примеры расчета показателей, использование в электросети

Иногда в процессе создания схем нужно получить точку с сигналом определённого уровня. Такая необходимость может возникнуть в разных ситуациях:

1.  К примеру, при создании опорной точки.
2.  При создании смещения напряжения.
3. При запитывании потребителя с малой мощностью, понижая уровни и ограничивая значения тока.

В таких ситуациях и применяются делители напряжения. Далее подробно рассмотрим принцип работы этих элементов в сети.

Значение понятия

Можно назвать делители напряжений устройством, с помощью которых возможно понизить уровни напряжения на вход относительно напряжений на выход.

Значения будут пропорционально равны значениям коэффициента передачи, при этом они будут ниже нуля. Прибор получил своё название из-за того, что последовательно соединяет несколько участков цепи.

Существует несколько видов делителей напряжения:

1. Линейный делитель. Есть как активное, так и реактивные сопротивления. О том, как находить коэффициенты передач, расскажем далее в нашей статье.
2. Нелинейный тип делителя. Среди них больше остальных выделяется параметрический стабилизатор напряжения, работу которого мы подробно рассмотрит ниже.

Как различаются и действуют

Для начала заметим, что все устройства этого вида в целом работают одинаково. Различия в работе могут зависеть от конструктивных особенностей устройства. Существует несколько ключевых видов в линейных схемах:

1. Резистивный делитель.
2. Ёмкостный делитель.
3. Индуктивный делитель.

Первые считаются самыми используемыми, поскольку они лёгкие в использование, а расчеты с ними провести проще всего. На примере делителей первого типа опишем работу приборов.

Все делители обладают напряжением на выход и вход, если в нём есть один резистор или несколько. Когда в элементе встречается больше двух резисторов, например 3, напряжений на выход будет 2.

Увеличение напряжения на выход растёт с количеством резисторов. Количество ступеней не имеет значения, их можно увеличить по вашему усмотрению.

Напряжение на входе равняется значению напряжений питания. Выходное напряжение в этом случае зависит от отношений резисторов в элементе, они располагаются в так называемых «плечах».

За плечо гашения отвечает первый резистор. Второй, нижний резистор, считается плечом на выход.

Предположим, что напряжение питания равняется десяти Вольтам. Сопротивление верхнего резистора составит восемьдесят пять Ом, сопротивление нижнего резистора будет равняться пятнадцати Омам. Рассчитаем напряжение на выходе.

Различаются и реактивные сопротивления. К ним относятся:

1. Ёмкостный делитель. Работает с использованием конденсаторов.
2. Индуктивный двигатель. Работает с помощью катушек индуктивности.

В целом, расчет в этом случае будет похож на пример, который мы описали выше. Тем не менее, формулы будут несколько отличаться.

При работе с использованием конденсаторов:

При работе с катушками:

Конечно, делители имеют свои особенности и различия. Делитель с резисторами используется как в цепях с переменным, так и в цепях с постоянным током.

Делители с катушками и конденсаторами могут функционировать только в цепях с переменными токами, поскольку именно по этой причине в них осуществляется реактивное сопротивление.

Обратите внимание. Иногда делители с конденсаторами работают и при постоянном токе, например, такой подход использован на входе компьютерного блока питания.

Реактивное сопротивление полезно, поскольку в процессе такой работы тепло почти не выделяется, соответственно не придётся беспокоиться о перегреве и пожарах. Резисторы выделяют больше тепла из-за активного сопротивления.

Использование в схемах на примерах

Существуют самые разные схемы, в которые включён делитель. Рассмотрим некоторые такие схемы.

Предположим, что мы составляем схему усилительного каскада для транзистора А-класса. Зная, как работает прибор, необходимо создать такие условия смещений на транзисторе, чтобы рабочая точка работала на линии ВАХ.

Нужно учитывать, что значения тока, проходящие через устройство, не должны быть слишком большими. Предположим, что значения тока на базе должны быть 0,1 миллиампер с учётом 0,6 В.

Чтобы найти значение сопротивления во всех плечах, нужно провести расчёты в противоположном порядке от того вычисления, что мы описали ранее. С помощью делителя найдём значение тока.

Кроме того, необходимо задавать ток по значению больше, чем ток нагрузки. Это нужно для того, чтобы значения тока нагрузки не влияли на числа напряжений в плечах. Тогда оно должно равняться двенадцати Вольтам.

Чтобы найти сопротивление, необходимо выполнить расчёт по следующей формуле:

Rд=Uпитания/I=12/0.001=12000 Ом

R2/R=U2/U

Иначе это вычисление может выглядеть так:

R2/(R1+R2)=U2/Uпитания

10/20=3/6

20*3/6=60/6/10

R2=(R1+R2)*U1/Uпитания=12000*0.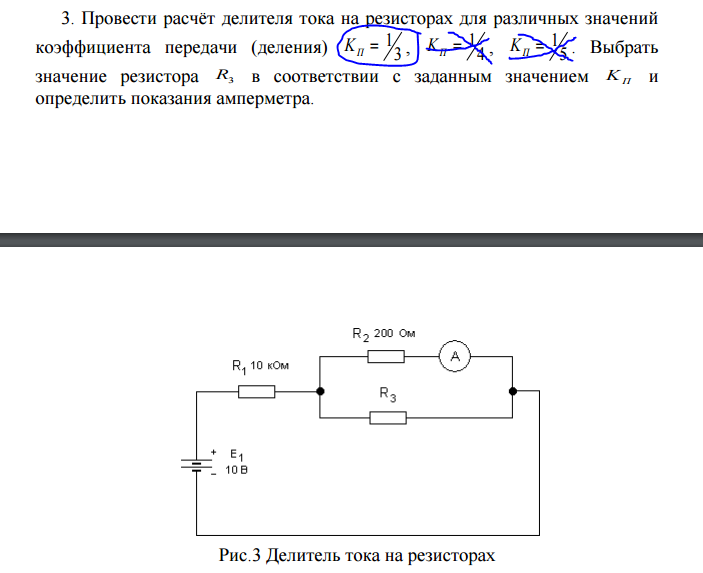 6/12=600

R1=12000-600=11400

Выполняем проверку:

U2=U*R2/(R1+R2)=12*600/12000=7200/12000=0,6 Вольт.

Тогда погашение первого плеча составит:

U2=U*R2/(R1+R2)=12*11400/12000=136800/12000=11,4 Вольт.

Это не является концом всех вычислений. Мощность резисторов тоже нужно определить, потому что если определить мощность примерно, детали могут сгореть. С током в один миллиампер на первом резисторе мощность составит:

P1=11,4*0,001=0,0114 Ватт

С током в один миллиампер на втором резисторе мощность составит:

P2=0,6*0,001=0,000006 Ватт

Значения получились очень маленькими. Если бы ток в делители составлял сто миллиампер один Ампер, какова тогда была бы мощность резистора?

В первом случае справедливо следующее вычисление:

P1=11,4*0,1=1,14 Ватт

P2=0,6*0,1=0,06 Ватт

Во втором случае справедливо следующее вычисление:

P1=11,4*1=11,4 Ватт

P2=0,6*1=0,6 Ватт

Такие цифры уже нельзя назвать маленькими, тем более при использовании усилителей. Хотя они являются не слишком эффективными, сегодня вместо них применяют схему с импульсами.

Линейные делители напряжения можно увидеть в схемах с самоделками. Кроме того, такие способы подключения деления иногда используют в электрическом оборудовании, где существуют особые требования для работы всей электрической цепи.

Другим примером являются делители, с помощью которых можно сформировать опорное напряжение в регулируемых стабилитронах ТЛ431.

Их чаще всего можно встретить в зарядных устройствах смартфонов или другой техники, обладающей блоками питания. Более наглядно принцип работы можно увидеть на схемах, приведённых ниже.

Опорное создано с помощью нескольких резисторов.

Микроконтроллеры могут послужить в качестве другого примера подключения. В цепи к таким контроллерам подключаются датчики. Мы рассмотрим контроллер модели АВР, с платами от Ардуино.

Разные измерительные приборы обладают разными измерительными пределами. Данные функции осуществляются за счёт групп резисторов.

При этом следует отметить, что такие делители применяются и для выполнения других функций.

Например, с их помощью можно гасить лишний ток с ограничениями светодиода. Так правильно распределяется нагрузка в лампах гирлянд, а ещё можно запитать устройства с малой мощностью.

Подробнее о нелинейном делителе

Параметрические стабилизаторы тоже относят к виду нелинейного делителя, о чём мы писали ранее. В их конструкцию всегда входят как резисторы, так и стабилитроны.

Причём вторые схематично похоже на диоды полупроводников, обладающий ещё одной небольшой чертой у катода.

Вычисление начинается со стабилизации элемента цепи. Если в сети есть стабилитрон с тремя целыми тремя десятыми Вольтами, а напряжение питание равняется десяти Вольтам, ток подаётся из даташита к стабилитрону.

Предположим, что он будет равняться двадцати миллиамперам, при этом нагрузка будет равняться десяти миллиамперам.

В этом случае получаем следующее:

R=12-3,3/0,02+0,01=8,7/0,03=290 Ом

Рассмотри принцип работы стабилизатора. При обратном включении стабилитроны начинают свою работу. Если выходное меньше значений напряжений стабилизации, ток не будет протекать.

Если напряжение питания будет повышено до стабилизации, случится пробами перехода PN. Тогда в нём произойдёт утечка тока, то есть ток стабилизации.

Его ограничивает первый резистор, погашающий разницу напряжения входа и напряжения стабилизации. Если значения максимального тока слишком завышены, случится пробой. В этом случае элемент цепи, в данном случае стабилитрон, сгорит.

Иногда стабилизаторы осуществляются с помощью диодов. U стабилизации равняется падению одного или нескольких диодов в цепи. При этом ток нужно задавать в соответствии с особенностью схем, хотя к подобному варианты люди прибегают нечасто.

Схемы с реализацией на диодах лучше назвать не стабилизатором, а ограничителем. Для цепей с переменным током такой вариант тоже может подойти.

Это основные моменты, которые следует знать о делителях напряжения и их работе. В некоторых схемах можно применять сразу несколько варианты реализаций делителя напряжения.

Потенциометры тоже являются делителями по своей сути, причем коэффициент передачи регулируется у них планов, вместе с постоянными резисторами. Расчёты и формулы при этом останутся такими же.

Как работает делитель напряжения – RxTx.su

Резистивный делитель напряжения — это простая схема, которая помогая уменьшить входное напряжение.

Суть схемы делителя напряжения — это распределить входное напряжение между компонентами схемы. Лучшим примером делителя напряжения являются два последовательно соединенных резистора. При этом входное напряжение прикладывается к двум резисторам, а вот выходное напряжение берется из точки между ними.

Такая схема используется для получения различных уровней напряжения от общего источника напряжения, но с одинаковым током для всех компонентов в последовательной цепи.

Схема делителя напряжения на резисторах. Входное напряжение — 5 В, выходное — 2.5 В.

Падение напряжения и входное напряжение в цепи делителя напряжения

Падение напряжения на резисторе R₂ — это и есть выходное напряжение, а также разделенное напряжение в цепи между резисторами.

Делитель напряжения относительно земли создается путем последовательного соединения двух резисторов. Входное напряжение подается на последовательные сопротивления R₁ и R₂, а выходным является напряжение на R₂. 

Отсюда следует, что одной и той же величине электрического тока, протекающего через каждый резистивный элемент цепи, деваться больше некуда. Таким образом обеспечивается падение напряжения I*R на каждом резистивном элементе.

Имея напряжение питания, мы можем применить закон Кирхгофа для напряжения и закон Ома, чтобы найти падение напряжения на каждом резисторе, полученное с точки зрения общего тока, протекающего через них.

Используя второй закон Кирхгофа (он же закон напряжения Кирхгофа), получаем:

\[U_{ВХ}=U_{R1}+U_{R2}\]

Представим U_R1 и U_R2, используя закон Ома:

\[U_{R1}=IR_{1}\]

\[U_{R1}=IR_{2}\]

Используя две приведенных выше формулы, получается:

\[U_{ВХ}=IR_{1}+IR_{2}=I(R_{1}+R_{2})\]

\[\implies I=\frac{U_{ВХ}}{R_1+R_2}\]

Формула делителя напряжения

В делителе напряжения выходное напряжение всегда уменьшает входное напряжение и ток, протекающий через последовательную цепь, который можно рассчитать с помощью закона Ома:

\[I=\frac{U}{R}\]

Поскольку ток одинаков для обоих резисторов, представим ток через резистор R₂, используя следующую формулу:

\[I_{R2}=\frac{U_{R2}}{R_2}=\frac{U_{ВХ}}{R_1+R_2}\]

Из приведенной выше формулы можно определить падение напряжения на резисторе R₂. Это и будет выходное напряжение делителя:

\[U_{R2}=U_{ВХ}(\frac{R_2}{R_1+R_2})\]

Аналогично, для резистора R₁ мы можем использовать формулу:

\[I_{R1}=\frac{U_{R1}}{R_1}=\frac{U_{ВХ}}{R_1+R_2}\]

А затем вычисляем падение напряжения на резисторе R₁:

\[U_{R1}=U_{ВХ}(\frac{R_1}{R_1+R_2})\]

Расчет делителя напряжения на резисторах

Задача: Рассчитать падение напряжения, создаваемое на каждом резисторе, и ток через резистор 30 Ом, соединенный последовательно с резистором 50 Ом, когда входное напряжение питания схемы составляет 10 вольт постоянного тока.

Расчет сопротивления

Рассчитаем общее сопротивление в цепи, просто сложив сопротивления двух резисторов, так как резисторы соединены последовательно.

\[R_{ОБЩ}=R_1+R_2=30+50=80\text{ Ом}\]

Расчет тока

Имея общее сопротивление, мы можем рассчитать ток, протекающий через резисторы.

\[I=\frac{U_{ВХ}}{R_{ОБЩ}}=\frac{10\text{ В}}{80\text{ Ом}}=125\text{ мА}\]

Расчет падения напряжения на резисторах

Используя приведенные выше уравнения, можно рассчитать падение напряжения на резисторах.

\[U_{R1}=IR_1=U_{ВХ}\frac{R_1}{R_1+R_2}=10(\frac{30}{30+50})=3.75\text{ В}\]

\[U_{R2}=IR_2=U_{ВХ}\frac{R_2}{R_1+R_2}=10(\frac{50}{30+50})=6.25\text{ В}\]

Делитель напряжения и правило 10%

При проектировании делителя напряжения для конкретной нагрузки вы должны знать ее напряжение питания и ее потребляемый ток.

Делитель напряжения должен иметь только 10% тока утечки. Это означает, что ток, проходящий через нагрузку, должен быть в десять раз больше тока, проходящий через нижнюю часть делителя напряжения (через резистор R₂) на землю.

Например:

Требование к данному делителю напряжения — обеспечивать напряжение 25В и ток 910мА на нагрузку от источника напряжения (батарея B1 на схеме) — 100 В.

Расчет сопротивлений R1 и R2 для делителя напряжения

Задача: Определить сопротивление резистора, используемого в схеме делителя напряжения. Ток через резистор делителя должен составлять примерно 10% от тока нагрузки. Ток, который не протекает ни через одно из устройств нагрузки, называется током утечки.

Расчет

Сначала определяемся с требуемой нагрузкой и доступным источником питания.

\[U_{ВХ}=100\text{ В};U_{НАГРУЗКИ}=25\text{ В};I_{НАГРУЗКИ}=910\text{ мА.}\]

Затем определим ток утечки, применив правило 10%.

\[I_{R2}=10\text{%} \times I_{НАГРУЗКИ}=0.1\times 910мА=91мА.\]

Получив ток утечки, рассчитаем сопротивление R2.

\[R2=\frac{U_{R2}}{I_{R2}}=\frac{25В}{91мА}=274.7\text{ Ом}\approx 275\text{ Ом}\]

Затем определим общий ток, сложив ток нагрузки и ток утечки.

\[I_{ОБЩ}=I_{НАГРУЗКИ}+I_{R2}=910мА+91мА\approx1\text{ A.}\]

Теперь из рассчитанных значений можем найти значение R1.

\[U_{R1}=U_{ОБЩ}-U_{R2}=100В-25В=75В\]

\[R_1=\frac{U_{R1}}{I_{ОБЩ}}=\frac{75\text{ В}}{\text{ 1А}}=75\text{ Ом}\]

Лестница из напряжений

Лестница из напряжения — это цепь, состоящая из нескольких резисторов, соединенных последовательно. Входное напряжение подается на всю цепь резисторов. Каждый резистор в цепи имеет более высокое падение напряжения, чем предыдущий.

Поскольку резисторы в лестнице включены последовательно, протекающий ток одинаков для всех резисторов. Чтобы получить его значение, следует общее напряжение разделить на общее сопротивление.

\[I=\frac{U_{ОБЩ}}{R_{ОБЩ}}=\frac{100\text{ В}}{50+50+50+50}=0.5\text{ А}\]

Падение напряжения на каждом резисторе можно рассчитать, умножив общий ток на сопротивление каждого резистора. Для конкретно случая получаем:

\[U_{R1}=U_{R2}=U_{R3}=U_{R4}=I\times R=0.5\text{ A}\times50\text{ Ом}=25\text{ В}\]

Напряжение относительно земли в любом узле может быть определено как сумма напряжений, падающих на каждом резисторе между этим узлом и землей.

\[U_{ОБЩ}=U_{R1}+U_{R2}+U_{R3}+U_{R4}\]

Надеюсь, эта статья помогла вам лучше понять что такое делитель напряжения. Если у вас есть вопросы, оставляйте их в комментариях ниже.

Компоненты

• Набор выводных резисторов (30 номиналов)
• Набор SMD резисторов типоразмера 0805 (33 номинала по 20 штук)

Как рассчитать делитель напряжения со смещением

\$\начало группы\$

У меня есть следующая схема:

^{смоделируйте эту схему – Схема создана с помощью CircuitLab не уверен, как это получилось.}

Если я просто использую делитель напряжения и вычитаю опорное напряжение 1,7, я получаю:

$$ 3,13 \times \frac{10}{(22+10)}-1,7 = -0,7218 $$

Что я делаю не так? Кстати, инженер-программист, а не инженер-электрик, поэтому я уверен, что это нубский вопрос.

• делитель напряжения
• смещение постоянного тока

\$\конечная группа\$

4

\$\начало группы\$

Здесь две разные проблемы.

1. Формула делителя напряжения применяется к напряжению на всем делителе:

^{имитация этой схемы – схема создана с помощью CircuitLab}

$$ V_2 = V_{tot} \cdot \frac{R2}{R1+R2} $$

То есть Vtot – это напряжение между узлами A и B.

2. Для расчета Vtot вы можете использовать LKT, и вы получите это:

$$ V_{общ.} = V_{синус} — V_1 $$

Эти выражения действительны для каждого момента , поэтому вы можете применить их, в частности, к пиковому значению синуса, которое, как вы говорите, равно 3,13.

Получается:

\$ V_{общий(пик)} = V_{синус(пик)} — V_1 = 3,13 В — 1,7 В = 1,43 В \$

\$ V_{2(пик)} = V_{общий(пик)} \cdot \frac{R2}{R1+R2} = 1,43 В \cdot \frac{100}{100+220} = 0,45 В \$

РЕДАКТИРОВАТЬ (предоставить полное решение, а не только подсказку)

Как только вы получите \$V_{2(пик)}\$, вы можете получить \$V_{выход(пик)}\$ с помощью добавление \$V_1\$:

\$ V_{выход(пик)} = V_{2(пик)} + V_1 = 0,45 В + 1,7 В = 2,15 В \$

Это результат моделирования с точностью до ошибки приближения.

Вот график различных напряжений с использованием LTspice:

, полученный из этой схемы:

\$\конечная группа\$

5

\$\начало группы\$

Вы говорите о двух разных «напряжениях».

1. Размах синусоиды 6,26 В с центром около 0 В.
2. Напряжение смещения 1,7 В постоянного тока.

Выходной сигнал схемы представляет собой синусоиду другой амплитуды и смещения, отличного от исходного.

Хорошим способом анализа такой цепи является использование суперпозиции (ищите суперпозицию в анализе цепей!): отделите части синусоиды от постоянного и переменного тока:

^{смоделируйте эту цепь CircuitLab}

Цепь постоянного тока можно перерисовать следующим образом, учитывая, что источник напряжения 0 В является коротким и может быть заменен проводом: выходного напряжения.

Переменная часть выходного напряжения уже представляет собой простую схему делителя — мы заменяем источник переменного тока 0 В V1 (это постоянный ток, поэтому 0 В в переменном токе!) проводом, чтобы вы могли решить это с помощью того, что вы уже знаете.

Выходное напряжение будет суммой «смещения» постоянного тока и синусоидального сигнала переменного тока.

Смещение постоянного тока $$1,7{\rm\ V} {220{\rm k} \более 100{\rm k}+220{\rm k}}.$$

Амплитуда переменного тока составляет $$3,13{\ rm \ V} {100 {\ rm k} \ over 100 {\ rm k} + 220 {\ rm k}}. $ $

Таким образом, выход представляет собой следующую функцию времени: 9{-1} t),$$, где \$t\$ — единица времени в системе СИ, т. е. секунды.

\$\конечная группа\$

\$\начало группы\$

Используйте принцип суперпозиции для анализа вклада каждого источника в отдельности, а затем суммируйте результаты. Таким образом, вклад усилителя при 3,13 В составляет 3,13×100/320=0,978125 В; вклад для V1 составляет 1,7×220/320=1,16875 В И общий результат равен 1,168750+0,975125=2,146875 В

. \$\конечная группа\$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Формула делителя напряжения — GeeksforGeeks

Делитель напряжения — это схема, которая используется для генерирования части входного напряжения в качестве выходного. Обычно он строится с использованием двух резисторов и источника напряжения, в котором резисторы соединены последовательно. Затем на эти два резистора подается напряжение. Он также известен как делитель потенциала, поскольку он преобразует высокое напряжение в низкое значение. Это последовательность резисторов или конденсаторов, которые можно подключить в любой точке цепи, чтобы создать точную пропорцию напряжения, приложенного между ее концами.

Формула

V _OUT = V _в × R ₂ /(R ₁ + R ₂ /(R ₁ + R ₂ /(R ₁ + R ₂ ). выходное напряжение,

В _в входное напряжение,

R ₁ входной резистор,

R ₂ выходной резистор.

Примеры задач

Задача 1. Рассчитайте выходное напряжение схемы делителя напряжения с двумя резисторами 3 Ом и 6 Ом и входным напряжением 15 В. Резистор 6 Ом подключен параллельно выходу Напряжение.

Solution:

We have,

R ₁ = 3

R ₂ = 6

V _in = 15

Using the formula we get,

V _out = 15 × (6/(3 + 6))

= 15 × 2/3

= 10 В

Задача 2. Рассчитайте выходное напряжение схемы делителя напряжения с двумя резисторами по 2 Ом и 5 Ом и входное напряжение 7 В. Резистор 5 Ом подключен параллельно выходному напряжению.

Solution:

We have,

R ₁ = 2

R ₂ = 5

V _in = 7

Using the formula we get,

V _out = 7 × (5/(2 + 5))

= 7 × 5/7

= 7 В

Задача 3. Рассчитайте входное напряжение схемы делителя напряжения с двумя резисторами по 3 Ом и 5 Ом и выходное напряжение 8 В. Резистор 5 Ом подключен параллельно выходному напряжению.

Решение:

Мы имеем,

R ₁ = 3

R ₂ = 5

V _OUT = 8

. = V _в × (5/(3 + 5))

=> 8 = V _в × 5/8

=> V _в = 64/5

=> V _в = 12,8 В

Задача 4. Рассчитать входное напряжение схемы делителя напряжения с двумя резисторами 4 Ом и 7 Ом и выходным напряжением 49 Ом.В. Резистор 7 Ом подключен параллельно выходному напряжению.

Решение:

Мы имеем,

R ₁ = 4

R ₂ = 7

V _OUT = 49

, используя Formula. = V _в × (7/(4 + 7))

=> 49 = V _в × 7/11

=> V _в = 539/7

=> V _в = 77 В

Задача 5. Рассчитать выходное сопротивление схемы делителя напряжения, имеющей входное сопротивление 3 Ом, входное напряжение 7 В и выходное напряжение 5 В.

Решение:

,

R ₁ = 3

V _в = 7

V _Out = 5

. = 7 × (r ₂ /(3 + R ₂ ))

=> 0,71 + 0,71 R ₂ = R ₂

=> 0,29 R ₂ = 0,71193

=>> 0,29 R ₂ = 0,71119103

=>> 0,29 R ₂ = 0,711193

=> 0,29 R ₂ = 0,71163

=> 0,29 r ₂ = 0,710003

. ₂ = 2,44 Ом

Задача 6. Рассчитать выходное сопротивление схемы делителя напряжения, имеющей входное сопротивление 6 Ом, входное напряжение 20 В и выходное напряжение 15 В.

Решение:

,

R ₁ = 6

V _в = 20

V _Out = 15

.