Радиальное напряжение — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Радиальное напряжение равно нулю на внешней и внутренней цилиндрических поверхностях диска, тангенциальное достигает максимума на внутренней поверхности. В другом крайнем случае при самом малом радиусе Хг напряжение аи уменьшается лишь на 20 % по сравнению с atn и примерно вдвое больше напряжений в центре сплошного диска при той же скорости вращения.  [1]

Остаточные объемные деформации вблизи подземной полости.  [2]

Радиальные напряжения характеризуются гладкими волновыми профилями. Остаточные объемные деформации имеют экстремум вблизи полости, что соответствует возникновению зоны повышенной пористости.  [3]

Радиальное напряжение о, у внутренней поверхности равно — р, а внешней — нулю, независимо от толщины цилиндра.  [4]

Радиальные напряжения

увеличивают обратимую часть упруго-пластической деформации, происходящей в течение цикла, и поэтому при их учете уменьшается величина необратимого формоизменения. В связи с этим при переходе от плоского напряженного состояния к объемному температура начала формоизменения повышается от 570 — 580 С до 630 — 640 С. При сопоставлении расчетных данных с экспериментальными обнаруживается качественное соответствие, однако количественно результаты отличаются друг от друга почти на порядок величины.  [5]

Напряжения в диске.| Граничные условия при расчете диска.  [6]

Радиальные напряжения на внешнем контуре Оу — ь ( рис. 45) создаются центробежными силами лопаток и замковой части диска. В центре диска беэ отверстия Ojo — rot iTO вытекает из условия осевой симметрии.  [7]

Радиальное напряжение в точках вдоль контура отверстия достигает наибольшей величины на средней линии спицы; оно понижается до минимума на полпути между двумя подобными точками, так что ось испытывает от ступицы переменное радиальное давление. Поперечное к радиусу или периферическое напряжение принимает минимальное значение в точках против спиц, а наибольшее-между ними.  [8]

Радиальные напряжения

на внутренней и наружной поверхностях равны нулю.  [9]

Радиальные напряжения обнаруживаются перед штампом нз расстоянии от вершины конуса, составляющем около 3 диаметров штампа. После прохода штампа радиальные напряжения падают постепенно и на расстоянии от основания конуса, составляющем около 1 диаметра штампа, остаются постоянными, образуя зону остаточных радиальных напряжений.  [10]

Распределение напряжений в стенках сосуда.  [11]

Радиальные напряжения и деформации максимальны на внутренних слоях и минимальны на внешней поверхности. При сосуществовании в стенке этих двух зон во внутренних слоях цилиндра напряженное состояние близко к двухосному сжатию, а во внешних к одноосному растяжению.

Этим и объясняется, что разрыв цилиндра начинается с наружной поверхности.  [12]

Радиальное напряжение у внутренней поверхности овального кольца будет при затяжке равно нулю, так как в этот период внутри арматуры избыточного давления нет.  [13]

Остаточные объемные деформации вблизи подземной полости ( / -, 2, Л 1, ай 2 — К.  [14]

Радиальные напряжения характеризуются гладкими волновыми профилями. Остаточные объемные деформации имеют экстремум вблизи полости, что соответствует возникновению зоны повышенной пористости.  [15]

Страницы:      1    2    3    4    5

Бурение — Стр 13

vk.com/club152685050 | vk.com/id446425943

Поскольку в процессе бурения удаляется порода, происходит перераспределение напряжений и возникают кольцевые напряжения.

Рис. 8-22 Распределение напряжений вокруг ствола скважины

Если скважина вертикальная, и нет тектонических напряжений, то горизонтальные напряжения (σH и σh) равны, и кольцевые напряжения равномерно распределены вокруг ствола скважины (рис.

8-23А).

Поскольку тектонические напряжения в той или иной степени существуют везде, то при любом распределении напряжений горизонтальные напряжения будут больше в одном направлении, чем в остальных. Наибольшие горизонтальные напряжения σH должны обойти скважину, как кольцевые напряжения. Это же относится и к наименьшим горизонтальным напряжениям σh. В результате возникают кольцевые напряжения, которые имеют максимальное значение на направлениях, отстоящих на 90° и 270° от направления действия наибольших главных горизонтальных напряжений (рис. 8-23В).

Когда σH и σh равны, кольцевые напряжения равномерно распределены вокруг ствола скважины.

Когда σH и σh не равны, кольцевые напряжения распределены вокруг ствола скважины неравномерно.

Рис. 8-23 Кольцевые напряжения на стенках скважины

129

vk.com/club152685050 | vk.com/id446425943

Если существует напряженное состояние, благоприятное для образования сброса, кольцевые напряжения на горизонтальном участке ствола будут иметь максимальное значение на боковых стенках

Рис. 8-24 Анизотропное распределение напряжений

Посмотрим на скважину, изображенную на рис. 8-24. Принимаем, что тектонические напряжения равны (о»н = 0″ь), тогда кольцевые напряжения на стенках скважины будут распределены равномерно по всей окружности сечения ствола, как показано на рис. 8-23А. Однако на горизонтальном участке ствола вертикальные напряжения от веса вышележащих пород будут больше действующих горизонтальных напряжений. В результате кольцевые напряжения будут иметь максимальное значение на боковых стенках, и наименьшие значения на верхней и нижней стенках (рис. 8-23В). Если плотность бурового раствора недостаточно велика, стенки обрушатся в скважину.

В горнодобывающей отрасли об этом знают уже в течение столетий. Вот почему в шахтных тоннелях крепь толще всего вдоль стен, а не на кровле или на полу (в большинстве случаев порода обрушивается в шахтных тоннелях не с кровли, а со стен. Это можно видеть и в голливудских фильмах).

Вероятнее всего, большие разности напряжений будут встречаться на небольших глубинах. Это объясняется тем, что на глубине породы становятся более пластичными из-за более высокого бокового давления. Пластичные породы деформируются до выравнивания напряжений. Этот феномен называется «правило Гейма»3. В горных районах, где высоки тектонические напряжения, кольцевые напряжения могут быть в три раза больше в одном направлении, чем в другом, особенно у поверхности. На очень больших глубинах напряжения почти выравниваются, даже в горных районах.

130

vk.com/club152685050 | vk.com/id446425943

Кольцевые напряжения отличаются не только в разных точках на стенке скважины, но и с удалением от стенки в пласт. Кольцевые напряжения имеют максимальное значение на стенке и уменьшаются до нуля на расстоянии примерно трех радиусов от стенки скважины (рис. 8-25). Нас интересуют наибольшие и наименьшие кольцевые напряжения (о»е) на стенке скважины. Эти напряжения можно найти по уравнению Кирша, приведенном в приложении В. Однако для нашего рассмотрения на уровне концепций лучше подходит графический метод, представленный Геком и Брауном

(Hoek & Brown)3.

Кольцевые напряжения имеют максимальное значение на стенке и уменьшаются до нуля на расстоянии примерно трех радиусов от стенки скважины.

Рис. 8-25 Изменение кольцевых напряжений с удалением от стенки скважины

Силовые линии поля напряжений

Hoek и Brown3 в своей книге «Подземные выработки в горных породах» использовали для описания поля напряжений вокруг скважины изящную аналогию с линиями тока. Силовые линии поля напряжений представляет собой воображаемые линии, вдоль которых действуют главные напряжения. Эти линии являются аналогом линий тока в плавном потоке.

Скважина круглого сечения вносит возмущение
в поле напряжений в горной породе таким же
образом, как круглая свая пирса в поток
обтекающей ее воды (рис. 8-26). Напряжения
вынуждены обтекать скважину так же, как вода
вынуждена обтекать сваю. Непосредственно
перед сваей и после сваи поток воды
замедляется, и линии тока отклоняются кнаружи.
По обе стороны от сваи поток ускоряется,
поскольку теперь воде нужно пройти через более
узкое пространство. То же самое происходит с
напряжениями, огибающими скважину. Силовые
линии поля напряжений расходятся перед
препятствием, а затем снова сходятся, пройдя	Скважина		круглого сечения	вносит
препятствие.	возмущение в поле напряжений в горной
В области, где силовые линии поля напряжений	породе таким же образом, как круглая свая
широко расходятся, сжимающие напряжения	пирса в поток обтекающей ее воды.
уменьшаются (и, возможно, переходят в	Сжимающие		напряжения	имеют
растягивающие). В области, где силовые линии	максимальное значение там, где линии
сходятся, сжимающие напряжения возрастают.	сходятся, и минимально значение там, где
	линии расходятся.

Рис. 8-26 Силовые линии поля напряжений3

131

vk.com/club152685050 | vk.com/id446425943

Изострессы

На рис. 8-27 показаны силовые линии поля напряжений с одной стороны скважины и линии равных напряжений (изострессы) с другой стороны скважины. Изострессы3 показывают соотношение наибольших главных напряжений в окрестности скважины и в пласте.

Как мы помним, нас интересуют именно максимальные кольцевые напряжения на стенках скважины. Указанное отношение можно определять начиная с точек, где изострессы пересекают стенки скважины. Как было указано выше, кольцевые напряжения имеют максимальное значение на направлениях, отстоящих на 900 и 2700 от направления действия наибольших горизонтальных напряжений, и изменяются по стенке скважины в зависимости от разности между наибольшим и наименьшим горизонтальными напряжениями.

Слева показаны силовые линии поля напряжений, а справа — изострессы. Изострессы построены по числам, показывающим соотношение наибольших главных напряжений, действующих в окрестности скважины и в пласте. В большинстве случаев наибольшими главными напряжениями в окрестности скважины являются кольцевые напряжения. Следует отметить, что при увеличении разности между горизонтальными напряжениями возрастают максимальные кольцевые напряжения (рис. А, В и F).

Рис. 8-27 Изострессы3

Когда скважина приобретает эллиптическое сечение вследствие эрозии из-за взаимодействия с бурильной колонной, максимальные кольцевые напряжения могут быть меньше, чем при круглом сечении, если большая ось эллипса ориентирована по направлению наибольших горизонтальных напряжений (рис.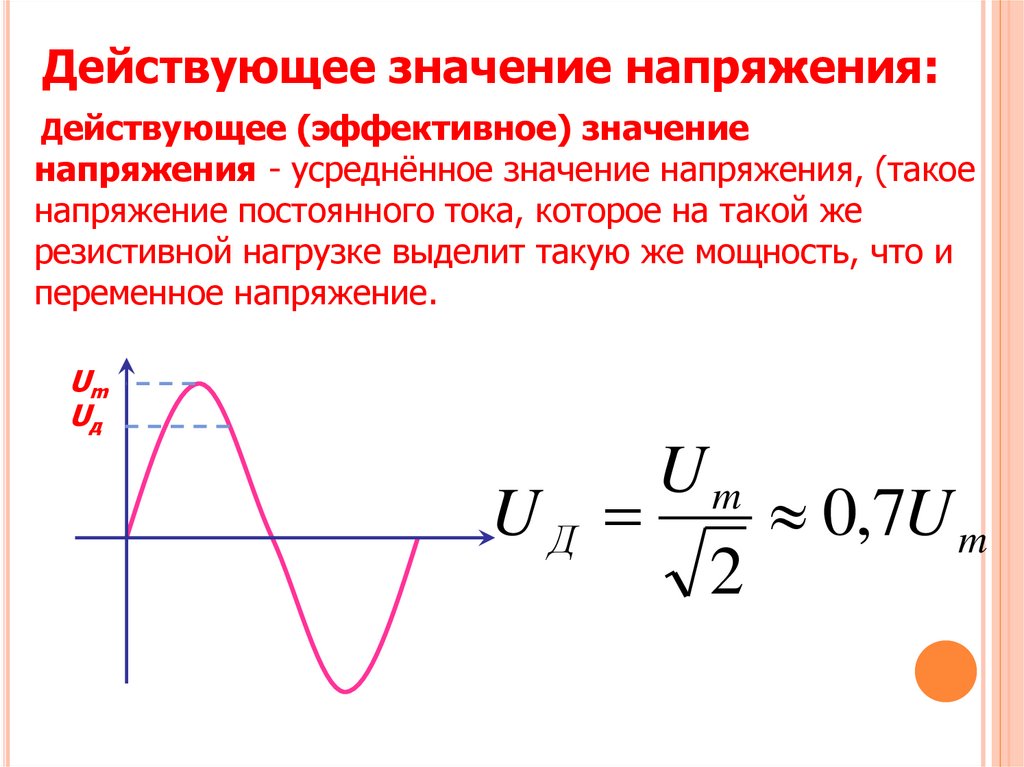 С и D). Если по направлению наибольших горизонтальных напряжений ориентирована малая ось эллипса, то максимальные кольцевые напряжения будут намного больше, чем при круглом сечении (рис. Е, G и H).

Из работы Hoek and Brown; «Underground Excavations in Rock».

132

vk.com/club152685050 | vk.com/id446425943

Судя по изострессам на рис. в и Н, при начале обрушения породы в скважину из-за потери устойчивости стенок ствола, потеря устойчивости нарастает. В интервале хрупких пород это часто ведет к почти мгновенному катастрофическому обвалу. Большинство глинистых пород при проникновении в них фильтрата бурового раствора начинает разрушаться не сразу. Это дает некоторое время для принятия исправительных мер.

Рис. 8-27 Изострессы (продолжение)

Эти изострессы получены путем приложения напряжений к фотоупругим материалам с различной степенью анизотропии напряжений и формой отверстий. Следует отметить, что все эти изострессы получены в отсутствие радиальных напряжений (нулевая плотность бурового раствора).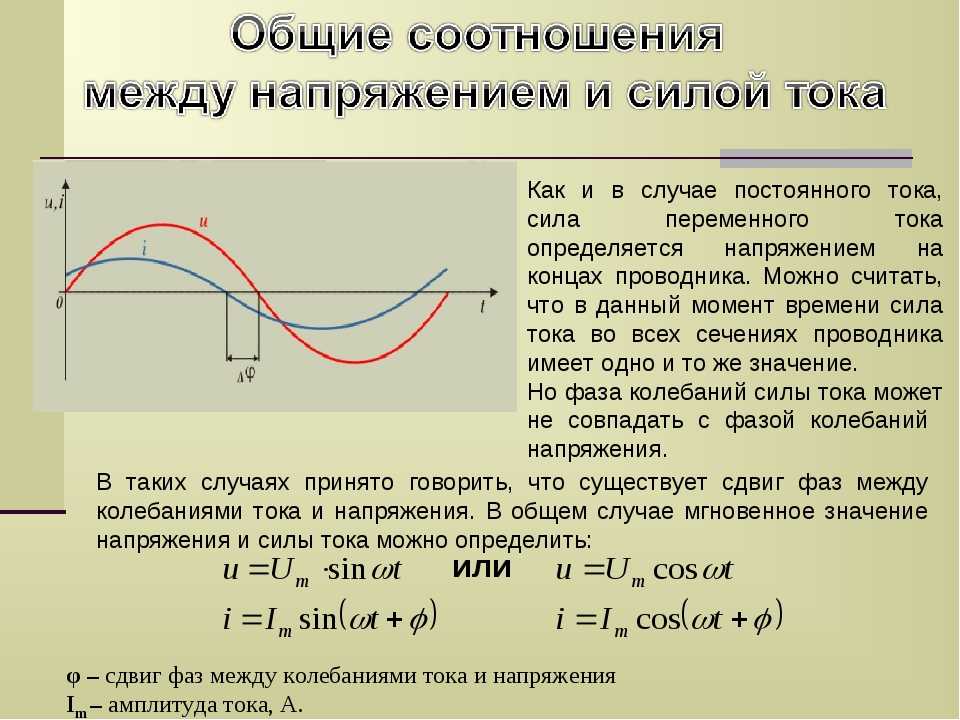

Как видно на рисунках с 8-27А по 8-27Н, форма сечения ствола оказывает значительное влияние на величину напряжений вокруг скважины. Можно заметить также влияние анизотропии напряжений на величину напряжений. Нас больше всего интересуют напряжения на стенках скважины. Обычно причиной обрушения породы являются касательные напряжения. Касательное напряжение пропорционально разности между максимальным кольцевым напряжением на стенке и радиальным напряжением, обусловленным весом бурового раствора.

133

vk.com/club152685050 | vk.com/id446425943

Возмущение поля напряжений сильнее всего проявляется около стенок скважины, а затем ослабевает с удалением от скважины в радиальном направлении. На расстоянии больше трех радиусов от стенки скважины поле напряжений остается невозмущенным (рис. 8-25). Обрушение породы вследствие потери устойчивости происходит в месте действия наибольших касательных напряжений, т.е. вблизи стенок. Однако зона деформации пластичных пород, таких как соль, мягкие глины и рыхлые пески, простирается в пласт на расстояние до трех радиусов от стенки скважины. 6

Следует отметить, что поведение глинистых пород изменяется со временем. Проникновение в пласт фильтрата бурового раствора приводит к возрастанию порового давления, в результате чего постепенно уменьшается радиальное напряжение и увеличивается кольцевое напряжение.

Радиальные напряжения

Давление столба бурового раствора создает радиальные напряжения на стенках скважины. Эти радиальные напряжения уменьшают сжимающие кольцевые напряжения. Кольцевые напряжения возникают из-за необходимости восполнения горизонтальных напряжений, действовавших в породе, удаленной при проводке скважины. Часть этих напряжений компенсирует давление бурового раствора, а остальное восполняют кольцевые напряжения. Чем больше часть напряжений, компенсируемая давлением бурового раствора, тем

меньше останется на долю кольцевых напряжений

(рис. 8-28).

Перераспределение	полного	напряжения		=
радиальные
напряжения + кольцевые напряжения			(8-4).

Помните образец породы в лаборатории (рис. 8-5)? Элементарный кубик породы на стенке скважины сжат кольцевыми напряжениями точно так же, как лабораторный образец сжат гидравлическим прессом (рис. 8-29). Если сжимающие напряжения превышают кажущуюся прочность породы, произойдет обрушение. Радиальные напряжения от давления бурового раствора уменьшают кольцевые напряжения, создавая боковое давление. С увеличением плотности бурового раствора увеличивается кажущаяся прочность породы и уменьшаются сжимающие кольцевые напряжения.

Горизонтальные напряжения в породе,

удаленной при бурении, восполняются радиальными и кольцевыми напряжениями.

Восполняемые напряжения = радиальные напряжения + кольцевые напряжения

Рис. 8-28 Перераспределение напряжений

Элементарный кубик породы на стенке скважины сжат кольцевыми напряжениями точно так же, как лабораторный образец сжат гидравлическим прессом. Радиальные напряжения создают боковое давление, в результате чего увеличивается кажущаяся прочность.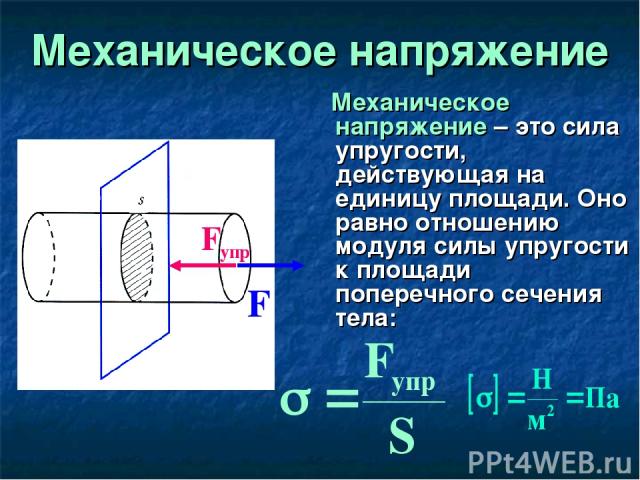

134	Рис. 8-29 Радиальные напряжения

vk.com/club152685050 | vk.com/id446425943

Можно увеличить плотность бурового раствора до значения, при котором кольцевые напряжения уменьшатся до нуля. Если же чрезмерно увеличить плотность бурового раствора, то кольцевые напряжения могут стать растягивающими, и порода может разрушиться из-за растяжения (рис. 8-30). Это и происходит при гидроразрыве пласта.

При увеличении плотности бурового раствора сжимающие кольцевые напряжения уменьшаются, и могут стать растягивающими

Рис. 8-30 Взаимосвязь между радиальными и кольцевыми напряжениями

Аналогичным образом, при уменьшении плотности бурового раствора кажущаяся прочность породы уменьшается . При выбросах из скважины часто выходят большие куски глинистой породы — до тех пор, пока ствол скважины не будет перекрыт пробкой из обвалившейся породы. Часто неправильно думают, что пробка образовалась из-за сильного потока при выбросе, который «ободрал» стенки ствола. На самом деле пробка образовалась из-за того, что при выбросе из скважины бурового раствора уменьшаются радиальные напряжения, а кольцевые напряжения возрастают. В результате касательные напряжения настолько превышают предел текучести породы, что она выдавливается и обрушивается в скважину.

Осевые напряжения

Осевые напряжения определяются суммой компонент вертикальных и горизонтальных напряжений, действующих в осевом направлении. В вертикальной скважине осевые напряжения равны вертикальным напряжениям. В горизонтальной скважине осевые напряжения определяются суммой компонент горизонтальных напряжений, действующих вдоль оси скважины.

Следует отметить, что сопротивление продольному перемещению бурильной колонны в скважине приводит к увеличению осевых напряжений.

Трехосное напряженное состояние в скважине

Трехосное напряженное состояние породы на стенках скважины (рис. 8-32) характеризуется следующими компонентами:

•σz (осевое напряжение)

•σr (радиальное напряжение)

•σθ (тангенциальное или кольцевое напряжение)

135

Осевые

напряжения

действуют вдоль оси скважины

Рис.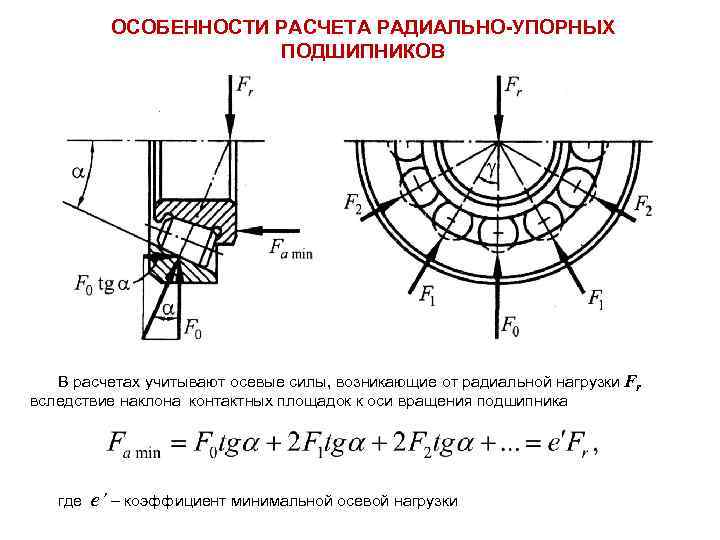 8-31 Осевые напряжения действуют вдоль оси скважины

Рис. 8-32 Трехосное напряженное состояние породы на стенках

vk.com/club152685050 | vk.com/id446425943

В этом руководстве мы не будем заниматься расчетом напряжений. Наша цель заключается в том, чтобы просто понять, что они из себя представляют, и как они влияют на устойчивость стенок скважины.

Порода вываливается из стенок тогда, когда комбинация из любых двух этих напряжений превышает определенный предел.

Два любых взаимно ортогональных напряжения создают касательное напряжение в плоскости, в которой действуют эти напряжения. Если касательное напряжение превысит предел прочности породы, она разрушается и обрушивается в скважину.

Круги напряжений (теория двойного угла)

Для представления напряжений в горной породе, действующих в плоскости, расположенной под любым углом относительно направления максимальных напряжений, часто используют круги напряжений (круги Мора). Этот метод полезен, когда мы знаем напряжения в определенном направлении и хотим знать напряжения в каком-то другом направлении. Кроме того, он полезен для определения главных напряжений и максимальных касательных напряжений.

Большинству инженеров и членов буровых бригад никогда не придется работать с кругами напряжений. Тем не менее, здесь предлагается краткое объяснение, поскольку огибающая предельных кругов напряжений часто используется для прогнозирования интервала допустимых значений плотности бурового раствора. Этот графический подход, проиллюстрированный на рис. 8-33, разработал немецкий инженер Отто Мор (1835 -1918 гг.).

Круги напряжений — графический метод представления главных напряжений и максимальных касательных напряжений в точке массива напряженной горной породы.

Ортогональные напряжения в точке представлены в координатах σ, τ. Точки А и В представляют наибольшее и наименьшее напряжения на некоторой поверхности.

Рис. 8-33 Круг напряжений

Главные напряжения существуют там, где касательные напряжения равны нулю. Наибольшее касательное напряжение численно равно радиусу круга.

Известные напряжения в элементарном кубике представлены на графике в координатах σ, τ (рис. 8-33). Фундаментальная концепция кругов напряжений заключается в том, что каждая точка окружности характеризует напряженное состояние в воображаемой плоскости, проходящей через породу под некоторым углом θ относительно плоскости, в которой действуют главные напряжения (главной плоскости).

Примечание: чтобы получить круг, все углы нужно удвоить.

136

vk.com/club152685050 | vk.com/id446425943

Например, на рис. 8-33 показано напряженное состояние образца породы, изображенного на рис. 8-34. Допустим, что мы хотим пробурить скважину через образец, изображенный на рис. 8-34, под некоторым углом. Напряженное состояние любого элементарного кубика на плоскости, расположенной под этим углом, показано в правом верхнем углу. Точки А и В характеризуют наибольшее и наименьшее сжимающие напряжения в образце до проводки скважины.

Главные напряжения в образце равны 10 тыс. фунт/дюйм2 и 5 тыс. фунт/дюйм2. Напомним, что в главных плоскостях касательные напряжения всегда равны нулю. Поэтому все точки, где действуют главные напряжения, лежат на оси σ. Максимальное касательное напряжение численно равно радиусу круга и действует в плоскости, расположенной под углом 45° относительно главной плоскости. В данном случае максимальное касательное напряжение равно 2,5 тыс. фунт/дюйм2.

Главные плоскости в этом образце ортогональны σv и σh. Справа показано напряженное состояние выделенного элемента, ориентированного под углом θ к главной плоскости. Максимальные и минимальные напряжения при таком расположении образца можно найти в круге напряжений по тригонометрическим формулам.

Рис. 8-34 Напряженное состояние в плоскости

По кругу напряжений видно, что при увеличении разности между наибольшим и наименьшим главными напряжениями возрастает максимальное касательное напряжение. Максимальное касательное напряжение всегда равно половине разности между максимальным и минимальным напряжениями (радиус круга напряжений).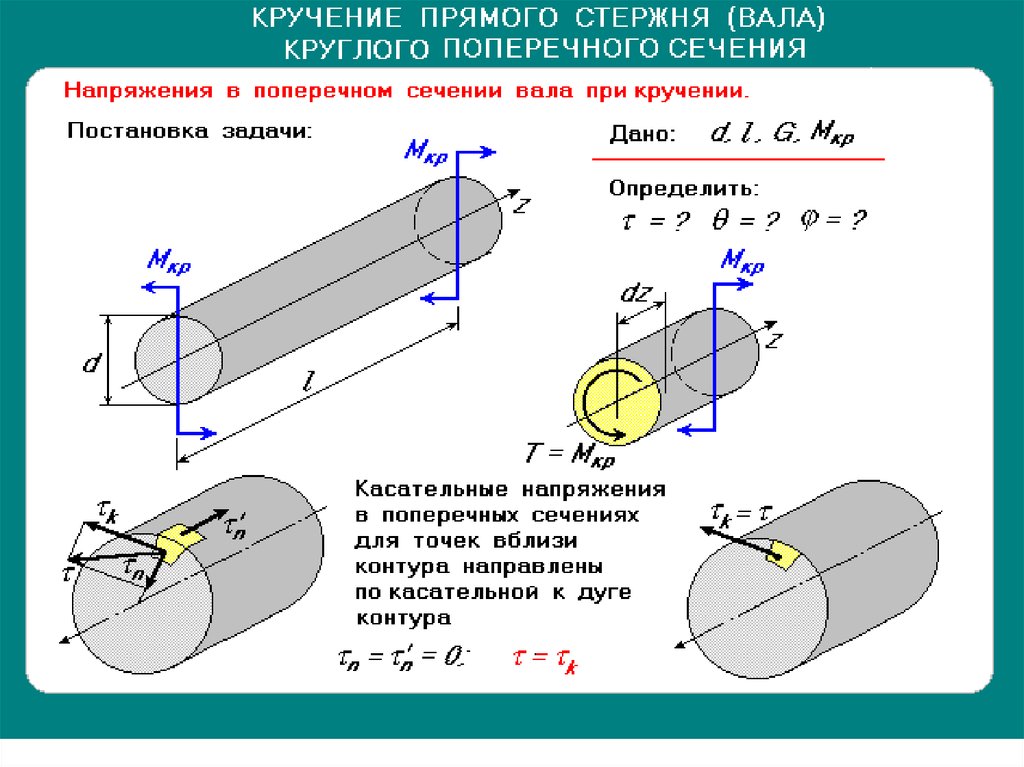 Это важно отметить, потому что

обрушение породы со стенок скважины обычно происходит из-за чрезмерных касательных напряжений!

Касательное напряжение всегда равно нулю на поверхности, где действуют главные напряжения.

Касательные напряжения не могут существовать на открытых поверхностях, находящихся в контакте с жидкостью, таких как стенки скважины. Поэтому после проводки скважины одна главная плоскость будет ориентирована параллельно траектории скважины, а другая будет ей ортогональна. Можно начертить новый круг напряжений для прогнозирования максимального касательного напряжения в таких условиях.

137

vk.com/club152685050 | vk.com/id446425943

Огибающая предельных кругов напряжений

Для большей части программы бурения можно спрогнозировать условия, при которых будет обеспечена устойчивость стенок скважины, или при которых будет потеряна устойчивость стенок скважины. Если мы знаем напряжения в естественных условиях залегания, нам нужно найти интервал допустимых плотностей бурового раствора, при которых не будет ни поглощений, ни обрушений породы. Типичный интервал допустимых значений плотности бурового раствора показан на рис. 5-1 и 8-40. Если плотность раствора слишком велика, возможны поглощения. Если плотность бурового раствора слишком низка, возможны обрушения породы. Для определения интервала допустимых значений плотности бурового раствора используется инструмент, называемый «огибающая предельных кругов напряжений».

Предварительно нужно провести испытания нескольких образцов породы из интересующего нас пласта, как показано на рис. 8-35. Образцы нагружаются до разрушения при различных значениях бокового давления. По данным каждого испытания строится предельный круг напряжений (рис. 8-35). Затем по верхам кругов проводится «огибающая предельных кругов напряжений». Эта линия определяет границу устойчивости. Если точка, характеризующая напряженное состояние, находится ниже этой линии (желтая область), то стенки скважины устойчивы. Если нет, стенки неустойчивы.

Определить интервал допустимых напряжений можно путем испытаний образцов при различных значениях бокового давления.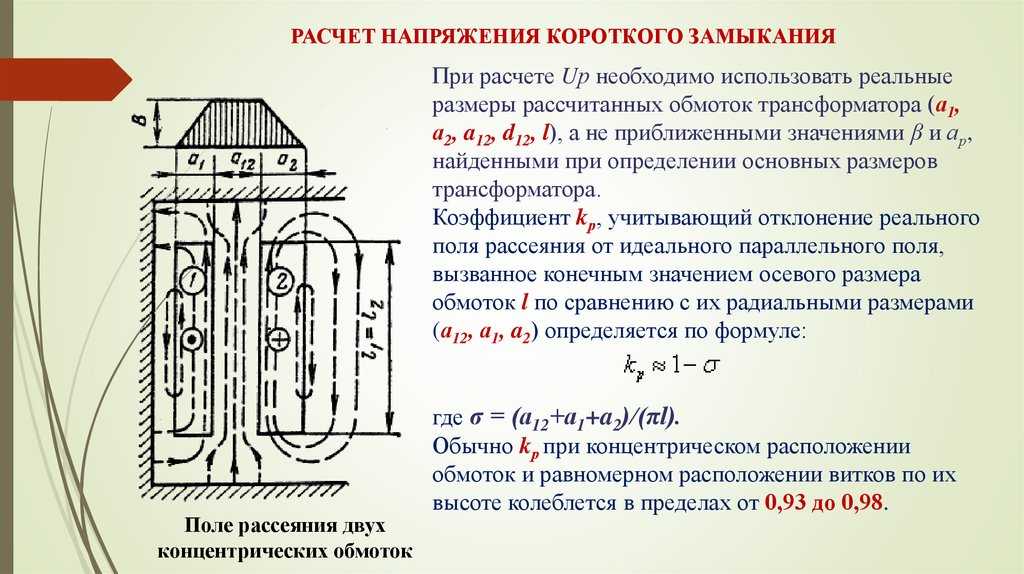

Рис. 8-35 Огибающая предельных кругов напряжений

Вспомним, что в большинстве случаев разрушение происходит из-за чрезмерного касательного напряжения. Вспомним также, что касательное напряжение возрастает с увеличением разности между наибольшим и наименьшим главными напряжениям (максимальное касательное напряжение характеризует радиус круга). Главными напряжениями, представленными на круге напряжений, обычно являются кольцевые напряжения, σθ, и радиальные напряжения, σr. При увеличении радиальных напряжений кольцевые напряжения уменьшаются. Таким образом, увеличение плотности бурового раствора влияет и на те и на другие напряжения и приводит к уменьшению круга напряжений, если радиальные напряжения меньше кольцевых, или к увеличению круга, если радиальные напряжения больше кольцевых (рис.8-39).

Огибающая предельных кругов напряжений помогает понять, как изменение параметров бурового раствора, таких как его плотность и температура, влияет на устойчивость стенок скважины. Но сначала посмотрим, какие факторы влияют на устойчивость стенок.

138

Что такое радиальное напряжение? — Определение из Trenchlesspedia

Что означает радиальное напряжение?

Радиальное напряжение в трубе можно определить как эффективное напряжение, действующее в радиальном направлении, т. е. в направлении, перпендикулярном продольной оси трубы. Напряжение действует в радиальном направлении, поэтому оно известно как радиальное напряжение. Кольцевое напряжение, продольное напряжение и радиальное напряжение действуют взаимно перпендикулярно друг другу. В подземных трубах эти различные напряжения действуют на трубу в зависимости от нагрузки и характеристик жидкости.

Реклама

Trenchlesspedia объясняет радиальное напряжение

Если давление действует изнутри цилиндра, максимальное напряжение возникает на внутренней поверхности, а минимальное напряжение возникает на внешней поверхности. Точно так же, если давление действует снаружи трубы, максимальное напряжение будет развиваться на внешней поверхности, а минимальное напряжение будет развиваться на внутренней поверхности. Радиальное напряжение представлено как σ _r . Для тонких труб величина радиального напряжения значительно меньше по сравнению с кольцевыми и продольными напряжениями, действующими на трубу, и поэтому ею часто пренебрегают.

Реклама

Поделись этим термином

Связанные термины

• Напряжение окружности
• Продольное напряжение
• Восстановление канализации
• Эффективное напряжение
• Гидравлический радиус

• Чувствительность к стрессу
• Напряжение на месте
• Коррозионное растрескивание под напряжением
• Минимальное напряжение на месте
• Стресс-тест на месте

Связанное Чтение

• Горизонтально-направленное бурение: 7 ключевых фактов, которые необходимо знать
• Испытание материалов на прочность и параметры
• Полное руководство по механике разрушения и испытаниям на безопасность материалов
• 3 эффективных способа обнаружения кольцевого напряжения в стенке трубы, пока не стало слишком поздно
• Процесс планирования: как подготовиться к успешному проекту бестраншейного строительства
• Планирование бурения скважины для бестраншейного проекта? Вот 5 важных факторов, которые следует учитывать

Теги

Разрыв трубыБестраншейная реабилитацияТехническое обслуживание

Актуальные статьи

Бестраншейная реабилитация

5 лучших способов соединения труб, на которые всегда можно положиться

Бестраншейное строительство

Понимание 4 этапов исследования места

Бестраншейная реабилитация

Как узнать, есть ли в вашем доме асбестоцементные трубы

Бестраншейное строительство

Микротоннелирование против.

Горизонтально-направленное бурение: понимание различий между этими ключевыми бестраншейными методами

Полное руководство для начинающих — Lambda Geeks

В этой статье мы обсудим различные факты, связанные с радиальным напряжением.

Внутреннее давление и внешнее давление сжимают сосуд под давлением в радиальном направлении, в результате чего возникают сжимающие напряжения, называемые радиальными напряжениями, общепринятое соглашение о знаках рассматривает сжимающие напряжения как отрицательные. Радиальное напряжение представлено как σ _r

Все три главных напряжения (кольцевое, осевое и радиальное) действуют на сосуд высокого давления взаимно перпендикулярно друг другу. Среди всех трех напряжений σ _r действует в направлении радиуса цилиндра или сферы.

Что такое радиальное напряжение?

Давления действуют в разных направлениях на цилиндрический или сферический объект , которые называются осевыми, радиальными и тангенциальными напряжениями.

Радиальные напряжения могут быть сформулированы как функция внутреннего давления и давления окружающей среды, а также внутреннего и внешнего радиусов сосуда высокого давления. На внутренней поверхности цилиндра σ _r такое же, как и внутреннее давление.

Снаружи соответствует внешнему давлению (14 фунтов на кв. дюйм или 0,1 МПа). По толщине цилиндра она меняется между этими значениями почти линейно. Если мы рассмотрим цилиндрическую трубу, по которой течет жидкость, различные типы нагрузок, такие как весовые нагрузки (вес трубы, вес жидкости и т. Д.), Давления (внутреннее и внешнее расчетное и рабочее давление), изменение температуры, случайные нагрузки (ударная сила, ударная сила) создавать напряжения в трубопроводной системе.

Эти нагрузки пытаются деформировать трубу, и из-за эффекта инерции труба создает некоторую внутреннюю силу сопротивления в виде напряжений.

Что такое радиальное напряжение в сосуде под давлением?

Радиальные напряжения по-разному действуют на сосуд высокого давления в зависимости от толщины его стенки и формы сосуда.

Если на внутреннюю поверхность цилиндра действует давление, то максимальные напряжения будут развиваться на внутренней поверхности, а если на внешнюю поверхность действует сила давления, то максимальные напряжения будут действовать на внешней поверхности.

Сосуды высокого давления представляют собой большие емкости, специально предназначенные для хранения жидкостей и газов, внутреннее давление всегда отличается от внешнего давления, внутреннее давление сосуда высокого давления обычно поддерживается на более высокой стороне. Клеточные организмы и артерии нашего тела являются естественным примером сосудов под давлением.

A Сварной стальной сосуд под давлением; Изображение предоставлено: Википедия

Сосуды под давлением, содержащие вакуум, поддерживаются при более низком внутреннем давлении, чем атмосферное.

Обычно для сосуда высокого давления можно предположить, что используемый материал является изотропным, деформации от давления малы, а толщина стенки сосуда намного меньше, чем внешний и внутренний радиусы сосуда.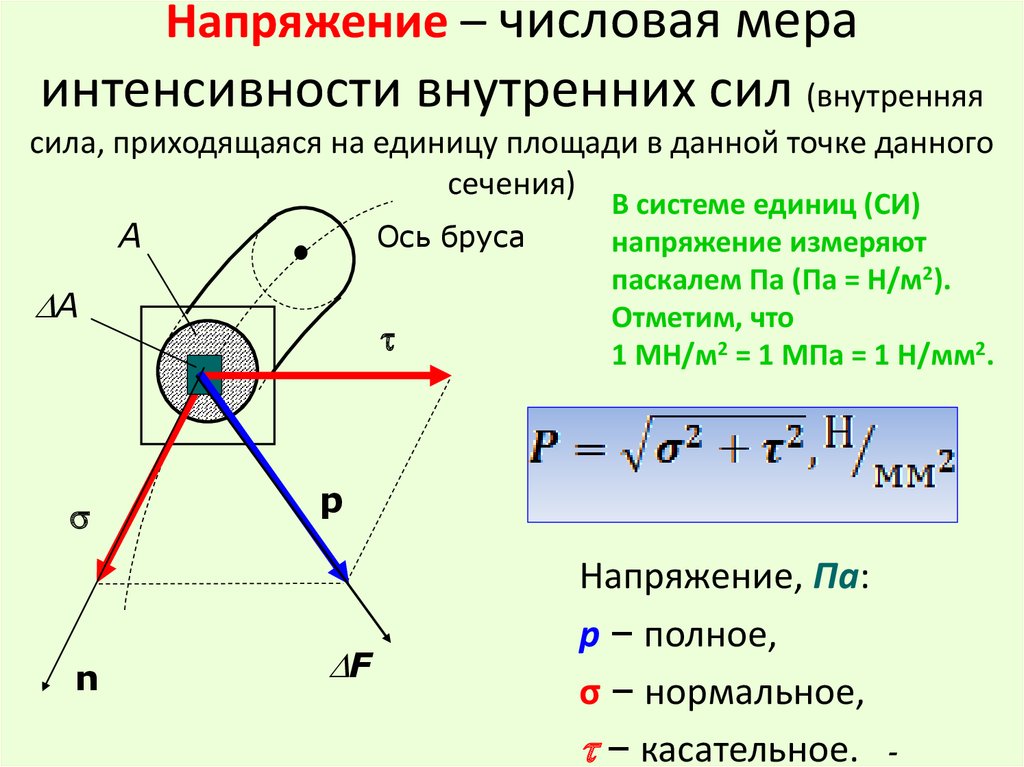 Аэрозольные баллончики, резервуары для подводного плавания и большие промышленные контейнеры, котлы и т. д. являются примерами сосудов высокого давления.

Что такое радиальное напряжение в трубопроводах?

Радиальное напряжение в трубопроводах возникает из-за внутреннего давления внутри трубы, создаваемого жидкостью или газом.

Радиальное напряжение действует в трубопроводах в виде нормального напряжения и действует параллельно радиусу трубы. Значение остается в пределах диапазона внутреннего расчетного давления и атмосферного давления, действующего на внутреннюю и внешнюю поверхности соответственно. σ _r , развернутое перпендикулярно поверхности, равно σ _r =-p.

По сравнению с другими нормальными напряжениями, действующими в трубопроводах, значение σ _r значительно меньше, поэтому продольное напряжение и окружное напряжение учитываются только при проектировании труб.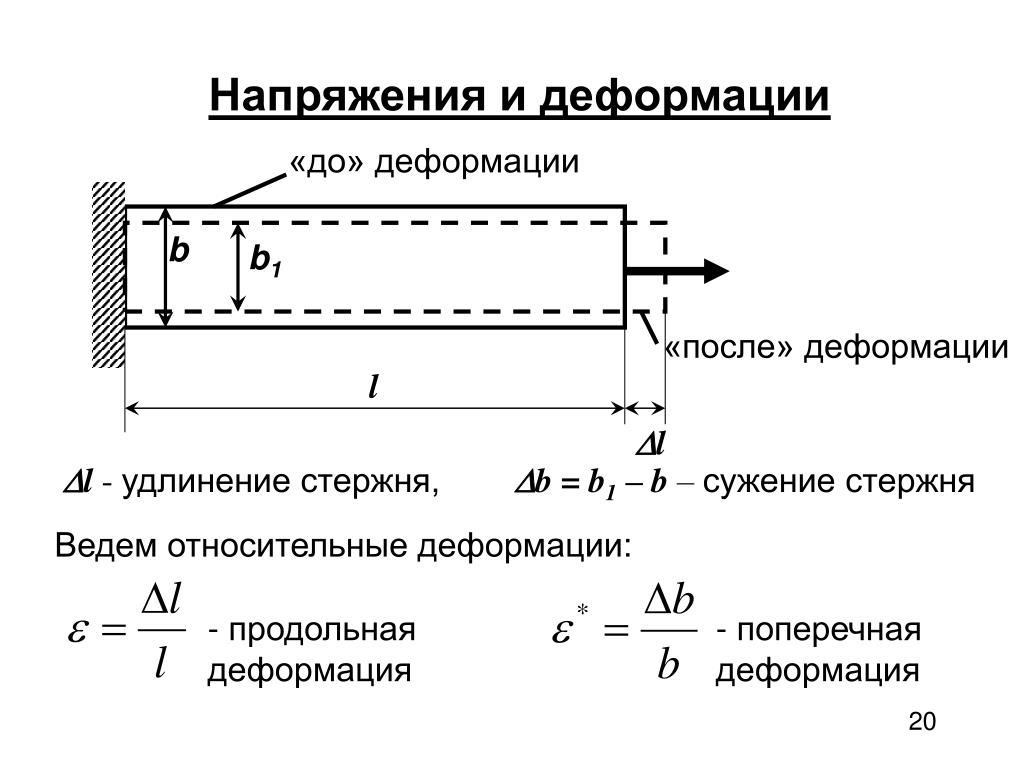 σ _r обычно игнорируется.

Как рассчитать радиальное напряжение в трубе?

Радиальное напряжение – это нормальное напряжение в стенке трубы, действующее в направлении, параллельном радиусу трубы.

σ _r действует в трубопроводах в виде нормального напряжения и действует параллельно радиусу трубы. Значение остается в пределах диапазона внутреннего расчетного давления и атмосферного давления, действующего на внутреннюю и внешнюю поверхности соответственно.

Рассмотрим σ _r в трубе под давлением, поперечное сечение стенки трубы характеризуется ее внутренним радиусом и внешним радиусом.

σ _r =-P _{целое число}

σ ^r =-P _амб

Знак минус обусловлен сжимающим характером напряжений.

В произвольном месте внутри стенки трубы силы вызывают сжатие, которому противодействует материал стенки трубы.

Величина сжимающего напряжения по толщине стенки трубы, выражение для распределения напряжения внутри стенки трубы дается теоремой Ламе.

Выражение для

Выражение содержит множество фиксированных значений, таких как r _o , r _i , p _i , p _o только радиус (r) только переменный.

Другими словами 

Радиальное напряжение уменьшается от значения внутреннего давления до значения внешнего давления.

Максимум σ _r просто значение внутреннего давления трубы

σ _rmax =p _int

Формула радиального напряжения

Нормальное напряжение, действующее в направлении или от центральной оси цилиндр известен как радиальное напряжение.

Набор уравнений, известных как уравнения Ламса, используется для расчета напряжений, действующих на сосуд высокого давления. В случае трубы σ _r варьируется между внутренним давлением и давлением окружающей среды.

σ _r =AB/r ²

σ _θ =A+B/r ²

Где A и B являются константами интегрирования и могут быть решены путем интегрирования.

И «r» — радиус, который может быть внутренним радиусом или может быть внешним радиусом.

Формула радиального напряжения для толстого цилиндра

Сосуд высокого давления считается толстым, если D/t< 20, где «D» — диаметр сосуда, а «t» — толщина стенки.

В случае толстого цилиндра действующими напряжениями являются в основном кольцевое или окружное напряжение и радиальное напряжение. Из-за внутреннего давления, действующего внутри сосуда, во внутренней стенке сосуда по радиусу сосуда возникают некоторые напряжения, известные как радиальные напряжения.

Уравнение Ламе используется для количественной оценки напряжений, действующих на толстый цилиндр.

где r _i = внутренний радиус цилиндра

ro = внешний радиус цилиндра

p _i = внутреннее абсолютное давление

p _o =внешнее абсолютное давление

На внутренней поверхности стенки цилиндра σ _r максимально и равно p _i – p _o т.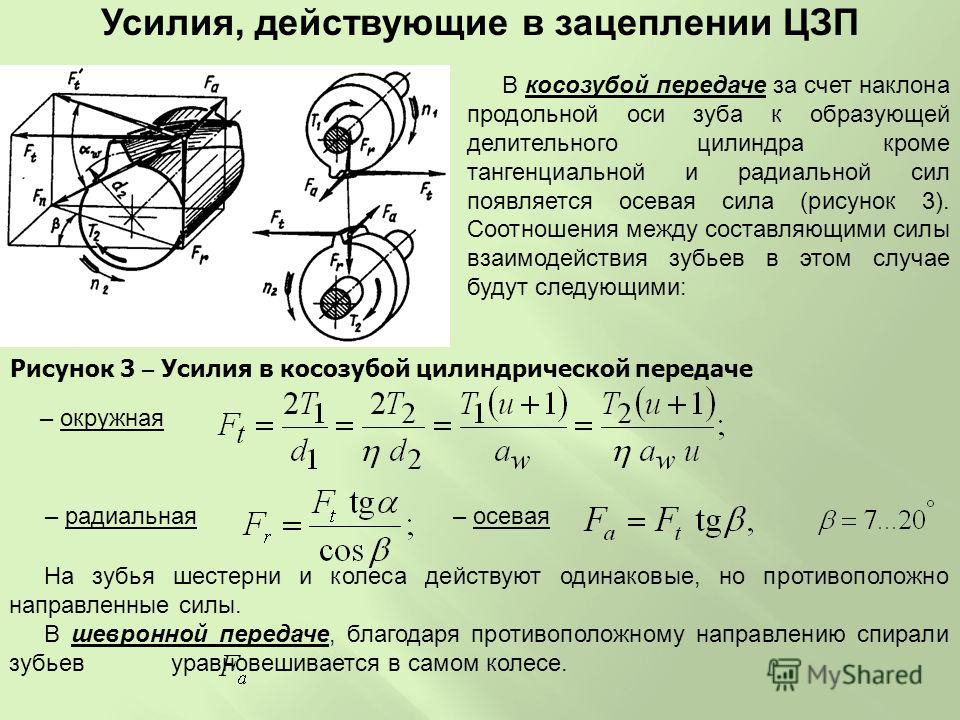 е. манометрическое давление.

Формула радиального напряжения для конического цилиндра

Влияние радиального напряжения в случае тонкого цилиндра не равно нулю, но не стоит учитывать его влияние при проектировании и расчете.

В случае тонкого цилиндра окружное напряжение и осевые напряжения намного больше, чем σ _r , поэтому для тонкого цилиндра радиальное напряжение обычно игнорируется. В случае толстого цилиндра σ 9Созданное 0011 r эквивалентно манометрическому давлению на внутренней поверхности цилиндра и нулю на внешней поверхности.

Формула радиального напряжения для сферы

Напряжения, действующие нормально к стенкам сферы, являются радиальными напряжениями.

σ _r , действующее на внешнюю стенку сферы, равно нулю, так как внешняя стенка является свободной поверхностью.

σ _r формула для сферы σ _r =-p _i /2, для средней толщины t/2

σ _r =-p, для внутреннего радиуса

σ _r =0, для внешнего радиуса

5 Istile?

Радиальные напряжения всегда имеют сжимающую природу.

Радиальное напряжение в сосуде под давлением возникает из-за действия внутреннего давления, создаваемого внутренней жидкостью, и давления окружающей среды на внешнюю поверхность. В произвольном месте внутри стенки сосуда под давлением силы вызывают сжатие, которому противодействует материал стенки.

p _i и p _e сжимают оболочку в радиальном направлении, создавая σ _r , согласно соглашению механики сплошной среды, эти напряжения отрицательны.

σ _r на внутреннем и внешнем радиусе соответственно

σ _ri =-p _i

σ _re =-p _e 90 конструкции среднее арифметическое напряжений даст радиальное напряжение σ _R ,

σ _R = (σ _RI +σ _RE )/2

σ _R =-(P _I +P _E )/2 EQ (1)

.

Где p _I = 0, p _E = 0,

EQ (1) дает

σ _R = -p _I /2

σ _R = -P _E / 2

Является ли радиальное напряжение отрицательным?

Радиальные напряжения действуют в радиальном направлении сосуда высокого давления и, как и касательное или кольцевое напряжение, также

, ответственный за диаметральную деформацию сосуда.

В общем случае радиальное напряжение имеет сжимающий характер и действует между внутренней и внешней поверхностью цилиндрического сосуда, и в соответствии с соглашением механики сплошной среды радиальное напряжение отрицательно.

Является ли радиальное напряжение основным напряжением?

Да, радиальное напряжение является основным напряжением.

Радиальное напряжение — это напряжение, направленное к главной оси сосуда высокого давления или от нее. В случае толстого цилиндра напряжение распределяется по толщине цилиндра. Максимальная σ _r получается на внутреннем радиусе цилиндра .

Является ли радиальное напряжение напряжением сдвига?

Напряжение сдвига τ — это составляющая напряжения, копланарная поперечному сечению материала.

Из-за расширения конструкции при сдвиге возникают радиальные напряжения, действующие в нормальном направлении поверхности раздела.