14) Элементарная работа силы; ее аналитическое выражение. Мощность.

Элементарная работа dA = F_ds, F_ – проекция силы на касательную к траектории, направленная в сторону перемещения, или dA = Fdscos.

Если  – острый, то dA>0, тупой – <0, =90^o: dA=0. dA= – скалярное произведение вектора силы на вектор элементарного перемещения точки ее приложения; dA= F_xdx+F_ydy+F_zdz – аналитическое выражение элементарной работы силы. Единицы работы:

[1 Дж (джоуль) = 1 Нм].

Элементарная работа силы равна проекции силы на направление перемещения точки , умноженной на элементарное перемещение ds или элементарная работа силы равна произведению модуля силы на элементарное перемещение ds и на косинус угла между направлением силы и направлением перемещения.

Мощность.

Мощность – величина, определяющая работу в единицу времени, Если изменение работы происходит равномерно, то

мощность постоянна: N=A/t. [1 Вт (ватт) =1 Дж/с, 1 кВт (киловатт) =

= 1000 Вт, 1л.с.(лошадиная сила) = 75 кгсм/с = 736 Вт]

Р-та силы на любом конечном перемещении М₀М₁: . Еслисила постоянна, то =Fscos.Ед.р-ты:[1 Дж (джоуль) = 1 Нм].

16) Работа силы тяжести, силы упругости

Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения (+ перемещение ↓, — перем ↑) A_1,2=±GH

Работа силы упругости.

Работа силы упругости: –работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

17) Понятие о силовом поле. Потенциальное силовое поле и силовая функция.

Силовым полем называется часть пространства, в каждой точке которого на помещенную туда материальную частицу действует определенная по модулю и направлению сила, зависящая от положения частицы.

Функция U от координат x, y, z, дифференциал которой = элементарной работе, называется

силовой функцией.

Силовое поле, для которого существует силовая функция, называется потенциальным силовым полем, а силы, действующие в этом поле, — потенциальными силами.

18) Потенциальная энергия.

Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той работе, которую произведут силы поля при перемещении точки из положения М в нулевое

Потенциальная энергия в любой точке силового поля равна значению силовой функции в этой точке, взятому с обратным знаком.

19) Примеры потенциальных силовых полей: однородное поле тяжести.

1)Сила тяжести

2)Сила упругости

3)Сила тяготения

20) Закон сохранения механической энергии.

При движении под действием потенциальных сил сумма кинетической и потенциальной энергий системы в каждом ее положении остается величиной постоянной.

Т+П=const

21) Малые колебания точки около положения устойчивого равновесия.

Малые колебания системы представляют собой такое движение системы, при котором значения обобщенных координат, определяющих положение системы, и обобщенных скоростей в любой момент времени настолько малы, что их можно рассматривать как величины первого порядка малости.

22) Свободные незатухающие колебания и их свойства.

или

Свойства:

1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следовательно, и период Т колебаний от начальных условий не завися и являются неизменными характеристиками данной колеблющейся системы.

Уравнение свободных колебаний при отсутствии сопротивления.

x=c₁cos(kt)+c₂sin(kt)

23) Частота и период свободных незатухающих колебаний.

Промежуток времени Т, в течение которого точка совершает одно полное колебание, называется периодом колебаний.

Величина , обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний.

24) Амплитуда и фаза свободных незатухающих колебаний.

Амплитуда наибольшее отклонение точки от положения равновесия.

X=asin(kt+α) a-амплитуда a=√x₀²+(x²\k² )

Фаза колебаний определяет положение точки в данный момент, направление ее последующего движения.

25) Дифференциальное уравнение свободных колебаний при сопротивлении, пропорциональном

скорости.

y+k²y=0

Уравнение свободных колебаний при сопротивлении, пропорциональном скорости.

y=Asin(kt+β)

26) Период свободных колебаний при сопротивлении, пропорциональном скорости.

T=2π\k=2π√ƒ_cт\g

Декремент колебаний.

Декремент обозначает убывание. Декремент- отвлеченное число e^—nT*\2

e^—nT*\2=A_i+1\A_i=(Ae^—n(t_i+T*\2))\Ae^—ntT*-период затух колебаний.

Логарифмический декремент колебаний.

Логорифмич декремент- натуральный логарифм декремента: -nT*\2

-nT*\2=-πn\√R²-n²

(n-коэф затухания)

27) Случай апериодического движения

Апериодическое движение точки при n  k или b  2. При n > k корни характеристич-ого ур-я вещественны, общее решение: , обозначая С₁=(В₁+В₂)/2, С₂=(В₁-В₂)/2, (ch, sh – гиперболические косинус и синус), если ввести В₁= Аsh, В₂= Аch, то – это уравнение не колебательного движения (апериодического), т.к. гиперболический синус не является периодической функцией. Приn = k корни характеристич. ур-я вещественны, равны и отрицательны: z

1=z₂= – n, общее решение: , или, движение также апериодическое.

Физика. Механика

Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы, сделанных из пластилина. Если эти шары летят друг на друга с одной и той же скоростью, то при соударении они прилипнут друг к другу и остановятся. В этом случае суммарный импульс обоих шаров остался равным нулю, хотя состояние системы изменилось. Шары при этом нагрелись. Этот пример показывает, что импульс не всегда может служить мерой движения. Такой мерой является энергия. В данном случае механическая энергия при ударе перешла в другой вид энергии (тепловую).

Сначала рассмотрим важную характеристику — работу. Пусть материальная точка движется по траектории AB (рис. 1). На точку во время движения действует в общем случае переменная сила F. На участке ds (настолько малом, что модуль перемещения равен пройденному пути) силу F можно считать постоянной.

Рис 4.1. Элементарная работа

Элементарная работа силы равна скалярному произведению вектора силы на вектор перемещения её точки приложения

Работа — скалярная величина, ее знак зависит от знака . Положительная работа совершается силой, если ее направление составляет острый угол с направлением движения тела. Отрицательная работа совершается силой, направление которой составляет тупой угол с направлением движения, при этом сила тормозит это движение. Величина

— это проекция силы F на направление перемещения. Следовательно,

Полная работа силы находится как сумма (интеграл) элементарных работ по всей траектории L точки:

При перемещении вдоль оси x работу графически можно представить как площадь под кривой F_x(x) (рис. 4.2), причем площади под осью абсцисс следует приписывать отрицательное значение.

Рис. 2. Графическая интерпретация работы силы. Здесь для краткости положено F = F_x(x)

Если перемещение ортогонально силе, то = 0 и работа равна нулю:

Последнее показывает, что понятие работы в механике отлично от обыденного представления о работе. Так, при перемещении груза с постоянной скоростью в горизонтальном направлении сила тяжести не совершает работы. Работа не совершается также и тогда, когда тело покоится, так как точка приложения силы не перемещается и = 0. Здесь и ниже и означают одно и то же — бесконечно малое перемещение, а ||=||= — соответствующий бесконечно малый путь.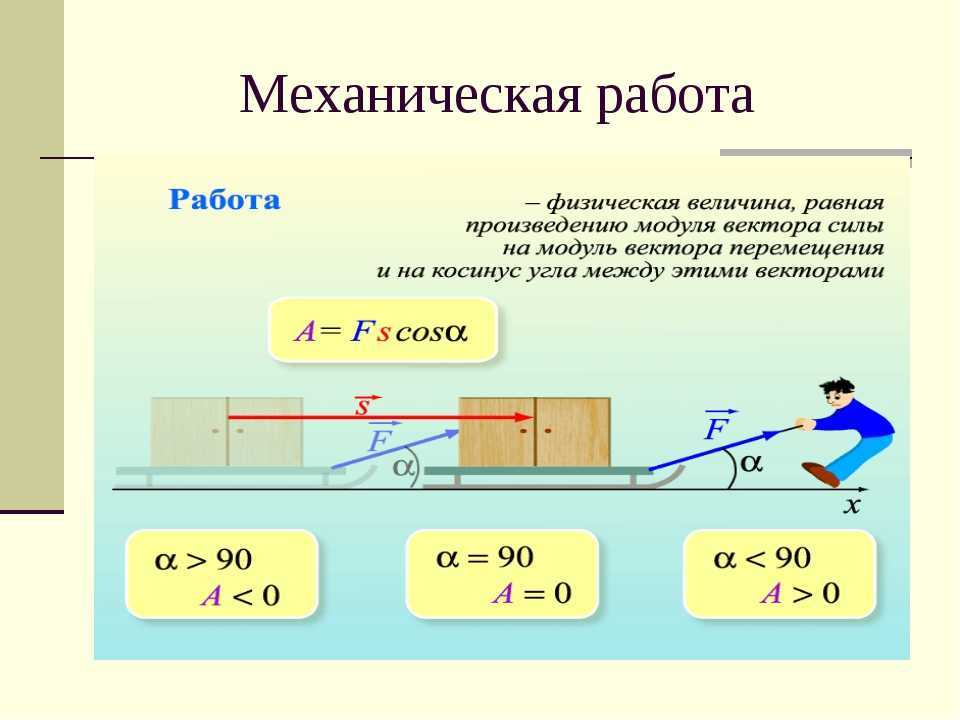

Если на тело действует несколько сил, то

то есть работа результирующей нескольких сил равна алгебраической сумме работ, совершаемых каждой из сил в отдельности.

Рассмотрим для примера работу, совершаемую внешней силой по сжатию и растяжению пружины с жесткостью . Направим ось 0x вдоль пружины, причем за начало координат 0 выберем положение свободного конца пружины, находящейся в ненагруженном состоянии. Процесс сжатия/растяжения представляем как последовательность равновесных состояний: в каждый момент времени прилагаем внешнюю силу, равную по величине силе упругости со стороны пружины. Тогда согласно закону Гука

где x — удлинение пружины. При положительных x (растяжение пружины) внешняя cила направлена направо, при отрицательных (сжатие) — налево (рис. 4.3).

Рис. 4.3. Работа, совершаемая при сжатии/растяжении пружины

Скалярное произведение для элементарной работы внешней силы имеет в этом случае вид

так что для полной работы упругой деформации пружины получаем

Заметим, что A не зависит от знака x: и при растяжении, и при сжатии пружины внешняя сила совершает одну и ту же положительную работу.

Дополнительная информация

http://www.plib.ru/library/book/17833.html – Хайкин С.Э. Физические основы механики, Наука, 1971 г.– стр. 476–479 (§ 111): выведено выражение для потенциальной энергии упруго деформированного тела.

7.2 Кинетическая энергия и теорема о работе-энергии

Чистая работа и теорема о работе-энергии

Мы знаем из изучения законов Ньютона в книге «Динамика: сила» и «Законы движения Ньютона», что результирующая сила вызывает ускорение. В этом разделе мы увидим, что работа, совершаемая результирующей силой, дает системе энергию движения, и в процессе мы также найдем выражение для энергии движения.

Давайте начнем с рассмотрения общей или чистой работы, выполненной в системе. Чистая работа определяется как сумма работы, выполненной всеми внешними силами, то есть чистая работа — это работа, выполненная чистой внешней силой FnetFnet size 12{F rSub { size 8{«net»} } } {}. В форме уравнения это Wnet=FnetdcosθWnet=Fnetdcosθ size 12{W rSub { size 8{«net»} } =F rSub { size 8{«net»} } d»cos»θ} {}, где θθ size 12{ θ} {} — угол между вектором силы и вектором смещения.

На рис. 7.3(a) показан график зависимости силы от смещения для составляющей силы в направлении смещения, то есть FcosθFcosθ размера 12{F»cos»θ} {} в зависимости от dd размера 12{d} {} график. В этом случае размер FcosθFcosθ 12{F»cos»θ} {} является постоянным. Вы можете видеть, что площадь под графиком равна FdcosθFdcosθ size 12{F»cos»θ} {}, или проделанной работе. На рис. 7.3(b) показан более общий процесс, когда сила изменяется. Площадь под кривой разбита на полосы, каждая из которых имеет среднюю силу пр» \) } } } {}. Проделанная работа равна (Fcosθ)i(ave)di(Fcosθ)i(ave)di size 12{ \( F»cos»θ \) rSub { size 8{i \(«ave» \) } } d rSub { size 8{i} } } {} для каждой полосы, а общая проделанная работа представляет собой сумму WiWi size 12{W rSub { size 8{i} } } {}. Таким образом, общая проделанная работа представляет собой общую площадь под кривой, полезное свойство, к которому мы обратимся позже.

Рисунок 7.3 (a) График зависимости FcosθFcosθ от размера dd 12{d} {}, когда размер FcosθFcosθ 12{F»cos»θ} {} является постоянным. Площадь под кривой представляет собой работу силы. (b) График зависимости FcosθFcosθ размера 12{F»cos»q} {} от размера dd 12{d} {}, в котором сила изменяется. Работа, выполненная для каждого интервала, равна площади каждой полосы; таким образом, общая площадь под кривой равна общей проделанной работе.

Связи с реальным миром: работа и направление

Подумайте о вождении автомобиля. Во время движения у вас есть поступательная скорость и, следовательно, кинетическая энергия. Когда вы нажимаете на тормоза, тормоза создают силу, противоположную направлению вашего движения (действующую через колеса). Тормоза работают на вашем автомобиле и уменьшают кинетическую энергию. Точно так же, когда вы ускоряетесь, двигатель (действующий через колеса) оказывает усилие в направлении движения. Двигатель работает на вашем автомобиле и увеличивает кинетическую энергию. Наконец, если вы проходите поворот с постоянной скоростью, у вас одинаковая кинетическая энергия как до поворота, так и после него. Сила, прилагаемая двигателем, была перпендикулярна направлению движения, поэтому не совершала работы и не изменяла кинетическую энергию.

Сетевую работу будет проще исследовать, если мы рассмотрим одномерную ситуацию, когда сила используется для ускорения объекта в направлении, параллельном его начальной скорости. Такая ситуация возникает для упаковки на роликовой конвейерной системе, показанной на рис. 7.4.

Рис. 7.4 Пакет на роликовой ленте толкают горизонтально на расстояние dd.

Сила тяжести и нормальная сила, действующие на упаковку, перпендикулярны смещению и не совершают работы. Кроме того, они также равны по величине и противоположны по направлению, поэтому они сокращаются при расчете результирующей силы. Чистая сила возникает исключительно из горизонтальной приложенной силы FappFapp и горизонтальной силы трения ff. Таким образом, как и ожидалось, чистая сила параллельна смещению, так что θ=0ºθ=0º и cosθ=1cosθ=1 размер 12{«cos»q=1} {}, а чистая работа определяется как

7. 7 Wnet=Fnetd.Wnet=Fnetd. size 12{W rSub { size 8{«net»} } =F rSub { size 8{«net»} } d} {}

Эффект чистой силы FnetFnet size 12{F rSub { size 8{«net»} } } {} заключается в ускорении пакета с v0v0 size 12{v rSub { size 8{0} } } {} до vv size 12 {т} {}. Кинетическая энергия упаковки увеличивается, указывая на то, что чистая работа, совершаемая над системой, положительна (см. пример 7.2). Применяя второй закон Ньютона и занимаясь алгеброй, мы можем прийти к интересному выводу. Подстановка Fnet=maFnet=ma size 12{F rSub { size 8{«net»} } = ital «ma»} {} из второго закона Ньютона дает

7.8 Wnet=безумие.Wnet=безумие. size 12{W rSub { size 8{«net»} } = ital «безумный»} {}

Чтобы получить соотношение между чистой работой и скоростью, придаваемой системе действующей на нее чистой силой, мы берем d=x−x0d=x−x0 size 12{d=x — x rSub { size 8{0} } } {} и использовать уравнение, изученное в Уравнениях движения для постоянного ускорения в одном измерении, для изменения скорости на расстоянии dd, если ускорение имеет постоянное значение aa; а именно, v2=v02+2adv2=v02+2ad. Обратите внимание, что в выражении для сети появляется aa. Решение для ускорения дает a=v2-v022da=v2-v022d. Когда aa подставляется в предыдущее выражение для WnetWnet, мы получаем

7.9 Wnet=mv2-v022dd.Wnet=mv2-v022dd.

Размер dd 12{d} {} отменяется, и мы переставляем это, чтобы получить

7.10 Wnet=12mv2−12mv0 2.Wnet=12mv2−12mv0 2. size 12{w»» lSub { size 8{ ital «net»} } = {{1} over {2} } ital «mv» rSup { size 8{2} } — { {1} over {2} } ital «mv»»» lSub { size 8{0} } «» lSup { size 8{2} } «.» } {}

Это выражение называется теоремой работы-энергии, и оно фактически применимо вообще — даже для сил, которые изменяются по направлению и величине — хотя мы вывели его для частного случая постоянной силы, параллельной перемещению. Из теоремы следует, что чистая работа над системой равна изменению величины 12mv212mv2 size 12{ { {1} над {2} } ital «mv» rSup { size 8{2} } } {}. Эта величина является нашим первым примером формы энергии.

Теорема о работе-энергии

Чистая работа системы равна изменению количества 12mv212mv2 size 12{ { { size 8{1} } over { size 8{2} } } ital «mv» rSup { size 8{ 2} } } {}.

7.11 Wnet=12mv2−12mv0 2.Wnet=12mv2−12mv0 2. size 12{w»» lSub { size 8{ ital «net»} } = {{1} over {2} } ital «mv» rSup { размер 8{2} } — { {1} более {2} } ital «mv»»» lSub { размер 8{0} } «» lSup { размер 8{2} } «.» } {}

Количество 12mv212mv2 size 12{ { {1} over {2} } ital «mv» rSup { size 8{2} } } {} в теореме о работе-энергии определяется как поступательная кинетическая энергия (KE) масса мм размер 12{m} {} движется со скоростью vv размер 12{v} {}. Поступательная кинетическая энергия отличается от вращательной кинетической энергии, которая рассматривается позже. В форме уравнения поступательная кинетическая энергия,

7.12 KE=12mv2,KE=12mv2, размер 12{«KE»= {{1} больше {2} } ital «mv» rSup {размер 8{2} } ,} {}

— это энергия, связанная с поступательным движением. Кинетическая энергия — это форма энергии, связанная с движением частицы, отдельного тела или системы объектов, которые движутся вместе.

Мы понимаем, что требуется энергия, чтобы разогнать объект, такой как автомобиль или пакет на рис. 7.4, до нужной скорости; однако может показаться немного удивительным, что кинетическая энергия пропорциональна квадрату скорости. Эта пропорциональность означает, например, что автомобиль, движущийся со скоростью 100 км/ч, имеет в четыре раза больше кинетической энергии, чем на скорости 50 км/ч, что помогает объяснить, почему столкновения на высокой скорости настолько разрушительны. Теперь мы рассмотрим ряд примеров, иллюстрирующих различные аспекты работы и энергии.

Применение научных методов: машинки на холме

Соберите пандус, подходящий для катания игрушечных машинок вверх и вниз. Затем запланируйте серию экспериментов, чтобы определить, как направление силы относительно скорости объекта изменяет кинетическую энергию объекта. Обратите внимание, что гравитация во всех случаях будет направлена ​​вниз. Что будет, если завести машину сверху? Как насчет дна, с возрастающей начальной скоростью? Если ваша рампа достаточно широкая, что произойдет, если вы отправите игрушечную машинку прямо через нее? Влияет ли изменение поверхности рампы на ваши результаты?

Пример ответа: Когда игрушечная машинка спускается по пандусу с компонентом силы тяжести в том же направлении, кинетическая энергия увеличивается. Отправка автомобиля вверх по пандусу уменьшает кинетическую энергию, поскольку гравитация препятствует движению. Отправка автомобиля боком не должна привести к каким-либо изменениям. Если у вас есть поверхность, которая создает большее трение, чем гладкая поверхность, например ковер, обратите внимание, что трение всегда препятствует движению и, следовательно, уменьшает кинетическую энергию.

Пример 7.2 Расчет кинетической энергии упаковки

Предположим, что пакет массой 30,0 кг на роликовом ленточном конвейере на рис.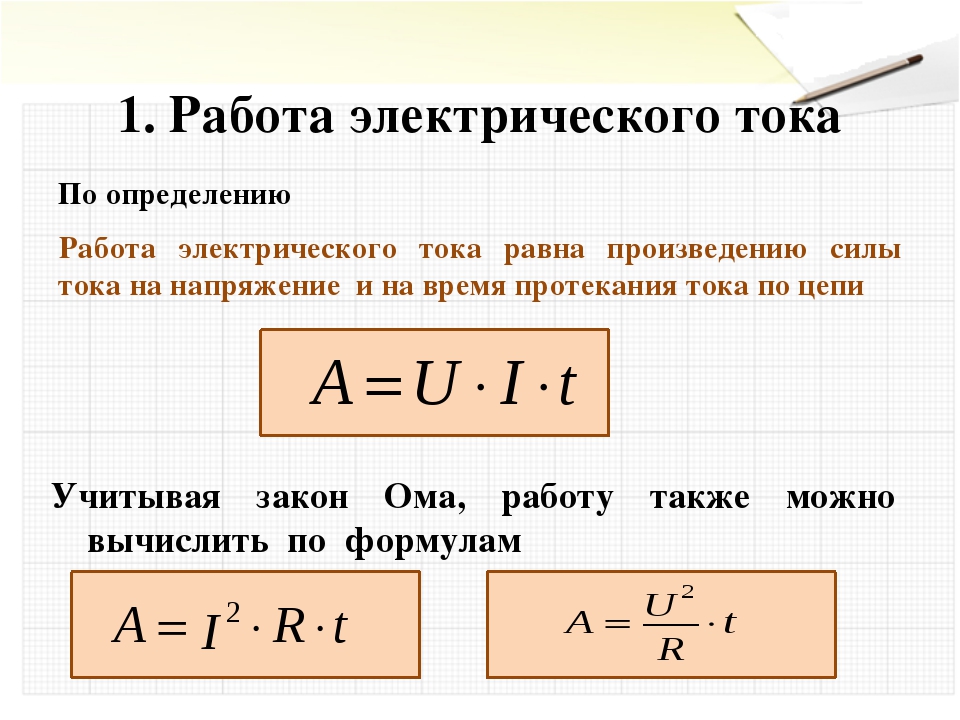 7.4 движется со скоростью 0,500 м/с. Какова его кинетическая энергия?

Стратегия

Поскольку масса mm и скорость vv заданы, кинетическая энергия может быть рассчитана по ее определению, приведенному в уравнении KE=12mv2KE=12mv2 size 12{«KE»= { {1} over {2 } } ital «mv» rSup {размер 8{2} } } {}.

Решение

Кинетическая энергия определяется выражением

7,13 KE=12mv2.KE=12mv2. size 12{«KE»= { {1} over {2} } ital «mv» rSup { size 8{2} } «.» } {}

Ввод известных значений дает

7,14 KE=0,5(30,0 кг)(0,500 м/с)2,KE=0,5(30,0 кг)(0,500 м/с)2, размер 12{«KE»=0 «.» 5 \( «30» «.» 0″ кг» \) \( 0 «.» «500»» м/с» \) rSup { размер 8{2} } ,} {}

что дает

7.15 KE=3,75 кг⋅м2/с2=3,75 Дж.KE=3,75 кг⋅м2/с2=3,75 Дж. размер 12{«KE»=3 «.» «75»‘»kg» cdot m rSup { размер 8{2} } «/s» rSup { размер 8{2} } =3 «.» «75» Дж «.» } {}

Обсуждение

Обратите внимание, что единицей кинетической энергии является джоуль, такая же, как единица работы, как упоминалось при первом определении работы. Интересно и то, что, хотя это достаточно массивный пакет, его кинетическая энергия невелика при такой относительно небольшой скорости. Этот факт согласуется с наблюдением, что люди могут перемещать такие пакеты, не утомляя себя.

Связи в реальном мире: центр масс

Предположим, у нас есть две экспериментальные тележки одинаковой массы, закрепленные вместе на гусенице со сжатой пружиной между ними. Когда защелка отпущена, пружина совершает над тележками работу 10 Дж. Мы увидим, как через пару разделов. Тележки перемещаются относительно пружины, являющейся центром масс системы. Однако центр масс остается неподвижным. Как можно учесть кинетическую энергию этой системы?

По теореме о работе-энергии работа, совершаемая пружиной над тележками, должна превращаться в кинетическую энергию. Итак, эта система имеет 10 Дж кинетической энергии. Полная кинетическая энергия системы равна кинетической энергии центра масс системы относительно фиксированного начала координат плюс кинетическая энергия каждой тележки относительно центра масс. Мы знаем, что центр масс относительно неподвижного начала координат не перемещается, и поэтому вся кинетическая энергия должна распределяться между тележками относительно центра масс. Поскольку тележки имеют одинаковую массу, каждая из них получает одинаковое количество кинетической энергии, поэтому каждая тележка имеет 5,0 Дж кинетической энергии.

В нашем примере силы между пружиной и каждой тележкой являются внутренними по отношению к системе. Согласно третьему закону Ньютона, эти внутренние силы будут сокращаться, так как они равны и противоположны по направлению. Однако это не означает, что эти внутренние силы не будут совершать работу. Таким образом, изменение кинетической энергии системы вызвано работой силы пружины и приводит к движению двух тележек относительно центра масс.

Пример 7.3 Определение работы по ускорению пакета

Предположим, что вы толкаете груз массой 30,0 кг, показанный на рис. 7.4, с постоянной силой 120 Н на расстояние 0,800 м, а средняя сила противодействующего трения составляет 5,00 Н.

(a) Рассчитайте чистую работу, выполненную на пакет. (б) Решите ту же задачу, что и в части (а), на этот раз найдя работу, совершаемую каждой силой, которая вносит вклад в результирующую силу.

Стратегия и концепция для (а)

Это движение в одномерной задаче. Сила, направленная вниз (от веса упаковки) и нормальная сила имеют одинаковую величину и противоположное направление, поэтому при расчете результирующей силы они компенсируются, в то время как приложенная сила, трение и перемещение горизонтальны (см. рис. 7.4). Как и ожидалось, чистая работа равна чистой силе, умноженной на расстояние.

Решение для (a)

Чистая сила представляет собой толкающую силу за вычетом силы трения, или Fnet = 120 Н – 5,00 Н = 115 NFnet = 120 Н – 5,00 Н = 115 Н размер 12{F rSub { размер 8{ «net»} } «= 120 Н – 5» «.» «00 Н = 115 Н»} {}. Таким образом, чистая работа равна

7,16 Wnet=Fnetd=115 N0,800 м=92,0 N⋅m=92,0 J.Wnet=Fnetd=115 N0,800 м=92,0 N⋅m=92,0 J. alignl { stack { размер 12 {W rSub { size 8{«net»} } =F rSub { size 8{«net»} } d= слева («115» N справа) слева (0 «.» «800» справа)} { } # » «=»92» «.» 0’N cdot m=»92″ «.» 0’J «.» {} } } {}

Обсуждение для (a)

Это значение представляет собой чистую работу, проделанную над упаковкой. Трение совершает отрицательную работу и удаляет часть энергии, затраченной человеком, и преобразует ее в тепловую энергию Чистая работа равна сумме работы, выполненной каждой отдельной силой

Стратегия и концепция (b)

К силам, действующим на упаковку, относятся сила тяжести, нормальная сила, сила трения и приложенная сила. Нормальная сила и сила тяжести перпендикулярны перемещению и, следовательно, не совершают работы.0005

Решение для (b)

Приложенная сила работает.

7.17 Wapp=Fappdcos0º=Fappd=120 N0.800 m= 96.0 J.Wapp=Fappdcos0º=Fappd=120 N0.800 m= 96.0 J.alignl { stack { size 12{W rSub { size 8{«app»} } =F rSub { size 8{«app»} } d»cos» влево (0° вправо)=F rSub { size 8{«app»} } d} {} # » «= влево («120 N» вправо ) влево (0 «.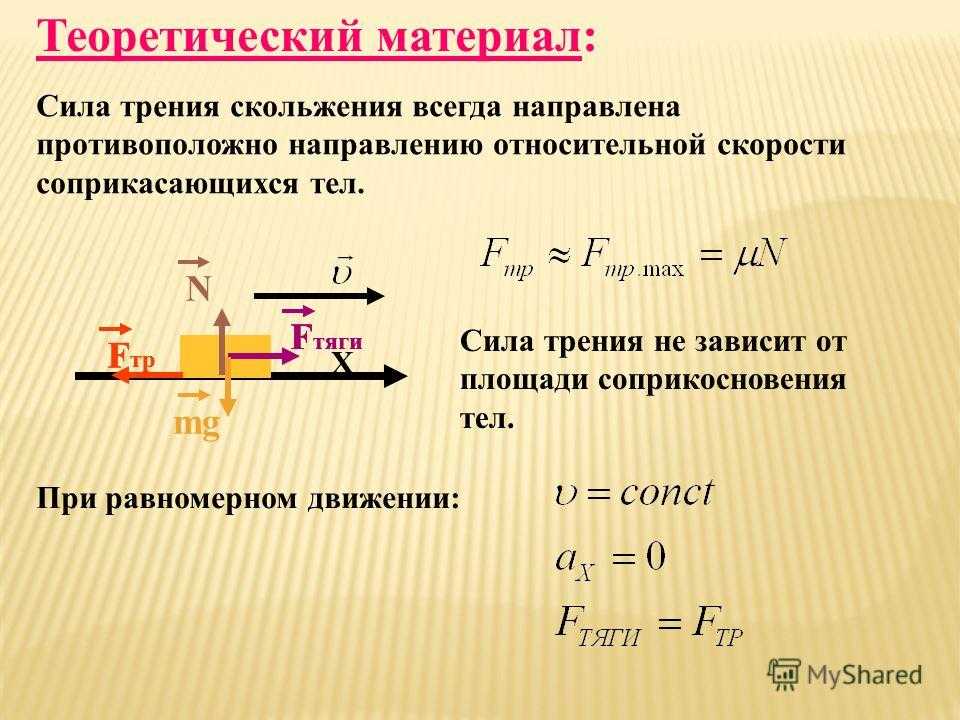 » «800»» м» вправо ) {} # » «=» 96″ «.» «0 Дж» «.» {} } } {}

Сила трения и перемещение направлены в противоположные стороны, так что θ=180ºθ=180º размер 12{θ=»180″°} {}, а работа, совершаемая трением, равна

7.18 Wfr=Ffrdcos180°=-Ffrd=-5.00 N0.800 м=-4.00 J.Wfr=Ffrdcos180°=-Ffrd=-5.00 N0.800 м=-4.00 J.alignl { stack { size 12{W rSub { size 8{«fr»} } =F rSub { size 8{«fr»} } d»cos» left («180″° right )= — F rSub { size 8{«fr»} } d} {} # » «= — левый (5 «.» «00 N» правый ) левый (0 «.» «800»» м» правый ) {} # ital » «= — 4 «.» «00»Дж».». {} } } {}

Таким образом, количество работы, выполненной силой тяжести, нормальной силой, приложенной силой и трением, составляет соответственно

7,19 Wgr=0,WN=0,Wapp=96,0 Дж, Wfr = -4,00 J.Wgr = 0, WN = 0, Wapp = 96,0 Дж, Wfr = -4,00 J.alignl { stack { size 12 {W rSub { size 8 {«gr»}} = 0,} {} # W rSub { size 8{N} } =0, {} # W rSub { size 8{«app»} } =»96″ «.» 0″ J,» {} # W rSub { size 8{«fr»} } = — 4 «.» «00» «Дж» «.» {} } } {}

Тогда общая работа, выполненная как сумма работы, выполненной каждой силой, будет равна

7,20 Wtotal=Wgr+WN+Wapp+Wfr=92,0 J. Wtotal=Wgr+WN+Wapp +Wfr=92,0 Дж. размер 12{W rSub {размер 8{«всего»}} =W rSub {размер 8{«gr»}} +W rSub {размер 8{N}} +W rSub {размер 8{» приложение»} } +W rSub {размер 8{«fr»} } =»92″ «.»0″ J»} {}

Обсуждение для (b)

Рассчитанная общая работа WtotalWtotal size 12{W rSub { size 8{«total»} } } {} как сумма работа каждой силы согласуется с работой, как и ожидалось, WnetWnet size 12{W rSub { size 8{«net»} } } {}, совершаемой суммарной силой. Работа, совершаемая совокупностью сил, действующих на объект, может быть рассчитано с использованием любого подхода

Пример 7.4 Определение скорости по работе и энергии

Найдите скорость пакета на рисунке 7.4 в конце толчка, используя понятия работы и энергии

Стратегия

Здесь можно использовать теорему о работе-энергии, поскольку мы только что рассчитали чистую работу, WnetWnet size 12{W rSub { size 8{«net»} } } {} и начальную кинетическую энергию, 12mv0212mv02 размер 12{ { {1} более {2} } ital «mv» rSub { размер 8{0} rSup { размер 8{2} } } } {}. Эти вычисления позволяют нам найти конечную кинетическую энергию, 12mv212mv2 размер 12{ { {1} над {2} } ital «mv» rSup { размер 8{2} } } {}, и, таким образом, конечную скорость vv размер 12{v } {}.

Решение

Теорема о работе-энергии в виде уравнения:

7.21 Wnet=12mv2−12mv02.Wnet=12mv2−12mv02. size 12{W rSub { size 8{«net»} } = {{1} over {2} } ital «mv» rSup { size 8{2} } — {{1} over {2} } ital «mv» rSub { размер 8{0} rSup { размер 8{2} } } «.» } {}

Решение для 12mv212mv2 размером 12{ { {1} over {2} } ital «mv» rSup { size 8{2} } } {} дает

7.22 12mv2=Wnet+12mv02.12mv2=Wnet+12mv02 . size 12{ { {1} over {2} } ital «mv»»» lSup { size 8{2} } =w rSub { size 8{ ital «net»} } + { {1} over {2} } ital «mv»»» lSub { размер 8{0} } «» lSup { размер 8{2} } «.» } {}

Таким образом,

7,23 12mv2=92,0 Дж+3,75 Дж=95,75 Дж.12mv2=92,0 Дж+3,75 Дж=95,75 Дж. размер 12{ { {1} над {2} } ital «mv» rSup { размер 8{ 2} } =»92″ «.» 0’J+3 «. » «75»‘J=»95″ «.» «75»‘J} {}

Решение конечной скорости по запросу и ввод известных значений дает

7,24 v=2(95,75 Дж)m=191,5 кг⋅м2/с230,0 кг=2,53 м/с.v=2 (95,75 Дж)м=191,5 кг⋅м2/с230,0 кг=2,53 м/с.

Обсуждение

Используя работу и энергию, мы не только приходим к ответу, но и видим, что конечная кинетическая энергия является суммой начальной кинетической энергии плюс чистая работа, выполненная на упаковке. Это означает, что работа действительно добавляет энергии упаковке.

Пример 7.5. Работа и энергия также могут показать расстояние

Как далеко уйдет пакет на рис. 7.4 после толчка, если предположить, что трение остается постоянным? Используйте соображения работы и энергии.

Стратегия

Мы знаем, что как только человек перестанет толкать, трение остановит упаковку. С точки зрения энергии трение совершает отрицательную работу до тех пор, пока оно не уберет всю кинетическую энергию упаковки. Работа, совершаемая трением, равна произведению силы трения на пройденное расстояние, умноженному на косинус угла между силой трения и перемещением; следовательно, это дает нам способ найти расстояние, пройденное после того, как человек перестанет толкать.

Решение

Нормальная сила и сила тяжести сокращаются при расчете результирующей силы. Тогда сила горизонтального трения является чистой силой, и она действует противоположно смещению, поэтому θ=180ºθ=180º. Чтобы уменьшить кинетическую энергию пакета до нуля, работа трения WfrWfr должна быть равна минус кинетическая энергия, с которой пакет стартовал, плюс то, что пакет накопил за счет толкания. Таким образом, Wfr=-95,75 JWfr=-95,75 Дж. Кроме того, Wfr=fd’cosθ= -fd’Wfr=fd’cosθ= -fd’, где d’d’ — расстояние, необходимое для остановки. Таким образом,

7,25 d′=−Wfrf=−−95,75 J5,00 N,d′=−Wfrf=−−95,75 J5,00 N, размер 12{ { {d}} sup { ‘ }= — { {W rSub { size 8{«fr»} } } over {f} } = — { { — «95» «.» «75»‘J} более {5 «. » «00 N»} } } {}

и т. д.

7,26 d′=19,2 м.d′=19,2 м. размер 12{ { {d}} суп { ‘ }=»19″ «.» 2″ м»} {}

Обсуждение

Это решение представляет собой разумное расстояние для перемещения упаковки на конвейерной системе с относительно низким трением. Обратите внимание, что работа, совершаемая трением, отрицательна — сила действует в направлении, противоположном движению, — поэтому она удаляет кинетическую энергию.

Некоторые примеры в этом разделе можно решить без учета энергии, но за счет упущенной возможности получить представление о том, какую работу и энергию выполняют в этой ситуации. В целом решения, связанные с энергией, обычно короче и проще, чем решения, использующие только кинематику и динамику.

Работа

Работа

Работа, совершаемая постоянной силой

Предположим, вы поднимаете предмет массой 20 кг с земли на высоту. 1,5 м. Предположим, что вы прилагаете постоянную силу в восходящем направлении. направление и что вы перемещаете объект вверх с постоянной скоростью. результирующая сила, действующая на объект, равна нулю. Сила, которую вы прилагаете, равна по величине и противоположно по направлению силе тяжести. Пока вы поднимаетесь объект, над которым вы работаете.

Работа Вт, совершаемая над объектом постоянной силой, определяется как W = Ф · д . Он равен величине силы, умноженной на расстояние до объекта. движется в направлении действия силы.
В приведенном выше примере F = мг = (20 кг) (9,8 м/с ² ) = 196 Н, W = (196 Н)(1,5 м) = 294 Нм.

Работа — это скаляр, число с единицами измерения. Единица работы СИ Нм = Джоуль (Дж).

---

Работа » скалярное произведение » или « скалярное произведение » силы и вектора смещения. Скалярное произведение двух векторов A и B — скалярная величина (число с единицами), равная произведение величин двух векторов и косинуса наименьшего угол между ними.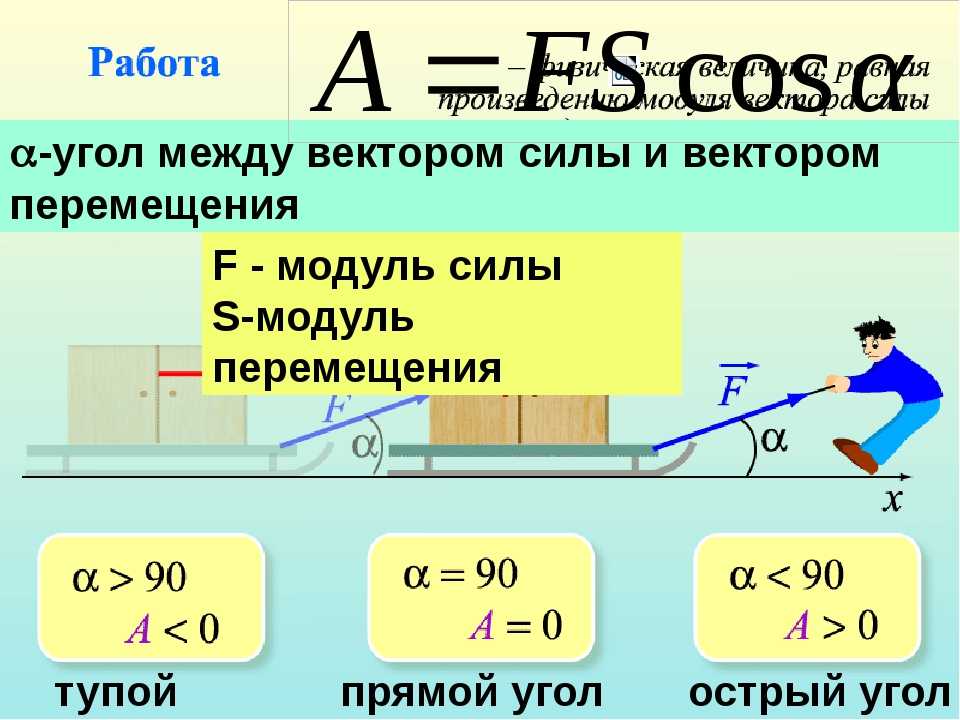

А · В = ABcosθ.

В терминах декартовых компонент векторов A и Б скалярное произведение записывается как

А · В = А _х В _х + А _у В _у + А _z Б _z .

Работа силы может быть положительной или отрицательной. Если составляющая силы в направление перемещения положительное, то работа положительна, а если составляющая силы в направлении перемещения отрицательна, то произведение отрицательное. В одном измерении скалярное произведение положительно, если два вектора параллельны друг другу, и отрицательно, если два вектора антипараллельны друг к другу, т. е. если они направлены в противоположные стороны.

Пример:

Предположим, вы забыли установить парковочный тормоз, и ваша машина начала катиться. вниз по холму. Вы тщетно пытаетесь остановить его, дергая изо всех сил. бампер, но машина продолжает двигаться вперед.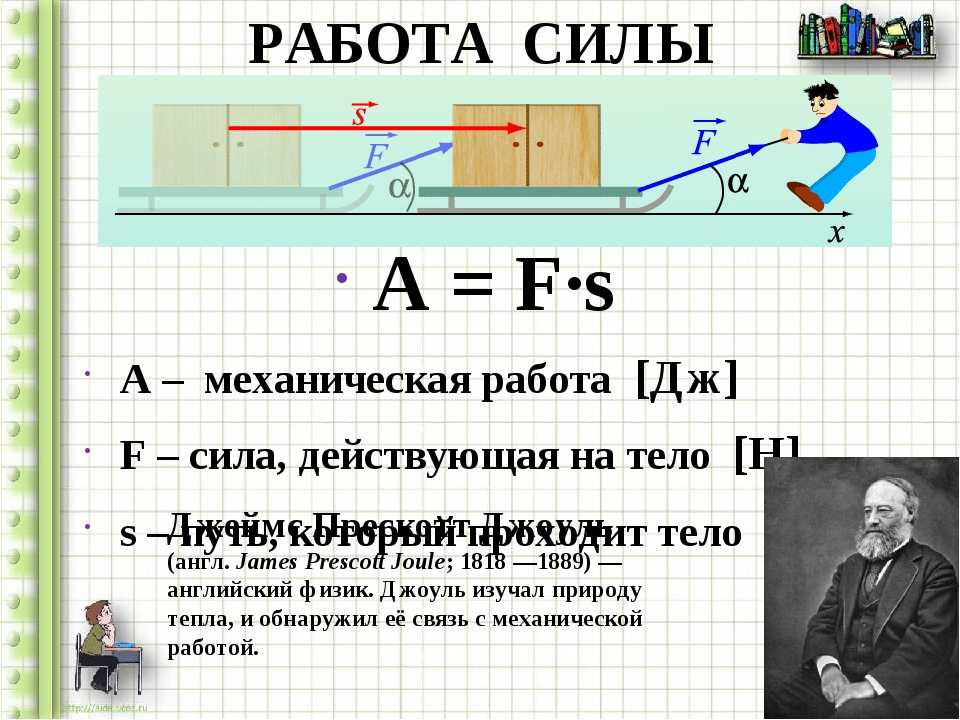 Вы прилагаете силу к автомобиль против направления движения. Расстояние, пройденное в направление силы отрицательное, вы совершаете с автомобилем отрицательную работу. Но автомобиль тянет вас по ходу движения с силой, равной величины (третий закон Ньютона). Машина производит на вас положительное впечатление.

---

Схема свободного тела объекта, поднимаемого с постоянная скорость на расстоянии d показано справа.
Суммарная сила, действующая на объект, равна нулю, F _a + F _г = 0,
Вектор смещения направлен вверх.
Работа, совершенная приложенной силой F _a , W = F _a · d = F _a д = мгд , положительный.
Работа силы тяжести F _g , W = F _г ·d = -F _г d = -mgd , отрицательно.
Суммарная работа всех сил, действующих на объект, W _net = F _net · d равна нулю.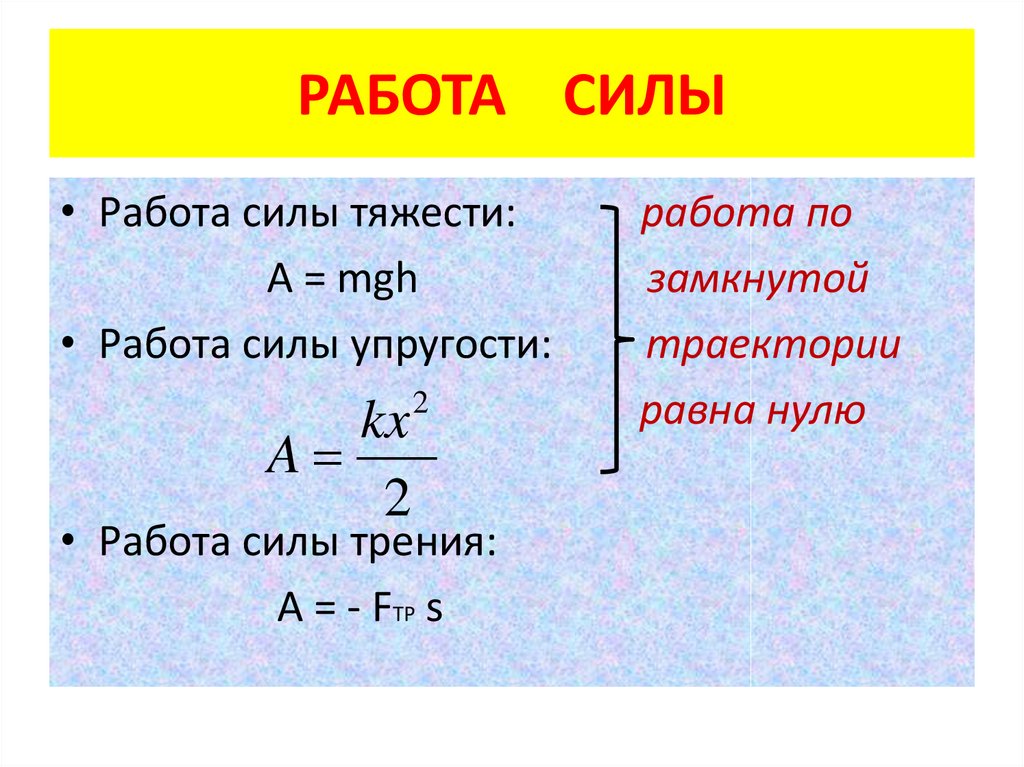

Проблема:

Для А = 3 i + дж — к , Б = — я + 2 я + 5 к , и С = 2 j — 3 k , найти С ·( А — В ).

Решение:

• Обоснование:
  Оцените скалярное произведение двух векторов.
• Детали расчета:
  A = 3 i + j — k . B = — i + 2 j + 5 k . А — В = 4 я — j — 6 k . С = 2 j — 3 k . С ·( А — В ) = -2 + 18 = 16.

Проблема:

Объясните, почему работа силы трения скольжения отрицательна. когда объект испытывает смещение на шероховатой поверхности?

Решение:

• Обоснование:
  Сила трения скольжения всегда направлена ​​в сторону, противоположную скорости v = d r /dt. Поэтому он указывает в направлении, противоположном направлению рабочий объем d r . dW = F _f · d r = -F _f др.

Проблема:

При движении частицы по окружности на нее действует сила, направленная центр вращения. Почему эта сила не действует на частицу?

Решение:

• Обоснование:
  Так как в любой точке окружности центростремительная сила перпендикулярна скорости v и, следовательно, к смещению d r скалярное произведение dW = F· d r это ноль.

Проблема:

Во время стрижки газона мальчик толкает газонокосилку на расстояние 350 м. траву с силой 90 Н, направленной по горизонтали. Какую работу выполнил мальчик?

Решение:

• Обоснование:
  Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = Fdcosθ.
  Здесь F и d указывают в одном направлении, θ = 0, cosθ = 1,
• Детали расчета:
  Вт = F · d = 90 Н * 350 м = 31500 Дж.

Проблема:

Покупатель в супермаркете толкает тележку с силой 35 Н. направлена ​​под углом 25 ^o вниз от горизонтали. Найдите работу, выполненную покупателем, когда он проходит по проходу длиной 50 м. длина.

Решение:

• Обоснование:
  Работа, совершаемая над объектом постоянной силой, определяется как W = F · d = F _x ∆x _{+ F y ∆y + F z ∆z.
  Тележка движется в направлении x, ∆y = ∆z = 0,
  X-компонента сила F x = Fcosθ = (35 Н)cos(25 ^o ).
  Работает только х-компонента силы, так как нет смещение тележки в направлении Y.}
• Детали расчета:
  Работа, совершаемая покупателем, равна W = F _x ∆x = (35 Н)cos(25 ^o )(50 м) = 1586 Дж.

---

Рампы

Предположим, вы хотите поднять свой мотоцикл на свой пикап. Вероятно, вы будете использовать рампу. Вы выберете длинная доска. Один конец доски будет опираться на кузов грузовика, а другой конец будет лежать на земле. Вы закатите свой мотоцикл эта рампа.

Вы прикладываете силу F _a , равную по величине и противоположное по направлению компоненту гравитационной силы параллельно рампе. Звездная величина F _a равна mgsinθ. Ты переместите мотоцикл на расстояние h/sinθ в направлении действия силы. Работа, которую вы совершаете, равна W = F·d = mgh, где mg — вес вашего мотоцикл и h высота кровати. Если бы вы подняли мотоцикл прямо, вы бы приложили силу, равную его весу. через расстояние ч. Когда вы катите его по рампе, вы должны нажать на это через гораздо большее расстояние. Чтобы выполнить ту же работу, вы, следовательно, нужна гораздо меньшая сила. Рампа обеспечивает механическое преимущество .

Работа = большая сила × малое расстояние = малая сила × большое расстояние .

---

Работа переменной силы в одном измерении

Если вы не знакомы с интегралами, пожалуйста, перейдите по этой ссылке, прежде чем продолжить.

Краткий обзор определенных интегралов

Работа, совершаемая переменной силой F только с x-компонентой определяется как
W = ∫ _xi ^xf F(x)dx = lim _∆x—>0 Σ _xi ^xf Ф(х)∆х.
(Символ Σ обозначает сумму. Σ _xi ^xf F∆x представляет собой сумму произведений F∆x из от начальной до конечной позиции с шагом ∆x.) 
Мы можем построить составляющую силы F воздействуя на объект в положении x по сравнению с положением x.
Работа силы равна площади под кривой.

График для постоянной силы, действующей от x _i до x _f показано справа.
Работа силы W = F(x _f — x _i ).

Работа, совершаемая переменной силой в трех измерениях

В трех измерениях работа, совершаемая переменной силой, равна W = ∫ _{r i} ^{r f} F ·dr = lim _{∆ r —>0} Σ _{r i} ^{r f} F ·∆ r .
Здесь d r — бесконечно малый отрезок пути от начального в конечное положение. По компонентам F и d r Интеграл может быть написан как
∫ _Путь ^{F · D R = ∫ _PATH F _X DX + ∫ _PATH 275 F _{F F F F F DX .0275 путь F z dz.}}

---

Подъем объекта вблизи поверхности Земли

Чтобы поднять предмет массой m так, чтобы его высота увеличилась на расстояние h, вы должны приложить среднюю силу mg на расстоянии h.
Работа, которую нужно выполнить, чтобы поднять предмет, равна W = mgh.

Проблема:

Ящик на 100 Н стоит на земле и крепится к одному концу веревки. Человек на балконе тянет веревку с постоянной силой 100 Н, подъем ящика на расстояние 3 м.
а) Какой объем работы выполняет человек?
б) Какую работу совершает сила тяжести?

Решение:

• Обоснование:
  Человек подтягивается, и ящик движется вверх в направлении действия силы.
  Работа, совершаемая человеком, положительна, W = Fd = mgd = (100 Н)d.
  Сила тяжести 100 Н направлена ​​вниз, в то время как ящик движется вверх. Гравитация совершает отрицательную работу.
• Детали расчета:
  (a) Работа, выполненная человеком, равна W = (100 Н) * (3 м) = 300 Дж.
  (б) Гравитация совершает 300 Дж отрицательной работы.

Проблема:

(a) Рассчитайте работу, выполненную на кабине лифта массой 1500 кг его трос, чтобы поднять его на 40 м с постоянной скоростью, при условии, что сила трения усредняется 100 Н.
б) Какую работу совершает над кабиной лифта гравитационная сила в этом процессе?

Решение:

• Рассуждение:
  Кабина лифта весит 1500*9,8 Н = 14700 Н. Чтобы заставить кабину двигаться со постоянной скорости, результирующая сила, действующая на него, должна быть равна нулю. Сила кабеля воздействующая на автомобиль должна иметь величину 14800 Н, чтобы компенсировать вес и сила трения 100 Н направлена ​​в противоположном направлении.