Работа силы Лоренца
М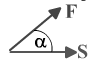 еханическая
работа А равна скалярному произведению
силы на перемещение, которое произошло
под действием этой силы:
еханическая
работа А равна скалярному произведению
силы на перемещение, которое произошло
под действием этой силы:
А = (FS) = FScosα
где α -угол между направлением силы и перемещения.
Е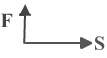 сли
этот угол равен 900, работа
силы равна нулю.
сли
этот угол равен 900, работа
силы равна нулю.
Поэтому полная работа силы Лоренца всегда равна нулю
Движение заряженной частицы в магнитном поле
Введение
Виды движения материальной точки:
равномерное прямолинейное, а=0, F=0
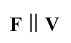
равноускоренное, a=const,
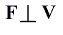
равномерное движение по окружности,
Рассмотрим различные случаи движения заряженной частицы в магнитном поле
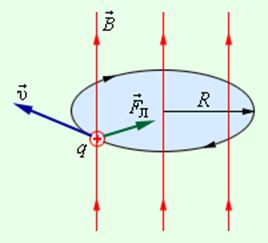
Частица влетает в магнитное поле перпендикулярно силовым линиям.
Определить направление силы Лоренца и нарисовать траекторию движения частицы.
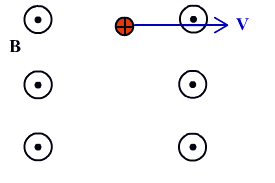
Сила, действующая на частицу, перпендикулярна скорости, поэтому траектория движения частицы
– окружность.
Определим радиус траектории частицы
По второму закону Ньютона F = ma
равнодействующая сила — сила Лоренца,
угол α равен 90 0F = BqVsinα = BqV
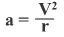
центростремительное ускорение
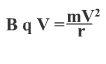
Подставляя F и а в уравнение 2го закона Ньютона, получаем
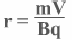
откуда для радиуса:
размерность радиуса – метр
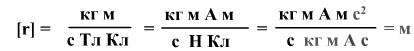
Задача: в камере Вильсона получены треки α-частицы и протона. Радиусы траекторий частиц одинаковы. Сравнить скорости движения частиц.
Пояснение: α- частица – это ядро гелия. В ее состав входит 2 протона и 2 нейтрона. Поэтому заряд α – частицы в 2 раза больше заряда протона, а масса – в 4 раза.
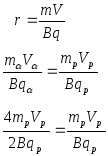
Дано
mα = 4 mp
qα = 2 qp
Rα = Rp
Vα/Vp — ?

Ответ: Vp=2Vα
Период обращения частицы в магнитном поле
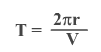
Период обращения частицы по окружности определяется формулой (1)
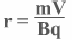
радиус окружности найден (2)
п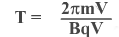
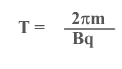
откуда
Размерность периода
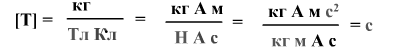
Вопрос: Как зависит период обращения частицы в магнитном поле от ее скорости?
Ответ: Период обращения частицы в магнитном поле не зависит от ее скорости
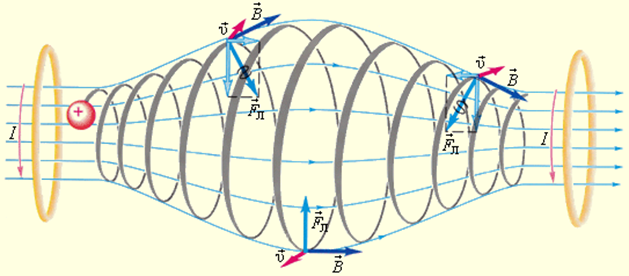
Частица влетает в магнитное поле под углом к силовым линиям
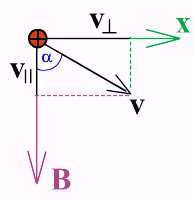
Выберем оси координат как показано на рисунке.
Обозначим на чертеже проекции скорости частицы на направление магнитной индукции и на ось Х
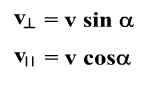
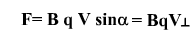
Сила Лоренца
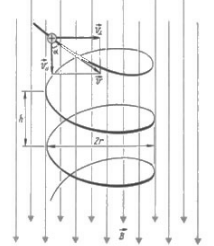
направлена перпендикулярно чертежу, от нас
радиус витка спирали
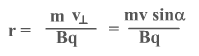
Частица влетает в магнитное поле параллельно силовым линиям
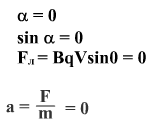
равнодействующая сил, приложенных к частице, равна нулю => движение равномерное прямолинейное, траектория движения частицы – прямая линия.
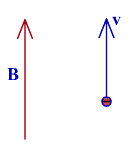
Вопрос А. Первоначально неподвижный электрон помещен в магнитное поле с индукцией В. Описать движение электрона. Пояснить ответ
Электрон будет оставаться в покое, потому что магнитное поле на покоющийся заряд не действует
Вопрос В. Частица движется в перекрывающихся магнитном и электрическом полях. Может ли ее движение быть равномерным прямолинейным?
Может, если векторная сумма силы Лоренца и электрической силы равна нулю. Это возможно, если поля перпендикулярны друг другу (см чертеж)
Р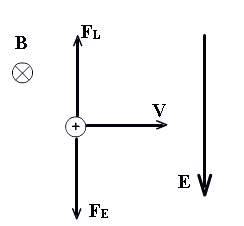
Движение частицы будет равномерным
прямолинейным, если действующие на нее силы
уравновешены. Это может произойти, например,
при таком расположении полей.
Условие равновесия: FL = FE; BqV = Eq; V = B/E
44. Действие магнитного поля на движущийся заряд. Сила Лоренца.
Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой F=
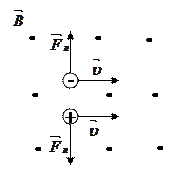
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
М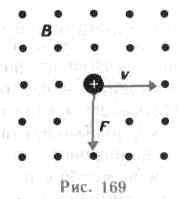
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F=QE + Q[vB]. Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
45. Движение заряженных частиц в магнитном поле. Ускорители элементарных частиц.
Н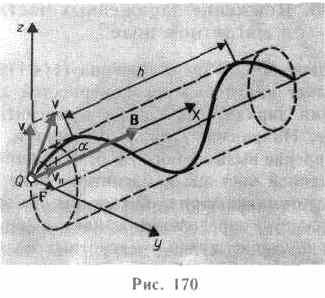 аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или . Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная
частица движется в магнитном поле со
скоростью v,
перпендикулярной вектору В, то сила
Лоренца F=Q[vB]
постоянна по модулю и нормальна к
траектории частицы. Согласно второму
закону Ньютона, эта сила создает
центростремительное ускорение. Отсюда
следует, что частица будет двигаться
по окружности, радиус r которой
определяется из условия QvB = mv2/r, откуда  Период
вращения частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот,
Период
вращения частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот, 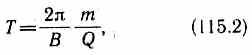 т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
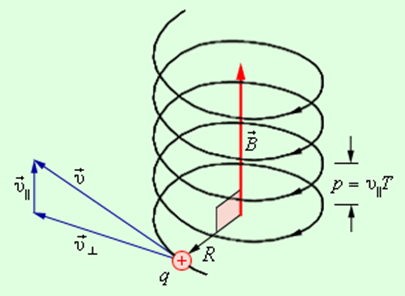
Если скорость v
заряженной частицы направлена под углом
а к вектору В (рис. 170), то ее движение
можно представить в виде суперпозиции:
1) равномерного прямолинейного
движения вдоль поля со скоростью
v||=vcos;
2) равномерного движения со скоростью
v┴= vsin
по окружности в плоскости, перпендикулярной
полю. В результате сложения обоих
движений возникает движение по спирали,
ось которой параллельна магнитному
полю. Шаг винтовой линии h=v||T=vTcos.
Радиус окружности определяется формулой  (в данном случае надо заменитьv на v┴=vsin).
(в данном случае надо заменитьv на v┴=vsin).
Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т.д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружности или спирали.
Рассмотрим некоторые типы ускорителей заряженных частиц.
1. Линейный ускоритель. Ускорение частиц осуществляется электростатическим полем, создаваемым, например, высоковольтным генератором Ван-де-Граафа. Заряженная частица проходит поле однократно: заряд Q, проходя разность потенциалов 1-2, приобретает энергию W=Q(1-2). Таким способом частицы ускоряются до 10 МэВ. Их дальнейшее ускорение с помощью источников постоянного напряжения невозможно из-за утечки зарядов, пробоев и т. д.
2. Линейный резонансный ускоритель. Ускорение заряженных частиц осуществляется переменным электрическим полем сверхвысокой частоты, синхронно изменяющимся с движением частиц. Таким способом протоны ускоряются до энергий порядка десятков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.
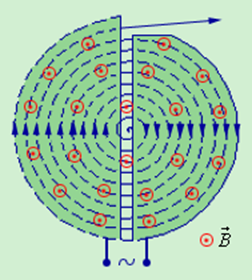
3. Циклотрон —
циклический резонансный ускоритель
тяжелых частиц (протонов, ионов).
Между полюсами 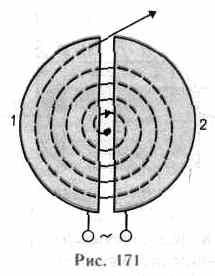 сильного
электромагнита помещается вакуумная
камера, в которой находятся два электрода
(1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
сильного
электромагнита помещается вакуумная
камера, в которой находятся два электрода
(1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.
Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма (условие «резонанса») — периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.
Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при E=0,5 МэВ m = 2m0, при E=10 МэВ m=28m0!).
4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, -частиц), в котором управляющее магнитное поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).
5. Синхротрон — циклический резонансный ускоритель ультрарелятивистских электронов, в котором управляющее магнитное поле изменяется во времени, а частота ускоряющего электрического поля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.
6. Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных частиц (протонов, ионов), в котором объединяются свойства фазотрона и синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одновременно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
7. Бетатрон — циклический индукционный ускоритель электронов, в котором ускорение осуществляется вихревым электрическим полем (см. §137), индуцируемым переменным магнитным полем, удерживающим электроны на круговой орбите. В бетатроне в отличие от рассмотренных выше ускорителей не существует проблемы синхронизации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W> 100 МэВ режим ускорения в бетатроне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20—50 МэВ.
Сила Лоренца
Цели:
- Учебные: ввести формулу силы Лоренца и формировать общеучебные навыки работы с компьютером и исследовательских умений;
- Развивающие: развитие логического мышления учащихся, по формированию умения строить индуктивные выводы;
- Воспитательные: формировать познавательный интерес; положительной мотивации к учению; дисциплинированности эстетического восприятия мира.
Организационные формы и методы обучения:
- традиционные – беседа на вводном этапе урока;
- инновационные – изучение нового учебного материала с помощью компьютера.
Средства обучения:
- инновационные – компьютеры, сетевая версия программы «Открытая физика 2.5»;
- печатные – лабораторные листы для компьютерного эксперимента.
План урока:
- Актуализация знаний и мотивация;
- Изучение новой темы на компьютере;
- Компьютерный эксперимент;
- Просмотр задач с готовыми решениями;
- Подведение итогов;
- Домашнее задание.
Ход урока
1. Актуализация знаний и мотивация.
Сообщение новой темы урока и беседа о возможностях программы «Открытая физика».
2. Изучение новой темы на компьютере.
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B, может быть выражена через силы, действующие на отдельные носители заряда.
F = IBΔl sin α
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику: I = qnυS.
Выражение для силы Ампера можно записать в виде:
F = qnSΔlυB sin α.
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
FЛ = qυB sin α.
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции.
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов υ, B и F для положительно заряженной частицы показано на рис.1
Рисунок 1
Сила Лоренца направлена перпендикулярно векторам υ и B
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость υ лежит в плоскости, перпендикулярной вектору B то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 2).
Рисунок 2.
Период обращения частицы в однородном магнитном поле равен
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 3.
Рисунок 3.
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
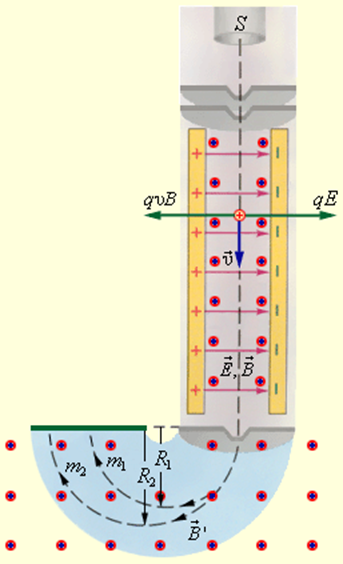
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость υ заряженных частиц направлена перпендикулярно векторам E и B.
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E /B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле B. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
3. Компьютерный эксперимент
Модель 1. Движение заряда в магнитном поле
На заряженную частицу с зарядом q, движущуюся со скоростью υ в магнитном поле с индукцией B, действует сила Лоренца:
FЛ = qυB sin α ,
где α – угол между векторами υ и B. Сила Лоренца работы не совершает, так как всегда направлена перпендикулярно скорости заряженной частицы. Если вектор скорости υ частицы в однородном магнитном поле B направлен перпендикулярно вектору магнитной индукции B то частица будет равномерно двигаться по окружности радиуса
R = mυ / qB.
Если скорость частицы имеет составляющую, параллельную вектору B то частица будет двигаться по спирали.
Компьютерная модель иллюстрирует движение заряженной частицы в однородном магнитном поле. Можно изменять значения составляющих скорости частицы и индукцию магнитного поля. Программа позволяет вычислить радиус траектории и время одного цикла. Обратите внимание, что сила Лоренца, действующая на движущуюся заряженную частицу, всегда перпендикулярна ее скорости.
Компьютерная лабораторная работа: Движение заряда в магнитном поле.
Вариант 1.
Класс _______________ Фамилия _______________ Имя _______________
Практические задания и вопросы
- Откройте в программе «Открытая Физика 2.5» в разделе «Электричество и магнетизм» компьютерную модель «Движение заряда в магнитном поле а».
- Выполните компьютерный эксперимент (задача 1)
- Запишите ответ 1-ой задачи B = ______
- Выполните компьютерный эксперимент (задача 2)
- Запишите ответ 2-ой задачи R = ______
- Выполните компьютерный эксперимент (задача 3)
- Запишите ответ 3-ей задачи R = ______, t = ______
- Выполните компьютерный эксперимент (задача 4)
- Запишите ответ 4-ой задачи R = ______
4. Просмотр задач с готовыми решениями.
В камере лабораторной установки создано магнитное поле, вектор магнитной индукции B которого направлен вертикально вверх и равен по модулю B = 1,2 мТл. В камеру влетает протон с кинетической энергией K = 5,3 МэВ. Вектор скорости протона направлен горизонтально. Определите ускорение a, с которым будет двигаться протон в камере, а также радиус R кривизны траектории. Масса протона mp = 1,67·10–27 кг.
Решение:
Сила Лоренца, действующая на движущуюся в магнитном поле заряженную частицу, зависит от ее скорости, которая может быть выражена через кинетическую энергию частицы
Протон движется с огромной скоростью. Однако эта скорость все же значительно меньше скорости света c = 3·108 м/с. Поэтому движение протона можно рассматривать на основе законов классической механики.
Сила Лоренца FЛ направлена перпендикулярно скорости частицы
FЛ = qυB sin α,
где q – заряд протона, равный элементарному заряду e = 1,602·10–19 Кл, α – угол между направлениями векторов υ и B. В условиях данной задачи α = 90°, sin α = 1. Сила Лоренца создает центростремительное ускорение a:
Под действием силы Лоренца протон будет двигаться в однородном магнитном поле по дуге окружности, радиус R которой находится из условия
Таким образом, в условиях лабораторного опыта отклонение вектора скорости протона от первоначального направления будет весьма малым.
5. Подведение итогов.
Посмотреть компьютерный журнал и выписать оценки учащихся по тестам.
6. Домашнее задание
§ 22, 23 Задачи 1-3 в конце параграфа. (Касьянов)
Сила Лоренца. Движение заряженных частиц в магнитном поле.
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле со скоростью , называется силой Лоренца.
— установлено опытным путем
Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление и для совпадают): если ладонь левой руки расположить так, чтобы вектор входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.
Для отрицательных зарядов берется противоположное направление.
Сила Лоренца всегда направлена перпендикулярно скорости заряда и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью , то результирующая сила
— формула Лоренца.
1. Движение заряженной частицы вдоль силовой линии, .
,
магнитное поле не действует на частицу.
Заряженная частица движется по инерции равномерно прямолинейно.
2. Движение заряженной частицы перпендикулярно силовым линиям, .
Пусть в однородное магнитное поле с индукцией влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью .
В каждой точке поля на частицу действует . Т.к. , то . Ускорение изменяет только направление скорости, , значит, . В этих условиях тело (заряженная частица) движется равномерно по окружности.
Согласно II закону Ньютона:
(1)
Т.к. все величины, входящие в (1), постоянны, радиус кривизны R будет оставаться постоянным. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше , тем меньше R. При , т.е. заряд движется по прямой.
Важным результатом для приложения является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.
если . (2)
Частицы, имеющие бóльшую скорость, движутся по окружности бóльшего радиуса, однако время одного полного оборота будет таким же, что и для более медленных частиц, движущихся по окружности меньшего радиуса. Данный результат положен в основу действия циклических ускорителей элементарных частиц.
3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции. Вектор скорости можно разложить на 2 составляющие:
В направлении сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с . В направлении, перпендикулярном , он движется по окружности со скоростью Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна .
Радиус витка с учетом (1):
(3)
Шаг винтовой линии (расстояние между соседними витками)
с учетом (2):
.
Если движение происходит в неоднородном магнитном поле, индукция которого возрастает в направлении движения частицы, то R уменьшается с ростом В согласно (3). На этом основана фокусировка пучка заряженных частиц в магнитном поле. Таким образом, с помощью неоднородного магнитного поля можно управлять пучками заряженных частиц, собирать их или рассеивать подобно тому, как управляют поведением пучков световых лучей с помощью оптических линз.
Рассмотренный принцип положен в основу действия электронных микроскопов.
Ускорители заряженных частиц.
Свойство независимости периода от скорости обращения используют для того, чтобы превратить траекторию ускоряемой частицы в спираль и уменьшить размеры ускорителя. Такой принцип положен в основу работы циклотрона — родоначальника целого семейства ускорителей с магнитным полем: синхротрона, синхрофазотрона и т.д.
Ускорительная камера циклотрона представляет собой вакуумную цилиндрическую коробку, помещенную между полюсами сильного электромагнита. Камера состоит из двух металлических половинок — дуантов, между которыми создается с помощью генератора переменное электрическое напряжение с амплитудой порядка (поле только в зазоре). Частицы вводятся внутрь камера с помощью специального впускного устройства (А).
При каждом пересечении зазора частица приобретает энергию E1 = qU. За N оборотов E = qUN, Emax~107эВ.
Большая энергия в циклотроне не может быть достигнута: как следует из теории относительности: m = f(V), а при росте массы уменьшается частота обращения.
В синхроциклотронах (фазотронах) медленно уменьшается частота подаваемого напряжения.
Фазотрон — изменяется .
В синхротронах меняется индукция магнитного поля .
Синхротрон — изменяется
В синхрофазотронах — изменяется и B.
E~109 — 1010 эВ.
Ускорители заряженных частиц — устройства, в которых создаются и управляются пучки высокоэнергетических заряженных частиц под действием электрических и магнитных полей.
Принцип автофазировки предложены советским физиком Векслером (1944 г.) и американским Мак-Милланом (1945 г.).
Магнитогидродинамический (МГД) генератор — установка для непосредственного преобразования тепловой энергии в электрическую (создан в 50-х годах).
Это источник тока, принцип действия которого основан на действии магнитного поля на заряженные частицы плазмы электролитов и жидких металлов. Плазма представляет собой поток раскаленного газа, все молекулы которого ионизированы высокой температурой (~2000K).
Поток плазмы, проходя через расширяющееся сопло, ускоряется до 2000-2500 м/с и попадает в сильное магнитное поле, разделяющее положительные и отрицательные заряды, отбрасывая их на электроды. При этом во внешней цепи возникает электрический ток.
т.к. Tпл >>Твн.среды, — велико.
Применение:
в ускорителях;
в НГД — генераторах;
датчиках Холла;
для осуществления управляемых термоядерных реакций;
при регистрации и исследовании заряженных частиц;
в магнетронах.
3.8. Сила лоренца. Движение зарядов в электрических и магнитных полях
Экспериментально
было установлено, что пучок электронов,
испускаемых катодной трубкой, отклоняется
во внешнем магнитном поле. Направление
отклонения перпендикулярно к вектору
индукции 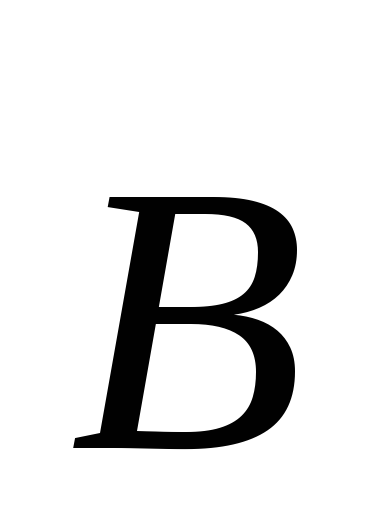 и вектору
и вектору скорости упорядоченного движения
электронов. Таким образом, на заряды,
движущиеся в магнитной поле, действует
сила, направление которой совпадает с
направлением векторного произведения
скорости упорядоченного движения
электронов. Таким образом, на заряды,
движущиеся в магнитной поле, действует
сила, направление которой совпадает с
направлением векторного произведения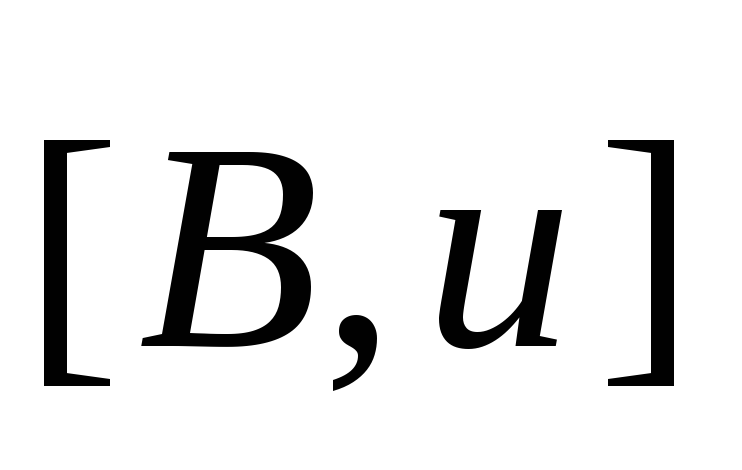 ,
если частицы отрицательно заряженные,
или
,
если частицы отрицательно заряженные,
или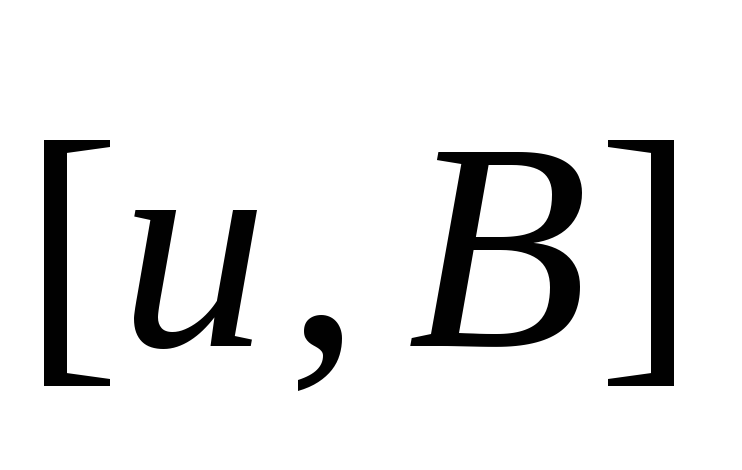 ,
если частицы заряжены положительно.
,
если частицы заряжены положительно.
Определим
силу, действующую на электрический
заряд, движущийся в магнитном поле. По
закону Ампера на элемент 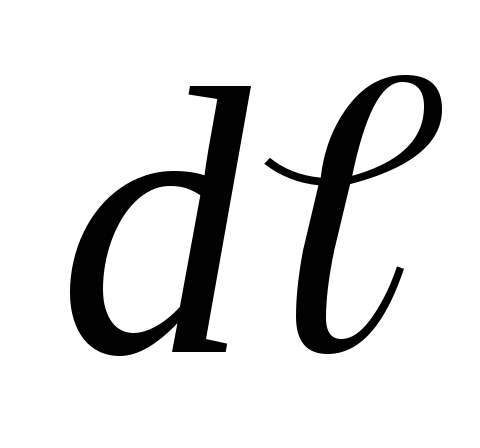 проводника с токомI,
действует сила
проводника с токомI,
действует сила
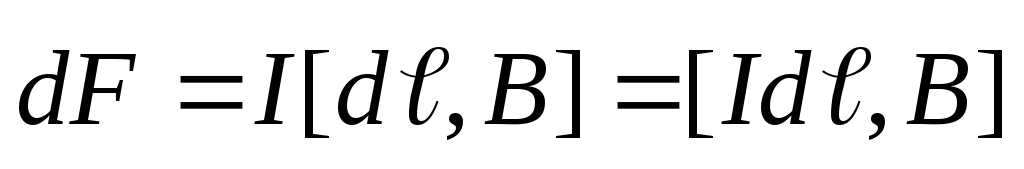 .
.
Ток
в проводнике определяется движением
зарядов, которые движутся со скоростью  :
: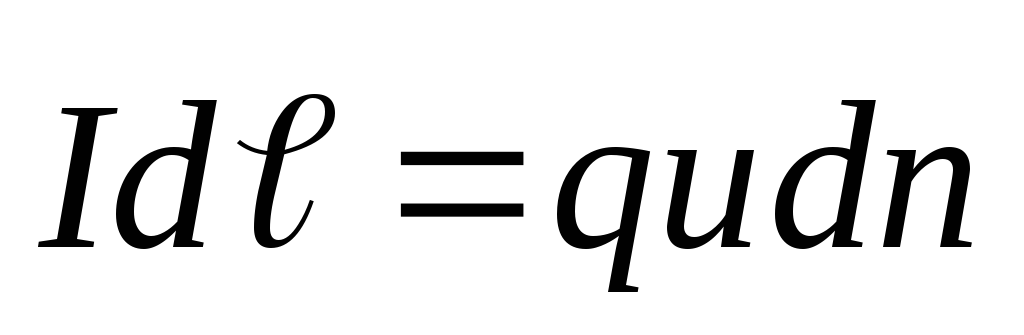 ,
гдеdn — число частиц в
элементе проводника
,
гдеdn — число частиц в
элементе проводника 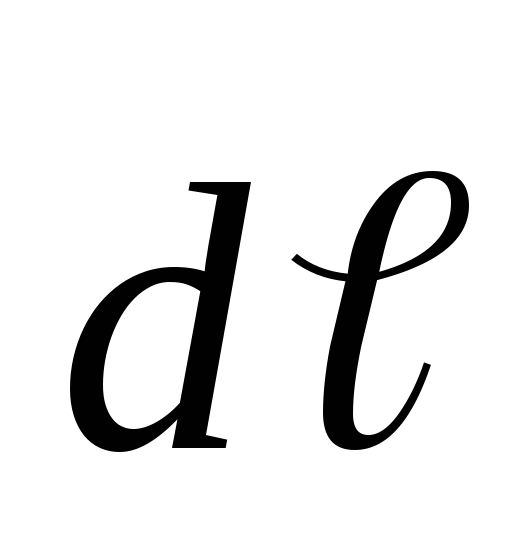 ,
,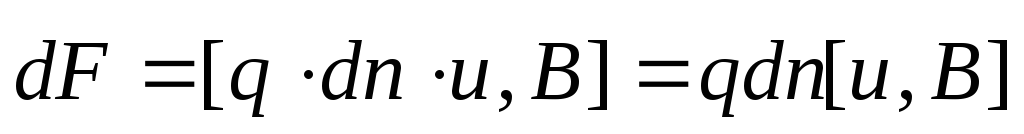 .
.
Определим силу, действующую на один заряд:
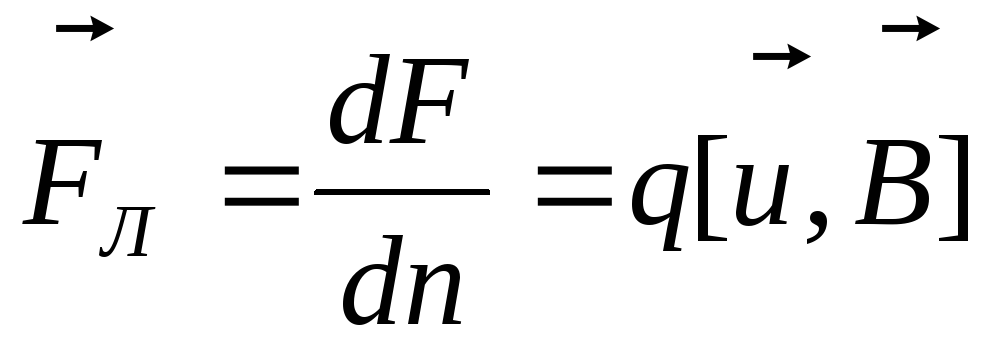 —
—
— это
сила Лоренца. Направление  определяется знаком зарядаq.
Сила Лоренца всегда направлена
перпендикулярно к скорости движения
заряда и играет роль центростремительной
силы. Сила Лоренца не совершает работы.
Она изменяет только направление скорости
движения заряда в магнитном поле.
Абсолютная величина скорости заряда и
его кинетическая энергия при движении
в магнитном поле не изменяется
определяется знаком зарядаq.
Сила Лоренца всегда направлена
перпендикулярно к скорости движения
заряда и играет роль центростремительной
силы. Сила Лоренца не совершает работы.
Она изменяет только направление скорости
движения заряда в магнитном поле.
Абсолютная величина скорости заряда и
его кинетическая энергия при движении
в магнитном поле не изменяется
 .
.
Но неизменность величины скорости и кинетической энергии заряженной частицы имеет место лишь в случае постоянного магнитного поля, не зависящего от времени, т.е. стационарного. Переменное же магнитное поле ускоряет заряженные частицы (т.е. меняет величину и направление скорости).
Рассмотрим движение частицы в однородном магнитном поле. Будем считать, что на частицу не действуют никакие электрические поля.
Пусть частица движется вдоль линий индукции магнитного поля (рис.3. 12), тогда угол
 м
м ежду
векторами
ежду
векторами и
и равен 0 или
равен 0 или ,
, ,
т.е. магнитное поле не действует на
частицу. Она будет двигаться по инерции
– прямолинейно и равномерно.
,
т.е. магнитное поле не действует на
частицу. Она будет двигаться по инерции
– прямолинейно и равномерно.Рассмотрим теперь частицу, которая движется перпендикулярно к линиям магнитной индукции
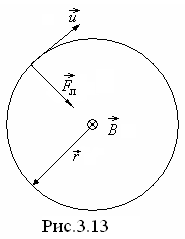
 (рис.3. 13):
(рис.3. 13): и
и  .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
.
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
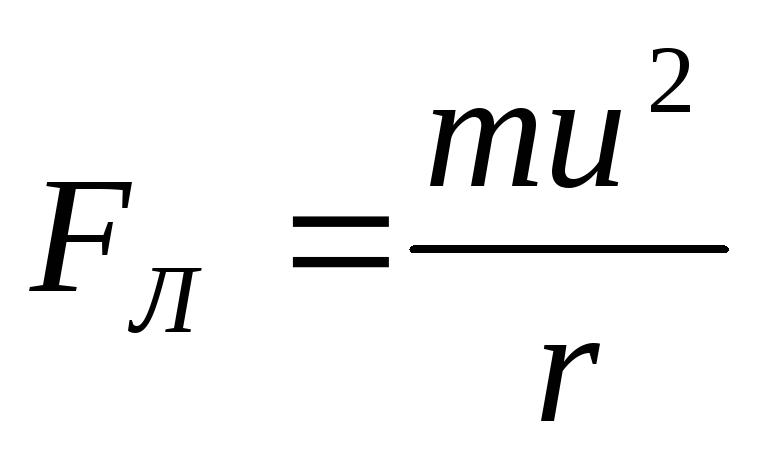 ,
,
где m – масса заряженной частицы, r – радиус кривизны ее траектории. Найдем r:
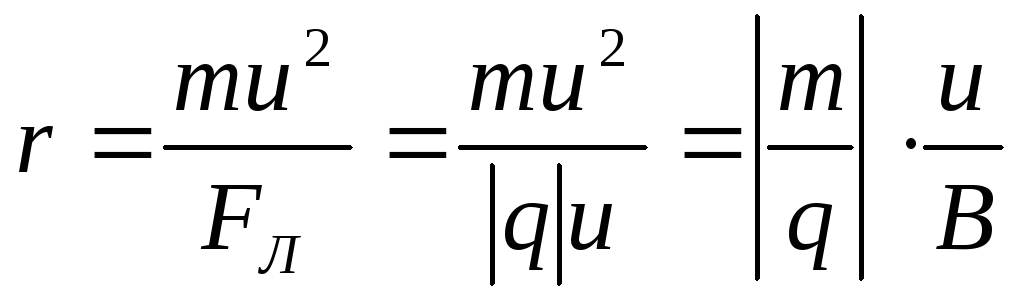 .
.
Скорость
частицы не меняется, индукция 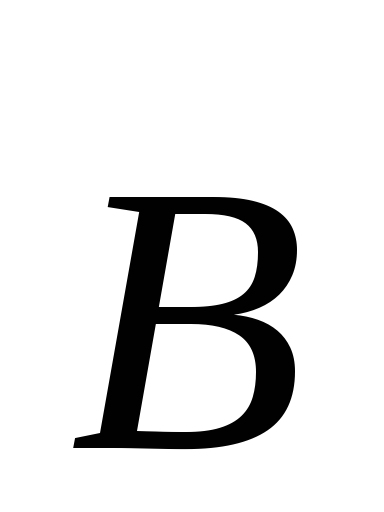 =const,
значит, r=const, и заряженная частица будет двигаться
по окружности, плоскость которой
перпендикулярна к магнитному полю.
=const,
значит, r=const, и заряженная частица будет двигаться
по окружности, плоскость которой
перпендикулярна к магнитному полю.
Направление
силы Лоренца 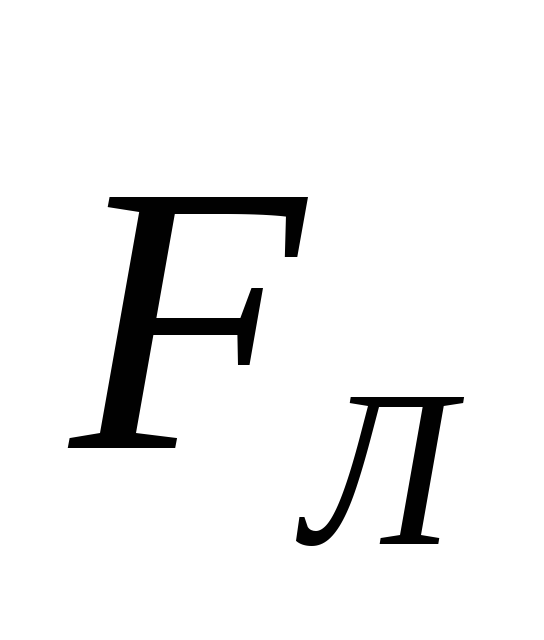 и направление вызываемого ею отклонения
заряженной частицы в магнитном поле
зависит от знака зарядаq.
Поэтому по направлению отклонения можно
судить о знаке заряда.
и направление вызываемого ею отклонения
заряженной частицы в магнитном поле
зависит от знака зарядаq.
Поэтому по направлению отклонения можно
судить о знаке заряда.
Частица движется в магнитном поле по окружности радиуса r равномерно. Период обращения, т.е. время одного полного оборота:
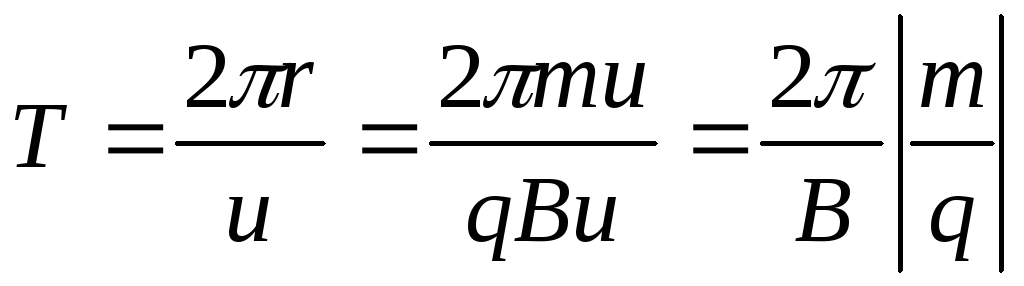
— период обращения частицы не зависит от
ее скорости. Этот период прямо
пропорционален индукции магнитного
поля.
период обращения частицы не зависит от
ее скорости. Этот период прямо
пропорционален индукции магнитного
поля.
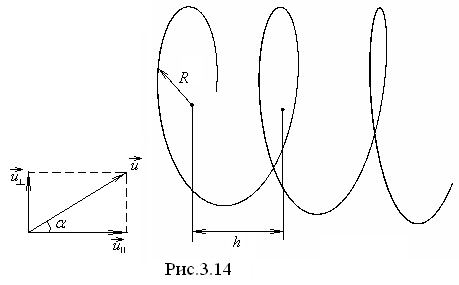
Рассмотрим более общий случай, когда скорость частицы направлена под произвольным острым углом
 к вектору
к вектору (рис.3.14). Разложим вектор
(рис.3.14). Разложим вектор на две составляющие:
на две составляющие:
—
параллельную вектору 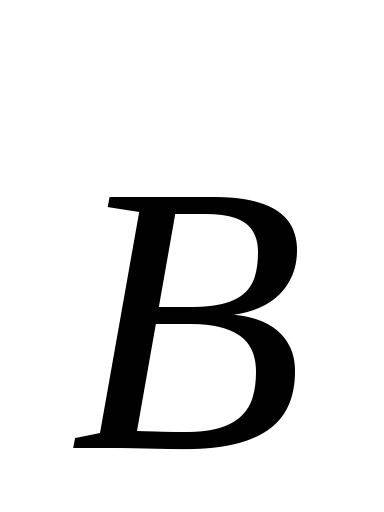 —
— 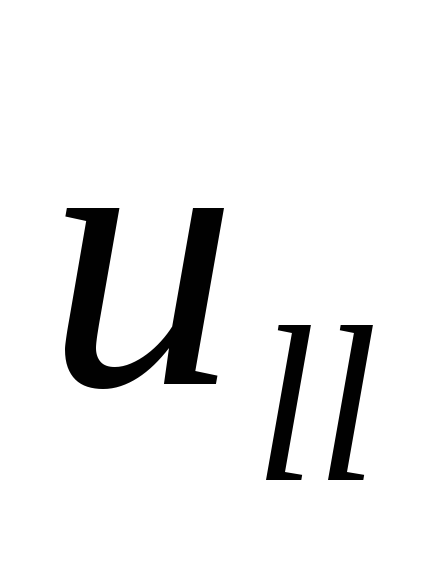 и перпендикулярную к
и перпендикулярную к  —
—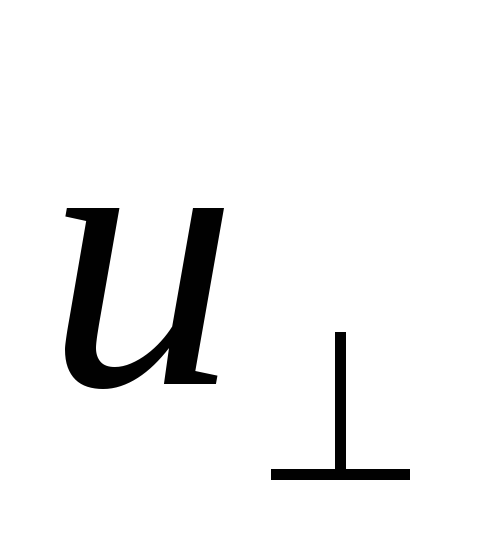 :
:
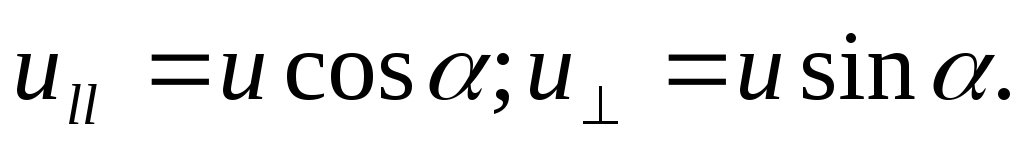 .
.
Скорость 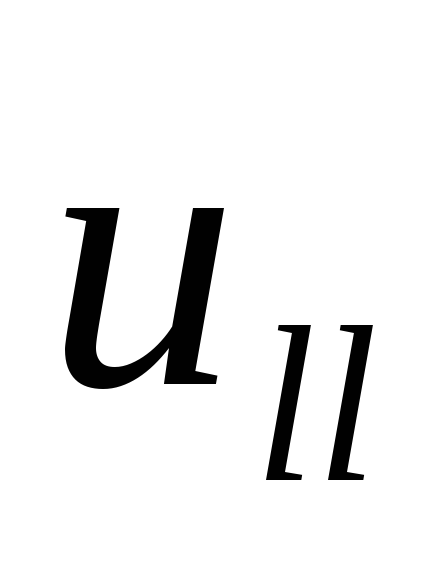 в магнитном поле не меняется, это скорость
поступательного движения частицы.
Благодаря же скорости
в магнитном поле не меняется, это скорость
поступательного движения частицы.
Благодаря же скорости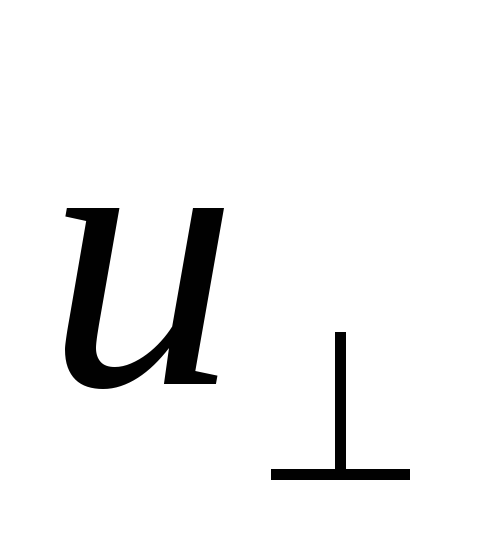 частица движется по окружности в
плоскости, перпендикулярной к
частица движется по окружности в
плоскости, перпендикулярной к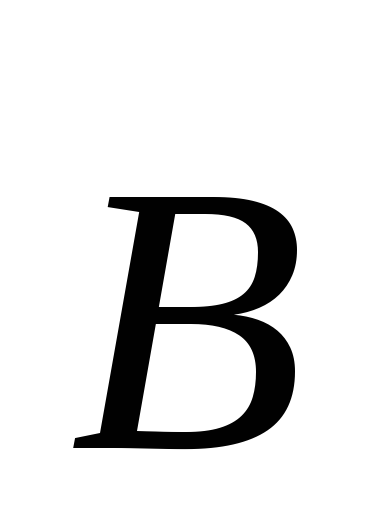 ,
тогда радиус этой окружности:
,
тогда радиус этой окружности:
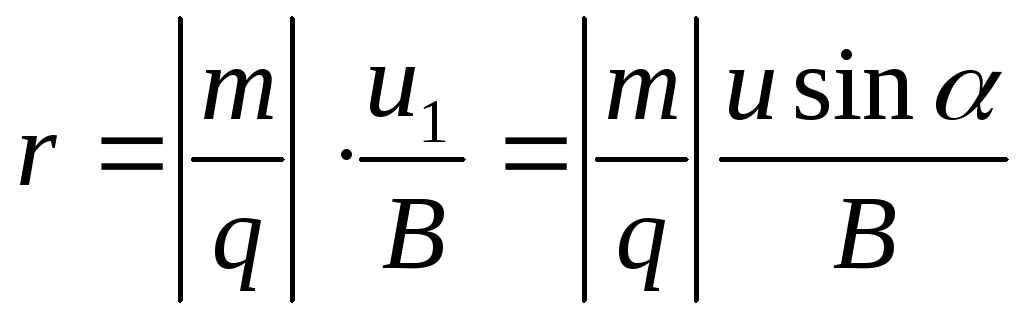 .
.
Таким
образом, частица одновременно совершает
два движения – поступательное со
скоростью 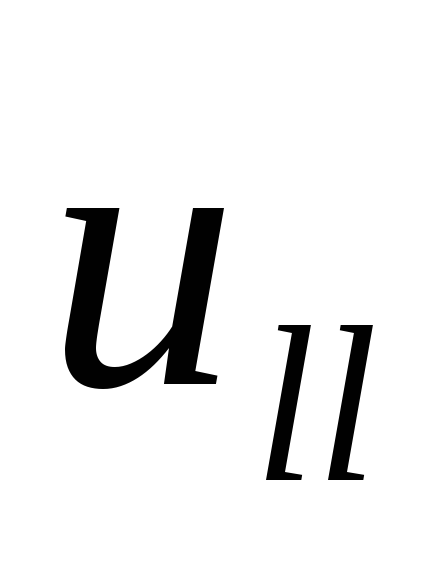 в направлении поля, т.е. перпендикулярном
к скорости вращения, и вращательное
в направлении поля, т.е. перпендикулярном
к скорости вращения, и вращательное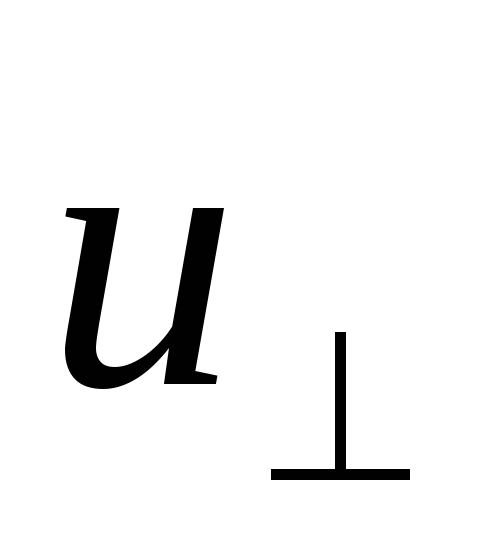 .
При этом траекторией движения будет
винтовая линия, ось которой совпадает
с линией индукции магнитного поля,
радиус витков
.
При этом траекторией движения будет
винтовая линия, ось которой совпадает
с линией индукции магнитного поля,
радиус витков
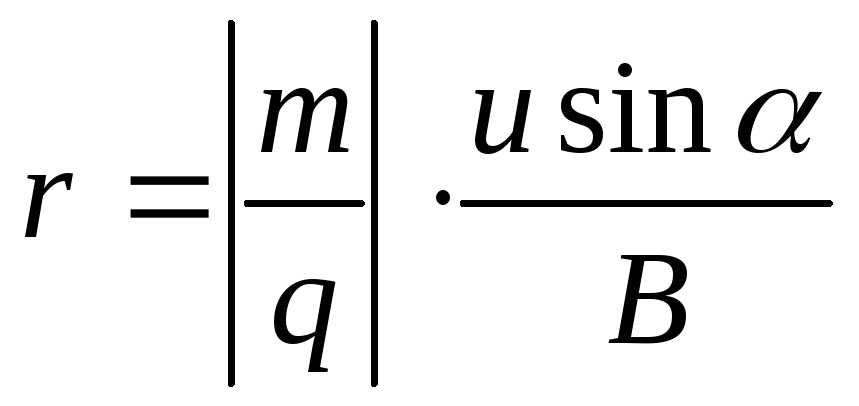 .
.
Шаг
винта 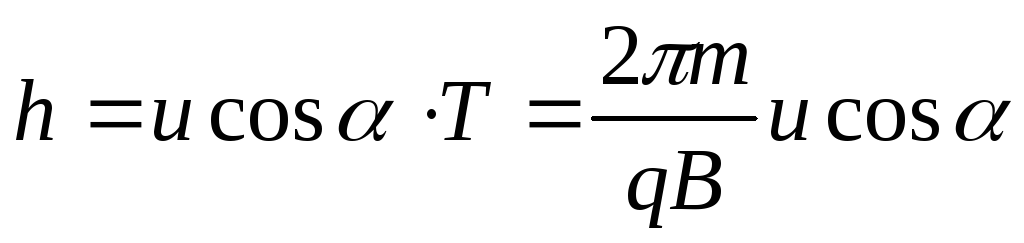 .
.
Рассмотрим движение заряженных частиц в электрическом и магнитном полях. Пусть узкий пучок одинаковых заряженных частиц (например, электронов) , попадает в точкеО
на перпендикулярный
к нему экран (рис.3.15). Определим смещение
следа пучка, вызываемое перпендикулярным
к пучку однородным электрическим полем,
действующем на пути длиной 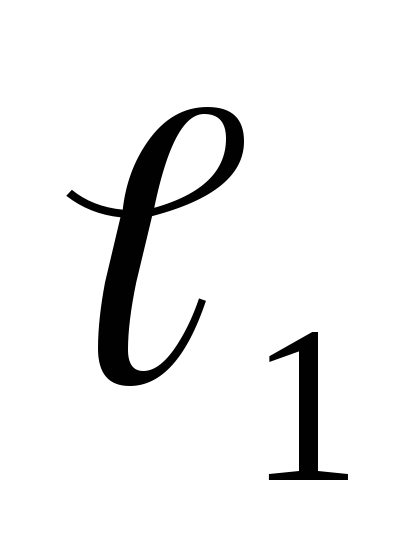 .
П
.
П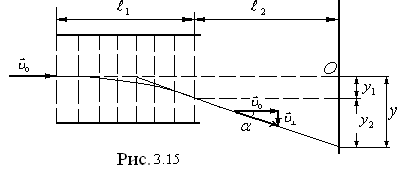 усть
первоначально скорость частицы равна
усть
первоначально скорость частицы равна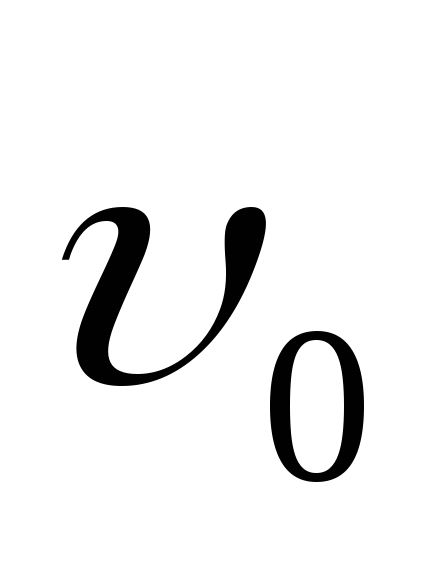 .
Войдя в область поля, каждая частица
будет двигаться с постоянным по величине
и направлению, перпендикулярным к
.
Войдя в область поля, каждая частица
будет двигаться с постоянным по величине
и направлению, перпендикулярным к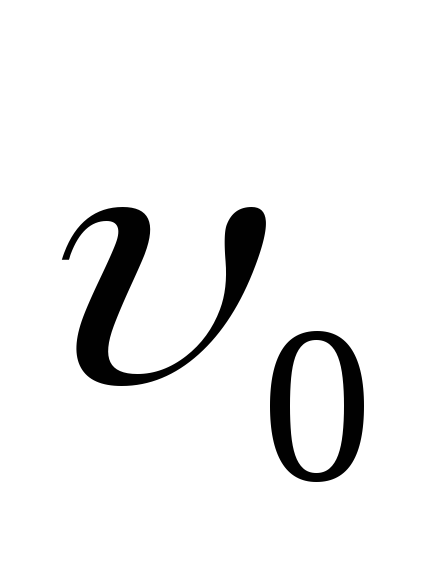 ускорением
ускорением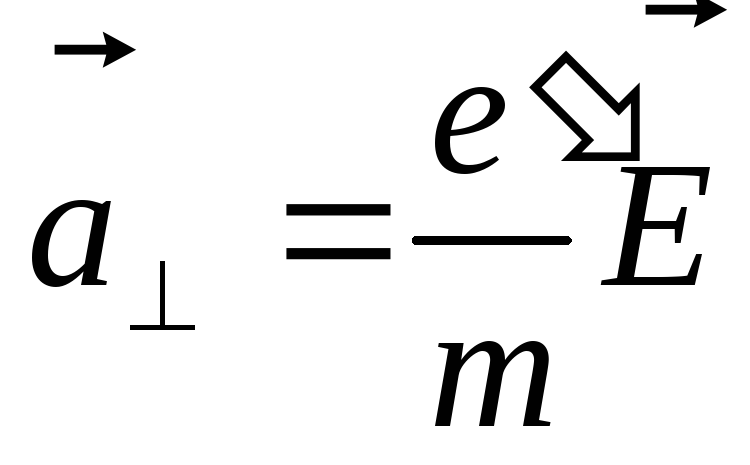 (e‘/m– удельный заряд частицы). Движение под
действием поля продолжается время
(e‘/m– удельный заряд частицы). Движение под
действием поля продолжается время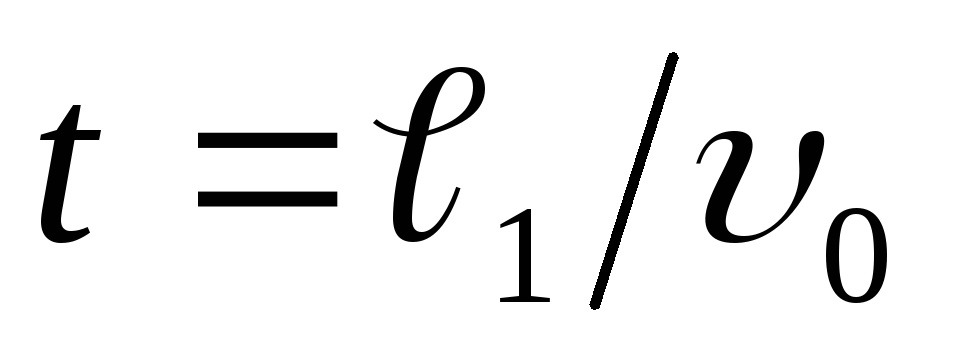 .
За это время частицы сместятся на
расстояние
.
За это время частицы сместятся на
расстояние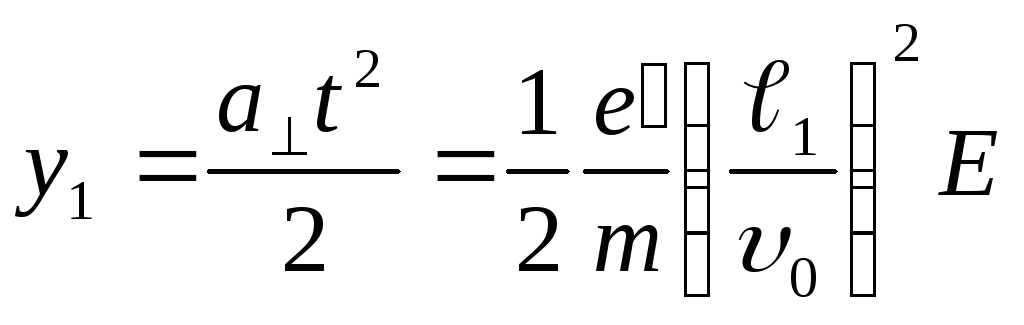 и приобретут перпендикулярную к
и приобретут перпендикулярную к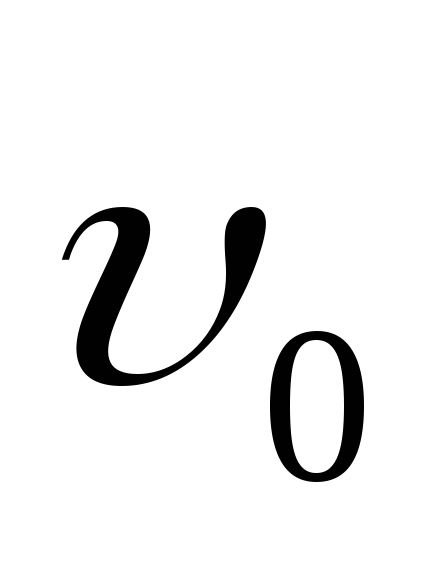 составляющую скорости
составляющую скорости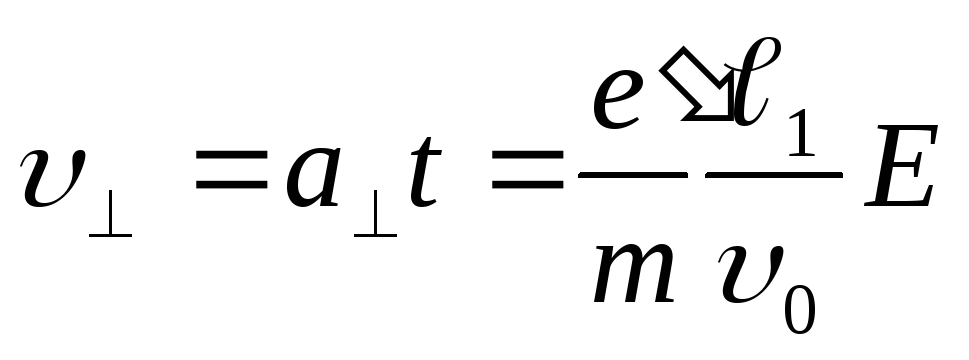 .
В дальнейшем частицы летят прямолинейно
в направлении, которое образует с
вектором
.
В дальнейшем частицы летят прямолинейно
в направлении, которое образует с
вектором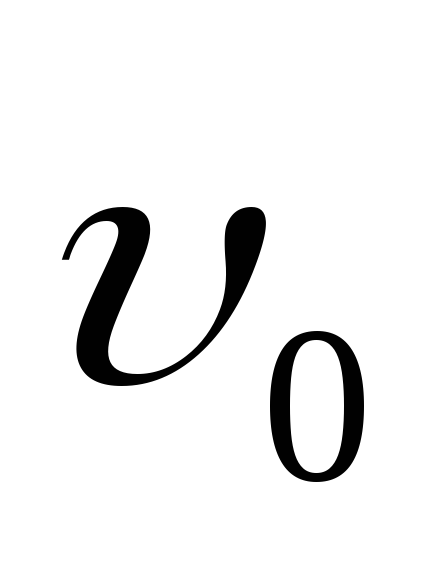 угол
угол ,
определяемый условием
,
определяемый условием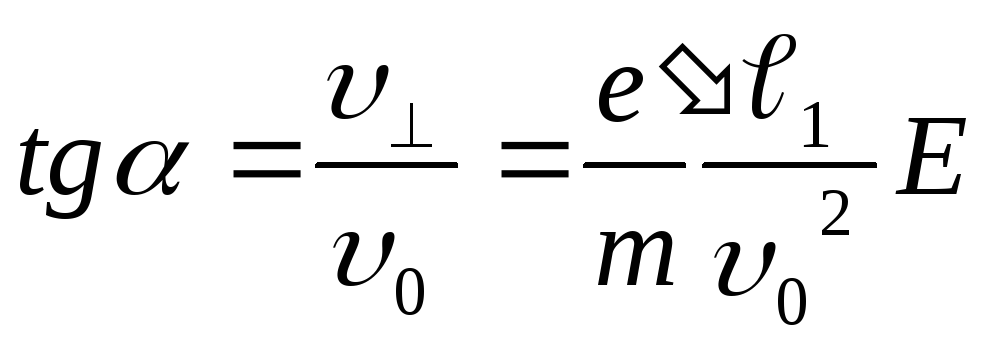 .
В результате в дополнение к смещению
.
В результате в дополнение к смещению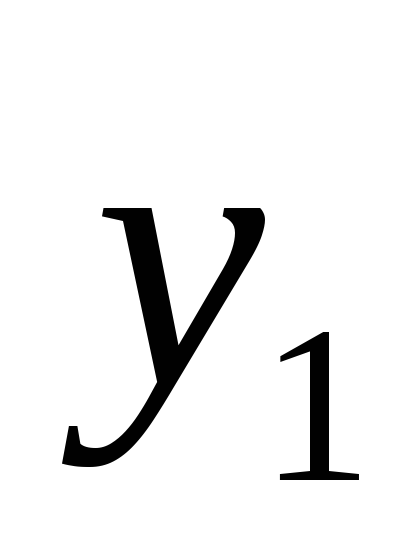 пучок
приобретет смещение
пучок
приобретет смещение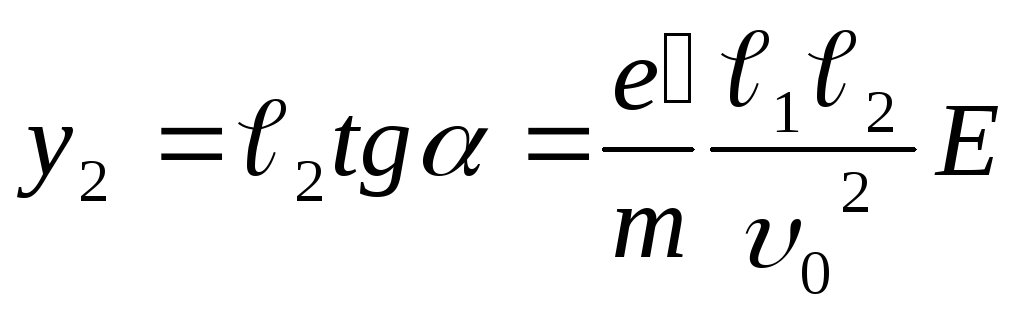 ,
где
,
где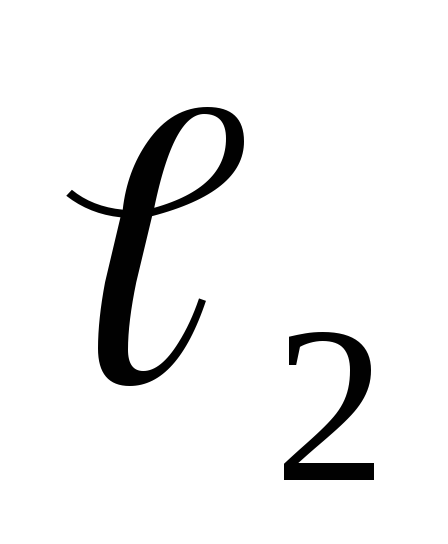 — расстояние от границы поля до экрана
. Таким образом, смещение пучка
относительно точкиОравно
— расстояние от границы поля до экрана
. Таким образом, смещение пучка
относительно точкиОравно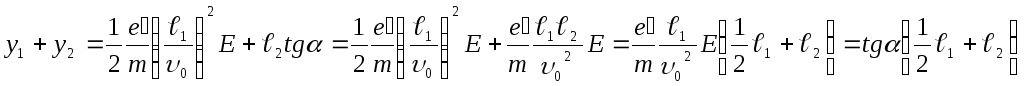 .
.
И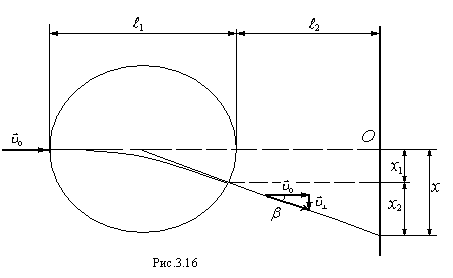 з
этого выражения следует, что частицы,
покинув поле, летят так, как если бы они
вылетели из центра конденсатора,
создающего поле, под углом
з
этого выражения следует, что частицы,
покинув поле, летят так, как если бы они
вылетели из центра конденсатора,
создающего поле, под углом .
.
Теперь предположим,
что на имеющем протяженность 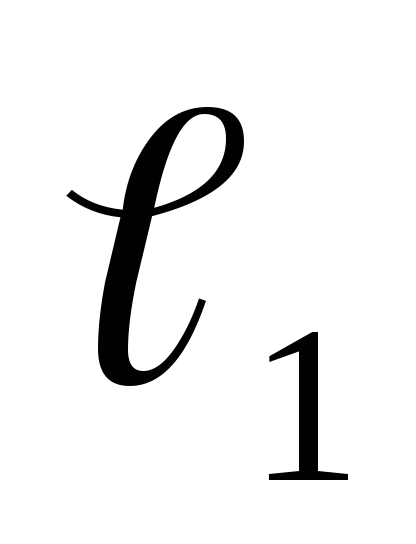 пути частиц включается перпендикулярное
к их скорости
пути частиц включается перпендикулярное
к их скорости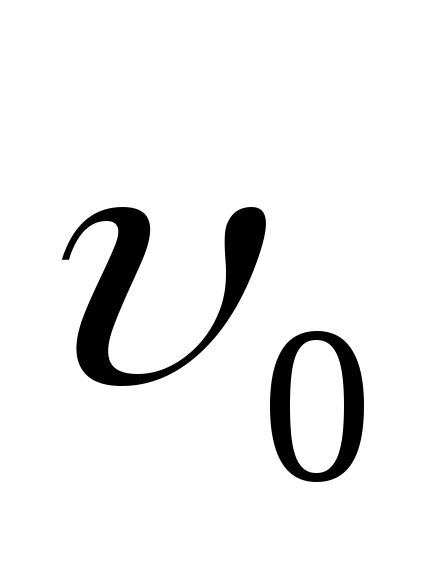 однородное магнитное поле (поле
перпендикулярно к плоскости рис. 3.16,
область поля обведена пунктирной
окружностью). Под действием поля
однородное магнитное поле (поле
перпендикулярно к плоскости рис. 3.16,
область поля обведена пунктирной
окружностью). Под действием поля
каждая частица
получит постоянное по величине ускорение 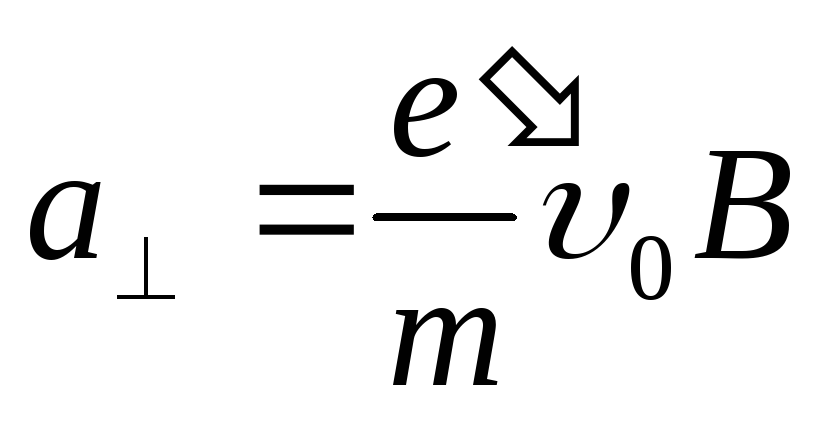 . Ограничиваясь случаем, когда отклонение
пучка полем невелико, можно считать ,
что ускорение
. Ограничиваясь случаем, когда отклонение
пучка полем невелико, можно считать ,
что ускорение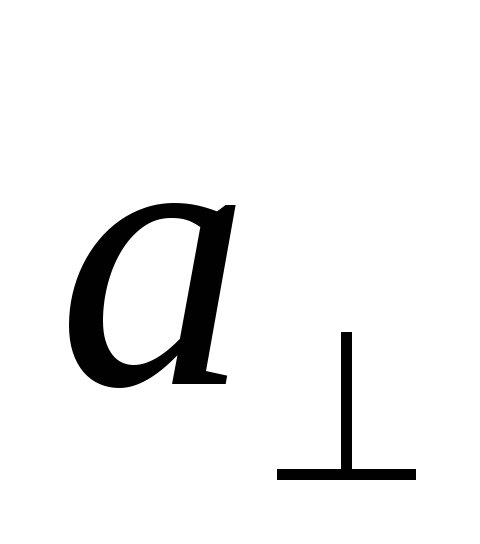
 также постоянно по направлению и
перпендикулярно к
также постоянно по направлению и
перпендикулярно к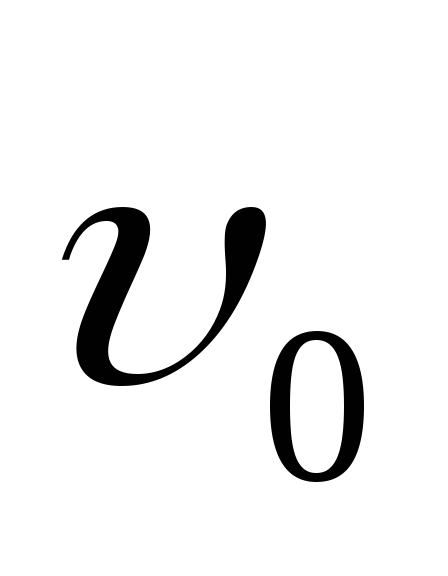 .
Тогда для расчета смещения можно
использовать полученные нами формулы,
заменив в них ускорение
.
Тогда для расчета смещения можно
использовать полученные нами формулы,
заменив в них ускорение значением
значением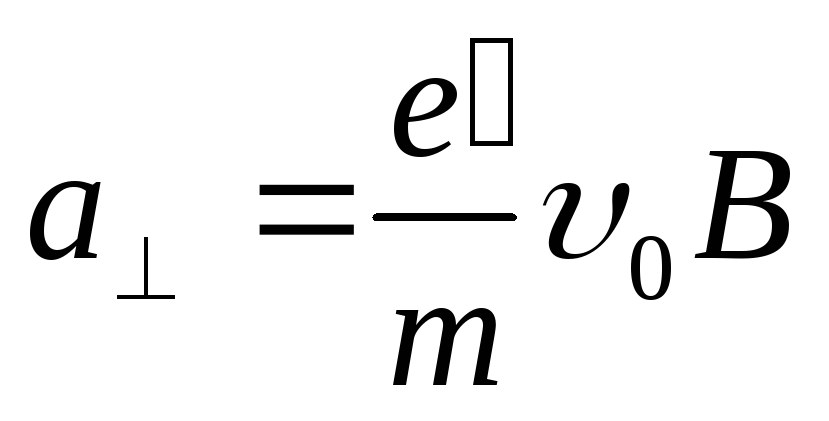 .
В результате для смещения, которое мы
теперь обозначим буквойх, получим
.
В результате для смещения, которое мы
теперь обозначим буквойх, получим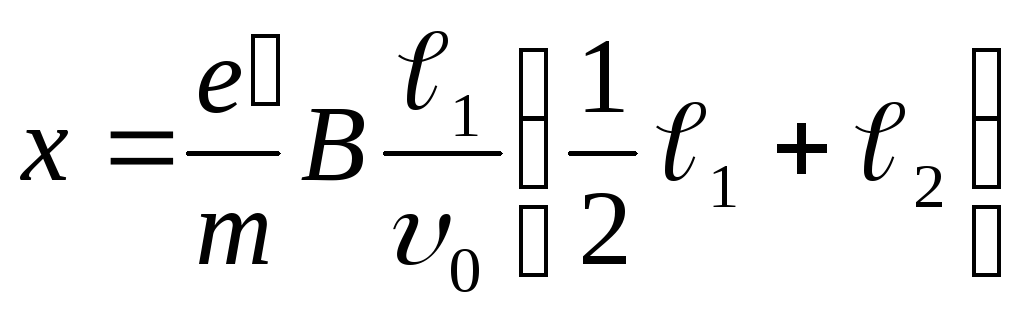 .
Угол, на который пучок отклонится
магнитным полем , определиться выражением
.
Угол, на который пучок отклонится
магнитным полем , определиться выражением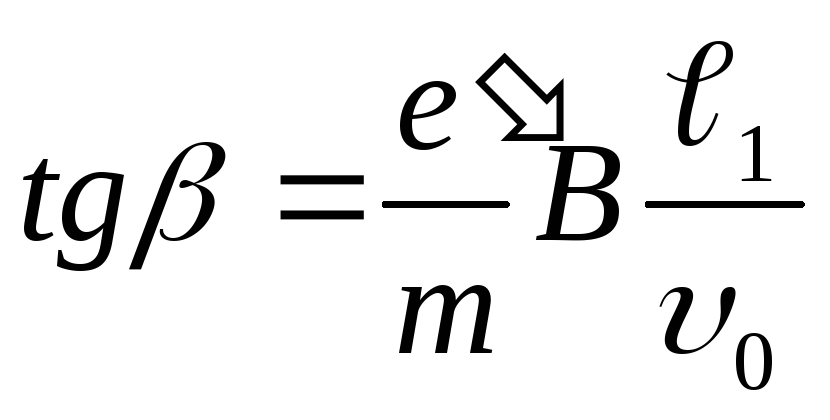 .
Тогда
.
Тогда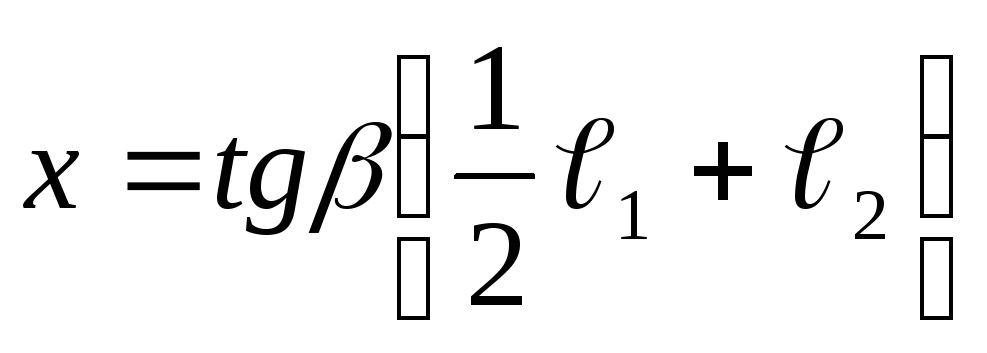 .
Следовательно, при малых отклонениях
частицы, покинув магнитное поле, летят
так, как если бы они вылетели из центра
поля под углом
.
Следовательно, при малых отклонениях
частицы, покинув магнитное поле, летят
так, как если бы они вылетели из центра
поля под углом .
Отметим, что как отклонениеуэлектрическим полем, так и отклонениехмагнитным полем пропорционально
удельному заряду частиц и напряженности
(или индукции) соответствующего поля.
Оба отклонения зависят также от
.
Отметим, что как отклонениеуэлектрическим полем, так и отклонениехмагнитным полем пропорционально
удельному заряду частиц и напряженности
(или индукции) соответствующего поля.
Оба отклонения зависят также от .
Частицы с одинаковым
.
Частицы с одинаковым и
и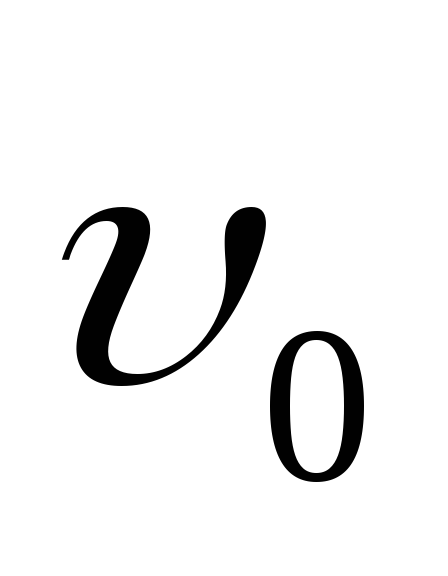 получают
в каждом из полей одинаковое отклонение
и, следовательно, попадают в одну и ту
же точку экрана.
получают
в каждом из полей одинаковое отклонение
и, следовательно, попадают в одну и ту
же точку экрана.
Отклонение пучка электронов электрическим или магнитным полем используется в электроннолучевых трубках (рис.3.17). Внутри трубки с электрическим отклонением кроме так называемого электронного прожектора, создающего узкий пучок быстрых электронов (электронный луч), помещаются две пары взаимно перпендикулярных пластин. Подавая напряжение на любую пару пластин, можно вызвать пропорциональное ему смещение электронного луча в направлении, перпендикулярном к данным пластинам. Экран трубки покрывают флуоресцирующим составом. Поэтому в месте попадания на экран электронного луча возникает ярко светящееся пятно. Электроннолучевые трубки применяются в осциллографах – приборах, позволяющих наблюдать и фотографировать быстропротекающие процессы. На одну пару отклоняющих пластин подают напряжение, изменяющееся линейно со временем, на другую пару исследуемое напряжение. Вследствие ничтожной инерционности электронного пучка его отклонение будет без запаздывания следовать за изменениями напряжений на отклоняющих пластинах, причем луч вычертит на экране осциллографа график зависимости исследуемого напряжения от времени. Многие неэлектрические величины могут быть с помощью соответствующих устройств (датчиков) преобразованы в электрические напряжения (или токи). Поэтому с помощью осциллографов исследуют самые различные по природе процессы. Электроннолучевая трубка является неотъемлемой частью телевизионных устройств. В телевидении чаще применяются трубки с магнитным управлением электронным лучом. У таких трубок вместо отклоняющих платин имеются две расположенные снаружи взаимно перпендикулярные системы катушек, каждая из которых создает перпендикулярное к лучу магнитное поле. Изменяя ток в катушках, вызывают перемещение светового пятна, создаваемого лучом на экране.
П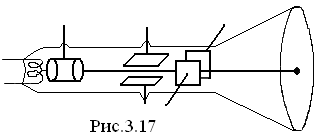
 ри
одновременном наложении электрического
и магнитного полей оба поля действуют
независимо одно от другого, так что
можно получить самые различные
результирующие движения и возможности
применения. В простейшем случае силы,
действующие со стороны электрического
и магнитного полей, взаимно компенсируются.
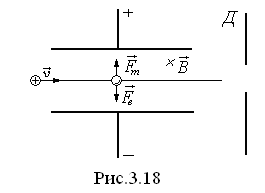
Так получают прибор, создающий однородный
по скорости пучок частиц (рис.3.18), он
называется селектор скоростей. Пусть
однородное магнитное поле, создаваемое
в пространстве между пластинами,
перпендикулярно плоскости рисунка.
Если в это пространство попадает пучок,
состоящий из частиц, скорости которых
различны, то на каждую частицу действует
сила Лоренса
ри
одновременном наложении электрического
и магнитного полей оба поля действуют
независимо одно от другого, так что
можно получить самые различные
результирующие движения и возможности
применения. В простейшем случае силы,
действующие со стороны электрического
и магнитного полей, взаимно компенсируются.
Так получают прибор, создающий однородный
по скорости пучок частиц (рис.3.18), он
называется селектор скоростей. Пусть
однородное магнитное поле, создаваемое
в пространстве между пластинами,
перпендикулярно плоскости рисунка.
Если в это пространство попадает пучок,
состоящий из частиц, скорости которых
различны, то на каждую частицу действует
сила Лоренса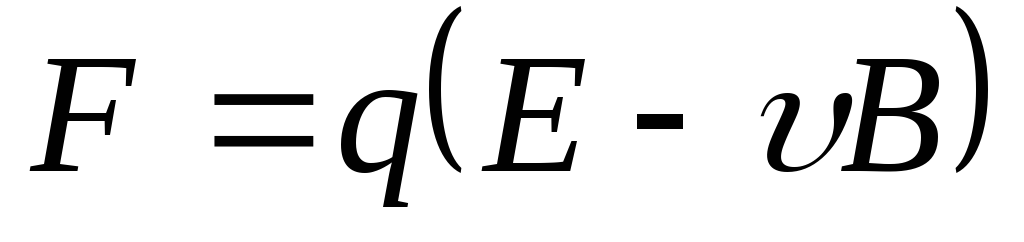 .
Если скорость частицы удовлетворяет
условию
.
Если скорость частицы удовлетворяет
условию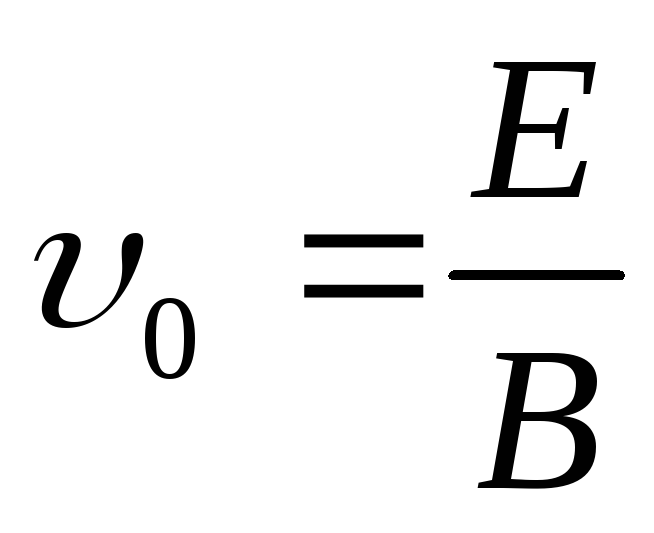 ,
то в любой момент времени сила равна
нулю, так что частица проходит через
диафрагму экранаД. Если же скорость
частицы больше или меньше, чем
,
то в любой момент времени сила равна
нулю, так что частица проходит через
диафрагму экранаД. Если же скорость
частицы больше или меньше, чем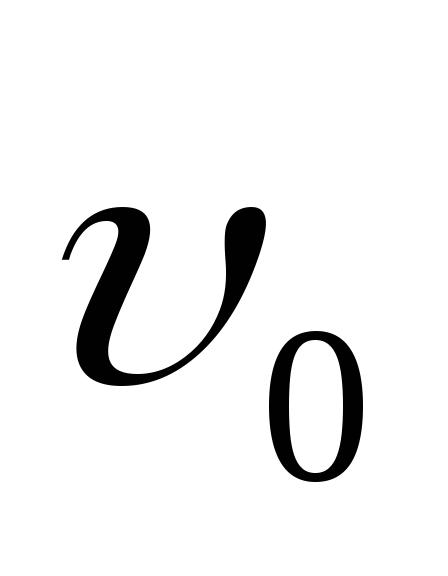 ,
частица отклоняется силой вверх или
вниз и ударяется об экранД. В
результате этого справа отДбудет
получаться пучок частиц, однородный по
скорости. Такое устройство можно
применять и для измерения скорости
частиц.
,
частица отклоняется силой вверх или
вниз и ударяется об экранД. В
результате этого справа отДбудет
получаться пучок частиц, однородный по
скорости. Такое устройство можно
применять и для измерения скорости
частиц.
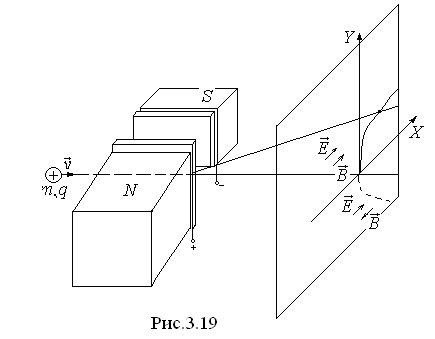
Е сли
электрическое и магнитное поля параллельны
(рис.3.19) , то отклонения частицы, вызываемые
полями, перпендикулярны друг другу,
для электрического поля
сли
электрическое и магнитное поля параллельны
(рис.3.19) , то отклонения частицы, вызываемые
полями, перпендикулярны друг другу,
для электрического поля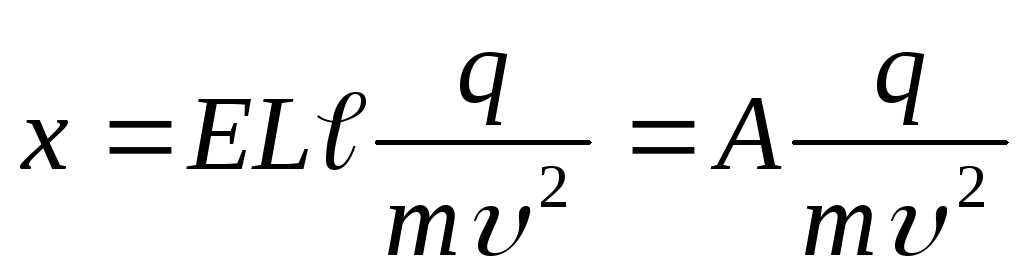 ,
для магнитного поля
,
для магнитного поля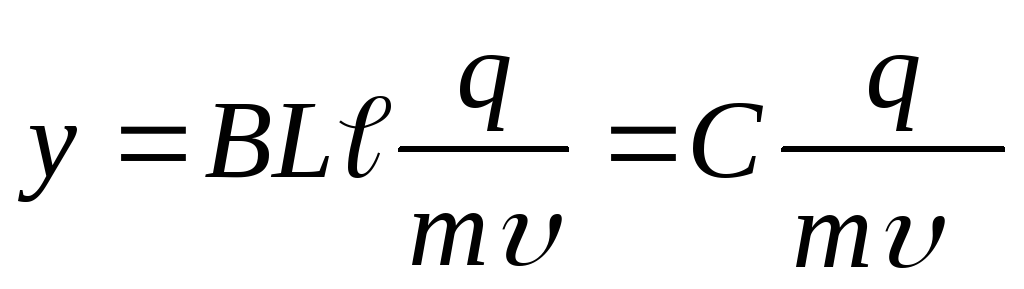 .
Частицы, обладающие одинаковым удельным
зарядом
.
Частицы, обладающие одинаковым удельным
зарядом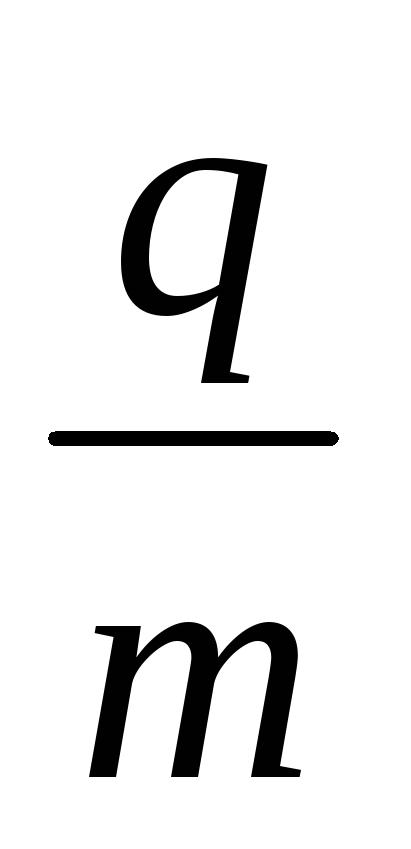 ,
попадают в зависимости от скорости в
разные точки. Эти точки образуют параболу
,
попадают в зависимости от скорости в
разные точки. Эти точки образуют параболу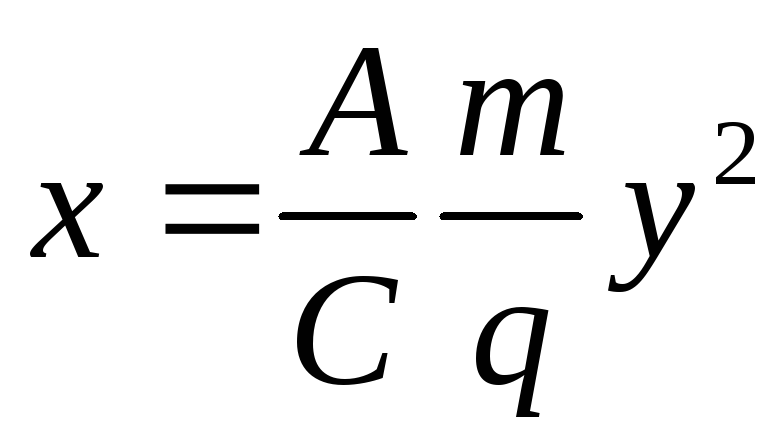 .
ВеличиныАиСявляются постоянными
прибора. Каждому отдельному типу ионов
соответствует своя парабола. Отличающиеся
друг от друга ионы, имеющие разные
скорости, разделяются в этом устройстве,
а ионы с одинаковым удельным зарядом и
любым значением скорости, попадают на
отдельную ветвь параболы, вызывая
почернение на фотопластинке (рис.3.20 ).
На этом принципе основана работа
параболического масс-спектрографа.
.
ВеличиныАиСявляются постоянными
прибора. Каждому отдельному типу ионов
соответствует своя парабола. Отличающиеся
друг от друга ионы, имеющие разные
скорости, разделяются в этом устройстве,
а ионы с одинаковым удельным зарядом и
любым значением скорости, попадают на
отдельную ветвь параболы, вызывая
почернение на фотопластинке (рис.3.20 ).
На этом принципе основана работа
параболического масс-спектрографа.
Рассмотрим движение
частиц в одновременно действующих
электрическом и магнитном полях
значительной протяженности. Е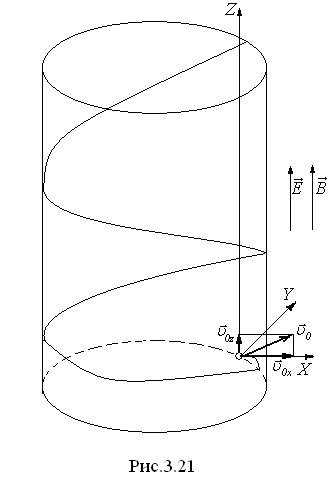 сли
частица не покидает поле, а движется в
нем постоянно, то магнитное поле вынуждает
ее двигаться по окружности в плоскости,
перпендикулярной к направлению поля,
а электрическое поле ускоряет ее. В
результате получается винтовая линия
с увеличивающимся шагом (рис.3.21).
сли
частица не покидает поле, а движется в
нем постоянно, то магнитное поле вынуждает
ее двигаться по окружности в плоскости,
перпендикулярной к направлению поля,
а электрическое поле ускоряет ее. В
результате получается винтовая линия
с увеличивающимся шагом (рис.3.21).
Н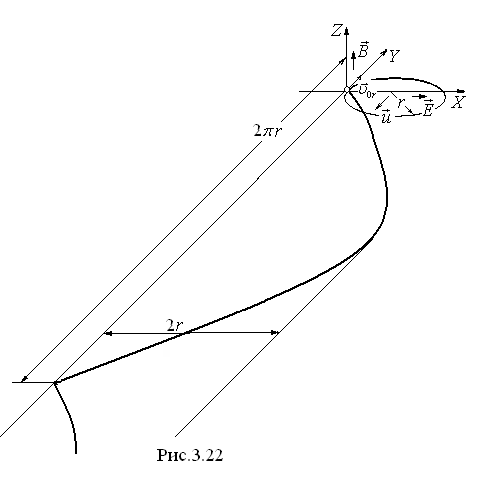 а
рис.3.22 показан случай, когда векторы
а
рис.3.22 показан случай, когда векторы и
и взаимно перпендикулярны , и частица
стартует из начала координат с начальной
скоростью, равной нулю. Уравнение
движения в этом случае имеет вид:
взаимно перпендикулярны , и частица
стартует из начала координат с начальной
скоростью, равной нулю. Уравнение
движения в этом случае имеет вид: .
Выберем новую систему координат, оси
которой в момент времени
.
Выберем новую систему координат, оси
которой в момент времени совпадают с осями старой системы, причем
новая система движется с постоянной
скоростью
совпадают с осями старой системы, причем
новая система движется с постоянной
скоростью относительно старой. Скорость частицы,
измеренная в неподвижной системе
координат, в любой момент времени равна
относительно старой. Скорость частицы,
измеренная в неподвижной системе
координат, в любой момент времени равна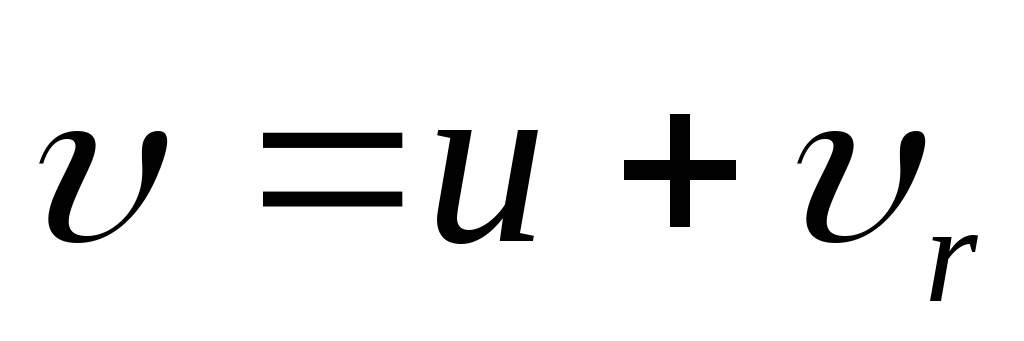 ,
где
,
где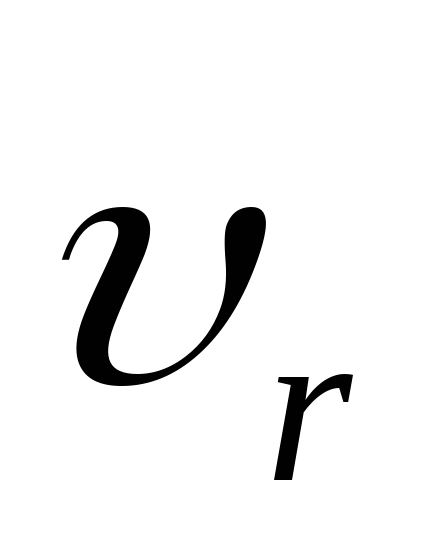 — скорость частицы в движущейся системе
координат. Уравнение движения принимает
вид
— скорость частицы в движущейся системе
координат. Уравнение движения принимает
вид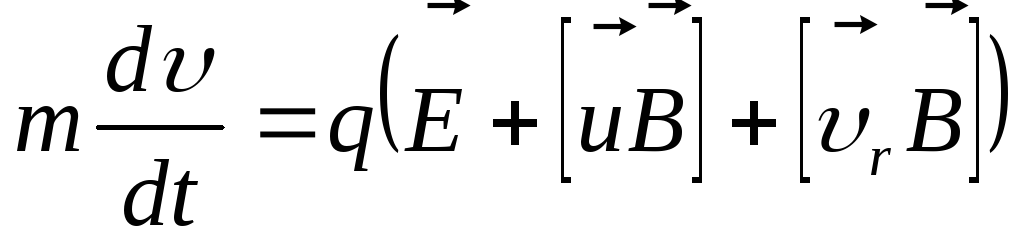 .
Выберем скорость
.
Выберем скорость таким образом, чтобы
таким образом, чтобы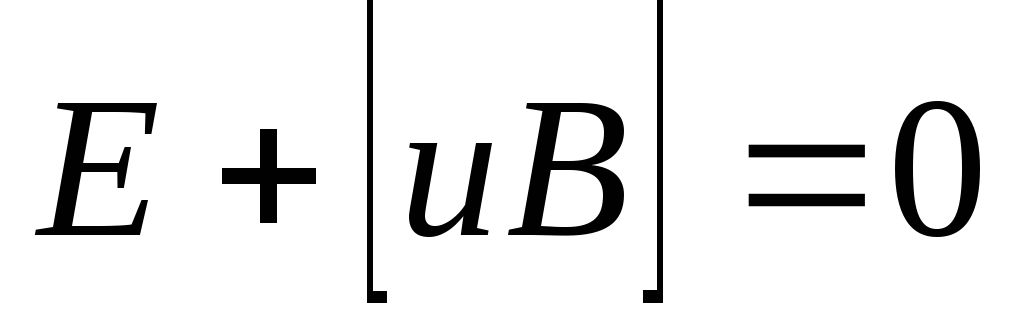 ,
т.е. скорость
,
т.е. скорость должна быть направлена против осиYи иметь значение
должна быть направлена против осиYи иметь значение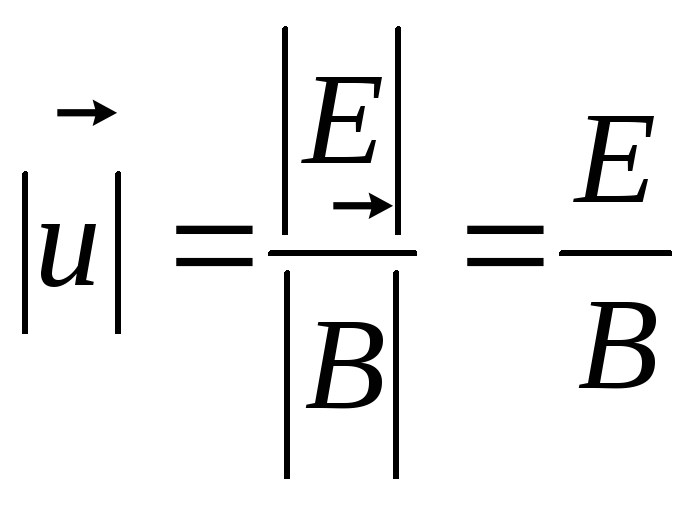 ,
или
,
или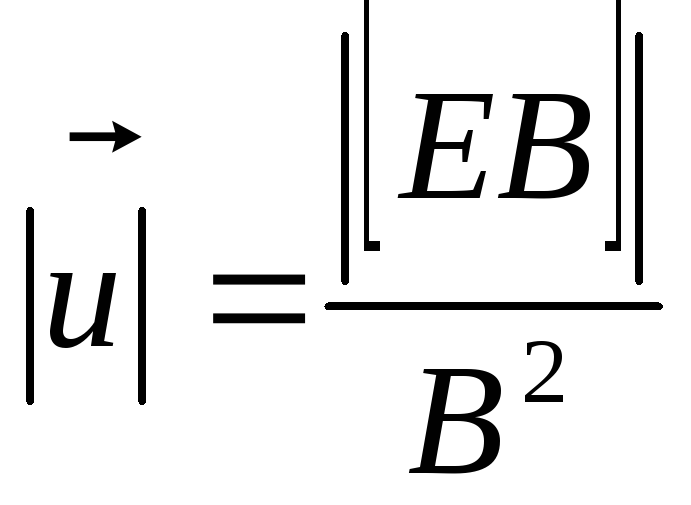 .
В движущейся системе отсчета уравнение
движения примет вид:
.
В движущейся системе отсчета уравнение
движения примет вид: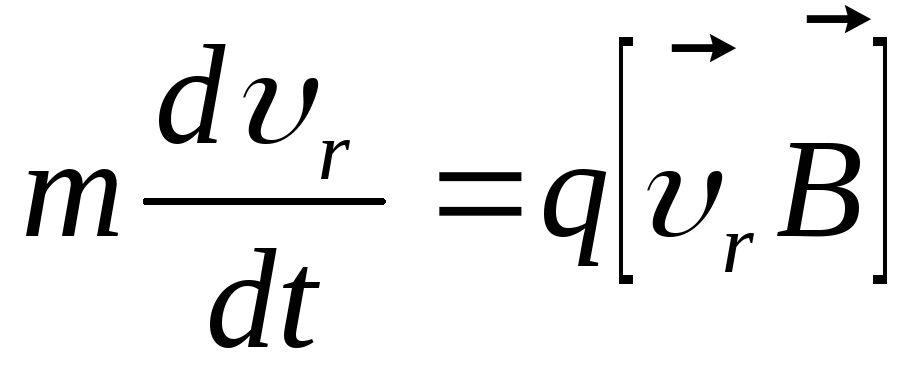 ,
так как производная постоянной
,
так как производная постоянной равна нулю.
равна нулю.
Частица в движущейся
системе отсчета ведет себя так, как если
бы существовало только магнитное поле.
Влияние электрического поля учтено
поступательной скоростью системы
отсчета. В движущейся системе отсчета
частица движется по окружности, если 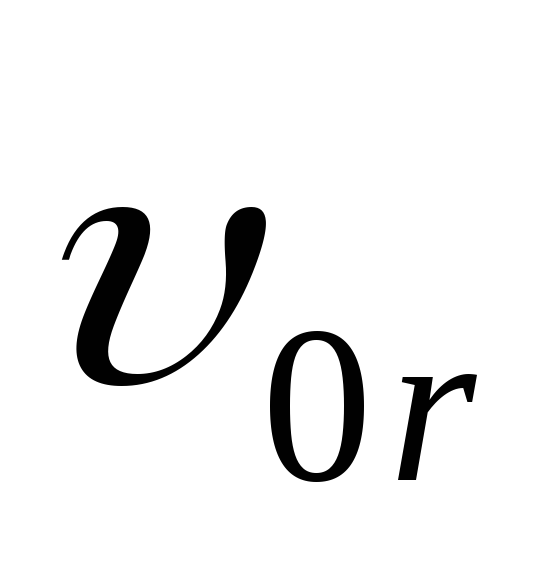 перпендикулярна к
перпендикулярна к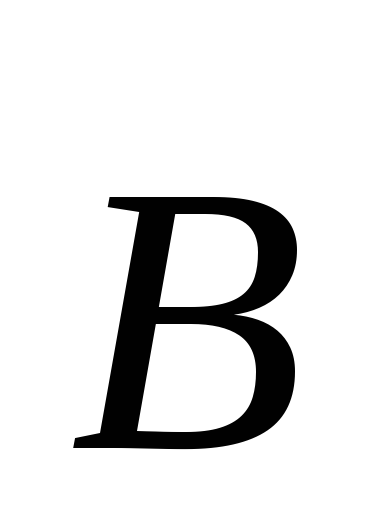 ,
и если система совершает равномерное
поступательное движение. Поэтому в
исходной системе отсчета траекторией
является циклоида.
,
и если система совершает равномерное
поступательное движение. Поэтому в
исходной системе отсчета траекторией
является циклоида.
Сила Лоренца. Движение заряженных частиц в магнитном поле.
Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на заряд q ,движущийся в магнитном поле 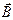 со скоростью
со скоростью 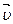 , называется силой Лоренца.
, называется силой Лоренца.
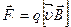 — установлено опытным путем
— установлено опытным путем
 Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление
Направление силы Лоренца определяется для положительных зарядов правилом левой руки (т.к. направление 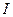 и
и 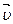 для
для 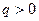 совпадают): если ладонь левой руки расположить так, чтобы вектор
совпадают): если ладонь левой руки расположить так, чтобы вектор 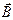 входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.
входил в нее, а 4 вытянутых пальца сонаправить с движением положительного заряда, то отогнутый большой палец покажет направление силы Лоренца.
Для отрицательных зарядов берется противоположное направление.
Сила Лоренца всегда направлена перпендикулярно скорости заряда 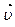 и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
и сообщает ему нормальное ускорение. Не изменяя модуля скорости, а лишь изменяя ее направление, сила Лоренца не совершает работы и кинетическая энергия заряженной частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля действует и электрическое поле напряженностью 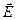 , то результирующая сила
, то результирующая сила
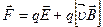 — формула Лоренца.
— формула Лоренца.
1. Движение заряженной частицы вдоль силовой линии, 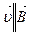 .
.
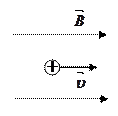
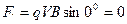 ,
,
магнитное поле не действует на частицу.
Заряженная частица движется по инерции равномерно прямолинейно.
2. Движение заряженной частицы перпендикулярно силовым линиям, 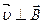 .
.
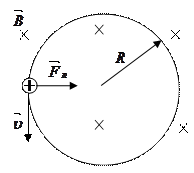 Пусть в однородное магнитное поле с индукцией
Пусть в однородное магнитное поле с индукцией 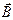 влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью
влетела заряженная частица массой m с зарядом q перпендикулярно магнитным силовым линиям со скоростью 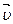 .
.
В каждой точке поля на частицу действует 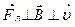 . Т.к.
. Т.к. 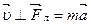 , то
, то 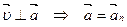 . Ускорение
. Ускорение 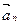 изменяет только направление скорости,
изменяет только направление скорости, 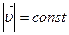 , значит,
, значит, 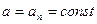 . В этих условиях тело (заряженная частица) движется равномерно по окружности.
. В этих условиях тело (заряженная частица) движется равномерно по окружности.
Согласно II закону Ньютона:
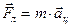
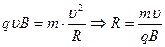 (1)
(1)
Т.к. все величины, входящие в (1), постоянны, радиус кривизны R будет оставаться постоянным. Постоянный радиус кривизны имеет только окружность. Следовательно, движение заряда в плоскости, перпендикулярной магнитному полю, будет происходить по окружности. Чем больше 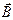 , тем меньше R. При
, тем меньше R. При 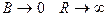 , т.е. заряд движется по прямой.
, т.е. заряд движется по прямой.
Важным результатом для приложения является тот факт, что период обращения заряда в однородном магнитном поле не зависит от его скорости.
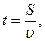 если
если 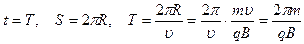 . (2)
. (2)
Частицы, имеющие бóльшую скорость, движутся по окружности бóльшего радиуса, однако время одного полного оборота будет таким же, что и для более медленных частиц, движущихся по окружности меньшего радиуса. Данный результат положен в основу действия циклических ускорителей элементарных частиц.
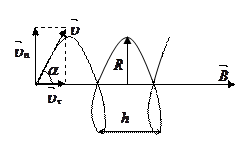 3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции. Вектор скорости можно разложить на 2 составляющие:
3. Движение заряженной частицы произвольно по отношению к линиям магнитной индукции. Вектор скорости можно разложить на 2 составляющие:
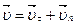
В направлении 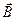 сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с
сила Лоренца на заряд не действует, поэтому в этом направлении он движется равномерно, прямолинейно с 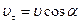 . В направлении, перпендикулярном
. В направлении, перпендикулярном 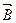 , он движется по окружности со скоростью
, он движется по окружности со скоростью 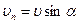 Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна
Движение заряда представляет собой суперпозицию этих двух движений и происходит по винтовой линии, ось которой параллельна 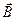 .
.
Радиус витка с учетом (1):
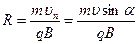 (3)
(3)
Шаг винтовой линии (расстояние между соседними витками)
с учетом (2):
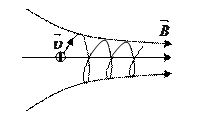
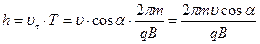 .
.
Если движение происходит в неоднородном магнитном поле, индукция которого возрастает в направлении движения частицы, то R уменьшается с ростом В согласно (3). На этом основана фокусировка пучка заряженных частиц в магнитном поле. Таким образом, с помощью неоднородного магнитного поля можно управлять пучками заряженных частиц, собирать их или рассеивать подобно тому, как управляют поведением пучков световых лучей с помощью оптических линз.
Рассмотренный принцип положен в основу действия электронных микроскопов.
Дата добавления: 2016-11-04; просмотров: 6420;
Похожие статьи:
Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
F = q n S Δl υB sin α. |
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна
FЛ = q υ B sin α. |
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью 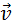 и вектором магнитной индукции
и вектором магнитной индукции 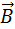 . Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов 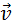 ,
, 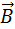 и
и 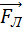 для положительно заряженной частицы показано на рис. 1.18.1.
для положительно заряженной частицы показано на рис. 1.18.1.
Сила Лоренца направлена перпендикулярно векторам 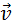 и
и 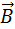
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость 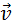 лежит в плоскости, перпендикулярной вектору
лежит в плоскости, перпендикулярной вектору 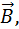 то частица будет двигаться по окружности радиуса
то частица будет двигаться по окружности радиуса
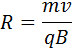
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
|
Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле |
Период обращения частицы в однородном магнитном поле равен
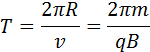
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
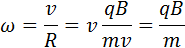
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
|
Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость 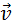 заряженных частиц направлена перпендикулярно векторам
заряженных частиц направлена перпендикулярно векторам 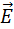 и
и 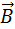
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила 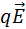 и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле 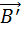 . Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
. Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
|
Рисунок 1.18.4. Селектор скоростей и масс-спектрометр |
Если скорость частицы 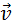 имеет составляющую
имеет составляющую 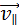 вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ+ вектора
вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ+ вектора 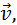 а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
|
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле |
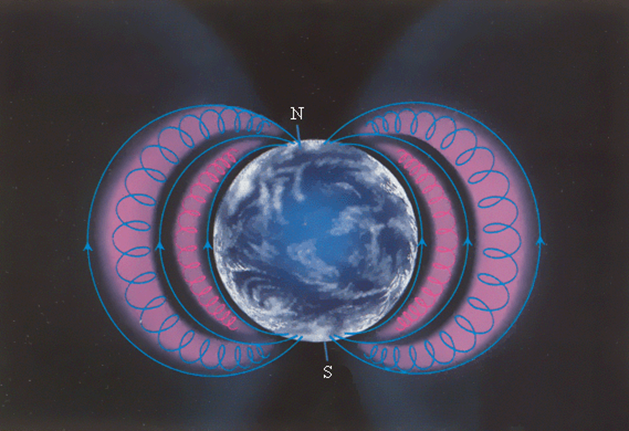
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
|
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током |
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что северный магнитный полюс Земли сейчас находится вблизи северного географического полюса и постепенно перемещается. Природа земного магнетизма до сих пор не изучена.
|
Рисунок 1.18.7. Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния |
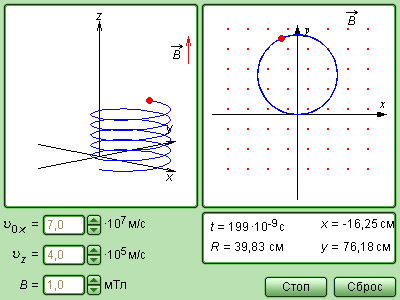 |
Модель. Движение заряда в магнитном поле |
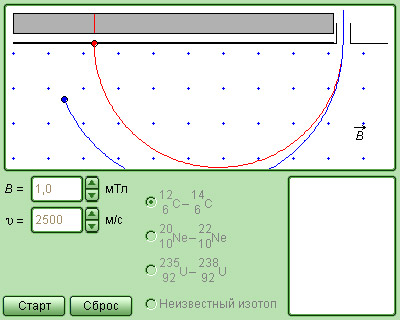 |
Модель. Масс-спектрометр |
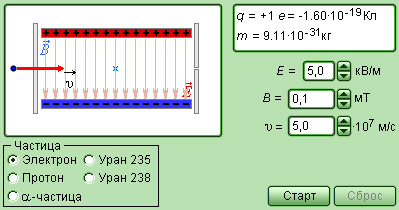 |
Модель. Селектор скоростей |


 м
м ежду
векторами
ежду
векторами и
и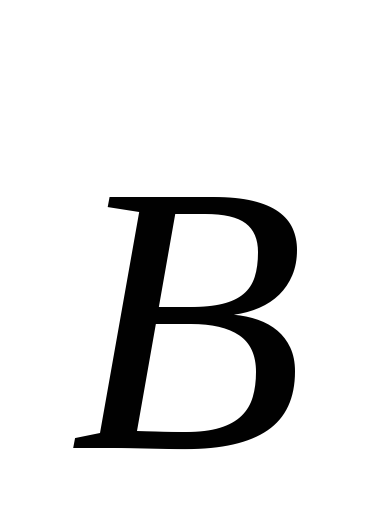 равен 0 или
равен 0 или ,
, ,
т.е. магнитное поле не действует на
частицу. Она будет двигаться по инерции
– прямолинейно и равномерно.
,
т.е. магнитное поле не действует на
частицу. Она будет двигаться по инерции
– прямолинейно и равномерно. (рис.3. 13):
(рис.3. 13):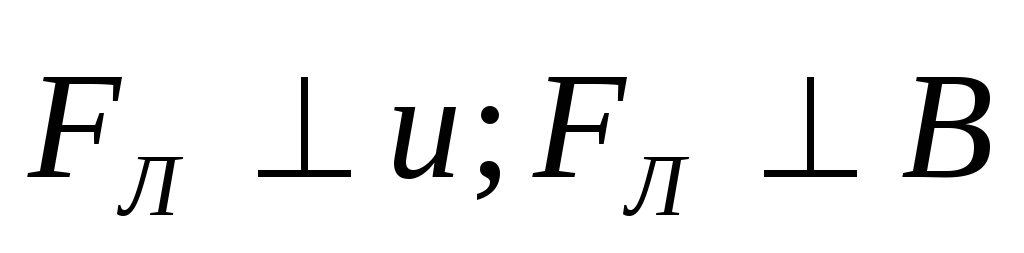 и
и 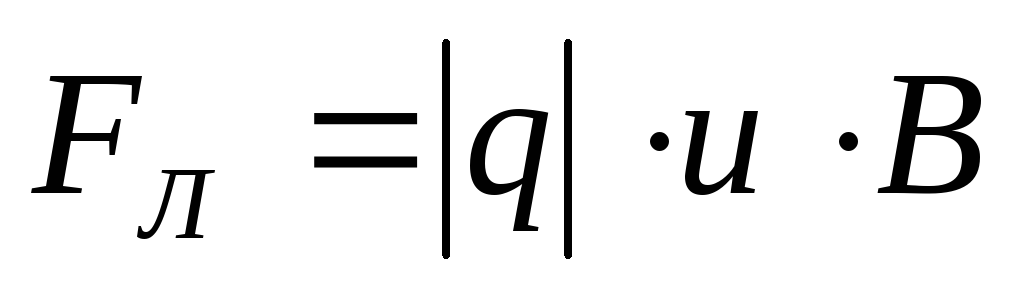 .
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой:
.
В этом случае частица движется в
плоскости, перпендикулярной к вектору
магнитной индукции, и сила Лоренца
является центростремительной силой: к вектору
к вектору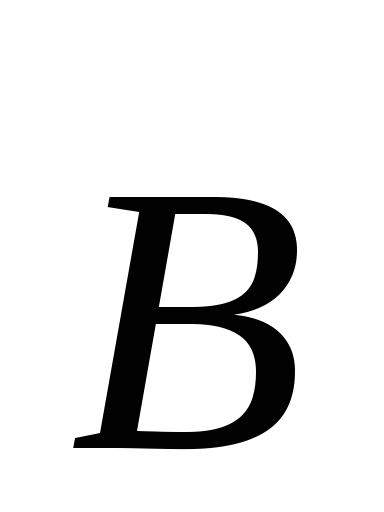 (рис.3.14). Разложим вектор
(рис.3.14). Разложим вектор на две составляющие:
на две составляющие: