создание, скалярное произведение, умножение, сложение, вычитание с подробными примерами
В этом уроке мы узнаем, как создать вектор с помощью библиотеки Numpy в Python. Мы также рассмотрим основные операции с векторами, такие как сложение, вычитание, деление и умножение двух векторов, векторное точечное произведение и векторное скалярное произведение.
Что такое вектор в Python?
Вектор известен как одномерный массив. Вектор в Python – это единственный одномерный массив списков, который ведет себя так же, как список Python. Согласно Google, вектор представляет направление, а также величину; особенно он определяет положение одной точки в пространстве относительно другой.
Векторы очень важны в машинном обучении, потому что у них есть величина, а также особенности направления. Давайте разберемся, как мы можем создать вектор на Python.
Создание вектора в Python
Модуль Python Numpy предоставляет метод numpy.array(), который создает одномерный массив, то есть вектор. Вектор может быть горизонтальным или вертикальным.
Вектор может быть горизонтальным или вертикальным.
Синтаксис:
np.array(list)
Вышеупомянутый метод принимает список в качестве аргумента и возвращает numpy.ndarray.
Давайте разберемся в следующих примерах.
Пример – 1: горизонтальный вектор
# Importing numpy
import numpy as np
# creating list
list1 = [10, 20, 30, 40, 50]
# Creating 1-D Horizontal Array
vtr = np.array(list1)
vtr = np.array(list1)
print("We create a vector from a list:")
print(vtr)
Выход:
We create a vector from a list: [10 20 30 40 50]
Пример – 2: Вертикальный вектор
# Importing numpy
import numpy as np
# defining list
list1 = [[12],
[40],
[6],
[10]]
# Creating 1-D Vertical Array
vtr = np.
array(list1)
vtr = np.array(list1)
print("We create a vector from a list:")
print(vtr)
Выход:
We create a vector from a list: [[12] [40] [ 6] [10]]
Базовые операции вектора Python
После создания вектора мы теперь будем выполнять арифметические операции над векторами.
Ниже приведен список основных операций, которые мы можем производить с векторами:
- сложение;
- вычитание;
- умножение;
- деление;
- точечное произведение;
- скалярные умножения.
Сложение двух векторов
В векторном сложении это происходит поэлементно, что означает, что сложение будет происходить поэлементно, а длина будет такой же, как у двух аддитивных векторов.
Синтаксис:
vector + vector
Давайте разберемся в следующем примере.
Пример –
import numpy as np list1 = [10,20,30,40,50] list2 = [11,12,13,14,15] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create vector from a list 2:") print(vtr2) vctr_add = vctr1+vctr2 print("Addition of two vectors: ",vtr_add)
Выход:
We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [11 12 13 14 15] Addition of two vectors: [21 32 43 54 65]
Вычитание
Вычитание векторов выполняется так же, как и сложение, оно следует поэлементному подходу, и элементы вектора 2 будут вычтены из вектора 1. Давайте разберемся в следующем примере.
Пример –
import numpy as np
list1 = [10,20,30,40,50]
list2 = [5,2,4,3,1]
vtr1 = np.array(list1)
vtr2= np.array(list2)
print("We create vector from a list 1:")
print(vtr1)
print("We create a vector from a list 2:")
print(vtr2)
vtr_sub = vtr1-vtr2
print("Subtraction of two vectors: ",vtr_sub)
Выход:
We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Subtraction of two vectors: [5 18 26 37 49]
Умножение векторов
Элементы вектора 1 умножаются на вектор 2 и возвращают векторы той же длины, что и векторы умножения.
Пример –
import numpy as np
list1 = [10,20,30,40,50]
list2 = [5,2,4,3,1]
vtr1 = np.array(list1)
vtr2= np.array(list2)
print("We create vector from a list 1:")
print(vtr1)
print("We create a vector from a list 2:")
print(vtr2)
vtr_mul = vtr1*vtr2
print("Multiplication of two vectors: ",vtr_mul)
Выход:
We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Multiplication of two vectors: [ 50 40 120 120 50]
Умножение производится следующим образом.
vct[0] = x[0] * y[0] vct[1] = x[1] * y[1]
Первый элемент вектора 1 умножается на первый элемент соответствующего вектора 2 и так далее.
Операция деления двух векторов
В операции деления результирующий вектор содержит значение частного, полученное при делении двух элементов вектора.
Давайте разберемся в следующем примере.
import numpy as np
list1 = [10,20,30,40,50]
list2 = [5,2,4,3,1]
vtr1 = np.array(list1)
vtr2= np.array(list2)
print("We create vector from a list 1:")
print(vtr1)
print("We create a vector from a list 2:")
print(vtr2)
vtr_div = vtr1/vtr2
print("Division of two vectors: ",vtr_div)
Выход:
We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Division of two vectors: [ 2. 10. 7.5 13.33333333 50. ]
Как видно из вышеприведенного вывода, операция деления вернула частное значение элементов.
Векторное точечное произведение
Векторное скалярное произведение выполняется между двумя последовательными векторами одинаковой длины и возвращает единичное скалярное произведение. Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.
Мы будем использовать метод .dot() для выполнения скалярного произведения. Это произойдет, как показано ниже.
vector c = x . y =(x1 * y1 + x2 * y2)
Давайте разберемся в следующем примере.
Пример –
import numpy as np list1 = [10,20,30,40,50] list2 = [5,2,4,3,1] vtr1 = np.array(list1) vtr2= np.array(list2) print("We create vector from a list 1:") print(vtr1) print("We create a vector from a list 2:") print(vtr2) vtr_product = vtr1.dot(vtr2) print("Dot product of two vectors: ",vtr_product)
Выход:
We create vector from a list 1: [10 20 30 40 50] We create vector from a list 2: [5 2 4 3 1] Dot product of two vectors: 380
Векторно-скалярное умножение
В операции скалярного умножения; мы умножаем скаляр на каждую компоненту вектора.
Пример –
import numpy as np
list1 = [10,20,30,40,50]
vtr1 = np.array(list1)
scalar_value = 5
print("We create vector from a list 1:")
print(vtr1)
# printing scalar value
print("Scalar Value : " + str(scalar_value))
vtr_scalar = vtr1 * scalar_value
print("Multiplication of two vectors: ",vtr_scalar)
Выход:
We create vector from a list 1: [10 20 30 40 50] Scalar Value : 5 Multiplication of two vectors: [ 50 100 150 200 250]
В приведенном выше коде скалярное значение умножается на каждый элемент вектора в порядке s * v =(s * v1, s * v2, s * v3).
Михаил Русаков
Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.
Еще для изучения:
Краткий курс высшей математики
Краткий курс высшей математики
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3.  УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8.  Пучок прямых Пучок прямых9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3.  ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. 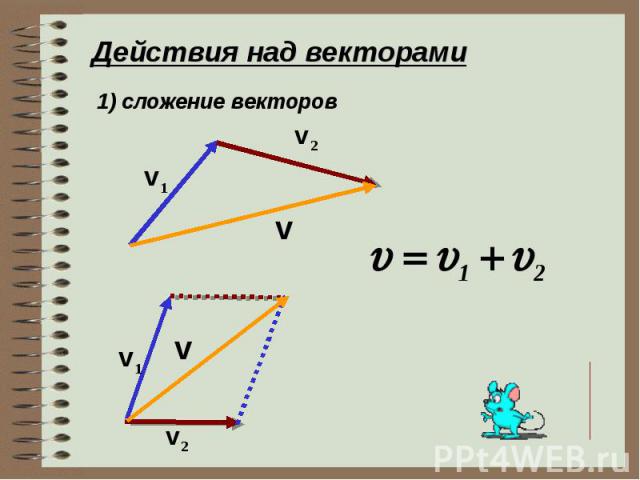 АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ§ 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V.  ТЕОРИЯ ПРЕДЕЛОВ ТЕОРИЯ ПРЕДЕЛОВ§ 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4.  Определение производной и ее механический смысл Определение производной и ее механический смысл5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6.  Дифференциалы высших порядков Дифференциалы высших порядков§ 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8.  ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3.  Интегралы видов Интегралы видов4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2.  Вычисление кривизны Вычисление кривизны3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2.  Полный дифференциал функции Полный дифференциал функции3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. 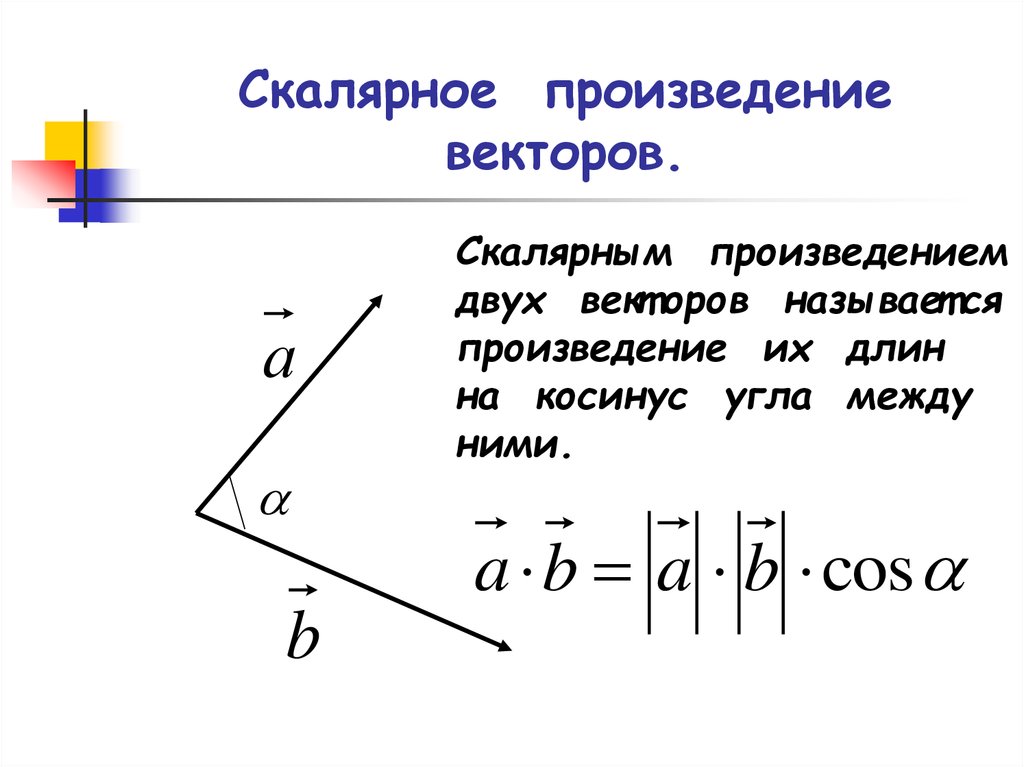 Приложения тройного интеграла Приложения тройного интеграла§ 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2.  Приближенное вычисление интегралов Приближенное вычисление интегралов§ 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2.  Линейные однородные дифференциальные уравнения второго порядка Линейные однородные дифференциальные уравнения второго порядка3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ |
Объяснение урока: Работа, совершаемая силой, выраженная в векторном представлении действуя на тело по вектору смещения с помощью скалярного произведения.
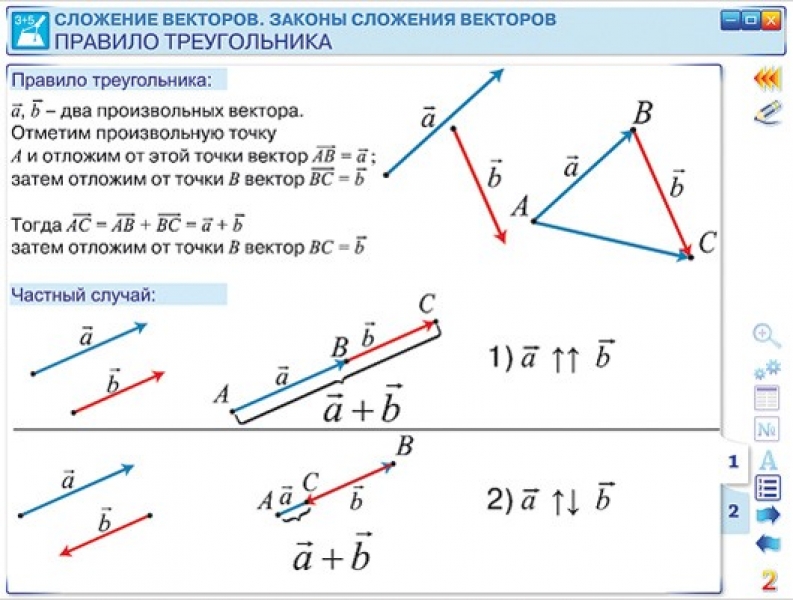
Работу, совершаемую силой над телом, можно определить следующим образом.
Определение: работа, совершаемая силой над телом
Работа, совершаемая силой над телом, зависит от силы, действующей на тело, и расстояние, на которое тело перемещается в направлении действия этой силы по формуле 𝑊=𝐹⋅𝑑(𝜃), потому что где 𝐹 — величина силы, 𝑑 — величина перемещение тела под действием силы, а 𝜃 – угол между направлениями 𝐹 и 𝑑.
Альтернативным способом представления работы, совершаемой силой над телом, является представление сила и перемещение как векторы, а не как величины векторов.
Произведение двух векторов ⃑𝑎 и ⃑𝑏 может быть скалярным произведением векторов, которое определяется как следует.
Определение: Скалярное произведение двух векторов
Скалярное произведение двух векторов определяется как
𝜃 — угол между ⃑𝑎 и
⃑𝑏. Угол берется против часовой стрелки от
от ⃑𝑎 до ⃑𝑏, как показано
следующий рисунок.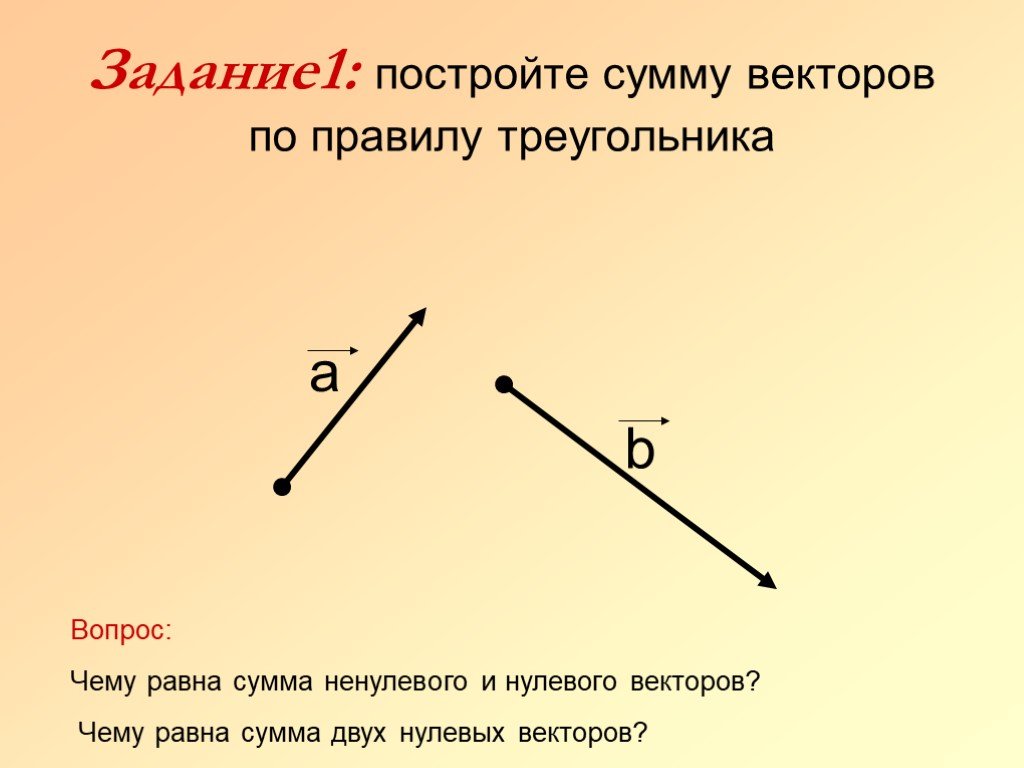
Работа, совершаемая силой с величиной 𝐹 при перемещении с величина 𝑑 равна ⃑𝐹⋅⃑𝑑⃑𝐹⋅⃑𝑑=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃).cos
Графическое представление ⃑𝐹 и ⃑𝑑 показывает, что произведение величины ⃑𝐹 и величина компонента ⃑𝑑 в направлении ⃑𝐹 есть равно ‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃)cos.
Скалярное произведение двух векторов, выраженных в компонентной форме, может быть определено без речь идет об угле между векторами.
Предположим теперь, что векторы ⃑𝐹 и ⃑𝑑 перпендикулярны, как показано на следующем рисунке.
Произведение определяется как ⃑𝐹⋅⃑𝑑=(4,−3)⋅(3,4)⃑𝐹⋅⃑𝑑=(4×3)+(−3×4)=12−12=0.
Скалярное произведение двух перпендикулярных векторов равно нулю. На тело не действуют никакие силы направление перемещения, поэтому сила не действует на тело.
Давайте рассмотрим пример использования векторной записи для определения работы силы.
Пример 1. Расчет работы силы, действующей на частицу, где сила и положение даны в виде векторов
Частица движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Сила
⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку
с вектором положения
−9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.
Сила
⃑𝐹=9⃑𝑖+⃑𝑗N действует на частицу. Частица движется из начала координат в точку
с вектором положения
−9⃑𝑖+6⃑𝑗 м. Найдите работу, совершенную силой.
Ответ
Работа силы равна скалярному произведению вектора силы и вектора смещения частицы. Вопрос не дает вектор смещения, однако он дает вектор положения. В вопросе также указано что частица движется в указанное положение от начала координат, поэтому вектор смещения частицы определяется выражением ⃑𝑑=(−9−0)⃑𝑖+(6−0)⃑𝑗,м который равен заданному вектору положения.
Работа силы 𝑊 определяется скалярным произведением векторов что определяется как 𝑊=(9,1)⋅(−9,6)𝑊=(9×−9)+(1×6)=−81+6=−75.
Таким образом, выполненная работа определяется выражением 𝑊=−75.J
Проделанная работа отрицательна. Если энергия частицы сохраняется,
то кинетическая энергия частицы должна уменьшаться. Если энергия частицы не сохраняется,
вместо этого проделанная работа может увеличить потенциальную энергию частицы.
Теперь давайте рассмотрим пример, когда на тело действуют несколько сил, вызывающих перемещение.
Пример 2. Нахождение работы равнодействующей двух сил, действующих на тело
Тело движется в плоскости, в которой ⃑𝑖 и ⃑𝑗 — перпендикулярные единичные векторы. Две силы ⃑𝐹=9⃑𝑖−2⃑𝑗N и ⃑𝐹=9⃑𝑖−7⃑𝑗N действовать на тело. Частица движется из точки с вектором положения −6⃑𝑖+2⃑𝑗 м к точке 2⃑𝑖+3⃑𝑗 м. Найдите работу равнодействующей сил.
Ответ
На тело действуют две силы. Силы являются векторами, и равнодействующая векторов может определяется суммированием компонент векторов. 𝑥-составляющая результирующей силы определяется выражением ⃑𝐹=9⃑𝑖+9⃑𝑖=18⃑𝑖,R а 𝑦-компонента равнодействующей силы определяется выражением ⃑𝐹=−2⃑𝑗−7⃑𝑗=−9⃑𝑗.R
Следовательно, результирующая сила, действующая на тело, равна
⃑𝐹=18⃑𝑖−9⃑𝑗.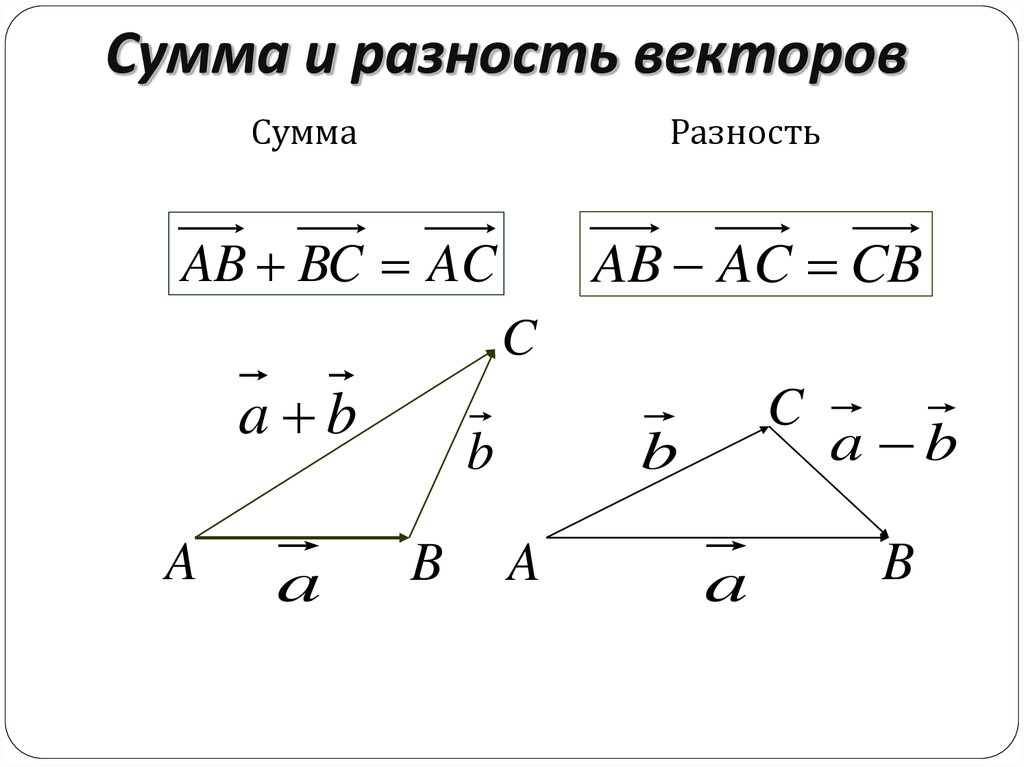 RN
RN
Конечный вектор положения тела равен 2⃑𝑖+3⃑𝑗, а вектор начального положения тела равен −6⃑𝑖+2⃑𝑗.
Таким образом, вектор смещения из начального положения в конечное положение равен ⃑𝑑=2⃑𝑖+3⃑𝑗−−6⃑𝑖+2⃑𝑗⃑𝑑=2−(−6)⃑𝑖+(3−2)⃑𝑗=8⃑𝑖+⃑𝑗.mm
.mm
.mm , у нас есть это
𝑊=⃑𝐹⋅⃑𝑑,R
что дает нам
𝑊=(18,−9)⋅(8,1)𝑊=(18×8)+(−9×1)=144−9=135.J Теперь рассмотрим пример, в котором ни одна из компонент ни вектор силы, ни компоненты вектора смещения не заданы напрямую.
Пример 3. Использование векторов для нахождения работы силы с направлением и величиной, заданными отдельно
Частица переместилась из точки 𝐴(7,−3) в точку
𝐵(−9,2) по прямой под действием
силы ⃑𝐹 величины
8√10 Н
действует в том же направлении, что и вектор
⃑𝑐=−3⃑𝑖−⃑𝑗. Рассчитать работу
совершается силой, учитывая, что величина смещения
измеряется в метрах.
Ответ
Мы можем назвать вектор смещения 𝐴𝐵, ⃑𝑑. Вектор ⃑𝑑 показан с вектором ⃑𝑐 на следующем рисунке.
Вектор ⃑𝑑 задается
⃑𝑑=(−9−7)⃑𝑖+(2−(−3))⃑𝑗=−16⃑𝑖+5⃑𝑗.m
Скалярное произведение ⃑𝑑 и ⃑𝑐
не равно скалярному произведению ⃑𝑑 и ⃑𝐹.
Величина ⃑𝐹 дана, но использовать ⃑𝐹 через точку
расчет продукта, необходимо определить компоненты ⃑𝑖 и ⃑𝑗 ⃑𝐹.
Поскольку ⃑𝐹 действует по линии ⃑𝑐,
⃑𝑖 компонент ⃑𝐹
должна иметь величину, которая
в три раза больше величины ⃑𝑗 компонента ⃑𝐹. Эти отношения
можно выразить как
𝐹=3𝐹.
𝐹 и 𝐹 две стороны прямоугольного треугольника
с гипотенузой длиной 8√10. Поэтому это
в случае, когда
И снова, так как 𝐹=3𝐹,𝐹=24.
Зная компоненты ⃑𝐹, можно выразить ⃑𝐹
как ⃑𝐹=−24⃑𝑖−8⃑𝑗.N
Таким образом, выполненная работа 𝑊
𝑊=(−24,−8)⋅(−16,5)𝑊=(−24×−16)+(−8×5)=384−40=344. J
J
Теперь давайте рассмотрим другой пример, где ни компоненты
вектора силы, ни компоненты вектора смещения не заданы напрямую.
Пример 4. Нахождение работы векторной силы, действующей на тело, движущееся между двумя точками
Частица переместилась из точки 𝐴(−2,−2) в точку
𝐵(6,10) по прямой под действием
сила ⃑𝐹=𝑘⃑𝑖−6⃑𝑗
действующий в направлении, противоположном перемещению 𝐴𝐵. Найдите работу силы ⃑𝐹.
Ответ
Вектор смещения ⃑𝑑 — это вектор, хвост которого находится в точке ⃑𝐴
и его голова в ⃑𝐵. Вектор ⃑𝑑 задается выражением
⃑𝑑=(6−(−2))⃑𝑖+(10−(−2))⃑𝑗=8𝑖+12⃑𝑗.m
Направление ⃑𝑑 𝐴𝐵. Направление, в котором ⃑𝐹
действует противоположно 𝐴𝐵, поэтому ⃑𝐹
должен действовать вдоль прямой 𝐵𝐴𝐵𝐴=−8⃑𝑖−12⃑𝑗
Δ𝑦Δ𝑥=−12−8=32.
Чтобы ⃑𝐹 имел то же направление, что и
𝐵𝐴,
доля 𝑦-компоненты над
его 𝑥-компонента должна быть равна
𝐵𝐴. Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Перестановка, чтобы сделать 𝑘 предмет уравнения дает
3𝑘=−6×2𝑘=−4.
Теперь мы можем выразить ⃑𝐹 как
⃑𝐹=−4⃑𝑖−6⃑𝑗.N
Таким образом, выполненная работа 𝑊 равна
𝑊=(−4,−6)⋅(8,12)𝑊=(−4×8)+(−6×12)=−32−72=−104.J
Неудивительно, что проделанная работа отрицательна, поскольку сила действует в направлении, противоположном перемещению.
Когда энергия частицы, на которую действует сила, сохраняется, путь, который проходит частица, чтобы сместить ее, когда на нее действует сила, не влияет на работу, совершаемую этой силой над частицей.
Теперь рассмотрим пример, в котором рассматривается работа, совершаемая силой за интервал времени.
Пример 5. Определение работы силы при задании смещения во времени
Частица движется в плоскости, в которой ⃑𝑖 и
⃑𝑗 — перпендикулярные единичные векторы. Его водоизмещение
от источника в момент времени 𝑡 секунд
определяется выражением ⃑𝑟=2𝑡+7⃑𝑖+(𝑡+7)⃑𝑗m и на него действует
силой ⃑𝐹=6⃑𝑖+3⃑𝑗Н. Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Ответ
Включение в этот пример не требует, чтобы его решение сильно отличалось от предыдущих примеров, так как скалярные произведения векторов используются таким же образом. Единственная новая особенность, обнаруженная в этом примере, заключается в том, что мы должны найти
перемещения, которые соответствуют двум разным временам.
Смещение частицы при 𝑡=3 с и
𝑡=2с
должны быть определены. Это делается путем замены
3 и 2 как значения 𝑡, чтобы дать
⃑𝑑 и ⃑𝑑,
соответственно, что дает нам
⃑𝑑=2×3+7⃑𝑖+(3+7)⃑𝑗=25⃑𝑖+10⃑𝑗,⃑𝑑=2×2+7⃑𝑖+(2+7)⃑𝑑 15⃑𝑖+9⃑𝑗.мм
Смещение частицы между 𝑡=3 с и
𝑡=2s равно ⃑𝑑
минус ⃑𝑑, заданный
⃑𝑑−⃑𝑑=Δ𝑑=25⃑𝑖+10⃑𝑗−15⃑𝑖+9⃑𝑗=10⃑𝑖+⃑𝑗.m
Скалярное произведение ⃐
и Δ𝑑 дает нам выполненную работу, 𝑊,
между 𝑡=3s и
𝑡=2с. С
⃑𝐹=6⃑𝑖+3⃑𝑗,N
это дано
𝑊=(6,3)⋅(10,1)𝑊=(6×10)+(1×3)=63. J
J
Ключевые точки
- Работа, совершаемая постоянной силой ⃑𝐹 при перемещении
⃑𝑑 равно скалярному произведению
⃑𝐹 и ⃑𝑑,
𝑊=⃑𝐹⋅⃑𝑑,
или 𝑊=‖‖⃑𝐹‖‖‖‖⃑𝑑‖‖(𝜃), cos
где 𝜃 — угол между ⃑𝐹 и ⃑𝑑.
- Скалярное произведение ⃑𝐹 и ⃑𝑑 можно определить без использования угла 𝜃
выражая ⃑𝐹 и ⃑𝑑 в компонентной форме.
- Если компоненты ⃑𝐹 и ⃑𝑑
находятся в перпендикулярных направлениях ⃑𝑖 и
⃑𝑗, то
⃑𝐹⋅⃑𝑑=𝐹,𝐹⋅𝑑,𝑑=(𝐹𝑑)+𝐹𝑑.
2.4 Работа с векторами | Введение в R
Манипулирование, суммирование и сортировка данных с помощью R — важный навык, который нужно освоить, но который поначалу многим кажется немного запутанным. Здесь мы рассмотрим несколько простых примеров с использованием векторов, чтобы проиллюстрировать некоторые важные концепции, но остановимся на этом более подробно в главе 3, где мы рассмотрим более сложные (и полезные) структуры данных.
Посмотрите это видео для быстрого ознакомления с работой с векторами в R с использованием позиционных и логических индексов
2.4.1 Извлечение элементов обычно называемые элементами) из вектора мы используем обозначение квадратной скобки
[ ] . Общий подход заключается в том, чтобы назвать объект, из которого вы хотите извлечь, а затем набор квадратных скобок с индексом элемента, который вы хотите извлечь, заключенный в квадратные скобки. Этот индекс может быть позицией или результатом логического теста. Позиционный индекс
Чтобы извлечь элементы на основе их позиции, мы просто записываем позицию внутри [ ] . Например, чтобы извлечь третье значение my_vec
my_vec # напомним себе, как выглядит my_vec
## [1] 2 3 1 6 4 3 3 7
my_vec[3] # извлечь третье значение
## [1] 1
# если вы хотите сохранить это значение в другом объекте
val_3 <- my_vec[3]
значение_3
## [1] 1
Обратите внимание, что позиционный индекс начинается с 1, а не с 0, как в некоторых других языках программирования (например, Python).
Мы также можем извлечь более одного значения, используя функцию c() внутри квадратных скобок. Здесь мы извлекаем элементы 1 st , 5 th , 6 th и 8 th из объекта my_vec
my_vec[c(1, 5, 6, 8)]
## [1] 2 4 3 7
Или мы можем извлечь диапазон значений, используя нотацию : . Чтобы извлечь значения из 3 rd в 8 th элементов
my_vec[3:8]
## [1] 1 6 4 3 3 7
Логический индекс
Еще один действительно полезный способ извлечения данных из вектора — использование логического выражения в качестве индекса. Например, чтобы извлечь все элементы со значением больше 4 в векторе my_vec
my_vec[my_vec > 4]
## [1] 6 7
Здесь логическое выражение my_vec > 4 , и R будет извлекать только те элементы, которые удовлетворяют этому логическому условию. Так как же это на самом деле работает? Если мы посмотрим на вывод только логического выражения без квадратных скобок, то увидим, что R возвращает вектор, содержащий либо ИСТИНА или ЛОЖЬ , которые соответствуют тому, выполняется ли логическое условие для каждого элемента. В этом случае только элементы 4 th и 8 th возвращают
В этом случае только элементы 4 th и 8 th возвращают TRUE , поскольку их значение больше 4.
my_vec > 4
## [1] FALSE FALSE FALSE TRUE FALSE FALSE FALSE TRUE
То, что на самом деле делает R под капотом, эквивалентно
my_vec[c(FALSE, FALSE, FALSE, TRUE, FALSE, FALSE, FALSE, TRUE)]
## [1] 6 7
, и будут извлечены только те элементы, которые TRUE .
В дополнение к операторам < и > вы также можете использовать составные операторы для увеличения сложности ваших выражений. Например, выражение «больше или равно» будет >= . Чтобы проверить, равно ли значение значению, нам нужно использовать двойной символ равенства == , а для «не равно» мы используем != (символ ! означает «не»).
my_vec[my_vec >= 4] # значения больше или равны 4
## [1] 6 4 7
my_vec[my_vec < 4] # значения меньше 4
## [1] 2 3 1 3 3
my_vec[my_vec <= 4] # значения меньше или равные 4
## [1] 2 3 1 4 3 3
my_vec[my_vec == 4] # значения равны 4
## [1] 4
my_vec[my_vec != 4] # значения не равны 4
## [1] 2 3 1 6 3 3 7
Мы также можем комбинировать несколько логических выражений, используя логические выражения. В R символы
В R символы и означают И, а | Символ означает ИЛИ. Например, чтобы извлечь из my_vec значения, которые меньше 6 И больше 2
val26 <- my_vec[my_vec < 6 & my_vec > 2]
значение26
## [1] 3 4 3 3
или извлечь из my_vec значения, которые больше 6 ИЛИ меньше 3
val63 <- my_vec[my_vec > 6 | мой_век < 3]
val63
## [1] 2 1 7
2.4.2 Замена элементов
Мы можем изменить значения некоторых элементов в векторе, используя нашу [ ] в сочетании с оператором присваивания <- . Например, чтобы заменить значение 4 th нашего объекта my_vec с 6 на 500
my_vec[4] <- 500
my_vec
## [1] 2 3 1 500 4 3 3 7
Мы также можем заменить более одного значения или даже заменить значения на основе логического выражения
# заменить 6-й и 7-й элементы на 100
my_vec[c(6, 7)] <- 100
my_vec
## [1] 2 3 1 500 4 100 100 7
# заменить элемент меньше или равный 4 на 1000
my_vec[my_vec <= 4] <- 1000
my_vec
## [1] 1000 1000 1000 500 1000 100 100 7
2.
 4.3 Упорядочивание элементов
4.3 Упорядочивание элементов В дополнение к извлечению определенных элементов из вектора мы также можем упорядочить значения, содержащиеся в векторе. Чтобы отсортировать значения от наименьшего к наибольшему значению, мы можем использовать функцию sort()
vec_sort <- sort(my_vec)
vec_sort
## [1] 7 100 100 500 1000 1000 1000 1000
Для обращения сортировки от высшего к низшему мы можем либо включить аргумент по убыванию = ИСТИНА при использовании sort() функция
vec_sort2 <- sort(my_vec, по убыванию = TRUE)
vec_sort2
## [1] 1000 1000 1000 1000 500 100 100 7
или сначала отсортируйте вектор с помощью функции sort() , а затем переверните отсортированный вектор с помощью функции rev() . Это еще один пример вложения одной функции в другую.
vec_sort3 <- rev(sort(my_vec))
vec_sort3
## [1] 1000 1000 1000 1000 500 100 100 7
Хотя сортировка одного вектора — это весело, возможно, более полезной задачей будет сортировка одного вектора в соответствии со значениями другого вектора. Для этого мы должны использовать
Для этого мы должны использовать функция order() в сочетании с [ ] . Чтобы продемонстрировать это, давайте создадим вектор с именем height , содержащий рост 5 разных людей, и другой вектор с именем p.names , содержащий имена этих людей (таким образом, Джоанна 180 см, Шарлотта 155 см и т. д.)
height < - с(180, 155, 160, 167, 181)
высота
## [1] 180 155 160 167 181
p.names <- c("Джоанна", "Шарлотта", "Хелен", "Карен", "Эми")
p.names
## [1] «Джоанна» «Шарлотта» «Хелен» «Карен» «Эми» Наша цель - упорядочить людей в p.names в порядке возрастания их роста . Первое, что мы сделаем, это воспользуемся функцией order() с переменной height для создания вектора с именем height_ord
height_ord <- order(height)
высота_орд
## [1] 2 3 4 1 5
Хорошо, что здесь происходит? Первое значение, 2 (помните, игнорируйте [1] ) следует читать как «наименьшее значение высоты — второй элемент вектора высоты ». Если мы проверим это, взглянув на вектор
Если мы проверим это, взглянув на вектор height выше, вы увидите, что элемент 2 имеет значение 155, что является наименьшим значением. Второе наименьшее значение в высоте — это 3 rd элемента высоты , который при проверке равен 160 и так далее. Наибольшее значение height — это элемент 5 , который равен 181. Теперь, когда у нас есть вектор позиционных индексов высот в порядке возрастания ( height_ord ), мы можем извлечь эти значения из нашего вектора p.names в следующем порядке:
names_ord <- p.names[height_ord]
имена_орд
## [1] «Шарлотта» «Хелен» «Карен» «Джоанна» «Эми»
Вы, вероятно, думаете: «Какая польза от этого?» Представьте, что у вас есть набор данных, который содержит два столбца данных, и вы хотите отсортировать каждый столбец. Если вы просто используете sort() для сортировки каждого столбца отдельно, значения каждого столбца станут несвязанными друг с другом. Используя «order()» в одном столбце, вектор позиционных индексов создается из значений столбца в порядке возрастания. Этот вектор можно использовать во втором столбце в качестве индекса элементов, который вернет вектор значений. на основе первого столбца.
Используя «order()» в одном столбце, вектор позиционных индексов создается из значений столбца в порядке возрастания. Этот вектор можно использовать во втором столбце в качестве индекса элементов, который вернет вектор значений. на основе первого столбца.
2.4.4 Векторизация
Одна из замечательных особенностей функций R заключается в том, что большинство из них векторизованы. Это означает, что функция будет работать со всеми элементами вектора без необходимости применять функцию к каждому элементу отдельно. Например, чтобы умножить каждый элемент вектора на 5, мы можем просто использовать
# создать вектор
my_vec2 <- c(3, 5, 7, 1, 9, 20)
# умножаем каждый элемент на 5
мой_vec2 * 5
## [1] 15 25 35 5 45 100
Или мы можем добавить элементы двух или более векторов
# создаем второй вектор
my_vec3 <- c(17, 15, 13, 19, 11, 0)
# добавляем оба вектора
мой_век2 + мой_век3
## [1] 20 20 20 20 20 20
# умножить оба вектора
мой_век2 * мой_век3
## [1] 51 75 91 19 99 0
Однако вы должны быть осторожны при использовании векторизации с векторами разной длины, так как R будет спокойно перерабатывать элементы в более коротком векторе, а не выдавать шаткий (ошибка).
# создаем третий вектор
my_vec4 <- c(1, 2)
# добавляем оба вектора - тихая переработка!
мой_век2 + мой_век4
## [1] 4 7 8 3 10 22
2.4.5 Отсутствующие данные
В R отсутствующие данные обычно обозначаются символом NA , означающим «Недоступно». Данные могут отсутствовать по целому ряду причин, может быть, ваша машина сломалась, может быть, вы сломались, может быть, погода была слишком плохой для сбора данных в определенный день и т. д. Отсутствующие данные могут быть болью в поговорке как от R перспектива, а также статистическая перспектива. С точки зрения R отсутствующие данные могут быть проблематичными, поскольку разные функции обрабатывают отсутствующие данные по-разному. Например, допустим, мы собирали показания температуры воздуха за 10 дней, но наш термометр сломался на 2-й день и снова на 9-й день.поэтому у нас нет данных для тех дней
temp <- c(7.2, NA, 7.1, 6.9, 6.5, 5.8, 5.8, 5.5, NA, 5.5)
температура
## [1] 7.2 NA 7.1 6.9 6. 5 5.8 5.8 5.5 NA 5.5
5 5.8 5.8 5.5 NA 5.5
Теперь мы хотим рассчитать среднюю температуру за эти дни, используя функцию mean()
mean_temp <- mean(temp)
средняя_температура
## [1] NA
Флиппин, черт возьми, что здесь произошло? Почему функция mean() возвращает NA ? На самом деле, R делает что-то очень разумное (по крайней мере, на наш взгляд!). Если вектор имеет отсутствующее значение, то единственное возможное значение, которое можно вернуть при вычислении среднего, равно 9.0155 Н/Д . R не знает, что вы, возможно, хотите игнорировать значения NA (R еще не умеет читать ваши мысли!). К счастью, если мы посмотрим на файл справки (используйте help("mean") — см. следующий раздел для более подробной информации), связанный с функцией mean() , мы увидим, что есть аргумент na.rm = для которого по умолчанию установлено значение FALSE .
na.rm — логическое значение, указывающее, следует ли удалять значения NA перед продолжением вычисления.
 J
J Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32.
Следовательно, мы имеем это
Δ𝑦Δ𝑥=−6𝑘=32. Какую работу совершает сила между 𝑡=2с и
𝑡=3s?
Какую работу совершает сила между 𝑡=2с и
𝑡=3s? J
J
[ ] . Например, чтобы извлечь третье значение my_vec 
функцию c() внутри квадратных скобок. Здесь мы извлекаем элементы 1 st , 5 th , 6 th и 8 th из объекта my_vec : . Чтобы извлечь значения из 3 rd в 8 th элементов my_vec my_vec > 4 , и R будет извлекать только те элементы, которые удовлетворяют этому логическому условию. Так как же это на самом деле работает? Если мы посмотрим на вывод только логического выражения без квадратных скобок, то увидим, что R возвращает вектор, содержащий либо ИСТИНА или ЛОЖЬ , которые соответствуют тому, выполняется ли логическое условие для каждого элемента. В этом случае только элементы 4 th и 8 th возвращают
В этом случае только элементы 4 th и 8 th возвращают TRUE , поскольку их значение больше 4. TRUE . < и > вы также можете использовать составные операторы для увеличения сложности ваших выражений. Например, выражение «больше или равно» будет >= . Чтобы проверить, равно ли значение значению, нам нужно использовать двойной символ равенства == , а для «не равно» мы используем != (символ ! означает «не»). В R символы
В R символы и означают И, а | Символ означает ИЛИ. Например, чтобы извлечь из my_vec значения, которые меньше 6 И больше 2 my_vec значения, которые больше 6 ИЛИ меньше 3 [ ] в сочетании с оператором присваивания <- . Например, чтобы заменить значение 4 th нашего объекта my_vec с 6 на 500 sort() по убыванию = ИСТИНА при использовании sort() функция sort() , а затем переверните отсортированный вектор с помощью функции rev() . Это еще один пример вложения одной функции в другую. Для этого мы должны использовать
Для этого мы должны использовать функция order() в сочетании с [ ] . Чтобы продемонстрировать это, давайте создадим вектор с именем height , содержащий рост 5 разных людей, и другой вектор с именем p.names , содержащий имена этих людей (таким образом, Джоанна 180 см, Шарлотта 155 см и т. д.) p.names в порядке возрастания их роста . Первое, что мы сделаем, это воспользуемся функцией order() с переменной height для создания вектора с именем height_ord 2 (помните, игнорируйте [1] ) следует читать как «наименьшее значение высоты — второй элемент вектора высоты ».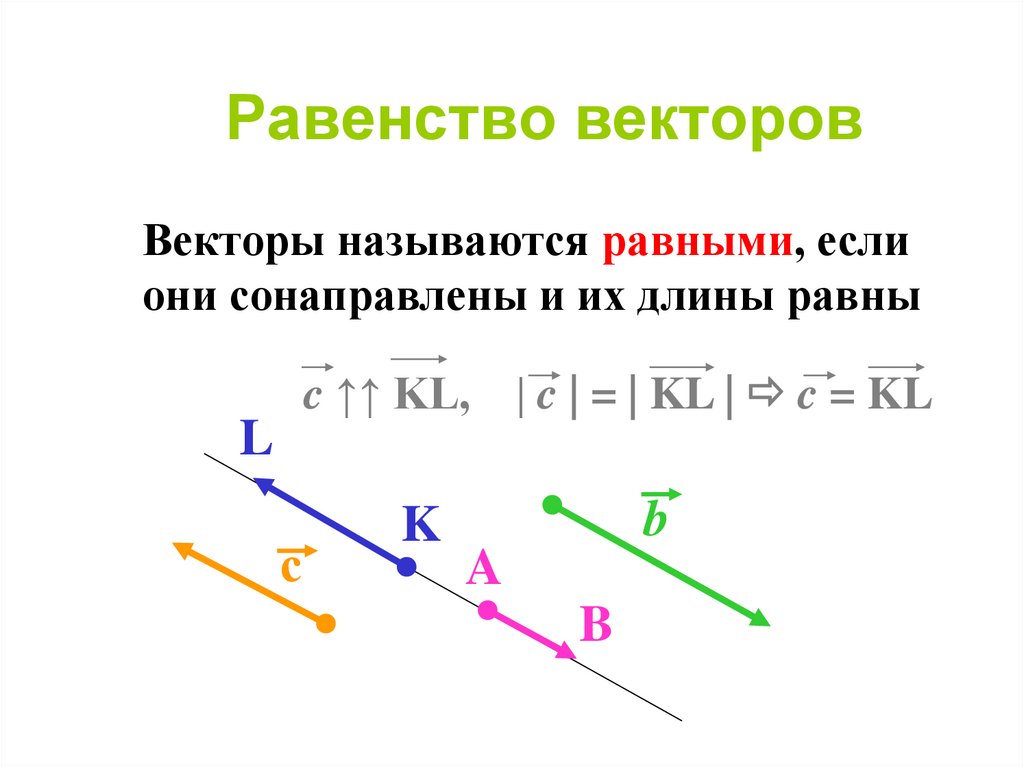 Если мы проверим это, взглянув на вектор
Если мы проверим это, взглянув на вектор height выше, вы увидите, что элемент 2 имеет значение 155, что является наименьшим значением. Второе наименьшее значение в высоте — это 3 rd элемента высоты , который при проверке равен 160 и так далее. Наибольшее значение height — это элемент 5 , который равен 181. Теперь, когда у нас есть вектор позиционных индексов высот в порядке возрастания ( height_ord ), мы можем извлечь эти значения из нашего вектора p.names в следующем порядке: sort() для сортировки каждого столбца отдельно, значения каждого столбца станут несвязанными друг с другом. Используя «order()» в одном столбце, вектор позиционных индексов создается из значений столбца в порядке возрастания. Этот вектор можно использовать во втором столбце в качестве индекса элементов, который вернет вектор значений. на основе первого столбца.
Используя «order()» в одном столбце, вектор позиционных индексов создается из значений столбца в порядке возрастания. Этот вектор можно использовать во втором столбце в качестве индекса элементов, который вернет вектор значений. на основе первого столбца.
NA , означающим «Недоступно». Данные могут отсутствовать по целому ряду причин, может быть, ваша машина сломалась, может быть, вы сломались, может быть, погода была слишком плохой для сбора данных в определенный день и т. д. Отсутствующие данные могут быть болью в поговорке как от R перспектива, а также статистическая перспектива. С точки зрения R отсутствующие данные могут быть проблематичными, поскольку разные функции обрабатывают отсутствующие данные по-разному. Например, допустим, мы собирали показания температуры воздуха за 10 дней, но наш термометр сломался на 2-й день и снова на 9-й день.поэтому у нас нет данных для тех дней 5 5.8 5.8 5.5 NA 5.5
5 5.8 5.8 5.5 NA 5.5 mean() mean() возвращает NA ? На самом деле, R делает что-то очень разумное (по крайней мере, на наш взгляд!). Если вектор имеет отсутствующее значение, то единственное возможное значение, которое можно вернуть при вычислении среднего, равно 9.0155 Н/Д . R не знает, что вы, возможно, хотите игнорировать значения NA (R еще не умеет читать ваши мысли!). К счастью, если мы посмотрим на файл справки (используйте help("mean") — см. следующий раздел для более подробной информации), связанный с функцией mean() , мы увидим, что есть аргумент na.rm = для которого по умолчанию установлено значение FALSE . na.rm — логическое значение, указывающее, следует ли удалять значения NA перед продолжением вычисления.




 4.3 Упорядочивание элементов
4.3 Упорядочивание элементов