При включении какого-либо конденсатора в электрическую цепь постоянного тока, происходит возникновение быстрого кратковременного импульса. С его помощью конденсатор заряжается до такой же степени, как источник энергии, после чего, всяческое движение электрического тока прекращается. Если его отключить от источника тока, то в очень скором времени, под воздействием нагрузки наступит полная разрядка. Когда в качестве индикатора подключается лампа, она моргает один раз, а, затем, гаснет, поскольку разрядка конденсатора при постоянном токе происходит в виде кратковременного импульса. Работа конденсатора при переменном токеСовершенно по-другому работает конденсатор в цепи переменного тока. В данном случае, конденсатор заряжается и разряжается, чередуясь с периодичностью колебаний, возникающих при переменном напряжении. Такая же лампа накаливания, помещенная в цепь в качестве индикатора, и подключенная последовательно, будет аналогично конденсатору излучать непрерывный свет, потому что частота колебаний промышленного уровня не воспринимается человеческим глазом.
В каждом конденсаторе имеется емкостное сопротивление, от которого зависят емкость и частота циклов переменного тока. По формуле, такая зависимость получается обратно пропорциональная. При наличии такого сопротивления не происходит превращения электрической и магнитной энергии в тепловую. При более высокой частоте электрического тока, емкостное сопротивление пропорционально снижается, и, наоборот. Эти важные свойства позволили применять конденсаторы в цепи переменного электрического тока в качестве гасящего элемента взамен резисторов в делителях напряжения. Данный фактор имеет особо важное значение при падениях напряжения. В подобной ситуации, вместо конденсатора пришлось бы применять мощные резисторы с большими размерами. Основное свойство конденсаторовПоскольку конденсатор в цепи переменного тока не подвержен нагреву, то и не наступает рассеивание энергии. Это обусловлено смещением между собой тока и напряжения в конденсаторе на 90 градусов. При наибольшем напряжении, ток имеет нулевое значение, а значит, не совершается никакой Однако, свое широкое применение конденсаторы нашли в различных видах частотных фильтров и резонансных схемах. |
Урок 45. Лабораторная работа № 11. Исследование зависимости силы тока от электроемкости конденсатора в цепи переменного тока
Лабораторная работа №11
Исследование зависимости силы тока от электроёмкости конденсатора в цепи переменного тока
Цель работы: изучить влияние электроёмкости на силу переменного тока.
Оборудование: набор неполярных конденсаторов известной ёмкости, регулируемый источник переменного тока ЛАТР, миллиамперметр с пределом измерения до 100 мА переменного тока, вольтметр с пределом измерения до 75 В переменного напряжения, соединительные провода.
Теория
Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.
Если же включить конденсатор в цепь переменного тока, то заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течёт переменный ток. Сила тока тем больше, чем больше ёмкость конденсатора и чем чаще происходит его перезарядка, т.е. чем больше частота переменного тока.
Сопротивление, обусловленное наличием электрической ёмкости в цепи переменного тока, называют ёмкостным сопротивлением XC. Оно обратно пропорционально ёмкости С и круговой частоте ω:
или, с учётом, что ω=2πν, где ν- частота переменного тока, (1).
Из закона Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление, действующее значение тока в цепи равно: (2).
Из формулы (2) следует, что в цепи с конденсатором переменный ток изменяется прямо пропорционально изменению ёмкости конденсатора при неизменной частоте тока.
Графически зависимость силы тока от электроёмкости конденсатора в цепи переменного тока изображается прямой линией (рис.1).
В этом и предстоит убедиться опытным путём в данной работе.
Ход работы.
1. Собрать электрическую схему согласно рисунка 2 и перечертить её в тетрадь:
2. Подготовить таблицу для результатов измерений и вычислений:
|
Частота тока ν, Гц |
Напряжение на конденсаторе U, В |
Ёмкость конденсатора С, мкФ |
Ток в цепи I, мА |
Ёмкостное сопротивление , Ом |
|
|
измеренное |
вычисленное |
||||
|
50 |
50 |
|
|
||
|
|
|||||
|
|
|
||||
|
|
|
||||
|
|
|
||||
3. Для каждого конденсатора из набора измерить силу тока при напряжении 50 В.
4. В каждом опыте рассчитать ёмкостное сопротивление по закону Ома для участка цепи переменного тока: , здесь I — действующее значение тока в мА, U=50 В — действующее значение напряжения.
5. В каждом опыте вычислите ёмкостное сопротивление по заданным значениям частоты переменного тока ν=50Гц и ёмкости конденсатора С: , здесь С — ёмкость в мкФ.
6. Сравните результаты расчётов в п.4 и в п.5 и сделайте вывод о выполнимости закона Ома для участка цепи переменного тока содержащего электроёмкость с учётом погрешности измерений.
7. Постройте график зависимости силы тока от электроёмкости конденсатора в цепи переменного тока:
8. Запишите вывод по результатам опытов и ответьте на контрольные вопросы.
Контрольные вопросы.
1. Почему постоянный ток не проходит через конденсатор?
2. Какое сопротивление называется ёмкостным? Почему оно является реактивным сопротивлением?
3. От чего и как зависит ёмкостное сопротивление?
4. Выполняется ли закон Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление?
5. Напряжение на конденсаторе изменяется по закону . Запишите уравнение переменного тока в цепи с конденсатором.
Конденсатор в цепи переменного тока
Физика > Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы
Изучите колебание, емкость, сопротивление и напряжение конденсатора в цепи переменного тока: использование фазового вектора, диаграмма, закон Ома, уравнения.
Напряжение на конденсаторе отстает от тока. Из-за разности фаз лучше всего ввести фазоры, чтобы охарактеризовать схемы.
Задача обучения
- Разобраться в преимуществе применения фазора.
Основные пункты
- Если конденсатор присоединен к переменному напряжению, то максимальное выступает пропорциональным максимальному току. Но они не возникают одновременно.
- Если питание переменного тока присоединено к резистору, то ток и напряжение выступают пропорциональными по отношению друг к другу. То есть, они достигнут пика в одно время.
- Среднеквадратичный ток в цепи с конденсатором определяется версией закона Ома: Irms = Vrms/XC, где XС – емкостное сопротивление.
Термины
- RMS – среднеквадратичное число; статическая мера величины.
Фазор
Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.
К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Aeiθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.

Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0
Конденсаторы в цепях переменного тока
Если питание переменного тока присоединено к резистору, то ток и напряжение выступают пропорциональными. То есть, достигают пика в одно время. Если к переменному напряжению подключен конденсатор, то максимальные ток и напряжение пропорциональны. Ток достигает максимума в точке ¼ цикла пикового напряжения (приводит к 90°).

Максимумы тока на ¼ цикла напряжения, в случаях, когда к переменному напряжению присоединен конденсатор
Для схемы с конденсатором значение V/I не выступает постоянным. Но Vmax/Imax полезное и именуется емкостью сопротивления. Это все еще напряжение, деленное на ток, а единица – Ом. Значение XC основывается на емкости и частоте: 
Конденсатор влияет на ток и при полном заряде способен полностью его остановить. Напряжение переменного тока поступает постоянно, поэтому есть среднеквадратичный ток, ограниченный конденсатором. Это эффективное сопротивление конденсатора к переменному току, поэтому среднеквадратичное (Irms) определяется версией закона Ома:
 (Vrms – среднеквадратичное напряжение).
(Vrms – среднеквадратичное напряжение).
Фазовое представление
Напряжение на конденсаторе в цепи переменного тока не поспевает за током, поэтому фазовый вектор повторяет его движение. На диаграмме стрелки совершают обороты против часовой стрелки в частоте v.

Схема фазора для цепи переменного тока с конденсатором
Поведение конденсатора в цепи переменного тока
Если говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут.
Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора.
Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор.
Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой хс и так же, как и обычное сопротивление, измеряется в омах. Величина хс зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:

Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора.
Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением хс=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).
Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи Ссв (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость Ссв нельзя брать слишком малой.
Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк Ск можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура — даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя — на контуре и подключенной к нему цепи детектор — телефон.


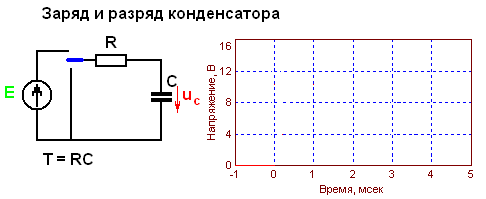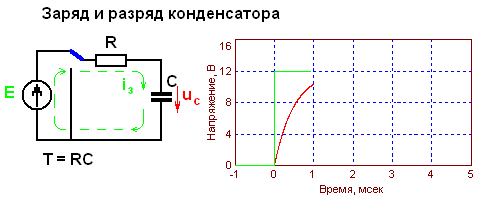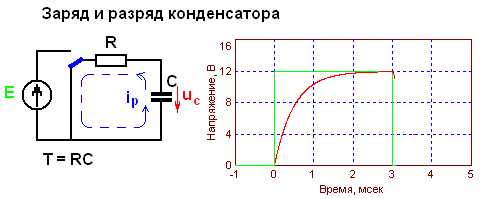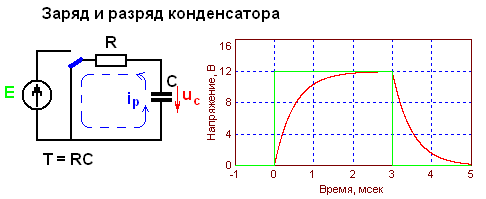
 работы и нагрева не происходит. Поэтому, конденсаторы в большинстве случаев, вполне успешно используются взамен резисторов. При этом, у них образуется недостаток, который должен быть учтен в обязательном порядке. Он заключается в изменении переменного тока в цепи, вызывающего изменение напряжения в нагрузке. Другим недостатком является отсутствие гальванической развязки, в связи с чем применение их имеет определенные ограничения и их используют при стабильном значении сопротивления. Такими нагрузками, чаще всего, выступают нагревательные элементы.
работы и нагрева не происходит. Поэтому, конденсаторы в большинстве случаев, вполне успешно используются взамен резисторов. При этом, у них образуется недостаток, который должен быть учтен в обязательном порядке. Он заключается в изменении переменного тока в цепи, вызывающего изменение напряжения в нагрузке. Другим недостатком является отсутствие гальванической развязки, в связи с чем применение их имеет определенные ограничения и их используют при стабильном значении сопротивления. Такими нагрузками, чаще всего, выступают нагревательные элементы.