Задача 2 — разбор задания ЕГЭ по предмету Информатика
- Newtonew
- ProTeachers
- MOOC 2016
- Большая переменная
Мы в соц.сетях:
- Статьи
- ·
- Разборы
- ·
- Новости
Написать статью
Решение №1
Давайте сначала определимся с тем, что у нас есть в задаче:
- логическая функция F, заданная некоторым выражением. Элементы таблицы истинности этой функции также представлены в задаче в виде таблицы. Таким образом, при подстановке конкретных значений x, y, z из таблицы в выражение результат должен совпасть с тем, который дан в таблицы (см.
 пояснение ниже).
пояснение ниже). - Переменные x, y, z и три столбца, которые им соответствуют. При этом мы в этой задаче не знаем, какой столбец какой переменной соответствует. То есть, в столбце Перем. 1 может быть как x, так и y или z.
- Нас просят как раз определить, какой столбец какой переменной соответствует.
Рассмотрим пример.
- Пусть Перем. 1 — это x, Перем. 2 — это y, Перем. 3 — это z.
- Рассмотрим, к примеру, вторую строку таблицы (можно было бы взять любую). В ней x = 0, y = 0, z = 1.
- При этом, согласно таблице, выражение F должно равняться 1.
ЕГЭ 2016, задача 2. Логическая функция F и таблица истинности.
Давайте подставим значения x,y,z в нашу формулу:
\((\neg z) \wedge x \vee x\wedge y = \\ = (\neg 1) \wedge 0 \vee 0\wedge 0 = \\ = 0\wedge 0 \vee 0\wedge 0 = \\ = 0 \vee 0 = 0\)- То есть, путём подстановки мы получили результат 0, хотя согласно таблице истинности результат должен равняться 1.
- Таким образом, невозможно, чтобы Перем.
 1 была x, Перем. 2 — y, а Перем. 3 — z, так как в этом случае результат подстановки формулы в таблицу в строку 2 не сходится со значением, указанным в этой же таблице.
1 была x, Перем. 2 — y, а Перем. 3 — z, так как в этом случае результат подстановки формулы в таблицу в строку 2 не сходится со значением, указанным в этой же таблице.
Решение
- Вернёмся теперь к решению. Давайте внимательно посмотрим на формулу: \((\neg z) \wedge x \vee x\wedge y\)
- В ней имеется две конструкции с конъюнкцией, соединённые дизъюнкцией. Как известно, чаще всего дизъюнкция истинна (для этого достаточно, чтобы одно из слагаемых было истинным).
- Давайте рассмотрим тогда внимательно строчки, где выражение F — ложно.
- Первая строчка нам неинтересна, так как в ней не определить, где что (все значения одинаковы).
- Рассмотрим тогда предпоследнюю строчку, в ней больше всего 1, но результат равен 0.
- Может ли z быть в третьем столбце? Нет, так как в этом случае в формуле будут везде 1, а, следовательно, и результат будет равняться 1, но согласно таблице истинности значение F в этой строке равно 0. Следовательно, z не может быть Перем.
 3.
3. - Аналогично для предыдущей строки имеем, что z не может быть Перем. 2.
- Следовательно, z — это Перем. 1
- Зная, что z — в первом столбце, рассмотрим третью строчку. Может ли x быть во втором столбце? Подставим значения:
\((\neg z) \wedge x \vee x\wedge y = \\ = (\neg 0) \wedge 1 \vee 1\wedge 0 = \\ = 1 \wedge 1 \vee 0 = \\ = 1 \vee 0 = 1\) - Однако, согласно таблице истинности, результат должен равняться 0.
- Следовательно, х не может быть Перем. 2.
- Следовательно, x — это Перем. 3.
- Следовательно, по методу исключения, y — это Перем. 2.
- Таким образом, ответ звучит следующим образом: zyx (z — Перем. 1, y — Перем. 2, x — Перем. 3).
Evgeny Smirnov
Сообщение:
Запрос успешно отправлен. В ближайшее время расширенный доступ будет предоставлен.
– Oбразование как Стиль ЖизниПрисылайте свои колонки
и предложения
У вас есть интересная новость
или материал из сферы образования
или популярной науки?
Расскажите нам!
[email protected]
© 2014-2023 Newtonew. 12+
12+
Просветительский медиа-проект об образовании,
посвящённый самым актуальным и полезным
концепциям, теориям и методикам, технологиям
и исследованиям, продуктам и сервисам. Мы
говорим о том, как развиваются и изменяются
образование и наука.
ЕГЭ спецпроект ProTeachers
MOOC 2016 Большая переменная
Физика: игра света
Маршрут в будущее
Считаные годы
Образование XXI века
Мы используем файлы cookie для улучшения пользовательского опыта. Подробнее вы можете посмотреть в нашем пользовательском соглашении.
App Store Google Play
Подписаться на рассылку
Авторизация на сайте
Вход через соц.сети:
ВКонтакте Facebook Google
Новый пользователь
Введите ваш email:
Введите пароль:
Повторите пароль:
назад
Напомнить пароль
Введите email, на который вы зарегистрированы:
назад
Пароль выслан
Мы выслали ваш пароль для входа в систему на указанный email.
Не забывайте о том, что вы можете авторизоваться в системе через социальные сети. Если при регистрации в соц.сетях вы указывали тот же email что и на нашем сайте, то после авторизации вы попадете в свой профиль.
Вход через соц.сети:
ВКонтакте Facebook Google
Подтвердите регистрацию
На указанный e-mail было отправлено письмо со ссылкой. Пожалуйста, перейдите по ссылке для подтверждения.
Вход через соц.сети:
ВКонтакте Facebook Google
Регистрация подтверждена
Вы успешно зарегистрировались
Способы задания функций алгебры логики.
При сопоставлении функций АЛ с дискретными автоматами аргументы функций, сопоставляются с входами, а сами функции с выходами дискретного автомата.
Поскольку
дискретный автомат имеет конечное число
входов, то мы будем иметь дело с функцией
конечного числа аргументов. Если автомат
имеет m входов, то количество входных
переменных тоже m и число возможных
комбинаций наборов значений этих входных
аргументов (переменных) К=2
Поскольку автомат имеет конечное число входов, его состояние описывается конечным числом значений функций выходов. Существует несколько способов задания функций АЛ и дискретного автомата.
1. Табличный способ. При этом способе функция задается в виде таблицы истинности, представляющей собой совокупность всех наборов переменных и соответствующих им значений функции.
Таблица истинности содержит 2m строк, m столбцов (по количеству входов) и один столбец для записи значения функции.
Например: пусть требуется задать функцию трех переменных F1(Х1,Х2,Х3) (рис. 1.4), т.е. автомат на три входа и на один выход, следовательно, M=3, К=8.
Следующий
способ задания дискретного автомата – числовой. В Этом случае функция задается в виде
десятичных эквивалентов номеров наборов
аргументов, при которых функция принимает
единичное значение.
.
Координатный способ. При этом способе дискретный автомат задается с помощью карты его состояния, которая известна как карта Карно.
Карта Карно содержит 2m клеток по числу наборов значений переменных. Каждая клетка определяется координатами строк и столбцов, соответствующими определенному набору переменных. Все входные переменные разбиваются на 2 группы так, что одна группа определяет координаты строк, а другая — координаты столбцов. В каждой клетке карты Карно проставляется соответствующее значение функции на заданном наборе. Пример задания функции трех переменных приведен на рис. 1.5. Числовое выражение этой функции выглядит так:
Пример
построения карты Карно для функции 4-х
переменных. Пусть функция задана в
числовой форме и имеет вид:
Пусть функция задана в
числовой форме и имеет вид:
,
следовательно, К=16, m=4.
Сначала проводим разметку координат карты Карно без указания значений функции. Для удобства воспользуемся указанием «шапки» в виде прямых линий, “под” которыми переменные входят в значение координат без отрицания (рис.1.6). Таким образом, по столбцам и по строкам переменные входят без отрицания в пределах линии-шапки.
Для
наглядности координаты клеток карты
Карно указаны в трех формах: в виде
наборов переменных; в виде двоичного
числа, соответствующего порядковому
номеру набора переменных; в десятичном
эквиваленте номеров наборов переменных.
На практике координаты внутри клеток
не записывают (рис. 1.7), в клетках
указываются единичные значения функции,
соответствующие “координатным” наборам
переменных. Нулевые значения функции
в клетки можно не записывать, т.е. клетки,
координаты которых определяются наборами
переменных с нулевыми значениями
функции, можно оставить пустыми.
Следует отметить, что перестановка местами переменных Х1 и Х2, а так же переменных Х3 и Х4 допускается, допускается также перестановка местами переменных Х1Х2 и Х4Х3. При построении карты Карно, т.е. при задании логической функции, указывают лишь внешние элементы разметки координат (рис. 1.7).
Аналитический способ задания функции алгебры логики. При этом способе функция задается в виде аналитического выражения, полученного путем применения каких-либо логических операций.
Например: .
Совершенная нормальная дизъюнктивная форма (СНДФ). По таблице истинности можно составить логическое выражение, содержащее наборы переменных, в которые входят все переменные с отрицанием или без. Одна из его форм называется СНДФ.
В
качестве примера получения СНДФ
рассмотрим случай задания логической
функции в виде таблицы истинности. Пусть
задана функция трех переменных. Таблица
истинности этой функции показана на
рис. 1.8. (очевидно, что значения функции
взяты произвольно и могут быть любыми).
Пусть
задана функция трех переменных. Таблица
истинности этой функции показана на
рис. 1.8. (очевидно, что значения функции
взяты произвольно и могут быть любыми).
Из таблицы истинности видно, что функция принимает значение логической единицы только на трех наборах переменных, т.е. на 2, 4 и 5-м наборах. Для второй строки (второго набора переменных) можно записать: Х1=0, Х2=1, Х3=0, следовательно, функция f(0,1,0)=1. Принято (по умолчанию) считать, что если переменная в «нормальном» состоянии имеет значение логической единицы, а в инверсном — логического нуля, тогда функцию для второй строки можно представить в виде `X1Х2X3 = 1. Для четвертой строки — `X1X2Х3 = 1 и для пятой строки — Х1X2Х3 = 1. Аналитическое выражение функции выглядит как
.
Каждое
произведение содержит все три переменные
с отрицанием или без отрицания и
соответствует только одной строке
набора переменных, на котором функция
принимает значение логической единицы. Произведения, в которых содержатся все
переменные с отрицанием или без,
называются конституентами единицы или минтермами.
Функция будет представлять логическую
сумму всех произведений, равных логической
единице. В нашем примере вся сумма
(дизъюнкция) соответствует совокупности
произведений переменных для трех строк.
Произведения, в которых содержатся все
переменные с отрицанием или без,
называются конституентами единицы или минтермами.
Функция будет представлять логическую
сумму всех произведений, равных логической
единице. В нашем примере вся сумма
(дизъюнкция) соответствует совокупности
произведений переменных для трех строк.
СНДФ любой функции записывается по таблице истинности согласно следующему правилу.
Для каждого набора переменных, на которых функция принимает значение логической 1, записываются конституенты, и все эти конституенты объединяются дизъюнктивно.
Переменные каждой строки, имеющие значение логического 0, в конституенты входят с отрицанием (записываются в произведение в инвертированном виде), а переменные, имеющие значения логической 1 — без отрицания.
Любую
логическую (булеву) функцию можно
представить дизъюнкцией конституент.
Если одно из произведений не содержит
хотя бы одной переменной, то такая форма
называется нормальной дизъюнктивной
формой (НДФ).
Например:.
Совершенная нормальная конъюнктивная форма (СНКФ). СНКФ можно построить по таблице истинности также как СНДФ. Для чего все значения функции представляют в инверсном виде и записывают СНДФ для инверсной функции. Далее, используя закон де Моргана, получают конъюнкцию всех дизъюнкций. В каждую дизъюнкцию входят все переменные строки таблицы, для которой функция до инвертирования принимала значение логической 1.
Если (хотя бы одна) дизъюнкции, которые называются также макстермами (конституентами нуля), не содержат отдельные переменные, то такая форма записи функции называется нормальной конъюнктивной формой (НКФ).
Пример записи СНКФ. Пусть функция представлена в виде таблицы истинности (рис. 1.9).
Элементарные
функции алгебры-логики. Среди
всех функций алгебры логики особое
место занимают функции одной и двух
переменных, называемые элементарными. В качестве логических операций над
переменными, эти функции позволяют
реализовать различные функции от любого
числа переменных.
В качестве логических операций над
переменными, эти функции позволяют
реализовать различные функции от любого
числа переменных.
Общее количество функций АЛ от m переменных R=2k, где k=2m. Рассмотрим элементарные функции от двух переменных
Переменные и их состояния | Обозначение функции | Назначение Функции | ||||
X1 X2 | 0 0 | 0 1 | 1 0 | 1 1 | ||
f0 | 0 | 0 | 0 | 0 | f0=0 | Генератор 0 |
f1 | 0 | 0 | 0 | 1 | f1=X1·X2 | «И» |
f2 | 0 | 0 | 1 | 0 | f2=X1· |
|
f3 | 0 | 0 | 1 | 1 | f3=X1 |
|
f4 | 0 | 1 | 0 | 0 | f4=·X2 |
|
f5 | 0 | 1 | 0 | 1 | f5=X2 |
|
f6 | 0 | 1 | 1 | 0 | f6=X1 X2 | Сумматор по модулю два |
f7 | 0 | 1 | 1 | 1 | f7=X1+X2 | «ИЛИ» |
f8 | 1 | 0 | 0 | 0 | f8= | «ИЛИ-НЕ» |
f9 | 1 | 0 | 0 | 1 | f9=X1~X2 | Функция равнозначности |
f10 | 1 | 0 | 1 | 0 | f10= | «НЕ» Х2 |
f11 | 1 | 0 | 1 | 1 | f11=X1+ |
|
f12 | 1 | 1 | 0 | 0 | f12= | «НЕ» Х1 |
f13 | 1 | 1 | 0 | 1 | f13=+X2 |
|
f14 | 1 | 1 | 1 | 0 | f14= | «И-НЕ» |
f15 | 1 | 1 | 1 | 1 | f15=1 | Генератор 1 |
6.
 2 Функции истинности 6.2 Функции истинности
2 Функции истинности 6.2 Функции истинностиПРИМЕЧАНИЕ. Здесь я должен использовать «*» для точка, «>» для подковы и «_» для тройника.
Переменные заявления и формы
Переменные оператора (p, q, r, É) используются для создания оператора формы. Таким образом, форма утверждения p v q может использоваться для обозначения любой дизъюнкции:
А против Б
(A * B) v [C É > (D _ E)]
~ C v (D * ~E)
Переменные оператора
(1) Вы должны иметь возможность заменить каждую переменную одним и тем же оператором
имя повсюду.
A v (B * A) является экземпляром p v (q * p), а A v (B * C) — нет.
Часть того, что показывает форма, состоит в том, что содержание первого дизъюнктивного
такое же, как содержание второго конъюнкта, каким бы ни было это содержание
может случиться.
Это не исключает возможности того, что q может обозначать тот же
содержание. (см. следующий слайд)
(2) Разные переменные могут иметь одно и то же имя оператора.
A v (A * A) и B v (B * B) являются экземплярами p v (q * p) как есть А в (Б*А)
q может обозначать то, что обозначает p, но ни одна переменная не может обозначать для разных вещей в одном заявлении.
A v (A * B) не является экземпляром, поскольку «p» не может обозначать одновременно «A» и «A».
«В» в том же заявлении.
(3) Переменные могут обозначать простые или составные операторы
Какие из следующих примеров являются примерами (p v q) É > п? (Читайте: условное предложение, антецедентом которого является дизъюнкция)
(~ A v B) É > (B * C)
~ (A v B) É > B
(B v B) É > B
[(B C) v B] É > (B * C)
Экземпляры (p v q) É p
(~ A v B) É > (B * C)
№. Замена p меняется.
~ (A v B) É > B
№. Антецедент — это отрицательная дизъюнкция, а не дизъюнкция.
(B v B) É > B
ДА. По форме подходит. (Оба p и q могут быть заменены одним и тем же содержимым. )
)
[(B C) v B] É > (B * C)
ДА. По форме подходит. (p заменяется составным оператором (B
*С).)
Функциональные заявления о достоверности
Значение истинности составного утверждения зависит от значений истинности составных частей.
Утверждения, не соответствующие действительности
«Люси считает, что Рикки в клубе» — составное утверждение.
чье истинностное значение не зависит от истинностного значения «Рики
в клубе»
Таблицы истинности
Таблицы истинности представляют собой организованную систему значений истинности, показывающую все
возможная комбинация назначений значений истинности для простых и составных
вовлеченные заявления.
Массив значений истинности всегда строится одинаково, чтобы ограничить ошибку
и гарантировать, что все возможные комбинации назначений значений истинности
учитываются.
Таблицы истинности можно использовать для определения логических операторов и связок.
Отрицание
Соединение
Разъединение
Материал Условный
Биусловный
Более длинные предложения
Если Люси носит кольцо-дешифратор и Этель знает пароль, то Рикки
подозревает шпиона.
(R * P) É > S
, где Люси носит кольцо, Этель не знает пароля и Рики
ничего не подозревает.
(Т * Ж) É > Ж
Чтобы найти истинность сложного предложения, определите сначала истинность значение союза (второстепенной связки), а затем определить истинностное значение условного предложения (большой связки).
(Т * Ж) Э > Ж
(F) > EF
Т
Другой пример
~ А в ~ ( А * ~ В )
Предположим, что А истинно, а В ложно.
Это дизъюнкция, поэтому «v» будет последним значением определенный.
Предложения слева и справа от «v» должны быть определены в отдельности.
Первая левая сторона
~ А в ~ (А * ~ В)
~ Т в ~ ( Т * ~ Ж )
F v ~ (А * ~ В)
Правая сторона сложнее
Начало внутри круглых скобок. Вы должны определить значение инвертированного
«Б» перед определяет значение союза. А ты
необходимо определить значение конъюнкции до того, как вы определите значение
отрицания союза.
Вы должны определить значение инвертированного
«Б» перед определяет значение союза. А ты
необходимо определить значение конъюнкции до того, как вы определите значение
отрицания союза.
Ф v ~ ( Т * ~ Ф )
Ф в ~ (Т * Т)
Ф в ~ ( Т )
Ф против Ф
Ф
Обычный язык и «если»
Вы провалите курс, если не будете посещать занятия каждую неделю.
Ф в А
Обратите внимание, что вы все еще можете посещать каждую неделю и потерпеть неудачу. Что правили выход в том, что вы не посещаете каждую неделю и не терпите неудачу (~ F A).
Это иногда называют включительно смысл «если».
Обычный язык и «если»
Вы сдадите экзамен, если не будете ленивы.
П в Л
Здесь оба не могут быть ложными (~P*~L) и вы не можете оба сдать экзамен
и быть ленивым (П*Л).
Это иногда называют исключительным смыслом «если».
Условное
Материальное состояние выражает отношения, основанные только на истине
значения следствия и антецедента.
В обычном языке мы часто используем условные предложения, чтобы выразить более значимые
отношения.
Так могут возникнуть загадки….
Условные обозначения материалов
p Éq истинно всякий раз, когда антецедент
если ложно.
Если Майкл Джексон кит, то он рептилия.
Если Клинтон выступает за злоупотребление наркотиками, то он хороший президент.
Эти условные предложения истинны, потому что они имеют ложные антецеденты. Если
вы думаете, что они ложны, возможно, вы думаете о другом
условно ….
Конфликтные кондиционалы
Если бы Майкл Джексон был китом, то он был бы рептилией.
Если бы Клинтон защищал злоупотребление наркотиками, то он был бы хорошим президентом.
Здесь мы предполагаем, что отношения между
предшествующим и последующим, чем тот факт, что последний не является ложным, когда
первое верно.
Истинно-функциональная полнота
Истинно-функциональная полнота
PL имеет пять операторов: тильда, клин, амперсанд, подкова и тройная черта. Мы знаем, что эти операторы являются функциями истинности. Они принимают значения истинности в качестве входных данных и возвращают значение истинности как выход. Наш вопрос в этом разделе следующий: можем ли мы описать все возможные функции истинности с использованием наших пяти операторов? То есть можем ли мы построить любое функция истинности от входа к выходу с использованием наших операторов? Если ответ да, тогда наша система логики равна правда-функционально полный. Это вопрос в том, что мы называем Metalogic , логика логики. Спрашивая об этом вопрос мы задаем вопрос о нашей системе логики, и в отвечая на него, мы доказываем что-то о нашей системе логики. Другой металогические вопросы появятся позже в тексте.
Упрощенная версия вопроса, который мы задаем, такова:
Можем ли мы построить все возможные таблицы истинности, используя наши пять операторов? Поскольку
таблица истинности представляет собой табличное выражение функции от входа к выходу, если мы
может построить все возможные таблицы истинности, то наша система функционально
полный.
Конечно, существует бесконечное количество таблиц истинности. Итак, как мы можем показать, что можем выразить их все на PL? Мы показываем что у нас есть рецепт построения любой возможной таблицы истинности.
Таблицы истинности бывают разных размеров. Мы помним, что число строк таблицы истинности равно 2 n , где n — количество отдельные буквы предложений в wff. Начнем с таблицы истинности для п=1. Это имеет две строки:
| А | ? |
| Т | ? |
| Ф | ? |
Здесь «A» может быть T или F. Каковы возможные выходы?
| А | ? |
| Т | Т |
| Ф | Т |
Мы могли бы получить все «T» для вывода. Тогда WFF мы
потребность — это тавтология. Таким образом, мы можем использовать «(A v ~A)», чтобы получить этот вывод.
Тогда WFF мы
потребность — это тавтология. Таким образом, мы можем использовать «(A v ~A)», чтобы получить этот вывод.
| А | (А в ~А) |
| Т | Т |
| Ф | Т |
Теперь рассмотрим возможный результат, при котором мы всегда получаем «Ф»:
| А | ? |
| Т | Ф |
| Ф | Ф |
Тогда нужная нам wff является противоречием. Таким образом, мы можем использовать
«(A & ~A)», чтобы дать нам этот вывод.
| А | (А и ~А) |
| Т | Ф |
| Ф | Ф |
Далее рассмотрим возможный выход, где выходом является то же, что и ввод:
| А | ? |
| Т | Т |
| Ф | Ф |
Для этого мы просто используем букву «А».
| А | А |
| Т | Т |
| Ф | Ф |
Наконец, рассмотрим, что происходит, когда мы переходим от входа «Т» на выход «F» или на вход «F» на выход «T»:
| А | ? |
| Т | Ф |
| Ф | Т |
Это наша старая добрая тильда!
| А | ~А |
| Т | Ф |
| Ф | Т |
Мы только что показали, что можем построить все возможные
функция от входных значений истинности к выходным значениям истинности для таблиц истинности с
одно предложение, отдельная буква. Теперь нам нужно показать, что мы можем сделать это для
таблицы истинности с двумя или более различными буквами предложений. Для любого такого
таблицы истинности, будет три разновидности: (1) таблицы истинности, которые
все «T» в последнем столбце, (2) таблицы истинности, в которых все «F» в последнем столбце
столбец и таблицы истинности, в которых есть хотя бы одна буква «Т» и хотя бы одна буква «F». Для
в первых двух случаях нам просто нужно построить тавтологии и противоречия.
Таким образом, если буква предложения «А» является одной из наших отдельных букв предложения, для
таблицы истинности со всеми «Т», мы убеждаемся, что мы отделить «(A v ~A) с
другие буквы предложения, и мы получим все буквы «Т» для последнего столбца. Для
таблицы истинности со всеми «F», мы соединяем «(A&~A) с буквами предложения
и мы получим все «F».
Теперь нам нужно показать, что мы можем сделать это для
таблицы истинности с двумя или более различными буквами предложений. Для любого такого
таблицы истинности, будет три разновидности: (1) таблицы истинности, которые
все «T» в последнем столбце, (2) таблицы истинности, в которых все «F» в последнем столбце
столбец и таблицы истинности, в которых есть хотя бы одна буква «Т» и хотя бы одна буква «F». Для
в первых двух случаях нам просто нужно построить тавтологии и противоречия.
Таким образом, если буква предложения «А» является одной из наших отдельных букв предложения, для
таблицы истинности со всеми «Т», мы убеждаемся, что мы отделить «(A v ~A) с
другие буквы предложения, и мы получим все буквы «Т» для последнего столбца. Для
таблицы истинности со всеми «F», мы соединяем «(A&~A) с буквами предложения
и мы получим все «F».
Теперь поговорим о таблицах истинности, где вывод
(последний столбец) содержит несколько F и несколько T. Мы формируем wff следующим образом: Начните с
первая строка, где все wff оказывается верным: построить соединение следующим образом: для каждого предложения
буква, если буква предложения назначена «T», тогда сделайте букву предложения a
соединение Если ему присвоено «F», сделайте отрицание буквы предложения a
соединение Мы будем называть каждое из этих соединений «ассоциированными соединениями» для
тот ряд. Делайте это для в каждой строке, где wff оказывается верным. Теперь возьмите эти союзы и сформируйте
дизъюнкция всех этих союзов, не забудьте использовать только союзы для
строки, которые верны в последнем столбце. Результирующий wff является wff с
рассматриваемая таблица истинности.
Делайте это для в каждой строке, где wff оказывается верным. Теперь возьмите эти союзы и сформируйте
дизъюнкция всех этих союзов, не забудьте использовать только союзы для
строки, которые верны в последнем столбце. Результирующий wff является wff с
рассматриваемая таблица истинности.
Например, давайте посмотрим на таблицу истинности:
| А | Б | ? |
| Т | Т | Ф |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
Следуя нашему рецепту, мы строим связанный
союзы (A &~B), для второй строки, и (~A & B)
для третьего ряда. Теперь мы разделяем связанные конъюнкции: (A &~B) v (~A & B). (Не беспокойтесь о группировке здесь.)
Эта дизъюнкция имеет рассматриваемую таблицу истинности:
Теперь мы разделяем связанные конъюнкции: (A &~B) v (~A & B). (Не беспокойтесь о группировке здесь.)
Эта дизъюнкция имеет рассматриваемую таблицу истинности:
| А | Б | (А и~В) v (~А и В) |
| Т | Т | Ф |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
И этот рецепт совершенно общий и будет работать для
таблицы истинности любого размера. Итак, мы доказали, что с помощью наших операторов (на самом деле,
просто используя отрицание, конъюнкцию и дизъюнкцию — нам не нужно было использовать
подкова или тройник) мы можем выразить любой функция истины. Следовательно, ЯП функционально завершен.
Следовательно, ЯП функционально завершен.
Вот еще. Для чего связан wff:
| А | Б | ? |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Ф |
Сначала мы перечисляем связанные союзы. Для первой строки это
(A&B), а для третьего (~A & B). Поскольку wff оказывается верным в первой и третьей строках, мы разделяем
соединения из этих строк и получить (A & B) v (~A & B).
| А | Б | (А и В) v (~А и В) |
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Ф |
В качестве упражнения постройте произвольную таблицу истинности и
затем создайте wff, который имеет эту таблицу истинности, используя приведенный выше рецепт.
Как еще
упражнение, объясните, как наше доказательство в этом разделе также является доказательством
ненужность подковы и тройки как операторов в PL.


 пояснение ниже).
пояснение ниже). 1 была x, Перем. 2 — y, а Перем. 3 — z, так как в этом случае результат подстановки формулы в таблицу в строку 2 не сходится со значением, указанным в этой же таблице.
1 была x, Перем. 2 — y, а Перем. 3 — z, так как в этом случае результат подстановки формулы в таблицу в строку 2 не сходится со значением, указанным в этой же таблице.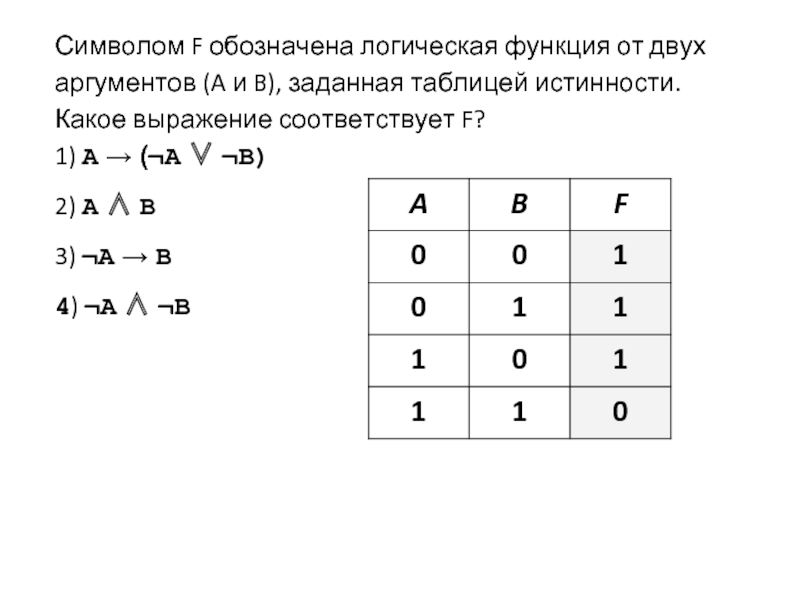 3.
3.