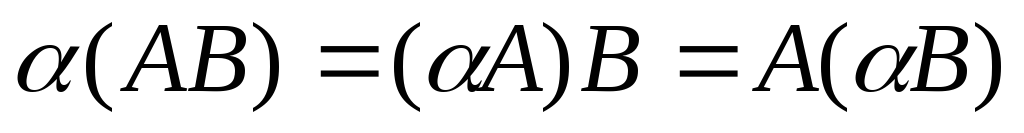Условились считать, что _ вектор сонаправлен с любым вектором
(*ответ*) нулевой
Условились, что любая точка плоскости также является вектором. В этом случае вектор называется _
(*ответ*) нулевым
единичным
ненаправленным
коллинеарным
Физические величины, характеризующиеся не только своим числовым значением, но и направлением в пространстве, называются _ величинами
(*ответ*) векторными
_ – направленный отрезок, для которого указано, какой из его концов считается началом, а какой — концом
(*ответ*) Вектор
Вектор, начало которого совпадает с его концом, называется _
(*ответ*) нулевым
точечным
конечным
абсолютным
Два ненулевых вектора, лежащие на параллельных прямых, называются _, если их концы лежат по одну сторону от прямой, проходящей через начала
Какие из следующих величин являются векторными:
(*ответ*) скорость
(*ответ*) сила
масса
длина
Верно ли утверждение?
«Отрезки, соединяющие середины противоположных сторон произвольного четырехугольника, точкой пересечения делятся пополам».
Введите «да», если утверждение верно, и «нет», если неверно
(*ответ*) да
Верно ли утверждение?
«Отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям и равен полусумме оснований».
Введите «да», если утверждение верно, и «нет», если неверно
(*ответ*) нет
Верны ли утверждения?
А) Прямая, проведенная через середины оснований трапеции, проходит через точку пересечения продолжений боковых сторон
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли утверждения?
А) Средняя линия трапеции проходит через середины ее диагоналей
В) Произведение любого вектора на единицу есть единичный вектор
Подберите правильный ответ
(*ответ*) А — да, В — нет
А — да, В — да
А — нет, В — да
А — нет, В — нет
Верны ли определения?
А) Произведением нулевого вектора на любое число считается нулевой вектор
В) Произведение любого вектора на число нуль есть нулевой вектор
Подберите правильный ответ
(*ответ*) А — да, В — да
А — нет, В — да
А — нет, В — нет
Лекция по теме «Умножение вектора на число»
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль |а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно.Произведение вектора а на число k обозначается так: ka.
Текст
Умножение вектора на число
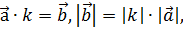
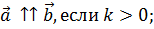
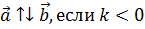
Рисунок векторов
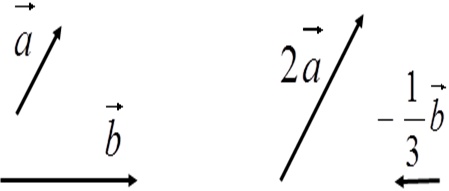
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.
Текст
Умножение вектора на число
 ││k
││k для любого k.
для любого k.
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства:
Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.
Текст
Свойства умножения вектора на число
Сочетательный закон
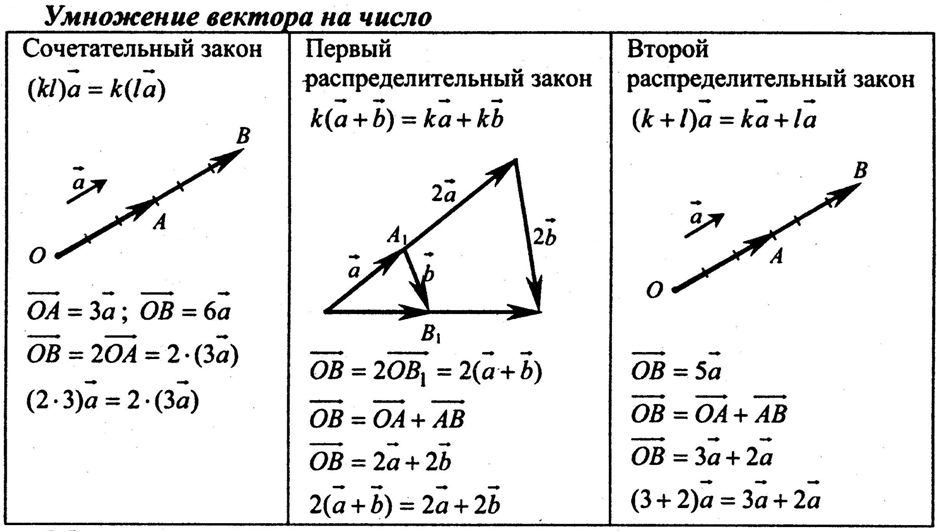
Рисунок векторов

Текст

Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.
На рисунке, на примере показано это свойство.
Текст
Свойства умножения вектора на число
Первый распределительный закон

Рисунок векторов
Текст

Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.
Текст
Свойства умножения вектора на число
Второй распределительный закон

Рисунок векторов

Текст

Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному.
Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
Текст
(-1)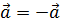 , так как
, так как
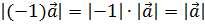 и
и
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:
Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.
Текст
Если 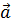 ││
││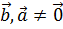 , то существует
, то существует
число k, что 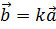
Решим задачу №347 (а)
Необходимо упростить выражение.
Текст
Задача №347(а)
Упростить выражение:
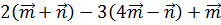
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.
Текст
Задача №347(а)
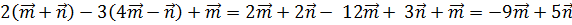
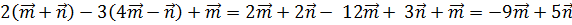 .
.
Произведение вектора на число — Студопедия
Произведением вектора  и числа λ называется вектор, обозначаемый
и числа λ называется вектор, обозначаемый 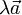 (или
(или  ), модуль которого равен
), модуль которого равен  , а направление совпадает с направлением вектора
, а направление совпадает с направлением вектора  , если
, если  , и противоположно ему, если
, и противоположно ему, если  . Если же
. Если же  , или вектор
, или вектор  нулевой, тогда и только тогда произведение
нулевой, тогда и только тогда произведение 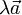 — нулевой вектор.
— нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе,
 .
.
Из определения произведения вектора на число легко вывести следующие свойства:
- если
 , то
, то  . Наоборот, если
. Наоборот, если  , то при некотором λ верно равенство
, то при некотором λ верно равенство  ;
; - всегда
 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт.
Немного истории
Я являюсь студентом уже 4 курса математического факультета, и до того как я начал заниматься программированием, я считал себя математиком на 100 процентов.
В конце первого курса мой преподаватель по информатике, который занимается олимпиадным программированием, обратил на меня внимание. Им как раз не хватало одного математика в команду. Так потихоньку меня начали приучать к олимпиадному программированию. Скажу честно, для меня это было очень сложно: для человека, который узнал слово Delphi на первом курсе. Однако мой преподаватель оказался очень грамотным специалистом и нашел хороший подход ко мне. Он начал давать мне математические задачи, который я сначала решал чисто математически, а уже потом писал код (с грехом пополам).
Мне очень нравится подход моего преподавателя: «разберись с этой темой, а потом расскажи нам, да так чтоб мы все поняли».
Итак, первой на самом деле важной задачей, с которой мне поручили разобраться, было именно вычислительная геометрия, необходимо было разобраться в типичных задач этого раздела информатики. И я решил подойти к этой задаче со всей ответственностью.
Я помню, как долго мучился с этими задачами, чтобы они прошли все тесты на сайте informatics.mccme. Зато теперь я очень рад, что прошел через все испытания и знаю, что же такое задачи вычислительной геометрии.
Вступление
«Вычислительная геометрия – это раздел информатики, изучающий алгоритмы решения геометрических задач. Такие задачи возникают в компьютерной графике, проектировании интегральных схем, технических устройств и др. Исходными данными в такого рода задачах могут быть множество точек, набор отрезков, многоугольники и т.п. Результатом может быть либо ответ на какой-то вопрос, либо какой-то геометрический объект».
Поскольку статья является достаточно большой я решил разбить ее на две части: первая часть посвящена многоугольникам, вторая – взаимному расположению различных геометрических объектов.
Немного теории о векторах
Отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Длиной ненулевого вектора AB называется длина отрезка AB. Длина нулевого вектора считается равной нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора AB и CD коллинеарны и если при этом лучи AB и CD сонаправлены, то векторы AB и CD называются сонаправленными, а если эти лучи не являются сонаправленными, то векторы AB и CD называются противоположно направленными. Нулевой вектор принято считать сонаправленным с любым вектором.
Скалярное произведение векторов
Скалярное произведение векторов — это число, равное произведению длин этих векторов на косинус угла между ними.
(a, b) = |a||b|cos∠(a, b)
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то скалярное произведение (a, b) = x1x2 + y1y2.
Косое произведение векторов
Псевдоскалярным или косым произведением векторов на плоскости называется число
[a, b] = |a||b|sinθ
где — угол вращения (против часовой стрелки) от a к b. Если хотя бы один из векторов a и b нулевой, то полагают [a, b] = 0.
Если векторы заданы своими координатами a(x1, y1), b(x2, y2) то косое произведение [a, b] = x1y2 — x2y1.
Геометрически косое произведение векторов представляет собой ориентированную площадь параллелограмма, натянутого на эти вектора.
Косое произведение векторов в задачах вычислительной геометрии занимает такое же почетное место, как рекурсии в комбинаторике. Это своего рода жемчужина вычислительной геометрии. Практически каждая задача вычислительной геометрии имеет более простое решение с помощью косового произведение вместо лобового решения.
А теперь займемся практикой
Начнем с треугольников
Задача №1
Задача очень простая, а именно: по введенным трем числам a, b, c определить существует ли треугольник с такими сторонами.
Решение
Понятно, что здесь нужно только проверить неравенство треугольника: a + b > c, a + c > b, b + c > a. Интересно, при изучении неравенства треугольника только ли у меня возник вопрос: не могут ли отрицательные числа тоже удовлетворять этим трем неравенствам? Оказывается, нет! Если мы сложим каждое неравенство, то получим a > 0, b > 0, c > 0. Поэтому неравенство треугольника является необходимым и достаточным условием существования треугольника.
Задача №2
Задача является очень похожей на предыдущую с той разницей, что треугольник задан не сторонами, а координатами вершин.
Решение
С первого взгляда решение кажется очевидным: вычислить стороны треугольника и свести задачу к предыдущей. Однако поскольку расстояние между двумя точками A(x1, y1), B(x2, y2) вычисляется по формуле √(x1-x2)2+(y1-y2)2 то при извлечении корня возможна потеря точности, что плохо скажется на проверке неравенства треугольника. Оказывается, что если треугольник задан координатами своих вершин, то вычислять длины его сторон и проверять неравенство треугольника не требуется. В этом случае треугольника не существует тогда и только тогда, когда данные три точки лежат на одной прямой. А это легко проверяется через косое произведение векторов. Если оно равно нулю, то векторы коллинеарные, то есть все три точки лежат на одной прямой.
Во всех следующих задачах будем считать, что треугольник существует, поскольку процедуру проверки существования треугольника мы только что рассмотрели.
Задача №3
Треугольник задан своими сторонами. Определить тип треугольника: тупоугольный, прямоугольный или остроугольный.
Решение
Вспомним, что представляют собой каждый вид треугольника.
Из курса геометрии известно, что напротив большей стороны лежит больший угол (он нам и нужен). Поэтому если мы выясним чему равен больший угол, то поймем тип треугольника:
- Угол больше 90° – треугольник тупоугольный
- Угол меньше 90°– треугольник остроугольный
- Угол равен 90°– треугольник прямоугольный
Очевидно, что если косинус угла больше нуля то угол меньше 90°, если он равен нулю, то угол равен 90°, если он меньше нуля, то угол больше 90°. Однако немного поразмыслив можно понять, что вычислять косинус угла не обязательно, необходимо учесть лишь его знак:
- Если cosα > 0, то a2 < b2 + c2 – треугольник остроугольный
- Если cosα = 0, то a2 = b2 + c2 – треугольник прямоугольный
- Если cosα < 0, то a2 > b2 + c2 – треугольник тупоугольный
Задача №4
Задача аналогична предыдущей задаче, только треугольник задан не своими сторонами, а координатами вершин.
Решение
Аналогично задаче 2 можно сказать, что эта задача полностью сводится к предыдущей задаче (так оно и есть). Однако, как и во второй задаче, решение можно упростить. Вообще, если треугольник задан координатами своих вершин, то всегда легче работать с ним через вектора, нежели вычислять стороны. Аналогично предыдущей задаче, необходимо определить каким является наибольший из углов треугольника. Вид угла легко определяется по знаку скалярного произведения образующих его векторов: оно положительно для острого угла, равно нулю для прямого угла и отрицательно для тупого угла. Поэтому необходимо посчитать все три скалярных произведения и перемножить их и по знаку данного числа можно судить о типе треугольника.
Задача №5
По данным сторонам треугольника найти его площадь.
Решение
Очевидно решение, заключается в применение формулы Герона.
Кстати, никого не интересовало доказательство этой формулы?
Вот и все!
Задача №6
Вычислить площадь треугольника заданного координатами своих вершин.
Решение
Не будем говорить о решении, которое сводится к предыдущей задачи, а попробуем воспользоваться геометрическим смыслом косового произведения. Геометрически косое произведение двух векторов определяет ориентированную площадь параллелограмма натянутого на эти вектора. Поскольку диагональ параллелограмма разбивает его на два равновеликих треугольника, то можем найти площадь нашего треугольника, как половину площади параллелограмма.
Для векторов a(x1, y1), b(x2, y2)
S = (x1y2 — x2y1) / 2 — ориентированная площадь треугольника
Задача №7
Дана точка и треугольник заданный координатами своих вершин. Определить лежит ли точка внутри, на границе или вне этого треугольника.
Решение
У этой задачи есть два принципиально разных решения. Начнем с наименее привлекательного.
Метод площадей
Если сумма площадей треугольников AKB, AKC, BKC (не ориентированных, а «обычных») больше площади треугольника ABC точка лежит вне треугольника. Если же сумма первых трех площадей равна четвертой, то нужно проверить, не равна ли нулю одна из трех площадей. Если равна, то точка лежит на границе треугольника, иначе – внутри.
Вычислять площади треугольников, естественно, надо через косое произведение векторов. Этот метод не очень хороший. Поскольку здесь используются сравнение чисел с плавающей точкой, а это в свою очередь может привести к принятию неверного решения при сравнении. Второй метод опять таки опирается на вектора, он намного эффективнее во всех отношениях.
Проверка полуплоскостей
Если хотя бы одна из сторон треугольника «разводит» противолежащую ей вершину и точку по разным полуплоскостям, то точка лежит вне треугольника. Иначе, если точка принадлежит хотя бы одной из прямых, содержащих стороны треугольника, то она находится на границе треугольника. Иначе точка лежит внутри треугольника.В первом примере сторона AB разводит вершину C и точку K по разным полуплоскостям, поэтому точка лежит снаружи.
Задача №8
Вычисление площади многоугольника заданного координатами своих вершин.
Решение
Под многоугольником будем подразумевать простой многоугольник, то есть без самопересечений. При этом он может быть как выпуклым, так и не выпуклым.
Данную задачу можно решить двумя способами: вычисляя ориентированные площади трапеций и треугольников.
Метод трапеций
Для того чтобы посчитать площадь многоугольника нужно разбить его на трапеции, так как это показано на рисунке, а затем сложить ориентированные площади полученных трапеций это будет ориентированной площадью исходного многоугольника.
S = SA1 A2 B2 B1 + SA2 A3 B3 B2 + SA3 A4 B5 B3 + SA4 A5 B6 B5 + SA5 A6 B4 B6 + SA6 A1 B1 B4
Площади трапеций считаем по известной формуле: полусумма оснований на высоту
SA1 A2 B2 B1 = 0.5 * (A1B1 + A2B2) *(B2 — B1)
Поскольку полученная площадь является ориентированной, необходимо вычислить ее модуль.
Метод треугольников
Аналогично предыдущему методу можно разбивать многоугольник не на трапеции, а на треугольники, как показано на рисунке. В результате, сложив ориентированные площади этих треугольников, мы получим опять-таки ориентированную площадь многоугольника.
S = SOA1A2 + SOA2A3 + SOA3A4 + SOA4A5 + SOA5A6 + SOA6A1
Как вы видите задача вычисления площади многоугольника достаточна проста. Не знаю, почему, но мне больше нравится решать эту задачу методом разбиения на трапеции (наверно потому, что на всех олимпиадах я ее так решал). Тем более, что при втором решении площади треугольников надо вычислять через косое произведение. О формуле Герона надо забыть!!!
Задача №9
Многоугольник задан координатами своих вершин в порядке его обхода. Необходимо проверить является ли многоугольник выпуклым.
Решение
Напомню, что многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону.
Задача опять сводится к вычислению косового произведения векторов, а именно у выпуклого многоугольника знаки косых произведений [Ai Ai+1, Ai+1 Ai+2] либо положительны, либо отрицательны. Поэтому если мы знаем направление обхода, то знак косых произведений для выпуклого многоугольника одинаков: он неотрицателен при обходе против часовой стрелки и неположителен при обходе по часовой стрелки.
Задача №10
Многоугольник (не обязательно выпуклый) на плоскости задан координатами своих вершин. Требуется подсчитать количество точек с целочисленными координатами, лежащих внутри него (но не на его границе).
Решение
Для решения этой задачи рассмотрим вспомогательную задачу: отрезок задан координатами своих концов, являющихся целыми числами. Необходимо посчитать количество целочисленных точек лежащих на отрезке. Понятно, что если отрезок вертикальный или горизонтальный, то необходимо вычесть координаты концов и добавить единицу. Интерес представляет случай, когда отрезок не является вертикальным или горизонтальным. Оказывается в этом случае необходимо достроить отрезок до прямоугольного треугольника и ответом будет число равное наибольшему общему делителю длин катетов этого треугольника плюс единица.
Для любого многоугольника с целочисленными координатами вершин справедлива формула Пика: S = n + m/2 — 1, где S – площадь многоугольника, n – количество целых точек лежащих строго внутри многоугольника, m – количество целых точек лежащих на границе многоугольника. Поскольку площадь многоугольника мы знаем как вычислять, то S известно. Так же мы можем вычислить количество целых точек лежащих на границе многоугольника, поэтому в формуле Пика остается лишь одна искомая неизвестная которую мы можем найти.
Рассмотрим пример:
S = 16 + 4 + 4,5 + 6 + 1 + 2 = 33,5
m = 15
n = 33,5 – 7,5 +1 = 27 — точек лежит строго внутри многоугольника
Вот так вот решается эта задачка!
Вот и все! Надеюсь, Вам понравилась статья, и я напишу ее вторую часть.
Координаты вектора
Пусть вектор имеет началом точку , а концом – точку . Координатами вектора называются числа . Обозначают так:
Координаты нулевого вектора равны нулю.
Длина вектора (или абсолютная величина вектора) выражается формулой
Равные векторы имеют равные соответствующие координаты.
И наоборот. Если у векторов соответствующие координаты равны, то векторы равны.
Сложение векторов
Суммой векторов и называется вектор с координатами
Умножение вектора на число
Произведением вектора на число называется вектор , то есть
Коллинеарные вектора
Пусть и – отличные от нуля коллинеарные векторы. Тогда существует число такое, что
Угол между векторами
Углом между любыми двумя ненулевыми векторами и называется угол между равными им векторами с общим началом (наименьший угол).
Угол между двумя векторами находится в промежутке .
Угол между одинаково направленными векторами равен нулю.
Скалярное произведение векторов
I. Скалярным произведением векторов и называется число , то есть
II. Скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между ними, то есть
Следовательно, если векторы перпендикулярны, то их скалярное произведение равно нулю. Верно и обратное.
Из формул I и II скалярного произведения вытекает, что угол между векторами можно найти, используя формулу:
Также, следствием, например, формулы II скалярного произведения есть следующий важный момент:
Диадное произведение векторов (базиса)
Скалярное произведение двух базисных векторов называется диадой:
eiej,
Свойства диад:
eiej= ejei
ei(aej + bek)=aeiej + beiek,
a,b — числа
Каждой диаде ставится в соответствие матрица 3*3, состоящая из нулей и одной единицы:


Лекция №3
Определение пространства Евклида
Норма(длина) вектора. Ортонормированный базис.
Определение пространства Евклида
Определение: вещественное пространство называется евклидовым,
если каждой паре векторов 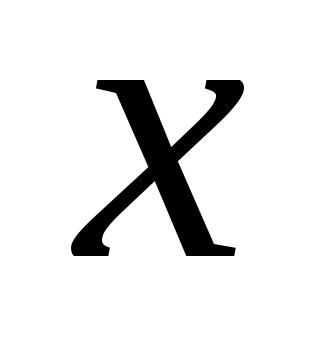 ,
, из
из поставлено в соответствие вещественное
число (
поставлено в соответствие вещественное
число ( ,
, ),
называемоескалярным
произведением,
причём выполнены следующие аксиомы:
),
называемоескалярным
произведением,
причём выполнены следующие аксиомы:
 –переместительный
закон
–переместительный
закон –сочетательный
закон
–сочетательный
закон –распределительный
закон
–распределительный
закон , при
, при  ,
, ,
,  ,
,
для произвольных
векторов  ,
, ,
, из
из и произвольного вещественного числа
и произвольного вещественного числа .
.
Зачастую в физике, механике и других дисциплинах приходится иметь дело с физическими величинами имеющими направление: сила, скорость и т.д. Их взаимодействие приводит к появлению понятия скалярного произведения векторов.
Скалярное
произведение ненулевых векторов  ,
, записывается следующим образом:
записывается следующим образом:
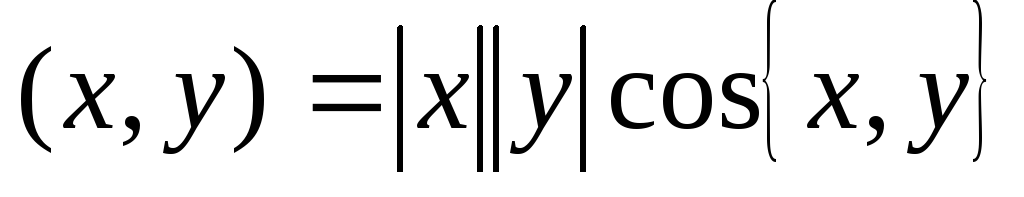 (3.1)
(3.1)
Если два вектора заданы базисом, то их скалярным произведением является сумма попарных произведений в соответствующих координатах:
Например возьмём
декартову систему координат, которая
является системой координат, евклидова
пространства. В этой системе выберем
векторы x и y,
записанные в ортах  :
:



Норма вектора. Ортонормированный базис
Согласно аксиоме
(4) скалярный квадрат  любого вектора есть неотрицательное
вещественное число .
любого вектора есть неотрицательное
вещественное число .
Определение:
Неотрицательное значение квадратного
корня из этого числа называется длиной (нормой) вектора x и обозначается  ,
т.е.
,
т.е.
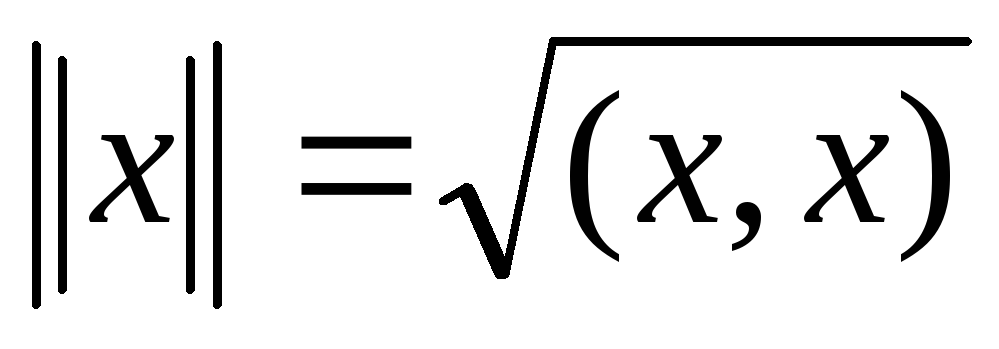
Свойства: отсюда видно , что
нулевой вектор является единственным вектором, длина которого равна нулю.

при умножении вектора на число, длина вектора умножается на модуль этого числа.

вектор длина которого равна единице называется нормированным,

Любой ненулевой вектор y можно нормировать, умножив его на некоторое число:

 –нормирующий
множитель.
–нормирующий
множитель.
Система векторов является нормированной, если нормированы все её векторы.
Одним из основных понятий также является понятие ортогональности.
Определение:
Считается, что векторы  ,
, ортогональны, если
ортогональны, если обозначение
обозначение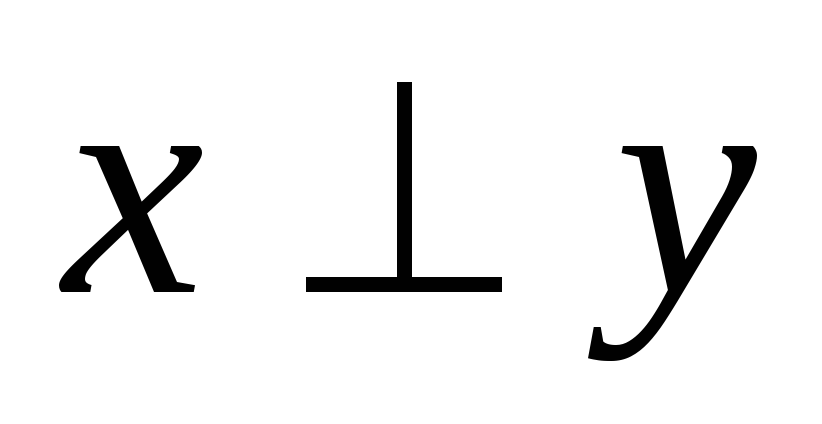 .
.
В декартовой системе координат это характеризуется перпендикулярностью векторов.
Теорема1: Всякая ортогональная система ненулевых векторов является линейно независимой.
Доказательство:
Пусть существует ортогональная система
ненулевых векторов  ,
выполняется равенство:
,
выполняется равенство:
 (3.7)
(3.7)
умножим обе части
скалярно на какой-нибудь вектор  :
:
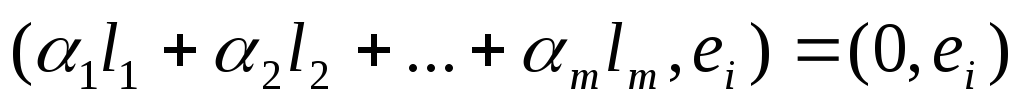
 ,
,
Так как векторы e1 ортогональны,
то все скалярные произведения кроме 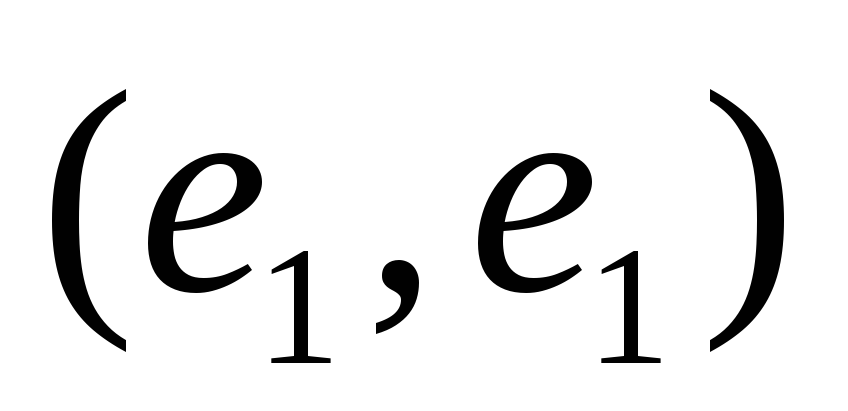 равны нулю. Получено:
равны нулю. Получено:
 ,
,
так как 
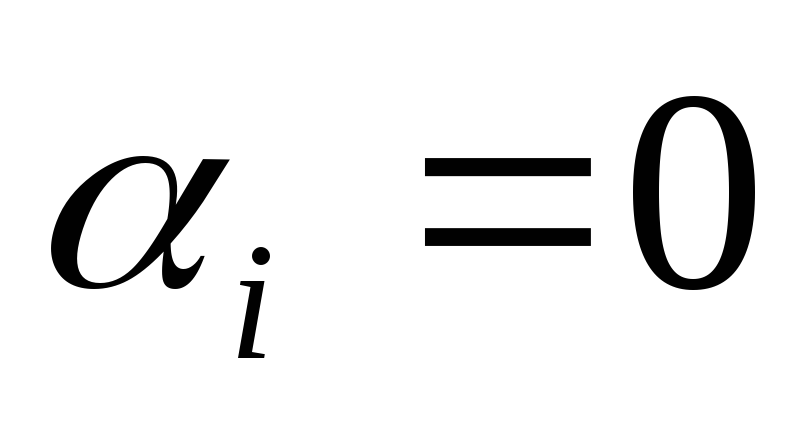 .
.
А это доказывает линейную независимость ортогональных векторов.
Если базис евклидова пространства представляет собой ортогональную систему векторов, то этот базис называют ортогональным.
В линейном пространстве все базисы равноправны. А в евклидовом пространстве скалярное умножение позволяет выделить среди всех базисов ортогональные и ортонормированные, которые играют роль, аналогичную роли прямоугольной системы координат в аналитической геометрии.
Определение: Ортогональный базис называют ортонормированным, если каждый вектор этого вектора имеет норму, равную единице.
Любой ортогональный базис легко преобразовать в ортонормированный, умножая векторы на соответствующие нормирующие коэффициенты. (разделив каждый вектор базиса на его длину).
Из любого произвольного базиса можно создать ортонормированный базис. Этот способ преобразования называется процессом ортогонализации Грама-Шмидта. Алгоритм заключается в следующем.
Пусть f=(f1,…,fn)
– некоторый базис n – мерного евклидова пространства  .
Преобразовывая этот базис, построим
ортонормированный базис
.
Преобразовывая этот базис, построим
ортонормированный базис .
Для этого последовательно вычислим
векторы
.
Для этого последовательно вычислим
векторы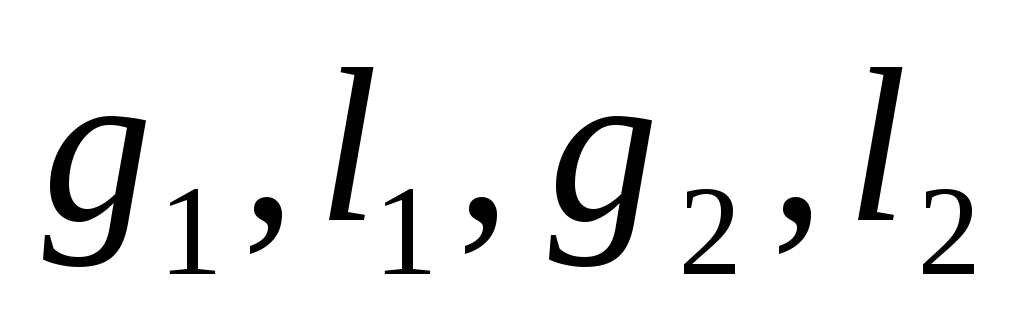 и так далее. По формулам:
и так далее. По формулам:
 ,
,
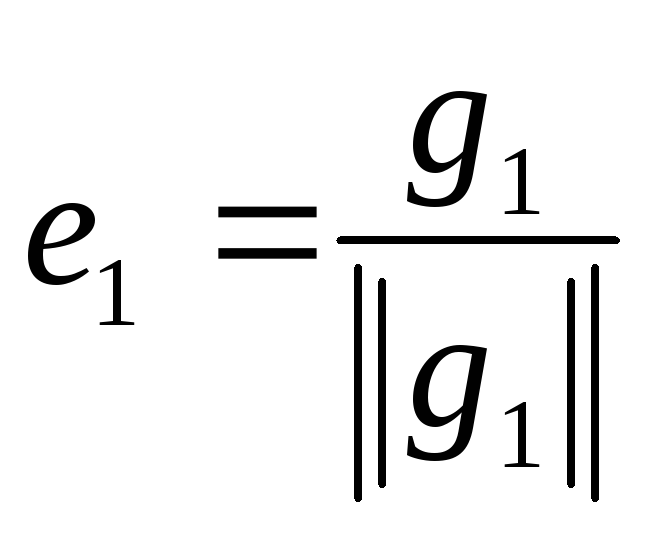 ,
,
 ,
,
 .
.
Процесс ортогонализации изображён на рисунке 1.






Для обоснования
алгоритма необходимо чтобы векторы 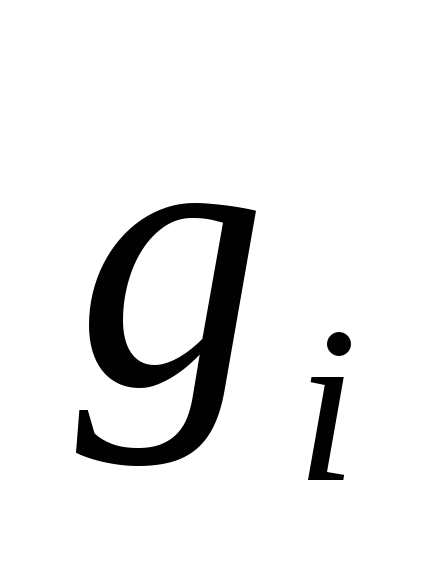 не были нулевыми и были попарно
ортогональными.
не были нулевыми и были попарно
ортогональными.
Докажем это. Предположим, что некоторый вектор gk+1=0, тогда:
 ,
(3.11)
,
(3.11)
то есть 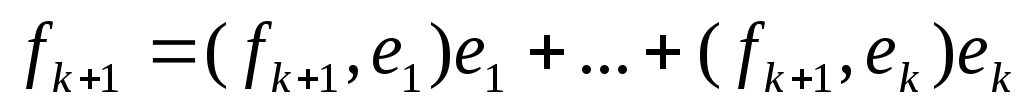 (3.12)
(3.12)
то есть вектор  является линейной комбинацией векторов
является линейной комбинацией векторов ,
которые в свою очередь выражаются через
векторы
,
которые в свою очередь выражаются через
векторы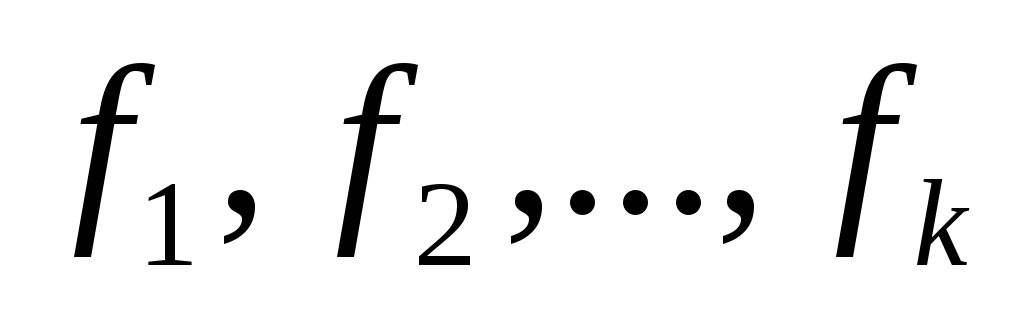 в силу 3.10. Это говорит о том что система
векторов
в силу 3.10. Это говорит о том что система
векторов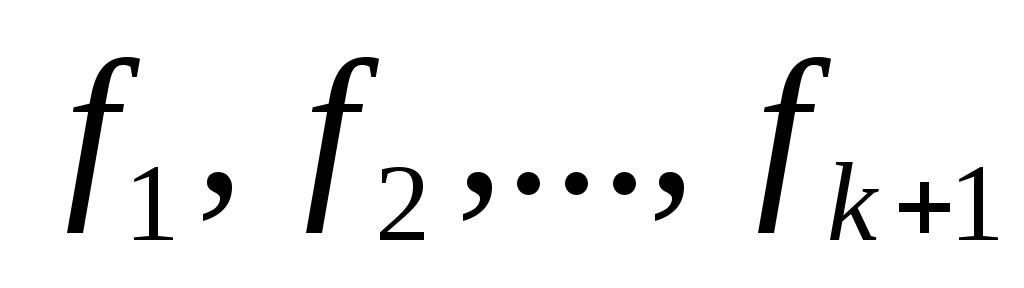 – линейно зависима. То есть утверждение
– линейно зависима. То есть утверждение привело к противоречию и поэтому его
можно считать неверным.
привело к противоречию и поэтому его
можно считать неверным.
Для определения
ортогональности, векторов скалярно
умножим (3.11) на вектор  ,
где
,
где .
.
(3.13)
Поскольку скалярное
произведение равно нулю, то вектор  ортогонален вектору
ортогонален вектору  .
.
Таким образом, в конечномерном (определённой размерности) евклидовом пространстве существует ортонормированный базис.
Лекция №4
Алгебра линейных операторов
Алгебра линейных операторов.
Числовые характеристики линейных операторов и его матрицы.
Собственны числа, векторы.
Характеристический многочлен.
Действия над линейными операторами
Основными алгебраическими действиями на линейными операторами являются следующие:
А) умножение линейных операторов
Б) умножение линейного оператора на число
В) сумма линейных операторов
Рассмотрим подробнее каждую из операций.
А) Пусть в линейном
пространстве 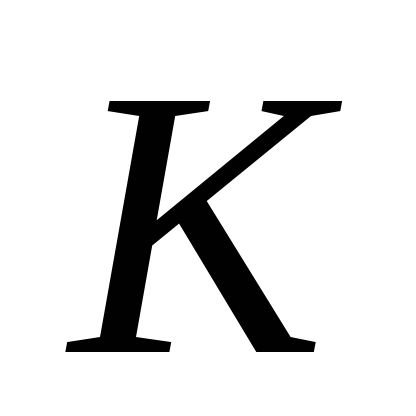 заданны два линейных преобразования
заданны два линейных преобразования и
и .
Применяя к произвольному вектору
.
Применяя к произвольному вектору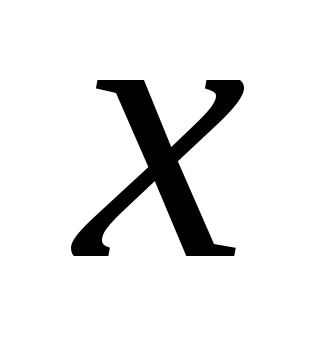 из
из сначала преобразование
сначала преобразование ,
а затем
,
а затем ,
получим некоторый вектор
,
получим некоторый вектор
 .
(1)
.
(1)
Определение: преобразование
переводящие 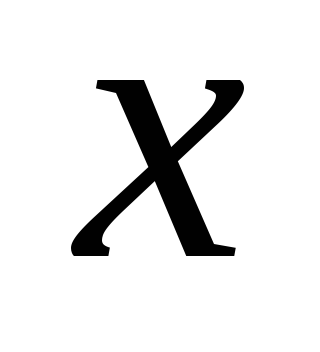 в
в называется произведением
называется произведением на
на .
.
 (2)
(2)
матрица
преобразования линейных операторов  и
и равна произведению матриц этих операторов:
равна произведению матриц этих операторов:
 (3)
(3)
Правило: обратное преобразование 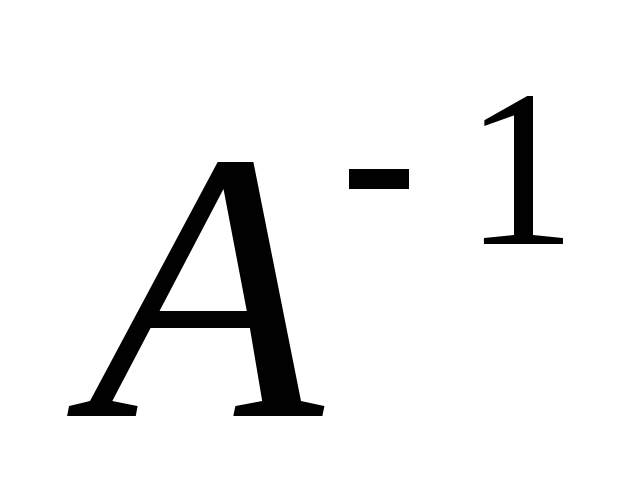 имеет обратную матрицу. Чтобы линейное
преобразование было обратным необходимо
и достаточно, чтобы была обратной и его
матрица.
имеет обратную матрицу. Чтобы линейное
преобразование было обратным необходимо
и достаточно, чтобы была обратной и его
матрица.
Б) Умножение линейного оператора на число.
Определение: Преобразование, полученное в результате
применения к некоторому вектору  сначала преобразования
сначала преобразования ,
а затем умножения нового вектора на
число
,
а затем умножения нового вектора на
число ,
называется произведением
,
называется произведением на
на и обозначается
и обозначается :
:
(4)
Матрица произведения числа на линейный оператор равна произведению этого числа на матрицу этого линейного оператора.
Свойствам произведений линейных операторов:
В) Сумма линейных операторов
Возьмём какие
либо два преобразования  и
и линейного пространства
линейного пространства и каждому вектору
и каждому вектору из
из поставим в соответствие вектор
поставим в соответствие вектор .
Преобразование переводящие
.
Преобразование переводящие в
в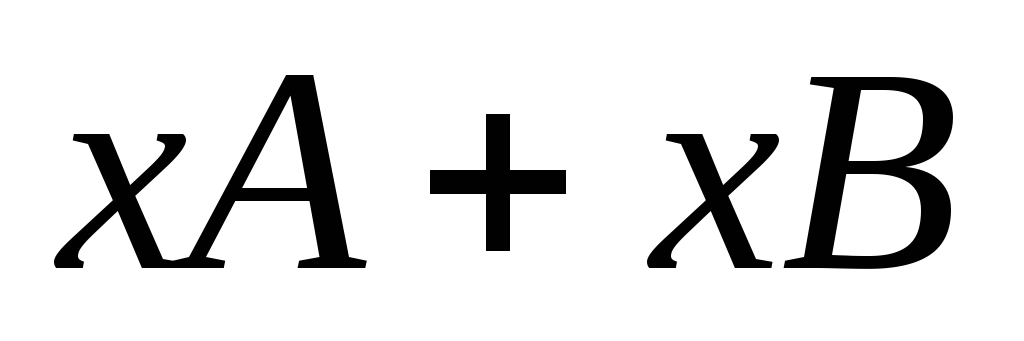 ,
обозначается
,
обозначается и называется суммой
и называется суммой и
и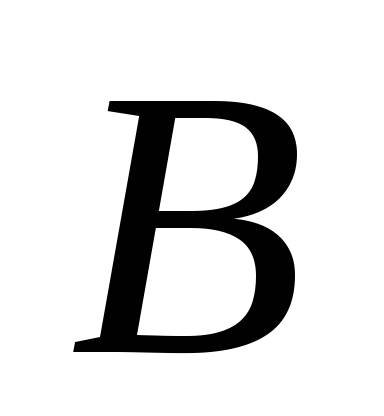 .
.
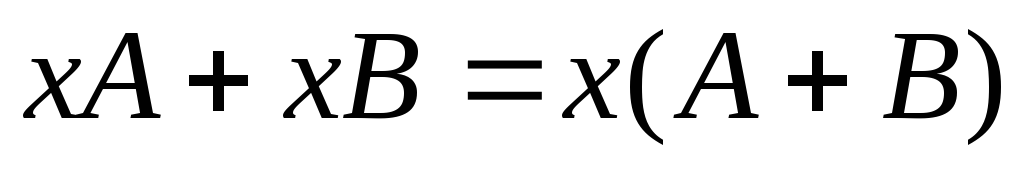 (5)
(5)
Матрица сумм преобразований равна сумме их матриц.
Свойства суммы линейных операторов:
Dot Product
Вектор имеет величину , величину (как долго) и направление :
Вот два вектора:
Их можно умножить на и , используя « Dot Product » (также см. «Перекрестный продукт»).
Расчет
Точечный продукт написан с использованием центральной точки:
a · b
Это означает продукт точки a и b
Мы можем рассчитать произведение точек двух векторов следующим образом:
a · b = | a | × | б | × cos (θ)
Где:
| a | это величина (длина) вектора a
| б | является величиной (длиной) вектора b
θ является углом между a и b
Таким образом, мы умножаем длину в раз на длину b , а затем умножаем на косинус угла между a и b
ИЛИ мы можем рассчитать это следующим образом:
a · b = a x × b x + a y × b y
Итак, мы умножаем x, умножаем y, затем добавляем.
Оба метода работают!
И результатом является число (называемое «скаляр», поэтому мы знаем, что это не вектор).
Пример: Рассчитать скалярное произведение векторов a и b :
a · b = | a | × | б | × cos (θ)
a · b = 10 × 13 × cos (59,5 °)
a · b = 10 × 13 × 0,5075 …
a · b = 65.98 … = 66 (округлено)
ИЛИ мы можем рассчитать это следующим образом:
a · b = a x × b x + a y × b y
a · b = -6 × 5 + 8 × 12
a · b = -30 + 96
a · b = 66
Оба метода дали один и тот же результат (после округления)
Также обратите внимание, что мы использовали минус 6 для x (он движется в отрицательном направлении x)
Примечание: вы можете использовать векторный калькулятор
чтобы помочь вам.
Почему cos (θ)?
Хорошо, чтобы умножить два вектора, имеет смысл умножить их длины вместе на , но только когда они указывают в одном направлении .
Итак, мы делаем одну «точку в том же направлении», что и другая, умножая на cos (θ):
| Мы берем компонент , который лежит рядом с b | Как свет, чтобы увидеть , где лежит тень |
ТОГДА МНОГИЕ!
Это работает точно так же, если мы «спроектировали» b вместе с a , а затем умножили: Потому что неважно, в каком порядке мы делаем умножение: | a | × | б | × cos (θ) = | a | × cos (θ) × | б | |
прямых углов
Когда два вектора расположены под прямым углом друг к другу, скалярное произведение равно и нулю .
Пример: вычисление продукта точки для:
a · b = | a | × | б | × cos (θ)
a · b = | a | × | б | × cos (90 °)
a · b = | a | × | б | × 0
a · b = 0
или мы можем рассчитать это следующим образом:
a · b = a x × b x + a y × b y
a · b = -12 × 12 + 16 × 9
a · b = -144 + 144
a · b = 0
Это может быть удобным способом узнать, находятся ли два вектора под прямым углом.
Три или более измерения
Все это прекрасно работает и в 3 (или более) измерениях.
И на самом деле может быть очень полезным!
Пример: Сэм измерил конечные точки двух полюсов и хочет знать угол между ними :
У нас есть 3 измерения, поэтому не забудьте про z-компоненты:
a · b = a x × b x + a y × b y + a z × b z
a · b = 9 × 4 + 2 × 8 + 7 × 10
a · b = 36 + 16 + 70
a · b = 122
Теперь для другой формулы:
a · b = | a | × | б | × cos (θ)
Но что такое | a | ? Это величина или длина вектора a .Мы можем использовать Пифагор:
- | a | = √ (4 2 + 8 2 + 10 2 )
- | a | = √ (16 + 64 + 100)
- | a | = √180
Аналогично для | b |:
- | б | = √ (9 2 + 2 2 + 7 2 )
- | б | = √ (81 + 4 + 49)
- | б | = √134
И мы знаем из приведенного выше расчета, что a · b = 122, поэтому:
a · b = | a | × | б | × cos (θ)
122 = √180 × √134 × cos (θ)
cos (θ) = 122 / (√180 × √134)
cos (θ) = 0.7855 …
θ = cos -1 (0,7855 …) = 38,2 … °
Готово!
Я однажды попробовал такой расчет, но работал все в углах и расстояниях … это было очень сложно, включало много тригонометрии, и мой мозг болел. Метод выше намного проще.
Крестовый продукт
Продукт с точками дает скалярный ответ (обычное число), и его иногда называют скалярным продуктом .
Но есть также перекрестный продукт, который дает вектор в качестве ответа, и его иногда называют векторным продуктом .
,векторов
Это вектор:
Вектор имеет величину , величину (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает в направлении.
Мы можем добавить два вектора, соединив их лицом к лицу:
И не имеет значения, в каком порядке мы их добавляем, мы получаем тот же результат:
Пример: самолет летит вдоль, указывая на север, но с северо-запада дует ветер.
Два вектора (скорость, вызванная пропеллером, и скорость ветра) приводят к тому, что скорость относительно земли немного снижается к востоку от севера.
Если бы вы смотрели на самолет с земли, казалось бы, он немного смещается вбок.
Вы когда-нибудь видели, чтобы это случилось? Возможно, вы видели птиц, борющихся против сильного ветра, который, кажется, летит вбок. Векторы помогают объяснить это.
Скорость, ускорение, сила и многое другое являются векторами.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который мы хотим вычесть,
- затем добавьте их как обычно:
а — б
Обозначение
Вектор часто пишется жирным шрифтом , например a или b .
| Вектор также можно записать буквами его головы и хвоста со стрелкой над ним, например: |
Расчеты
Сейчас… как мы делаем расчеты?
Самый распространенный способ — сначала разбить векторы на части x и y, например:
Вектор a разбивается на
два вектора a x и a y
(мы увидим позже, как это сделать.)
Добавление векторов
Затем мы можем добавить векторы , добавив части x и , добавив части y :
Вектор (8, 13) и вектор (26, 7) складываются в вектор (34, 20)
Пример: добавьте векторы a = (8, 13) и b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем такой вектор, каждая часть называется компонентом :
Вычитание векторов
Чтобы вычесть, сначала переверните вектор, который мы хотим вычесть, затем добавьте.
Пример: вычесть k = (4, 5) из v = (12, 2)
a = v + — k
a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ это может быть записано с двойными вертикальными чертами (чтобы не путать его с абсолютным значением):
|| a ||
Мы используем теорему Пифагора для ее вычисления:
| a | = √ (x 2 + y 2 )
Пример: какова величина вектора b = (6, 8)?
| б | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против Скаляр
Скаляр имеет величину (размер) только .
Скалярное: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто пишется жирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому с является вектором, имеет величину и направление
- , но с просто значение, как 3 или 12.4
Пример: k b на самом деле является скалярным k, умноженным на вектор b .
Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем, насколько велик или мал вектор.
Пример: умножить вектор м = (7, 3) на скаляр 3
| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
Он все еще указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (точечный продукт и перекрестный продукт)
Как мы умножаем два вектора вместе? Существует несколько способов! (Прочитайте эти страницы для более подробной информации.) |
больше чем 2 размера
Векторы также отлично работают в 3 или более измерениях:
Вектор (1, 4, 5)
Пример: добавьте векторы a = (3, 7, 4) и b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора w = (1, -2, 3)?
| Вт | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4 размерами (но это трудно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (-1, -2, −3, −4)
= (3 -1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины x и y (или наоборот):
| <=> | ||
| Вектор a в Полярном Координаты | Вектор a в декартовом Координаты |
Вы можете прочитать, как преобразовать их в полярных и декартовых координатах, но вот краткое резюме:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) до полярных координат (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут коробку.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с силой 120 Ньютонов при 45 °, как показано
Что такое объединенная сила и ее направление?
Давайте добавим два вектора головы к хвосту:
Первое преобразование из полярного в декартово (до 2 десятичных знаков):
Сэм Вектор:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Алекс Вектор:
- x = r × cos ( θ ) = 120 × cos (−45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (−45 °) = 120 × -0,7071 = −84,85
Теперь у нас есть:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ верен, но давайте обратимся к полярности, как вопрос был в полярности:
- r = √ (x 2 + y 2 ) = √ (184.85 2 + 88,36 2 ) = 204,88
- θ = загар -1 (у / х) = загар -1 (88,36 / 184,85) = 25,5 °
И у нас есть этот (округленный) результат:
И это похоже на Сэма и Алекса:
Они могли бы получить лучший результат, если бы были плечом к плечу!
,Модуль 24 — Векторы — Урок 1
В этом уроке вы научитесь определять векторы на TI-89 и выполнять три типа умножения векторов. Будут обсуждены единичные векторы, и будут определены два формата, используемые для обозначения векторов.
Определение векторов
Величины, которые имеют величину и направление, называются векторами и часто представлены направленными отрезками, как показано ниже.
Показанный вектор имеет начальную точку в точке O и конечную точку в точке P .
Представление векторов в скобках
Векторы могут быть представлены на TI-89, давая координаты кончика стрелки. Например, вектор, который идет от начала координат до точки (3, 2), представлен на TI-89 с пометкой [3, 2].Обратите внимание на использование скобок вместо скобок для обозначения количества как вектора.
- Выполнить NewProb
- Сохраните вектор [3, 2] в переменной a на вашем TI-89 Скобки находятся над и ключи.
| |||
Определение единичных векторов i и j
Вектор i имеет длину в одну единицу и направлен вдоль положительной оси x , а вектор j имеет длину в одну единицу и направлен вдоль положительной оси и .Поскольку векторы i и j имеют длину в одну единицу, они называются единичными векторами. И , и , и , и показаны ниже вместе с вектором [3, 2].
Представление векторов с использованием i и j
Другая нотация использует единичные векторы i и j для представления вектора. Вектор [3, 2] также можно записать в виде
a = 3 i + 2 j
Обратите внимание, что a , i и j выделены жирным шрифтом, чтобы показать, что они являются векторами.
Нахождение длины вектора
Длина или величина любого вектора a = [x, y] равна
Длина а = [3, 2] составляет единицы.
Умножение вектора
Есть три типа умножения, которые включают векторы.Два типа создают вектор, а оставшийся тип создает действительное число. Каждый тип умножения обсуждается ниже.
Скалярное Умножение Векторов
Letting c представляет собой
| |||
Координаты c a находятся путем умножения каждой координаты a на c .
c a = c [ a 1 , a 2 ] = [ ca 1 , ca 2 ]
- Сохраните вектор [3, -1] в переменной a на своем калькуляторе и умножьте вектор на скаляр 2.
- Умножьте вектор [2, -5] на скаляр 3, не сохраняя вектор в переменной.
Использование команды V
Вектор, который указывает в том же направлении, что и и , и имеет звездную величину, можно найти с помощью команды unitV .
Определите единичный вектор, который указывает в том же направлении, что и , а = [3, 2].
- Откройте математическое меню, нажав
- Откройте подменю Matrix, выбрав 4: Matrix и нажав
- Выделите L: Vector ops
- Откройте подменю векторной операции, нажав
Пункт меню «1: unitV (» должен быть выделен.
- Нажмите вставить его в строку редактирования
- Введите единицу V (а)
Каждый компонент a был умножен на величину, обратную величине a , чтобы создать единичный вектор, который указывает в том же направлении, что и a . Обратите внимание, что фракции были
| |||
Нахождение точечных продуктов векторов
Второй тип умножения называется -точечным произведением .Точечное произведение двух векторов [ a 1 , a 2 ] и [ b 1 , b 2 ] определено как a 1 · b 1 + a 2 · b 2 .
Точечное произведение a и b можно найти с помощью команды dotP , которая находится в меню Math Matrix: Vector ops.
- Сохраните вектор -2 i + 5 j в b
Вычислить скалярное произведение а · б .
- Откройте подменю Matrix меню Math.
- Откройте подменю Vector ops в подменю Matrix.
- Вставить точку P (в строку редактирования
- Введите точку P (a, b)
Точечное произведение a · b равно 4.
Обратите внимание, что результатом точечного произведения двух векторов является действительное число , а не вектор. Точечное произведение такое же, как произведение величины на , величины на и косинуса угла между на и на .
Если это угол между а и б
Точечные продукты широко используются в физике.Например, они используются для расчета работы, выполняемой силой, действующей на объект.
Проецирование одного вектора на другой вектор
Проекция может рассматриваться как тень одного вектора на другом. Когда два вектора имеют одинаковую начальную точку, проекция b на a параллельна a и имеет длину тени b .Диаграмма ниже иллюстрирует проекцию b на a , записанную как proj a b и показанную как более темный вектор.
Проекции и точечные продукты
Величина проекции b на a , | proj a b | также называется компонентом из b вдоль a , и она равна | б | соз ,Обратите внимание, что компонент b вдоль a равен a · b / | а |.
Нахождение формулы для точечных продуктов на вашем калькуляторе
Формула для нахождения точечного произведения двух векторов [ a 1 , a 2 ] и [ b 1 , b 2 ] может быть получена на TI-89.
- Введите dotP ([a1, a2], [b1, b2])
24.1.1. Напишите формулу для нахождения скалярного произведения двух векторов. Нажмите здесь для ответа.
Определение кросс-продуктов
Третий тип умножения называется кросс-произведением и используется в геометрии и во многих ситуациях в физике и технике.Суммарное произведение a x b двух трехмерных векторов представляет собой вектор, который перпендикулярен и a и b . Если это угол между a и b , тогда длина a x b определяется как
Перекрестное произведение определено только для 3-мерных векторов, но TI-89 вычисляет перекрестное произведение 2-мерных векторов, рассматривая их как 3-мерные векторы с 0 в качестве третьего компонента.
В поисках перекрестных товаров
Перекрестное произведение можно рассчитать с помощью команды crossP , которая находится в меню «Математическая матрица векторных операций».
Найдите перекрестное произведение a x b ранее определенных векторов a = [3, 2] и b = [-2, 5].
[3, 2, 0] x [-2, 5, 0] = [0, 0, 19] = 0 i + 0 j + 19 k
Результатом перекрестного произведения является вектор , который имеет три компонента, что означает, что это трехмерный вектор.Единичный вектор k указывает вдоль положительной оси z. Вектор 0 i + 0 j + 19 k направлен вверх вдоль положительной оси z и имеет длину 19.
Перекрестное произведение двух векторов a и b всегда перпендикулярно каждому из двух векторов. Его величина равна величине a , умноженной на величину компонента b , перпендикулярного a .
24.1.2 Найти перекрестное произведение трехмерных векторов a = 2 i + j — 4 k и b = — i — 2 j + k . Опишите взаимосвязь между a , b и их перекрестным произведением. Нажмите здесь, чтобы проверить свой ответ.
,

 .
. , то
, то  . Наоборот, если
. Наоборот, если  , то при некотором λ верно равенство
, то при некотором λ верно равенство 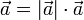 °, то есть каждый вектор равен произведению его модуля на орт.
°, то есть каждый вектор равен произведению его модуля на орт. –переместительный
закон
–переместительный
закон –сочетательный
закон
–сочетательный
закон –распределительный
закон
–распределительный
закон , при
, при  ,
, ,
, 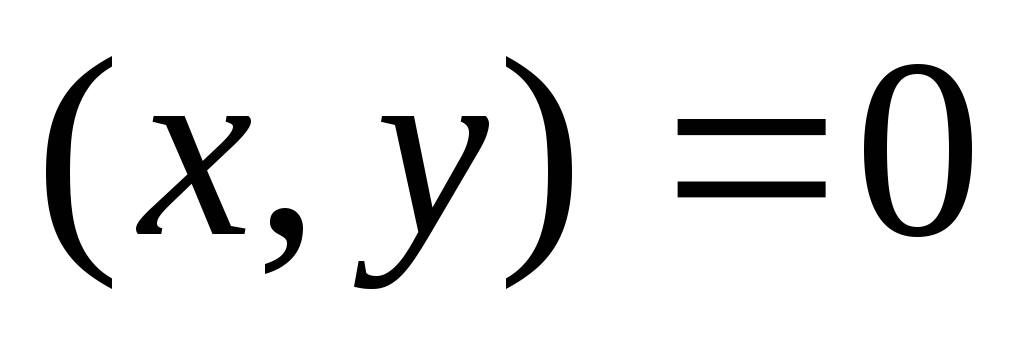 ,
,