Применение сил Ампера и Лоренца в науке и технике. Амперметр, телеграф, электромагниты, масс-анализаторы

Почему одних ученых история вносит на свои страницы золотыми буквами, а некоторых стирает бесследно? Каждый пришедший в науку обязан оставить в ней свой след. Именно по величине и глубине этого следа судит история. Так, Ампер и Лоренц внесли неоценимый вклад в развитие физики, что дало возможность не только развивать научные теории, но получило весомую практическую ценность. Как появился телеграф? Что такое электромагниты? На все эти вопросы даст ответ сегодняшний урок.

Для науки представляют огромную ценность полученные знания, которые впоследствии могут найти свое практическое применение. Новые открытия не только расширяют исследовательские горизонты, но и ставят новые вопросы, проблемы.

Выделим основные открытия Ампера в области электромагнетизма.

Во-первых, это взаимодействия проводников с током. Два параллельных проводника с токами притягиваются друг к другу, если токи в них сонаправлены, и отталкиваются, если токи в них противонаправлены (рис. 1).

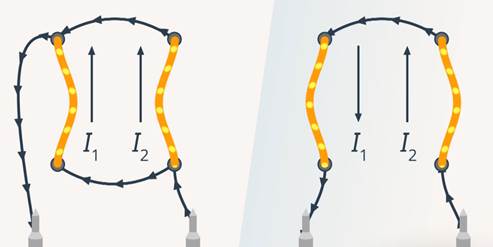
Рис. 1. Проводники с током

Закон Ампера гласит:

Сила взаимодействия двух параллельных проводников пропорциональна произведению величин токов в проводниках, пропорциональна длине этих проводников и обратно пропорциональна расстоянию между ними.

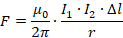
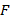– сила взаимодействия двух параллельных проводников,

– величины токов в проводниках,

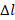 − длина проводников,

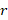 – расстояние между проводниками,

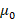 – магнитная постоянная.

Открытие этого закона позволило ввести в единицы измерения величину силы тока, которой до того времени не существовало. Так, если исходить из определения силы тока как отношения количества заряда перенесенного через поперечное сечение проводника в единицу времени, то мы получим принципиально не измеряемую величину, а именно количество заряда, переносимое через поперечное сечение проводника. На основании этого определения мы не сможем ввести единицу измерения силы тока. Закон Ампера позволяет установить связь между величинами сил тока в проводниках и величинами, которые можно измерить опытным путем: механической силой и расстоянием. Таким образом, получена возможность ввести в рассмотрение единицу силы тока – 1 А (1 ампер).

Ток в один ампер – это такой т

определение, формула, правило левой руки

Определение силы Лоренца

Немного истории

Формула силы Лоренца

Правило левой руки

Применение силы Лоренца

Рекомендованная литература и полезные ссылки

Сила Лоренса, видео

Определение силы Лоренца

Сила Лоренца представляет собой комбинацию магнитной и электрической силы на точечном заряде, который вызван электромагнитными полями. Или другими словами, сила Лоренца – это сила, действующая на всякую заряженную частицу, которая падает в магнитном поле с определенной скоростью. Ее величина зависит от величины магнитной индукции В, электрического заряда частицы q и скорости, с которой частица падает в поле – V. О том какая формула расчета силы Лоренца, а также ее практическое значение в физике читайте далее.

Немного истории

Первые попытки описать электромагнитную силу были сделаны еще в XVIII веке. Ученые Генри Кавендиш и Тобиас Майер высказали предположение, что сила на магнитных полюсах и электрически заряженных объектах подчиняется закону обратных квадратов. Однако экспериментальное доказательство этого факта не было полным и убедительным. Только в 1784 году Шарль Августин де Кулон при помощи своего торсионного баланса смог окончательно доказать это предположение.

В 1820 году физиком Эрстедом был открыт факт, что на магнитную стрелку компаса действует ток вольта, а Андре-Мари Ампер в этом же году смог разработать формулу угловой зависимости между двумя токовыми элементами. По сути, эти открытия стали фундаментом современной концепции электрических и магнитных полей. Сама же концепция получила свое дальнейшее развитие в теориях Майкла Фарадея, особенно в его представлении о силовых линиях. Лорд Кельвин и Джеймс Максвелл дополнили теории Фарадея подробным математическим описанием. В частности Максвеллом было создано так званное, «уравнение поля Максвелла» – представляющее собой систему дифференциальных и интегральных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Джей Джей Томпсон был первым физиком, кто попытался вывести из уравнения поля Максвелла электромагнитную силу, которые действует на движущийся заряженный объект. В 1881 году он опубликовал свою формулу F = q/2 v x B. Но из-за некоторых просчетов и неполного описания тока смещения она оказалась не совсем правильной.

И вот, наконец, в 1895 году голландский ученый Хендрик Лоренц вывел правильную формулу, которая используется и поныне, а также носит его имя, как и та сила, что действует на летящую частицу в магнитном поле, отныне называется «силой Лоренца».

Хендрик Лоренц.

Формула силы Лоренца

Формула для расчета силы Лоренца выглядит следующим образом:

Где q – электрический заряд частицы, V – ее скорость, а B – величина магнитной индукции магнитного поля.

При этом поле B выступает в качестве силы, перпендикулярной к направлению вектора скорости V нагрузок и направлению вектора B. Это можно проиллюстрировать на диаграмме:

Правило левой руки

Правило левой руки позволяет физикам определять направление и возврат вектора магнитной (электродинамической) энергии. Представьте себе, что наша левая рука расположена таким образом, что линии магнитного поля направлены перпендикулярно внутренней поверхности руки (так, что они проникают внутрь руки), а все пальцы за исключением большого указывают на направление протекания положительного тока, отклоненный большой палец указывает на направление электродинамической силы, действующий на положительный заряд, помещенный в это поле.

Вот так это будет выглядеть схематически.

Есть также и второй способ определения направления электромагнитной силы. Он заключается в расположении большого, указательного и среднего пальцев под прямым углом. В этом случае указательный палец будет показывать направление линий магнитного поля, средний – направление движение тока и большой – направление электродинамической силы.

Применение силы Лоренца

Сила Лоренца и ее расчеты имеет свое практическое применение при создании как специальных научных приборов – масс-спектрометров, служащих для идентификации атомов и молекул, так и создании многих других устройств самого разнообразного применения. Среди устройств есть и электродвигатели, и громкоговорители, и рельсовые пистолеты.

Также способность силы Лоренса связывать механическое смещение с электрическим током представляет большой интерес для медицинской акустики.

Рекомендованная литература и полезные ссылки

• Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
• Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренса, видео

Сила Лоренца — Википедия

Материал из Википедии — свободной энциклопедии

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью v{\displaystyle \mathbf {v} }, заряд q {\displaystyle q\ } лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического E{\displaystyle \mathbf {E} } и магнитного B{\displaystyle \mathbf {B} } полей. В Международной системе единиц (СИ) выражается как:

F=q(E+[v×B]).{\displaystyle \mathbf {F} =q\left(\mathbf {E} +[\mathbf {v} \times \mathbf {B} ]\right).}

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[3].

Заряженная частица[править | править код]

Сила F{\displaystyle \mathbf {F} }, действующая на частицу с электрическим зарядом q{\displaystyle q}, движущуюся со скоростью v{\displaystyle \mathbf {v} }, во внешнем электрическом E{\displaystyle \mathbf {E} } и магнитном B{\displaystyle \mathbf {B} } полях, такова:

F=q(E+v×B),{\displaystyle \mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ),}

где ×{\displaystyle \times } — векторное произведение. Все величины, выделенные жирным, являются векторами. Более явно:

F(r,t,q)=qE(r,t)+qr˙×B(r,t),{\displaystyle \mathbf {F} (\mathbf {r} ,t,q)=q\mathbf {E} (\mathbf {r} ,t)+q\mathbf {\dot {r}} \times \mathbf {B} (\mathbf {r} ,t),}

где r{\displaystyle \mathbf {r} } — радиус-вектор заряженной частицы, t{\displaystyle t} — время, точкой обозначена производная по времени.

Непрерывное распределение заряда[править | править код]

Для непрерывного распределения заряда, сила Лоренца принимает вид:

dF=dq(E+v×B),{\displaystyle d\mathbf {F} =dq\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right),}

где dF{\displaystyle d\mathbf {F} } — сила, действующая на маленький элемент dq{\displaystyle dq}.

4-сила выражается через вектор 4-скорости частицы по формуле

Fμ=qFνμuν,{\displaystyle {\mathcal {F}}^{\mu }=qF^{\nu \mu }u_{\nu },}

где Fμ{\displaystyle {\mathcal {F}}^{\mu }} — 4-сила, q{\displaystyle q} — заряд частицы, Fνμ{\displaystyle F^{\nu \mu }} — тензор электромагнитного поля, uν{\displaystyle u_{\nu }} — 4-скорость.

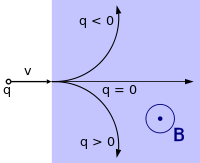Направление движения частицы в зависимости от её заряда при векторе магнитной индукции, перпендикулярном вектору скорости (к нам из плоскости рисунка, перпендикулярно ей)

В однородном магнитном поле, направленном перпендикулярно вектору скорости, под действием силы Лоренца заряженная частица будет равномерно двигаться по окружности постоянного радиуса r{\displaystyle r} (называемого также гирорадиусом). Сила Лоренца в этом случае является центростремительной силой:

СГС	СИ
mv2r=|q|cvB⇒r=cm|q|⋅vB{\displaystyle {mv^{2} \over r}={|q| \over c}vB\Rightarrow r={cm \over |q|}\cdot {v \over B}}	mv2r=|q|vB⇒r=m|q|⋅vB{\displaystyle {mv^{2} \over r}=|q|vB\Rightarrow r={m \over |q|}\cdot {v \over B}}

Работа силы Лоренца будет равна нулю, поскольку векторы силы и скорости всегда ортогональны. При скорости v {\displaystyle v\ }, намного меньшей скорости света, круговая частота ω {\displaystyle \omega \ } не зависит от v {\displaystyle v\ }:

СГС	СИ
ω=|q|Bmc{\displaystyle \omega ={|q|B \over mc}}	ω=|q|Bm{\displaystyle \omega ={|q|B \over m}}

Если заряженная частица движется в магнитном поле так, что вектор скорости v {\displaystyle v\ } составляет с вектором магнитной индукции B{\displaystyle \mathbf {B} } угол α {\displaystyle \alpha \ }, то траекторией движения частицы является винтовая линия с радиусом r {\displaystyle r\ } и шагом винта h {\displaystyle h\ }:

СГС	СИ
r=mc|q|⋅vsin⁡αB{\displaystyle r={mc \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅mc|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {mc \over |q|}\cdot v\cos \alpha }	r=m|q|⋅vsin⁡αB{\displaystyle r={m \over |q|}\cdot {v\sin \alpha \over B}}, h=2πB⋅m|q|⋅vcos⁡α{\displaystyle h={2\pi \over B}\cdot {m \over |q|}\cdot v\cos \alpha }

Эксперимент, показывающий воздействие силы Лоренца на заряженные частицы Пучок электронов, движущихся по круговой траектории под воздействием магнитного поля. Свечение вызвано возбуждением атомов остаточного газа в баллоне

1. ↑ Такая двойственность применения термина «сила Лоренца», очевидно, объясняется историческими причинами: дело в том, что сила, действующая на точечный заряд со стороны только электрического поля была известна задолго до Лоренца — Закон Кулона был открыт в 1785 году. Лоренц же получил общую формулу для действия и электрического и магнитного полей, отличающуюся от прежней как раз выражением для магнитного поля. Поэтому то и другое, вполне логично, называют его именем.
2. ↑ Болотовский Б. М. Оливер Хевисайд. — Москва: Наука, 1985. — С. 43-44. — 260 с.
3. ↑ Матвеев А. Н. Механика и теория относительности. — 3-е изд. — М. Высшая школа 1976. — С. 132.

Сила Лоренца: определение, направление, формула, применение

Мари Ампер доказал, что при наличии электрического тока в проводнике, оказавшемся в магнитном поле, он взаимодействует с силами этого поля. Учитывая то, что электрический ток – это не что иное, как упорядоченное движение электронов, можно предположить, что электромагнитные поля подобным образом действуют также на отдельно взятую заряженную частицу. Это действительно так. На точечный заряд действует сила Лоренца, модуль которой можно вычислить по формуле.

Определение и формула

Хендрик Лоренц доказал, что электромагнитная индукция взаимодействует с заряженными частицами. Эти взаимодействия приводят к возникновению силы Лоренца. Рассматриваемая сила возникает под действием магнитной индукции. Она перпендикулярна вектору скорости движущейся частицы (см. рис. 1). Необходимым условием возникновения этой силы является движение электрического заряда.

Рис. 1. Выводы Лоренца

Обратите внимание на расположение векторов (рисунок слева, вверху). Векторы, указывающие направления скорости и силы Лоренца, лежат в одной плоскости XOY, причём они расположены под углом 90º. Вектор магнитной индукции сориентирован вдоль оси Z, перпендикулярной плоскости XOY, а значит, в выбранной системе координат он перпендикулярен к векторам силы и скорости.

По закону Ампера:

Учитывая, что

(здесь j – плотность тока, q – единичный заряд, n – количество зарядов на бесконечно малую единицу длины проводника, S – сечение проводника, символом v обозначен модуль скорости движущейся частицы), запишем формулу Ампера в виде:

Так, как nSdl – общее число зарядов в объёме проводника, то для нахождения силы, действующей на точечный заряд, разделим выражение на количество частиц:

Модуль F вычисляется по формуле:

Из формулы следует:

1. Сила Лоренца приобретает максимальное значение, если угол α прямой.
2. Если точечный заряд, например, электрон, попадает в среду однородного магнитного поля, обладая некой начальной скоростью, перпендикулярной к линиям электромагнитной индукции, тогда вектор F будет перпендикулярен к вектору скорости. На точечный заряд будет действовать центробежная сила, которая заставит его вращаться по кругу. При этом работа равняется нулю (см. рис.2).
3. Если угол между вектором индукции и скоростью частицы не равняется 90º, тогда заряд будет двигаться по спирали. Направление вращения зависит от полярности заряда (рис. 3).

Рис. 2. Заряженная частица между полюсами магнитовРис. 3. Ориентация вектора в зависимости от полярности заряда

Из рисунка 3 видно, что вектор F направлен в противоположную сторону, если знак заряда меняется на противоположный (при условии, что направления остальных векторов остаются неизменными).

Траекторию движения частицы правильно называть винтовой линией. Радиус этой винтовой линии (циклотронный радиус) определяется перпендикулярной к полю составной начальной скорости частицы. Шаг винтовой линии, вдоль которой перемещается частица, определяется составной начальной скорости заряда, вошедшего в однородное магнитное поле. Эта составная направлена параллельно к электромагнитным линиям.

В чём измеряется?

Размерность силы Лоренца в международной системе СИ – ньютон (Н). Разумеется, модуль силы Лоренца настолько крохотная величина, по сравнению с ньютоном, что её записывают в виде К×10^-n Н, где 0<К<1, а n – порядок числа 10.

Когда возникает?

Магнитные поля не реагируют на неподвижный электрический заряд, так же как не действует сила Ампера на обесточенный проводник.

Для возникновения силы Лоренца необходимо выполнить три условия:

1. У частицы должен быть отрицательный или положительный заряд.
2. Заряженная частица должна находиться в магнитном поле.
3. Частица должна быть в движении, то есть вектор v ≠ 0.

Если хотя бы одно из условий не выполняется, сила Лоренца не возникает.

Формула силы Лоренца при наличии магнитного и электрического полей

Рассмотрим случай, когда заряженная частица находится в движении в двух полях одновременно (в электрическом и магнитном), тогда на заряд подействуют две составляющие:

Тогда:

Поскольку эту формулу вывел Лоренц, то её также называют именем учёного-физика.

Направление силы Лоренца

Мы уже упоминали, что направление возникшей силы Лоренца, кроме магнитных параметров, определяется (в том числе) полярностью заряда. Если бы мы имели возможность наблюдать заряженную элементарную частицу, пребывающую в магнитном поле, то по вектору её перемещения можно было бы определить направление вектора силы F.

Но на практике наблюдать элементарные заряды очень сложно из-за крохотных размеров. Поэтому для определения этого направления применяют способ, известен, как правило левой руки (рис. 4).

Рис. 4. Нахождение вектора силы Лоренца

Ладонь необходимо развернуть так, чтобы вектор индукции входил в неё. В случае с положительным зарядом, вытянутые пальцы располагают по движению частицы. (для отрицательного заряда пальцы направляют в противоположную сторону). Большой палец под прямым углом указывает искомое направление.

Если известна ориентация вектора скорости частицы, то определить направления остальных векторов можно, применяя правило правой руки, которое понятно из рисунка 5.

Рис. 5. Пример применения правила правой руки

Применение на практике

Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.

Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.

Рис. 6. Применение учения Лоренца

На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.

Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).

Рис. 7. Измерение текучести жидких веществ

Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.

Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.

На основании действия силы Лоренца создано много других устройств, используемых на практике.

Сила ? Лоренца — как действует и в чем ? измеряется? Как определить силу Лоренца?

Автор Даниил Леонидович На чтение 8 мин. Просмотров 1.2k. Опубликовано 18 ноября

Нигде еще школьный курс физики так сильно не перекликается с большой наукой, как в электродинамике. В частности, ее краеугольный камень – воздействие на заряженные частицы со стороны электромагнитного поля, нашло широкое применение в электротехнике.

Формула силы Лоренца

Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда. Но сперва нужно разобраться, что же оно собой представляет.

Определение и формула силы Лоренца

В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.

Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.

Вычисляют ее по специальной формуле:

FЛ=qvB,

здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).

Направление силы Лоренца

Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.

Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица. В таком случае большой палец покажет, куда она отклонится.

Интересно!

Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.

Следствия свойств силы Лоренца

Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:

FЛ=qvBsinα,

sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.

Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.

В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:

R=mvqB

Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.

Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:

R=mvsinαqB

h=2mvcosαqB

Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.

Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.

Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.

Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.

Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.

Формула силы Лоренца при наличии магнитного и электрического полей

Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:

FЛ=qE+vB

где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.

Единицы измерения силы Лоренца

Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.

Напряженность электрического поля

Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:

E=Fq

Единицей измерения является Н/Кл или В/м.

Примеры задачи

Задача 1

На заряд в 0,005 Кл, который движется в магнитном поле с индукцией 0,3 Тл, действует сила Лоренца. Вычислить ее, если скорость заряда 200 м/с, а движется он под углом 450 к линиям магнитной индукции.

Дано: q = 0,005 Кл B = 0,3 Тл v = 200 м/с α = 450

Решение: В условиях задачи нет упоминания электрического поля, поэтому силу Лоренца можно найти по следующей формуле: FЛ=qvBsinα=0,005×200×0,3×sin 450 =0,3×22=0,21 Н

Задача 2

Определить скорость тела, имеющего заряд и которое движется в магнитном поле с индукцией 2 Тл под углом 900. Величина, с которой поле воздействует на тело, равна 32 Н, заряд тела – 5 × 10-3 Кл.

Дано: q = 0,005 Кл B = 2 Тл FЛ = 32 Н α = 900

Решение: Чтобы найти скорость заряда, необходимо несколько видоизменить формулу для нахождения силы Лоренца:   FЛ=qvBsinαv=FЛqBsinα v=320,005×2×sin900=320,01×1=32000мс=32 км/с

Задача 3

Электрон движется в однородном магнитном поле под углом 900 ее силовым линиям. Величина, с которой поле воздействует на электрон, равна 5 × 10-13 Н. Величина магнитной индукции равна 0,05 Тл. Определить ускорение электрона.

Дано: q = -1,6 × 10-19 Кл B = 0,05 Тл FЛ = 5 × 10-13 Н α = 900

Решение: В этой задаче сила Лоренца ко всему прочему еще и заставляет двигаться электрон по окружности. Поэтому здесь под ускорением следует понимать центростремительное ускорение: aц=v2R На данный момент неизвестны ни скорость электрона, ни радиус окружности, по которой он движется.   v=FЛqBsinα=5×10-13-1,6×10-19×0,05∙sin900=6×107мс R=mvqB=9×10-31×6×107-1,6×10-19×0,05=6,8×10-3мс

aц=v2R=6×10726,8×10-3=5×1017мс2

Электродинамика оперирует такими понятиями, которым трудно подобрать аналогию в обычном мире. Но это совсем не значит, что их невозможно постичь. С помощью различных наглядных экспериментов и природных явлений процесс познания мира электричества может стать по настоящему захватывающим.

Урок физики: Применение силы Лоренца.

Урок 7. Применение силы Лоренца

 

Цель: показать практическую значимость силы Лоренца.

Ход урока

I. Организационный момент

 

II. Повторение изученного

— Какую силу называют силой Лоренца?

— Чему равна сила Лоренца?

— Что такое электрическое поле?

— Какое поле называют однородным?

— В каком случае электрическое поле разгоняет заряженную частицу, а в каком тормозит?

— Что такое магнитное поле?

— Как определить направление магнитной силы Лоренца?

— Как движется частица в магнитном поле в разных случаях?

 

III. Выполнение лабораторной работы

Лабораторная работа

Цели: ознакомление с устройством электронно-лучевой трубки осциллографа, использование знаний о силе Лоренца для определения скорости движения заряда.

Оборудование: подковообразный магнит с рассчитанным модулем В магнитной индукции, линейка, осциллограф (электроннолучевая трубка).

Ход работы

1. Установите след электронного луча (светящуюся точку) в центре экрана, вращая ручки вертикального и горизонтального смещения луча осциллографа. Осторожно прижмите подкову магнита к экрану и измерьте линейкой смещение луча по Y.

2. Зарисуйте положение магнита относительно экрана, начальное и конечное положение луча на экране. Укажите направление линий магнитной индукции между полюсами магнита. Определите направление движения электронов.

3. Радиус кривизны найдите по формуле:

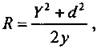
где R — радиус кривизны; d — толщина слоя, где действует магнитное поле; у — смещение.

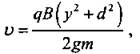
где q и m — табличные данные.

4. Если известно напряжение между ускоряющими электродами осциллографа, то можно провести оценку:

 

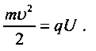
IV. Изучение нового материала

Рассмотрим некоторые из многочисленных применений силы Лоренца, которые встречаются в науке и технике.

1. Управление электронным пучком.

Как видно из лабораторной работы, с помощью магнитных полей можно изменить направление движения электронов. Впервые управлять электронными лучами научился Дж.-Дж. Томсон.

2. Определение скорости движения частиц.

3. Действие магнитного поля на движущиеся заряженные частицы используется для преобразования кинетической энергии плазменной струи в электрическую (МГД-генераторы) (магнитогидродинамики).

Поток плазмы направляется в поперечное магнитное поле, которое действует на движущиеся заряженные частицы  направленное перпендикулярно к скорости их движения. В результате положительные ионы отклоняются вверх, а электроны и отрицательные ионы — вниз.

Верхний катод электризуется положительно, а нижний — отрицательно, их выводы являются полюсами генератора. Между электродами ток течет снизу вверх. Происходит уменьшение скорости струи и ее кинетической энергии. На МГД-генераторе кинетическая энергия плазменной струи преобразовывается непосредственно в электрическую энергию.

Совместное использование на тепловых электростанциях гидродинамического метода преобразования энергии и обычных паротурбинных установок позволяет значительно повысить экономическую эффективность электростанций.

4. Определение знака заряда движущейся частицы.

5. Магнитные ловушки.

6. Определение удельного заряда и массы частиц.

7. Ускорители заряженных частиц.

8. Электронный микроскоп.

 

V. Закрепление изученного материала

— Каким методом можно определить скорость заряженных частиц?

— Как с помощью магнитного поля можно узнать заряжена ли частица?

— Опишите принцип действия циклотрона.

 

VI. Подведение итогов урока

Домашнее задание

П. 6; упр. № 1 (3 : 4).

 

Дополнительный материал

Полярные сияния

Одним из красивейших оптических явлений природы является полярное сияние.

В большинстве случаев полярные сияния имеют зеленый или сине-зеленый оттенок с изредка появляющимися пятнами или каймой розового или красного цвета.

Полярные сияния наблюдают в двух основных формах — в виде лент и в виде облакоподобных пятен. Когда сияние интенсивно, оно приобретает форму лент. Теряя интенсивность, оно превращается в пятна. Однако многие ленты исчезают, не успев разбиться на пятна. Ленты как бы висят в темном пространстве неба, напоминая гигантский занавес или драпировку, тянущуюся обычно с востока на запад на тысячи километров. Высота этого занавеса составляет несколько сотен километров, толщина не превышает нескольких сотен метров, причем он так нежен и прозрачен, что сквозь него видны звезды. Нижний край занавеса довольно резко и отчетливо очерчен и часто подкрашен в красный или розоватый цвет, напоминающий кайму занавеса, верхний — постепенно теряется в высоте и это создает особенно эффектное впечатление глубины пространства.

Различают четыре типа полярных сияний:

— Однородная дуга — светящаяся полоса имеет наиболее простую, спокойную форму. Она более яркая снизу и постепенно исчезает кверху на фоне свечения неба.

— Лучистая дуга — лента становится несколько более активной и подвижной, она образует мелкие складки и струйки.

— Лучистая полоса — с ростом активности более крупные складки накладываются на мелкие.

При повышении активности складки или петли расширяются до огромных размеров, нижний край ленты ярко сияет розовым свечением. Когда активность спадает, складки исчезают и лента возвращается к однородной форме. Это наводит на мысль, что однородная структура является основной формой полярного сияния, а складки связаны с возрастанием активности.

Часто возникают сияния иного вида. Они захватывают весь полярный район и оказываются очень интенсивными. Происходят они во время увеличения солнечной активности. Эти сияния представляются в виде беловато-зеленой шапки. Такие сияния называют шквалами.

По яркости сияния разделяют на четыре класса, отличающиеся друг от друга на один порядок (то есть в 10 раз). К первому классу относятся сияния еле заметные и приблизительно равные по яркости Млечному Пути, сияния же четвертого класса освещают Землю так ярко, как полная Луна.

Надо отметить, что возникшее сияние распространяется на запад со скоростью 1 км/с. Верхние слои атмосферы в области вспышек сияний разогреваются и устремляются вверх, что сказалось на усиленном торможении искусственных спутников Земли, проходящих эти зоны.

Во время сияний в атмосфере Земли возникают вихревые электрические токи, захватывающие большие области. Они возбуждают дополнительные неустойчивые магнитные поля, так называемые магнитные бури. Во время сияний атмосфера излучает рентгеновские лучи, которые, по-видимому, являются результатом торможения электронов в атмосфере.

Интенсивные вспышки сияния часто сопровождаются звуками, напоминающими шум, треск. Полярные сияния вызывают сильные изменения в ионосфере, что в свою очередь влияет на условия радиосвязи. В большинстве случаев радиосвязь значительно ухудшается. Возникают сильные помехи, а иногда полная потеря приема.

Как возникают полярные сияния. Земля представляет собой огромный магнит, южный полюс которого находится вблизи северного географического полюса, а северный — вблизи южного. Силовые линии магнитного поля Земли, называемые геомагнитными линиями, выходят из области, прилегающей к северному магнитному полюсу Земли, охватывают земной шар и входят в него в области южного магнитного полюса, образуя тороидальную решетку вокруг Земли.

Долго считалось, что расположение магнитных силовых линий симметрично относительно земной оси. Теперь выяснилось, что так называемый «солнечный ветер» — поток протонов и электронов, излучаемых Солнцем, налетая на геомагнитную оболочку Земли с высоты около 20000 км, оттягивает ее назад, в сторону от Солнца, образуя у Земли своеобразный магнитный «хвост».

Электрон или протон, попавшие в магнитное поле Земли, движутся по спирали, как бы навиваясь на геомагнитную линию. Электроны и протоны, попавшие из солнечного ветра в магнитное поле Земли, разделяются на две части. Часть из них вдоль магнитных силовых линий сразу стекает в полярные области Земли; другие попадают внутрь тероида и движутся внутри него, вдоль замкнутой кривой ABC. Эти протоны и электроны в конце концов по геомагнитным линиям также стекают в область полюсов, где возникает их увеличенная концентрация. Протоны и электроны производят ионизацию и возбуждение атомов и молекул газов. Для этого они имеют достаточно энергии, так как протоны прилетают на Землю с энергиями 10000- 20000 эВ (1 эВ = 1,6 ·10 Дж), а электроны с энергиями 10-20 эВ. Для ионизации же атомов нужно: для водорода — 13,56 эВ, для кислорода — 13,56 эВ, для азота — 124,47 эВ, а для возбуждения еще меньше.

Возбужденные атомы газов отдают обратно полученную энергию в виде света, наподобие того, как это происходит в трубках с разреженным газом при пропускании через них токов.

Спектральное исследование показывает, что зеленое и красное свечение принадлежит возбужденным атомам кислорода, инфракрасное и фиолетовое — ионизованным молекулам азота. Некоторые линии излучения кислорода и азота образуются на высоте 110 км, а красное свечение кислорода — на высоте 200-400 км. Другим слабым источником красного света являются атомы водорода, образовавшиеся в верхних слоях атмосферы из протонов, прилетевших с Солнца. Захватив электрон, такой протон превращается в возбужденный атом водорода и излучает красный свет.

Вспышки сияний происходят обычно через день-два после вспышек на Солнце. Это подтверждает связь между этими явлениями. Исследование при помощи ракет показало, что в местах большей интенсивности сияний имеется более значительная ионизация газов электронами.

В последнее время ученые установили, что полярные сияния более интенсивны у берегов океанов и морей.

Но научное объяснение всех явлений, связанных с полярными сияниями, встречает ряд трудностей. Например, неизвестен точно механизм ускорения частиц до указанных энергий, не вполне ясны их траектории в околоземном пространстве, не все сходится количественно в энергетическом балансе ионизации и возбуждения частиц, не вполне ясен механизм образования свечения различных видов, неясно происхождение звуков.



Т. Применения силы Лоренца — PhysBook

Использование силы Лоренца. Масс-спектрограф

Действие, оказываемое магнитным полем на движущиеся заряженные частицы, очень широко используют в технике.

Например, отклонение электронного пучка в кинескопах телевизоров осуществляют с помощью магнитного поля, которое создают специальными катушками. В ряде электронных приборов магнитное поле используется для фокусировки пучков заряженных частиц.

В созданных в настоящее время экспериментальных установках для осуществления управляемой термоядерной реакции действие магнитного поля на плазму используют для скручивания ее в шнур, не касающийся стенок рабочей камеры. Движение заряженных частиц по окружности в однородном магнитном поле и независимость периода такого движения от скорости частицы используют в циклических ускорителях заряженных частиц — циклотронах.

Действие силы Лоренца используют и в приборах, называемых масс-спектрографами, которые предназначены для разделения заряженных частиц по их удельным зарядам.

Схема простейшего масс-спектрографа показана на рисунке 1.

Рис. 1

В камере 1, из которой откачан воздух, находится источник ионов 3. Камера помещена в однородное магнитное поле, в каждой точке которого индукция \(~\vec B\) перпендикулярна плоскости чертежа и направлена к нам (на рисунке 1 это поле обозначено кружочками). Между электродами А ч В приложено ускоряющее напряжение, под действием которого ионы, вылетающие из источника, разгоняются и с некоторой скоростью попадают в магнитное поле перпендикулярно линиям индукции. Двигаясь в магнитном поле по дуге окружности, ионы попадают на фотопластинку 2, что позволяет определить радиус R этой дуги. Зная индукцию магнитного поля В и скорость υ ионов, по формуле

\(~\frac q m = \frac {v}{RB}\)

можно определить удельный заряд ионов. А если заряд иона известен, можно вычислить его массу.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 328.