Единицы измерения

В современном мире существует множество единиц измерения для различных величин. Не всеми ими часто пользуются, но все они имеют право на существование. Чаще всего использование той или иной единицы измерения зависит от местоположения. Например, мы привыкли измерять длину в миллиметрах, сантиметрах, метрах, километрах. Однако, покупая телевизор иностранного производства, мы неизбежно сталкиваемся с такой единицей измерения длины, как дюйм, ведь обычно именно в дюймах указывается длина диагонали телевизора. Представьте, например, вы покупаете телевизор, как сейчас модно, через интернет-магазин. На сайте указано, что диагональ его составляет 24 дюйма. И тут возникает проблема: а сколько это 24 дюйма? И на помощь приходит математика. Еще один пример: любой школьник, изучающий физику, слышал о системе СИ единиц измерения. Более того, от каждого школьника современная программа требует уметь переводить единицы измерения в систему СИ при решении школьных задач по физике. Таких примеров можно привести множество. Суть в том, что нужно уметь ориентироваться в единицах измерения различных величин и, при необходимости, уметь переводить одни единицы измерения в другие.

Приведем наиболее часто встречающиеся единицы измерения основных величин.

Масса: миллиграмм, грамм, килограмм (СИ), центнер, тонна.

1 тонна = 10 центнеров = 1 000 кг = 1 000 000 г = 1 000 000 000 мг.

Длина: миллиметр, сантиметр, метр (СИ), километр, фут, дюйм.

1 км = 1 000 м = 100 000 см = 1 000 000 мм

1 м = 3,2808399 фута = 39,3707 дюйма

Площадь: см², м² (СИ), акр, фут², гектар, дюйм².

1 м² = 10 000 см² = 0,00024711 акра = 10,764 фута = 0,0001 гектара = 1 550 дюйма².

Объем: сантиметр³, метр³ (СИ), фут³, галлон, дюйм³, литр.

1 м³ = 1 000 000 см³ = 35,32 фута³ = 220 галлонов = 61 024 дюйм³ = 1 000 литров (дм³).

Как правило, у школьников не возникает проблем с переводом больших единиц измерения в меньшие.

Например:

23 м = 2 300 см = 23 000 мм.

43 кг = 43 000 г.

Когда же речь заходит о переводе меньших единиц в большие, тут, как правило, возникают проблемы. Давайте разберемся, как лучше поступать в таких ситуациях.

Пример.

Пусть нам нужно перевести 28 мм в метры. Такая задача часто возникает в физике, когда требуется перевести единицы измерения в систему СИ.

Решение.

Действуем следующим образом:

1) Строим цепочку единиц измерения от большей к меньшей:

м -> см -> мм.

2) Вспоминаем: 1 м = 100 см, 1 см = 10 мм.

3) Теперь идем в обратном порядке: 1 мм = 0,1 см, 1 см = 0,01 м.

Значит, 1 мм = 0,1 см = 0,1 · 0,01 = 0,001 м.

4) 28 мм = 28 · 0,001 = 0,028 м.

Ответ. 28 мм = 0,028 м.

Пример.

Пусть нам требуется перевести 25 литров в метры³.

Решение.

Пользуемся той же схемой.

1) Строим цепочку единиц измерения от большей к меньшей, но пока без кубов.

м -> дм.

2) Вспоминаем: 1 м = 10 дм.

3) Теперь идем в обратном порядке: 1 дм = 0,1 м.

Значит, 1 литр = 1 дм³ = 0,001 м³.

4) 25 литров = 25 дм³ = 25 · 0,001 = 0,025 м

3.

Ответ. 25 литров = 0,025 м³.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Перевод единиц

В этом уроке мы научимся переводить физические величины из одной единицы измерения в другую.

Перевод единиц измерения длины

Из прошлых уроков мы знаем, что основные единицы измерения длины это:

• миллиметры;
• сантиметры;
• дециметры;
• метры;
• километры.

Любая величина, которая характеризует длину, может быть переведена из одной единицы измерения в другую.

Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если длина дана не в метрах, а в другой единице измерения, то её обязательно нужно перевести в метры, поскольку метр является единицей измерения длины в системе СИ.

Чтобы переводить длину из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один сантиметр состоит из десяти миллиметров или один километр состоит из тысячи метров.

Покажем на простом примере, как можно рассуждать при переводе длины из одной единицы измерения в другую. Предположим, что имеется 2 метра и нужно перевести их в сантиметры.

Сначала нужно узнать сколько сантиметров содержится в одном метре. В одном метре содержится сто сантиметров:

1 м = 100 см

Если в 1 метре содержится 100 сантиметров, то сколько сантиметров будет содержаться в двух метрах? Ответ напрашивается сам — 200 см. А эти 200 см получаются, если 2 умножить на 100.

Значит, чтобы перевести 2 метра в сантиметры, нужно 2 умножить на 100

2 × 100 = 200 см

Теперь попробуем перевести те же 2 метра в километры. Сначала надо узнать сколько метров содержится в одном километре. В одном километре содержится тысяча метров:

1 км = 1000 м

Если один километр содержит 1000 метров, то километр который содержит только 2 метра будет намного меньше. Чтобы его получить нужно 2  разделить на 1000

2 : 1000 = 0,002 км

Поначалу бывает трудно запомнить, какое действие применять для перевода единиц — умножение или деление. Поэтому на первых порах удобно пользоваться следующей схемой:

Суть данной схемы заключается в том, что при переходе из старшей единицы измерения в младшую применяется умножение. И наоборот, при переходе из младшей единицы измерения в более старшую применяется деление.

Стрелки, которые направлены вниз и вверх указывают на то, что осуществляется переход из старшей единицы измерения в младшую и переход из младшей единицы измерения в более старшую соответственно. В конце стрелки указывается какую операцию применить: умножение или деление.

Например, переведём 3000 метров в километры, пользуясь данной схемой.

Итак, мы должны перейти из метров в километры. Другими словами, перейти из младшей единицы измерения в более старшую (километр старше метра). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:

Теперь нужно узнать, сколько метров содержится в одном километре. В одном километре содержится 1000 метров. А чтобы узнать, сколько километров составляют 3000 таких метров, нужно 3000 разделить на 1000

3000 : 1000 = 3 км

Значит, при переводе 3000 метров в километры, получим 3 километра.

Попробуем перевести те же 3000 метров в дециметры. Здесь мы должны перейти из старших единиц в младшие (дециметр младше метра). Смотрим на схему и видим, что стрелка указывающая переход из старших единиц в младшие, направлена вниз и в конце стрелки указано, что мы должны применить умножение:

Теперь нужно узнать, сколько дециметров в одном метре. В одном метре 10 дециметров.

1 м = 10 дм

А чтобы узнать сколько таких дециметров в трёх тысячах метрах, нужно 3000 умножить на 10

3000 × 10 = 30 000 дм

Значит при переводе 3000 метров в дециметры, получим 30000 дециметров.

---

Перевод единиц измерения массы

Из прошлых уроков мы знаем, что основные единицы измерения массы это:

• миллиграммы;
• граммы;
• килограммы;
• центнеры;
• тонны.

Любая величина, которая характеризует массу, может быть переведена из одной единицы измерения в другую.

Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если масса дана не в килограммах, а в другой единице измерения, то её обязательно нужно перевести в килограммы, поскольку килограмм является единицей измерения массы в системе СИ.

Чтобы переводить массу из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения. То есть нужно знать, что к примеру один килограмм состоит из тысячи граммов или один центнер состоит из ста килограммов.

Покажем на простом примере, как можно рассуждать при переводе массы из одной единицы измерения в другую. Предположим, что имеется 3 килограмма и нужно перевести их в граммы.

Сначала нужно узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:

1 кг = 1000 г

Если в 1 килограмме 1000 граммов, то сколько граммов будут содержаться в трёх таких килограммах? Ответ напрашивается сам — 3000 граммов. А эти 3000 граммов получаются путем умножения 3 на 1000. Значит, чтобы перевести 3 килограмма в граммы, нужно 3 умножить на 1000

3 × 1000 = 3000 г

Теперь попробуем перевести те же 3 килограмма в тонны. Сначала нужно узнать сколько килограммов содержатся в одной тонне. В одной тонне содержится тысяча килограмм:

1 т = 1000 кг

Если одна тонна содержит 1000 килограмм, то тонна которая содержит только 3 килограмма будет намного меньше. Чтобы её получить нужно 3 разделить на 1000

3 : 1000 = 0,003 т

Как и в случае с переводом единиц измерения длины, на первых порах удобно пользоваться следующей схемой:

Данная схема позволит быстро сориентироваться какое действие выполнить для перевода единиц — умножение или деление.

Например, переведём 5000 килограмм в тонны, пользуясь данной схемой.

Итак, мы должны перейти из килограммов в тонны. Другими словами, перейти из младшей единицы измерения в более старшую (тонна старше килограмма). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:

Теперь нужно узнать сколько килограмм содержатся в одной тонне. В одной тонне содержится 1000 килограмм. А чтобы узнать, сколько тонн составляет 5000 килограмм, нужно 5000 разделить на 1000

5000 : 1000 = 5 т

Значит, при переводе 5000 килограмм в тонны, получается 5 тонн.

Попробуем перевести 6 килограммов в граммы. В данном случае мы переходим из старшей единицы измерения в младшую. Поэтому будем применять умножение.

Сначала надо узнать сколько граммов содержится в одном килограмме. В одном килограмме содержится тысяча граммов:

1 кг = 1000 г

Если в 1 килограмме 1000 граммов, то в шести таких килограммах будет в шесть раз больше граммов. Значит 6 нужно умножить на 1000

6 × 1000 = 6000 г

Значит, при переводе 6 килограммов в граммы, получим 6000 грамм.

---

Перевод единиц измерения времени

Из прошлых уроков мы знаем, что основные единицы измерения времени это:

• секунды;
• минуты;
• часы;
• сутки.

Любая величина, которая характеризует время, может быть переведена из одной единицы измерения в другую.

Кроме того, при решении задач по физике, обязательно нужно соблюдать требования международной системы СИ. То есть если время дано не в секундах, а в другой единице измерения, то его обязательно нужно перевести в секунды, поскольку секунда является единицей измерения времени в системе СИ.

Чтобы переводить время из одной единицы измерения в другую, нужно знать из чего состоит та или иная единица измерения времени. То есть нужно знать, что к примеру один час состоит из шестидесяти минут или одна минута состоит из шестидесяти секунд и т.д.

Покажем на простом примере, как можно рассуждать при переводе времени из одной единицы измерения в другую. Предположим, что требуется перевести 2 минуты в секунды.

Сначала надо узнать сколько секунд содержится в одной минуте. В одной минуте содержатся шестьдесят секунд:

1 мин = 60 с

Если в 1 минуте 60 секунд, то сколько секунд будет в двух таких минутах? Ответ напрашивается сам — 120 секунд. А эти 120 секунд получаются путём умножения 2 на 60. Значит, чтобы перевести 2 минуты в секунды, нужно 2 умножить на 60

2 × 60 = 120 с

Теперь попробуем перевести те же 2 минуты в часы. Поскольку мы переводим минуты в часы, то сначала надо узнать сколько минут содержится в одном часе. В одном часе содержится шестьдесят минут:

1 ч = 60 м

Если один час содержит 60 минут, то час который содержит только 2 минуты будет намного меньше. Чтобы его получить нужно 2 минуты разделить на 60

При делении 2 на 60 получается периодическая дробь 0,0 (3). Эту дробь можно округлить до разряда сотых. Тогда получим ответ 0,03

2 : 60= 0,03 ч

При переводе единиц измерения времени также применима схема, подсказывающая что применять — умножение или деление:

Например, переведём 25 минут в часы, пользуясь данной схемой.

Итак, мы должны перейти из минут в часы. Другими словами, перейти из младшей единицы измерения в более старшую (часы старше минут). Смотрим на схему и видим, что стрелка указывающая переход из младших единиц в более старшие, направлена вверх и в конце стрелки указано, что мы должны применить деление:

Теперь нужно узнать, сколько минут содержится в одном часе. В одном часе содержится 60 минут. А час, который содержит только  25 минут будет намного меньше. Чтобы его найти, нужно 25 разделить на 60

При делении 25 на 60 получается периодическая дробь 0,41 (6). Эту дробь можно округлить до разряда сотых. Тогда получим ответ 0,42

25 : 60 = 0,42 ч

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Единицы длины. Единицы площади. Таблица единиц площади

Вы знакомы с различными единицами длины. Какими единицами длины удобно пользоваться при измерении толщины спички или длины тельца божьей коровки? Я думаю, вы назвали миллиметры.

Какими единицами длины удобно пользоваться при измерении длины карандаша? Конечно, сантиметрами (см. рис. 1).

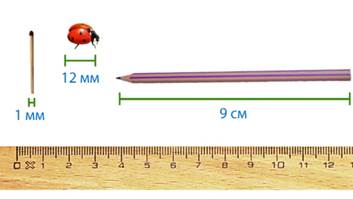
Рис. 1. Измерение длин

Какими единицами длины удобно пользоваться при измерении ширины или длины окна? Удобно измерять дециметрами.

А длину коридора или длину забора? Воспользуемся метрами (см. рис. 2).

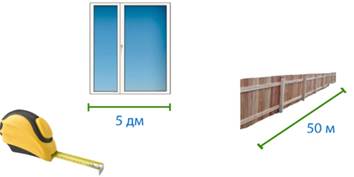
Рис. 2. Измерение длин

Для измерения более крупных расстояний, например, расстояний между городами, используют более крупную, чем метр, единицу длины – километр (см. рис. 3).

 

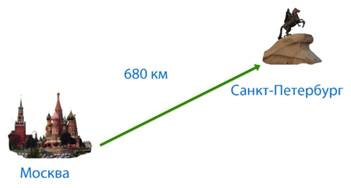
Рис. 3. Измерение длин

В 1 километре 1000 метров.

Выразите расстояние в километрах.

1 километр – это тысяча метров, значит, число тысяч будет обозначать километры.

8000 м = 8 км

385007 м = 385 км 7 м

34125 м = 34 км 125 м

В числе количество сотен, десятков и единиц указывают метры.

Можно рассуждать по-другому: 1 км в тысячу раз больше 1 метра, значит, число километров должно быть в 1000 раз меньше числа метров. Поэтому 8000 : 1000 = 8, число 8 означает количество километров.

385007 : 1000 = 385 (ост. 7). Число 385 обозначает километры, остаток – количество метров.

34125 : 1000 = 34 (ост. 125), то есть 34 километра 125 метров.

Прочитайте таблицу единиц длины (см. рис. 4). Постарайтесь ее запомнить.

Рис. 4. Таблица единиц длины

Для измерения площадей используют разные мерки. Квадратный сантиметр – это квадрат со стороной в 1 см (см. рис. 5), квадратный дециметр – это квадрат со стороной в 1 дм (см. рис. 6), квадратный метр – это квадрат со стороной в 1 м (см. рис. 7).

 

Рис.5. Квадратный сантиметр 

 

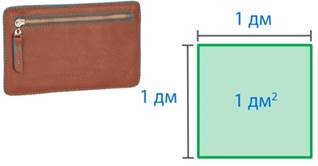
Рис. 6. Квадратный дециметр

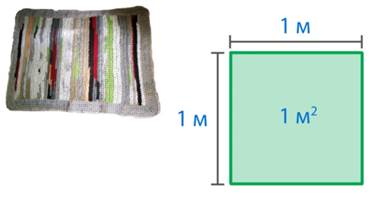
Рис. 7. Квадратный метр

Для измерения больших площадей используют квадратный километр – это квадрат, сторона которого равна 1 км (см. рис. 8).

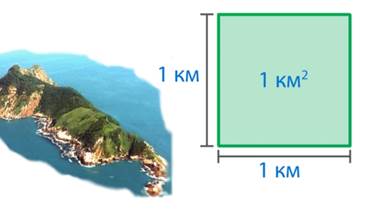
Рис. 8. Квадратный километр

Слова «квадратный километр» сокращенно при числе записывают так – 1 км², 3 км², 12 км². В квадратных километрах измеряют, например, площади городов, площадь Москвы S = 1091 км².

Вычислим, сколько квадратных метров в одном квадратном километре. Чтобы найти площадь квадрата, надо длину умножить на ширину. Нам дан квадрат со стороной в 1 км. Мы знаем, что 1 км = 1000 м, значит, чтобы найти площадь такого квадрата, умножим 1000 м на 1000 м, получится 1 000 000 м² = 1 км².

Выразите в квадратных метрах 2 км². Будем рассуждать так: так как 1 км² – это 1 000 000 м², то есть число квадратных метров в миллион раз больше, чем число квадратных километров, поэтому умножим 2 на 1 000 000, получим 2 000 000 м².

56 км²: умножим 56 на 1 000 000, получим 56 000 000 м².

202 км² 15 м²: 202 ∙1 000 000  + 15 = 202 000 000 м² + 15 м² = 202 000 015 м².

Для измерения маленьких площадей используются квадратный миллиметр (мм²). Это квадрат, сторона которого равна 1 мм. Слова «квадратный миллиметр» при числе записывают так: 1 мм², 7 мм², 31 мм².

Вычислим, сколько квадратных миллиметров в одном квадратном сантиметре. Чтобы найти площадь квадрата, надо длину умножить на ширину. Нам дан квадрат со стороной 1 см. Мы знаем, что 1 см = 10 мм. Значит, чтобы найти площадь такого квадрата, умножим 10 мм на 10 мм, получится 100 мм².

Выразите в квадратных миллиметрах 4 см². Будем рассуждать так: так как 1 см² – это 100 мм², то есть число мм² в 100 раз больше числа см², поэтому умножим 4 на 100, получим 400 мм².

16 см²: умножим 16 на 100 = 1600 мм².

31 см² 7 мм²: это 31 ∙ 100 + 7 = 3100 + 7 = 3107 мм².

В жизни часто употребляются такие единицы площади, как ар и гектар. Ар – это квадрат со стороной 10 м (см. рис. 9). При числах ар записывают короче: 1 а, 5 а, 12 а.

 

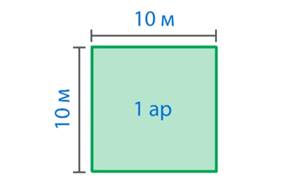
Рис. 9. 1 ар

1 а = 100 м², поэтому его часто называют соткой.

Гектар – это квадрат со стороной в 100 м (см. рис. 10). Слово «гектар» при числах сокращенно записывают так: 1 га,6 га, 23 га. 1 га = 10000 м².

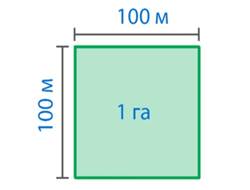
Рис. 10. 1 гектар

Вычислите, сколько аров в 1 гектаре.

1 га = 10000 м²

1 а = 100 м², значит, 10000 : 100 = 100 а

1 га = 100 а

Теперь внимательно рассмотрите таблицу единиц площади (см. рис. 11), постарайтесь ее запомнить.

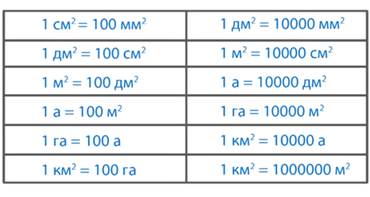
Рис. 11. Таблица единиц площади

На уроке мы познакомились с новой единицей длины – км и единицами площади – м², км², а, га.

 

Список рекомендованной литературы

1. Башмаков М.И. Нефёдова М.Г. Математика. 4 класс. М.: Астрель, 2009.
2. М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. Математика. 4 класс. Часть 1 из 2, 2011.
3. Демидова Т. Е. Козлова С. А. Тонких А. П. Математика. 4 класс 2-е изд., испр. — М.: Баласс, 2013.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. School.xvatit.com (Источник).
2. Mer.kakras.ru (Источник).
3. Dpva.info (Источник).

 

Домашнее задание

1. Найдите площадь квадрата со стороной 15 дм.
2. Выразите: в квадратных метрах: 5 га; 3 га 18 а; 247 соток; 16 а;
3. в гектарах: 420 000 м²; 45 км² 19 га;
4. в арах: 43 га; 4 га 5 а; 30 700 м²; 5 км2 13 га;
5. в гектарах и арах: 930 а; 45 700 м².

 

«Единицы измерения» — Яндекс.Знатоки

Единиц измерения сущетвует огромное количество. Во-первых, для разных измерений используются разные системы единиц, которые нельзя сравнивать между собой. Что больше – грамм или метр? Что меньше – литр или секунда? На эти вопросы нельзя дать ответ. Поэтому не может быть одной наименьшей единицы измерения вообще. Можно только говорить о наименьшей единице длины, наименьшей единице времени и т.д.

Но и для конкретного измерения, скажем, длины, всё не так просто. Если мы найдём наименьшую единицу, что помешает нам или кому-либо ещё придумать новую единицу ещё меньше? Ничего! А может быть, такая единица уже существует и где-то используется, просто она пока не получила широкой известности? Всё может быть!

Тем не менее, давайте попробуем найти ответ, например, для единиц днины. Возьмём систему СИ (международную систему единиц). В этой системе основной единицей длины является метр. К названию единицы можно приписывать стандартные префиксы, которые уменьшают или увеличивают эту единицу. Например, префикс «кило» даёт нам километр (1000 метров), а префикс «микро» даёт микрометр (0.001 метр). Чтобы получить наименьшую единицу, надо использовать префикс йокто. Один йоктометр равен 10⁻²⁴ метра или, если записать это в виде десятичной дроби, 0.000000000000000000000001 метра.

Но есть известная единица длины ещё меньше йоктометра. В далёком 1899г немецкий физик Макс Планк придумал систему единиц, основанную только на фундаментальных свойствах и постоянных нашей вселенной, таких, как скорость света. Вот, что писал Планк о своей системе:

…мы получаем возможность установить единицы длины, массы, времени и температуры, которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений»

Система планковских единиц не используется широко, потому что все единицы в ней получились очень малы, их неудобно использовать на практике. Однако, если искать наименьшие единицы измерения, именно планковские единицы могут быть ответом на вопрос.

И правда, планковская длина равна 1,616 229(38)⋅10⁻³⁶ метра, т.е. почти в 600 миллиардов раз меньше йоктометра.

Похоже, победителем в конкурсе за звание наименьшей единицы длины с большим отрывом побеждает планковская длина.

о физических явлениях и законах природы

Отличие физики от всех других наук заключается в том, что она изучает самые основные, фундаментальные законы нашего мира. Изучая, описывает их языком математики.

Например, закон гравитации — фундаментальный закон. Но он не совсем точен, ибо нет связи его с квантовой теорией. Тоже относится и к другим нашим законам — они не точны. Где-то на краю их всегда лежит тайна, всегда есть, над чем поломать голову. Может быть, это — свойство природы, а может быть, и нет, но это свойственно тем законам, которые известны нам сегодня. Может быть, все дело тут в неполноте нашего знания.

Законы просты, их легко сформулировать так, чтобы не оставалось никаких лазеек для двусмысленности и для иного толкования. Они просты и поэтому прекрасны. Просты по форме. Закон действует сложно, но его коренная идея проста. Это и роднит все наши законы. Сами по себе они всегда оказываются простыми, хотя в природе действуют сложным образом.

Физические законы универсальны. Например, гравитация, простирается на огромные расстояния. Если увеличить расстояние в десять миллионов миллионов раз, то мы получим Солнечную систему. Увеличим еще в десять миллионов миллионов раз — и вот вам галактики, которые притягиваются друг к другу по тому же самому закону. Вышивая свой узор, Природа пользуется лишь самыми длинными нитями, и всякий, даже самый маленький образчик его может открыть нам глаза на строение целого.

УТВЕРЖДЕНО
Приказ Министерства образования Республики Беларусь
от 20.12.2012г №931

МЕХАНИКА.

1) Механическое движение. Относительность движения. Характеристики механического движения: путь, перемещение. Скорость. Закон сложения скоростей.

2) Равномерное движение. Графическое представление равномерного движения.

3) Неравномерное движение. Средняя и мгновенная скорости. Ускорение. Прямо¬линейное движение с постоянным ускорением. Графическое представление равно¬ускоренного движения.

4) Движение материальной точки по окружности с постоянной по модулю линей¬ной скоростью. Угловая скорость. Период и частота равномерного вращения. Центростремительное ускорение.

5) Свободное падение тел. Ускорение свободно падающего тела. Движение тела, брошенного горизонтально.

6) Взаимодействие тел. Первый закон Ньютона.

7) Сила. Сложение сил.

8) Инертность тел. Масса. Плотность вещества.

9) Второй закон Ньютона.

10) Третий закон Ньютона.

11) Закон всемирного тяготения. Сила тяжести.

12) Силы упругости. Закон Гука.

13) Силы трения. Коэффициент трения.

14) Импульс. Закон сохранения импульса. Реактивное движение.

15) Механическая работа. Мощность.

16) Кинетическая энергия. Теорема об изменении кинетической энергии.

17) Потенциальная энергия. Потенциальная энергия гравитационных и упругих взаимодействий.

18) Закон сохранения механической энергии.

19) Колебательное движение. Амплитуда, период, частота и фаза колебаний. Уравнение гармонических колебаний. Пружинный и математический маятники. Превращения энергии при колебательных движениях.

20) Распространение колебаний в упругой среде. Волны. Скорость распространения волны, частота и длина волны, связь между ними.

21) Давление. Закон Паскаля. Гидростатическое давление. Сообщающиеся сосуды.

22) Атмосферное давление. Опыт Торричелли.

23) Закон Архимеда. Плавание тел.

знать/понимать:

физические явления: механическое движение: равномерное, равноускоренное движение; равномерное вращательное движение;

смысл физических понятий: путь, перемещение, скорость, средняя скорость пути и перемещения, мгновенная скорость, ускорение; угловая и линейная скорости, период и частота равномерного вращения, центростремительное ускорение, масса, плотность, сила (тяжести, упругости, трения), давление, атмосферное давление, импульс тела, импульс силы, гравитационное поле, работа, мощность, кинетическая энергия, потенциальная энергия, коэффициент полезного действия; период, амплитуда, частота, фаза колебаний, длина волны, скорость распространения волны;

смысл физических законов, принципов, правил, постулатов: I, II, III законов Ньютона, всемирного тяготения, Гука, сохранения механической энергии, сохранения импульса, Архимеда, Паскаля

уметь решать задачи:

на применение кинематических законов поступательного движения, закона сложения скоростей, на определение периода, частоты, на связь угловой и линейной скоростей, на определение центростремительного ускорения при равномерном вращательном движении, на применение законов Ньютона, Гука, всемирного тяготения, сохранения импульса и механической энергии, Архимеда; на расчет работы и мощности, на движение тел под действием силы тяжести, упругости, трения; на определение периода, частоты и фазы колебаний, периода колебаний математического и пружинного маятников, скорости распространения и длины волны;

ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ И ТЕРМОДИНАМИКИ.

1) Основные положения молекулярно-кинетической теории.

2) Идеальный газ. Основное уравнение молекулярно-кинетической теории идеального газа. Закон Дальтона.

3) Температура — мера средней кинетической энергии теплового движения частиц. Шкала температур Цельсия. Абсолютная шкала температур — шкала Кельвина.

4) Уравнение состояния идеального газа (уравнение Клапейрона—Менделеева). Изотермический, изобарный и изохорный процессы в идеальном газе.

5) Внутренняя энергия термодинамической системы. Работа и количество теплоты как меры изменения внутренней энергии. Удельная теплоемкость.

6) Внутренняя энергия одноатомного идеального газа.

7) Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе.

8) Циклические процессы. Физические основы работы тепловых двигателей. Коэффициент полезного действия теплового двигателя и его максимальное значение.

9) Плавление и кристаллизация. Удельная теплота плавления.

10) Испарение и конденсация. Кипение жидкости. Удельная теплота парообразования.

11) Насыщенный пар. Влажность.

12) Горение. Удельная теплота сгорания топлива.

знать/понимать:

физические явления: переход вещества из одного агрегатного состояния в другое;

смысл физических понятий: внутренняя энергия, внутренняя энергия одноатомного идеального газа, температура, количество теплоты, удельная теплоемкость, удельная теплота сгорания, удельная теплота плавления, удельная теплота парообразования;

смысл физических законов, принципов, правил, постулатов: закона Дальтона, первого закона термодинамики, газовых законов;

уметь решать задачи:

на расчет количества вещества, средней квадратичной скорости и средней кинетической энергии теплового движения молекул, параметров состояния идеального газа (давления, объема, температуры) с использованием основного уравнения молекулярно-кинетической теории и уравнения Клапейрона—Менделеева; на применение закона Дальтона; на расчет работы, количества теплоты, изменения внутренней энергии одноатомного идеального газа при изотермическом, изохорном, изобарном процессах с использованием первого закона термодинамики, на применение уравнения теплового баланса при переходе вещества из одного агрегатного состояния в другое; на определение коэффициента полезного действия тепловых двигателей;

ЭЛЕКТРОДИНАМИКА.

1) Электрический заряд. Закон сохранения электрического заряда.

2) Взаимодействие точечных зарядов. Закон Кулона.

3) Электростатическое поле. Напряженность электростатического поля. Поле точечного заряда. Однородное электростатическое поле. Графическое изображение электростатических полей.

4) Потенциальный характер электростатического поля. Потенциал электростатического поля точечного заряда. Разность потенциалов. Напряжение. Связь между напряжением и напряженностью однородного электростатического поля.

5) Принцип суперпозиции электростатических полей.

6) Диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества.

7) Электроемкость. Конденсаторы.

8) Энергия электростатического поля конденсатора.

9) Электрический ток. Условия существования электрического тока. Источники электрического тока. Сила и направление электрического тока.

10) Закон Ома для однородного участка электрической цепи. Электрическое сопротивление. Удельное сопротивление. Последовательное и параллельное соединение проводников.

11) Электродвижущая сила источника тока. Закон Ома для полной электрической цепи.

12) Работа и мощность электрического тока. Закон Джоуля—Ленца. Коэффициент полезного действия источника тока.

13) Постоянные магниты. Взаимодействие магнитов. Магнитное поле.

14) Действие магнитного поля на проводник с током. Закон Ампера. Индукция магнитного поля. Графическое изображение магнитных полей. Принцип суперпозиции магнитных полей.

15) Движение заряженных частиц в магнитном поле. Сила Лоренца.

16) Магнитный поток. Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца.

17) Явление самоиндукции. Индуктивность.

18) Энергия магнитного поля.

19) Колебательный контур. Свободные электромагнитные колебания в контуре. Формула Томсона. Превращения энергии в идеальном колебательном контуре.

20) Переменный электрический ток. Действующие значения силы тока и напряжения.

21) Электромагнитные волны и их свойства. Скорость распространения электромагнитных волн. Шкала электромагнитных волн.

знать/понимать:

физические явления:электрические взаимодействия; тепловое действие тока; магнитные взаимодействия; электромагнитная индукция, самоиндукция; электромагнитные волны;

смысл физических понятий: электромагнитное поле; проводник, диэлектрик, электрический заряд, точечный электрический заряд, элементарный заряд, напряженность электрического поля, потенциал электрического поля, разность потенциалов, электрическое напряжение; электроемкость, диэлектрическая проницаемость вещества, энергия электрического и магнитного полей; источник тока, сила электрического тока, электрическое сопротивление, удельное электрическое сопротивление, электродвижущая сила источника тока; индукция магнитного поля, магнитный поток, электродвижущая сила индукции и самоиндукции, индуктивность; амплитудное и действующее значения напряжения и силы переменного тока;

смысл физических законов, принципов, правил, постулатов: законов сохранения электрического заряда, Кулона, принципа суперпозиции электрических и магнитных полей; законов Ома для однородного участка цепи, для полной цепи, Джоуля — Ленца; Ампера; электромагнитной индукции Фарадея, правила Ленца;

уметь решать задачи:

на применение закона сохранения заряда и закона Кулона; на расчет напряженности и потенциала электростатического поля; на применение принципа суперпозиции для напряженности и потенциала электростатического поля; на определение напряжения, работы сил электрического поля, связи напряжения и напряженности однородного электростатического поля, электроемкости конденсатора, энергии электростатического поля конденсатора;

на расчет электрических цепей с использованием формулы для электрического сопротивления, закона Ома для однородного участка цепи и полной цепи и закономерностей последовательного и параллельного соединения резисторов; на расчет работы и мощности электрического тока, на применение закона Джоуля—Ленца; на определение коэффициента полезного действия источника тока;

на определение силы Ампера, силы Лоренца; на применение принципа суперпозиции для магнитных полей; на расчет характеристик движения заряженной частицы в однородном магнитном поле перпендикулярно линиям магнитной индукции; на расчет магнитного потока; на применение правила Ленца, определение электродвижущей силы индукции; на расчет электродвижущей силы, возникающей в прямолинейном проводнике, равномерно движущемся в однородном магнитном поле, энергии магнитного поля, электродвижущей силы самоиндукции и индуктивности катушки;

на определение периода, частоты и энергии свободных электромагнитных колебаний в колебательном контуре; на расчет действующих значений напряжения и силы переменного тока; на применение формул, связывающих длину волны с частотой и скоростью;

ОПТИКА

1) Источники света. Прямолинейность распространения света. Скорость распространения света.

2) Отражение света. Закон отражения света. Зеркала. Построение изображений в плоском зеркале.

3) Закон преломления света. Показатель преломления. Полное отражение.

4) Призма. Ход лучей в призме.

5) Линзы. Фокусное расстояние и оптическая сила тонкой линзы. Построение изображений в тонких линзах. Формула тонкой линзы.

6) Интерференция света.

7) Дифракция света. Дифракционная решетка.

8) Дисперсия света. Спектр.

знать/понимать:

физические явления: прямолинейность распространения света, отражение и преломление света, дифракция и интерференция света, поглощение и дисперсия света;

смысл физических понятий: световой луч, показатель преломления; фокусное расстояние и оптическая сила тонкой линзы; оптическая разность хода, постоянная дифракционной решетки;

смысл физических законов, принципов, правил, постулатов: законов отражения и преломления света;

уметь решать задачи:

на применение законов отражения и преломления света, формулы тонкой линзы; на использование условий максимума и минимума интерференции, формулы дифракционной решетки;

ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

1) Постулаты специальной теории относительности.

2) Закон взаимосвязи массы и энергии.

знать/понимать:

смысл физических законов, принципов, правил, постулатов: постулатов Эйнштейна; законов взаимосвязи массы и энергии;

уметь решать задачи:

на применение закона взаимосвязи массы и энергии;

ОСНОВЫ КВАНТОВОЙ ФИЗИКИ

1) Фотоэлектрический эффект. Экспериментальные законы внешнего фотоэффекта.

2) Фотон. Уравнение Эйнштейна для фотоэффекта.

3) Ядерная (планетарная) модель атома. Квантовые постулаты Бора.

4) Излучение и поглощение света атомом. Спектры.

знать/понимать:

физические явления: фотоэффект;

смысл физических понятий: внешний фотоэффект, фотон, энергия и импульс фотона, красная граница фотоэффекта, работа выхода;

смысл физических законов, принципов, правил, постулатов: внешнего фотоэффекта;

уметь решать задачи:

на вычисление частоты и длины волны при переходе электрона в атоме из одного энергетического состояния в другое; на применение формул, связывающих энергию и импульс фотона с частотой соответствующей волны; уравнения Эйнштейна для внешнего фотоэффекта;

АТОМНОЕ ЯДРО И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ

1) Протонно-нейтронная модель строения ядра атома.

2) Энергия связи атомного ядра.

3) Ядерные реакции. Радиоактивность. Закон радиоактивного распада.

4) Элементарные частицы.

знать/понимать:

физические явления: радиоактивность, деление ядер;

смысл физических понятий: ядерная модель атома, энергия связи ядра, дефект масс, энергетический выход ядерной реакции, период полураспада; элементарные частицы;

смысл физических законов, принципов, правил, постулатов: радиоактивного распада, постулатов Бора, правил смещения при ?-, ?-распадах;

уметь решать задачи:

на определение продуктов ядерных реакций; на расчет энергии связи, энергетического выхода ядерных реакций; на применение закона радиоактивного распада и правил смещения при ?-, ?—распадах.

Конвертер величин

---

Длина — это расстояние между двумя наиболее удаленными точками одного объекта. Обычно длина это наибольшая из трех физических характеристик объекта – длины, ширины, высоты.

Расстояние – это степень удаленности двух объектов друг от друга.

Измеряются длина и расстояние в системных единицах измерения – метр. Обозначение единиц измерения длины в СИ: м – русское, m – международное.

В системе СИ метр — это расстояние, пройденное светом в вакууме за время 1/299 792 458 секунд.

В различных сферах ряда государств применяются внесистемные единицы измерения длины, например: сантиметр, нанометр, фут, дюйм, ярд, миля и другие многочисленные единицы.

Такое многообразие связано с национальными система измерения различных государств, которые складывались столетиями, а иногда и тысячелетиями. С введением международной СИ, применение национальных единиц измерения не прекратилось, так как переход к международной СИ требует значительных финансовых и временных затрат.

К примеру, во многих англоязычных странах основной единицей измерения длины и расстояния, является дюйм, а система измерения называется не метрической, а дюймовой. Применение дюйма в качестве основной единицы сложилось исторически, и теперь быстро перейти на международную метрическую систему весьма затруднительно.

Применение внесистемных единиц измерения в различных областях науки и техники, связано с неудобством стандартных системных величин. Если к примеру речь идет о очень больших расстояниях, таких как объекты вселенной, то измерения расстояний в миллиардах километрах очень неинформативно и не удобно. Поэтому в астрономии более распространены единицы измерения – один световой год, парсек, астрономическая единица. А к примеру, в микромире наиболее удобно применять малые единицы измерения – микрон, нанометр.

Система относительных единиц — Википедия

Материал из Википедии — свободной энциклопедии

Система относительных единиц (англ. per-unit system) — способ расчета параметров в системах передачи электроэнергии, при котором значения системных величин (напряжений, токов, сопротивлений, мощностей и т. п.) выражаются как множители определенной базовой величины, принятой за единицу. Это упрощает вычисления, так как величины, выраженные в относительных единицах, не зависят от уровня напряжения. Так, для устройств (например, трансформаторов) одного типа, импеданс, падение напряжения и потери мощности при различных уровнях напряжения будут различаться по абсолютной величине, но выраженные относительно базовых величин, будут примерно одинаковы. После расчета полученные результаты могут быть переведены обратно в системные единицы (вольты, амперы, омы, ватты и т. п.), если известны базовые величины, принятые за основу.

Относительные единицы используются обычно при расчетах передаваемой мощности; однако, поскольку параметры оборудования (трансформаторов, моторов и генераторов) часто указываются в относительных величинах, каждый электроинженер должен быть знаком с их концепцией.

В системе относительных единиц используются единицы мощности, напряжения, силы тока, импеданса и адмиттанса. Только две из них являются независимыми; обычно в качестве независимых величин выбираются мощность и напряжение, что продиктовано природой реальных энергосистем. Все системные величины в сети выражаются как множители выбранных базовых значений. Например, для мощности в качестве базы может быть выбрана номинальная мощность трансформатора (или иногда произвольная мощность, такая, что полученные относительные значения облегчают вычисления). В качестве базы для напряжения обычно выбирается номинальное напряжение шины. В технической литературе на английском языке различные типы величин обозначаются одним и тем же символом pu (иногда p.u.). Из контекста должно быть понятно, идет ли речь о напряжении, силе тока и т. д.