Сила тяжести — урок. Физика, 7 класс.
Силу гравитации, с которой Земля притягивает тело, находящееся на её поверхности или вблизи неё, называют силой тяжести. Эта сила направлена к центру Земли.
Сила гравитации Земли для нас является самой важной, поэтому ей и дано особое название.
Земля притягивает всё, что находится вокруг неё: твёрдые тела, жидкости, газы.
Из-за того, что есть сила тяжести, возможно существование атмосферы (молекулы газа не улетают в космос), воды морей и океанов удерживаются на своих местах, если какой-либо предмет приподнимают и роняют, этот предмет падает вниз — в направлении Земли.
Силу, с которой Земля притягивает тела, можно рассчитать по формуле F=m⋅g, где \(m\) — масса тела, а \(g\) — ускорение свободного падения.
Ускорение свободного падения — это ускорение, которое вблизи Земли приобретает тело, падающее свободно и беспрепятственно. Вблизи поверхности Земли значение \(g\) равно примерно \(9,81\) мс2, для приблизительных расчётов можно использовать значение \(10\) мс2.
Что означает эта единица измерения?
Скорость свободно падающего тела каждую секунду увеличивается на \(9,81\) метров в секунду (м/с).
Если предмет падает, например, в течение \(4\) секунд, то скорость его падения в самом начале равна \(0\) м/с;
за \(1\)-ю секунду он достигает скорости \(9,81\) м/с;
за \(2\)-ю секунду он достигает скорости: \(9,81\), умноженное на \(2\) м/с \(=\) \(19,62\) м/с;
за \(3\)-ю секунду он достигает скорости: \(9,81\), умноженное на \(3\) м/с \(=\) \(29,43\) м/с;
за \(4\)-ю секунду тело достигает скорости: \(9,81\), умноженное на \(4\) м/с \(=\) \(39,24\) м/с, что приблизительно составляет \(141\) км/ч.
Обрати внимание!
Интересно, что кирпич и яблоко падают с одинаковой скоростью. Только падение лёгких предметов сопротивление воздуха замедляет сильнее, например, птичье перо из-за сопротивления воздуха будет падать медленнее.
Ускорение свободного падения на поверхности Луны составляет только \(1,62\) мс2.На Юпитере значение \(g\) приблизительно равно \(26,2\) мс2, это примерно так же, как если бы человек в дополнение к своим \(60\) кг веса взвалил бы на плечи ещё примерно \(102\) кг.
ФИЗИКА: Задачи на силу тяжести и вес тела
Задачи на силу тяжести
и вес тела с решениями
Формулы, используемые на уроке «Задачи на силу тяжести и вес тела»
Название величины | Обозначение | Единицы измерения | Формула |
Масса | m | кг | m = F / g |
Вес тела | P | H | P = m *g |
Сила тяжести | Fтяж | H | Fтяж = mg |
Постоянная (сила тяжести, действующая на тело массой 1 кг) | g = 10 H/кг | H/кг |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Определите силу тяжести, действующую: а) на человека массой m = 100 кг; б) на автомобиль массой М = 1,5 т; в) на монет массой m = 5 г.

Задача № 2. Какова масса свинцового шара, если он весит 600 Н?
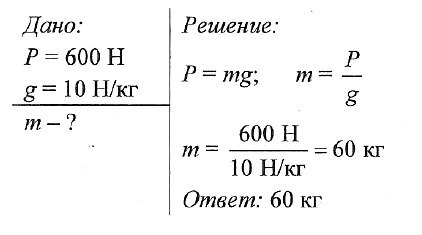
Задача № 3. Масса футбольного мяча 400 г. Вычислите вес мяча и силу тяжести, действующую на него.
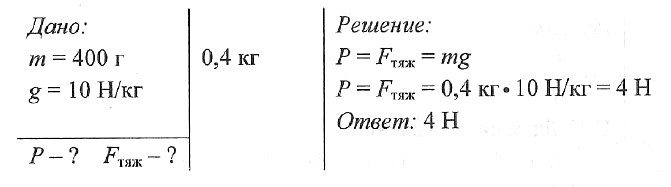
Задача № 4. Чему равна сила тяжести тела, масса которого 4 кг?

Задача № 5. Какой вес имеет вода объемом 3 дм3?

Задача № 6. Подвешенная к потолку люстра действует на потолок с силой 49 Н. Какова масса люстры?

Задача № 7. Изобразите графически силу тяжести и вес гири массой 1 кг.
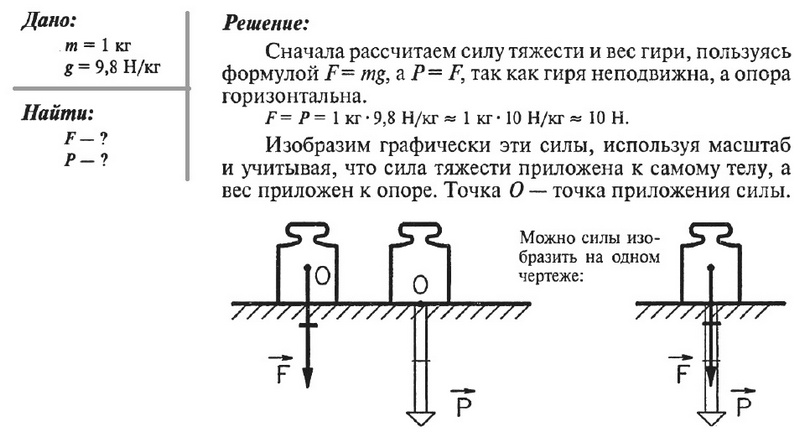
Задача № 8. Изобразите графически силы, действующие на шар, висящий на нити.
Решение. На шар, висящий на нити, действуют несколько сил: сила тяжести, приложенная к шару, сила упругости нити, приложенная к нити, и вес тела, приложенный к подвесу. Шар неподвижен, поэтому численно эти силы равны, следовательно, длина стрелок, изображающих силы, будет одинакова.
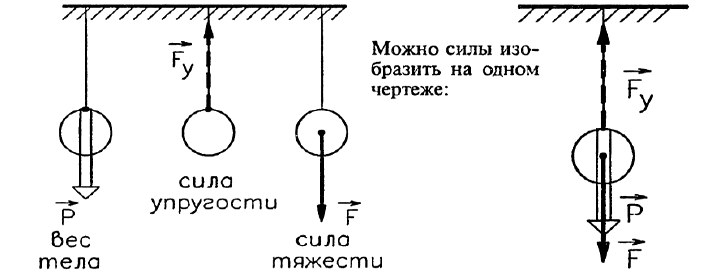
Задача № 9 (повышенной сложности). Как изменяются сила тяжести, действующая на космонавта, и его вес, когда он перемещается с Земли на орбитальную станцию?
ОТВЕТ: сила тяжести — незначительно, а вес будет равен нулю.
РЕШЕНИЕ: Сила тяжести уменьшается незначительно (менее чем на 10% при высоте орбиты 300 км), так как она зависит только от массы тела и расстояния до центра Земли, которое при перемещении на орбитальную станцию изменяется всего на несколько процентов. Если бы не сила притяжения к Земле, орбитальная станция покинула бы околоземную орбиту и улетела далеко в космическое пространство. А вот
Краткая теория к задачам на силу тяжести и вес тела

Конспект урока «Задачи на силу тяжести и вес тела с решениями»
Следующая тема: «Задачи на давление твердых тел».
Что такое сила тяжести и каково ее значение для жизни на Земле :: SYL.ru
Семнадцатый век недаром называют веком великих астрономических открытий. Многолетние наблюдения Галилея, Коперника, Тихо Браге дали возможность сформировать Иоганну Кеплеру законы движения небесных тел. Для того чтобы объяснить, почему планеты находятся в бесконечном движении, что заставляет их оставаться на своей орбите и что такое сила тяжести, понадобился гений — Исаак Ньютон.

Гипотезы гения
Свои законы о движении Исаак Ньютон сформулировал не для теории, а для практического применения. Обобщая данные многолетних астрономических наблюдений и благодаря своим законам о движении, этот великий ученый смог ответить на вопрос, который ставил в тупик не одно поколение ученых: «Что удерживает планеты на своих орбитах?» Ведь до Ньютона учеными выдвигались разные предположения – от хрустальных сфер до магнитных флюидов. Благодаря первому закону Ньютона стало ясно, что для равномерного прямолинейного движения сила не нужна. Сила необходима для того, чтобы заставить планеты двигаться по криволинейной орбите. Если применить формулу силы из второго закона Ньютона, то она будет равна произведению ускорения на массу. Ньютон пришел к выводу, что ускорение должно быть равным v2 /R. Так более легкое небесное тело, Луна например, будет вращаться вокруг более тяжелого, но никогда не станет к нему приближаться. Это можно представить себе как падение с касательной к окружности на саму окружность. В точке соприкосновения скорость может быть постоянной или равной нулю, но ускорение присутствует всегда. Постоянное движение по заданной орбите без отсутствия видимого ускорения — вот ответ Ньютона на вопрос о движении планет.

Притяжение
Так, Луна движется вокруг Земли, а Земля – вокруг Солнца, повинуясь некой силе. Гениальность Ньютона проявилась в том, что он объединил силу притяжения небесных тел с силой тяжести, которая известна каждому жителю Земли. Существует легенда, что к правильным выводам Ньютона подтолкнуло обычное яблоко, упавшее ему на голову. Притяжение яблока и Луны к Земле описывается по абсолютно одинаковым законам – сделал вывод исследователь. Свое второе название сила тяжести получила от слова «гравис», что означает «вес».
Гравитация
Обобщив законы движения планет, Ньютон выяснил, что сила их взаимодействия может быть вычислена по формуле:
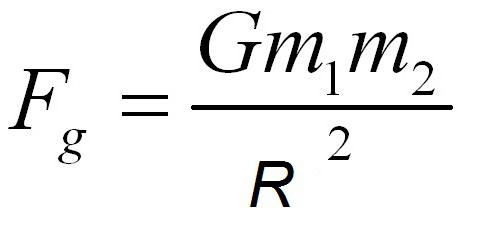
Где m1 m2 — массы взаимодействующих тел, R — расстояние между ними, а G – некий коэффициент пропорциональности, получивший название гравитационной постоянной. Слово «гравитация» подобрано абсолютно правильно, ведь происходит оно от слова «вес». Точное число постоянной Ньютону известно не было, гораздо позже значение G установил Кавендиш. Можно видеть, что на действие силы притяжения влияют массы тел и учитывается расстояние между ними. Никакие другие факторы на силу притяжения влиять не могут.
Значение закона притяжения
Данный закон универсален и может применяться к любым двум телам, имеющим массу. В случае, когда масса одного взаимодействующего тела много больше массы другого, можно говорить о частном случае гравитационной силы, для которого имеется специальный термин «сила тяжести». Это понятие применяется для задач, вычисляющих силу притяжения на Земле или других небесных телах. Если подставить значение силы тяжести в формулу второго закона Ньютона, то получим значение F=ma. Здесь а – ускорение силы тяжести, которое заставляет тела стремиться друг к другу. В задачах, связанных с использованием ускорения свободного падения, его обычно обозначают буквой g. С помощью разработанного им интегрального исчисления Ньютон математически доказал, что сила тяжести в шаре всегда сосредоточена в центре большего тела. В паре яблоко-Земля вектор ускорения направлен к центру земли, в паре Земля-Солнце направлен к Солнцу и так далее.
Зависимости силы тяжести от широты
Сила тяжести на Земле зависит от высоты тела под поверхностью планеты и от широты, на которой проводится эксперимент. Высота тела влияет на значение R, как видно, чем дальше расстояние от поверхности Земли, тем величина g меньше. Связь силы тяжести с широтой объясняется тем, что Земля имеет форму не шара, а геоида. У полюсов она немного сплюснута. Поэтому расстояние от центра Земли до экватора и до полюса будет разным – до 10 %. Такое расхождение делает весьма неудобным расчеты, например расчеты грузов трансконтинентальных перевозок. Поэтому за основу принимают показатель силы притяжения на средних широтах 9,81 м/с2 .
Вес тела
В быту широко применяется такое понятие, как вес тела. В физике он обозначается буквой P. Вес – это сила, с которой тело давит на опору. В бытовом понятии вес часто подменяется понятием «масса», хотя это совершенно разные величины. В зависимости от того, какое значение принимает сила тяжести, изменяется и вес тела. Например, вес свинцовой детали на Земле и Луне будет отличаться. А вот масса остается неизменной и на Земле, и на Луне. Кроме этого, в определенных случаях вес тела может быть нулевым. Вес — величина, имеющая направление, а масса — скаляр.
Но так как согласно третьему закону Ньютона действие равно противодействию, вес тела равен силе реакции опоры.
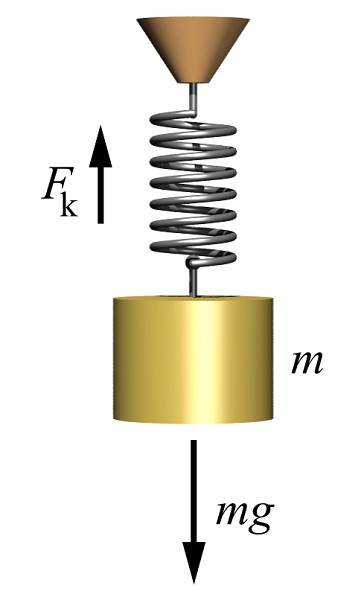
Так как силу реакции простой опоры измерить довольно трудно, то опыт можно «перевернуть», подвесив какое-либо тело на пружину и измеряя степень растяжения этой пружины. При этом сила, растягивающая пружину с грузом, будет иметь вполне логичное F=mg, где m — масса, а g — ускорение свободного падения.
Перегрузка
Если груз с пружинкой поднять вверх, то ускорение силы тяжести и ускорение подъема будут направлены в противоположные стороны. Представить это можно так: F = m(g+a). Сила тяжести, а соответственно, и его вес, возрастают.
Для увеличения веса, связанного с дополнительным ускорением, существует специальный термин – перегрузка. Действие перегрузки испытывал каждый из нас, поднимаясь на лифте или взлетая на самолете. Особенно сильную перегрузку испытывают на себе космонавты и летчики сверхзвуковых самолетов при взлете своих летательных аппаратов.
Невесомость
Когда телу придается ускорение в направлении силы тяжести, то есть вниз в нашем случае, тогда F=m(g-a). Так, вес тела становится меньше. В предельном случае, когда a=g и направлены они в разные стороны, можно говорить о нулевом весе, то есть тело падает с постоянной скоростью. Состояние, при котором вес тела является нулевым, называют невесомостью. Человек испытывает состояние невесомости в космическом корабле, когда он движется с выключенными двигателями. Невесомость – обычное состояние для космонавтов и летчиков, летающих на сверхзвуковых самолетах.

Значение силы тяжести
Без силы тяжести не происходило бы многих, кажущихся нам естественными, вещей – не сходили бы лавины с гор, не шли бы дожди, не текли бы реки. Атмосфера Земли сохраняется благодаря силе тяжести. Для сравнения, планеты с меньшей массой, такие как Луна или Меркурий, растеряли свою атмосферу очень быстро и остались беззащитными перед потоком жесткого космического излучения. Атмосфера Земли играла решающую роль при возникновении жизни на Земле, ее видоизменении и сохранении.

Кроме силы тяжести, на Земле действует сила притяжения Луны. Благодаря ее близкому (в космических масштабах) соседству на Земле существуют приливы и отливы, сдвигаются континенты, а многие биологические ритмы совпадают с лунным календарем.
Таким образом, силу тяжести нужно рассматривать не как досадную помеху, а как полезный и необходимый закон природы.
Сила тяжести и вес тела
В § 2-а мы начали знакомство с явлением гравитации вообще и земным тяготением в частности. Теперь настало время более подробного изучения силы тяжести на Земле и других планетах.
На рисунке изображён опыт с двумя гирями и динамометрами. Вы видите, что при массе гири 200 г (то есть 0,2 кг) на неё действует сила тяжести 2 Н, а при массе 500 г (то есть 0,5 кг) – сила тяжести 5 Н. Обратим внимание на закономерность:
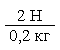 | = 10 Н/кг | и |  | = 10 Н/кг |
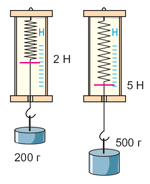 |
Проделав опыты с многими телами, мы обнаружим ту же самую закономерность: отношение силы тяжести, действующей на тело, к массе этого тела является постоянной величиной, не зависящей ни от силы тяжести, ни от массы тела. Эту величину называют коэффициентом силы тяжести:
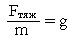 |
Формулу для вычисления коэффициента «g» можно преобразовать, поместив слева силу тяжести:
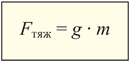 | Fтяж – сила тяжести, Н m – масса тела, кг g – коэффициент, Н/кг |
В опыте с двумя гирями мы выяснили, что вблизи поверхности Земли коэффициент «g» имеет значение 10 Н/кг (более точные значения 9,78 Н/кг и 9,83 Н/кг – см. далее в таблице).
Опыты показывают, что по мере удаления от Земли сила тяжести ослабевает. Например, на высоте 300 км значение коэффициента «g» уменьшается приблизительно до 9 Н/кг.
Повторяя опыт с гирями и динамометрами в различных местах Земли, а также на поверхности Луны, Марса и так далее, можно выяснить, что коэффициент «g» зависит от места наблюдения:
Коэффициенты силы тяжести, Н/кг
| Луна | 1,7 | Земля: | » 10 | |
| Марс | 3,8 | а) полюс | 9,83 | |
| Юпитер | 24 | б) экватор | 9,78 |
В обыденной жизни под словом «вес» мы зачастую подразумеваем массу тела, не делая различия между этими терминами. Однако это неверно.
 |
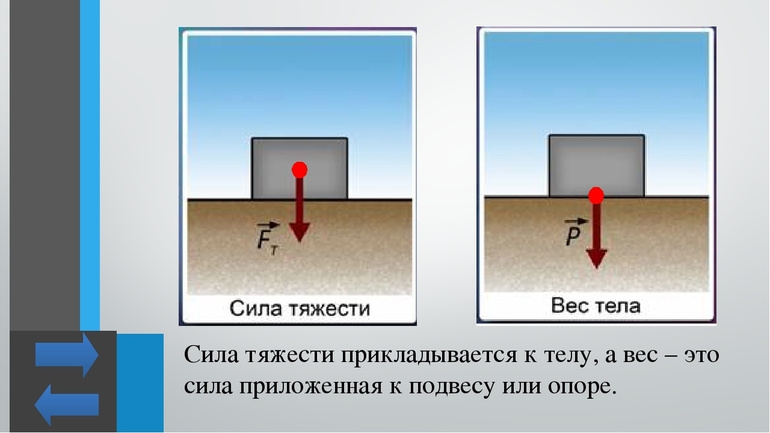
Весом тела называют силу, с которой тело давит на опору или тянет подвес. Например, на рисунке медведь действует на опору – прогнувшуюся доску. Согласно определению, сила давления медведя на доску – вес медведя. На рисунке правее медведь действует на подвес – канат. Эта сила тоже является весом, но уже медведя вместе с доской.
Часто вес тела равен действующей на него силе тяжести. В виде формулы это записывается так:
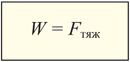 | W – вес тела, Н Fтяж – сила тяжести, Н |
Однако эта формула верна не всегда. Например, если тело погружено в жидкость или газ. В этом случае возникает выталкивающая сила, обычно приводящая к уменьшению веса. Многочисленные опыты показывают, что вес тела равен действующей на него силе тяжести, когда тело и его опора (подвес) покоятся или движутся вместе равномерно и прямолинейно, и не действуют другие силы, кроме силы тяжести. Это – границы применимости формулы W = Fтяж
Забегая вперед, скажем, что когда тело или его опора (подвес) движутся непрямолинейно или неравномерно, вес тела никогда не равен силе тяжести. Он может быть как больше, так и меньше неё, а также направлен в другую сторону.
Referat. Сила тяжести — PhysBook
Сила тяжести
Частным, но крайне важным для нас видом силы всемирного тяготения является сила притяжения тел к Земле. Эту силу называют силой тяжести. Согласно закону всемирного тяготения, она выражается формулой
\(~F_T = G \frac{mM}{(R+h)^2}\) , (1)где m – масса тела, М – масса Земли, R – радиус Земли, h – высота тела над поверхностью Земли. Сила тяжести направлена вертикально вниз, к центру Земли.
- Более точно, помимо этой силы, в системе отсчета, связанной с Землей, на тело действует центробежная сила инерции \(~\vec F_c\) , которая возникает из-за суточного вращения Земли, и равна \(~F_c = m \cdot \omega^2 \cdot r\) , где m – масса тела; r – расстояние между телом и земной осью. Если высота тела над поверхностью Земли мала по сравнению с ее радиусом, то \(~r = R \cos \varphi\) , где R – радиус Земли, φ – географическая широта, на которой находится тело (рис. 1). С учетом этого \(~F_c = m \cdot \omega^2 \cdot R \cos \varphi\) .
Рис. 1
Силой тяжести называется сила, действующая на любое находящееся вблизи земной поверхности тело.
Она определяется как геометрическая сумма действующей на тело силы гравитационного притяжения к Земле \(~\vec F_g\) и центробежной силы инерции \(~\vec F_c\) , учитывающей эффект суточного вращения Земли вокруг собственной оси, т.е. \(~\vec F_T = \vec F_g + \vec F_c\) . Направление силы тяжести является направлением вертикали в данном пункте земной поверхности.
НО величина центробежной силы инерции очень мала по сравнению с силой притяжения Земли (их отношение составляет примерно 3∙10-3), то обычно силой \(~\vec F_c\) пренебрегают. Тогда \(~\vec F_T \approx \vec F_g\) .
Ускорение свободного падения
Сила тяжести сообщает телу ускорение, называемое ускорением свободного падения. В соответствии со вторым законом Ньютона
\(~\vec g = \frac{\vec F_T}{m}\) .С учетом выражения (1) для модуля ускорения свободного падения будем иметь
\(~g_h = G \frac{M}{(R+h)^2}\) . (2)На поверхности Земли (h = 0) модуль ускорения свободного падения равен
\(~g = G \frac{M}{R^2}\) ,а сила тяжести равна
\(~\vec F_T = m \vec g\) .Модуль ускорения свободного падения, входящего в формулы, равен приближенно 9,8 м/с2.
Из формулы (2) видно, что ускорение свободного падения не зависит от массы тела. Оно уменьшается при подъеме тела над поверхностью Земли: ускорение свободного падения обратно пропорционально квадрату расстояния тела от центра Земли.
Однако если высота h тела над поверхностью Земли не превышает 100 км, то при расчетах, допускающих погрешность ≈ 1,5%, этой высотой можно пренебречь по сравнению с радиусом Земли (R = 6370 км). Ускорение свободного падения на высотах до 100 км можно считать постоянным и равным 9,8 м/с2.
И все же у поверхности Земли ускорение свободного падения не везде одинаково. Оно зависит от географической широты: больше на полюсах Земли, чем на экваторе. Дело в том, что земной шар несколько сплюснут у полюсов. Экваториальный радиус Земли больше полярного на 21 км.
Другой, более существенной причиной зависимости ускорения свободного падения от географической широты является вращение Земли. Второй закон Ньютона справедлив в инерциальной системе отсчета. Такой системой является, например, гелиоцентрическая система. Систему же отсчета, связанную с Землей, строго говоря, нельзя считать инерциальной. Земля вращается вокруг своей оси и движется по замкнутой орбите вокруг Солнца.
Вращение Земли и сплюснутость ее у полюсов приводит к тому, что ускорение свободного падения относительно геоцентрической системы отсчета на разных широтах различно: на полюсах gпол ≈ 9,83 м/с2, на экваторе gэкв ≈ 9,78 м/с2, на широте 45° g ≈ 9,81 м/с2. Впрочем, в наших расчетах мы будем считать ускорение свободного падения приближенно равным 9,8 м/с2.
Из-за вращения Земли вокруг своей оси ускорение свободного падения во всех местах, кроме экватора и полюсов, не направлено точно к центру Земли.
Кроме того, ускорение свободного падения зависит от плотности пород, залегающих в недрах Земли. В районах, где залегают породы, плотность которых больше средней плотности Земли (например, железная руда), g больше. А там, где имеются залежи нефти, g меньше. Этим пользуются геологи при поиске полезных ископаемых.
Вес тела
Вес тела – это сила, с которой тело, вследствие его притяжения к Земле, действует на опору или подвес.
Рассмотрим, например, тело, подвешенное к пружине, другой конец которой закреплен (рис. 2). На тело действует сила тяжести \(~\vec F_T = m \vec g\) направленная вниз. Оно поэтому начинает падать, увлекая за собой нижний конец пружины. Пружина окажется из-за этого деформированной, и появится сила упругости \(~\vec F_{ynp}\) пружины. Она приложена к верхнему краю тела и направлена вверх. Верхний край тела будет поэтому «отставать» в своем падении от других его частей, к которым сила упругости пружины не приложена. Вследствие этого и тело деформируется. Возникает еще одна сила упругости – сила упругости деформированного тела. Она приложена к пружине и направлена вниз. Вот эта сила и есть вес тела.
Рис. 2
По третьему закону Ньютона обе эти силы упругости равны по модулю и направлены в противоположные стороны. После нескольких колебаний тело на пружине оказывается в покое. Это значит, что сила тяжести \(~m \vec g\) по модулю равна силе упругости Fупр пружины. Но этой же силе равен и вес тела.
Таким образом, в нашем примере вес тела, который мы обозначим буквой \(~\vec P\) , по модулю равен силе тяжести:
\(~P = m g\) .Второй пример. Пусть тело А находится на горизонтальной опоре В (рис. 3). На тело А действует сила тяжести \(~m \vec g\) и сила реакции опоры \(~\vec N\) . Но если опора действует на тело с силой \(~\vec N\) то и тело действует на опору с силой \(~\vec P\) , которая в соответствии с третьим законом Ньютона равна по модулю и противоположна по направлению \(~\vec N\) \[~\vec P = -\vec N\] . Сила \(~\vec P\) и есть вес тела.
Рис. 3
Если тело и опора неподвижны или движутся равномерно и прямолинейно, т. е. без ускорения, то, согласно второму закону Ньютона,
\(~\vec N + m \vec g = 0\) .Так как
\(~\vec N = -\vec P\) , то \(~-\vec P + m \vec g = 0\) .Следовательно,
\(~\vec P = m \vec g\) .Значит, если ускорение а = 0, то вес тела равен силе тяжести.
Но это не значит, что вес тела и сила тяжести, приложенная к нему, одно и то же. Сила тяжести приложена к телу, а вес приложен к опоре или подвесу. Природа силы тяжести и веса тоже различна. Если сила тяжести является результатом взаимодействия тела и Земли (сила тяготения), то вес появляется в результате совсем другого взаимодействия: взаимодействия тела А и опоры В. Опора В и тело А при этом деформируются, что приводит к появлению сил упругости. Таким образом, вес тела (как и сила реакции опоры) является частным видом силы упругости.
Вес обладает особенностями, существенно отличающими его от силы тяжести.
Во-первых, вес определяется всей совокупностью действующих на тело сил, а не только силой тяжести (так, вес тела в жидкости или воздухе меньше, чем в вакууме, из-за появления выталкивающей (архимедовой) силы). Во-вторых, вес тела, существенно зависит от ускорения, с которым движется опора (подвес).
Вес тела при движении опоры или подвеса с ускорением
Можно ли увеличить или уменьшить вес тела, не изменяя самого тела? Оказывается, да. Пусть тело находится в кабине лифта, движущегося с ускорением \(~\vec a\) (рис. 4 а, б).
а
б
Согласно второму закону Ньютона
\(~\vec N + m \vec g = m \vec a\) , (3)где N – сила реакции опоры (пола лифта), m – масса тела.
По третьему закону Ньютона вес тела \(~\vec P = -\vec N\) . Поэтому, учитывая (3), получим
Направим координатную ось Y системы отсчета, связанной с Землей, вертикально вниз. Тогда проекция веса тела на эту ось будет равна
\(~P_y = m (g_y — a_y)\) .Так как векторы \(~\vec P\) и \(~\vec g\) сонаправлены с осью координат Y, то Рy = Р и gy = g. Если ускорение \(~\vec a\) направлено вниз (см. рис. 4, а), то ay = а, и равенство принимает следующий вид:
\(~P = m (g — a)\) .Из формулы следует, что лишь при а = 0 вес тела равен силе тяжести. При а ≠ 0 вес тела отличается от силы тяжести. При движении лифта с ускорением, направленным вниз (например, в начале спуска лифта или в процессе его остановки при движении вверх) и по модулю меньшим ускорения свободного падения, вес тела меньше силы тяжести. Следовательно, в этом случае вес тела меньше веса того же тела, если оно находится на покоящейся или равномерно движущейся опоре (подвесе). По этой же причине вес тела на экваторе меньше, чем на полюсах Земли, так как вследствие суточного вращения Земли тело на экваторе движется с центростремительным ускорением.
Рассмотрим теперь, что произойдет, если тело движется с ускорением \(~\vec a\), направленным вертикально вверх (см. рис. 4, б). В данном случае получаем
\(~P = m (g + a)\) .Вес тела в лифте, движущемся с ускорением, направленным вертикально вверх, больше веса покоящегося тела. Увеличение веса тела, вызванное ускоренным движением опоры (или подвеса), называется перегрузкой. Перегрузку можно оценить, найдя отношение веса ускоренно движущегося тела к весу покоящегося тела:
Тренированный человек способен кратковременно выдерживать примерно шестикратную перегрузку. Значит, ускорение космического корабля, согласно полученной формуле, не должно превосходить пятикратного значения ускорения свободного падения.
Невесомость
Возьмем в руки пружину с подвешенным к ней грузом, а лучше пружинные весы. По шкале пружинных весов можно отсчитать вес тела. Если рука, держащая весы, покоится относительно Земли, весы покажут, что вес тела по модулю равен силе тяжести
Невесомость объясняется тем, что сила всемирного тяготения, а значит, и сила тяжести сообщают всем телам (в нашем случае – грузу и пружине) одинаковое ускорение
Это же можно доказать и математически. При свободном падении тела \(~\vec a = \vec g\) и \(~P = m (g — g) = 0\) .
Литература
- Кикоин И.К., Кикоин А.К. Физика: Учеб. для 9 кл. сред. шк. – М.: Про-свещение, 1992. – 191 с.
- Луцевич А.А., Яковенко С.В. Физика: Учеб. пособие. – Мн.: Выш. шк., 2000. – 495 с.
- Физика: Механика. 10 кл.: Учеб. для углубленного изучения физики / М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
Формула силы тяжести
Здесь – сила тяжести, – масса, — ускорение свободного падения.
Единица измерения силы – Н (ньютон).
Для тела, находящегося на определённой высоте над Землёй сила тяжести может быть найдена по формуле:
Здесь – гравитационная постоянная, – масса тела, – масса Земли ( кг), – высота тела над Землёй, – радиус Земли ( м).
Из-за того, что Земля имеет сплюснутую форму, то есть её радиус не везде одинаков, ускорение свободного падения меняется в зависимости от географической широты, от на экваторе до на полюсах. – его среднее значение.
Сила тяжести действует на тело, имеющее опору или подвес. Если тело их не имеет, то есть находится в состоянии свободного падения, то говорят, что тело находится в невесомости. Сила тяжести всегда направлена к центру Земли.
Примеры решения задач по теме «Сила тяжести»
| Понравился сайт? Расскажи друзьям! | |||
Сила тяжести ℹ️ определение, причины возникновения, обозначение и единицы измерения, направление, формулы, зависимость величины от массы и ускорения свободного падения, примеры расчетов

Общие сведения
Силой тяжести (Fт) называется величина, действующая на физическое тело, которое находится на поверхности Земли или другого астрономического объекта. Последним может быть любая планета, астероид, звезда и даже черная дыра. Следует отметить, что Fт Земли отличается от других, поскольку все зависит от следующих факторов:
- Гравитационного поля.
- Центробежной силы инерции при вращении.
Необходимо отметить, что Fт является векторной величиной. Иными словами, она имеет направление. Единицей измерения является ньютон (Н).
Существуют также и другие классы составляющих (сила притяжения Солнца и Луны), однако они не учитываются, поскольку являются очень малыми величинами. Fт сообщает физическим телам ускорение свободного падения, которое считается величиной постоянной (константой) для отдельного астрономического тела. Она не зависит от его массы.
Гравитационное притяжение
Гравитационным притяжением, или силой Всемирного тяготения, называется величина взаимодействия двух физических тел с массами M и m, зависящая также от расстояния между ними (причем M > m). Кроме того, следует обратить внимание на константу, называемую гравитационной постоянной G.
Гравитационная составляющая играет важную роль не только для выполнения расчетов в физике, но и в сохранении жизни. С помощью этой силы строятся Солнечные системы, которые объединяются в Галактики. В Солнечной системе Земля находится на нужном расстоянии от Солнца, тем самым на первой существует жизнь. Кроме того, постоянно происходит расширение Вселенной. На основании этого явления осуществляется образование новых Галактик.
Впервые закон всемирного тяготения огласил Исаак Ньютон. У него следующая формулировка: сила взаимодействия двух тел с массами m1 и m2, совершающих работу в пространстве и находящихся на расстоянии r друг от друга, прямо пропорциональна произведению их масс на гравитационную постоянную G и обратно пропорциональна квадрату расстояния между ними.
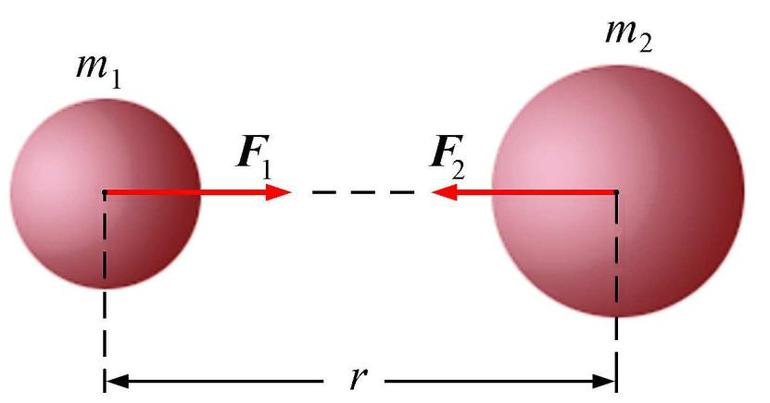
Запись в виде формулы выглядит таким образом: F = (G * m1 * m2) / r 2. Если тело находится над поверхностью Земли, то нужно записать соотношение с учетом радиуса планеты R и его высоты над поверхностью h таким способом: F = (G * m1 * m2) / [R + h]^2.
Коэффициент G равен примерно 6,67 * 10^(-11) м3 / (кг * с2). Следует отметить, что существует определенное условие, при котором можно воспользоваться этой формулой. В этом случае следует учитывать скорость света c = 3 * 108 м/с, а также радиус астрономического тела R. Соотношение имеет такой вид: G * M / (R * c 2) <<1. Следовательно, скорость движения тела должна быть намного меньше скорости света, то есть v << c.
Для совершения точных расчетов следует брать мощность излучения потоков фотонов и других элементарных частиц. Для этих целей применяются специализированные калькуляторы, а также приложения, позволяющие создавать рисунки или схемы действия всех сил и их составляющих.
Центробежная сила
Центробежной силой называется физическая величина, характеризующая составляющую действующих сил инерции. Это понятие вводят при переходе из инерциальной системы отсчета в неинерциальную, что позволяет без проблем рассчитать ускорение некоторых тел, используя баланс сил.
Вектор центробежной силы инерции Земли или другого астрономического тела всегда направлен по касательной воображаемой окружности, с которой оно аппроксимируется. Иногда физики избегают этого понятия, поскольку благодаря научно-техническому прогрессу можно рассчитывать ускорения с помощью специального программного обеспечения. Программы сами переходят из одной инерциальной системы в другую, используя методы параллельного переноса одной границы в другую с учетом теории относительности Альберта Эйнштейна, а также закона всемирного тяготения Исаака Ньютона.
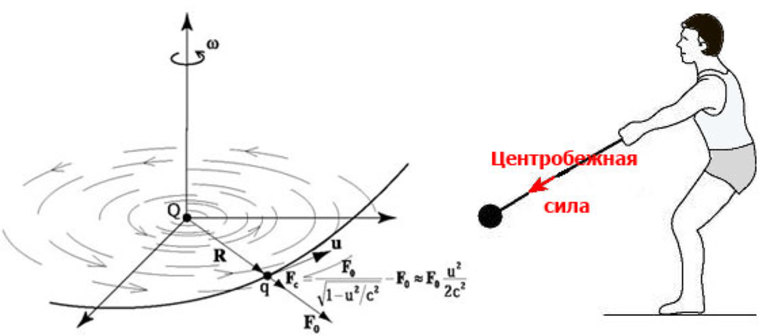
Существуют также и другие сложные алгоритмы, позволяющие производить расчеты не только на Земле, но и на других космических телах. Это очень важно, поскольку при использовании такой методики были получены ускорения свободного падения (g) на различных планетах и телах. Кроме того, с учетом Fт и других сил и факторов на орбиту были выведены искусственные спутники Земли, осуществляющие информационный обмен в гражданской и военной сферах деятельности человека.
Следует отметить, что центробежная сила обозначается Fc и определяется по формуле: Fc = m * w 2 * r, где m — масса тела, а r — расстояние между физическим телом или материальной точкой и земной осью. Когда величина r является меньше радиуса Земли, тогда соотношение приобретает такой вид: Fc = m * w2 * R * cos (q), где q — географическая широта, на которой расположено тело.
Ускорение свободного падения
Fт, действуя на тело, сообщает ему g. Используя II закон Ньютона, эту величину можно выразить в таком виде: g = Fт / m. В этом случае модуль g с высоты h будет эквивалентен такому соотношению: g (h) = (G * M) / (R + h)^2. Тогда на поверхности Земли при h = 0 формулу можно править таким методом: g (h) = (G * M) / R2.

Fт определяется по такому равенству: Fт = m * g. Для Земли величина g примерно равна 9,81 м/с2. По формуле видно, что g не зависит от массы тела, а обратно пропорционально зависит от квадрата расстояния искомого тела до центра Земли. Однако на поверхности планеты не всегда одинаковое ускорение. Сила тяжести увеличивается на полюсах Земного шара, а уменьшается на экваторе. Следовательно, увеличивается или уменьшается величина g. Это явление объясняется тем, что шар немного сплюснут по полюсам. Радиус экватора на 21,25 км больше, чем на последних.
Однако g зависит не только от широты. Следующим фактором является тип системы. Они бывают инерциальными и неинерциальными. Примером первой считается гелиоцентрическая система, а второй — Земля. В последнем случае она движется по орбите вокруг Солнца, а не стоит на месте.
Еще одним фактором, от которого зависит g, является плотность (p) залегания пород. Если p больше средней плотности Земли (залежи железной руды), то g становится больше. Далее следует разобраться в физическом смысле g.

Этот процесс проще понять на примере падающего тела с высоты 50 метров:
- На начальном уровне его скорость эквивалентна 0. Ее следует определять по такой формуле: v = g * t
- На 1 секунде (t = 1): 9,81 * 1 = 9,81 (м/с).
- При t = 2: 9,81 * 2 = 19,62 (м/с).
- t = 3: 9,81 * 3 = 29,43 (м/с).
- t = 4: 9,81 * 4 = 39,24 (м/с).
- t = 5: 9,81 * 5 = 49,05 (м/с).
Иными словами, оно равномерно разгоняется до определенной скорости с течением времени. Такое движение называется равноускоренным. Если перевести скорость на пятой секунде в км/ч, то значение будет эквивалентно величине 176,58. Однако при падении тела необходимо учитывать сопротивляемость воздуха, поскольку перо и яблоко падают не с одинаковыми показателями.
Вес тела
Весом тела (P) называется сила действия тела на опору или подвес в результате притяжения Земли. Для демонстрации этого явления необходимо рассмотреть пример взаимодействия пружины и тела, прикрепленного к ней. Под действием Fт пружина деформируется и появляется новая величина, называемая силой упругости Fупр. Необходимо отметить, что векторы Fупр и Fт направлены в противоположные стороны. Направление силы тяжести, а точнее ее вектора, осуществляется всегда вниз, а Fупр — вверх.
Кроме того, необходимо отметить, что при растяжении пружины верхняя часть тела «деформируется», отставая от всех его точек. Эта величина и называется весом тела. Формула для его определения имеет такой вид: P = Fт = m * g.
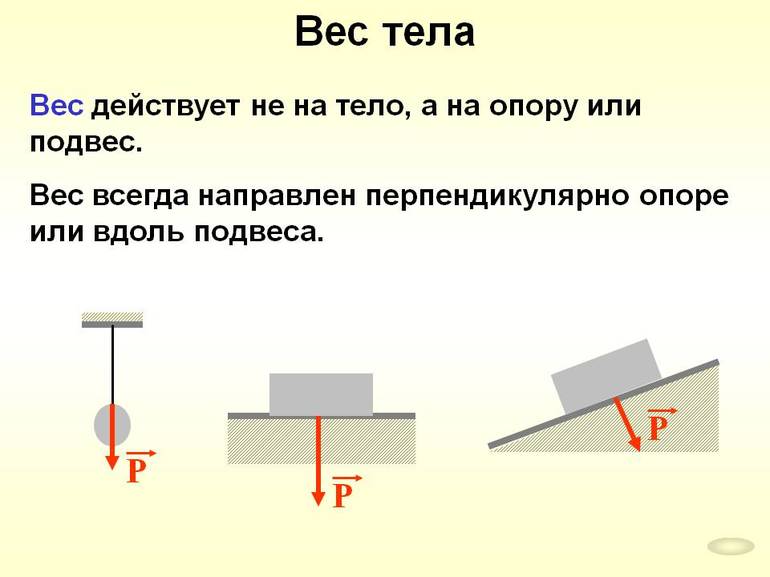
При использовании опоры, на которой лежит физическое тело, величина P будет равна реакции опоры, направленной вверх. Следовательно, модули N и Fт равны, поскольку тело не падает. Значит P определяется по следующей формуле: P = N = |Fт| = m * g. Однако природа возникновения P и Fт различна, поскольку первая приложена к подвесу или опоре. Она является результатом взаимодействия тела и последней. Вторая — взаимодействие тела и силы тяготения. Кроме того, она приложена только к телу. В этих ключевых аспектах и заключается основная разница между P и Fт.
Вес тела обладает некоторыми особенностями. Сила тяжести — составляющая P. Первый состоит из совокупности сил (реакция опоры или сила упругости, сила тяжести и тяги). А также P зависит от скорости движения подвеса или выталкивающей силы в жидкостях.
Понятие невесомости
Для понимания явления невесомости следует проделать опыт с весами и телом. Если держать весы, к которым привязано тело, то можно увидеть вес последнего, равного по модулю Fт = m * g. Однако при выпускании весов из рук показание начнет стремительно приближаться к нулевому значению. Это связано с тем, что P и Fт компенсируют друг друга, поскольку в одном и другом случаях величина g одинакова.
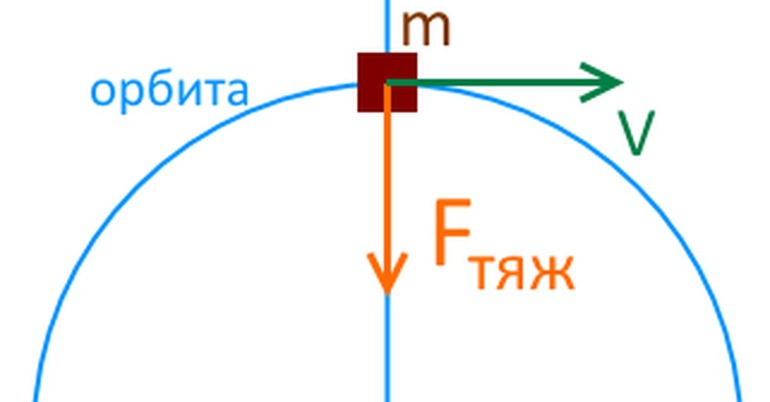
Математически такое явление можно записать следующим образом: P = m * (g — g) = 0. Запись показывает, что физическое тело не деформируется, поскольку движется в одном направлении с вектором Fт. Далее следует рассмотреть Космос. В нем также присутствует невесомость, но другого вида. Если космический корабль находится далеко от Земли, то силы притяжения на него практически не действуют, а, следовательно, значение Fт стремится к 0. Расчет выполняется по такой методике:
- Записывается формула силы тяжести Fт: Fт = m * g.
- Величина параметра g стремится к бесконечно малому значению, равному 0 (g -> 0), поскольку находится из уравнения: 0 = m * g. Из равенства можно вычислить g = 0 / m = 0.
- Подставив g -> 0 в формулу веса тела, можно получить такое тождество: P = m * g = m * 0 = 0.
Методика позволяет при помощи математических преобразований находить любые значения физических величин. Выражение g -> 0 показывает, что g практически равно 0. Очень важную роль сила тяжести играет в природе, поскольку влияет на некоторые необходимые для жизни процессы.
Значение в природе
Ученые установили, что без Fт невозможно существование жизни и Вселенной, поскольку она необходима для термоядерного синтеза на Солнце. Если бы не было ее, то звезды в процессе своей эволюции на конечных стадиях взрывались, распыляя в космическое пространство мощные потоки радиоактивной энергии, губительной для всего живого.
Кроме того, с ее участием формируется структура внутренней оболочки Земли. Следует обратить внимание на метеориты, которые образуются в космическом пространстве в результате уничтожения звезд или других элементов Галактики. Планеты, обладающие большей силой гравитации, помогают отвести нежелательные космические тела от нашей планеты. Например, при помощи мощного телескопа можно рассмотреть поверхность Юпитера, на которой заметно множество кратеров. Подобные изменения рельефа присутствуют также и на Марсе. Несмотря на меньшие размеры, он обладает большей массой, чем Земля, а, следовательно, и гравитационное поле мощнее.
Круговорот вещества и энергии зависит от потенциальной энергии Fт, которая постоянно переходит в кинетическую и обратно. Кроме того, при помощи этой силы удерживается атмосфера, влияющая на жизнь и защищающая от губительного излучения космического пространства и близлежащей звезды — Солнца. В результате этого существует такая характеристика, как атмосферное давление. Оно является результатом воздействия Fт на слои атмосферы.
Благодаря Fт живые организмы ориентируются в пространстве при помощи определенных рецепторов. У человека за это отвечает вестибулярный аппарат. Кроме того, постоянное воздействие Fт стало причиной образования прочного скелета у позвоночных.
Таким образом, сила тяжести играет важную роль в существовании жизни на Земле, поскольку от нее зависит множество явлений и процессов, а также в построении Вселенной.

