Что такое электростатическое поле?, Где используются ЭСП?, Как влияет ЭСП на организм человека?, Как осуществляется гигиеническое нормирование электростатических полей?, Какие защитные средства от воздействия ЭСП? охраной труда Библиотека украинские учебникив

Постоянное электростатическое поле (ЭСП) — это поле неподвижных электрических зарядов, осуществляющее взаимодействие между ними

Статический ток — это совокупность явлений, связанных с возникновением и сохранением свободного электрического заряда на поверхности и в объеме диэлектрических и полупроводниковых веществ, материалов, изделий или на изолированных проводника.

Возникновение зарядов статического электричества происходит при деформации, дроблении веществ, относительном перемещении двух тел, находящихся в контакте, слоев жидкости и сыпучих материалов, при интенсивном п перемешивании, кристаллизации, а также вследствие инд.

ЭСП характеризуется напряженностью (Б). Напряженность. ЭСП — это отношение силы, действующей в поле на точечный электрический заряд, к величине этого заряда. Единицей измерения напряженности. ЭСП является вольт на метр (В / м мм).

ЭСП создается в энергетических установках и при электротехнических процессах зависимости от источника образования они могут существовать в виде собственного электростатического поля (поля неподвижных зарядов) или стац ционарного электрического поля (электрическое поле постоянного тока).

Где используются ЭСП?

ЭСП имеют широкое применение при електрогазоочищенни, электростатической сепарации материалов, электростатическом нанесении лакокрасочных и полимерных материалов и в других производственных процессах

В радиоэлектронной промышленности статический ток образуется при транспортировке, шлифовке, полировке радиотелевизионных приемников, в помещениях вычислительных центров, а также в других процессах где е используются диэлектрические материалы, являющиеся побочным и нежелательным производственных факторов.

ЭСП возникающие при обработке химического волокна, имеет высокие диэлектрические свойства. Уровень напряженности. ЭСП на прядильном и ткацком оборудовании достигает 20-60 кВ / м

В химической промышленности при производстве пластических материалов и изделий из них (шинный корд, линолеум и др.) образуются электростатические заряды и поля напряженностью 240-250 кВ / м

Как влияет ЭСП на организм человека?

Биологическое действие. ЭСП на организм человека определяет наибольшую чувствительность к электростатических полей нервной, сердечно-сосудистой, нейрогуморальной и других систем организма

У рабочих, работающих в зоне действия электрического поля, наблюдаются разнообразные жалобы на раздражительность, головная боль, нарушение сна, снижение аппетита и т др.

У людей, подпадающих под действие. ЭСП, характерна появление своеобразных»фобий», обусловленных страхом ожидания разряда. Склонность к»фобий»преимущественно сопровождается повышенной эмоциональной возбудимостью

Как осуществляется гигиеническое нормирование электростатических полей?

Напряженность электростатического поля нормируется стандартом. ГОСТ 121045-84″Электростатические поля. Допустимые уровни на рабочих местах и ??требования к проведению контроля»

Приведенный стандарт распространяется на. ЭСП, возникающие при эксплуатации электрического оборудования высокого напряжения постоянного тока и электризации диэлектрических материалов. Настоящий стандарт устанавливает доп допустимых уровни напряженности электростатических полей на рабочих местах, а также общие требования к проведению контроля и средств защитыу.

Допустимые уровни напряженности. ЭСП устанавливаются в зависимости от времени пребывания на рабочих местах

Предельно допустимый уровень напряженности. ЭСП (Е, ра») принимается согласно стандарту 60 кВ / м в течение одного часа

Если напряженность электростатических полей до 20 кВ / м, время пребывания в. ЭСП не регламентируется

В диапазоне напряженности от 20 до 60 кВ / м, допустимое время пребывания работающих в. ЭСП без средств защиты (/, год) определяется по формуле:

где. Е ^ — фактическое значение напряженности. ЭСП, кВ / м

Для определения напряженности. ЭСП используются измеритель напряженности электростатического поля

Какие защитные средства от воздействия ЭСП?

Использование средств защиты работающих обязательно в тех случаях, когда фактические уровни напряженности. ЭСП на рабочих местах превышают 60 кВ / м

Для защиты от воздействия. ЭСП используют: экранирование источников поля рабочего места, нейтрализаторы статического сотрясения, ограничение времени работы и т др.

При выборе средств защиты от статического электричества должны быть учтены особенности технологических процессов, физико-химические свойства обрабатываемых материалов, микроклимат производственных помещений и т и др.. Приведенные факторы определяют дифференцированный подход при разработке защитных средствеів.

Уменьшение генерации электростатических зарядов или отвод их с наэлектризованных материалов достигается путем:

1) заземление металлических и электропроводных элементов технологического оборудования;

2) увеличение поверхностей и объемной проводимости диэлектриков;

3) установление нейтрализаторов статического электричества

Защитное заземление производится независимо от использования других методов защиты. Заземлению подлежат не только элементы технологического оборудования, но. И изолированные электропроводящие участки технологическо ного оборудования.

Достаточно эффективным средством защиты является увеличение влажности воздуха до 65-75%, если это возможно по условиям технологического процесса

Среди средств индивидуальной защиты используют антистатическое обувь, антистатические халаты, комбинезоны, заземлены браслеты для защиты рук и другие средства, которые могут обеспечивать электростатическое за аземлення тела человек.

Слободянюк А.И. Физика 10/10.3 — PhysBook

Содержание книги

Предыдующая страница

§10. Проводники и диэлектрики в электростатическом поле

10.3 Применение электростатических свойств проводников.

Приведем некоторые примеры использования рассмотренных свойств поведения проводников в электрическом поле.

Электростатическая защита.

Иногда возникает необходимость изолировать некоторые тела, приборы от воздействия внешних электрических полей. Для такой изоляции их помещают внутрь металлического корпуса. Мы показали, что при помещении проводника во внешнее электрическое поле, индуцированные заряды возникают только на поверхности проводника, а поле внутри проводника оказывается равным нулю.

Пусть, например, металлический шар помещен в однородное электрическое поле напряженностью \(~\vec E_0\) (рис. 236). Под действием этого поля на поверхности шара возникнут индуцированные заряды, поверхностная плотность которых σ₀, будет различна в различных точках поверхности шара. Эти заряды приведут к изменению электрического поля: внутри шара напряженность поля станет равной нулю, снаружи – силовые линии поля будут перпендикулярны поверхности шара. Если теперь внутри шара вырезать произвольную полость, то от этой «операции» распределение поля и индуцированных зарядов не изменится, так как изъята та часть шара, где нет ни зарядов, ни поля. Аналогичные рассуждения можно распространить на произвольную полость внутри проводящего тела произвольной формы, находящегося в произвольном электростатическом поле – в любом случае поле внутри полости будет отсутствовать. Говорят, что проводящая оболочка экранирует внешнее электрическое поле.

Более того, можно показать, что аналогичного эффекта достигается даже в том случае, если сплошную проводящую оболочку заменить на металлическую сетку с мелкими ячейками. В этом случае электрическое поле проникает за сетку на глубину порядка размеров ячейки сетки.

Подчеркнем, что сплошная металлическая оболочка экранирует электрическое поле, находящееся снаружи от оболочки, но не те, которые находятся внутри нее. Пусть точечный заряд +q₀ находится внутри металлической сферической оболочки (рис. 237). Этот заряд создает электрическое поле, которое индуцирует электрические заряды, как на внутренней, так и на внешней поверхностях оболочки. Рассмотрим, как в этом случае изменится распределение электрического поля.

На внутренней поверхности распределятся отрицательные заряды с некоторой поверхностной плотностью σ₁. Внутри металла напряженность поля равна нулю, поэтому отрицательные индуцированные заряды σ₁ полностью экранируют поля заряда q₀ . Используя теорему Гаусса, легко показать, что суммарный заряд, индуцированный на внутренней поверхности, равен —q₀. Суммарный заряд оболочки остается равным нулю, следовательно, на ее внешней поверхности индуцируется положительный заряд равный +q₀. На поверхностное распределение этого заряда σ₂, заряды внутренней поверхности и заряд полости не действуют, поэтому они распределятся по поверхности оболочки равномерно, и вне оболочки будут создавать электрическое поле эквивалентное полю точечного заряда +

q₀, помещенного в центр сферической оболочки. Подчеркнем такое распределение поля вне оболочки не зависит от положения заряда внутри полости – смещение этого заряда приведет к изменению поля внутри полости, изменению распределения зарядов на внутренней поверхности, но не изменяет поля вне оболочки.

Чтобы «убрать» поле снаружи от оболочки ей необходимо сообщить дополнительный отрицательный заряд, такого эффекта можно добиться, заземлив оболочку.

Заземление.

Как распределяются заряды между двумя связанными проводящими телами?

С точки зрения здравого смысла на теле больших размеров должен накапливаться больший электрический заряд. Чтобы обосновать это утверждение, рассмотрим два проводящих шара, радиусы которых обозначим

R₁, R₂, находящиеся на большом расстоянии l друг от друга (l >> R₁, R₂), и соединенных проводником (рис. 238). Если этой системе сообщить электрический заряд Q, то заряды шаров q₁, q₂ распределятся так, чтобы их потенциалы были равны; суммарный же заряд системы, конечно, останется равным сообщенному заряду q₁ + q₂ = Q. Так как расстояние между шарами значительно больше их радиусов, то при расчете потенциала каждого шара можно пренебречь их взаимным влиянием и воспользоваться формулой для потенциала уединенного шара

\(~\varphi_1 = \frac{q_1}{4 \pi \varepsilon_0 R_1} ; \varphi_2 = \frac{q_2}{4 \pi \varepsilon_0 R_2}\) .

Приравнивая эти потенциалы, получим, что заряды шаров пропорциональны их радиусам

\(~\frac{q_1}{q_2} = \frac{R_1}{R_2}\) ,

или

\(~q_1 = \frac{R_1}{R_1 + R_2} Q ; q_2 = \frac{R_2}{R_1 + R_2} Q\) . (1)

Качественно аналогичный вывод справедлив и для проводящих тел произвольной формы. Если одно из тел значительно больше другого, то практически весь заряд окажется на большем теле. Действительно, из формул (1) следует, что при R₂ >> R₁

\(~q_1 \approx 0 ; q_2 \approx Q\) . (2)

Именно это обстоятельство используется для того, чтобы разрядить небольшое заряженное тело – его необходимо соединить с телом больших размеров. Так если к заряженному электроскопу прикоснуться рукой, то заряд перераспределится между электроскопом и телом человека, но так как размер последнего значительно больше размеров электроскопа, то можно считать, что весь заряд «сбежит» на человека. Часто в качестве тела больших размеров используют весь земной шар. Приборы, на которых не должен собираться электрический заряд «заземляют», для чего подключают их к массивному проводнику, закопанному в землю. В этом случае можно считать, что соотношения (2) выполняются точно. На схемах для указания того, что тело или прибор заземлены, используется специальное обозначение — .

В теоретических расчетах полагают, что заземление – есть соединение данного тела с телом бесконечно больших размеров, так что потенциал этого тела не изменяется при сообщении ему произвольного заряда и, наоборот, при необходимости это тело может сообщить произвольный заряд, не изменяя его потенциала, который естественно можно положить равным нулю. Поэтому также можно сказать, что заземление – это «соединение с бесконечностью», а потенциал заземленного тела равен нулю, кроме того, суммарный заряд заземленного тела может изменяться.

Уместно привести следующую аналогию. Если небольшое тело находится в тепловом контакте с окружающей средой, то с течением времени его температура станет равной температуре окружающей среды, независимо от того, было тело первоначально нагрето или охлаждено. То есть окружающая среда может получить любое количество теплоты, или отдать любое количество теплоты, а при этом ее температура не изменяется. Такая модель окружающей среды называется термостатом. Заземление в электростатике играет такую же роль, как окружающая среда (термостат) в теории тепловых явлений.

Если рассмотренную в предыдущем разделе сферическую оболочку заземлить, то положительные заряды на внешней поверхности «исчезнут – уйдут в землю», поэтому поле вне оболочки также исчезнет (рис. 239). Можно рассуждать и в обратном порядке: если внутрь полости заземленной оболочки поместить электрический заряд, то его поле индуцирует заряды противоположного знака на внутренней поверхности, эти заряды «прибегут из заземления».

Заметим, что поле внутри заземленной полости полностью определяется ее формой и распределением зарядов внутри нее и не зависит от формы всего тела и заряда последнего.

Генератор Ван-дер-Граафа.

Как мы показали, в условиях равновесия электрический заряд распределяется по внешней поверхности проводника – это позволяет в некоторых случаях накапливать на проводниках значительные электрические заряды.

Можно провести следующий эксперимент. На изолирующей ручке расположен небольшой металлический шарик (рис. 240). Если этому шарику сообщить небольшой электрический заряд

q₀ (например, с помощью стеклянной палочки) и прикоснуться шариком к поверхности сферической насадки электроскопа, то только часть этого заряда перейдет на электроскоп. Если затем опять зарядить шарик до прежнего значения заряда q₀ и опять прикоснуться к внешней поверхности насадки, то меньшая часть заряда шарика перейдет на электроскоп. Таким способом можно сообщить электроскопу только конечный заряд, сколько бы раз мы не подзаряжали шарик. Действительно, когда потенциалы уединенного шарика и электроскопа сравняются, то перераспределение зарядов прекратится. Приближенно максимальный заряд электроскопа Q_max при таком способе зарядки можно оценить из условия равенства потенциалов, поэтому \(~Q_{max} \approx q_0 \frac{R}{r}\) , где R — радиус насадки электроскопа, r — радиус шарика. Если же зарядку электроскопа проводить с помощью такого же шарика, но прикасаясь к внутренней поверхности насадки, то электроскопу можно сообщить гораздо больший заряд. Действительно, если прикоснуться шариком к внутренней поверхности, то весь его заряд перейдет на внешнюю поверхность насадки, независимо от того, какой заряд на ней находится. В этом случае максимальный заряд электроскопа будет определяться внешними причинами – при очень большом заряде насадке начнется утечка зарядов через окружающую среду, т.е. через воздух.

По этому принципу работают устройства, позволяющие накапливать очень большие заряды (соответственно создающие большие разности потенциалов). Одним из первых таких устройств (заметим, использующихся до настоящего времени) является электростатический генератор Ван-дер-Граафа, принципиальная схема которого показана на рисунке 241. В генераторе Ван-дер-Граафа резиновая лента приводится в движение с небольшой скоростью электродвигателем. При движении лента проходит между электрически заряженными пластинами. Возникшие на ленте индуцированные заряды снимаются с внешней поверхности ленты с помощью контактной щетки и подаются на внутреннюю поверхность металлическом купола генератора, создавая достаточно сильные электростатические поля (высокие напряжения) в окружающем купол пространстве. Заряды с внутренней стороны ленты отводятся через шину заземления. Максимальный электрический заряд купола (и его потенциал) ограничиваются только утечкой заряда с купола через воздух. Такие генераторы используются для создания высокой разности потенциалов в линейных ускорителях частиц. Диаметр купола генератора может составлять несколько метров, а создаваемая разность потенциалов несколько миллионов вольт.

Следующая страница

Применение метода аналогии при изучении электростатического поля

 

В  рамках школьной программы   гравитационное поле Земли  рассматривается не  так подробно, как электростатическое с его силовыми и энергетическими характеристиками. Отдельно изучается сила тяжести как сила, действующая со стороны Земли на любое тело, находящееся вблизи ее поверхности. Но, изучая электростатику, мы не ограничиваемся рассмотрением только кулоновской силы как силы, действующей со стороны одного заряженного тела на другое. Мы рассматриваем посредник этого взаимодействия – электростатическое поле. Вводим характеристики электростатического поля – напряженность и потенциал, изучаем  их взаимосвязь и зависимость от других величин. Даем понятие силовых линий для графического изображения поля с целью более четкого представления учащимися распределения поля в пространстве.  Разбираем  большое количество задач на расчет характеристик электростатических полей и электростатических взаимодействий.

Тогда как на изучение гравитационной силы уделяется один урок в ряду изучения различных видов сил, изучению электростатического взаимодействия выделяется целый раздел школьного курса физики. Каковы же результаты такого обучения? Возьмем данные анализа результатов выполнения заданий по физике Единого государственного экзамена [1]. В разделе «понимание физического смысла понятий электростатики»  приведены результаты выполнения следующего задания:

Напряженность электрического поля измеряют с помощью пробного заряда. Если значение этого заряда увеличить в n раз, то модуль напряженности:

1) не изменится;

2) увеличится в n раз;

3) уменьшится в n раз;

4) увеличится в n² раз.

«Менее 1/6 части выпускников выбрали первый ответ, показав непонимание того, что при увеличении пробного заряда во столько же раз увеличивается и сила, действующая на него со стороны поля, а отношение этих величин остается постоянным. Причем ученики сильной группы выполнили задание так же плохо. Это свидетельствует о том, что учащиеся не понимают физического смысла понятия напряженность. Ученики умеют подставлять цифры в формулы для напряженности, но не понимают ее смысла. В какой-то степени проявляется психологический настрой. Так, если спрашивают про какие-либо изменения физических величин, то ответ, где звучит, что величина не изменяется, не может быть верным. Между тем в физике многие величины вводятся только потому, что они сохраняются или не зависят от устройства, которое используется для их измерения. Такой физической величиной является напряженность электрического поля и его потенциал. В качестве «прибора», который определяет эти величины, используется пробный электрический заряд. Он может быть разным по значению, и сила, действующая на него в электрическом поле, или работа, совершенная при его перемещении, будет разная для разных пробных зарядов, но отношение силы к пробному заряду или отношение работы к пробному заряду останется одинаковым как для одного, так и для другого заряда [1].»  При этом аналогичный факт независимости ускорения свободного падения от массы падающего тела принимается и хорошо усваивается с седьмого класса.

Практически нет  студента ВУЗа, который не знает, как рассчитывается сила тяжести и что такое ускорение свободного падения. А вот как найти кулоновскую силу и что такое напряженность поля вряд ли помнит половина нынешних студентов гуманитарных направлений.  

Причина понятна. Изучение  механических явлений дается проще, так как большую часть их мы постоянно наблюдаем в жизни. А уж результат действия силы тяжести каждый из нас постоянно чувствует на себе. Даже результат отсутствия действия силы тяжести мы часто наблюдаем в телевизионных репортажах с космических летательных аппаратов.

Но наблюдать электростатическое взаимодействие в повседневной жизни нам приходится не часто. Даже притяжение волос к расческе вызывает у учащихся некоторое удивление. Живя в макромире, мы сложно представляем себе процессы, причиной которых является поведение элементарных заряженных частиц. Например, мы хорошо себе представляем механические колебательные и волновые процессы, так как постоянно наблюдаем их в жизни (колесо, маятник;   вращение планет Солнечной системы; движение Луны вызывает приливы и отливы на Земле;   ветры возбуждают колебания и волны на поверхности водоемов и т.д). Но мы не можем наблюдать колебания заряда в контуре и распространение в пространстве радиоволн.

Проблему сложного изучения электромагнитных колебаний и волн в рамках школьной программы мы решаем, применяя аналогию как метод познания. Аналогию электромагнитных и механических колебаний. Впервые с механическими колебаниями учащиеся знакомятся в IX классе. Но перед началом изучения электромагнитных колебаний  в  XI классе механические колебания рассматриваются дополнительно с более детальным их описанием. Затем проводится аналогия электромагнитных и механических колебаний: «Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями, например с колебаниями тела, закрепленного на пружине. Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин. При механических колебаниях периодически изменяются координата тела x и проекция его скорости v_x,  а при электромагнитных колебаниях меняются заряд конденсатора q и сила тока i в цепи. Одинаковый характер изменения величин ( механических и электрических ) объясняется тем, что имеется аналогия в условиях, при которых порождаются механические и электромагнитные колебания [2].» Соответствие между механическими и электрическими величинами при колебательных процессах сводится в таблицу [2]:

механические величины	электрические величины
координата x	заряд q
скорость vx	сила тока i
масса m	индуктивность L
жесткость пружины k	величина, обратная емкости 1/C
потенциальная энергия kx2/2	энергия электрического поля q2/2C
кинетическая энергия mvx2/2	энергия магнитного поля Li2/2

 

Такой метод изучения  материала по электромагнитным колебаниям дает  ощутимые результаты: делает процессы более понятными, помогает уяснить смысл характеристик, позволяет лучше запомнить основные формулы и уравнения, аналогичные усвоенным уже в механике.

Этот положительный пример применения метода аналогии можно использовать и при изучении других электромагнитных явлений. В частности, электростатического поля по аналогии с полем гравитационным.  Для этого перед началом изучения электростатического поля необходимо более детально рассмотреть гравитационное поле,  в частности  гравитационное поле Земли. Рассмотреть ускорение свободного падения как силовую векторную характеристику поля, зависящую от расстояния от источника поля и массы Земли как источника поля.   Ввести понятие силовых линий гравитационного поля Земли для графического его изображения.

Соответствие между механическими и электрическими величинами при  этом можно свести в таблицу:

механические величины	электрические величины
масса    М, m	заряд  Q, q
ускорение свободного падения   g=F/m	напряженность E=F/q
ускорение свободного падения поля тела массой М                 g=GM/r2	напряженность поля точечного заряда Q                          E=kQ/r2
гравитационная сила    F=GMm/r2	кулоновская сила  F=kQq/r2
потенциальная энергия тела в поле силы тяжести              Ep=mgh	потенциальная энергия заряда в электростатическом поле    Wp=qEd
потенциальная энергия тела единичной массы         Ep/m	потенциал                                          φ= Wp/q
изменение потенциальной энергии тела единичной массы           g∆h	разность потенциалов    ∆ φ=E∆d
работа поля тяжести Земли по перемещению в нем тела  А= m g∆h	работа электростатического поля  по перемещению в нем заряженного тела  А=q E∆d

 

Масса тела – характеристика тела, определяющая его гравитационное взаимодействие с другими телами. Заряд – характеристика тела, определяющая его электрическое взаимодействие с другими заряженными телами. Воспринимая эту аналогию, учащиеся должны правильно понимать, что заряд не существует раздельно от вещества, это величина, характеризующая вещество с точки зрения его электрического взаимодействия. Так же как масса не может существовать отдельно от вещества. Ускорение свободного падения  можно представить как силовую векторную характеристику гравитационного поля Земли, но  при этом важно не потерять первоначального смысла ускорения. Как силовая векторная характеристика гравитационного поля ускорение свободного падения  должно  иметь  определение: сила, действующая со стороны гравитационного поля на тело единичной массы   g=F/m.  Здесь необходимо подчеркнуть  независимость ускорения свободного падения от массы тела,  на которое рассматривается действие гравитационного поля, что очень важно для понимания по аналогии независимости  напряженности электростатического поля от величины пробного заряда. Ускорение свободного падения  гравитационного поля, созданного телом массой   М, зависит от этой массы и расстояния  r  от  этого тела (от центра тела) до точки пространства, в которой исследуется поле   g=GM/r². Необходимо подробно проанализировать эту зависимость, что поможет учащимся понять и запомнить по аналогии формулу зависимости напряженности электростатического поля, созданного зарядом Q , от этого заряда и расстояния  r  от  этого тела (от центра тела) до точки пространства, в которой исследуется поле  E=kQ/r².  В силу введенного определения g=F/m вектор ускорения свободного падения в каждой точке поля совпадает по направлению с вектором силы тяжести (масса – всегда положительный скаляр). Аналогично вектор напряженности в каждой точке электростатического поля совпадает по направлению с силой, действующей со стороны поля на положительный заряд. Но в отличие от массы заряд тела может быть отрицательным. В этом случае вектор напряженности будет   направлен противоположно силе, действующей на него. Если гравитационное взаимодействие представляет собой только притяжение, то электростатическое – притяжение и отталкивание. Но здесь необходимо подчеркнуть, что направление вектора напряженности поля не зависит от знака пробного заряда, хотя определяется им, точно так же как модуль вектора напряженности не зависит от величины пробного заряда, но определяется им. Вообще понятия пробного заряда и заряда, создающего поле, можно более четко развести по аналогии с массой притягиваемого тела и массой Земли, т.е. массой тела, создающего гравитационное поле. Но учащиеся так же должны понимать и их равноправность (гравитационное поле создается и бабочкой, притягивающей к себе Землю). Можно ввести понятие силовых линий гравитационного поля как линий, касательными к которым в каждой точке поля будут вектора ускорения свободного падения  g. Затем по аналогии  определить силовые линии электростатического поля. Большое сходство имеется между графическим изображением гравитационного поля Земли и графическим изображением электростатического поля одиночного заряда или заряженного шара. Но и при  изучении однородного электростатического поля можно  ограничиться рассмотрением силовых линий гравитационного поля в малой области пространства над поверхностью Земли, в пределах которой вектора ускорения свободного падения и силовые линии поля можно считать взаимно параллельными. Самое сложное для учащихся понятие при изучении электростатики – потенциал поля. Потенциал электростатического  поля в некоторой точке пространства определяется как скалярная энергетическая характеристика поля, показывающая, какой энергией обладает единичный пробный заряд, помещенный в данную точку поля. К сожалению, аналогичной величины для гравитационного поля не вводится.  Подобная  ситуация возникает и при  проведении  аналогии механических и электромагнитных колебаний с жесткостью пружины и величиной, обратной электроемкости конденсатора. Это не большая проблема. Можно ввести величину, равную  потенциальной энергии взаимодействия с Землей тела единичной массы  E_p/m= gh  как скалярную энергетическую характеристику гравитационного поля Земли , что  должно помочь  более четкому пониманию относительности потенциала электростатического поля. Так как высота тела – понятие относительное,   зависящее от выбора  уровня отсчета высоты, то и потенциальная энергия тела единичной массы – величина относительная. Достаточно легко понимается то, что  тело имеет разную потенциальную энергию взаимодействия с Землей относительно второго и  четвертого этажей здания. По аналогии не сложно понять, что и потенциал поля зависит от выбора поверхности нулевого потенциала. Эквипотенциальные поверхности не сложно будет представить по аналогии с поверхностью равной высоты над Землей (точнее равного расстояния от ее центра). Более важной  при исследовании электростатического поля  характеристикой является  разность потенциалов между двумя точками поля  ∆ φ=E∆d  – величина абсолютная, как и изменение потенциальной энергии тела при перемещении его в гравитационном поле Земли.  Полная аналогия   проявляется в  работе данных полей и в свойстве их потенциальности.  Учащиеся хорошо понимают и запоминают формулу для расчета работы  гравитационного поля Земли по перемещению в нем тела  А= m g∆h, где изменение высоты тела ∆h  есть проекция вектора перемещения  s  на направление ускорения свободного падения, т.е. А= m g s cosα,  α – угол между векторами  g  и  s. Не сложно понимается, что при перемещении тела перпендикулярно силовым линиям поля (вдоль поверхности равной высоты) работа не совершается. И легко объясняется, почему работа гравитационного поля при перемещении тела по замкнутой траектории равна нулю. Этим же  свойством потенциальных полей обладает и поле электростатическое. Аналогичная формула для расчета работы электростатического поля по перемещению заряженного тела   А=q E∆d, где ∆d- проекция вектора перемещения  s  на направление силовых линий поля   Е, т.е.  А=q E s cosα,  α – угол между векторами  Е   и   s.  Аналогично гравитационному электростатическое поле не совершает работы по перемещению заряда вдоль эквипотенциальной поверхности, и так же работа  электростатического  поля при перемещении заряженного тела по замкнутой траектории равна нулю.

Такая общность свойств гравитационного и электростатического полей позволяет учащимся понять и усвоить теоретический материал и научиться применять эти знания при решении задач по электростатике.

Применяя аналогию  между электростатическим и гравитационным полями, а так же между электромагнитными и механическими  колебаниями, мы сталкиваемся с некоторой проблемой —  двойственностью массы. В первом случае масса  рассматривается как  мера гравитационного взаимодействия (гравитационная масса), а во втором – как мера инертности (инерциальная масса). Можно обратить внимание на несоответствие аналогий в двух разных таблицах:

механические величины	электрические величины
масса  m	заряд  q
масса m	индуктивность L

 

 

Но эта проблема представляется мне много менее сложной, чем непонимание учащимися электромагнитных процессов. Тем более, что редко кто из учащихся может заметить такое противоречие самостоятельно.  Целесообразнее преподнести это учащимся не как противоречие, а как двойственность свойств этой величины. Двойственность массы воспринимается учащимися также нормально, как и корпускулярно-волновой дуализм электромагнитного излучения.

 

 

 

Библиографический список

1. Единый государственный экзамен: Контрольные измерительные материалы: Физика / Авт.-сост. В.А.Орлов, Н.К.Ханнанов; М-во образования РФ. – М.: Просвещение, 2003. – 222с.

2. Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 11 кл. сред.шк. М.: Просвещение. Стр. 288

 

 

Применение электрического поля — Справочник химика 21

    Таким образом, скорость процесса разделения водонефтяных эмульсий в отстойнике определяется осаждением взвешенных капель и их коалесценцией. На скорости этих процессов влияют температура подогрева разделяемой эмульсии и добавляемые в нефть реагенты — деэмульгаторы. К управляющим параметрам можно отнести и химические вещества, называемые флокулянтами [36, 37]. Они так же, как и деэмульгаторы, способствуют коагуляции (или флокуляции) диспергированных капель, т. е. объединению их в группы, что в свою очередь приводит к ускорению процесса коалесценции. На скорость процесса коалесценции можно влиять и другими способами применением электрических полей [4—6], коалесцирующих фильтров [38], ультразвука [39, 40], магнитных полей [41] и др. Однако из всех этих способов при подготовке нефти применяют в основном только электрические поля и реже — коалесцирующие фильтры. [c.26]
    Применение электрического поля [c.187]

    Очистка масел в электрическом поле является одним из сравнительно новых способов и недостаточно широко применяется на практике. В то же время электрокинетические свойства нефтяных масел, являющихся диэлектриками, определяют возможность и целесообразность их очистки с применением электрического поля. Практический опыт подтверждает, что такая очистка нефтяных масел от твердых загрязнений и воды в некоторых случаях довольно эффективна, однако отсутствие единой теории электрокинетических явлений в жидкой диэлектрической среде тормозит развитие этого перспективного метода очистки. [c.167]

    По применению электрических полей переменного и постоянного тока. В СССР электродегидраторы работают в основном с полями переменного тока как в промысловых, так и в нефтезаводских установках подготовки нефти. Наряду с эффективностью обработки водонефтяных эмульсий В/Н (вода в нефти) с большой обводненностью в полях переменного тока такие системы имеют более простое и доступное электрооборудование. [c.368]

    Поэтому для ускорения процесса разрушения эмульсии ее наряду с отстоем одновременно подвергают и другим мерам воздействия, направленным на укрупнение капель воды, увеличение разности плотностей, снижение вязкости нефти. Основными мерами являются подогрев эмульсии (термообработка) введение в нее деэмульгатора (химическая обработка) применение электрического поля (электрообработка). Существуют и другие меры воздействия на эмульсию, например перемешивание, вибрация, обработка ультразвуком, фильтрация, способствующие в основном укрупнению капелек воды. [c.34]

    Отстой полученной эмульсии проводили в стеклянных воронках при 60 и 80 °С с применением электрического поля средней напряженности [c.74]

    Аппараты для разделения водонефтяных эмульсий с применением электрических полей называются электродегидраторами. По типу используемого напряжения их делят на электродегидраторы, работающие на напряжении промышленной частоты и электростатические дегидраторы (или разделители), работающие на постоянном электрическом токе. В начале 50-х годов делались попытки создать высокочастотные электродегидраторы [56], однако практического применения они не нашли. [c.37]

    В связи с повышением требований к чистоте жидкостей гидросистем, от которой зависит надежность устройств, как у нас, так и за рубежом разрабатываются способы и устройства очистки этих жидкостей с применением электрических полей [2, 47]. Очистительные устройства, как правило, используют принцип заряжения дисперсных частиц в поле и их осаждение на электроде. Под действием поля сил точечных зарядов частицы могут осаждаться на диэлектрических поверхностях. По данным американского Инженерно-технического общества технологии смазки , электростатический фильтр с пористыми керамическими матрицами в качестве осадителей очищает гидравлические жидкости, смазочные масла, топливные жидкости, трансформаторные масла с эффективностью до 90-99 %. По литературным данным, производительность фильтров достигает 2 м /мин, размер улавливаемых дисперсных частиц-до 100 мк [39]. [c.52]

    На лабораторной установке было проведено исследование электрообезвоживания нефти ряда месторождений страны. В таблице приведены некоторые результаты для нефти новых месторождений Западной Сибири, п/о Мангышлак и Оренбургской обл., для сравнения там же приводятся результаты обработки нефти в тех же условиях, но без наложения электрического поля. Полученные данные убедительно показывают эффективность применения электрического поля для обезвоживания нефтей, качество обработанной нефти, как правило, получается выше при меньшем расходе реагента и более низкой температуре, чем при теплохимическом обезвоживании. [c.89]

    При обработке же нефти на И ступени с применением электрического поля качество полученной нефти было значительно выше, содержание воды колебалось в пределах 0,11—0,22%, а содержание солей составляло 85—115 мг/л. Качество нефти, обработанной с применением реагента АНП-2, в этом случае было примерно таким же, как и с реагентом диссольван. Таким образом, по полученным лабораторным данным можно сделать вывод, что при помощи реагента АНП-2 можно как обезвоживать, так и обессоливать нефть. [c.191]

    Приведены результаты исследования на описанной установке процесса электрообезвоживания нефтей новых месторождений Западной Сибири, п/о Мангышлак, Оренбургской области. Результаты проведенных испытаний показали высокую эффективность применения электрического поля для обезвоживания нефтяных эмульсий перечисленных месторождений. [c.215]

Применение теоремы Гаусса для расчёта электрических полей

2. 1. Поле бесконечной заряженной нити

Рассмотрим поле, созданное зарядом, равномерно распределенным по бесконечной нити. Эту задачу мы решили на прошлой лекции, воспользовавшись принципом суперпозиции электрических полей (см. 1.11).

Теперь покажем, несколько проще можно рассчитать это поле с помощью теоремы Гаусса.

Определим напряжённость поля на расстоянии rот нити, заряженной с постоянной линейной плотностью:

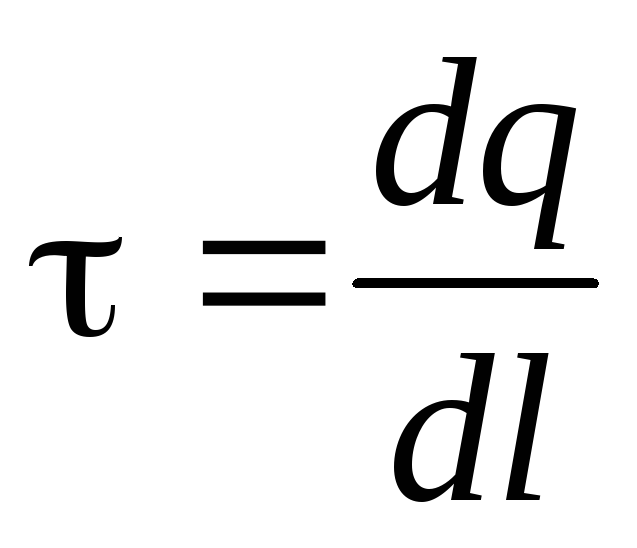, [Кл/м] (2.10)

Окружим нить замкнутой цилиндрической поверхностью (рис. 2.7.). Высота цилиндра — h, а радиус его основания —r.

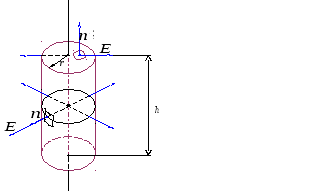
Рис. 2.7.

Поле, созданное заряженной нитью, обладает цилиндрической симметрией. В связи с этим векторы напряжённости во всех точках боковой поверхности цилиндра будут одинаковы по модулю и направлены радиально, то есть перпендикулярно к боковой поверхности цилиндра. На основаниях цилиндра векторы , направленные по-прежнему радиально, «скользят» по основанию, образуя прямой угол с нормалью.

Вычислим поток вектора через поверхность выбранного цилиндра. Полный поток через эту замкнутую «гауссову» поверхность складывается из потока через боковую поверхность цилиндра и через два его основания:

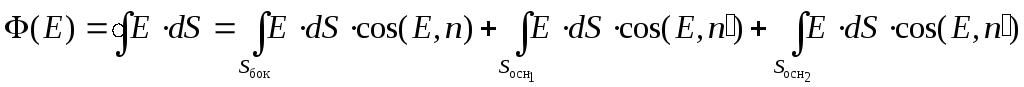
Последние два интеграла равны нулю, так как «скользящие» по основаниям цилиндра векторы не пронизывают их и не создают никакого потока. Формально эти два интеграла равны нулю, так как между векторамии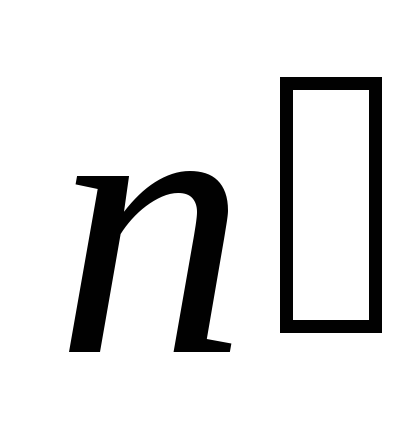прямой угол и. Таким образом

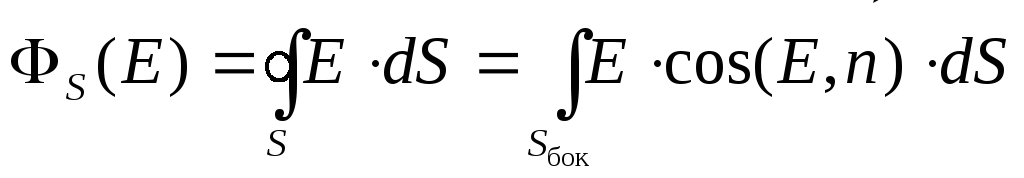
Во всех точках боковой поверхности цилиндра E=Е_r=constи.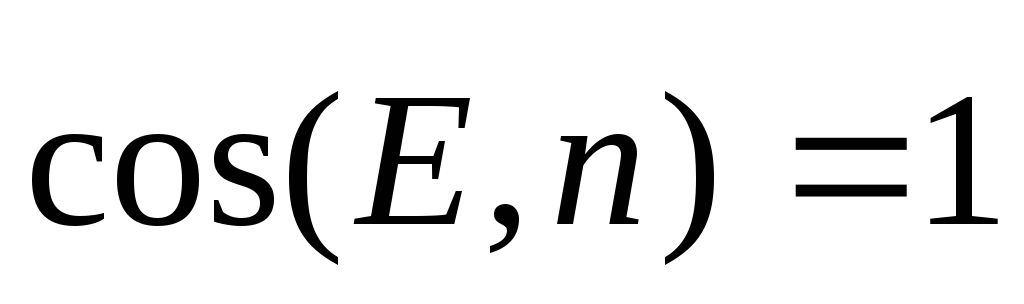

Поэтому поток через боковую поверхность цилиндра равен

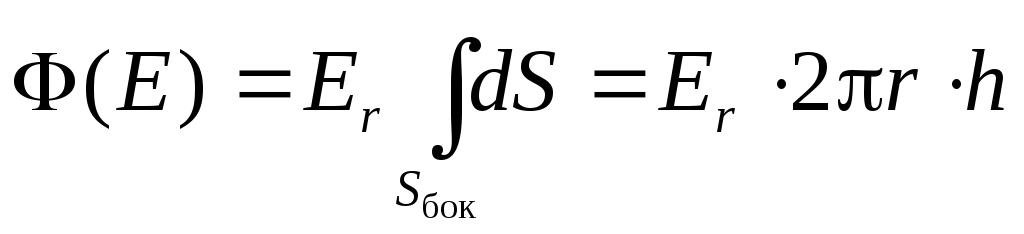(2.11)

Это поток вектора напряжённости электрического поля, вычисленный по определению потока.

Теперь воспользуемся теоремой Гаусса, отметив предварительно, что «заряд, заключённый внутри гауссовой поверхности» в данном случае сосредоточен на отрезке нити h— на оси цилиндра:

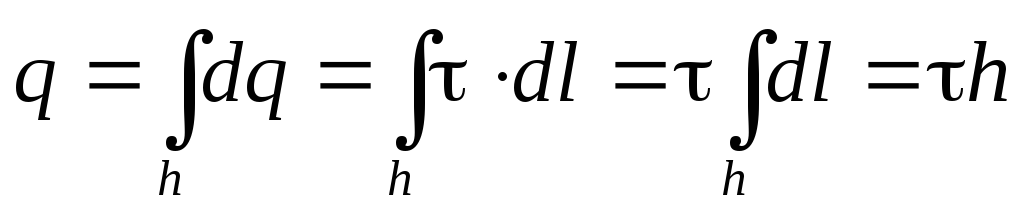
Таким образом

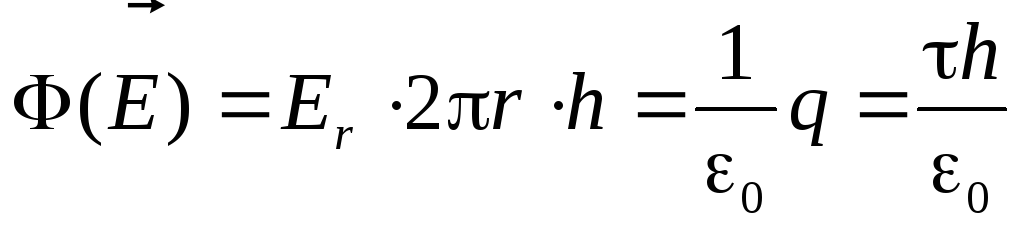(2.12)

Отсюда теперь легко получить знакомую нам гиперболическую зависимость напряжённости поля от расстояния до нити — r(см. 1.11).

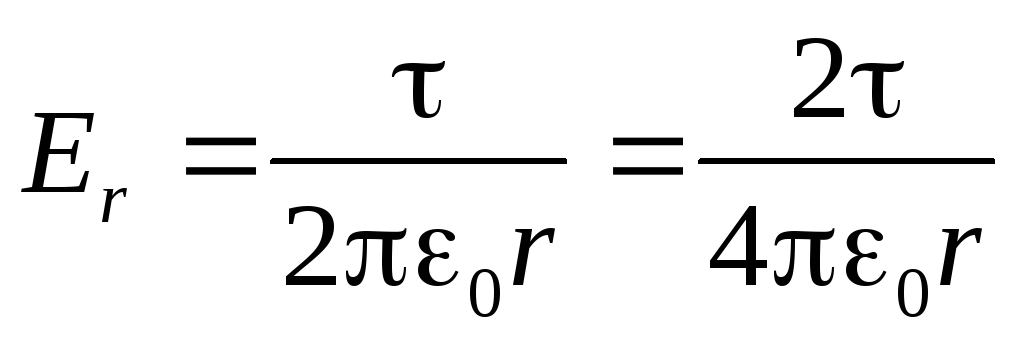(2.13)

2. Поле бесконечной равномерно заряженной плоскости. Поле плоского конденсатора

Пусть электрическое поле создаётся зарядом, равномерно распределённым по поверхности безграничной плоскости, с поверхностной плотностью (рис. 2.8.)

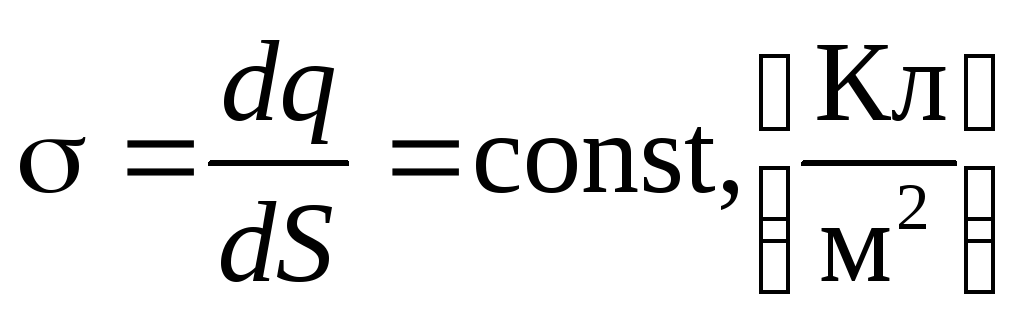
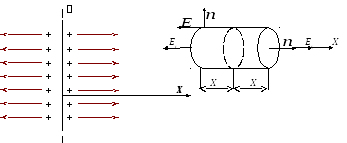
Рис. 2.8.

Из симметрии задачи следует, что поле повсюду направлено перпендикулярно к поверхности. Выясним, как меняется напряжённость поля по мере удаления от заряженной плоскости.

В качестве гауссовой поверхности удобно выбрать цилиндр. Ось цилиндра направим перпендикулярно плоскости, его основание расположим на расстоянии Хсимметрично по обе стороны от поверхности.

Вычислим поток вектора напряжённости через боковую поверхность и основания цилиндра. Как следует из рис. 2.8., поток вектора напряжённости через боковую поверхность цилиндра равен нулю, так как здесь повсюду векторы напряжённости «скользят» по поверхности и.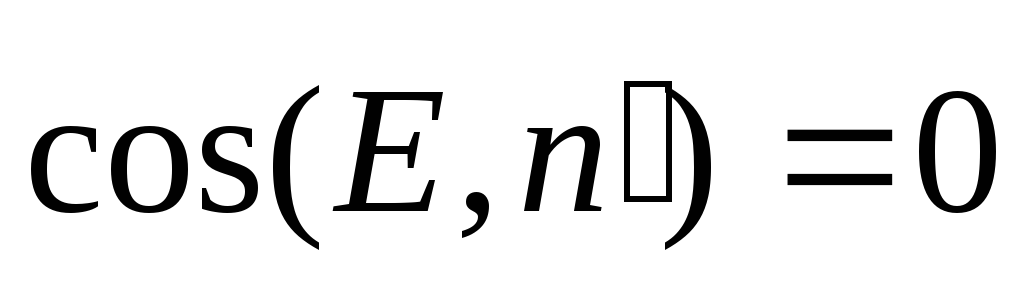

Тогда полный поток через замкнутую цилиндрическую поверхность можно записать как поток через два основания цилиндра.

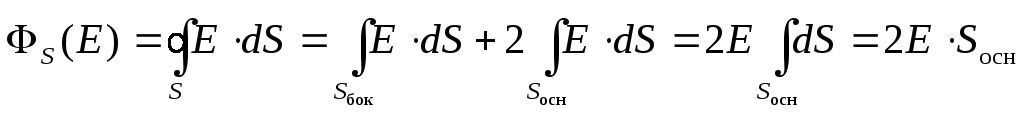(2.14)

Это величина, рассчитанная по определению потока.

Теперь воспользуемся теоремой Гаусса, заметив, что заряд q, «находящийся внутри гауссовой поверхности», в данном случае сосредоточен на площадкеS=S_осн, «вырезанной» цилиндром на бесконечной плоскости

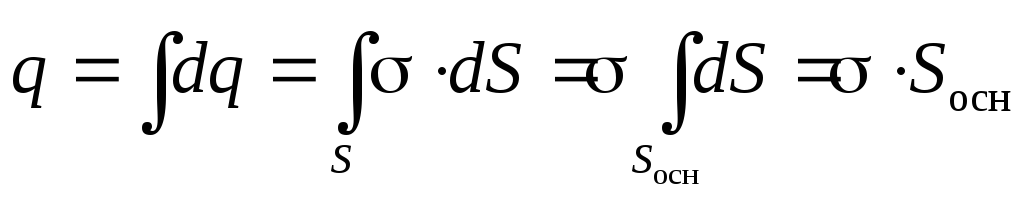(2.15)

Объединим результаты(2.15) и (2.14) в уравнение Гаусса:

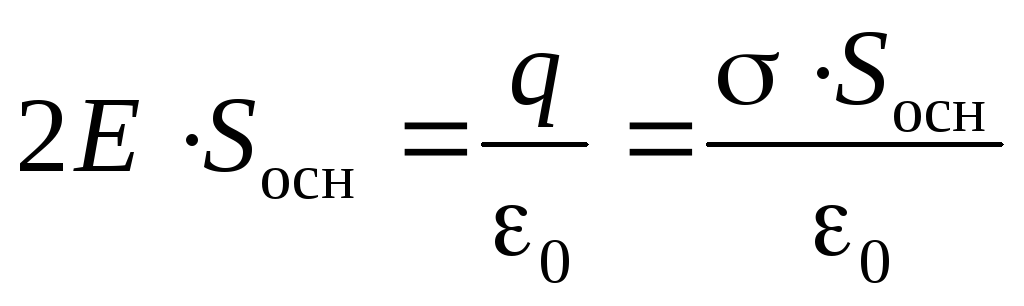
Откуда следует

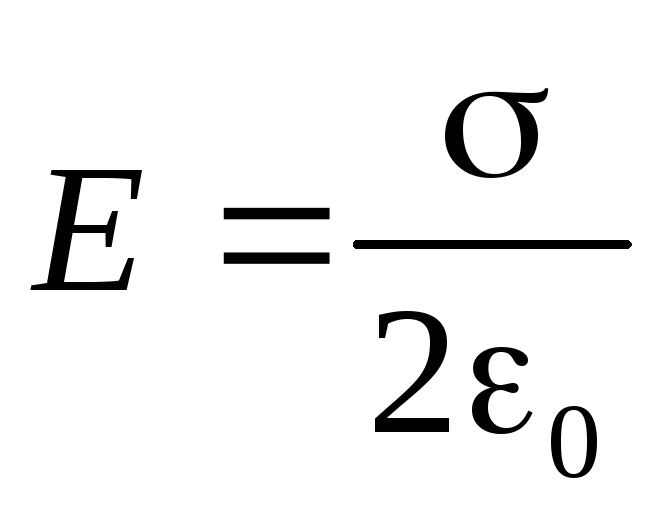(2.16)

Вывод. Поле, созданное бесконечной равномерно заряженной плоскостью, однородно. Оно не меняется с расстоянием от заряженной поверхности ни по величине, ни по направлению.

Теперь рассмотрим еще один важный пример. Пусть поле создаётся двумя бесконечными плоскостями, заряженными разноименно, но с одинаковой по величине поверхностной плотностью заряда (рис. 2.9.). Это важная идеализация электростатики — плоский конденсатор. Каждая обкладка этого конденсатора создаёт однородное поле, напряжённость которого мы только что установили (2.16):

.

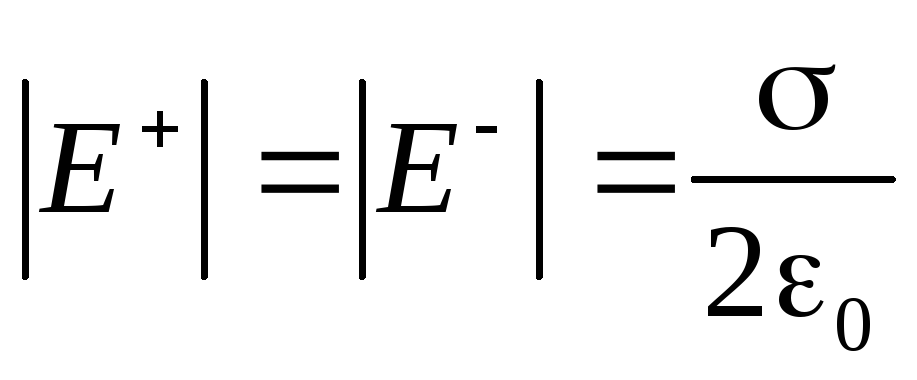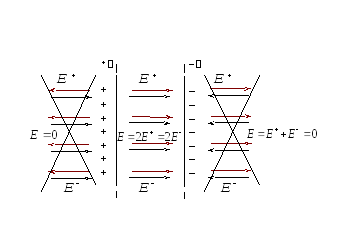
Рис. 2.9.

Силовые линии поля положительно заряженной плоскости направлены от неё, а отрицательной — к плоскости. При сложении этих полей, напряжённость результирующего поля вне конденсатора оказывается равной нулю, а внутри конденсатора, где эти поля совпадают по направлению, — поле удваивается:

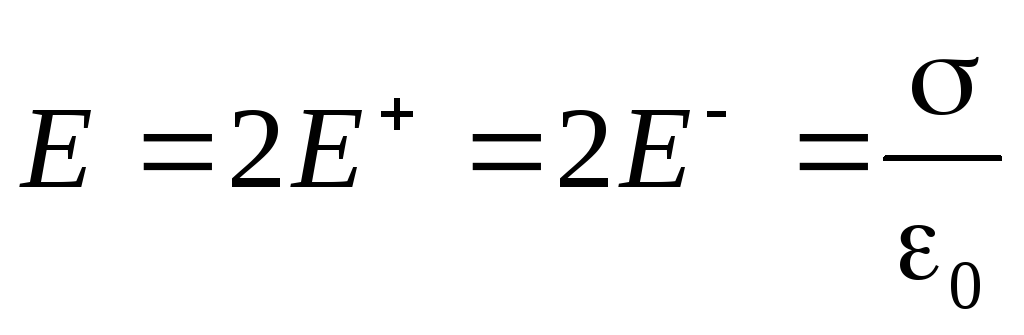. (2.17)

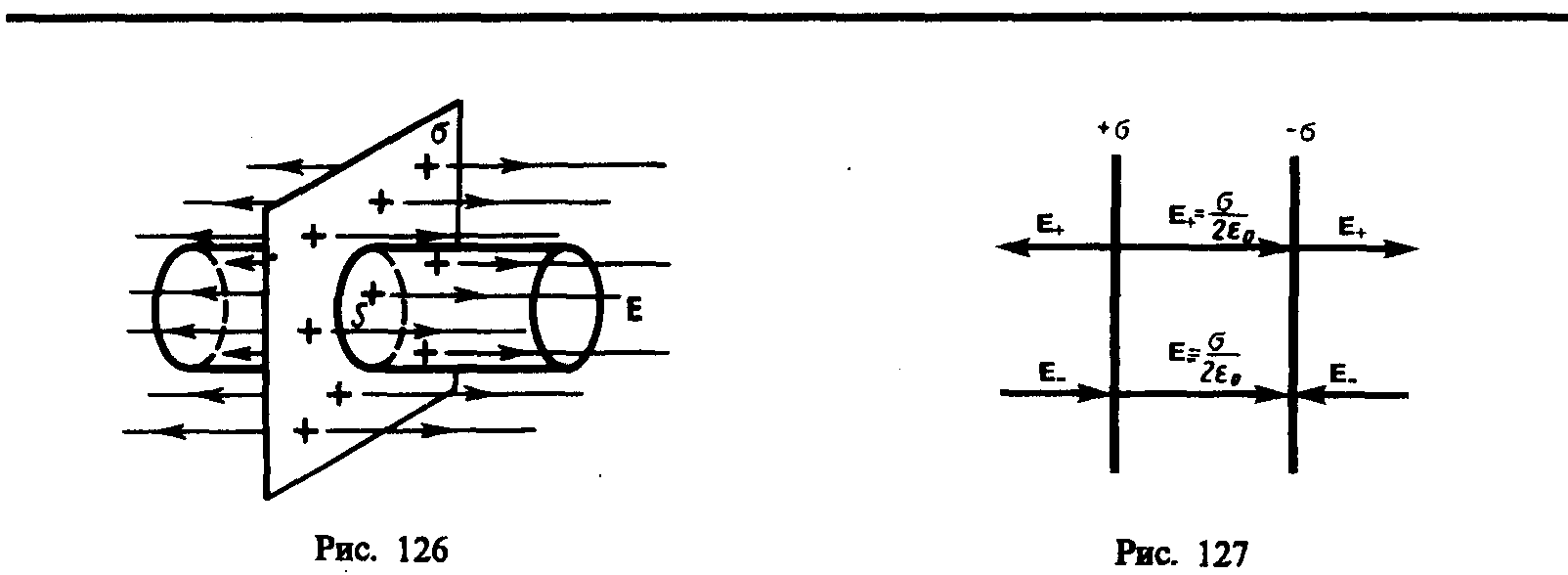
§ 82. Применение теоремы Гаусса к расчету некоторых электростатических полей в вакууме

1. Поле равномерно заряженной бесконечной плоскости.Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью + (=dQ/dS — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соs=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основанияЕ_nсовпадает сЕ), т. е. равен 2ES.Заряд, заключенный внутри построенной цилиндрической поверхности, равенS.Согласно теореме Гаусса (81.2), 2ES=S/₀,откуда

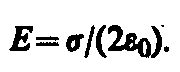(82.1)

Из формулы (82.1) вытекает, что Ене зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскостиоднородно.

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей(рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + и –. Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поляE=0. В области между плоскостямиE =E₊ +E_–(E₊ иE_–определяются по формуле (82.1)), поэтому результирующая напряженность

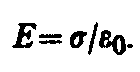(82.2)

Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.

3. Поле равномерно заряженной сферической поверхности.Сферическая поверхность радиусаR собщим зарядомQзаряжена равномерно с поверхностной плотностью+. Благодаря равномер­ному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметри­ей. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиусаr,имеющую общий центр с заряженной сферой. Еслиr>R,roвнутрь поверхности попадает весь зарядQ,создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 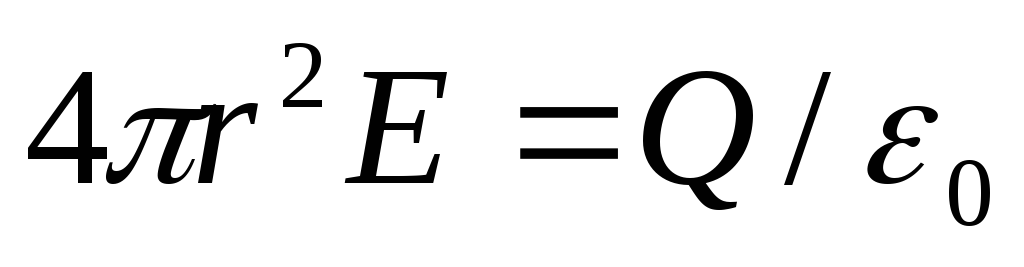,откуда

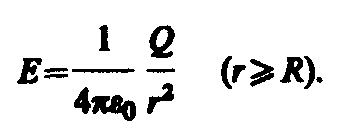(82.3)

При r>Rполе убывает с расстояниемrпо такому же закону, как у точечного заряда. График зависимостиЕ от rприведен на рис. 129. Еслиr‘<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).

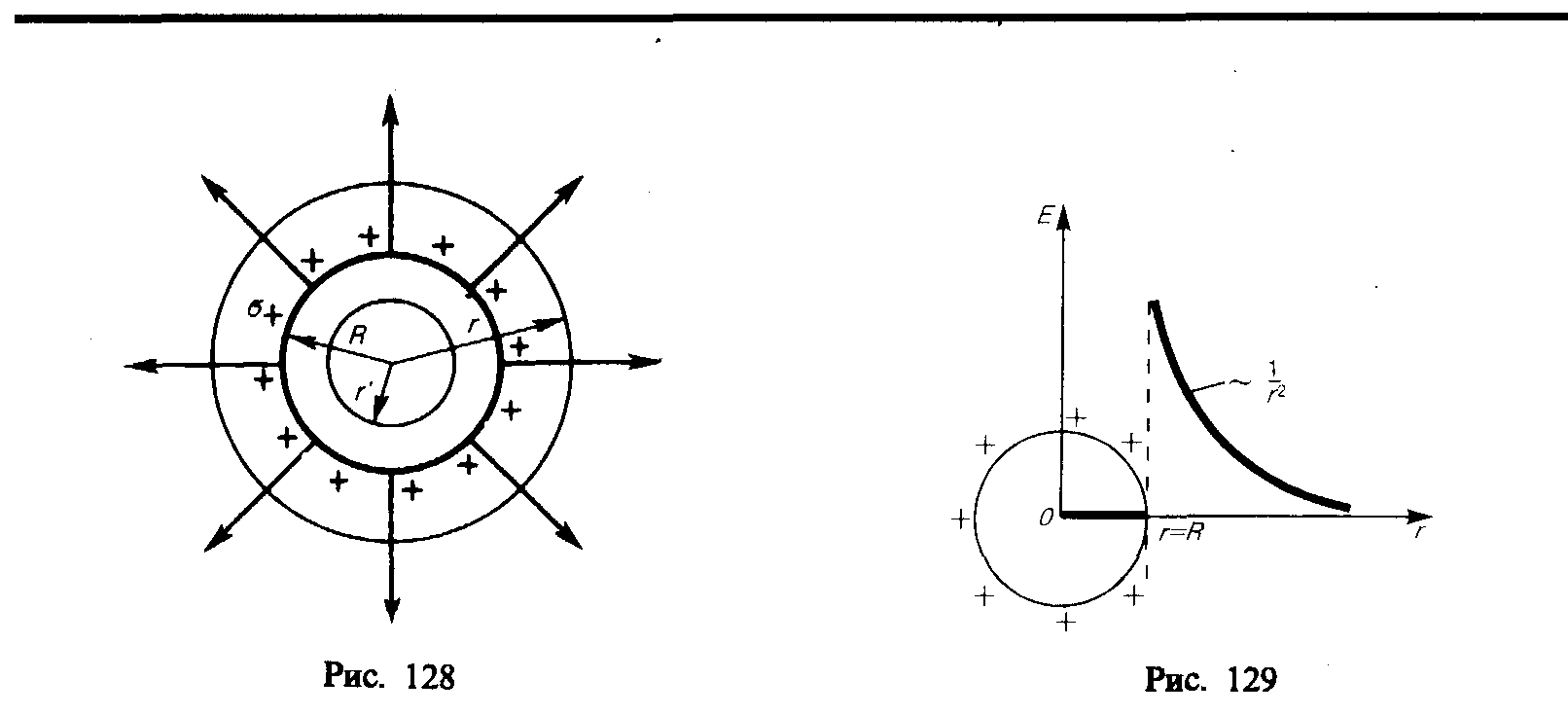
4. Поле объемно заряженного шара. Шар радиусаR с общим зарядомQзаряжен равномерно с объемной плотностью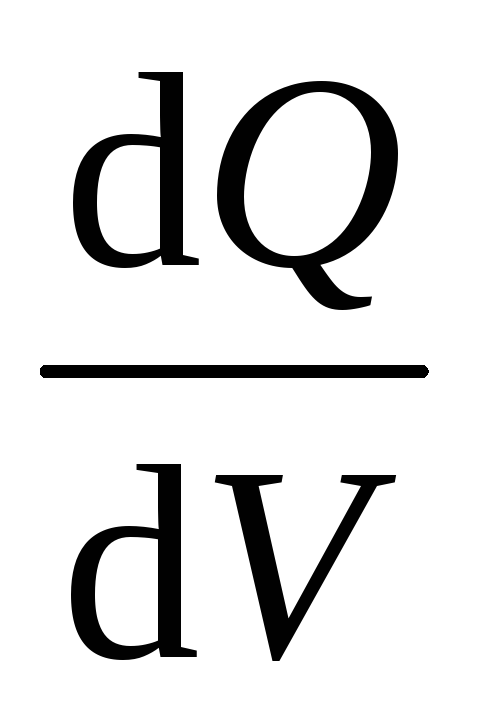 (=– заряд, приходящийся на единицу объема). Учитывая соображения

симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r‘<Rохватывает зарядQ‘=⁴/₃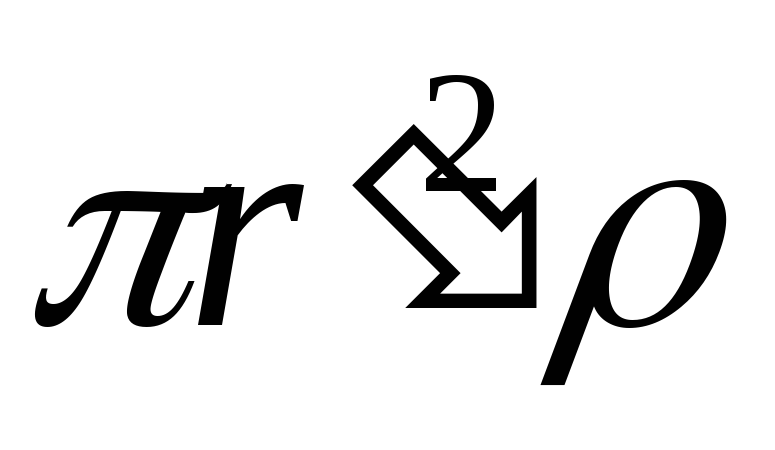.Поэтому, согласно теореме Гаусса (81.2),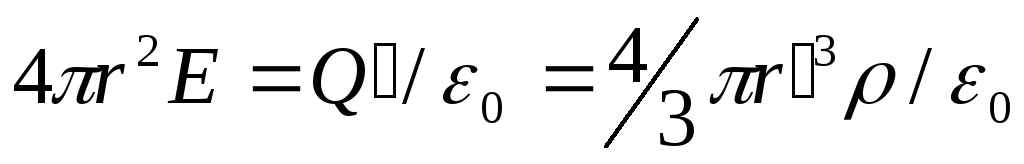. Учитывая, что 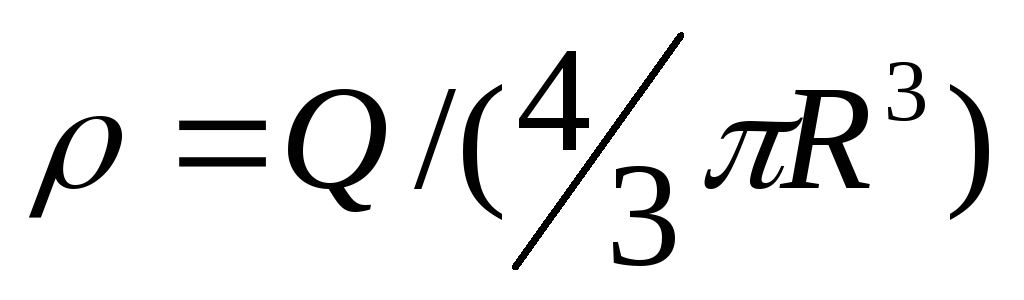,получаем

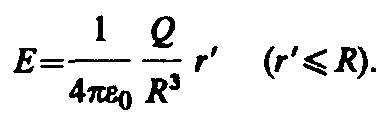(82.4)

Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием r‘согласно выражению (82.4). График зависимостиЕотrдля рассмотренного случая приведен на рис. 130.

5. Поле равномерно заряженного бесконечного цилиндра (нити).Бесконечный цилиндр радиусаR(рис. 131) заряжен равномерно с линейной плотностью 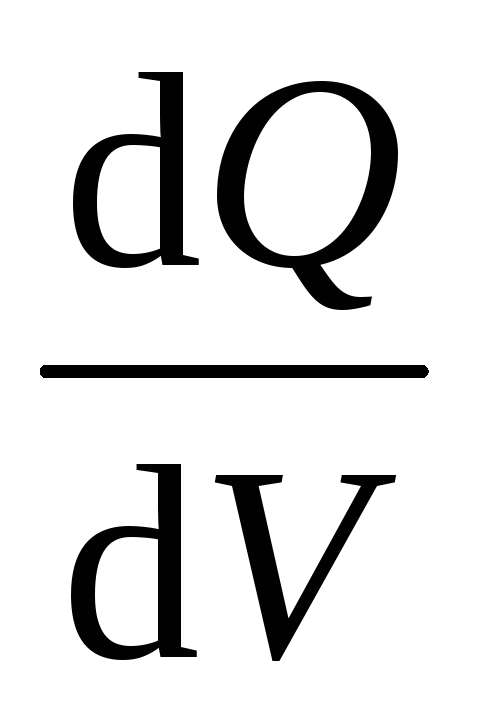(=– заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиусаrи высотойl. Поток вектораЕсквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2rlЕ.По теореме Гаусса (81.2), приr>R2rlЕ=l/₀, откуда

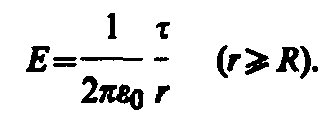(82.5)

Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой областиE=0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определя­ется выражением (82.5), внутри же его поле отсутствует.