Параллельное соединение проводников | 8 класс

Содержание

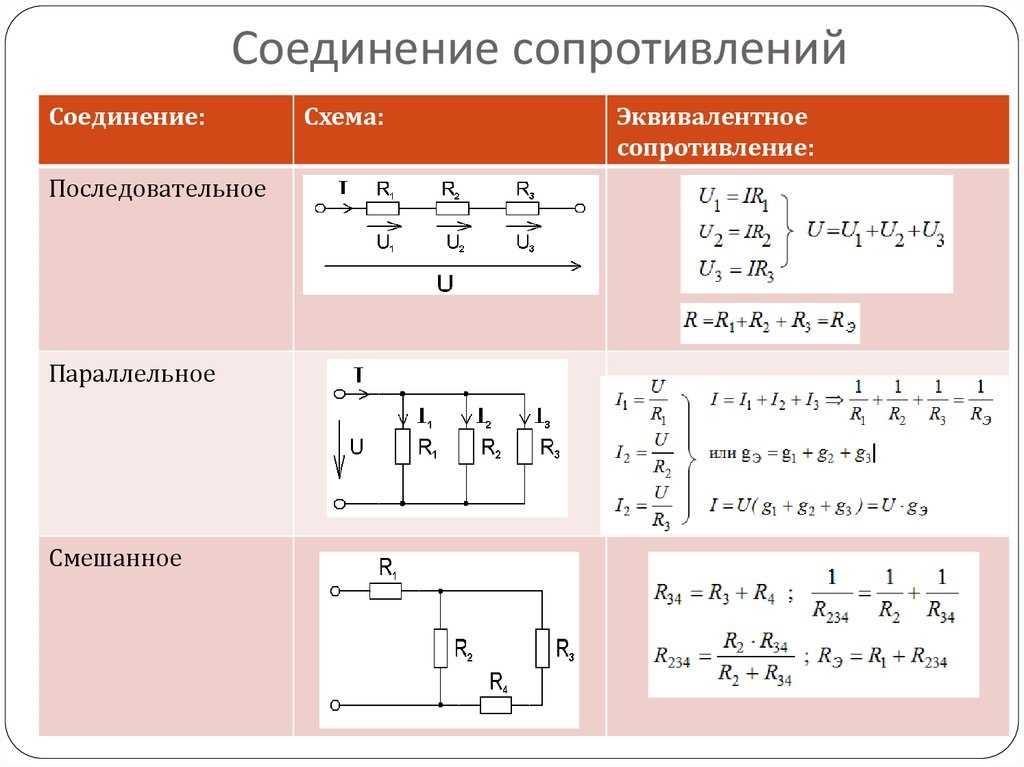
На прошлом уроке мы рассмотрели последовательное соединение проводников. При нем сила тока на всех участках цепи одинакова ($I = I_1 = I_2 = … = I_n$), а сопротивление всей цепи складывается из сопротивлений всех проводников, составляющих ее ($R = R_1 + R_2 + … + R_n$). Напряжение (подобно сопротивлению) всей цепи рассчитывается сложением напряжений на концах всех элементов, составляющих такую электрическую цепь ($U = U_1 + U_2 + … + U_n$).

На данном уроке мы рассмотрим другой вид соединения проводников — параллельный. Так мы подсоединяли вольтметр, когда измеряли напряжение на каком-либо участке цепи. Сейчас же мы рассмотрим закономерности для силы тока, сопротивления и напряжения в цепи для такого типа соединения.

Параллельное включение элементов в электрическую цепь

Какое соединение проводников называют параллельным?

Соберем электрическую цепь с таким соединением. Цепь будет состоять из источника тока, ключа и двух электроламп. Электролампы включены в цепь параллельно (рисунок 1).

Рисунок 1. Электрическая цепь с параллельным подключением электроламп

Схема этой электрической цепи изображена на рисунке 2.

Рисунок 2. Схема электрической цепи с параллельным подключением электроламп

На схеме обозначены две точки A и B. Важный момент:

При параллельном соединении все входящие в него проводники одним своим концом присоединяются к точке A, а вторым концом — к другой точке B.

Так мы можем подключить еще несколько ламп или некоторое количество других потребителей электроэнергии. Поэтому все закономерности, которые мы рассмотрим далее, будут справедливы для любого количества параллельно подключенных в цепь проводников между точками A и B.

{"questions":[{"content":"Если вы хотите включить в электрическую цепь параллельно три электролампы, то необходимо, чтобы [[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["провода, идущие от электроламп, одним своим концом были присоединены к одной определенной точке, а вторым проводом — к другой определенной точке цепи","провода, идущие от электроламп, были соединены сначала друг с другом, а далее — с остальными элементами цепи","хотя бы одна электролампа была подключена в цепь последовательно"],"answer":[0]}}}]}

Напряжение в цепи при параллельном соединении проводников

Вольтметр подсоединяется в цепь параллельно. Взгляните на рисунок 3.

Рисунок 3. Схема цепи для измерения вольтметром напряжения при параллельном соединении проводников

Можно ли сказать, что мы измеряем напряжение только на одной из ламп? Нет. Получается, что одновременно мы измеряем напряжения и на одной, и на другой лампе. Мы приходим к следующему заключению.

Напряжение на участке цепи AB и на концах всех параллельно соединенных проводников одно и то же:
$U = U_1 = U_2 = … = U_n$.

Значит, напряжение — это электрическая величина, которая одинакова для всех проводников, соединенных параллельно.

По этой причине в быту и технике очень удобно применять параллельный тип соединения проводников. Почему?

Во-первых, в таком случае все потребители электроэнергии изготавливаются в расчете на одну и ту же величину напряжения. Во-вторых, если исключить из цепи один потребитель, то другие продолжат работать. Цепь останется замкнутой.

{"questions":[{"content":"Какая величина одинакова для всех проводников, соединенных параллельно?[[choice-7]]","widgets":{"choice-7":{"type":"choice","options":["напряжение","сила тока","сопротивление"],"explanations":["","Сила тока одинакова для всех проводников, если они соединены последовательно. ","Сопротивление — определенная величина для каждого проводника."],"answer":[0]}}}]}

Сила тока в цепи при параллельном соединении проводников

Теперь рассмотрим, что происходит с силой тока при параллельном подключении.

Взгляните на рисунок 4, а. В точке B ток разветвляется на два тока: $I_1$ и $I_2$.

Рисунок 4. Разветвление тока при параллельном подключении проводников

Эти два тока сходятся снова в точке A. По смыслу этот момент очень похож на разветвление реки (рисунок 4, б) на два потока воды, которые через какое-то расстояние вновь сходятся в одно русло.

Как выражается сила тока в цепи до ее разветвления через силы токов в отдельных ветвях разветвления?

Сила тока в неразветвленной части цепи равна сумме сил токов в отдельных параллельно соединенных проводниках:
$I = I_1 + I_2 + … + I_n$.

{"questions":[{"content":"Сила тока на участке цепи после разветвления (на участке с параллельно включенным в цепь проводником) будет[[choice-12]]","widgets":{"choice-12":{"type":"choice","options":["меньше силы тока до разветвления цепи","больше силы тока до разветвления цепи","будет равна силе тока до разветвления цепи"],"explanations":["Так как после разветвления ток разделяется на несколько токов, то сила тока на каждом параллельно соединенном проводнике будет меньше, чем до разветвления. ","",""],"answer":[0]}}}]}

Сопротивление в цепи при параллельном соединении проводников

Перейдем к сопротивлению. При параллельном соединении можно представить все проводники как один. Этот один проводник будет явно больше в диаметре, чем каждый из них по отдельности. Получается, что площадь поперечного сечения проводника как бы увеличивается при таком соединении.

Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Чем больше поперечное сечение, тем меньше сопротивление.

Значит, общее сопротивление цепи уменьшается. Оно становится меньше сопротивления каждого из проводников, которые входят в такую электрическую цепь.

В цепи на рисунке 1 у нас две одинаковые лампы с сопротивлениями $R_1$. Общее сопротивление цепи $R$  будет в два раза меньше сопротивления каждой лампы: $R = \frac{R_1}{2}$.

Общее сопротивление цепи при параллельном соединении проводников рассчитывается по формуле:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + … + \frac{1}{R_n}$.

Как изменяется общее сопротивление разветвления после увеличения числа проводников в разветвлении?

Очевидно, что чем больше проводников будет в разветвлении, тем меньше будет общее сопротивление цепи.

{"questions":[{"content":"При параллельном включении в цепь дополнительного проводника общее сопротивление цепи [[choice-18]]","widgets":{"choice-18":{"type":"choice","options":["уменьшится","увеличится","не изменится"],"answer":[0]}}}]}

Пример параллельного соединения проводников

Взгляните на рисунок 5. Здесь изображена часть схемы электрической цепи. Здесь параллельно включены электрические лампы, нагревательные приборы и электродвигатель.

Рисунок 5. Параллельное включение в цепь различных потребителей электроэнергии

Где может использоваться такая схема соединения?
Например, в жилых помещениях. В точках A и B провода вводятся в квартиру.

Также в наших квартирах все стандартные розетки находятся под одинаковым напряжением в $220 \space В$. Большинство производителей техники изготавливают приборы как раз под это напряжение.

Использовать параллельное подключение к одной и той же цепи очень удобно, поскольку в нее могут быть включены самые разные потребители энергии (рисунок 6).

Рисунок 6. Подключение к сети различных бытовых приборов

Благодаря такому способу подключения, выключая свет в своей квартире, мы не выключаем его и у наших соседей. Любые электроприборы могут работать независимо от подключения или отключения в сеть других.

На практике также часто можно увидеть смешанное соединение проводников. В таких цепях присутствует и последовательный тип соединении, и параллельный.

{"questions":[{"content":"На какое напряжение рассчитано большинство бытовых электроприборов?[[choice-21]]","widgets":{"choice-21":{"type":"choice","options":["$220 \\space В$","$200 \\space В$","$100 \\space В$","На произвольное значение"],"answer":[0]}}}]}

Пример задачи

В осветительную сеть комнаты включены две электрические лампы, сопротивления которых равны $200 \space Ом$ и $300 \space Ом$. Напряжение в сети составляет $120 \space В$. Определите силу тока в каждой лампе, силу тока в проводящих проводах (то есть силу тока до разветвления), общее сопротивление участка, состоящего из двух ламп.

Подразумевается, что лампы подключены в сеть параллельно. Запишем условие задачи и решим ее.

Дано:
$R_1 = 200 \space Ом$
$R_2 = 300 \space Ом$
$U = 120 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$
$R — ?$

Решение:

Запишем закон Ома для участка цепи с первой лампой:
$I_1 = \frac{U_1}{R_1}$.

Значение сопротивления нам известно. Что с напряжением на этом участке?
Так как лампы подсоединены параллельно, то напряжение на каждой будет равно напряжению во всей цепи:
$U_1 = U_2 = U = 120 \space В$
Тогда мы можем рассчитать силу тока в каждой лампе.

Сила тока в первой лампе:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{120 \space В}{200 \space Ом} = 0.6 \space А$.

Сила тока во второй лампе:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{120 \space В}{300 \space Ом} = 0.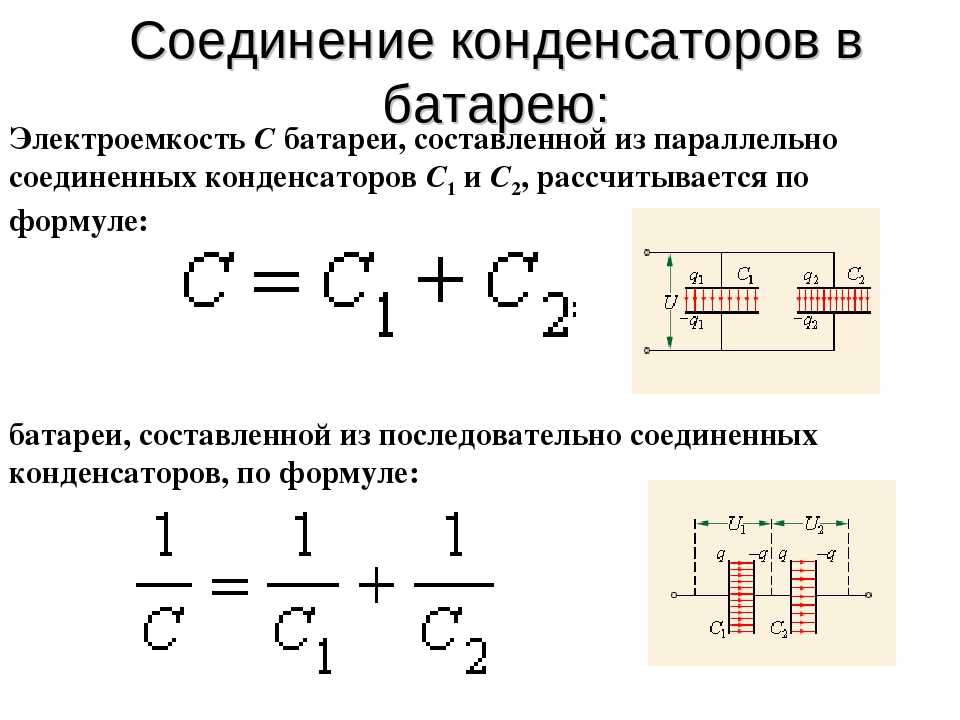 4 \space А$.

Сила тока до разветвления будет равна сумме сил этих двух токов в лампах:
$I = I_1 + I_2$,
$I = 0.6 \space А + 0.4 \space А = 1 \space А$.

Общее сопротивление цепи мы можем определить двумя способами.

Способ №1
Используя закон Ома для участка цепи, состоящего из двух параллельно соединенных ламп:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{120 \space В}{1 \space А} = 120 \space Ом$.

Способ №2
Используя формулу для расчета сопротивления при параллельном соединении проводников:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{200 \space Ом} + \frac{1}{300 \space Ом} = \frac{5}{600 \space Ом} = \frac{1}{120 \space Ом}$.

Отсюда, $R = \frac{1}{\frac{1}{120 \space Ом}} = 120 \space Ом$.

При решении этой задачи мы убедились, что общее сопротивление цепи меньше сопротивления каждого из параллельно подключенных проводников: $R < R_1 < R_2$.

Ответ: $I_1 = 0.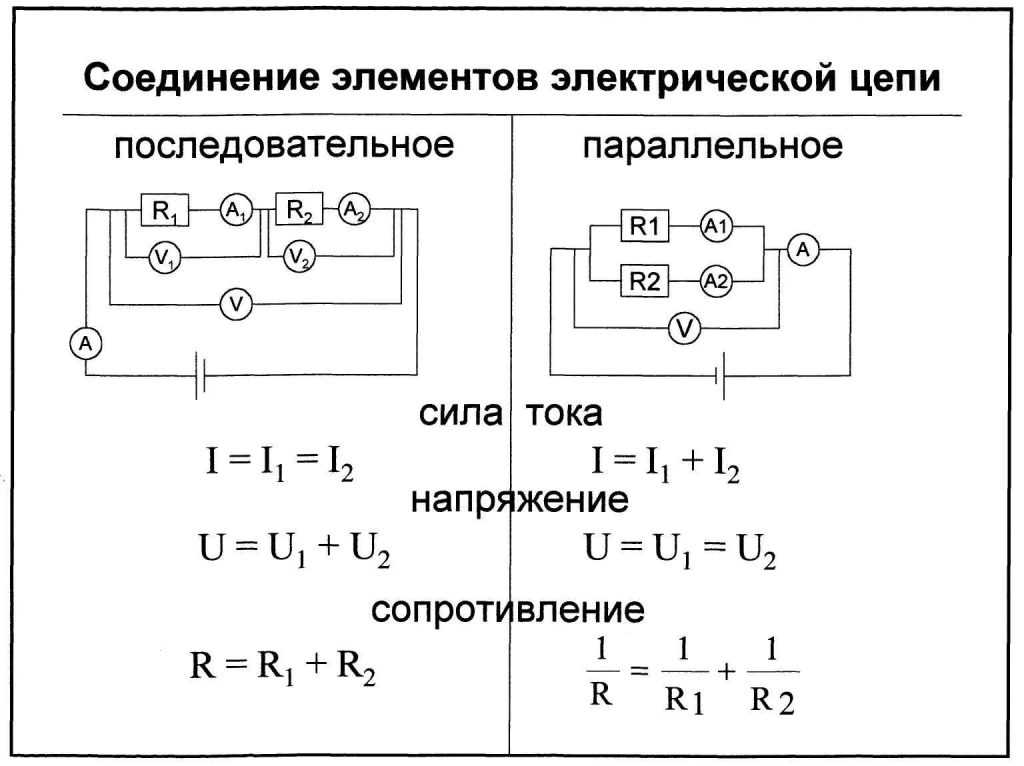 6 \space А$, $I_2 = 0.4 \space А$, $I = 1 \space А$, $R = 120 \space Ом$.

Упражнения

Упражнение №1

Два проводника сопротивлением $10 \space Ом$ и $15 \space Ом$ соединены параллельно и подключены к напряжению в $12 \space В$. Определите силу тока в каждом проводнике и силу тока до разветвления.

Дано:
$R_1 = 10 \space Ом$
$R_2 = 15 \space Ом$
$U = 12 \space В$

$I_1 — ?$
$I_2 — ?$
$I — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение будет одинаковое как во всей цепи, так и на концах каждого из двух проводников.

Запишем закон Ома для первого проводника и рассчитаем силу тока в нем:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{12 \space В}{10 \space Ом} = 1.2 \space А$.

То же самое сделаем для второго проводника:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{15 \space Ом} = 0.8 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом проводнике:
$I = I_1 + I_2$,
$I = 1. 2 \space А + 0.8 \space А = 2 \space А$.

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.8 \space А$, $I = 2 \space А$.

Упражнение №2

Почему бытовые приборы в помещении необходимо соединять параллельно?

Потому что бытовые приборы рассчитаны на то же напряжение, которое подается от городской сети — $220 \space В$. При параллельном соединении это напряжение будет одинаковым на всех участках цепи.

Также параллельное соединение позволяет включать и выключать приборы независимо друг от друга, что невозможно при последовательном соединении.

Упражнение №3

Три потребителя с сопротивлениями $20 \space Ом$, $40 \space Ом$ и $24 \space Ом$ соединены параллельно. Напряжение на концах этого участка цепи равно $24 \space В$. Определите силу тока в каждом потребителе, общую силу тока в участке цепи и сопротивление участка цепи.

Дано:
$R_1 = 20 \space Ом$
$R_2 = 40 \space Ом$
$R_3 = 24 \space Ом$
$U = 24 \space В$

$I_1 — ?$
$I_2 — ?$
$I_3 — ?$
$I — ?$
$R — ?$

Показать решение и ответ

Скрыть

Решение:

Напряжение на концах этого участка цепи будет равно напряжению на концах каждого потребителя, так как они соединены параллельно: $U_1 = U2 = U_3 = U = 24 \space В$.

Используя закон Ома для участка цепи, рассчитаем силу тока на каждом потребителе электроэнергии.

Для первого потребителя:
$I_1 = \frac{U}{R_1}$,
$I_1 = \frac{24 \space В}{20 \space Ом} = 1.2 \space А$.

Для второго потребителя:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{24 \space В}{40 \space Ом} = 0.6 \space А$.

Для третьего потребителя:
$I_3 = \frac{U}{R_3}$,
$I_3 = \frac{24 \space В}{24 \space Ом} = 1 \space А$.

Сила тока до разветвления в цепи будет равна сумме сил тока в каждом потребителе электроэнергии:
$I = I_1 + I_2 + I_3$,
$I = 1.2 \space А + 0.6 \space А + 1 \space А = 2.8 \space А$.

Теперь используем закон Ома, представляя участок цепи с тремя потребителями как единый участок цепи:
$I = \frac{U}{R}$,
$R = \frac{U}{I}$,
$R = \frac{24 \space В}{2.8 \space А} \approx 8.6 \space Ом$. 

Ответ: $I_1 = 1.2 \space А$, $I_2 = 0.6 \space А$, $I_3 = 1 \space А$, $I = 2.8 \space А$, $R \approx 8. 6 \space Ом$.

Упражнение №4

Два проводника имеют сопротивления, равные $5 \space Ом$ и $500 \space Ом$. Почему при последовательном соединении этих проводников их общее сопротивление будет больше $500 \space Ом$, а при параллельном соединении меньше $5 \space Ом$?

При последовательном соединении проводников общее сопротивление цепи будет равно сумме сопротивлений составляющих ее проводников.
Общее сопротивление при последовательном соединении:
$R = R_1 + R_2 = 5 \space Ом + 500 \space Ом = 505 \space Ом$.

Это значение действительно больше, чем $500 \space Ом$.

При параллельном соединении общее сопротивление мы рассчитываем следующим образом:
$\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}$,
$\frac{1}{R} = \frac{1}{5 \space Ом} + \frac{1}{500 \space Ом} = \frac{101}{500 \space Ом}$,
$R = \frac{1}{\frac{101}{500 \space Ом}} = \frac{500 \space Ом}{101} \approx 5 \space Ом$.

Согласитесь, что $5 \space Ом$ намного меньше, чем $500 \space Ом$.

Можно посмотреть на этот вопрос и с другой стороны. Сопротивление рассчитывается по формуле $R = \frac{\rho l}{S}$. Оно прямо пропорционально длине проводника и обратно пропорционально площади его поперечного сечения.

При последовательном соединении проводников мы можем сказать, что длина проводника увеличивается. Значит, увеличивается и сопротивление. Общее сопротивление будет больше, чем сопротивление каждого отдельного проводника.

А при параллельном соединении увеличивается площадь поперечного сечения. Значит,  сопротивление будет уменьшаться. Получается, что общее сопротивление такой цепи будет меньше сопротивления каждого из проводников.

Упражнение №5

На рисунке 7 изображена схема смешанного соединения проводников, сопротивления которых: $R_1 = 4 \space Ом$, $R_2 = 6 \space Ом$, $R_3 = 12 \space Ом$, $R_4 = 2 \space Ом$. Амперметр показывает силу тока $1 \space А$. Определите напряжение между точками В и С и силу тока в каждом проводнике.

Рисунок 7. Схема электрической цепи со смешанным соединением проводников к упражнению №5

Дано:
$R_1 = 4 \space Ом$
$R_2 = 6 \space Ом$
$R_3 = 12 \space Ом$
$R_4 = 2 \space Ом$
$I_3 = 1 \space А$

$U — ?$
$I_1 — ?$
$I_2 — ?$
$I_4 — ?$

Показать решение и ответ

Скрыть

Решение:

Амперметр подсоединен последовательно с проводником $R_3$. Он показывает силу тока $I_3 = 1 \space А$. Это сила тока после разветвления.

Используя закон Ома для этого проводника, рассчитаем напряжение на его концах:
$I_3 = \frac{U_3}{R_3}$,
$U_3 = I_3R_3$,
$U_3 = 1 \space А \cdot 12 \space Ом = 12 \space В$.

Так как проводники $R_3$ и $R_2$ подключены в цепь параллельно, то напряжение на каждом из этих проводников будет равно напряжению на участке цепи, который их включает. Это и есть напряжение между точками B и C:
$U = U_3 = 12 \space В$.

По закону Ома рассчитаем силу тока на проводнике $R_2$:
$I_2 = \frac{U}{R_2}$,
$I_2 = \frac{12 \space В}{6 \space Ом} = 2 \space А$.

Теперь мы можем рассчитать силу тока до его разветвления — на проводниках $R_1$ и $R_4$. При этом $I_1 = I_4 = I$, потому что эти проводники включены в цепь последовательно. Это значит, что сила тока в любом участке такой цепи будет одинаковой. В нашем случае на проводнике $R_1$ и $R_4$.

Рассчитаем эту силу тока, используя величины, полученные с параллельно соединенных проводников. Сила тока до разветвления будет равна сумме сил тока в каждом проводнике после разветвления:
$I = I_2 + I_3$,
$I = 1 \space А + 2 \space А = 3 \space А$.

Ответ: $U = 12 \space В$, $I_1 = I_4 = I = 3 \space А$, $I_2 =  2 \space А$, $I_3 = 1 \space А$. 

Основы электроники

Основы

Основы электроники и схемотехники начинаются с изучения последовательных и параллельных соединений электронных компонентов и их свойств.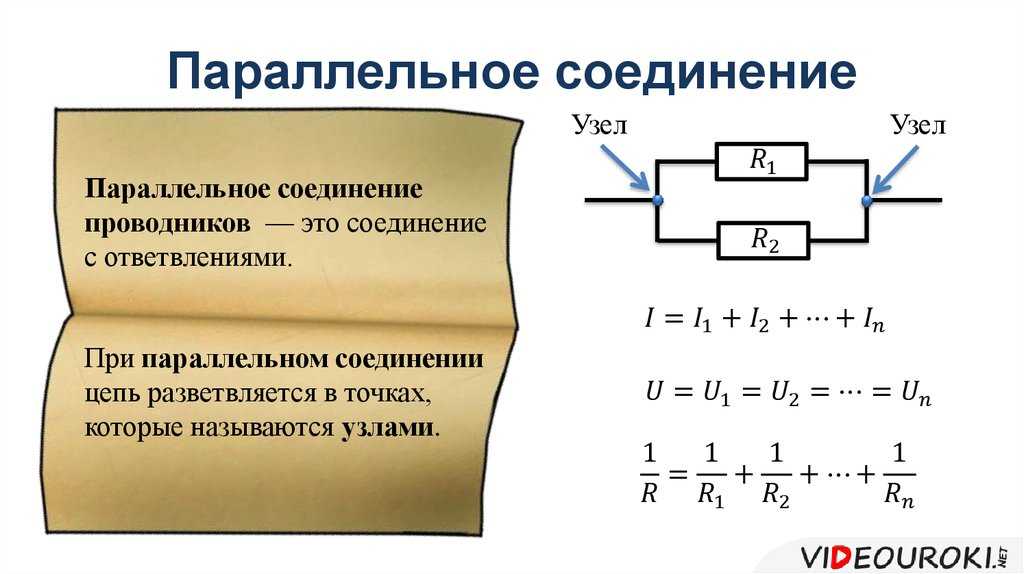

Последовательное и параллельное соединение батарей

При последовательном соединении общее напряжение (Вольты) батареи равно сумме напряжений входящих в нее элементов. Получившаяся батарея будет иметь ту же емкость, что и одиночный элемент. При этом через все элементы будет течь одинаковый ток (Амперы), а максимально допустимый ток, который можно получить при разрядке батареи, равен максимальному току, который можно получить от одного элемента.

При параллельном соединении одинаковых элементов общее напряжение батареи (Вольты) будет равно напряжению одного элемента, а общий ток (Амперы) будет равен сумме токов каждого элемента. Емкость такой батареи равна сумме емкостей входящих в нее элементов.

Резюмируя, можно сказать, что последовательное соединение элементов в батарее увеличивает напряжение (Вольты), а параллельное соединение увеличивает ток (Амперы) и емкость (Амперы/Час).

На практике при создании BEAM-роботов своими руками чаще всего используют последовательно соединенные пальчиковые батареи по 1,5 вольта. Таким образом, три батареи дают 4,5 вольта, а четыре – 6 вольт.

Соединяют батареи как при помощи пайки, используя короткие отрезки проводов, так и применяя специальные отсеки для батарей.

Последовательное и параллельное соединение резисторов

При последовательном соединении общее сопротивление составного резистора будет равно сумме сопротивлений отдельных резисторов.

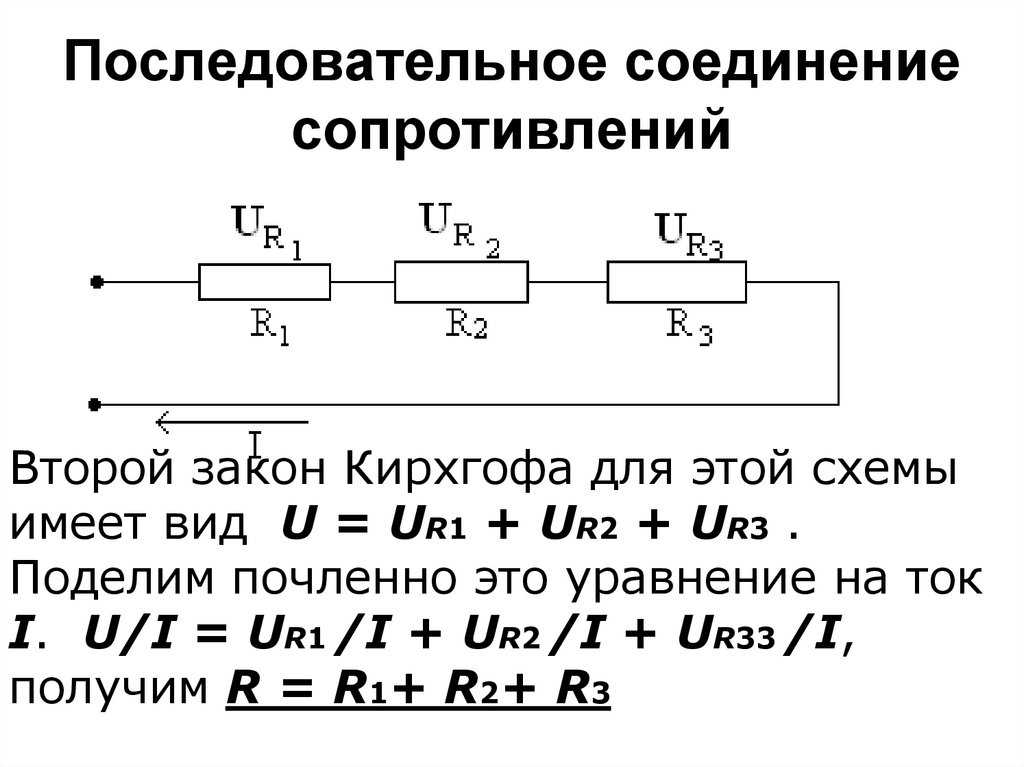
При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.

При использовании такого соединения резисторов, через каждый резистор потечет свой ток. Сила этого тока для каждого резистора будет обратно пропорциональна его сопротивлению.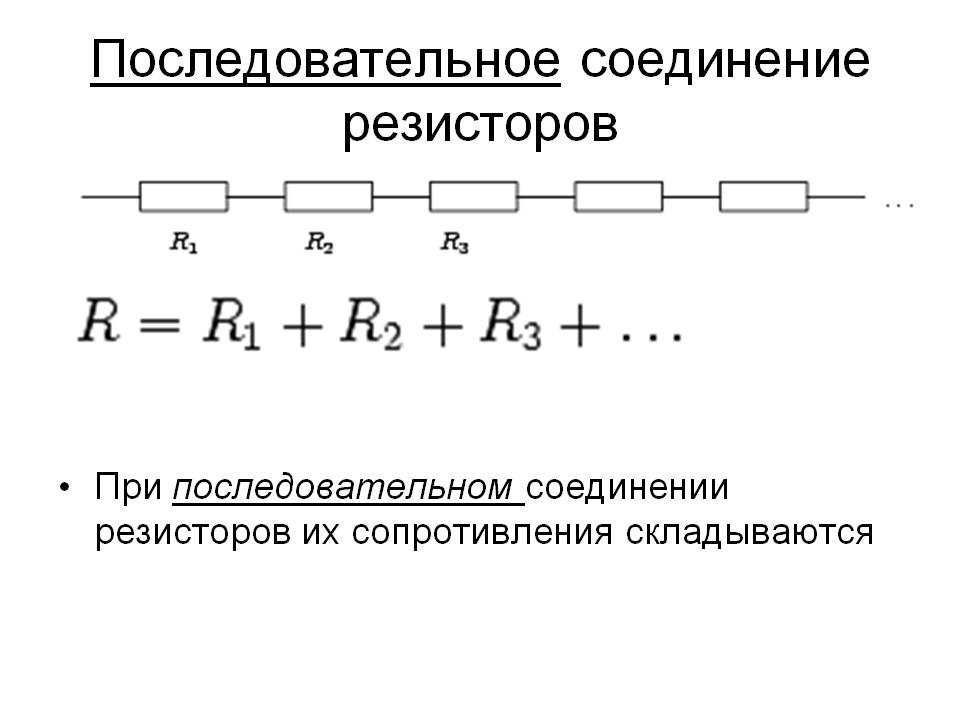

Таким образом, общая проводимость участка цепи с параллельным соединением резисторов увеличится, а его общее сопротивление наоборот уменьшится.

Для расчета сопротивления двух параллельно соединенных резисторов формула примет следующий вид:

Для трех:

При параллельном соединении двух одинаковых резисторов, их общее сопротивление будет равным половине сопротивления одного из резисторов:

Для N одинаковых резисторов:

Для параллельно подсоединенных резисторов с различным сопротивлением, их общее сопротивление окажется всегда меньше самого маленького из сопротивлений.

Если резисторы на участке цепи соединены между собой частично параллельно, а частично последовательно, то такое соединение называют смешанным. В зависимости от итогового типа соединения, смешанные соединения могут быть параллельного и последовательного типов.

Соединение резисторов

Используя приведеные выше формулы, мы можем, например, из трех резисторов получить сборки с шестью различными сопротивлениями. Рассмотрим это на примере трех резисторов с сопротивлением 1К (1 килоом) каждый.

Соединение конденсаторов

Для параллельного соединения конденсаторов, их общая емкость складывается. При этом допустимое напряжение для всего набора конденсаторов будет равно самому малому значению допустимого напряжения из всего набора.




При последовательном соединении уменьшается общая емкость и увеличивается общее напряжение конденсаторов.




Общее напряжение в данном случае будет равно сумме всех напряжений конденсаторов.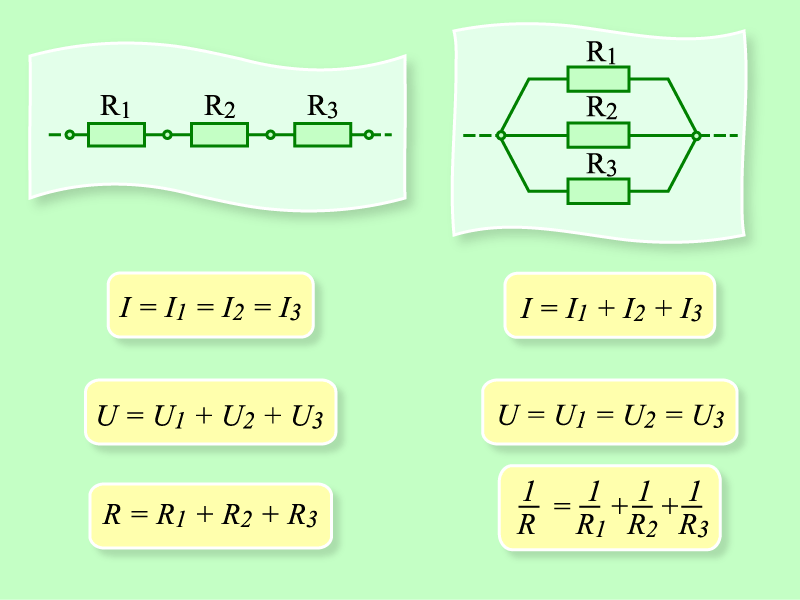

Закон Ома

Для вычисления напряжения, тока и сопротивления в цепи используют самый главный закон в электронике и электротехнике, который был эмпирически открыт в 1826 году Георгом Омом и получил его имя.

Соглано закону Ома для участка цепи, сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка цепи и обратно пропорциональна сопротивлению этого участка:

Где

I – величина тока, протекающего через участок цепи;
U – величина приложенного напряжения к участку цепи;
R – величина сопротивления рассматриваемого участка цепи.

При помощи второго варианта закона Ома для участка цепи можно вычислить приложенное напряжение к участку цепи, если мы знаем величину тока, протекающего через участок, и сопротивление этого участка.

Третий вариант закона Ома для участка цепи, позволяет вычислить сопротивление участка цепи по известным величинам напряжения и тока.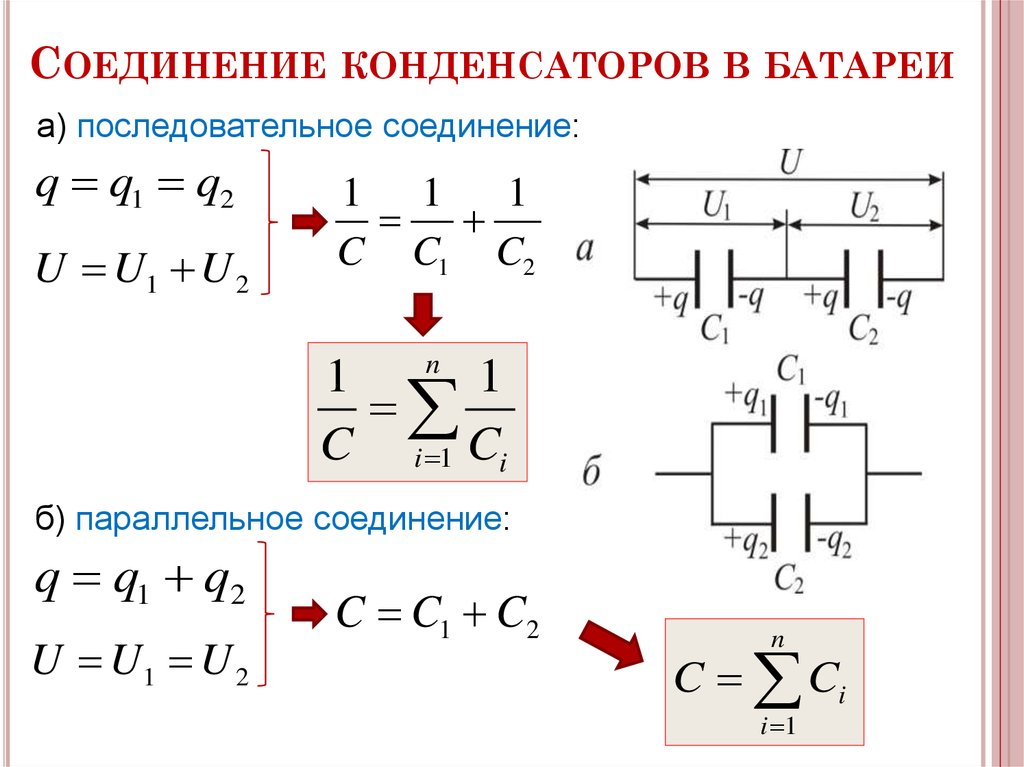

Используя третий вариант закона Ома можно, например, расчитать сопротивление ограничительного резистора для подключения светодиода к электрической цепи с напряжением, превышающим рабочее напряжение светодиода.

Подключение светодиодов

Предположим, что мы хотим подключить светодиод с рабочим напряжением 2В (2 вольта) и потреблением тока 20mA (20 миллиампер) к электрической батарее с напряжением 6В (6 вольт). Нам необходимо расчитать сопротивление ограничительного резистора. Падение напряжения на резисторе должно составлять 6В — 2В = 4В. Так как сила тока на всех участках цепи одинаковая, значит на нашем резисторе будет столько же ампер, сколько и на светодиоде, а именно 20mA = 0,02A. Используя закон Ома вычислим сопротивление резистора.




Сопротивление ограничительного резистора лучше выбирать с небольшим запасом. В нашем случае оно может быть 220 Ом.


Подключение светодиода

Основы схемотехники

При создании схем следует помнить о том, что можно разветвлять проводники, но нельзя соединять напрямую проводники, по которым могут проходить сигналы с разными значениями, иначе возникнет короткое замыкание.

электрических цепей — Почему добавляется напряжение, когда батареи соединены последовательно, а не параллельно?

Возможно, было бы полезно рассмотреть задействованную электронную динамику и знать о разнице в параметрах схемы, которую две конфигурации (последовательная и параллельная) приводят к электронному результату.

Два источника питания, включенных параллельно, вместе выдают такое же напряжение, как если бы они были единственным присутствующим источником питания, но общий ток (измеряемый в амперах) двух источников питания суммируется (если два источника выдают одинаковое напряжения, то это означает, что сила тока всей цепи удваивается, но напряжение остается прежним).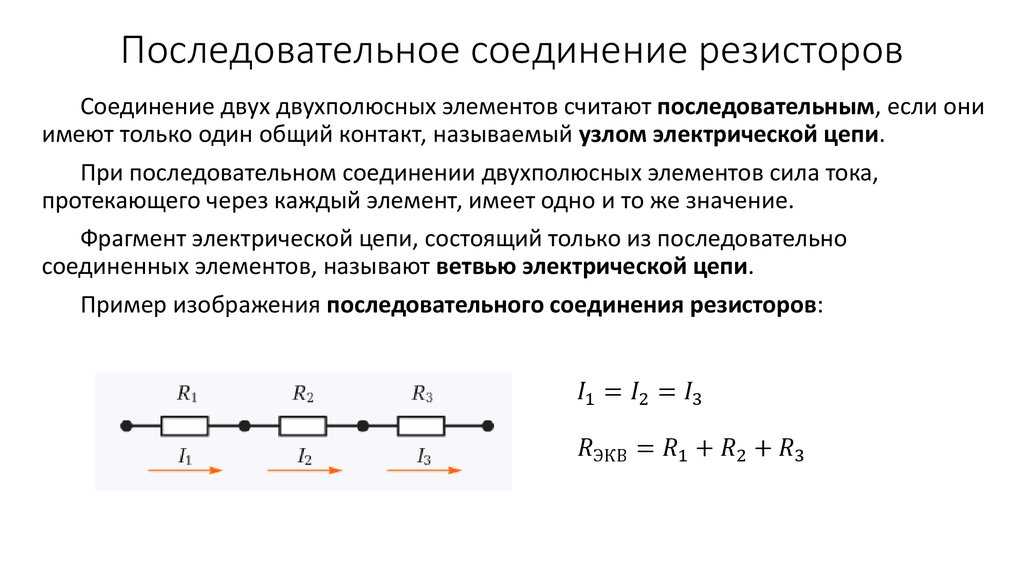

При последовательном соединении верно обратное: сила тока, подаваемая в цепь двумя источниками питания, равна силе тока, подаваемого любым из источников по отдельности, а общее напряжение удваивается (опять же, при условии, что два источника имеют одинаковую мощность). размеры и мощность).

Так что это компромисс, когда вы объединяете два или более источников энергии, что-то должно измениться, иначе не было бы смысла это делать, по логике вещей что-то должно увеличиться. Компромисс заключается в том, что что-то является либо током, либо напряжением, и какое из них определяется конфигурацией источников питания.

Имейте в виду, эти значения не обязательно являются удвоенными , это работает только тогда, когда оба источника питания идентичны друг другу.

Редактирование технических деталей электроники для подтверждения моего ответа

---

 Закон напряжения Кирхгофа: (параллельная цепь)
   «Алгебраическая сумма всех напряжений вокруг любой замкнутой цепи должна равняться 0». 
   (Следствие сохранения энергии).
   Пусть V = напряжение
   V(источник1) + [-V(источник2)] = 0
   V(всего) = V1 = V2
   I(всего) = I1 + I2
 

И

 Текущий закон Кирхгофа: (последовательная цепь)
   «Алгебраическая сумма всех токов, входящих в узел и выходящих из него, должна равняться 0».
   (Следствие сохранения заряда).
   Пусть ток=I
   I(вход) + [-I(выход)] = 0
   I(всего) = I1 = I2
   V(всего) = V1 + V2
 

Есть то, что известно как:

 идеальный источник напряжения - имеет нулевое внутреннее сопротивление/импеданс, так что
   изменения сопротивления/импеданса нагрузки не изменят напряжение
   поставляется.
   (см. теорему Тевенина). Это ваша параллельная схема с двумя источниками.
 

И

 идеальный источник тока - имеет бесконечное внутреннее сопротивление/импеданс
   (и, следовательно, нулевая проводимость источника, поскольку проводимость является обратной
   импеданса или сопротивления), чтобы изменения импеданса/сопротивления нагрузки
   не изменит подаваемый ток. 
   (см. теорему Нортона). Это цепь источника серии 2.
 

Дополнительная информация:

 Теорема Тевенина:
   «Для линейных электрических сетей любое сочетание источников напряжения,
   источники тока и резисторы с двумя выводами электрически
   эквивалентно одному источнику напряжения V и одному резистору R.
   Любая двухполюсная линейная двусторонняя сеть постоянного тока может быть заменена
   эквивалентная схема, состоящая из источника напряжения и последовательного резистора.
   Источник напряжения равен разности потенциалов между двумя
   клеммы, подключенные к этим клеммам. Последовательное сопротивление (или
   импеданс) является эквивалентным сопротивлением/импедансом с учетом двух
   терминальные порты со всеми источниками питания в паре неактивны».
   Или сформулировать по-другому, чтобы отразить концепции идеального источника:
   «Любой источник электрического сигнала эквивалентен идеальному источнику напряжения в
   серии с импедансом источника».
 

И

 Теорема Нортона:
   «Любые два терминала сети, состоящей из линейных пассивных и активных
   элементы цепи могут быть заменены эквивалентным источником тока и
   параллельное сопротивление.  Ток источника – это ток, измеренный в
   короткое замыкание на клеммной паре. Параллель
   сопротивление - это эквивалентное сопротивление, смотрящее на клеммную пару
   со всеми неактивными независимыми источниками питания».
   Или сформулировать по-другому, чтобы отразить концепции идеального источника:
   «Любой источник электрического сигнала эквивалентен идеальному источнику тока в
   параллельно входу источника».
 

электрических цепей — Почему напряжение не увеличивается при параллельном соединении аккумуляторов?

tl;dr Батареи не создают электрических полей для перемещения зарядов. Они перемещают заряды, что создает электрические поля.

батарея […] создает некоторое электрическое поле, которое перемещается по цепи и создает силу, воздействующую на электроны в проводнике для производства тока.

Это описание если не совсем неверно, то по крайней мере вводит в заблуждение. Батарея не является источником электрическое поле , оно является источником электрического потенциала . Представьте себе батарею с клеммами в виде пары параллельных токопроводящих пластин с воздушным зазором между ними (это конденсатор): при смещении пластин друг к другу напряженность поля (между пластинами) увеличивается, а при раздвинуть их, напряженность поля уменьшается. Верхнего предела силы поля нет (ну, пока оно не достигнет напряжения пробоя и не начнется дуговой разряд), как нет и нижнего предела — сила поля не определяется батареей. Таким образом, сама батарея напрямую не создает электрического поля между своими клеммами.

Более того, электрическое поле не «движется» по цепи; заряды делают. В простой установке постоянного тока, такой как батарея, пропускающая ток через резистор, все электрические поля стабильны во времени — зарядов перемещаются по цепи, а само поле — нет. Сказать, что электрическое поле движется по цепи, это все равно, что сказать, что гравитация движется по американским горкам. Движущиеся электрические поля вступают в игру с цепями переменного тока и устройствами с движущимися частями, такими как электродвигатели; но даже неподвижное электрическое поле заставляет заряды двигаться через проводник (в конце концов, это, по сути, определение «проводника»).

Так как работает ток? Батареи являются источником электрического потенциала , который измеряется в вольтах. Потенциал — это своего рода давление, и в типичной батарее это давление вызвано химическими реакциями внутри батареи, перекачивающими электроны с одного контакта (+) на противоположный (-). Разность потенциалов между клеммами действительно создает электрическое поле. В приведенном выше эксперименте, где клеммы батареи представляют собой параллельные плоские пластины, разделенные расстоянием $d$, вы можете вычислить напряженность поля между ними как просто $E = {V \over d}$. Но поле — это всего лишь способ наблюдения за разностью потенциалов между клеммами: в первую очередь это не причина движения зарядов (это, опять же, химические реакции, происходящие внутри батареи).

Давление относительно, и электрический потенциал ничем не отличается. Чтобы быть строго точным, то, что обеспечивает батарея, представляет собой разность электрических потенциалов («напряжение») между двумя ее клеммами. По сути, это измерение того, насколько мощный электронный насос находится внутри батареи. Вот почему параллельное соединение двух одинаковых батарей не добавляет их напряжения: поскольку они обе обеспечивают одну и ту же разность потенциалов между клеммами (+) и (-), по сути, нет никакой разницы между двумя батареями, соединенными параллельно, и двумя изолированными. , отсоединенные аккумуляторы. Электрический потенциал между клеммами (+) и (-) одинаков, и обе батареи «согласуются» с ним, поэтому нет причин для протекания тока между ними. (Соединение двух несоответствие батарей, соединенных параллельно приведет к протеканию тока в направлении, определяемом тем, какая батарея имеет более высокое напряжение.)

Параллельное соединение двух батарей делает изменением поведения системы под нагрузкой. Если вы подключите нагрузку, скажем, резистор 1 кОм, к клеммам одной 1,5-вольтовой батареи, ток через резистор составит 1,5 мА, и все они питаются от одной батареи.