| Последовательное соединение | Fiziku5

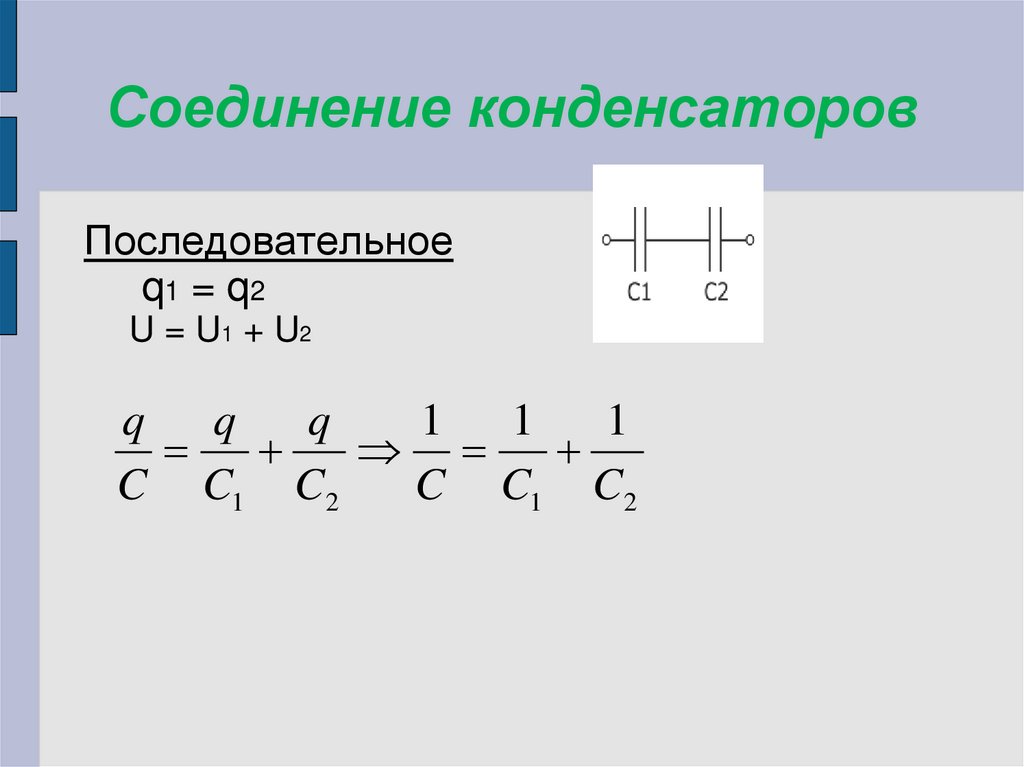
Последовательное соединение

Рассмотрим последовательное соединение конденсаторов. Для последовательного соединения можно указать, что падение потенциала на всей цепи равно сумме разностей потенциалов на обкладках всех конденсаторов, составляющих батарею:

При суммировании получим:

.

Рис. 6.2.

Тогда для каждого конденсатора:

тогда

Итак, при последовательном соединении конденсаторов величина, обратная эквивалентной емкости, равна сумме величин, обратных емкостям конденсаторов, составляющих батарею. Поэтому эквивалентная емкость меньше, чем наименьшая емкость, включенная в цепь.

Параллельное соединение

Рис. 6.3.

При таком соединении U=const, а . Тогда:

т. е. при параллельном соединении конденсаторов их емкости складываются.

6.3. Энергия и плотность энергии заряженного конденсатора

Рассмотрим заряженный конденсатор.

Обкладки конденсатора взаимодействуют, а внутри конденсатора происходит поляризация диэлектрика. При этом совершается работа, следовательно, можно говорить об энергии электростатического поля. Чтобы вычислить энергию поля найдем работу по зарядке конденсатора.

Рис. 6.4.

(6.5)

т. е. поле внутри конденсатора обладает энергией:

(6.6)

Такой же энергией обладает любое электростатическое поле. Если конденсатор плоский, то , тогда:

– объемная плотность энергии электростатического поля, тогда:

(6.8)

Для анизотропных диэлектриков:

.

Конденсаторы используются для накапливания энергии и выпрямления переменного и постоянного тока в электронных устройствах.

В России запатентовано устройство, которое представляет собой батарею конденсаторов, способное заменить аккумулятор в автомобилях. Выгода очевидна: конденсаторы не замерзают, в них не надо добавлять воду и т. д.

Тесты к лекции №6.

Тест 6.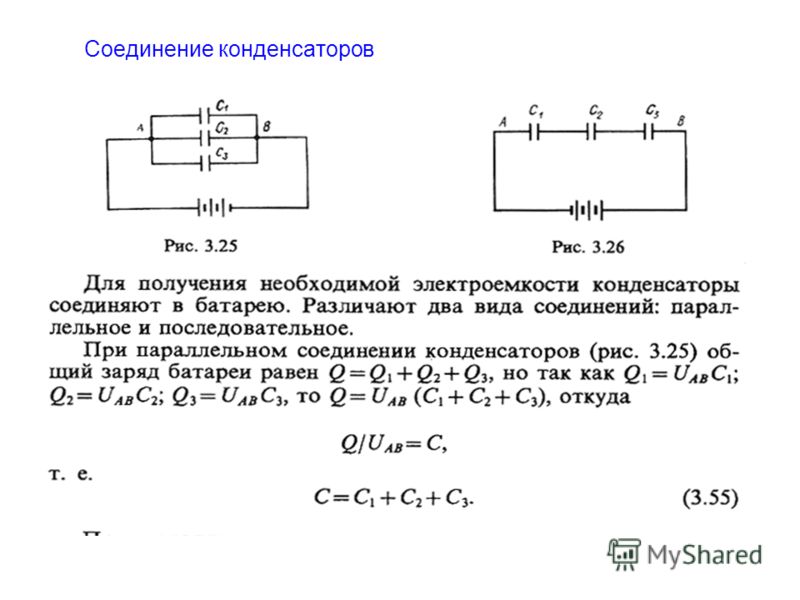 1. Имеется плоский конденсатор. От чего зависит его электроемкость?

£ площади обкладки.

£ величины зазора между обкладками.

£ диэлектрической проницаемости среды между обкладками.

£ толщины обкладок конденсатора.

£ покрытия конденсатора.

Тест 6.2. Формула емкости плоского конденсатора.

£

£

£

£

Тест 6.3. По форме конденсаторы бывают…

£ плоские;

£ сферические

£ кубические

£ цилиндрические

£ ромбические

£ нитевидные

Тест 6.4. Зависимость электроемкости плоского конденсатора от площади перекрытия обкладок определяется формулой:

£C~S

£

£

£

£

Тест 6.5. Физическая величина, численно равная заряду, при сообщении которого потенциал проводника повышается на единицу, называется:

£ диэлектрическая проницаемость;

£ дипольный момент

£ электроемкость.

£ Работа

£ Энергия

£ Плотность заряда

Тесты к главе №2.

Тест 1.Электростатическая индукция — это …

£ явление поляризации электростатическим полем.

£ выстраивание диполей вдоль приложенного поля.

£ разность потенциалов положительной и отрицательной обкладок.

£ возникновение электростатического поля.

Тест 2. Как называют вещество, в котором электрические заряды могут свободно перемещаться по всему его объему?

£ диэлектрик.

£ конденсатор.

£ проводник.

Тест 3. Диполь – это система, состоящая из…

£ Двух равных по модулю и соединенных вместе одноименных зарядов

£ Двух равных по модулю и разнесенных друг от друга разноименных зарядов

£ Двух равных по модулю и разнесенных друг от друга одноименных зарядов

£ Двух не равных по модулю и соединенных вместе разноименных зарядов

Тест.4. Верно ли утверждение, что заряды на обкладках конденсатора должны быть одинаковы по модулю и противоположны по знаку.

£ верно.

£ не верно.

£ верно, если конденсатор находиться в магнитном поле.

£ верно, если конденсатор находиться в электрическом поле.

Тест 5. Укажите выражение, определяющее энергию поля заряженного конденсатора.

£

£

£

£

Тест 6. Зависимость электроемкости плоского конденсатора от расстояния между его обкладками определяется формулой:

£

£

£

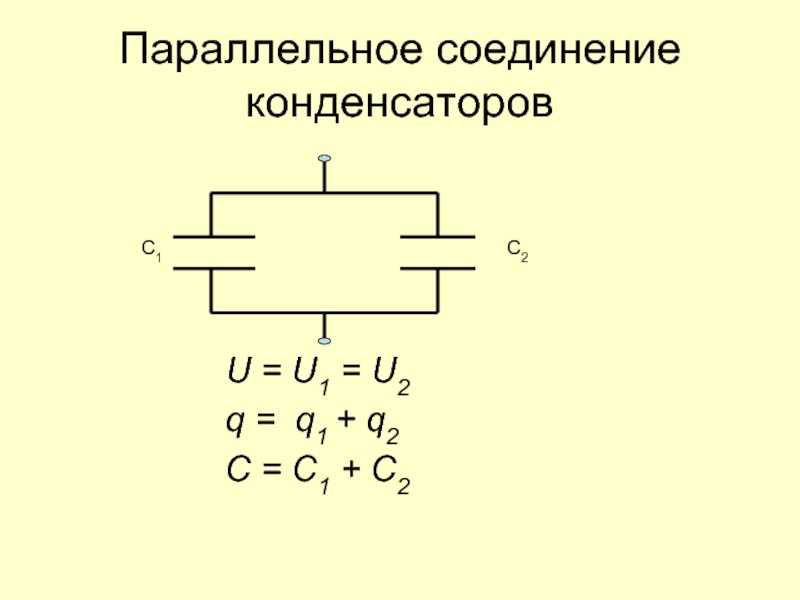
Соединение конденсаторов Параллельное соединение конденсаторов

1. При параллельном соединении конденсаторов к каждому кон­денсатору приложено одинаковое напряжениеU, а величина за­ряда на обкладках каждого конденсатора Q пропорциональна его емкости (рис. 2).

Рис.2 U=U₁=U₂=U₃

2. Общий заряд

   Q всех конденсаторов

3. Общая емкость С, или емкость батареи, параллельно включенных конденсаторов равна сумме емкостей этих конденсаторов.

Параллельное подключение конденсатора к группе других включенных конденсаторов увеличивает общую емкость батареи этих конденсаторов. Следовательно, параллельное соединение конденсаторов при­меняется для увеличения емкости.

4)Если параллельно включены т одинаковых конденсаторов ем­костью С´ каждый, то общая (эквивалентная) емкость батареи этих конденсаторов может быть определена выражением

Последовательное соединение конденсаторов

Рис.3

1. На обкладках последовательно соединенных конденсаторов, подключенных к источнику постоянного тока с напряжением U, появятся заряды одинаковые по величине с противоположными знаками.

Q=Q₁=Q₂=Q₃

2. Напряжение на конденсаторах распределяется обратно пропорционально емкостям конденса­торов:

3. Обратная величина общей емкости последовательно соединенных конденсаторов равна сумме обратных величин емкостей этих кон­денсаторов.

При последовательном включении двух конденсаторов их об­щая емкость определяется следующим выражением:

Если в цепь включены последовательно п одинаковых конден­саторов емкостью С каждый, то общая емкость этих конденса­торов:

Из (14) видно, что, чем больше конденсаторов п соединено последовательно, тем меньше будет их общая емкость С, т. е. по­следовательное включение конденсаторов приводит к уменьше­нию общей емкости батареи конденсаторов.

На практике может оказаться , что допустимое ра­бочее напряжение U_p конденсатора меньше напряжения, на кото­рое необходимо подключить конденсатор. Если этот конденсатор подключить на такое напряжение, то он выйдет из строя, так как будет пробит диэлектрик. Если же последовательно включить не­сколько конденсаторов, то напряжение распределится между ними и на каждом конденсаторе напряжение окажется мень­ше его допустимого рабочего U_p.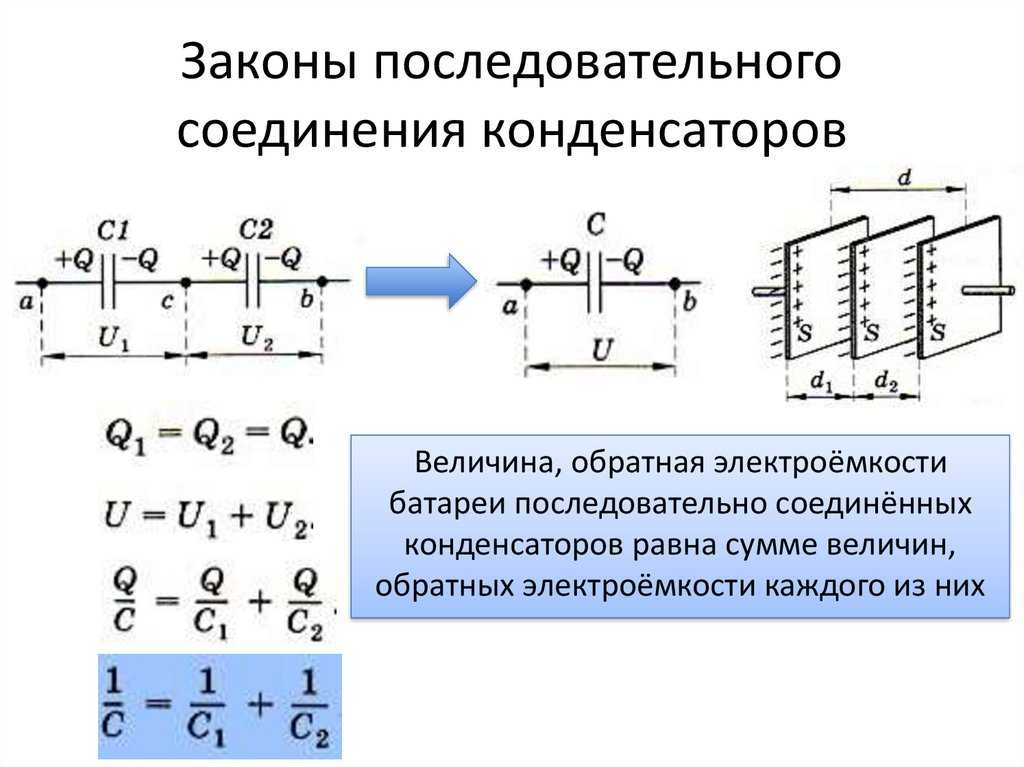 Следовательно, последовательное соединение конденсаторов применяют для того, чтобы напряжение на каждом конденсаторе не превышало его рабочего напряжения

U_p.

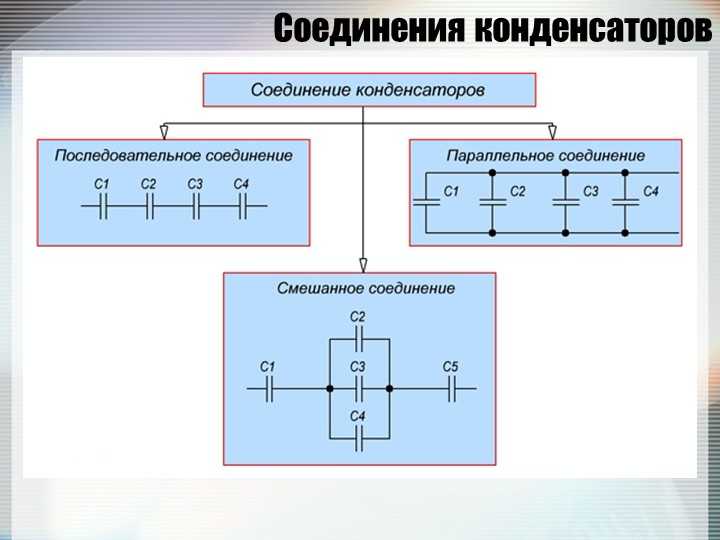
Смешанное соединение конденсаторов

Смешанное соединение (последовательно-параллельное) кон­денсаторов применяют тогда, когда необходимо увеличить ем­кость и рабочее напряжение батареи конденсаторов.

Рассмотрим смешанное соединение конденсаторов на ниже­приведенных примерах.

Энергия конденсаторов

где Q — заряд конденсатора или конденсаторов, к которым при­ложено напряжение U; С — электрическая емкость конденсатора или батареи соединенных конденсаторов, к которой приложено напряжение U.

Таким образом, конденсаторы служат для накопления и сохра­нения электрического поля и его энергии.

15.Дайте определение понятиям трех лучевая звезда и треугольник сопротивлений.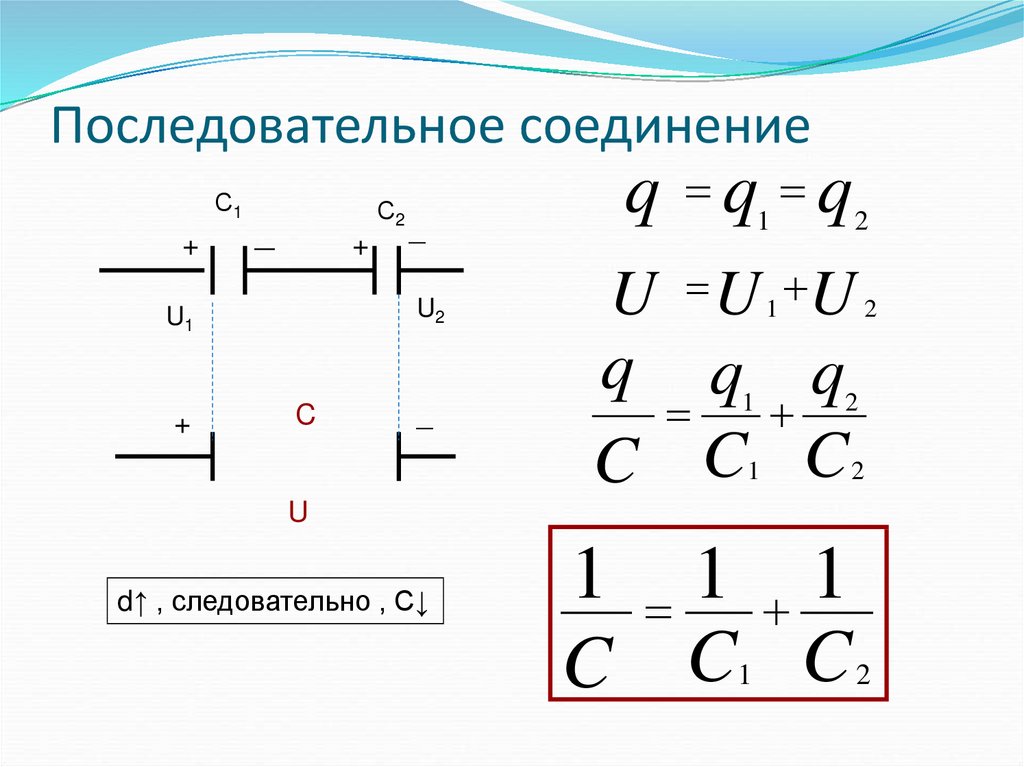 Запишите формулы для преобразования трех лучевой звезды сопротивлений в треугольник сопротивлений и наоборот. Преобразуйте схему к двум узлам (Рисунок 5)

Рисунок 5- Схема электрическая

6.СХЕМЫ ЗАМЕЩЕНИЯ

Для облегчения расчета составляется схема замещения электрической цепи, т. е. схема, отображающая свойства цепи при определенных условиях.

На схеме замещения изображают все элементы, влиянием которых на результат расчета нельзя пренебречь, и указывают также электрические соединения между ними, которые имеются в цепи.

1.Схемы замещения элементов электрических цепей

На расчетных схемах источник энергии можно представить ЭДС без внутреннего сопротивления, если это сопротивление мало по сравнению с сопротивлением приемника (рис. 3.13,6).

Приr= 0 внутреннее падение напряженияUо = 0, поэтому

напряжение на зажимах источника при любом токе равно

ЭДС: U=E=const.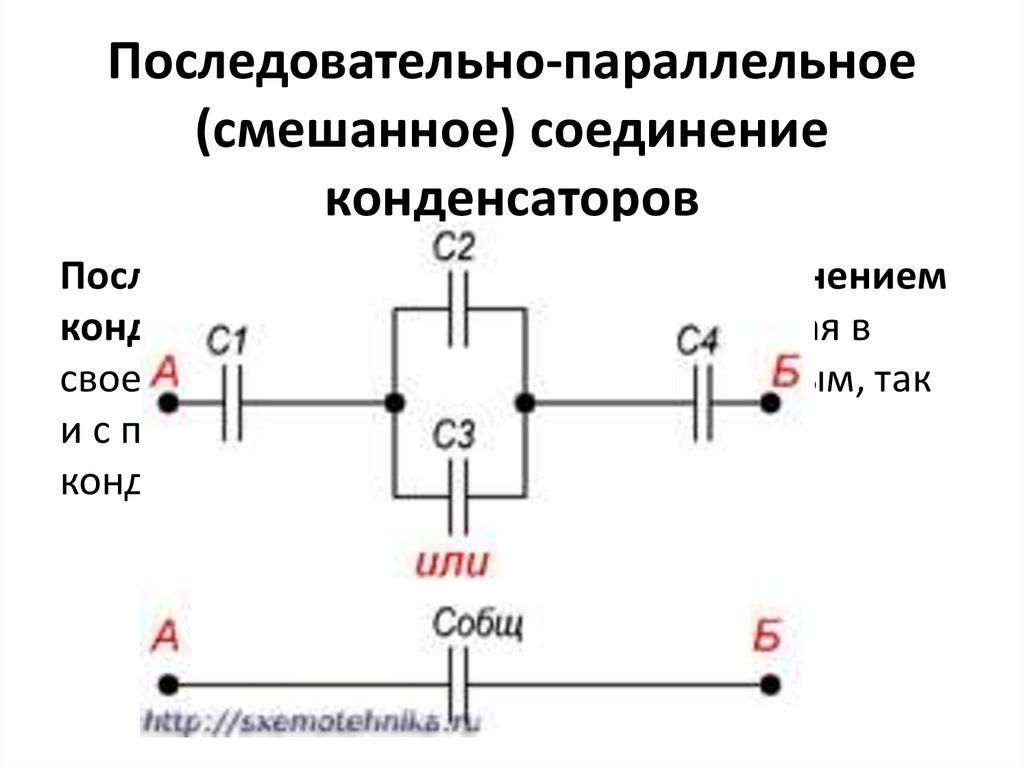

В некоторых случаях источник электрической энергии на расчетной схеме заменяют другой (эквивалентной) схемой (рис. 3.14, а), где вместо ЭДСЕ источник характеризуется его током короткого замыканияI_K, а вместо внутреннего со­противления в расчет вводится внутренняя проводимостьg=1/r.

Возможность такой замены можно доказать, разделив равенство (3.1) на r:

U/r = E/r—I,

где U/r = Io—некоторый ток, равный отношению напряжения на зажимах источника к внутреннему сопротивлению;E/r = I_K — ток короткого замыкания источника;

Вводя новые обозначения, получим равенство I_K = Io + I, которому удовлетворяет эквивалентная схема рис. 3.14,а.

В этом случае при любой величине напряжения на зажимах; источника его ток остается равным току короткого замыкания (рис. 3.14,6):

I=I_к=const.

Источник с неизменным током, не зависящим от внешнего сопротивления, называют источником тока.

Один и тот же источник электрической энергии может быть заменен в расчетной схеме источником ЭДС или источником тока.

Емкость

— Почему заряд постоянен при последовательном соединении?

спросил 7 лет, 3 месяца назад

Изменено 5 лет, 8 месяцев назад

Просмотрено 3к раз

$\begingroup$

Почему каждый конденсатор при последовательном соединении имеет одинаковый заряд? Я понимаю, что напряжения и емкости на последовательно соединенных парах пластин конденсаторов различаются, но почему необходимо, чтобы заряд был постоянным?

• заряд
• емкость

$\endgroup$

$\begingroup$

Представьте себе два последовательно соединенных конденсатора.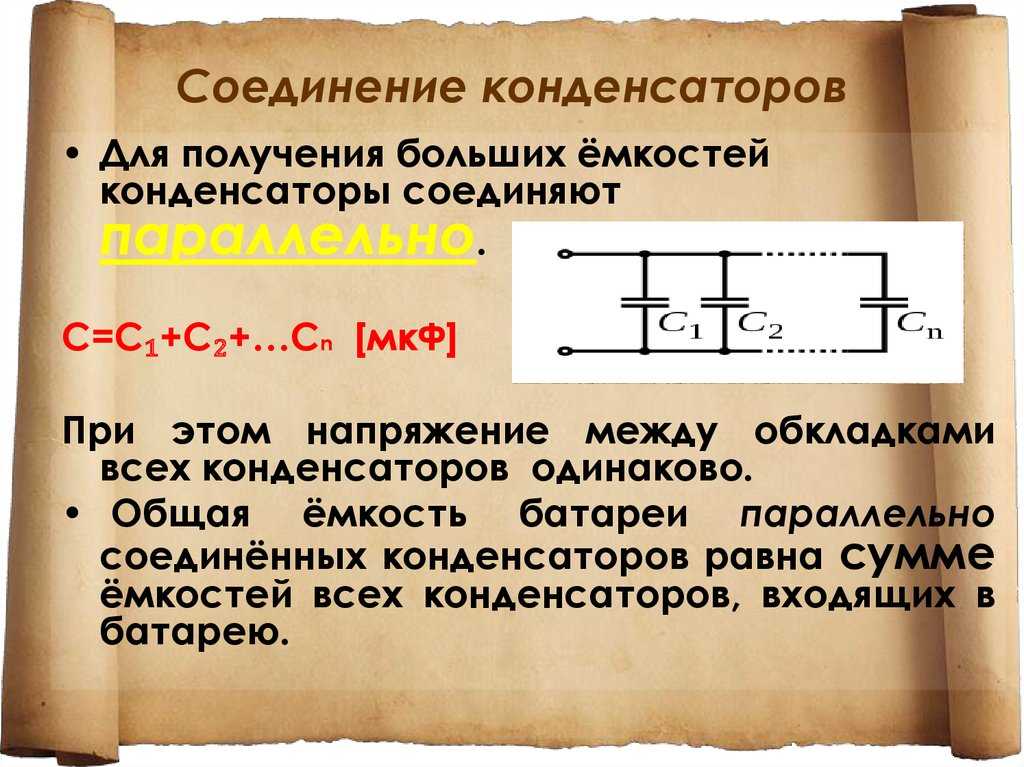

• Если электроны напр. переместитесь на левую пластину конденсатора $C_2$, эта пластина приобретет некоторый отрицательный суммарный заряд, назовем его $-Q$.

• Отрицательный заряд на левой пластине отталкивает одноименный заряд на правой пластине (электроны отталкиваются от правой пластины и отталкиваются вправо). Таким образом, эта правая тарелка $C_2$ получает сеть положительный заряд на ту же сумму, $+Q$.

• Электроны (количество отрицательных зарядов $-Q$) «отталкиваются» как можно дальше вправо; то есть на левую пластину $C_1$. Таким образом, эта пластина получает чистый отрицательный заряд в размере $-Q$.

• Как и раньше, теперь на правой пластине $C_1$ индуцируется суммарный заряд $+Q$.

Это должно быть сбалансировано таким образом. Если одна пластина конденсатора имеет другую величину заряда, чем другая, то больше/меньше заряда будет отталкиваться, а равновесие еще не достигнуто. Только равные (но противоположные по знаку) заряды на противоположных пластинах будут в равновесии.

А с правой пластины $C_2$ на левую пластину $C_1$ отталкиваемые электроны, отсутствие которых вызывает заряд $+Q$ на правой пластине $C_2$, сами перемещаются на левую пластину $C_1 $, которые для этого обязательно должны получить такую ​​же сумму заряда, но с противоположным знаком.

$\endgroup$

$\begingroup$

Этот сайт Техасского университета, я думаю, дает хорошее объяснение.

В основном, когда у вас есть два конденсатора, соединенных последовательно, скажем, $C_1$ и $C_2$, тогда общий заряд в средней проводке, соединяющей два компонента, должен оставаться постоянным, так как он не может никуда уйти.

Любое накопление заряда на внешней пластине $C_1$ создает накопление виртуального заряда на его внутренней пластине, но общий заряд в средней проводке должен оставаться постоянным, поэтому в точке $ будет создаваться равный, но противоположный виртуальный заряд. Внутренняя пластина C_2$. Виртуальный заряд на $C_2$ вызовет накопление фактического заряда на его внешней пластине, поэтому общий заряд на $C_1$ будет равен общему заряду на $C_2$.

Вы можете думать об этом как о граничном условии между конденсаторами, в некотором смысле заставляющем колебания заряда распространяться по структуре.

$\endgroup$

$\begingroup$

Потому что любой избыток заряда на одном конденсаторе может исходить только от другого конденсатора. Следовательно, ни один из них не может приобрести или потерять заряд без того, чтобы другой не изменился точно на ту же величину.

$\endgroup$

Зарегистрируйтесь или войдите

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

домашнее задание и упражнения — Постоянная времени цепи — конденсаторы параллельно или последовательно?

спросил 5 лет, 6 месяцев назад

Изменено 5 лет, 6 месяцев назад

Просмотрено 4к раз

$\begingroup$

Когда я заряжаю цепь, как показано, где переключатель находится в положении A, p.d. на C1 10 В, что правильно.

Однако, когда я разряжаю цепь, меняя переключатель S с A на B, общая емкость цепи составляет 200 мкФ, так как C1 и C2 включены параллельно.

Это должно означать, что постоянная времени цепи разряда равна 93 = 20s$$

Однако в решении постоянная времени цепи разряда указана как 5 секунд, где указано, что C1 и C2 соединены последовательно, когда переключатель находится в положении B.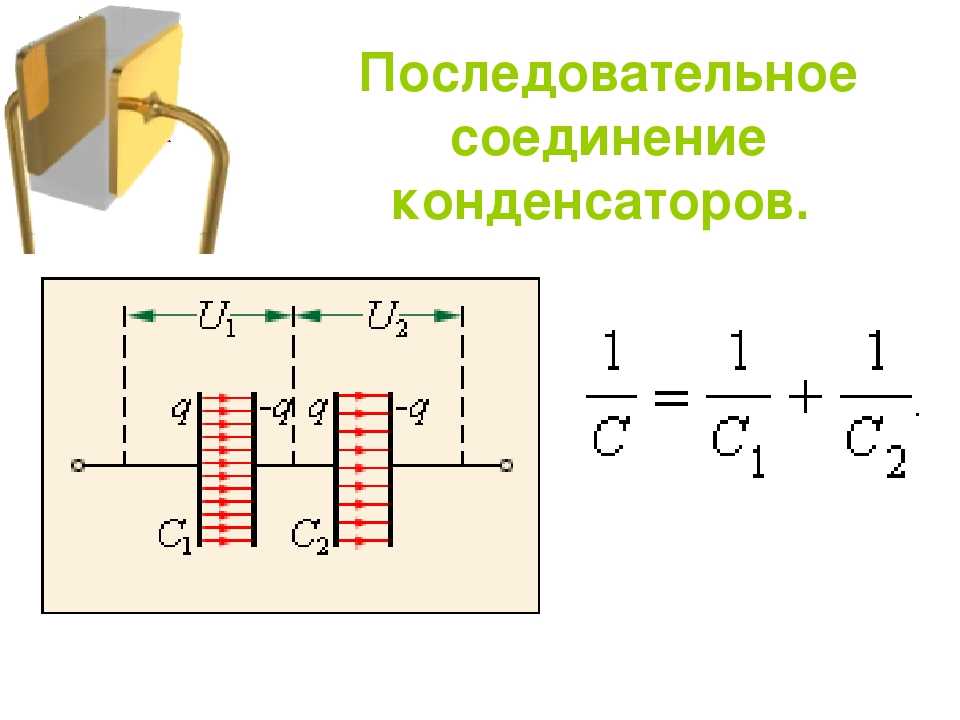

Кто прав, решения или я?

• домашние задания и упражнения
• электрические цепи
• электрические сопротивления
• емкости

$\endgroup$

9

$\begingroup$

общая емкость цепи составляет 200 мкФ, так как C1 и C2 находятся в параллельно.

Они не параллельны ни для одного из положений переключателя.

Когда переключатель находится в положении A, C2 и резистор 100 кОм соединены последовательно, но один конец резистора «болтается», поэтому ток через последовательную комбинацию не проходит.

Когда переключатель находится в положении B, C1 помещается в серию с комбинацией C2 + серия 100k RC. Это должно быть очевидно, так как есть только один путь для тока, все три элемента схемы имеют одинаковый ток .