Как выбрать оптимальные полевые транзисторы для синхронных выпрямителей
16 июня 2017
автомобильная электроникауправление питаниемпотребительская электроникаавтоматизацияответственные применениялабораторные приборыInfineonстатьядискретные полупроводникиMOSFET
Применение синхронных выпрямителей – лучший способ снижения потерь во вторичных цепях преобразователей энергии. А полевые транзисторы из линейки OptiMOS™ производства Infineon с напряжением 30…150 В отлично подходят для этой цели.
Постоянное ужесточение требований к удельной мощности и энергосбережению преобразователей электрической энергии требует увеличения эффективности всех ступеней преобразования. Основным видом потерь во вторичных цепях преобразователей с гальванической развязкой являются потери проводимости выпрямительных диодов, которые можно уменьшить, используя синхронное выпрямление (рисунок 1).
Замена диодов полевыми транзисторами (MOSFET) приводит к появлению новых задач – оптимизации эффективности системы и предотвращению выбросов перенапряжения.
Принципы синхронного выпрямления
Для правильного выбора транзисторов синхронного выпрямителя необходимо четкое понимание механизма возникновения потерь. В первую очередь необходимо различать потери проводимости (статические потери), зависящие от тока нагрузки, и потери переключения (динамические потери). Потери проводимости напрямую зависят от сопротивления транзисторов в открытом состоянии RDS(on) и падения напряжения на внутренних диодах VSD. Причем увеличение тока нагрузки приводит к увеличению потерь проводимости. Для предотвращения одновременного включения транзисторов синхронного выпрямителя, приводящего к токовым перегрузкам транзисторов, необходимо наличие некоторого времени задержки, при котором один транзистор должен быть гарантированно закрыт перед открытием другого. Именно в этот промежуток времени ток протекает через внутренний диод, и в нем возникают дополнительные потери.
Рис. 1. Схемы диодного и синхронного выпрямителей
Динамические потери MOSFET также вносят большой вклад в общую картину. Они зависят от частоты коммутации fSW и выходного тока преобразователя IOUT. Для включения транзистора емкость затвора необходимо зарядить до величины Qg, а напряжение на затворе должно достигнуть порога переключения. Для выключения MOSFET емкость «затвор-исток» должна быть разряжена, что означает рассеивание заряда Qg на сопротивлении затвора и внутреннем сопротивлении драйвера. При существующей технологии производства потери управления для транзисторов с малым сопротивлением канала – больше, чем для высокоомных, поскольку увеличение размера кристалла приводит к увеличению заряда затвора Qg.
Другая важная часть динамических потерь связана с наличием выходной емкости Coss и зарядом обратного восстановления Qrr.
В первом приближении зарядом обратного восстановления Qrr для транзисторов серии OptiMOS™ можно пренебречь, поскольку его вклад в общие потери мощности незначителен. В нашем случае зарядом Qrr считается только заряд восстановления внутреннего диода MOSFET, в то время как величина заряда Qrr, которая указывается в документации, измеряется в соответствии со стандартами JEDEC, и поэтому содержит не только заряд восстановления внутреннего диода, но и некоторые составляющие выходного заряда транзистора. К тому же, при синхронном выпрямлении реальные значения заряда обратного восстановления диода Qrr – меньше значений, указанных в документации. В ней приводятся значения для максимально допустимого тока стока транзистора при условии, что диод находился в проводящем состоянии длительное время, более 500 мкс, и при ограниченной скорости изменения тока di/dt на уровне 100 А/мкс. В реальном устройстве токи транзистора обычно не превышают трети максимально допустимого тока стока, внутренний диод находится в проводящем состоянии 20…100 нс, а скорость изменения тока di/dt достигает 800 А/мкс.
Оптимизация выбора транзисторов синхронного выпрямителя
Оптимальный выбор транзисторов синхронного выпрямителя, направленный на максимальную эффективность, заключается в поиске сбалансированного соотношения потерь проводимости и переключения. При малом токе нагрузки потери проводимости играют второстепенную роль. В этом случае потери переключения, которые приблизительно постоянны во всем диапазоне нагрузок, являются доминирующими. При большом токе нагрузки потери проводимости максимальны и поэтому вносят наибольший вклад в общие потери мощности (рисунок 2).
Рис. 2. Зависимость потерь мощности от выходного тока
При выборе транзисторов особое внимание необходимо уделить выбору сопротивления в проводящем состоянии RDS(on). В качестве примера рассмотрим семейство транзисторов 60 В OptiMOS™, работающих при условиях, приведенных на рисунке 3. На нем видно, что отклонение сопротивления RDS(on) от точки оптимального выбора приводит к увеличению общих потерь пропорционально увеличению RDS(on).
Рис. 3. Зависимость потерь мощности от сопротивления RDS(on)
В любом случае необходимо помнить, что график на рисунке 3 был построен для конкретных условий, и ситуация может существенно поменяться при изменении частоты преобразования (рисунок 4в, г) или тока, протекающего через транзисторы (рисунок 4а, б).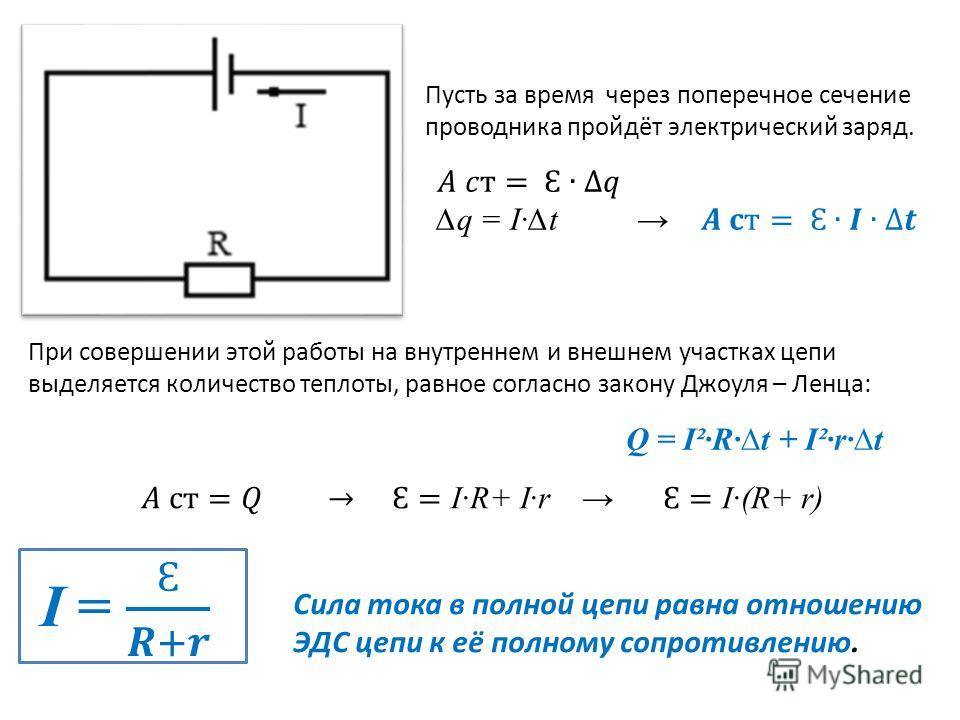
Если взять в качестве примера рисунок 4а, где ток транзистора уменьшен до 5 А, а частота преобразования осталась 175 кГц, потери переключения теперь составляют значительную часть общих потерь и оптимальным является использование транзистора BSC039N06NS. В другом случае частота преобразования уменьшена до 100 кГц при сохранении тока транзистора на уровне 15 А (рисунок 4в). В этом случае оптимальным решением является выбор транзистора BSC016N06NS, при использовании которого обеспечивается минимальный уровень потерь.
Рис. 4. Зависимость потерь мощности от сопротивления RDS(on) при различных значениях частоты преобразования fsw и тока транзистора IMosfet
Еще одной важной проблемой оптимизации синхронных выпрямителей является правильный выбор корпуса транзистора. Действительно, повысить эффективность выпрямителя можно простым путем замены корпуса ТО-220 на SuperSO8. Причиной этого является уменьшение доли сопротивления корпуса в величине RDS(on).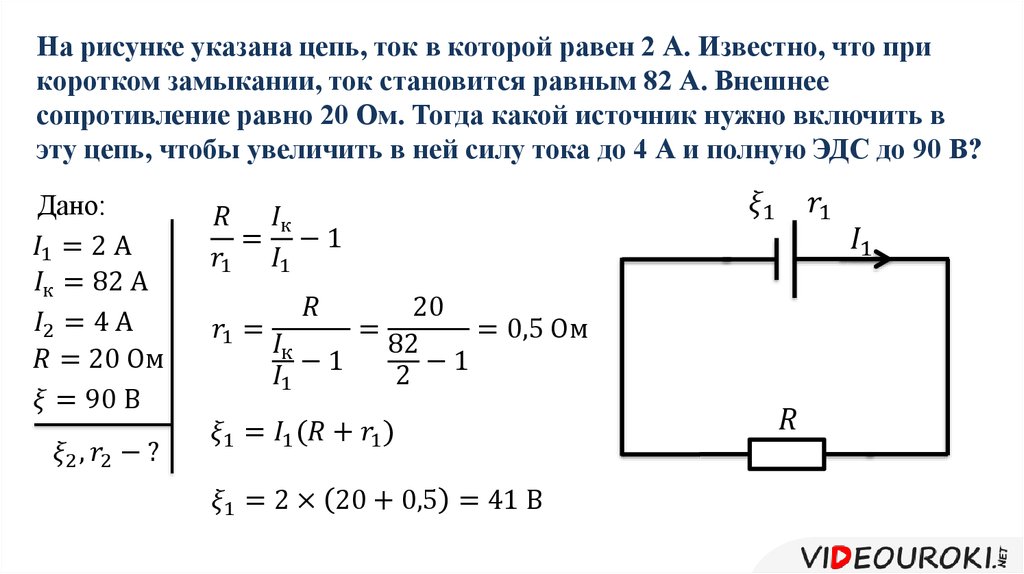
При каком токе необходимо оптимизировать транзисторы?
Чтобы получить высокое значение КПД синхронного выпрямителя во всем диапазоне токов нагрузки необходимо правильно выбрать ток MOSFET, воспользовавшись четырехквадрантными оптимизирующими зависимостями. Оптимизация, выполненная для максимальной нагрузки, даст высокое значение КПД при больших выходных токах. Однако в этом случае при небольшой нагрузке выпрямителя значение КПД резко уменьшится, а количество параллельно соединенных транзисторов окажется недопустимо большим. Поэтому необходимо выбрать такое значение тока транзистора, при котором КПД будет иметь относительно постоянное значение во всем диапазоне токов.
Для иллюстрации этой проблемы на рисунке 5 показаны зависимости КПД синхронного выпрямителя с выходным напряжением Vout = 12 В, напряжением вторичной обмотки трансформатора 24 В, напряжением затвора 10 В и частотой преобразования 200 кГц, рассчитанные для различных вариантов оптимизации. Если обратиться к оптимизирующим зависимостям (о методике их использования будет рассказано далее) для 40 В OptiMos BSC010N04LS (рисунок 8), то при оговоренном выше режиме работы (VT = 24 В, f = 200 кГц) и токе 20 А оптимальным будет применение одного транзистора. В этом случае, в соответствии с рисунком 5, максимум КПД будет располагаться в области небольших токов нагрузки. В случае оптимизации при токе транзистора 40 А оптимальным будет применение двух транзисторов. В этом случае максимум КПД сместится в область больших токов нагрузки. Обычно сбалансированное значение КПД достигается, если оптимизация выполняется при 20…30% от максимальной мощности выпрямителя. Если выпрямитель большую часть времени функционирует при небольших нагрузках – имеет смысл уменьшить ток, при котором выполняется оптимизация, до величины 10…20% от максимального выходного тока.
Если же нагрузка такова, что большую часть времени выпрямитель работает при уровне мощности более половины от максимального, оптимизацию необходимо выполнять для тока значением до 60% от максимального выходного тока. Оптимизации для 100% нагрузки следует избегать, поскольку в этом случае с уменьшением нагрузки КПД выпрямителя существенно уменьшается, а количество параллельно соединенных транзисторов значительно возрастает.
Рис. 5. Зависимость КПД от тока нагрузки при различных значениях тока оптимизации
Выбор полевых транзисторов по четырехквадрантным оптимизирующим зависимостям для синхронного выпрямления
Для выбора транзисторов предлагаются оптимизирующие зависимости, которые позволяют легко отыскать наиболее подходящий полевой транзистор для синхронного выпрямителя с использованием всего трех параметров: напряжения вторичной обмотки трансформатора, частоты преобразования и среднего значения тока транзистора. Пример выбора транзистора показан на рисунке 6.
Рис.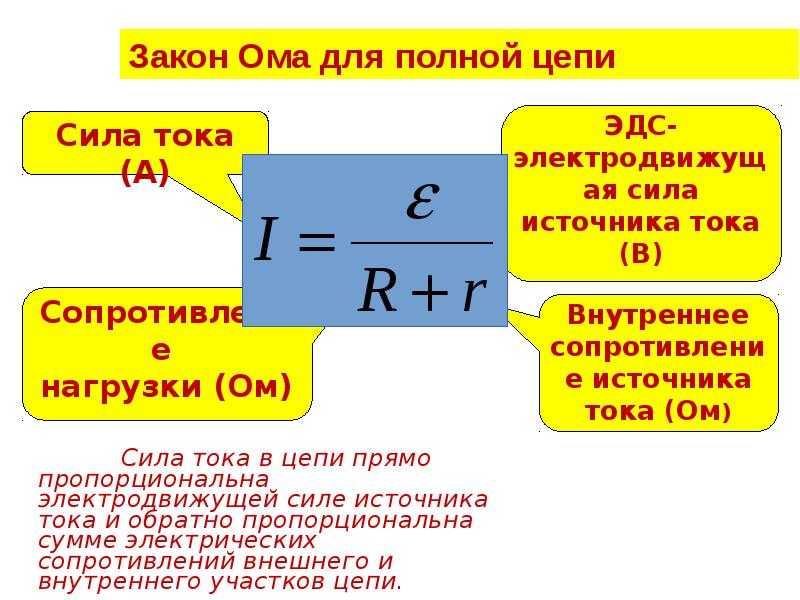
6. Выбор транзистора по оптимизирующим зависимостям
На первом этапе необходимо выбрать один из транзисторов, присутствующих на графиках. Из точки на оси Х, которая соответствует напряжению вторичной обмотки трансформатора, проводят вертикальную линию вниз до пересечения с линией, соответствующей выбранному транзистору. Из этой точки проводят горизонтальную линию влево до точки пересечения с линией, соответствующей частоте преобразования. После этого проводят вертикальную линию вверх до пересечения с линией, соответствующей выбранному току транзистора. Далее из этой точки проводят горизонтальную линию вправо до пересечения с вертикальной линией, соответствующей выбранному транзистору, по которой можно определить оптимальное число параллельно соединенных транзисторов.
Хорошим соотношением будет уровень тока в 20…30% от полной нагрузки. Оптимальным значением RDS(on) для данного случая будет точка пересечения с положительной частью оси Y. Данную процедуру можно выполнить для разных моделей транзисторов.
Наименьшие потери, а следовательно, и максимальное значение КПД выпрямителя будут при использовании тех транзисторов, для которых эквивалентное сопротивление RDS(on) будет наименьшим.
Данная методика рассчитана на работу транзисторов выпрямителя в режиме оптимального переключения. В любом другом случае, например, в случае динамического включения или лавинного пробоя, приведенные зависимости будут неточными. Наилучшие результаты были получены для топологий с жесткой коммутацией. Использование данной методики для резонансных схем с режимами мягкой коммутации приведет к большим расхождениям, поскольку в данном случае динамические потери будут ниже нуля. В этом случае оптимальное значение сопротивления RDS(on) будет меньше расчетного. Обратите внимание на то, что даже при работе первичной стороны в квазирезонансном режиме, например, при использовании мостового инвертора Phase Shift ZVS, синхронный выпрямитель может работать в режиме жесткого переключения и может быть оптимизирован с использованием приведенных зависимостей.
Все оптимизирующие зависимости, приведенные в данной статье (рисунки 7…14), были построены для идеализированных полевых транзисторов. На практике результаты расчетов по идеализированным зависимостям могут отличаться от реального значения потерь. Поэтому полученные результаты необходимо рассматривать не более чем как индикатор наилучшего возможного случая или предупреждение о выборе недостаточного или избыточного количества транзисторов. Если оптимальное количество параллельно соединенных транзисторов, полученное по графикам, находится между двумя значениями, следует помнить, что выбор меньшего количества транзисторов увеличит КПД выпрямителя при меньших токах нагрузки, а большего – при больших. Кроме того, необходимо учитывать наличие снабберных цепей, включенных параллельно транзисторам, которые также могут влиять на выбор транзисторов.
Оптимизация во всем диапазоне токов нагрузки не может быть выполнена с помощью расчета при одном значении выходного тока. Для этого необходимо выполнить несколько тестовых расчетов при различных токах нагрузки, и, анализируя полученные результаты, осуществить выбор модели и количества транзисторов в соответствии с требованиями, предъявляемыми к выпрямителю.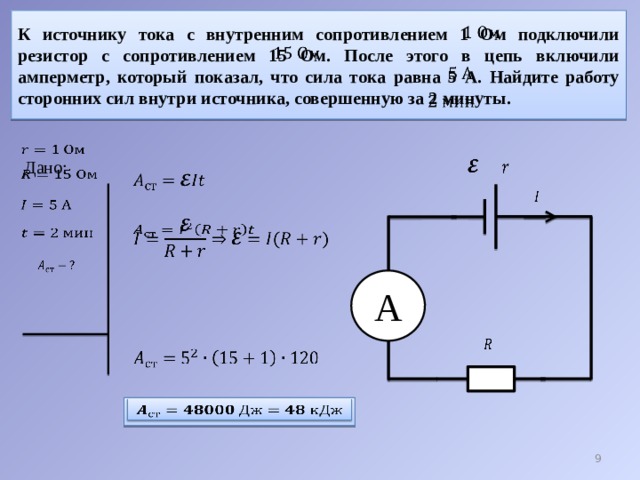
Рис. 7. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 30 В | Рис. 8. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 40 В |
Рис. 9. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 60 В | Рис. 10. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 75 В |
Рис. 11. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 80 В | Рис. 12. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 100 В |
Рис. 13. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 120 В | Рис. 14. Выбор транзистора по оптимизирующим зависимостям OptiMOS™ 150 В |
•••
[PDF] Электрический конденсатор Лабораторная работа № 10 .
Лабораторная работа № 10
Электрический конденсатор . Цель работы: исследование зависимости заряда конденсатора от разности потенциалов между пластинами.
Расчет емкости конденсатора. Изучение процесса зарядки конденсатора. Проверка работы батареи конденсаторов параллельного и последовательного соединения, расчет емкости батарей. Оборудование: два конденсатора С ~ 10-50 мкФ, резистор R ~ 10кОм Порядок выполнения работы: 1. В начале работы соберите представленную на рисунке схему. На этой схеме U обозначена клемма питания на устройстве сопряжения. V1 и V2 – служат для измерения тока и напряжения в цепи. 2. В работе напряжение, подаваемое компьютером на конденсатор, будет меняться с течением времени. Компьютером измеряется напряжение на конденсаторе и ток в цепи, и строятся соответствующие графики. Измерение заряда конденсатора производится косвенно. Заряд равен произведению силы тока на время протекания заряда по проводнику. Q = I T Объясните, в каком случае допустимо рассчитывать заряд таким образом. Далее на экране появится график зависимости заряда на конденсаторе от поданного на него напряжения. 3. Повторите предыдущий эксперимент с конденсатором другой емкости.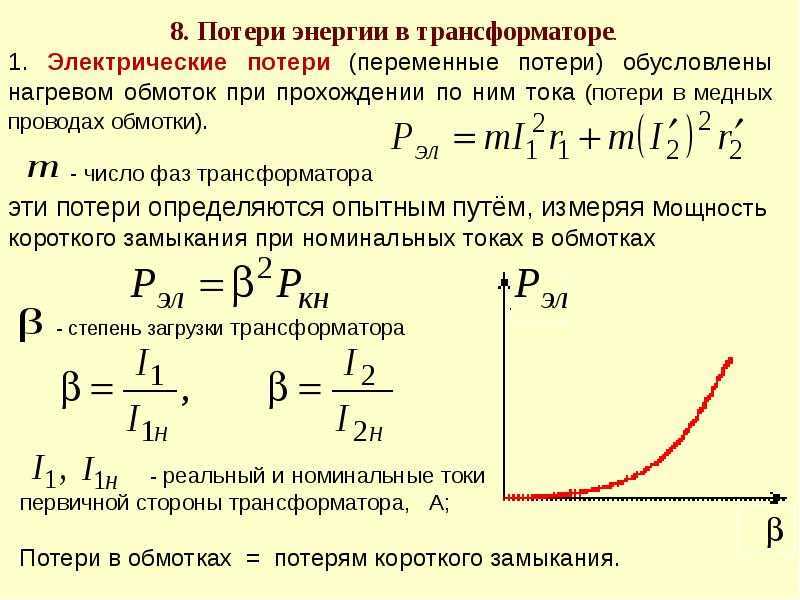
4. Соберите батарею из двух последовательно соединенных конденсаторов. Повторите первый эксперимент. 5. Соберите батарею из двух параллельно соединенных конденсаторов. Повторите первый эксперимент. 6. На полученных графиках с помощью подвижного курсора определите значения емкостей использованных конденсаторов. 7. В последнем эксперименте на конденсатор будет подана постоянная разность потенциалов и измерена сила тока в цепи при зарядке конденсатора. На экране появится график зависимости тока зарядки от времени. 8. Рассчитайте погрешность измерения емкости. Дополнительные вопросы: 1. Зачем на конденсатор в первом эксперименте подается возрастающее напряжение? 2. Сравните те емкости (с погрешностями!), которые Вы использовали в эксперименте, с теми, которые были измерены компьютером. 3. Почему в последнем эксперименте ток спадает со временем? Если можете, напишите дифференциальное уравнение, описывающее этот процесс.
Лабораторная работа №11
Движение заряженной частицы в однородном магнитном поле . Цель работы: определить скорость движения электрона, угол вылета и удельный заряд электрона. Оборудование: водородная лампа с электронной пушкой, вольтметр, амперметр, линейка Порядок выполнения работы: 1. Изучите схему, представленную на рисунке. 2. Для прогрева схема требует 5 минут. После, регулируя рукоятками «Фокус» и «Анод», добейтесь замыкания луча в кольцо. Траектория движения электронов в нижней точке кольца должна быть наиболее узкой. 3. Измерьте диаметр кольца, анодное напряжение и ток в катушках. Полученные данные представьте в виде таблицы. Проделайте серию экспериментов не менее 8 раз при различных значениях тока и напряжения. Придумайте наилучший, по вашему мнению, способ измерения диаметра кольца. e Кл м V( ) I(A) U(B) R(м) B(Тл) m кг с
4. Поверните трубку нежно на небольшой угол. Добейтесь наименьшего радиуса траектории электронов и наибольшей ее четкости. Для определения угла между скоростью электронов и вектором магнитной индукции проведите измерения анодного напряжения, тока в катушках, диаметра кольца и шага винта траектории. Полученные значения представьте в виде таблицы. м V( ) I(A) U(B) R(м) H(м) B(Тл) cos с 5. Рассчитайте погрешности. Сравните усредненное значение
e m
с табличным
значением. 6. Дайте теоретическое обоснование формулам (1), (2) и (3), используемым в работе.
0,71 0 nI , где 0 — магнитная постоянная, n – число витков в катушках (n=245), r r – радиус катушек (r=12,5 0,5 см)
B
e 2U 2 2 m R B eRB V m cos( )
HBe 2mV
(1) (2) (3)
Дополнительные вопросы: Объясните причину размытости кольца, наблюдаемого в эксперименте. Предложите способ получения пучка электронов с близкими по величине скоростями («монокинетичный пучок»).
Лабораторная работа №12
Исследование полной однородной цепи постоянного тока . Цель работы: исследовать вольтамперную характеристику полной цепи постоянного тока, определить ЭДС источника, внутреннее сопротивление и ток короткого замыкания. Оборудование: вольтметр, амперметр, источник постоянного напряжения, реостат (Rn~1000 Ом), резистор r ~1000 Ом Порядок выполнения работы: 1. Соберите схему, представленную на рисунке. 2. Подаваемое напряжение не должно превышать 40В. 3. Снимите вольтамперную характеристику нагрузки (сделайте не менее 10 измерений при различных положениях ползунка реостата). 4. Постройте график ВАХ. Добавить линейную интерполяцию (коэффициент достоверности должен быть не менее 0.95, иначе эксперимент необходимо переделать). 5. Определите по графику значения ЭДС и тока короткого замыкания. 6. Рассчитайте внутреннее сопротивление источника. Дополнительные вопросы: Что означает тангенс угла наклона графика U(I). Какой угол содержит информацию о текущем значении сопротивления реостата?
Лабораторная работа № 13
Мощность и КПД полной цепи постоянного тока. Цель работы: Исследовать реальную электрическую цепь, определить мощность и КПД цепи. Оборудование: резистор r ~ 400Ом, Rmax ~ 1 кОм
Порядок выполнения работы: 1. В начале работы соберите представленную на рисунке схему. На этой схеме U обозначена клемма питания на устройстве сопряжения. V1 и V2 – служат для измерения тока и напряжения в цепи. 2. Изменяя сопротивление нагрузки (для этого надо двигать ползунок реостата), получите зависимость силы тока в цепи и напряжения на нагрузке. Измерение проводить не менее 10 секунд. 3. Получите графики зависимости мощности и КПД цепи. 4. Рассчитайте погрешности. Дополнительные вопросы: Объясните вид полученных в работе графиков, напишите формулы зависимости измеренных величин от сопротивления нагрузки R. При каком значении сопротивления нагрузки выделяется наибольшая мощность? Чему при этом сопротивлении равен КПД цепи? В каких электрических цепях выгодно получать наибольший КПД, а в каких – наибольшую выделяемую мощность?
Лабораторная работа № 14
Зависимость сопротивления от температуры. Цель работы: Исследовать зависимость сопротивления металлов, электролитов и полупроводников от температуры. Работа может быть выполнена целиком или по частям. Оборудование: резистор Rэт ~ 400 Ом, сменный блок, в котором может быть установлен исследуемый объект (терморезистор, ванночка с электролитом или колодка с полупроводником). Порядок выполнения работы: 1. В начале работы соберите представленную на рисунке схему. На этой схеме U обозначена клемма питания на устройстве сопряжения. V1 и V2 – служат для измерения тока и напряжения в цепи. 2. Поместите термометр в термостат с исследуемым терморезистором. Запишите погрешность прибора. Сам термостат поместите в сосуд с водой, нагреваемой с помощью электроплитки. Проведите 5-8 измерений при разных значениях температуры. В результате на экране появится график зависимости сопротивления проводника от температуры. С помощью подвижного курсора определите значения температуры и сопротивления, необходимые для расчета температурного коэффициента сопротивления данного металла. Введите расчетную формулу. 3. Повторите эксперимент, поместив в сменный блок ванночку с электролитом. 4. Повторите эксперимент, поместив в сменный блок колодку с полупроводником. 5. Рассчитайте погрешности. Дополнительные вопросы: Как в данном эксперименте измерено сопротивление проводника? Почему графики зависимости сопротивления проводника от температуры выглядят по-разному в 1, 2 и 3 экспериментах?
Лабораторная работа №1 5
Изучение явления самоиндукции. Цель работы: исследовать особенности явления самоиндукции, измерить индуктивность катушки и ЭДС самоиндукции. Оборудование: катушка 3600 витков RL 50 Ом, резистор R0~50 150 Ом Порядок выполнения работы: 1. Соберите схему, представленную на рисунке. 2. От компьютера в схему подается линейно возрастающее напряжение, поэтому ток в цепи также растет, причем параметры схемы подобраны таким образом, что зависимость I(t) практически линейна. При изменении силы тока в катушке возникает ЭДС самоиндукции, в данных условиях эксперимента практически постоянная. 3. В первой части работы по графикам I(t) и U(t), пользуясь подвижным курсором, измерьте ЭДС самоиндукции, и значения тока в разные моменты времени. Рассчитайте значение индуктивности катушки L. 4. Во второй части эксперимента будет повторен первый эксперимент с увеличенным в два раза полным сопротивлением цепи. Для этого надо изменить R0 так, чтобы соблюдалось равенство R02= 2*R01+RL ( ). 5. Третий эксперимент предлагается провести аналогично предыдущим, но время нарастания тока автоматически будет уменьшено вдвое. 6. Во всех трех заданиях необходимо записывать значения токов и времени. 7. В каждом из экспериментов рассчитайте индуктивность катушки с погрешностью. Дополнительные вопросы: Выведите равенство ( ). Объясните, как были измерены значения силы тока и ЭДС самоиндукции. Объясните, как изменялись графики I(t) и U(t), при изменении условий эксперимента, и как при этом менялось значение ЭДС самоиндукции.
Теорема о максимальной передаче мощности (MPTT)
В этом уроке мы узнаем о теореме о максимальной передаче мощности (MPTT). Это один из основных, но важных законов, определяющий необходимое условие максимальной передачи мощности (не путать с максимальной эффективностью).
Краткое описание
Введение
В любой электрической цепи электрическая энергия от источника питания передается на нагрузку, где она преобразуется в полезную работу. Практически вся подаваемая мощность не будет присутствовать на нагрузке из-за эффекта нагрева и других ограничений в сети. Следовательно, существует определенная разница между притягивающей и доставляющей силами.
Величина нагрузки всегда влияет на количество мощности, передаваемой от источника питания, т. е. любое изменение сопротивления нагрузки приводит к изменению мощности, передаваемой на нагрузку. Таким образом, теорема о передаче максимальной мощности обеспечивает идеальные условия для передачи максимальной мощности в нагрузку. Посмотрим «как».
Теорема о передаче максимальной мощности Заявление
Теорема о передаче максимальной мощности утверждает, что в линейной двусторонней сети постоянного тока максимальная мощность передается на нагрузку, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
Если это независимый источник напряжения, то его последовательное сопротивление (внутреннее сопротивление R S ) или если это независимый источник тока, то его параллельное сопротивление (внутреннее сопротивление R S ) должно быть равно сопротивлению нагрузки R L для обеспечения максимальной мощности нагрузки.
Доказательство теоремы о передаче максимальной мощности
Теорема о передаче максимальной мощности обеспечивает значение сопротивления нагрузки, при котором в нагрузку передается максимальная мощность.
Рассмотрим показанную ниже сеть постоянного тока с двумя клеммами (левая цепь). Условие максимальной мощности определяется путем получения выражения для мощности, поглощаемой нагрузкой, с использованием метода сеточного или узлового тока, а затем получения результирующего выражения относительно сопротивления нагрузки R L .
Это достаточно сложная процедура. Но в предыдущих уроках мы видели, что сложную часть сети можно заменить эквивалентом Thevenin, как показано ниже.
Первоначальная схема с двумя выводами заменена эквивалентной схемой Тевенина при переменном сопротивлении нагрузки. Ток через нагрузку для любого значения сопротивления нагрузки составляет
Из приведенного выше выражения отдаваемая мощность зависит от значений R TH и R L . Однако, поскольку эквивалент Тевенина является константой, мощность, передаваемая от этого эквивалентного источника к нагрузке, полностью зависит от сопротивления нагрузки R L . Для нахождения точного значения RL применим дифференцирование P L относительно R L и приравняем его к нулю, как показано ниже:
Следовательно, это условие согласования нагрузки, при которой максимальная мощность передача происходит, когда сопротивление нагрузки равно сопротивлению Тевенина цепи. Подставив R TH = R L в предыдущее уравнение, мы получим:
Максимальная мощность, подаваемая на нагрузку,
Общая мощность, передаваемая из источника:
P T = I L 2 * (R TH + R L )
P T = 2 * L
P T = 2 * I L ) 2 R L …………….(2)
Следовательно, теорема о передаче максимальной мощности выражает состояние, при котором на нагрузку передается максимальная мощность, т. е. когда сопротивление нагрузки равно эквивалентному сопротивлению Тевенина. цепи. На рисунке ниже показана зависимость мощности, подаваемой на нагрузку, от сопротивления нагрузки.
Обратите внимание, что отдаваемая мощность равна нулю, когда сопротивление нагрузки равно нулю, поскольку в этом состоянии на нагрузке нет падения напряжения. Также мощность будет максимальной, когда сопротивление нагрузки равно внутреннему сопротивлению цепи (или эквивалентному сопротивлению Тевенина). Опять же, мощность равна нулю, так как сопротивление нагрузки достигает бесконечности, поскольку ток через нагрузку отсутствует.
Эффективность передачи мощности
Мы должны помнить, что эта теорема утверждает только максимальную передачу мощности, но не максимальную эффективность. Если сопротивление нагрузки меньше сопротивления источника, мощность, рассеиваемая на нагрузке, уменьшается, а большая часть мощности рассеивается на источнике, тогда КПД становится ниже.
Рассмотрим общую мощность, выдаваемую из уравнения источника (уравнение 2), в котором мощность рассеивается на эквивалентном сопротивлении Тевенина R TH источником напряжения V TH .
Таким образом, КПД при условии передачи максимальной мощности:
КПД = Выход / Вход × 100
= I L 2 R L / 2 I L 2 R L × 100
= 50 %
Следовательно, при условии максимальной передачи мощности КПД составляет 50 %, что означает, что в нагрузку передается только половина генерируемой мощности, а при других условиях в нагрузку передается небольшой процент мощности, как указано в зависимости эффективности от максимальной передачи мощности представлены на кривых ниже.
Для некоторых применений желательно передавать максимальную мощность в нагрузку, чем достигается высокий КПД, например, в усилителях и цепях связи.
С другой стороны, желательно достичь более высокой эффективности, чем максимальная передача мощности, в случае систем передачи электроэнергии, где к нагрузке приложено большое сопротивление нагрузки (намного большее значение, чем внутреннее сопротивление источника). Несмотря на то, что эффективность высока, мощность в этих случаях будет меньше.
Теорема о передаче максимальной мощности для цепей переменного тока
В активной сети можно утверждать, что максимальная мощность передается на нагрузку, когда полное сопротивление нагрузки равно комплексно-сопряженному эквивалентному полному сопротивлению данной сети, если смотреть из клеммы нагрузки.
Рассмотрим приведенную выше эквивалентную схему Тевенина между клеммами нагрузки, в которой ток, протекающий через цепь, задается как: L = R L + JX L
Z TH = R TH + JX TH
Следовательно, I = v TH / (R L + JX L + JX + JX + JX + JX + JX + JX + JX + JX + JX + JX + JX / jx / JX / jx / jx ; + R TH + jX TH )
I = V TH / ((R L + R TH ) + j(X L + X TH ))
7 P 9002 Мощность, отдаваемая нагрузке,L = I 2 * R L
P L = V 2 TH * R L / (R L + R TH ) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 . L + X TH ) 2 ) ……(1)
Для максимальной мощности производная приведенного выше уравнения должна быть равна нулю, после упрощения получаем
x L + x TH = 0
x L = — x TH
Уравнение выше в уравнении 1,
P L = V 2 9007 TH L = V 2 9007 TH L × R L / ((R L + R TH ) 2
Опять же, для максимальной передачи мощности вывод приведенного выше уравнения должен быть равен нулю, и после упрощения мы получаем:
R L + R TH = 2 R L
Р Л = Р ТХ
Следовательно, максимальная мощность будет передана в нагрузку от источника, если R L = R TH и X L = – X TH в цепи переменного тока. Это означает, что импеданс нагрузки должен быть равен комплексно-сопряженному эквивалентному импедансу цепи,
Z L = Z TH
Где Z TH — комплексно-сопряженное эквивалентное сопротивление цепи.
Эта максимальная передаваемая мощность, P MAX = V 2 TH / 4 R TH или V 2 TH / 4 R L
Пример применения передачи максимальной мощности к цепи постоянного тока
Рассмотрим приведенную ниже цепь, для которой мы определяем значение сопротивления нагрузки, получающей максимальную мощность от источника питания, и максимальную мощность при условии передачи максимальной мощности.
Отсоедините сопротивление нагрузки от клемм нагрузки «a» и «b». Чтобы представить данную схему как эквивалент Тевенина, мы должны определить напряжение Тевенина V TH и эквивалентное сопротивление Thevenin R TH .
Напряжение Thevenin или напряжение на клеммах ab равно В ab = В a – В b
В a = В × R2 / (R1 + R2)
= 30 × 20 / × (20 + 15)
= 17,14 В
В б = В × R4/ (R3 + R4)
= 30 × 5 / (10 + 5)
= 10 В
В аб = 17,14 – 10
= 7,14 В
В TH = В аб = 7,14 Вольт
Рассчитайте эквивалентное сопротивление Thevenin R TH , заменив источники их внутренними сопротивлениями (здесь предположим, что источник напряжения имеет нулевое внутреннее сопротивление, поэтому возникает короткое замыкание).
Эквивалентное сопротивление Thevenin или сопротивление на клеммах ab равно
R TH = Rab = [R1R2 / (R1 + R2)] + [R3R4 / (R3 + R4)]
= [(15 × 20) / (15 + 20)] + [(10 × 5) / (10+ 5)]
= 8,57 + 3,33
R TH = 11,90 Ом
Эквивалентная схема Thevenin с приведенными выше расчетными значениями путем повторного подключения сопротивления нагрузки показана ниже.
Согласно теореме о передаче максимальной мощности, значение R L должно быть равно R TH , чтобы передать максимальную мощность в нагрузку.
Следовательно, R L = R TH = 11,90 Ом
Максимальная мощность, передаваемая при этом условии,
P МАКС = V 2 TH / 4 R TH
= (7,14) 2 / (4 × 11,90)
= 50,97 / 47,6
= 1,07 Вт
Применение передачи максимальной мощности к цепи переменного тока
Приведенная ниже сеть переменного тока состоит из импеданса нагрузки Z L , реактивная и резистивная части которого могут варьироваться. Следовательно, мы должны определить значение импеданса нагрузки, при котором максимальная мощность отдается от источника, а также значение максимальной мощности.
Чтобы найти значение импеданса нагрузки, сначала мы находим эквивалентную схему Тевенина на клеммах нагрузки. Чтобы найти напряжение Thevenin, отключите импеданс нагрузки, как показано на рисунке ниже.
По правилу делителя напряжения,
В TH = 20∠0 × [j6 / (4 + j6)]
= 20∠0 × [6∠90 / 7,21∠56,3]
= 20∠0 × 0,825∠33,7
В TH = 16,5∠33,7 В
Замыкая источник напряжения, мы вычисляем эквивалентное сопротивление цепи Тевенина, как показано на рисунке.
Следовательно,
Z TH = (4 × j6) / (4 + j6)
= (4 × 6∠90) / (7,21∠56,3)
= 3,33∠33,7 0r 2,77 + j1,85 Ом
Таким образом, эквивалентная схема Thevenin между клеммами нагрузки показана ниже.
Следовательно, для передачи максимальной мощности на нагрузку значение импеданса нагрузки должно быть
Z L = Z TH
= 2,77 – j1,85 Ом
Максимальная отдаваемая мощность, P MAX
= V 2 TH / 4 R TH
= (16,5) 2 /4(2,77)
= 272,25 / 11,08
= 24,5 Вт
Практическое применение теоремы о максимальной передаче мощности
Рассмотрим практический пример динамика с импедансом 8 Ом. Он управляется усилителем звука с внутренним сопротивлением 500 Ом. Эквивалентная схема Тевенина также показана на рисунке.
Согласно теореме о максимальной передаче мощности мощность на нагрузке максимальна, если сопротивление нагрузки равно 500 Ом (такое же, как внутреннее сопротивление). В противном случае внутреннее сопротивление должно быть изменено на 8 Ом для достижения условия максимальной передачи мощности. Однако изменить ни один из них невозможно.
Таким образом, это состояние несоответствия импеданса, и его можно преодолеть, используя согласующий трансформатор импеданса с коэффициентом преобразования импеданса 500:8.
Эффективность цепей преобразования мощности
by Steve Roberts, Recom
Краткий обзор показывает источники неэффективности как линейных, так и импульсных источников питания.
Большинство инженеров знают, что одной из причин широкого распространения импульсных источников питания является их высокая энергоэффективность. Но многие инженеры недостаточно хорошо разбираются в технологии источников питания, чтобы объяснить причины эффективности и неэффективности импульсного режима. Поэтому полезно рассмотреть, как обычные линейные источники питания рассеивают энергию и почему их энергоэффективность так низка. Также может быть полезно понять, где происходит утечка энергии из конструкций с переключением режимов. Различные компоненты имеют различные источники потерь энергии. И разные конструкции с импульсным режимом теряют энергию по-разному
Сначала рассмотрим типовые стабилизаторы для линейных источников питания. Обычно они состоят из транзистора, включенного последовательно между входным и выходным напряжениями. Этот проходной транзистор является регулирующим элементом, эффективно функционирующим как переменный резистор. Он ограничивает ток, протекающий от входа к выходу. Резистивный делитель подает на вход усилителя ошибки напряжение, равное опорному напряжению. Усилитель ошибки формирует выходной сигнал, управляющий проходным транзистором. Действие таково, что разность напряжений между входами усилителя ошибки всегда равна нулю. Другими словами, усилитель ошибки реагирует на такие изменения, как увеличение нагрузки или повышение или понижение входного напряжения.
КПД η линейного регулятора определяется отношением выдаваемой выходной мощности P OUT к потребляемой мощности P IN :
η = P OUT /P IN
По закону Ома, P out = 0 I 0 out 19019; P в = V в х I в ; I в = I из + I Q ; где I Q — ток покоя линейного регулятора при отсутствии нагрузки. Уравнение можно переписать:
η = (V OUT I OUT )/V IN (I OUT +I Q )
Теперь рассмотрим пример типичного 5-вольтового трехвыводного регулятора напряжения с входным напряжением 10 В постоянного тока, выходным током 1 А и током покоя 5 мА. Тогда расчет КПД будет следующим:
η = 5 В x 1 А/10 В x 1,005 А = 0,49
Таким образом, общий КПД составляет 49%. Обратите внимание, что рассеиваемая мощность преобразователя превышает 5 Вт, подаваемые на нагрузку. Если входное напряжение снижается до минимума 7 В постоянного тока, КПД возрастает до 70 %, но это максимальная практическая эффективность, поскольку регулятору требуется около 2 В запаса для надлежащего регулирования.
Из уравнений КПД сразу видно, что КПД регулятора этого типа напрямую зависит от входного напряжения и нагрузки. И энергоэффективность не постоянна. Это также означает, что регулятор напряжения должен быть оснащен достаточно большим радиатором, чтобы обеспечить безопасную работу в наихудших условиях максимального входного напряжения и максимального выходного тока.
Теперь рассмотрим переключающие регуляторы. В отличие от линейных стабилизаторов, которые сбрасывают избыточную мощность в виде тепла для ограничения выходного напряжения, импульсные стабилизаторы используют свойства накопления энергии индуктивными и емкостными компонентами для передачи мощности дискретными энергетическими пакетами. Пакеты энергии хранятся либо в магнитном поле катушки индуктивности, либо в электрическом поле конденсатора. Коммутационный контроллер гарантирует, что в каждом пакете передается только та энергия, которая фактически требуется нагрузке. Вот почему эта топология является энергоэффективной.
Наиболее распространенным способом передачи энергии от входа к выходу в импульсном регуляторе является ШИМ (широтно-импульсная модуляция), где импульс переменной ширины с фиксированным временным интервалом модулирует количество энергии, передаваемой от входа к выходу. Коэффициент заполнения ШИМ, δ, представляет собой отношение времени включения t на (время, в течение которого энергия забирается из источника) к периоду T (обратное значение частоты переключения ƒ OSC ):
δ = t ON /T, где T = 1/ƒ OSC
Для многих импульсных стабилизаторов регулируемое выходное напряжение прямо пропорционально коэффициенту заполнения ШИМ. Контур управления использует рабочий цикл «большого сигнала» для управления силовым переключающим элементом. Напротив, линейный регулятор использует «слабосигнальный» сервоконтур для ограничения тока через проходной транзистор.
Одна из причин, по которой ШИМ-управление намного эффективнее линейного управления, заключается в том, что основные потери возникают при каждом изменении состояния переключателя, а не постоянно. Полевые транзисторы, которые полностью открыты или полностью закрыты, рассеивают небольшую мощность.
По сравнению с линейными регуляторами процесс определения эффективности импульсных регуляторов значительно сложнее. Линейный регулятор легко предопределяет потери постоянного тока; самое большое рассеяние имеет место в проходном транзисторе. Импульсный регулятор, однако, имеет не только потери постоянного тока, но и потери переменного тока, возникающие в переключателях и компонентах для накопления энергии.
Например, общие потери выключателя складываются не только из потерь во включенном и выключенном состояниях, но и из потерь при переходе от включения к выключению. В случае трансформатора общие потери рассчитываются из суммы потерь переменного тока (сердечник), переменного тока (обмотка) и постоянного тока (обмотка). Потери в сердечнике трансформатора обусловлены в основном взаимодействием магнитного потока с материалом сердечника (гистерезисные потери, потери на вихревые токи). Потери в обмотке в основном связаны с материалом обмотки трансформатора (омические потери, скин-эффекты). В любом случае конечным эффектом является повышение температуры трансформатора.
Чтобы рассчитать КПД преобразователя постоянного тока, потери каждой части цикла преобразования должны быть найдены путем усреднения потерь по всему диапазону рабочего цикла ШИМ. Потери в магнитных, индуктивных и емкостных компонентах можно контролировать и минимизировать для достижения высокой эффективности преобразования. Обычно только около 4% входной мощности теряется и преобразуется в тепло.
Неизолированные преобразователи, как правило, более эффективны, чем их изолированные аналоги, поскольку в преобразовании энергии участвует меньшее количество деталей; неизолированные преобразователи не используют трансформаторы, поэтому потери трансформатора отсутствуют. Тем не менее, несмотря на более высокую степень сложности, КПД изолированного DC/DC преобразователя может достигать более 85%, в зависимости от номинальной мощности.
Эффективность импульсного преобразователя может быть разной для разных входных напряжений и разных нагрузок. Обычно выражается как отношение выходной мощности к входной мощности. При нулевой нагрузке КПД всегда равен нулю. Спецификация в процентах является обычной, но ее также можно указать в виде нормализованного числа (≤ 1). Обычно данные предоставляются при нескольких условиях, таких как номинальное входное напряжение и полная нагрузка.Одной из основных причин снижения эффективности импульсных схем являются выходные диоды. Если выходной ток равен 1 А, а прямое падение напряжения на диоде равно 0,6 В, то только на диоде будет потеряно 600 мВт. Таким образом, преобразователи постоянного тока с высоким выходным током часто используют полевые транзисторы с синхронным переключением для уменьшения потерь выпрямления.
Возможно, вас удивит тот факт, что маломощные преобразователи обычно имеют более низкий КПД, чем более мощные преобразователи, особенно с учетом более высоких потерь I²R, возникающих при более высоких выходных токах. Однако существенное значение имеет внутреннее энергопотребление коммутационных контроллеров, шунтирующих регуляторов и оптронов («хозяйственное» потребление). Если общая хозяйственная потребность составляет 1 Вт, то 10-ваттный преобразователь не может иметь КПД более 90%. Но максимально возможный КПД преобразователя мощностью 100 Вт будет 99%.
Хозяйственные потери также объясняют, почему все DC/DC преобразователи имеют КПД 0% в условиях холостого хода, поскольку преобразователи все еще потребляют энергию, но не выдают выходной мощности. Полевые транзисторы потребляют больше энергии при переключении, чем в постоянно включенном или выключенном состоянии. Это связано с тем, что их внутренняя емкость затвора должна заряжаться и разряжаться для переключения выхода. Пиковые токи затвора 2 А и более не являются чем-то необычным. Преобразователь постоянного тока, работающий без нагрузки, по-прежнему будет переключать полевые транзисторы сотни тысяч раз в секунду, поэтому нет ничего необычного в том, что преобразователь постоянного тока продолжает работать в горячем состоянии без какой-либо нагрузки.
Учет паразитных характеристик
Уровень энергоэффективности топологий импульсных преобразователей различается. Одна из причин заключается в том, что используемые ими компоненты не идеальны. Описания топологий преобразователя в учебниках предполагают идеальные компоненты и игнорируют паразитные эффекты. Однако фактом жизни является то, что катушки индуктивности имеют емкостные и резистивные элементы и наоборот. Таким образом, выбор компонентов, используемых в импульсном источнике питания, оказывает большое влияние на его характеристики. Критические компоненты, такие как элементы переключения и выпрямления, магнитные компоненты и фильтрующие конденсаторы, влияют как на частоту переключения, так и на общий КПД преобразователя.
В частности, полупроводниковые переключатели обладают многими неидеальными свойствами. Полевые транзисторы предъявляют к цепи управления высокие пиковые токи, особенно ток, необходимый для зарядки и разрядки паразитной емкости Миллера между затвором и стоком. Диоды имеют параллельную эквивалентную емкость, что замедляет их скорость переключения и, конечно же, внутреннее прямое падение напряжения. Потери в индукторе сильно зависят от выбора материала сердечника и имеют эксплуатационные потери, возникающие из-за рассеяния I²R в обмотке и емкостей связи между витками. Конденсаторы обладают паразитными эффектами, такими как эквивалентное последовательное сопротивление (ESR) и эквивалентная последовательная индуктивность (ESL). Все эти эффекты зависят от частоты, поэтому катушка индуктивности может вести себя как конденсатор на высоких частотах, точно так же, как конденсатор может вести себя как катушка индуктивности.
Трансформеры имеют аналогичные проблемы. Недостатком использования трансформатора является то, что передача энергии от первичной обмотки к вторичной связана с дополнительными потерями. Таким образом, в то время как понижающий регулятор может достигать 9КПД преобразования 7%, трансформаторные преобразователи с трудом превышают 90%.
Одной из основных причин неэффективности импульсных схем являются потери мощности, связанные с выходными диодами. Альтернативой может быть замена диода полевым транзистором, включенным с противофазным сигналом к сигналу ШИМ. R DS,ON полевого транзистора имеет низкий уровень и не имеет прямого падения напряжения диода. Повышение эффективности может быть значительным в условиях полной нагрузки, так как мощность, обычно рассеиваемая на запирающем диоде, может быть уменьшена в четыре раза в типичном 15-ваттном синхронном преобразователе средней мощности. Однако при низкой нагрузке (<10% полной нагрузки) синхронная конструкция может быть фактически менее эффективной, чем асинхронная, отчасти из-за дополнительных потерь в цепи переключения полевого транзистора нижнего плеча, которая также рассеивает мощность при зарядке и разрядке нижнего плеча. Емкость затвора полевого транзистора. Другая причина заключается в том, что в асинхронной схеме обратный ток катушки индуктивности блокируется диодом, но в синхронной схеме могут протекать как положительные, так и отрицательные токи катушки индуктивности. Любой отрицательный ток представляет собой дополнительную потерю мощности, которую не видит асинхронная схема. Паразитные элементы
Паразитные эффекты в трансформаторах включают емкости межобмоточной связи для первичной и вторичной обмоток, индуктивность намагничивания сердечника и индуктивности рассеяния как для первичной, так и для вторичной обмотки.
Индуктивность рассеяния особенно опасна, так как снижает эффективность и создает излучаемые электромагнитные помехи.Эти паразитные эффекты трансформатора сильно влияют на работу преобразователя. Емкость связи вызывает проблемы ЭМС в синфазном режиме. Насыщение сердечника, вызванное индуктивностью намагничивания, ограничивает ток трансформатора. Индуктивность рассеяния особенно опасна, так как снижает эффективность и создает излучаемые электромагнитные помехи.
Индуктивность рассеяния также является причиной всплесков напряжения, возникающих при быстром изменении тока в обмотках. Такие перенапряжения нагружают первичный ключ и вторичные диоды, поэтому они должны быть рассчитаны либо на то, чтобы выдерживать пиковое напряжение, либо снабжены параллельной демпфирующей сетью для рассеивания энергии в пиках.
Однако энергия всплесков и мощность, которую должен поглотить демпфер, представляют собой потери энергии, которые снижают эффективность преобразователя. Энергию шипов и мощность, которую должен поглотить демпфер, можно рассчитать по формуле:
E = 1/2 L Утечка I 2 Утечка
P = 1/2 L Утечка I 2 Утечка ƒ
A Snubber не может устранить проигрышной мощности, построенный в сил, построенный SPIKES, построенный SPIKES, построенный в сил. . Мощность, которая в противном случае рассеивалась бы в переключателе или выпрямительном диоде, теперь вместо этого рассеивается на сетевых резисторах-демпферах.
Помимо всплесков, вызванных паразитной индуктивностью рассеяния, любая связанная реактивная система также будет демонстрировать резонансные частоты. Большинство конструкций на основе трансформаторов пытаются либо свести эти паразитные элементы к минимуму, либо выбрать рабочие частоты, при которых резонанс не является проблемой. Однако конструкция квазирезонансного или резонансного преобразователя преднамеренно способствует возникновению резонанса за счет увеличения индуктивности обмотки или добавления дополнительных катушек индуктивности, поскольку управление этим резонансом может облегчить создание эффективной конструкции преобразователя.
Как упоминалось ранее, одним из основных источников снижения эффективности любого преобразователя является рассеивание мощности на выходных диодах. Диоды Шоттки с низким прямым падением напряжения иногда могут служить альтернативой маломощным преобразователям, но они дороги, если их размеры позволяют выдерживать более высокие токи. Даже в этом случае прямое падение составляет около 200 мВ, поэтому потери мощности могут быть значительными.
Большим шагом вперед в повышении эффективности стала разработка синхронного выпрямления.
Одной из основных причин снижения эффективности любого преобразователя является рассеивание мощности на выходных диодах. Большим шагом вперед в повышении эффективности стала разработка синхронного выпрямления. Здесь полевые транзисторы служат выпрямляющими элементами и включаются во время прямой части цикла и выключаются во время обратной части цикла. Недостатком этих устройств является то, что они должны активно управляться, поэтому требуются дополнительные схемы синхронизации и управления.В типичной схеме с диодным выпрямлением один диод действует как выпрямитель, а другой — как шунтирующий диод. Оба диода попеременно нагружаются примерно одинаковым током. Потери от прямого падения напряжения на диодах — это просто падение напряжения, умноженное на ток диода. При типичном прямом напряжении 0,5 В можно предположить относительную рассеиваемую мощность 0,5 Вт на ампер. Таким образом, выходной преобразователь 3,3 В/10 А будет иметь потери преобразования напряжения 15 % без учета каких-либо других потерь преобразования. Мощность, рассеиваемая диодом, будет составлять 5 Вт, поэтому диод, вероятно, должен быть установлен на радиаторе, чтобы иметь какой-либо полезный рабочий диапазон температур.
К счастью, полевые транзисторы можно использовать в качестве выпрямляющих элементов, включая их во время прямой части цикла и выключая во время обратной части цикла. Их преимущество в качестве быстрых переключателей с низким сопротивлением во включенном состоянии делает их пригодными для использования в качестве выпрямителей.
Недостатком полевых транзисторов является то, что они должны активно управляться, поэтому требуются дополнительные схемы синхронизации и управления. Синхронные выпрямители должны определять внутренние напряжения, чтобы правильно включать и выключать два полевых транзистора синхронно с формой выходного сигнала, отсюда и название этой топологии.
Для сравнения, диоды являются пассивными устройствами, для работы которых не требуется дополнительная схема, но низкое сопротивление полевых транзисторов в открытом состоянии, составляющее около 10 мОм, более чем компенсирует недостаток более сложной схемы для преобразователей с высоким выходным током.
Наконец, несколько слов о расчете эффективности: Эффективность преобразования напряжения определяется отношением выходной мощности к входной мощности. При нулевой нагрузке КПД всегда равен нулю. Спецификация в процентах является обычной, но ее также можно указать в виде нормализованного числа (≤ 1). Обычно данные предоставляются при нескольких условиях, таких как номинальное входное напряжение и полная нагрузка.
