11.3. ИДЗ–3. Приложения производной
1 Найти глобальный экстремум функции на отрезке .
1.1 .
1.2 .
1.3 .
1.4 .
1.5 .
1.6 .
1.7 .
1.8 .
1.9 .
1.10 .
1.11 .
1.12 .
1.13 .
1.14 .
1.15 .
1.16 .
1.17 .
1.18 .
1.19 .
1.20 .
1.21 .
1.22 .
1.23 .
1.24 .
1.25 .
1.26 .
1.27 .
1.28 .
1.29 .
1.30 .
2 Решить геометрические задачи:
2.1 Найдите прямоугольный треугольник наибольшей площади, если сумма катета и гипотенузы его постоянна.
2.2 При каких линейных размерах закрытая цилиндрическая банка данной вместимости V будет иметь наименьшую полную поверхность?
2.3 В данный круговой сегмент, не превышающий полукруга, вписать прямоугольник наибольшей площади.
2.4 В эллипс вписать прямоугольник со сторонами, параллельными осям эллипса, площадь которого наибольшая.
2.5 Боковое ребро правильной треугольной пирамиды имеет постоянную заданную длину и составляет с плоскостью основания угол .
2.6 В полушар радиуса R вписать прямоугольный параллелепипед с квадратным основанием наибольшего объёма.
2.7 В данный шар радиуса R вписать цилиндр наибольшего объёма.
2.8 В шар радиусом R Вписать цилиндр с наибольшей полной поверхностью.
2.9 Около шара радиуса r описать конус наименьшего объёма.
2.10 Через вершину М квадрата CEMK провести прямую, пересекающую лучи CK и CE в точках A и B так, чтобы площадь DABC была наименьшей.
2.11 Две стороны параллелограмма лежат на сторонах данного треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма является наибольшей?
2.12 Найти наибольший объём конуса с образующей L.
2.13 В прямой круговой конус с углом в осевом сечении и радиусом основания R вписать цилиндр с наибольшей полной поверхностью.
2.
14 Найти кратчайшее расстояние точки M(P,P) от параболы .
2.15 Найти наибольшую хорду эллипса , , проходящую через вершину .
2.16 Через точку эллипса провести касательную, образующую с осями координат треугольник наименьшей площади.
2.17 Найти основания и высоту равнобочной трапеции, которая при данной площади S имеет наименьший периметр; угол при большем основании трапеции равен .
2.18 Какова должна быть высота равнобедренного треугольника, вписанного в окружность диаметра D, чтобы площадь треугольника была наибольшей?
2.19 В прямоугольный треугольник с гипотенузой 10 см и углом 30° вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы площадь его была наибольшей?
2.20 Требуется огородить забором прямоугольный участок земли площадью в 294 м2 и разделить затем этот участок забором на две равные части. При каких линейных размерах участка длина всего забора окажется наименьшей?
2.
21 Прямоугольный лист жести имеет линейные размеры дм. В четырех его углах вырезают одинаковые квадраты и делают открытую коробку, загибая края под прямым углом. Какова наибольшая вместимость полученной коробки?
2.22 В прямоугольный треугольник с гипотенузой 24 см и углом 60° вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть длины сторон прямоугольника, чтобы его площадь была наибольшей?
2.23 Две стороны параллелограмма лежат на сторонах данного треугольника, а одна из его вершин принадлежит третьей стороне. При каких условиях площадь параллелограмма является наибольшей?
2.24 Среди равнобедренных треугольников с данной боковой стороной найти треугольник наибольшей площади.
2.25 Боковые стороны и меньшее основание трапеции имеют одинаковые длины по 10 см. Найти размер большего основания, при котором площадь трапеции была бы наибольшей.
2.26 Найти длины сторон прямоугольника наибольшей площади, вписанного в прямоугольный треугольник со сторонами 18, 24 и 30 см и имеющего с ним общий прямой угол.
2.27 Величина угла при основании равнобедренного треугольника равна . При каком значении отношение длин радиусов вписанной и описанной окружностей является наибольшим?
2.28 Каким должен быть радиус основания и высота цилиндрического бака, чтобы при данном объеме на его изготовление пошло наименьшее количество листового металла?
2.29 В прямоугольный треугольник с гипотенузой 12 см и углом 60° вписан прямоугольник, основание которого расположено на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы площадь его была наибольшей?
2.30 Боковые стороны и меньшее основание трапеции имеют одинаковые длины по 15 см. Найти размер меньшего основания, при котором площадь трапеции была бы наибольшей.
3 Решить физические задачи:
3.1 Тяжелую балку длиной 13 м, расположенную вертикально, опускают на землю так, что нижний её конец прикреплен к вагонетке, а верхний удерживается канатом, намотанным на ворот. Канат сматывается со скоростью 2 м/мин. С каким ускорением откатывается вагонетка в момент, когда она npoйдёт расстояние 5 м?
3.
2 Антенна радара находится на расстоянии 1000 м по горизонтали от стартовой площадки и все время направлена на ракету, которая поднимается с постоянным ускорением 20 м/с2. Какова угловая скорость антенны в момент, когда ракета находится не высоте 1000 м?
3.3 Лошадь бежит по окружности со скоростью 20 м/с. В центре окружности находится фонарь. Забор касается окружности в точке, из которой лошадь начинает бег. С какой скоростью перемешается тень лошади вдоль забора в момент, когда лошадь пробежит 1/8 окружности?
3.4 Резервуар, имеющий форму полушара радиуса , заполняется водой. Скорость заполнения резервуара равна . Определите скорость подъёма воды в резервуаре в момент, когда вода поднялась на высоту .
3.5 Длина вертикально стоящей лестницы равна 5 м. Нижний конец лестницы начинает отодвигаться от стены с постоянной скоростью 2 м/с. Чему равно ускорение верхнего конца лестницы в момент, когда нижний конец отодвинулся от стены на 1 м?
3.6 Канат висячего моста, имеющего форму цепной линии, т.
3.7 В точках A и B находятся источники света силы и соответственно, 27. Найдите на отрезке наименее освещенную точку (освещенность прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния до него).
3.8 Бревно длиной 10 м с помощью подъёмного крана поднимается вертикально вверх за один из его концов. При этом второй конец волочится по земле со скоростью 0,05 м/с. С какой скоростью перемещается верхний конец бревна в момент, когда его нижний конец находится на расстоянии 3 м от вертикали?
3.9 Мальчик надувает воздушный шар, радиус которого возрастает с постоянным ускорением 0,2 см/с2. С какой скоростью увеличивается объём шара в момент, когда площадь его поверхности равна См2 (радиус шара в начальный момент времени равнялся нулю)?
3.
10 Человек, рост которого 1,7 м, удаляется от точечного источника света, расположенного на высоте 3 м, с постоянным ускорением 0,1 м/с2. С каким ускорением перемещается тень его головы?
3.11 Скорость тела, движущегося по окружности радиуса 1 м, меняется по закону . Найдите величину ускорения тела в момент времени c.
3.12 Зависимость пути, пройденного телом, движущимся по окружности радиуса , от времени задается уравнением (). Чему равна величина скорости тела в момент, когда оно пройдёт путь ?
3.13 Частица движется с постоянной по величине скоростью по кривой . Найдите величину ускорения частицы в момент, когда .
3.14 При изобарном нагревании n молей идеального газа его объём с течением времени меняется по закону (, A
3.15 Зависимость электрического заряда, проходящего через проводник с сопротивлением R, от времени имеет вид .
Исследуйте на экстремум функцию , выражающую зависимость от времени мгновенной тепловой мощности, выделяемой в проводнике.
3.16 Предмет, находившийся первоначально на расстоянии от собирающей линзы, начинают удалять от неё с постоянным ускорением A. Чему равна скорость движущегося изображения в момент, когда предмет находится от линзы на расстоянии
3.17 Дождевая капля, начальная масса которой , падает под действием силы тяжести, равномерно испаряясь, так, что убыль массы пропорциональна времени с коэффициентом пропорциональности K. В какой момент времени после начала падения кинетическая энергия капли будет наибольшей (сопротивлением воздуха пренебречь)?
3.18 Груз весом P, лежащий на горизонтальной плоскости, требуется сдвинуть с места приложенной силой. При каком наклоне этой силы к горизонту величина её будет наименьшей, если коэффициент трения груза равен ?
3.19 Найдите максимальную возможную температуру молей идеального газа, если его давление Р и объём V связаны зависимостью (, , ).
3.20 Электрические заряды +Q1, —Q2, +Q3 расположены на одной прямой так, что заряд —Q2 находится между зарядами +Q1 и +Q3 на расстоянии А от заряда +Q1. На каком расстоянии от заряда —Q2 должен находиться заряд +Q3, чтобы его потенциальная энергия была минимальной (потенциал поля точечного заряда Q равен )?
3.21 Определить наименьший возможный объём V , занимаемый одним молем идеального газа, если его температура Т и давление P связаны соотношением (, , ).
3.22 Магнитный поток Ф через неподвижный контур, имеющий сопротивление R, изменяется с течением времени T по закону , где A положительная постоянная. В какой момент времени сила индукционного тока достигает максимального значения?
3.23 Найдите максимально возможную температуру одного моля идеального газа, если его давление и объём Связаны соотношением (, ).
3.24 Над центром круглого стола радиуса R висит лампа.
При какой высоте лампы над столом освещенность края стола будет наилучшей (освещенность прямо пропорциональна косинусу угла падения лучей света и обратно пропорциональна квадрату расстояния до источника света)?
3.25 Определите наибольшее возможное давление одного моля идеального газа, если температура и объём газа связаны соотношением ().
3.26 Резервуар, имеющий форму усеченного конуса, заполняется водой. Скорость заполнения резервуара равна 1 м3/мин. Определите скорость подъёма воды в резервуаре в момент, когда он заполнится на половину своего объёма (высота резервуара равна 3 м, радиус нижнего основания 2 м, верхнего – 5м).
3.27 Известно, что, мощность , отдаваемая электрическим элементом, определяется по формуле , где — постоянная электродвижущая сила элемента, – постоянное внутреннее сопративление, – внешнее сопративление. Каким должно быть внешнее сопративление , чтобы мощность была наибольшей?
3.28 На прямой между двумя источниками света силы и найти наименее освещенную точку, если расстояние между источниками равно 24 м (освещенность прямо пропорциональна силе света источника и обратно пропорциональна квадрату расстояния до него).
3.29 Бревно длиной 15 м с помощью подъёмного крана начинают поднимать вертикально вверх за один из его концов. При этом второй конец волочится по земле со скоростью 0,09 м/с. С какой скоростью перемещается верхний конец бревна в момент, когда его нижний конец находится на расстоянии 5 м от вертикали?
3.30 Зависимость пути, пройденного телом, движущимся по окружности радиуса R, от времени задается уравнением (). Чему равна величина скорости тела в момент, когда оно пройдёт путь ?
4 Провести полное исследование и построить график функции:
4.1 а) ; б) , .
4.2 а) ; б) , .
4.3 а) ; б) . .
4.4 а) ; б) , .
4.5 а) ; б) , .
4.6 а) ; б) , .
4.7 а) ; б) .
4.8 а) ; б) .
4.9 а) ; б) .
4.10 а) ; б) .
4.11 а) ; б) .
4.12 а) ; б) .
4.13 а) ; б) .
4.14 а) ; б) .
4.15 а) ; б) .
4.16 а) ; б) .
4.17 а) ; б) .
4.18 а) ; б) .
4.19 а) ; б) .
4.20 а) ; б) .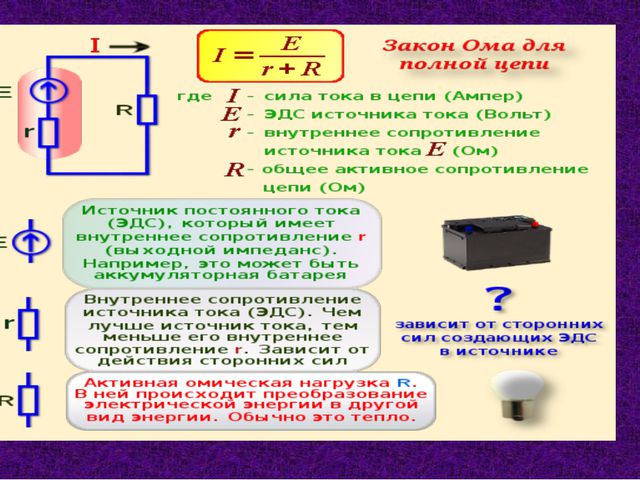
4.21 а) ; б) , .
4.22 а) ; б) , .
4.23 а) ; б), , .
4.24 а) ; б) , .
4.25 а) ; б) .
4.26 а) ; б) .
4.27 а) ; б) .
4.28 а) ; б) .
4.29 а) ; б) .
4.30 а) ; б) .
| < Предыдущая | Следующая > |
|---|
Компоненты формации Основными атмосферными компонентами, которые приводят к потенциалу торнадо, являются нестабильность — теплый влажный воздух у земли, с более прохладным сухим воздухом наверху и сдвиг ветра — изменение скорости и/или направления ветра с высотой. Нестабильная воздушная масса способствует развитию сильных восходящих потоков, в то время как сдвиг ветра еще больше увеличивает силу восходящего потока и способствует вращению, из-за которого возникают торнадо. Все грозы могут вызывать торнадо, но наиболее часто торнадоподобным типом грозы является суперячейка. Обнаружение Наш доплеровский радар WSR-88D может обнаруживать циркуляцию, связанную с торнадо, вызывающим грозу. После выявления циркуляции выдается предупреждение. Однако доплеровский радар не идеален, потому что он может показывать только вращение вверху и не показывает, что может происходить на земле. Вот тут-то и появляются наши наблюдатели за штормами. Только отзывы от кого-то в этом районе могут подтвердить, связана ли радиолокационная сигнатура с торнадо. Северная и Центральная Джорджия История торнадо Грузия испытала почти все силы торнадо, от EF-0 до EF-4. Хотя государство никогда не сталкивалось с EF-5, это не значит, что этого не может быть! На приведенном ниже графике показаны как прошлые следы, так и сила торнадо в северной и центральной Джорджии.
Информация по безопасности Прежде чем действовать, важно иметь план обеспечения безопасности.
Ущерб от торнадо в округе Коуэта, показанный ниже, является примером важности перемещения во внутреннюю комнату. При этом все наружные стены были разрушены. | |||||||
Эта очень сильная, долгоживущая гроза содержит циркуляцию наверху (мезоциклон), которая усиливается вверх через грозу и вниз к земле. При благоприятных условиях будут возникать торнадо. Суперячейки могут производить сильные, жестокие торнадо или несколько торнадо в течение нескольких часов. Две самые последние крупные вспышки суперклеток в северной или центральной Джорджии произошли во время торнадо в Вербное воскресенье 27,19 марта.94 и вспышка юго-восточного торнадо 27-28 апреля 2011 г.
Торнадо могут быстро развиваться, поэтому будьте готовы действовать быстро! Руководство по обеспечению готовности к грозам, смерчам и молниям предлагает следующие правила безопасности при смерчах:
Водород — информация об элементе, свойства и использование
Стенограмма:
(Промо)
Вы слушаете Химию в ее стихии, представленную вам Chemistry World , журналом Королевского химического общества.
(Конец акции)
Мира Сентилингам
На этой неделе мы узнаем, каково это быть на вершине и номером один, когда мы встречаем Короля Стихий.
Вот Брайан Клегг.
Брайан Клегг
Забудьте о Даунинг-стрит, 10 или Пенсильвания-авеню, 1600, самом престижном адресе во вселенной . — номер один в периодической таблице, водород. В науке простота и красота часто приравниваются — и это делает водород таким прекрасным, как он есть, один протон и одинокий электрон составляют самый компактный из существующих элементов.
Водород существует с тех пор, как атомы впервые образовались в остатках Большого взрыва, и на сегодняшний день он является самым распространенным элементом. Несмотря на то, что миллиарды лет бесчисленные звезды превращают водород в гелий, он по-прежнему составляет 75 процентов обнаруживаемого содержимого Вселенной.
Этот легкий, бесцветный, легко воспламеняющийся газ сохраняет свою уникальность благодаря тому, что содержит только названные изотопы (и при этом одни из самых известных), дейтерий с добавленным нейтроном в ядре и тритий с двумя нейтронами.
Водород необходим для жизни, Вселенной и почти всего.
Жизнь, по сути, многократно зависит от него. Без водорода у нас не было бы Солнца, дающего нам тепло и свет. Не было бы полезных органических соединений для формирования строительных блоков жизни. И самого необходимого для существования жизни вещества, воды, не существовало бы.
Только благодаря особой уловке водорода мы вообще можем использовать воду. Водород образует слабые связи между молекулами, зацепляясь за соседние атомы кислорода, азота или фтора. это эти водородные связи , которые придают воде многие ее свойства. Если бы их не было, температура кипения воды была бы ниже -70 градусов по Цельсию. Жидкой воды на Земле не было бы.
Водород был невольным открытием Парацельса, швейцарского алхимика шестнадцатого века, также известного как Теофраст Филиппус Ауреолус Бомбастус фон Гогенхайм. Он обнаружил, что что-то легковоспламеняющееся пузырится из металлов, которые были брошены в сильные кислоты, не подозревая о химической реакции, которая приводит к образованию солей металлов и выделению водорода, что-то, что многие другие, включая Роберта Бойля, независимо обнаружили на протяжении многих лет.
Однако первым, кто осознал, что водород является уникальным веществом, которое он назвал «горючим воздухом», был Генри Кавендиш, благородный предок Уильяма Кавендиша, который позже дал свое имя тому, что впоследствии стало самой известной в мире физической лабораторией в Кембридже. . Между 1760-ми и 1780-ми годами Генри не только выделил водород, но и обнаружил, что при его сжигании он соединяется с кислородом (или «дефлогистированным воздухом», как его называли) с образованием воды. Эти неуклюжие термины были отметены французским химиком Антуаном Лавуазье, который навсегда изменил химические названия, назвав горючий воздух «водородом», геном или создателем гидро, воды.
Поскольку водород очень легкий, этот чистый элемент редко встречается на Земле. Оно бы просто уплыло. Основные компоненты воздуха, азот и кислород, в четырнадцать и шестнадцать раз тяжелее, что придает водороду исключительную плавучесть. Эта легкость водорода сделала его естественным для одного из первых практических применений — наполнения воздушных шаров.
Ни один воздушный шар не парит так хорошо, как водородный.
Первый такой воздушный корабль был создан французским ученым Жаком Шарлем в 1783 году, который был вдохновлен успехом братьев Монгольфье с горячим воздухом за пару месяцев до того, как использовать водород в воздушном шаре из шелка, пропитанного каучуком. У водорода, казалось, было гарантированное будущее в летательных аппаратах, подкрепленное изобретением дирижаблей, построенных на жесткой раме, называемых дирижаблями в Великобритании, но более известных под своим немецким прозвищем Цеппелины, в честь их восторженного промоутера графа Фердинанда фон Цеппелина.
Эти дирижабли вскоре стали небесными лайнерами, безопасно и плавно перевозя пассажиров через Атлантику. Но, несмотря на исключительную легкость водорода, у него есть еще одно свойство, которое погубило дирижабли, — водород легко воспламеняется. Разрушение огромного цеппелина «Гинденбург», вероятно, в результате пожара, вызванного статическим электричеством, было заснято шокированной публикой по всему миру.
Водородный дирижабль был обречен.
Тем не менее, водород остается важным игроком в сфере транспорта из-за высокой эффективности его сгорания. Многие ракеты НАСА, в том числе вторая и третья ступени программы «Аполлон» «Сатурн-5» и главные двигатели космического корабля «Шаттл», работают на сжигании жидкого водорода с чистым кислородом.
Совсем недавно водород был предложен в качестве замены ископаемого топлива в автомобилях. Здесь у него есть большое преимущество перед бензином в том, что он сжигает только воду. Выбросов парниковых газов не происходит. Наиболее вероятным способом использования водорода является не его взрывное сжигание, а использование его в топливном элементе, где электрохимическая реакция используется для производства электроэнергии для питания автомобиля.
Однако не все убеждены, что будущее за водородными автомобилями. Нам понадобится сеть водородных заправочных станций, а он остается опасным взрывоопасным веществом. В то же время он менее эффективен, чем бензин, так как в литре бензина примерно в три раза больше больше полезной энергии в нем, чем в литре жидкого водорода (если использовать сжатый газообразный водород, то может уйти до десяти раз больше).
Другой проблемой является получение водорода. Это происходит либо из углеводородов, потенциально оставляющих осадок парниковых газов, либо из электролиза воды с использованием электричества, которое не может быть получено экологически чистым способом.
Но даже если мы не получим автомобили на водородном топливе, у водорода все еще есть будущее в более драматическом источнике энергии — ядерном синтезе, источнике энергии солнца. Термоядерные электростанции через десятки лет не станут практичными, но они дают надежду на чистую, обильную энергию.
Как бы мы ни использовали водород, мы не можем отнять у него первое место. Это numero uno, высшее, царь стихий.
Мира Сентилингам
Итак, это самый распространенный элемент, он необходим для жизни на Земле, служит топливом для космических ракет и может решить нашу зависимость от ископаемого топлива. Вы можете понять, почему Брайан Клегг ставит водород на первое место. На следующей неделе мы встретимся с хранителем времени периодической таблицы.
