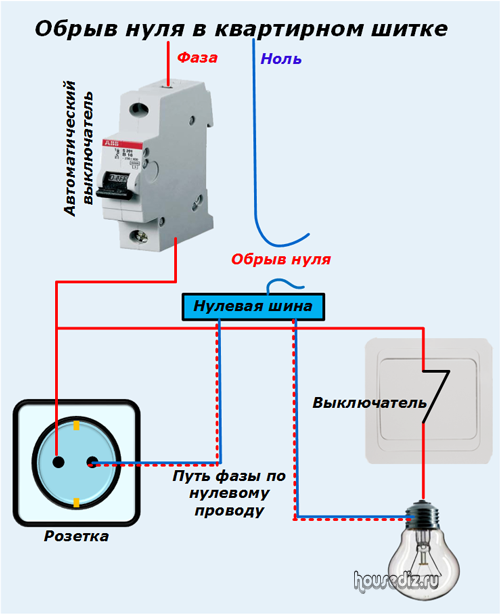
Как найти фазу и ноль
Домашнему мастеру «
В ходе строительных и ремонтных работ бывают ситуации, когда надо найти фазу и ноль в проводке, по которой наши дома и квартиры получают переменный ток. Обычно проводка состоит из двух проводов, только по одному из которых непосредственно идёт ток – такой провод называется «фаза». Ну, а оставшийся – это «ноль».
Заранее убедитесь, что вы достаточно подготовлены для работы с электричеством. Процесс определения «фазы» и «ноля» связан с реальной угрозой для жизни и здоровья, т.к. есть опасность пострадать от поданного в сеть напряжения. Возможно, есть смысл поручить эту работу профессионалам. Даже если вы абсолютно уверены в своих знаниях и опыте, надо всегда соблюдать предельную осторожность.
А теперь давайте попробуем разобраться, как найти фазу и ноль в домашней электропроводке.
Инструмент, который поможет найти фазу
Успешно справиться с поставленной задачей, вам поможет:
- индикаторная отвертка для определения наличия напряжения;
- кусачки, нож и плоскогубцы для снятия изоляции и отделения проводов друг от друга;
- вольтметр для определения «земли» и «ноля» в трёхжильном проводе.

Последовательность действий
- 1. Проверьте, чтобы помещение было полностью обесточено. Все переключатели на распределяющем щите должны находиться в выключенном состоянии.
- 2. С помощью инструментов зачистите изоляцию на концах проводов, которые будут проверяться. Нельзя допускать случайного соприкосновения двух проводов, поэтому разведите их подальше друг от друга.
- 3. Приготовив индикаторную отвертку, подайте на провода напряжение, включив переключатели на щите.
- 4. При работе с индикатором важно правильно взяться за него. Ни в коем случае нельзя касаться рабочей части отвертки. Необходимо браться только за её корпус, при этом указательный палец должен лежать на конце рукоятки, выполненном из металла.
- 5. Прикоснитесь кончиком индикатора к каждому проводу. Тот, на котором индикатор загорится – это и есть «фаза». Другой, соответственно, «ноль».

- 6. Иногда провод бывает трёхжильным, третьим проводом является «земля». Тут всё делаем точно также, но после определения «фазы» нужно будет узнать, какой из двух оставшихся проводов «ноль», а какой – «земля». Для этого необходимо подключить к вольтметру поочередно две пары проводов, соединяя «фазу» с каждым из оставшихся проводов. При сочетании «фазы» и «ноля» полученное напряжение будет больше.
Конечно, можно довериться электрикам, делавшим проводку, и выбирать провода по цвету изоляции. Но это сработает только в том случае, если работники были добросовестными. В целом процесс поиска фазы несложен, но требует особого внимания и осторожности. Нельзя недооценивать опасность удара током, поэтому всегда соблюдайте меры безопасности при работе с электричеством.
Домашнему мастеру «
Как в электрической сети определить фазу и ноль мультиметром?
Пример HTML-страницыОчень часто при проведении ремонтных или монтажных работ, связанных с электричеством в квартире, доме, гараже или даче, возникает необходимость найти ноль и фазу. Это необходимо для правильного подключения розеток, выключателей, осветительных приборов. Большинство людей, даже не имеющих специального технического образования, воображают, что для этого есть специальные показатели. Мы бегло рассмотрим этот метод, а также расскажем об еще одном устройстве, без которого не может обойтись ни один профессиональный электрик. Поговорим о том, как определить фазу и ноль мультиметром.
Это необходимо для правильного подключения розеток, выключателей, осветительных приборов. Большинство людей, даже не имеющих специального технического образования, воображают, что для этого есть специальные показатели. Мы бегло рассмотрим этот метод, а также расскажем об еще одном устройстве, без которого не может обойтись ни один профессиональный электрик. Поговорим о том, как определить фазу и ноль мультиметром.
Содержание
- Понятия нуля и фазы
- Самые простые способы
- Для исполнения цвета прожилок
- Индикаторная отвертка
- Мультиметр. Что это за устройство?
- Как пользоваться устройством?
- Некоторые правила использования мультиметра
Понятия нуля и фазы
Прежде чем определять нулевую фазу, было бы неплохо вспомнить немного физики и понять, что это за концепции и почему они используются в розетке.
Орлов Анатолий Владимирович
Начальник службы РЗиА Новгородских электрических сетей
Задать вопрос
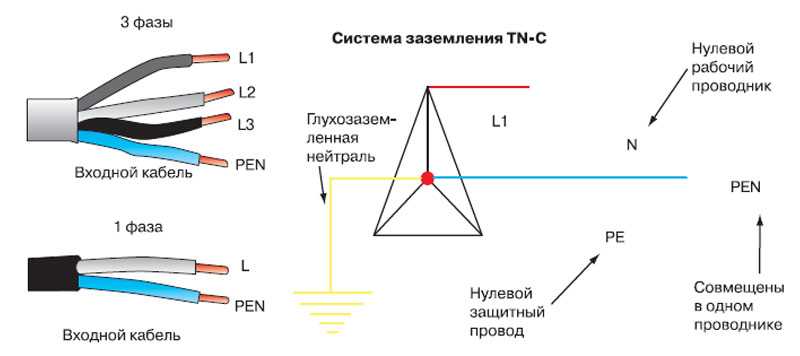
Все электрические сети (как бытовые, так и промышленные) делятся на два типа: постоянного и переменного тока. Еще со школы мы помним, что ток — это движение электронов в определенном порядке. При постоянном токе электроны движутся в одном направлении. При переменном токе это направление постоянно меняется.
Еще со школы мы помним, что ток — это движение электронов в определенном порядке. При постоянном токе электроны движутся в одном направлении. При переменном токе это направление постоянно меняется.
Нас больше интересует сеть переменных, которая состоит из двух частей:
- Фаза работы (обычно называемая просто «фазой»). На него подается рабочее напряжение.
- Пустая фаза, называемая «нулем» в электричестве. Необходимо создать замкнутую сеть для подключения и эксплуатации электрических устройств, она же служит для заземления сети.
Когда мы подключаем устройства к однофазной сети, не имеет особого значения, где именно находится пустая или рабочая фаза. Но когда мы монтируем в квартире электропроводку и подключаем ее к общей домашней сети, нужно это знать.
Разница между нулем и фазой на видео:
Самые простые способы
Есть несколько способов найти фазу и ноль. Рассмотрим их кратко.
Рассмотрим их кратко.
Для исполнения цвета прожилок
Самый простой, но в то же время и самый ненадежный способ — определить фазу и ноль по цветам изоляционных оболочек проводников. Как правило, фазовый провод имеет вариант черного, коричневого, серого или белого цвета, а ноль — синего или синего цвета. Чтобы держать вас в курсе, есть также зеленые или желто-зеленые провода, так обозначаются провода защитного заземления.
При этом никаких устройств не нужно, смотрели по цвету провода и определяли, фаза он или ноль.
Но почему этот метод самый ненадежный? И нет гарантии, что при установке электрики соблюдали цветовую кодировку жил и ничего не перепутали.
Цветовая кодировка ниток в следующем видео:
Индикаторная отвертка
Более верный метод — использовать индикаторную отвертку. Он состоит из непроводящего корпуса и встроенного резистора с индикатором, представляющего собой обычную неоновую лампу.
Например, при подключении переключателя важно не путать ноль с фазой, так как это устройство переключения работает только для одного диапазона фаз. Проверка индикаторной отверткой выглядит следующим образом:
- Отключите общий ввод автомата на квартиру.
- С помощью ножа зачистите тестируемые проводники от изоляционного слоя толщиной 1 см и отделите их на безопасном расстоянии друг от друга, чтобы полностью исключить возможность контакта.
- Подайте напряжение, включив входной автоматический выключатель.
- Острием отвертки коснитесь оголенных проводов. Если при этом загорается окошко индикатора, это означает, что провод соответствует первой фазе. Отсутствие свечения говорит о том, что найденная нить нулевая.
- Отметьте нужную жилу маркером или куском изоленты, затем снова выключите общий автомат и подключите коммутационный аппарат.
Более сложные и точные проверки выполняются с помощью мультиметра.
Поиск фазы индикаторной отверткой и мультиметром на видео:
youtube.com/embed/_WggwlRKU3o?feature=oembed» frameborder=»0″ allowfullscreen=»allowfullscreen»>Мультиметр. Что это за устройство?
Мультиметр (электрики также называют его тестером) — это комбинированный прибор для электрических измерений, сочетающий в себе множество функций, основными из которых являются омметр, амперметр и вольтметр.
Эти устройства разные:
- аналог;
- цифровой;
- легкий портативный для некоторых основных измерений;
- комплекс стационарный с множеством возможностей.
С помощью мультиметра можно не только определить землю, ноль или фазу, но и измерить ток, напряжение, сопротивление на участке цепи, проверить целостность электрической цепи.
Устройство представляет собой дисплей (или экран) и переключатель, который можно устанавливать в различные положения (вокруг восемь секторов). Вверху (в центре) есть сектор «ВЫКЛ», когда переключатель установлен в это положение, это означает, что устройство выключено. Для измерения напряжения вам необходимо установить переключатель в секторах «ACV» (для переменного напряжения) и «DCV» (для постоянного напряжения).
Для измерения напряжения вам необходимо установить переключатель в секторах «ACV» (для переменного напряжения) и «DCV» (для постоянного напряжения).
В комплекте мультиметра еще два измерительных щупа: черный и красный. Черный зонд подключается к нижнему разъему с пометкой «COM», это соединение является постоянным и используется для любых измерений. Красный зонд, в зависимости от измерений, вставляется в среднее или верхнее гнездо.
Как пользоваться устройством?
Выше мы рассмотрели, как найти фазный провод с помощью индикаторной отвертки, но отличить ноль от земли таким инструментом не получится. Итак, давайте узнаем, как проверить жилы мультиметром.
Петров Василий Александрович
Электромонтер 6 разряда, ООО «Петроэнергоспецмонтаж», 18 лет стажа
Задать вопрос
Подготовительный этап выглядит точно так же, как работа индикаторной отверткой. При отключенном напряжении зачистите концы проводов и обязательно разделите их, чтобы не вызвать случайный контакт и возникновение короткого замыкания.
 Подайте напряжение, теперь все дальнейшие работы будут с мультиметром:
Подайте напряжение, теперь все дальнейшие работы будут с мультиметром:Выберите на приборе диапазон измерения переменного напряжения выше 220 В. Как правило, в режиме «ACV» стоит знак со значением 750 В, установите переключатель в это положение.
- В устройстве есть три гнезда, в которые вставляются наконечники. Находим среди них то, что обозначено буквой «V» (т.е для измерения напряжения). Вставьте в него щуп.
- Коснитесь очищенных стержней зондом и посмотрите на экран устройства. Если вы видите небольшое значение напряжения (до 20 В), вы касаетесь фазного провода. Если на экране нет показаний, вы нашли ноль с помощью мультиметра.
Для определения «земли» очистите небольшой участок на любом металлическом элементе бытовых коммуникаций (это могут быть водопроводные или отопительные трубы, батареи).
В этом случае мы будем использовать два гнезда «COM» и «V», мы будем вставлять измерительные щупы. Установите устройство в режим «ACV» на значение 200 В.
У нас есть три провода, среди них нам нужно найти фазу, ноль и землю. Одним щупом касается чистого места на трубке или аккумуляторе, вторым — проводника. Если на дисплее отображается значение порядка 150–220 В, значит, вы нашли фазный провод. Для нулевого провода при аналогичных измерениях показание колеблется в пределах 5-10В, при касании «земли» на экране ничего не будет отображаться.
Отметьте каждую жилу маркером или изолентой и, чтобы убедиться, что измерения верны, сделайте измерения относительно друг друга.
Прикоснитесь двумя щупами к фазному и нейтральному проводам, на экране должна появиться цифра в пределах 220 В. Фаза с землей даст немного более низкие показания. А если коснуться нуля и земли, на экране отобразится значение от 1 до 10 В.
Некоторые правила использования мультиметра
Прежде чем определять фазу и ноль мультиметром, ознакомьтесь с некоторыми правилами, которые необходимо соблюдать при работе с прибором:
- Никогда не используйте мультиметр во влажной среде.

- Не используйте неисправные наконечники.
- Во время измерения не изменяйте пределы измерения и не перемещайте переключатель.
- Не измеряйте параметры, значение которых превышает верхний предел измерения устройства.
Как измерить напряжение мультиметром — в следующем видео:
Обратите внимание на важный нюанс использования мультиметра. Поворотный переключатель всегда должен быть изначально установлен в максимальное положение, чтобы избежать повреждения электронного устройства. А в дальнейшем, если показания будут ниже, переключатель перемещается в нижние отметки для более точных измерений.
0.00%
Осталось:
Понравилась статья? Поделиться с друзьями:
непрерывных сигналов — Как связаны графики полюс-ноль, графики амплитудной характеристики и графики фазовой характеристики?
Чтобы ответить на этот вопрос, важно понимать
- что такое преобразование Лапласа интуитивно делать,
- как преобразование Лапласа связано с комплексными входными и комплексными функциями вывода,
- как можно построить сложные входные и сложные выходные функции,
- что за полюс и ноль визуально есть, а
- что означают «отклик амплитуды» и «отклик фазы» $h(t)$.

Примечание: весь код, используемый для создания графиков в этом ответе, можно найти здесь.
Функции являются основой теории DSP, и в этом контексте она ничем не отличается. Функция $h(t)$, например, принимает действительное число $t$, которое может представлять время, и можно предположить, что оно выводит другое действительное число $h(t)$, которое может представлять напряжение, ток и т. д. Аналогичным образом мы могли бы определить другую функцию $f(x)$, которая принимает комплексное число $x$ и выводит другое комплексное число $f(x)$. Мы также могли бы определить другую функцию $g(x)$, которая принимает комплексное число $x$ и выводит действительное число $g(x)$. Учитывая, что $\mathbb{R}$ — это набор действительных чисел, а $\mathbb{C}$ — это набор комплексных чисел, для сокращения мы используем обозначение
$$
ч:\mathbb{R} \стрелка вправо \mathbb{R} \\
f:\mathbb{C} \стрелка вправо \mathbb{C} \\
g:\mathbb{C} \стрелка вправо \mathbb{R} \\
$$
Эти виды функций просты для понимания: они принимают число (действительное или сложное) и выводят другое число (действительное или сложное).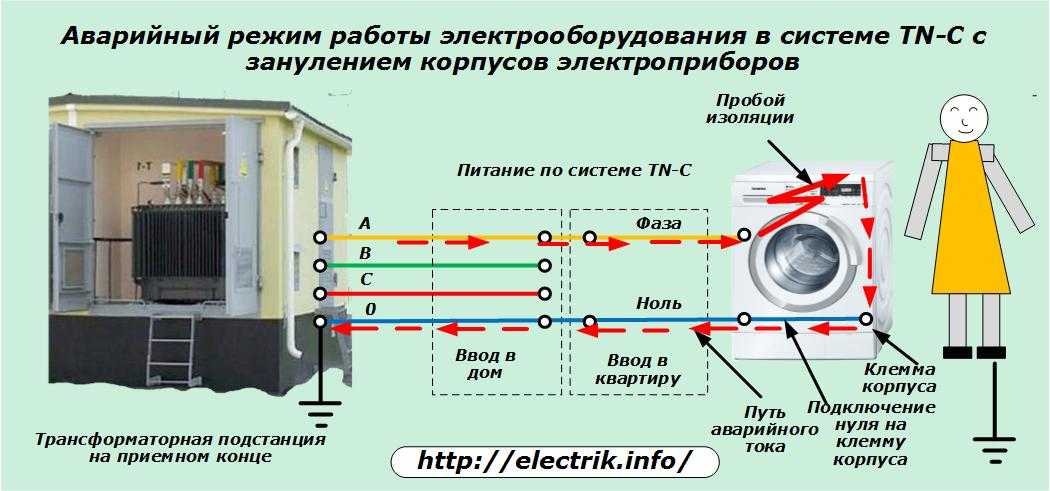
Точнее, если $h:\mathbb{R} \rightarrow \mathbb{R}$ является входной функцией и $f:\mathbb{C } \rightarrow \mathbb{C}$ — выходная функция, тогда мы могли бы определить 9{-st} \ \text{d}t $$ мы могли бы сократить это определение до $$ \mathcal{L}\{h(t)\} = H(s) $$ Обратите внимание, что функция сложного входа и выхода $f(x)$ была заменена функцией сложного входа и выхода $H(s)$. Это всего лишь изменение обозначения, и оно не имеет значения, так как и $x$, и $s$ считаются комплексными числами.
Мы можем легко построить функцию реального входа и реального выхода $h(t)$, поскольку она состоит только из двух изменяющихся чисел: входа и выхода.
Здесь мы отложили ввод по оси x и вывод по оси y.
Предположим, мы вычисляем преобразование Лапласа $h(t)$, чтобы получить $H(s)$. Если $H(s)$ представляет собой комплексную входную и комплексную функцию на выходе, можем ли мы построить ее, как мы сделали с примером $h(t)$, приведенным выше? Проблема с попыткой сделать это заключается в том, что для представления входных данных для $H(s)$ нам нужны два числа: действительная часть $s$ и мнимая часть $s$. Точно так же для представления комплексного выхода $H(s)$ нам нужны два числа: действительная часть $H(s)$ и мнимая часть $H(s)$. Всего 4 числа: 2 для ввода и 2 для вывода, что означает, что нам понадобится 4-мерный график для представления $H(s)$! 92} \\ \theta &= \text{atan2}\left(b,a\right) \end{выравнивание} $$ где $\text{atan2}$ — функция atan2. Следовательно, хороший способ визуально представить $H(s)$ – это
- . Представить входные данные для $H(s)$, равные $s$, в виде комплексного числа в прямоугольной форме ($a+bi$).
 ,
, - Представьте вывод $H(s)$ как комплексное число в полярной форме, а затем
- Создайте два 3D-графика: один для величины $C$ выходного сигнала, а другой для угла (фазы) $\theta$ выходного сигнала. Точнее, первый трехмерный график состоит из $C$ по оси z и $a$ и $b$ по осям x и y соответственно, а второй трехмерный график состоит из $\theta$ по оси z и $a$ и $b$ по осям x и y соответственно. 92)\справа)
\end{выравнивание}
$$
Наконец, последним шагом является создание двух 3D-графиков, одного для $C$ и другого для $\theta$. Эти графики показаны ниже.
Обратите внимание, что разрывы графика для $\theta$ связаны с функцией atan2.
Вот где становится интересно. Предположим, мы наносим на график величину ($C$) и фазу ($\theta$) комплексной входной и комплексной выходной функции $$ H (s) = \ frac {(s — 0,5)} {(s — 1,5) (s + 2)} $$
На графике величины для $H(s)$ видно, что $|H(s)|$ стремится к бесконечности вблизи $s = 1,5$ и $s = -2$. Обратите внимание, что если вы возьмете очень длинный и тонкий флагшток и установите его на $s = 1,5$, поверхность $|H(s)|$ никогда не коснется его.


Мы можем даже увеличить фиолетовые контуры выше, а затем построить двухмерные версии амплитудной и фазовой характеристик, используя пакет
scipy, и мы увидим, что они точно такие же:Вспомним, что полюса $H(s )$ выше равны $s = 1,5$ и $s = -2$. Основываясь на приведенных выше графиках, можно было бы ожидать, что по мере приближения этих полюсов к воображаемой оси отклик величины будет «подтягиваться» при $\omega = 0$. Например, предположим, что мы перемещаем полюсы $H(s)$ в точки $s = 0,1$ и $s = -0,5$ так, что $$ H (s) = \ frac {(s — 0,5)} {(s — 0,1) (s + 0,5)} $$ Соответствующие величины и фазовые характеристики равны
Обратите внимание, что отклик величины очень высок при $\omega = 0$ (некоторая прозрачность была добавлена к поверхностным графикам, чтобы сделать контуры более четкими).
 На самом деле это пример очень селективного полосового/фильтра нижних частот. Мы можем разработать другие фильтры, используя этот метод, заметив, что нули «отягивают» отклики амплитуды вниз. Например, вот фильтр верхних частот:
$$
H (s) = \ frac {s (s + 0,5j) (s — 0,5j)} {(s — (-0,5 + 1,5j)) (s — (-0,5 — 1,5j))}
$$
На самом деле это пример очень селективного полосового/фильтра нижних частот. Мы можем разработать другие фильтры, используя этот метод, заметив, что нули «отягивают» отклики амплитуды вниз. Например, вот фильтр верхних частот:
$$
H (s) = \ frac {s (s + 0,5j) (s — 0,5j)} {(s — (-0,5 + 1,5j)) (s — (-0,5 — 1,5j))}
$$Из этого обсуждения становится ясно, что трехмерные графики амплитуды и фазы $H(s)$ можно использовать для определения двухмерной амплитуды и фазы ответов $h(t)$ есть. Кроме того, поскольку Z-преобразование является частным случаем преобразования Лапласа, аналогичная интерпретация может быть получена для сигналов с дискретным временем. Раздел 6.2 Ричарда Лайонса «Понимание цифровой обработки сигналов » расширяет это объяснение более подробно. Наконец, инструмент MATLAB Filter Designer позволяет вам в интерактивном режиме перемещать полюса и нули и наблюдать за соответствующими амплитудными и фазовыми откликами, что я считаю чрезвычайно полезным.

fft — Эквивалент фильтрации нулевой фазы в частотной области («filtfilt»)
спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 669 раз
$\begingroup$
В связи с этим вопросом @Molem7b5, что было бы эквивалентом в частотной области (реализация фильтра посредством сложения с перекрытием ДПФ) для нуль-фазового фильтра, реализованного с помощью MATLAB/Octave/Python scipy.signal
filtfiltкоманда?- fft
- конечный импульс-отклик
- перекрытие-сложение
$\endgroup$
$\begingroup$
По сути, filtfilt делает следующее
$$y[n] = x[n] \ast h[n] \ast h[-n]$$
Это свертка с импульсной характеристикой, а затем обратное время импульсная характеристика (в любом порядке, поскольку свертка коммутативна).




 Подайте напряжение, теперь все дальнейшие работы будут с мультиметром:
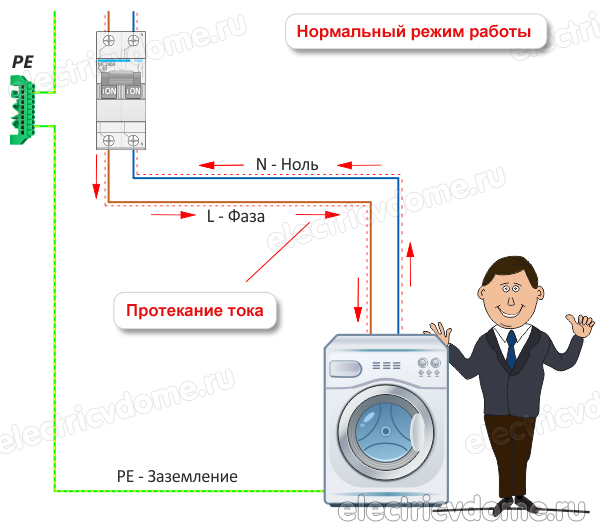
Подайте напряжение, теперь все дальнейшие работы будут с мультиметром: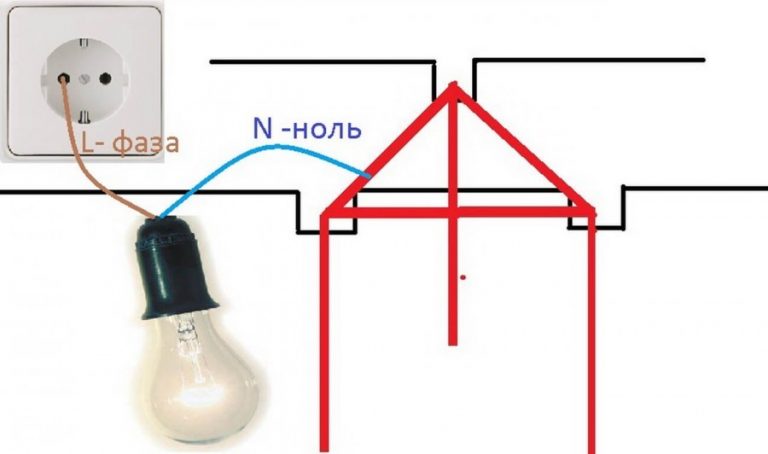

 ,
,

 На самом деле это пример очень селективного полосового/фильтра нижних частот. Мы можем разработать другие фильтры, используя этот метод, заметив, что нули «отягивают» отклики амплитуды вниз. Например, вот фильтр верхних частот:
$$
H (s) = \ frac {s (s + 0,5j) (s — 0,5j)} {(s — (-0,5 + 1,5j)) (s — (-0,5 — 1,5j))}
$$
На самом деле это пример очень селективного полосового/фильтра нижних частот. Мы можем разработать другие фильтры, используя этот метод, заметив, что нули «отягивают» отклики амплитуды вниз. Например, вот фильтр верхних частот:
$$
H (s) = \ frac {s (s + 0,5j) (s — 0,5j)} {(s — (-0,5 + 1,5j)) (s — (-0,5 — 1,5j))}
$$
