Сопротивление в цепи переменного тока. (11 класс)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс
НАГРУЗКА В ЦЕПИ ПЕРЕМЕННОГОТОКА
РЕАКТИВНАЯ
Индуктивная
АКТИВНАЯ
Емкостная
3. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
• Электрические устройства, преобразующиеэлектрическую энергию во внутреннюю,
называются активными сопротивлениями.
15 Ом
4.
 АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА• От чего зависит активное сопротивление
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА• От чего зависит активное сопротивлениепроводника?
5. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим сначала цепь, состоящую из одного лишь
сопротивления , подключённого к синусоидальной ЭДС:
• Из второго правила Кирхгофа для такой цепи
можно сделать следующие три вывода:
• 1) ток через сопротивление совершает гармонические колебания в
одной фазе с напряжением;
• 2) максимальная сила тока (достигается при значении синуса,
равном единице) ;
• 3) связь амплитуд силы тока и напряжения на сопротивлении
формально совпадает с законом Ома для участка цепи с постоянным
током.
6. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
iu
R
7. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
• Емкостное сопротивление — величина,характеризующая сопротивление, оказываемое
переменному току электрической емкостью
8. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
9.
 ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАРассмотрим цепь, состоящую из одной лишь ёмкости , подключенной к
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАРассмотрим цепь, состоящую из одной лишь ёмкости , подключенной ксинусоидальной ЭДС. Второе правило Кирхгофа для такой цепи
Тогда сила тока .
Величина
называется ёмкостным сопротивлением.
Можно сделать следующие три вывода:
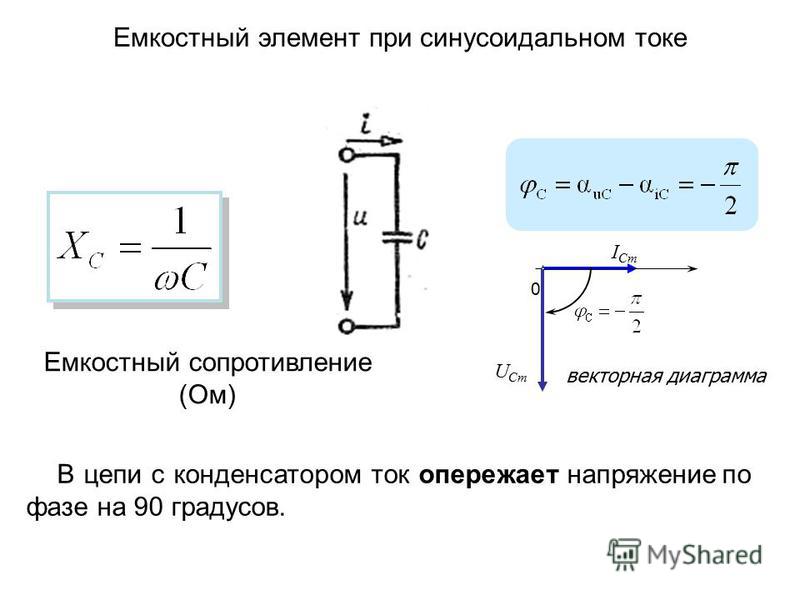
1) ток в цепи совершает гармонические колебания, опережая по фазе
напряжение на
;
2) максимальная сила тока
;
3) связь амплитуд силы тока и напряжения на конденсаторе формально
совпадает с законом Ома для участка цепи в случае постоянных токов.
10. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
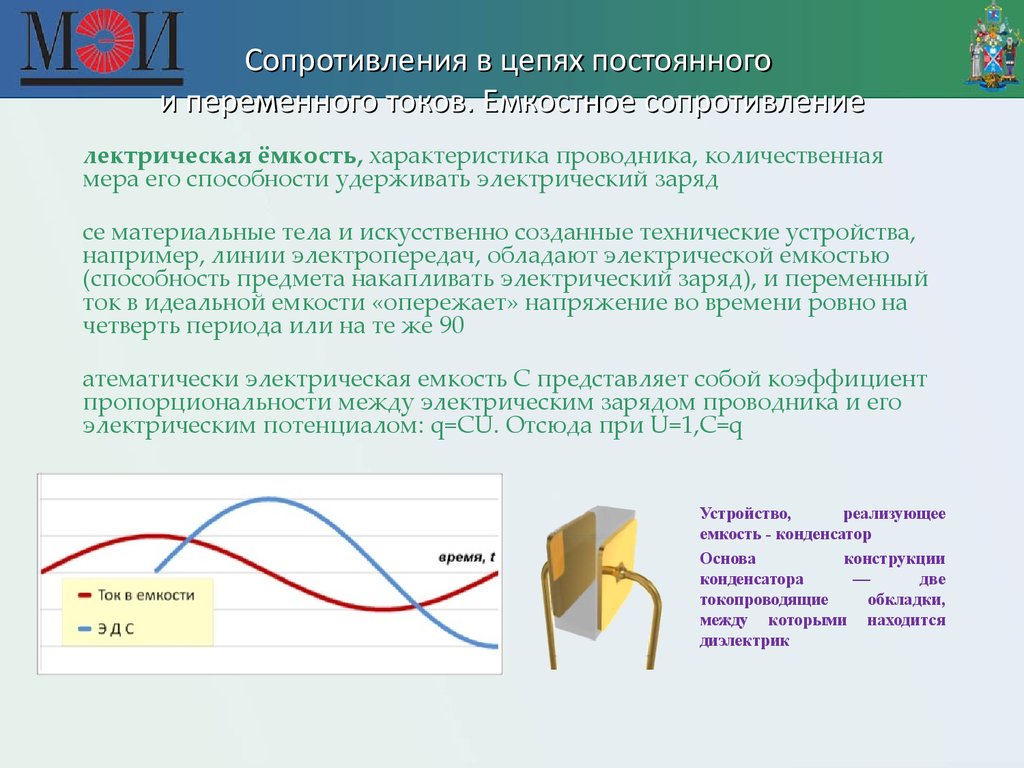
Почему конденсатор оказывает конечноесопротивление переменному току? Ведь между
обкладками конденсатора – диэлектрик, а
значит, цепь разомкнута, и её сопротивление
должно быть очень большим. Этот факт имеет
простое объяснение. Переменный
электрический ток не проходит сквозь
конденсатор, а представляет собой
периодически повторяющийся процесс
зарядки и разрядки конденсатора.

11. ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i,u
i
u
t
0
Uc
Ic
12. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Индуктивное сопротивление- величина,характеризующее сопротивление, оказываемое
переменному току индуктивностью цепи
13. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
14. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим цепь, состоящую из одной лишь катушки индуктивности ,присоединённой к синусоидальной ЭДС. Второе правило Кирхгофа для
такой цепи
Интегрируя, получаем:
Величина
называется индуктивным сопротивлением.
Можно сделать следующие три вывода:
1) ток через индуктивность совершает гармонические колебания и отстаёт
от напряжения по фазе на
;
2) максимальная сила тока
;
3) связь амплитуд силы тока и напряжения на индуктивности формально
совпадает с законом Ома для участка цепи в случае постоянных токов.
15.
 ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАi,
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКАi,u
i
u
t
U
0
16. ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
17. Сравнить накал лампочек, подключённых к синусоидальному и постоянному напряжениям. Накал лампочек для рисунка (а) одинаков.
Одинаковый накал лампочек на рис (а)означает, что напряжения источника
постоянного тока равно эффективному
напряжению источника переменного тока
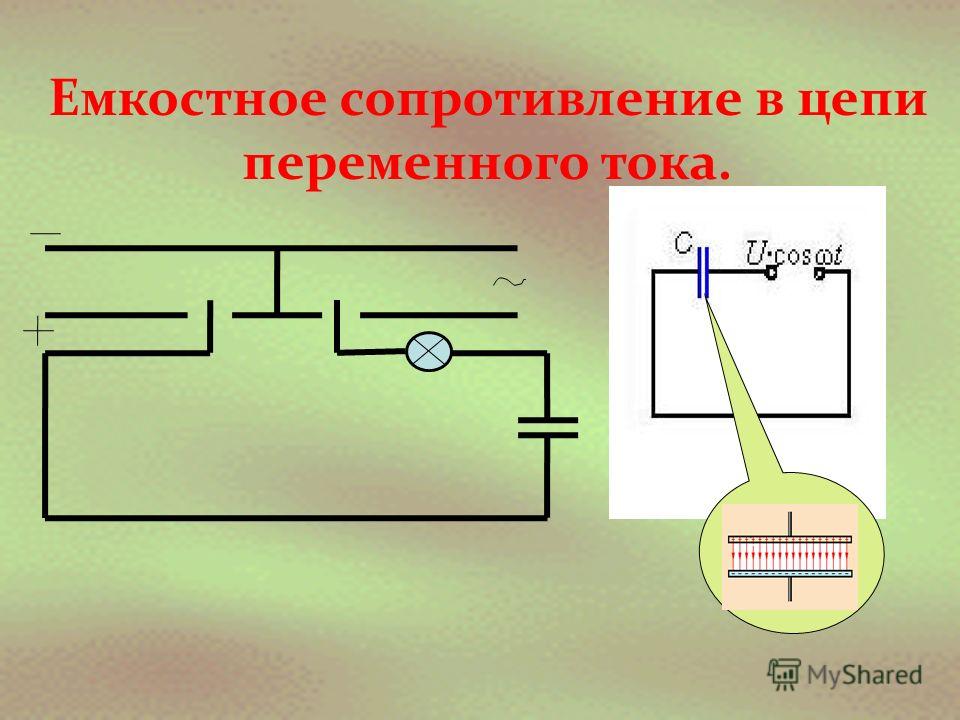
Если в обе цепи включить конденсатор
достаточно большой ёмкости (б), то лампочка в
цепи источника переменного тока будет попрежнему гореть ярко, поскольку ёмкостное
сопротивление переменному току обратно
пропорционально ёмкости и, следовательно,
будет мало. В цепи постоянного тока накал
отсутствует, поскольку между обкладками
конденсатора диэлектрик, и цепь разомкнута.
анализируя формулу
.
Постоянный ток означает, что циклическая частота
,
и, значит,
.
Если в обе цепи включить катушку достаточно большой индуктивности, то ток в цепи источника
переменного тока будет мал из-за большого индуктивного сопротивления, лампочка погаснет, а в цепи
источника постоянного тока лампочка по-прежнему будет гореть ярко, поскольку индуктивное
сопротивление постоянному току равно нулю.
 Действительно, в случае постоянного тока
Действительно, в случае постоянного тока,и
индуктивное сопротивление
.
18. Метод векторных диаграмм
1) Векторнаправлен вдоль оси 0x
так как напряжение на активном
сопротивлении колеблется в одной фазе
с током.
U 0 U 0 R U 0 L U 0C
2) напряжение на индуктивности
опережает ток по фазе на
, вектор
повёрнут относительно оси 0x на угол
против часовой стрелки, т.е. направлен
вдоль положительного направления оси
0y.
3) напряжение на ёмкости отстаёт от
тока по фазе на
, вектор
повёрнут относительно оси 0x на угол
по часовой стрелке, т.е. направлен
вдоль отрицательного направления
оси 0y.
Сначала удобно сложить противоположно направленные вектора
и
сумма равна вектору, направленному вдоль оси 0y и по величине равному
. Их
,
где реактивное сопротивление цепи. Далее по теореме Пифагора
находим величину результирующего вектора
Величина
называется полным
сопротивлением цепи.

20. закон Ома для переменного тока
21. Пример Рассчитать допустимую амплитуду напряжения генератора в электрической цепи на рис, если пробой конденсатора наступает
при напряжении U=500 В.Параметры схемы: C=10 мкФ, L= 1Гн, R=3 Ом, частота
генератора 50 Гц.
22. Cдвиг фаз между током в цепи и суммарным напряжением на концах цепи
• Сдвиг фаз равен углумежду векторами
и . Из
прямоугольного
треугольника
1
L
I0 X X
C
tg
I0R R
R
English Русский Правила
Сопротивление в цепи переменного тока. (11 класс) презентация, доклад
АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
11 класс
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Электрические устройства, преобразующие электрическую энергию во внутреннюю, называются активными сопротивлениями.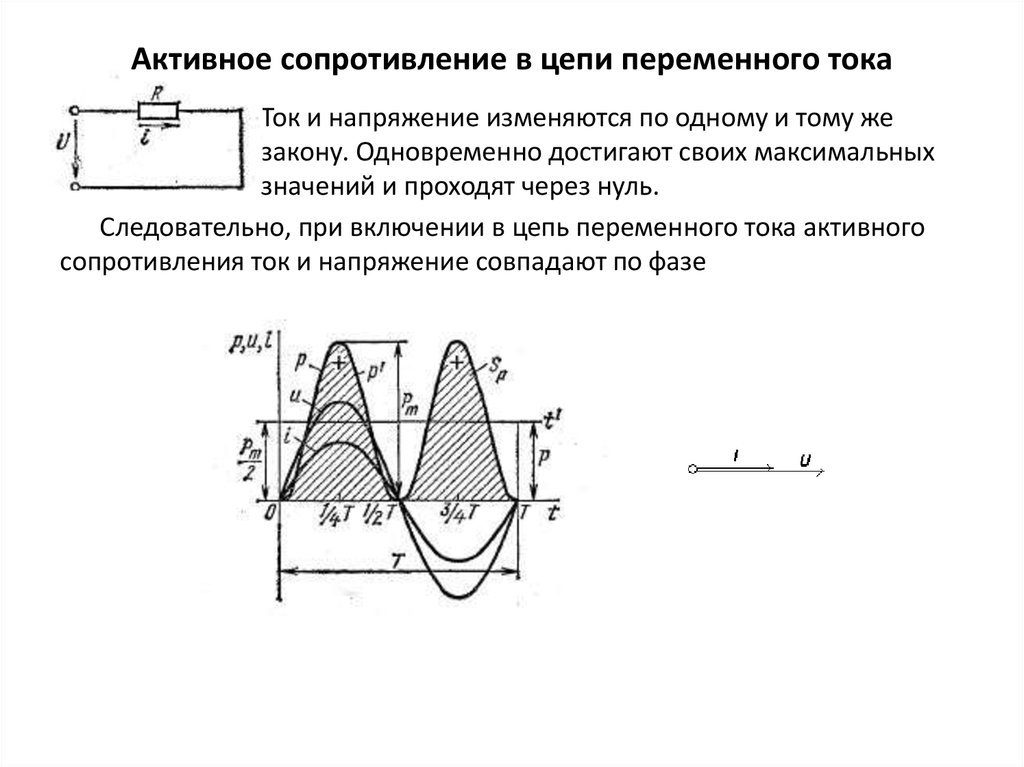
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
От чего зависит активное сопротивление проводника?
Удельное сопротивление проводника
Длина проводника в метрах
Площадь поперечного сечения проводника в мм2
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим сначала цепь, состоящую из одного лишь сопротивления , подключённого к синусоидальной ЭДС:
Из второго правила Кирхгофа для такой цепи
можно сделать следующие три вывода:
1) ток через сопротивление совершает гармонические колебания в одной фазе с напряжением;
2) максимальная сила тока (достигается при значении синуса, равном единице) ;
3) связь амплитуд силы тока и напряжения на сопротивлении формально совпадает с законом Ома для участка цепи с постоянным током.
АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i
u
R
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Емкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим цепь, состоящую из одной лишь ёмкости , подключенной к синусоидальной ЭДС. Второе правило Кирхгофа для такой цепи
Второе правило Кирхгофа для такой цепи
Тогда сила тока .
Величина называется ёмкостным сопротивлением.
Можно сделать следующие три вывода:
1) ток в цепи совершает гармонические колебания, опережая по фазе напряжение на ;
2) максимальная сила тока ;
3) связь амплитуд силы тока и напряжения на конденсаторе формально совпадает с законом Ома для участка цепи в случае постоянных токов.
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Почему конденсатор оказывает конечное сопротивление переменному току? Ведь между обкладками конденсатора – диэлектрик, а значит, цепь разомкнута, и её сопротивление должно быть очень большим. Этот факт имеет простое объяснение. Переменный электрический ток не проходит сквозь конденсатор, а представляет собой периодически повторяющийся процесс зарядки и разрядки конденсатора.
ЕМКОСТНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i, u
t
i
u
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Индуктивное сопротивление- величина, характеризующее сопротивление, оказываемое переменному току индуктивностью цепи
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Рассмотрим цепь, состоящую из одной лишь катушки индуктивности , присоединённой к синусоидальной ЭДС. Второе правило Кирхгофа для такой цепи
Интегрируя, получаем:
Величина называется индуктивным сопротивлением. Можно сделать следующие три вывода:
1) ток через индуктивность совершает гармонические колебания и отстаёт от напряжения по фазе на ;
2) максимальная сила тока ;
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i, u
t
i
u
I
U
0
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Сравнить накал лампочек, подключённых к
синусоидальному и постоянному напряжениям.
Накал лампочек для рисунка (а) одинаков.
Одинаковый накал лампочек на рис (а) означает, что напряжения источника постоянного тока равно эффективному напряжению источника переменного тока
Если в обе цепи включить конденсатор достаточно большой ёмкости (б), то лампочка в цепи источника переменного тока будет по-прежнему гореть ярко, поскольку ёмкостное сопротивление переменному току обратно пропорционально ёмкости и, следовательно, будет мало. В цепи постоянного тока накал отсутствует, поскольку между обкладками конденсатора − диэлектрик, и цепь разомкнута.
анализируя формулу . Постоянный ток означает, что циклическая частота , и, значит, .
Если в обе цепи включить катушку достаточно большой индуктивности, то ток в цепи источника переменного тока будет мал из-за большого индуктивного сопротивления, лампочка погаснет, а в цепи источника постоянного тока лампочка по-прежнему будет гореть ярко, поскольку индуктивное сопротивление постоянному току равно нулю. Действительно, в случае постоянного тока , и индуктивное сопротивление .
Метод векторных диаграмм
1) Вектор направлен вдоль оси 0x так как напряжение на активном сопротивлении колеблется в одной фазе с током.
2) напряжение на индуктивности опережает ток по фазе на , вектор повёрнут относительно оси 0x на угол против часовой стрелки, т.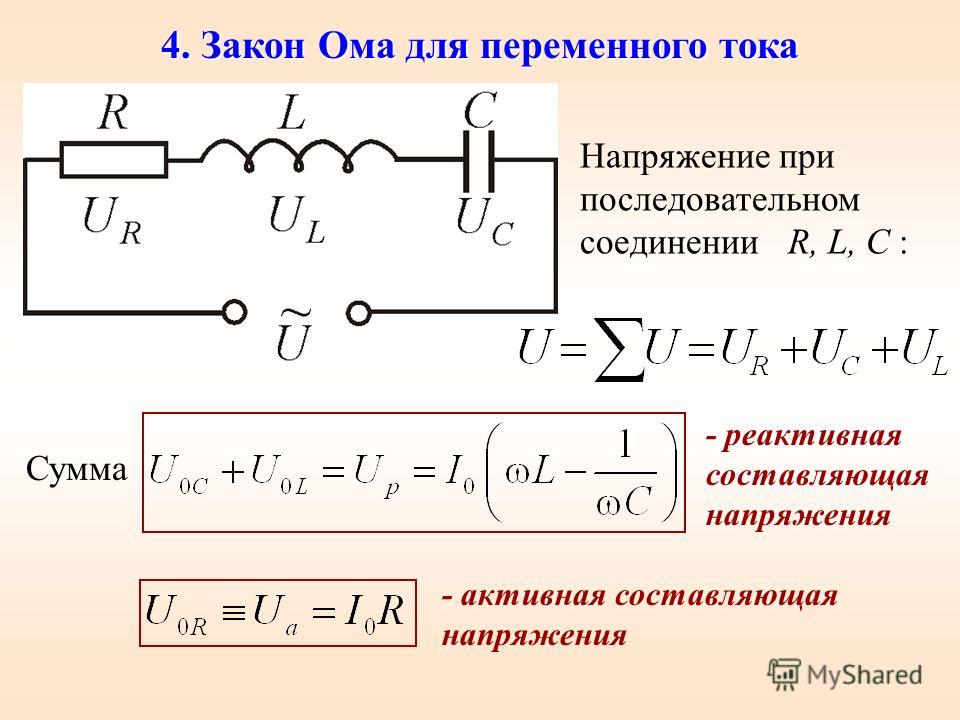 е. направлен вдоль положительного направления оси 0y.
е. направлен вдоль положительного направления оси 0y.
3) напряжение на ёмкости отстаёт от тока по фазе на , вектор повёрнут относительно оси 0x на угол по часовой стрелке, т.е. направлен вдоль отрицательного направления оси 0y.
Сначала удобно сложить противоположно направленные вектора и . Их сумма равна вектору, направленному вдоль оси 0y и по величине равному
, где − реактивное сопротивление цепи. Далее по теореме Пифагора находим величину результирующего вектора
Величина
называется полным сопротивлением цепи.
закон Ома для переменного тока
Пример Рассчитать допустимую амплитуду напряжения генератора в электрической цепи на рис, если пробой конденсатора наступает при напряжении U=500 В.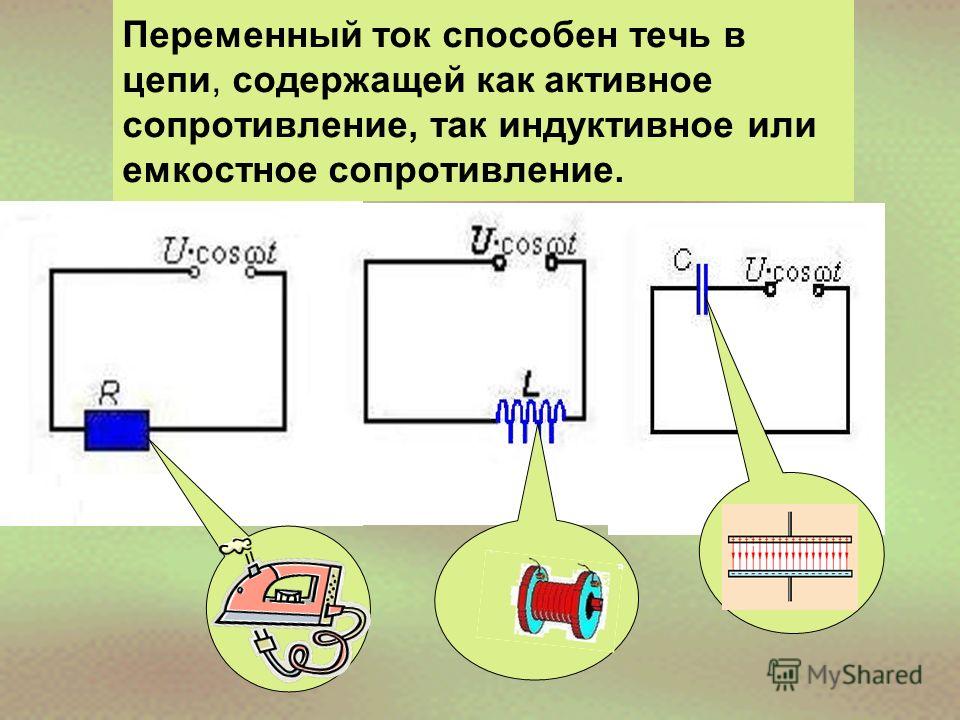
Cдвиг фаз между током в цепи и суммарным напряжением на концах цепи
Сдвиг фаз равен углу между векторами и . Из прямоугольного треугольника
Презентация к уроку 11 класс:Активное индуктивное сопротивление в цепи переменного тока доклад, проект
СОПРОТИВЛЕНИЯ
В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
РЕЗОНАНС В
ПОСЛЕДОВАТЕЛЬНОЙ
ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ
Тема урока:
«СОПРОТИВЛЕНИЯ
В ЦЕПИ ПЕРЕМЕННОГО ТОКА»
Учитель физики
МАОУ «СОШ №7»г.Улан-Удэ
Культикова С.А.
R,C,L в цепи переменного тока
Вопросы для изучения:
Действующие значения тока и напряжения.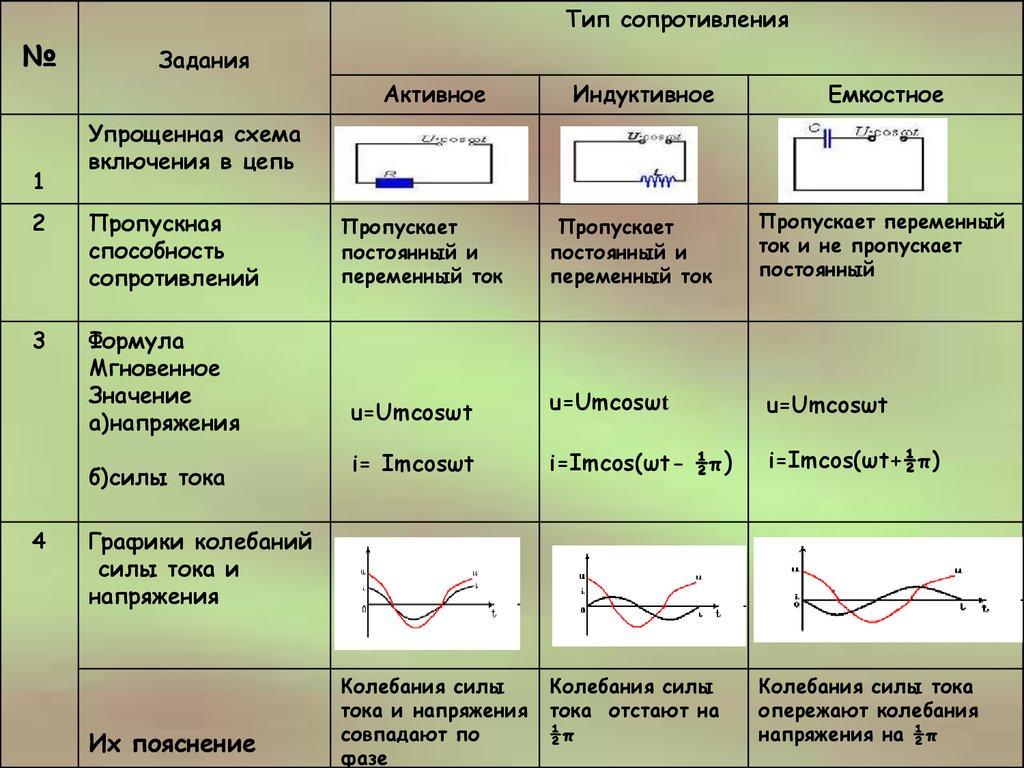 Активное сопротивление в цепи ~ тока
Активное сопротивление в цепи ~ тока
Конденсатор в цепи ~ тока
Индуктивность в цепи ~ тока
Использование частотных свойств конденсатора и катушки индуктивности
R C L
@ Краснополянская школа № 1 Домнин Константин Михайлович 2006 год
в цепи переменного тока -1
1.Действующие значения тока и напряжения. Активное сопротивление в цепи переменного тока
Действующие значения тока и напряжения, виды сопротивлений
Рассмотрим активное сопротивление в цепи переменного тока:
R
Мгновенное значение силы тока через активное сопротивление пропорционально мгновенному значению напряжения
Колебания напряжения и силы тока на активном сопротивлении совпадают по фазе
РЕЗИСТОР В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
u = Um cos ω t – мгновенное значение напряжения
i = Im cos ω t – мгновенное значение силы тока
– действующее значение
силы тока
– действующее значение
напряжения
– закон Ома для цепи переменного тока с
резистором, R – активное сопротивление
P = IU = I2R – действующее значение мощности
РЕЗИСТОР В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
i
i, u
t
u
В цепи переменного тока, содержащей активное сопротивление, колебания силы тока i и напряжения и совпадают по фазе
2. Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока
C
Конденсатор в цепи переменного тока
Давайте вспомним, что такое конденсатор
Конденсатор – это система из двух проводников, разделенных слоем диэлектрика (воздуха, слюды, керамики …)
Ясно, что конденсатор – это разрыв в цепи (подобно разомкнутому выключателю), поэтому постоянный ток конденсатор не проводит
Конденсатор в цепи переменного тока
Итак, конденсатор проводит переменный ток, однако он оказывает току сопротивление, которое называется емкостным сопротивлением
— емкостное сопротивление
— циклическая частота протекающего тока
С – электроемкость конденсатора
— частота тока
КОНДЕНСАТОР В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
– закон Ома для цепи переменного тока с
конденсатором
– емкостное сопротивление
q = C Um cos ω t — мгновенное значение заряда
u = Um cos ω t — мгновенное значение напряжения
i = q΄= – С Um ω sin ω t
Im = Um C ω — максимальное значение силы тока
i = Im cos (ω t + π) — мгновенное значение силы тока
i
i, u
t
u
КОНДЕНСАТОР В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
В цепи переменного тока, содержащей конденсатор, колебания силы тока i опережают колебания напряжения u на
КОНДЕНСАТОР В ЦЕПИ
ПЕРЕМЕННОГО ТОКА
3. Индуктивность в цепи переменного тока
Индуктивность в цепи переменного тока
L
Индуктивность в цепи переменного тока
Давайте вспомним, что такое индуктивность
Индуктивность L– это физическая величина, подобная массе в механике. Как в механике для изменения скорости тела нужно время, и масса является мерой этого времени (инерция), так и электродинамике для изменения тока через проводник нужно время и индуктивность является мерой этого времени (самоиндукция)
Катушка индуктивности – это обычный проводник с необычной формой, обладающий активным сопротивлением.
Поэтому катушка хорошо проводит постоянный ток, значение которого ограничено только его активным сопротивлением
L
Явление самоиндукции возникает только в моменты включения и выключения (препятствует любому изменению тока)
Индуктивность в цепи переменного тока
Посмотрим, как ведет себя индуктивность в цепи переменного тока:
~
Источник ~ тока, обладающий и r
Замкнем цепь и сравним яркость горения лампочек 1 и 2
Л1
Л2
В цепи сопротивление R поберем равным активному сопротивлению L
R
L
Лампочка Л1 горит гораздо ярче, чем Л2
Почему ?
Индуктивность в цепи переменного тока
Все дело в явлении самоиндукции, возникающей в катушке при любом изменении тока, которое мешает этому изменению – поэтому у катушки индуктивности кроме активного сопротивления провода, из которого она сделана, появляется еще одно сопротивление, обусловленное явлением самоиндукции и называемое индуктивным сопротивлением X L
— циклическая частота протекающего тока
L – индуктивность катушки
— частота тока
КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
i = Im sin ωt — мгновенное значение силы тока
еi = – L i΄= – L Im ω cos ωt
и = – еi = Um sin (ωt + ) – мгновенное значение напряжения
Um = L Im ω
– закон Ома для цепи переменного тока с
катушкой индуктивности
XL = ω L – индуктивное сопротивление
i
i, u
t
u
КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
В цепи переменного тока, содержащей катушку индуктивности, колебания напряжения и опережают колебания силы тока i на
КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
ЗАКОН ОМА ДЛЯ ЦЕПИ ПЕРЕМЕННОГО ТОКА, СОДЕРЖАЩЕЕЙ РЕЗИСТОР, КОНДЕНСАТОР, КАТУШКУ ИНДУКТИВНОСТИ
РЕЗОНАНС В ПОСЛЕДОВАТЕЛЬНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний тока при совпадении частот ω0 = ω, где
ω 0 – собственная частота колебаний контура;
ω – частота питающего напряжения
Когда в цепи наблюдается резонанс
Амплитуда установившихся колебаний
, при R → 0, I → ∞
При максимальной силе тока:
==> T = Tсоб (ω = ωсоб )
5. Использование частотных свойств конденсатора и катушки
Использование частотных свойств конденсатора и катушки
Таким образом, в цепи переменного тока можно выделить 3 вида сопротивлений (или три вида элементов, оказывающих сопротивление току)
СОПРОТИВЛЕНИЕ
активное
реактивное
индуктивное
емкостное
Реальные электрические цепи содержат все виды сопротивлений (активное, индуктивное и емкостное), поэтому ток в реальной цепи зависит от ее полного (эквивалентного) сопротивления, а сдвиг фаз определяется величиной L и C цепи
R
XL
XC
Тестирование
запущено
Название сайта: zzi.sh
Код nue2655
Название теста:
11класс активное, индуктивное, ёмкостное
сопротивление
ДОМАШНЕЕ ЗАДАНИЕ
Работа с теорией
§§ 27-31.
Выписать формулы,
определения
https://kulitikova. wixsite.com/cji37
wixsite.com/cji37
«4-5» Выполнение письменной работы на gmail.com
СПАСИБО ЗА УРОК!
АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс
АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс — скачать презентациюНажмите для полного просмотра!
Вы можете ознакомиться и скачать
АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс .
Презентация содержит 22 слайдов.
Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс
Слайд 2
Описание слайда:
Заполнить таблицу
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Электрические устройства, преобразующие электрическую энергию во внутреннюю, называются активными сопротивлениями. Электрические устройства, преобразующие электрическую энергию во внутреннюю, называются активными сопротивлениями.
Слайд 5
Описание слайда:
От чего зависит активное сопротивление проводника? От чего зависит активное сопротивление проводника?
Слайд 6
Описание слайда:
МГНОВЕННОЕ ЗНАЧЕНИЕ НАПРЯЖЕНИЯ на зажимах цепи меняется по гармоническому закону: МГНОВЕННОЕ ЗНАЧЕНИЕ НАПРЯЖЕНИЯ на зажимах цепи меняется по гармоническому закону: МГНОВЕННОЕ ЗНАЧЕНИЕ СИЛЫ ТОКА
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Емкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью Емкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Слайд 14
Описание слайда:
Слайд 15
Описание слайда:
Одинаков ли цвет фигур?
Слайд 16
Описание слайда:
Слайд 17
Описание слайда:
Слайд 18
Описание слайда:
Слайд 19
Описание слайда:
Слайд 20
Описание слайда:
Слайд 21
Описание слайда:
Слайд 22
Описание слайда:
Литература
Мякишев Г. Я., Буховцев Б.Б. «Физика 11»
http://www.uzdog.su/viewtopic.php?p=2612
Я., Буховцев Б.Б. «Физика 11»
http://www.uzdog.su/viewtopic.php?p=2612
Теги АКТИВНОЕ, ЕМКОСТНОЕ И ИНДУКТИВНОЕ СОПРОТИВЛЕНИЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА 11 класс
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Mypresentation.ru
Загрузить презентациюЗакрыть (X)
Презентация «Переменный ток» (47 слайдов)
Слайд 1
1
ПЕРЕМЕННЫЙ ТОК –
– электрический ток, который с
течением времени изменяется.
Слайд 2
2
Мгновенное значение силы переменного тока
меняется во времени по гармоническому
(синусоидальному) закону
U =Um cos t
i = Im cos (t+)
Слайд 3
3
Скрелин Вариант 1.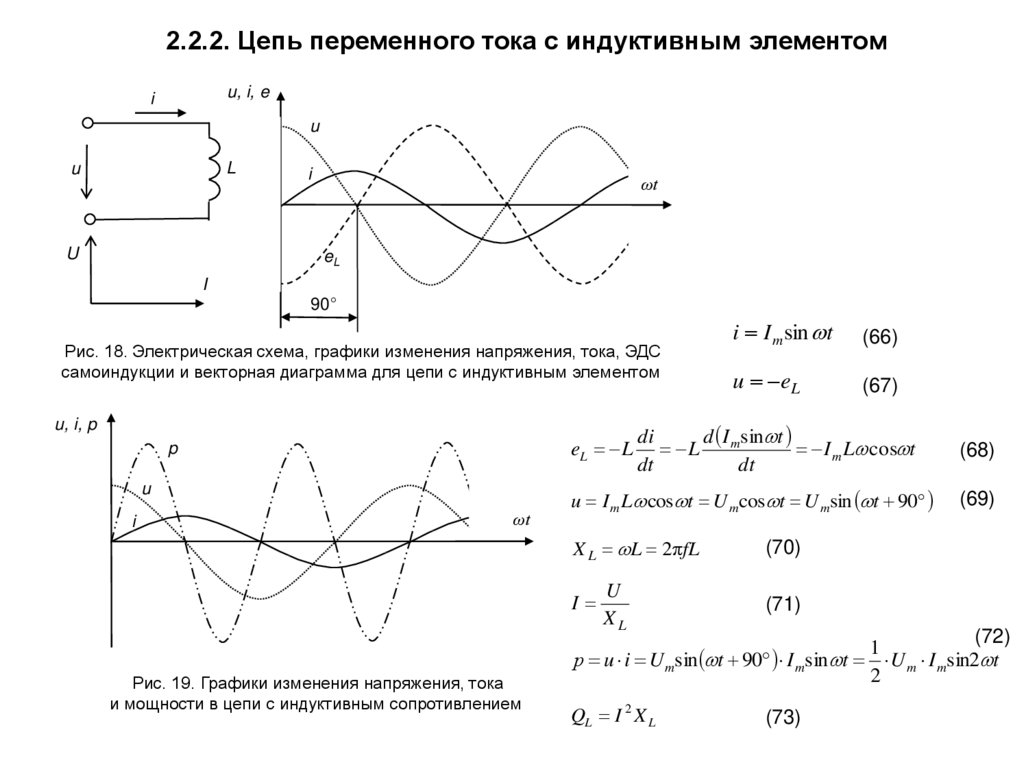 /II
/II
Т
U
Т=0,012 с
Um = 20 В
Слайд 4
4
КОРОЛЬ ЭКСПЕРИМЕНТА
МАЙКЛ
ФАРАДЕЙ
1791 г.
1867 г.
Слайд 5
5
ГЛАВНОЕ ОТКРЫТИЕ ДЭВИ – ФАРАДЕЙ —
английский физик. Родился 22 сентября 1791 в предместье Лондона в семье кузнеца. С 12 лет работал разносчиком газет, затем учеником в переплетной мастерской. Занимался самообразованием, читал книги по химии и электричеству. В 1813 один из заказчиков подарил Фарадею пригласительные билеты на лекции Г.Дэви в Королевском институте, сыгравшие решающую роль в судьбе Фарадея..
Слайд 6
6
Майкл
Фарадей
Слайд 7
7
Рамка крутится в магните
Не ленитесь, посмотрите
Рамка крутится, “поёт”,
Переменный ток идёт.
Кольца, щётки, проводок
Быстро пролетел урок.
Ф=ВS cos
Производную поймай-ка,
Или, попросту, возьми,
Фарадея помяни !
Ф=ВS cos t
= — В S sin t
Ф=10 cos2 t
= — 20 sin(2t)
=20 cos(2t+/2)
Слайд 8
8
Ф=10 cos2 t
=20 cos(2t+/2)
Слайд 9
9
Принцип действия генератора Выработка электроэнергии. swf
swf
Слайд 10
10
Электродинамические машины
различной конструкции школьные
Слайд 11
11
АКТИВНОЕ
СОПРОТИВЛЕНИЕ –
ЭЛЕКТРИЧЕСКАЯ
ЭНЕРГИЯ
НЕОБРАТИМО
ПРЕОБРАЗУЕТСЯ
ВО ВНУТРЕННЮЮ
ЭНЕРГИЮ
Слайд 12
12
Слайд 13
13
Слайд 14
14
ЗАКОН ОМА
Слайд 15
15
КАТУШКА
В ЦЕПИ
ПЕРЕМЕННОГО
ТОКА
Колебания тока на катушке
отстают от колебаний напряжения
на четверть периода
Слайд 16
16
Уравнения:
U=U0coswt
i =I0 cos(wt — p/2)
Слайд 17
17
График тока сдвинут вправо на /2.
Слайд 18
18
ИНДУКТИВНОЕ СОПРОТИВЛЕНИЕ –
физическая величина, характеризующая дополнительное влияние катушки, которое она оказывает протеканию через нее переменного тока (помимо активного сопротивления). Возникновение индуктивного сопротивления в цепи переменного тока обусловлено явлением самоиндукции.
Возникновение индуктивного сопротивления в цепи переменного тока обусловлено явлением самоиндукции.
Слайд 19
19
КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА
Колебания тока опережают колебания напряжения на четверть периода
График тока сдвинут влево на /2.
Слайд 20
20
Слайд 21
21
Слайд 22
22
Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями
Слайд 23
23
О Б О З Н А Ч Е Н И Я
U
Um
Uд
i
Im
Iд
R
L
C
Z
XL
X C
t
0
Слайд 24
24
Ф О Р М У Л Ы
U=Um cos t
I=Im cos (t+0)
= t+0
Слайд 25
25
Слайд 26
26
Слайд 27
27
Слайд 28
28
Слайд 29
29
Слайд 30
30
Задачи
Слайд 31
31
По графику, изображенному
на рисунке, определите амплитуду ЭДС, период тока и частоту. Напишите уравнение ЭДС.
Напишите уравнение ЭДС.
Задача №1
Слайд 32
32
По графику, изображенному на рисунке, определите амплитуду силы тока, период и частоту. Напишите уравнение мгновенного значения силы переменного тока
Задача №2
Слайд 33
33
Задача №3
По графику, изображенному
на рисунке, определите амплитуду ЭДС, период тока и частоту. Напишите уравнение ЭДС.
Слайд 34
34
Задача №4
По графику, изображенному на рисунке, определите амплитуду силы тока, период и частоту. Напишите уравнение мгновенного значения силы переменного тока
Слайд 35
35
Задача №5
По графику, изображенному на рисунке, определите амплитуду напряжения , период и частоту. Напишите уравнение мгновенного значения напряжения переменного тока
Слайд 36
36
Значение силы тока, измеренное
в Амперах, задано уравнением
I = 0,28 sin50t,
где t выражено в секундах.
Определите амплитуду силы тока,
частоту и период.
Задача №6
Слайд 37
37
Значение ЭДС, измеренное
в Вольтах, задано уравнением
е = 50 cos5t,
где t выражено в секундах.
Определите амплитуду ЭДС,
период и частоту.
Задача №7
Слайд 38
38
Амплитуда ЭДС переменного тока с частотой 50 Гц равна
100 В. Каковы значения ЭДС
через 0,0025 и 0,005 с,
считая от начала периода?
Задача № 8
Слайд 39
39
Каково индуктивное сопротивление проводника
с индуктивностью 0,05 Гн
в цепи переменного тока
частотой 50 Гц?
Задача № 9
Слайд 40
40
Определите емкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно
10 МОм
Задача №10
Слайд 41
41
В цепь переменного тока
с действующим значением напряжения 220 В включено активное сопротивление 50 Ом. Найдите действующее и амплитудное значения силы тока.
Задача №11
Слайд 42
42
Индуктивное сопротивление катушки 80 Ом. Определите индуктивность катушки, если частота переменного тока 1000 Гц.
Определите индуктивность катушки, если частота переменного тока 1000 Гц.
Задача №12
Слайд 43
43
Определите период переменного тока, для которого конденсатор емкостью 2 мкФ представляет сопротивление 8 Ом
Задача №13
Слайд 44
44
Зачет Скрелин Вопросы к карточкам II серии —
Графики напряжения переменного тока
1. Какова циклическая частота тока?
2. Определите амплитудное значение напряжения.
3. Вычислите действующее значение напряжения.
4. Вычислите: а) амплитудное и б) действующее значения тока при включении в цепь только активного сопротивления R, указанного в карточке. Перечертите данный график изменения напряжения со временем и на том же чертеже изобразите графическую зависимость силы тока от времени, выбрав подходящий масштаб.
5. Какова будет средняя мощность тока в этом случае?
Слайд 45
45
Слайд 46
46
Слайд 47
47
6. Вычислите реактивное и полное сопротивление, если в цепь будут включены последовательно активное сопротивление R и катушка с индуктивностью L,. 7. Вычислите амплитудное значение тока в этой цепи.
8. Каков окажется коэффициент мощности и угол сдвига фазы тока относительно напряжения?
Начертите графики изменения напряжения и тока со временем на одном чертеже, выбрав удобный масштаб.
9. Вычислите среднюю мощность для этого случая.
10. Какой емкости конденсатор следует включить последовательно в данную цепь, чтобы получить резонансное увеличение тока?
11. Какое амплитудное напряжение возникнет в этой цепи на индуктивном и емкостном сопротивлениях?
7. Вычислите амплитудное значение тока в этой цепи.
8. Каков окажется коэффициент мощности и угол сдвига фазы тока относительно напряжения?
Начертите графики изменения напряжения и тока со временем на одном чертеже, выбрав удобный масштаб.
9. Вычислите среднюю мощность для этого случая.
10. Какой емкости конденсатор следует включить последовательно в данную цепь, чтобы получить резонансное увеличение тока?
11. Какое амплитудное напряжение возникнет в этой цепи на индуктивном и емкостном сопротивлениях?
Презентация «Переменный ток» | Электронный образовательный ресурс:
Слайд 1
Переменный ток.
Слайд 2
Содержание Тема 1 Фаза. Сдвиг фаз. Тема 2 Получение переменного тока Тема 3 Параметры переменного тока Тема 4 Расчет цепей переменного тока 4.1 Виды нагрузок переменного тока 4.2 Активное сопротивление ( R) в цепи переменного тока 4.3 Цепь с индуктивным сопротивлением (катушкой L ) 4.4 Цепь с емкостным сопротивлением (конденсатором С ) 4.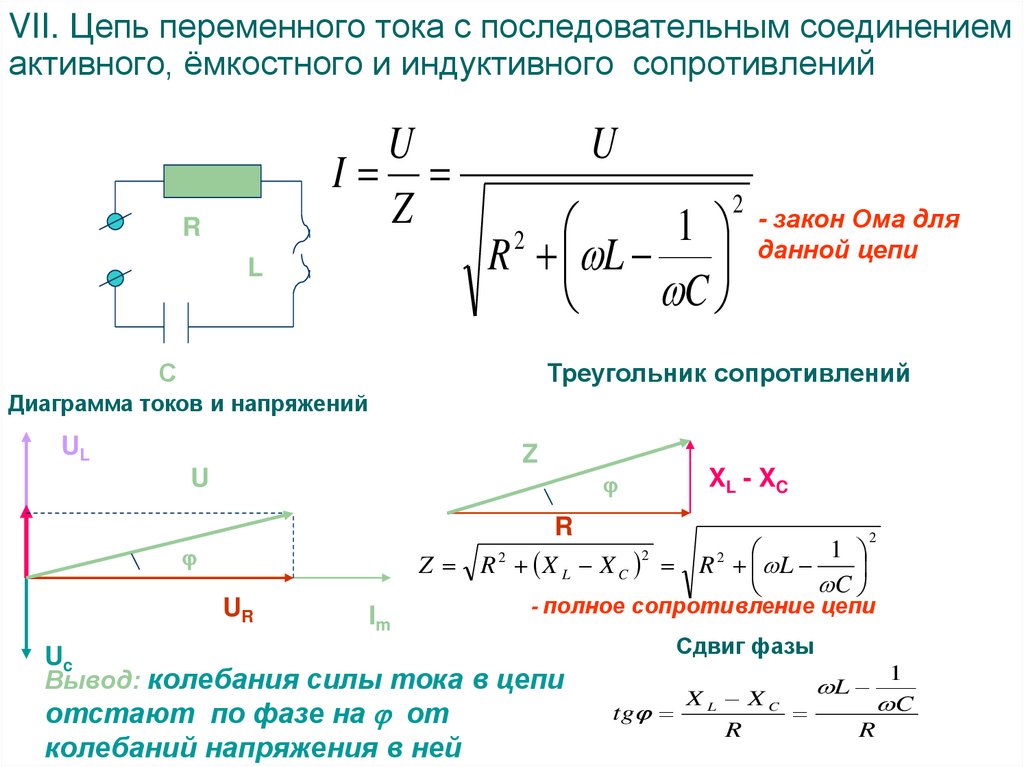 5 Расчет цепи с резистором и катушкой 4.6 Расчет цепи с резистором и конденсатором 4.7 Расчет цепи с резистором , катушкой и конденсатором 4.8 Расчет разветвленной цепи переменного тока Тема 5.Резонансные режимы цепи 5.1 Резонанс напряжений 5.2 Резонанс тока
5 Расчет цепи с резистором и катушкой 4.6 Расчет цепи с резистором и конденсатором 4.7 Расчет цепи с резистором , катушкой и конденсатором 4.8 Расчет разветвленной цепи переменного тока Тема 5.Резонансные режимы цепи 5.1 Резонанс напряжений 5.2 Резонанс тока
Слайд 3
В магнитном поле вращаются два витка. В них наводится ЭДС одной частоты и амплитуды, но так как витки находятся под разными углами к нейтральной линии ОО, то е 1 = Е m ·sin ( ω ·t )+ψ 1 е 2 = Е m ·sin ( ω ·t )+ ψ 2 Т. Е. ЭДС своих амплитудных значений достигают не одновременно. ( ω ·t +ψ ) –фаза В момент времени t=0 ЭДС отличны от нуля и равны: е 1 = Е m ·sin ψ 1 е 2 = Е m ·sin ψ 2 Углы ψ 1 и ψ 2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами. Т.к. начальные фазы ЭДС различны ,то максимальные значения ЭДС достигают не одновременно, а со сдвигом во времени. ψ 1 — ψ 2 = φ Тема 1 Фаза. Сдвиг фаз
Слайд 4
Синусоидальная величина на временной диаграмме характеризуется: 1.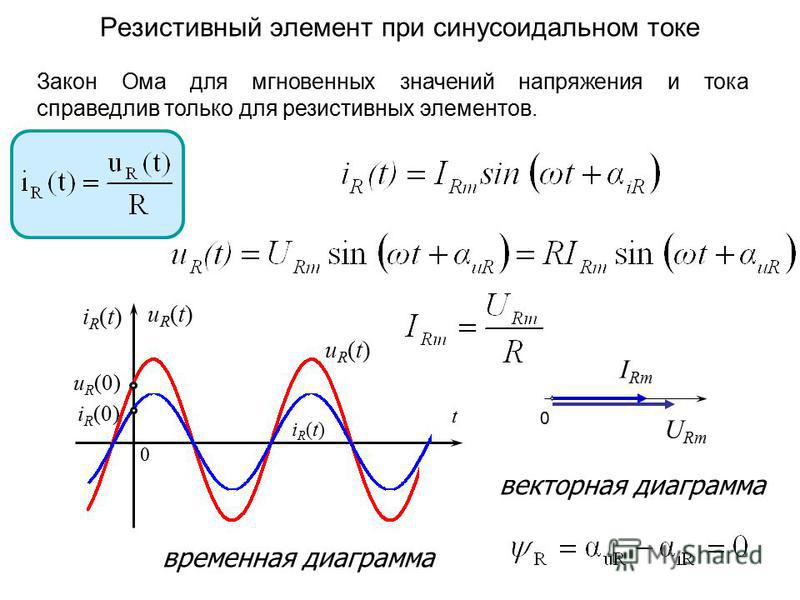 Амплитудой 2.Частотой или периодом 3.Начальной фазой Переменный ток, напряжение и ЭДС можно представить в виде: Временной диаграммы Уравнения Вектора Графически синусоидальные величины изображаются в виде вращающегося вектора Предполагается вращение против часовой стрелки с частотой вращения ω . Длина вектора — действующее ( амплитудное) значение. Проекция на вертикальную ось есть мгновенное значение Совокупность двух и более векторов называется векторной диаграммой. Переменная величина на векторной диаграмме характеризуется: Действующим значением Начальной фазой
Амплитудой 2.Частотой или периодом 3.Начальной фазой Переменный ток, напряжение и ЭДС можно представить в виде: Временной диаграммы Уравнения Вектора Графически синусоидальные величины изображаются в виде вращающегося вектора Предполагается вращение против часовой стрелки с частотой вращения ω . Длина вектора — действующее ( амплитудное) значение. Проекция на вертикальную ось есть мгновенное значение Совокупность двух и более векторов называется векторной диаграммой. Переменная величина на векторной диаграмме характеризуется: Действующим значением Начальной фазой
Слайд 5
Если одновременно и с одной скоростью вращать два вектора, то о синусоидальных величинах можно сказать, что они: Совпадают по фазе Уравнение (начальные фазы одинаковые) i 1 = Е m ·sin ( ω ·t ) i 2 = Е m ·sin ( ω ·t ) Векторная диаграмма(сдвиг по фазе равен нулю) Временная диаграмма (одновременно достигаются нулевые и амплитудные значения.
Слайд 7
2 . Сдвинуты по фазе Временная диаграмма (не одновременно достигаются нулевые и амплитудные значения). Положительное значение начальных фаз откладывается влево, отрицательное – вправо. Векторная диаграмма Уравнение (начальные фазы не совпадают) u(t) = U m sin ω t i (t) = I m sin( ω t -90)
Положительное значение начальных фаз откладывается влево, отрицательное – вправо. Векторная диаграмма Уравнение (начальные фазы не совпадают) u(t) = U m sin ω t i (t) = I m sin( ω t -90)
Слайд 8
Тема 2 Получение переменного тока Ток, периодически меняющийся по величине и направлению, называется переменным током. Если кривая изменения тока описывается синусоидой, то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток несинусоидальный. Практически в домашних условиях применяют однофазный переменный ток, который получают с помощью генераторов переменного тока . Устройство и принцип действия этих генераторов основывается на явлении электромагнитной индукции — возникновение электрического тока в замкнутом проводнике при изменении магнитного потока, проходящего через него. Это явление было открыто английским ученым М.Фарадеем (1791-1867) в 1831 г. Простейший генератор – рамка, вращающаяся в магнитном поле постоянного магнита. Концы рамки присоединены к двум медным кольцам 3 и 4, на которых наложены две угольные щетки 5 и 6. Во внешней цепи будет протекать изменяющийся по направлению и величине ток.
Во внешней цепи будет протекать изменяющийся по направлению и величине ток.
Слайд 9
Переменный ток, напряжение и ЭДС изменяются по синусоидальному закону: i = I m sin(ωt+ ψ i ) u= U m sin ω t + ψ u е = Е m sin ω t + ψе где i —мгновенное значение тока; I m —амплитудное (наибольшее) значение тока; t — время, ω –угловая частота, i (t) = I m sin( ω t ) i (t) = I m sin( ω t — ψ i )
Слайд 10
Тема 3 Параметры переменного тока. u , i , е — значение переменного тока, напряжения и ЭДС в любой момент времени, называемое мгновенным значением переменной величины. I m U m Е m — Амплитуда — это наибольшее положительное или отрицательное значение переменного тока. I , U , Е — действующее значение переменного тока – это такой постоянный ток, который за время одного периода оказывает такое тепловое (механическое и др.) действие, как и данный переменный ток. I = I m /√2 ≈ 0,707· I m U = U m / √2 ≈ 0,707· U m Е = Е m / √2 ≈ 0,707· Е m Измерительные приборы, включенные в цепь переменного тока, показывают действующие значения тока или напряжения.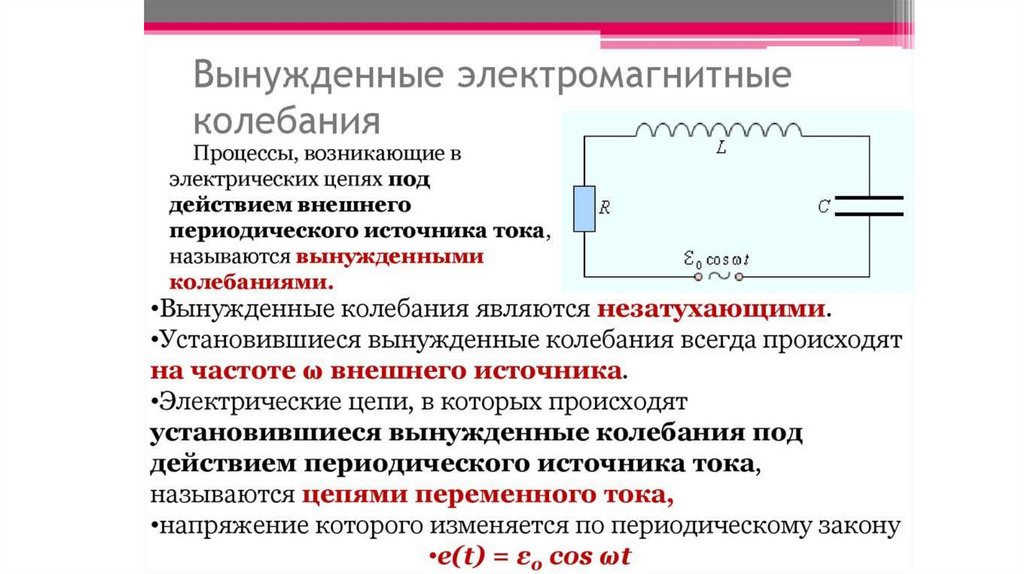 4.Т (сек.) — период — время, в течение которого происходит полное изменение (колебание) тока в проводнике. 5 .( f ) –частота — число полных колебаний тока за одну секунду. Частота измеряется в герцах (Гц) в честь немецкого ученого Г. Герца (1857-1894). При частоте в 1 Гц происходит одно полное колебание тока за одну секунду. Стандартной частотой переменного тока в России является частота 50 Гц, что соответствует 50 полным колебаниям тока за одну секунду. Частота измеряется с помощью частотомеров.
4.Т (сек.) — период — время, в течение которого происходит полное изменение (колебание) тока в проводнике. 5 .( f ) –частота — число полных колебаний тока за одну секунду. Частота измеряется в герцах (Гц) в честь немецкого ученого Г. Герца (1857-1894). При частоте в 1 Гц происходит одно полное колебание тока за одну секунду. Стандартной частотой переменного тока в России является частота 50 Гц, что соответствует 50 полным колебаниям тока за одну секунду. Частота измеряется с помощью частотомеров.
Слайд 11
Частота — величина, обратная периоду. Следовательно, f = 1/T или T = 1/ f Частота переменного тока зависит от частоты вращения ротора генератора и числа пар полюсов индуктора f =p . n \ 60 , Гц где p —число пар полюсов индуктора; n —частота вращения ротора в минуту, об\мин . Если генератор имеет одну пару полюсов, то ротор такого генератора совершает 3000 об/мин для получения переменного тока частотой 50 Гц. 6. ω ( рад\сек )– угловая частота или угловая скорость вращения равна углу поворота вектора в единицу времени , ω = α \ t .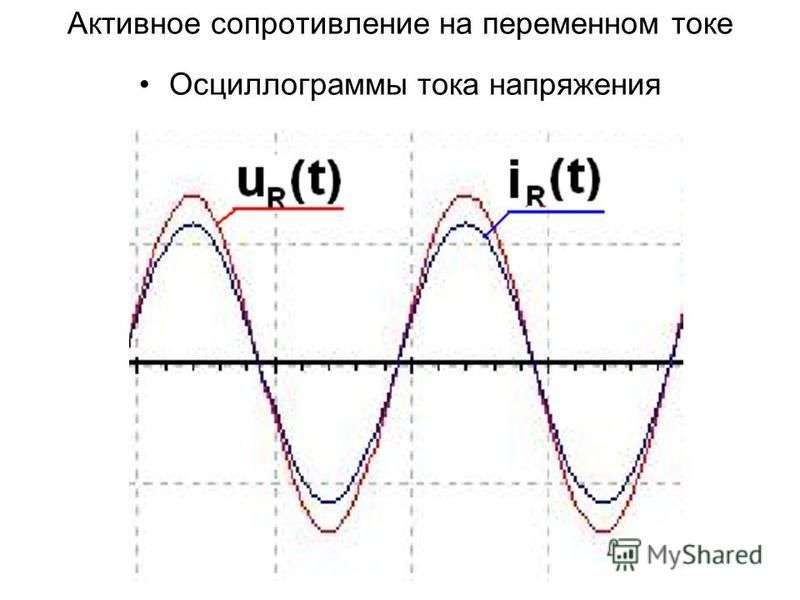 , угол α называется фазным углом или фазой. Часто вместо градуса применяют радиан – угол, дуга которого равна радиусу. ω =2·π·f= 2·π\Т , рад\сек . (град. –начальная фаза или угол. Задача. Определить амплитудное значение напряжения в сети, если при сопротивлении цепи 40 Ом амперметр показывает ток 5,5 А. Из закона Ома напряжение равно U = Ir . Подставив вместо I и r их значения, получим действующее значение напряжения U = 5,5×40 = 220 В. А так как U m = √2U, то U m = 1,41×220 = 310,2 В.
, угол α называется фазным углом или фазой. Часто вместо градуса применяют радиан – угол, дуга которого равна радиусу. ω =2·π·f= 2·π\Т , рад\сек . (град. –начальная фаза или угол. Задача. Определить амплитудное значение напряжения в сети, если при сопротивлении цепи 40 Ом амперметр показывает ток 5,5 А. Из закона Ома напряжение равно U = Ir . Подставив вместо I и r их значения, получим действующее значение напряжения U = 5,5×40 = 220 В. А так как U m = √2U, то U m = 1,41×220 = 310,2 В.
Слайд 12
Задача. Найти частоту тока, если период, если период равен 5∙10 -8 сек. f = 1/T = 0,2∙10 8 Гц или 20 МГц. Задача. Определить частоту переменного тока, получаемого от генератора с 8 полюсами, скорость вращения ротора равна 750 об\мин . Решение. f =p . n \ 60 = 4 ∙750\60 = 50 Гц. Задача. Определить скорость вращения ротора двадцатиполюсного генератора, если частотомер показал частоту тока 25 Гц. n =60 f \ р = 60 ∙25\10 =150 об\мин . Задача . ЭДС изменяется по закону: е =8,45 sin 1256 t + Π \4 Определить Е, Т, f , ω, ψ Е m Решение Ψ = 90град. = Π \4 рад. Е m =8,45 В Е=0,707×8,45=5,97 В ω=1256 рад\сек f = ω\2 Π = 1256\6,28 = 200 Гц T = 1/ f = 1\200 =0,005 сек.
= Π \4 рад. Е m =8,45 В Е=0,707×8,45=5,97 В ω=1256 рад\сек f = ω\2 Π = 1256\6,28 = 200 Гц T = 1/ f = 1\200 =0,005 сек.
Слайд 13
Задача Действующее значение тока в цепи равно 2,9 А., начальная фаза -2\3 π, частота 50 Гц . Записать выражения изменения тока i и определить его амплитуду. Решение. i = I m sin(ωt+ ψ i ) ω =2·π·f=2 ·з,14·50 =314 рад\сек I m = 1,41×2,9 = 4 А i = 4·sin(314·t — 2\3 π )
Слайд 14
Тема 4 Расчет цепей переменного тока 4.1 Виды нагрузок переменного тока Для цепей переменного тока, в отличие от постоянного, закон Ома несколько изменяется, так как некоторые виды нагрузок ведут себя при прохождении изменяющегося во времени тока по-разному. Активная (резистивная) нагрузка. Сопротивление резистора не зависит от частоты. Пример — электрическая лампочка, нагревательный элемент (ТЭН), электрическая плита. Индуктивная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в магнитное поле, а течении следующей половины преобразует энергию магнитного поля в электрический ток.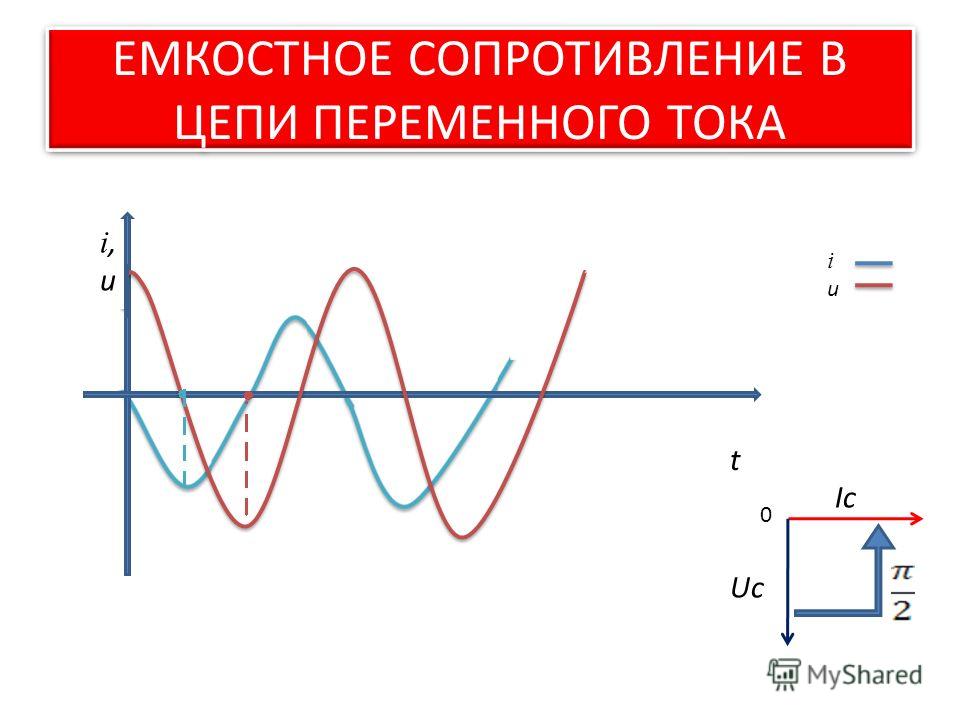 Пример — дроссель или катушка индуктивности. Сопротивление обозначается X L измеряется в Омах и зависит прямо пропорционально от частоты переменного тока. Ёмкостная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в электрическое поле, а течении следующей половины преобразует энергию электрического поля в электрический ток. Пример — конденсатор. Сопротивление обозначается X C измеряется в Омах и зависит обратно пропорционально от частоты переменного тока.
Пример — дроссель или катушка индуктивности. Сопротивление обозначается X L измеряется в Омах и зависит прямо пропорционально от частоты переменного тока. Ёмкостная (реактивная) нагрузка преобразует в течение одной половины полупериода энергию электрического тока в электрическое поле, а течении следующей половины преобразует энергию электрического поля в электрический ток. Пример — конденсатор. Сопротивление обозначается X C измеряется в Омах и зависит обратно пропорционально от частоты переменного тока.
Слайд 15
В природе не существует ничего идеального, чистые реактивные нагрузки в электротехнике не встречаются. Любая нагрузка имеет КПД ниже 100%, и часть энергии рассеивается в виде тепловых потерь, излучения и т.д. Поэтому в реальной, электротехнике применяется понятие активно-индуктивной нагрузки. Активно-индуктивная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной индуктивности. Пример- трансформатор, электродвигатель, электромагнитное пускорегулирующее устройство для люминесцентных ламп, катушка зажигания в автомобиле.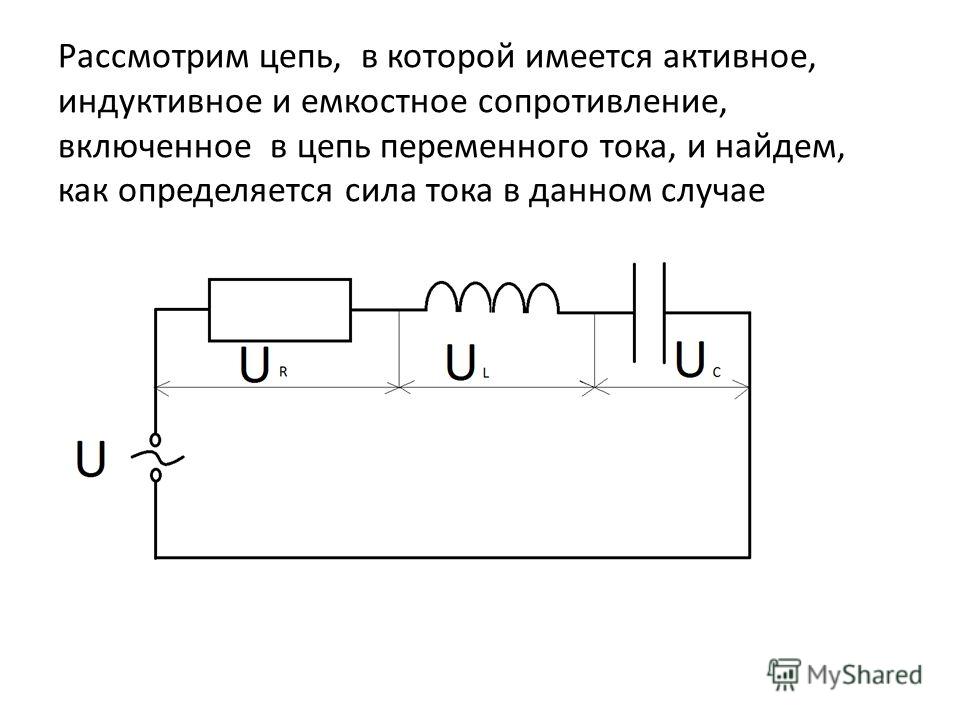 Для этого вида нагрузок характерен бросок напряжения в момент размыкания электрической цепи. Активно-ёмкостная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной ёмкости. Пример- конденсатор, электронные блоки питания галогенных или люминесцентных ламп.
Для этого вида нагрузок характерен бросок напряжения в момент размыкания электрической цепи. Активно-ёмкостная нагрузка может рассматриваться как последовательное или параллельное соединение активного сопротивления и идеальной ёмкости. Пример- конденсатор, электронные блоки питания галогенных или люминесцентных ламп.
Слайд 16
Для этих нагрузок характерен бросок тока в момент замыкания электрической цепи. При протекании тока через активно-реактивную нагрузку часть тока будет протекать через прибор, не производя никакой полезной работы. При этом максимумы и минимумы тока и напряжения будут достигаться в разное время, а кривые изменения по времени тока и напряжения будут не совпадать – оставаясь, при этом, периодическими функциями. Происходит сдвиг тока и напряжения по фазе. Косинус угла между током и напряжением является важной величиной в электротехнике и обозначается cos ( φ ). Для компенсации cos ( φ ) и сокращения расходов на электроэнергию применяются конденсаторные установки.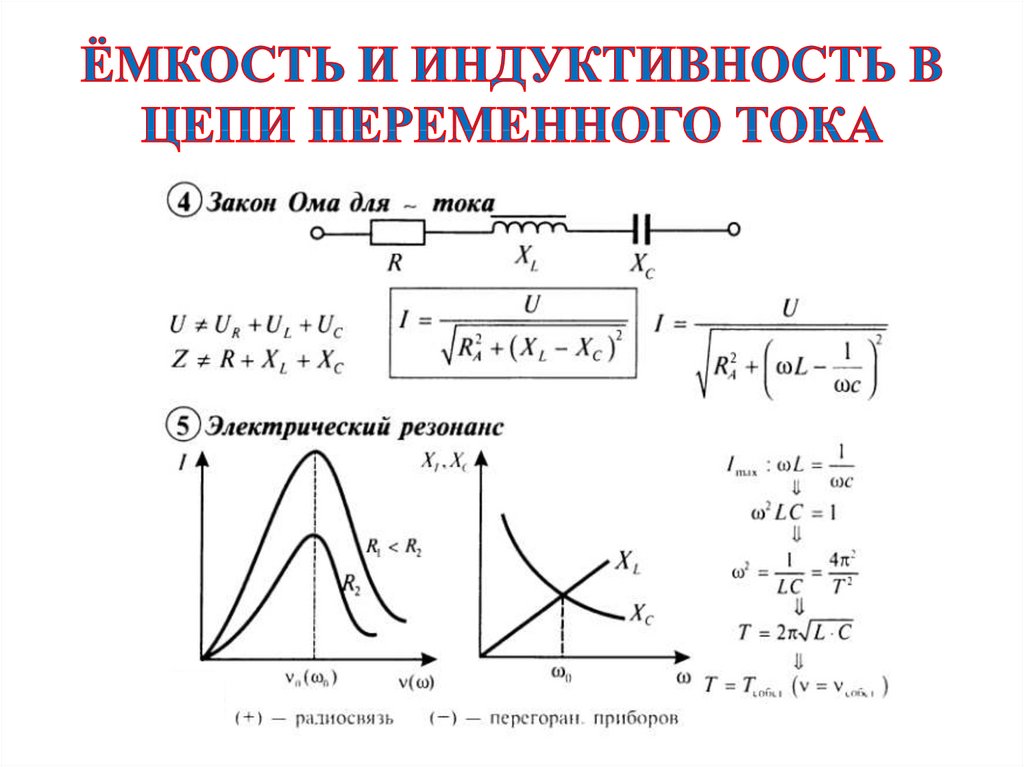 Физический смысл cos ( φ ) – КПД установки. Этот коэффициент показывает, какая часть тока преобразуется в полезную работу, а какая часть тока течёт в проводниках вхолостую, перегружая проводники. Чем выше cos ( φ ), тем лучше КПД установки. У активных проводников он равен 1, а у идеальных ёмкостных и индуктивных проводников равен 0.
Физический смысл cos ( φ ) – КПД установки. Этот коэффициент показывает, какая часть тока преобразуется в полезную работу, а какая часть тока течёт в проводниках вхолостую, перегружая проводники. Чем выше cos ( φ ), тем лучше КПД установки. У активных проводников он равен 1, а у идеальных ёмкостных и индуктивных проводников равен 0.
Слайд 17
Тема 4.2 Активное сопротивление ( R) в цепи переменного тока Активное сопротивление – сопротивление проводника переменному току. Электрическое (омическое) – сопротивление проводника постоянному току. Активное больше омического из-за поверхностного эффекта – вытеснение носителей зарядов на поверхность проводника. Однако при частоте 50 Гц эти сопротивления можно считать одинаковыми . Временная диаграмма Начальные фазы одинаковы ψ u = ψ i . Векторные диаграммы. Фазовый сдвиг меду током и напряжением в цепи равен нулю u = U m sin ω t i = I m sin ω t i = I m sin( ω t + ψ i ). u = U m sin( ω t + ψ u )
Слайд 18
Цепь обладает только активной мощностью, которая всегда положительная Р = I 2 R = U I = U 2 \ R Вт Закон Ома справедлив для мгновенных, максимальных и действующих значений тока I = U \ R I m = U m \ R Вывод: В цепи с активным сопротивлением ток и напряжение совпадают по фазе. Фаза – величина, определяющая взаимоотношение во времени тока и напряжения в электрической цепи . Задача 1. В цепь переменного тока с сопротивлением 55 Ом подключили генератор, амплитуда напряжения которого равна 310,2 В. Определить : показания амперметра и вольтметра, мощность цепи. Решение. U = U m \ √ 2= 310,2\1,41 =220 В I = U\ R = 220\55 = 4 А Р= U I =220∙4 = 880 Вт
Фаза – величина, определяющая взаимоотношение во времени тока и напряжения в электрической цепи . Задача 1. В цепь переменного тока с сопротивлением 55 Ом подключили генератор, амплитуда напряжения которого равна 310,2 В. Определить : показания амперметра и вольтметра, мощность цепи. Решение. U = U m \ √ 2= 310,2\1,41 =220 В I = U\ R = 220\55 = 4 А Р= U I =220∙4 = 880 Вт
Слайд 19
Задача 2. Решение. Im =14,1 А I = Im \ √ 2= 14,1 \1,41 = 10 А U R 1 = I ∙ R 1 = 10∙10 = 100 В U R 2 = I ∙ R 2 = 10∙10 = 100 В U общ. = 100+100 = 200 В Р = U I = 200∙10 = 2000 Вт Задача 3. Дано: R = 3,6 Ом Р = 120 Вт Определить: I , I m , U , U m Решение. Р= I 2 ∙ R , поэтому I = √ Р \ R = √120 \ 3,6 = 5,77 А Im = I ∙ √ 2= 5,77∙1,41 = 8,14 А U m = Im ∙ R = 8,14 ∙3,6 = 29 В U = I ∙ R = 5,77∙3,6 = 20,77 В
Слайд 20
Тема 4.3 Цепь с индуктивным сопротивлением (катушкой L) Переменный ток, протекая по виткам катушки, создает переменное магнитное поле, которое пересекает витки катушки, создавая в них ЭДС самоиндукции.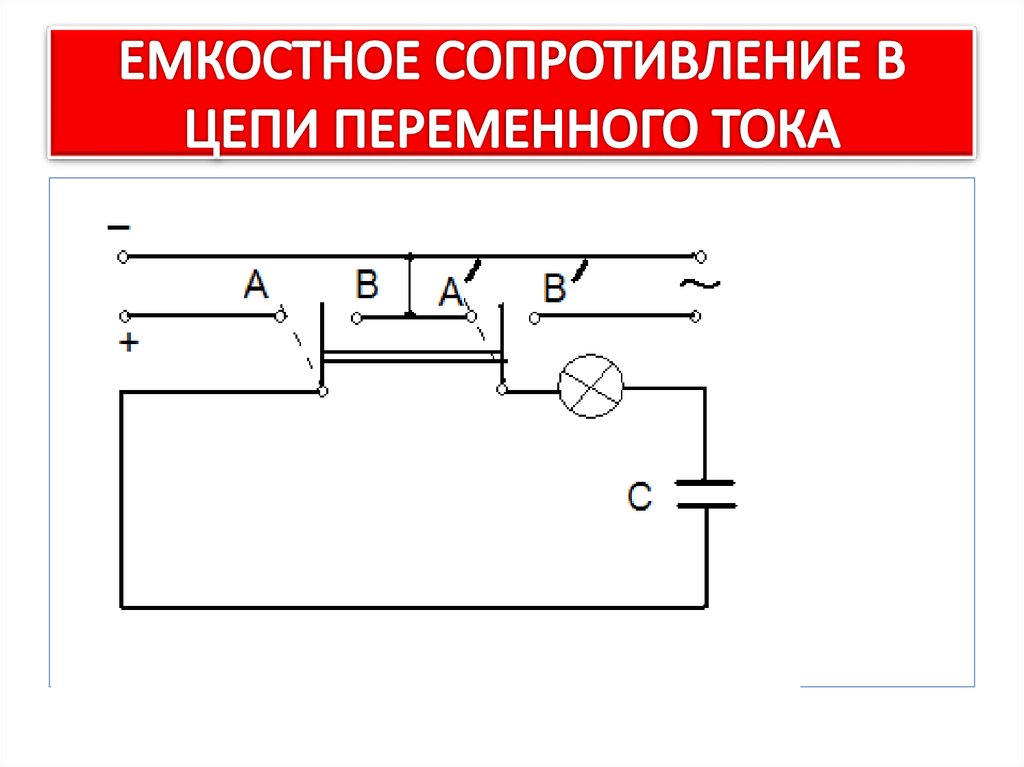 Согласно закону Ленца, эта ЭДС всегда противодействует причине, ее вызывающей, т.е. ток сразу установится не может. Вывод: Ток в цепи с катушкой отстает от напряжения на 90 град. (Π \ 2) или напряжение опережает ток на угол Π \ 2. u = U m sin ω t i = I m sin ( ω t — Π \ 2. ). Векторная диаграмма Напряжение опережает ток на 90 градусов
Согласно закону Ленца, эта ЭДС всегда противодействует причине, ее вызывающей, т.е. ток сразу установится не может. Вывод: Ток в цепи с катушкой отстает от напряжения на 90 град. (Π \ 2) или напряжение опережает ток на угол Π \ 2. u = U m sin ω t i = I m sin ( ω t — Π \ 2. ). Векторная диаграмма Напряжение опережает ток на 90 градусов
Слайд 21
Мгновенная мощность меняет знак 4 раза. В первую четверть периода – положительная, энергия накапливается в магнитном поле катушки. Катушка – приемник энергии. Во вторую четверть – отрицательная, энергия обратно возвращается в сеть. Катушка – источник энергии. Работа не производится. Происходит обмен энергией между катушкой и источником. Расхода энергии не будет, несмотря на то, что в цепи есть ток и напряжение. Активная мощность равна нулю. Провода загружаются реактивной мощностью. Q L = I 2 X L = U I ВАр X L = ω L =2π f L – индуктивное сопротивление катушки. L – индуктивность катушки, Гн f – частота , Гц ω – угловая частота, рад\сек Закон Ома I = U \ X L Im = Um \ X L Задача 1 Решение I = U \ XL отсюда XL= U\ I = 220 \ 0 , 5 = 440 Ом XL = 2π f L отсюда L = XL \ 2π f = 440 \ 2∙ π ∙50 = 1,4 Гн U = 220 В I = 0,5 А F = 50 Гц Определить : L — ?
Слайд 22
Задача 2 Дано: L = 0,01 Гн f = 300 Гц U = 82 В Определить: I — ? Написать закон изменения тока i и напряжения u Решение. XL = 2π f L = 6,28 ∙300 ∙0,01 = 18,84 Ом I = U \ XL = 82 \ 18,84 = 4,35 А Im = I∙ √ 2= 1,41∙ 4,35 = 6,13 А ω =2π f = 6,28∙300 = 1884 рад\сек Um = U∙√ 2 = 82∙1,41 =115,62 В u = U m sin ω t = 115,62 sin 1884 t i = I m sin ( ω t — Π \ 2. ) = 6 ,13 sin 1884 t — Π\2 Начертить векторную диаграмму тока и напряжения
XL = 2π f L = 6,28 ∙300 ∙0,01 = 18,84 Ом I = U \ XL = 82 \ 18,84 = 4,35 А Im = I∙ √ 2= 1,41∙ 4,35 = 6,13 А ω =2π f = 6,28∙300 = 1884 рад\сек Um = U∙√ 2 = 82∙1,41 =115,62 В u = U m sin ω t = 115,62 sin 1884 t i = I m sin ( ω t — Π \ 2. ) = 6 ,13 sin 1884 t — Π\2 Начертить векторную диаграмму тока и напряжения
Слайд 23
Задача 3 Закон изменения напряжения в цепи u = 113,5 sin 126 t + Π\2. Индуктивность катушки L = 0,5 Гн. Определить ток в цепи, период, реактивную мощность и закон изменения тока. Решение. ω =2π f = 126 рад\сек f = ω \ 2π =126\6,28 = 20 Гц Т =1 \ f = 1\20 = 0,05 сек X L = ω L =126 ∙ 0,5 = 63 Ома Im = Um \ X L =113,5\63 = 1,8 А I = I m \ √ 2= 1 ,8 \ 1,41 = 1,28 А Q L = I 2 X L = 1,28 2 ∙63 = 103 ВАр i = 1,8 sin 126 t
Слайд 24
Вопросы по теме Какой фазовый сдвиг между током и напряжением в цепи с катушкой? Какой мощностью обладает данная цепь и чему она равна? Чему равна активная мощность цепи? Напишите закон Ома для цепи с катушкой. Начертите векторную диаграмму тока и напряжения для цепи с катушкой.
Слайд 25
Тема 4.4 Цепь с емкостным сопротивлением (конденсатором С ) За один период конденсатор дважды заряжается и разряжается и в его цепи протекает ток, не совпадающий по фазе с напряжением. Вывод: В цепи с конденсатором ток опережает напряжение на 90 град. Временная диаграмма Векторная диаграмма Закон изменения тока и напряжения u C = U m sin ω t i = I m sin( ω t + 90 )
Слайд 26
Цепь обладает только реактивной мощностью Q с = I 2 X с = U I ВАр , Q берется со знаком (-), т.к. угол φ
Слайд 27
ЗАДАЧА 1. В цепь включен конденсатор. Напряжение в цепи 220 В, ток 440 А, частота 50 Гц. Определить емкость конденсатора. Решение. X c = U \ I = 220\440 = 0,5 Ом X C = 1 \ 2π fC , отсюда C = 1\ 2π f X C = 1\ 2∙3,14∙ 50∙0,5 = 0,006 Ф Задача 2 Дано: С = 2,5 мкФ u = 24 sin 1884 t +15 Определить: I, i , ВД Решение. ω =2π f , отсюда f = ω \ 2π = 1884 \6,28 = 300 Гц X C = 1 \ 2π f C = 1\ 2∙3,14∙ 300 ∙2,5∙10 -6 = 212 Ом U = U m \ √2= 24\1,41 = 17 В I = U \ X c = 17\212 = 0,08 А I m = I∙ √2 = 1,41∙0,08 = 0,11 А i = 0,11 sin( 1884 t + 105 )
Слайд 28
Вопросы по теме. Какой фазовый сдвиг между током и напряжением в цепи с конденсатором? Какой мощностью обладает данная цепь и чему она равна? Чему равна активная мощность цепи? Напишите закон Ома для цепи с конденсатором. Начертите векторную диаграмму тока и напряжения для цепи с конденсатором
Какой фазовый сдвиг между током и напряжением в цепи с конденсатором? Какой мощностью обладает данная цепь и чему она равна? Чему равна активная мощность цепи? Напишите закон Ома для цепи с конденсатором. Начертите векторную диаграмму тока и напряжения для цепи с конденсатором
Слайд 29
Тема 4.5 Расчет цепи с резистором и катушкой По закону Кирхгофа можно записать : ῡ= ῡ R + ῡ L Алгебраически складывать нельзя, только векторно , т.к. напряжение постоянно меняет свое направление. Падение напряжения на сопротивлениях: U R =I ×R, ( Ом) U L =I ×X L ( Ом ) Векторная диаграмма напряжений цепи Из теоремы Пифагора можно записать, что общее напряжение цепи равно Закон Ома для цепи: где z – полное сопротивление цепи , Ом
Слайд 30
ВЫВОД: в такой цепи напряжение опережает ток на угол φ (положительный). Задача 1. Катушка индуктивности подключена к сети с напряжением U = 100 В. Ваттметр показывает значение P K = 600 Вт, амперметр: I = 10 А. Определить параметры катушки R K , L K .
Слайд 31
1. Вычисление полного сопротивления катушки Z К = U / I = 100 / 10 = 10 Ом. 2. Вычисление активного сопротивления катушки R К Ваттметр измеряет активную мощность, которая в данной схеме потребляется активным сопротивлением R К . R К = P К / I 2 = 600 / 100 = 6 Ом. 3 . Вычисление индуктивности катушки L К X К = 2πf L К ; L К = X К / (2πf) = 8 / (2π×50) = 0,025 Гн . Дополнительные вопросы к задаче 1. Как решить задачу другим способом? Параметры катушки индуктивности можно определить, рассчитав полную мощность S К и реактивную мощность катушки Q К . S К = U I = 100 · 10 = 1000 ВА . R К = P К / I 2 = 6 Ом; X К = Q К / I 2 = 8 Ом;
Слайд 32
Тема 4.6 Расчет цепи с резистором и конденсатором По закону Кирхгофа ῡ = ῡ R + ῡ C Падение напряжения на сопротивлениях: U R = I × R , (Ом) U с =I ×X C ( Ом)
Слайд 33
ВЫВОД: в такой цепи ток опережает напряжение на угол φ (отрицательный). Реактивная мощность берется со знаком (-) ЗАДАЧА. Дано: X с = 8 Ом R = 6 Ом. I = 5 А Определить: U -? Решение. U = I ∙ √ R 2 + X L 2 = 5∙ √ 8 2 + 6 2 = 5∙√ 100 = 50 В
I = 5 А Определить: U -? Решение. U = I ∙ √ R 2 + X L 2 = 5∙ √ 8 2 + 6 2 = 5∙√ 100 = 50 В
Слайд 34
Тема 4.7 Расчет цепи с резистором , катушкой и конденсатором Для напряжений выполняется второй закон Кирхгофа в векторной форме. Ú = Ú R + Ú L + Ú C . Напряжения на элементах определяются по формулам U R = I R, ψ uR = ψ i ; U L = I X L , ψ uL = ψ i + 90° ; U C = I X C , ψ uC = ψ i — 90°. В зависимости от величин L и С в формуле , возможны следующие варианты: 1. X L > X C ; 2. X L
Слайд 35
1 вариант : X L > X C , тогда U L > U C . Строим векторную диаграмму Вывод: Так как ток отстает от напряжения на угол φ (угол φ > 0), то цепь имеет индуктивный характер Самостоятельно нарисовать треугольник сопротивлений и мощности в цепи.
Слайд 36
Треугольник сопротивлений Векторная диаграмма тока и напряжения Треугольник мощностей
Слайд 37
2 вариант : X L
Слайд 38
Вывод: Так как ток опережает напряжение на угол φ (угол φ
Слайд 39
Решение Вычисление сопротивлений участков и всей цепи Индуктивное реактивное сопротивление X L = 2πf L = 2×3,14×200×6,37·10 -3 = 8 Ом. Емкостное реактивное сопротивление X C = 1 / (2πf C) = 1 / (2×3,14×200×159·10 -6 ) = 5 Ом. Полное сопротивления всей цепи: X = X L — X C = 8-5 = 3 Ом; 2. Вычисление тока и напряжений на участках цепи Ток в цепи I = U / Z = 120 / 5 = 24 А. Напряжения на участках: U R = R I = 96 В; U L = X L I = 192 В; U C = X C I = 120 В. 3. Вычисление мощностей Активная мощность P = R I 2 = U R I = 2304 Вт. Реактивные мощности: Q L = X L I 2 = U L I = 4608 вар; Q C = X C I 2 = U C I = 2880 вар. Полная мощность цепи
Емкостное реактивное сопротивление X C = 1 / (2πf C) = 1 / (2×3,14×200×159·10 -6 ) = 5 Ом. Полное сопротивления всей цепи: X = X L — X C = 8-5 = 3 Ом; 2. Вычисление тока и напряжений на участках цепи Ток в цепи I = U / Z = 120 / 5 = 24 А. Напряжения на участках: U R = R I = 96 В; U L = X L I = 192 В; U C = X C I = 120 В. 3. Вычисление мощностей Активная мощность P = R I 2 = U R I = 2304 Вт. Реактивные мощности: Q L = X L I 2 = U L I = 4608 вар; Q C = X C I 2 = U C I = 2880 вар. Полная мощность цепи
Слайд 40
4. Угол сдвига фаз В данной цепи ток отстает по фазе от напряжения на угол 37 град.
Слайд 41
4.8 Расчет разветвленной цепи переменного тока Переменный ток I можно рассматривать как геометрическую сумму двух составляющих: активной Iа и реактивной Iр . Разложение тока на активную и реактивную составляющие Активная составляющая совпадает по направлению с напряжением и равна: Реактивная составляющая перпендикулярная вектору напряжения и равна:
Слайд 42
Токи в ветвях: Углы сдвига фаз между напряжением и токами в ветвях Построив векторы токов I 1 , и I 2 и сложив их по правилу параллелограмма, получим вектор тока I, протекающего на общем участке цепи, который равен Векторная диаграмма напряжений и токов параллельной цепи переменного тока
Слайд 43
Тема 5.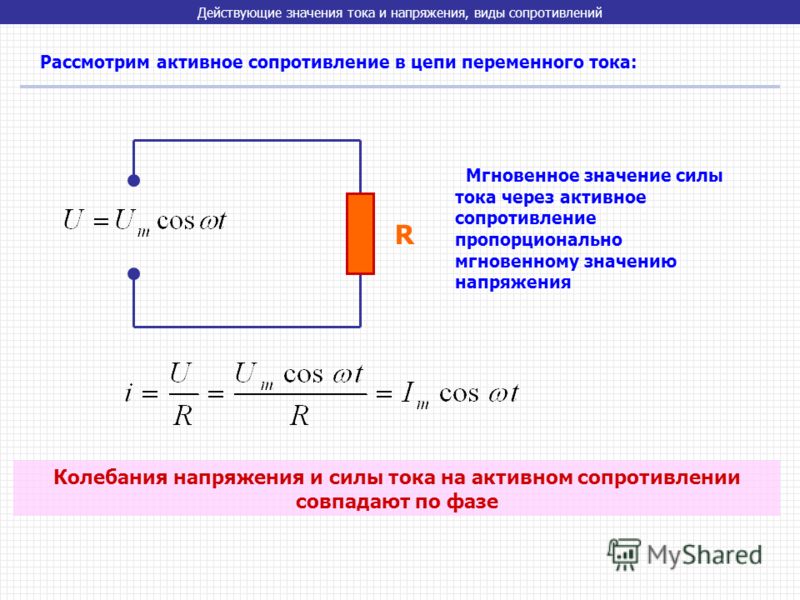 Резонансные режимы цепи 5.1 Резонанс напряжений Режим работы неразветвленной электрической цепи , когда ток и напряжение совпадают по фазе, а сопротивление цепи является чисто активным . Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Условия резонанса: Цепь неразветвленная X L = X C Свойства цепи при резонансе Т.к. реактивные сопротивления равны, падения напряжения на индуктивности и емкости равны и много больше напряжения цепи. U L = U C >>U Падение напряжения на активном сопротивлении совпадает по фазе с напряжением цепи U R = U
Резонансные режимы цепи 5.1 Резонанс напряжений Режим работы неразветвленной электрической цепи , когда ток и напряжение совпадают по фазе, а сопротивление цепи является чисто активным . Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной. Условия резонанса: Цепь неразветвленная X L = X C Свойства цепи при резонансе Т.к. реактивные сопротивления равны, падения напряжения на индуктивности и емкости равны и много больше напряжения цепи. U L = U C >>U Падение напряжения на активном сопротивлении совпадает по фазе с напряжением цепи U R = U
Слайд 44
3.Ток в цепи максимальный и равен Полное сопротивление минимальное и равно Z = R Реактивная мощность равна нулю. Коэффициент мощности равен единице: cos φ = P/S = R / Z = 1. Явление резонанса находит применение в радиотехнике для получения максимального тока и напряжения в контуре. ( антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей). Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков . Резонансная частота
( антенный контур радиопередатчика настраивают на резонанс напряжений для того, чтобы ток в антенне был максимальным. Тогда дальность действия передатчика будет наибольшей). Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков . Резонансная частота
Слайд 46
5.2 Резонанс тока Режим работы разветвленной электрической цепи , когда ток и напряжение в неразветвленной части цепи совпадают по фазе. Условия резонанса: Цепь разветвленная X L = X C Свойства цепи при резонансе Общий ток может быть значительно меньше токов в каждой ветви. Ток и напряжение совпадают по фазе. 3.При резонансе токов коэффициент мощности равен единице: cos φ = 1. 4. Полная мощность равна активной мощности: S = P. 5. Реактивная мощность равна нулю: Q = QL — QC = 0.
Слайд 47
Задача 1 Дано: U = 220 B, f = 50 Гц, R = 22 Ом, L = 350 мГн, С = 28,9 мкФ. Найти: I , U L , U C , φ-? Индуктивное сопротивление X L = ωL = 2πf L = 2 · 3,14 · 50 · 0,35 = 110 Ом ; Емкостное сопротивление X C = 1 / ωC = 1 / (2πf C) = 110 Ом ; Полное сопротивление Z = R = 22 Ом , Угол сдвига между током и напряжением φ =0
Слайд 48
Ток в цепи I = U / R = 220 / 22 = 10 А Напряжение на индуктивности и емкости U L = U C = I X L = 10 · 110 = 1100 В . Задача 2 Определить частоту сети, при которой в цепи возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры: r = 20 Ом, L = 0,1 Гн, С = 5 мкф . Решение. Резонансная частота Индуктивное сопротивление цепи при резонансе xL = 2 π f 0 L = 6,28 • 224 • 0,l = 140 Ом. Напряжение на индуктивности при резонансе UL / U = IxL / Ir, UL = U xL / r = U 140 /20 = 7 U . Напряжение на индуктивности при резонансе в 7 раз больше напряжения се ти.
Задача 2 Определить частоту сети, при которой в цепи возникает резонанс напряжений. Определить также, во сколько раз напряжение на индуктивности больше напряжения сети при резонансе, если цепь имеет следующие параметры: r = 20 Ом, L = 0,1 Гн, С = 5 мкф . Решение. Резонансная частота Индуктивное сопротивление цепи при резонансе xL = 2 π f 0 L = 6,28 • 224 • 0,l = 140 Ом. Напряжение на индуктивности при резонансе UL / U = IxL / Ir, UL = U xL / r = U 140 /20 = 7 U . Напряжение на индуктивности при резонансе в 7 раз больше напряжения се ти.
Слайд 49
Контрольные вопросы 1.Что такое резонанс напряжений, чем он характеризуется? 2.Что такое резонанс токов, чем он характеризуется? 3.В чем физическая сущность резонансных режимов?
Слайд 50
По векторным диаграммам определить способы соединения катушки, резистора и конденсатора, а также характер цепи.
Что такое чисто резистивная цепь и каковы ее характеристики?| Блог Advanced PCB Design
Задолго до того, как Борг произнес одну из моих любимых фраз: «Сопротивление бесполезно», я понял, какое влияние сопротивление оказывает на все аспекты нашей жизни.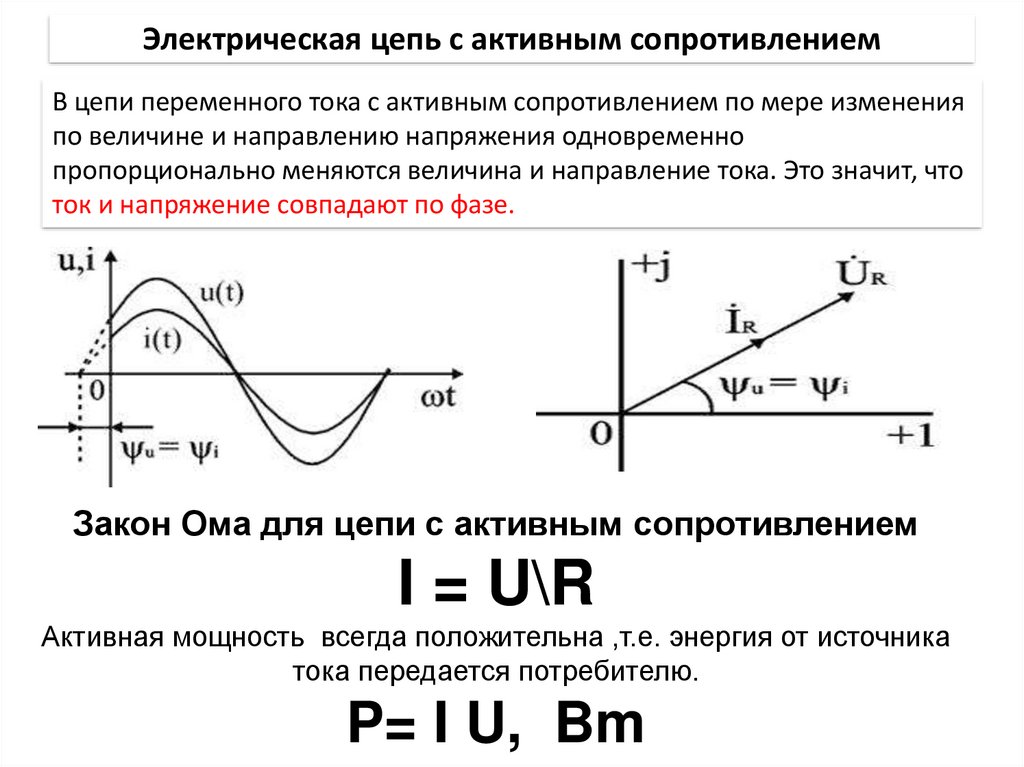 Более того, даже самые ранние мои детские воспоминания содержат учения из библейской школы, в которых особое внимание уделялось сопротивлению искушению.
Более того, даже самые ранние мои детские воспоминания содержат учения из библейской школы, в которых особое внимание уделялось сопротивлению искушению.
Более того, одним из лучших примеров важности сопротивления и его эффектов является существование группы формул, называемых законом Ома. Я уверен, что вы знаете, что закон Ома представляет собой набор уравнений, которые можно использовать для расчета взаимосвязи между током, сопротивлением и напряжением в электрической цепи. Так что да, сопротивление влияет на все аспекты нашей жизни, от религии до области электроники.
Кроме того, с точки зрения электрической цепи свойство или характеристика сопротивления может также определять цепь в целом. Кроме того, тип электрической цепи, о которой я говорю, называется чисто резистивной цепью.
Что такое чистые резистивные цепи?
Чисто резистивная цепь — это цепь, индуктивность которой настолько мала, что при типичной частоте ее реактивное сопротивление незначительно по сравнению с ее сопротивлением. Кроме того, в чисто резистивной цепи все используемое напряжение расходуется на преодоление омического сопротивления самой цепи. Кроме того, чисто резистивная цепь называется безиндуктивной.
Кроме того, в чисто резистивной цепи все используемое напряжение расходуется на преодоление омического сопротивления самой цепи. Кроме того, чисто резистивная цепь называется безиндуктивной.
Более того, в чисто резистивной цепи фазовый угол между током и напряжением равен нулю. Кроме того, если бы мы должны были выразить мгновенный ток и мгновенное приложенное напряжение типичной чисто резистивной цепи, это указывало бы, что подаваемое напряжение и ток действительно находятся в фазе друг с другом.
Кроме того, если мы рассмотрим графическое представление той же цепи, мы увидим из ее кривой мощности, что ни одна часть цикла мощности не становится отрицательной в любое время. Поэтому в чисто резистивной цепи мощность никогда не равна нулю. Причем это связано с тем, что мгновенные значения тока и напряжения всегда бывают отрицательными или положительными. Кроме того, частота цикла мощности чисто резистивной цепи вдвое больше, чем частота волн тока и напряжения.
Соотношение между током и напряжением показывает, с каким сопротивлением работают ваши цепи.
Чисто резистивная цепь переменного тока
Цепь, которая содержит только чистое сопротивление (Ом) в цепи переменного тока, называется чисто резистивной цепью переменного тока. С технической точки зрения эта схема не содержит ни емкости, ни индуктивности. Переменное напряжение и ток синхронно перемещаются вперед в дополнение к обратному в любом направлении цепи. Следовательно, переменное напряжение и ток имеют форму синусоидальной волны и поэтому называются синусоидальной формой волны.
В этих цепях резисторы рассеивают мощность, а фазы тока и напряжения остаются неизменными. Ток и напряжение достигают своего максимального значения одновременно. Стоит отметить, что резистор является пассивным компонентом, он не производит и не потребляет электроэнергию. Итак, какое влияние оказывает резистор на мощность в чисто резистивной цепи? Он преобразует доступную энергию в тепло.
Я уверен, вы знаете, что в цепи переменного тока отношение тока к напряжению зависит от фазового угла, разности фаз и частоты питания. Кроме того, значение сопротивления резистора останется постоянным независимо от частоты питания.
Более подробно о чисто резистивной цепи
Изучая мощность в чисто резистивной цепи, мы можем наблюдать по приведенным ниже сигналам (красный, синий и розовый) общие характеристики типичной цепи. Из аналитического представления видно, что напряжение и ток находятся в фазе друг с другом. Вы также можете заметить, что значения напряжения и тока одновременно достигают своего максимума. И вы можете убедиться, что кривая мощности постоянно положительна для всех значений, относящихся к напряжению и току.
Сигналы являются полезным представлением любого ожидаемого выхода или входа для схемы.
Я уверен, вы помните, что в цепи питания постоянного тока побочный продукт тока и напряжения все еще называется мощностью. Хотя это то же самое в цепи переменного тока, разница здесь в том, что в цепи переменного тока мы принимаем во внимание мгновенные значения тока и напряжения. Следовательно, мгновенную мощность, которую мы находим в чисто резистивной цепи, мы представляем следующим уравнением.
Хотя это то же самое в цепи переменного тока, разница здесь в том, что в цепи переменного тока мы принимаем во внимание мгновенные значения тока и напряжения. Следовательно, мгновенную мощность, которую мы находим в чисто резистивной цепи, мы представляем следующим уравнением.
Мгновенная мощность, P = VI
Коэффициент мощности чисто резистивных цепей
Во-первых, что подразумевается под фразой «коэффициент мощности»? Что ж, в электротехнике мы определяем коэффициент мощности (PF или cosφ) как отношение между мощностью, которую вы можете использовать в электрической цепи (действительная мощность, P), и мощностью, вычисленной путем умножения напряжения и тока в цепи ( кажущаяся мощность, S). Кроме того, мы определяем PF как имеющий диапазон от нуля до единицы.
В цепи постоянного тока результат V x I дает нам мощность (P) в ваттах (Вт), потребляемую цепью. Однако в цепи переменного тока это будет отклоняться. Потому что в цепи переменного тока результат V x I дает нам полную мощность (S), а не реальную мощность (P), поскольку ток и напряжение не совпадают по фазе.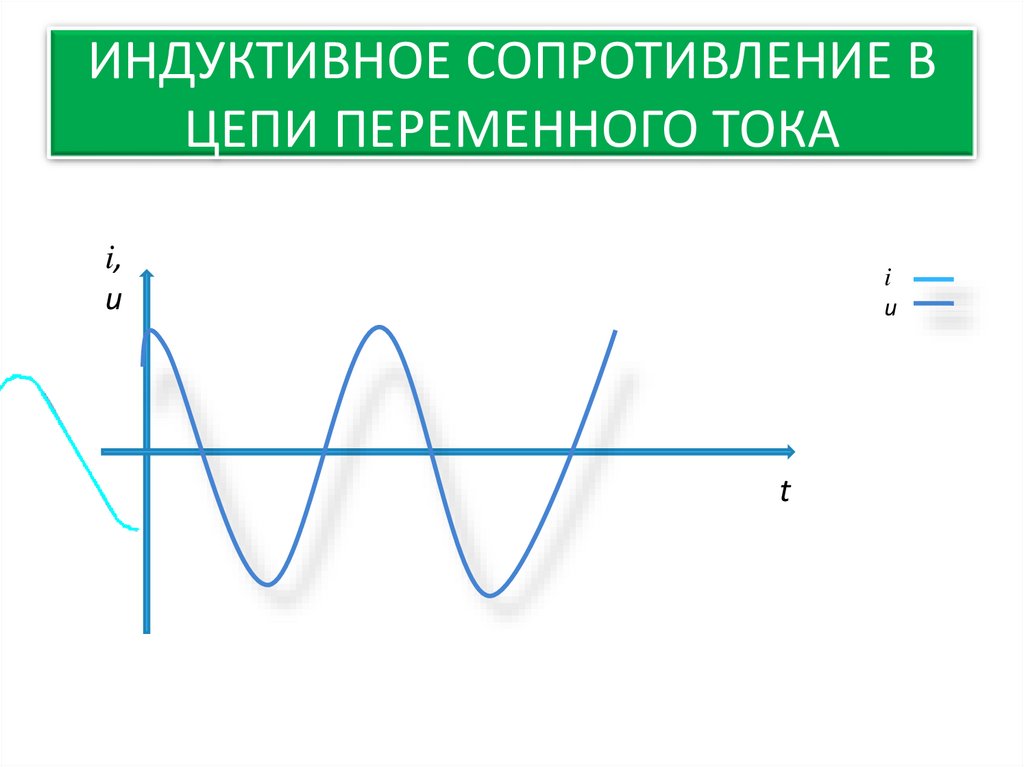
Далее мы можем определить коэффициент мощности в цепи переменного тока следующим образом:
Определить коэффициент мощности как косинус фазового угла между током и напряжением
Определить PF или cos φ как сопротивление (R) ÷ импеданс (Z)
PF или cos φ также определяется как: активная мощность (P) ÷ полная мощность (S)
Следовательно, поскольку напряжение и ток совпадают по фазе для чисто резистивной цепи, ее коэффициент мощности равен 1.
В чисто индуктивных или чисто емкостных цепях ток на 90° не совпадает по фазе с напряжением цепи; таким образом, cos φ = 90o. Следовательно, PF этих цепей равен нулю. PF цепи серии RLC находится между нулем и единицей.
Чисто резистивная цепь имеет уникальные характеристики, отличающиеся от характеристик других типов цепей.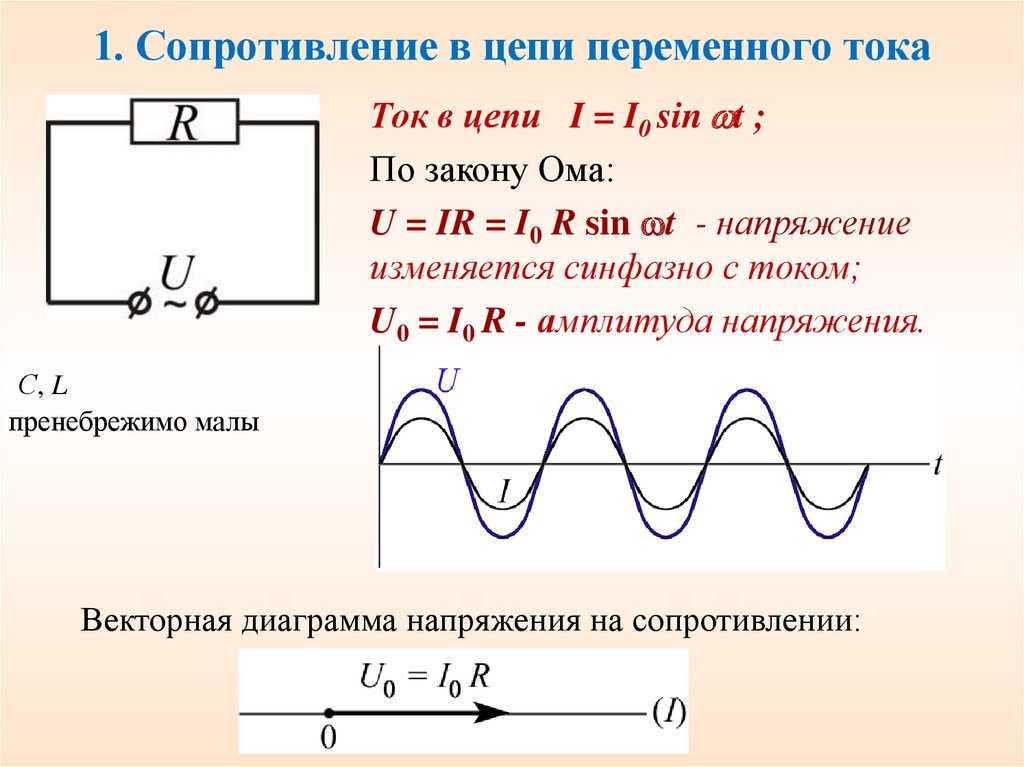 Однако без этих типов схем такие устройства, как лампы накаливания, были бы невозможны.
Однако без этих типов схем такие устройства, как лампы накаливания, были бы невозможны.
Работа с любым сопротивлением цепей и источниками питания становится проще благодаря набору инструментов для проектирования и анализа от Cadence. Помимо множества возможностей моделирования и анализа, OrCAD PCB Designer представляет собой непревзойденный вариант компоновки для интеграции любых результатов проектирования в ваш рабочий процесс.
Если вы хотите узнать больше о том, как у Cadence есть решение для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о проектировании и компоновке печатных плат, а также ознакомиться с новинками нашего набора инструментов для проектирования и анализа.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.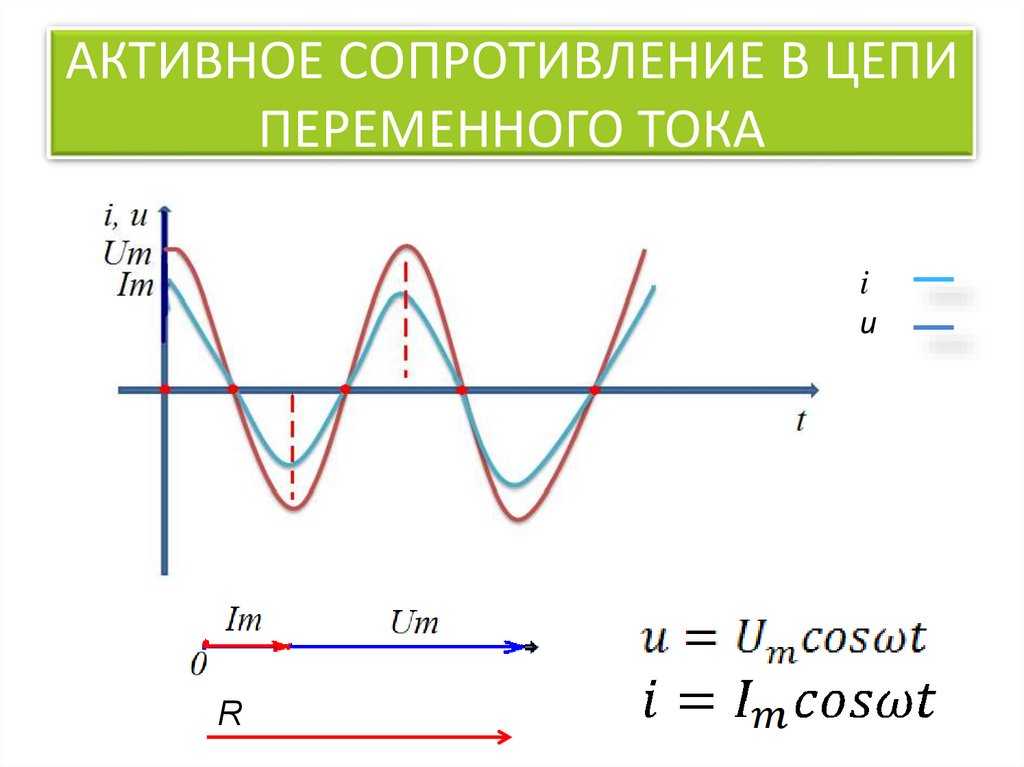
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Архивы цепей переменного тока — Электрические концепции
от администратора
Определение: Комплексная мощность в основном представляет собой электрическую мощность в виде комплексного числа. Как и комплексное число, оно состоит из действительной и мнимой частей. Действительная часть представляет собой активную мощность, тогда как мнимая часть представляет собой реактивную мощность. Обычно обозначается символом S. Если активная и реактивная мощность равны P … Читать далее
Если активная и реактивная мощность равны P … Читать далее
от администратора
Активные и пассивные элементы — это два разных типа элементов схемы. Эта классификация основана на способности элемента цепи отдавать энергию в виде напряжения или тока. Если элемент цепи может подавать энергию в цепь, он называется активным элементом, тогда как если элемент потребляет … Читать далее
Категории Цепь переменного тока 2 Комментарииот администратора
Односторонние и двусторонние элементы представляют собой два разных типа элементов электрических / электронных схем на основе их характеристик V-I при изменении полярности напряжения. В этой статье подробно описаны односторонние и двусторонние элементы и схемы с соответствующими схемами.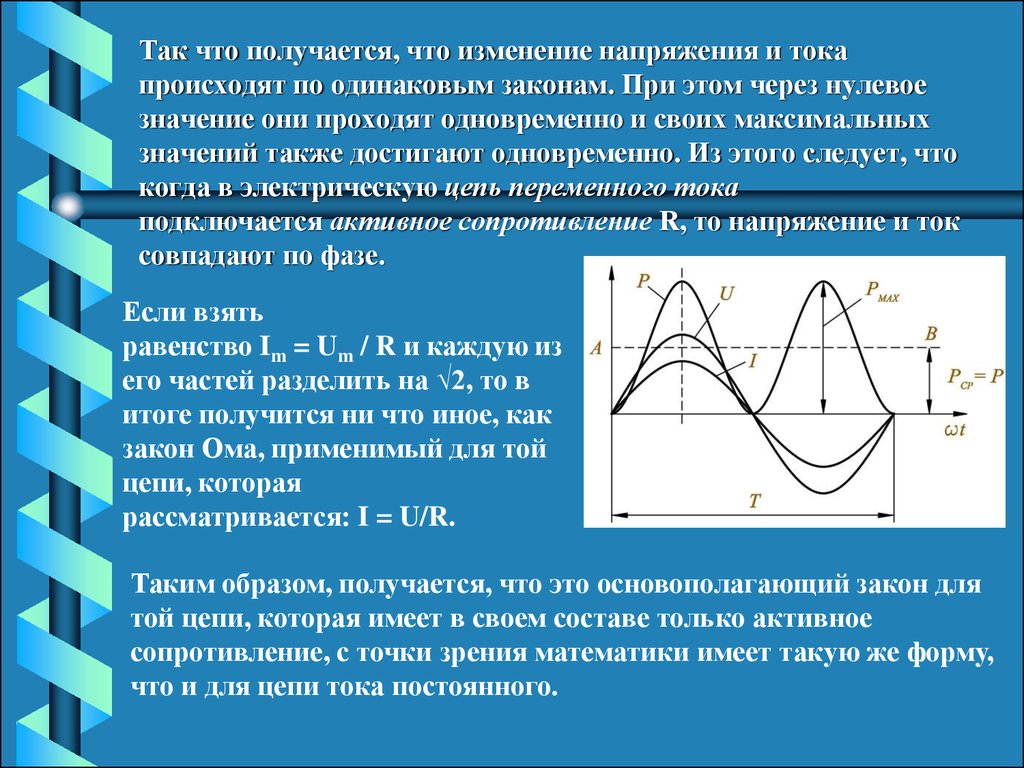 Односторонние элементы: Односторонние элементы в электрической цепи определяются как элемент, чей V-I … Читать далее
Односторонние элементы: Односторонние элементы в электрической цепи определяются как элемент, чей V-I … Читать далее
от администратора
Определение: Треугольник импеданса представляет собой прямоугольный треугольник, основание, перпендикуляр и гипотенуза которого представляют сопротивление, реактивное сопротивление и импеданс соответственно. По сути, это геометрическое представление импеданса цепи. Объяснение треугольника импеданса: импеданс состоит из двух компонентов, а именно. сопротивление и реактивность. Следовательно, она может быть выражена в этих двух компонентах. Пусть полное сопротивление … Читать далее
Категории Цепь переменного тока 2 Комментарииот администратора
Реактивное сопротивление определяется электрической величиной, из-за которой переменному току противодействует катушка индуктивности или конденсатор или их комбинация в цепи. Импеданс — это чистый противодействующий фактор переменному току. Реактивное сопротивление также можно назвать импедансом, обеспечиваемым катушкой индуктивности или конденсатором. Реактивное сопротивление обозначается X, а полное сопротивление … Читать далее
Импеданс — это чистый противодействующий фактор переменному току. Реактивное сопротивление также можно назвать импедансом, обеспечиваемым катушкой индуктивности или конденсатором. Реактивное сопротивление обозначается X, а полное сопротивление … Читать далее
от администратора
Что такое оператор j? j Оператор — это математический оператор, который при умножении на любой вектор поворачивает этот вектор на 90 градусов против часовой стрелки. Подобно тому, как символы x, +, – и т. д. используются с числами для обозначения определенных операций, которые необходимо выполнить с этими числами, оператор j используется для обозначения счетчика часов … Читать далее
Рубрики Цепь переменного тока 1 Комментарийот администратора
Основное различие между сопротивлением и импедансом заключается в том, что сопротивление противостоит потоку постоянного и переменного тока, тогда как импеданс противодействует только потоку переменного тока.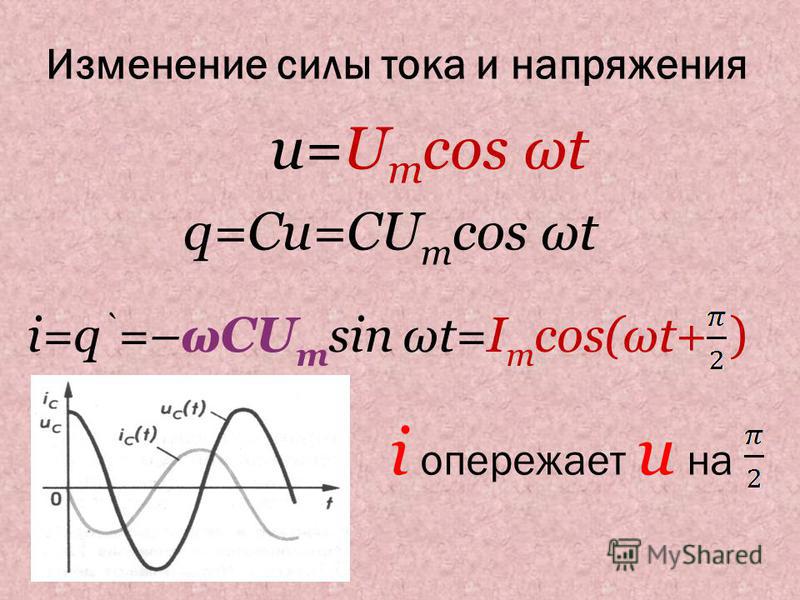 Импеданс имеет значение только в цепи переменного тока. В цепи постоянного тока это не имеет никакого значения. Еще одно важное различие между сопротивлением и импедансом заключается в том, что импеданс может… Читать далее
Импеданс имеет значение только в цепи переменного тока. В цепи постоянного тока это не имеет никакого значения. Еще одно важное различие между сопротивлением и импедансом заключается в том, что импеданс может… Читать далее
от администратора
Формулировка теоремы о передаче максимальной мощности в цепи переменного тока: В цепи переменного тока теорема о передаче максимальной мощности формулируется следующим образом: В линейной сети, имеющей источники энергии и полное сопротивление, максимальное количество мощности передается от источника к сопротивлению нагрузки, если сопротивление нагрузки является комплексно-сопряженным полным сопротивлением … Читать далее
Рубрики Цепь переменного тока Оставить комментарийот admin
Что такое правило деления напряжения? Правило разделения напряжения гласит, что общее напряжение, прикладываемое к последовательному соединению нескольких резисторов, делится между резисторами пропорционально их сопротивлению. Это означает, что падение напряжения будет максимальным на резисторе с максимальным значением сопротивления. Аналогично, минимальной она будет для резистора, имеющего … Читать далее
Рубрики Цепь переменного тока 1 Комментарийот администратора
Что такое текущее правило деления? Правило разделения тока гласит, что общий ток, разделенный на параллельную комбинацию двух сопротивлений или импедансов, обратно пропорционален значению сопротивления/импеданса. Это в основном говорит нам, как ток делится на параллельно подключенное сопротивление. Это правило применимо для АС … Читать далее
Рубрики Цепь переменного тока Оставить комментарий Цепи LCR серии— GeeksforGeeks
В отличие от постоянного тока (DC), который течет только в одном направлении, Переменный ток (AC) — это электрический ток, который время от времени меняет направление и постоянно меняет свою величину с течением времени. Переменный ток — это тип электричества, который доставляется компаниям и домам, и это тип электричества, который используется потребителями, когда они подключают кухонные приборы, телевизоры, вентиляторы и электрические лампы к настенной розетке. Аккумулятор фонарика часто является источником питания постоянного тока. При изменении тока или напряжения сокращения AC и DC часто используются для обозначения просто переменного и постоянного тока.
Переменный ток — это тип электричества, который доставляется компаниям и домам, и это тип электричества, который используется потребителями, когда они подключают кухонные приборы, телевизоры, вентиляторы и электрические лампы к настенной розетке. Аккумулятор фонарика часто является источником питания постоянного тока. При изменении тока или напряжения сокращения AC и DC часто используются для обозначения просто переменного и постоянного тока.
В большинстве электрических цепей наиболее распространенной формой волны переменного тока является синусоида, положительный полупериод которой соответствует положительному направлению тока и наоборот. На самом деле ток может не изменить направление (как для помеченной пульсирующей формы волны). Различные формы сигналов, такие как треугольные волны или прямоугольные волны, используются в различных приложениях, таких как гитарные усилители. К переменному току относятся также аудио- и радиосигналы, передаваемые по электрическим линиям. Такая информация, как звук (аудио) или изображения (видео), иногда передается посредством модуляции несущего сигнала переменного тока в этих формах переменного тока. Частота этих токов обычно выше частоты токов электропередачи.
Частота этих токов обычно выше частоты токов электропередачи.
Цепь LCR серии
Цепь LCR состоит из трех компонентов: катушки индуктивности (L), конденсатора (C) и резистора (R). Настроенная или резонансная схема — это другое название. Цепь последовательного LCR состоит из этих устройств, которые соединены последовательно. В результате резистор, конденсатор и катушка индуктивности будут иметь одинаковое количество тока, протекающего через них.
Напряжение V S подается на последовательную цепь LCR в приведенной выше схеме, которая изображает простую последовательную цепь LCR.
Импеданс — это величина сопротивления, которое цепь оказывает току. Это эффективное сопротивление переменному току в электрической цепи, состоящей из множества электрических компонентов. Это вызвано взаимодействием омического сопротивления, емкостного сопротивления и индуктивного сопротивления. Если R обозначает сопротивление, X L обозначает индуктивное сопротивление, X C обозначает емкостное сопротивление, тогда Z обозначает импеданс.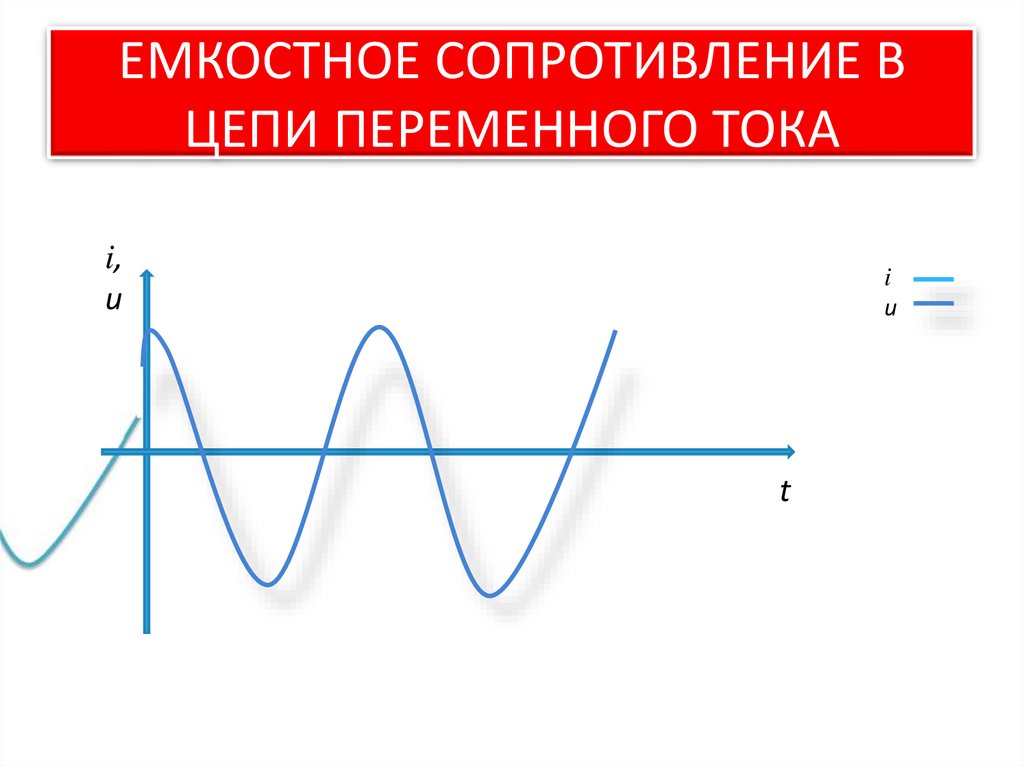
Z=√ R 2 +(X C −X L ) 2
Расчет переменного напряжения, приложенного к последовательной цепи LCR питание от сети переменного тока. Переменное напряжение V подается от источника напряжения, где
V=V м sin(ωt)
где
- В м – амплитуда приложенного напряжения, а
- ω — частота приложенного напряжения.
Если q — заряд конденсатора, а I — ток, протекающий в цепи в любой момент t, уравнение напряжения для цепи можно записать следующим образом:
Суммарная ЭДС в цепи: В (напряжение источника ) = Падение напряжения на резисторе + Падение напряжения на конденсаторе + ЭДС Фарадея самоиндукции в дросселе
V=L(di/dt) + IR + q/C
Собственная индуктивность дросселя обозначается L.
Подставляя переменное напряжение вместо выражения, мгновенный ток I или его фаза, соответствующая приложенному переменному напряжению V. Мы знаем, что ток равен скорости, с которой электрический заряд течет в единицу времени, т. е.
Мы знаем, что ток равен скорости, с которой электрический заряд течет в единицу времени, т. е.
I=dq/dt
по времени получаем:
dI/dt=d 2 q/dt 2
Уравнение напряжения относительно q получается путем подстановки вышеуказанного значения в уравнение (1):
В sin ) = L(d 2 q/dt 2 ) + (dq/dt)R + q/C ……(2)
Уравнение для вынужденного или затухающего гармонического осциллятора аналогично этому уравнению.
q = q m sin(ωt+θ)
Дифференцирование обеих сторон по времени,
dq/dt = q m ωcos(ωt+θ)
d 2 q/dt 2 =–q m ω 2 sin(ωt+θ)
Подставляя эти значения в уравнение (2), получаем )] …..(3)
Здесь,
- Емкостное сопротивление: X C =1/ωC
9021 X L =ωL- Impedance: Z= √R2+(X C −X L ) 2
Substituting the above values in equation (3), so we get:
V M sin (ωt) = Q M ωz [r/z cos (ωt+θ)+(x C –x L )/zsin (ωt+θ)] … (4)
Рассмотрим,
R/Z = cos∅
(X C –X L )/Z = sin∅
Разделение двух уравнений:
(x C –x L )/R = TAN∅
∅ = TAN —1 (X C4444444444444444). /R)
/R)
Подставив вышеуказанные значения в уравнение (4):
В м sin(ωt)=q м ωZ[cos(ωt+θ–∅)]
Сравнение LHS В правой части этого уравнения получаем
V м =q м ωZ=I м Z
Ток в схеме LCR,
I = DQ/DT
или,
I = Q M ωcos (ωt+θ)
I 33333333333 M . θ) [где, Q M ω = I M ]
, так как θ — ∅ = — π/2
θ = — π/2 + ∅
Мы получаем,
I = m cos(ωt–π/2+∅)
I = I m sin(ωt+∅)
Здесь I m =V m /Z = V m / √R 2 +(X C –X L ) 2 and ∅=tan –1 (X C –X L /R)
- Таким образом, при θ=0 ∘ , В результате приложенное напряжение и мгновенный ток совпадают по фазе
- При θ=90 ∘ , Приложенное напряжение равно не в фазе с мгновенным током.

Резонанс цепи LCR
Если выход цепи достигает максимума на определенной частоте, говорят, что она находится в резонансе. Явление резонанса связано с системами, которые имеют тенденцию колебаться с определенной частотой, известной как собственная частота системы. Наблюдается, что амплитуда колебаний учитывается, когда источник энергии приводит в движение такую систему с частотой, близкой к собственной частоте.
Мы обнаружили, что амплитуды напряжения, частоты и тока связаны друг с другом в следующем ряду цепей LCR: R 2 +(X C –X L ) 2
where,
- X C =1/ωC and
- X L =ωL
I м =V м /Z=V m / √R 2 +(1/ωC−ωL) 2
Когда импеданс цепи низкий, ток, протекающий через нее, максимален.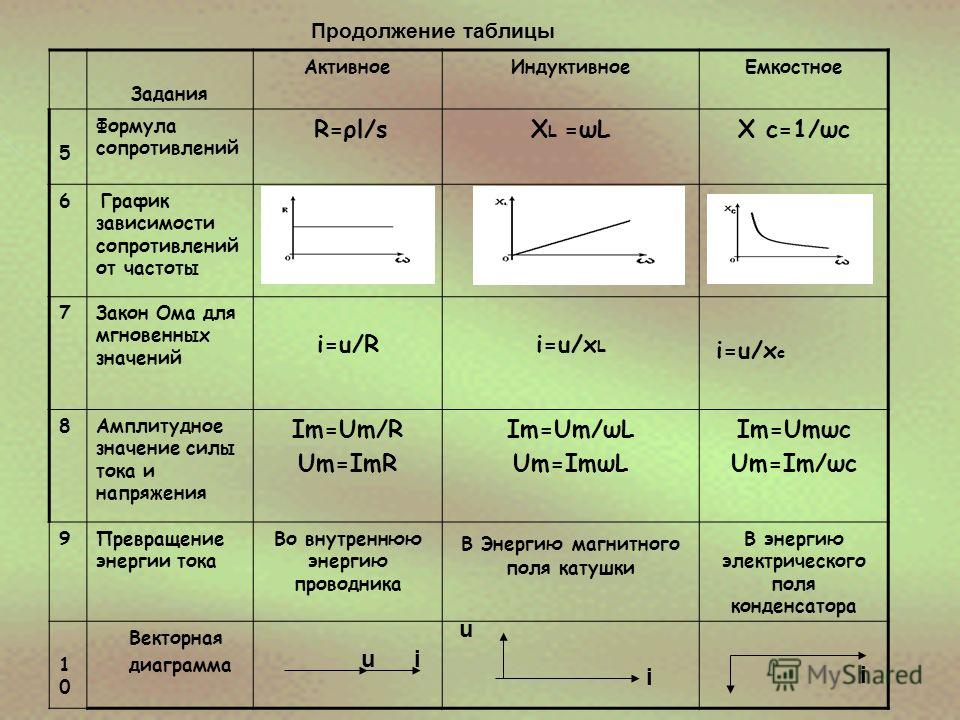 Для этого мы изменяем значение частоты, пока не получим X C = X L при заданной частоте ω 0 , а импеданс
Для этого мы изменяем значение частоты, пока не получим X C = X L при заданной частоте ω 0 , а импеданс
Z=√ R 2 +(X C −X L ) 2 = √ R 2 +0 = R
Таким образом, ток будет максимальным, т. е.
I=V m /R
Когда импеданс последовательной цепи LCR, Z=R, равен сопротивлению. Эта частота ω 0 называется резонансной частотой контура.
For, X C =X L
1/ω 0 C=ω 0 L
Or,
ω 0 = 1/√LC
Резонанс возникает в последовательной цепи LCR, когда емкостное и индуктивное сопротивления равны по величине, но разнесены по фазе на 180 градусов.
Для последовательной цепи LCR разность фаз,
∅=tan –1 (X C –X L / R)
Для, X C =X L, 90∅ 0, схема находится в резонансе.
x C > x L , ∅ <0, схема преимущественно емкости
x C
Power Factor, CosΦ=Active power/Total Power
CosΦ=I 2 R / I 2 Z
=R/Z
= R / √(R) 2 +( X L −X C ) 2
Потребляемая мощность: Резистор является единственным компонентом в цепи, который потребляет мощность; индуктор и конденсатор — нет. Следовательно,
P=VI CosΦ
=(IZ)×I×R/Z
= I 2 R
Добротность последовательного резонансного контура: Добротность контура (добротность) определяется как отношение реактивной мощности к активной, т.
е.
Добротность = реактивная мощность /Активная мощность
Q -Factor = I 2 x L /I 2 R = = I 2 x C /I 2 R . /R = 1/ωCR
В резонансе
ω 0 =1/√LC
Итак,
Q 0 −фактор=1/R × √L/C
Примеры задач
91:169 30 Ом, L = 15 мГн, C = 51 мкФ. Если напряжение и частота источника равны 12 В и 60 Гц соответственно, какова сила тока в цепи?
Решение:
x L = 2 × 3,14 × 60 × 0,015 = 5,655 ω
x C = 1/2 × 3,14 × 6051515151515151 гг.0003
z = √ (30) 2 + (52-5.655) 2 = 55,21 ω
I = 12/55,21 = 217 мА
Задача 2: a stirc rlc orcistc orcistc orcistc orcistc orcistc rlc rlc. резистор ом, конденсатор 51 мкФ и катушка индуктивности 25 мГн. Если частота источника 50 Гц, а ток в цепи 350 мА, каково приложенное напряжение?
Если частота источника 50 Гц, а ток в цепи 350 мА, каково приложенное напряжение?
Решение:
Учитывая, что
R = 20 Ом
X L = 2 × 3,14 × 50 × 0,025 = 7,85 Ом
x C = 1/2 × 3,14 × 50 × 0,000051 = 62,445 ω
z = √ (20) 2 + (7,85-62,445) 2 = 58,15 ω
9008. 0,35 = 20 В
Проблема 3. В источнике переменного тока 240 В, 50 Гц применена катушка с индуктивностью 0,08 Гн и сопротивлением 4 Ом, соединенная последовательно с конденсатором 8 мкФ. Вычислить импеданс
Решение:
Здесь
X L = ωL = 2πfL=2π×50×0,08=25,12 Ом
X C =1/ωC=1/2πfL=1/2π×50×8×10 −6 = 398,09 Ом
Таким образом,
Полное сопротивление цепи
Z=√1(R) 2 +(x L -x C ) 2
= √ (4) 2 +(25,12–398,09) 2
= 908,09) 2
= .
09) 2
= .09) 2 9000 3 9086 = .09) 2
66 = 9019,09) 2 66 = 9019,09) 2 = 908,09) 2= 908,09). Вопрос 1: Каковы условия резонанса для последовательной цепи LCR?
Ответ:
Емкостное и индуктивное сопротивления равны и сдвинуты по фазе на 180 градусов при резонансе.
Вопрос 2: Каково сопротивление последовательной цепи LCR?
Ответ:
Суммарное воздействие омического сопротивления и реактивного сопротивления дает эффективное сопротивление электрической цепи или компонента переменному току.
Полное сопротивление последовательной цепи LCR выражается как
Z=√R 2 +(X C −X L ) 2
Вопрос 3: Какова острота резонанса?
Ответ:
Добротность определяет остроту резонанса.
- Коэффициент добротности — это безразмерный параметр, характеризующий потери энергии в резонансном элементе, таком как механический маятник, элемент механической конструкции или электронная схема, такая как резонансная цепь.
- Q часто используется вместе с катушкой индуктивности.
- Острота резонанса пропорциональна скорости затухания энергии колебательной системы.
Анализ передаточной функции | Основная теория переменного тока (AC)
Чрезвычайно важной темой в технике является передаточная функция . Проще говоря, передаточная функция — это отношение выхода к входу для любой физической системы, обычно с выходом и входом, являющимися математическими функциями \(s\). Другими словами, мы выражаем как выход системы, так и соответствующий вход этой системы в терминах экспоненциально растущих/затухающих синусоидальных волн, а затем находим отношение этих двух выражений.
К сожалению, преподавание передаточных функций и их связи с явлениями реального мира часто запутывается из-за сильного упора на математику.
Цель этого раздела состоит в том, чтобы представить эту концепцию очень «мягко» и постоянно ссылаясь на реальные приложения. Если я смогу сделать что-нибудь, чтобы помочь приподнять завесу тайны, окружающую такие понятия, как передаточные функции, переменная \(s\) и графики нулевого полюса, тогда техники и инженеры смогут оценить мощь этого аналитического метода. и иметь возможность обмениваться большим количеством идей на одном и том же «языке».
Простым примером передаточной функции является усиление электронного усилителя. Как учат все студенты электроники, «усиление» — это отношение выходного сигнала к входному сигналу для схемы. Начинающие учащиеся учатся представлять коэффициенты усиления цепи в виде скалярных значений (например, «Усилитель имеет коэффициент усиления по напряжению 24»), сначала в виде простых коэффициентов, а затем в виде цифр в децибелах (например, «Усилитель имеет коэффициент усиления по напряжению 27,6 дБ»). Одним из недостатков этого подхода является то, что он чрезмерно упрощает ситуацию, когда коэффициент усиления рассматриваемой схемы зависит от частоты и/или скорости нарастания/спада сигнала, что бывает довольно часто.
Если мы воспользуемся инженерным подходом к выражению выходных и входных сигналов как функций \(s\), мы получим более полную картину поведения этой схемы в широком диапазоне условий.
Другим простым примером передаточной функции является то, что мы только что видели в этой книге: импеданс реактивного электрического компонента, такого как конденсатор или катушка индуктивности. Здесь речь идет о соотношении между напряжением и током. Если мы считаем, что ток через компонент является «входным» сигналом, а напряжение на компоненте является «выходным» сигналом — оба выражения выражены в терминах \(s\) — тогда импеданс \(Z(s) = {V( s) \over I(s)}\) — передаточная функция для этого компонента. Это поднимает важный вопрос о передаточных функциях: то, что мы определяем как «вход» и «выход» системы, совершенно произвольно, пока существует реальная связь между двумя сигналами.
Если мы запишем обобщенные входные/выходные передаточные функции \(s\) для цепи переменного тока, мы можем математически проанализировать эту передаточную функцию, чтобы получить представление о поведении и характеристиках этой цепи.
Особенности передаточных функций, представляющие интерес для нас, включают:
- Нули : любое значение(я) \(s\), приводящее к нулевому значению передаточной функции (т.е. нулевое усиление)
- Полюса : любое значение(я) \(s\), приводящее к бесконечному значению передаточной функции (т.е. максимальный коэффициент усиления)
нули цепи переменного тока говорят нам, где цепь не реагирует на входные воздействия. полюса цепи переменного тока говорят нам, где схема способна генерировать выходной сигнал без входного стимула (т. е. ее естественный или неуправляемый режим(ы) реакции).
Для четкого понимания концепции передаточных функций очень полезны практические примеры. Здесь мы рассмотрим несколько очень простых цепей переменного тока, чтобы понять, что такое передаточные функции и какую пользу они приносят системному анализу.
Пример: схема фильтра нижних частот LR
Сначала давайте начнем с простой схемы фильтра нижних частот, состоящей из катушки индуктивности и резистора, соединенных последовательно:
Полное сопротивление каждого компонента как функция \( s\) показано на диаграмме: импеданс индуктора равен \(sL\), а импеданс резистора просто \(R\).
Любому изучающему электронику должно быть ясно, что эти два компонента будут функционировать как делитель напряжения , при этом выходное напряжение составляет некоторую часть входного напряжения. Зная это, мы можем написать передаточную функцию для этой схемы на основе формулы делителя напряжения, которая говорит нам, что отношение выходного напряжения к входному напряжению такое же, как отношение выходного импеданса к общему импедансу:
\[\hbox{Передаточная функция} = {V_{out}(s) \over V_{in}(s)} = {R \over {R + sL}} = {R \over {R + (\ sigma + j \omega) L}}\]
Эта передаточная функция позволяет нам вычислить «выигрыш» системы для любого заданного значения \(s\), что подводит нас к следующему шагу нашего анализа. На этом этапе мы зададим себе три вопроса:
- Как эта система реагирует, когда \(s = 0\)?
- При каком значении (значениях) \(s\) передаточная функция приближается к нулевому значению?
- При каком значении (значениях) \(s\) передаточная функция приближается к бесконечности?
Первый из этих вопросов относится к ситуации, когда на вход системы подается устойчивый сигнал постоянного тока.
Если \(s = 0\), то и \(\sigma\), и \(\omega\) должны быть равны нулю. Нулевое значение для \(\sigma\) означает, что сигнал не растет и не затухает с течением времени, а остается на каком-то неизменном значении. Нулевое значение для \(\omega\) означает, что сигнал не колеблется. Эти два условия могут относиться только к устойчивому сигналу постоянного тока, приложенному к цепи. Подставляя ноль вместо \(s\), получаем:
\[{R \over {R + 0 L}}\]
\[{R \over R} = 1\]
Следовательно, передаточная функция этой цепи равна единице (1) в условиях постоянного тока. Это именно то, чего можно было бы ожидать, если бы катушка индуктивности была соединена последовательно с резистором, а выходное напряжение падало бы на резистор. Если в подаваемом сигнале нет изменений, то магнитное поле катушки индуктивности также будет неизменным, а это означает, что на ней будет падать нулевое напряжение (при условии, что это чистая катушка индуктивности без сопротивления провода), в результате чего все входное напряжение падает на резисторе.
Второй вопрос относится к состоянию, когда выходной сигнал этой схемы равен нулю. Любые значения \(s\), приводящие к нулевому выходу системы, называются нулями передаточной функции. Исследуя передаточную функцию для этой конкретной схемы фильтра нижних частот LR, мы видим, что это может быть верным только в том случае, если \(s\) становится бесконечно большим, потому что \(s\) находится в знаменателе дроби:
\ [{R \over {R \pm \infty L}} = 0\]
Это согласуется с поведением фильтра нижних частот: по мере увеличения частоты (\(\omega\)) выходной сигнал фильтра уменьшается . Однако передаточная функция не только говорит нам, как эта схема будет реагировать на изменение частоты, но также говорит нам, как схема будет реагировать на нарастающие или затухающие сигналы. Здесь мы видим, что бесконечно большие значения \(\сигма\) также приводят к нулевому выходному сигналу: катушка индуктивности, которая имеет тенденцию противодействовать любому току с высокой скоростью изменения, не позволяет большому напряжению развиваться на резисторе, если вход сигнал очень быстро нарастает или затухает.
Третий вопрос относится к условию, когда либо числитель передаточной функции стремится к бесконечности, либо ее знаменатель приближается к нулю. Любые значения \(s\), имеющие этот результат, называются полюсами передаточной функции. Поскольку числитель в этом конкретном случае является константой (\(R\)), только нулевое значение знаменателя может привести к тому, что передаточная функция достигнет бесконечности:
\[{R \over {R + sL}} = \infty \hbox{ только если } R + sL = 0\]
Если необходимым условием для «полюса» является то, что \(R + sL = 0\), то мы можем решить для \(s\) следующим образом:
\[R + sL = 0\]
\[sL = -R\]
\[s = -{R \over L}\]
Таким образом, эта передаточная функция для этого простого фильтра нижних частот схема имеет один полюс, расположенный в \(s = — R / L\). Поскольку и \(R\), и \(L\) являются действительными числами (не мнимыми) с положительными значениями, то значение \(s\) для полюса должно быть действительным числом с отрицательным значением.
Другими словами, решение для \(s\) на этом полюсе есть все \(\сигма\) и никакое \(\омега\): это относится к экспоненциально затухающему сигналу постоянного тока .
На данном этапе важно рассмотреть, что означает это состояние «полюса» в реальной жизни. Представление о том, что схема способна генерировать выходной сигнал при нулевом входном сигнале, может показаться абсурдным, но оно имеет смысл, если рассматриваемая схема способна накапливать и выделять энергию. В этой конкретной схеме катушка индуктивности является компонентом, накапливающим энергию, и она способна создавать падение напряжения на резисторе с нулевым входным напряжением в режиме «разрядки».
Иллюстрация помогает понять это. Если условие «полюса» таково, что \(V_{in}(s) = 0\), мы можем показать это, замкнув накоротко вход нашей схемы фильтра, чтобы обеспечить условие нулевого входа:
Если предположить, что катушка индуктивности была «заряжена» энергией до короткого замыкания входа, выходное напряжение обязательно возникнет на резисторе по мере разрядки катушки индуктивности.
Другими словами, катушка индуктивности ведет себя как электрический источник , в то время как резистор ведет себя как электрическая нагрузка : соединенные последовательно, они, конечно, должны иметь один и тот же ток, но их соответствующие напряжения равны по величине и противоположны по полярности в соответствии с с законом напряжения Кирхгофа. Кроме того, значение \(s\) в этом «полюсном» состоянии точно говорит нам, как быстро будет затухать выходной сигнал: он будет делать это со скоростью \(\sigma = -R / L\). Напомним, что член роста/убывания переменной \(s\) обратно пропорционален постоянной времени системы (\(\sigma = 1 / \tau\)). Следовательно, \(\сигма\) значение \(R / L\) эквивалентно постоянной времени \(L / R\), что, как узнают все начинающие студенты электроники, заключается в том, как мы вычисляем постоянную времени для простая схема индуктор-резистор.
Передаточные функции легче понять, если графически изобразить их в виде трехмерных поверхностей: действительная и мнимая части переменной \(s\) занимают горизонтальные оси, а величина дроби передаточной функции отображается как высота.
Вот график полюс-ноль передаточной функции этой схемы фильтра нижних частот со значением резистора \(R = 5 \> \Omega\) и значением индуктивности \(L = 10 \hbox{H} \):
Этот поверхностный график делает значение термина «полюс» совершенно очевидным: форма функции выглядит точно так же, как резиновый коврик, натянутый в одной точке физическим полюсом. Здесь «полюс» поднимается на бесконечную высоту при значении \(s\), где \(\sigma\) = \(-0,5\) постоянных времени в секунду и \(\omega\) = 0 радиан в секунду. . Видно, что высота поверхности уменьшается на всех краях графика по мере увеличения значения \(\sigma\) и \(\omega\).
«Нуль» этой передаточной функции не так очевиден, как полюс, поскольку значение функции не равно нулю до тех пор, пока \(s\) не станет бесконечным, что, конечно, не может быть нанесено на какую-либо конечную область. Достаточно сказать, что ноль этой передаточной функции лежит во всех горизонтальных направлениях на бесконечном расстоянии от начала координат (центра), что объясняет, почему поверхность наклоняется к нулю везде с увеличением расстояния от полюса.
Одной из ценных идей, которую дает трехмерный график полюс-ноль, является реакция системы на входной сигнал постоянной величины и переменной частоты. Это обычно называют частотная характеристика системы, ее графическое представление называется графиком Боде . Мы можем проследить график Боде для этой системы, открыв срез трехмерной поверхности в поперечном сечении вдоль плоскости, где \(\сигма = 0\) (т.е. показав, как система реагирует на синусоидальные волны различной частоты, которые не t растут или затухают со временем):
Здесь нанесена только половина поверхности полюс-ноль, чтобы лучше показать поперечное сечение по оси \(j \omega\). Жирная красная кривая отслеживает край поверхности передаточной функции, начиная с нулевой частоты (DC) до все более положительных значений \(j \omega\). Таким образом, красная кривая представляет собой график Боде для этого фильтра нижних частот, начиная с максимального значения 1 (\(V_{out} = V_{in}\) для входного сигнала постоянного тока) и приближаясь к нулю по мере увеличения частоты.
Какими бы проницательными ни были трехмерные графики полюс-ноль, их сложно рисовать вручную, и даже с помощью компьютера может потребоваться много времени для настройки. По этой причине графики полюс-ноль традиционно рисовались в двумерном, а не в трехмерном формате, с высоты птичьего полета, глядя на плоскость \(s\). Поскольку этот вид скрывает любые особенности высоты, полюса и нули вместо этого расположены на плоскости \(s\) символами \(\times\) и \(\circ\) соответственно. Здесь показан пример традиционного графика полюс-ноль для нашего фильтра нижних частот:
Следует признать, что этот тип графика полюс-ноль гораздо менее интересен для просмотра, чем трехмерная поверхность, построенная компьютером, но, тем не менее, содержит полезную информацию о системе. Единственный полюс, лежащий на действительной (\(\сигма\)) оси, говорит нам, что система не будет совершать автоколебаний (т.е. \(\омега = 0\) на полюсе), и что она по своей природе устойчива: импульс, его естественная тенденция состоит в том, чтобы затухать до стабильного значения с течением времени (т.
Е. \ (\ sigma < 0 \)).
Следует отметить, что передаточные функции и графики полюс-ноль применимы не только к схемам фильтров. На самом деле любая физическая система, имеющая ту же характеристику «низких частот», что и эта схема фильтра, может быть описана той же передаточной функцией и теми же графиками полюс-ноль. Электрические цепи оказались удобными приложениями, потому что характеристики их отдельных компонентов так легко представить как функции \(s\). Однако, если мы можем охарактеризовать компоненты другой физической системы в одних и тех же терминах, применяются те же математические инструменты.
Пример: RC-схема фильтра верхних частот
В нашем следующем ознакомительном примере мы рассмотрим еще одну простую схему фильтра, на этот раз состоящую из конденсатора и резистора, с выходным сигналом, принимаемым через резистор. Как и прежде, мы можем получить передаточную функцию, выразив \(V_{out} / V_{in}\) как отношение импеданса резистора к общему последовательному импедансу резистор-конденсатор (рассматривая это как схему делителя напряжения):
\[\hbox{Передаточная функция} = {V_{out}(s) \over V_{in}(s)} = {R \over {R + {1 \over sC}}}\]
После написания этой начальной передаточной функции, основанной на импедансах компонентов, мы будем алгебраически манипулировать ею, чтобы исключить составные дроби.
Это поможет нам проанализировать отклик цепи по постоянному току, нули и полюса:
\[R \over {R + {1 \over sC}}\]
\[R \over {{sRC \over sC} + {1 \over sC}}\]
\[R \over {1 + sRC \over sC}\]
\[sRC \over 1 + sRC\]
Эта передаточная функция позволяет нам рассчитать коэффициент усиления ” системы для любого заданного значения \(s\), что подводит нас к следующему шагу нашего анализа. Еще раз зададим себе три вопроса о передаточной функции:
- Как эта система реагирует, когда \(s = 0\)?
- При каком значении (значениях) \(s\) передаточная функция приближается к нулевому значению?
- При каком значении (значениях) \(s\) передаточная функция приближается к бесконечности?
Отвечая на первый вопрос, видим, что передаточная функция равна нулю при \(s = 0\):
\[{0RC \over 1 + 0RC}\]
\[{0 \over 1 + 0} = {0 \over 1} = 0\]
Конечно, значение 0 для \(s\) означает воздействие постоянного сигнала постоянного тока: такого, который не растет, не затухает со временем и не колеблется.
Следовательно, эта схема резистор-конденсатор будет выдавать нулевое напряжение при воздействии на входной сигнал постоянного тока. Это имеет концептуальный смысл, когда мы исследуем саму схему: напряжение входного сигнала постоянного тока означает, что конденсатор не будет испытывать никаких изменений напряжения с течением времени, а это означает, что он не будет пропускать ток через резистор. Без тока через резистор не будет выходного напряжения. Таким образом, конденсатор «блокирует» входной сигнал постоянного тока, не давая ему достичь выхода. Именно такое поведение мы и ожидаем от такой схемы, которую любой изучающий электронику должен сразу распознать как простую схему.0021 фильтр верхних частот : постоянный ток — это состояние нулевой частоты, которое должно быть полностью заблокировано любой схемой фильтра с характеристикой верхних частот.
Ответ на наш первый вопрос является также ответом на второй вопрос: «Какое значение \(s\) делает передаточную функцию равной нулю?» Здесь мы видим, что только при значении \(s = 0\) значение всей передаточной функции будет равно нулю.
Любые другие значения \(s\) — даже бесконечные — дают ненулевые результаты. В отличие от последней схемы (резисторно-индукторный фильтр нижних частот) эта схема имеет единственную «нулевую» точку в своей передаточной функции: одно конкретное место на графике полюс-ноль, где значение функции уменьшается до нуля.
Когда мы рассматриваем третий вопрос («Какое значение(я) \(s\) заставляет передаточную функцию приближаться к бесконечности?»), мы поступаем так же, как и раньше: находим значение(я) \(s) \), что сделает знаменатель дроби передаточной функции равным нулю. Если мы приравняем часть знаменателя к нулю и решим для \(s\), мы получим полюс для схемы:
\[1 + sRC = 0\]
\[sRC = -1\]
\[s = -{1 \over RC}\]
Мы знаем, что и \(R\), и \(C\) — действительные числа, а не мнимые. Это говорит нам о том, что \(s\) также будет действительным числом на полюсе. То есть \(s\) будет состоять из всех \(\sigma\) и ни одного \(\omega\). Тот факт, что значение \(\сигма\) отрицательное, говорит нам о том, что полюс представляет собой состояние экспоненциальный спад , точно такой же, как и в случае резисторно-индуктивного ФНЧ.
Как и прежде, это означает, что схема будет генерировать сигнал выходного напряжения без сигнала входного напряжения, когда скорость затухания сигнала равна \(\sigma = -1 / RC\).
Напомним, что скорость затухания переменной \(s\) (\(\sigma\)) есть не что иное, как величина, обратная постоянной времени системы (\(\tau\)). Таким образом, скорость затухания, равная \(1 / RC\), приравнивается к постоянной времени \(\tau = RC\), что, как известно всем изучающим электронику, является тем, как мы вычисляем постоянную времени для любой простой схемы резистор-конденсатор.
Используя компьютер для построения трехмерного представления этой передаточной функции, мы ясно видим и полюс, и ноль как сингулярности. Здесь я предположил резистор 10 Ом и конденсатор 0,2 Ф, чтобы разместить полюс в том же месте, что и в схеме фильтра нижних частот \(s = -0,5 + j0\), для справедливого сравнения:
Здесь мы видим как полюс в точке \(s = -0,5 + j0\), так и нуль в точке \(s = 0 + j0\) совершенно ясно: полюс представляет собой особую точку бесконечной высоты, а нуль особая точка нулевой высоты.
Трехмерная поверхность передаточной функции выглядит как резиновый лист, растянутый на бесконечную высоту в полюсе и вытянутый до уровня земли в нуле.
Как и в последнем примере, мы можем перестроить передаточную функцию таким образом, чтобы показать вид в поперечном сечении при \(\sigma = 0\), чтобы показать частотную характеристику этой схемы фильтра верхних частот:
Снова жирная красная кривая показывает край поверхности передаточной функции, начиная с нулевой частоты (DC) до возрастающих положительных значений \(j \omega\). Таким образом, красная кривая представляет собой график Боде для этого фильтра верхних частот, начиная с минимального значения 0 (\(V_{out} = 0\) для входного сигнала постоянного тока) и приближаясь к единице (1) по мере увеличения частоты. Естественно, это тип отклика, который мы ожидаем увидеть от схемы фильтра верхних частот.
Более традиционный двумерный график полюс-ноль для этой схемы определяет положение полюса с помощью символа «\(\times\)», а ноль — с помощью символа «\(\circ\)»:
Пример: LC-контур
Далее мы исследуем передаточную функцию для контура , состоящего из конденсатора и катушки индуктивности.
Мы предполагаем использование здесь чистых реактивных сопротивлений без электрического сопротивления или других потерь энергии любого рода, просто для анализа идеального случая. Выходное напряжение в этой конкретной схеме будет приниматься через дроссель:
Запись передаточной функции для этой цепи резервуара (еще раз) заключается в выражении отношения между полным сопротивлением выходного компонента и полным сопротивлением цепи:
\[\hbox{Передаточная функция} = {V_{out} (s) \over V_{in}(s)} = {sL \over {sL + {1 \over sC}}}\]
Алгебраические манипуляции с этой функцией для устранения составных дробей:
\[sL \over { sL + {1 \over sC}}\]
\[sL \over {{sLsC \over sC} + {1 \over sC}}\] 92\) терминов, а не \(s\) терминов. Это делает его функцией второго порядка , которая будет давать очень разные результаты на графике полюс-ноль, чем те, которые мы видели со схемами фильтра резистор-индуктор или резистор-конденсатор.
Снова задаем себе те же три вопроса:
- Как эта система реагирует, когда \(s = 0\)?
- При каком значении (значениях) \(s\) передаточная функция приближается к нулевому значению?
- При каком значении (значениях) \(s\) передаточная функция приближается к бесконечности? 92 = -{1 \over LC}\]
\[s = \sqrt{-{1 \over LC}}\]
\[s = \pm j \sqrt{1 \over LC}\]
Учитывая тот факт, что и \(L\), и \(C\) являются действительными, положительными числами, и, следовательно, решение для \(s\) требует извлечения квадратного корня из отрицательного действительного числа, мы видим, что значение \(s\) должны быть мнимыми.
Мы также видим здесь, что в этой передаточной функции есть два полюса: один при \(s = 0 + j \sqrt{1 \over LC}\), а другой при \(s = 0 — j \sqrt{1 \ над LC}\).
Используя компьютер для построения трехмерного представления этой передаточной функции, мы ясно видим один нуль в точке \(s=0\) и два полюса, симметрично расположенные вдоль оси \(j \omega\). Здесь я принял конденсатор 0,2 Ф и катушку индуктивности 5 Гн для номиналов компонентов: при \(s = 0 — j1\)) говорит нам, что схема способна генерировать колеблющийся выходной сигнал (\(\omega\) = 1 радиан в секунду частоты) при постоянной величине (\(\sigma = 0\)) без входного сигнала. Это возможно только потому, что мы предположили идеальный конденсатор и идеальную катушку индуктивности без каких-либо потерь энергии. Если мы зарядим один или оба этих компонента, а затем немедленно замкнем накоротко вход схемы, чтобы убедиться, что \(V_{in} = 0\), он будет вечно колебаться на своей резонансной частоте.
Ранее мы отмечали, что полюсами в этой схеме были \(s = 0 + j \sqrt{1 \over LC}\) и \(s = 0 — j \sqrt{1 \over LC}\).
Другими словами, его резонансная частота равна \(\omega = \sqrt{1 \over LC}\). Вспоминая, что определение \(\omega\) — это радианы вращения фазора в секунду, и что на один полный оборот (цикл) приходится \(2 \pi\) радиан, мы можем вывести известную формулу резонансной частоты для простого Цепь LC:
\[\omega = \sqrt{1 \over LC}\]
\[\hbox{. . . заменив } 2 \pi f \hbox{ на } \omega \hbox{ . . .}\]
\[2 \pi f = \sqrt{1 \over LC}\]
\[f = {1 \over 2 \pi \sqrt{LC}}\]
Взяв поперечное сечение этой поверхности график в \(\sigma = 0\), чтобы получить частотную характеристику (график Боде) LC-контура, мы видим, что выходной сигнал этой схемы начинается с нуля, когда частота (\(\omega\)) равна нулю, затем выход достигает пика на резонансной частоте (\(\omega\) = 1 рад/сек), затем выход приближается к единице (1) по мере увеличения частоты после резонанса:
Более традиционный двумерный график полюс-ноль для эта схема показывает ноль и два полюса, используя символы «\(\circ\)» и «\(\times\)»:
Пример: схема полосового фильтра RLC
В нашем следующем примере схемы мы добавим резистор последовательно с катушкой индуктивности и конденсатором, чтобы исследовать их влияние на передаточную функцию.
92\) срок. Еще раз повторим наши три вопроса:Взяв наше выходное напряжение на резисторе, мы должны ожидать, что эта схема покажет поведение фильтрации в полосе пропускания с максимальным напряжением, развивающимся на резисторе на одной частоте, где импедансы катушки индуктивности и конденсатора компенсируются:
- Как эта система реагирует, когда \(s = 0\)?
- При каком значении (значениях) \(s\) передаточная функция приближается к нулевому значению?
- При каком значении (значениях) \(s\) передаточная функция приближается к бесконечности?
Ответы на первые два вопроса одни и те же: числитель передаточной функции будет равен нулю при \(s = 0\), что является единственным нулем функции. Вспоминая, что условие \(s = 0\) представляет собой входной сигнал постоянного тока (отсутствие роста или затухания во времени и отсутствие колебаний), это имеет смысл: наличие последовательного конденсатора, блокирующего постоянный ток, в этой цепи обеспечивает выходной сигнал.
2LC + 1\) должны отмечать расположение полюсов на плоскости \(s\). 92\)) слагаемое
\(b\) — коэффициент первой степени (\(x\)) слагаемого
\(c\) — коэффициент нулевой степени (постоянного) слагаемого
Рассмотрение снова знаменатель нашей передаточной функции, мы видим, что \(s\) является независимой переменной, и поэтому \(LC\) должен быть коэффициентом «\(a\)», \(RC\) должен быть «\ (b\)», а 1 должен быть коэффициентом «\(c\)». Подстановка этих переменных в квадратичную формулу даст нам формулу для вычисления полюсов этой цепи резистор-индуктор-конденсатор: 92 — 4LC\). Эта часть квадратичной формулы называется дискриминантом , и ее значение определяет как количество корней, так и их действительный или мнимый характер. Если дискриминант равен нулю, у нашего многочлена будет один действительный корень и, следовательно, у нашей схемы будет только один полюс. Если дискриминант больше нуля (т.е. положительное значение), то будет два действительных корня и, следовательно, два полюса, лежащие на оси \(\сигма\) (т.
е. нет мнимых \(j \омега\) частей). Если дискриминант меньше нуля (т. е. отрицательное значение), то у нашего многочлена будет два комплексных корня и, следовательно, два комплексных полюса, имеющих как действительную, так и мнимую части.
Рассмотрим на мгновение, что означает знак дискриминанта на практике. Полюс, который является чисто реальным, означает значение для \(s\), которое полностью равно \(\сигма\), а не \(\омега\): представляет собой состояние роста или распада, но без колебаний. Это похоже на то, что мы видели со схемами фильтров нижних/высоких частот LR или RC, где схема в состоянии разрядки могла генерировать выходной сигнал даже с закороченными входными клеммами, чтобы гарантировать отсутствие входного сигнала.
Если у нас есть положительное значение дискриминанта, что дает два реальных полюса, это означает два разных возможных значения для \(\сигма\) (скорость роста/убывания), которые могут возникнуть без ввода сигнала в схему. Такое поведение возможно только с двумя компонентами, накапливающими энергию в цепи: своего рода с двойной постоянной времени , когда разные части цепи разряжаются с разной скоростью.
Отсутствие какой-либо мнимой части внутри \(s\) означает, что схема по-прежнему не будет генерировать автоколебания.
Если у нас есть отрицательное значение дискриминанта, что дает два комплексных полюса , это означает два разных значения для \(s\), имеющих как действительную, так и мнимую части. Поскольку действительная часть (\(\sigma\)) представляет рост/спад, а мнимая часть (\(\omega\)) представляет колебание, комплексные полюса говорят нам, что схема сможет совершать автоколебания, но не с постоянной величиной. как с идеальной (без потерь) схемой бака. На самом деле интуиция должна подсказывать нам, что эти сложные полюса должны иметь отрицательные действительные значения, представляющие затухающие колебания, потому что это нарушило бы Закон сохранения энергии, если бы наша схема начала самоколебаться с возрастающей амплитудой. 92 = 4LC\]
\[RC = \sqrt{4LC}\]
\[RC = 2 \sqrt{L} \sqrt{C}\]
\[R = {2 \sqrt{L} \sqrt{C} \over C}\]
\[R = {{2 \sqrt{L} \sqrt{C}} \over {\sqrt{C} \sqrt{C}}}\]
\[R = {2 \sqrt{L} \over \sqrt{C}} = 2 \sqrt{L \over C}\]
Это критическое значение \(R\), приводящее к одному реальному полюсу, является минимальным величина сопротивления, необходимая для предотвращения автоколебаний.
Если схема работает в этот момент, говорят, что она критически демпфирована . Большие значения \(R\) приведут к множеству реальных полюсов, где говорят, что схема передемпфирована . Меньшие значения \(R\) допускают возникновение некоторых автоколебаний, и говорят, что схема недостаточно демпфирована .
Иногда инженеры-электрики намеренно устанавливают резисторы в цепи, содержащие как индуктивность, так и емкость, специально для демпфирования колебаний. В таких случаях резистор называется антирезонансным резистором , потому что его назначение — бороться с резонансными колебаниями, которые в противном случае возникали бы при обмене энергией между собой индуктивных и емкостных элементов схемы. Если намерение инженера состоит в том, чтобы установить в цепь сопротивление, достаточное для предотвращения колебаний без создания ненужных временных задержек, то лучшим значением резистора будет то, которое вызывает критическое демпфирование.
Напомним, что тема передаточных функций, полюсов и нулей относится к любой линейной системе , а не только к цепям переменного тока.
Механические системы, контуры управления с обратной связью и многие другие физические системы могут быть охарактеризованы таким же образом с использованием одних и тех же математических инструментов. Этот конкретный вопрос демпфирования чрезвычайно важен в приложениях, где колебания вредны. Рассмотрим конструкцию системы подвески автомобиля, в которой взаимодополняющие энергоаккумулирующие явления натяжения пружины и массы автомобиля вызывают колебания после удара о возмущение дорожного покрытия. Работа амортизатора заключается в том, чтобы действовать как «резистор» в этой системе и рассеивать энергию, чтобы свести к минимуму колебания после неровностей дороги. Амортизатор меньшего размера не будет достаточно хорошо рассеивать энергию возмущения, и поэтому подвеска автомобиля будет демонстрировать сложные полюса (т. е. будут некоторые затяжные колебания после удара). Амортизатор слишком большого размера будет слишком «жестким» и позволит слишком большому количеству энергии удара пройти к раме автомобиля и пассажирам.
Однако амортизатор идеального размера будет «критически демпфировать» систему, чтобы полностью предотвратить колебания и обеспечить максимально плавную езду.
Подобным образом, колебания, следующие за возмущением, нежелательны в системе управления с обратной связью, целью которой является поддержание переменной процесса как можно ближе к заданному значению. Контур обратной связи с недостаточным демпфированием будет иметь тенденцию к чрезмерным колебаниям после возмущения. Контур обратной связи с чрезмерным демпфированием не будет колебаться, но потребуется чрезмерное количество времени, чтобы вернуться к заданному значению, что также нежелательно, поскольку это означает, что больше времени будет потрачено вне заданного значения. Контур обратной связи с критическим демпфированием — это наилучший компромисс, когда колебания устранены, а время сходимости сведено к минимуму.
Чтобы полностью проиллюстрировать характеристики передаточной функции этой схемы, мы сделаем это для трех различных номиналов резисторов: один, где \(R\) дает критическое демпфирование (один реальный полюс), другой, где \(R\) обеспечивает критическое демпфирование схема с избыточным демпфированием (два реальных полюса) и одна, где \(R\) делает схему с недостаточным демпфированием (два сложных полюса).
Мы будем использовать трехмерный график, чтобы показать отклик передаточной функции в каждом случае. Чтобы не противоречить нашему предыдущему примеру с емкостной схемой, мы примем то же значение емкости конденсатора 0,2 фарад и то же значение катушки индуктивности 5 генри. Значение резистора будет изменено в каждом случае, чтобы создать различные условия демпфирования. 9{-1}\]
Интересно, что только \(L\) и \(R\) определяют скорость затухания (\(\sigma\), действительную часть \(s\)) в критически затухающем состоянии. Это ясно видно, если мы установим дискриминант равным нулю в квадратичной формуле и найдем переменные для сокращения:
\[s = {{-RC \pm \sqrt{0}} \over 2LC} = -{R \ over 2L}\]
Далее мы построим ту же передаточную функцию с большим номиналом резистора (15 Ом), чтобы обеспечить избыточное демпфирование:
Мы ясно видим 9{-1}\), более медленная из этих двух скоростей затухания доминирует в переходной характеристике схемы в течение длительных периодов времени.
Далее мы построим ту же передаточную функцию с меньшим номиналом резистора (5 Ом), чтобы обеспечить недостаточное демпфирование:
Мы снова ясно видим два полюса , но ни один из них не расположен на оси. Они представляют собой два комплексных значения для \(s\), описывающих поведение схемы при нулевом входе. Мнимая (\(j \omega\)) часть \(s\) говорит нам о том, что схема способна к автоколебаниям. Отрицательная действительная (\(\сигма\)) часть \(s\) говорит нам, что эти колебания уменьшаются по величине со временем. Используя квадратичную формулу для решения этих двух полюсов: 9{-1}\]
Расчетное значение \(\omega\) 0,866 радиан в секунду меньше, чем резонансная частота 1 радиан в секунду, рассчитанная для контура чистого резервуара, имеющего те же \(L\) и \(C \) значений, показывая, что демпфирующий резистор искажает «центральную» частоту этого полосового фильтра RLC. Вычисленное значение \(\сигма\) постоянной времени \(-0,5\) в секунду (эквивалентное постоянной времени \(\тау\) = 2 секунды) описывает скорость, с которой синусоидальные колебания затухают по величине.
{-1}\)).
Если мы сравним двухмерные графики полюс-ноль для каждого из трех значений резистора в этой цепи RLC, мы можем сравнить характеристики с избыточным, критическим и недостаточным демпфированием:
— графики в разрезе передаточной функции при \(\sigma = 0\), чтобы показать частотную характеристику этого полосового фильтра RLC, мы видим, что характеристика становится «острее» (более избирательной) по мере уменьшения значения резистора и перемещения полюсов. ближе к оси \(j \omega\). Специалисты по электронике связывают это с добротность или \(Q\) схемы полосового фильтра, схема, демонстрирующая более высокое «качество» выбора полосы пропускания по мере увеличения отношения реактивного сопротивления к сопротивлению: и каждый полюс на графике полюс-ноль имеет одинаковую (бесконечную) высоту, полюса сужаются при удалении друг от друга и расширяются при близком расстоянии друг от друга. По мере уменьшения сопротивления в этой цепи и удаления полюсов друг от друга и приближения к оси \(j \omega\) их ширина сужается, а пик АЧХ становится уже и круче.
Резюме анализа передаточной функции
Вот краткое изложение некоторых основных понятий, важных для анализа передаточной функции:
- Переменная \(s\) является выражением нарастающих/затухающих синусоидальных волн, состоящих из действительная часть и мнимая часть (\(s = \sigma + j \omega\)). Действительная часть \(s\) (\(\sigma\)) — это скорость роста/затухания, говорящая нам, насколько быстро сигнал растет или затухает во времени, при этом положительные значения \(\sigma\) представляют рост, а отрицательные значения \(\сигма\), представляющие распад. Эта скорость роста/затухания обратно пропорциональна 9{-1}\)).
- Важное допущение, которое мы делаем при анализе передаточной функции (функций) любой системы, заключается в том, что система является линейной (т. характеристики системы не меняются с течением времени). Если мы хотим проанализировать нелинейную систему с помощью этих инструментов, мы должны ограничить себя диапазонами работы, в которых отклик системы приблизительно линейный, а затем допустить небольшие ошибки между результатами нашего анализа и реальным откликом системы.
- Для любой линейной стационарной системы (системы «LTI») \(s\) является описательным для всей системы. Другими словами, для определенного значения \(s\), описывающего вход в эту систему, то же самое значение \(s\) будет также описывать выход этой системы.
- Передаточная функция является выражением коэффициента усиления системы , измеренного как отношение выходного сигнала к входному. В технике передаточные функции обычно представляют собой математические функции \(s\) (т.е. \(s\) — независимая переменная в формуле). При таком выражении передаточная функция для системы говорит нам, какой выигрыш будет иметь система при любом заданном значении \(s\).
- Передаточные функции полезны для анализа поведения электрических цепей, но они не ограничиваются этим приложением. Любая линейная система, будь то электрическая, механическая, химическая или какая-либо другая, может быть охарактеризована с помощью передаточных функций и проанализирована с использованием одних и тех же математических методов.
Таким образом, передаточные функции и переменная \(s\) являются общими инструментами, не ограничивающимися анализом электрических цепей.
- ноль — это любое значение \(s\), которое приводит к тому, что передаточная функция имеет нулевое значение (т. е. нулевое усиление или отсутствие выходных данных при любой величине входных данных). Это говорит нам, где система будет наименее отзывчивой. На трехмерном графике полюс-ноль каждый нуль отображается как нижняя точка, где поверхность касается плоскости \(s\). На традиционном двумерном графике полюс-ноль каждый нуль отмечен символом круга (\(\circ\)). Мы можем найти ноль(и) системы, найдя значение(я) \(s\), которое сделает Числитель передаточной функции равен нулю, так как числитель передаточной функции представляет собой выходной член системы.
- Полюс — это любое значение \(s\), которое приводит к тому, что передаточная функция имеет бесконечное значение (т. е. максимальный коэффициент усиления, дающий выходной сигнал без каких-либо входных данных).
Это говорит нам о том, на что способна система, когда она не «управляется» каким-либо входным стимулом. Полюса обычно связаны с накапливающими энергию элементами в пассивной системе, потому что единственный способ, которым обесточенная система может генерировать выход с нулевым входом, — это если в этой системе есть элементы, накапливающие энергию, разряжающиеся на выходе. На трехмерном графике полюс-ноль каждый полюс выглядит как вертикальный выступ на поверхности, уходящий в бесконечность. На традиционном двумерном графике полюс-ноль каждый полюс отмечен символом (\(\times\)) . Мы можем найти полюс(ы) системы, найдя значение(я) \(s\), которое сделает Знаменатель передаточной функции равен нулю, так как знаменатель передаточной функции представляет входной член системы.
- Системы второго порядка способны к автоколебаниям. Об этом свидетельствуют полюса, имеющие мнимые значения. Эти колебания могут быть полностью незатухающими (т. Е. \ (s \) полностью мнимыми, с \ (\ sigma = 0 \)), и в этом случае система может вечно колебаться сама по себе.
Если в системе второго порядка присутствуют элементы, рассеивающие энергию, колебания будут затухать (т.е. затухать по величине с течением времени).
- Система с недостаточным демпфированием демонстрирует сложные полюса, где \(s\) имеет как мнимые (\(j \omega\)) значения частоты, так и реальные (\(\sigma\)) значения затухания. Это означает, что система может совершать автоколебания, но только с уменьшением амплитуды с течением времени.
- Система с критическим демпфированием имеет диссипативное поведение, достаточное для полного предотвращения автоколебаний, демонстрируя единственный полюс, имеющий только реальное (\(\sigma\)) значение и не имеющий мнимого (\(j \omega\)) ценность.
- Система с избыточным демпфированием имеет чрезмерное рассеяние и имеет несколько реальных полюсов. Каждый из этих реальных полюсов представляет различную скорость затухания (\(\сигма\)) или постоянную времени (\(\тау = 1/\сигма\)) в системе.
Когда эти скорости затухания существенно отличаются друг от друга, самая медленная из них будет доминировать в поведении системы в течение длительных периодов времени.
Основы измерения электрической мощности
Основы измерения электрической мощностиПонимание производства электроэнергии, потери мощности и различных типов измеряемой мощности может быть пугающим. Ниже приведен обзор основных измерений электрической и механической мощности.
Электрический ток, напряжение и сопротивлениеЛюбое обсуждение электричества неизбежно приводит к электрическому току, напряжению и сопротивлению. Эти концепции показаны ниже на рисунке 1. Электрический ток представляет собой поток самого электричества и измеряется в единицах, называемых амперами (А). Напряжение — это сила, которая заставляет электричество течь, и измеряется в единицах, называемых вольтами (V или U). Сопротивление выражает сложность, с которой протекает электричество, и измеряется в единицах, называемых омами (Ом).
На рисунке ниже эти отношения показаны в виде электрических цепей. В электрической цепи электрический ток проходит через различные типы нагрузки, включая сопротивление, индуктивность и емкость, от положительной полярности источников питания, таких как батареи, а затем возвращается к отрицательной полярности источника питания. Термин «нагрузка» обычно используется для обозначения чего-то, что получает электричество от источника питания и работает (обеспечивает свет, в случае лампочки).
Рисунок 1 – Основные компоненты электрической цепи МощностьЭлектрическая энергия может быть преобразована в другие формы энергии и использована. Например, его можно преобразовать в тепло в электронагревателе, в крутящий момент в двигателе или в свет в люминесцентной или ртутной лампе. В подобных примерах работа, совершаемая электричеством за определенный период времени (или затрачиваемая электрическая энергия), называется электрической мощностью.
Единицей электрической мощности является ватт (Вт). 1 ватт эквивалентен работе в 1 джоуль, выполненной за 1 секунду.
В электрических системах напряжение — это сила, необходимая для перемещения электронов. Ток — это скорость потока заряда в секунду через материал, к которому приложено определенное напряжение. Взяв напряжение и умножив его на соответствующий ток, можно определить мощность.
Мощность постоянного тока (постоянного тока)Постоянный ток или постоянный ток относится к системам питания, в которых используется одна полярность напряжения и тока, однако амплитуда может изменяться (циклически или случайным образом).
Рисунок 2. Базовая схема, показывающая напряжение и ток с источником постоянного напряжения электрический ток, напряжение и сопротивление. Закон Ома гласит, что электрический ток течет пропорционально напряжению. Ниже показана формула для выражения отношения между током (I) и напряжением (U).Согласно этой формуле ток (I) уменьшается по мере увеличения значения R и, наоборот, ток (I) увеличивается по мере уменьшения значения R. R здесь представляет собой сопротивление (или электрическое сопротивление). Другими словами, мы видим, что по мере увеличения или уменьшения сопротивления (R) ток течет с меньшей или большей легкостью. Эту формулу можно переписать, как показано ниже. Если известны два значения тока, напряжения и сопротивления, можно получить оставшееся значение.
Мощность постоянного тока (DC) P (Вт) определяется путем умножения приложенного напряжения (U) на ток I (А), как показано выше. В приведенном ниже примере количество электроэнергии, определяемое предыдущим уравнением, извлекается из источника питания и потребляется сопротивлением R (в омах) каждую секунду. По закону Ома мы можем переписать формулу следующим образом:
В электрических цепях постоянного тока поддерживается постоянный ток и напряжение без циклических изменений.
Источник переменного тока (AC)Таким образом, очень просто получить мощность постоянного тока (P) с результирующей формой волны, показанной ниже.
Источник питания, обычно используемый в Японии, работает при напряжении 100 В переменного тока. Эти 100 В представляют собой напряжение, выраженное как среднеквадратичное значение (среднеквадратичное значение).
100 В от настенных розеток наблюдаются в виде чистых синусоидальных волн, как показано на рисунке ниже. Мы можем видеть, что полярность меняется циклами, и что напряжения постоянно колеблются. Формы сигналов напряжения переменного тока имеют чистые синусоидальные волны, такие как график на рис. 3, а также множество других волн, таких как искаженные волны, такие как обычные формы, такие как треугольная и прямоугольная волна. Чтобы установить размер этих волн переменного тока и напряжения, нам нужны значения, которые используют тот же стандарт. Поэтому используется среднеквадратичное значение (rms), которое было установлено на основе постоянного тока и напряжения.
Рисунок 3. Изменение полярности переменного напряжения в синусоидальных, треугольных и прямоугольных формах Среднеквадратичное значение (среднеквадратичное значение)Среднеквадратичное значение чаще всего используется при выражении значений переменного тока и напряжения, и измеряется в Arms и Urms. В приведенном выше примере 100 В — это напряжение, выраженное как среднеквадратичное значение (среднеквадратичное значение).
Простое среднее значение синусоиды равно нулю, поэтому требуется другое уравнение. Вот почему используется среднеквадратичное значение (rms), которое было установлено на основе постоянного тока и напряжения. Он основан на количестве работы, выполняемой определенным количеством постоянного тока и напряжения, и выражает, используя те же значения, что и для постоянного тока и напряжения, величину переменного тока и напряжения, которые выполняют ту же работу.
Если теплотворная способность при подаче напряжения постоянного тока на резистор такая же, как теплотворная способность при подаче переменного тока другой формы волны, то среднеквадратичное значение напряжения переменного тока такое же, как и для напряжения постоянного тока.
Например, теплотворная способность при подаче постоянного напряжения 100 В на резистор 10 Ом такая же, как теплотворная способность при подаче переменного тока 100 В на тот же резистор. Понятие среднеквадратичного значения то же самое для электрического тока.
Рис. 4. Равная теплотворная способность сигналов постоянного и переменного тока
Теплотворная способность относится к количеству выполненной работы, поэтому следующая формула рассчитывает мощность как теплотворную способность.
В качестве примера на следующей диаграмме показаны колебания мощности в зависимости от времени при подаче постоянного тока 1 A и переменного тока 1 ампер на резистор 10 Ом.
Рис. 5. Зависимость мощности от времени при постоянном и переменном токе
Поскольку при постоянном токе нет колебаний значения тока, значение мощности остается постоянным и составляет 10 Вт. Однако, поскольку значение тока постоянно колеблется при переменном токе, значение мощности колеблется со временем.
То, что эти два типа мощности (теплотворная способность) равны, равнозначно утверждению, что средние значения Pdc и P1 – Pn равны. Это выражается в виде формулы ниже.
Здесь резистор (R) постоянный, поэтому им можно пренебречь. Следующее выражает результирующую связь между постоянным током и переменным током.
Если максимально уменьшить интервал между I1 и In в этой формуле, в конечном итоге Irms дает квадратный корень из площади части, заключенной в сигнале, деленный на время. Это выражается в виде формулы ниже.
Важно знать, что постоянный ток силой 1 А выполняет такую же работу, что и переменный среднеквадратичный ток силой 1 А. При постоянном и устойчивом постоянном токе вы можете получить значение мощности, просто умножив ток на напряжение.
Однако переменный ток не так прост, как постоянный, из-за разности фаз между током и напряжением. Ниже приведены три типа переменного тока. Как правило, мощность и потребляемая мощность относятся к активной мощности.
Мощность в системах переменного токаКак и в случае с постоянным током, значение мощности (мгновенное значение мощности) в определенный момент времени для переменного тока можно получить путем умножения напряжения и тока для этого момента времени.
При переменном токе, поскольку и ток, и напряжение циклически колеблются, значения мощности также постоянно колеблются. Это показано на следующей диаграмме.
В качестве энергии в секунду мощность может быть получена из среднего значения мгновенной энергии, т. е. площади части, заключенной в форме волны, по времени. Формула выглядит следующим образом:
Например, если к резистору приложен ток 1 ампер и напряжение 100 ампер, как показано ниже, мощность становится равной 100 Вт при расчете по приведенной выше формуле.
При подаче тока и напряжения на резистор результирующие формы сигналов показаны на рис. 6 ниже.
Рис.6. Отсутствие разности фаз при чисто резистивной нагрузке
Говорят, что ток и напряжение находятся «в фазе» по полярности и времени, когда кривые тока и напряжения проходят через нуль. Ток и напряжение всегда совпадают по фазе, когда нагрузка состоит только из сопротивления.
Когда в нагрузке помимо сопротивления есть катушка, возникает фазовый сдвиг между сигналами напряжения и тока. Это отставание называется разностью фаз и показано на рис. 7.9.0003
Рисунок 7. Разность фаз, характерная для индуктивной и емкостной нагрузки
Разность фаз обычно выражается как Φ (фи), а единицей измерения являются радианы, но часто указывается в градусах. В приведенном ниже примере точка A начинается с точки P и совершает один оборот по окружности O. Расстояние между точкой A и прямой линией, проходящей через центр O и точку P (красная линия) в качестве оси Y и ∠AOP (φ), так как ось X приводит к синусоидальной волне ниже.
Рис.8. Синусоидальная волна, показанная с фазой
На Рис. 9 показаны кривые тока и напряжения, сдвинутые по фазе на 60°. При рассмотрении положения на окружности напряжения (u) и тока (i) в соответствии с приведенным выше примером ∠uoi постоянна в каждый момент времени. Угол этого ∠uoi указывает размер разности фаз между напряжением (u) и током (i).
Рис. 9. Синусоиды напряжения и тока с разностью фаз
Три типа нагрузки цепи переменного тока показаны на рис. 10. Как показано ниже, разность фаз между током и напряжением возникает в зависимости от типа нагрузки.
Рис. 10. Фазное и векторное представление цепей переменного тока с резистивной, индуктивной или емкостной нагрузкой
С фазами ток может отставать по отношению к напряжению или опережать его. Ток отстает на 90⁰, когда нагрузка состоит только из индуктивности, и опережает на 90⁰, когда только емкость. Когда существуют все три типа, разность фаз колеблется в соответствии с соотношением размеров каждого компонента.
Мощность переменного тока с разницей фазДалее, давайте посмотрим на мощность, когда есть разность фаз между током и напряжением.
При наличии разности фаз между током и напряжением происходит мгновенное изменение энергии, как показано на рис. 11.
Когда ток или напряжение равны 0, мгновенная мощность становится равной 0. полярность напряжения меняется в промежутках между ними, мгновенная мощность становится отрицательной. Мощность представляет собой среднее значение мгновенной энергии, поэтому мощность становится меньше, чем когда ток и напряжение совпадают по фазе (пунктирная линия).
Рисунок 11. Мгновенная энергия, когда напряжение и ток имеют разность фазТреугольник мощности и коэффициент мощности
Цепи переменного тока, содержащие емкость, индуктивность или и то, и другое, содержат активную и реактивную мощности. Треугольник мощности, показанный на рис. 12, помогает проиллюстрировать энергопотребление в индуктивной или емкостной цепи.
Треугольник мощности представляет собой прямоугольный треугольник, показывающий соотношение четырех основных элементов: активной мощности, реактивной мощности, полной мощности и коэффициента мощности.
Рис. 12. Треугольник мощности показывает соотношение активной и реактивной мощности.Активная мощность
Активная мощность (P) — это реальная мощность, которую устройство потребляет и выполняет реальную работу в электрической цепи. Активная мощность рассчитывается ниже в ваттах (Вт).
Реактивная мощностьРеактивная мощность (Q) — это мощность, которая не потребляется устройством и передается туда и обратно между источником питания и нагрузкой. Иногда называемая безваттной мощностью, реактивная мощность забирает мощность из цепи из-за фазового сдвига, создаваемого емкостными и/или индуктивными компонентами. Этот фазовый сдвиг уменьшает количество активной мощности для выполнения работы и усложняет расчет мощности.
Полная мощностьРеактивная мощность рассчитывается ниже и выражается в реактивных вольт-амперах (ВАр). В цепи постоянного тока нет реактивной мощности.
Полная мощность (S) — это гипотенуза треугольника мощности, состоящая из сложения векторов активной мощности (P) и реактивной мощности (Q). Расчет полной мощности представляет собой произведение среднеквадратичного значения напряжения на среднеквадратичное значение тока в вольт-амперах (ВА).
Коэффициент мощностиПри определении коэффициента мощности для синусоидальных волн коэффициент мощности равен косинусу угла между напряжением и током (Cos Φ). Он определяется как коэффициент мощности «смещения» и верен только для синусоидальных волн. Для всех других форм сигналов (не синусоидальных волн) коэффициент мощности определяется как мощность в ваттах, деленная на полную мощность в амперах напряжения. Это называется «истинным» коэффициентом мощности и может использоваться для всех форм сигналов, как синусоидальных, так и несинусоидальных, с использованием квалификатора λ (лямбда).
Коэффициент мощности (λ) увеличивается или уменьшается в зависимости от величины разности фаз (φ). Рисунок 13 иллюстрирует это явление. Рис. 13. Коэффициент мощности с различной разностью фаз разность фаз увеличивается; коэффициент мощности равен 0,5 (активная мощность составляет 1/2 полной мощности) при разности фаз 60⁰ и 0 при разнице фаз 90⁰. Коэффициент мощности 0 означает, что ток течет к нагрузке, но она не совершает никакой работы.
Векторное отображение переменного тока
Смещение по времени между напряжением и током называется разностью фаз, а Φ — фазовым углом. Смещение по времени в основном вызвано нагрузкой, на которую подается питание. В общем, разность фаз равна нулю, когда нагрузка является чисто резистивной. Ток отстает от напряжения, когда нагрузка индуктивная. Ток опережает напряжение, когда нагрузка емкостная.
Рис. 14. Сдвиг фаз между напряжением и током при чисто индуктивной или емкостной нагрузке
Векторный дисплей используется для четкой передачи зависимости величины и фазы между напряжением и током.
Положительный фазовый угол представлен углом против часовой стрелки относительно вертикальной оси.
Рис. 15. Векторная диаграмма отображает отношения амплитуды и фазы между напряжением и током
Системы питания переменного тока
Питание переменного тока может быть однофазным или многофазным. Однофазное электричество используется для питания обычных бытовых и офисных электроприборов, но для распределения электроэнергии и подачи электроэнергии непосредственно на более мощное оборудование почти повсеместно используются трехфазные системы переменного тока.
Схемы однофазной проводкиСуществуют две распространенные конфигурации проводки для однофазных цепей. Наиболее распространена однофазная двухпроводная схема. Другая — однофазная трехпроводная схема, обычно встречающаяся в бытовых приборах.
Однофазная 2-проводная система (1P2W)Обеспечивает подачу однофазного переменного тока с использованием двух проводников.
Самая простая система, она используется при подключении источников питания ко многим электрическим устройствам, таким как бытовая электроника. При подключении ваттметра к однофазной двухпроводной системе перед подключением необходимо учитывать несколько моментов.
Рис. 16. Различные схемы подключения однофазной двухпроводной системыВлияние паразитной емкости
При измерении однофазного устройства влияние паразитной емкости на точность измерения можно свести к минимуму, подключив клемму токового входа прибора к стороне, ближайшей к потенциалу земли источника питания. Рисунок 17. Схема подключения для минимизации паразитной емкости Когда измеренный ток относительно мал, подключите клемму измерения тока между клеммой измерения напряжения и нагрузкой.
Рис. 18. Схема подключения при относительно большом измеренном токеДвухфазная трехпроводная система (1P3W)
Обеспечивает подачу однофазного переменного тока по трем проводникам.
Однофазная трехпроводная система является наиболее распространенной системой распределения электроэнергии. Электричество, поставляемое большинству домохозяйств, подается с помощью этой системы. Следующее требует двух ваттметров для измерения двух напряжений (U1, U2) и двух токов (I1, I2).
Рисунок 19. Трехпроводная система с расщепленной фазойСхемы подключения трехфазной сети
В отличие от однофазных систем, по проводникам трехфазного источника питания течет переменный ток одинаковой частоты. и амплитуда напряжения относительно общего эталона, но с разницей фаз в одну треть периода. Трехфазные системы имеют преимущества перед однофазными, которые делают их пригодными для передачи энергии и в таких приложениях, как асинхронные двигатели.
Характеристики трехфазных систем
- Ток и напряжение на каждой фазе имеют разность фаз 120° в сбалансированной системе.
- Линейное напряжение — это напряжение, измеренное между любыми двумя линиями в трехфазной цепи.
- Фазное напряжение — это напряжение, измеренное на нагрузке в фазе
- Линейный ток — это ток в любой одной линии между трехфазным источником и нагрузкой.
- Фазный ток – это ток через любой компонент, состоящий из трехфазного источника или нагрузки.
- При соединении треугольником линейное напряжение совпадает с фазным напряжением. Для синусоидальных волн линейный ток в √3 раза превышает фазный ток.
- При соединении звездой линейное напряжение в √3 раза превышает фазное напряжение, а токи одинаковы.
- Трехфазные источники питания могут передавать в три раза больше энергии, используя всего в 1,5 раза больше проводов, чем однофазные источники питания (т. е. три вместо двух). Таким образом, отношение емкости к материалу проводника удваивается.
- Трехфазные системы также могут создавать вращающееся магнитное поле с заданным направлением и постоянной величиной, что упрощает конструкцию электродвигателей.
В предыдущем обсуждении источник питания и нагрузка были соединены двумя проводниками.
Это известно как однофазная двухпроводная система. При питании переменным током существует однофазное и трехфазное питание со следующими доступными системами электропитания. Трехфазное питание можно использовать в трехпроводной или четырехпроводной конфигурации в режиме звезды или треугольника.
На диаграммах на рис. 20 показаны источник и нагрузка в конфигурации «треугольник» или «звезда» (звезда).
Рис. 20. Трехфазные конфигурации треугольника и звезды (WYE)Теорема Блонделя
При обсуждении измерений мощности с помощью ваттметров часто ссылаются на теорему Блонделя при определении правильного метода подключения ваттметров и количества ваттметров. необходимы для наиболее точного измерения. Теорема утверждает, что мощность, подводимая к системе из N проводников, равна алгебраической сумме мощностей, измеренных N ваттметрами. Кроме того, если общая точка расположена на одном из проводников, то счетчик этого проводника может быть удален и требуется только N-1 счетчиков.
Трехфазное соединение звездой (3P4W)Измерение относительно простое, если объектом измерения является трехфазная 4-проводная система. Как показано на схеме ниже, трехфазная четырехпроводная схема предполагает подключение ваттметров к каждой фазе на основе нейтрального проводника. Получите мощность для каждой фазы, измеряя напряжение (фазное напряжение) и ток (фазный ток) для каждой фазы с помощью разных ваттметров. В сумме это даст значение трехфазной мощности переменного тока. Для измерения трехфазной четырехпроводной мощности требуются три ваттметра.
Рис. 21. Трехфазное соединение звездой (3P4W)
Полная мощность, активная мощность и реактивная мощность для трехфазной мощности представляют собой сумму каждой фазы.
Трехфазный ваттметр Delta Two (3P3W)Измерение в трехфазной 3-проводной системе немного сложнее, поскольку нейтральный проводник использовался в качестве основы для трехфазной 4-проводной системы.
система отсутствует и фазное напряжение не может быть измерено. Измерение в трехфазной трехпроводной системе включает получение значения трехфазной мощности переменного тока с использованием метода, называемого методом двух ваттметров.
Применяя теорему Блонделя и используя метод двух ваттметров, мы можем получить значения трехфазной мощности переменного тока. Схема подключения для метода двух ваттметров и векторная карта приведены ниже.
Вывод теоремы Блонделя приведен ниже.
Вышеприведенный расчет показывает, что мы можем получить значения трехфазной мощности переменного тока из двухлинейных значений мощности и двухфазных значений тока. Поскольку этот метод требует контроля только двух токов и двух напряжений вместо трех, упрощается установка и конфигурация проводки. Он также может точно измерять мощность в сбалансированной или несбалансированной системе. Его гибкость и недорогая установка делают его подходящим для производственных испытаний, в которых требуется измерение только мощности или нескольких других параметров.
Другими словами, для трехфазного измерения мощности мощность может быть получена путем измерения мощности для каждой фазы и расчета суммы. Для метода двух ваттметров уравнение показано ниже.
Трехфазное соединение треугольником (3V3A)Существует еще один метод измерения в трехфазной трехпроводной системе: трехфазное трехфазное измерение (3V3A). Как и метод двух ваттметров, этот метод измеряет ток фазы T и линейное напряжение между R и S. Ниже представлена схема подключения.
Рис. 22. Трехфазное соединение треугольником (3V3A)
Поскольку трехфазный трехфазный метод (3V3A) измеряет ток фазы T, он позволяет увидеть баланс токов между фазами, что было невозможно при использовании метод двух ваттметров. Для инженерных и научно-исследовательских и опытно-конструкторских работ лучше всего подходит трехфазный
трехпроводный с трехваттметровым методом, так как он дает дополнительную информацию, которую можно использовать для балансировки нагрузки и определения истинного коэффициента мощности.
Векторное отображение измерений трехфазного переменного токаВ этом методе используются все три напряжения и все три тока. Измеряются все три напряжения (от R до T, от S до T, от R до S).
Мы будем использовать трехфазную систему Y «звезда», чтобы проиллюстрировать концепцию трехфазного векторного отображения. В звездной системе напряжения и токи каждой фазы смещены на 120°. Нейтральная точка Y-системы находится в центре, где теоретически сумма всех напряжений и токов равна нулю.
При проведении измерений в звездной системе, где присутствует физический нейтральный провод; напряжения будут измеряться относительно этой нейтральной точки, это называется «фазным напряжением». При проведении измерений в звездной системе, где отсутствует физический нейтральный провод; напряжения будут измеряться относительно друг друга, это называется «линейное напряжение» или «соединение треугольником». Схема соединения треугольником образует равносторонний треугольник с интервалом между напряжениями 60 градусов, в отличие от соединения звезды, где напряжение изменяется на 120 градусов.
Величина линейного напряжения измеряется выше, чем фазное напряжение в √3 раза. Токи в звездной системе всегда измеряются последовательно относительно нейтральной точки, при этом угловое измерение относительно векторов напряжения обозначается Φ. Рисунок 23 иллюстрирует взаимосвязь между измерением напряжения по схеме треугольника и по схеме звезда с помощью векторной диаграммы.
Рисунок 23 – Векторная диаграмма трехфазных дельта- и звездных измерений.Измерение трехфазного коэффициента мощности
Общий коэффициент мощности для трехфазной цепи определяется путем суммирования общей мощности в ваттах, деленной на общее значение ВА.
При использовании метода двух ваттметров сумма общей мощности (W1 + W2) делится на количество ВА. Однако, если нагрузка несбалансированная (фазные токи разные), это может привести к ошибке при расчете коэффициента мощности, поскольку при расчете используются только два измерения ВА.
Два VA усредняются, потому что предполагается, что они равны; однако, если это не так, получается ошибочный результат. Поэтому лучше всего использовать метод трех ваттметров для несбалансированных нагрузок, поскольку он обеспечит правильный расчет коэффициента мощности как для сбалансированных, так и для несбалансированных нагрузок.
При использовании метода трех ваттметров все три измерения ВА используются при расчете приведенного выше коэффициента мощности.
ГармоникиГармоники относятся ко всем синусоидальным волнам, частота которых является целым кратным основной волны (обычно синусоидальный сигнал линии электропередачи 50 Гц или 60 Гц или от 0 до 2 кГц для вращающихся машин). Гармоники — это искажение формы волны нормального электрического тока, обычно передаваемое нелинейными нагрузками. В отличие от линейных нагрузок, где потребляемый ток пропорционален входному напряжению и соответствует форме волны, нелинейные нагрузки, такие как двигатели с регулируемой скоростью, потребляют ток короткими прерывистыми импульсами.
Когда основная волна и последующие гармонические компоненты объединяются, формы сигналов искажаются, и возникает интерференция.
Рис. 24. Искаженные формы сигналов состоят из нескольких гармонических составляющих
Гармоники необходимо контролировать, поскольку они могут вызывать ненормальный шум, вибрацию, нагрев или неправильную работу устройств и сокращать срок их службы. Для контроля гармоник существуют национальные и международные стандарты, такие как IEC61000-3. Поэтому инженерам необходимо обнаруживать гармоники и оценивать их влияние на компоненты, системы и подсистемы в приложении. Размер и разность фаз следует измерять не только для основной частоты, но и для каждой более высокочастотной составляющей. Высокоточные анализаторы мощности могут измерять гармоники выше 500-го порядка.
Для вращающихся машин основные амплитуды являются единственными составляющими, которые эффективно способствуют вращению оси. Все остальные гармонические составляющие приводят к потерям в виде тепла и вибрации.
Измерение гармоникИспользуя режим измерения гармоник, можно измерить размер и разность фаз для каждой основной частоты, а также гармоники для каждой степени, включенной в ток, напряжение и мощность. В случае основной частоты (первичной составляющей) 50 Гц, например, третья составляющая составляет 150 Гц, пятая составляющая — 250 Гц и т. д., и возможно измерение до 500-й составляющей на частоте 2,5 кГц.
Рис. 25. Сумма нечетных гармонических составляющих в искаженном сигнале соотношение содержания и фазы в списке.
Рис. 26. Гистограмма, показывающая энергию гармоник в зависимости от порядкаЗаключение
При измерении мощности необходимо учитывать множество факторов, включая входную мощность, КПД инвертора, КПД, гармоники и коэффициент мощности. Эти измерения включают сложные уравнения, поэтому большинство компаний используют анализаторы мощности для автоматического получения результатов.
Прецизионный высокочастотный анализатор мощности является важным инструментом для измерения как механической, так и электрической мощности. Его функции анализа и показания могут помочь улучшить работу и даже продлить срок службы двигателя. Выбор правильного анализатора и его правильная реализация требуют знаний; однако при правильном использовании данные анализатора мощности обеспечат точные и очень ценные данные.
Gale Apps — Технические трудности
Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.
org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.
zeroc.Ice.UnknownException unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0 в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64) в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70) в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248) в java.base/java.util.Objects.checkIndex(Objects.java:372) в java.base/java.util.ArrayList.get(ArrayList.java:458) в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60) в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53) в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.
java:30) в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17) в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244) на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71) на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52) на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130) на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.
java:82) на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44) на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31) в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57) на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61) на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1) в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97) в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406) в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221) в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.
java:2706) на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292) в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203) в com.zeroc.IceInternal.ThreadPool.run(ThreadPool.java:412) в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7) в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781) в java.base/java.lang.Thread.run(Thread.java:834) » org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348) org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310) org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.
invoke(MonitoringIceProxyFactoryBean.java:71) org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186) org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215) com.sun.proxy.$Proxy151.authorize(Неизвестный источник) com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61) com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65) com.gale.apps.
controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57) com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22) jdk.internal.reflect.GeneratedMethodAccessor288.invoke (неизвестный источник) java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43) java.base/java.lang.reflect.Method.invoke(Method.java:566) org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205) org.
springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150) org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808) org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87) org.
springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067) org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963) org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006) org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898) javax.servlet.http.HttpServlet.service(HttpServlet.java:626) org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883) javax.
servlet.http.HttpServlet.service(HttpServlet.java:733) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.
apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.
springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126) org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64) org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.
springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.
java:201) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202) org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97) org.apache.catalina.authenticator.
AuthenticatorBase.invoke(AuthenticatorBase.java:542) org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143) org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92) org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687) org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78) org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357) org.apache.coyote.http11.Http11Processor.
service(Http11Processor.java:374) org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65) org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893) org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707) org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49) java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128) java.base/java.util.concurrent.ThreadPoolExecutor$Worker.



 е.
е.