Правило Ленца простыми словами: формулировка, формулы, примеры применения
В этой статье мы рассмотрим, что такое правило Ленца и какого его практическое применение. Это правило позволяет быстро определить направление индукционного тока. На самом деле, правило Ленца тесно связано с принципом сохранения энергии – об этом также читайте в этой статье.
Рис. 1. Электрический генератор начала 20-го века. Его принцип работы соответствует правилу Ленца. (Автор: Сергей Прокудин-Горский [Public domain], via Wikimedia Commons)Формулировка
Правило Ленца обычно формулируется следующим образом:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Википедия
Давайте расшифруем это предложение.
Давайте расшифруем это предложение. Давайте начнем с причины. Причиной протекания индукционного тока является изменяющийся поток магнитной индукции B через поверхность, охватываемую контуром, в котором должен протекать электрический ток.
Противодействие причине здесь заключается в том, что когда поток увеличивается, магнитное поле Bind, создаваемое индукционным током, направлено так, чтобы уменьшить поток. И наоборот, когда поток уменьшается, индуцированное магнитное поле направлено так, чтобы усилить поток. В общем, если поле B перпендикулярно плоской поверхности, охватывающей замкнутый проводник, то
Когда ФB уменьшается, то Вind параллельно В.
Когда ФB увеличивается, то Bind антипараллельно B.
В более общем случае необходимо задать условие для углов между этими векторами.
Как только мы установили, как направлен вектор магнитной индукции Bind (внутри контура), мы должны связать индукционный ток с этим вектором и определить его направление.
Пример правила Ленца в действии
Теперь мы покажем правило Ленца в действии; вот конкретный пример.
В магнитном поле, создаваемом прямолинейным проводником с током, имеется круговой контур (кольцо), лежащий в одной плоскости с проводником (рис. 2а.). Ток в прямолинейном проводнике течет вверх. В каком направлении будет течь электрический ток в кольце, если мы прижмем его к проводнику?
2а.). Ток в прямолинейном проводнике течет вверх. В каком направлении будет течь электрический ток в кольце, если мы прижмем его к проводнику?
Ток в прямолинейном проводнике создает вокруг себя магнитное поле. Для определения направления вектора магнитной индукции в кольце мы используем хорошо известный метод правой руки. Мы располагаем большой палец так, как направлен электрический ток, а пальцы покажут нам магнитное поле, “оборачивающееся” вокруг этого электрического тока. Справа от проводника, где находится кольцо, линии поля идут “внутрь”, как показано на рис. 2б.
Рис. 2б. Определение направления вектора магнитной индукции в кольцеСближение кольца вызывает увеличение потока магнитного поля, проникающего через кольцо (увеличивается значение магнитной индукции B). Согласно правилу Ленца, ток в кольце должен протекать таким образом, чтобы вектор магнитного поля Bind, создаваемого этим током, был направлен противоположно вектору, вызывающему явление индукции B. То есть, вектор Bind направлен “в нашу сторону”. (рис. 2в).
То есть, вектор Bind направлен “в нашу сторону”. (рис. 2в).
Снова применим правило правой руки. На этот раз мы укажем большим пальцем вектор индукции Bind, а остальные пальцы покажут нам направление индукционного тока. Он будет протекать против часовой стрелки.
Правило Ленца и закон сохранения энергии
То, что “скрывается” под правилом Ленца – это фундаментальный принцип сохранения энергии в физике. Вы узнаете об этом, прочитав данный подраздел.
Посмотрите на следующую экспериментальную установку (см. рисунок 3).
Рис. 3. Правило Ленца – Экспериментальная установка с лестничными качелямиДля эксперимента подвесьте качели проводника в магнитном поле подковообразного магнита. Подковообразный магнит располагается так, чтобы северный полюс находился внизу, а южный – вверху. Вы подключаете проводник к амперметру вне магнитного поля, поэтому во всей цепи нет источника.
В эксперименте мы теперь перемещаем качели проводника в направлении, перпендикулярном силовым линиям магнитного поля, в нашем случае “из подковообразного магнита”. Для перемещения качающегося проводника нужна сила F. Когда частицы движутся в магнитном поле, действует сила Лоренца, происходит разделение зарядов, а значит, и возникает индукционный ток. Это можно наблюдать по отклонению стрелки амперметра.
Для перемещения качающегося проводника нужна сила F. Когда частицы движутся в магнитном поле, действует сила Лоренца, происходит разделение зарядов, а значит, и возникает индукционный ток. Это можно наблюдать по отклонению стрелки амперметра.
Для определения направления индукционного тока применяется правило левой руки. Большой палец указывает направление, в котором электроны перемещаются под действием силы F, т.е. “из подковы”. Ваш указательный палец указывает направление магнитного поля, от северного к южному полюсу. Наконец, средний палец указывает направление, в котором электроны притягиваются силой Лоренца. На конце проводника, в сторону которого указывает ваш средний палец, образуется избыток электронов и это приводит к изменению направления тока.
Однако, в силу правила Ленца, точно в тот же момент должна действовать противодействующая сила F‘, направленная в противоположную сторону от причины F. Эта противодействующая сила создается индукционным током, который, так сказать, пытается восстановить исходное состояние.
Вы можете еще раз проверить направление силы F‘ с помощью правила левой руки. На этот раз большой палец указывает направление движения электронов. Итак, в проводнике, который перемещается под действием силы F внутри магнита , большой палец направлен в плоскость рисунка, а указательный палец снова направлен от северного полюса к южному. Затем средний палец указывает направление силы F’. Это направление согласуется с правилом Ленца и действует в направлении, противоположном направлению движения проводника. Чтобы проиллюстрировать это, мы провели эти рассуждения одно за другим. В реальном эксперименте, однако, все это происходит параллельно.
Можно также сравнить правило Ленца с поведением детей (аналог индукционного тока). Когда их родители (аналог причины) говорят им что-то, они сначала хотят сделать прямо противоположное. Если вы будете помнить об этой мнемонике, вы гарантированно не забудете правило Ленца.
Сохранение энергии для индукции также может быть соблюдено только с помощью правила Ленца.
Чтобы проверить это, вы можете провести следующий мысленный эксперимент. Если бы сила из F‘ была направлена в противоположную сторону, то есть равна силе F, раскачивание качелей ускорялось бы все больше и больше. И это без добавления дополнительной энергии извне. Таким образом, можно было бы создать вечный двигатель, что противоречит закону сохранения энергии.
Применение
Правило Ленца необходимо для многих применений в технике. Например, в вихретоковом тормозе. Этот тормоз не изнашивается, поскольку отсутствует трение. Тормозная сила генерируется магнитными полями. Например, такие тормоза есть у поездов и грузовиков. Электродвигатели также работают по этому принципу.
Правило Ленца защитит вас, даже если в вашу машину ударит молния. Клетка Фарадея также основана на этом принципе.
Все металлодетекторы, которые вы знаете по аэропортам или магазинам, работают одинаково. Они генерируют магнитное поле с помощью катушки. Если в магнитном поле находится металлический предмет, в нем индуцируются вихревые токи. Согласно правилу Ленца, эти токи направлены таким образом, что противодействуют причине возникновения тока. Поэтому магнитное поле детектора становится слабее. Это также уменьшает ток в металлодетекторе, эта разница измеряется, что приводит, например, к сигналу тревоги.
Согласно правилу Ленца, эти токи направлены таким образом, что противодействуют причине возникновения тока. Поэтому магнитное поле детектора становится слабее. Это также уменьшает ток в металлодетекторе, эта разница измеряется, что приводит, например, к сигналу тревоги.
Металлодетекторы также используются в некоторых светофорах, только здесь катушка расположена в асфальте под машинами. Таким образом, светофор, так сказать, замечает, что автомобиль ждет, и по возможности переключает его на зеленый. Как видите, правило Ленца важно для многих областей электротехники, а также в повседневной жизни.
Список использованной литературы
- Мякишев Г. Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В. А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.
Правило Ленца для электромагнитной индукции
Содержание:
Электромагнитная индукция:
Неоценимая заслуга в изучении явления электромагнитной индукции принадлежит известному английскому физику М.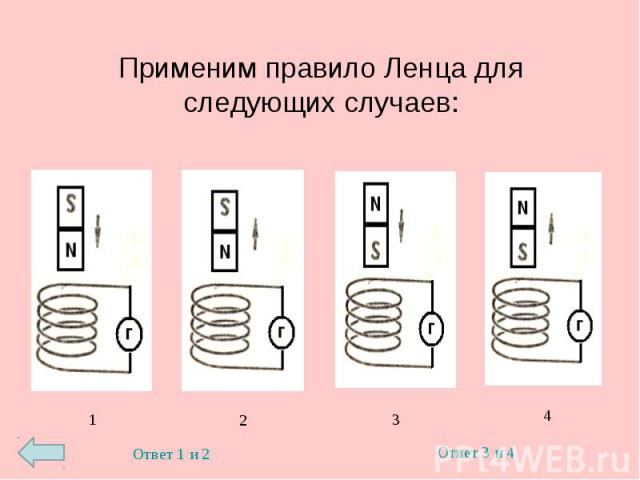 Фарадею — непревзойденному мастеру проведения физического эксперимента.
Фарадею — непревзойденному мастеру проведения физического эксперимента.
| Фарадей Майкл (1791-1867) — выдающийся английский физик, основоположник учения об электромагнитном поле, один из основателей электрохимии, исследователь взаимодействия вещества и магнитного поля. |
Обнаружение в 1820 г. датским физиком X. Эрстедом связи магнитного поля с электрическим током положило начало фундаментальным исследованиям открытого явления. Обладая широким научным кругозором, выдающийся физик и исследователь М. Фарадей предусмотрел возможность обратной связи магнитного поля и электрического тока, когда появление магнитного поля приводит к возникновению электрического тока. В результате длительных научных поисков он в 1821 г. получил первые положительные результаты: добился того, что в замкнутых проводниках, находящихся в переменном магнитном поле, возникал электрический ток.
Явление возникновения электрического тока в замкнутом проводнике, который расположен в переменном магнитов ном поле, называется электромагнитной индукцией.
Опишем основные опыты М. Фарадея, которые можно повторить и на школьном оборудовании.
C клеммами гальванометра соединим длинный проводник, пасть которого укреплена в штативе.
Постоянный подковообразный магнит сначала будем приближать к проводнику, а потом удалять от него (рис. 2.26). При этом увидим, что стрелка гальванометра будет отклоняться сначала в одну сторону, потом в противоположную.
Изменим условия опыта. Укрепим теперь подковообразный магнит в лапках штатива, а проводник, присоединенный к клеммам гальванометра, будем вводить в между полюсное пространство и выводить из него (рис. 2.27). Стрелка гальванометра также будет отклоняться сначала в одну, а потом в противоположную сторону.
Pиc. 227. Опыт с движущимся проводником
Видоизменим опыт. Одну из катушек присоединим к клеммам гальванометра, а вторую включим в электрическую цепь, состоящую из источника постоянного тока и выключатели. Замкнув цепь второй катушки, будем приближать ее к первой катушке (рис. 2.28). Отклонение стрелки гальванометра засвидетельствует появление тока в цепи первой катушки. Направление этого тока изменится, если вторую катушку удалять от первой. При неподвижных катушках ток будет отсутствовать.
Рис. 228. Опыт с движущейся катушкой с током
Разместив вторую катушку неподвижно на первой, начнем замыкать и размыкать цепь второй катушки (рис. 2.29). Когда цепь будет замыкаться, стрелка гальванометра отклонится в одну сторону. При размыкании стрелка отклонится в противоположную сторону.
Pиc. 229. Замыкание и размыкание цепи второй катушки
Изменим условия последнего опыта. Включим в цепь второй катушки реостат и снова замкнем цепь.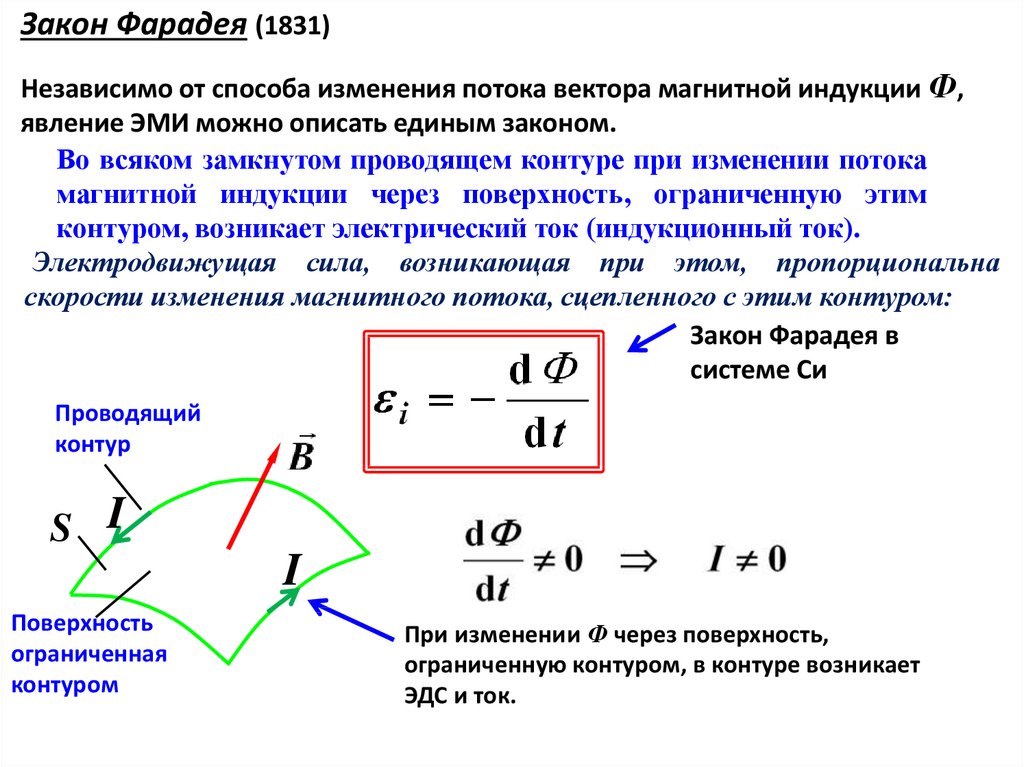 Когда стрелка остановится на нулевом делении, начнем изменять силу тока, перемещая ползунок реостата (рис. 2.30).
Когда стрелка остановится на нулевом делении, начнем изменять силу тока, перемещая ползунок реостата (рис. 2.30).
Рис. 230. Сила тока в катушке изменяется с помощью реостата
При увеличении силы тока в цепи первой катушки стрелка гальванометра будет отклоняться в одну сторону. При уменьшении силы тока отклонение стрелки будет противоположным.
После этого, не изменяя положения катушек и не разрывая цепи второй катушки, введем в катушки стальной стержень (рис. 2.31). Стрелка и в этом случае отклонится от положения равновесия и возвратится в начальное положение. Во время вынимания стержня из катушки заметим, что стрелка гальванометра отклоняется в противоположную сторону.
Pиc. 231. Опыт, когда движется стальной стержень
Электрический ток, возникающий в замкнутом проводнике в изменяющемся магнитном поле, называют индукционным.
Результаты всех опытов свидетельствуют, что при любом изменении магнитного поля или движении замкнутого проводника в магнитном поле возникает электрический ток. Его направление зависит от характера изменения магнитного поля: при увеличении магнитной индукции ток имеет одно направление, при уменьшении — противоположное.
Его направление зависит от характера изменения магнитного поля: при увеличении магнитной индукции ток имеет одно направление, при уменьшении — противоположное.
На практике направление тока в проводнике, который возникает вследствие электромагнитной индукции, определяют по правилу правой руки (рис. 2.32): если правую руку разместить в поле так, чтобы линии магнитной индукции входили в ладонь, а отставленный большой палец показывал направление движения проводника, то вытянутые пальцы руки покажут направление тока в проводнике.
Рис. 2.32 Правило правой руки
Чтобы ток в проводниках протекал длительное время, необходимо, чтобы все это время существовала разность потенциалов. А это возможно при непрерывном движении проводника. При этом будет происходить разделе ние в проводнике положительно и отрицательно заряженных частиц под действием силы Лоренца, которая имеет неэлектростатическое происхождение. Это приводит к возникновению ЭДС индукции.
Определим способ рассчета ЭДС, для случая, когда прямой проводник, который является частью электрической цепи, равномерно движется в магнитном поле. Вызванное силой Лоренца движение заряженных частиц образует электрический ток, а в это время на него в магнитном поле будет действовать сила Ампера (рис. 2.33):
где В — модуль вектора магнитной индукции; I — сила тока в проводнике; l длина проводника; — угол между направлением тока в проводнике и вектором магнитной индукции.
Возникающий ток в проводнике всегда будет иметь направление, при котором сила Ампера «тормозит» движение проводника. Чтобы проводник двигался равномерно (условие существования электрического тока), к нему нужно приложить силу, которая по модулю равна силе Ампера, а по направлению противоположна:
Рис. 2.33. К объяснению ЭДС индукции
Если за определенное время △t проводник сместится па △s, то работа будет равна
Таким образом,
Приняв во внимание, что по определению сила тока равна а ЭДС равна . И произведя определенные математические преобразования, получим
И произведя определенные математические преобразования, получим
Таким образом, для случая, когда проводник движется равномерно в однородном магнитном поле, значение ЭДС индукции зависит от магнитной индукции поля, длины
Правило установлено известным русским физиком Э.Х. Ленцем как обобщение многочисленных опытов по определению направления индукционного тока. C этой целью Э.Х. Ленц исследовал взаимодействие замкнутого проводника и переменного магнитного поля, которое вызвало индукционный ток в этом проводнике.
Чтобы лучше понять сущность этого правила, рассмотрим опыт.
На легком горизонтальном рычаге, который имеет вертикальную ось вращения, находятся два легких металлических кольца, одно из которых сплошное, я второе разрезано (рис. 2.35). Рычаг посажен на тонкое стальное острие так, чтобы трение было минимальным.
Pиc. 235. Прибор для демонстрации правила Ленца
235. Прибор для демонстрации правила Ленца
Введем в сплошное кольцо катушку с ферромагнитным сердечником (электромагнитом), включенным в электрическую цепь из источника тока и выключателя (рис. 2.36).
Рис. 236. К правилу Ленца
В момент .замыкания цепи кольцо, как бы отталкиваясь от катушки, сместится на определенное расстояние и развернет рычаг на некоторый угол.
В момент появления тока в электромагните электропроводное кольцо, находящееся возле полюса электромагнита, всегда — притягивается к нему.
Если опыт повторить, изменив направление тока в катушке, то будем наблюдать тот же эффект. Таким образом, определяющим в данном случае является не направление магнитной индукции, а характер изменения магнитной индукции.
Если опыт попытаться пронести с разрезанным кольцом, то подобного эффекта наблюдать не сможем. Это свидетельствует, что отталкивание кольца связано с индукционным током, который возникает в сплошном кольце.
При размыкании цепи питания электромагнита проводящее кольцо будет двигаться от него.
Чтобы разобраться в дальнейших рассуждениях, необходимо вспомнить, что параллельные проводники, в которых ток проходит в одном направлении, притягиваются, а в противоположных отталкиваются. Таким образом, если кольцо отталкивается от катушки, то в нем индуцируется ток, противоположный току в катушке по направлению.
Взаимно противоположными будут и магнитные индукции полей этих токов.
Обобщив результаты опытов, можно сделать выводы, к которым пришел Э.Х. Ленц: магнитное поле индукционного тока всегда противодействует изменениям, которые вызвали этот так.
Правило Ленца: индукционный ток в замкнутом проводнике имеет такое направление, что его магнитное поле компенсирует изменение магнитного поля, которое вызвало этот ток.
Магнитный потокЭлектромагнитную индукцию можно наблюдать в двух случаях: когда проводник движется в однородном магнитном поле или неподвижный проводник находится и магнитном поле, магнитная индукция которого изменяется со временем. Нa практике, как правило, случается так, что одновременно изменяется магнитная индукция и положение проводника в магнитном поле. Примером может быть движение проводника в неоднородном магнитном поле. Так как в этом случае расчеты сложнее» для их упрощения ввели физическую величину, которая одновременно зависит и от индукции магнитного поля, и от параметров движения проводника. Эта величина получила название магнитного потока.
Нa практике, как правило, случается так, что одновременно изменяется магнитная индукция и положение проводника в магнитном поле. Примером может быть движение проводника в неоднородном магнитном поле. Так как в этом случае расчеты сложнее» для их упрощения ввели физическую величину, которая одновременно зависит и от индукции магнитного поля, и от параметров движения проводника. Эта величина получила название магнитного потока.
Представим себе проводник в виде замкнутого кольца, которое находится в магнитном поле (рис. 2.38-а). Приведем кольцо в движение так, чтобы оно двигалось в плоскости, перпендикулярной к линиям магнитного поля. При этом количество линий индукции магнитного поля, которые проходят через него, будет уменьшаться, и в кольце возникнет индукционный ток (рис. 2.38-б).
Pис. 238. Движение кольца в магнитом поле
Если теперь кольцо проводника поместить в магнитное поле, индукция которого изменяется, то количество линий магнитной индукции, которые проходят через контур, также будет изменяться и в проводнике возникнет индукционный ток (рис. 2.39).
2.39).
Pиc. 239. Изменение магнитного потока через кольцо
Оба описанных случая можно объяснить проще, если для каждого их них учитывать произведение площади кольца на значение магнитной индукции магнитного поля. Именно это произведение изменялось в обоих случаях. Фактически это произведение характеризовало поток линий магнитной индукции, которые пронизывают контур определенной площади, или просто — магнитный поток.
Магнитный поток Ф зависит не только от модуля магнитной индукции и площади контура, но и от угла, который образуют нормаль с плоскостью контура и вектором магнитной индукции поля (рис. 2.40). Поэтому в общем виде значении магнитного потока записывается как
где Ф — магнитный поток; В — модуль магнитной индукции поля; — угол между нормалью к плоскости контура и вектором магнитной индукции.
Величина, которая описывает магнитное поле и равна произведению магнитной индукции на площадь замкнутого контура и косинус угла (между вектором магнитной индукции и нормалью к контуру), называется магнитным потоком, или потоком магнитной индукции.
Анализ формулы показывает, что минимальное значение магнитного потока (Ф = 0) будет тогда, когда = 90º, т. е. плоскость контура параллельна линиям магнитного поля. Если = 0, то магнитный поток при всех равных условиях будет максимальным (Ф = BS).
Магнитный поток — скалярная величина. В СИ магнитный поток измеряется в веберах (Вб), на честь известного немецкого физика В. Вебера.
Если магнитная индукция магнитного поля 1 Тл, а площадь контура, сквозь который проходит магнитный поток, 1 м2, то магнитный поток равен 1 веберу (1 Вб):
1 Вб = 1 Тл • 1 м2.
Любые изменения магнитного поля или площади контура вызывают явление электромагнитной индукции.
| Вебер Вильгельм Эдуард (1804-1881) — немецкий физик, основные работы посвящены электромагнетизму, работал также над проблемами акустики, теплоты, молекулярной физики, земного магнетизма.  |
Таким образом, любое изменение магнитного потока обусловливает возникновение электрического тока в замкнутом проводящем контуре. C учетом закона Ома для полной цепи последний вывод можно записать так: любое, изменение. магнитного потока приводит к возникновению ЭДС индукции.
Проанализировав результаты экспериментальных исследований электромагнитной индукции, можно найти общую формулу для выражения особенностей этого явления, которые отражают сущность закона электромагнитной индукции: при изменении магнитного потоки в замкнутых проводниках возникает электрический ток, вызванный ЭДС индукции, которая пропорциональна скорости изменения магнитного потока:
или
где электродвижущая сила индукции; -скорость изменения магнитного потока Ф; k — коэффициент пропорциональности.
Закон электромагнитной индукции: электродвижущая сила индукции пропорциональна скорости изменения магнитного потока.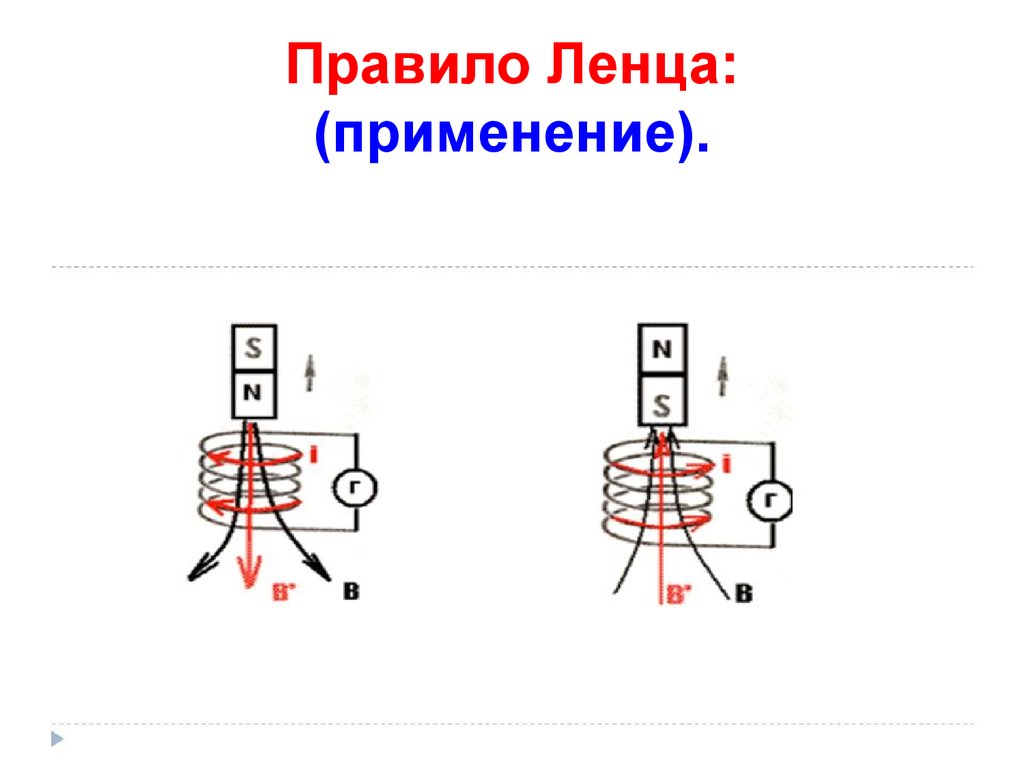
При использовании единиц СИ коэффициент k = 1. Приняв во внимание, что индукционный ток противодействует изменению магнитного потока (правило Ленца), окончательно имеем:
Так как согласно закону Ома то можно записать его для случая электромагнитной индукции в виде , где — сопротивление контура, а r=0.
Заряд, который проходит в контуре вследствие электромагнитной индукции: Q = I∆t.
Учитывая, что заряд скалярная величина, а знак минус можно опустить, получим:
Магнитный поток, пронизывающий катушку, которая состоит из 75 витков, равен 4,8 ∙ 10-3 Вб. На протяжении какого времени исчезнет этот поток, если в катушке индуцируется ЭДС индукции 0,74 В?
Дано: | Решение ЭДС индукции возникает в катушке потому, что магнитный поток, пронизывающий ее, изменяется на △Φ = Φ2 — Φl.  В каждом В каждомвитке катушки при этом будет возникать ЭДС индукции в соответствии с законом ΔΦ электромагнитной индeкции: |
| ∆t — ? |
Общая ЭДС будет в N раз больше: . Отсюда: .
Подставив значения физических величин, получим
Ответ: ток исчезнет через 0,48 с.
Электродинамический микрофонОдним из примеров практического применения явления электромагнитной индукции является электродинамический микрофон. C помощью этого прибора звуковые колебания превращаются в колебания электрического тока, которые усиливаются при помощи специальных электронных усилителей и используются в быту, научных исследованиях, производстве.
Микрофоны превращают звуковые колебания в электрические.
Обязательной частью электродинамического микрофона является постоянный магнит, изготовленный в виде кольца (рис. 2.41).
К одному из полюсов магнита приклеен цилиндрический стержень 1 из мягкого ферромагнетика (железа). К другому — ферромагнитная пластина 2 из такого же ферромагнетика. В центре этой пластины находится круглое отверстие, которое охватывает стержень. Диаметр отверстия несколько больше диаметра стержня, поэтому между стержнем и пластиной образуется узкая щель 5, в которой сосредоточен весь магнитный поток магнита.
К другому — ферромагнитная пластина 2 из такого же ферромагнетика. В центре этой пластины находится круглое отверстие, которое охватывает стержень. Диаметр отверстия несколько больше диаметра стержня, поэтому между стержнем и пластиной образуется узкая щель 5, в которой сосредоточен весь магнитный поток магнита.
На стержне находится мембрана 3, которая колеблется под действием звуковых волн. К нижней части мембраны приклеена небольшая катушка 4 с некоторым количеством витков изолированного провода. Катушка помещена в кольцевую щель
между полюсами постоянного магнита.
В электродинамическом микрофоне катушка находится в магнитном поле.
Концы катушки соединены гибкими проводниками со специальными клеммами. Если на мембрану микрофона попадают звуковые волны, то она начинает колебаться вместе с катушкой. При колебании катушки магнитный поток, пронизывающий ее, изменяется и в ней индуцируется ЭДС индукции.
В движущейся катушке, находящейся в магнитном поле, возникает ЭДС индукции.
Если катушка включена в цепь электронного усилителя, то электрические колебания усиливаются и могут быть или записаны на магнитный либо оптический диск, или сразу
воспроизведены громкоговорителем.
Принцип действия электродинамического микрофона используется в различных датчиках для изучения и контроля колебательных процессов.
СамоиндукцияКаждый проводник, в котором существует электрический ток, создает «собственное» магнитное поле. Это поле образуется сразу же, как только в проводнике начинает про ходить электрический ток. Если индукция магнитного поля перед замыканием цепи была равна нулю, то через некоторое время после замыкания она будет иметь максимальное значение B, соответствующее силе тока в проводнике. Таким образом, момент возникновения электрического тока можно читать моментом начала изменения магнитного потока. А любое изменение магнитного потока, по закону электромагнитной индукции, порождает вихревое электрическое поле, способствующее появлению ЭДС индукции во всех проводниках,находящихся в магнитном поле.
Явление самоиндукции выявил Д. Генри в 1832 г.
Не может быть исключения и для проводника, который является «источником» этого поля. Вихревое поле создает и в нем ЭДС индукции , которую назвали ЭДС самоиндукции.
Наличие ЭДС самоиндукции можно подтвердить опытом. Для этого составим электрическую цепь из источника тока, выключателя и электрической лампочки (рис. 2.43). При
замыкании цепи лампочка зажигается практически мгновенно. Если же в цепь включить катушку с железным сердечником, то максимальная яркость свечения лампочки устанавливается постепенно (рис. 2.44).
Pиc. 2.43. Лампочка загорается сразу после замыкания цепи | Рис 2.44 В цепи с катушкой лампочка загорается постепенно |
Это является свидетельством того, что ток в цепи увеличивается во мгновенно, а на протяжении некоторого времени.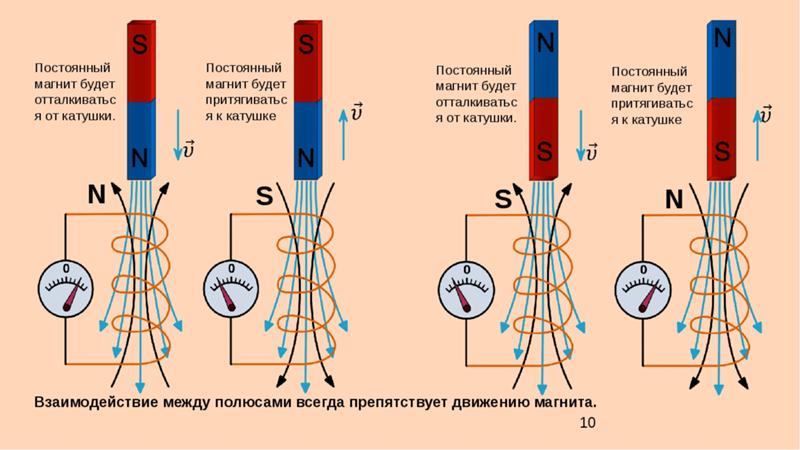 Посмотрев на графики рисунков 2.45 и 2.46, можно сказать, что в цепи, где находится катушка из 100 витков, ток нарастает быстрее, чем в цепи, в которой находится катушка из 1000 витков. На прохождение тока н цепи существенно влияет также ферромагнитный сердечник в катушке (рис. 2.47).
Посмотрев на графики рисунков 2.45 и 2.46, можно сказать, что в цепи, где находится катушка из 100 витков, ток нарастает быстрее, чем в цепи, в которой находится катушка из 1000 витков. На прохождение тока н цепи существенно влияет также ферромагнитный сердечник в катушке (рис. 2.47).
Pиc. 2.45. График силы тока при замыкании цепи с катушкой из 100 витков | Рис. 2.46. График силы тока при замыкании цепи с катушкой из 1000 витков |
Рис. 2.47. График силы тока при замыкании цепи с катушкой (сердечником) |
Поскольку ЭДC самоиндукции противодействует ЭДС источники тока, то можно сделать вывод, что ЭДС самоиндукции зависит от характеристик катушки или проводника, включенного в электрическую цепь.
А магнитный поток, создаваемый катушкой или проводником, будет пропорционален силе тока в них: Ф ~ I. Если внести коэффициент пропорциональности, то можно получить более точное соотношение и новую формулу: Ф = L ∙ I. Здесь коэффициент пропорциональности L учитывает электромагнитные свойства катушки (проводника) и называется индуктивностью. Индуктивность определяется формой и размерами проводника, а также магнитными свойствами среды.
Если внести коэффициент пропорциональности, то можно получить более точное соотношение и новую формулу: Ф = L ∙ I. Здесь коэффициент пропорциональности L учитывает электромагнитные свойства катушки (проводника) и называется индуктивностью. Индуктивность определяется формой и размерами проводника, а также магнитными свойствами среды.
Физическую величину, которая характеризует электромагнитные свойства катушки или проводника, называют индуктивностью.
Если при изменении силы тока в проводнике на 1 А за 1 с в нем индуцируется ЭДС самоиндукции 1 В, то этот проводник имеет индуктивность 1 Гн.
В СИ индуктивность измеряют в генри (Гн) в честь известного американского физика Д. Генри.
Единица 1 генри имеет довольно большой размер, поэтому применяют, как правило, долевые единицы:
- 1 миллигенри = 1 мГн = 10-3 Гн;
- 1 микрогенри = 1 мкГн = 10-6 Гн.
Если в любом проводнике изменяется электрический ток, то это приводит к изменению магнитного потока ΔΦ — LΔI, которое вызывает ЭДС самоиндукции:
Явление самоиндукции наблюдается также при размыкании цепи c током. Составим цепь из источника тока, выключателя, катушки и лампочки. Лампу накаливания, сопротивление которой значительно меньше сопротивления катушки, включим параллельно катушке (рис. 2.48). Если замкнуть цепь, то накаливание волоска лампочки будет происходить постепенно, как
Составим цепь из источника тока, выключателя, катушки и лампочки. Лампу накаливания, сопротивление которой значительно меньше сопротивления катушки, включим параллельно катушке (рис. 2.48). Если замкнуть цепь, то накаливание волоска лампочки будет происходить постепенно, как
бы с задержкой. Если после полного загорания лампы разомкнуть ключ, то она ярко вспыхнет. Это будет проявлением самоиндукции. В результате размыкания цепи возникнет ЭДС самоиндукции, которая поддержит ток в цепи лампочки и катушки.
Рис. 2.48. Схема электрической цепи для наблюдения явления самоиндукции при размыкании
Определить индуктивность катушки, если сила тока в ней изменяется на 50 А за 1 с и при этом появляется ЭДС самоиндукции 0,08 В.
Дано: | Решение По закону ЭДС самоиндукции Отсюда Подставив значения физических величин, получим |
| L— ? |
Ответ: индуктивность катушки 1,6 мГн.
Самоиндукция подтверждает действие закона сохранения и превращения энергии в электромагнитных явлениях.
Как известно, вследствие явления самоиндукции при замыкании цепи возникает ЭДС самоиндукции . Если же сила тока не изменяется, ЭДС самоиндукции не возникает. Такое положение в электрической цепи обусловлено тем, что за счет энергии источника тока выполняется работа по компенсации ЭДС самоиндукции. Это аналогично случаю, когда для сообщения скорости неподвижному телу необходимо выполнить определенную работу по преодолению инерции.
Любые изменения силы тока в катушке вызовут появление ЭДС индукции и приведут к выполнению работы источником тока для компенсации ее действия. Эта работа равна энергии магнитного поля катушки или проводника.
Для компенсации ЭДС самоиндукции источник тока выполнит работу по перемещению заряженных частиц, общий заряд которых равен Q. Приняв во внимание, что, и то, что , получим значение выполненной работы для явления самоиндукции:
ЭДС самоиндукции зависит от индуктивности проводника и скорости изменения силы тока в нем.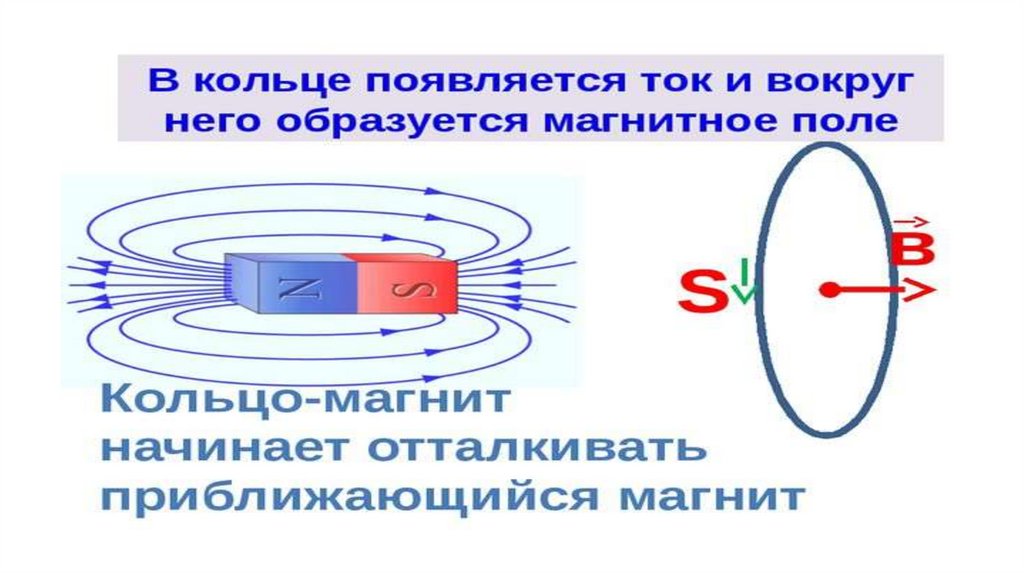
При этом сила тока в цепи изменяется от пуля до Imax которое равно I0. По определению Q=IΔt.
Поскольку при замыкании цепи сила тока не имеет постоянного значения, то для упрощения расчетов будем считать,что сила тока линейно изменяется на протяжении всего времени. Тогда сила тока
Таким образом,
Изменение силы тока ΔI за интервал времени Δt равно I0.
Работа, выполненная источником тока, равна энергии магнитного поля катушки с током:
Энергия магнитного поля катушки с током пропорциональна индуктивности катушки и квадрату силы тока в ней.
Правило ⚠️ Ленца для электромагнитной продуции: формулировка
Содержание:
- Явление электромагнитной индукции
- Направление индукционного тока: правило Ленца
- Правило Ленца: примеры
Содержание
- Явление электромагнитной индукции
- Направление индукционного тока: правило Ленца
- Правило Ленца: примеры
Явление электромагнитной индукции
Определение
Электромагнитная индукция – это физическое явление, при котором в изолированном проводнике возникает ток вследствие того, что через него проходит магнитный поток.
Закон ЭИ открыл Майкл Фарадей в 1831 году. Он понял, что электродвижущая сила аналогична скорости, с которой меняется магнитный поток. При этом величина ЭС не зависима от трансформации магнитного поля или движения контура. Такой электрический ток является индукционным. Благодаря ЭИ механическая энергия преобразовывается в электрическую.
Направление индукционного тока: правило Ленца
Ленц продолжил искания Фарадея. С помощью открытого им в 1833 году правила можно определить путь ИТ. Оно читается так: индукционный ток протекает таким образом, чтобы собственным магнитным полем противостоять изменению магнитного потока, который и вызвал его.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Единица измерения ИТ – тесла, обозначается как сочетание букв Тл.
Формула выглядит следующим образом: \(\frac{\bigtriangleup Ф}{\bigtriangleup t}>0,\;е_i<0\). Индукционный ток \( i_{инд.}\) течет в сторону выбранного положительного направления обхода замкнутого пути.
Индукционный ток \( i_{инд.}\) течет в сторону выбранного положительного направления обхода замкнутого пути.
Проиллюстрируем данное положение. Виток проводника находится в неоднородном магнитном поле, которое создается движущимся магнитом. Вследствие того, что В увеличивается, то векторы Вi и В нельзя назвать параллельными. Магнитное поле, которое создается ИТ, не дает магнитному потоку измениться.
ПЛ – это частный случай закона сохранения энергии, который имеет вид \(\bigtriangleup Е+\bigtriangleup U=A+Q.\)
Правило Ленца: примеры
1. Представим, что прямоугольный контур расположен в однородном магнитном поле \overrightarrow В. По отношению к плоскости замкнутого пути оно направлено перпендикулярно. При этом одна из сторон передвигается по двум другим сторонам с определенной скоростью. Сила Лоренца воздействует на свободные заряды той части контура, которая находится в движении. Главная составляющая СЛ здесь направлена вдоль проводника. Она связана с переносной скоростью зарядов \(\overrightarrow v\). Модель данной силы будет равняться: \(F_Л=е\overrightarrow vВ\). Работа силы \(F_Л\) на пути l: \(А=F_Л\times l=evBl\). Электродвижущая сила равна: \(\delta_{инд.}=\frac Ае=vBl\). В недвижимых частях замкнутого пути сторонняя сила приравнивается к 0. Через некоторое время площадь контура изменится: \(\bigtriangleup S=lv\bigtriangleup t\). То же самое будет происходить с магнитным потоком: \(\bigtriangleup Ф=Вlv\bigtriangleup t\). Из этого следует, что \(\left|\delta_{инд.}\right|=\left|\frac{\bigtriangleup Ф}{\bigtriangleup t}\right|\). Значит, ПЛ действительно для данной ситуации.
Она связана с переносной скоростью зарядов \(\overrightarrow v\). Модель данной силы будет равняться: \(F_Л=е\overrightarrow vВ\). Работа силы \(F_Л\) на пути l: \(А=F_Л\times l=evBl\). Электродвижущая сила равна: \(\delta_{инд.}=\frac Ае=vBl\). В недвижимых частях замкнутого пути сторонняя сила приравнивается к 0. Через некоторое время площадь контура изменится: \(\bigtriangleup S=lv\bigtriangleup t\). То же самое будет происходить с магнитным потоком: \(\bigtriangleup Ф=Вlv\bigtriangleup t\). Из этого следует, что \(\left|\delta_{инд.}\right|=\left|\frac{\bigtriangleup Ф}{\bigtriangleup t}\right|\). Значит, ПЛ действительно для данной ситуации.
2. Пример без расчетов. Представим катушку C, которая замкнута через гальванометр G. Приблизим к одному из его концов магнит. Сделаем это со стороны северного полюса. В катушке появится электрический ток, который можно увидеть из-за того, что стрелка гальванометра станет отклоняться. Если посмотреть на этот винтовой проводник со стороны магнита, то можно заметить, что индукционный ток направлен против часовой стрелки. Поток вектора магнитной индукции пронизывает ветки катушки. Если мы приблизим к ней магнит, то этот поток увеличится, потому что возрастет МИ поля магнита. Магнитное поле ИТ направлено наружу по правилу буравчика. Это значит, что оно восполняет нарастание поля магнита. А это соответствует правилу Ленца.
Поток вектора магнитной индукции пронизывает ветки катушки. Если мы приблизим к ней магнит, то этот поток увеличится, потому что возрастет МИ поля магнита. Магнитное поле ИТ направлено наружу по правилу буравчика. Это значит, что оно восполняет нарастание поля магнита. А это соответствует правилу Ленца.
Насколько полезной была для вас статья?
Рейтинг: 2.50 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Явление электромагнитной индукции. Правило Ленца. Закон Фарадея и его вывод
Явление электромагнитной индукции. Правило Ленца. Закон Фарадея и его вывод.
Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Электромагнитная
индукция была открыта Майклом
Фарадеем 29
августа[источник не указан 273 дня] 1831
года.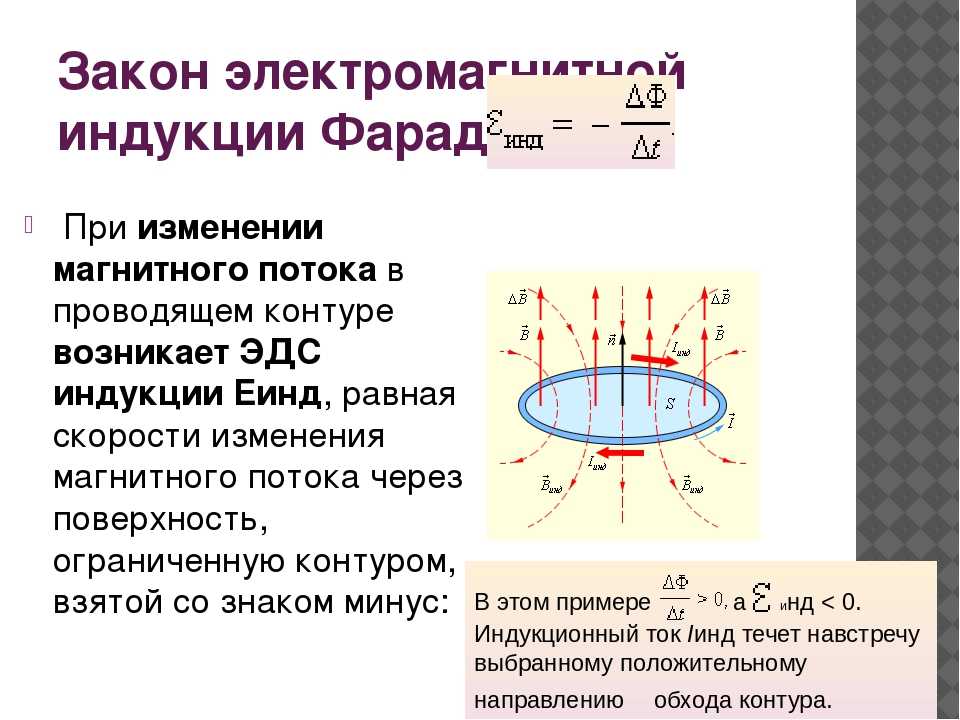 Он обнаружил, что электродвижущая
сила, возникающая в замкнутом проводящем
контуре, пропорциональна скорости
изменениямагнитного
потока через
поверхность, ограниченную этим контуром.
Величинаэлектродвижущей
силы (ЭДС)
не зависит от того, что является причиной
изменения потока — изменение самого
магнитного поля или движение контура
(или его части) в магнитном поле.Электрический
ток,
вызванный этой ЭДС, называется индукционным
током.
Он обнаружил, что электродвижущая
сила, возникающая в замкнутом проводящем
контуре, пропорциональна скорости
изменениямагнитного
потока через
поверхность, ограниченную этим контуром.
Величинаэлектродвижущей
силы (ЭДС)
не зависит от того, что является причиной
изменения потока — изменение самого
магнитного поля или движение контура
(или его части) в магнитном поле.Электрический
ток,
вызванный этой ЭДС, называется индукционным
током.
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, натянутую на этот контур.
Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
— электродвижущая сила,
— число витков,
— магнитный поток через один виток,
— потокосцепление катушки.
Векторная форма
[править]В дифференциальной форме закон Фарадея можно записать в следующем виде:
(в системе СИ)
или
(в системе СГС).
В интегральной форме (эквивалентной):
(СИ)
или
(СГС)
Здесь — напряжённость электрического поля, — магнитная индукция, — произвольная поверхность, — её граница. Контур интегрирования подразумевается фиксированным (неподвижным).
Следует отметить, что закон Фарадея в такой форме, очевидно, описывает лишь ту часть ЭДС, что возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учете последнего см. ниже).
Если
же, скажем, магнитное поле постоянно, а
магнитный поток изменяется вследствие
движения границ контура (например, при
увеличении его площади), то возникающая
ЭДС порождается силами, удерживающими
заряды на контуре (в проводнике) исилой
Лоренца,
порождаемой прямым действием магнитного
поля на движущиеся (с контуром) заряды. При этом равенство продолжает
соблюдаться, но ЭДС в левой части теперь
не сводится к (которое
в данном частном примере вообще равно
нулю). В общем случае (когда и магнитное
поле меняется со временем, и контур
движется или меняет форму) последняя
формула верна так же, но ЭДС в левой
части в таком случае есть сумма обоих
слагаемых, упомянутых выше (то есть
порождается частично вихревым
электрическим полем, а частично силой
Лоренца и силой реакции движущегося
проводника).
При этом равенство продолжает
соблюдаться, но ЭДС в левой части теперь
не сводится к (которое
в данном частном примере вообще равно
нулю). В общем случае (когда и магнитное
поле меняется со временем, и контур
движется или меняет форму) последняя
формула верна так же, но ЭДС в левой
части в таком случае есть сумма обоих
слагаемых, упомянутых выше (то есть
порождается частично вихревым
электрическим полем, а частично силой
Лоренца и силой реакции движущегося
проводника).
Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[2] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[3]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.

Однако
возможность (пусть с некоторыми
оговорками, уточняющими область
применимости) совпадающей формулировки
«правила потока» с законом электромагнитной
индукции нельзя назвать чисто случайной.
Дело в том, что, по крайней мере для
определенных ситуаций, это совпадение
оказывается очевидным проявлением принципа
относительности.
А именно, например, для случая относительного
движения катушки с присоединенным к
ней вольтметром, измеряющим ЭДС, и
источника магнитного поля (постоянного
магнита или другой катушки с током), в
системе отсчета, связанной с первой
катушкой, ЭДС оказывается равной именно
циркуляции электрического поля, тогда
как в системе отсчета, связанной с
источником магнитного поля (магнитом),
происхождение ЭДС связано с действием
силы Лоренца на движущиеся с первой
катушкой носители заряда. Однако та и
другая ЭДС обязаны совпадать, поскольку
вольтметр показывает одну и ту же
величину, независимо от того, для какой
системы отсчета мы ее рассчитали.
Потенциальная форма
[править]При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
(в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока , пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением[1]:
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
Правило
Ленца носит обобщённый характер и
справедливо в различных физических
ситуациях, которые могут отличаться
конкретным физическим механизмом
возбуждения индукционного тока. Так,
если изменение магнитного потока вызвано
изменением площади контура (например,
за счёт движения одной из сторон
прямоугольного контура), то индукционный
ток возбуждается силой Лоренца,
действующей на электроны перемещаемого
проводника в постоянном магнитном поле.
Если же изменение магнитного потока
связано с изменением величины внешнего
магнитного поля, то индукционный ток
возбуждается вихревым электрическим
полем, появляющимся при изменении
магнитного поля. Однако в обоих случаях
индукционный ток направлен так, чтобы
скомпенсировать изменение потока
магнитного поля через контур.
Так,
если изменение магнитного потока вызвано
изменением площади контура (например,
за счёт движения одной из сторон
прямоугольного контура), то индукционный
ток возбуждается силой Лоренца,
действующей на электроны перемещаемого
проводника в постоянном магнитном поле.
Если же изменение магнитного потока
связано с изменением величины внешнего
магнитного поля, то индукционный ток
возбуждается вихревым электрическим
полем, появляющимся при изменении
магнитного поля. Однако в обоих случаях
индукционный ток направлен так, чтобы
скомпенсировать изменение потока
магнитного поля через контур.
Если
внешнее магнитное поле, пронизывающее
неподвижный электрический контур,
создаётся током, текущим в другом
контуре, то индукционный ток может
оказаться направлен как в том же
направлении, что и внешний, так и в
противоположном: это зависит от того,
уменьшается или увеличивается внешний
ток. Если внешний ток увеличивается, то
растёт создаваемое им магнитное поле
и его поток, что приводит к появлению
индукционного тока, уменьшающего это
увеличение. В этом случае индукционный
ток направлен в сторону, противоположную
основному. В обратном случае, когда
внешний ток уменьшается со временем,
уменьшение магнитного потока приводит
к возбуждению индукционного тока,
стремящегося увеличить поток, и этот
ток направлен в ту же сторону, что и
внешний ток.
В этом случае индукционный
ток направлен в сторону, противоположную
основному. В обратном случае, когда
внешний ток уменьшается со временем,
уменьшение магнитного потока приводит
к возбуждению индукционного тока,
стремящегося увеличить поток, и этот
ток направлен в ту же сторону, что и
внешний ток.
Правило Ленца | Презентация к уроку по физике (11 класс) на тему:
Слайд 1
Курсовая работа Правило Ленца. Явление самоиндукции. Работу выполнила Романова Галина Алексеевна учитель физики МОУ СОШ №2 Вязьма 2011 г.
Слайд 2
Содержание 1.Явление ЭМИ и опыт Фарадея 2.Опыт Ленца. Правило Ленца и закон сохранения энергии 3.Явление самоиндукции 4.Индуктивность 5.Следствия самоиндукции 6.Энергия магнитного поля тока
Слайд 3
Цель : научиться определять направление индукционного тока; на примере правила Ленца сформулировать представление о фундаментальности ЗСЭ; разъяснить сущность явления самоиндукции; вывести формулу для расчета энергии магнитного поля, выяснить физический смысл этой формулы.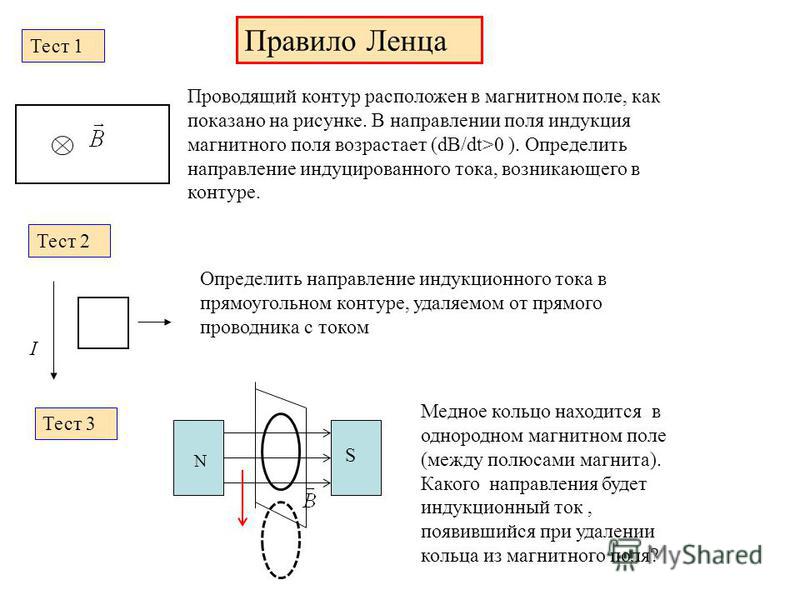
Слайд 4
Опыт Фарадея: направление отклонения стрелки амперметра (а, значит, и направление тока) может быть различным.
Слайд 5
В чем заключается явление ЭМИ? Если в цепи, содержащей замкнутый контур (катушку) менять силу тока, то в самом контуре возникнет ещё и индукционный ток. Этот ток также будет подчиняться правилу Ленца.
Слайд 6
Демонстрация явления электромагнитной индукции
Слайд 7
Опыт Ленца Если приблизить магнит к проводящему кольцу, то оно начнет отталкиваться от магнита. Это отталкивание можно объяснить только тем, что в кольце возникает индукционный ток, обусловленный возрастанием магнитного потока через кольцо, а кольцо с током взаимодействует с магнитом.
Слайд 8
Демонстрация опыта Ленца
Слайд 9
Если магнитный поток через контур возрастает , то направление индукционного тока в контуре таково, что вектор магнитной индукции созданного этим током поля направлен противоположно вектору магнитной индукции внешнего магнитного поля. Если магнитный поток через контур уменьшается , то направление индукционного тока таково, что вектор магнитной индукции созданного этим током поля сонаправлен вектору магнитной индукции внешнего поля.
Если магнитный поток через контур уменьшается , то направление индукционного тока таково, что вектор магнитной индукции созданного этим током поля сонаправлен вектору магнитной индукции внешнего поля.
Слайд 10
Правило Ленца : индукционный ток имеет такое направление, что созданный им магнитный поток всегда стремится скомпенсировать то изменение магнитного потока, которое вызвало данный ток. Правило Ленца является следствием закона сохранения энергии.
Слайд 11
Парение магнита над сверхпроводящей чашей Магнит падает; возникает переменное магнитное поле; возникает вихревое электрическое поле; в сверхпроводнике возникают незатухающие кольцевые токи; согласно правилу Ленца направление этих токов таково, что магнит отталкивается от сверхпроводника; магнит «парит» над чашей.
Слайд 12
Явление самоиндукции
Слайд 13
САМОИНДУКЦИЯ – возникновение вихревого электрического поля в проводящем контуре при изменении силы тока в нем; частный случай электромагнитной индукции . Вследствие самоиндукции замкнутый контур обладает «инертностью»: силу тока в контуре, содержащем катушку, нельзя изменить мгновенно .
Вследствие самоиндукции замкнутый контур обладает «инертностью»: силу тока в контуре, содержащем катушку, нельзя изменить мгновенно .
Слайд 14
Проявление явления самоиндукции Замыкание цепи При замыкании в электрической цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое электрическое поле, направленное против тока, т. е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи. В результате Л1 загорается позже, чем Л2.
Слайд 15
Размыкание цепи При размыкании электрической цепи ток убывает, возникает уменьшение магнитного потока в катушке, возникает вихревое электрическое поле, направленное как ток, т. е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи. В результате Л при выключении ярко вспыхивает.
Слайд 16
Вывод формулы ЭДС самоиндукции Если магнитное поле создано током, то можно утверждать, что Ф ~ В ~ I , т.е. Ф ~ I или Ф= LI , где L – индуктивность контура (или коэффициент самоиндукции).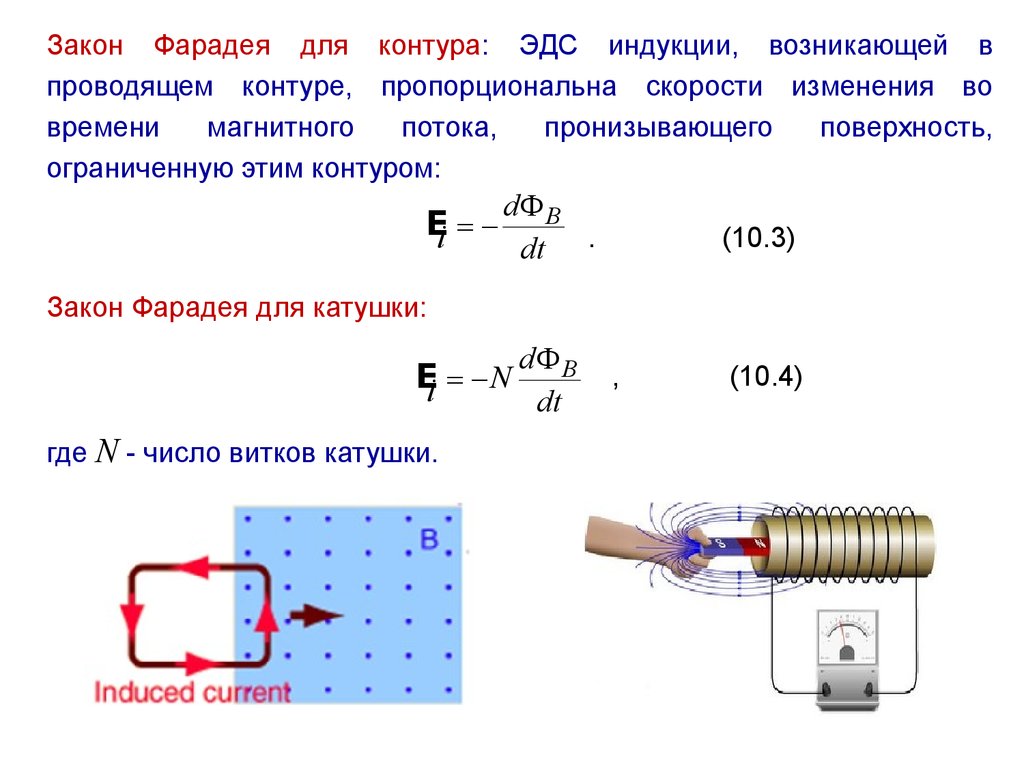 Тогда
Тогда
Слайд 17
Физический смысл индуктивности Индуктивность — физическая величина, численно равна я ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Слайд 18
Явление самоиндукции особенно резко проявляется в цепи, содержащей в себе катушку с железным сердечником, т. к. железо значительно увеличивает магнитный поток катушки, а следовательно, и величину ЭДС самоиндукции при его изменении.
Слайд 19
Следствия самоиндукции Вследствие явления самоиндукции при размыкании цепей, содержащих катушки со стальными сердечниками (электромагниты, двигатели, трансформаторы) создается значительная ЭДС самоиндукции и может возникнуть искрение или даже дуговой разряд.
Слайд 20
Аналогия между установлением в цепи тока величиной I и процессом набора телом скорости V 1. Установление в цепи тока I происходит постепенно. 2. Для достижения силы тока I необходимо совершить работу. 3. Чем больше L , тем медленнее растет I . 4. 1. Достижение телом скорости V происходит постепенно. 2. Для достижения скорости V необходимо совершить работу. 3. Чем больше m , тем медленнее растет V . 4.
2. Для достижения скорости V необходимо совершить работу. 3. Чем больше m , тем медленнее растет V . 4.
Слайд 21
Вопросы к проверочной работе по теме «Явление ЭМИ. Самоиндукция» 1.Определение явления ЭМИ 2.Правило Ленца 3.Закон ЭМИ(определение, формула) 4.Определение явления самоиндукции 5.ЭДС самоиндукции(формула) 6.Индуктивность(определение, формула, единица измерения) 7.Энергия магнитного поля тока(формула)
Слайд 22
Использованные ресурсы 1.Л.Э.Генденштейн, Ю.Л.Дик.- М.: Мнемозина,2009.-272с.:ил. 2.ОК «1С: Школа. Физика. 7-11 классы: Библиотека наглядных пособий.» 3. http : //files. shcool – collection . edu.ru 4. http://class-fizika.narod.ru
Слайд 23
Спасибо за внимание!
С этим файлом связано 1 файл(ов). Среди них: Итоговая контрольная работа.docx. Показать все связанные файлы Подборка по базе: Золотое правило нравственности.docx, Как правило.docx, Блоки. Золотое правило механики 7 класс. 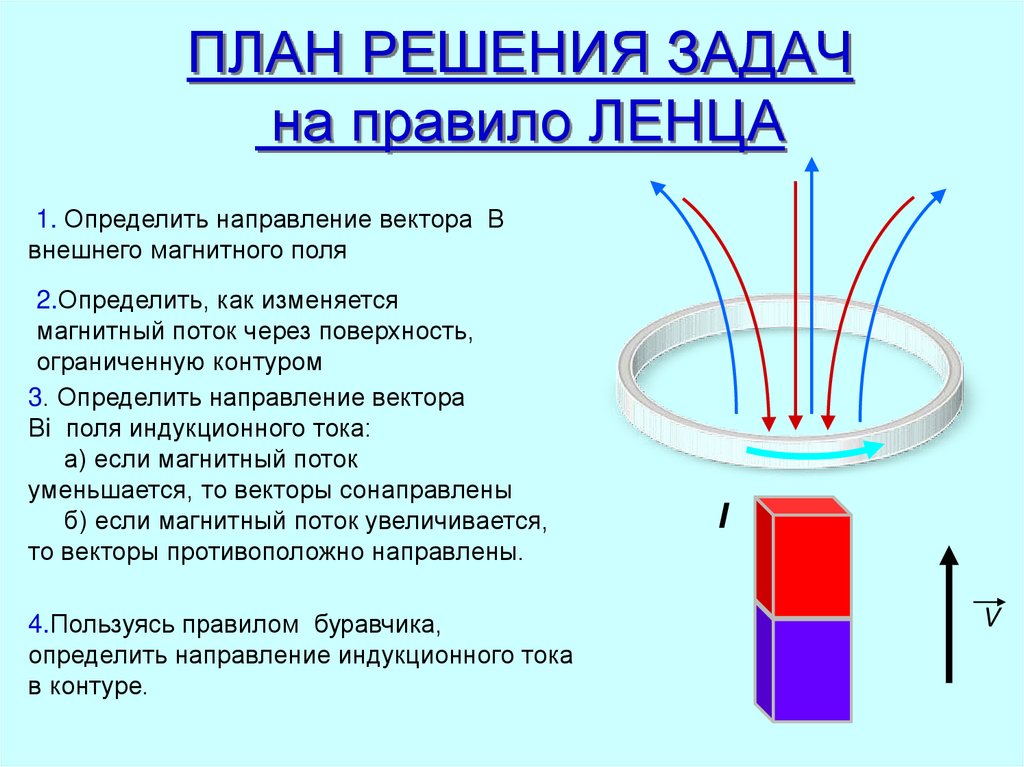 pptx, урок ОРКСЭ Золотое правило нравственности.doc, ПЗ №2 Правило Лопиталя_Бернулли от 08.04.2021.doc, Золотое правило механики.pptx, «Первое правило бизнеса – поступай с другим так, как он хотел бы, ПР правило левой руки.docx, Блок Золоое правило механики.pptx, обособление дееприч с правилом.docx pptx, урок ОРКСЭ Золотое правило нравственности.doc, ПЗ №2 Правило Лопиталя_Бернулли от 08.04.2021.doc, Золотое правило механики.pptx, «Первое правило бизнеса – поступай с другим так, как он хотел бы, ПР правило левой руки.docx, Блок Золоое правило механики.pptx, обособление дееприч с правилом.docx
|
| Φ= B · S · cos α, |
где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис.
 1.20.1).
1.20.1).| |
| Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обхода контура связаны правилом правого буравчика |
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется Вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
| 1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
| |
| Рисунок 1.20.2. Иллюстрация правила Ленца. В этом примере , а . Индукционный ток Iинд течет навстречу выбранному положительному направлению обхода контура |
Правило Ленца отражает тот экспериментальный факт, что и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью по двум другим сторонам (рис. 1.20.3).
| |
| Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон |
На свободные заряды на этом участке контура действует сила Лоренца.
 Одна из составляющих этой силы, связанная с переносной скорость зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен
Одна из составляющих этой силы, связанная с переносной скорость зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен| FЛ = eυB |
Работа силы FЛ на пути l равна
| A = FЛ · l = eυBl. |
По определению ЭДС
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
Для того, чтобы установить знак в формуле, связывающей и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный . За время Δt на сопротивлении R выделится джоулево тепло
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Джеймсом Максвеллом в 1861 г.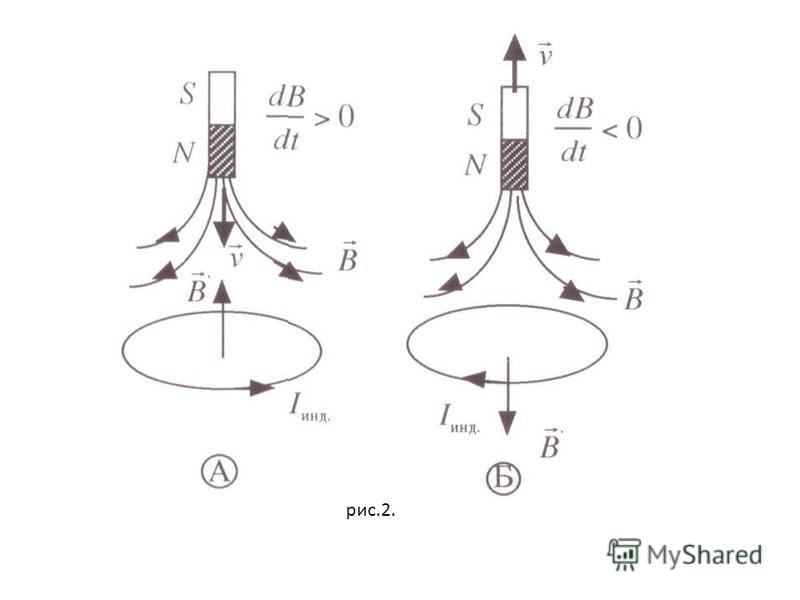
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Вихревые токи
В электрических аппаратах, приборах и машинах металлические детали иногда движутся в магнитном поле или неподвижные металлические детали пересекаются силовыми линиями меняющегося по величине магнитного поля. В этих металлических деталях индуктируется ЭДС самоиндукции.
Под действием этих э. д. с. в массе металлической детали протекаютвихревые токи (токи Фуко), которые замыкаются в массе, образуя вихревые контуры токов.
Вихревыми токами (также токами Фуко) называются электрические токи, возникающие вследствие электромагнитной индукции в проводящей среде (обычно в металле) при изменении пронизывающего ее магнитного потока.
Вихревые токи порождают свои собственные магнитные потоки, которые, по правилу Ленца, противодействуют магнитному потоку катушки и ослабляют его. Кроме того, они вызывают нагрев сердечника, что является бесполезной тратой энергии.
Пусть имеется сердечник из металлического материала. Поместим на этот сердечник катушку, по которой пропустим переменный ток. Вокруг катушки окажется переменный магнитный ток, пересекающий сердечник. При этом в сердечнике станет наводиться индуцированная ЭДС, которая, в свою очередь, вызывает в сердечнике токи, называемые вихревыми. Эти вихревые токи нагревают сердечник. Так как электрическое сопротивление сердечника невелико, то наводимые в сердечниках индуцированные токи могут оказываться достаточно большими, а нагрев сердечника — значительным.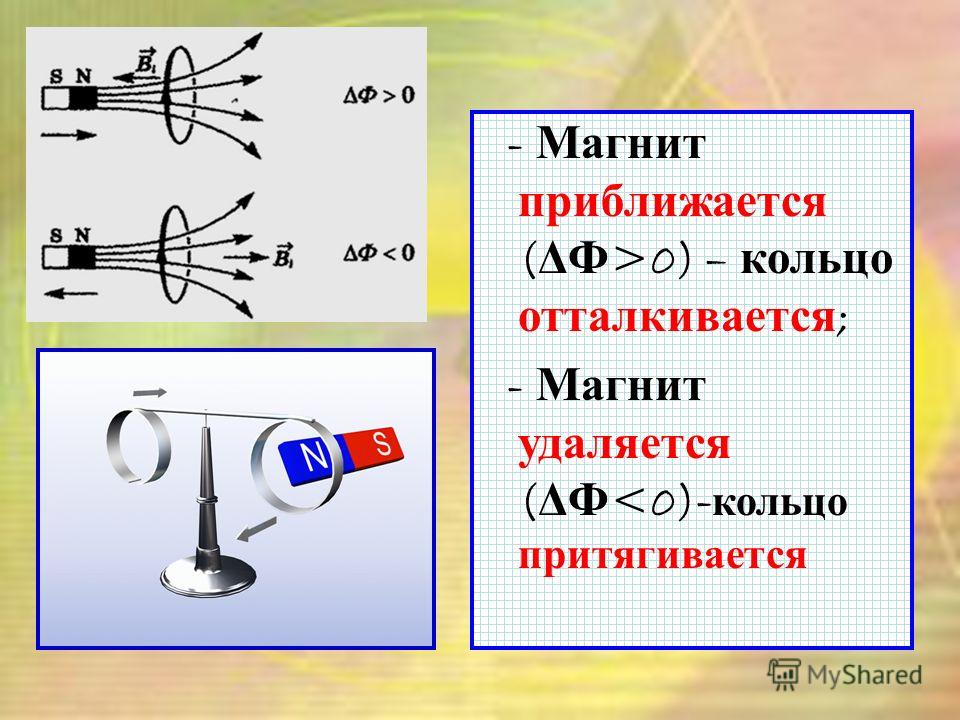
Возниконвение токов Фуко (вихревых токов)
Впервые вихревые токи были обнаружены французским учёным Д.Ф. Араго (1786 — 1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции.
Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Он назвал явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.
В качестве примера на рисунке показаны вихревые токи, индуктируемые в массивном сердечнике, помещенном в катушку, обтекаемую переменным током. Переменное магнитное поле индуктирует токи, которые замыкаются по путям, лежащим в плоскостях, перпендикулярных направлению поля.
Вихревые токи: а — в массивном сердечнике, б — в пластинчатом сердечнике
Способы уменьшения токов Фуко
Мощность, затрачиваемая на нагрев сердечника вихревыми токами, бесполезно снижает КПД технических устройств электромагнитного типа.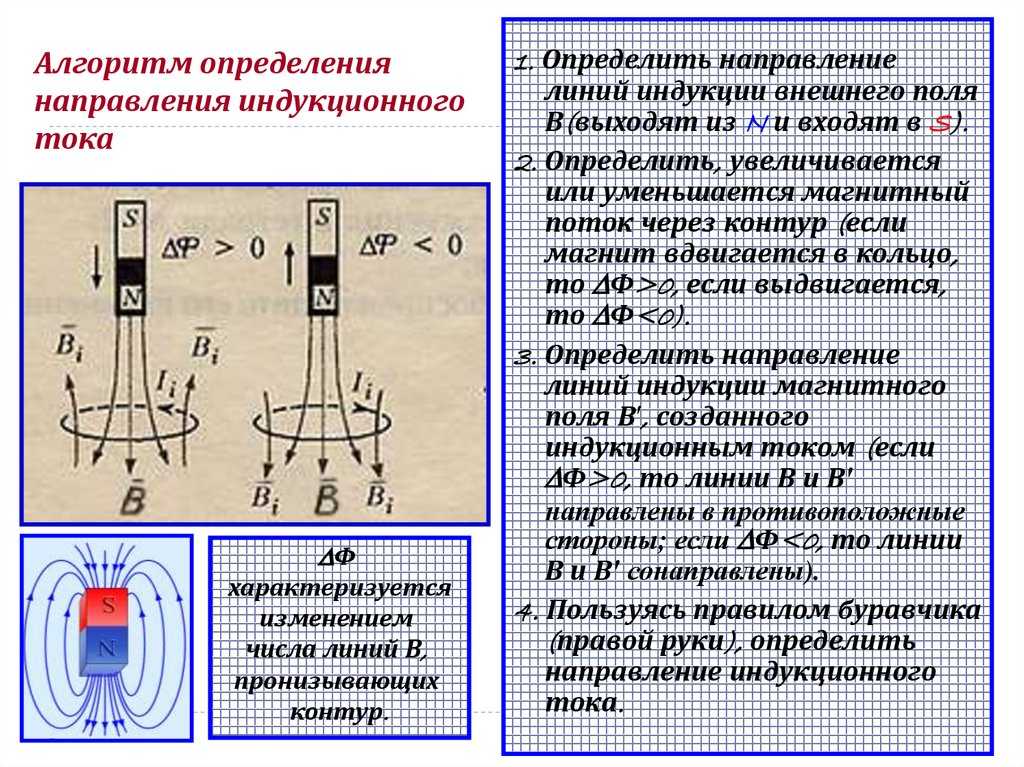
Чтобы уменьшить мощность вихревых токов, увеличивают электрическое сопротивление магнитопровода, для этого сердечники набирают из отдельных тонких (0,1- 0,5 мм) пластин, изолированных друг от друга с помощью специального лака или окалины.
Магнитопроводы всех машин и аппаратов переменного тока и сердечники якорей машин постоянного тока собирают из изолированных друг от друга лаком или поверхностной непроводящей пленкой (фосфатированных) пластин, выштампованных из листовой электротехнической стали. Плоскость пластин должна быть параллельна направлению магнитного потока.
При таком делении сечения сердечника магнитопровода вихревые токи существенно ослабляются, так как уменьшаются магнитные потоки, которыми сцепляются контуры вихревых токов, а следовательно, понижаются и индуктируемые этими потоками э. д. с, создающие вихревые токи.
В материал сердечника также вводят специальные добавки, также увеличивающие егоэлектрическое сопротивление. Для увеличения электрического сопротивления ферромагнетика электротехническую сталь приготовляют с присадкой кремния.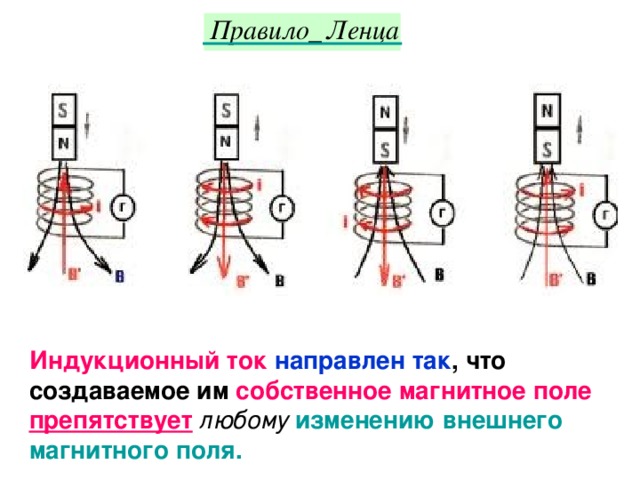
Сердечники некоторых катушек (бобин) набирают из кусков отожженной железной проволоки. Полоски железа располагают параллельно линиям магнитного потока. Вихревые же токи, протекающие в плоскостях, перпендикулярных направлению магнитного потока, ограничиваются изолирующими прокладками. Для магнитопроводов приборов и устройств, работающих на высокой частоте, применяют магнетодиэлектрики. Чтобы снизить вихревые токи в проводах, последние изготавливают в виде жгута из отдельных жил, изолированных друг от друга.
Лицендрат — это система переплетенных медных проводов, в которой каждая жила изолирована от соседних. Лицендрат предназначен для использования на высокочастотных токах для предотвращения возникновения паразитных токов и токов Фуко.
Применение токов Фуко
Полезное применение вихревые токи нашли в устройстве магнитного тормоза диска электрического счетчика. Вращаясь, диск пересекает магнитные силовые линии постоянного магнита. В плоскости диска возникают вихревые токи, которые, в свою очередь, создают свои магнитные потоки в виде трубочек вокруг вихревого тока.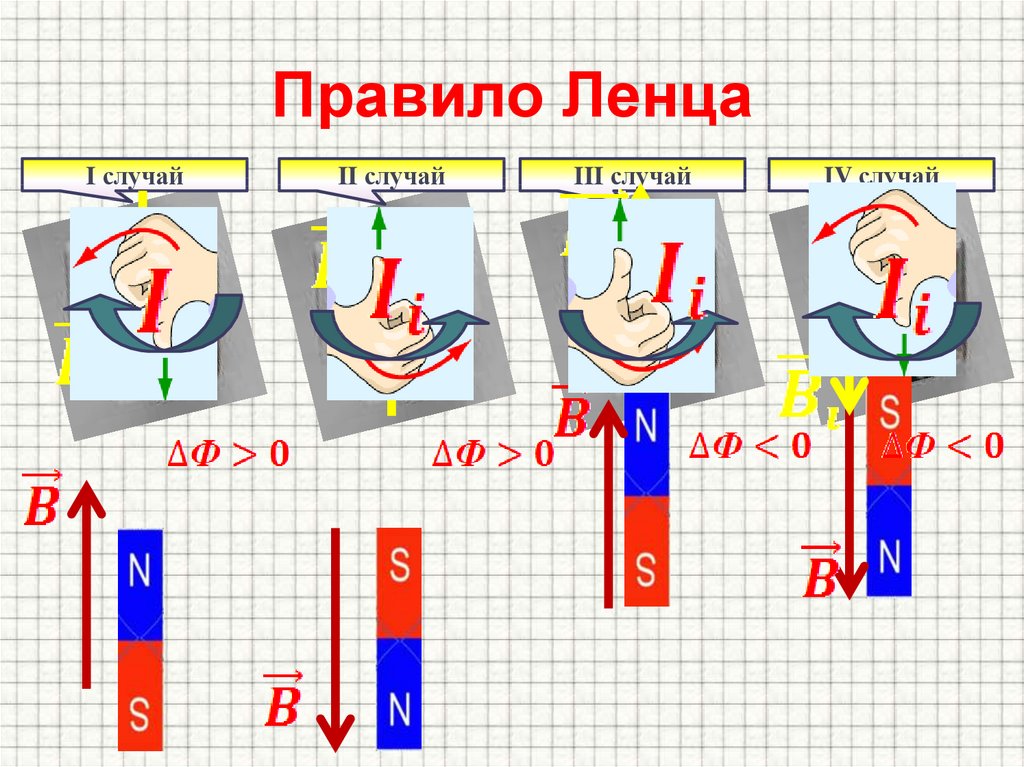 Взаимодействуя с основным полем магнита, эти потоки тормозят диск.
Взаимодействуя с основным полем магнита, эти потоки тормозят диск.
В ряде случаев, применяя вихревые токи, можно использовать технологические операции, которые невозможно применить без токов высокой частоты. Например, при изготовления вакуумных приборов и устройств из баллона необходимо тщательно откачать воздух и иные газы. Однако в металлической арматуре, находящейся внутри баллона, имеются остатки газа, которые можно удалить только после заваривания баллона. Для полного обезгаживания арматуры вакуумный прибор помещают в поле высокочастотного генератора, в результате действия вихревых токов арматура нагревается до сотен градусов, остатки газа при этом нейтрализуются.
Вихревые токи находят полезное применение также при индукционной плавке металлов и поверхностной закалке токами высокой частоты.
САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
Самоиндукция. Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется.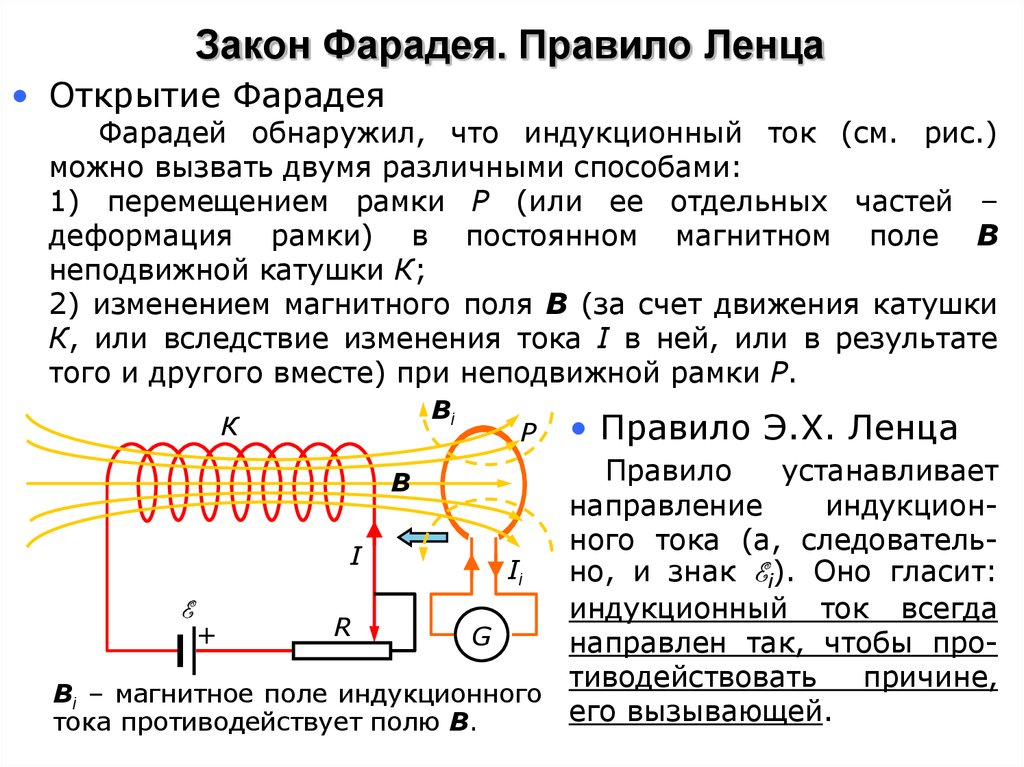 Поэтому в том же самом проводнике, по которому идет переменный ток, возникает ЭДС индукции. Это явление называют самоиндукцией.
Поэтому в том же самом проводнике, по которому идет переменный ток, возникает ЭДС индукции. Это явление называют самоиндукцией.
При самоиндукции проводящий контур выполняет двойную роль: переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, то появляется ЭДС индукции . По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
Явление самоиндукции можно наблюдать в простых опытах. На рисунке 2.13 показана схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (рис. 2.14).
ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (рис. 2.14).
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на рисунке 2.15. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. в результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции больше ЭДС батареи элементов.
Индуктивность. Модуль вектора индукции магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф В I.
Можно, следовательно, утверждать, что
Ф = LI, (2.7)
где L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком.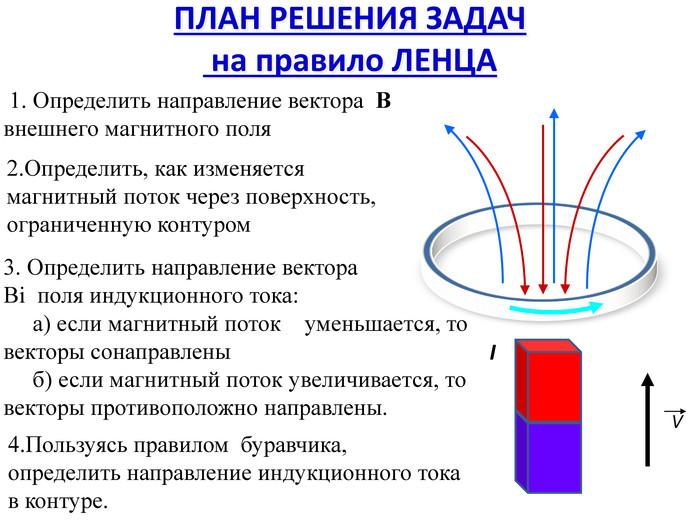 Величину L называют индуктивностью контура, или его коэффициентом самоиндукции.
Величину L называют индуктивностью контура, или его коэффициентом самоиндукции.
Используя закон электромагнитной индукции и выражение (2.7), получаем равенство
если считать, что форма контура остается неизменной и поток меняется только за счет изменения силы тока.
Из формулы (2.8) следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока в нем на 1 А за 1 с.
Индуктивность, подобно электроемкости, зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Очевидно, что индуктивность одного проволочного витка меньше, чем у катушки (соленоида), состоящей из N таких же витков, так как магнитный поток катушки увеличивается в N раз.
Единицу индуктивности в СИ называют генри (обозначается Гн). Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В:
Индуктивность проводника равна 1 Гн, если в нем при равномерном изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В:
Аналогия между самоиндукцией и инерцией. Явление самоиндукции подобно явлению инерции и механике. Так, инерция приводит к тому, что под действием силы тело не мгновенно приобретает определенную cкорость, а постепенно. Тело нельзя мгновенно затормозить, как 6ы велика ни былa тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция поддерживает его некоторое время, несмотря на сопротивление цепи.
Явление самоиндукции выполняет очень важную роль в: электротехнике и радиотехнике. Индуктивность цепи «оказывает существенное влияние на прохождение по цепи переменного электрического тока. Подробно об этом будет рассказано в главе 4.
При изменении силы тока в проводнике в нем возникает вихревое электрическое поле. Это поле тормозит электроны ири возрастании силы тока и ускоряет при убывании.
Это поле тормозит электроны ири возрастании силы тока и ускоряет при убывании.
формул в рабочих процессах и проверке — ленивые или жадные оцениваются?
Я попробовал разобраться с этим.
Чтобы уменьшить шум, я попытался использовать самое обременительное (и наименее полезное) правило проверки, которое смог придумать. Моя надежда заключалась в том, что я смогу получить четкий и хотя бы несколько значимый результат при небольшом размере выборки.
(
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
...повторяется 46 раз...
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
)
Я провел
- 3 набора тестов,
- 10 повторений каждого набора (ну… 16 первого набора, 11 второго и 10 третьего)
- каждая итерация пытается вставить 10 записей (которые имеют отношение поиска к возможности)
Точки данных были собраны из столбца Millis в представлении «Анализ» в консоли разработчика. Я предполагаю, что это имеет некоторую связь с ограничением регулятора времени процессора.
Я предполагаю, что это имеет некоторую связь с ограничением регулятора времени процессора.
Мои уровни журнала были:
БД: INFO, Выноски: INFO, ApexCode: DEBUG, Проверка: FINEST, Рабочий процесс: INFO, Профилирование: FINEST, Visualforce: INFO, Система: DEBUG
Я использовал приведенное выше правило проверки в качестве основы. Каждый набор тестов модифицировал это базовое правило проверки одним единственным способом.
Я предполагаю, что распределение результатов во всех тестовых наборах является гауссовым.
тестовый набор 1 выполнил следующее правило проверки:
верно && (
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
...повторяется 46 раз...
BEGINS(Возможность__r.Учетная запись.Владелец. Профиль.LastModifiedById, '005') &&
)
Профиль.LastModifiedById, '005') &&
)
тестовый набор 2 выполнил следующее правило проверки:
ложь && (
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
...повторяется 46 раз...
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
)
тестовый набор 3 выполнил следующее правило проверки:
(
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
...повторяется 46 раз...
BEGINS(Возможность__r.Учетная запись.Владелец.Профиль.LastModifiedById, '005') &&
) && ЛОЖЬ
Правило проверки в первом наборе тестов всегда будет давать сбой (т. е. результат формулы проверки будет истинным), и ему необходимо оценить каждую часть формулы.
е. результат формулы проверки будет истинным), и ему необходимо оценить каждую часть формулы.
Правило проверки во втором наборе тестов всегда проходит успешно, и ему не нужно оценивать каждую часть формулы (если в формулах используется ускоренная оценка), но все же можно оценивать каждую часть формулы.
Правило проверки во втором тесте всегда проходит, но необходимо будет оценить каждую часть формулы (поскольку определяющий фактор находится в конце формулы).
Мои результаты были следующими
Набор тестов 1:
25.99, 24.62, 25.62, 29.19, 24,63, 25,20, 26,12, 24,74, 29,80, 23,64, 24,17, 24,91, 23,40, 32,67, 30,25, 29,19
Среднее значение: 26,50875, стандартное отклонение: 2,78372, отклонение: 7,74912
Тестовый набор 2:
18.81, 17.65, 18.84, 17.81, 17.38, 17.99, 18.61, 19.25, 17.37, 17.42, 18.41
Среднее значение: 18,14, стандартное отклонение: 0,6727, отклонение: 0,45252
Тестовый набор 3:
24.
90, 27.75, 23.68, 24.04, 28.36, 24.27, 24.65, 24.60, 24.69, 23.31
Среднее значение: 25,025, стандартное отклонение: 1,67622, отклонение: 2,80972
Данные из тестового набора 3 очень похожи на данные из тестового набора 1 и очень отличаются от данных из тестового набора 2. 3 стандартных отклонения выше среднего для набора тестов 2: 20,1581. 3 стандартных отклонения ниже среднего для тестового набора 3 составляет 19,99634
Из этого я думаю, что могу сделать следующие выводы:
- Формулы правил проверки оцениваются лениво
- Формулы правил проверки используют ускоренную оценку
- Если у вас есть состояние, которое с большей вероятностью может сократить остальную часть формулы, поместите его ближе к началу вашей формулы
Размер выборки очень мал, так что примите это во внимание.
Однако, по моему опыту, правила проверки не начинают вносить существенный вклад в лимит времени ЦП, пока вы не начнете работать с тысячами записей в одном контексте выполнения.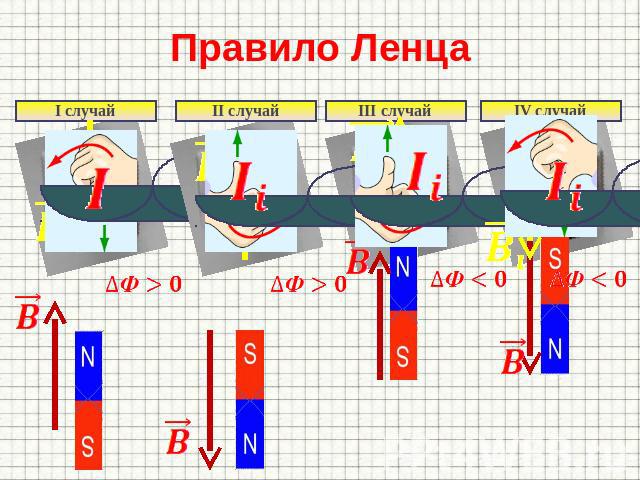
Мои извинения всем статистикам, читающим это, поскольку я, вероятно, убил статистический анализ.
Роб Иствэй
05 июня 2018
Сезон экзаменов, и ленивому студенту пора понять, как мало правок можно пройти, не обнаружив огромных пробелов в своих знаниях.
Слушатель программы Radio 4 More or Less прислал интересный запрос по этому поводу, и меня попросили изучить математику, стоящую за ним.
Предположим, вы сдаете экзамен по истории и в программе 20 тем. Экзамен в конце года будет состоять из двенадцати вопросов, каждый по отдельной теме. На экзамене от кандидата требуется ответить всего на три вопроса.
Сколько тем вам нужно пересмотреть, чтобы быть на 100% уверенным, что у вас будет как минимум три вопроса, которые вы сможете решить на этом экзамене?
Это хорошая маленькая головоломка, и вы, возможно, захотите найти ответ, прежде чем читать дальше.
*****
Чтобы выяснить, сколько тем вам нужно пересмотреть, представьте себе сценарий худшего случая. В этом мифическом экзамене по истории максимальное количество тем, которые вы могли повторить, только чтобы обнаружить, что ни одна из них не подходит на экзамене, равно восьми (= 20 — 12). Так что, если вы повторите восемь предметов плюс еще три — т.е. всего 11 тем, — то у вас гарантированно будет как минимум три вопроса на выбор на экзамене.
В этом мифическом экзамене по истории максимальное количество тем, которые вы могли повторить, только чтобы обнаружить, что ни одна из них не подходит на экзамене, равно восьми (= 20 — 12). Так что, если вы повторите восемь предметов плюс еще три — т.е. всего 11 тем, — то у вас гарантированно будет как минимум три вопроса на выбор на экзамене.
Существует простая формула для расчета минимального уровня пересмотра для любого экзамена такого типа. Предположим, есть:
T Темы в программе
Q Вопросы на экзамене (каждая на другую тему)
. На вопросы Дан
, чтобы быть на 100%, что не менее А. вопросов возникнет в темах, которые студент пересмотрел, количество пересмотренных тем, R , is :
R >= T – Q + A
Просто чтобы подтвердить, что это работает – если есть 20 тем и 12 вопросов, из которых нужно ответить на 3, R = 20-12+3 = 11 .
Но может ли ленивый ученик сэкономить еще больше усилий? Для экзамена 20 : 12 : 3 выше, если студент повторяет только десять тем вместо одиннадцати, он все равно почти наверняка получит как минимум три вопроса по измененным темам. Шансы составляют 99,9.6%* . Так что, хотя пересмотр всего десяти тем — это риск, он очень мал.
И ленивому студенту становится лучше. Они по-прежнему могут быть на 95 % уверены в том, что получат три вопроса, даже если пересмотрят только семь тем из 20.
Однако риск быстро возрастает, как только количество исправлений падает ниже этого уровня. Если они пересматривают только четыре темы, шанс получить три вопроса падает до менее чем 50-50.
Вот таблица, показывающая, как растет риск по мере уменьшения ширины ревизии:
Количество вопросов. Пересмотренная вероятность> = 3 вопроса, возникающих*
9 99,7%
8 98,5%
7 94,8%
6 86,3%
5 70,4% (в настоящее время вступает в высокую территорию)
4 46,6%
3 19,3%
Есть ли простая обратная сторона правила конверта, чтобы выяснить, сколько мало ленивого студента нужно пересмотреть, чтобы иметь хороший удар на экзамене? Да, есть, но помните, что это всего лишь грубое руководство, а не окончательное правило.
Если вы хотите, чтобы вероятность появления вопросов по темам, которые вы пересмотрели, составляла не менее 90 %, число тем R, которые вы должны тщательно пересмотреть, очень приблизительно определяется следующим образом:
R = T x A + 1 (если Q> a и если A> 2) **
Q
Имеет ли смысл следовать этому правилу? Если вы игрок, которому не хватает времени на учебу, то может быть. Но помните, формула предполагает, что если возникнет вопрос по изученной вами теме, вы сможете успешно его решить. Также предполагается, что никакие вопросы не устанавливают связи между темами. Настоящие экзамены редко бывают такими. Так что обычно стоит иметь хотя бы пару запасных тем в рукаве на всякий случай.
Так что мой совет? Ну, конечно, я советую любому студенту тщательно изучить всю программу, чтобы вы были полностью готовы справиться со всем, что возникнет на экзамене. Как всегда. (Нет).
* Один из способов вычислить это — рассчитать вероятность того, что на экзамене появятся ровно две, одна или ноль тем, и вычесть это значение из 100%, чтобы получить вероятность того, что на экзамене появятся как минимум 3 темы. Обратите внимание, что если вы повторите десять тем, вероятность того, что на экзамене появится ровно 1 или 0 тем, равна нулю.
Обратите внимание, что если вы повторите десять тем, вероятность того, что на экзамене появится ровно 1 или 0 тем, равна нулю.
** Обратите внимание, что эта формула обратной стороны конверта не работает, если все вопросы являются обязательными. Когда Q = A, формула предполагает, что вам нужно изучить темы T + 1, что означает выход за рамки учебного плана! И формула становится гораздо менее надежной, когда вы должны ответить только на 1 или 2 вопроса из немногочисленных на экзамене.
Ленивый расчет | Coding Diet
Во многих случаях при программировании необходимо принять решение о том, следует ли
до сохранить некоторое состояние или (пере) вычислить его по мере необходимости. Очевидно каждый
ситуация иная, и поэтому нет единственного ответа, который подходит. В этом
сообщение я собираюсь попытаться объяснить различие и преимущества/недостатки
того или иного подхода. Я надеюсь, что простое воспоминание о том, что этот выбор существует,
заставить меня сделать явный выбор, чтобы я мог подумать об этом немного больше.
Различие
Различие немного похоже на различие между активным вычислением и ленивым вычислением. оценка, но это не то же самое. Различие здесь заключается в сопровождении кода. Я начну с очень простого примера, а затем перейду к более реалистичному примеру. который включает доступ к базе данных, что делает решение немного более интересным.
Предположим, у вас есть очень простой класс , представляющий человека и детей.
что они могут иметь:
класс Person(object):
def __init__(я, пол):
self.gender = пол
self.boys = []
self.girls = []
защита have_baby_girl (я)
девушка = человек('женщина')
self.girls.append (девушка)
вернуть девушку
защита have_baby_boy (я):
мальчик = Человек('мужчина')
self.boys.append (мальчик)
вернуть мальчика
Теперь предположим, что где-то в вашем коде вы хотите вернуть количество дочерних элементов
что есть у конкретного человека.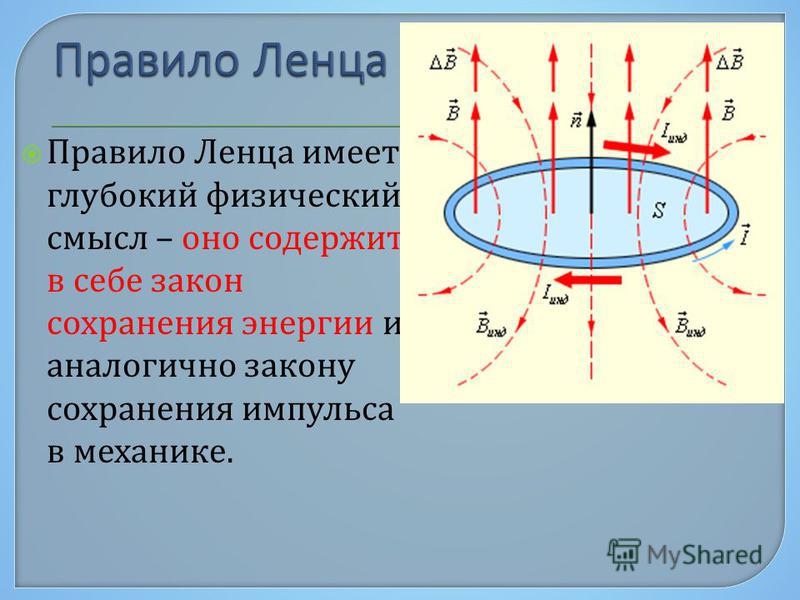 Вы можете либо отслеживать это, либо вычислять его
на лету, вот версия для отслеживания:
Вы можете либо отслеживать это, либо вычислять его
на лету, вот версия для отслеживания:
класс Человек(объект):
def __init__(я, пол):
self.gender = пол
self.boys = []
self.girls = []
self.number_of_children = 0
защита have_baby_girl (я)
девушка = человек('женщина')
self.girls.append (девушка)
self.number_of_children += 1
вернуть девушку
защита have_baby_boy (я):
мальчик = Человек('мальчик')
self.boys.append (мальчик)
self.number_of_children += 1
вернуть мальчика
Вот возможная версия расчета на лету:
класс Человек(объект):
def __init__(я, пол):
self.gender = пол
self.boys = []
self.girls = []
@имущество
def number_of_children (я):
вернуть len(self.boys) + len(self.girls)
защита have_baby_girl (я)
девушка = человек('женщина')
self.girls.append (девушка)
вернуть девушку
защита have_baby_boy (я):
мальчик = Человек('мальчик')
self. boys.append (мальчик)
вернуть мальчика
boys.append (мальчик)
вернуть мальчика
В данном конкретном случае я предпочитаю расчет на лету. Мне нравится
что мне не нужно было изменять какой-либо существующий код, мне нужно было только добавить кое-что. Если я
добавить какой-либо другой метод (предположим, принять метод ), затем в отслеживании
version я должен убедиться, что обновляю нашу переменную состояния number_of_children соответственно. Наконец, если мы изменим наше определение того, что такое «ребенок»,
предположим, что они должны быть моложе 18 лет, тогда отслеживание этого может
вообще не работает, а если и работает, то мне нужно быть очень осторожным при обновлении родителей
всякий раз, когда ребенок стареет.
С точки зрения производительности, это часто сложно правильно оценить. По сути,
ты спрашиваешь, неужели расчет государства на лету дороже,
чем код, чтобы отслеживать его. Это, конечно, сильно зависит от того, как часто вы проверяете
штат. Вы можете проделать большую работу, чтобы отслеживать переменную состояния, которая
никогда не проверяли или проверяли очень редко.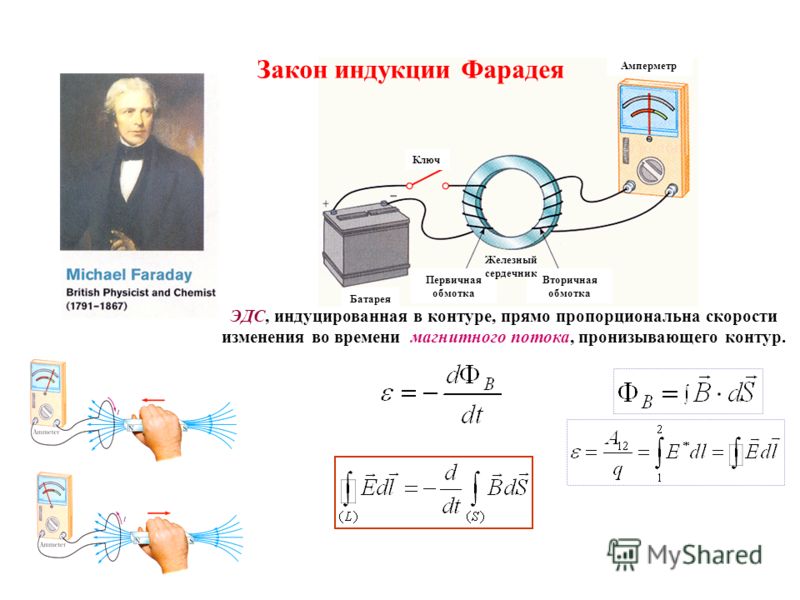 С другой стороны, если это
часто проверяются, но не обновляются, подход «расчет на лету»,
может без необходимости повторять одно и то же вычисление много раз.
С другой стороны, если это
часто проверяются, но не обновляются, подход «расчет на лету»,
может без необходимости повторять одно и то же вычисление много раз.
В качестве примечания есть ленивый пакет для Python, который позволяет вычислять атрибуты один раз, когда это необходимо, а затем сохраняет результат для последующего поиска. Конечно, если вы обновите что-нибудь расчет зависит от того, что вы должны убедиться, что сохраненный результат недействителен. я обнаружил это полезно в том случае, если атрибут никогда не нужно будет пересчитывать, но, возможно, вообще никогда не потребуется рассчитывать (и это дорого).
Более интересный пример
Для событий в памяти, таких как приведенный выше простой пример, часто выбирают довольно ясно. Код часто становится яснее, если вы вычисляете его на лету и только прибегать к отслеживанию, когда вычисление значения требует больших затрат, используются очень часто или особенно просты для отслеживания.
Однако выбор становится более интересным, когда вычисление значения
включает некоторое внешнее состояние, даже если его отслеживание выполняется на
внешнее состояние. Распространенным случаем является хранение состояния в базе данных. В Питоне,
вы вполне можете использовать ORM для доступа к внешнему состоянию.
Распространенным случаем является хранение состояния в базе данных. В Питоне,
вы вполне можете использовать ORM для доступа к внешнему состоянию.
Рассмотрим веб-сайт онлайн-игры, в которой участвуют четыре игрока. Давайте предположим, что игра пошаговая, и игроки не должны входить в систему для на протяжении всей продолжительности, но просто встаньте на их очередь, когда они в сети. Игра затем может находиться в нескольких состояниях: ожидание игроков, выполнение, завершение. Итак, в какой-то ORM вы могли бы описать игру как:
класс Игра(база данных.Модель):
player_one_id = Столбец (Целое число, Внешний ключ ('user.id'))
player_two_id = Столбец (Целое число, Внешний ключ ('user.id'))
player_three_id = Столбец (Целое число, Внешний ключ ('user.id'))
player_four_id = Столбец (Целое число, Внешний ключ ('user.id'))
winner_id = столбец (целое число, ForeignKey ('user.id'))
.... куча других столбцов, которые собственно и описывают состояние игры... .
.
Предположим, вы хотите отобразить список запущенных игр для пользователя. сделать что-то вроде этого:
класс Игра(база данных.Модель):
... как прежде ...
state_names = ['ожидание', 'выполняется', 'завершено']
состояние = столбец (перечисление (* state_names), nullable = False, по умолчанию = 'ожидание')
@статический метод
def running_games (пользователь):
игры = Game.query.filter(
Game.state == 'работает',
или же_(
Game.player_one_id == user.id,
Game.player_two_id == user.id,
Game.player_three_id == user.id,
Game.player_four_id == user.id,
)
).все()
вернуть игры
@статический метод
защита open_games (пользователь):
игры = Game.query.filter(
Game.state == 'ожидание',
а также_(
Game.player_one_id != user.id,
Game.player_two_id != user.id,
Game. player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
Используя этот способ, вы должны убедиться, что когда четвертый игрок присоединяется к в игре состояние устанавливается на «работает», а когда игра заканчивается, состояние устанавливается до «завершено» вместе с установленным «победителем».
Вместо этого можно использовать вычисление на лету, например:
class Game(database.Model):
... как прежде ...
# Нет столбца состояния
@статический метод
def running_games (пользователь):
игры = Game.query.filter(
Game.player_one_id != Нет,
Game.player_two_id != Нет,
Game.player_three_id != Нет,
Game.player_four_id != Нет,
или же_(
Game.player_one_id == user.id,
Game.player_two_id == user.id,
Game.player_three_id == user.id,
Game.player_four_id == user. id,
),
Game.winner_id == Нет
).все()
вернуть игры
@статический метод
защита open_games (пользователь):
игры = Game.query.filter(
или же_(
Game.player_one_id == Нет,
Game.player_two_id == Нет,
Game.player_three_id == Нет,
Game.player_four_id == Нет,
)
а также_(
Game.player_one_id != user.id,
Game.player_two_id != user.id,
Game.player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
id,
),
Game.winner_id == Нет
).все()
вернуть игры
@статический метод
защита open_games (пользователь):
игры = Game.query.filter(
или же_(
Game.player_one_id == Нет,
Game.player_two_id == Нет,
Game.player_three_id == Нет,
Game.player_four_id == Нет,
)
а также_(
Game.player_one_id != user.id,
Game.player_two_id != user.id,
Game.player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
Это можно немного упростить, если предположить, что игроки заполняют слоты по порядку.
таким образом, никогда не бывает, чтобы Game.player_four_id не было None , в то время как
один из других есть.
В этом конкретном случае я думаю, что отслеживание немного проще.
Но это сильно зависит от логики присоединения к игре, хода и
окончание игры. В частности, когда игра закончена, вы должны установить
В частности, когда игра закончена, вы должны установить колонка winner_id в любом случае, так что это не слишком обременительно для
дополнительно установить столбец состояния .
Однако во многих ситуациях вычисление на лету более эффективно.
соответствующий. Распространенный случай, когда правила изменения состояния могут измениться.
Например, в случае с игрой мы можем решить, что пока есть два
игроки, люди могут играть в игру, которая, следовательно, работает под управлением . Люди могут
присоединиться к запущенной игре , если она не заполнена, и может покинуть запущенную игру .
В этом случае функция вычисления на лету просто обновляет правила, когда игра под управлением . Тем не менее, keep-track-of-it не только должен обновлять свои правила для
когда изменять состояние (включая возврат игры с , работающей под управлением , на ждет , когда кто-то выходит из игры для двух игроков), но также должен пройти
базу данных и измените столбец состояния любых существующих игр.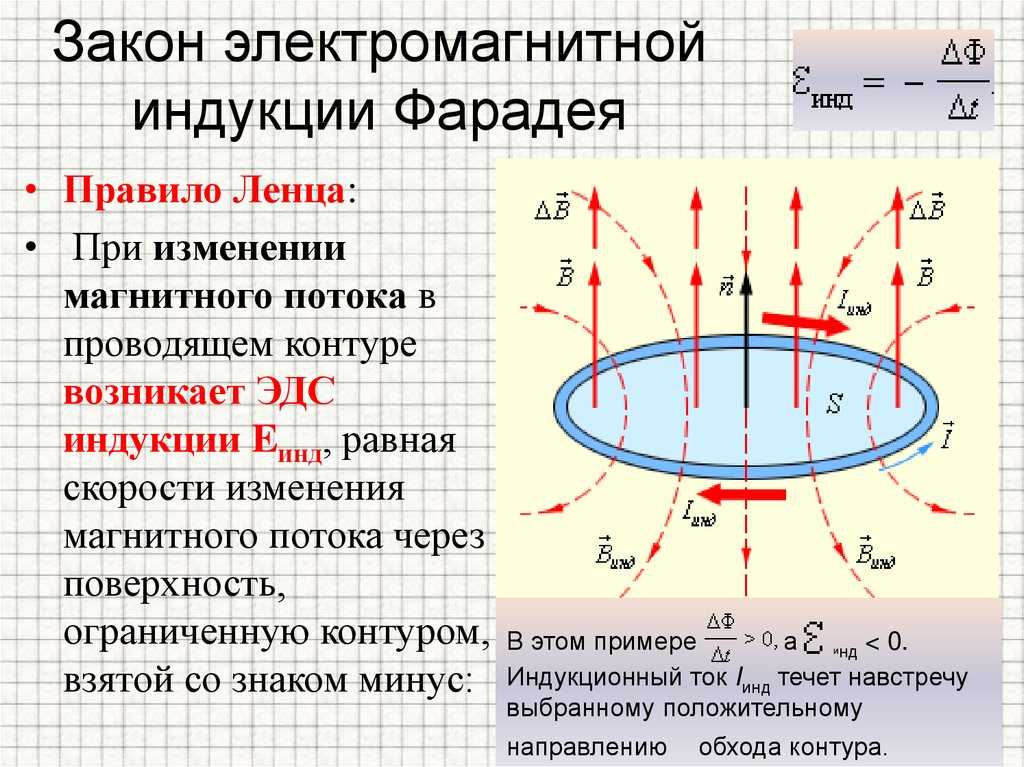 Для этого
код обновления базы данных по существу должен будет имитировать
Для этого
код обновления базы данных по существу должен будет имитировать расчет на лету код в любом случае.
Заключение
Часто приходится делать выбор между сохранением какого-либо состояния заранее, и вычислять его всякий раз, когда это требуется. Оба полезны и должны использоваться в зависимости от ситуации. Напоминание о том, что есть такой выбор, может помочь программист, чтобы явно сделать этот выбор и, возможно, даже записать причины для этого.
Тест ленивых столкновений, простая мера смертоносности столкновений в D&D: SlyFlourish.com
Впервые в Sly Flourish? Начните здесь !
от Mike, 2 марта 2020 г.
Lazy Encounter Benchmark: Столкновение может быть смертельным, если сумма CR монстров превышает одну четверть суммы уровней персонажей или половину суммы уровней персонажей, если персонажи выше 4-го уровня.
Этот ленивый тест столкновений абстрагирует математику, лежащую в основе рейтингов построения столкновений и испытаний монстров, чтобы помочь вам оценить, может ли ваш сюжетный бой закончиться смертельным исходом.
Этот тест ленивых встреч использует два шага, и все они могут быть выполнены без какого-либо онлайн-инструмента или ссылочной таблицы.
- В данном столкновении выберите монстров, которые имеют смысл в текущей истории, месте и ситуации.
- Определите, может ли столкновение быть смертельным. Столкновение может быть смертельным, если сумма рейтингов опасности монстров превышает одну четверть суммы уровней персонажей или половину суммы уровней персонажей, если персонажи выше 4-го уровня.
Второй шаг требует некоторой работы, чтобы понять, но как только вы увидите примеры, мы надеемся, что они вам понравятся. Как только это произойдет, вы можете держать это руководство в голове и использовать его в качестве меры, чтобы определить, приближаются ли столкновения к смертельным.
Простой пример: Орки
Допустим, у нас есть четыре персонажа 3-го уровня, и они наткнулись на банду из десяти орков. Такова ситуация. Это первый шаг. Мы еще не беспокоились о «балансировке» этой встречи, она исходила из того, что имеет смысл в данной ситуации.
Мы еще не беспокоились о «балансировке» этой встречи, она исходила из того, что имеет смысл в данной ситуации.
Шаг 2. Является ли это столкновение смертельным?
Начнем с суммирования всех рейтингов опасности орков (по 1/2 каждого). Это дает нам 5. Затем мы суммируем все уровни персонажей, что дает нам 12. Поскольку персонажи ниже 5-го уровня, мы делим сумму уровней персонажей на четыре, что дает нам 3.
Так как 3 (одна четверть суммированного уровни персонажа) меньше 5 (сумма CR монстров), это потенциально смертельное столкновение.
У нас есть несколько вариантов. Мы можем уменьшить количество орков с десяти до шести. Сумма CR монстров (3) теперь соответствует сумме уровней персонажей (также 3). Это, вероятно, тяжелый бой, но, возможно, не смертельный.
Вместо этого мы можем решить остаться с десятью орками, но разбить их на несколько групп. Четверо орков могут уйти из лагеря, чтобы поохотиться, или могут разделиться на две группы по два человека, чтобы охранять лагерь.
Сюжет по-прежнему управляет схваткой, но наш тест говорит нам, что в данной ситуации, например, сразиться с десятью орками одновременно, это может быть смертельно опасно.
Другой пример: Аболет
Допустим, мы запускаем приключение Стайс из Призраки Солтмарша . Злодей в Styes — особенно неприятный aboleth . Аболеты используют чуулов в качестве своих личных телохранителей, так что у нашего аболета будет несколько чуулов, слоняющихся поблизости. Аболет также медленно превращает жителей Стайеса в морских отродий , так что некоторые из них тоже околачиваются поблизости.
Когда персонажи попадают в святилище аболета, его, скорее всего, охраняют несколько чуулов, а вокруг прячутся морские отродья. Скажем, два чуула и четыре морских икринки.
Это шаг 1. Это текущая история. Мы еще не занимались математикой. Мы только что следили за историей о том, что персонажи вот-вот столкнутся с аболетом, а вокруг аболета ошиваются чуулы и морские отродья.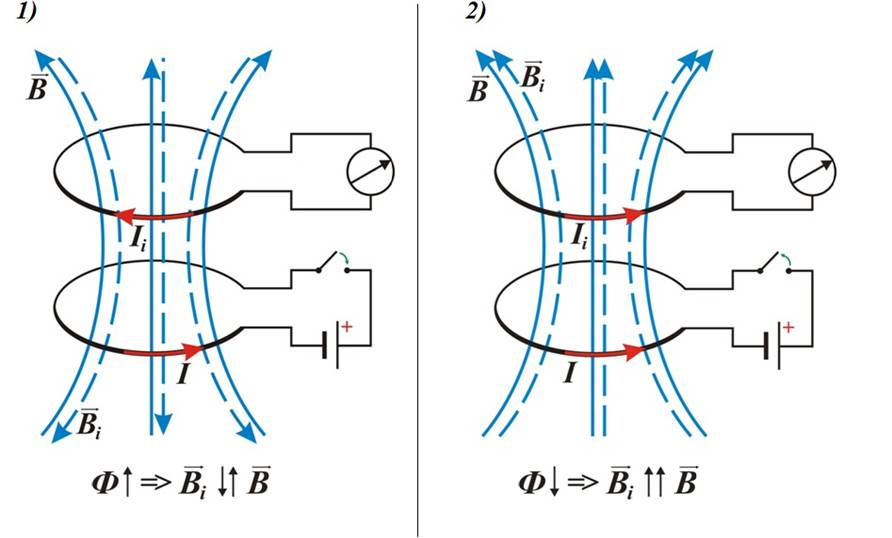
Теперь давайте определим, является ли эта встреча смертельной. Начнем со сложения всех CR наших монстров. Аболет — CR 10. Два чуула — CR 4 каждый. Четыре морских отродья имеют CR 1 каждый. Всего 22.
Допустим, у нас есть пять персонажей 7-го уровня. Мы суммируем все их уровни вместе до 35. Мы делим это число на два (округляя вниз), потому что они 7-го уровня. Если бы они были 4-го уровня, мы бы их четвертовали. Половина от 35, округленных в меньшую сторону, равна 17. Это меньше, чем 22, которые мы рассчитали для монстров. Таким образом, это потенциально смертельная встреча.
Но нам нравится наша история, поэтому мы оставим морских отродий. В основном они будут слугами аболета, не участвующими в боевых действиях, если только аболету не будет угрожать опасность. Тогда они будут защищать аболет как вторую линию обороны.
Зная, что это столкновение перерастает в смертельную опасность, мы можем быть готовы к этому , когда запустим нашу игру. Мы можем скорректировать очки жизни, снизив их для чуулов, если дела пойдут слишком плохо. Мы можем оставить морских отродий в качестве некомбатантов. Если мы получим больше персонажей, мы можем добавить больше монстров и пересчитать.
Мы можем скорректировать очки жизни, снизив их для чуулов, если дела пойдут слишком плохо. Мы можем оставить морских отродий в качестве некомбатантов. Если мы получим больше персонажей, мы можем добавить больше монстров и пересчитать.
Преимущества для этого эталона
Этот эталон построения встреч имеет множество преимуществ по сравнению с другими.
Во-первых, он хорошо масштабируется для любого количества символов. Поскольку вы суммируете все уровни персонажей, это работает одинаково, если у вас есть три персонажа или шесть. Нам не нужно переходить к другому столбцу в таблице; мы просто добавляем все это вместе.
Во-вторых, масштабируется вверх и вниз в зависимости от уровня сложности. Если у нас есть пять персонажей 12-го уровня (общее смертельное значение CR равно 30), мы можем использовать тот же показатель для гулей CR 1 (более 30 могут быть смертельными), CR 9.огненные гиганты (более трех могут быть смертельными) или любое сочетание существ с высоким и низким CR. Мы просто суммируем все CR всех монстров, которых мы рассматриваем, и смотрим, превышает ли он пороговое значение.
Мы просто суммируем все CR всех монстров, которых мы рассматриваем, и смотрим, превышает ли он пороговое значение.
В-третьих, мы можем быстро сделать это в уме. Пока вы помните , столкновение может быть смертельным, если общая сумма рейтингов опасности монстров превышает одну четверть суммы уровней персонажей или половину уровней персонажей, если персонажи выше 4-го уровня 9.0115 у вас есть то, что вам нужно. Немного быстрой математики даст вам ответ. Вы можете записать этот порог в свои заметки во время подготовки к игре, просто чтобы он был под рукой.
Допущения эталонного теста
Этот эталонный тест работает при использовании нескольких допущений.
Во-первых, предполагается, что в бою участвует не более одного легендарного монстра. Математика все равно сработает, но сражения с несколькими легендарными монстрами будут ужасными. Используйте только одного легендарного монстра в бою.
Во-вторых, предполагается, что вы используете более одного монстра в бою. Этот тест не особенно хорошо подходит для сравнения одного врага с персонажами. Вместо этого он хорошо работает для групп монстров с любым диапазоном CR.
Этот тест не особенно хорошо подходит для сравнения одного врага с персонажами. Вместо этого он хорошо работает для групп монстров с любым диапазоном CR.
В-третьих, вместо того, чтобы использовать его в качестве бюджета встречи, всегда начинается с шага 1 . Сначала выбирает монстров, подходящих для текущей ситуации , а затем использует тест, чтобы увидеть, будет ли эта ситуация смертельной.
Простой инструмент для несовершенной системы
Любой Мастер, игравший в эту игру достаточно долго, признает, что любая система измерения боевой сложности в D&D несовершенна . Многие переменные изменяют сложность встречи, включая определенные сборки персонажей, групповую синергию, эффекты окружающей среды, опыт игрока, магические предметы, определенные заклинания или способности и так далее. Этот простой тест не предназначен для того, чтобы быть идеальным индикатором. Это свободный, простой в реализации бенчмарк, который даст вам 9 баллов. 0098 грубая идея если столкновение может быть смертельным.
0098 грубая идея если столкновение может быть смертельным.
Простые рекомендации для гибкого D&D
Рекомендации и инструменты, подобные этому, помогают нам оставаться быстрыми и гибкими при запуске нашей игры. Они дают нам инструменты, необходимые для импровизации, когда наши игры развиваются в направлениях, которых мы не ожидали. Сохраните этот тест ленивых встреч в своем наборе инструментов DM на основе мозга и используйте его, чтобы помочь вам проводить самые веселые встречи, какие только можете.
Этот сайт использует партнерские ссылки на Amazon и DriveThruRPG. Спасибо за поддержку!
Ленивый способ решения дифференциальных уравнений
Яго Леаль | Ленивый способ решения дифференциальных уравнений Еще в колледже я посещал занятия по решению дифференциальных уравнений.
Моими любимыми, безусловно, были те, что были на физическом факультете, потому что
они научили нас всевозможным формулам, методам и рядам, чтобы на самом деле
вычислять решения вместо того, чтобы зацикливаться на регулярности и сходимости
выпуски 1 . Многие техники, особенно
те, что для уравнений с аналитическими коэффициентами, иногда ощущались немного
механический. На самом деле, это почти всегда происходит так: получите уравнение,
Тейлор все расширяет, собирает термины по индексам, а потом решает
рекуррентные соотношения, чтобы найти ряд Тейлора для решения.
Многие техники, особенно
те, что для уравнений с аналитическими коэффициентами, иногда ощущались немного
механический. На самом деле, это почти всегда происходит так: получите уравнение,
Тейлор все расширяет, собирает термины по индексам, а потом решает
рекуррентные соотношения, чтобы найти ряд Тейлора для решения.
Ну, несколько дней назад Жуан Пайшао прислал мне ссылку на статью Д. Павловича и М. Х. Эскардо 2 под названием «Исчисление в Коиндуктивная форма». В нем авторы показывают, что если мы посмотрим на Тейлора ряды как потоки действительных чисел, затем решая эти дифференциальные уравнения становятся так же просто, как записать их как !
Конечно, я очень загорелся этой идеей и должен был воплотить ее в жизнь.
код. В конце концов, это воплощение декларативного программирования!
статья действительно читабельна, и я призываю вас взглянуть на нее. Есть
много математических подробностей, которые я не буду касаться и даже целое
обсуждение того, как эти же методы применяются к преобразованиям Лапласа.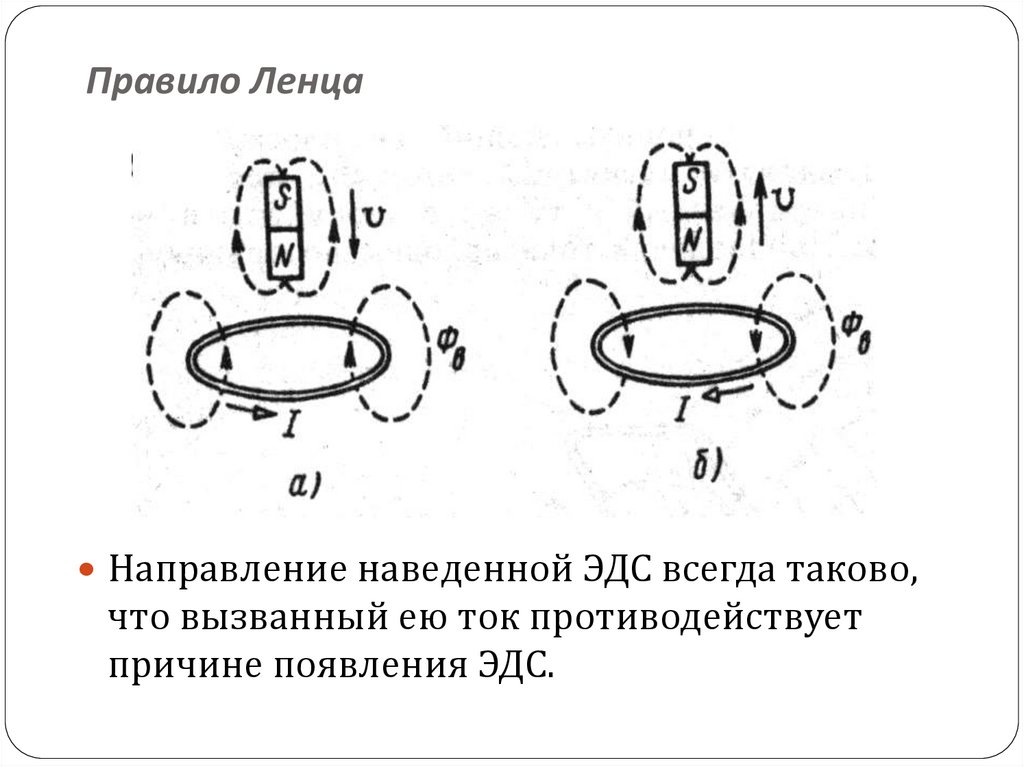 В качестве
закуска к тому, что мы собираемся делать, рассмотрим начальное значение
проблема 92) * у + 2 * разн у + 4
В качестве
закуска к тому, что мы собираемся делать, рассмотрим начальное значение
проблема 92) * у + 2 * разн у + 4
Исчисление с бесконечными списками
{-# LANGUAGE DeriveFunctor, DeriveFoldable, NoMonomorphismRestriction #-}
импортировать Data.Foldable (в список) Во-первых, отказ от ответственности: я не буду касаться вопросов конвергенции в этом почта. Для нас все будет красиво, идеально и аналитическо. Из конечно, поскольку от игнорирования этих вещей у меня мурашки бегут по спине, давайте просто согласимся, что каждый раз, когда я говорю «гладкий», я на самом деле имею в виду «аналитика в достаточно большом районе вокруг любых точек, в которых мы находимся». учитывая". Отлично, теперь пришло время вычислений. 9{а+х} f'(т) дт.
Игнорирование всего смысла, стоящего за интегралом, производной, оценкой и т. д. мы можем рассматривать это как рецепт: гладкие функции эквивалентны парам содержащий число и другую гладкую функцию. я не знаю о тебе но для меня это очень похоже на рекурсивный тип данных!
поток данных a = a :> поток a вывод (Функтор, Складной) инфикср 2 :>
Тип данных Stream a представляет собой список с бесконечным
количество элементов. Чтобы увидеть это, все, что вам нужно сделать, это развернуть
определение. В нашем контексте это означает, что гладкая функция может быть
представить бесконечным списком своих производных в точке: 9к/к!\}.
Чтобы увидеть это, все, что вам нужно сделать, это развернуть
определение. В нашем контексте это означает, что гладкая функция может быть
представить бесконечным списком своих производных в точке: 9к/к!\}.
На этом мы закончили. Что ж… На самом деле мы еще не закончили, еще много классных вещей, которые я хочу показать вам. Тем не менее определение выше уже достаточно, чтобы воспроизвести метод степенных рядов для решения ОДУ. Не верите мне? Давайте тогда решим некоторые знакомые уравнения.
Экспоненциальная функция является единственным решением y' = y, y(0) = 1, который становится следующей рекурсией в Haskell:
пр = 1 :> пр
Давайте проверим начальные коэффициенты ex на ghci на
подтверждают, что они соответствуют производной \exp в нуле: в точности являются производными от
\ехр:
ghci> возьми 10 (в список ex) [1,1,1,1,1,1,1,1,1,1]
Способ определения синуса и косинуса как решений системы ODE в Haskell становится взаимно рекурсивным определением:
синус = 0 :> косинус косинус = 1:> fmap инвертировать синус
Как и ожидалось, эти потоки следуют одному и тому же чередующемуся шаблону
0, 1, 0, -1, \ldots как Тейлор
коэффициенты.
ghci> возьми 10 (до списка синуса) [0,1,0,-1,0,1,0,-1,0,1] ghci> возьми 10 (в список косинусов) [1,0,-1,0,1,0,-1,0,1,0]
Несмотря на то, что мы знаем, как рассчитать коэффициенты Тейлора, они только средство для достижения цели. Основная причина, по которой хотят решить дифференциальную уравнений заключается в вычислении функций , а не рядов. Давайте тогда взломать аппроксимацию функции бедняка для этих разложений Тейлора. Для простоты я буду использовать фиксированное количество 100 коэффициентов. Этот работает для этой демонстрации, но в любой реальной программе лучше вызовите некоторый анализ, чтобы узнать правильное количество терминов для вашего желаемая оценка ошибки. Затем создадим функцию более высокого порядка, которая преобразует потоки действительных чисел в функции с действительными значениями.
-- | Превратите Stream f в функциональное приближение -- своего ряда Тейлора вокруг точки а. -- То есть eval a f ≈ f(a + x) eval :: Fractional a => a -> Stream a -> a -> a eval a f x = foldr1 (\ fa f' -> fa + (x - a) * f') (возьмем 100 Тейлор) куда taylor = zipWith (/) (toList f) факториалы факториалы = пусть жиры = 1 : zipWith (*) жиры [1..] в fmap от Интегральные жиры
С нашим оценщиком в руках пришло время протестировать наши предыдущие потоки в некоторые известные значения:
ghci> оценка 0 ex 0 1,0 ghci> оценка 0 ex 1 2,718281828459045 ghci> fmap (eval 0 sine) [0, pi/2, pi, 2*pi] [0,0,1,0,0,0,0,0] ghci> fmap (значение косинуса 0) [0, pi/2, pi, 2*pi] [1.0,0.0,-1.0,1.0]
Неплохо, да? Всего несколько строк кода, и у нас уже есть способность решать и аппроксимировать некоторые классические дифференциальные уравнения! Все благодаря лени Haskell и TFC. Наш решатель готов, но в коде по-прежнему отсутствует более понятный интерфейс для управления потоками и представляют собой дифференциальные уравнения. Давайте определим некоторые функции для смягчить это.
Из предыдущего обсуждения мы можем получить производную потока просто отбрасывая первый член.
-- | Представление производной в ряд Тейлора. diff :: Поток a -> Поток a разность (_ :> f') = f'
Можно встроить любую константу в виде потока с производной
нуль. Кроме того, давайте определим поток
Кроме того, давайте определим поток x , представляющий
тождественная функция 3 , чтобы наши уравнения выглядели
немного лучше.
-- | Ряд Тейлора для постоянного нуля. ноль :: Num a => Поток a ноль = 0 :> ноль -- | Ряд Тейлора для тождественной функции `f x = x`. x :: Num a => Поток a х = 0 :> 1 :> ноль
Наконец, наши коллеги-математики и физики, которые, возможно,
использовать этот код наверняка захочет произвести арифметические манипуляции на
сериал. Мы можем добиться этого с помощью традиционного Num , Дробные экземпляры и Плавающие экземпляры . По-прежнему
с этими сообщениями исчисления, эти экземпляры соответствуют известному
формулы для производных. Начнем с уроков арифметики.
instance Num a => Num (поток a), где -- Старая добрая линейность (+) (fa :> f') (ga :> g') = fa + ga :> f' + g' (-) (fa :> f') (ga :> g') = fa - ga :> f' - g' отрицание = fmap отрицание -- Правило Лейбница применяется к потокам (*) f@(fa :> f') g@(ga :> g') = fa * ga :> f' * g + f * g' fromInteger n = fromInteger n :> ноль abs = ошибка "Абсолютное значение не является гладкой функцией" signum = ошибка «Нет четко определенного знака для серии» instance Fractional a => Fractional (Stream a), где -- Правило деления из исчисления.2 fromRational n = fromRational n :> ноль
Для экземпляра Floating мы будем использовать цепное правило
и тот факт, что мы знаем производные для всех методов в классе.
Я рекомендую взглянуть на реализацию, которую мы сделали в предыдущем посте для двойных номеров.
Они поразительно похожи, что, конечно, не случайно. Главный
идея состоит в том, что применение аналитического g к
поток f, если он такой же, как
вычисление производных для g \circ
ф. Таким образом, все наши методы Floating будут выглядеть так:
это:
12154172]
Наконец, мы должны обсудить пару предостережений этого метода. Решение
ОДУ через ряд Тейлора может быть медленным… Вот почему на практике
это будет использоваться только для самых хороших уравнений. Есть
также вопрос конвергенции, который мы решили проигнорировать во время этого
почта. Не все функции
Не все функции Floating a => a -> a аналитически везде, а когда эта гипотеза не выполняется, метод
просто молча потерпит неудачу и вернет мусор, такой как бесконечность или NaN для коэффициентов. Тем не менее, этот «автомат»
решение в значительной степени эквивалентно тому, что можно было бы сделать, чтобы решить это
вид уравнения от руки, включая эти же вопросы. На самом деле, я бы
даже рискну сказать, что внутренности Haskell гораздо более оптимизированы, чем
можно было бы надеяться, что при решении вручную.
Это действительно автомат метод
Подводя итог, хочу отметить классный факт, что я только понял после написания всего поста: есть прямая связь между этим методом решения ОДУ и прямым автоматическим дифференциация! 92 = 0, из чего следует, что для любого аналитическая функция удовлетворяет
f(a + \varepsilon) = f(a) + f'(a)\varepsilon.
Это эквивалентно разложению Тейлора f вокруг
и усечение ряда после членов первого порядка. Однако ничего
действительно заставляет нас остановиться на достигнутом! Поскольку производная аналитического
функция также является аналитической, мы можем снова разложить ее по Тейлору, чтобы получить
вторая производная и так далее. Рекурсивно повторяя эту процедуру, мы
получить полное расширение Тейлора. Итак, если вместо термина \varepsilon, который обращается в нуль во втором порядке, мы
применить f к a
+ x, мы получаем все производные от f
в а.
Однако ничего
действительно заставляет нас остановиться на достигнутом! Поскольку производная аналитического
функция также является аналитической, мы можем снова разложить ее по Тейлору, чтобы получить
вторая производная и так далее. Рекурсивно повторяя эту процедуру, мы
получить полное расширение Тейлора. Итак, если вместо термина \varepsilon, который обращается в нуль во втором порядке, мы
применить f к a
+ x, мы получаем все производные от f
в а.
То же самое мы делали все вместе с Streams; единственный
разница в том, что мы пишем a :> 1 для представления a + x. Итак, аналогично с двойными числами, мы
можно определить процедуру для вычисления всех производных полиморфный f в точке a путем применения f к подходящему потоку.
-- | Поток со всеми производными от f в a. diffs f a = f (a :> 1)
Благодарности
Этот пост появился благодаря энтузиазму Жоао Пайшао и
Лукас Руфино. Жоао прислал мне газету, и мы втроем весело поболтали. о его значении, включая недоумение вместе о том, как
нам действительно нужно было немного кода, чтобы реализовать это.
о его значении, включая недоумение вместе о том, как
нам действительно нужно было немного кода, чтобы реализовать это.
Ссылки
Числовая.AD.Mode.Tower модуль объявления упаковка.
Павлович Д. и М. Х. Эскардо. «Исчисление в коиндуктивном Форма." В материалах года 13-го ежегодного симпозиума IEEE по Логика в информатике , 408. LICS '98. США: компьютер IEEE Society, 1998.
Руттен, Ян Дж. М. М. «Коиндуктивное исчисление потоков». Математические структуры в информатике 15 (2005): 93–147.
Надеюсь, мои коллеги-математики не отлучат меня от церкви за такой комментарий. Д:↩︎
«Исчисление в коиндуктивной форме», в Материалы 13-го ежегодного симпозиума IEEE по логике в компьютерах Science , LICS '98 (США: IEEE Computer Society, 1998), 408.↩︎
Это ужасное имя для использования на самом высоком уровне. определение.↩︎
Распространяйте информацию
© Iago Leal de Freitas, 2020-2022Сделано с маркой и пандок
Источник на Github
Исчисление II для чайников Шпаргалка
Обновлено: 31 августа 2021 г.
Из книги: Исчисление II для чайников
Исчисление II для чайников
Исследуйте книгу Купить на Amazon
По своей природе исчисление может быть интимным. Но вы можете немного избавиться от страха перед изучением исчисления, поняв его основные принципы, такие как производные и первообразные, интегрирование и решение сложных функций. Также откройте для себя несколько основных правил, применяемых в исчислении, таких как правило Крамера, правило постоянного множителя и некоторые другие, и вы будете на пути к успеху в курсе.Самые важные производные и первообразные, которые нужно знать
В таблице ниже показано, как дифференцировать и интегрировать 18 наиболее распространенных функций. Как видите, интегрирование меняет дифференцирование на противоположное, возвращая функцию в исходное состояние, вплоть до константы C .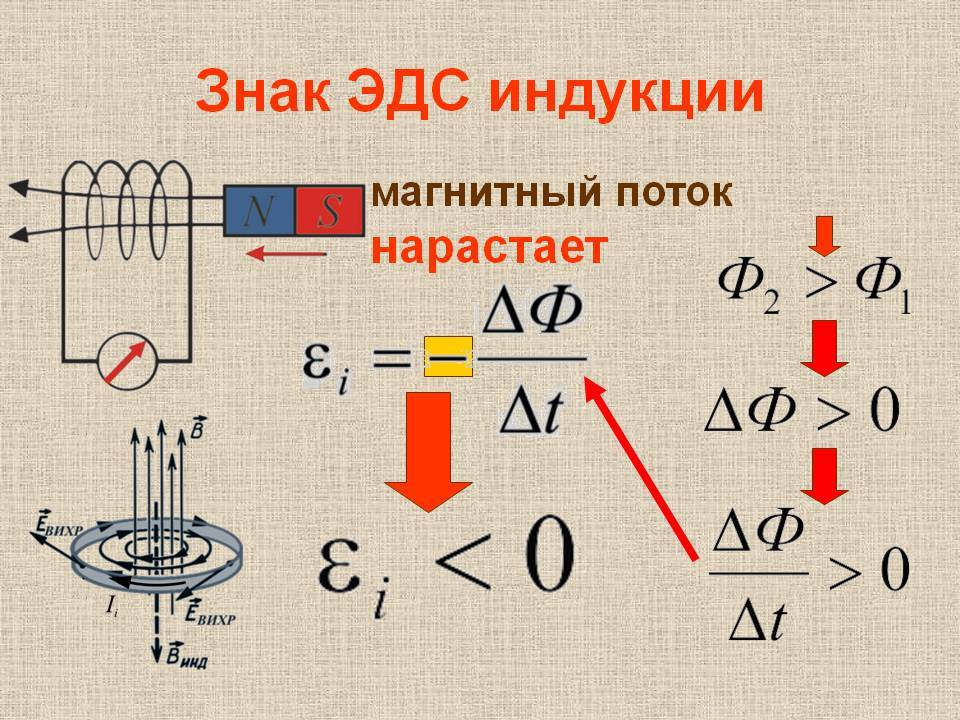
Формула суммы Римана для определенного интеграла
Формула суммы Римана дает точное определение определенного интеграла как предела бесконечного ряда. Формула суммы Римана выглядит следующим образом :
Ниже приведены шаги для аппроксимации интеграла с использованием шести прямоугольников:
Увеличьте количество прямоугольников ( n ), чтобы создать лучшее приближение:
Упростите эту формулу, вынеся w из каждого члена:
Используйте символ суммирования, чтобы сделать эту формулу еще более компактной:
Значение w равно ширине каждого прямоугольника:
Каждое h значение является высотой другого прямоугольника:
Итак, вот формула суммы Римана для , аппроксимирующая интегралом с использованием n прямоугольников:
Для лучшего приближения используйте предел
, чтобы количество прямоугольников приближалось к бесконечности :
Интегрирование по частям с помощью DI-агонального метода
DI-агональный метод в основном представляет собой интегрирование по частям с помощью диаграммы, которая помогает вам систематизировать информацию. Этот метод особенно полезен, когда вам нужно интегрировать по частям более одного раза, чтобы решить проблему. Используйте следующую таблицу для интегрирования по частям с помощью DI-агонального метода:
Этот метод особенно полезен, когда вам нужно интегрировать по частям более одного раза, чтобы решить проблему. Используйте следующую таблицу для интегрирования по частям с помощью DI-агонального метода:
Правило суммы, правило постоянной кратности и правило степени для интеграции
При выполнении интеграции необходимо знать три важных правила: правило суммы, правило постоянной кратности и правило степени.
Правило суммы для интеграции говорит вам, что можно интегрировать длинные выражения почленно. Вот он формально:
Правило множественной константы для интегрирования говорит вам, что можно переместить константу за пределы интеграла перед интегрированием. Здесь это выражено в символах:
Правило мощности для интеграции позволяет интегрировать любую реальную степень x (кроме –1). Вот формальная формулировка правила мощности:
., где n ≠ –1
Как решать интегралы с подстановкой переменных
В исчислении вы можете использовать подстановку переменных для вычисления сложного интеграла. Подстановка переменных позволяет интегрировать, когда правило суммы, постоянное множественное правило и правило мощности не работают.
Подстановка переменных позволяет интегрировать, когда правило суммы, постоянное множественное правило и правило мощности не работают.
Объявить переменную u , установите его равным алгебраическому выражению, которое появляется в интеграле, а затем подставьте u вместо этого выражения в интеграле.
Дифференцируйте и , чтобы найти
, а затем изолировать все переменные x по одну сторону от знака равенства.
Сделайте еще одну замену, чтобы заменить dx и все остальные вхождения x в интеграл на выражение, включающее дю .
Интегрируйте, используя u в качестве новой переменной интегрирования.
Выразите этот ответ в терминах x .
Как использовать интегрирование по частям
При выполнении вычислений формула интегрирования по частям дает возможность разложить произведение двух функций на его множители и интегрировать его в измененной форме. Чтобы использовать интегрирование по частям в Calculus, выполните следующие действия:
Чтобы использовать интегрирование по частям в Calculus, выполните следующие действия:
Разложите весь интеграл (включая dx ) на два множителя.
Пусть множитель без dx равен u , а множитель с dx равен dv .
Дифференцируйте u , чтобы найти du , и проинтегрируйте dv , чтобы найти v .
Используйте формулу:
Оцените правую часть этого уравнения, чтобы решить интеграл.
Как решать составные функции, внутренняя функция которых равна ax + b
Некоторые интегралы составных функций f ( g ( x )) легко и быстро вычислить в исчислении. К ним относятся составные функции, для которых вы знаете, как интегрировать внешнюю функцию f , а внутренняя функция g ( x ) имеет вид x + b , то есть она дифференцируется в константу .
Вот несколько примеров:
Решение составных функций, внутренняя функция которых равна ax
При построении математических задач некоторые интегралы составных функций f ( g ( x )) легко решить быстро. К ним относятся составные функции, для которых вы знаете, как интегрировать внешнюю функцию f , а внутренняя функция g ( x ) имеет вид x , то есть она дифференцируется до константы.
Вот несколько примеров:
Об этой статье
Эта статья взята из книги:
- Исчисление II для чайников,
Об авторе книги:
Марк Зегарелли, репетитор по математике и писатель с 25-летним кристально чистая и веселая информация для обычных читателей.



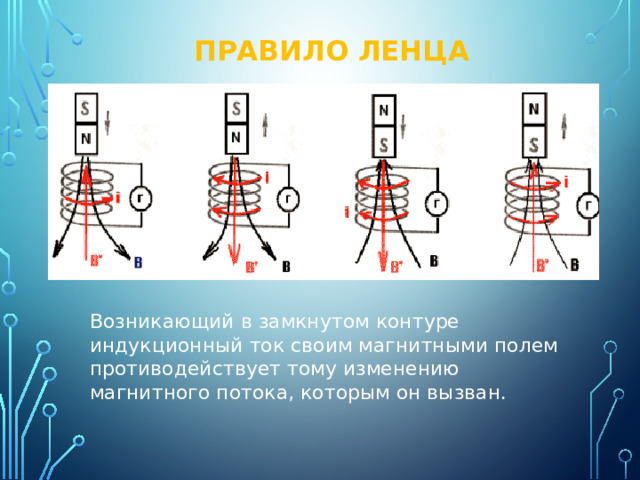 Профиль.LastModifiedById, '005') &&
)
Профиль.LastModifiedById, '005') &&
)
 90, 27.75, 23.68, 24.04, 28.36, 24.27, 24.65, 24.60, 24.69, 23.31
90, 27.75, 23.68, 24.04, 28.36, 24.27, 24.65, 24.60, 24.69, 23.31 boys.append (мальчик)
вернуть мальчика
boys.append (мальчик)
вернуть мальчика
 .
.
 player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
 id,
),
Game.winner_id == Нет
).все()
вернуть игры
@статический метод
защита open_games (пользователь):
игры = Game.query.filter(
или же_(
Game.player_one_id == Нет,
Game.player_two_id == Нет,
Game.player_three_id == Нет,
Game.player_four_id == Нет,
)
а также_(
Game.player_one_id != user.id,
Game.player_two_id != user.id,
Game.player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
id,
),
Game.winner_id == Нет
).все()
вернуть игры
@статический метод
защита open_games (пользователь):
игры = Game.query.filter(
или же_(
Game.player_one_id == Нет,
Game.player_two_id == Нет,
Game.player_three_id == Нет,
Game.player_four_id == Нет,
)
а также_(
Game.player_one_id != user.id,
Game.player_two_id != user.id,
Game.player_three_id != user.id,
Game.player_four_id != user.id,
)
).все()
вернуть игры
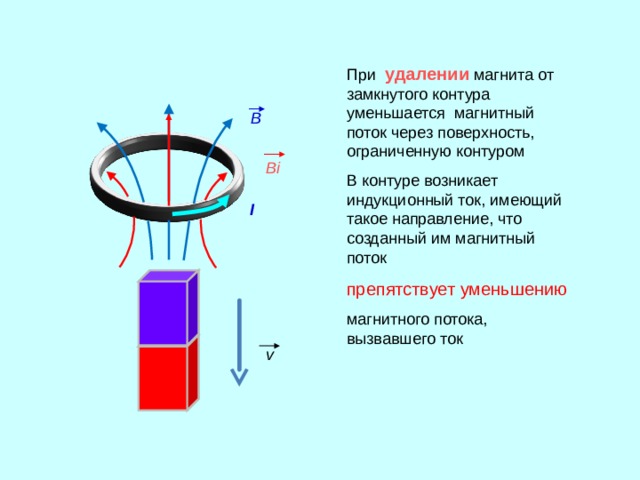 .]
в fmap от Интегральные жиры
.]
в fmap от Интегральные жиры 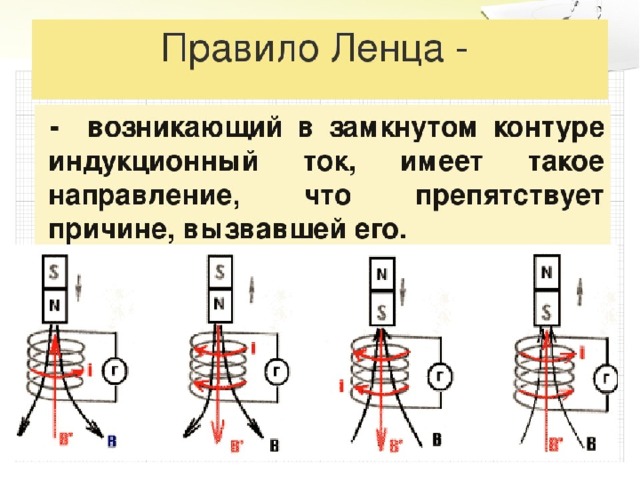 2
fromRational n = fromRational n :> ноль
2
fromRational n = fromRational n :> ноль