Открытая Физика. Магнитное взаимодействие токов

Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. В Европе он появился приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.

Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.

По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.

Источниками магнитного поля являются движущиеся электрические заряды (токи).

Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).

Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.

Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие

только на движущиеся заряды (токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E→ электрического поля. Такой характеристикой является вектор магнитной индукции B→, который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.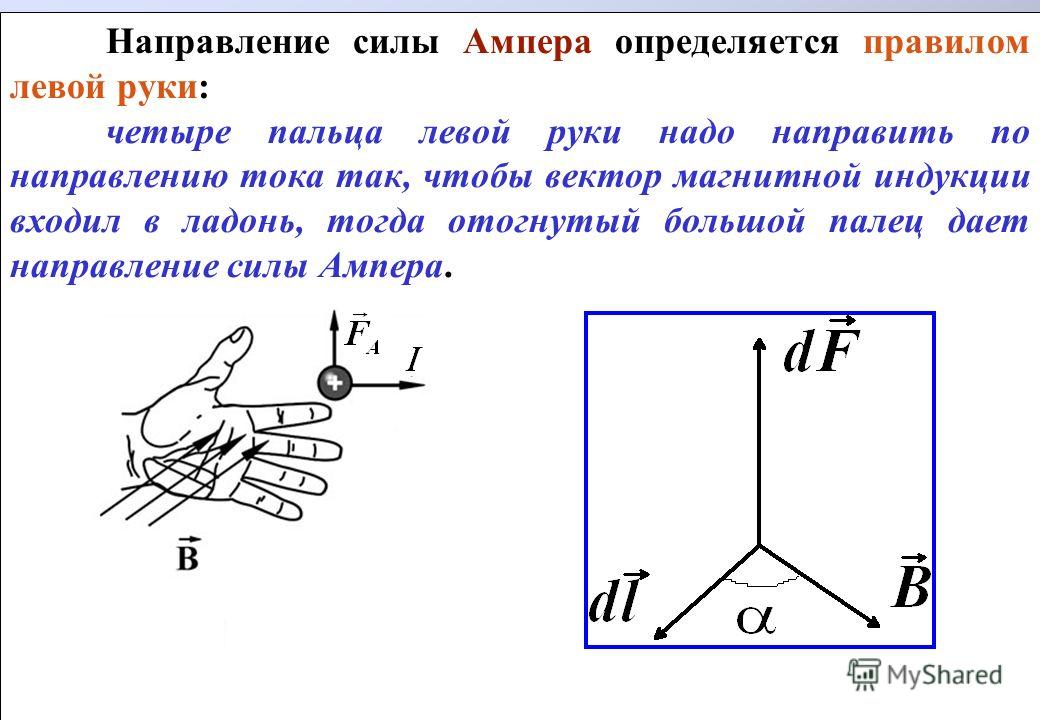

За положительное направление вектора B→ принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора B→. Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор B→ направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.

Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции

Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током.

Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора B→, но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δ

l, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции: F ~ IΔl sin α.

Эта сила называется силой Ампера. Она достигает максимального по модулю значения

F_max, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора B→ определяется следующим образом:

Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl: B=FmaxIΔl.

В общем случае сила Ампера выражается соотношением: F = IBΔl sin α.

Это соотношение принято называть законом Ампера.

В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл). 1 Тл=1 HАċм.

Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5ċ10^–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.

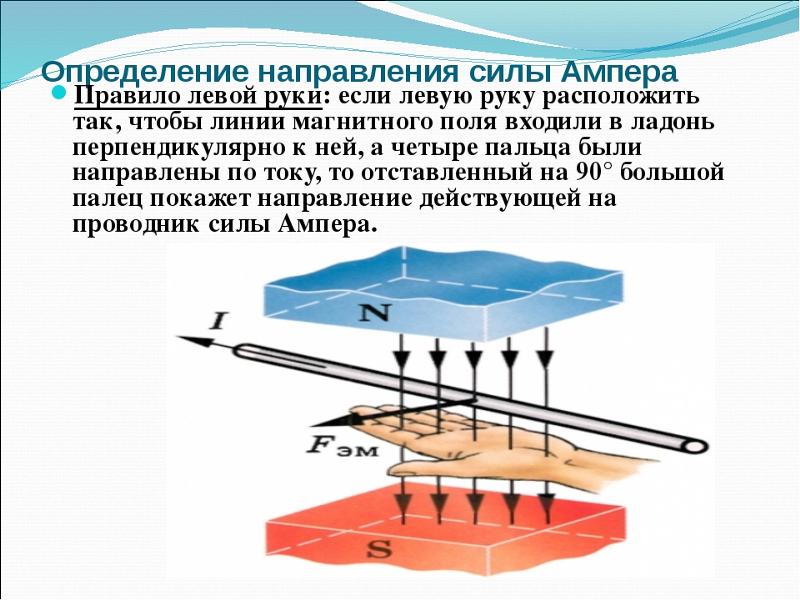
Сила Ампера направлена перпендикулярно вектору магнитной индукции B→ и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции B→ входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

Правило левой руки и правило буравчика

Если угол α между направлениями вектора B→ и тока в проводнике отличен от 90°, то для определения направления силы Ампера F→ более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор B→ и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора B→. Поступательное перемещение буравчика будет показывать направление силы Ампера F→ (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.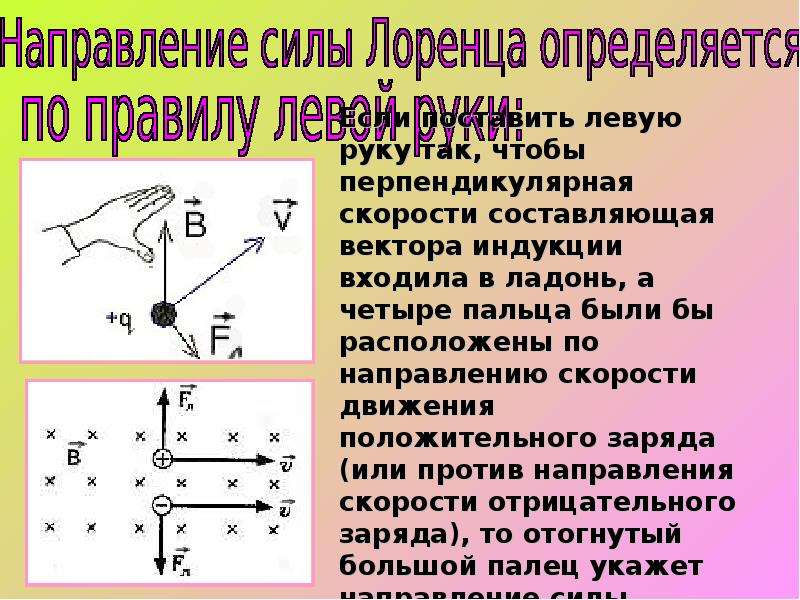

Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.

Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.

Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока

I₁ и I₂ в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними: F=kI1I2ΔlR.

В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде: k = μ₀ / 2π,

где μ₀ – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно μ₀ = 4π·10^–7 H/A² ≈ 1,26·10^–6 H/A²

.

Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид: F=μ02πI1I2ΔlR.

Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы B→1 и B→2 магнитной индукции параллельных токов I₁ и I₂ лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить

sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением B=μ02πIR.

Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора B→ магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора B→, если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).

Магнитное поле прямолинейного проводника с током Магнитное взаимодействие параллельных и антипараллельных токов

Рис. 1.16.4 поясняет закон взаимодействия параллельных токов.

Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:

Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10^–7 Н на каждый метр длины.

Взаимодействие параллельных токов Рамка с током в магнитном поле

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.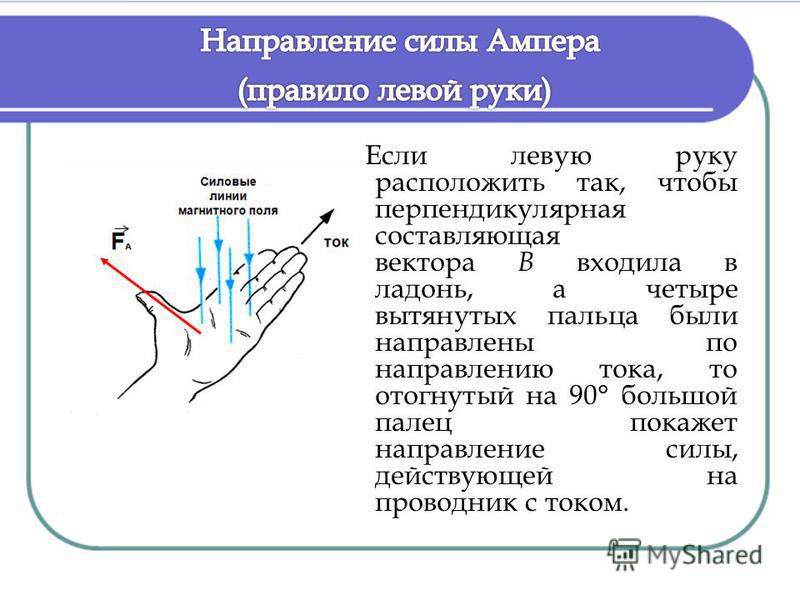
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376171 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА
уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Владимир Александрович Кузьмин

«

Тренинг у Кузьмина В. А. проходил в экстремальных условиях. Мой модем совершенно не держал соединение. За время часового тренинга связь прерывалась практически постоянно. Ясно, что в таких условиях чрезвычайно непросто чему-то учить. Однако Владимир Александрович проявил удивительную выдержку и терпение. Неоднократно он перезванивал мне на сотовый телефон, чтобы дать пояснения или комментарии. Ценой больших усилий нам удалось рассмотреть три программы: ConceptDraw MINDMAP Professional Ru, GeoGebra и Ultra Flash Video FLV Converter. Владимир Александрович открыл мне курс на платформе dist-tutor.info и научил подключать и настраивать Виртуальный кабинет, порекомендовав изучать возможности этого ресурса, чтобы постепенно уходить от использования Skype. В итоге, занятие мне очень понравилось! Спокойное объяснение материала, дружелюбный настрой, подбадривание дистанционного ученика даже в самых непростых ситуациях — вот далеко не полный перечень качеств Владимира Александровича как дистанционного педагога. Мне следует учиться у такого замечательного репетитора!

«

Вячеслав Юрьевич Матыкин

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки. Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

Видео с вопросами: Определение направления магнитной силы на проводе с током

На схеме показан участок провода, расположенный под углом 90° к магнитному полю напряженностью 0,1 Тл. По проводу течет ток силой 2 А. Как направлена ​​сила, действующая на провод из-за магнитного поля?

Стенограмма видео

На схеме показан участок провода, расположенный на 90 градусов в магнитном поле 0,1 тесла. По проводу течет ток в два ампера. Как направлена ​​сила, действующая на провод со стороны магнитного поля?

На нашей диаграмме мы видим этот отрезок провода с током в нем, направленный к верхней части экрана. Наш провод с током существует в магнитном поле B, направленном вправо. Наш вопрос просит нас определить направление силы, действующей на провод из-за магнитного поля. Мы знаем, что ток в этом проводе возникает из-за движения микроскопически малых объектов, обладающих электрическим зарядом. Когда каждый отдельный заряженный объект движется через магнитное поле В, на него действует магнитная сила.

Направление этой силы определяется так называемым правилом правой руки. Скажем, у нас есть объект с зарядом 𝑞, и представим далее, что этот объект движется вправо со скоростью 𝑣. Если наш движущийся заряд проходит через однородное магнитное поле, назовем его В, то мы можем правой рукой определить направление магнитной силы, действующей на заряд 𝑞. Для этого указываем пальцами правой руки в направлении 𝑞 раз 𝑣. Если предположить, что заряд 𝑞 имеет положительное значение, то 𝑞, умноженное на 𝑣, указывает вправо. Далее сгибаем пальцы правой руки в направлении магнитного поля В. Мы видим, что здесь это направление в экран. Сделав все это, большой палец на правой руке теперь указывает в направлении действия магнитной силы на заряд 𝑞.

Правило правой руки, как мы описали его здесь, применимо к отдельным зарядам, но мы все же можем применить это правило к нашему проводу с током, потому что ток состоит из отдельных зарядов. Если мы найдем направление магнитной силы на один из этих зарядов, оно будет таким же, как направление этой силы на любые другие заряды того же знака. Нам показывают, что ток в этом проводе течет снизу вверх нашего экрана. Условно ток определяется как поток положительного заряда. Следовательно, для нашего провода с током 𝑞 умножить на 𝑣 указывает на верхнюю часть экрана.

Мы также видим, что магнитное поле B направлено вправо. Что мы сделаем, так это расположим нашу правую руку так, чтобы наши пальцы могли указывать вверх в направлении 𝑞 раз 𝑣, но также могли сгибаться в этом направлении, чтобы они могли указывать в направлении магнитного поля B. Для нашего правой рукой, чтобы сделать это, нужно немного покрутить. Однако когда мы можем это сделать, наша рука устроена так, что большой палец указывает на экран. Мы знаем, что это направление магнитной силы, действующей на положительные заряды в токе. И это говорит нам ответ на наш вопрос. Направление силы, действующей на провод из-за магнитного поля, направлено внутрь экрана.

Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.

Сила, действующая на движущийся заряд в магнитном поле – Колледж физики

Резюме

• Опишите влияние магнитных полей на движущиеся заряды.
• Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
• Рассчитайте магнитную силу, действующую на движущийся заряд.

Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.

Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитная сила  [латекс]\boldsymbol{F}[/латекс] на заряд [латекс]\boldsymbol{q}[/латекс], движущийся со скоростью [латекс]\boldsymbol{v}[/латекс] в магнитном поле напряженности [латекс]\boldsymbol{B}[/латекс] равно

[латекс]\boldsymbol{F = qvB \;\textbf{sin} \theta},[/latex]

, где [latex]\boldsymbol{\theta}[/latex] — угол между направлениями [latex]\textbf{v}[/latex] и [latex]\textbf{B}[/latex]. Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля [latex]\boldsymbol{B}[/latex] — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля [латекс]\boldsymbol{B}[/латекс] называется тесла (T) в честь эксцентричного, но гениального изобретателя Николы Теслы (1856–1943).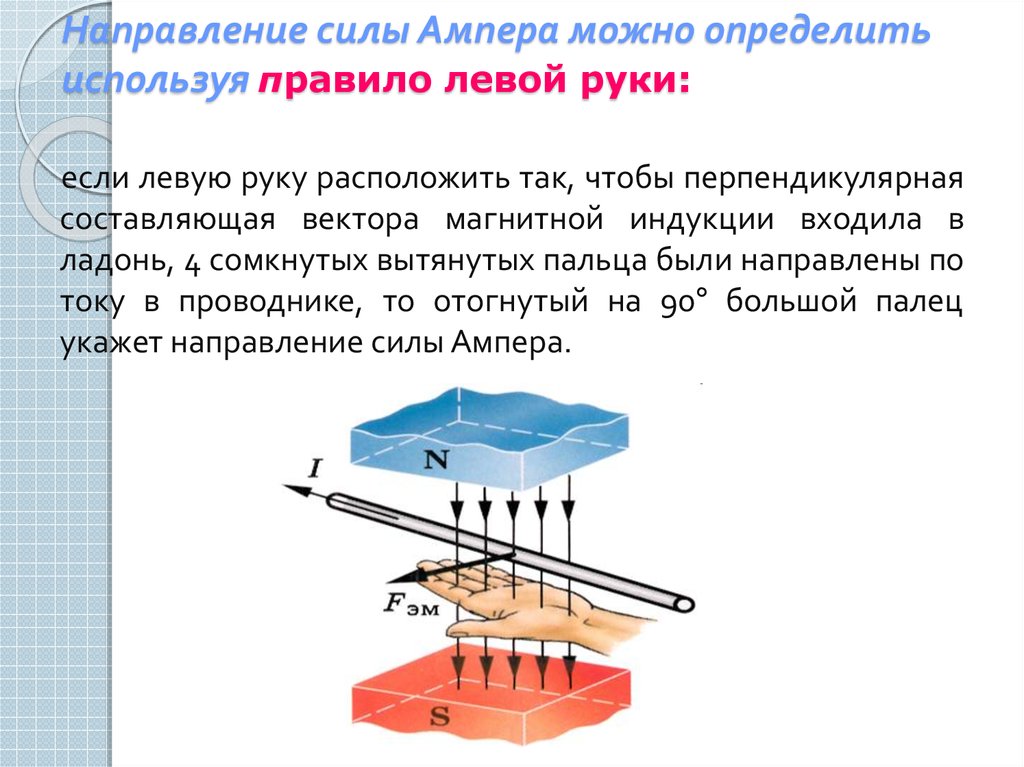 Чтобы определить, как тесла относится к другим единицам СИ, мы решаем [латекс]\boldsymbol{F = qvB \;\textbf{sin} \theta}[/latex] для [латекс]\boldsymbol{B}[/латекс].

[латекс]\boldsymbol{B =}[/латекс] [латекс]\boldsymbol{\frac{F}{qv \;\textbf{sin} \;\theta}}[/latex]

Поскольку [латекс]\boldsymbol{\textbf{sin} \;\theta}[/latex] не имеет единиц измерения, тесла равен

.

[латекс]\boldsymbol{1 \;\textbf{T} =}[/latex] [латекс]\boldsymbol{\frac{1 \;\textbf{N}}{\textbf{C} \cdot \;\ textbf{м/с}}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol{\frac{1 \;\textbf{N}}{\textbf{A} \cdot \;\textbf{м}}}[/латекс] 9{-5} \;\textbf{T}}[/latex], или 0,5 г.

Направление магнитной силы [латекс]\textbf{F}[/латекс] перпендикулярно плоскости, образованной [латекс]\текстбф{в}[/латекс] и [латекс]\текстбф{В}[ /латекс], как определено правилом правой руки 1 (или RHR-1), которое показано на рисунке 1. RHR-1 утверждает, что для определения направления магнитной силы на положительно движущемся заряде вы большой палец правой руки в направлении [латекс]\textbf{v}[/латекс], пальцы в направлении [латекс]\текстбф{В}[/латекс], а перпендикуляр к ладони указывает на направление [латекс]\textbf{F}[/латекс]. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена ​​в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена ​​прямо противоположно силе на положительном заряде.

Рисунок 1. Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B , и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q , v , B и синусу угла между v и B .

Соединения: заряды и магниты

На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.

Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне

За исключением компасов, вы редко видите или лично испытываете на себе силы из-за слабого магнитного поля Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)

Рис. 2. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, подвергается действию силы, которая направлена ​​прямо вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.

Стратегия

Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение [латекс]\boldsymbol{F = qvB \;\textbf{sin} \;\theta}[/latex] для нахождения силы.

9{-11} \;\textbf{N}} \end{array}.[/latex]

Обсуждение

Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное влияние, особенно на субмикроскопические частицы. Некоторые из них рассматриваются в главе 22.5 «Сила движущегося заряда в магнитном поле: примеры и приложения».

• Магнитные поля воздействуют на движущийся заряд силой q , величина которой равна

  [латекс]\boldsymbol{F = qvB \;\textbf{sin} \;\theta},[/latex]

  , где [latex]\boldsymbol{\theta}[/latex] — угол между направлениями [latex]\textbf{v}[/latex] и [latex]\textbf{B}[/latex].

• Единицей СИ для напряженности магнитного поля [латекс]\textbf{B}[/латекс] является тесла (Тл), которая связана с другими единицами соотношения

  [латекс]\boldsymbol{1 \;\textbf{T} =}[/latex] [латекс]\boldsymbol{\frac{1 \;\textbf{N}}{\textbf{C} \cdot \;\ textbf{м/с}}}[/латекс] [латекс]\boldsymbol{=}[/латекс] [латекс]\boldsymbol{\frac{1 \;\textbf{N}}{\textbf{A} \cdot \;\textbf{м}}}[/латекс]

• Направление силы, действующей на движущийся заряд, задается правилом правой руки 1 (RHR-1): Направьте большой палец правой руки в направлении [латекс]\boldsymbol{v}[/latex], пальцы в направлении [латекс]\boldsymbol{B}[/латекс], а перпендикуляр к ладони указывает в направлении [латекс]\boldsymbol{F}[/латекс].
• Сила перпендикулярна плоскости, образованной [латексом]\textbf{v}[/латексом] и [латексом]\текстбф{В}[/латексом]. Поскольку сила равна нулю, если [латекс]\textbf{v}[/латекс] параллелен [латексу]\текстбф{В}[/латексу], заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.

Задачи и упражнения

1: Каково направление магнитной силы, действующей на положительный заряд, который движется так, как показано в каждом из шести случаев, показанных на рисунке 3?

Рисунок 3.

2: Повторите главу 22.4 Задачи и упражнения 1 для отрицательного заряда.

3: Каково направление скорости отрицательного заряда, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 4, если предположить, что он движется перпендикулярно [латексу]\boldsymbol{B}[/latex] ?

Рисунок 4.

4: Повторите главу 22.4 Задачи и упражнения 3 для положительного заряда.

5: Каково направление магнитного поля, которое создает магнитную силу на положительном заряде, как показано в каждом из трех случаев на рисунке ниже, при условии, что [latex]\textbf{B}[/latex] перпендикулярно [латексу]\textbf{v}[/латексу]?

Рисунок 5.