Вычитание векторов. Правило вычитания векторов. Геометрия вычитание векторов.
- Альфашкола
- Статьи
- Правила вычитания векторов
В этой статье мы узнаем как вычесть вектора. Вектор — это величина, имеющая величину размер и направление. Вычитание вектора равносильно добавлению вектора с отрицательным знаком. Разность векторов \(\overline{a}\) и \(\overline{-b}\) равна сумме \(\overline{a}\) и \(\overline{-b}\):
Перемещение векторов
Наша задача — найти способ четко и последовательно представлять векторы. Графически это просто: поскольку мы можем перемещать вектор в любом месте, давайте всегда будем располагать «хвост» вектора в начале координатной плоскости. Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Теперь, когда хвост вектора помещен в конец другого вектора (помните, мы можем перемещать вектор в любом месте, пока мы сохраняем его направление и длину). Проводим от начала вектора \(\overline{b}\) (вычитаемого вектора) вектор \(\overline{c}\) к началу вектора \(\overline{a}\) (уменьшаемого вектора) получаем разость вектор \(\overline{c}\) :
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Сабина Витальевна Рабцевич
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-11 классов, информатике 5-11 классы, а также Scratch.
Камо Аркадьевич Филипосян
Репетитор по математике
Стаж (лет)
Образование:
Самаркандский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 8-11 классов и по физике для 7-9 классов.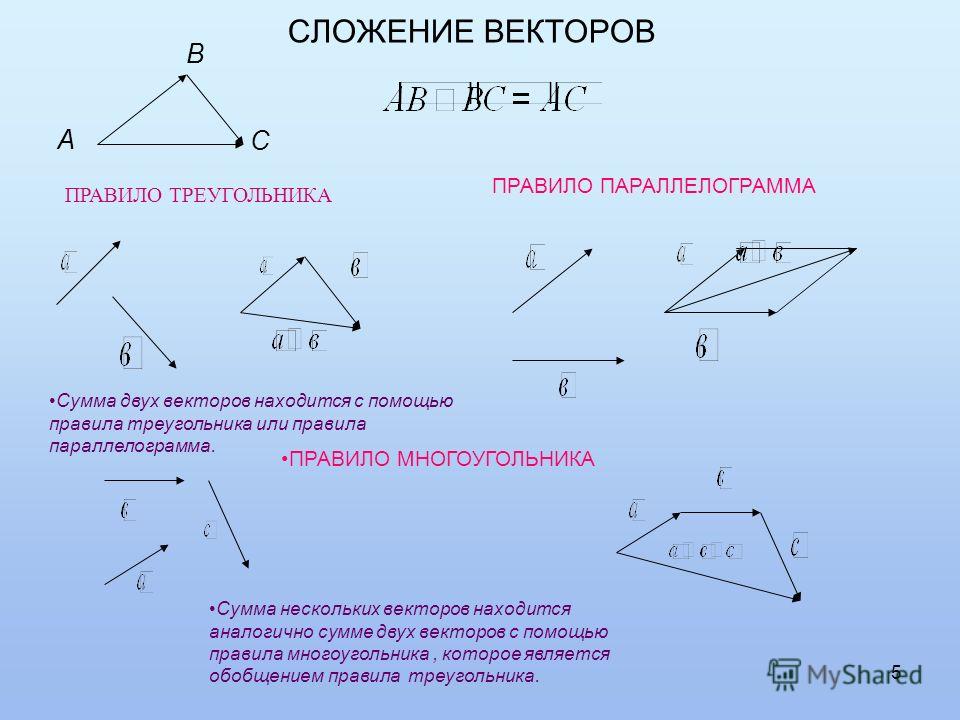 Я твёрдо убежден, что образовательный процесс должен быть пронизан живой, позитивной энергией учителя, находящий ключ к сердцу ученику с помощью индивидуальных подходов к урокам, подаче нового материала. Мое кредо – «Математика – ключ к новым возможностям, добыть его мало, надо найти замок открываемый этим ключом»! Могу помочь с высшей математикой (Арифметика и теория чисел, математическая логика, математический анализ, линейная алгебра, аналитическая геометрия, обыкновенные дифференциальные уравнения.)
Я твёрдо убежден, что образовательный процесс должен быть пронизан живой, позитивной энергией учителя, находящий ключ к сердцу ученику с помощью индивидуальных подходов к урокам, подаче нового материала. Мое кредо – «Математика – ключ к новым возможностям, добыть его мало, надо найти замок открываемый этим ключом»! Могу помочь с высшей математикой (Арифметика и теория чисел, математическая логика, математический анализ, линейная алгебра, аналитическая геометрия, обыкновенные дифференциальные уравнения.)
Анжела Валентиновна Самсонова
Репетитор по математике
Стаж (лет)
Образование:
Костанайской педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Информатика: 5-11 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ОГЭ, ЕГЭ.
Похожие статьи
- Пропорция в математике
- Корень
- НИУ ВШЭ: Маркетинг и рыночная аналитика
- ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 1)
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 4)
- Задачи на исследование функций
- Осенняя фотосессия: идеи для креативных снимков
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Коллинеарность векторов: условия, правила и примеры
Ученики 9-го класса, помимо понятия вектора, должны знать, что такое коллинеарные векторы, а также условия коллинеарности векторов.
Вектор — это направленный отрезок. Вектор обозначается двумя заглавными латинскими буквами со стрелочкой над ними или одной маленькой со стрелочкой над ней .
Нулевой вектор — вектор, начало которого совпадает с концом. То есть в геометрической интерпретации это просто точка.
Теперь, когда мы вспомнили базовые понятия, можно переходить к определению коллинеарных векторов.
Что значит «коллинеарные векторы»
Коллинеарные векторы — это ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Причем считается, что нулевой вектор коллинеарен каждому другому вектору. То есть, попросту говоря, коллинеарность — это параллельность векторов. Если векторы и коллинеарны, то это записывают так: .
Коллинеарные векторы можно разделить по направлению на две группы: сонаправленные и противоположно направленные.
Векторы и лежат на параллельных прямых, а также имеют одно направление, поэтому и — сонаправленные векторы: .
Векторы и лежат на параллельных прямых, но имеют разное направление, поэтому и — противоположно направленные векторы: .
Задача № 1
Благодаря клетчатому фону мы можем определить, что все векторы на рисунке коллинеарны, то есть лежат на параллельных прямых. Осталось посмотреть на направление векторов и сделать выводы:
,
,
,
.
Но не забываем о нулевом векторе — он будет сонаправлен с каждым вектором.
Но согласитесь, что визуальная оценка параллельности не самая точная вещь на планете, а математика славится своей точностью и четкостью. Поэтому возникает вопрос: как проверить коллинеарность векторов алгебраическими способами? Для этого существуют признаки коллинеарности векторов. Рассмотрим их.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Запишитесь и участвуйте в розыгрыше 8 уроков
Признаки коллинеарности векторов
Первый критерий коллинеарности векторов: векторы и коллинеарны, если .
Второй критерий коллинеарности векторов: два вектора коллинеарны, если отношения их координат равны.
Но здесь важно понимать, что это условие параллельности векторов работает только для всех ненулевых координат. Значит, если хотя бы один компонент вектора равен нулю, то правило неприменимо.
Третий критерий коллинеарности векторов, который могут применять одиннадцатиклассники, взрослые и все, кто увлечен математикой: два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Применим условия коллинеарности векторов при решении задач.
Задача № 2
Докажите, что векторы и коллинеарны.
У нас с вами есть два способа определить или доказать коллинеарность векторов, однако в координатах каждого вектора есть нули — значит, подходит только первый критерий, который еще называется свойством коллинеарных векторов: если , то .
Для начала определим . А теперь проверим, выполняется ли условие , значит, . Что и требовалось доказать.
Задача № 3
Какие из векторов , и коллинеарны?
А здесь очень удобно использовать второй критерий коллинеарности векторов, который звучит так: отношения соответствующих координат коллинеарных векторов равны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — верно, значит, .
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Проверим коллинеарность векторов и : должно выполняться условие , т. е. — неверно, значит, и неколлинеарны.
Задача № 4
Определите, при каком значении k векторы и коллинеарны.
Так как по условию векторы должны быть коллинеарны, а в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности, а именно — должно выполняться условие , то есть .
По свойству пропорции выразим k:
;
k = 27.
Значит, при k = 27 векторы и коллинеарны.
Если же вам нужно проверить коллинеарность векторов в пространстве, а не на плоскости, то все эти условия продолжают работать, но помните, что к проверке присоединяется третья координата векторов. Рассмотрим пару примеров.
Задача № 5
Докажите, что векторы и коллинеарны.
Поступим аналогично решению в задаче 2 — применим первый критерий, который еще называется свойством коллинеарных векторов, т. е. если , то .
Для начала определим . А теперь проверим, выполняется ли условие . Что и требовалось доказать.
Задача № 6
Аналогично задаче 4: так как по условию векторы должны быть коллинеарны и в их координатах не содержится нуля, то можно использовать второй критерий коллинеарности. А именно — должно выполняться условие , то есть .
Рассмотрим первую и вторую дроби, по свойству пропорции выразим k:
;
k = 27.
Рассмотрим первую и третью дроби, по свойству пропорции выразим f:
;
f = 2.
Значит, при k = 27 и f = 2 векторы и коллинеарны.
Векторы — удивительная тема, с помощью которой можно решить многие физические задачи, легко и просто доказать самые сложные геометрические теоремы. Сегодня вы узнали, какие векторы называются коллинеарными, но это лишь один аспект большой главы о векторах. Чтобы узнать остальные действия с векторами, познакомиться с интересными задачами и способами решений, приходите на онлайн-курсы математики для детей в Skysmart.
Вектор
В математике и физике, вектор является величиной, которая характеризуется своим направлением, а также численным значением. Когда же используются векторы и зачем они нужны? Векторы используют для записи тех величин, которые обыкновенными числами записать невозможно. Допустим, нам необходимо описать положение предмета относительно некоторой точки. Разумеется, мы можем вычислить расстояние между точкой и предметов и записать его обыкновенным числом, но это не будет полной характеристикой. А вот если мы запишем данную величину вектором, то помимо расстояния, мы будем еще знать направление, в котором данный предмет находится относительно заданной точки.
А вот если мы запишем данную величину вектором, то помимо расстояния, мы будем еще знать направление, в котором данный предмет находится относительно заданной точки.
Графически все векторы изображаются, как направленные отрезки определенной заданной длины.
Что же такое свободные векторы? По-другому свободные векторы можно еще назвать и равными. Это такие векторы, у которых совпадает, как модульная величина (то есть отрезок по значению одинаковый), так и направление.
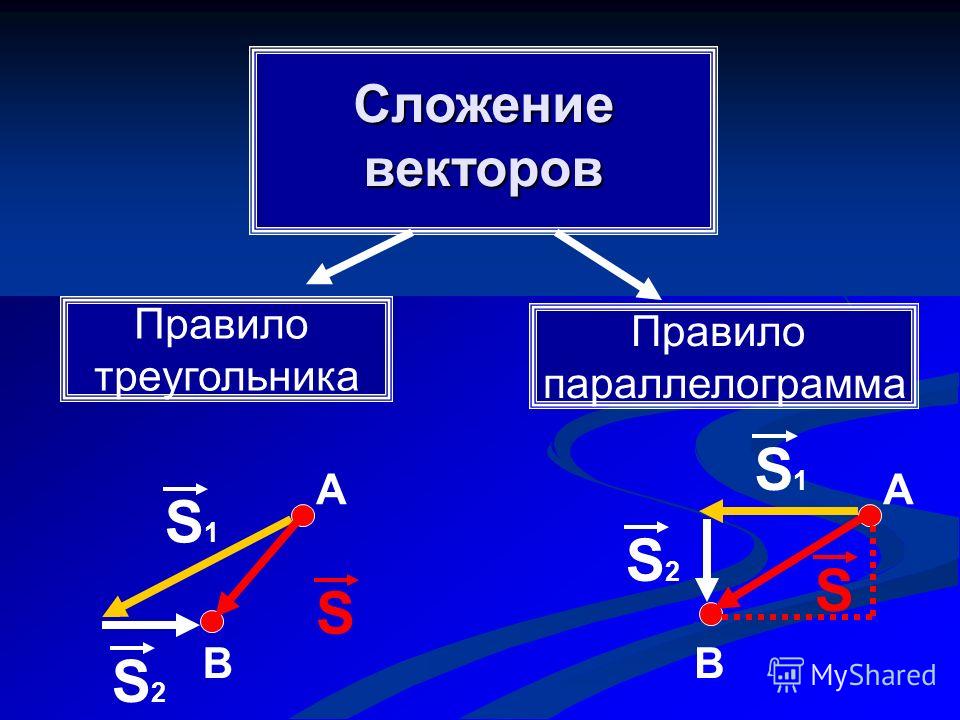
А теперь поговорим не много о действиях над векторами. Зачем вообще придумали слаживать вектора? На самом-то деле, просто решили, что можно вывести один вектор, который бы оказывал тоже воздействие, что и два других вектора. Как вы догадались, два других вектора, это наши слагаемые, а один вектор, который оказывает такое же воздействие – это наша сумма. Вектора складываются несколькими способами, в математики они называются «правилами». Первый – «правило треугольника», второй – «правило «параллелограмма». Стоит отметить и то, что мы можем сложить и три, и четыре , и пять векторов, но делать это надо постепенно, то есть попарно.
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Свойства сложения векторов | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Координаты произведения вектора на число | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Свойства умножения | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Скалярное произведение векторов | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Косинус угла между векторами | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Свойства скалярного произведения | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒ Рассмотрим два произвольных ненулевых вектора и : Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора : Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего пути с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы. Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов. Умножение вектора на число Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные». Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены. Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация: (векторы сонаправлены) или (векторы направлены противоположно). Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при . Правило умножения вектора на число легче понять с помощью рисунка:
9. Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.\ Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Все выше упомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда. 1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA1−→−, CC1−→− и AD−→−, то есть эти векторы компланарны. Также компланарны векторы AA1−→−, AB−→− и CC1−→−, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC1−→− совпадет с вектором AA1−→−. 2. Например, векторы AB−→−, AD−→− и AA1−→− не компланарны, так как их нельзя разместить в одной и той же плоскости. Признак компланарности трёх векторов: Пусть векторы a⃗ и b⃗ не коллинеарны. Если для вектора c⃗ существует единственная пара реальных чисел x и y, такая, чтоc⃗ =x⋅a⃗ +y⋅b⃗ , то векторы a⃗ , b⃗ и c⃗ компланарны. Справедливо и обратное утверждение: Если три вектора a⃗ , b⃗ и c⃗ компланарны и векторы a⃗ и b⃗ не коллинеарны, то вектор c⃗ можно разложить по векторам a⃗ и b⃗ одним единственным образом. 10. Координаты точки, координаты вектора Если даны две точки плоскости и , то вектор имеет следующие координаты: Если даны две точки пространства и , то вектор имеет следующие координаты: То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Обязательно нужно понимать различие между координатами точек и координатами векторов: Координаты точек – это обычные координаты в прямоугольной системе координат. Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости . Записи координат точек и координат векторов вроде бы схожи: , а смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства
11.Координаты суммы и разности векторов, произведение на число Сложение векторов (сумма векторов) a + b есть операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai + bi Вычитание векторов (разность векторов) a — b есть операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: сi = ai — bi В случае пространственной задачи сумму и разность векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующими формулами: a + b = {ax + bx; ay + by; az + bz} a — b = {ax — bx; ay — by; az — bz} Пример 3. Решение: a + b = {1 + 4; 2 + 8; 5 + 1} = {5; 10; 6} Пример 4. Найти разность векторов a = {1; 2; 5} и b = {4; 8; 1}. Решение: a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4} ⇐ Предыдущая12345Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Требования для добавления векторной графики в Adobe Stock
Хотите, чтобы ваша векторная графика была принята в коллекцию Adobe Stock? Узнайте, как обеспечить соответствие нашим стандартам качества, а также техническим и юридическим требованиям, и узнайте, как успешно загружать файлы.
Вы можете отправлять векторы через порталы Adobe Stock Contributor в виде файлов AI, EPS или SVG. Если вы отправляете иллюстрации, которые не являются векторными изображениями, см. раздел Требования к фотографии и иллюстрациям.
Компании, рекламные агентства, дизайн-студии и маркетологи хотят покупать великолепные, характерные векторные изображения, например:
Вот некоторые правила, которые помогут вам добиться успеха: компоненты
Сделайте : Избегайте текста, если он не является необходимой частью вашей композиции, поскольку покупателям может потребоваться выбрать замещающий шрифт.
Сделать : Сведите использование автотрассировки к минимуму.
Не : добавляйте растровые изображения (JPEG) в векторные файлы или растрируйте любые элементы.
Не : Включите свою подпись или имя в произведение искусства.
Контуры
Выполните : Используйте правильное количество опорных точек — не так много, чтобы фигура стала неровной, и не так мало, чтобы кривые выглядели неестественно или плоско.
Выполнить : Закрыть пути для всех фигур с заливкой.
Сделайте : рассмотрите возможность использования различных толщин обводки на изображении.
Сделать : Загляните в Illustrator Learning & Support, чтобы получить учебные пособия по самым разным темам: от создания изображений с помощью фигур до использования динамических символов.
Организация файла
Выполните : Назовите слои.
Выполнить : удалить скрытые и пустые слои.
Выполнить : удалить неиспользуемые элементы панели.
Сделать : Разблокировать все слои и подслои.
Сделайте : Убедитесь, что все ваши рисунки находятся на одной монтажной области, и удалите все, что находится за пределами монтажной области.
Варианты
Сделайте : Загрузите до трех значимых вариантов каждого вектора, если хотите. Простые цветовые вариации не считаются значимыми вариациями для редактируемых векторов. Варианты должны изменить стиль, тему или состав файла таким образом, чтобы он был полезен потенциальному покупателю. Подробнее
Не следует: Загружать одно и то же изображение с разными типами обводки или цветом фона.
Не следует: Загружать одно и то же изображение с разными тенями, эффектами или перевернутыми изображениями.
Вот пример приемлемого и неприемлемого варианта:
Перед отправкой
Убедитесь, что ваши градиенты сохраняют целостность в режимах :Просмотрите свои градиенты, чтобы сохранить их целостность в режимах :Просмотрите и нет растровых изображений.
Выполните : Увеличьте масштаб до 100 % или ближе и осмотрите изображение, чтобы убедиться, что оно не содержит случайных опорных точек или плохо соединенных линий.
Сделайте : Отправьте формы разрешения для любого используемого справочного материала или узнаваемых людей или имущества, даже если узнаваемым лицом являетесь вы или имущество принадлежит вам.
Отправьте со следующими техническими рекомендациями:
- Только форматы AI, EPS и SVG
- Рекомендуемое минимальное разрешение монтажной области: 15MP (мегапикселей)
- Максимальное разрешение монтажной области: 65MP (мегапикселей)
- Максимальный размер файла: 45 МБ (мегабайт)
- Цветовой режим документа: RGB
- Смещение монтажной области: (0,0) верхний левый угол
Файлы EPS следует либо экспортировать с разрешением более 15 МП, либо экспортировать с предустановками прозрачности «Высокое разрешение», чтобы изображения для предварительного просмотра отображались с оптимальным качеством. Файлы EPS размером более 15 Мп могут экспортировать пресеты прозрачности EPS с плотностью 72 пикселей на дюйм, чтобы они оставались меньше максимального размера файла 45 МБ.
Файлы EPS размером более 15 Мп могут экспортировать пресеты прозрачности EPS с плотностью 72 пикселей на дюйм, чтобы они оставались меньше максимального размера файла 45 МБ.
Узнайте больше о вариантах экспорта векторов здесь.
Следуйте этим рекомендациям:
- Отправляйте упорядоченные векторные файлы с полезными помеченными слоями и группами.
- Отправьте размеры, точные для предполагаемого использования файла.
- Оптимизируйте опорные точки, упростив пути или объединив объекты.
- Обведите все штрихи в виде контуров или фигур.
- Текст должен быть минимизирован, но при включении обведен контуром.
- Подгонка монтажной области под арт.
- Удалите фон или используйте чистый фон, чтобы клиентам было легко загрузить актив и использовать его в виде файла вектора, PNG или JPG.
Вот пример отправки с хорошо организованными слоями и группами:
А вот еще несколько рекомендаций для успешной отправки:
Узнайте больше о передовых технических методах создания великолепных векторов и узнайте, как использовать Adobe Пути, штрихи и опорные точки Illustrator для оптимизации векторных файлов.
Правильный размер векторов.
Хотя векторы можно масштабировать, мы рекомендуем создавать их в пригодных для использования размерах, чтобы клиенты могли редактировать их как есть. Клиенты смогут загружать векторные файлы в форматах PNG и JPEG, а небольшие векторные файлы будут загружаться как изображения с низким разрешением, если не в масштабе.
Категория | Примеры содержания | Минимальный размер | Максимальный размер |
|---|---|---|---|
Элементы дизайна и наборы | Значки, логотипы, узоры, символы, надписи | 1000×1000 пикселей | 4800×4800 пикселей |
Сцены и иллюстрации | Сцены с персонажами, мультфильмы, цифровые изображения | 1200×1200 пикселей | 4800×4800 пикселей |
Макеты с мелким шрифтом | Открытки, визитки, ярлыки | 1000×1000 пикселей | 3600×3600 пикселей |
Большие макеты для печати | Листовки, плакаты, конверты | 2400×2400 пикселей | 4800×4800 пикселей |
Маленькие цифровые конструкции | Социальные сети, мобильный пользовательский интерфейс, небольшая реклама | 1000×1000 пикселей | 3600 x 3600 пикселей |
Большой цифровой дизайн | Веб-макеты, настольные пользовательские интерфейсы, большие объявления | 1200×1200 пикселей | 7200×7200 пикселей |
Получите более подробные рекомендации по размеру от Adobe Stock.
Используйте эффективные заголовки и ключевые слова.
Если у вашего файла нет заголовка или встроенных ключевых слов, Adobe Stock будет использовать технологию Adobe Sensei, чтобы автоматически предлагать заголовок и до 25 ключевых слов, чтобы сэкономить ваше время. Прочитайте их и отредактируйте, измените порядок или удалите ключевые слова по мере необходимости, а затем расположите их в порядке важности, так как первые 10 перечисленных ключевых слов имеют приоритет в результатах поиска.
Если вы уже добавили заголовки и ключевые слова к изображениям предварительного просмотра в формате JPEG в Adobe Photoshop Lightroom, Lightroom Classic, Photoshop, Adobe Bridge или другом приложении для редактирования изображений, Adobe Stock сохранит их. Вы всегда можете отредактировать эти метаданные перед отправкой контента.
Не используйте названия товарных знаков (например, Porsche, iPad или Ferrari), характеристики камеры (например, Nikon или 12MP) или типы контента (например, вектор или иллюстрацию) в качестве ключевых слов или в заголовке.
Узнайте больше о названиях и ключевых словах или см. раздел Иллюстрация в справочнике исполнителя для получения примеров и дополнительной информации.
Знать основы законодательства.
Содержимое Adobe Stock должно соответствовать всем законам об авторском праве, товарных знаках, правах на неприкосновенность частной жизни, правах собственности и многом другом. Просмотрите Юридические рекомендации раздел данного руководства пользователя, чтобы убедиться, что вы понимаете ключевые юридические термины и знаете, когда вам нужно включить разрешение модели и/или разрешение собственности с отправкой.
Пара ключевых моментов, которые нужно знать:
- Если вы создаете векторную графику на основе фотографии или произведения искусства, вам необходимо предоставить разрешение на собственность, даже если фотография или иллюстрация является вашей собственной работой.
- Мы не принимаем векторы, содержащие логотипы, товарные знаки, названия компаний или торговые марки.
 — хотя вы можете отправить работу, в которой эти вещи были удалены в цифровом виде. Иллюстрации с изображением брендов или продуктов могут рассматриваться как иллюстративные редакционные материалы.
— хотя вы можете отправить работу, в которой эти вещи были удалены в цифровом виде. Иллюстрации с изображением брендов или продуктов могут рассматриваться как иллюстративные редакционные материалы.
Будьте осторожны, не спамьте.
Выберите только лучшие векторы и убедитесь, что каждая отправка предлагает что-то свое. Не отправляйте несколько изображений с минимальными изменениями. Отправка нескольких копий похожего или идентичного контента может быть воспринята нашей командой модераторов как спам. Использование длинных, не описательных, повторяющихся или нерелевантных заголовков и ключевых слов также может быть воспринято как спам. Рассылка спама строго запрещена и может привести к тому, что мы заблокируем вашу учетную запись или закроем ее навсегда. Узнать больше
Экспортированные изображения для предварительного просмотра, включенные в заархивированные папки, больше не обрабатываются через портал авторов. Мы рекомендуем загружать только отдельные файлы AI, EPS или SVG. Изображения для предварительного просмотра будут автоматически сгенерированы из этих векторных файлов, поэтому обязательно соблюдайте приведенные выше технические рекомендации по отправке, чтобы избежать каких-либо проблем с созданием изображений для предварительного просмотра.
Изображения для предварительного просмотра будут автоматически сгенерированы из этих векторных файлов, поэтому обязательно соблюдайте приведенные выше технические рекомендации по отправке, чтобы избежать каких-либо проблем с созданием изображений для предварительного просмотра.
Adobe Artists:
9\circ)$ как представляющий «5 км к северо-востоку», т. е. этот вектор может быть смещением вектор , указывая, скажем, на то, что ваша бабушка прошла 5 километров в сторону северо-восток в школу в снегу. С другой стороны, тот же вектор может обозначать скорость, указывая на то, что ваша бабушка шла со 5 км/ч на северо-восток. То, что вектор не указывает, где произошло это блуждание: вектор представляет величину, а направление, но не место. Наглядно полезно изобразить вектор в виде стрелки; направление вектора, естественно, направление, в котором указывает стрелка; величина вектора отражается на длине стрелы. Оказывается, многие величины ведут себя как векторы, например,
перемещение, скорость, ускорение, сила. Мы уже можем получить некоторые
представление об их полезности с использованием векторов смещения. Предположим, что ваш
бабушка прошла 5 км на СВ и 2 км на ЮЮВ; если позволяет местность,
и, возможно, вооружившись компасом, как могла ваша бабушка
шел прямо к месту назначения? Мы можем использовать векторы (и немного
геометрия), чтобы ответить на этот вопрос. Начнем с того, что отметим, что поскольку
векторы не включают спецификацию положения, мы можем «поместить»
их в любом удобном месте. Таким образом, мы можем представить вашу бабушку
путешествие в виде двух векторов смещения, проведенных лоб в лоб:
9\circ$
к северу от востока (примерно на восток-восток) доставит вашу бабушку
школа. Этот вид расчетов настолько распространен, что мы удостоим его
имя: мы говорим, что третий вектор является суммой двух других векторов. Есть
еще один распространенный способ изобразить сумму двух векторов. Поместите векторы
хвост к хвосту, а затем завершите указанный ими параллелограмм; в
сумма двух векторов является диагональю
параллелограмм:
Мы уже можем получить некоторые
представление об их полезности с использованием векторов смещения. Предположим, что ваш
бабушка прошла 5 км на СВ и 2 км на ЮЮВ; если позволяет местность,
и, возможно, вооружившись компасом, как могла ваша бабушка
шел прямо к месту назначения? Мы можем использовать векторы (и немного
геометрия), чтобы ответить на этот вопрос. Начнем с того, что отметим, что поскольку
векторы не включают спецификацию положения, мы можем «поместить»
их в любом удобном месте. Таким образом, мы можем представить вашу бабушку
путешествие в виде двух векторов смещения, проведенных лоб в лоб:
9\circ$
к северу от востока (примерно на восток-восток) доставит вашу бабушку
школа. Этот вид расчетов настолько распространен, что мы удостоим его
имя: мы говорим, что третий вектор является суммой двух других векторов. Есть
еще один распространенный способ изобразить сумму двух векторов. Поместите векторы
хвост к хвосту, а затем завершите указанный ими параллелограмм; в
сумма двух векторов является диагональю
параллелограмм:
пример, если два исходных вектора представляют собой силы, действующие на
объект, сумма двух векторов является чистой или эффективной силой на
объект, и хорошо нарисовать всех троих хвостами в
расположение объекта. \circ)$. Давайте
нарисуйте его снова, но наложите систему координат. Если мы положим хвост
стрелка в начале координат, конец стрелки заканчивается в
точка $\ds (5/\sqrt2,5/\sqrt2)\приблизительно(3.54, 3.54)$.
\circ)$. Давайте
нарисуйте его снова, но наложите систему координат. Если мы положим хвост
стрелка в начале координат, конец стрелки заканчивается в
точка $\ds (5/\sqrt2,5/\sqrt2)\приблизительно(3.54, 3.54)$.
стрелка, при условии, что мы знаем, что конец стрелки был помещен в $(0,0)$. Тогда на самом деле вектор всегда можно определить как $(3.54,3.54)$, где бы он ни находился; мы просто должны помнить что числа 3,54 должны быть интерпретированы как изменение от положение хвоста, а не фактические координаты наконечника стрелки; чтобы подчеркнуть это, мы будем писать $\langle 3.54,3.54\rangle$, чтобы обозначить вектор и $(3.54,3.54)$ для обозначения точки. Тогда, если вектор $\langle 3.54,3.54\rangle$ нарисован хвостом в $(1,2)$, это выглядит как это:
вектор, представляющий первую часть пути, равен $\ds \langle 5/\sqrt2,5/\sqrt2\rangle$, а вторая часть пути представлен $\langle 2\cos(-3\pi/8),2\sin(-3\pi/8)\rangle \приблизительно\угол 0,77,-1,85 \угл$. Мы можем представить сумму этих с обычной картинкой головы до хвоста:
точки $\ds (5/\sqrt2+2\cos(-3\pi/8),5/\sqrt2+2\sin(-3\pi/8))$ или
приблизительно $(4.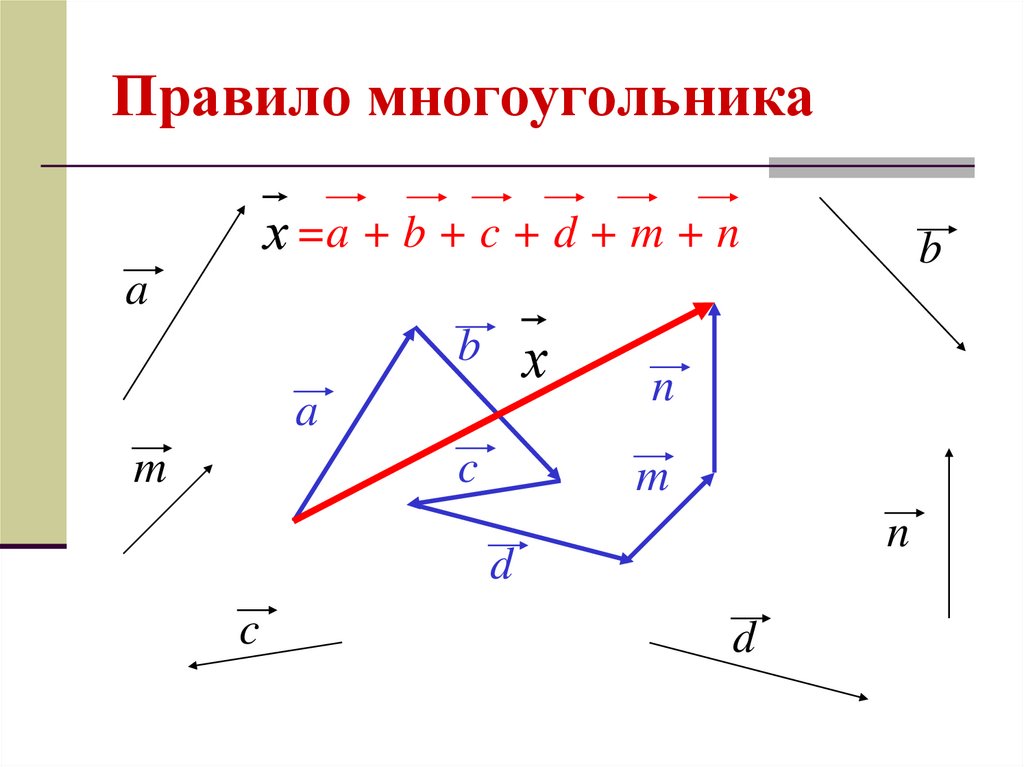 2}$.
2}$.
В трех измерениях векторы по-прежнему являются величинами, состоящими из
величина и направление, но, конечно, возможно гораздо больше
направления. Неясно, как мы могли бы представить направление
явно, но координатная версия векторов делает столько же
смысл в трех измерениях, как в двух. Под $\langle 1,2,3\rangle$ мы подразумеваем
вектор, голова которого находится в $(1,2,3)$, если его хвост находится в начале координат. В качестве
раньше мы могли разместить вектор где угодно; если у него есть хвост
в $(4,5,6)$, то его голова находится в $(5,7,9))$. Остается верным, что
арифметика легко выполняется с векторами в такой форме:
$$\выравнивание{
&a\langle v_1,v_2,v_3\rangle=\langle av_1,av_2,av_3\rangle\cr
&\langle v_1,v_2,v_3\rangle + \langle w_1,w_2,w_3\rangle
=\langle v_1+w_1,v_2+w_2,v_3+w_3\rangle\cr
&\langle v_1,v_2,v_3\rangle — \langle w_1,w_2,w_3\rangle
=\лангле v_1-w_1,v_2-w_2,v_3-w_3\рангл\кр}
$$
Величина вектора снова равна расстоянию от начала координат до
наконечник стрелы или
$\ds |\langle v_1,v_2,v_3\rangle|=\sqrt{v_1^2+v_2^2+v_3^2}$.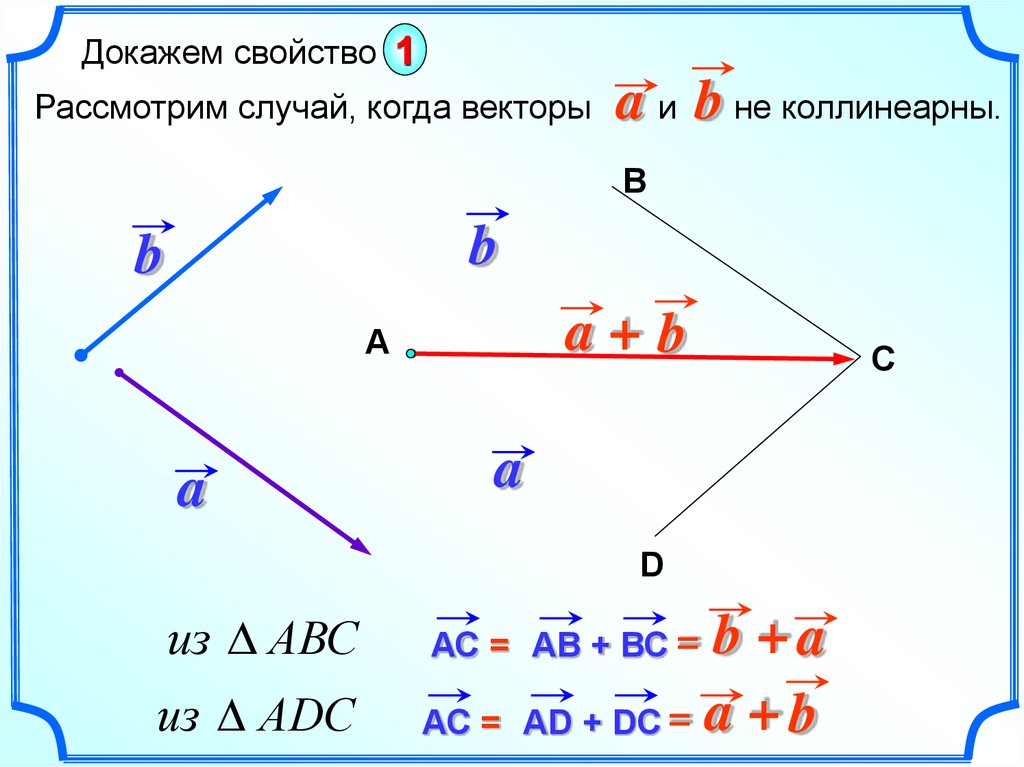
Рисунок 12.2.1. Вектор $\langle 2,4,5\rangle$ с хвостом в начале координат.
Три особенно простых вектора оказываются весьма полезными: ${\bf i}=\langle1,0,0\rangle$, ${\bf j}=\langle0,1,0\rangle$ и ${\bf k}=\langle0,0,1\rangle$. Они играют почти ту же роль для векторы, которые оси играют за точки. В частности, обратите внимание, что $$\выравнивание{ \langle v_1,v_2,v_3\rangle &= \langle v_1,0,0\rangle + \langle 0,v_2,0\rangle + \langle 0,0,v_3\rangle\cr &=v_1\langle1,0,0\rangle + v_2\langle0,1,0\rangle + v_3\langle0,0,1\rangle\cr &= v_1{\bf i} + v_2{\bf j} + v_3{\bf k}\cr }$$
Мы часто хотим создать вектор, который указывает из одной точки другому. То есть, если $P$ и $Q$ — точки, мы ищем вектор $\bf x$ такой, что когда хвост $\bf x$ помещается в $P$, его голова находится в $Q$; мы называем этот вектор как $\ds \overrightarrow{\strut PQ}$. Если мы знаем координаты $P$ и $Q$, координаты вектора легко найти.
Пример 12.2.1
Предположим, что $P=(1,-2,4)$ и $Q=(-2,1,3)$.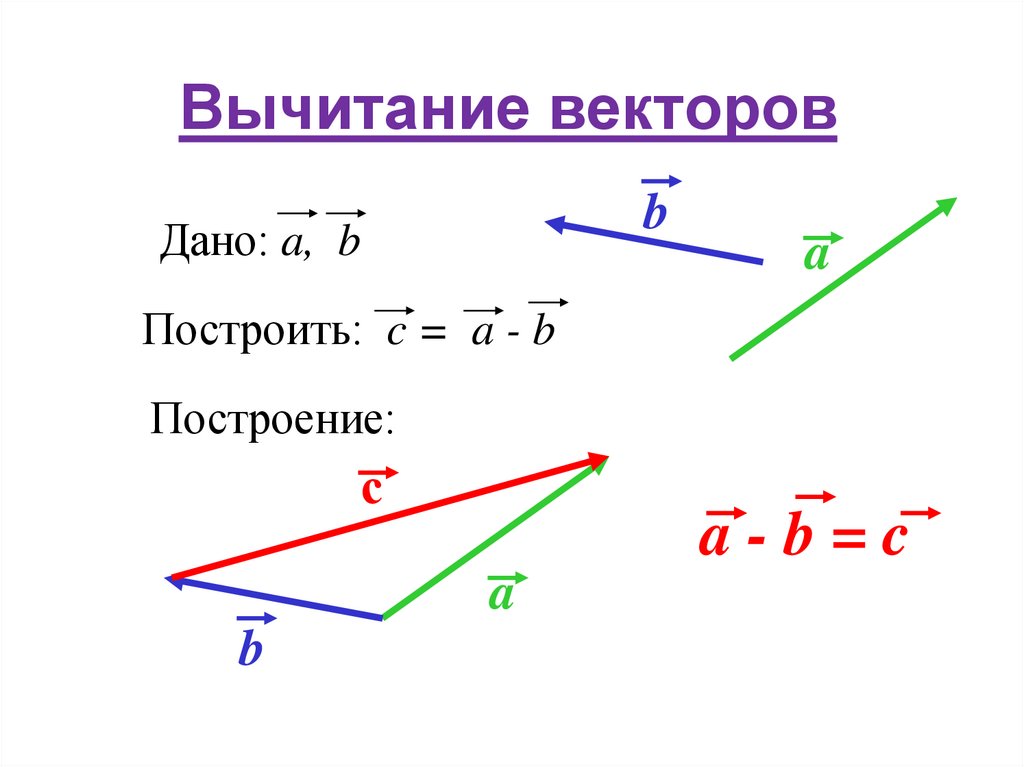 Вектор
$ \ ds \ overrightarrow {\ распорка PQ} $
является
$\langle -2-1,1- -2,3-4\rangle=\langle -3,3,-1\rangle$ и
$\ds \overrightarrow{\strut QP}=\langle 3,-3,1\rangle$.
Обратите внимание, что это то же самое, что вычитание векторов с хвостами в точках.
начало координат и головы в $P$ и $Q$:
$\langle -2,1,3\rangle-\langle 1,-2,4\rangle=\langle -3,3,-1\rangle$.
$\квадрат$
Вектор
$ \ ds \ overrightarrow {\ распорка PQ} $
является
$\langle -2-1,1- -2,3-4\rangle=\langle -3,3,-1\rangle$ и
$\ds \overrightarrow{\strut QP}=\langle 3,-3,1\rangle$.
Обратите внимание, что это то же самое, что вычитание векторов с хвостами в точках.
начало координат и головы в $P$ и $Q$:
$\langle -2,1,3\rangle-\langle 1,-2,4\rangle=\langle -3,3,-1\rangle$.
$\квадрат$
Арифметика с векторами обладает некоторыми знакомыми свойствами, перечисленными в следующая теорема. Все это довольно легко доказать, просто представление векторов в стандартной форме.
Теорема 12.2.2. Если ${\bf u}$, ${\bf v}$ и ${\bf w}$ — векторы, а $a$ и $b$ — вещественные числа, затем
1. $\ds {\bf u}+{\bf v}={\bf v}+{\bf u}$
2. $a{\bf u}={\bf u}a$
3. $a({\bf u}+{\bf v})=a{\bf u}+a{\bf v}$
4. $(a+b){\bf u}= a{\bf u} + b{\bf u}$
5. $({\bf u}+{\bf v})+{\bf w}={\bf u}+({\bf v}+{\bf w})$
6. $|a{\bf u}|=|a||{\bf u}|$
Доказательство. Мы делаем один из них в качестве примера, часть 3. Пишем
${\bf u}=\langle x_1, y_1, z_1\rangle$,
${\bf v}=\langle x_2, y_2, z_2\rangle$. затем
$$\выравнивание{
a ({\ bf u} + {\ bf v}) & = a (\ langle x_1, y_1, z_1 \ rangle + \ langle x_2, y_2, z_2 \ rangle) \ cr
&=a\langle x_1+x_2,y_1+y_2,z_1+z_2\rangle\cr
&=\langle a(x_1+x_2),a(y_1+y_2),a(z_1+z_2)\rangle\cr
&=\langle ax_1+ax_2,ay_1+ay_2,az_1+az_2\rangle\cr
&=\langle ax_1,ay_1,az_1\rangle+\langle ax_2,ay_2,az_2\rangle\cr
&=a\langle x_1,y_1,z_1\rangle+a\langle x_2,y_2,z_2\rangle\cr
& = а {\ bf и} + а {\ bf v} \ cr
}$$
$\qed$
Мы делаем один из них в качестве примера, часть 3. Пишем
${\bf u}=\langle x_1, y_1, z_1\rangle$,
${\bf v}=\langle x_2, y_2, z_2\rangle$. затем
$$\выравнивание{
a ({\ bf u} + {\ bf v}) & = a (\ langle x_1, y_1, z_1 \ rangle + \ langle x_2, y_2, z_2 \ rangle) \ cr
&=a\langle x_1+x_2,y_1+y_2,z_1+z_2\rangle\cr
&=\langle a(x_1+x_2),a(y_1+y_2),a(z_1+z_2)\rangle\cr
&=\langle ax_1+ax_2,ay_1+ay_2,az_1+az_2\rangle\cr
&=\langle ax_1,ay_1,az_1\rangle+\langle ax_2,ay_2,az_2\rangle\cr
&=a\langle x_1,y_1,z_1\rangle+a\langle x_2,y_2,z_2\rangle\cr
& = а {\ bf и} + а {\ bf v} \ cr
}$$
$\qed$
Вы можете использовать Sage для выполнения векторной арифметики.
Пример 12.2.1 Нарисуйте вектор $\langle 3,-1\rangle$ хвостом в источник.
Пример 12.2.2 Нарисуйте вектор $\langle 3,-1,2\rangle$ хвостом в источник.
Пример 12.2.3 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой
в $(1,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой
в $(3,1)$.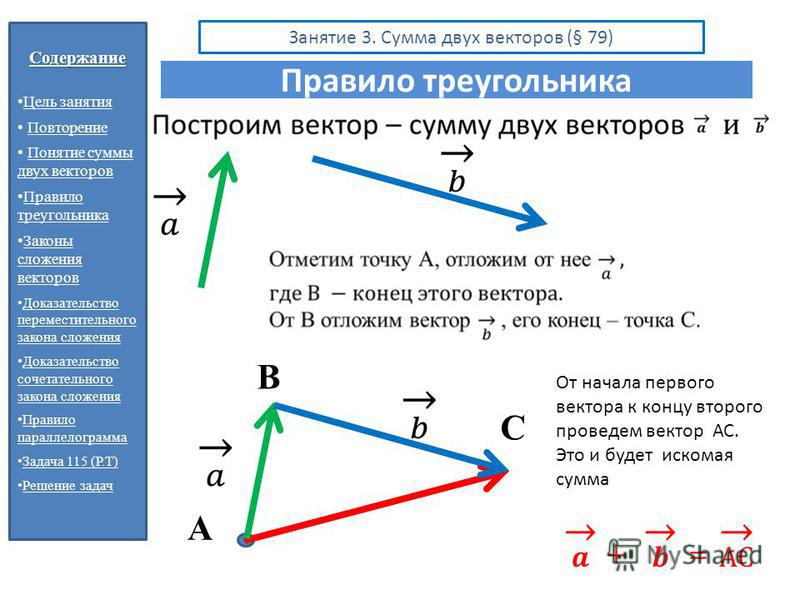 Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с
хвост в $(1,2)$ и голова в $(3,1)$. Нарисуйте $\bf C$ хвостом в начале координат.
Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с
хвост в $(1,2)$ и голова в $(3,1)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.4 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой в $(-1,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой в $(3,3)$. Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с хвост в $(-1,2)$ и голова в $(3,3)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.5 Пусть ${\bf A}$ — вектор с хвостом в начале координат и головой в $(5,2)$; пусть ${\bf B}$ — вектор с хвостом в начале координат и головой в $(1,5)$. Нарисуйте ${\bf A}$ и ${\bf B}$, а также вектор ${\bf C}$ с хвост в $(5,2)$ и голова в $(1,5)$. Нарисуйте $\bf C$ хвостом в начале координат.
Пример 12.2.6 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$,
$|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для
${\bf v} = \langle 1,3\rangle$ и ${\bf w} = \langle -1,-5\rangle$. (отвечать)
(отвечать)
Пример 12.2.7 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,2,3\rangle$ и ${\bf w} = \langle -1,2,-3\rangle$. (отвечать)
Пример 12.2.8 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,0,1\rangle$ и ${\bf w} = \langle -1,-2,2 \rangle$. (отвечать)
Пример 12.2.9 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 1,-1,1\rangle$ и ${\bf w} = \langle 0,0,3\rangle$. (отвечать)
Пример 12.2.10 Найти $|{\bf v}|$, ${\bf v}+{\bf w}$, ${\bf v}-{\bf w}$, $|{\bf v}+{\bf w}|$, $|{\bf v}-{\bf w}|$ и $-2{\bf v}$ для ${\bf v} = \langle 3,2,1\rangle$ и ${\bf w} = \langle -1,-1,-1\rangle$. (отвечать)
Пример 12.2.11 Пусть $P=(4,5,6)$, $Q=(1,2,-5)$. Находить
$\ds \overrightarrow{\strut PQ}$. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 1. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 4.
(отвечать)
Находить
$\ds \overrightarrow{\strut PQ}$. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 1. Найдите вектор с
в том же направлении, что и $\ds \overrightarrow{\strut PQ}$
но с длиной 4.
(отвечать)
Пример 12.2.12 Если $A, B$ и $C$ — три точки, найдите $ \ ds \ overrightarrow {\ распорка AB} + \overrightarrow{\распорка до н.э.}+ \overrightarrow{\распорка CA}$. (отвечать)
Пример 12.2.13 Рассмотрим 12 векторов, хвосты которых находятся в центре часы и их соответствующие головки на каждой из 12 цифр. Что такое сумма этих векторов? Что, если мы удалим вектор, соответствующий до 4 часов? Что, если вместо этого все векторы имеют свои решки на 12 часов, а головы на остальные цифры? (отвечать)
Пример 12.2.14 Пусть $\bf a$ и $\bf b$ — ненулевые векторы в двух измерениях.
которые не параллельны и не антипараллельны. Покажите алгебраически, что если
$\bf c$ — любой двумерный вектор, существуют скаляры $s$ и $t$
такое, что ${\bf c}=s{\bf a}+t{\bf b}$.
Пример 12.2.15 Верно ли утверждение из предыдущего упражнения, если векторы $\bf a$, $\bf b$ и $\bf c$ — трехмерные векторы? Объяснять.
Пример 12.2.16 Докажите остальные части Теорема 12.2.2.
Операции с векторами — GeeksforGeeks
В физике в основном есть два типа величин — векторы и скаляры. Векторы — это величины, с которыми связаны как направление, так и величина, в то время как скаляры — это величины, с которыми связана единственная величина. Со скалярными величинами можно работать, используя простые алгебраические правила, но это не относится к векторным величинам, с ними нельзя обращаться таким же образом. Таким образом, важно знать, какие и сколько различных операций можно произвести над этими величинами. Рассмотрим подробнее некоторые из этих операций.
Математические операции с векторами
Поскольку векторы содержат направления, с этими величинами следует обращаться таким образом, чтобы учитывать их направления. Основные правила алгебры вообще не применимы к векторам, например, простое сложение величин двух векторов в большинстве случаев даст неправильный ответ. В следующем списке перечислены некоторые распространенные операции, выполняемые над векторами в области физики:
Основные правила алгебры вообще не применимы к векторам, например, простое сложение величин двух векторов в большинстве случаев даст неправильный ответ. В следующем списке перечислены некоторые распространенные операции, выполняемые над векторами в области физики:
- Сложение/вычитание двух векторов.
- Умножение вектора на скаляр.
- Продукт двух векторов:
- DOT Product
- Cross-Product
⇢ (Перестановочное свойство)
Треугольный закон сложения векторов Рассмотрим векторы, указанные на рисунке выше. Линия PQ представляет вектор «p», а QR представляет вектор «q». Линия QR представляет результирующий вектор. AC направлен от A к C.
Линия PQ представляет вектор «p», а QR представляет вектор «q». Линия QR представляет результирующий вектор. AC направлен от A к C.
Линия AC представляет собой
Величина результирующего вектора определяется выражением
Представляет собой угол между двумя векторами. Пусть \phi будет углом между результирующим вектором и вектором p.
Умножение векторов на скалярУмножение вектора a на постоянный скаляр k дает вектор, направление которого остается тем же, но величина изменяется в k раз. На рисунке показан вектор до и после умножения на константу k. В математических терминах это можно переписать как
, если k > 1, величина вектора увеличивается, а уменьшается, когда k < 1.
Произведение векторов
Векторы можно умножать друг на друга, но нельзя делить. В случае умножения есть в основном два вида умножения — скалярное и векторное. Скалярное умножение (также известное как скалярное произведение) — это вид умножения, в результате которого получается скалярная величина. Умножение векторов (также известное как перекрестное произведение) — это вид умножения, в результате которого получается векторная величина. Векторные произведения используются для определения других производных векторных величин.
Умножение векторов (также известное как перекрестное произведение) — это вид умножения, в результате которого получается векторная величина. Векторные произведения используются для определения других производных векторных величин.
Скалярный продукт
Рассмотрим два вектора и . Скалярное произведение этих двух векторов определяется уравнением
Здесь θ — угол между двумя векторами.
В случае, если векторы заданы их компонентами. например, a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. В этом случае скалярный продукт определяется как
a.b = a 1 b 1 i + a 2 b 2 j + a 3 b 3 k
Vector Product Consider two vectors \vec{A } и \vec{B} . Векторное произведение этих двух векторов обозначается . Направление этого вектора перпендикулярно обоим векторам. Величина этого вектора определяется выражением
Векторное произведение этих двух векторов обозначается . Направление этого вектора перпендикулярно обоим векторам. Величина этого вектора определяется выражением
Здесь θ — угол между двумя векторами.
Правило правой руки используется для определения направления результирующего вектора векторного произведения. Обратите внимание, что в отличие от сложения и скалярного произведения векторное произведение не является коммутативным по своей природе.
В случае, если векторы заданы их компонентами. например, a = a 1 i + a 2 j + a 3 k и b = b 1 i + b 2 j + b 3 k. В этом случае векторное произведение определяется выражением
Примеры задач
Вопрос 1. Вектор определяется выражением v = 2i + j. Найдите модуль вектора, когда он масштабируется на константу 0,4.
Ответ:
для вектора, v = ai + bj
|в| =
0,4|v| = |0,4 В|
а = 2, б = 1
|0,4v|
⇒ |0,4(2i + j)|
⇒ |0,8i + 0,4j|
|в| =
⇒ |v| =
⇒ |v| = √0,8
Вопрос 2: Два вектора величиной 5 и 10. Эти векторы имеют между собой угол 60°. Найдите величину результирующих векторов.
Эти векторы имеют между собой угол 60°. Найдите величину результирующих векторов.
Ответ:
Пусть два вектора заданы p и q. Тогда результирующий вектор «r» определяется как
|р| = 5, |q| = 10 и
⇒
⇒
⇒
⇒
. Найдите модуль результирующих векторов и угол, образуемый результирующим вектором.
Ответ:
Пусть два вектора заданы p и q. Тогда результирующий вектор «r» определяется как
|р| = 4, |q| = 4 и
⇒
⇒
⇒
⇒ |r| = 4 √ 3
угол, образованный равнодействующей к. Найдите скалярное произведение этих двух векторов.
Ответ:
Дано:
a = 2i + j + k
b = i + j + k
a.b
⇒ (2i + j + k ).(i + j + k)
⇒ 2,1 + 1,1 + 1,1
⇒ 4
Вопрос 5.
Два вектора задаются формулой a = 2i + j + k и b = i + j + k. Найдите векторное произведение этих двух векторов.
Ответ:
Дано:
A = 2i + J + K
B = I + J + K
3.3 Дополнение вектор и субтрокция: аналитические методы — Колледж
3,3 Вектор и субтрокция: аналитические методы — Колледж 2E
3,3. Цели обучения
К концу этого раздела вы сможете:
- Понимать правила сложения и вычитания векторов с использованием аналитических методов.
- Применение аналитических методов для определения векторов вертикальной и горизонтальной составляющих.
- Применение аналитических методов для определения величины и направления результирующего вектора.
Аналитические методы сложения и вычитания векторов используют геометрию и простую тригонометрию, а не линейку и транспортир графических методов. Часть графической техники сохранена, потому что векторы по-прежнему представлены стрелками для облегчения визуализации.
Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Разложение вектора на перпендикулярные компоненты
Аналитические методы и прямоугольные треугольники идут рука об руку в физике, потому что (среди прочего) движения вдоль перпендикулярных направлений независимы. Нам очень часто нужно разделить вектор на перпендикулярные компоненты. Например, имея такой вектор, как AA на рис. 3.24, мы можем захотеть найти, какие два перпендикулярных вектора, AxAx и AyAy, нужно сложить, чтобы получить его.
Рисунок 3,24 Вектор AA с хвостом в начале координат x , y — система координат, показана вместе с ее x — и y -компонентами, AxAx и AyAy.
Эти векторы образуют прямоугольный треугольник. Аналитические отношения между этими векторами резюмируются ниже.
AxAx и AyAy определяются как компоненты AA вдоль осей x и y . Три вектора AA, AxAx и AyAy образуют прямоугольный треугольник:
Ax + Ay = A.Ax + Ay = A.
3,3
Обратите внимание, что эта связь между компонентами вектора и результирующим вектором сохраняется только для векторных величин (которые включают как величину, так и направление). Отношения не применимы только к величинам. Например, если Ax=3 мAx=3 м на восток, Ay=4 мAy=4 м на север, и A=5 мА=5 м на северо-восток, то верно, что векторы Ax + Ay = AAx + Ay = A. Однако это не правда, что сумма модулей векторов тоже равна. То есть
3 м+4 м ≠ 5 м3 м+4 м ≠ 5 м
3,4
Таким образом,
Ax+Ay≠AAx+Ay≠A
3,5
Если вектор AA известен, то известны его модуль AA (его длина) и его угол θθ (его направление).
Чтобы найти AxAx и AyAy, его компоненты x и y , мы используем следующие соотношения для прямоугольного треугольника.
Ax=AcosθAx=Acosθ
3,6
и
Ay=Asinθ.Ay=Asinθ.
3,7
Рисунок 3,25 Величины компонент вектора AxAx и AyAy можно связать с результирующим вектором AA и углом θθ тригонометрическими тождествами. Здесь мы видим, что Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ.
Предположим, например, что AA является вектором, представляющим общее перемещение человека, идущего по городу, рассматриваемому в Кинематике в двух измерениях: введение и сложение и вычитание векторов: графические методы.
Рисунок 3,26 Мы можем использовать соотношения Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ для определения величины векторов горизонтальной и вертикальной составляющих в этом примере.
Тогда A=10.
3A=10.3 блоков и θ=29,1ºθ=29,1º , чтобы
Ax=Acosθ=(10,3 блока)(cos29,1°)=9,0 блокаAx=Acosθ=(10,3 блока)(cos29,1°)=9,0 блока
3,8
Ay=Asinθ=(10,3 блока)(sin29,1° )=5,0 блоков.Ay=Asinθ=(10,3 блоков)(sin29,1º)=5,0 блоков.
3,9
Вычисление результирующего вектора
Если известны перпендикулярные компоненты AxAx и AyAy вектора AA, то AA можно найти и аналитически. Чтобы найти величину AA и направление θθ вектора по его перпендикулярным компонентам AxAx и AyAy относительно оси x , мы используем следующие соотношения:
A=Ax2+Ay2A=Ax2+Ay2
3.10
θ=tan−1(Ay/Ax).θ=tan−1(Ay/Ax).
3.11
Рисунок 3,27 Величина и направление результирующего вектора могут быть определены, когда горизонтальная и вертикальная составляющие А Икс А Икс а также А у А у были определены.
Обратите внимание, что уравнение A=Ax2+Ay2A=Ax2+Ay2 — это всего лишь теорема Пифагора, связывающая катеты прямоугольного треугольника с длиной гипотенузы. Например, если AxAx и AyAy составляют 9 и 5 кварталов соответственно, тогда A=92+52=10,3A=92+52=10,3 квартала, что опять-таки соответствует примеру человека, идущего по городу. Наконец, направление θ=загар–1(5/9)=29,1ºθ=загар–1(5/9)=29,1º , как прежде.
Определение векторов и компонентов векторов аналитическими методами
Уравнения Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ используются для нахождения перпендикулярных компонент вектора, то есть для перехода от AA и θθ к AxAx и AyAy. Уравнения A=Ax2+Ay2A=Ax2+Ay2 и θ=tan–1(Ay/Ax)θ=tan–1(Ay/Ax) используются для нахождения вектора по его перпендикулярным компонентам, т. е. для перехода от AxAx и AyAy в AA и θθ. Оба процесса имеют решающее значение для аналитических методов сложения и вычитания векторов.
Добавление векторов с использованием аналитических методов
Чтобы увидеть, как складывать векторы, используя перпендикулярные компоненты, рассмотрите рис.
3.28, на котором векторы AA и BB складываются для получения результирующего RR.
Рисунок 3,28 Векторы AA и BB — это два этапа ходьбы, а RR — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления RR.
Если AA и BB представляют два этапа ходьбы (два перемещения), то RR — это полное перемещение. Человек, совершающий прогулку, оказывается на вершине RR. Есть много способов попасть в одну и ту же точку. В частности, человек мог ходить первым в x -направление, а затем в y -направление. Этими путями являются x — и y -компоненты результирующего, RxRx и RyRy. Если мы знаем RxRx и RyRy мы можем найти РР и θθ с помощью уравнений A=Ax2+Ay2A=Ax2+Ay2 и θ=tan–1(Ay/Ax)θ=tan–1(Ay/Ax). Когда вы используете аналитический метод сложения векторов, вы можете определить компоненты или величину и направление вектора.
Шаг 1. Определите оси X и Y, которые будут использоваться в задаче. Затем найдите компоненты каждого добавляемого вектора вдоль выбранных перпендикулярных осей . Используйте уравнения Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ, чтобы найти компоненты. На рис. 3.29 эти компоненты аксакс, АйАй, BxBx и ByBy. Углы, которые векторы AA и BB образуют с осью x , равны θAθA и θBθB соответственно.
Рисунок 3,29 Чтобы сложить векторы AA и BB, сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы AxAx, AyAy, BxBx и ByBy, показанные на изображении.
Шаг 2. Найдите компоненты равнодействующей вдоль каждой оси путем сложения компонентов отдельных векторов вдоль этой оси . То есть, как показано на рисунке 3.30,
Rx=Ax+BxRx=Ax+Bx
3.
12
и
Ry=Ay+By.Ry=Ay+By.
3.13
Рисунок 3.30 Сумма векторов AxAx и BxBx дает величину RxRx результирующего вектора в горизонтальном направлении. Точно так же величины векторов AyAy и ByBy складываются, чтобы получить величину RyRy результирующего вектора в вертикальном направлении.
Компоненты вдоль одной оси, скажем, оси x , являются векторами вдоль одной линии и, таким образом, могут складываться друг с другом, как обычные числа. То же самое верно для компонентов вдоль оси y . (Например, пройти 9 кварталов на восток можно двумя этапами: первые 3 квартала на восток и вторые 6 кварталов на восток, всего 9, потому что они идут в одном направлении.) Таким образом, разложение векторов на компоненты вдоль общие оси облегчают их добавление. Теперь, когда компоненты RR известны, можно найти его величину и направление.
Шаг 3.
Чтобы получить величину RR равнодействующей, используйте теорему Пифагора:
R=Rx2+Ry2.R=Rx2+Ry2.
3.14
Шаг 4. Чтобы получить направление равнодействующей относительно оси x : /Rx).
3.15
Следующий пример иллюстрирует этот метод сложения векторов с использованием перпендикулярных компонентов.
Пример 3.3
Добавление векторов с помощью аналитических методов
Добавьте вектор AA к вектору BB, показанному на рис. 3.31, используя перпендикулярные компоненты вдоль осей x и y . Оси x — и y — направлены соответственно с востока на запад и с севера на юг. Вектор АА представляет собой первый этап ходьбы, при котором человек проходит 53,0 м 53,0 м в направлении 20,0º20,0º к северу от востока.
Вектор BB представляет собой вторую ветвь, смещение 34,0 м34,0 м в направлении 63,0º63,0º к северу от востока.
Рисунок 3.31 Вектор AA имеет величину 53,0 м 53,0 м и направление 20,0º20,0º к северу от оси x . Вектор BB имеет величину 34,0 м34,0 м и направление 63,0º63,0º к северу от оси x . Вы можете использовать аналитические методы для определения величины и направления RR.
Стратегия
Компоненты AA и BB вдоль осей x и y представляют собой ходьбу строго на восток и строго на север, чтобы добраться до одной и той же конечной точки. После обнаружения они объединяются для получения результирующего.
Решение
Следуя описанному выше методу, мы сначала находим компоненты АА и ББ по осям x — и y -. Обратите внимание, что А=53,0 мА=53,0 м, θА=20,0ºθА=20,0º, B=34,0 мB=34,0 м и θB=63,0°, θB=63,0°.
Мы находим компоненты x , используя Ax=AcosθAx=Acosθ, что дает
Ax=AcosθA=(53,0 м)(cos 20,0º)=(53,0 м)(0,940)=49,8 мAx=AcosθA=(53,0 м )(cos 20,0º)=(53,0 м)(0,940)=49,8 м
3,16
и
Bx=BcosθB=(34,0 м)(cos 63,0º)=(34,0 м)(0,454)=15,4 м. Bx=BcosθB=(34,0 м)(cos 63,0º)=(34,0 м)(0,454)=15,4 м.
3,17
Аналогично, компоненты y находятся с использованием Ay=AsinθAAy=AsinθA:
Ay=AsinθA=(53,0 м)(sin 20,0º)=(53,0 м)(0,342 м)=18,1 =(53,0 м)(sin 20,0º)=(53,0 м)(0,342)=18,1 м
3,18
и
By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891) =30,3 м.By=BsinθB=(34,0 м)(sin 63,0º)=(34,0 м)(0,891)=30,3 м.
3.19
Таким образом, x — и y -компоненты равнодействующей равны
Rx=Ax+Bx=49
3,20
и
Ry=Ay+By=18,1 м+30,3 м=48,4 м.
Ry=Ay+By =18,1 м+30,3 м=48,4 м.
3,21
Теперь мы можем найти величину равнодействующей по теореме Пифагора: )2 м
3,22
так что
R=81,2 м. R=81,2 м.
3,23
Наконец, находим направление равнодействующей:
θ=tan−1(Ry/Rx)=+tan−1(48,4/65,2).θ=tan−1(Ry/Rx)=+ тангенс −1 (48,4/65,2).
3,24
Таким образом,
θ=tan−1(0,742)=36,6°. θ=tan−1(0,742)=36,6°.
3,25
Рисунок 3,32 Используя аналитические методы, мы видим, что магнитуда RR составляет 81,2 м81,2 м и его направление 36,6º36,6º к северу от востока.
Обсуждение
Этот пример иллюстрирует сложение векторов с использованием перпендикулярных компонентов. Вычитание вектора с использованием перпендикулярных компонент очень похоже — это просто добавление отрицательного вектора.
Вычитание векторов осуществляется добавлением отрицательного вектора.
То есть A−B≡A+(–B)A−B≡A+(–B). Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты –B–B – минусы компонентов ББ. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R равны =Ay+(–By)Ry=Ay+(–By)
3.27
и остальная часть описанного выше метода аналогична методу добавления. (См. рис. 3.33.)
Анализ векторов с использованием перпендикулярных компонент очень полезен во многих областях физики, поскольку перпендикулярные величины часто не зависят друг от друга. Следующий модуль Projectile Motion — один из многих, в котором использование перпендикулярных компонентов помогает сделать картинку более ясной и упростить физику.
Рисунок 3,33 Вычитание двух векторов показано на рис. 3.28. Компоненты –B–B являются негативами компонентов BB. Метод вычитания такой же, как и для сложения.
Исследования ФЕТ
Добавление вектора
Узнайте, как добавлять векторы. Перетащите векторы на график, измените их длину и угол и суммируйте их вместе. Величина, угол и компоненты каждого вектора могут отображаться в нескольких форматах.
Определение, формула, правила и примеры
Возможно, мы этого не осознаем, но каждый день мы что-то добавляем. Мы делаем это, когда идем в продуктовый магазин, чтобы купить что-то, мы делаем это, когда добавляем ингредиенты в еду во время приготовления пищи и даже когда играем с друзьями. Это часть нашей повседневной жизни, и ее также можно применять к более сложным вещам, таким как векторы.
В этой статье мы узнаем о векторах и различных способах добавления векторов.
Определение сложения векторов
Сложение векторов можно определить как процедуру сложения двух или более векторов.
Вектор, образованный сложением векторов, называется результирующим вектором и обычно обозначается как .
Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.
Формула сложения векторов
Предположим, что A и B являются точками на плоскости с их координатами, заданными как и соответственно. Тогда формула сложения векторов для может быть записана как:
Свойства сложения векторов
Коммутативность: Изменение порядка векторов не меняет сумму.
Ассоциативность: Изменение группировки сложений не меняет сумму.
Нулевой элемент: Добавление точки с нулем равно точке. Если нулевой элемент , то
Аддитивная обратная: Если точка A , то ее обратная . Когда эти векторы складываются, в результате получается ноль.
Графическое сложение векторов
Как можно графически выполнить сложение векторов? Ниже приведены различные методы.
Треугольный закон векторного сложения
Закон треугольника — это закон сложения векторов. Он также известен как метод «голова к хвосту» , потому что головы и хвосты задействованных векторов помещаются друг на друга при попытке найти их сумму. На рисунке ниже показано, как выглядят голова и хвост вектора.
Показ головы и хвоста вектора
Посмотрим, как используется этот закон. Рассмотрим векторы A и B ниже.
Отображение двух векторов A и B
Чтобы сложить два вектора, используя метод «голова к хвосту», выполните следующие процедуры.
- Поместите конец второго вектора на начало первого вектора.
- Чтобы найти сумму, нарисуйте результирующий вектор, чтобы соединить конец первого вектора с головой второго вектора.
Сложение двух векторов
На рисунке выше .
Если есть третий вектор, вы продолжаете размещать хвост третьего вектора на голове второго вектора. Результирующий вектор будет нарисован так, чтобы соединить хвост первого вектора с головой второго вектора.
Вектор можно перемещать вдоль своей плоскости до тех пор, пока длина/направление не меняются.
Закон сложения векторов в виде параллелограмма
Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны, исходящие из общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то результирующий вектор можно найти из диагонали этого параллелограмма.
Чтобы найти:
Сложите хвосты векторов вместе
Завершите параллелограмм, нарисовав две параллельные стороны.
После завершения параллелограмма нарисуйте диагональ, начинающуюся в вершине исходного вектора, как показано на рисунке ниже.
Демонстрация сложения двух векторов
Закон параллелограмма также можно использовать, когда вам заданы векторы, определенные как координаты.
Для точек и сумму можно найти по закону параллелограмма, показанному на рис. 2.
Отображение суммы двух точек вектора
Вычитание вектора
Чтобы понять вычитание, нужно сначала понять, что такое отрицательное значение вектора. Допустим, есть вектор A. Отрицательное значение этого вектора определяется как -A. Отрицательный вектор вектора А имеет ту же величину, что и вектор А, однако они направлены в противоположные стороны.
Разность между вектором А и отрицанием вектора А
Закон параллелограмма для векторного вычитания
Чтобы найти , его следует рассматривать как . Имея это в виду, мы получим следующий рисунок:
Закон параллелограмма для вычитания векторов
Примеры сложения векторов
Давайте рассмотрим несколько примеров.
Если и — две векторные точки, какова сумма векторов?
Ответ.
Формула сложения векторов:
Полученные точки равны и
Из заданных точек:
Если подставить в формулу сложения векторов, то получится:
Если и — две векторные точки, найти сумму векторов.
Ответ.
Полученные точки:
Формула сложения векторов:
Из точек, которые мы имеем:
Применение формулы сложения векторов:
Возьмем другой пример.
Игрушечная машинка перемещается на 10 см на восток и на 24 см на север. Используя закон треугольника, найдите результирующий вектор двух векторов.
Ответ.
У нас есть два вектора величиной 10 см и 24 см. Назовем их A и B.
Направление — восток, а направление — север. Таким образом, мы имеем:
Обратите внимание, что хвост второго вектора помещается на голову первого вектора, как и говорит закон. Чтобы найти результирующий вектор, мы завершим треугольник, нарисовав линию, соединяющую хвост первого вектора с головой второго вектора, а затем добавим обе величины.
Назовем результирующий вектор C.
Результирующий вектор:
Возьмем другой пример.
Рассмотрим векторы в восточном направлении, в северном направлении и в восточном направлении.
Используя правило треугольника, найдите результирующий вектор.
Ответы.
Во-первых, нам нужно нарисовать векторы в соответствии с их направлениями. При этом имейте в виду, что хвост одного вектора должен располагаться над головой другого вектора.
Как видно из рисунка выше, хвост второго вектора помещается на начало первого вектора, а хвост третьего вектора — на начало второго вектора.
Результирующий вектор будет суммой величин всех векторов.
Чтобы найти результирующий вектор, была проведена линия, соединяющая хвост первого вектора с головой третьего вектора. результирующий вектор:
Используя рисунок выше, найдите векторы по закону параллелограмма.
Решение
- Чтобы найти , можно применить закон параллелограмма, как показано на рисунке. Диагональ параллелограмма представляет собой сумму векторов, как на рисунке ниже.
- Чтобы найти , нужно сначала инвертировать вектор B, а затем применить закон параллелограмма, как показано на рисунке ниже.
- Чтобы найти , сложение векторов можно выполнить с помощью закона параллелограмма, как показано на рисунке ниже.
- Чтобы найти , сначала нужно обратить вектор C, а затем применить закон параллелограмма, как показано на рисунке ниже.
Сложение векторов – ключевые выводы
- Сложение векторов можно определить как процедуру сложения двух или более векторов.
- Формула сложения векторов для заданных точек:
- Согласно закону параллелограмма, если два вектора можно представить как две смежные стороны от общей вершины, а затем дополнить их так, как если бы они образовывали параллелограмм, то сумму можно найти из диагонали этого параллелограмма.
- Как и при обычном сложении, порядок сложения векторов не имеет значения.
- Вычитание векторов имеет ту же операцию, что и сложение векторов, после инвертирования связанных векторов.
Объяснение урока: Операции с векторами в 2D
В этом объяснении мы узнаем, как выполнять операции над векторами алгебраически, такие как сложение векторов, вычитание векторов, и скалярное умножение в двух измерениях.
Давайте вспомним векторные операции, которые мы будем использовать, начиная со сложения и вычитания двумерных векторов.
Определение: сложение и вычитание двумерных векторов
Чтобы сложить или вычесть пару двумерных векторов, мы складываем или вычитаем соответствующие компоненты двух векторов. Если ⃑𝑣=(𝑎,𝑏) и ⃑𝑤=(𝑐,𝑑), то ⃑𝑣+⃑𝑤=(𝑎+𝑐,𝑏+𝑑),⃑𝑣-⃑𝑤=(𝑎-𝑐,𝑏-𝑑).
Далее вспомним скалярное умножение двумерного вектора.
Определение: скалярное умножение двумерных векторов
Чтобы умножить двумерный вектор на скаляр, мы умножаем каждый компонент вектора на скаляр. Учитывая вектор ⃑𝑣=(𝑎,𝑏) и скаляр 𝑐, 𝑐⃑𝑣=(𝑐𝑎,𝑐𝑏).
Мы также помним, что двумерный вектор может быть выражен через фундаментальные единичные векторы ⃑𝑖 и ⃑𝑗, которые определяются ⃑𝑖=(1,0),⃑𝑗=(0,1).
Начиная с компонентной формы вектора, мы можем применить векторное сложение и скалярное умножение для записи (𝑎,𝑏)=(𝑎,0)+(0,𝑏)=𝑎(1,0)+𝑏(0,1)=𝑎⃑𝑖+𝑏⃑𝑗.
Это объясняет, как достигается преобразование между этими двумя формами вектора. Мы также можем выполнять алгебраические операции над векторы с использованием фундаментальных векторов. В этом случае мы можем рассматривать фундаментальные единичные векторы ⃑𝑖 и ⃑𝑗 как неопределенные и собрать подобные термины вместе. Например, добавление два вектора можно записать как 𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑖+𝑑⃑𝑗 = 𝑎⃑𝑖+𝑏⃑𝑗+𝑐⃑𝑖+𝑑⃑𝑗 = 𝑎⃑𝑖+𝑐⃑𝑖+𝑏⃑𝑗+𝑑⃑𝑗 = (𝑎+𝑐) ⃑𝑖+(𝑏+𝑑) ⃑𝑗.
Этот процесс приводит к той же формуле для сложения двух векторов, что и приведенная выше в компонентной форме. Точно так же скалярное умножение можно записать как 𝑐𝑎⃑𝑖+𝑏⃑𝑗=𝑐𝑎⃑𝑖+𝑐𝑏⃑𝑗, что снова совпадает с приведенной выше формулой для вектора в компонентной форме. Как мы видим здесь, одним из преимуществ Использование фундаментальных единичных векторов заключается в том, что это делает алгебраические операции над векторами более похожими на соответствующие алгебраические операции над действительными числами.
Мы можем комбинировать несколько алгебраических операций с двумерными векторами. Поскольку алгебраические операции над векторами напоминают соответствующие операции действительных чисел, мы можем определить порядок операций, следуя порядку операций вещественные числа. Помните, что порядок операций над действительными числами определяется аббревиатурой PEMDAS, обозначающей круглые скобки. степень, умножение, деление, сложение и вычитание. Мы также помним, что порядок между сложением и вычитанием часто выполняется в том порядке, в котором написано выражение. Например, чтобы вычислить 9−2+4, мы бы сначала вычислить вычитание 9−2=7, а затем вычислить сложение 7+4=11.
Поскольку векторные операции не включают возведение в степень и деление, нам нужно рассмотреть только эти четыре операции: круглые скобки, умножение, сложение и вычитание.
Правило: порядок векторных операций
Когда мы вычисляем алгебраическое выражение, включающее двумерные векторы, которое включает скалярное умножение, сложение и вычитание, мы должны следовать порядку операций, указанному ниже:
- Круглые скобки
- Скалярное умножение
- Сложение и вычитание
В нашем первом примере мы объединим скалярное умножение с вычитанием двумерных векторов.
Пример 1. Вычисление выражений, включающих вычитание и скалярное умножение заданных векторов в двух измерениях
Учитывая, что ⃑𝐴=(2,−4) и ⃑𝐵=(−7,−6), найдите ⃑𝐴−4⃑𝐵.
Ответ
В этом примере нам нужно вычислить ⃑𝐴−4⃑𝐵, что включает вычитание и скалярное умножение двумерных векторов. Напомним, что порядок векторных операций задается
- скобки,
- скалярное умножение,
- сложение и вычитание.
Итак, мы можем начать с вычисления скалярного умножения 4⃑𝐵. Напомним, что задан вектор ⃑𝑣=(𝑎,𝑏) и скаляр 𝑐, скалярное умножение определяется 𝑐⃑𝑣=(𝑐𝑎,𝑐𝑏).
Следовательно, 4⃑𝐵=4(−7,−6)=(−28,−24).
Далее мы можем вычислить вычитание. Напомним, что мы можем вычесть пару векторов, вычитая соответствующие компоненты из двух векторов. Это дает нам ⃑𝐴−4⃑𝐵=(2,−4)−(−28,−24)=(2−(−28),−4−(−24))=(30,20).
В предыдущем примере мы вычислили алгебраическое выражение, включающее двумерные векторы, которые использовали скалярное умножение и вычитание векторов.
Используя эти понятия, мы иногда можем записать вектор в терминах двух векторов. Эта идея похожа на то, как мы можем написать любой вектор через фундаментальные единичные векторы ⃑𝑖 и ⃑𝑗, где мы пишем (𝑎,𝑏)=𝑎⃑𝑖+𝑏⃑𝑗.
Имея два двумерных вектора ⃑𝐴 и ⃑𝐵, мы иногда можем написать третий 2D-вектор ⃑𝐶 через ⃑𝐴 и ⃑𝐵 если мы найдем скаляры 𝑎 и 𝑏, удовлетворяющие ⃑𝐶=𝑎⃑𝐴+𝑏⃑𝐵.
Если мы вычислим скалярное умножение и сложение двумерных векторов в правой части этого уравнения, мы можем получить пару уравнений с участием 𝑎 и 𝑏. Мы должны иметь в виду, что эта система уравнения не всегда имеют решение, и в этом случае мы не можем выразить вектор ⃑𝐶 через ⃑𝐴 и ⃑𝐵. Но когда эта система уравнений приводит к решениям 𝑎 и 𝑏, то мы можем выразить ⃑𝐶 через ⃑𝐴 и ⃑𝐵.
Хотя этот процесс выражения двумерного вектора через два вектора является чисто алгебраическим, полезно визуализировать его с помощью график, чтобы понять, почему это возможно. Рассмотрим три вектора ⃑𝐴, ⃑𝐵 и ⃑𝐶, указанные ниже.
Давайте посмотрим, что означают эти операции графически, чтобы выразить ⃑𝐶 как 𝑎⃑𝐴+𝑏⃑𝐵=⃑𝐶.
Мы знаем, что скалярное умножение вектора приводит к растяжению или сжатию вектора, а также изменению направления вектора, если скаляр отрицателен. Это означает, что векторы 𝑎⃑𝐴 и 𝑏⃑𝐵 — масштабированные (или обращенные) версии векторов ⃑𝐴 и ⃑𝐵 соответственно. Мы также знаем, что сумма двух двумерных векторов образует диагональ параллелограмма образованные двумя векторами. Следовательно, приведенное выше уравнение означает, что мы можем масштабировать векторы ⃑𝐴 и ⃑𝐵, чтобы нарисовать параллелограмм с диагональю ⃑𝐶, как показано ниже.
В следующем примере мы запишем вектор через два других вектора.
Пример 2. Использование операций над векторами для выражения вектора через два других вектора −1) с точки зрения ⃑𝐴 и ⃑𝐵.
Ответ
В этом примере нам нужно выразить вектор ⃑𝐶 через два вектора ⃑𝐴 и ⃑𝐵. Это означает, что мы хотим найти скаляры 𝑎 и 𝑏 такие, что 𝑎⃑𝐴+𝑏⃑𝐵=⃑𝐶.
Левая часть этого уравнения содержит скалярное умножение и сложение двумерных векторов. Мы знаем, что скаляр умножение должно быть вычислено до сложения векторов. Напомним, что для вектора ⃑𝑣=(𝑎,𝑏) и скаляра 𝑐 скалярное умножение определяется выражением 𝑐⃑𝑣=(𝑐𝑎,𝑐𝑏).
Это приводит к 𝑎⃑𝐴=𝑎(−4,−1)=(−4𝑎,−𝑎),𝑏⃑𝐵=𝑏(−2,−1)=(−2𝑏,−𝑏).
Далее добавим два вектора. Напомним, что мы можем сложить пару векторов, добавив соответствующие компоненты два вектора. Следовательно, 𝑎⃑𝐴+𝑏⃑𝐵=(−4𝑎,−𝑎)+(−2𝑏,−𝑏)=(−4𝑎−2𝑏,−𝑎−𝑏).
Так как это должно равняться вектору ⃑𝐶, мы получаем (−4𝑎−2𝑏,−𝑎−𝑏)=(−8,−1).
Мы знаем, что два вектора равны, если равны соответствующие компоненты векторов. Это приводит к паре одновременные уравнения: −4𝑎−2𝑏=−8, −𝑎−𝑏=−1.
Чтобы решить эту пару одновременных уравнений, давайте сначала разделим обе части первого уравнения на −2: 2𝑎+𝑏=4,−𝑎−𝑏=−1.
Тогда сложение этих двух уравнений приводит к 𝑎=3. Подстановка этого значения во второе уравнение приводит к −3−𝑏=−1.
Преобразуя это уравнение так, чтобы 𝑏 было субъектом, мы получаем 𝑏=−2. Следовательно, ⃑𝐶 можно записать как 3⃑𝐴−2⃑𝐵.
Далее мы рассмотрим пример с векторными операциями, где векторы определяются своими конечными точками. Если нам дадут баллы 𝐴(𝑥,𝑦) и 𝐵(𝑥,𝑦), вектор 𝐴𝐵 определяется разностью векторов положения 𝑂𝐵 и 𝑂𝐴. Это ведет к 𝐴𝐵=𝑂𝐵−𝑂𝐴=(𝑥,𝑦)−(𝑥,𝑦)=(𝑥−𝑥,𝑦−𝑦).
Напомним также, что 𝐴𝐵+𝐵𝐶=𝐴𝐶.
Это уравнение можно изобразить на следующем графике.
В следующем примере мы найдем недостающие координаты точки, когда нам дано уравнение, включающее двумерные векторные операции.
Пример 3. Нахождение пропущенных координат из векторных уравнений
На решетке, где 𝐴𝐶=(3,3), 𝐵𝐶=(13,−7) и −4), найдите координаты точки 𝐶.
Ответ
В этом примере нам нужно найти координаты точки 𝐶 из заданного векторного уравнения. На В левой части данного уравнения мы видим два вектора 𝑂𝐶 и 𝐴𝐵.
Напомним, 𝑂𝐶 — вектор положения точки 𝐶, что означает, что компоненты этого вектора задаются соответствующими координатами 𝐶. Так как мы не знаем координаты 𝐶, обозначим координаты 𝐶 на (𝑥,𝑦). Затем, 𝑂𝐶=(𝑥,𝑦).
Далее рассмотрим другой вектор в данном уравнении, 𝐴𝐵. Отметим, что это не один из предоставленные векторы. Однако мы можем найти этот вектор, используя заданные векторы, вспомнив 𝐴𝐵+𝐵𝐶=𝐴𝐶.
Обозначим 𝐴𝐵=(𝑎,𝑏). Подставляя 𝐵𝐶=(13,−7) и 𝐴𝐶=(3,3) в уравнение выше приводит к (𝑎,𝑏)+(13,−7)=(3,3).
Напомним, что мы можем сложить пару векторов, сложив соответствующие компоненты двух векторов. Это ведет к (𝑎+13,𝑏−7)=(3,3).
Следовательно, мы должны иметь 𝑎+13=3,𝑏−7=3.
Перестановка этих двух уравнений приводит к 𝑎=−10 и 𝑏=10. Это дает нам 𝐴𝐵=(−10,10).
Тогда данное уравнение можно записать в виде 2(𝑥,𝑦)+2(−10,10)=(−4,−4).
Левая часть этого уравнения содержит скалярное умножение и сложение двумерных векторов.
Мы знаем, что нам нужно вычислить скалярное умножение перед сложением. Напомним, что мы можем вычислить скалярное умножение двумерного вектора, умножив каждую компоненту вектора скаляром. Это означает 2(𝑥,𝑦)=(2𝑥,2𝑦),2(-10,10)=(-20,20).
Тогда уравнение можно записать в виде (2𝑥,2𝑦)+(−20,20)=(−4,−4).
Сложение векторов слева, (2𝑥−20,2𝑦+20)=(−4,−4).
Приравнивание соответствующих компонентов двух векторов приводит к паре уравнений: 2𝑥−20=−4,2𝑦+20=−4.
Перестановка этих уравнений приводит к 𝑥=8,𝑦=−12, что дает 𝑥- и 𝑦-координаты 𝐶. Следовательно, координаты 𝐶 есть (8,−12).
В следующем примере мы рассмотрим векторную операцию, включающую три вектора.
Пример 4. Сложение, вычитание и скалярное умножение векторов
Учитывая, что ⃑𝐵=(−9,−3), ⃑𝐶=(−4,−2) и ⃑𝐷=(−2,9), определить вектор ⃑𝐴, удовлетворяющий уравнению ⃑𝐴=−4⃑𝐵+2⃑𝐶−6⃑𝐷.
Ответ
В этом примере нам нужно вычислить правую часть уравнения, чтобы найти вектор ⃑𝐴.
Выражение, которое нам нужно вычислить, включает скалярное умножение, сложение и вычитание двумерных векторов. Напомним, что порядок векторных операций равен
- скобки,
- скалярное умножение,
- сложение и вычитание.
Поскольку в этом выражении нет скобок, начнем с вычисления скалярных умножений. Напомним, что мы можем умножить вектор на скаляр, умножив каждый компонент вектора на скаляр. Следовательно, −4⃑𝐵=−4(−9,−3)=(36,12),2⃑𝐶=2(−4,−2)=(−8,−4),6⃑𝐷=6(−2,9)=(− 12,54).
Теперь, когда мы закончили эту часть, мы можем следовать порядку сложения и вычитания, как написано. Поскольку выражение мы хотим вычислить −4⃑𝐵+2⃑𝐶−6⃑𝐷, нам нужно вычислить сложение −4⃑𝐵+2⃑𝐶 сначала. Напомним, что мы можем складывать или вычитать 2D-векторы, добавляя или вычитая соответствующие компоненты двух векторов. Используя векторы, которые мы вычислили выше, мы имеем −4⃑𝐵+2⃑𝐶=(36,12)+(−8,−4)=(36+(−8),12+(−4))=(28,8).
Наконец, мы можем вычислить вычитание: −4⃑𝐵+2⃑𝐶−6⃑𝐷=(28,8)−(−12,54)=(28−(−12),8−54)=(40,−46).
Следовательно, ⃑𝐴=(40,−46).
В последнем примере мы вычислим векторную операцию, включающую 3 вектора, и вычислим величину результирующего вектора.
Пример 5. Нахождение нормы результата операций над векторами ‖‖−2⃑𝐴−2⃑𝐵+2⃑𝐶‖‖.
Ответ
В этом примере нам нужно вычислить величину вектора, полученного в результате векторных операций. Сначала вычислим результат векторных операций: −2⃑𝐴−2⃑𝐵+2⃑𝐶.
Это выражение, которое нам нужно вычислить, включает скалярное умножение, сложение и вычитание двумерных векторов. Напомним, что порядок векторных операций задается
- скобками,
- скалярным умножением,
- сложением и вычитанием.
Поскольку в этом выражении нет скобок, начнем с вычисления скалярного умножения. Напомним, что мы можем умножить вектор на скаляр, умножив каждый компонент вектора на скаляр.
Следовательно, −2⃑𝐴=−2(−3,5)=(6,−10),2⃑𝐵=2(2,0)=(4,0),2⃑𝐶=2(−4,5)=(−8,10) .
Теперь, когда мы закончили эту часть, мы можем приступить к сложению и вычитанию векторов в заданном порядке. С наше выражение равно −2⃑𝐴−2⃑𝐵+2⃑𝐶, нам нужно вычислить вычитание −2⃑𝐴−2⃑𝐵 сначала. Напомним, что мы можем складывать или вычитать 2D-векторы, добавляя или вычитая соответствующие компоненты двух векторов. Используя векторы, которые мы вычислили выше, мы имеем −2⃑𝐴−2⃑𝐵=(6,−10)−(4,0)=(6−4,−10−0)=(2,−10).
Наконец, мы можем вычислить сложение: −2⃑𝐴−2⃑𝐵+2⃑𝐶=(2,−10)+(−8,10)=(2+(−8),−10+10)=(−6,0).
Мы получили, что вектор, полученный в результате векторных операций, равен (−6,0). Сейчас мы нужно найти модуль этого вектора. Напомним, что величина двумерного вектора определяется выражением ‖(𝑎,𝑏)‖=√𝑎+𝑏.
Поскольку наш вектор равен (−6,0), мы можем применить эту формулу с 𝑎=−6 и 𝑏=0, чтобы получить ‖(−6,0)‖=(−6)+0=6.
Следовательно, ‖‖−2⃑𝐴−2⃑𝐵+2⃑𝐶‖‖=6.


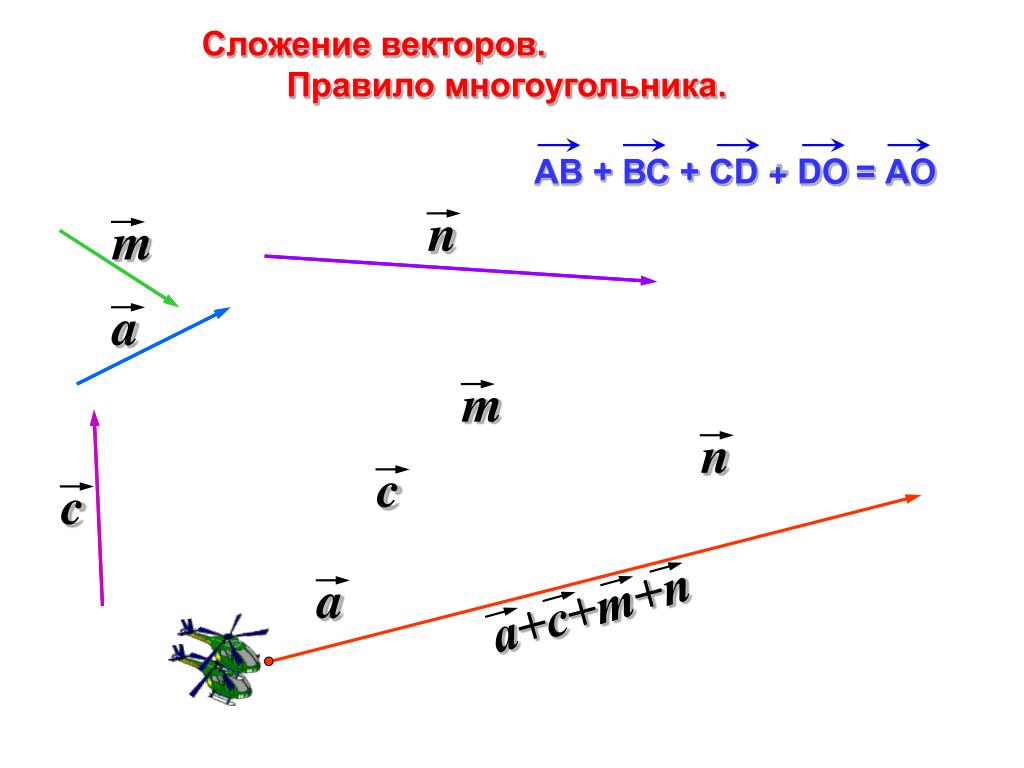
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
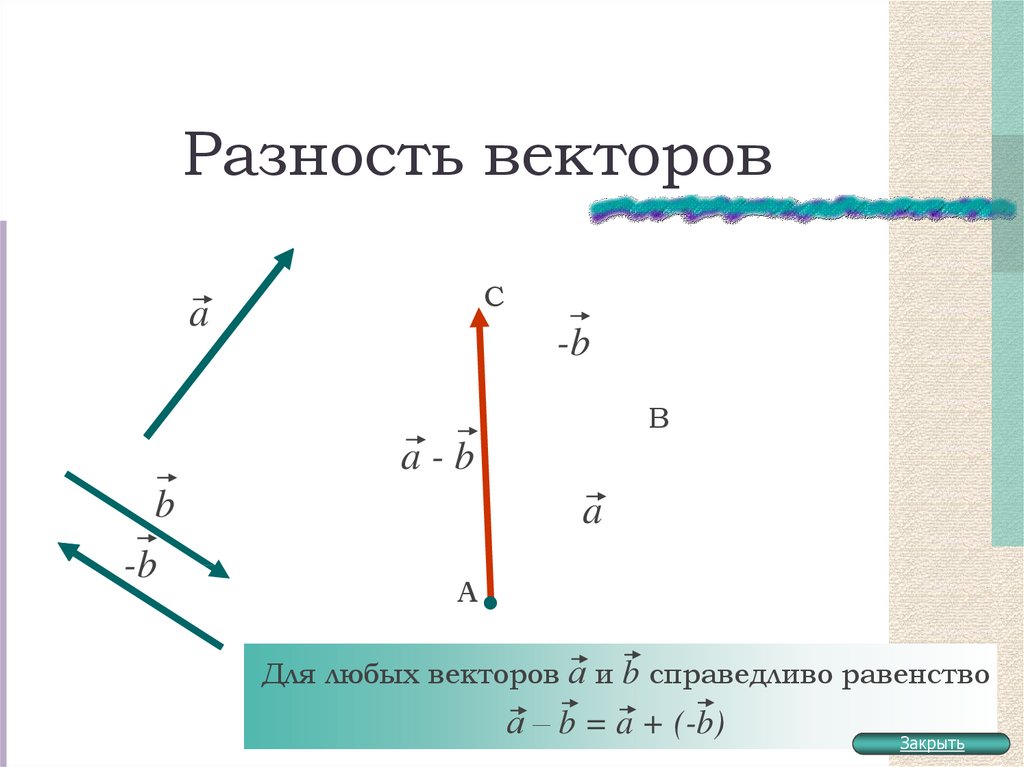
 Коллинеарные и компланарные векторы
Коллинеарные и компланарные векторы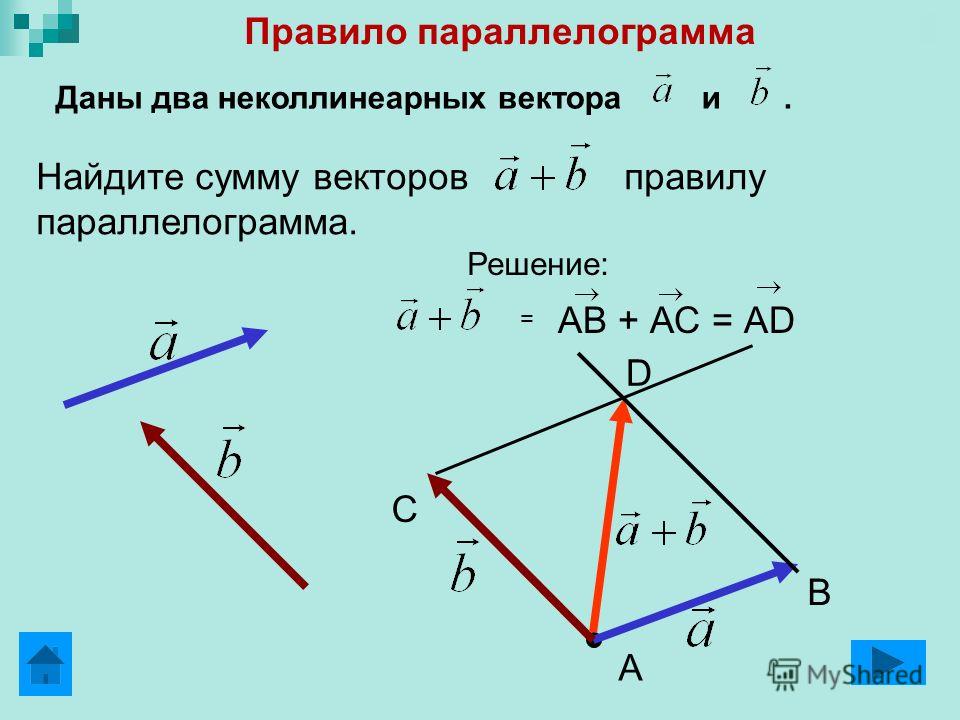
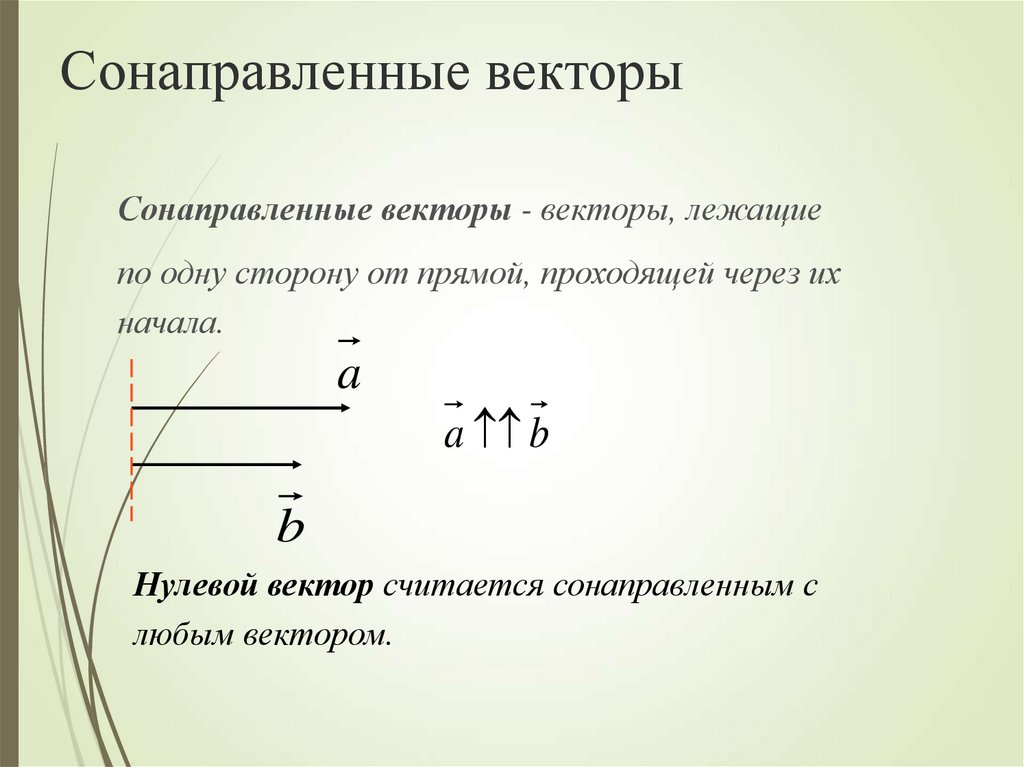 Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.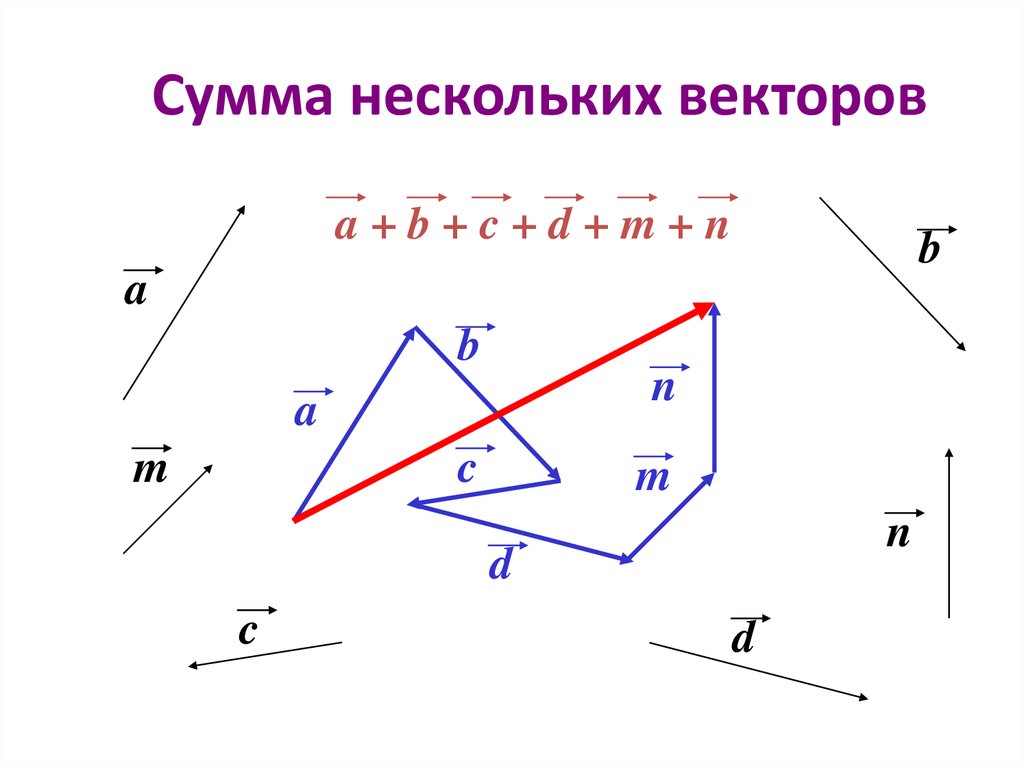 Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}.
Найти сумму векторов a = {1; 2; 5} и b = {4; 8; 1}. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.011 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.011 с.) — хотя вы можете отправить работу, в которой эти вещи были удалены в цифровом виде. Иллюстрации с изображением брендов или продуктов могут рассматриваться как иллюстративные редакционные материалы.
— хотя вы можете отправить работу, в которой эти вещи были удалены в цифровом виде. Иллюстрации с изображением брендов или продуктов могут рассматриваться как иллюстративные редакционные материалы.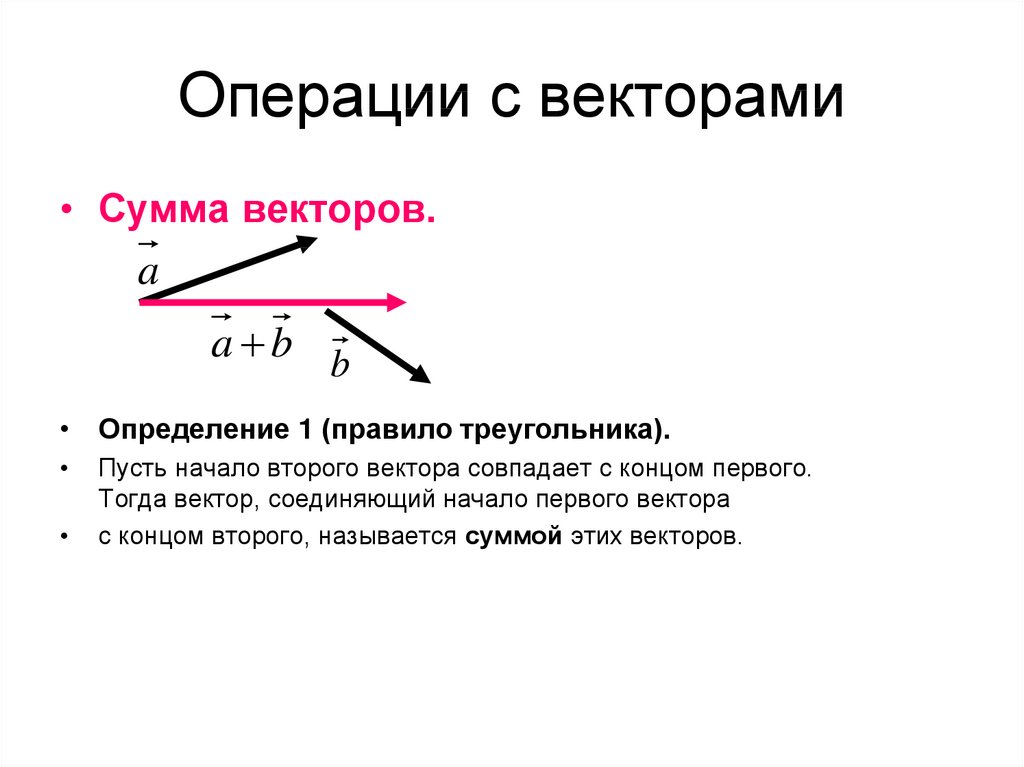 Два вектора задаются формулой a = 2i + j + k и b = i + j + k. Найдите векторное произведение этих двух векторов.
Два вектора задаются формулой a = 2i + j + k и b = i + j + k. Найдите векторное произведение этих двух векторов.  Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины.
Однако аналитические методы более лаконичны, точны и точны, чем графические методы, которые ограничены точностью, с которой может быть выполнен чертеж. Аналитические методы ограничены только точностью и точностью, с которой известны физические величины. Эти векторы образуют прямоугольный треугольник. Аналитические отношения между этими векторами резюмируются ниже.
Эти векторы образуют прямоугольный треугольник. Аналитические отношения между этими векторами резюмируются ниже.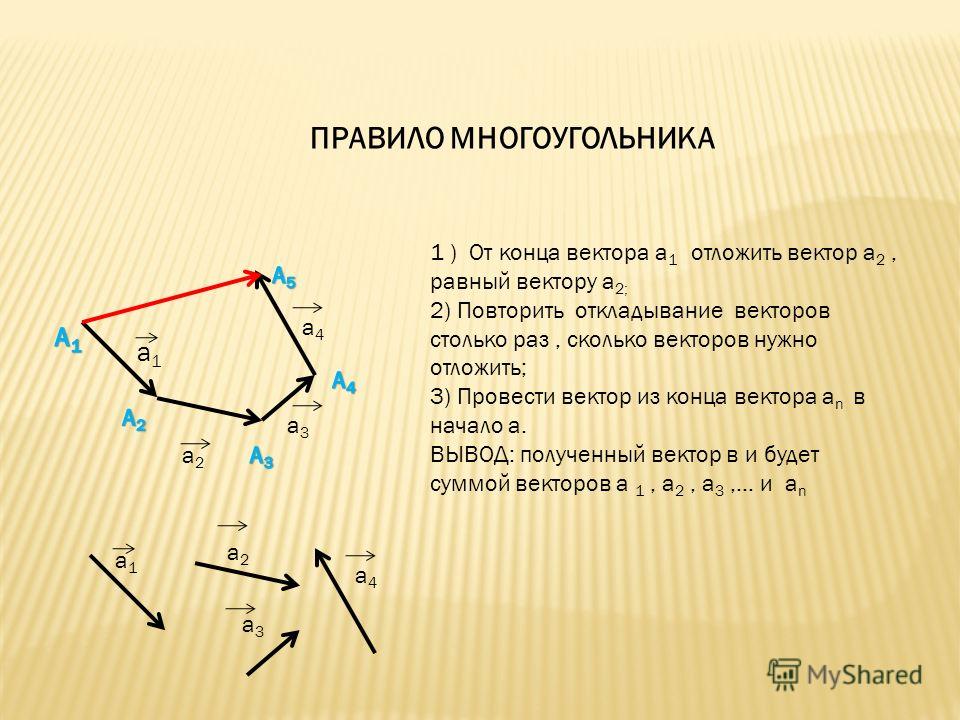 Чтобы найти AxAx и AyAy, его компоненты x и y , мы используем следующие соотношения для прямоугольного треугольника.
Чтобы найти AxAx и AyAy, его компоненты x и y , мы используем следующие соотношения для прямоугольного треугольника.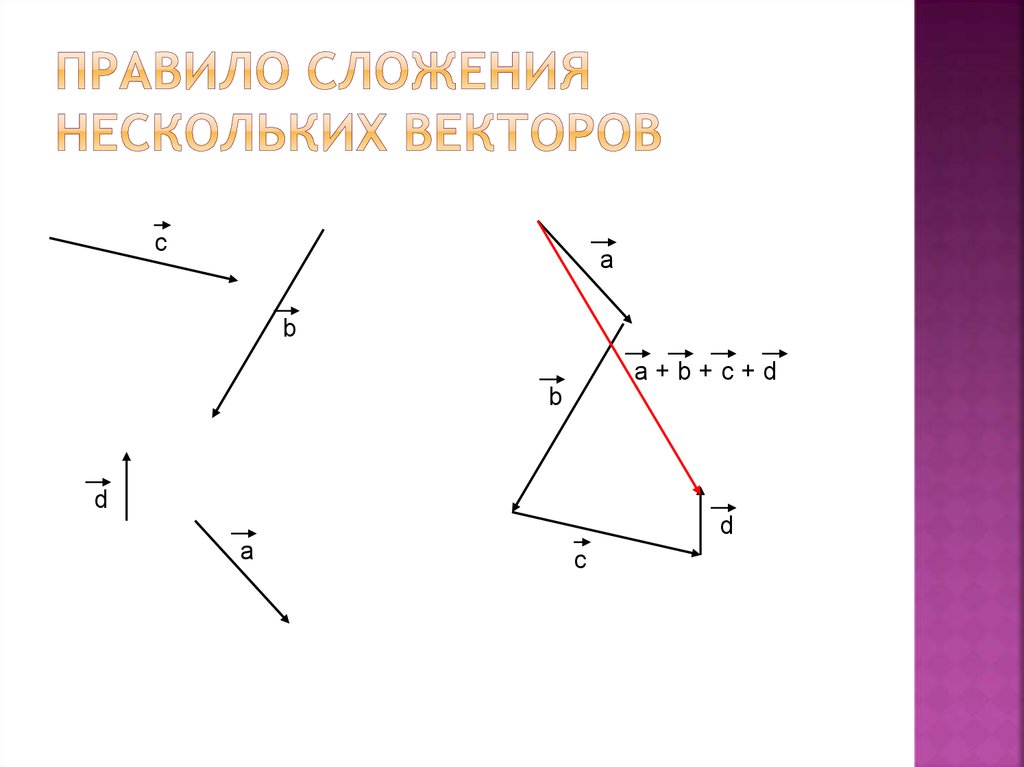 3A=10.3 блоков и
θ=29,1ºθ=29,1º
, чтобы
3A=10.3 блоков и
θ=29,1ºθ=29,1º
, чтобы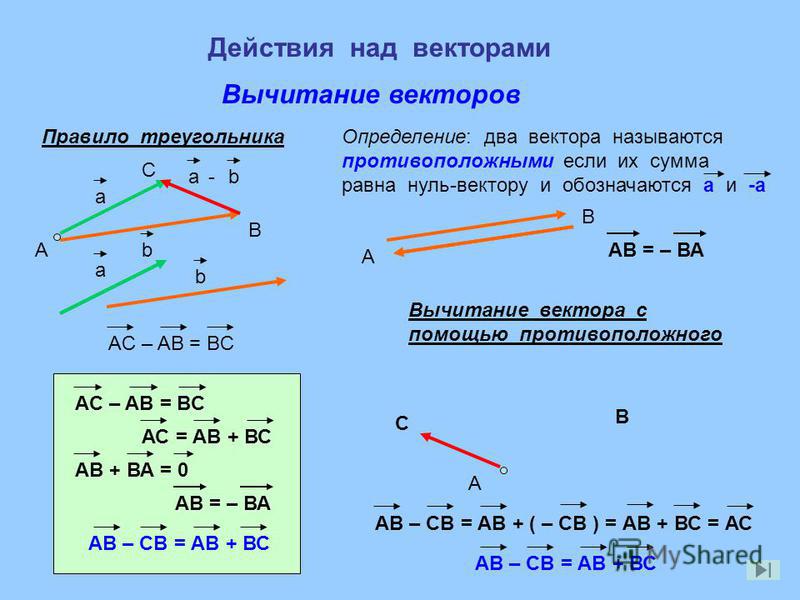
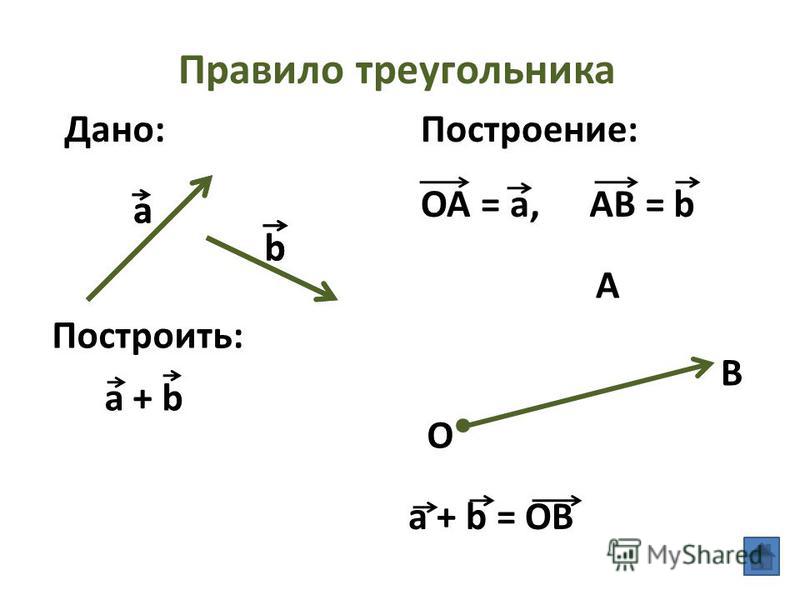 3.28, на котором векторы AA и BB складываются для получения результирующего RR.
3.28, на котором векторы AA и BB складываются для получения результирующего RR.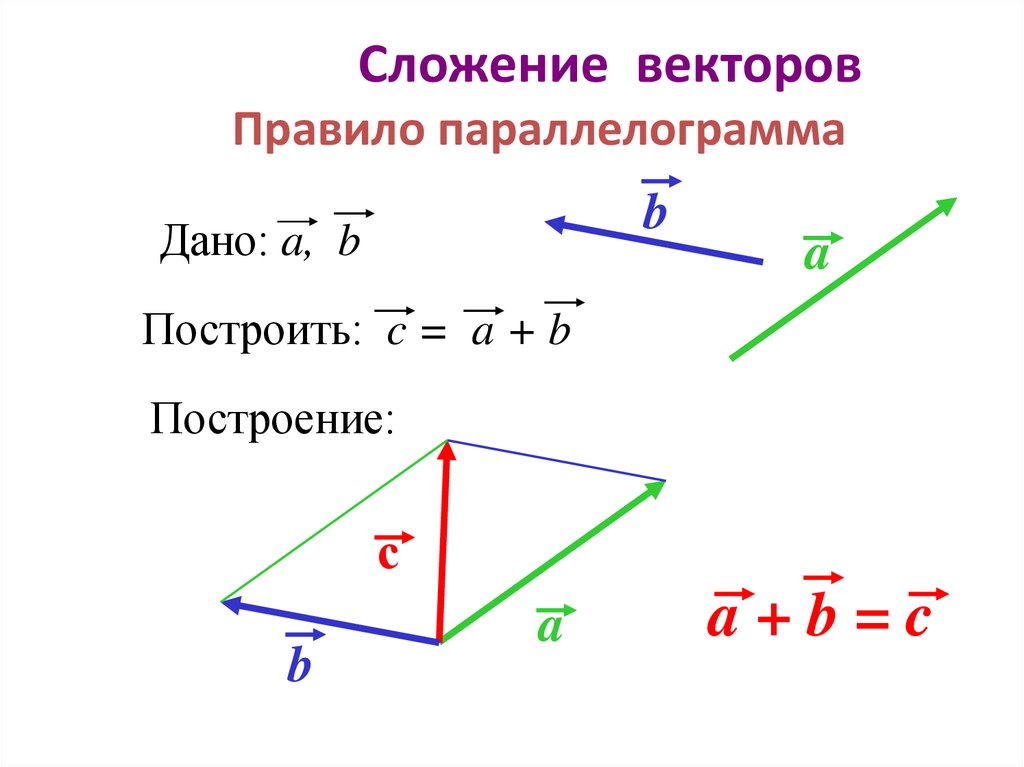
 12
12 Чтобы получить величину RR равнодействующей, используйте теорему Пифагора:
Чтобы получить величину RR равнодействующей, используйте теорему Пифагора:  Вектор BB представляет собой вторую ветвь, смещение 34,0 м34,0 м в направлении 63,0º63,0º к северу от востока.
Вектор BB представляет собой вторую ветвь, смещение 34,0 м34,0 м в направлении 63,0º63,0º к северу от востока. Мы находим компоненты x , используя Ax=AcosθAx=Acosθ, что дает
Мы находим компоненты x , используя Ax=AcosθAx=Acosθ, что дает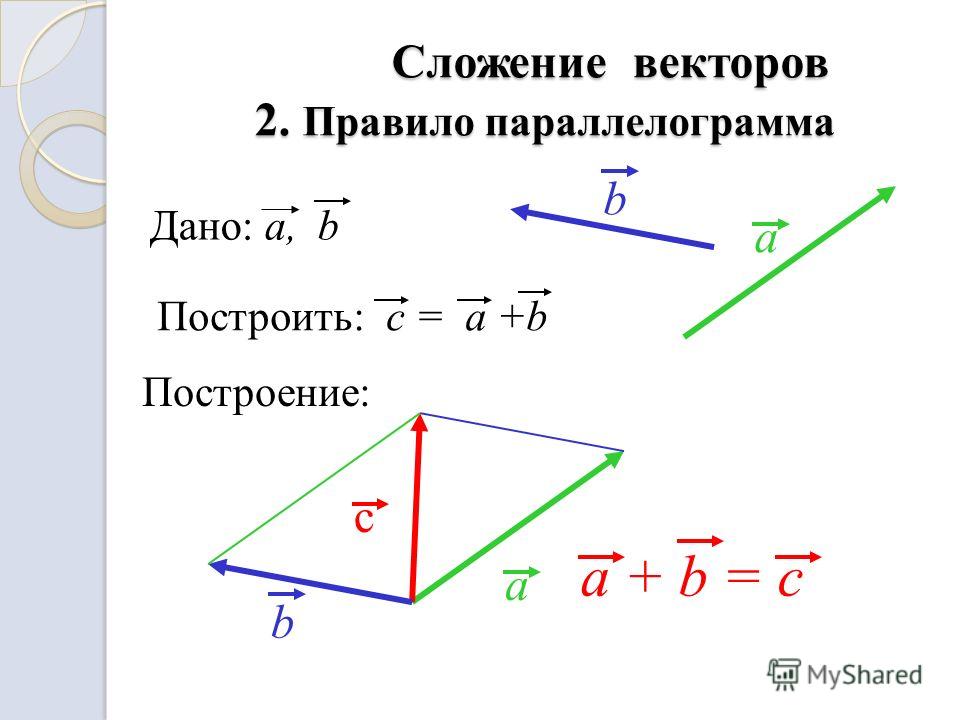 Ry=Ay+By =18,1 м+30,3 м=48,4 м.
Ry=Ay+By =18,1 м+30,3 м=48,4 м.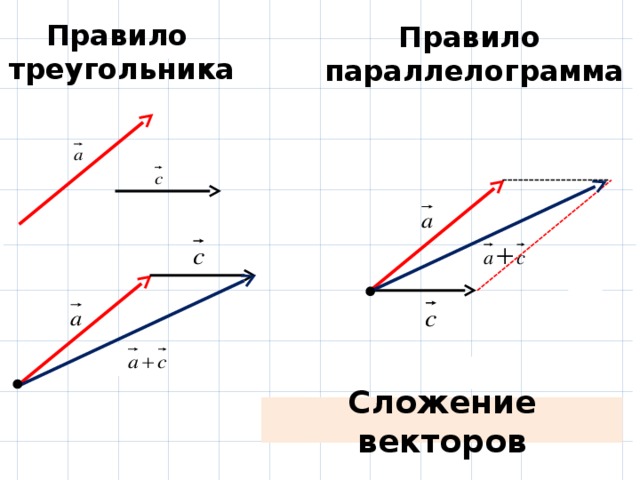 То есть A−B≡A+(–B)A−B≡A+(–B). Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты
–B–B – минусы компонентов
ББ. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R равны =Ay+(–By)Ry=Ay+(–By)
То есть A−B≡A+(–B)A−B≡A+(–B). Таким образом, метод вычитания векторов с использованием перпендикулярных компонент идентичен методу сложения . Компоненты
–B–B – минусы компонентов
ББ. Таким образом, x — и y -компоненты результирующего A−B = RA−B = R равны =Ay+(–By)Ry=Ay+(–By)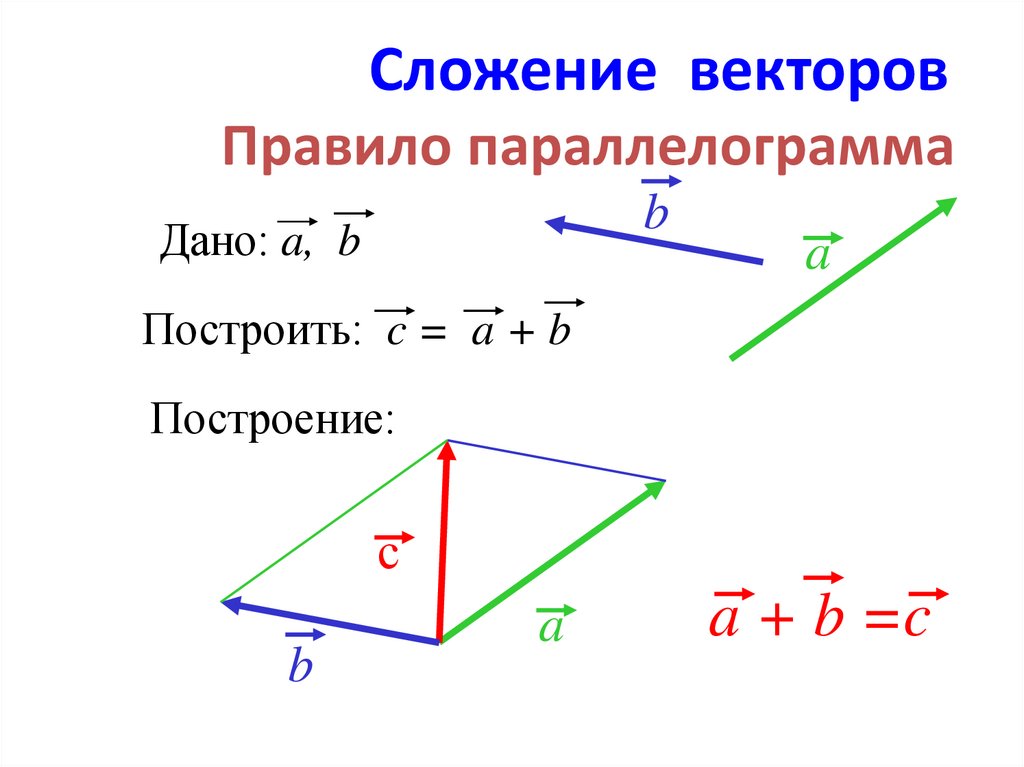
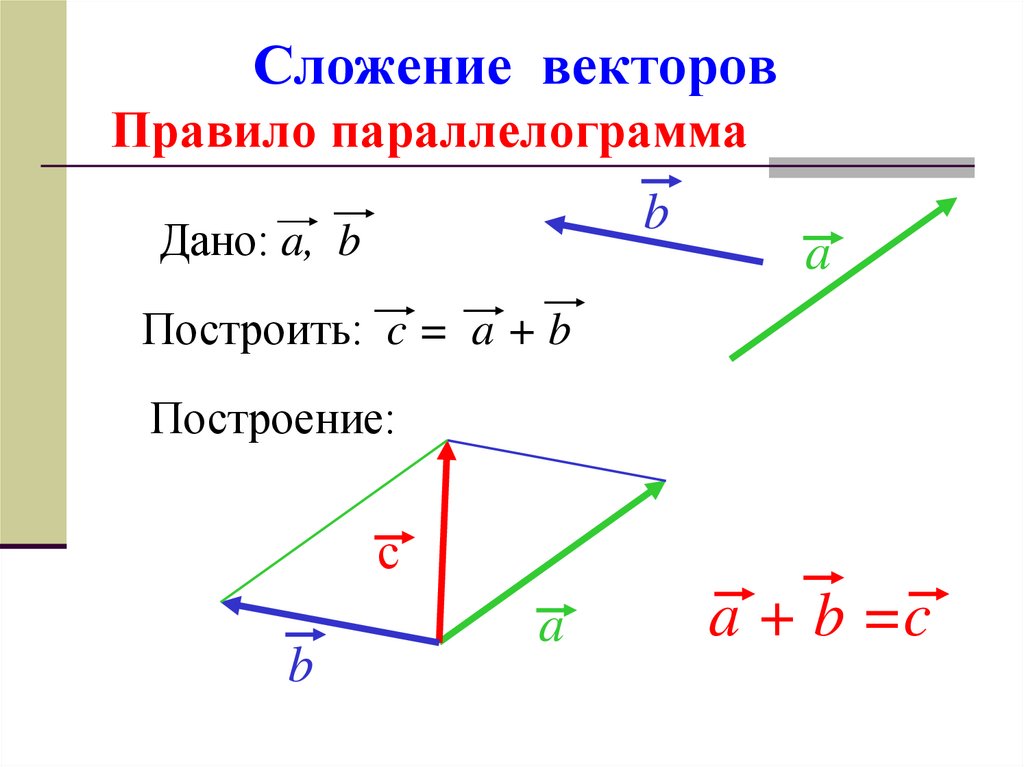 Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.
Способ добавления этих векторов может различаться в зависимости от того, заданы ли они в виде точек или в геометрическом представлении. Хотя сложение можно выполнить с помощью математики для точек, практично использовать закон параллелограмма, когда они представлены геометрически.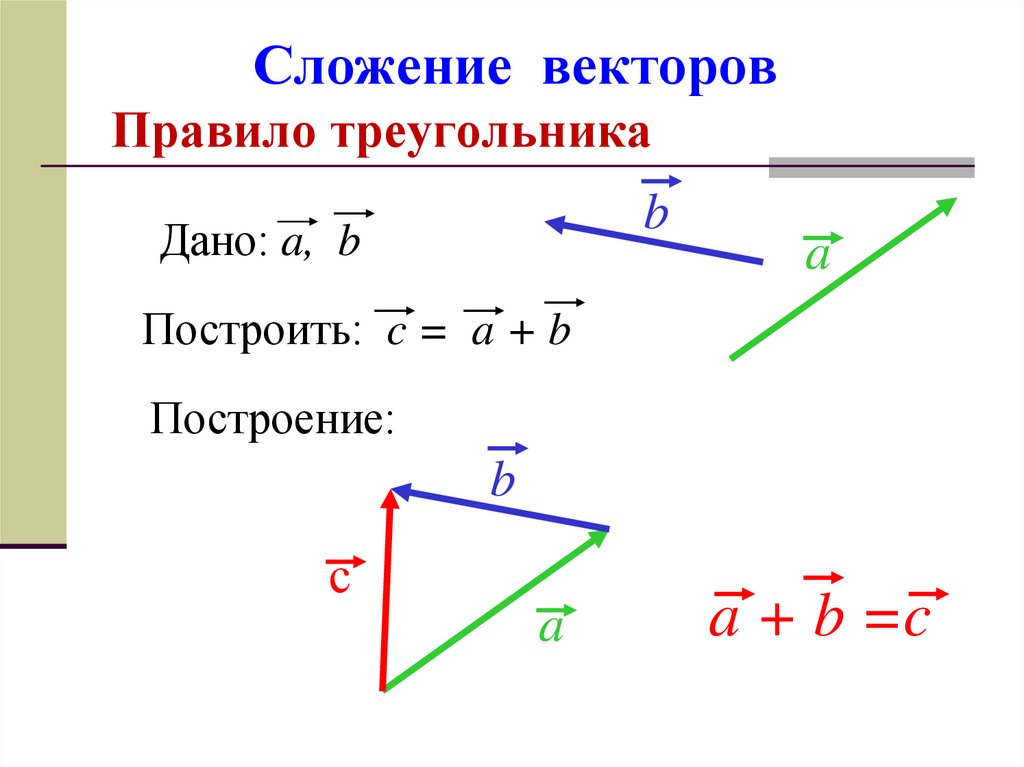
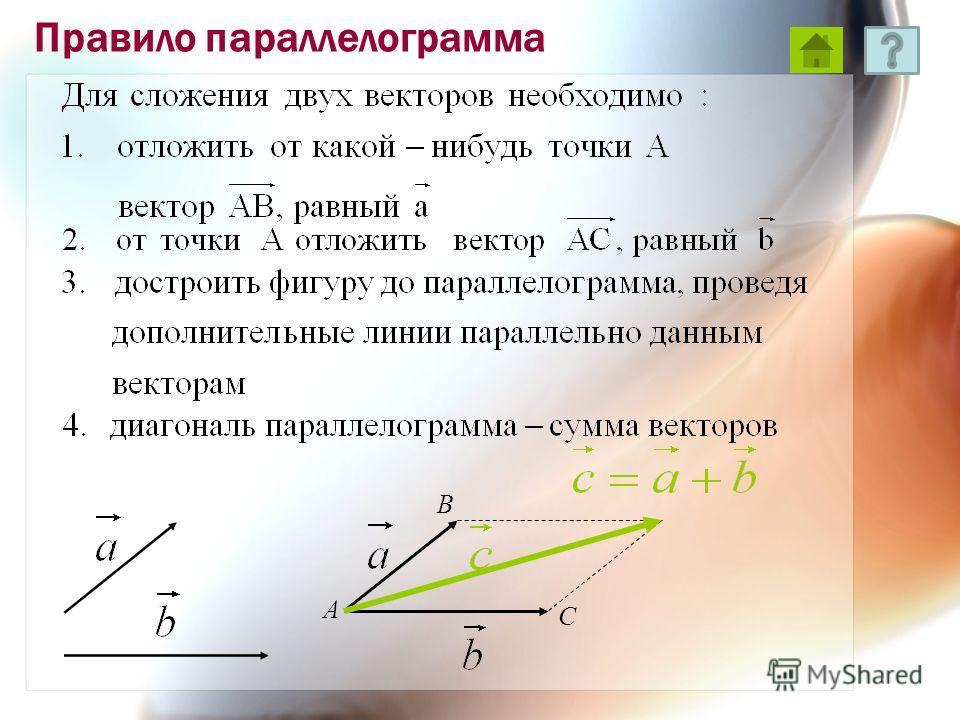
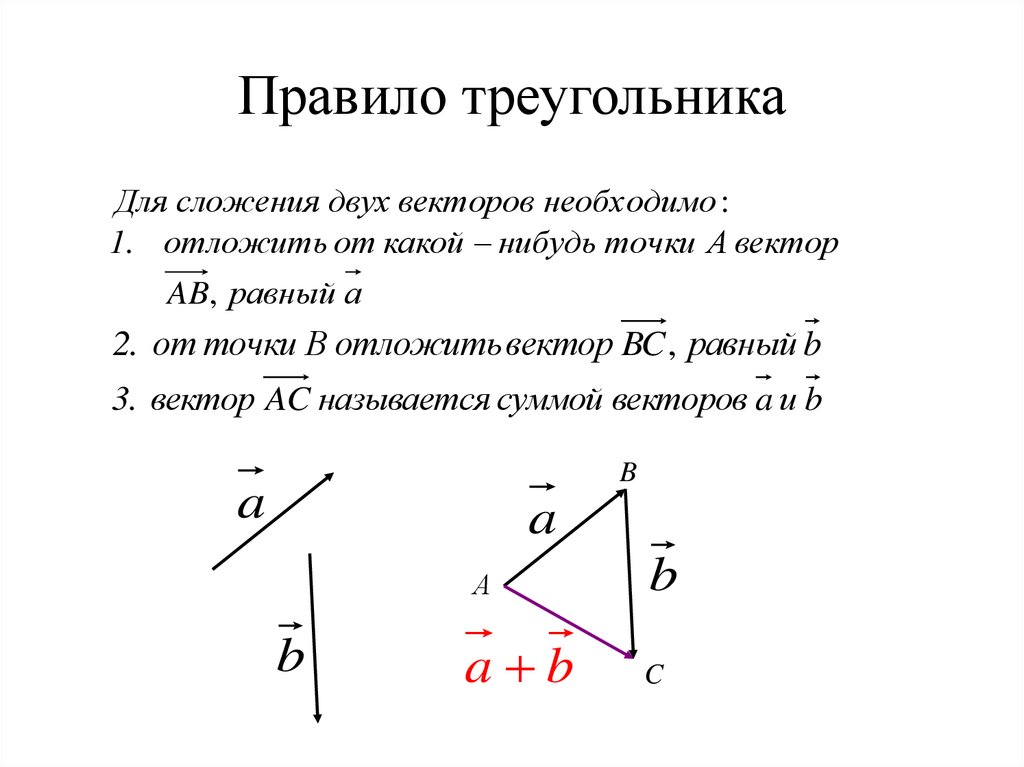
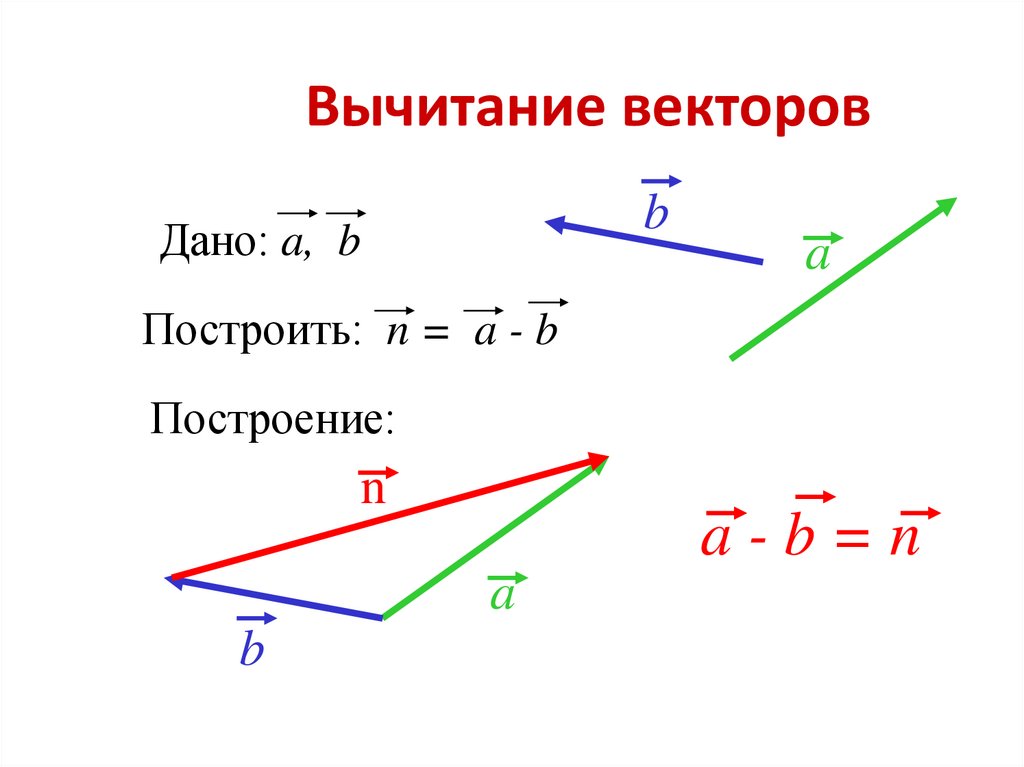
 Используя правило треугольника, найдите результирующий вектор.
Используя правило треугольника, найдите результирующий вектор.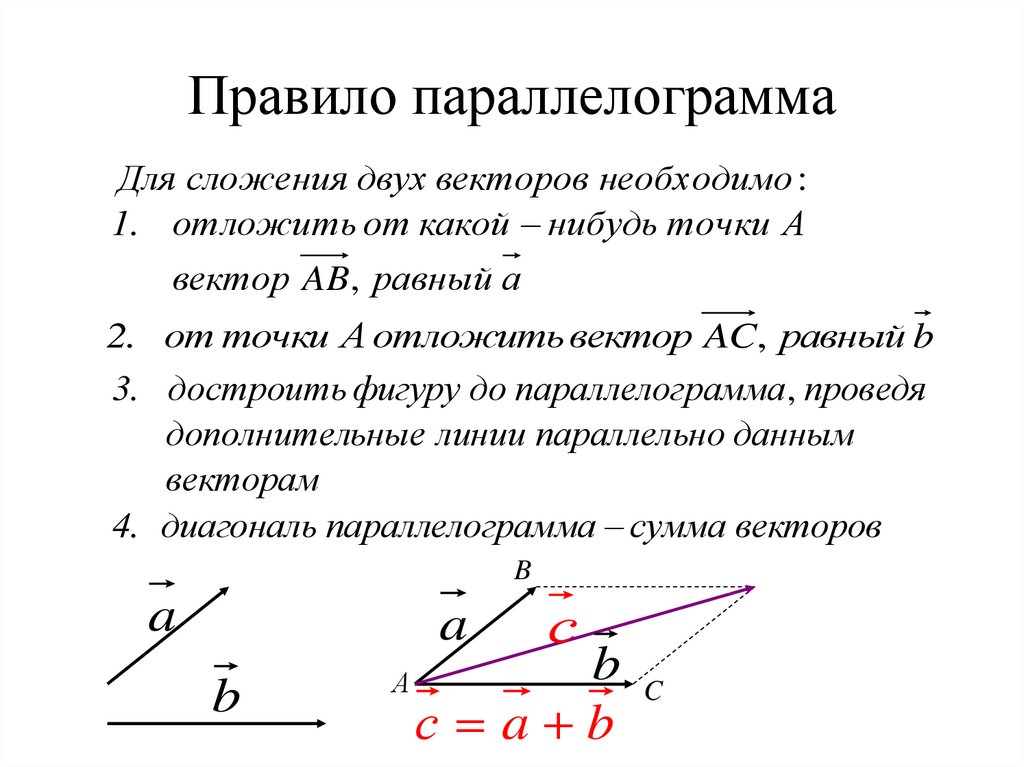
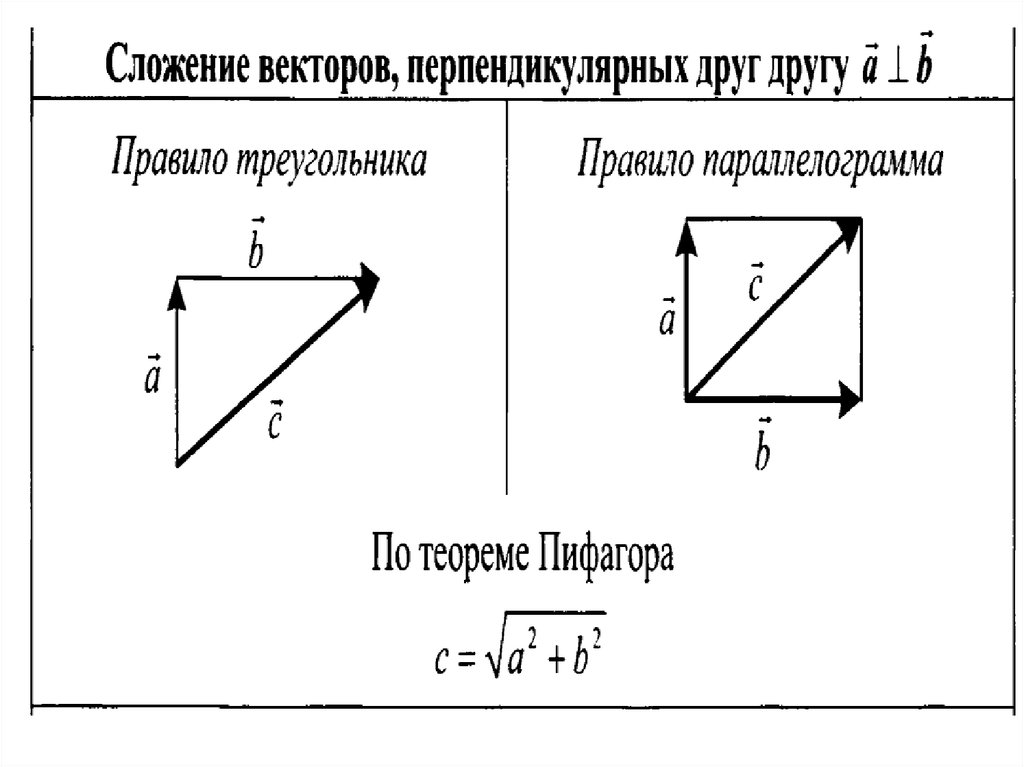
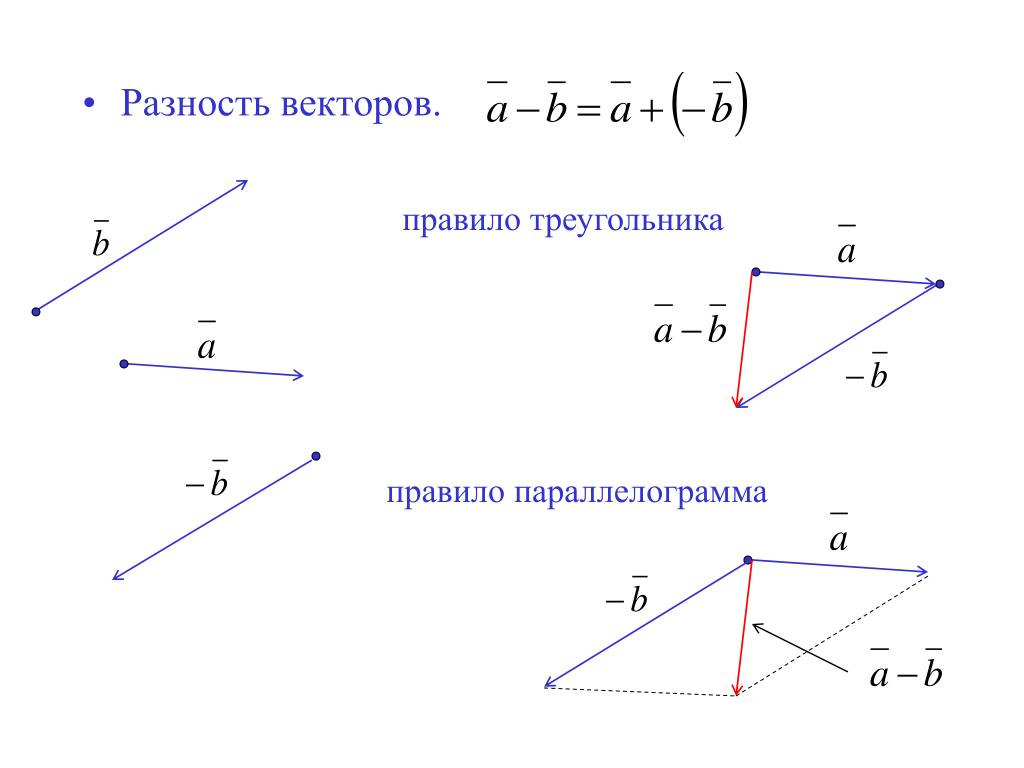


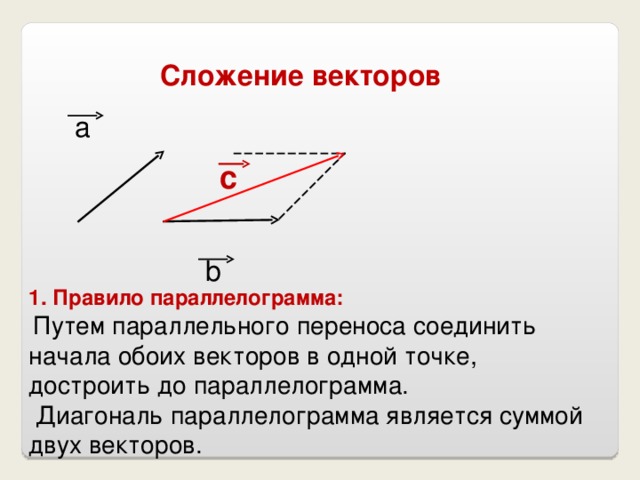
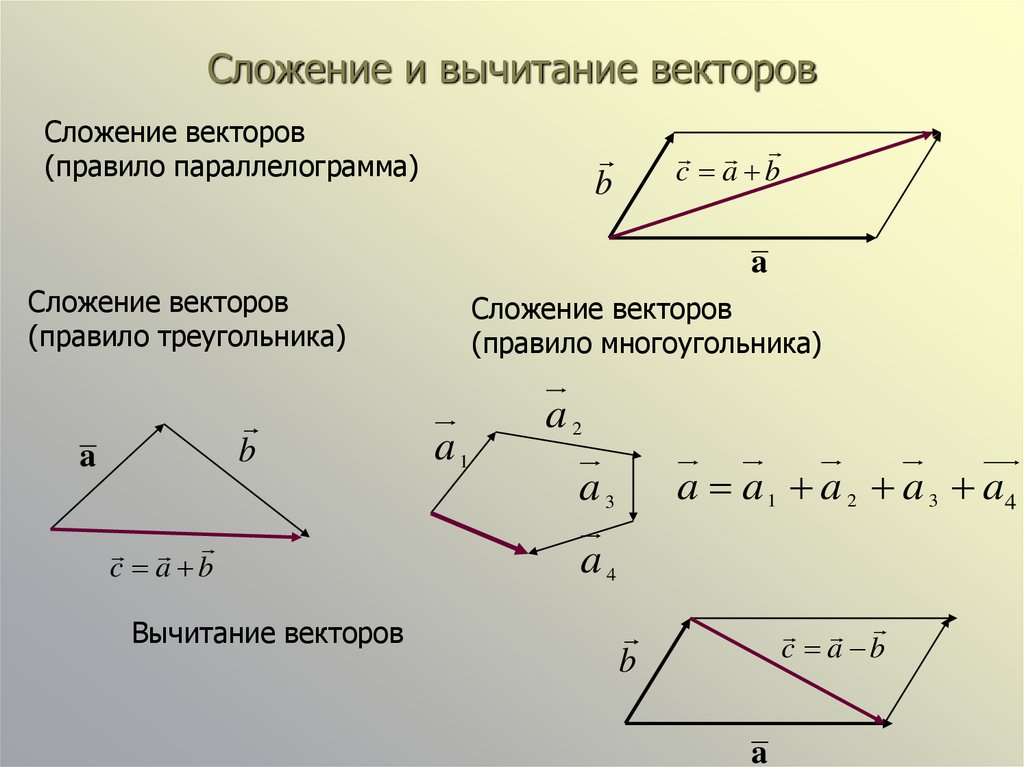

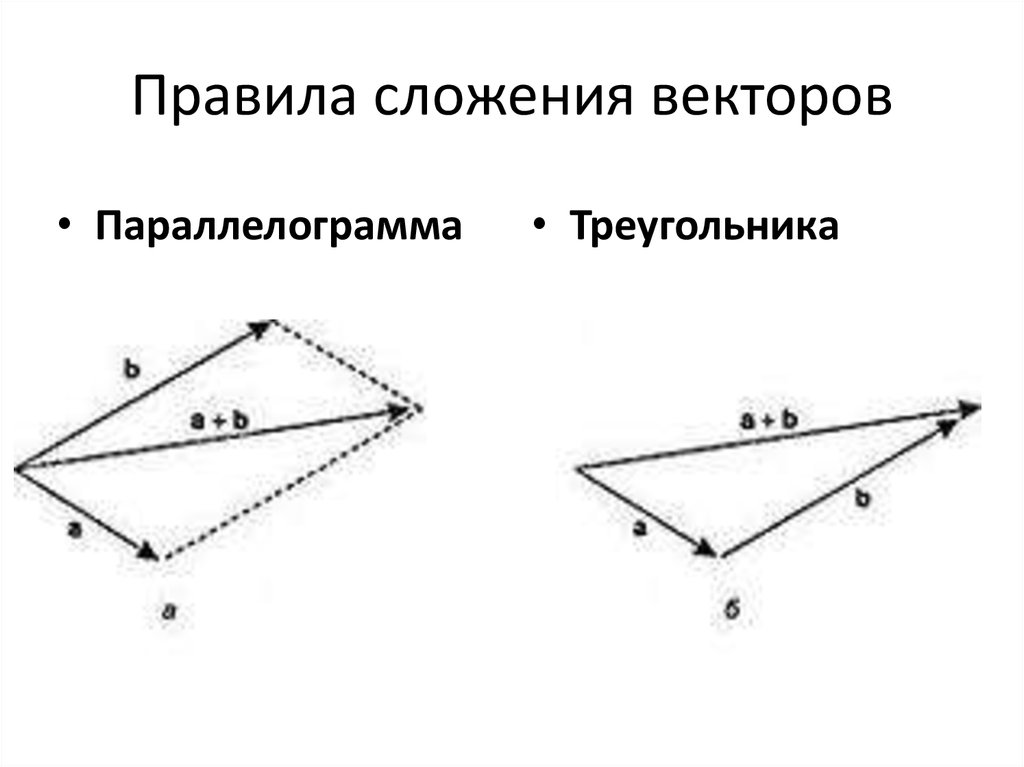
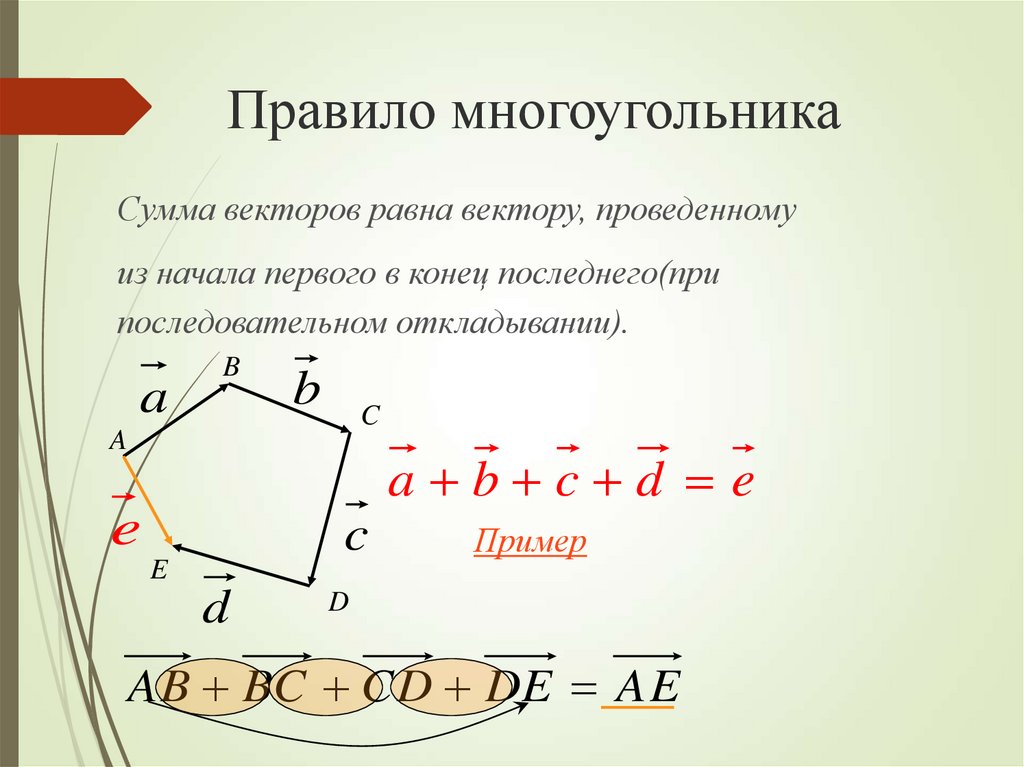 Напомним, 𝑂𝐶 — вектор положения точки
𝐶, что означает, что компоненты этого вектора задаются соответствующими координатами
𝐶. Так как мы не знаем координаты 𝐶, обозначим координаты
𝐶 на (𝑥,𝑦). Затем,
𝑂𝐶=(𝑥,𝑦).
Напомним, 𝑂𝐶 — вектор положения точки
𝐶, что означает, что компоненты этого вектора задаются соответствующими координатами
𝐶. Так как мы не знаем координаты 𝐶, обозначим координаты
𝐶 на (𝑥,𝑦). Затем,
𝑂𝐶=(𝑥,𝑦).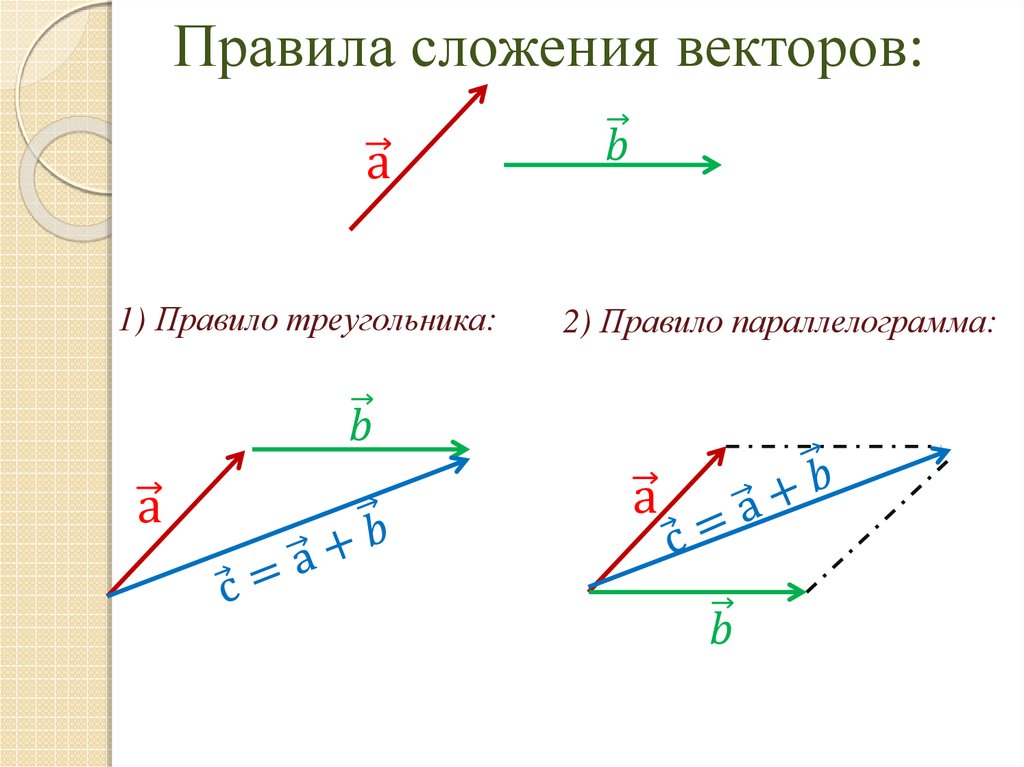 Мы знаем, что нам нужно вычислить
скалярное умножение перед сложением. Напомним, что мы можем вычислить скалярное умножение двумерного вектора, умножив
каждую компоненту вектора скаляром. Это означает
2(𝑥,𝑦)=(2𝑥,2𝑦),2(-10,10)=(-20,20).
Мы знаем, что нам нужно вычислить
скалярное умножение перед сложением. Напомним, что мы можем вычислить скалярное умножение двумерного вектора, умножив
каждую компоненту вектора скаляром. Это означает
2(𝑥,𝑦)=(2𝑥,2𝑦),2(-10,10)=(-20,20).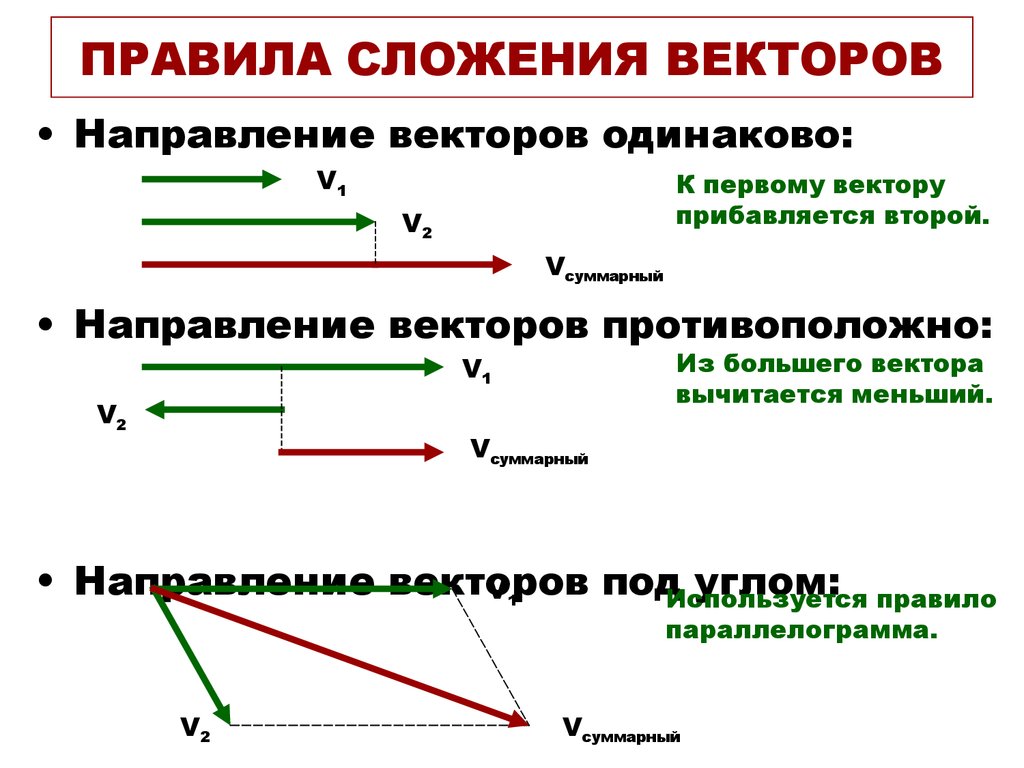 Выражение, которое нам нужно вычислить, включает скалярное умножение, сложение и вычитание двумерных векторов. Напомним, что
порядок векторных операций равен
Выражение, которое нам нужно вычислить, включает скалярное умножение, сложение и вычитание двумерных векторов. Напомним, что
порядок векторных операций равен
 Следовательно,
−2⃑𝐴=−2(−3,5)=(6,−10),2⃑𝐵=2(2,0)=(4,0),2⃑𝐶=2(−4,5)=(−8,10) .
Следовательно,
−2⃑𝐴=−2(−3,5)=(6,−10),2⃑𝐵=2(2,0)=(4,0),2⃑𝐶=2(−4,5)=(−8,10) .