4.2. Основные законы алгебры логики и правила преобразования логических выражений. Информатика: аппаратные средства персонального компьютера
4.2. Основные законы алгебры логики и правила преобразования логических выражений. Информатика: аппаратные средства персонального компьютераВикиЧтение
Информатика: аппаратные средства персонального компьютера
Яшин Владимир Николаевич
Содержание
4.2. Основные законы алгебры логики и правила преобразования логических выражений
В алгебре логики имеются законы, которые записываются в виде соотношений. Логические законы позволяют производить равносильные (эквивалентные) преобразования логических выражений. Преобразования называются равносильными, если истинные значения исходной и полученной после преобразования логической функции совпадают при любых значениях входящих в них логических переменных.
Для простоты записи приведем основные законы алгебры логики для двух логических переменных
1. Закон противоречия:
2. Закон исключенного третьего:
3. Закон двойного отрицания:
4. Законы де Моргана:
5. Законы повторения: A & A = A; A v A = A; В & В = В; В v В = В.
6. Законы поглощения: A ? (A & B) = A; A & (A ? B) = A.
7. Законы исключения констант: A ? 1 = 1; A ? 0 = A; A & 1 = A; A & 0 = 0; B ? 1 = 1; B ? 0 = B; B & 1 = B; B & 0 = 0.
8. Законы склеивания:
9. Закон контрапозиции: (A ? B) = (B ? A).
Для логических переменных справедливы и общематематические законы. Для простоты записи приведем общематематические законы для трех логических переменных
1. Коммутативный закон: A & B = B & A; A ? B = B ? A.
2. Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C.
Ассоциативный закон: A & (B & C) = (A & B) & C; A ? (B ? C) = (A ? B) ? C.
3. Дистрибутивный закон: A & (B ? C) = (A & B) ? (A & C).
Как уже отмечалось, с помощью законов алгебры логики можно производить равносильные преобразования логических выражений с целью их упрощения. В алгебре логики на основе принятого соглашения установлены следующие правила (приоритеты) для выполнения логических операций: первыми выполняются операции в скобках, затем в следующем порядке: инверсия (отрицание), конъюнкция ( & ), дизъюнкция (v), импликация (?), эквиваленция (?)
Выполним преобразование, например, логической функции
применив соответствующие законы алгебры логики.
Данный текст является ознакомительным фрагментом.
Пользовательский интерфейс и основные правила работы с программой
Пользовательский интерфейс и основные правила работы с программой
После запуска программы на экране отображается ее пользовательский интерфейс, который представлен на рис.
Правила написания выражений
Правила написания выражений В процессе чтения этой главы мы изучили множество выражений JavaScript. Но так и не узнали, по каким правилам они пишутся. Настала пора восполнить пробел в наших знаниях.— Между операндами, операторами, вызовами функций и методов и ключевыми
Правила написания выражений
Правила написания выражений В процессе чтения этой главы мы изучили множество выражений JavaScript. Но так и не узнали, по каким правилам они пишутся. Настала пора восполнить пробел в наших знаниях.— Между операндами, операторами, вызовами функций и методов и ключевыми
Основные законы теории цепей
Основные законы теории цепей
При изучении электрических цепей широко применяется второй закон Кирхгофа, согласно которому алгебраическая сумма напряжений на замкнутом контуре равна 0. Первый закон Кирхгофа относится к токам, подходящим к узлу, и утверждает, что
Первый закон Кирхгофа относится к токам, подходящим к узлу, и утверждает, что
Глава 1 Основные правила оформления рефератов, курсовых и дипломных работ
Глава 1 Основные правила оформления рефератов, курсовых и дипломных работ • Общие сведения об оформлении• Структура работы• Межгосударственный стандарт ГОСТ 7.1—2003• Заголовки• Оформление текста (границы, абзацы, размер шрифта,
2.2. Основные правила форматирования
2.2. Основные правила форматирования Форматирование текстаТекст в редакторе Word можно набирать разными шрифтами. Программа предусматривает установку размера, типа и начертания шрифта. Перед форматированием необходимо выделить фрагмент текста, который требуется
6. Выражения реляционной алгебры
6.
Глава 1 Основные правила оформления рефератов, курсовых и дипломных работ
Глава 1 Основные правила оформления рефератов, курсовых и дипломных работ Сведения о правилах оформления рефератов, курсовых и дипломных работ обычно предоставляют студентам в каждом учебном заведении. В большинстве случаев можно выделить основные общие требования и
2.2. Основные правила форматирования
 Перед форматированием необходимо выделить фрагмент текста, который требуется
Перед форматированием необходимо выделить фрагмент текста, который требуется5.2.1. Основные правила эксплуатации ноутбука
5.2.1. Основные правила эксплуатации ноутбука Не нужно загромождать воздушное пространство на расстоянии примерно 10–15 см вокруг ноутбука — оно необходимо для нормальной вентиляции.Не курите рядом с ноутбуком, чтобы пепел не падал на клавиатуру.Не нужно принимать пищу и
5.1.3. Основные правила набора текста
5.1.3. Основные правила набора текста При работе с электронным документом помимо правил русского языка следует знать и использовать правила набора текста? Переход на новую строку в процессе набора текста происходит автоматически, не требуя ввода специального символа?
Основные правила работы за компьютером
Основные правила работы за компьютером Многие родители, родственники, руководители учебных заведений задаются не праздным вопросом о том, существуют ли правила работы с компьютером, позволяющие сохранить здоровье и продуктивно работать? Разные исследователи и научные
Основные правила композиции
Основные правила композиции
Ваши фотографии должны смотреться красиво и привлекательно, а для этого при построении кадра необходимо соблюдать несложные правила, которые обеспечат снимкам наилучший вид. Эти правила нужно «пропустить через себя», то есть добиться того,
Эти правила нужно «пропустить через себя», то есть добиться того,
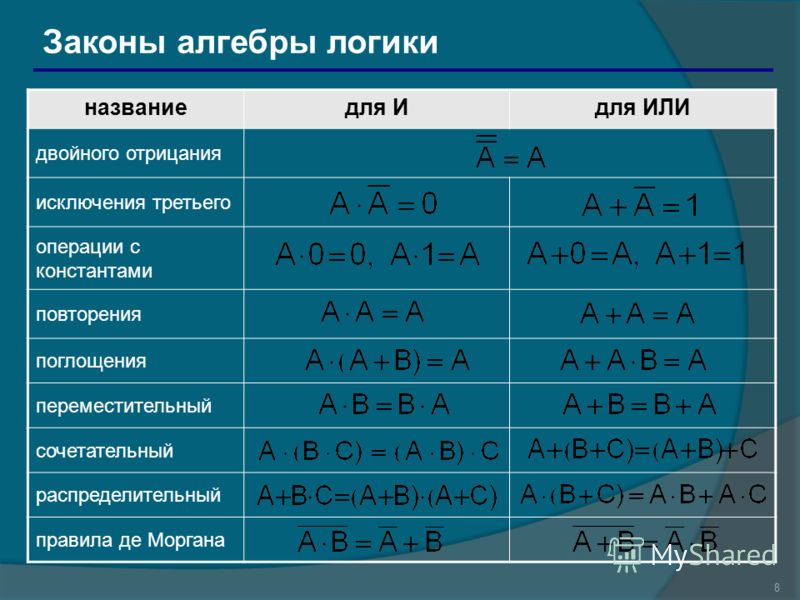
5.1.3 Законы (правила преобразования) алгебры логики
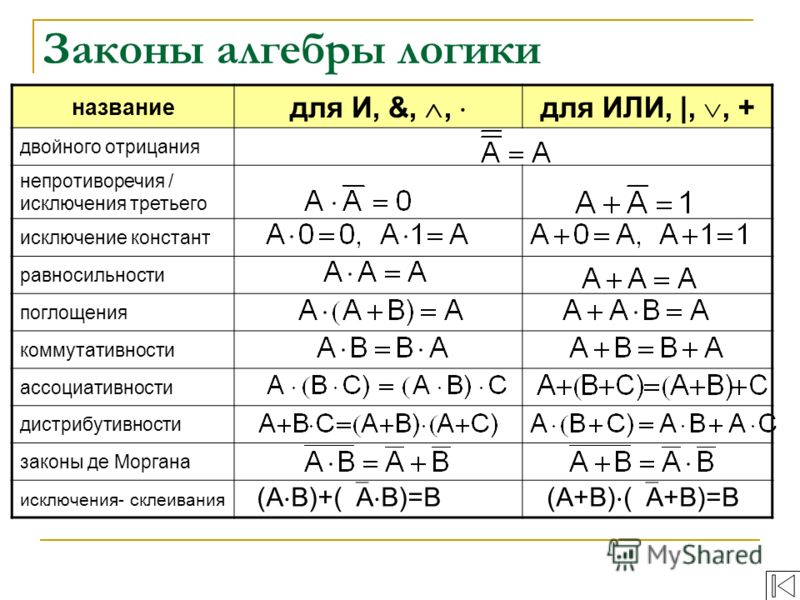
Таблица 5.3 Правила преобразования алгебры логики
Логические формулы
Закон
a b = b a ; a + b = b + a
Переместительный
( a + b ) c = a c + b c
Распределительный
( a + c ) ( b + c ) = a b + c
Распределительный
a.
 a
= a ; a + a = a
a
= a ; a + a = aПовторения
a .1 = a ; a + 1 = 1
Множества
Дополнения
де Моргана
де Моргана
Склеивания
Докажем справедливость неочевидных преобразований:
;
;
.
Справедливость привил де Моргана докажем, сравнив таблицы соответствия.
№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
2 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
3 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
4 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
Сравнивая восьмой
и девятый столбцы, докажем равенство
.
Сравнивая седьмой и десятый столбцы, докажем равенство .
Преобразование ДНФ в СДНФ.
Совершенные формы единственны и обычно являются исходными для минимизации по алгоритмам, обеспечивающим получения минимальных логических формул.
Для развертывания ДНФ в каждое слагаемое добавляется недостающая переменная, используя правило , и раскрываются скобки.
Процедура повторяется до тех пор, пока слагаемые не станут содержать все переменные.
Пример. ДНФ = , преобразуем в СДНФ
Преобразование КНФ в СКНФ.
В каждую сумму добавляем недостающую переменную, используя правило . Разворачиваем результат в КНФ, используя правило
.
Процедура повторяется до тех пор, пока суммы не станут содержать все переменные.
Пример. КНФ= , преобразуем вCRYA
Минимизация
логических функций (уменьшение числа
букв в логической формуле) необходима
для реализации функции минимальным
числом логических элементов. Минимизация
осуществляется путем преобразования
логической формулы по правилам,
приведенным в табл.4.3, или по карте
Карно.
Минимизация
осуществляется путем преобразования
логической формулы по правилам,
приведенным в табл.4.3, или по карте
Карно.
Условия минимизации:
Задана логическая функция в виде логической формулы, таблицы состояния, СДНФ, карты Карно.
Система элементарных логических функций, которой будет реализована минимальная формула.
Сложность реализации (цена) каждой элементарной функции.
Критерий минимизации (экономичность, быстродействие, минимум элементов и т.д.).
Реально разработаны
алгоритмы минимизирующие число букв в
логическом выражении в элементном
базисе И. ИЛИ, НЕ. Считается, что инверсия
не требует дополнительных затрат. Такие
алгоритмы хорошо подходят для релейных
схем. Для бесконтактных логических
элементов минимизация заключается в
минимизации корпусов микросхем, что
трудно формализовать.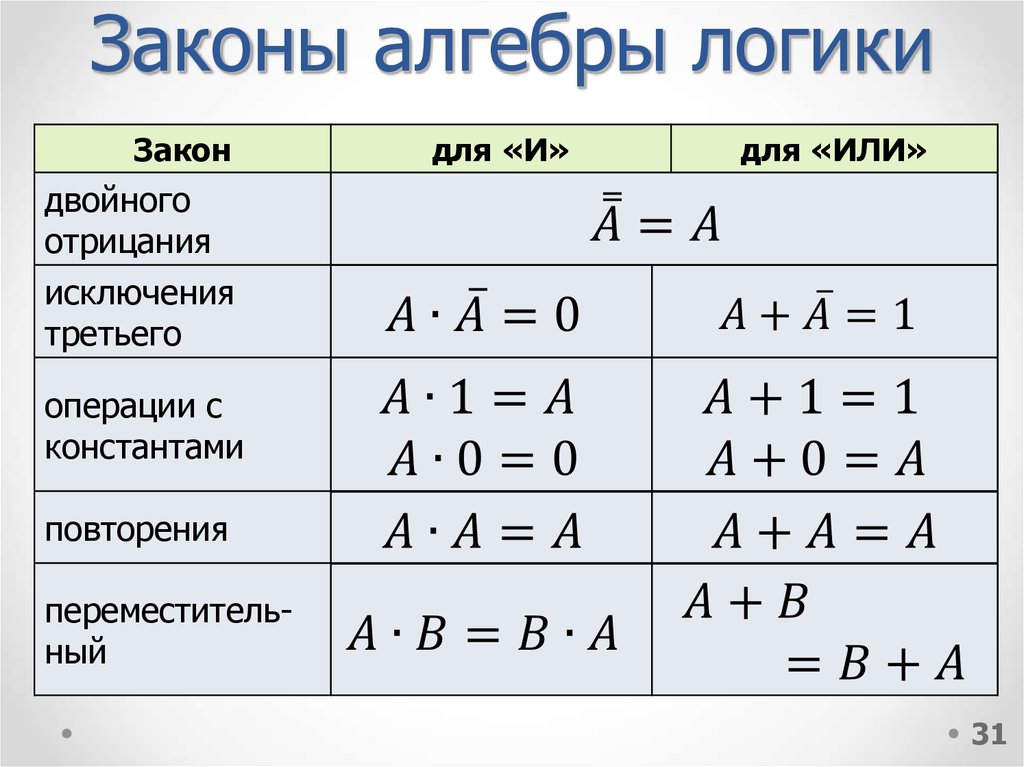
Непосредственная минимизация по алгоритму Квайна
Исходной является СДНФ. Соседними слагаемыми называются такие, которые отличаются значением только одной переменной, то есть в одном слагаемом переменная без инверсии, в другом с инверсией.
1. Для каждой пары соседних слагаемых применяют операцию склеивания .
2. Приводят подобные слагаемые по правилу а + а = а.
3. повторяют пункты 1 и 2 пока это возможно.
4. Применяют, если это возможно, формулу .
Пример. Минимизировать СДНФ .
Имеем три пары соседних слагаемых (каждое слагаемое может многократно входить в пару).
Соседние слагаемые | Результат склеивания |
Минимизация логической функции с помощью карты Карно
Минимизация логической функции с помощью карты Карно осуществляется по следующему алгоритму:
Для получения ДНФ все единицы объединяются в прямоугольные контуры, не содержащие внутри нулей, с числом клеток в контуре , гдеn = 0, 1, 2, 3,.
 ..
..Контур проводится через соседние клетки, т.е. клетки, отличающие значением только одной переменной.
Контуры могут частично накладываться друг на друга и должны иметь максимальные возможные размеры.
Единичному контуру соответствует произведение переменных, в области единичного значения которых он находится полностью, т.е. границ их изменения не пересекает.
ДНФ получается в виде суммы значений всех единичных контуров.
Для получения минимальной ДНФ размеры контуров должны быть максимальны, а их число минимально.
Для получения КНФ все нули объединяются в прямоугольные контуры, не содержащие внутри единиц, с числом клеток в контуре , гдеn = 0, 1, 2, 3…
Контур проводится через соседние клетки, т.е. клетки, отличающие значением только одной переменной.

Контуры могут частично накладываться друг на друга и должны иметь максимальные возможные размеры.
Нулевому контуру соответствует сумма инвертированных значений переменных, в области единичного или нулевого значения которых он находится полностью, т.е. границ их изменения не пересекает.
КНФ получается в виде произведения значений всех нулевых контуров.
Для получения минимальной КНФ размеры контуров должны быть максимальны, а их число минимально.
Пример: Минимизировать карту Карно, приведенную на рис.4.2.
Рис.5.2 Карта Карно с единичными и нулевыми контурами
Анализ единичных контуров дает следующее выражение для ДНФ
(5.3)
/ \
контур 1 контур 2
Анализ нулевых контуров дает следующее выражение для КНФ
(5. 4)
4)
/ \
контур 3 контур 4
Переход от логической формулы к логической схеме
Логические элементы, при построении логической схемы, располагаются в том же порядке, в каком выполняются логические операции в формуле. При этом формула преобразуется так, чтобы группы операций соответствовали функциям, выполняемым элементами, на базе которых строится схема.
Пример: Постройте логическую схему на базе элементов «И-НЕ» и «НЕ» для логической формулы .
Преобразуем формулу, выразив ее через операции «И-НЕ» и «НЕ», для чего применим закон двойного отрицания, а затем правило де Моргана
. (5.5)
Логическая схема, соответствующая преобразованному выражению (4.5) приведена на рис.4.3.
Рис.5.3 Схемная реализация формулы (4.5).
Пример: Постройте логическую схему на базе элементов «ИЛИ-НЕ» и «НЕ» для логической формулы .
Преобразуем формулу, выразив ее через операции «ИЛИ-НЕ» и «НЕ», для чего применим закон двойного отрицания, а затем правило де Моргана
. (5.6)
(5.6)
Логическая схема, соответствующая преобразованному выражению (5.6) приведена на рис.5.4. Следует отметить, что структура реализации формул (5.5) и (5.6) отличаются лишь инвертором в схеме рис. 5.4, то есть реализация в базисе ИЛИ-НЕ оказалась более сложной. Однако, если за исходную формулу взять КНФ, то реализация в базисе ИЛИ-НЕ окажется более компактной, чем реализация в базисе И-НЕ.
Рис5.4 Схемная реализация формулы (5.6)
Законы и правила булевой алгебры
следующий → ← предыдущая В упрощении булевых выражений важную роль играют законы и правила булевой алгебры. Прежде чем понять эти законы и правила булевой алгебры, разберитесь с концепцией сложения и умножения логических операций. Логическое сложение Операция сложения в булевой алгебре аналогична операции ИЛИ. В цифровых схемах операция ИЛИ используется для вычисления суммирующего члена без использования операции И. Булево умножениеОперация умножения в булевой алгебре аналогична операции И. В цифровых схемах операция И вычисляет произведение без использования операции ИЛИ. AB, AB, ABC и ABCD — вот некоторые из примеров термина продукта. Значение термина произведения истинно, когда все литералы истинны, и ложно, когда любой из литералов ложен. Законы булевой алгебрыСуществуют следующие законы булевой алгебры: Коммунативное правоЭтот закон гласит, что независимо от того, в каком порядке мы используем переменные. Это означает, что порядок переменных не имеет значения. В булевой алгебре операции ИЛИ и сложения аналогичны. На приведенной ниже диаграмме вентиль ИЛИ показывает, что порядок входных переменных вообще не имеет значения. Для двух переменных переместительный закон сложения записывается как: А+В = В+А Для двух переменных коммутативный закон умножения записывается как: А. Ассоциативный законЭтот закон гласит, что операция может выполняться в любом порядке при одинаковом приоритете переменных. Поскольку «*» и «/» имеют одинаковый приоритет. На приведенной ниже диаграмме ассоциативный закон применяется к вентилю ИЛИ с двумя входами. Для трех переменных ассоциативный закон сложения записывается как: А + (В + С) = (А + В) + С Для трех переменных ассоциативный закон умножения записывается как: А(ВС) = (АВ)С Согласно этому закону, независимо от того, в каком порядке группируются переменные, при выполнении И более двух переменных. На приведенной ниже диаграмме ассоциативный закон применяется к вентилю И с двумя входами. Распределительный закон: В соответствии с этим законом, если мы выполняем операцию ИЛИ двух или более переменных, а затем выполняем операцию И результата с одной переменной, то результат будет аналогичен выполнению операции И этой одиночной переменной с каждыми двумя или более переменным, а затем выполнить операцию ИЛИ этого продукта. Для трех переменных распределительный закон записывается как: А(В + С) = АВ + АС Правила булевой алгебрыСуществуют следующие правила булевой алгебры, которые в основном используются для обработки и упрощения логических выражений. Эти правила играют важную роль в упрощении логических выражений.
Правило 1: А + 0 = АДопустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию ИЛИ с 0, результат будет таким же, как и входная переменная. Итак, если значение переменной равно 1, то результатом будет 1, а если значение переменной равно 0, то результатом будет 0. Схематически это правило можно определить как: Правило 2: (А + 1) = 1Допустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию ИЛИ с 1, результатом всегда будет 1. Таким образом, если значение переменной равно 1 или 0, то результатом всегда будет 1. Схематически , это правило можно определить как: Правило 3: (А.0) = 0 Допустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию AND с 0, результатом всегда будет 0. Это правило гласит, что входная переменная, объединенная AND с 0, всегда равна 0. Правило 4: (А.1) = АДопустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию И с 1, результат всегда будет равен входной переменной. Это правило гласит, что входная переменная, объединенная по И с 1, всегда равна входной переменной. Схематически это правило можно определить как: Правило 5: (А + А) = АДопустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию ИЛИ с той же переменной, результат всегда будет равен входной переменной. Это правило утверждает, что входная переменная, объединенная ИЛИ с самой собой, всегда равна входной переменной. Схематически это правило можно определить как: Правило 6: (А + А’) = 1 Допустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию ИЛИ с дополнением этой переменной, результат всегда будет равен 1. Это правило гласит, что переменная, объединенная ИЛИ с ее дополнением, равна 1 всегда. Правило 7: (А.А) = АДопустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию И с той же переменной, результат всегда будет равен только этой переменной. Это правило гласит, что переменная, объединенная по И с самой собой, всегда равна входной переменной. Схематически это правило можно определить как: Правило 8: (А.А’) = 0Допустим; у нас есть входная переменная A, значение которой равно 0 или 1. Когда мы выполняем операцию И с дополнением этой переменной, результат всегда будет равен 0. Это правило гласит, что переменная, объединенная И с ее дополнением, равна 0 всегда. Схематически это правило можно определить как: Правило 9: А = (А’)’ Это правило гласит, что если мы выполним двойное дополнение переменной, результат будет таким же, как исходная переменная. Итак, когда мы выполняем дополнение переменной A, результатом будет A’. Далее, если мы снова выполним дополнение A’, мы получим A, т. Правило 10: (А + АВ) = АМы можем доказать это правило, используя правило 2, правило 4 и распределительный закон: A + AB = A(1 + B) Факторинг (распределительный закон) Правило 11: А + АВ = А + ВМы можем доказать это правило, используя приведенные выше правила как: A + AB = (A + AB)+ AB Правило 10: A = A + AB Правило 12: (А + В)(А + С) = А + ВСМы можем доказать это правило, используя приведенные выше правила как: (A + B)(A + C)= AA + AC + AB + BC Распределительный закон Следующая темаЛогические вентили ← предыдущая следующий → |
Законы и теоремы булевой алгебры
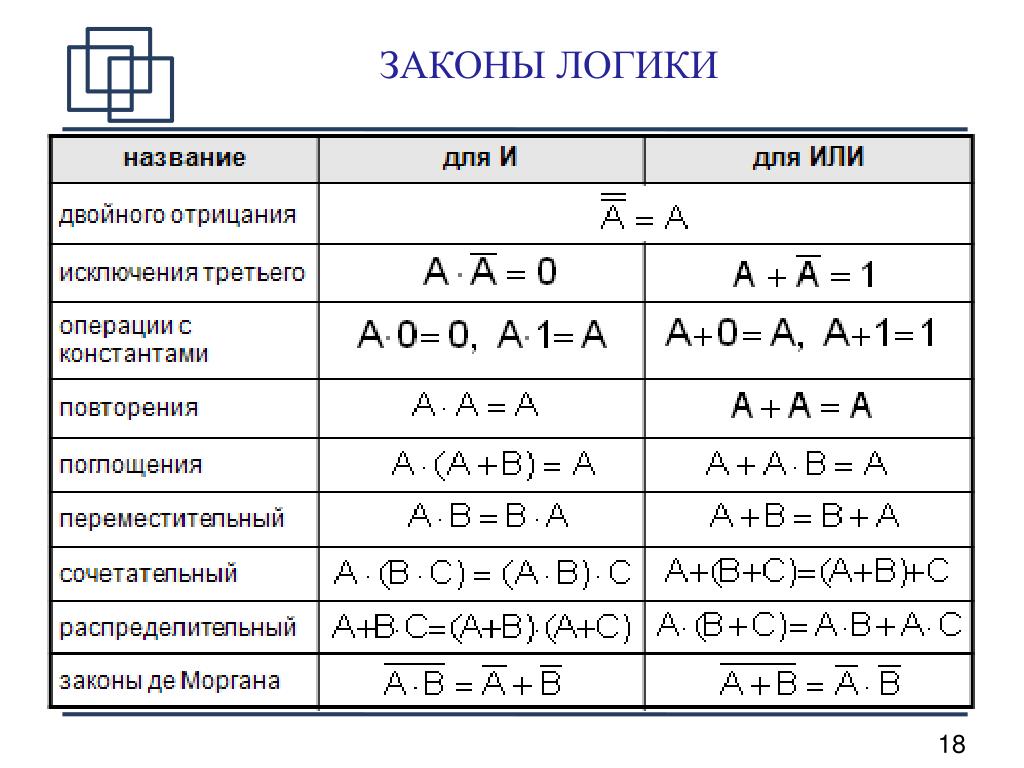
Законы и теоремы булевой алгебры| 1а. | Х • 0 = 0 | 1б. | Х + 1 = 1 | Закон об аннулировании | ||
| 2а. | Х • 1 = Х | 2б. | Х + 0 = Х | Закон о личности | ||
| 3а. | Х • Х = Х | 3б. | Х + Х = Х | Закон идемпотента | ||
| 4а. | Х • Х = 0 | 4б. | Х + Х = 1 | Закон о дополнении | ||
5. | Х = Х | Закон о двойном отрицании | ||||
| 6а. | Х • У = У • Х | 6б. | Х + У = У + Х | Коммунативное право | ||
| 7а. | X (Y Z) = (X Y) Z = (X Z) Y = X Y Z | Ассоциативный закон | ||||
| 7б. | X + (Y + Z) = (X + Y) + Z = (X + Z) + Y = X + Y + Z | Ассоциативный закон | ||||
| 8а. | Х • (Г + Z) = Х У + Х Z | 8б. | X + Y Z = (X + Y) • (X + Z) | Распределительный закон | ||
| 9а. | Х • У = Х + У | 9б. | Х + У = Х • У | Теорема де Моргана | ||
| 10а. | Х • (Х + У) = Х | 10б. | Х + Х У = Х | Закон о поглощении | ||
| 11а. | (X + Y) • (X + Y) = X | 11б. | ||||


 a
= a ; a + a = a
a
= a ; a + a = a ..
..
 A + B, A + B’, A + B + C’ и A’ + B + + D’ — вот некоторые из примеров «суммы». Значение термина суммы истинно, когда один или несколько литералов истинны, и ложно, когда все литералы ложны.
A + B, A + B’, A + B + C’ и A’ + B + + D’ — вот некоторые из примеров «суммы». Значение термина суммы истинно, когда один или несколько литералов истинны, и ложно, когда все литералы ложны.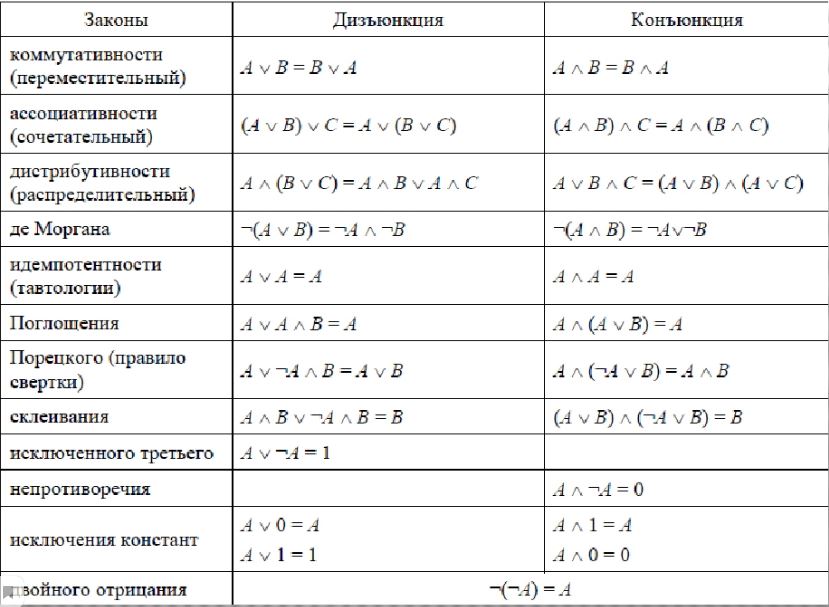 Б. = Б.А.
Б. = Б.А. Этот закон объясняет процесс факторинга.
Этот закон объясняет процесс факторинга.
 Схематически это правило можно определить как:
Схематически это правило можно определить как: Схематически это правило можно определить как:
Схематически это правило можно определить как: е. исходную переменную.
е. исходную переменную. 1 + AB + BC Факторинг (дистрибутивное право)
1 + AB + BC Факторинг (дистрибутивное право)