5. Практическая работа 2. Алгебра логики

6. Защитить выполненную работу у преподавателя.

Вопросы для самоконтроля

1.Что такое система счисления?

2.Чем характеризуется система счисления?

3.Виды систем счисления.

4.Десятичная система счисления. Основание. Представление чисел.

5.Двоичная система счисления. Основание.

6.Восьмеричная и шестнадцатеричная системы счисления.

7.Перевод чисел из любой системы счисления в десятичную.

8.Перевод чисел из десятичной в любую другую систему счисления.

9.Почему для машинной арифметики используется двоичная система счисления?

10.Для чего используется шестнадцатеричная система счисления?

Цель работы: Ознакомиться с основными арифметическими операциями, базовыми логическими элементами (И, И-НЕ, ИЛИ, ИЛИ-НЕ, исключающее ИЛИ) и изучить методы построения на их основе простейших логических схем.

Задания к практической работе № 2:

1.В приложении №2 выбрать свой вариант индивидуального задания.

2.Выполнить его, пользуясь данными методическими указаниями (глава 2. Алгебра логики).

3.Оформить работу по образцу приложения № 4.

4.Результат работы предъявить преподавателю.

5.Ответить на вопросы для самоконтроля к практической работе №2.

6.Защитить выполненную работу у преподавателя.

Решение логических задач средствами алгебры логики

Задача: Составить таблицу истинности для данной формулы: (x ~ z) | ((x y) ~ (y z)).

Решение: В таблицу истинности данной формулы полезно включить таблицы истинности промежуточных функций:

xyz	x ~ z	x y	y z	(x y) ~ (y z)	(x~ z)|((x y) ~ (yz)
000	1	0	0	1	0
001	0	0	0	1	1
010	1	0	0	1	0
011	0	0	1	0	1
100	0	0	0	1	1
101	1	0	0	1	0
110	0	1	0	0	1
111	1	1	1	1	0

21

Конспект урока по теме Алгебра логики 10 класс | Электронный образовательный ресурс по информатике и икт (10 класс):

Конспект урока информатики в 10 классе по теме «Логика» с использованием ЭОР.

Учителя информатики ГБОУ школы №454 Колпинского района Санкт-Петербурга Черноивановой Екатерины Вадимовны

Цели урока: сформировать у учащихся понятие форм мышления, логическое высказывание, логические величины и операции. Научить составлять простые логические выражения.

Задачи: 

1. Учебно – образовательные: 

• сформировать у учащихся понятие форм мышления, логическое высказывание, логические величины и операции;
• научить составлять простые логические выражения.

2. Развивающие:

• создать условия для повышения познавательного интереса учащихся;
• развитие памяти, внимания, логического мышления,
• развитие умения проводить анализ, сравнение, обобщение;
• развитие практических умений и навыков работы интерактивной доской.

3. Воспитательные:

• формирование отношения сотрудничества при работе,
• аккуратность, бережное обращение с техникой;
• культуры общения учащихся на уроке.

Тип урока: урок изучения и закрепления нового материала

Формы работы учащихся: фронтальная, коллективная и индивидуальная работа.

Учебно-методический комплекс:

Технические средства обучения:

компьютер, мультимедийный проектор, интерактивная доска.

Открытые электронные ресурсы по теме:

http://lbz.ru/metodist/authors/informatika/3/eor10.php

http://kpolyakov.spb.ru/school/ege.htm

Глоссарий по теме:

алгебра логики, импликация, эквиваленция, предикат, высказывание, конъюнкция, дизъюнкция.

Ресурсы:

Учебник Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса — М.: БИНОМ. Лаборатория знаний, 2017 (с.174—197)

электронное приложение к учебнику.

План урока:

1. Организационный момент                                         3 минуты
2. Изучение нового материала                                        15 минут
3. Практическая часть. Закрепление изученного                7+15 минут
4. Подведение итогов (рефлексия)                                4 минуты
5. Домашняя работа                                                1 минута

Структура урока:

1. Организационный момент. 

Учитель: Для начала давайте решим несколько шуточных задач:

Ученики: Решают следующие задачи, устно дают ответы:

• Вы сидите в вертолете, перед вами конь, сзади верблюд. Где Вы находитесь?
• Какое слово начинается с трех букв «Г» и заканчивается тремя буквами «Я»?
• Вы зашли в темную комнату. В ней есть газовая и бензиновая лампа. Что вы зажжете в первую очередь?
• Обычно месяц заканчивается 30 или 31 числом. В каком месяце есть 28 число?
• Когда человек бывает в комнате без головы?

Учитель: Давайте подумаем, к какому же типу относятся данные задачи?

Ученики: Отвечают, что задачи такого плана можно отнести к логике.

Учитель: Конечно же, мы отнесем их логическим, то есть от нашего умения мыслить мы  можем прийти к правильному решению.  А как человек мыслит? Что в нашей речи является высказыванием, а что нет?

2. Изучение нового материала. 

(Слайд 2-3)

Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Алгебра логики возникла в середине 19 века в трудах английского математика Джорджа Буля. Её создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Логическая переменная – обозначает любое высказывание и может принимать логическое значение «истина» или «ложь» (1 или 0)

Предикат – высказывание с неизвестной

Предпосылка – часть высказывания

Примеры:

6-четное число	высказывание	Истинно
Рим – столица Франции	высказывание	Ложно
Ученик 10 класса	Не высказывание, т. к. ничего не утверждает об ученике	—
Информатика – интересный предмет	Не высказывание, т.к. слишком неопределённое понятие «интересный предмет»	—
У него голубые глаза (Высказывательная форма)	Не высказывание, т.к. для выяснения их истинности или ложности нужны дополнительные сведения, о каком человеке идёт речь.	—

Зачастую трудно установить истинность высказывания, например высказывание «площадь поверхности Индийского океана равна 75 млн. км2» в одной ситуации можно посчитать ложным (указанное значение неточное и вообще постоянно меняется), а в другой истинным (если рассматривать его как некоторое приближение, приемлемое на практике).

(Слайд 4-10)

Логические операции

• Дизъюнкция – логическое сложение
• Конъюнкция – логическое умножение
• Инверсия – отрицание
• Импликация – следование «Если А то В»
• Эквиваленция – сравнение «Если А то и В»

Дизъюнкция – логическая операция, которая принимает значение истина, если истина хотя бы одна предпосылка.

Обозначение: ⋁, +, ИЛИ, |.

A	B	A + B
0	0	0
0	1	1
1	0	1
1	1	1

Конъюнкция – логическая операция, которая принимает значение истина, если истина обе предпосылки.

Обозначение: ⋀, *, И, &

A	B	A * B
0	0	0
0	1	0
1	0	0
1	1	1

Инверсия – логическая операция, которая меняет значение предпосылки.

Обозначение: ⌝A,  ‾ , НЕ

A	⌝A
0	1
1	0

---

Импликация – логическая операция, которая принимает значение ЛОЖЬ, только если первая предпосылка истина (1), а вторая ложь (0).

Обозначение: ⟶ 

A	B	A ⟶ B
0	0	1
0	1	1
1	0	0
1	1	1

Эквиваленция – логическая операция, которая принимает значение истина, если обе предпосылки одинаковые.

Обозначение: ⟷, ≡

A	B	A ≡ B
0	0	1
0	1	0
1	0	0
1	1	1

Порядок операций:

1. Действия в скобках                (…)
2. Инверсия                        ⌝A,  ‾ , НЕ
3. Конъюнкция                        ⋀, *, И, &
4. Дизъюнкция                        ⋁, +, ИЛИ, |
5. Импликация,                        ⟶ 
   Эквиваленция                        ⟷, ≡

3. Практическая часть.

1) Установите, какие из следующих предложений являются логическими высказываниями, а какие нет (объясните, почему) :

1. Солнце есть спутник Земли
2. 2+3=5
3. Сегодня отличная погода
4. В романе Л.Н Толстого «Война и мир» 3 432 536 слов
5. Санкт-Петербург расположен на Неве
6. Музыка И.С.Баха слишком сложна
7. Первая космическая скорость равна 7,8км/с
8. Железо – металл
9. Если один угол в треугольнике прямой, то треугольник будет тупоугольным
10. Если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный

2) Укажите, какие из высказываний предыдущего упражнения истинны, какие – ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить.

3) Приведите примеры истинных или ложных высказываний (по два) из:

• Арифметики
• Физики
• Биологии
• Информатики
• Геометрии
• Жизни

Ответы:

1. а, г, д, ж, з, и, к – высказывания; б, в, е – не высказывания

2) истинные: д, з, к;        Ложные: а, и;         Истинность трудно установить: г;        Можно рассматривать и как истинное, и как ложное в зависимости от требуемой точности представления: ж.

(Слайд 10)

Пример составления таблиц истинности для логических операций на примере функции F=( (⌝X ⋀ Y) ⟶ Z) ⋁ (⌝Z ⋀ Y)

Количество строк в таблице истинности высчитывается по формуле N=2i, где i – это количество переменных в формуле!

Решение:

X	Y	Z	1)⌝ X	2)⌝ X ⋀ Y	3) 2⟶ Z	4) ⌝ Z	5) ⌝ Z ⋀ Y	6) F=3 ⋁ 5
0	0	0	1	0	1	1	0	1
0	0	1	1	0	1	0	0	1
0	1	0	1	1	0	1	1	1
0	1	1	1	1	1	0	0	1
1	0	0	0	0	1	1	0	1
1	0	1	0	0	1	0	0	1
1	1	0	0	0	1	1	1	1
1	1	1	0	0	1	0	0	1

(Слайд 11)

Самостоятельное решение заданий по составлению таблиц истинности.

1. F=( (Z ⋀⌝ Y) ≡ X) ⋁ (⌝Z ⟶ Y)
2. F=( Y ⋁ Z) ⋀⌝(X ≡ Y) ⋀⌝X
3. F=((Z ⟶W) ⋁(Y ≡ W)) ⋀ ((X ⋁ Z) ≡ Y)

4. Подведение итогов.

• О чём мы сегодня с вами узнали на уроке?
• Приведите пример высказываний, которые вы сегодня (вчера) слышали на других уроках

Разбор решённых заданий.

Выставление отметок

5. Домашнее задание:

Выучить основные определения, знать обозначения.

Учебник §18-19: стр. 187-188  № 1, 6; стр. 196 №3 (письменно).

Алгебра, логика и приложения — Серия книг

Просмотреть все Серия книг

СЕРИЯ КНИГ

---

---

• Названия серии
• Авторы

12 заголовков серий

На странице

122448

Сортировка

Дата публикацииЗаголовок (по возрастанию)Заголовок (по убыванию)

---

Включить будущие заголовки

Дисплей

Упорядоченные алгебраические структуры

1-е издание

К W. Charles Holland
1 апреля 2001 г.

Эта книга является результатом конференции по упорядоченным алгебраическим структурам, проходившей в Нанкине. Он охватывает ряд тем: теория решеток, упорядоченные полугруппы, частично упорядоченные группы, полностью упорядоченные группы, упорядоченные группы и упорядоченные поля….

Введение в теорию моделей

1-е издание

By Philipp Rothmaler
31 октября 2000 г.

Теория моделей исследует математические структуры с помощью формальных языков. В этом отношении особенно полезными оказались так называемые языки первого порядка. Этот текст знакомит с теорией моделей логики первого порядка, избегая синтаксических вопросов, не слишком относящихся к теории моделей. В этом духе …

Гиперидентичности и клоны

1-е издание

Автор: Клаус Денеке, С.Л. Висмат
08 августа 2000 г.

Теории и результаты о гипертождествах были опубликованы в различных областях литературы за последние 18 лет.

Hyperidentities and Clones впервые объединяет их в согласованную структуру. Автор также включает некоторые приложения гипертождеств к функционалу…

Почти полностью разложимые группы

1-е издание

By A Mader
09 марта 2000 г.

Почти вполне разложимая абелева группа является расширением конечной прямой суммы подгрупп аддитивной группы рациональных чисел с помощью конечной абелевой группы. Примеры легко написать и они часто используются, но, как известно, их трудно изучать и классифицировать из-за … По М Дросте, Р. Гобель
29 января 1998 г.

Содержит 25 обзоров по алгебре и теории моделей, написанных ведущими экспертами в этой области. Обзоры основаны на выступлениях на конференциях, состоявшихся в Эссене, 1994 г., и Дрездене, 1995 г. Каждый вклад написан таким образом, чтобы подчеркнуть идеи, которые обсуждались на конференциях, …

Билинейная алгебра: введение к алгебраической теории квадратичных форм

1-е издание

Казимеж Шимичек
05 сентября 1997 г.

Давая доступное элементарное введение в алгебраическую теорию квадратичных форм, эта книга охватывает как теорию Витта, так и теорию квадратичных форм Пфистера. Ведущими темами являются геометрия билинейных пространств, классификация билинейных пространств вплоть до изометрии в зависимости от …

Полилинейная алгебра

1-е издание

By Russell Merris
20 августа 1997

Прототипом полилинейной операции является умножение. Действительно, каждое полилинейное отображение можно разложить на множители через тензорное произведение. Помимо своего внутреннего интереса, тензорное произведение имеет фундаментальное значение во множестве дисциплин, начиная от матричных неравенств и групповых …

Упражнения по алгебре

1-е издание

Автор: Александра Ивановна Кострикин
09 февраля 1996 г.

Семантика языков программирования и теория моделей

1-е издание

Манфред Дросте, Юрий Гуревич
10 сентября 1993 г.

Основы теории модулей и колец

1-е издание

By Robert Wisbauer
05 сентября 1991 г.

Этот том представляет собой всеобъемлющее введение в теорию модулей и связанную с ней часть теории колец, включая оригинальные результаты, а также самые последние работы. Это полезное и стимулирующее исследование для тех, кто плохо знаком с предметом, а также для исследователей, и служит справочным томом. Начиная…

Теоретическая алгебра моделей с особым акцентом на поля, кольца и модули

1-е издание

К году Кристиан. U Jensen, Helmt Lenzing
26 июля 1989 г.

В этом томе освещаются связи между теорией моделей и алгеброй. Работа содержит окончательный отчет об алгебраически компактных модулях, тему, имеющую центральное значение как для теории модулей, так и для теории моделей. На конкретных примерах особое внимание уделяется теоретико-модельным понятиям, таким как…

Линейная алгебра и геометрия

1-е издание

By Суетин П. К., Кострикин Александра Ивановна, Манин Ю.И.
14 июля 1989 г.

Углубленный учебник по линейной алгебре и геометрии охватывает широкий круг классических и современных тем. В отличие от существующих учебников по подходу, работа иллюстрирует многосторонние приложения и связи линейной алгебры с функциональным анализом, квантовой механикой и алгебраическими и…

приложений булевой алгебры: Клод Шеннон и схемотехника

Автор(ы):

Джанет Хейн Барнетт (Университет штата Колорадо, Пуэбло) логика проектирования электрических цепей . (Источник: Архив истории математики MacTutor)

Введение

В 1938 году американский математик и инженер-электрик Клод Э. Шеннон (1916–2001) защитил магистерскую диссертацию по электротехнике в Массачусетском технологическом институте. Ванневер Буш (1890–1974), декан инженерного факультета Массачусетского технологического института и изобретатель первого механического компьютера под названием «машина дифференциального анализатора», был настолько впечатлен диссертацией Шеннона, что спонсировал ее публикацию в инженерном журнале.

Эта отмеченная наградами статья «Символический анализ реле и коммутационных цепей» [4] произвела революцию в изучении переключателей и реле, которые, в свою очередь, формируют схему, лежащую в основе двоичной арифметики современных компьютеров.

Вдохновлен Идею из своего изучения символической логики в курсе философии бакалавриата, Шеннон описал общую проблему, которую необходимо решить, и предложенный им подход к ней следующим образом [4, стр. 713]:

В цепях управления и защиты сложных электрических систем часто необходимо выполнять сложные взаимосвязи контактов реле и переключателей. Примеры таких схем встречаются в автоматических телефонных станциях, промышленных устройствах управления двигателями и почти в любых схемах, предназначенных для автоматического выполнения сложных операций. В этой статье будет проведен математический анализ некоторых свойств таких сетей. …

Метод решения этих проблем можно кратко описать следующим образом: любая цепь представлена ​​набором уравнений, члены уравнений соответствуют различным реле и переключателям в цепи. Разработано исчисление для манипулирования этими уравнениями с помощью простых математических процессов, большинство из которых похожи на обычные алгебраические алгоритмы. Показано, что это исчисление в точности аналогично исчислению предложений, используемому при символическом изучении логики.

Рисунок 2. Идеи логики, высказанные Джорджем Булем (1815-1864), полезны при проектировании электрических цепей
.
(Источник: Архив MacTutor)

«Исчисление предложений, используемых в символическом исследовании логики», на которое ссылается здесь Шеннон, сегодня более широко известно под названием «булева алгебра» в честь викторианского математика Джорджа Буля (1815–1864), чья собственная новаторская работа по изучению логики в [1, 2] положили начало этой важной области математики.

Из работ многих людей, которые внесли свой вклад в историю рождения и развития булевой алгебры как абстрактной математической структуры и мощного прикладного инструмента, мы создали три основных исходных модуля проекта, подходящие для студентов вводных или промежуточных курсов дискретной математики. :

• проект, который развивает элементарную теорию множеств на основе оригинальных выдержек из собственных работ Буля и двух первых математиков, внесших изменения в подход Буля к логике, представленный в Convergence статья «Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К.С. Пирс»;
• проект, в котором исследуется структура булевой алгебры как абстрактной аксиоматизированной структуры, представленный в статье Convergence , Булева алгебра как абстрактная структура: Эдвард В. Хантингтон и аксиоматизация; и
• настоящий проект «Приложения булевой алгебры: Клод Шеннон и проектирование схем», в котором исследуется применение булевой алгебры к конкретной проблеме проектирования схем.

Все три проекта являются частью более крупной коллекции, опубликованной в Convergence, , и весь вводный курс дискретной математики может быть изучен на основе подборки проектов из этой коллекции. Дополнительные проекты см. в разделе «Основные исторические источники в классе: дискретная математика и информатика».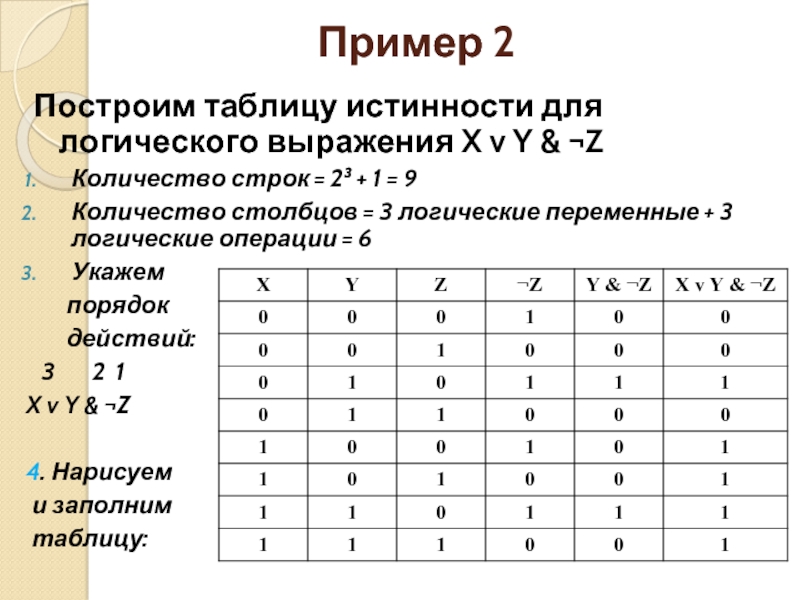

Наш проект Applications of Boolean Algebra: Claude Shannon and Circuit Design готов для студентов, а исходный код Latex также доступен для преподавателей, которые могут захотеть изменить проект для студентов. Подробные «Примечания для инструктора», представленные далее, также прилагаются к самому проекту.

Рис. 3.   Будучи исследователем в Bell Labs, Клод Шеннон основал теорию информации. Позже он стал профессором Массачусетского технологического института. (Источники: Convergence Portrait Gallery, MIT News)

Примечания для инструктора

Проект «Применения булевой алгебры: Клод Шеннон и проектирование схем» предназначен для вводного или промежуточного курса дискретной или конечной математики, который рассматривает логические алгебра либо с математической точки зрения, либо с точки зрения информатики. Проект предполагает некоторое (очень минимальное) знакомство с операциями объединения и пересечения множеств. Этот предварительный материал можно получить, выполнив сопутствующий (булев) проект, описанный ниже, прочитав стандартный учебник по элементарным операциям над множествами или прочитав короткое обсуждение/лекцию в классе. Хотя для какой-либо части проекта не требуется каких-либо других специальных предварительных знаний, разделы 3 и 4 действительно предполагают более высокий уровень математической зрелости учащихся, примерно соответствующий уровню учащегося, завершившего исчисление I (для Раздел 3) и Исчисление II (для Раздела 4).

Основанный на отмеченной наградами статье Клода Шеннона «Символический анализ реле и коммутационных цепей» [4], этот проект начинается с краткого обзора двух исторических предшественников работы Шеннона. Первая из них — это оригинальная работа Джорджа Буля о «логике классов», включенная отчасти для того, чтобы дать учащимся связь с другим конкретным примером булевой алгебры, который они могут использовать; вторая из них — работа Эдварда Хантингтона по аксиоматизации булевых алгебр, включенная отчасти для того, чтобы подчеркнуть для студентов взаимосвязь между абстрактными аксиоматическими структурами и конкретными моделями как примерами этих структур. Раздел 2 проекта вводит и развивает использование логических выражений для представления параллельных и последовательных цепей. В конкретном контексте двузначной булевой алгебры, связанной с этими схемами, в этом разделе развиваются стандартные свойства булевой алгебры; конкретные вопросы проекта в этом разделе также позволяют учащимся попрактиковаться в использовании этих тождеств для упрощения логических выражений и управления ими. В разделе 3 понятие «дизъюнктивная нормальная форма» для логических выражений вводится в контексте проектирования схем. Затем в разделе 4 исследуется более сложный метод применения булевой алгебры к проблеме упрощения сложных схем.

Так как многие понятия в этом проекте разрабатываются с помощью упражнений, инструкторам рекомендуется заранее проработать все упражнения, чтобы определить, какие из них, если таковые имеются, она может пропустить. Для полного завершения проекта требуется примерно четыре 50-минутных урока. Раздел 4 можно легко опустить для тех, кто хочет, чтобы студенты изучали только более фундаментальные понятия булевой алгебры, или для использования со студентами, которые еще не достигли необходимого уровня математической зрелости для более поздних разделов. Оба раздела 3 и 4 также могут быть опущены по тем же причинам. Инструкторам, решившим заполнить раздел 4, рекомендуется, чтобы студенты также заполняли раздел 3.

В качестве дополнения к этому проекту доступны два других проекта по булевой алгебре, каждый из которых или оба могут использоваться независимо от этого проекта. Первый сопутствующий проект «Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс» подходит в качестве предварительного либо к проекту Хантингтона, либо к проекту Шеннона. Без явного введения современных обозначений для операций над множествами (до заключительного раздела) этот проект развивает современное понимание этих операций и их основных свойств в контексте ранних попыток разработать символическую алгебру для логики. Постоянно повышая уровень абстракции, этот проект также закладывает основу для более абстрактного обсуждения булевой алгебры как дискретной структуры и исследует множество других математических тем, включая понятие обратной операции, вопросы, связанные с математической записью. , а также стандарты строгости и доказательства.

Второй сопутствующий проект «Булевая алгебра как абстрактная структура: Эдвард В. Хантингтон и аксиоматизация» можно использовать либо как предварительный, либо как продолжение проекта Шеннона по проектированию схем. Этот проект исследует раннюю аксиоматизацию булевой алгебры как абстрактной структуры, основанную на статье Хантингтона 1904 года «Наборы независимых постулатов для алгебры логики» [3]. В дополнение к введению теперь стандартных аксиом для структуры булевой алгебры, проект иллюстрирует, как использовать эти постулаты для доказательства некоторых основных свойств булевых алгебр. Конкретные вопросы проекта также дают учащимся возможность попрактиковаться в использовании символических обозначений и побуждают их анализировать логическую структуру выраженных в количественном выражении утверждений. В проекте также исследуется использование Хантингтоном двузначной булевой алгебры на \(K=\{0,1\}\) — впервые изученной Джорджем Булем в его работе по логике классов — в качестве модели для установления независимости и непротиворечивость одного из его наборов постулатов. В заключительном разделе проекта обсуждаются современные (студенческие) обозначения и аксиомы для булевых алгебр, а также предлагаются несколько практических упражнений для закрепления идей, разработанных в предыдущих разделах.

Реализация со учащимися любого из этих проектов может быть достигнута путем индивидуальной работы, работы в малых группах и/или обсуждения в классе; рекомендуется сочетание этих учебных стратегий, чтобы воспользоваться разнообразием вопросов, включенных в проект.

Загрузите проект Applications of Boolean Algebra: Claude Shannon and Circuit Design в формате pdf, готовый для использования в классе.

Загрузите редактируемый исходный файл Latex для этого проекта.

Дополнительные проекты см. в разделе «Основные исторические источники в классе: дискретная математика и информатика».

Библиография

[1] Boole, G., Mathematical Analysis of Logic, MacMillan, Barclay & MacMillan, Cambridge, 1847. Переиздано Open Court, La Salle, 1952.

[2] Boole, G., Исследование законов мысли, на которых основаны математические теории логики и вероятностей, Уолтон и Маберли, Лондон, 1854 г. Переиздано Dover Publications, Нью-Йорк, 1958.

[3] Хантингтон, Е. В., Наборы независимых постулатов для алгебры логики, Transactions of the American Mathematical Society, 5:3 (1904), 288-309.

[4] Шеннон, С. Е., Символический анализ реле и коммутационных цепей, Американский институт инженеров-электриков, 57 (1938), 713-723. Перепечатано в Claude Elwood Shannon: Collected Papers, NJA Sloane and AD Wyner (редакторы), IEEE Press, New York, 1993, 471-495.

Благодарность

Разработка учебных материалов по дискретной математике была частично поддержана Национальным научным фондом в рамках Программы усовершенствования курсов, учебных планов и лабораторий в рамках грантов DUE-0717752 и DUE-0715392, за что авторы выражают им наибольшую признательность. Любые мнения, выводы и выводы или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда.