Физика Потенциальная энергия заряженного тела в однородном электростатическом поле
Материалы к уроку
Конспект урока
Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел действующие между ними силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит, система заряженных тел обладает потенциальной энергией, называемой электростатической или электрической.
Энергия взаимодействия электронов с ядром в атоме и энергия взаимодействия атомов друг с другом в молекулах (химическая энергия) – это в основном электрическая энергия.
С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом.
При перемещении заряда действующая на него со стороны поля сила совершает работу. Поэтому можно утверждать, что заряженное тело в электрическом поле обладает энергией. Однородное поле создают, например, большие металлические пластины, имеющие заряды противоположного знака. Это поле действует на заряд с постоянной силой, равной произведению напряженности поля на заряд.
Это подобно тому, как Земля действует с постоянной силой, равной произведению массы на ускорение свободного падения, на камень вблизи ее поверхности. Работа электрического поля не зависит от формы траектории, подобно тому, как не зависит от формы траектории работа силы тяжести.
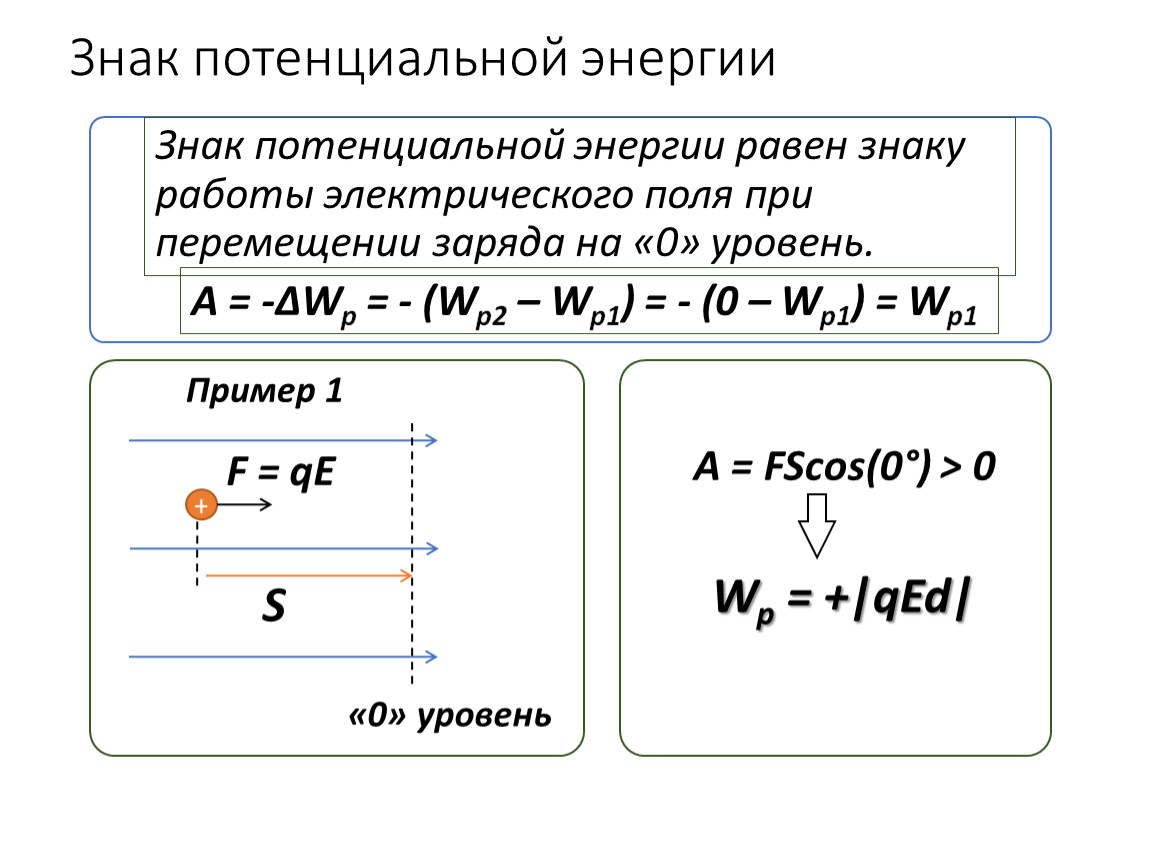
Проведем аналогию с потенциальной энергией Земли. Знак потенциальной энергии зависит только от знака высоты (от выбора «0» уровня). Знак энергии заряда, находящегося в электрическом поле, зависит от направления поля, знака заряда и выбора «0» уровня.
Рассмотрим потенциальную энергию взаимодействия точечных зарядов. Пусть два точечных заряда (кю1) q1 и (кю2) q2 находятся в вакууме на расстоянии (эр) r друг от друга. Потенциальная энергия их взаимодействия равна отношению произведения этих зарядов и электрической постоянной к расстоянию между зарядами. В данной формуле есть две особенности.
Иными словами, когда заряды расположены бесконечно далеко друг от друга, потенциальная энергия их взаимодействия полагается равной нулю (что логично — в этом случае заряды уже «не взаимодействуют»). Во-вторых, q1 и q2 — это алгебраические величины зарядов, т. е. заряды с учётом их знака. Например, потенциальная энергия взаимодействия двух одноимённых зарядов будет положительной. Почему? Если мы отпустим их, они начнут разгоняться и удаляться друг от друга.
Эта формула помогает также вычислить потенциальную энергию системы зарядов, если число зарядов больше двух. Для этого нужно просуммировать энергии каждой пары зарядов. Проиллюстрируем сказанное примером. На рисунке изображено взаимодействие трёх зарядов. Если заряды (кю1, кю2, кю3) q1, q2, q3 находятся в вершинах треугольника со сторонами (а, бэ, цэ) a, b, c, то потенциальная энергия их взаимодействия равна сумме потенциальных энергий взаимодействий зарядов 1-2, 2-3 и 3-1.
Сравним работы по перемещению заряда в электрическом поле из точки А в точку В (бэ) и из точки А в точку С (цэ). Работы по перемещению равны, так как разность потенциалов точек начала и конца перемещений заряда равна.
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
1.
4. Работа сил электростатического поля и потенциальная энергия заряженных частиц. Потенциал, разность потенциалов — ЗФТШ, МФТИПусть точечный заряд `q` находится в однородном электрическом поле с напряжённостью `vecE`. (Обобщение на случай неоднородного
Работой силы со стороны электрического поля при перемещении заряда `q` из точки `1` в точку `2` называют величину (сумму работ на отдельных участках)
где `vecF_i` — сила, действующая на заряд на малом участке `Deltavecr_i`, `vecF_iDeltavecr_i` — скалярное произведение векторов.
Заметим, что работа силы электростатического поля (1.4.2) определяется лишь начальной и конечной точками (двумя радиус-векторами `vecr_1` и `vecr_2`) и не зависит от конкретной траектории, по которой двигался заряд (в ответ вошла лишь разность этих векторов). Силы, обладающие тем свойством, что работа этих сил не зависит от траектории, называют консервативными силами, а соответствующие поля —
По общей теореме механики изменение кинетической энергии заряда равно сумме работ всех сил:
Если заряд двигался только под действием сил электрического поля (не было никаких ниточек, за которые бы мы тянули заряд, не было силы трения и др.
2)/2` — кинетическая энергия заряда, равенство (1.4.4’) – это просто
т. е. в процессе движения сумма кинетической и потенциальной энергий не изменяется (сохраняет своё значение).
Если приписать точке `A` с радиус-вектором `vecr_0` потенциальную энергию, равную нулю, то это эквивалентно выбору константы `Pi_0=+qvecEvecr_0`. Выбрав в качестве точки `A` начало координат `(vecr_0=0)`, получаем `Pi_0=0` и `Pi(vecr)=-qvecEr`.
Важнейшим понятием в учении об электричестве является потенциал. Перепишем выражение для работы сил электростатического поля в виде
введя потенциал однородного электростатического поля по формуле
`varphi_0` — произвольная постоянная.
В силу равенства (1.4.7) и, соответственно, потенциал измеряется в единицах Дж/Кл = В (вольт).
По формуле (1.4.8) найдём ещё изменение потенциала при переходе от одной точки поля к другой — с радиус-векторами `vecr_1` и `vecr_2`:
Заметим, что если перемещение перпендикулярно электрическому полю, `Deltavecr_|_vecE`, то скалярное произведение `vecEDeltavecr=0`, т. е. `Deltavarphi=0`: перемещаясь в плоскости перпендикулярно вектору напряжённости электрического поля `vecE`, переходим от одной точки к другой с таким же потенциалом. О таких плоскостях (в общем случае – о поверхностях) говорят как об эквипотенциальных поверхностях.
А как будет изменяться потенциал при переходе от одной эквипотенциальной плоскости к другой? Рассмотрим перемещение вдоль электрического поля `Deltavecr«||«vecE`. Направим ось `X` параллельно электрическому полю (не обязательно по полю, м. б., и против поля, так что проекция `E_x` вектора `vecE` на ось `X` может иметь любой знак).
Согласно основным свойствам скалярного произведения векторов `(vecavecb=|veca|*|vecb|cosalpha=a_xb_x+a_yb_y+a_zb_z)` имеем
а для приращения потенциала
Формуле (1.4.10’) можно придать ещё следующий вид. Пусть ось `X` направлена по полю `(E=E_x>0)` и пусть `d=x_2-x_1`. Введём разность потенциалов (напряжение) по формуле `U=varphi_1-varphi_2`. Тогда согласно (1.4.10’) получаем `U=Ed`.
До сих пор мы рассматривали лишь однородное электростатическое поле. Простейшим примером неоднородного поля является поле точечного заряда. К сожалению, нахождение работы сил даже этого сравнительно простого поля без привлечения высшей математики весьма затруднительно. Поэтому формулу для неё приведём без вывода.
Пусть имеется неподвижный точечный заряд `q` и пусть другой заряд `q_0` перемещается в поле этого заряда. Пусть он переместился из точки `1`, характеризуемой радиус-вектором `vecr_1`, в точку `2` — с радиус-вектором `vecr_2` по, вообще говоря, криволинейной траектории.
Можно показать (вывод можно найти в книге `[3]`), что в этом случае работа сил электростатического поля будет равна
где `r_1=|vecr_1|`, `r_2=|vecr_2|`. Далее действуем, как и в случае однородного поля. Если в процессе движения заряда `q_0` никаких других сил, кроме кулоновской силы со стороны заряда `q` не действовало, то по теореме об изменении кинетической энергии имеем:
Определяя потенциальную энергию взаимодействия точечных зарядов `q` и `q_0` находящихся на расстоянии `r` друг от друга, формулой
где `Pi_0` — произвольная постоянная, мы можем придать равенству (1.4.12) вид закона сохранения энергии `K_2+Pi_2=K_1+Pi_1`.
В случае точечных зарядов весьма часто константу `Pi_0` выбирают равной нулю так, чтобы потенциальная энергия взаимодействия двух зарядов стремилась к нулю при разнесении зарядов на бесконечно большое расстояние друг от друга (когда они перестанут «чувствовать» друг друга). В этом случае
Пусть в одну и ту же точку поля точечного заряда `q` на расстоянии `r` от него поочерёдно помещаются разные пробные заряды `q_1`, `q_2`, `.
..`. Энергии этих зарядов будут разными `Pi_1`, `Pi_2`, `…`. Существенно, однако, что отношение этих энергий в величинам пробных зарядов будет одним и тем же
Последним равенством определяется потенциал `varphi(r)` точечного заряда `q` на расстоянии `r` от него. Заметим, что согласно (1.4.11) потенциал `varphi(r)=q/(4pi epsilon_0r)` равен работе сил электростатического поля заряда `q` при перемещении единичного положительного точечного заряда из точки на расстоянии `r` от заряда `q` на бесконечность. Потенциал, как и потенциальная энергия, определён, вообще говоря, неоднозначно — с точностью до произвольной константы
которую весьма часто выбирают равной нулю с тем, чтобы при удалении от заряда на бесконечно большое расстояние потенциал заряда в этих (бесконечно удалённых точках) стремился к нулю.
Согласно формуле (1.4.14′) потенциал точечного заряда одинаков во всех точках, равноудалённых от него. Это означает, что эквипотенциальными поверхностями в данном случае будут концентрические сферы.
Как и в случае однородного поля, в каждой точке поля напряжённость перпендикулярна эквипотенциальной поверхности.
Если электростатическое поле создаётся несколькими зарядами `q_1,q_2,…`, потенциал в произвольной точке поля равен сумме потенциалов, создаваемых каждым из зарядов в той точке:
что, как и в случае напряжённостей полей, называют принципом суперпозиции. Важно, что напряжённости полей надо складывать векторно, а потенциалы — алгебраически (т. е. все же с учётом знаков).
Электрическая потенциальная энергия
Электрическая потенциальная энергияСледующий: Электрический потенциал Вверх: Электрический потенциал Предыдущий: Электрический потенциал Рассмотрим заряд, помещенный в однородное электрическое поле. ( например, , поле между двумя противоположно заряженными, параллельными проводящие пластины). Предположим, что мы очень медленно смещаем заряд на вектор смещения по прямой.
Какую работу мы должны выполнить
чтобы этого добиться? Итак, сила, которую мы должны приложить к заряду, равна
равна и противоположна электростатической силе, действующей на заряд
( т. е. , мы должны преодолеть электростатическую силу на заряде, прежде чем мы
свободно перемещать его).
Количество работы, которую мы выполнили бы при перемещении заряда, является просто произведением силы
мы
силы, а перемещение заряда в направлении этой силы .
Предположим, что вектор смещения образует угол с
электрическое поле. Следует, что | (76) |
Таким образом, если мы перемещаем положительный заряд в направлении электрического поля, то мы делать отрицательную работу ( т.е. , получаем энергию). Так же, если мы переместим положительный заряд в направлении, противоположном электрическому полю затем совершаем положительную работу ( т.
е. , мы теряем энергию). Рассмотрим набор точечных зарядов,
распределены в пространстве, которые жестко зажаты в положении так, что не могут
двигаться. Мы уже знаем, как рассчитать электрическое поле, создаваемое таким
распределение заряда (см. раздел 3). В общем, это электро
поле будет
неоднородный. Предположим, что мы поместили заряд в поле, скажем, в точке
и
затем медленно
переместите его по некоторой кривой траектории в другую точку. Какую работу мы должны совершить, чтобы
добиться этого? Разделим путь заряда от точки к точке
на ряд прямолинейных отрезков, где й отрезок
имеет длину
и образует угол с
локальное электрическое поле. Если мы сделаем достаточно большой, то мы можем
адекватно представлять любой криволинейный путь между и , и мы также можем гарантировать
примерно равномерный на ом сегменте пути. простым
обобщение уравнения (76), работу, которую мы должны совершить при перемещении
заряд от точки к точке
| (77) |
Наконец, беря предел, в котором уходит в бесконечность, правая часть приведенное выше выражение становится линейным интегралом:
| (78) |
Теперь рассмотрим частный случай, когда точка совпадает с точкой
.
Другими словами, случай, когда мы перемещаем заряд по замкнутому контуру в электрическом
поле. Какую работу мы должны совершить, чтобы достичь этого?
На самом деле можно доказать, используя довольно мощную математику, что
чистая работа, совершаемая при перемещении заряда по замкнутому контуру в
электрическое поле, создаваемое фиксированными зарядами, равно ноль . Однако,
нам не нужно быть математическими гениями, чтобы понять, что это
разумный результат.
Предположим ради аргумента, что чистая работа совершается, когда мы берем заряд вокруг некоторого
замкнутый контур в электрическом поле отличен от нуля. Другими словами, мы теряем энергию.
каждый раз мы берем заряд по петле в одном направлении, но получаем энергию
каждый раз мы берем заряд по петле в обратном направлении. Этот
следует из уравнения (77), потому что когда мы переключаем направление циркуляции
вокруг петли электрическое поле на th сегменте пути не изменяется, но,
так как заряд движется по отрезку в обратном направлении, , и поэтому,
.
Выберем перемещение заряда по контуру в направлении
в котором мы получаем энергию. Итак, мы перемещаем заряд один раз по петле, и
мы получаем определенное количество энергии в процессе. Откуда берется эта энергия? Давайте
рассмотреть возможности. Может быть, электрическое поле подвижного заряда
совершает отрицательную работу над фиксированными зарядами, поэтому
что последние заряды теряют энергию, чтобы компенсировать энергию, которая
мы получаем? Но фиксированные заряды не могут двигаться, и поэтому
работать с ними невозможно. Может быть, электрическое поле
теряет энергию, чтобы компенсировать энергию,
мы получаем? (Вспомните из предыдущего раздела, что существует энергия, связанная с
с электрическим полем, заполняющим пространство). Но все обвинения ( т.е. ,
фиксированные расходы и подвижные расходы)
находятся в одном и том же положении до и после того, как мы возьмем
подвижный заряд вокруг петли, поэтому электрическое поле одинаково до и
после (поскольку по закону Кулона электрическое поле зависит только от положений
и величины зарядов), и, следовательно, энергия поля должна быть
то же самое до и после.
Таким образом, мы имеем ситуацию, в которой мы принимаем
заряжаться по замкнутому контуру в электрическом поле и получать энергию в процессе,
но ничто не теряет энергию. Другими словами, энергия появляется из
«разреженный воздух», что явно нарушает первый закон термодинамики.
Единственный способ избежать этого абсурдного вывода состоит в том,
если принять следующее правило:
Работа, совершаемая при переносе заряда по замкнутому контуру в электрическом поле, создаваемое фиксированными зарядами, равно нулю.
Одним из следствий приведенного выше правила является то, что работа, совершаемая при перемещении
заряд между двумя точками и в таком электрическом поле независимых пути, пройденного между этими точками. Это легко доказывается. Учитывать
два разных пути, 1 и 2, между точками и .
Пусть работа, проделанная при взятии заряда на себя
путь 1 быть , а работа, проделанная при переносе заряда с на вдоль
путь 2 быть .
Давайте возьмем на себя ответственность
от к по пути 1, а затем от к по пути 2. Сеть
работа, проделанная для взятия заряда по этому замкнутому контуру, равна .
Так как мы знаем, что эта работа должна быть равна нулю, отсюда немедленно следует, что . Таким образом,
у нас новое правило:
Работа, совершаемая при переносе заряда между двумя точками в электрическом поле генерируемая фиксированными зарядами, не зависит от пути, пройденного между точками.
Сила, обладающая особым свойством, состоящим в том, что работа, выполненная при ее преодолении,
для перемещения тела между двумя точками пространства не зависит от
путь между этими точками называется консервативной силой .
Очевидно, что электростатическая сила между неподвижными зарядами
консервативная сила. Другим примером консервативной силы является сила
силы тяжести (работа, совершаемая при подъеме массы, зависит только от разности
по высоте между начальной и конечной точками, а не по пути
между этими точками).
Трение — очевидный пример неконсервативного
сила.
Предположим, что мы очень медленно перемещаем заряд из точки в точку.
в электрическом поле, создаваемом фиксированными зарядами. Работа, которую мы должны выполнить, чтобы
достичь этого можно вычислить
используя уравнение (78). Так как мы теряем энергию при движении заряда от
, что-то должно получить эту энергию. Давайте на время предположим, что это
что-то заряд. Таким образом, заряд получает энергии, когда
мы перемещаем его из точки в точку. Какова природа этого прироста энергии?
Это, конечно, не выигрыш в кинетической энергии, так как мы двигаем частицу медленно : т. е. , так что он всегда обладает незначительной кинетической энергией.
На самом деле, если мы хорошенько подумаем, то увидим, что выигрыш в энергии
заряд зависит только от его позиции . Для фиксированной начальной точки работа
делается при переносе заряда из точки в точку, зависит только от
положение точки , а не, например, на пути между
и .
Мы обычно называем энергией тело, которым оно обладает в силу своего положения. потенциальная энергия : напр. , масса имеет определенную гравитационную потенциальную энергию которая зависит от его высоты над землей. Таким образом, мы можем сказать, что когда
заряд переносится из точки в точку в электрическом поле, создаваемом фиксированными зарядами его электрическая потенциальная энергия увеличивается на величину:
| (79) |
Здесь обозначает электрическую потенциальную энергию заряда в точке , и т. д. Это определение однозначно определяет разность в потенциальной энергии между точками и (поскольку не зависит от пройденного пути между этими точками), но абсолютное значение потенциальной энергии точка остается произвольной.
Мы видели, что когда заряженную частицу перемещают из точки в точку в электрическом поле, ее электрическая потенциальная энергия увеличивается на указанную величину.
в уравнении (79). Но как частица хранит эту энергию? В самом деле, частица
вообще не хранит энергию. Вместо этого энергия запасается в электрическом поле.
окружающих частицу. Можно рассчитать это увеличение
энергия поля напрямую (если мы знаем формулу, связывающую плотность энергии
электрического поля к величине поля), но это очень утомительный
расчет. Гораздо проще вычислить работу, затраченную на
заряжать от точки к точке, через уравнение. (78), а затем используйте
закон сохранения энергии, чтобы сделать вывод, что энергия электрического поля должна
увеличились на сумму. Тот факт, что мы условно приписываем эту энергию
возрастать к частице, а не к полю, через понятие электрического
потенциальной энергии, не имеет значения для всех практических целей. Например, мы называем
деньги, которые у нас есть в банке, «наши», несмотря на то, что банк владеет ими,
потому что мы знаем, что банк вернет нам деньги в любое время, когда мы их попросим.
Точно так же, когда мы перемещаем заряженную частицу в
электрического поля от точки к точке, то энергия поля увеличивается на величину
(работа, которую мы совершаем при перемещении частицы из в ), но мы можем
безопасно связывать
эта энергия увеличивается вместе с частицей, потому что мы знаем, что если частица
вернуться к точке, тогда поле даст все
энергия возвращается к частице без потерь .
Кстати, мы можем быть уверены, что
поле возвращает частице энергию без потерь, потому что если есть
если бы были какие-либо потери, то это означало бы, что ненулевая работа совершается при взятии заряженного
частица вокруг замкнутого контура в электрическом поле, создаваемом фиксированными зарядами. Мы называем силовым полем, которое
сохраняет энергию без потерь a консервативное поле . Таким образом, электрическое поле, а точнее
электростатическое поле ( т.е. , электрическое поле, создаваемое
стационарные заряды), является консервативным. Из вышесказанного должно быть ясно
обсуждения, что понятие потенциальной энергии имеет смысл только в том случае, если поле
которая порождает рассматриваемую силу, является консервативной.
Гравитационное поле — еще один пример консервативного поля. оказывается
что, когда мы поднимаем тело на определенную высоту, увеличение гравитационного
потенциальная энергия тела фактически запасается в окружающей
гравитационное поле ( т.
е. , в искажениях пространства-времени вокруг
тело). Можно определить увеличение энергии гравитационного
поле напрямую, но это очень сложно
расчет с использованием общей теории относительности.
С другой стороны, очень легко вычислить работу, совершаемую при подъеме тела.
Таким образом, удобно рассчитать прирост энергии
поля от проделанной работы, и
затем приписать это увеличение энергии телу с помощью концепции
гравитационно потенциальная энергия.
В заключение можно оценить увеличение электрической потенциальной энергии заряда при оно взято между двумя различными точками в электростатическом поле от работу, совершаемую при перемещении заряда между этими двумя точками. Энергия на самом деле хранится в электрическом поле, окружающем заряд, но мы можем смело приписать эту энергию заряду, потому что мы знаем, что поле хранит энергию без потерь, и будет возвращать энергию заряду всякий раз, когда это требуется для этого законы физики.
Следующий: Электрический потенциал Вверх: Электрический потенциал Предыдущий: Электрический потенциал Ричард Фицпатрик 2007-07-14
7.
2: Электрическая потенциальная энергия — LibreTexts по физике- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4386
- OpenStax
- OpenStax
Цели обучения
К концу этого раздела вы сможете:
- Определять работу, совершаемую электрической силой
- Определение электрической потенциальной энергии
- Применение работы и потенциальной энергии в системах с электрическими зарядами
Когда свободный положительный заряд q ускоряется электрическим полем, ему придается кинетическая энергия (рис. \(\PageIndex{1}\)). Этот процесс аналогичен ускорению объекта гравитационным полем, как если бы заряд двигался вниз по электрическому холму, где его потенциальная электрическая энергия преобразуется в кинетическую энергию, хотя, конечно, источники сил очень разные.
Исследуем работу, совершаемую электрическим полем над зарядом q в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.
Электростатическая или кулоновская сила консервативна, а это означает, что работа, совершаемая над q , не зависит от пройденного пути, как мы покажем позже. Это в точности аналогично силе гравитации. Когда сила консервативна, можно определить потенциальную энергию, связанную с силой. Обычно легче работать с потенциальной энергией (поскольку она зависит только от положения), чем непосредственно вычислять работу.
Чтобы показать это явно, рассмотрим электрический заряд \(+q\), зафиксированный в начале координат, и переместим другой заряд \(+Q\) к q таким образом, что в каждый момент приложенная сила \(\ vec{F}\) точно уравновешивает электрическую силу \(\vec{F}_e\) на Q (Рисунок \(\PageIndex{2}\)).
Работа, совершаемая приложенной силой \(\vec{F}\) к заряду Q , изменяет потенциальную энергию Q . Мы называем эту потенциальную энергию электрической потенциальной энергией 9.2} \шляпа{г},\]
, где мы определили положительное направление, направленное от начала координат, а r — это расстояние от начала координат. Направления как смещения, так и приложенной силы в системе на рисунке \(\PageIndex{2}\) параллельны, и, таким образом, работа, проделанная над системой, положительна.
Мы используем букву U для обозначения потенциальной электрической энергии, которая измеряется в джоулях (Дж). Когда консервативная сила совершает отрицательную работу, система приобретает потенциальную энергию. Когда консервативная сила совершает положительную работу, система теряет потенциальную энергию \(\Delta U = — W\). В системе на рисунке \(\PageIndex{3}\) сила Кулона действует в направлении, противоположном смещению; следовательно, работа отрицательна.
Однако мы увеличили потенциальную энергию в двухзарядной системе.
Пример \(\PageIndex{1}\): Кинетическая энергия заряженной частицы
Заряд \(+3,0-nC\) Q изначально находится в состоянии покоя на расстоянии 10 см (\(r_1\)) от заряд \(+5,0-нКл\) q зафиксирован в начале координат (рис. \(\PageIndex{3}\)). Естественно, кулоновская сила разгоняет Q от q , достигая в итоге 15 см (\(r_2\)).
Рисунок \(\PageIndex{3}\): Заряд Q отталкивается от q , совершая над ним работу и получая кинетическую энергию. 9{-7} \, J. \nonumber \end{align} \nonumber\]Это также значение кинетической энергии в точке \(r_2\).
Значение
Заряд Q первоначально находился в состоянии покоя; электрическое поле q совершило работу над q , поэтому теперь q имеет кинетическую энергию, равную работе, совершаемой электрическим полем.
Упражнение \(\PageIndex{1}\)
Если Q имеет массу \(4,00 \, \мкг\), какова скорость Q 9{-9}kg}} = 15 \, м/с.\)
В этом примере работа Вт , совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери U , или отрицательный \(\Дельта U\). Значение для U можно найти в любой точке, взяв одну точку за точку отсчета и рассчитав работу, необходимую для перемещения заряда в другую точку.
Электрическая потенциальная энергия
Работа Вт , совершаемая для ускорения положительного заряда из состояния покоя, положительна и является результатом потери в U или отрицательный \(\Delta U\). Математически
\[W = — \Delta U. \label{7.1}\]
Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное представление об энергии и преобразовании энергии без необходимости иметь дело с силой напрямую.
Например, гораздо чаще используется концепция электрической потенциальной энергии, чем непосредственное рассмотрение кулоновской силы в реальных приложениях. 92} \hat{r} \cdot \hat{r} dr \nonumber \\[4pt] &= \underbrace{kqQ \dfrac{1}{r_2}}_{конечная \, точка} — \underbrace{kqQ \ dfrac{1}{r_1}}_{начальная \,точка}. \конец{выравнивание}\]
Обратите внимание, что этот результат зависит только от конечных точек и не зависит от выбранного пути. Чтобы изучить это глубже, сравните путь \(P_1\) к \(P_2\) с путем \(P_1 P_3 P_4 P_2\) на рисунке \(\PageIndex{4}\).
Рисунок \(\PageIndex{4}\): Два пути перемещения \(P_1\) в \(P_2\). Работа на отрезках \(P_1P_3\) и \(P_4P_2\) равна нулю из-за того, что электрическая сила перпендикулярна перемещению по этим путям. Поэтому работы по путям \(P_1P_2\) и \(P_1P_3P_4P_2\) равны. Отрезки \(P_1P_3\) и \(P_4P_2\) представляют собой дуги окружностей с центрами q . Поскольку сила, действующая на Q , направлена либо к q , либо от нее, сила, уравновешивающая электрическую силу, не совершает никакой работы, поскольку она перпендикулярна смещению вдоль этих дуг.
Таким образом, единственная работа выполняется вдоль отрезка \(P_3P_4\), который идентичен \(P_1P_2\).
Одним из следствий этого вычисления работы является то, что если бы мы обошли путь \(P_1P_3P_4P_2P_1\), чистая работа была бы равна нулю (рисунок \(\PageIndex{5}\)). Напомним, что так мы определяем, является ли сила консервативной или нет. Следовательно, поскольку электрическая сила связана с электрическим полем соотношением \(\vec{F} = g\vec{E}\), электрическое поле само по себе консервативно. то есть
\[\oint \vec{E} \cdot d\vec{l} = 0.\]
Обратите внимание, что Q является константой.
Рисунок \(\PageIndex{5}\): Замкнутая траектория в электрическом поле. Чистая работа вокруг этого пути равна нулю. Другое следствие состоит в том, что мы можем определить электрическую потенциальную энергию. Напомним, что работа, совершаемая консервативной силой, также выражается как разность потенциальной энергии, соответствующей этой силе. Следовательно, работа \(W_{ref}\) по доставке заряда из контрольной точки в интересующую точку может быть записана как 9r = kqQ\left[ \dfrac{1}{r} — \dfrac{1}{r_{ref}}\right].
\]
Второй член можно принять за произвольный постоянный опорный уровень, который служит нулевой отметкой:
\[U(r) = k\dfrac{qQ}{r} — U_{ref}.\]
Удобный выбор ссылки, основанный на нашем здравом смысле, состоит в том, что когда два заряда бесконечно далеко друг от друга, между ними нет взаимодействия. (Вспомните обсуждение эталонной потенциальной энергии в книге «Потенциальная энергия и сохранение энергии».) Принятие потенциальной энергии этого состояния равной нулю удаляет член \(U_{ref}\) из уравнения (точно так же, как когда мы говорим, что земля нулевой потенциальной энергии в задаче гравитационной потенциальной энергии), а потенциальная энергия Q , когда он отделен от q расстоянием r , принимает вид
\[\underbrace{U(r) = k\dfrac{qQ}{r}}_{ноль \, ссылка \, at \, r = \infty}.\]
Эта формула симметрична относительно \(q\) и \(Q\), поэтому ее лучше всего описывать как потенциальную энергию двухзарядной системы.
Пример \(\PageIndex{2}\): Потенциальная энергия заряженной частицы
Заряд \(+3.0-nC\) Q первоначально покоится на расстоянии 10 см \((r_1)\) от заряд \(+5,0-нКл\) q фиксируется в начале координат (рис. \(\PageIndex{6}\)). Естественно, кулоновская сила разгоняет Q от q , достигая в итоге 15 см \((r_2)\).
Рисунок \(\PageIndex{6}\): Заряд \(Q\) отталкивается от \(q\), совершая над ним работу и теряя потенциальную энергию.Как изменится потенциальная энергия двухзарядной системы от \(r_1\) до \(r_2\)?
Стратегия
Рассчитайте потенциальную энергию по приведенному выше определению: 9{-7} \, J. \end{align} \]
Значение
Изменение потенциальной энергии, как и ожидалось, отрицательно и равно по величине изменению кинетической энергии в этой системе. Напомним из примера \(\PageIndex{1}\), что изменение кинетической энергии было положительным.
Упражнение \(\PageIndex{2}\)
Какова потенциальная энергия Q относительно нулевой точки на бесконечности в точке \(r_2\) в приведенном выше примере?
Раствор
9{-7} \, Дж\), что означает, что когда Q приближается к бесконечности, его кинетическая энергия в три раза превышает кинетическую энергию в точке \(r_2\), поскольку вся потенциальная энергия преобразуется в кинетическую.В соответствии с законом Кулона силы, возникающие при воздействии нескольких зарядов на пробный заряд \(Q\), накладываются друг на друга; они могут быть рассчитаны индивидуально, а затем добавлены. Это означает, что интегралы работы и, следовательно, результирующие потенциальные энергии демонстрируют одинаковое поведение. Для демонстрации этого рассмотрим пример сборки системы из четырех зарядов.
Пример \(\PageIndex{3}\): Сборка четырех положительных зарядов
Найдите объем работы, которую должен выполнить внешний агент при сборке четырех зарядов \(+2.
0-\mu C\), \(+3.0-\mu C\), \(+4,0-\mu C\) и \(+5,0-\mu C\) в вершинах квадрата со стороной 1,0 см, начиная каждый заряд с бесконечности (рис. \(\PageIndex{7} \)).
Стратегия
Мы вводим заряды по одному, задавая им начальные местоположения в бесконечности и вычисляя работу, чтобы привести их из бесконечности в их конечное местоположение. Делаем это в порядке возрастания заряда.
Решение
Шаг 1. Сначала доведите заряд \(+2,0-\мкКл\) до начала координат. Так как других зарядов на конечном расстоянии от этого заряда еще нет, то работы по доведению его из бесконечности не совершается,
\[W_1 = 0.\]
C\) заряд, фиксированный в начале координат, привести заряд \(+3,0-\mu C\) к \((x,y,z) = (1,0 \, см, \, 0, \, 0)\) ( Рисунок \(\PageIndex{8}\)). Теперь приложенная сила должна совершать работу против силы заряда \(+2,0-\мкС\), зафиксированного в начале координат.
Совершенная работа равна изменению потенциальной энергии заряда \(+3,0-\мкС\): 9{-2} m} \nonumber \\[4pt] &= 5.4 \, J.\nonumber \end{align} \nonumber\]
Шаг 3. Удерживая заряды \(+2.0-\mu C\) и \(+3.0-\mu C\) на своих местах, поднесите заряд \(+4.0-\mu C\) к \((x,y,z) = (1,0 \, см, \, 1,0 \, см, \, 0)\) (рисунок)\(\PageIndex{9}\). Работа, проделанная на этом шаге, равна
\[\begin{align} W_3 &= k\dfrac{q_1q_3}{r_{13}} + k \dfrac{q_2q_3}{r_{23}} \nonumber \\[4pt ] &= \влево(9{-2} m}\right] \nonumber \\[4pt] &= 15.9 \, J. \nonumber \end{align} \nonumber\]
Рисунок \(\PageIndex{9}\): Шаг 3. работать \(W_3\), чтобы вывести заряд \(+4.0-\mu C\) из бесконечности.Шаг 4. Наконец, оставив первые три заряда на своих местах, довести заряд \(+5,0-\mu C\) до \((x,y,z) = (0, \, 1,0 \, см, \, 0)\) (Рисунок \(\PageIndex{10}\)). Здесь проделана работа:
\[\begin{align} W_4 &= kq_4 \left[ \dfrac{q_1}{r_{14}} + \dfrac{q_2}{r_{24}} + \dfrac{q_3} {r_{34}}\right], \nonumber \\[4pt] &= \left(9{-2}m} \right] \nonumber \\[4pt] &= 36,5 \, J.
\nonumber \end{align} \nonumber\]
Следовательно, общая работа, проделанная приложенной силой при сборке четырех зарядов, равна сумме работ по перемещению каждого заряда из бесконечности в его конечное положение:
\[\begin{align} W_T &= W_1 + W_2 + W_3 + W_4 \nonumber \\[4pt] &= 0 + 5,4 \, J + 15,9 \, J + 36,5 \, J \nonumber \\[4pt] &= 57,8 \, J. \nonumber \end{align} \номер\]
Значение
Работа над каждым зарядом зависит только от его парного взаимодействия с другими зарядами. Нет необходимости рассматривать более сложные взаимодействия; работа над третьим зарядом зависит только от его взаимодействия с первым и вторым зарядами, взаимодействие между первым и вторым зарядом не влияет на третий.
Упражнение \(\PageIndex{3}\)
Является ли электрическая потенциальная энергия двух точечных зарядов положительной или отрицательной, если заряды одного знака? Противоположные знаки? Как это связано с работой, необходимой для сближения зарядов с бесконечности?
Решение
положительное, отрицательное, и эти величины равны работе, которую вам нужно совершить, чтобы принести заряды из бесконечности
Обратите внимание, что электрическая потенциальная энергия положительна, если два заряда одного типа, положительного или отрицательного, и отрицательна, если два заряда противоположного типа.
Это имеет смысл, если вы думаете об изменении потенциальной энергии \(\Delta U\) по мере того, как вы приближаете два заряда или отдаляете их друг от друга. В зависимости от относительных типов зарядов вам, возможно, придется воздействовать на систему или система будет воздействовать на вас, то есть ваша работа будет либо положительной, либо отрицательной. Если вам нужно совершить над системой положительную работу (фактически сблизить заряды), то энергия системы должна увеличиться. Если вы сблизите два положительных заряда или два отрицательных заряда, вы должны совершить над системой положительную работу, которая повысит их потенциальную энергию. Поскольку потенциальная энергия пропорциональна 1/ r потенциальная энергия увеличивается, когда r уменьшается между двумя положительными или двумя отрицательными зарядами.
С другой стороны, если вы сблизите положительный и отрицательный заряды, вы должны совершить отрицательную работу над системой (заряды притягивают вас), а значит, вы заберете энергию у системы.
