Потенциал электростатического поля и разность потенциалов. Школьный курс физики
Главная | Физика 10 класс | Потенциал электростатического поля и разность потенциалов
Потенциал электростатического поля.
Введём ещё одну количественную характеристику электростатического поля — потенциал, не зависящую от помещённого в поле заряда.
Потенциалом электростатического поля в данной точке называют скалярную физическую величину, равную отношению потенциальной энергии пробного заряда, помещённого в данную точку поля, к этому заряду.
Потенциал обозначается буквой фи φ.
Как вы уже знаете, напряжённость электростатического поля является его силовой характеристикой, так как она определяет силу, действующую на заряд q в данной точке поля. Потенциал φ — энергетическая характеристика поля, которая позволяет определить потенциальную энергию заряда q

Пусть в начальном положении 1 потенциальная энергия заряда q равна Wpl = φplq, а в конечном положении 2 — Wp2 = φp2q. Работа сил электростатического поля по перемещению пробного заряда q из одной точки поля в другую равна A12 = -(Wp2 — Wpl), или
Итак, работа электростатического поля по перемещению пробного заряда q из одной точки поля в другую равна произведению модуля заряда на разность потенциалов между положениями 1 и 2
C точки зрения теории близкодействия на заряд непосредственно действуют не другие заряды, а созданное ими электрическое поле. При перемещении заряда действующая на него со стороны поля сила совершает работу. (В дальнейшем для краткости мы будем говорить о
работе поля. ) Поэтому можно определить не только потенциальную энергию системы заряженных частиц, но и потенциальную энергию отдельного заряженного тела в электрическом поле.
) Поэтому можно определить не только потенциальную энергию системы заряженных частиц, но и потенциальную энергию отдельного заряженного тела в электрическом поле.
Разность потенциалов.
Подобно потенциальной энергии заряда, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала. Этот уровень выбирается произвольно, и поэтому потенциал одной определённой точки поля может иметь любое значение. Для описания электростатического поля вводят также физическую величину — разность потенциалов. Она не зависит от выбора нулевого уровня отсчёта потенциала.
Разность потенциалов между двумя точками поля — это скалярная физическая величина, равная отношению работы сил электростатического поля при перемещении пробного заряда из начальной точки в конечную, к этому заряду.
 Если же заряд будет отрицательным, то работа сил электростатического поля отрицательна.
Если же заряд будет отрицательным, то работа сил электростатического поля отрицательна.
Наряду с потенциалом, разность потенциалов также является энергетической характеристикой электростатического поля.
Часто вместо понятия «разность потенциалов» используют понятие «напряжение» (его обозначают буквой U). В случае если работу по перемещению заряда совершают только кулоновские силы, эти понятия совпадают.
Разность потенциалов между двумя точками поля равна единице, если при перемещении заряда 1 Кл из одной точки в другую электростатическое поле совершает работу 1 Дж.
В СИ эту единицу называют вольт (В): 1B = 1 Дж/1 Кл.
Используя определение разности потенциалов, можно придать потенциалу в точке электростатического поля простой физический смысл. Если потенциал бесконечно удалённой точки принять за нулевой φ∞ = 0, то A1∞ = q(φ1 — φ2) = q
Потенциал электростатического поля в данной точке численно равен работе, совершаемой силами электростатического поля по перемещению заряда 1 Кл из этой точки поля в бесконечно удалённую точку.
Эквипотенциальные поверхности.
При перемещении заряда под углом 90° к линиям напряжённости сила электростатического поля не совершает работу (в этом случае сила перпендикулярна перемещению). Отсюда следует, что если провести поверхность, перпендикулярную в каждой точке линиям напряжённости, то при перемещении заряда вдоль этой поверхности работа полем не совершается. Это, в свою очередь, означает, что все точки поверхности, перпендикулярной линиям напряжённости, имеют один и тот же потенциал.
Эквипотенциальная поверхность — поверхность, во всех точках которой потенциал имеет одно и то же значение.
Эквипотенциальные поверхности однородного электростатического поля представляют собой плоскости (рис. 9.35), а поля точечного заряда — концентрические сферы (рис. 9.36).
9.35), а поля точечного заряда — концентрические сферы (рис. 9.36).
Рис. 9.35
Рис. 9.36
Подобно линиям напряжённости, эквипотенциальные поверхности качественно характеризуют распределение ноля в пространстве. При этом вектор напряжённости перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала. Это особенно очевидно на примере поля точечного положительного заряда. Потенциал убывает по мере удаления от заряда, и напряжённость поля направлена от заряда вдоль радиусов концентрических сфер (см. рис. 9.36). Чем больше напряжённость поля, тем меньше расстояние между соседними эквипотенциальными поверхностями.
Эквипотенциальные поверхности системы положительного и отрицательного точечных зарядов изображены на рисунке 9.37.
Рис. 9.37
Напряжённость электростатического поля и разность потенциалов.
Установим связь между напряжённостью электростатического поля и разностью потенциалов.
При перемещении заряда q из точки 1 электростатического поля в точку 2, расположенную на расстоянии d от точки 1 (рис. 9.38), силы электростатического поля совершают работу:
Рис. 9.38
C другой стороны, в однородном поле работа сил электростатического поля равна:
Приравнивая правые части этих выражений, можно записать:
Отсюда
Выражение, связывающее напряжённость электрического поля и разность потенциалов, можно использовать только для однородного поля.
В СИ единицу напряжённости устанавливают на основе разности потенциалов. Её называют вольт на метр (1 В/м).
1 В/м — напряжённость такого однородного поля, в котором разность потенциалов между двумя точками, расположенными на рас стоянии 1 м вдоль силовой линии, равна 1 В.
Эту единицу измерения используют чаще, чем Н/Кл.
Вопросы:
1. Что называют:
а) потенциалом электростатического поля в данной точке;
б) разностью потенциалов между двумя точками поля?
2.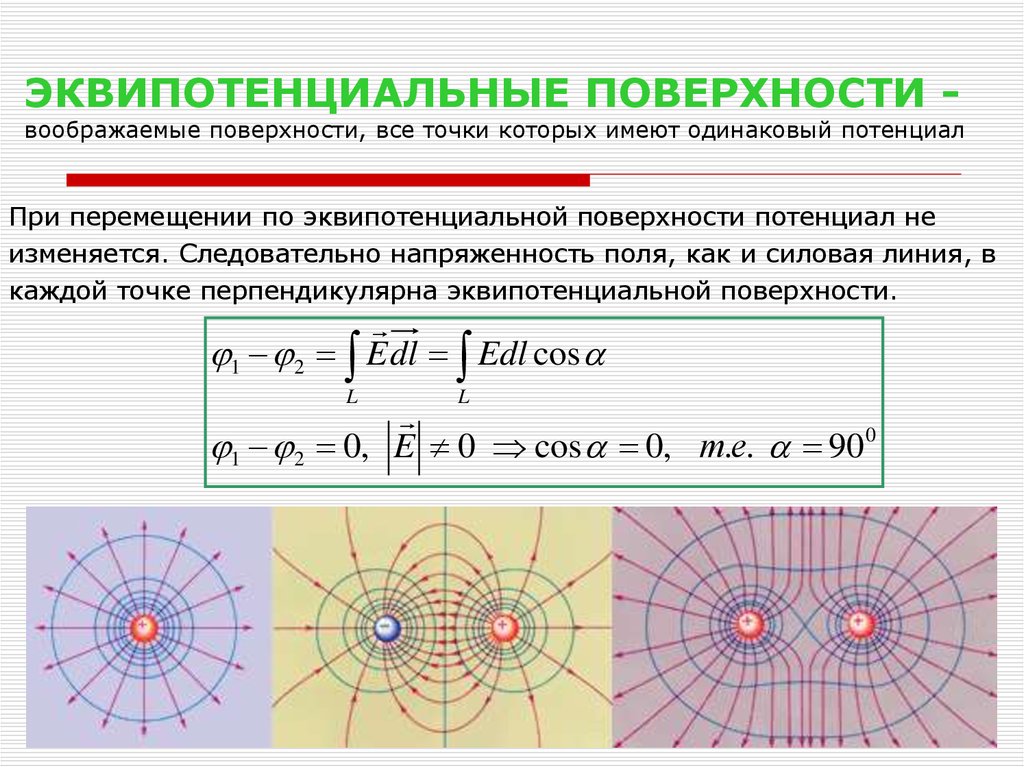
а) положительную работу;
б) отрицательную работу?
3. В чём состоит физический смысл потенциала?
4. Какую поверхность называют эквипотенциальной? Приведите примеры таких поверхностей.
5. Как связаны между собой напряжённость однородного электрического поля и разность потенциалов?
Пример решения задачи
В однороднохм электростатическом поле, модуль напряжённости которого равен 103 В/м, перемещается пробный заряд на расстояние 12 см под углом 30° к линиям напряжённости этого поля. Определите работу сил электростатического поля по перемещению этого заряда. Модуль заряда равен 5 ∙ 10 -8
Рис. 9.39
В однородном электростатическохм поле на заряд действует постоянная сила K = q. При перемещении заряда из точки А в точку C по прямой AC сила K совершает работу:
Подставляя числовые данные, получим:
Ответ: A ≈ 5,2 ∙ 10 -6 Дж.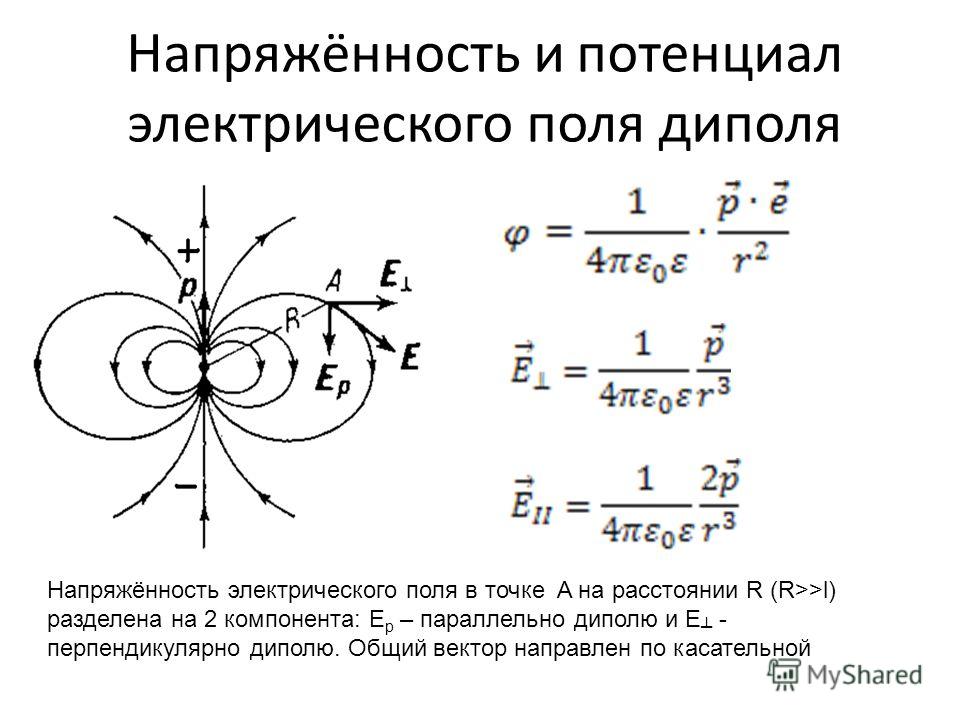
Упражнения:
1. В однородном электростатическом поле, напряжённость которого равна 1 кВ/м, переместили заряд -25 нКл в направлении силовой линии на расстояние 2 см. Найдите работу поля, изменение потенциальной энергии и напряжение между начальной и конечной точками траектории.
2. Чему равна разность потенциалов между двумя точками однородного электростатического поля, если при перемещении заряда 2 мкКл из одной точки в другую поле совершает работу, равную 8 • 10 -4 Дж?
3. Два одноимённых точечных заряда, модули которых равны 5 нКл, расположены на расстоянии 1 м друг от друга. Определите работу внешних сил по сближению этих зарядов до расстояния, равного 0,1 м.
4. Разность потенциалов между двумя параллельными разноимённо заряженными металлическими пластинами равна 1 кВ, а расстояние между ними составляет 10 см. Какая сила будет действовать на заряд 0,1 мКл, помещённый между пластинами?
5. Между двумя параллельными разноимённо заряженными горизонтальными пластинами с разностью потенциалов между ними 0,7 кВ висит капелька масла радиусом 1,5 мкм. Расстояние между пластинами равно 0,4 см, плотность масла 0,8 г/см3. Найдите модуль заряда капли.
Расстояние между пластинами равно 0,4 см, плотность масла 0,8 г/см3. Найдите модуль заряда капли.
Предыдущая страницаСледующая страница
Какую величину называют потенциалом электрического поля?
Какую величину называют потенциалом электрического поля?
Эта величина и называется потенциалом электрического поля. Разность потенциалов двух точек, умноженная на величину заряда , равна работе, необходимой для перемещения этого заряда между этими точками. … Потенциал поля в некоторой точке равен работе по перемещению единичного заряда из этой точки на бесконечность.
Какие основные характеристики электрического поля существуют?
Электрическое поле всегда существует вокруг электрического заряда и имеет две характеристики: силовую (напряженность электрического поля в данной точке) и энергетическую (потенциал электрического поля в данной точке).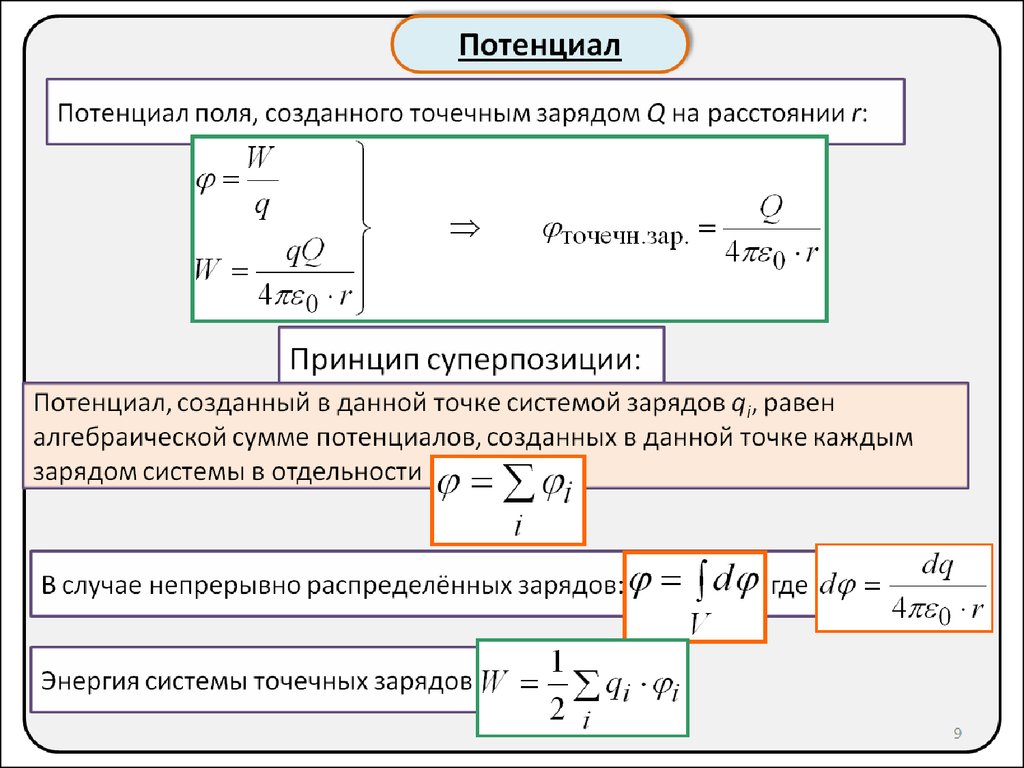
Что характерно для однородного электрического поля?
Электрическое поле называют однородным, если вектор его напряженности одинаков во всех точках поля. Основные характеристики электростатического поля: напряженность потенциал
Какая из характеристик электрического поля является его основной силовой характеристикой?
Индукция электрического поля. Напряженность электрического поля является силовой характеристикой поля и определяется не только зарядами, создающими поле, но зависит и от свойств среды, в которой находятся эти заряды.
Какая физическая величина является силовой характеристикой электрического поля?
Для количественного определения электрического поля вводится силовая характеристика — напряжённостьэлектрического поля — векторная физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда.
Какая характеристика электрического поля отражает его скрытую энергию?
Потенциал поля φ – это скрытая энергетическая характеристика поля, которая проявляется при внесении в поле пробного тела (пробной массы или пробного заряда) и зависит от источника поля и от расстояния от него до точки в поле. Потенциал φ – скалярная величина.
В чем проявляется магнитное действие электрического тока?
Ответ, проверенный экспертом 1. Магнитное действие электрического тока — способность электрического тока, проходящего по проводникам второго рода, порождать вокруг этих проводов магнитное поле. … Получаете, что на концах такого магнита будут одинаковые полюса.
Что называют силовыми линиями электрического поля?
Силовые линии электрического поля Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля.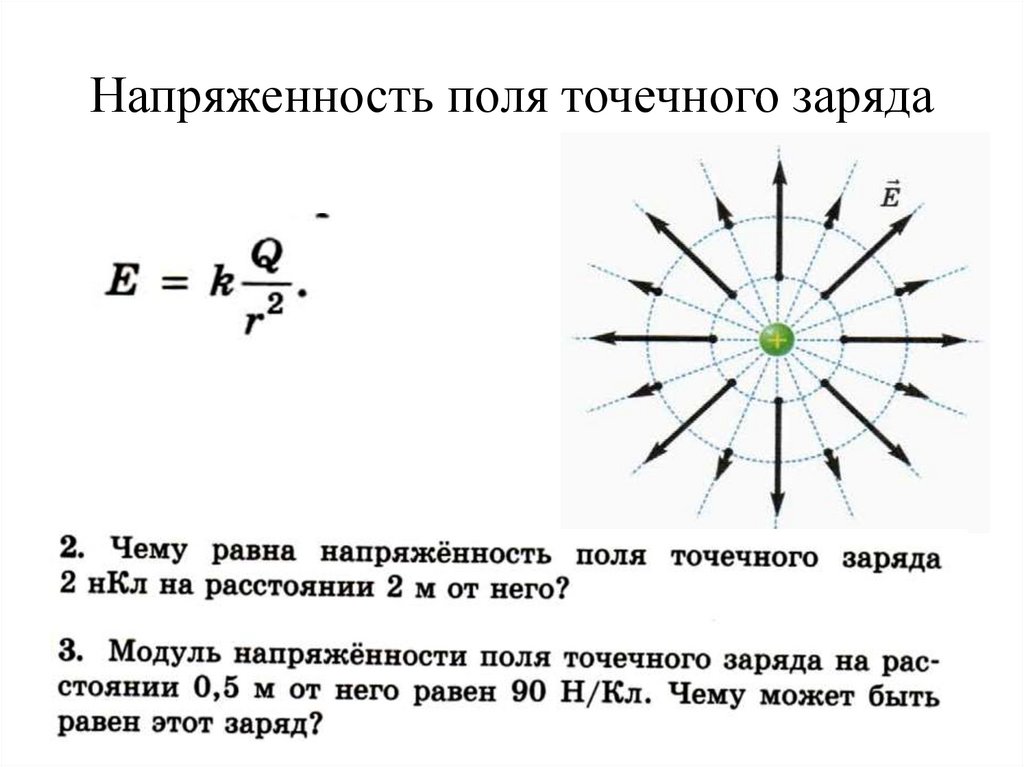
Что называют напряжённость электрического поля?
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда: Напряженность электрического поля – векторная физическая величина.
Какие линии называют силовыми линиями напряженности как определяют их направление?
Линии, касательные к которым совпадают с направлением вектора напряженности электрического поля, называются линиями напряженности электрического поля, или силовыми линиями.
Как зависит напряженность электрического поля?
Напряженность — силовая характеристика электрического поля. — величина постоянная в данной точке данного поля. силы, действующей на заряд, помещенный в данную точку данного поля, к величине этого заряда. Напряженность не зависит от величины заряда, помещенного в поле.
Где напряженность больше?
Линии напряженности направлены в сторону уменьшения потенциала. Значит, потенциал на поверхности В больше, чем на поверхности А. Напряженность больше, где линии напряженности гуще. Значит, напряженность в точке С больше, чем в точке D.
В чем измеряется напряженность магнитного поля?
В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр. 1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.
Какие бывают электрические поля?
Электрические поля бывают двух видов: однородные и неоднородные.
Какие виды электрических полей существуют в природе?
Известны такие их типы:
- Электрослабое Электромагнитное поле (см. тж. Фотон) Электрическое поле Магнитное поле Поле — переносчик слабого взаимодействия (см. тж. W- и Z-бозоны)
- глюонное поле (см.
 тж. Глюон) поле ядерных сил
тж. Глюон) поле ядерных сил - Гравитационное поле
Как возникает электрическое поле?
Электростатическое поле возникает в системе неподвижно распределенных электрических зарядов., причем взаимодействие осуществляется не мгновенно, а распространяется в вакууме с некоторой конечной скоростью, равной скорости света.
Где образуется магнитное поле?
Магнитное поле представляет собой один из видов материи. … Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле.
Когда возникает магнитное поле вокруг проводника?
При прохождении тока по прямолинейному проводнику вокруг него возникает магнитное поле (рис. 38). … Направление магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.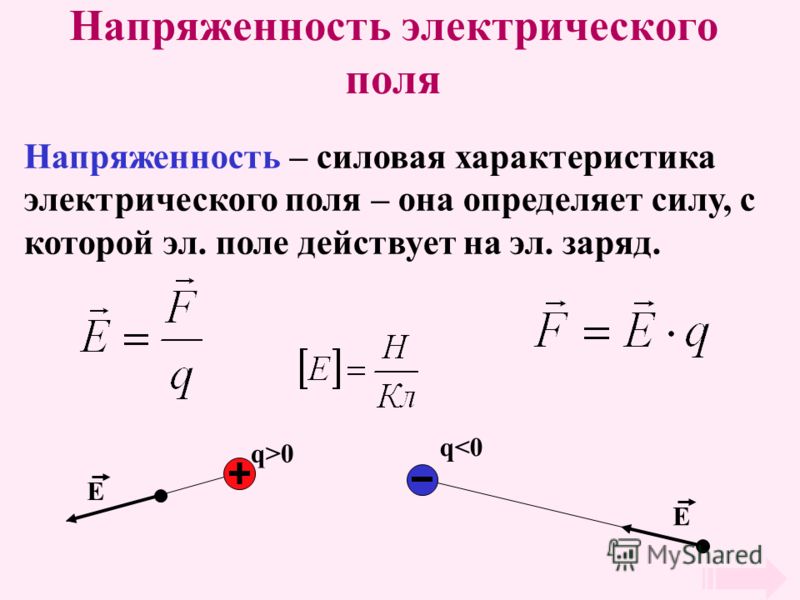 Направление магнитных силовых линий можно определить по правилу буравчика.
Направление магнитных силовых линий можно определить по правилу буравчика.
Где используется магнитное поле?
В первом случае магнитное поле применяют в сепараторах в целях очистки различных пищевых сред от металлических ферромагнитных примесей и в устройствах для разделения заряженных частиц. Во втором — в целях изменения физико-химических свойств воды. … Магнитное сопротивление постоянно только для немагнитных участков цепи.
Потенциал электростатического поля
Электри́ческий заря́д (коли́чество электри́чества) — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
Элемента́рный
электри́ческий заря́д
— фундаментальная физическая постоянная,
минимальная порция (квант) электрического
заряда,
наблюдающегося в природе у свободных
долгоживущих частиц. Согласно изменениям
определений основных единиц СИ равен
точно 1,602 176 634⋅10−19 Кл в Международной системе единиц (СИ).
Закон Кулона – сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля (например, в электромагнитных волнах).
Напряжённость
электри́ческого по́ля — векторная
физическая величина, характеризующая
электрическое поле в данной точке и
равная отношению силы, действующей на
неподвижный точечный заряд, помещённый
в данную точку поля, к величине этого
заряда. Напряжённость
поля точечного заряда
– вектор напряжённости
в любой точке электрического поля
направлен вдоль прямой, соединяющей
эту точку и заряд,
и совпадает с силой, действующей на
точечный положительный заряд,
помещённый в данную точку.
Принцип суперпозиции электрических полей – если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0. где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2.
Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Теорема Гаусса в дифференциальной форме.
Вопрос
№4 Вычисление
полей с помощью теоремы Гаусса. Поле
равномерно заряженной плоскости,
бесконечного цилиндра, сферы. Поле шара,
равномерно заряженного по объёму.
(Теорему Гаусса см в вопросе №3)
Поле
равномерно заряженной плоскости,
бесконечного цилиндра, сферы. Поле шара,
равномерно заряженного по объёму.
(Теорему Гаусса см в вопросе №3)
Поле равномерно заряженной плоскости Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле: (dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.)
Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S.
В симметричных, относительно плоскости точках, напряженность будет одинакова по величине и противоположна по направлению.
Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (см рис).
Тогда
Применим теорему Остроградского-Гаусса.
Поток ФЕ через боковую часть поверхности цилиндра равен нулю, т.
 к.
к.
Для основания цилиндра
Суммарный поток через замкнутую поверхность (цилиндр) будет равен:
Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим: ; откуда следует, что
Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости
Поле заряженного бесконечно длинного цилиндра (нити)
Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью (dq – заряд, сосредоточенный на отрезке цилиндра).
Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.
Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси).
Для оснований цилиндров
Для боковой поверхности т.
 е.
зависит от расстояния r.
е.
зависит от расстояния r.Следовательно, поток вектора через рассматриваемую поверхность, равен
При r>R на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда
Если r<R; E(r)=0, т.к. внутри замкнутой поверхности зарядов нет. График зависимости E(r):
Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.
Поле заряженной сферы
Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, – в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r.
Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда
,
Как
видно, вне сферы поле тождественно полю
точечного заряда той же величины,
помещенному в центр сферы.
Поле объемного заряженного шара
Для поля вне шара радиусом R получается тот же результат, что и для пустотелой сферы, т.е. справедлива формула: .
Но внутри шара при сферическая поверхность будет содержать в себе заряд, равный (ρ – объемная плотность заряда, равная: ; – объем шара).
Тогда по теореме Остроградского-Гаусса запишем:
, т.е. внутри шара
Вопрос №5 Потенциальность электростатического поля. Потенциал электростатического поля. Потенциал поля точечного заряда, равномерно заряженной металлической сферы.
Потенциальность электростатического поля
Пусть
точечный заряд q перемещается
по произвольной траектории в
электростатическом поле из точки 1 в
точку 2 под
действием нескольких сил. Нас интересует
сила Fэ,
действующая на заряд со стороны
электростатического поля. При заданном
перемещении заряда она совершает
работу Aэ.
Э та работа не зависит от траектории, по которой перемещается заряд в электростатическом поле, а определяется только его начальным и конечным положениями (расположением точек 1 и 2). Это свойство называется потенциальностью (консервативностью). Следует понимать, что именно электростатическое поле является потенциальным, произвольное электрическое − нет.
Потенциалом φ электростатического поля называется скалярная (числовая) функция φ=φ(x,y,z) координат пространства такая, что работа сил Aэ электростатического поля при перемещении произвольного точечного заряда q по произвольной траектории из точки 1 в точку 2 равна разности значений этой функции в этих точках, умноженной на q:
Aэ=q⋅(φ1−φ2),
(φ1=φ(x1,y1,z1) − потенциальная энергия в точке 1, φ2=φ(x2,y2,z2) − потенциальная энергия в точке 2).
Потенциал поля точечного заряда
Подставим в соотношение для определения потенциала выражение для напряженности электрического поля точечного заряда:
.
При интегрировании учтем, что .
После интегрирования получаем:
.
Потенциал точечного заряда пропорционален величине заряда и убывает обратно пропорционально расстоянию, стремясь на бесконечности к нулю.
Потенциал поля равномерно заряженной металлической сферы Получим выражение потенциала поля сферы радиуса , равномерно заряженной зарядом , как функцию расстояния до ее центра. Нулевое положение выберем на бесконечности. Возможны два случая.
В силу эквивалентности полей равномерно заряженной сферы и точечного заряда, напряженность поля в любой точке внешней области не изменится, если весь заряд сферы собрать в ее центре. Стало быть, не изменится и работа поля при движении пробного заряда по любой траектории во внешней области. А, значит, и выражение потенциальной энергии заряда в поле заряда также не изменится.
Таким образом, потенциальная энергия взаимодействия пробного заряда, находящегося за пределами равномерно заряженной сферы и самой этой сферы определяется соотношением:
Тогда,
по определению потенциала, для внешней
области.
При движении из внутренней области на бесконечность, заряд неизбежно пересечет границу сферы. Тогда его потенциальная энергия, по определению равная работе кулоновских сил , разлагается в сумму
Но, так как внутри равномерно заряженной сферы напряженность равна нулю, то и потенциал во всей внутренние области равен:
Вопрос №6 Связь между напряжённостью электростатического поля и потенциалом. Эквипотенциальные поверхности. Уравнение Пуассона.
Связь между напряжённостью электростатического поля и потенциалом
Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl, можно найти так:
(El – проекция на ; dl– произвольное направление перемещения заряда).
С другой стороны, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl: , отсюда
Для ориентации dl (направление перемещения) в пространстве, надо знать проекции на оси координат:
По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть
– вектор,
показывающий направление наибыстрейшего
увеличения функции.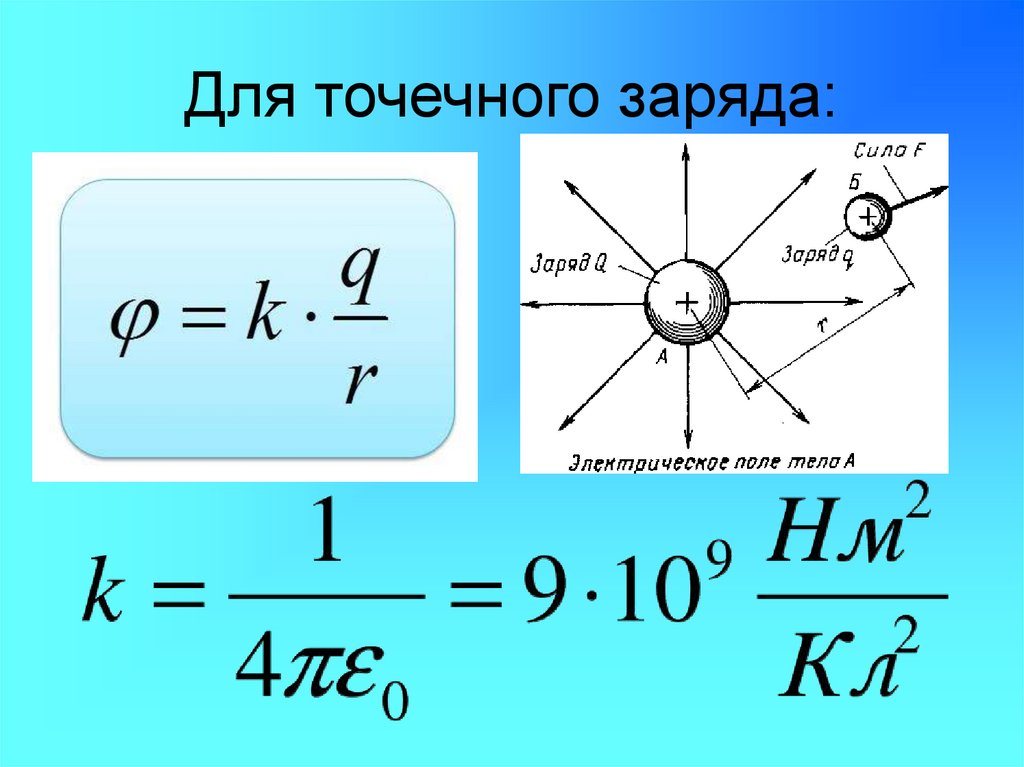
Тогда коротко связь между и φ записывается так: или , где (набла) означает символический вектор, называемый оператором Гамильтона.
Знак минус говорит о том, что вектор направлен в сторону уменьшения потенциала электрического поля.
Эквипотенциальные поверхности Совокупность точек, имеющих равный потенциал, образуют так называемые эквипотенциальное поверхности, или поверхности равного потенциала.
С
их помощью также можно графически
изобразить электростатическое поле.
Направление нормали к эквипотенциальной
линии будет совпадать с направлением
вектора
в
той же точке. Эквипотенциальные
поверхности можно провести через любую
точку поля. Следовательно, таких
поверхностей может быть построено
бесконечное множество. Однако, проводят
поверхности таким образом, чтобы разность
потенциалов для двух соседних поверхностей
была всюду одна и та же. Тогда по густоте
эквипотенциальных поверхностей можно
судить о величине напряженности. Чем
гуще располагаются эквипотенциальные
поверхности, тем быстрее изменяется
потенциал при перемещении вдоль нормали
к поверхности.
Уравнение Пуассона
Произвольное векторное поле E→(r→) характеризуется тремя скалярными функциями Ej(r→), где j пробегает значения x, y, z (если говорить о декартовой системе координат). Поэтому одного уравнения недостаточно, чтобы найти электрическое поле. Однако электростатическое поле потенциально. Это накладывает столь сильное ограничение, что все три компоненты E→ можно выразить через одну скалярную функцию — электрические потенциал ϕ. Подставляя E→ = −gradϕ. в уравнение divE→ = 4πρ, получаем уравнение Пуассона Δϕ = −4πρ.
где дифференциальный оператор Δ = divgrad называется оператором Лапласа, или лапласианом. В декартовой системе координат уравнение записывается следующим образом: ∂2ϕ ∂x2 + ∂2ϕ ∂y2 + ∂2ϕ ∂z2 = −4πρ.
В произвольной криволинейной системе координат для вычисления оператора Δ необходимо исходить из инвариантных определений дивергенции и градиента.
Уравнение
Пуассона относится к классу дифференциальных
уравнений в частных производных. Иногда
специальным выбором системы координат
его удается свести к обыкновенному
дифференциальному уравнению. Это
случается, если в такой специальной
системе координат плотность заряда и
потенциал зависят от одной координаты.
Один пример такого рода рассмотрен
далее в качестве задачи.
Иногда
специальным выбором системы координат
его удается свести к обыкновенному
дифференциальному уравнению. Это
случается, если в такой специальной
системе координат плотность заряда и
потенциал зависят от одной координаты.
Один пример такого рода рассмотрен
далее в качестве задачи.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Процедура выполнения команд. Интересное: Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Потенциал – это энергетическая характеристика поля. φ = Wр/q– потенциал электрического поля в данной точке, это физическая величина, показывающая, чему равна потенциальная энергия заряда, равного + 1 Кл, в данной точке поля. [φ] = Дж/Кл = В (Вольт).Потенциал величина скалярная. φ>0, если заряд создающий поле положителен. φ<0, если заряд, создающий поле отрицателен. Если в данной точке электрическое поле создают несколько зарядов, то φ = φ1 ± φ2± φ3 +….–принцип суперпозиции потенциалов – потенциал электрического поля, созданного несколькими зарядами, в данной точке равен алгебраической сумме потенциалов, созданных в этой точке, каждым зарядом в отдельности. φ = qEd/q = Еd– потенциал однородного электростатического поля, где d — расстояние( вдоль силовой линии) от отрицательно заряженной плоскости( нулевой уровень потенциальной энергии) до той точки, где находится заряд. φ1 – φ2 = A/q = U —разность потенциалов между точками – это физическая величина, показывающая, какую работу совершает электрическое поле перемещая заряд в + 1 Кл между данными точками поля. Напряженность и разность потенциалов для однородного электростатического поля связаны между собой формулой: U = E∆d – где ∆d – расстояние между точками , для которых находят разность потенциалов. Вектор напряженности электрического поля всегда направлен от точек с большим потенциалом к точкам с меньшим потенциалом. 2 Звуковые волны. Ультразвук и его использование в технике и медицине. Акустика – это учение о звуке. Звук– это продольная механическая волна с частотой от 16 Гц до 20000 Гц, воспринимаемые человеком. Любое колеблющееся со звуковой частотой тело может являться источником звука. При колебаниях такое тело сжимает прилегающий к одной из его сторон слой воздуха, создавая сжатие (зона повышенного давления). Примеры источников звука: голосовые связки, камертон, громкоговоритель. Тело воспринимающее звук называют приемником звука (ухо, микрофон). Звук распространяется во всех упругих средах: газах, жидкостях, твердых телах. Звук не может распространяться в вакууме. Пористые тела плохо проводят звук( звукоизоляция). Скорость звука различна в разных средах: она наибольшая в твердых телах (в стали около 5 км/с), наименьшая в газе (332 м/с при 00С в воздухе). В жидкостях она больше чем в газе, но меньше чем в твердом теле (в воде около 1,4 км/с). В данной среде скорость звука зависит от температуры, например для воздуха скорость звука растет с повышением температуры (при 200С скорость звука около 343 м/с). Эхо – это отражённый звук. Продольные механические волны с частотой меньше 16 Гц называю инфразвуком, мы их не слышим Продольные механические волны с частотой больше 20кГц называют ультразвуком, мы их тоже не слышим. В медицине широко используют УЗИ – ультразвуковое исследование внутренних органов человека. Физические основы использования УЗ в медицине. 1) Диагностика — используется зависимость скорости распространения звуковой волны от состояния организма. 2) Терапия – используется способность УЗ волны создавать в жидкости сжатия и разряжения, которые приводят к разрыву сплошности жидкости (кавитации). 3) Хирургия — используется способность УЗ волны разрушать ткани – ультразвуковой скальпель. Можно рассекать мягкие и костные ткани и дробить камни в почках. 4) УЗ –кардиография, определение размера сердца в динамике; 5) Эхо энцефалография – определение отека и опухоли мозга, прибор – эхоэнцефалограф; 6) УЗ – локация, определение размеров глазных сред в офтальмологии; 7) УЗИ – исследование внутренних органов – поджелудочной железы, почек, печени. 8) УЗ в акушерстве и гинекологии – определение развития плода, внематочной беременности и опухолей. Преимущество УЗ перед рентгеном – меньше вредность, недостаток – меньше четкость изображения. УЗ – терапия. Используется прогревание (при помощи кавитации) и обработка ран и травм для профилактики раневой инфекции (используется свойство УЗ уничтожать микроорганизмы). УЗ можно также стерилизовать инструменты и хирургическое белье.
3.Решите задачу: определите массу водорода, находящегося в баллоне емкостью 20 л при давлении 830 к Па, если температура газа равна 17º С. Решение: из уравнения состояния идеального газа PV=(m/M)RT и M=M010-3кг/моль, R=8,31 Дж/моль К, определяем массу водорода 138г.
Билет №29 Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
94.
 Потенциал электростатического поля и разность потенциалов
Потенциал электростатического поля и разность потенциаловПотенциал физика
Обладает ли электрическое поле энергией? В чём это выражается?
В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это Силовая характеристика. Теперь введём энергетическую характеристику — потенциал.
Потенциал поля. Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.
Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (Wп2 — Wп1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14. 14).
14).
Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно,
Это позволяет ввести новую количественную характеристику поля — Потенциал, не зависящую от заряда, помещённого в поле.
Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.
Согласно данному определению потенциал равен:
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это Энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
Разность потенциалов. Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.
Так как потенциальная энергия Wn = дчр, то работа сил поля равна:
Разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:
Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
Единица разности потенциалов. Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.
Выразим единицу разности потенциалов через основные единицы СИ. Так как
Вопросы к параграфу
1. Какие поля называют потенциальными?
2. Как разность потенциалов между двумя точками поля зависит от работы электрического поля?
Образцы заданий ЕГЭ
А1. Выберите правильное соотношение разности потенциалов между точкой G и точками В, С и D (см. рис.) в однородном электростатическом поле.
А2. Работа поля по перемещению заряда q — 10 -5 Кл из одной точки в другую равна 10 Дж. Разность потенциалов между этими точками равна
1) 10 -4 В 2) 10 4 В 3) -10 6 В 4) 10 6 В
А3. Для перемещения заряда 10 6 Кл из точки, потенциал которой равен 2 В, в точку, потенциал которой равен 6 В, надо совершить работу, равную
Напряжённость поля — векторная величина.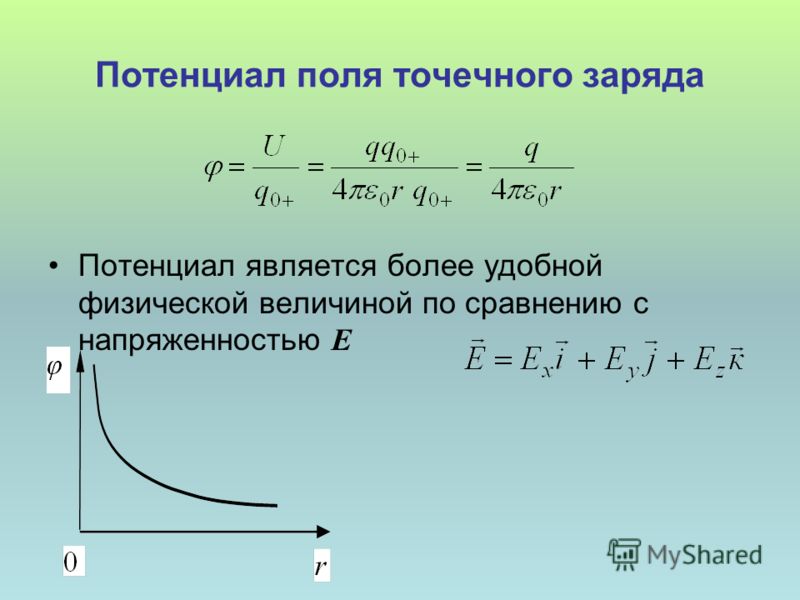 Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это Энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это Энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен.
Www. xn--24-6kct3an. xn--p1ai
25.08.2018 21:23:57
2018-08-25 21:23:57
Источники:
Http://www. xn--24-6kct3an. xn--p1ai/%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_%D0%B4%D0%BB%D1%8F_10_%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B0_%D0%9C%D1%8F%D0%BA%D0%B8%D1%88%D0%B5%D0%B2/94.html
Потенциал, работа электростатического поля. Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы — учебные курсы » /> » /> .keyword { color: red; }
Потенциал физика
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются Консервативными, а само поле называется Потенциальным.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется Потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще Электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.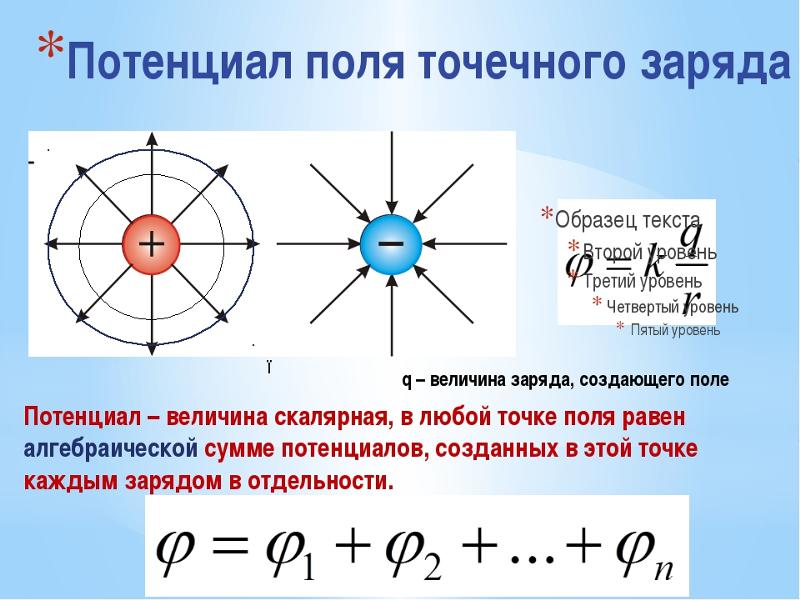
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Зависимость напряженности и потенциала от расстояния
Потенциал поля, созданного равномерно заряженной сферой радиусом R и зарядом q на расстоянии r от центра сферы, равен
Напряжение в природе
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.
Энергия взаимодействия зарядов*
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются Консервативными, а само поле называется Потенциальным.
Электрический угорь способен создавать напряжение до 650 В.
Fizmat. by
01.11.2020 17:52:37
2020-11-01 17:52:37
Источники:
Http://fizmat. by/kursy/jelektrichestvo/potencial
Урок 27. напряжённость и потенциал электростатического поля. разность потенциалов — Физика — 10 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Потенциал физика
Напряжённость — отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.
Потенциал точки электростатического поля — отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.
Напряжение – разность потенциалов.
Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.
Напряжённость направлена в сторону убывания потенциала.
Эквипотенциальные поверхности – поверхности равного потенциала.
Свободные заряды — заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля.
Электростатическая индукция – явление разделения зарядов и их распределение по поверхности проводника во внешнем электрическом поле.
Основная и дополнительная литература
Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 290 – 320.
Рымкевич А. П. Сборник задач по физике. 9 – 11 класс. М. Дрофа, 1999 – С. 93 — 102
Теоретический материал для самостоятельного изучения
Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создаёт в окружающем пространстве электрическое поле.
Электрическое поле — это особый вид материи, посредством которой происходит взаимодействие зарядов. Скорость распространения электрического поля в вакууме равна 300000 км/с.
Напряжённость Е — силовая характеристика электрического поля.
Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами однородно
Главное свойство электрического поля – это действие его на электрические заряды с некоторой силой.
Напряжённость-это отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.
Если в данной точке пространства различные заряженные частицы создают поля, напряжённости которых Е1, Е2, то результирующая напряжённость поля в этой точке равна геометрической сумме напряжённостей этих полей. В этом состоит принцип суперпозиции полей.
Заряд, помещенный в электрическое поле обладает потенциальной энергией.
Потенциалом φ точки электростатического поля называют отношение потенциальной энергии Wn заряда, помещённого в данную точку, к этому заряду q.
Напряжение – это работа, совершаемая полем при перемещении заряда 1Кл.
Примеры и разбор решения заданий
1. К каждой позиции первого столбца подберите соответствующую позицию второго
Потенциальная энергия заряда в однородном электростатическом поле
Решение: вспомнив формулы величин, можем установить:
Потенциальная энергия заряда в однородном электростатическом поле
2. В однородном электрическом поле напряжённостью 1 В/м переместили заряд -25 нКл в направлении силовой линии на 2 см. Найти работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками перемещения.
Работа электрического поля при перемещении заряда вдоль силовой линии:
При этом изменение потенциальной энергии равно:
Напряжение между начальной и конечной точками перемещения равно:
ΔA = -25 · 10 -9 Kл · 10 3 B/м · 0,02 м = -0,5 мкДж;
Ответ:
Ответ:
Напряжённость Е — силовая характеристика электрического поля.
Resh. edu. ru
28.01.2019 14:21:17
2019-01-28 14:21:17
Источники:
Https://resh. edu. ru/subject/lesson/5899/conspect/
Потенциал поля
Потенциал поля
Реферат по физике студента гр. 617-07 ИТ Даутова Салавата
Ферганский филиал Ташкентского университета информационных технологий
Фергана — 2008 г.
Выясним, как можно найти работу электрических сил при перемещении заряда q в однородном электрическом поле (Е=const). Пусть заряд q находится в точке В однородного электрического поля (рис.1).
Рис.1. Работа сил электрического поля по перемещению заряда q из точки В в точку С не зависит от формы пути.
Из механики известно, что работа равна произведению силы на путь и на косинус угла между ними. Поэтому работа электрических сил при перемещении заряда q в точку С по прямой BnC выразится следующим образом:
ABnC = F • BC • cos α = qE • BC • cos α
Так как BC•cos α=BD (см. рис. 1), то имеем
рис. 1), то имеем
ABnC = qE • BD.
Работа сил поля при перемещении заряда q в точку С по пути BDC равна сумме работ на отрезках BD и DC, т. е.
ABDC = ABD + ADC = qE • BD + qE • DC • cos 90º.
Поскольку cos 90º=0, работа сил поля на участке DC равна нулю. Поэтому
ABDC = qE • BD.
Следовательно, когда перемещение заряда происходит по линии напряжённости, а затем перпендикулярно к ней, то силы поля совершают работу только при перемещении заряда вдоль линии напряжённости поля.
Выясним теперь, чему будет равна работа сил поля на криволинейном участке BmC. Разобьём этот участок на малые отрезки, сто каждый из них можно принять за прямую линию (см. рис. 1). По доказанному выше работа на каждом таком участке будет равна работе на соответствующем отрезке линии напряжённости li. Тогда вся работа на пути BmC будет равна сумме работ на отрезках l1, l2 и т. д. Таким образом,
д. Таким образом,
ABmC = qE • (l1 + l2 +…+ lk).
Поскольку сумма в скобках равна длине BD, имеем
ABmC = qE • BD.
Итак, мы доказали, что в однородном электрическом поле работа электрических сил не зависит от формы пути. Например, при перемещении заряда q между точками В и С эта работа во всех случаях равна qE•BD. Можно доказать, что этот вывод справедлив и для неоднородного поля. Следовательно, если распределение а пространстве электрических зарядов, создающих электрическое поле, не изменяется со временем, то силы поля являются консервативными.
Поскольку работа сил поля на участке BnC и BmC одинакова (см. рис.2), то на замкнутом пути работа сил поля равна нулю. Действительно, если на участке BmC работа сил поля положительна, то на участке CnB она отрицательна. Итак, работа сил электрического поля по замкнутому контуру всегда равна нулю.
Рис. 2. Работа электрических сил на замкнутом пути равна нулю.
При действии только консервативной силы работа является единственной мерой изменения энергии. Поле консервативной силы, т. е. поле, в котором работа не зависит от формы пути, называется потенциальным. Примерами потенциальных полей являются поле тяготения и электрическое поле.
Поскольку силы электрического поля консервативные, то работа сил этого поля при перемещении заряда из точки В в С (см. рис. 2) может служить мерой изменения потенциальной энергии заряда в электрическом поле. Если обозначить потенциальную энергию заряда в точке В через ПВ, а в точке С – через ПС, то
ABC = ПВ — ПС. (1)
В более общем случае, если заряд перемещается в электрическом поле из точки 1, где его потенциальная энергия была П1, в точку 2, где его энергия оказывается равной П2, работа сил поля
А1 2 = П1 — П2 = — (П2 — П1) = — ∆П2 1,
Где ∆П2 1=П2-П1 представляет собой приращение потенциальной энергии заряда при его перемещении из точки 1 в точку 2. Итак
Итак
А1 2 = — ∆П2 1. (1а)
Из формулы (1а) видно, что А1 2 и ∆П2 1 всегда имеют противоположные знаки.
Действительно, если заряд q перемещается под действием сил поля (т. е. работа сил поля А1 2 положительна), то при этом потенциальная энергия заряда уменьшается (т. е. П2 0).
Из формулы (1) видно, что с помощью измерения работы можно узнать лишь изменение потенциальной энергии заряда q между двумя точками В и С, но нет способов, позволяющих однозначно оценить величину его потенциальной энергии в какой-либо точке поля. Чтобы устранить эту неопределённость, можно условно принять за нуль потенциальную энергию в любой произвольно выбранной точке поля. Тогда и во всех других точках потенциальная энергия будет определена однозначно. Условились потенциальную энергию заряда, находящегося в точке, бесконечно отдалённой от заряженного тела, создающего поле, считать за нуль:
П∞ = 0. (2)
Тогда для случая перемещения заряда q Из точки В в бесконечность получим
АВ∞ = Пв – П∞ = ПВ. (2а)
(2а)
Следовательно, при таком условии потенциальная энергия заряда, находящегося в какой-либо точке поля, будет численно равна работе, совершаемой силами поля при перемещении данного заряда из этой точки в бесконечность. Таким образом, если поле создано положительным зарядом, то потенциальная энергия другого положительного заряда, находящегося в какой-либо точке этого поля, будет положительной, а если поле создано отрицательным зарядом, то потенциальная энергия положительного заряда в этом поле будет отрицательной. Для отрицательного заряда, помещённого в электрическое поле, будет всё наоборот.
Когда поле создано сразу несколькими зарядами, то потенциальная энергия заряда q, помещённого в какую-либо точку В такого поля, равна алгебраической сумме энергий, обусловленных полем (в точке В) каждого заряда в отдельности. Вспомним, что напряжённости электрических полей отдельных зарядов в каждой точке пространства тоже складываются (геометрически). Таким образом, если в пространстве одновременно существуют поля нескольких зарядов, то эти поля просто накладываются друг на друга. Такое свойство полей называется суперпозицией.
Таким образом, если в пространстве одновременно существуют поля нескольких зарядов, то эти поля просто накладываются друг на друга. Такое свойство полей называется суперпозицией.
Отметим ещё, что в электротехнике за нуль часто принимают потенциальную энергию заряда, находящегося на Земле. В этом случае потенциальная энергия заряда в какой-либо точке поля В численно равна работе, совершаемой силами поля при перемещении этого заряда из точки В на поверхность Земли.
Было установлено, что потенциальная энергия электрического заряда зависит от его положения в электрическом поле. Поэтому целесообразно ввести энергетическую характеристику точек электрического поля.
Поскольку сила, действующая на заряд q в электрическом поле, прямо пропорциональна величине заряда q, то работа сил поля при перемещении заряда также прямо пропорциональна величине заряда q. Следовательно, и потенциальная энергия заряда в произвольной точке В электрического поля прямо пропорциональна величине этого заряда:
ПВ = φВq. (3)
(3)
Коэффициент пропорциональности φВ для каждой определённой точки поля остаётся постоянным и может служить энергетической характеристикой поля в этой точке.
Энергетическая характеристика электрического поля в данной точке называется потенциалом поля в этой точке. Потенциал измеряется потенциальной энергией единичного положительного заряда, находящегося в заданной точке поля:
φВ = ПВ/q. (3а)
Потенциал поля электрического поля численно равен работе, совершаемой силами поля при перемещении единичного положительного заряда из этой точки в бесконечность.
φ2
Рис. 3. Во всех точках, находящихся на одинаковом расстоянии от точечного заряда, потенциал одинаков.
Потенциал поля в данной точке может быть рассчитан теоретически. Он определяется величиной и расположением зарядов, создающих поле, а также окружающей средой. Ввиду сложности таких расчётов здесь мы их приводить не будем. Запишем лишь формулу для потенциала поля точечного заряда q, полученную в результате такого расчёта.
Запишем лишь формулу для потенциала поля точечного заряда q, полученную в результате такого расчёта.
Если расстояние от заряда q до точки 1, в которой вычисляется потенциал, обозначить через r1 (рис. 3), то можно показать, что потенциал в этой точке
φ1 = q/4πεcr1. (4)
Отметим, что по этой же формуле вычисляется потенциал поля, созданного зарядом q, который равномерно распределён по поверхности шара, для всех точек, находящихся вне шара. В этом случае r1 обозначает расстояние от центра шара до точки 1.
Следует обратить внимание на то, что потенциал поля положительного заряда уменьшается при удалении от заряда, а потенциал поля отрицательного заряда – увеличивается. Поскольку потенциал является величиной скалярной, то, когда поле создано многими зарядами, потенциал в любой точке поля равен алгебраической сумме потенциалов, созданных в этой точке каждым зарядом в отдельности.
Работу сил поля можно выразить с помощью разности потенциалов. Вспомни, что работа при перемещении заряда между точками 1 и 2 (см. рис. 3) определяется формулой (1а):
Вспомни, что работа при перемещении заряда между точками 1 и 2 (см. рис. 3) определяется формулой (1а):
А1 2 = — ∆П2 1 = — (П2 – П1).
Заменив П его значением из формулы (3), получим
А1 2 = — (φ2qПр – φ1qПр) = — qПр (φ2 – φ1) = — qПр∆φ.
Но это можно записать и так:
А1 2 = qПр (φ1 – φ2).
Разность потенциалов (φ1 – φ2) называют напряжением между точками 1 и 2 и обозначается U1 2. Таким образом,
А1 2 = qПрU1 2.
Опустив индексы, получим
А = qU. (5)
Следовательно, работа сил поля при перемещении заряда q между двумя точками поля прямо пропорциональна напряжению между этими точками.
Выведем из (5) единицу напряжения:
U = A/q; U = 1 Дж/1Кл = кг • м2/с3 • А = 1 В (вольт).
В системе СИ за единицу измерения напряжения принимается вольт. Вольтом называется такое напряжение (разность потенциалов) между двумя точками поля, при котором, перемещая заряд в 1 Кл из одной точки в другую, поле совершает работу в 1 Дж. Отметим, что на практике заряды всегда перемещаются между двумя определёнными точками поля, поэтому чаще важно знать напряжение между отдельными точками, а не их потенциалы.
Вольтом называется такое напряжение (разность потенциалов) между двумя точками поля, при котором, перемещая заряд в 1 Кл из одной точки в другую, поле совершает работу в 1 Дж. Отметим, что на практике заряды всегда перемещаются между двумя определёнными точками поля, поэтому чаще важно знать напряжение между отдельными точками, а не их потенциалы.
Из формулы (4) видно, что во всех точках поля, находящихся на расстоянии r1 от точечного заряда q (см. рис. 3), потенциал φ1 будет одинаковый. Все эти точки находятся на поверхности сферы, описанной радиусом r1 из точки, в которой находится точечный заряд q.
Поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной (от латинского «экви» — равный). Разрезы таких поверхностей с потенциалами φ1 и φ2 на рис. 3 показаны окружностями. Для эквипотенциальной поверхности справедливо соотношение
φ = const. (6)
Оказывается, что линии напряжённости электрического поля всегда нормальны к эквипотенциальным поверхностям. Это означает, что работа сил поля при перемещении заряда по эквипотенциальной поверхности равна нулю.
Это означает, что работа сил поля при перемещении заряда по эквипотенциальной поверхности равна нулю.
Поскольку работа сил поля при перемещении заряда q определяется только разностью потенциалов между началом и концом пути, то при перемещении заряда q с одной эквипотенциальной поверхности на другую (потенциалы которых φ1 и φ2) эта работа не зависит от формы пути и равна А = q(φ1 – φ2).
В дальнейшем следует помнить, что под действием сил поля положительные заряды всегда перемещаются от большего потенциала к меньшему, а отрицательные – наоборот.
Список литературы
Л.С. Жданов «Учебник по физике для средних специальных учебных заведений», изд. «Наука», 1977г.
Электрическая потенциальная энергия (U) и электрический потенциал (В): (Примечания к C
Электрическая потенциальная энергия (U) и электрический потенциал (V): ( Заметки из лекций C. Erkals PHYS 221 )
электрическое поле между его большими пластинами. Это достигается подключением каждой пластины к одному из выводов
источник питания (например, аккумулятор).
Это достигается подключением каждой пластины к одному из выводов
источник питания (например, аккумулятор).
Рисунок 1: Электрическое поле создается заряженными пластинами разделены расстоянием l. обвинения на пластинах +Q и Q.
Рис. 2: Электрический заряд q перемещается из точки A в направлении точка B с внешней силой T против электрической силы qE.
Рис. 3, 4: При перемещении на расстояние d его потенциальная энергия в точке B равна qEd относительно точки A.
Рис. 5. При выходе из положения B (T = 0) оно ускоряется к нижней пластине. Как он движется по направлению к нижней пластине ее потенциальная энергия уменьшается, а ее кинетическая энергия увеличивается. Когда он достигает нижней пластина (где мы можем выбрать Потенциальную энергию равной нулю), ее потенциал энергия в точке A полностью преобразуется в кинетическую энергию в точке B:
Обратите внимание, что qEd — это работа, совершаемая полем в виде заряда
движется под действием силы qE из В в А.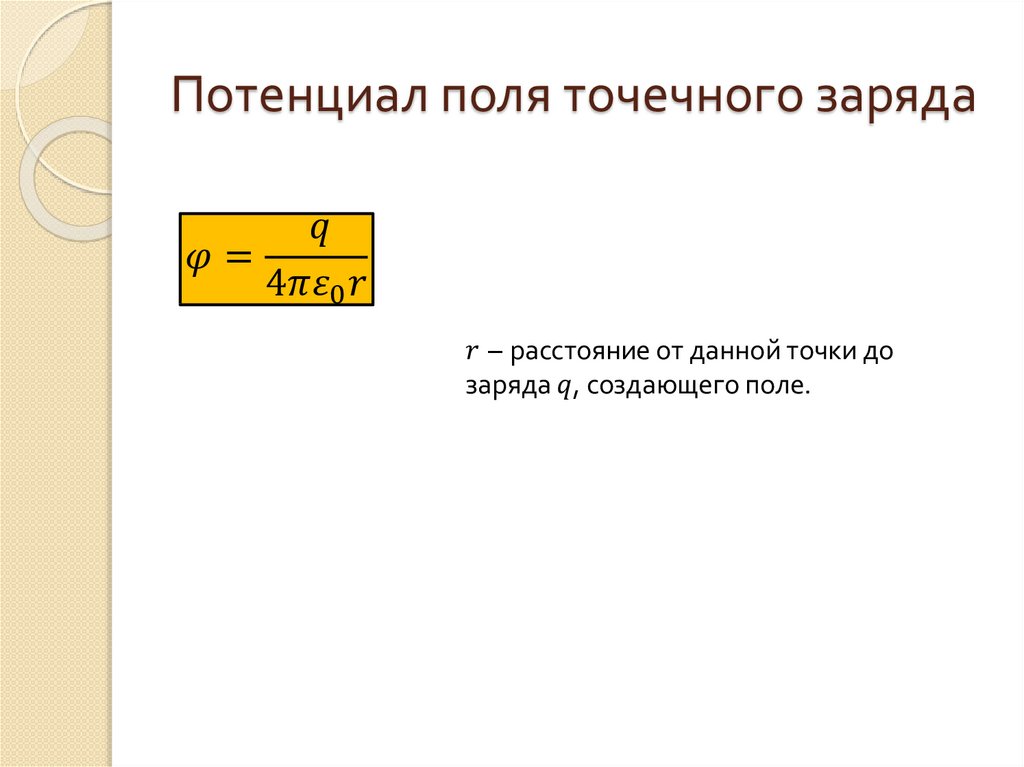 Здесь m — масса заряда q, а v — его скорость при достижении
точка А. Здесь мы предполагали, что электрические
поле однородное! Работа, проделанная полем E:
Здесь m — масса заряда q, а v — его скорость при достижении
точка А. Здесь мы предполагали, что электрические
поле однородное! Работа, проделанная полем E:
Давайте вспомним теорему о кинетической энергии-работе (рабочая энергия принцип):
где мы ввели понятие потенциальной энергии и консервативная сила (сила, под действием которой можно определить потенциальную энергию так, что совершенная работа зависит только от разницы потенциальной энергии функция оценивается в конечных точках).
Эмпирическое правило для принятия решения о том, является ли EPE возрастание:
Если заряд движется в направлении, в котором он
нормально двигаться, его электрическая потенциальная энергия уменьшается. Если заряд перемещается в направлении, противоположном
чтобы он нормально двигался, его электрическая потенциальная энергия увеличивается. Эта ситуация аналогична ситуации
постоянное гравитационное поле (g = 9,8 м/с 2 ). Когда вы поднимаете предмет, вы
увеличивает свою гравитационную потенциальную энергию.
Точно так же, когда вы опускаете объект, его гравитационная энергия
уменьшение.
Эта ситуация аналогична ситуации
постоянное гравитационное поле (g = 9,8 м/с 2 ). Когда вы поднимаете предмет, вы
увеличивает свою гравитационную потенциальную энергию.
Точно так же, когда вы опускаете объект, его гравитационная энергия
уменьшение.
Общая формула для разности потенциалов:
Работа, совершаемая полем E при воздействии на заряд q для перемещения это из точки А в точку Б определяется как разность электрических потенциалов между точки A и B:
Ясно, что функция потенциала V может быть поставлена в соответствие каждой
точка в пространстве, окружающем распределение заряда (например, параллельная
тарелки). Приведенная выше формула обеспечивает
простой рецепт для расчета работы, совершаемой при перемещении заряда между двумя точками
где мы знаем величину разности потенциалов. Приведенные выше утверждения и формула справедливы независимо от
пути, по которому перемещается заряд. Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив
интегрирование по простому пути (например, по прямой) из точки A
чье расстояние от Q равно r до бесконечности.
Путь выбирается по радиальной линии так, чтобы становится просто Edr.
Поскольку электрическое поле Q равно кОм/р,
обвинение. Обратите внимание, что потенциальная функция
скалярная величина, в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал
энергия системы зарядов или зарядовых распределений. Предположим, мы вычисляем работу, совершенную против
электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от
заряд Q. Работа определяется:
Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив
интегрирование по простому пути (например, по прямой) из точки A
чье расстояние от Q равно r до бесконечности.
Путь выбирается по радиальной линии так, чтобы становится просто Edr.
Поскольку электрическое поле Q равно кОм/р,
обвинение. Обратите внимание, что потенциальная функция
скалярная величина, в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал
энергия системы зарядов или зарядовых распределений. Предположим, мы вычисляем работу, совершенную против
электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от
заряд Q. Работа определяется:
Обратите внимание, что если q отрицательно, его знак должен использоваться в
уравнение! Таким образом, система
состоящий из отрицательного и положительного точечных зарядов, имеет отрицательный
потенциальная энергия.
Отрицательная потенциальная энергия означает, что необходимо совершить работу против электрического поля при раздвигании зарядов!
Теперь рассмотрим более общий случай, связанный с потенциал в окрестности ряда зарядов, как показано на рисунке ниже:
Пусть r 1 ,r 2 ,r 3 расстояния зарядов до точки поля А, и r 12 , r 13 , r 23 представляют расстояние между зарядами. Электрический потенциал в точке А равен:
Пример:
Если мы принесем заряд Q из бесконечности и поместим его в точку А проделанная работа будет:
Полная электрическая потенциальная энергия этой системы
зарядов, а именно работа, необходимая для приведения их в текущую позицию, может быть
рассчитывается следующим образом: сначала принесите q1 (ноль работы, так как нет заряда
вокруг еще), то в поле q1 вносим q2, то в поля q1 и q2
принести Q3. Добавьте всю работу, необходимую для
вычислить общую работу. Результат
будет:
Добавьте всю работу, необходимую для
вычислить общую работу. Результат
будет:
Определение электрического поля по электрическому потенциалу:
Составляющая E в любом направлении является отрицательной скорость изменения потенциала с расстоянием в этом направлении:
Символ называется градиентом. Электрическое поле – это градиент электрического потенциала. Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.
Эквипотенциальные поверхности:
Это воображаемые поверхности, окружающие заряд.
распределение. В частности, если
распределение заряда сферическое (точечный заряд или равномерно заряженная сфера),
поверхности сферические, концентрические с центром заряда
распределение. Линии электрического поля
всегда перпендикулярны эквипотенциальным поверхностям. Уравнение подразумевает, что из-за
отрицательный знак, направление E противоположно направлению, в котором V
увеличивается; E направлена от высших к низшим уровням V (от высших
потенциал к более низкому потенциалу). Другая
Другими словами, градиент скаляра (в данном случае поля E) нормальен к поверхности
постоянного значения (эквипотенциальная поверхность) скаляра и в направлении
максимальная скорость изменения постоянного скаляра.
Помните об этом утверждении, когда будете проводить эксперимент.
Другая
Другими словами, градиент скаляра (в данном случае поля E) нормальен к поверхности
постоянного значения (эквипотенциальная поверхность) скаляра и в направлении
максимальная скорость изменения постоянного скаляра.
Помните об этом утверждении, когда будете проводить эксперимент.
Баллы | безграничная физика |
Электрический потенциал от точечного заряда
Электрический потенциал точечного заряда Q определяется выражением
В=kQr\text{V}=\frac{\text{kQ}}{\text{r}}V=rkQ
.
Цели обучения
Выразите электрический потенциал, создаваемый точечным зарядом, в форме уравнения
Ключевые выводы
Ключевые моменты
- Напомним, что электрический потенциал определяется как потенциальная энергия на единицу заряда, т.е.
V=PEq\text{V}=\frac{\text{PE}}{\text{q}}V=qPE
.
- Разность потенциалов между двумя точками ΔV часто называют напряжением и определяется как
ΔV=VB−VA=ΔPEq\Delta \text{V} = \text{V}_{\text{B}} — \text{ V} _ {\ text {A}} = \ frac {\ Delta \ text {PE}} {\ text {q}} ΔV = VB − VA = qΔPE
. Потенциал на бесконечном расстоянии часто принимается равным нулю. - Случай электрического потенциала, генерируемого точечным зарядом, важен, поскольку он часто встречается. Сферическая сфера заряда создает внешнее поле точно так же, как, например, точечный заряд.
- Уравнение для электрического потенциала точечного заряда:
V=kQr\text{V}=\frac{\text{kQ}}{\text{r}}V=rkQ
, где k — постоянная равно 9,0×10 9 Н⋅м 2 /C 2 .
Ключевые термины
- электрический потенциал : Потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
- напряжение : Величина электростатического потенциала между двумя точками в пространстве.

Электрический потенциал от точечного заряда
Обзор
Напомним, что электрический потенциал определяется как электрическая потенциальная энергия на единицу заряда
V=PEq\text{V}=\frac{\text{PE}}{\text{q}}V=qPE
Электрический Потенциал говорит вам, сколько потенциальной энергии будет иметь один точечный заряд в данном месте. Электрический потенциал в точке равен потенциальной электрической энергии (измеряемой в джоулях) любой заряженной частицы в этом месте, деленной на заряд (измеряемый в кулонах) частицы. Поскольку заряд пробной частицы был разделен, электрический потенциал является «свойством», относящимся только к самому электрическому полю, а не к пробной частице. Другой способ сказать это так: поскольку PE зависит от q, q в приведенном выше уравнении уравновешивается, поэтому V не зависит от q.
Разность потенциалов между двумя точками ΔV часто называется напряжением и определяется как
ΔV=VB−VA=ΔPEq\Delta \text{V} = \text{V}_{\text{B}} — \ text{V}_{\text{A}} = \frac{\Delta \text{PE}}{\text{q}}ΔV=VB−VA=qΔPE
Точечные сборы
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда (как на металлическом шаре, см. рисунок ниже) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование исчисления для нахождения работы, необходимой для перемещения пробного заряда q с большого расстояния до расстояния r от точечного заряда Q , и учитывая связь между работой и потенциалом (W=–qΔV), можно показать, что электрический потенциал V точечного заряда равно
Кроме того, сферические распределения заряда (как на металлическом шаре, см. рисунок ниже) создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование исчисления для нахождения работы, необходимой для перемещения пробного заряда q с большого расстояния до расстояния r от точечного заряда Q , и учитывая связь между работой и потенциалом (W=–qΔV), можно показать, что электрический потенциал V точечного заряда равно
V=kQr\text{V}=\frac{\text{kQ}}{\text{r}}V=rkQ
(точечный заряд)
, где k — константа, равная 9,0×10 9 Н⋅м 2 /C 2 .
Генератор Ван де Граафа : Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре. 9{2}}E=qF=r2kQ
Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре. 9{2}}E=qF=r2kQ
Электрический потенциал — это скаляр, а электрическое поле — это вектор. Обратите внимание на симметрию между электрическим потенциалом и гравитационным потенциалом: оба падают как функция расстояния в первой степени, в то время как электрическое и гравитационное поля падают как функция расстояния во второй степени.
Наложение электрического потенциала
Чтобы найти общий электрический потенциал, обусловленный системой точечных зарядов, нужно сложить отдельные напряжения в виде чисел.
Цели обучения
Объясните, как находится общий электрический потенциал, обусловленный системой точечных зарядов
Ключевые выводы
Ключевые моменты
- Электрический потенциал В является скаляром и не имеет направления, тогда как электрическое поле E является вектором .

- Чтобы найти напряжение, обусловленное комбинацией точечных зарядов, необходимо сложить отдельные напряжения в виде чисел. Так, например, в электрический потенциал в точке L входит сумма потенциальных вкладов зарядов Q 1 , Q 2 , Q 3 , Q 4 и Q 5 так, что
VL=k[Q1d1+Q2d2+Q3d3+Q4d4+Q5d5]\text{V}_{\text{V}_ {L}} = \ text {k} [\ frac {\ text {Q} _ {1}} {\ text {d} _ {1}} + \ frac {\ text {Q} _ {2}} { \text{d}_{2}}+\frac{\text{Q}_{3}}{\text{d}_{3}}+\frac{\text{Q}_{4}}{ \text{d}_{4}}+\frac{\text{Q}_{5}}{\text{d}_{5}}]VL=k[d1Q1+d2Q2 +d3Q3+d4Q4+d5Q5]
. - Чтобы найти полное электрическое поле, необходимо сложить отдельные поля в виде векторов, принимая во внимание величину и направление. Это согласуется с тем фактом, что V тесно связано с энергией, скаляром, тогда как E тесно связано с силой, вектором.
- Суммирование всех вкладов напряжения для нахождения полного потенциального поля называется суперпозицией электрического потенциала.
 Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительным методом решения задач с электрическими полями является суммирование напряжений.
Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительным методом решения задач с электрическими полями является суммирование напряжений.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
- скаляр : Величина, имеющая величину, но не направление; сравнить вектор.
- суперпозиция : суммирование двух или более полей, занимающих одно и то же пространство.
Наложение электрического потенциала
Мы видели, что электрический потенциал определяется как количество потенциальной энергии на единицу заряда, которую пробная частица имеет в данном месте в электрическом поле, т.е.
V=PEq\text{V}=\frac{\text{ PE}}{\text{q}}V=qPE
Мы также видели, что электрический потенциал точечного заряда равен
9{2}}E=qF=r2kQ с той разницей, что электрическое поле падает пропорционально квадрату расстояния, а потенциал падает линейно с расстоянием. Это аналогично связи между гравитационным полем и гравитационным потенциалом.
Это аналогично связи между гравитационным полем и гравитационным потенциалом.
Наложение электрического потенциала : Электрический потенциал в точке L представляет собой сумму напряжений от каждого точечного заряда (скаляры).
Напомним, что электрический потенциал В является скаляром и не имеет направления, тогда как электрическое поле E — вектор. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Так, например, на рисунке выше электрический потенциал в точке L представляет собой сумму потенциальных вкладов зарядов Q 1 , Q 2 , Q 3 , Q 4 и Q 5 , так что
VL=k[Q1d1+Q2d2+Q3d3+Q4d4+Q5d5]\text{V}_{\text{L}}=\text{k}[\frac{\text{Q}_{1}}{ \text{d}_{1}}+\frac{\text{Q}_{2}}{\text{d}_{2}}+\frac{\text{Q}_{3}}{ \text{d}_{3}}+\frac{\text{Q}_{4}}{\text{d}_{4}}+\frac{\text{Q}_{5}}{ \text{d}_{5}}]VL=k[d1Q1+d2Q2+d3Q3+d4Q4+d5Q5]
Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что V тесно связано с энергией, скаляром, тогда как E тесно связано с силой, вектором.
Это согласуется с тем фактом, что V тесно связано с энергией, скаляром, тогда как E тесно связано с силой, вектором.
Суммирование всех вкладов напряжения для нахождения полного потенциального поля называется суперпозицией электрического потенциала. Суммирование напряжений, а не суммирование электрических, значительно упрощает расчеты, поскольку добавление потенциальных скалярных полей намного проще, чем добавление электрических векторных полей. Обратите внимание, что в некоторых случаях вам может потребоваться суммировать потенциальные вклады из источников, отличных от точечных сборов; однако это выходит за рамки данного раздела.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, Конкретная атрибуция
- электрический потенциал.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Электрический потенциал. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- напряжение. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 13 декабря 2012 г. Предоставлено : OpenStax CNX.
 Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Авторство
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Авторство - Колледж OpenStax, Электрический потенциал в однородном электрическом поле. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Лицензия : CC BY: Attribution
- Электрический потенциал. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Колледж OpenStax, Колледж физики. 18 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- скалярная. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- вектор.
 Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike - Колледж OpenStax, Колледж физики. 13 декабря 2012 г. Предоставлено : OpenStax CNX. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Атрибуция
- Потенциальный электрический результат. Предоставлено : Wikimedia. Лицензия : Общественное достояние: Не известно Авторское право
Электростатика — Каков электрический потенциал в точке?
$\begingroup$
1) Что означает электрический потенциал в точке точно ? Мой учитель говорит мне, что ток течет от более высокого потенциала к более низкому, но когда я спрашиваю его о причине, он не может дать мне убедительного ответа.
2) А кто-нибудь может объяснить, как электрический потенциал связан с потенциальной энергией и выполненной работой?
3) Кроме того, когда я сослался на учебник по физике, в нем говорилось, что, поскольку сила Кулона и сила гравитации математически подобны, электрический потенциал является эквивалентом заряда потенциальной энергии массы. Поэтому я связал электрический потенциал, например, с потенциальной энергией шара. Мяч падает с высоты на землю из-за Потенциальной энергии — точно так же ток течет от более высокого потенциала к более низкому. Верна ли эта аналогия?
Поэтому я связал электрический потенциал, например, с потенциальной энергией шара. Мяч падает с высоты на землю из-за Потенциальной энергии — точно так же ток течет от более высокого потенциала к более низкому. Верна ли эта аналогия?
Даже если вышеприведенная аналогия верна, я все равно не могу понять, почему между двумя электродами гальванического элемента течет ток. Единственное объяснение, которое предлагает мой учитель, состоит в том, что существует разность потенциалов и, таким образом, ток течет от более высокого потенциала к более низкому. Это объяснение бесполезно, так как я вообще не понимаю, что такое потенциал!
4) Если аналогия верна, то как электроны в электрохимической ячейке движутся без электрического поля, сообщая электрическую потенциальную энергию? (как в гравитационной энергии, где потенциальная энергия присутствует только при наличии гравитационной силы? В космосе ни один объект любой массы не имеет веса)
- электростатика
- потенциал
- потенциал-энергия
- работа
$\endgroup$
$\begingroup$
Я бы посоветовал вам прочитать статью в Википедии об электрохимических элементах.
Вы увидите, что там химическая энергия преобразуется в электрическую, т.е. создается коллективное электрическое поле от всех молекул, участвующих в химической реакции. Таким образом, аналогия с гравитационным полем верна.
Энергия поступает от химического действия, а в перезаряжаемых батареях — от цепи зарядки. У заряженной батареи есть разность потенциалов между двумя ее полюсами, поэтому, когда, например, вводится лампочка, электроны в проводах движутся в направлении наименьшего потенциала и по пути зажигают лампочку из-за встречающегося сопротивления.
$\endgroup$
1
$\begingroup$
Если взять электрический потенциал, то
электрический потенциал в данной точке есть величина потенциала точки в этой точке на единицу заряда.
Но гораздо лучшее определение:
электрического потенциала в точке определяется как количество работы, совершаемой в перемещение единичного положительного заряда из бесконечности в эту точку.
после этого
разность потенциалов между двумя точками определяется как величина работа, совершаемая при перемещении единичного положительного заряда из одной точки в другую против поля
Я предполагаю, что вы поняли связь между потенциалом и выполненной работой
поскольку сила Кулона и гравитационная сила обратно пропорциональны квадрату расстояния, было заявлено, что сила Кулона и гравитационная сила математически подобны
Сейчас идет к части, почему ток течет от более высокого потенциала к более низкому потенциалу,
В природе все системы стремятся достичь минимальной энергии, потому что чем меньше энергия, тем больше стабильность (поэтому атомы в возбужденном состоянии быстро достигают основного состояния, высвобождая энергию) аналогично току( который есть не что иное, как поток электронов) хотят течь из более высокого потенциала
$\endgroup$
$\begingroup$
Электрический потенциал — это потенциальная энергия на единицу заряда, которую заряженный объект имел бы в точке пространства. Электрическое поле направлено в направлении градиента потенциала, поэтому объекты ощущают силу, направленную вниз по градиенту потенциала, так же, как вода ощущает силу, направленную вниз по склону. Вода движется вниз, поэтому заряды падают по градиенту потенциала. Чтобы подняться, нужна энергия.
Электрическое поле направлено в направлении градиента потенциала, поэтому объекты ощущают силу, направленную вниз по градиенту потенциала, так же, как вода ощущает силу, направленную вниз по склону. Вода движется вниз, поэтому заряды падают по градиенту потенциала. Чтобы подняться, нужна энергия.
Электрический потенциал является фундаментальной величиной электромагнитного поля. Он определяется тем свойством, что это потенциальная энергия на единицу заряда. Концепция не может быть сокращена дальше.
$\endgroup$
$\begingroup$
потенциал в точке А равен заряду электрической потенциальной энергии на единицу пробного заряда при его перемещении из исходной точки в точку А.
$\endgroup$
1
Электростатический потенциал – формула и производные
Электростатический потенциал
Объект обладает электростатической потенциальной энергией в силу двух элементов, которые представляют собой его относительное положение по отношению к другим электрически заряженным объектам и заряд, которым он обладает. Величина электростатического потенциала зависит от количества работы, затраченной на перемещение тела против электрического поля из одной точки в другую.
Величина электростатического потенциала зависит от количества работы, затраченной на перемещение тела против электрического поля из одной точки в другую.
Когда мы двигаем тело против электрического поля, происходит прирост некоторого количества энергии, которая называется электростатической потенциальной энергией. Электростатическая потенциальная энергия для любого заряда получается делением электростатической потенциальной энергии на величину заряда.
Что такое электростатическая потенциальная энергия?
Электростатическая потенциальная энергия конкретного заряда или системы зарядов определяется как количество работы, которую совершает внешний агент, приводя этот конкретный заряд или систему зарядов к настоящей конфигурации из бесконечности без какого-либо ускорения.
Определение потенциальной электростатической энергии:
Потенциальная электростатическая энергия определяется как полная потенциальная энергия, которой обладает единичный заряд, если он находится в точке космического пространства.
Электростатическая потенциальная энергия — это скалярная величина, имеющая только величину без направления. Мы можем измерить его в джоулях, что представлено буквой V. Его размерная формула: ML 2 T -3 A -1
Электростатический потенциал
Обозначается V, ∆V, U, ∆U
Размерная формула: ML 2 T -3 A -1
Нормальная формула: Напряжение = Энергия/Заряд электростатического потенциала
SI: 90 ВольтЭлектростатическая потенциальная энергия объекта зависит от двух ключевых элементов — его электрического заряда и его положения относительно других объектов, обладающих электрическим зарядом.
Формула электростатического потенциала:
Потенциальной энергией обладает заряд, находящийся в электрическом поле, которая измеряется работой, совершаемой при перемещении заряда из бесконечности в некоторую точку, противоположную электрическому полю. Если мы разнесем два заряда q1 и q2 друг от друга на расстояние d, электростатическая потенциальная энергия системы будет равна:
U = [1/(4πεo)] × [q1q2/d]
Если мы приблизим два заряда (два электрона или протона) друг к другу, произойдет увеличение электростатической потенциальной энергии системы. Если два разноименных заряда (электрон и протон) приблизить друг к другу, то произойдет уменьшение электростатической потенциальной энергии системы.
Если два разноименных заряда (электрон и протон) приблизить друг к другу, то произойдет уменьшение электростатической потенциальной энергии системы.
Электростатический потенциал в конкретной точке вокруг точечного заряда q можно определить по формуле:
В = k × [q/r]
Здесь
В обозначает электростатическую потенциальную энергию
r обозначает расстояние между конкретной точкой, окружающей заряд, до точечного заряда
q обозначает точечный заряд
k обозначает постоянную Кулона, значение которой равно 9,0 × 10 9 N
Между двумя произвольными зарядами q1 и q2, отстоящими друг от друга на расстояние r, электростатический потенциал определяется законом Кулона, который математически может быть выражен как:
U = k × [q1q2/r2]
Здесь
U представляет электростатическую потенциальную энергию
q1 и q2 представляют два заряда
Обратите внимание, что электростатический потенциал на бесконечности равен нулю (как в приведенной выше формуле , r = ∞ )
Вывод электростатического потенциала:
Рассмотрим заряды q1 и q2, расположенные на расстоянии r друг от друга. Суммарный электростатический потенциал зарядов определяется как полная работа, совершаемая внешней силой по доведению зарядов до заданной точки из бесконечности. Это можно записать как
Суммарный электростатический потенциал зарядов определяется как полная работа, совершаемая внешней силой по доведению зарядов до заданной точки из бесконечности. Это можно записать как
-∫ (ra→rb) F.dr = – (Ua – Ub)
Здесь мы можем заметить, что точка rb расположена в бесконечности, а точка ra – это r.
Приведенную выше формулу можно переписать после подстановки значений в виде
-∫ (r →∞) F.dr = – (Ur – U∞)
Поскольку бесконечность равна нулю,
-∫ (r →∞) F.dr = -UR
Если между двумя зарядами используется закон Кулона, то можно записать следующее:
⇒ -∫ (r → ∞) [-kqqo]/r2 dr = -UR
Или, -k × qqo × [1/r] = UR
Отсюда UR = -kqqo/r
Электростатический потенциал точечного заряда
Рассмотрим два точечных заряда q и Q в присутствии друг друга на расстоянии бесконечности между ними.
UE (r) = ke × [qQ/r]
Здесь ke = 1/4πεo = постоянная Кулона
Рассмотрим точечный заряд q, отделенный от нескольких других точечных зарядов Qi с бесконечным расстоянием между ними.
UE (r) = ke q × ∑ni = 1 [Qi /ri]
Электростатический потенциал при множественных зарядах
Для трех зарядов:
С учетом трех зарядов q1, q2 и q3, расположенных в вершинах треугольника, электростатическая потенциальная энергия этой системы определяется выражением:
U =U12 + U23 + U31 = ( 1/4πεo) × [q1q2/d1 + q2q3/d2 + q3q1/d3]
Для четырех зарядов:
С учетом четырех зарядов q1, q2, q3 и q4, расположенных в углах квадрата, электростатическая потенциальная энергия этой системы: ) + (q3q1/√2d)]
A Частный случай:Рассмотрим заряд Q, в поле которого заряд q тащится против электрического поля между расстояниями a и b от Q. Полная проделанная работа может быть определена как:
Вт = (Vb – Va) × q = [1/4πεo × (Qq/b)] – [1/4πεo × (Qq/a)] = Qq/4πεo[1/b – 1/a] = (Qq/4πεo) [(a-b)/ab]
Важные моменты
В средней точке между двумя противоположными и равными зарядами электростатическая потенциальная энергия равна нулю. Однако электрическое поле не равно нулю.
Однако электрическое поле не равно нулю.
В точке говорят, что электростатический потенциал равен одному вольту, если мы рассматриваем один джоуль работы, выполняемой для перемещения 1 кулона заряда против электрического поля.
Если мы переместим отрицательный заряд из точки A в точку B, то произойдет увеличение электростатического потенциала системы.
Базовый уровень, используемый для описания электростатического потенциала в точке, равен бесконечности. Сила, действующая на пробный заряд на эталонном уровне, обозначается как ноль.
Считается, что поверхность Земли имеет нулевой потенциал, поскольку она настолько велика, что добавление или удаление заряда не приведет к изменению ее электрического состояния.
Что такое разность электрических потенциалов?
Разность потенциалов E между двумя точками в электрической цепи может быть определена как количество работы, совершаемой внешним агентом для перемещения единицы заряда Q между двумя точками.
В математических терминах
E = W/Q
Здесь
Вт означает работу, проделанную при перемещении заряда между двумя точками.
E означает разность электрических потенциалов между двумя точками.
Q представляет количество заряда в кулонах.
Решенные задачи на электростатический потенциал:
Q1: Рассмотрим объект массой 40 мг, несущий заряд, равный 5×10-9 Кл, движущийся в направлении фиксированного положительного точечного заряда с величиной, равной 10 -8 C. При расстоянии 10 см между объектом и неподвижным точечным зарядом его скорость равна 50 см/с. Вычислите заряд расстояния, на котором объект на мгновение останавливается от фиксированного точечного заряда. Определить, постоянно ли ускорение во время движения или нет.
Решение: Предположим, что объект на мгновение останавливается, когда между ним и фиксированным зарядом находится расстояние r; из закона сохранения энергии можно сказать:
Полная энергия системы = Константа
(К. Э + Ф.Э) = константа
Э + Ф.Э) = константа
(1/2)mu2 + 1/4πεo × [Qq/a] = (1/4πεo) × [Qq/r]
Если подставить данную информацию в приведенную выше формулу, то можно написать:
1/2 × 40 × 10 -6 × 1/2 × 1/2 = 9 × 10 9 × 10-8 × 5 × 10 -9 × [ 1/r – 1/(10 × 10 -2)]
или, [1/r – 10] = (5×10 -5 )/(9×5×10 -8 )= 100/9
или, 1/r = (100/9) + 10 = 190/9 м
или, r = 4,7 × 10 -2 м
As, F = [1/4πεo] × [Qq/r2]
Таким образом, ускорение может быть выражено как F/m ∝ 1/r2
Следовательно, мы определяем, что ускорение в этом случае непостоянно .
Q2. Рассмотрим шар с зарядом 10-7 Кл и массой 5 грамм с потенциалом 500 В, который движется из точки в точку В с нулевым потенциалом. Вычислите скорость мяча в точке А, если в точке В она равна 25 см.
Решение: Предположим, что скорость мяча в точке А равна u.
Работа, совершенная полем над зарядом:
Вт = q × (ВА – ВБ) = 10 -7 × (500 – 0) = 5 × 10 -5 Дж
Кинетическая энергия здесь равна вырос.
Следовательно, W = (1/2) mv 2 – (1/2) mu 2
5 × 10 -5 = (1/2) × 5/1000 [(1/4) 2 – и 2 ]
2 × 10 -2 = 1/16 – и 2
u 2 = (1/16) – 0,02
= (1 – 0,32)/16
= 0,0425
Отсюда u =0,206 м/с = 2,06 см/с.
А, u = 20,6 см/сек.
Заключение
Часто задаваемые вопросы (FAQ)
1. Что такое электростатическая потенциальная энергия?
Электростатическая потенциальная энергия определяется как полная потенциальная энергия, которой обладает единичный заряд, если он находится в точке космического пространства.
2. Приведите несколько примеров электростатической потенциальной энергии.
Примеры потенциальной электростатической энергии:
- Выключенная лампа накаливания
- Неработающая радиомачта
- Перед переключением фар вашего автомобиля
- Выключенный телефон
2.
 3 Электрический потенциал, обусловленный точечным зарядом
3 Электрический потенциал, обусловленный точечным зарядомЦели обучения
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Объясните точечные заряды и составьте уравнение для электрического потенциала точечного заряда
- Различие между электрическим потенциалом и электрическим полем
- Определить электрический потенциал точечного заряда при заданном заряде и расстоянии
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферические распределения заряда — как на металлическом шаре — создают внешние электрические поля точно так же, как точечный заряд. Электрический потенциал, обусловленный точечным зарядом, является, таким образом, случаем, который нам необходимо рассмотреть. Использование исчисления для нахождения работы, необходимой для перемещения пробного заряда qq размер 12{q} {} с большого расстояния до расстояния rr размера 12{r} {} от точечного заряда Q,Q, размер 12{Q} {} и отметив связь между работой и потенциала W=–qΔV,W=–qΔV, размер 12{ левый (W= — q?V правый)} {} можно показать, что электрический потенциал ВВ размером 12{В} {} точечного заряда is
2,37 V = kQ r (точечный заряд), V = kQ r (точечный заряд), размер 12{V= {{ ital «kQ»} over {r}} \(«Point Charge» \),} { }
, где k – константа, равная 9,0×109 Н·м2/C2,9,0×109 Н·м2/C2.
Электрический потенциал VV размером 12 {В} {} точечного заряда
Электрический потенциал VV размером 12 {В} {} точечного заряда определяется выражением
2,38 В = kQ r (точечный заряд). V = kQ r (точечный заряд). size 12{V= { { ital «kQ»} over {r} } \(«Point Charge» \) ,} {}
Потенциал на бесконечности выбран равным нулю. Таким образом, размер VV 12{V} {} для точечного заряда уменьшается с расстоянием, тогда как размер EE 12{E} {} для точечного заряда уменьшается с расстоянием в квадрате
2.39 E=Fq=kQr2.E=Fq=kQr2. size 12{ left (E=F/q right )= ital «kQ/r» rSup { size 8{2} } } {}
Напомним, что электрический потенциал VV size 12{V} {} является скаляром и имеет нет направления, тогда как электрическое поле EE размером 12{E} {} является вектором. Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторов , принимая во внимание величину и направление. Это согласуется с тем фактом, что размер ВВ 12{V} {} тесно связан с энергией, скаляром, тогда как размер EE 12{Е} {} тесно связан с силой, вектором.
Это согласуется с тем фактом, что размер ВВ 12{V} {} тесно связан с энергией, скаляром, тогда как размер EE 12{Е} {} тесно связан с силой, вектором.
Пример 2.6 Какое напряжение создает небольшой заряд на металлическом шаре?
Заряды статического электричества обычно находятся в диапазоне от нанокулонов nCnC размера 12{ слева («nC» справа)} {} до микрокулонов µCµC размера 12{ слева (мкКл справа)} {}. Чему равно напряжение на расстоянии 5,00 см от центра металлического шара диаметром 1 см, имеющего статический заряд от −3,00 нКл до 3,00 нКл?
Стратегия
Как мы обсуждали в разделе «Электрический заряд и электрическое поле», заряд на металлическом шаре распространяется равномерно и создает поле, похожее на поле точечного заряда, расположенного в его центре. Таким образом, мы можем найти напряжение, используя уравнение V=kQ/r.V=kQ/r. размер 12{V= ital «kQ»/r} {}
Решение
Подставляя известные значения в выражение для потенциала точечного заряда, получаем 2 м=–539 V. V=kQr=8,99×109 Н·м2/C2–3,00×10–9 C5,00×10–2 м=–539 V.alignl { stack { размер 12{V=k { {Q} over {r} } = слева (9 «.» «00» умножить на «10» rSup {размер 8{9} } «N» cdot m rSup {размер 8{2} } /C rSup {размер 8{2}} правильно ) { { — 3 «.» «00» умножить на «10» rSup {размер 8{ — 9} } «C»} более {5 «.» «00» умножить на «10» rSup { size 8{«–2»} } «m»} } } {} # = — «540»»V» «.» {} } } {}
V=kQr=8,99×109 Н·м2/C2–3,00×10–9 C5,00×10–2 м=–539 V.alignl { stack { размер 12{V=k { {Q} over {r} } = слева (9 «.» «00» умножить на «10» rSup {размер 8{9} } «N» cdot m rSup {размер 8{2} } /C rSup {размер 8{2}} правильно ) { { — 3 «.» «00» умножить на «10» rSup {размер 8{ — 9} } «C»} более {5 «.» «00» умножить на «10» rSup { size 8{«–2»} } «m»} } } {} # = — «540»»V» «.» {} } } {}
Обсуждение
Отрицательное значение напряжения означает, что положительный заряд будет притягиваться с большего расстояния, поскольку потенциал ниже — более отрицательный — чем на больших расстояниях. И наоборот, отрицательный заряд будет отталкиваться, как и ожидалось.
Пример 2.7 Что такое избыточный заряд генератора Ван де Граафа
Демонстрационный генератор Ван де Граафа имеет металлическую сферу диаметром 25,0 см, которая производит напряжение 100 кВ вблизи своей поверхности (см. рис. 2.11). Какой избыточный заряд находится на шаре? Предположим, что каждое числовое значение здесь показано тремя значащими цифрами.
Рисунок 2.11 Напряжение этого демонстрационного генератора Ван де Граафа измеряется между заряженной сферой и землей. Потенциал Земли принимается равным нулю в качестве эталона. Потенциал заряженной проводящей сферы такой же, как и у равного точечного заряда в ее центре.
Стратегия
Потенциал на поверхности будет таким же, как у точечного заряда в центре сферы на расстоянии 12,5 см. Радиус шара 12,5 см. Таким образом, мы можем определить избыточный заряд, используя уравнение
2,41 В=kQr.V=kQr. размер 12{V= ital «kQ»/r} {}
Решение
Решение для QQ и ввод известных значений дает
2,42 Q=rVk=0,125м100×103V8,99×109 Н·м2/C2= 1,39×10–6C=1,39 мкКл.Q=rVk=0,125м100×103V8,99×109 Н·м2/C2=1,39×10–6C=1,39 мкКл.alignl { stack { size 12{Q= { { ital «rV «} над {k} } = {{ влево (0 «.» «12» «м» вправо) влево («100″´»10» rSup {размер 8{3} } «V» вправо)} более {9 «.» «00»´»10″ rSup { размер 8{9} } «N» cdot m rSup { размер 8{2} } /C rSup { размер 8{2} } } } } {} # =1 «. » «39»´»10″ rSup { размер 8{-6} } «C=1» «.» «39 «mC «.» {} } } {}
» «39»´»10″ rSup { размер 8{-6} } «C=1» «.» «39 «mC «.» {} } } {}
Обсуждение
Это относительно небольшая плата, но он создает довольно большое напряжение. Здесь у нас есть еще одно указание на то, что трудно хранить изолированные заряды.
Напряжения в обоих этих примерах могут быть измерены с помощью измерителя, который сравнивает измеренный потенциал с потенциалом земли. Часто берется потенциал земли. быть равным нулю, вместо того, чтобы считать потенциал на бесконечности равным нулю.Важна разность потенциалов между двумя точками, и очень часто существует молчаливое предположение, что какая-то точка отсчета, такая как Земля или очень удаленная точка, находится при нулевом потенциале. Как отмечено в книге «Электрическая потенциальная энергия: разность потенциалов», это аналогично принятию уровня моря как h=0h=0 size 12{h=0} {} при рассмотрении гравитационной потенциальной энергии, PEg=mgh.PEg=mgh .size 12{«PE» rSub {size 8{g} } = ital «mgh»} {}
- Печать
- Поделиться
Solutions HW # 4 — Physics 122
Solutions HW # 4 — Physics 122Проблема 1
Электростатический потенциал точечного заряда q равен
На основании этого уравнения мы можем заключить, что:
- Потенциал вблизи отрицательно заряженного объекта становится все более
отрицательный.

- Потенциал вблизи положительно заряженного объекта становится все более положительный.
- Потенциал вблизи заряженного объекта пропорционален заряду объекта.
Электрическое поле E и потенциал V связаны следующим образом:
На основании этого уравнения делаем вывод, что чем больше разница в электростатический потенциал на определенном расстоянии, тем больше величина электрического поля в этом положении.
Проблема 2
С помощью контурного графика можно определить разность потенциалов [Delta]V между начальным и конечным положением заряда q (убедитесь, что вы получили знак правильный) . Начальная и конечная потенциальная энергия заряда равно (q V1) и (q V2) соответственно. Работа, необходимая для перемещения заряда Таким образом, q равно -[Delta]U = -(q V2 — q V1) = -q [Delta]V.
Проблема 3
Электрическое поле направлено перпендикулярно эквипотенциальным контурам. С помощью линейки на рисунке можно определить изменение потенциала на
единица расстояния:
С помощью линейки на рисунке можно определить изменение потенциала на
единица расстояния:
Убедитесь, что вы используете правильные единицы для [Delta]V и [Delta]d.
Проблема 4
Используйте тот же метод, что и в задаче 3, чтобы вычислить величину электрическое поле E. Тогда величина силы, действующей на заряд q, будет быть q E.
Проблема 5
Выберите определенную точку на эквипотенциальной поверхности, ближайшую к заряду. представляет интерес. Значение потенциала в этой точке равно
Несмотря на то, что два других заряда находятся дальше, у них все равно будет существенное влияние на потенциал из-за зависимости 1/r потенциал. Используйте заданное соотношение зарядов и измеренных расстояний определить неизвестный заряд.
Проблема 6
Рассмотрим шар радиуса R с полным зарядом Q. Электрическое поле вне сферы находится точечный заряд Q, расположенный в центре сфера:
Таким образом, величина электрического поля на поверхности сферы равна равно
Таким же образом мы можем определить электростатический потенциал на поверхность сферы:
Комбинируя два последних уравнения, получаем:
Проблема 7
Используя выражение для V(R), мы можем определить заряд на куполе:
Проблема 8
Рассмотрим сферическую оболочку с внутренним радиусом ri и внешним радиусом ro.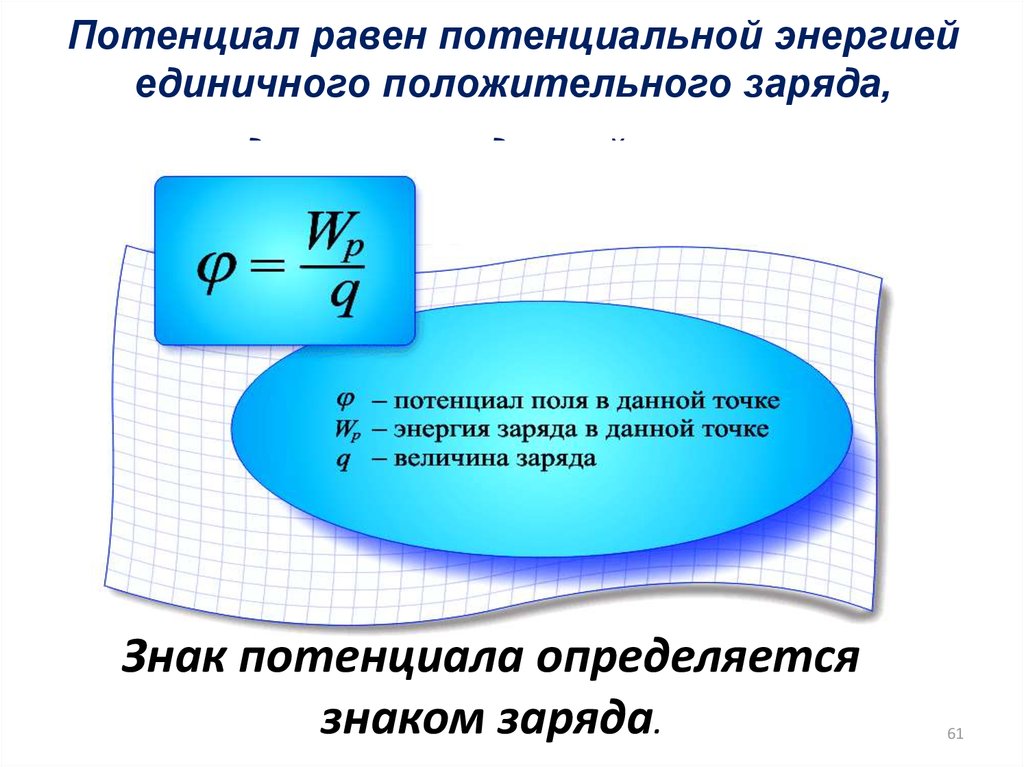 Предполагая
что общий заряд оболочки равен Q, плотность заряда оболочки
равно
Предполагая
что общий заряд оболочки равен Q, плотность заряда оболочки
равно
Электрическое поле, создаваемое распределением заряда, будет иметь сферическую форму. симметрии и может быть легко получено с помощью закона Гаусса:
Для получения электростатического потенциала в определенной точке Р, расположенной расстоянии r от центра сферической оболочки, мы должны проинтегрировать электрическое поле на пути от бесконечности до этой точки P. Рассмотрим три особые случаи:
- при r > ro:
- при ro > r > ri:
- при ri > r:
Таким образом, потенциал в центре сферической оболочки равен:
Проблема 9
Поскольку электрическое поле внутри сферической оболочки равно 0 Н/Кл, потенциал постоянен внутри сферической оболочки. Потенциал на внутри оболочки, таким образом, будет равен потенциалу в центре. Таким образом:
Проблема 10
Потенциал на внешней поверхности оболочки можно получить из общее решение, обсуждавшееся в задаче 8:
Проблема 11
Электростатический потенциал вне заряженной сферы радиусом R и общий заряд Q равен электростатическому потенциалу, создаваемому точечный заряд Q, расположенный в центре сферы:
Таким образом, электростатический потенциал на поверхности сферы равен до
Это уравнение можно использовать для выражения заряда Q через потенциал на сфере и радиусе R:
Проблема 12
Электрическое поле внутри металлического шара равно нулю.


 тж. Глюон) поле ядерных сил
тж. Глюон) поле ядерных сил к.
к.
 е.
зависит от расстояния r.
е.
зависит от расстояния r. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует…
Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует…
 Заряд, помещённый в данную точку поля обладает потенциальной энергией Wр.
Заряд, помещённый в данную точку поля обладает потенциальной энергией Wр.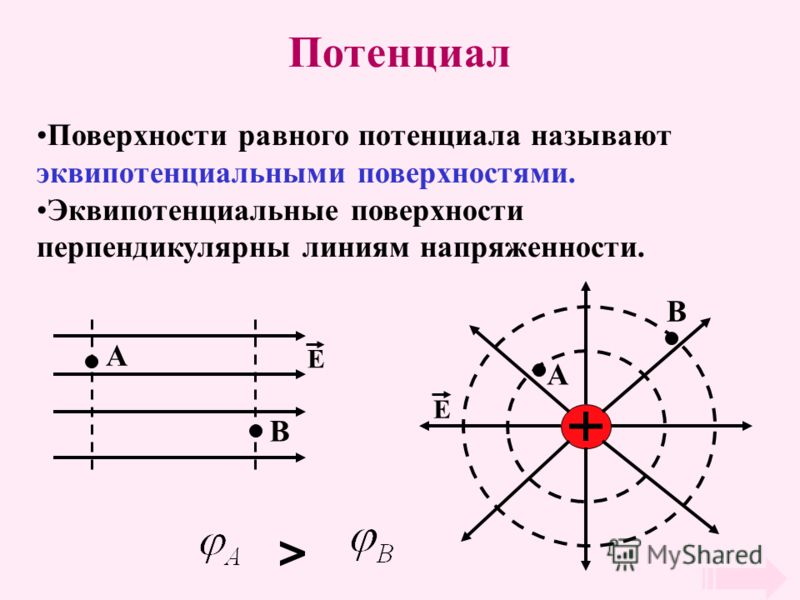
 При этом с другой стороны возникает разрежение (зона пониженного давления). Эти сгущения и разрежения, распространяясь в среде, и создают звуковую волну.
При этом с другой стороны возникает разрежение (зона пониженного давления). Эти сгущения и разрежения, распространяясь в среде, и создают звуковую волну. Летучие мыши, киты, дельфины излучают и улавливают ультразвук. Летучие мыши в полной темноте ориентируются благодаря отраженному ультразвуку. Для получения ультразвука используются специальные ультразвуковые генераторы. Мощная ультразвуковая волна способна дробить тела, помещенные в жидкость, например, дробить камни в желчном пузыре и почках, убивать микробов, стерилизовать молоко. Ультразвуковая волна слабо затухает в воде, поэтому её используют в гидроакустике. Гидролокатор (эхолот)посылает импульс ультразвуковых волн, а затем улавливает отраженный сигнал. L = vt/2–расстояние до объекта от которого произошло отражение, где t- время прохождения сигнала до объекта и обратно, v- скорость ультразвука.
Летучие мыши, киты, дельфины излучают и улавливают ультразвук. Летучие мыши в полной темноте ориентируются благодаря отраженному ультразвуку. Для получения ультразвука используются специальные ультразвуковые генераторы. Мощная ультразвуковая волна способна дробить тела, помещенные в жидкость, например, дробить камни в желчном пузыре и почках, убивать микробов, стерилизовать молоко. Ультразвуковая волна слабо затухает в воде, поэтому её используют в гидроакустике. Гидролокатор (эхолот)посылает импульс ультразвуковых волн, а затем улавливает отраженный сигнал. L = vt/2–расстояние до объекта от которого произошло отражение, где t- время прохождения сигнала до объекта и обратно, v- скорость ультразвука. Кавитация закрывается с выделением тепла.
Кавитация закрывается с выделением тепла.



 Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительным методом решения задач с электрическими полями является суммирование напряжений.
Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительным методом решения задач с электрическими полями является суммирование напряжений. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike  Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Авторство
Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Авторство  Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike 
