§ 84. Потенциал электростатического поля
Тело, находящееся в потенциальном поле сил (а электростатическое поле является потенциальным), обладает потенциальной энергией, за счет которой силами поля совершается работа (см. §12). Как известно (см. (12.2)), работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу
(83.1) сил электростатического поля можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q0 в начальной и конечной точках поля заряда Q:
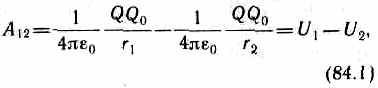
откуда следует, что потенциальная энергия заряда Q0 в поле заряда Q равна
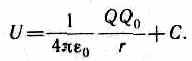
Она, как и в механике, определяется не однозначно, а с точностью до произвольной постоянной С. Если считать, что при удалении заряда в бесконечность (r->) потенциальная энергия обращается в нуль (U=0), то С=0 и потенциальная энергия заряда Q0, находящегося в поле заряда Q на расстоянии r от него, равна
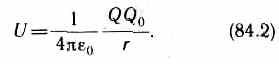
Для одноименных зарядов Q0Q>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов Q0Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
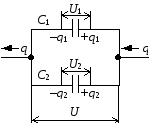
Если поле создается системой n точечных зарядов Q1, Q2, …, Qn, то работа электростатических сил, совершаемая над зарядом Q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия U заряда Q0, находящегося в этом поле, равна сумме его потенциальных энергий Ui, создаваемых каждым из зарядов в отдельности:
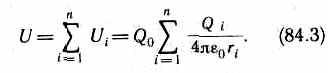
Из формул (84.2) и (84.3) вытекает, что отношение
=U/Q0. (84.4)
138
Потенциал в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.
Из формул (84.4) и (84.2) следует, что потенциал поля, создаваемого точечным зарядом Q, равен
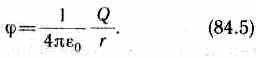
Работа, совершаемая силами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2 (см. (84.1), (84.4), (84.5)), может быть представлена как
A12==U1-U2=Q0(1-2), (84.6)
т. е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Разность потенциалов двух точек 1 и 2 в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из точки 1 в точку
Работа сил поля при перемещении заряда Q0 из точки 1 в точку 2 может быть записана также в виде

Приравняв (84.6) и (84.7), придем к выражению для разности потенциалов:
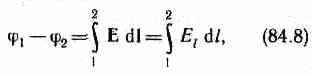
где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траектории перемещения.
Если перемещать заряд
A=Q0,
Таким образом, потенциал — физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.
Из выражения (84.4) следует, что единица потенциала — вольт (В): 1В есть потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1В=1Дж/Кл). Учитывая размерность вольта, можно показать, что введенная в § 79 единица напряженности электростатического поля действительно равна 1 В/м: 1Н/Кл=1Н• м/(Кл•м)=1 Дж/(Кл•м)=1 В/м.
Из формул (84.3) и (84.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:
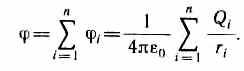
Потенциал электростатического поля и разность потенциалов
Потенциал электростатического поля и разность потенциалов
Обладает ли электрическое поле энергией? В чём это выражается?
Как рассчитать энергию поля?
В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.
Потенциал поля.
Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.
На замкнутой траектории работа электростатического поля всегда равна нулю.
Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным.
Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (Wп2 — Wп1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14.14).
Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещённого в поле заряда.
Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещённого в поле.
Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.
Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.
Согласно данному определению потенциал равен:
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
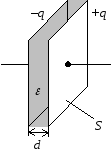
Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
Разность потенциалов.
Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.
Изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.
Так как потенциальная энергия Wn = дчр, то работа сил поля равна:
А = — (Wп2 — Wп1) = -q(φ2 — φ1) = q(φ1 — φ2) = qU. (14.17)
Здесь
разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Разность потенциалов называют также напряжением.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:
Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
Единица разности потенциалов.
Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.
Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.
Выразим единицу разности потенциалов через основные единицы СИ. Так как
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара. Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля. Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Работа в электрическом поле. Потенциал
Работа сил электростатического поля. Понятие потенциала
Когда пробный заряд q перемещается в электрическом поле, можно говорить о работе, совершаемой в данный момент электрическими силами. Для малого перемещения ∆l→ формулу работы можно записать так: ∆A=F·∆l·cos α=Eq∆lcos α=Elq∆l.

Рисунок 1.4.1. Малое перемещение заряда и работа, совершаемая в данный момент электрическими силами.
Теперь посмотрим, какую работу по перемещению заряда совершают силы в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени. Такое поле еще называют электростатическим. У него есть важное свойство, о котором мы поговорим в этой статье.
Определение 1При перемещении заряда из одной точки электростатического поля в другую работа сил электрического поля будет зависеть только от величины этого заряда и положением начальной и конечной точки в пространстве. Форма траектории при этом не имеет значения.
У гравитационного поля есть точно такое же свойство, что неудивительно, поскольку соотношения, с помощью которых мы описываем кулоновские и гравитационные силы, одинаковы.
Исходя из того, что форма траектории не имеет значения, мы можем также сформулировать следующее утверждение:
Определение 2Когда заряд в электростатическом поле перемещается по любой замкнутой траектории, работа сил поля равна 0. Поле, обладающее таким свойством, называется консервативным, или потенциальным.
Ниже приведена иллюстрация силовых линий в кулоновском поле, образованных точечным зарядом Q, а также две траектории перемещения пробного заряда q в другую точку. Символом ∆l→ на одной из траекторий обозначается малое перемещение. Запишем формулу работы кулоновских сил на нем:
∆A=F∆lcos α=Eq∆r=14πε0Qqr2∆r.
Следовательно, зависимость существует только между работой и расстоянием между зарядами, а также их изменением Δr. Проинтегрируем данное выражение на интервале от
Потенциал в электростатике
Определение 1
Электростатический потенциал представляет скалярную энергетическую характеристику электростатического поля, характеризующую потенциальную энергию, обладателем которой является единичный положительный пробный заряд, который поместили в данную точку поля. В качестве единицы измерения потенциала в системе единиц выступает вольт.
Электростатическое поле
Электростатическое поле представляет образованное неподвижными в пространстве и неизменными во времени электрозарядами поле (при условии отсутствия электрических токов). Электрическое поле, таким образом, считается особым видом материи, связанным с электрическими зарядами и передающим воздействия зарядов друг на друга.
Так, при присутствии в пространстве системы заряженных тел, то в каждой его точке будет фиксироваться существование силового электрического поля, определяемого через силу, воздействующую на пробный точечный заряд, помещенный в данное поле. Пробный заряд должен при этом быть ничтожно малым, чтобы не оказать влияние на характеристику электростатического поля.
Рисунок 1. Электростатическое поле. Автор24 — интернет-биржа студенческих работ
Электрическое поле называют однородным в ситуации, если вектор его напряженности оказывается одинаковым во всех точках поля. В качестве главных характеристик электростатического поля выделяют следующие:
- напряженность;
- потенциал.
Силовые линии такого поля обладают такими свойствами:
- Они будут всегда замкнутыми, то есть начинающимися на положительных зарядах и заканчивающимися на отрицательных. Они не пересекаются между собой и не касаются друг друга.
- Плотность линий тем больше, чем большей будет напряжённость. Другими словами, напряжённость поля является прямо пропорциональной количеству силовых линий, пересекающих площадку единичной площади, чье расположение будет перпендикулярно линиям.
Замечание 1
Электростатическое поле оказывает непосредственное воздействие на любое количество зарядов, при этом возникнет сложная система взаимодействий. Напряженность системы можно рассматривать с точки зрения суперпозиции, поэтому суммарное влияние числа зарядов является векторной суммой всех напряженностей поля.
В соответствии с этим, чем больше таких линий, тем интенсивнее оказывается силовое воздействие. В металлах (и иных проводящих материалах) напряженность поля будет отсутствовать (за счет встречно направленного действия поля свободных носителей заряда, пребывающих в структуре кристаллической решетки).
Фактически, силы оперативно уравниваются, фиксируется отсутствие тока, а линии напряженности не способны проникнуть в такой проводник. Помимо векторных величин, поле может описываться скалярными значениями (идеальный случай), взятыми в каждой точке. Такие значения в электростатике характеризуют потенциал поля.
Определение электростатического потенциала
Тело, пребывающее в потенциальном поле сил (а электростатическое поле считается потенциальным), имеет потенциальную энергию, посредством которой силами поля будет совершаться работа. Работа консервативных сил будет выполняться за счет убыли потенциальной энергии
Электростатический потенциал является специальным термином в случае возможной замены общего термина в электродинамике (скалярный потенциал). Исторически в физике первым наблюдается появление термина «электростатический потенциал», а уже скалярный потенциал электродинамики стал его обобщением.
В связи с тем, что потенциал (равно как и потенциальная энергия) может определяться с точностью до произвольной постоянной (и все величины, которые возможно измерить: напряженности поля, силы, остаются неизменными в независимости от выбора способа постоянной величины) непосредственным физическим смыслом (если не имеются в виду квантовые эффекты) обладает не сам потенциал, а разность потенциалов.
При этом принято считать, что прочие заряды при подобной операции «заморожены» (неподвижны в момент такого перемещения (подразумевается воображаемое, а не реальное перемещение). При этом, в редких случаях, с целью снятия неоднозначности, используют определенные «естественные» условия.
Рисунок 2. Потенциал электростатического поля. Автор24 — интернет-биржа студенческих работ
Так, например, часто потенциал определяется таким образом, чтобы его значение оказывалось равнозначно нулевому на бесконечности для какого-либо точечного заряда. В такой ситуации для любой конечной системы зарядов будет выполнимо на бесконечности аналогичное условие, а над произволом выбора константы при этом можно будет не задумываться.
Особенности кулоновского потенциала
Иногда такой термин, как «кулоновский потенциал» применяется при обозначении электростатического потенциала (в формате полного синонима). При этом они несколько различны касательно области применения.
Замечание 2
Зачастую, под «кулоновским потенциалом» понимают электростатический потенциал одного (или, возможно, нескольких) точечного заряда, который получен посредством сложения кулоновского потенциала каждого из них.
Зачастую даже в ситуации с потенциалом, созданным непосредственно непрерывно распределенными зарядами, если его и называют «кулоновским», то это может означать его выражение в виде суммы числа элементов (пусть и бесконечного), на которые разбивается заряженный объем, однако при этом потенциал каждого рассчитывается в виде потенциала точечного заряда.
При этом, в связи с тем, что электростатический потенциал может быть, в принципе, выражаться подобным образом практически всегда, разграничение терминов в таком случае становится довольно размытым.
Рисунок 3. Кулоновские силы. Автор24 — интернет-биржа студенческих работ
Под «кулоновским» также понимается потенциал любой природы (иными словами, он не обязательно должен быть электрическим), который при наличии точечного или сферически симметричного источника будет зависимым от расстояния на $\frac {1}{г}$ (гравитационный потенциал в теории тяготения Ньютона, например, хоть его часто называют «ньютоновским», поскольку он был исследован раньше)). Особенно это происходит в случае необходимости обозначения всего класса потенциалов (в отличие от потенциалов с некоторыми другими «зависимостями» от расстояния.
4.Потенциальная энергия. Потенциал электростатического поля. Связь между напряженностью и потенциалом поля.
Потенциальная
энергия — часть механической энергии системы
тел; работа, которую необходимо совершить
против действующих сил, чтобы перенести
тело из некой точки отсчёта в данную
точку.
— часть механической энергии системы
тел; работа, которую необходимо совершить
против действующих сил, чтобы перенести
тело из некой точки отсчёта в данную
точку.
Величина потенциальной энергии — относительна. Она отсчитывается от некой точки пространства, выбор которой определяется удобством дальнейших вычислений. Понятно также, что корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тел, но не от пути их перемещения. Такие силы называются консервативными.
Электростатический потенциал— скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля.
Электростатический
потенциал равен отношению потенциальной
энергии взаимодействия заряда с полем
к величине этого заряда. Напряжённость
электростатического поля Е и потенциал
φ связаны соотношением: 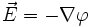
5.Поток вектора напряженности. Теорема Остроградского-Гаусса для электростатического поля в вакууме.
Поток векторного поля через гиперповерхность — поверхностный интеграл второго рода по поверхности S.
В ряде случаев принцип суперпозиции для вычисления напр. поля применять трудно, в таких случаях напряженность электростатического поля вычисляют с помощью теоремы Гаусса.
Теорема Гаусса:Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключенному внутри этой поверхности электрическому заряду.
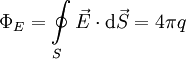
Теорема Гаусса:Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
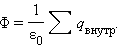
6.Применение теоремы Гаусса к расчету электростатических полей (сфера, шар)
7.Применение теоремы Гаусса к расчету электростатических полей (Полный цилиндр, сплошной цилиндр)
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
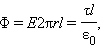
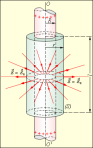
где τ – заряд единицы длины цилиндра. Отсюда
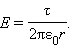
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое длинного полого цилиндра равно нулю. Поле внутри однородно заряженного длинного полого цилиндра равно нулю.
9. Диполь в электрическом поле. Неполярные и полярные диэлектрики. Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательного электрических зарядов. Другими словами, электрический диполь представляет из себя совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Произведение вектораl, проведённого от отрицательного заряда к положительному, и помноженного на абсолютную величину зарядовq, называется дипольным моментом:p=ql.
Диэлектрик— вещество, плохо проводящее или совсем не проводящее электрический ток. Плотность свободных носителей заряда в диэлектрике не превышает 10(в 8 степени)шт/см³. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле.
Неполярные диэлектрики— состоят из неполярных молекул, у которых центры тяжести положительного и отрицательного зарядов совпадают. Следовательно неполярные молекулы не обладают электрическим моментом и их электрический момент p = q • l = 0. Примером практически неполярных диэлектриков, применяемых в качестве электроизоляционных материалов, являются углеводороды, нефтяные электроизоляционные масла, полиэтилен, полистирол и др.
Полярные диэлектрики— состоят из полярных молекул, обладающих электрическим моментом. В таких молекулах из-за их асимметричного строения центры масс положительных и отрицательных зарядов не совпадают. При замещении в неполярных полимерах некоторой части водородных атомов другими атомами или не углеводородными радикалами получаются полярные вещества. При определении полярности вещества по химической формуле следует учитывать пространственное строение молекул. К полярным диэлектрикам относятся феноло-формальдегидные и эпоксидные смолы, кремнийорганические соединения, хлорированные углеводороды и др.
10.Поляризация диэлектриков. Типы поляризации. Вектор поляризации. Поляризация диэлектриков— явление, связанное с поляризацией связанных зарядов в диэлектрике и поворотом электрических диполей под воздействием внешнего электрического поля. Поляризацию диэлектриков характеризуетвектор электрической поляризации. В зависимости от механизма поляризации, поляризация диэлектриков делится на несколько видов, среди которых можно отметить —электронную, ионную и ориентационную поляризацию.Поляризация диэлектриков имеет максимальное значение в статических электрических полях. В переменных полях, в связи с наличием инерции электронов, ионов и электрических диполей, вектор электрической поляризации зависит от частоты.
Количественной мерой поляризации диэлектрика является вектор поляризации . Вектором поляризации (поляризованностью(и это дипольный момент единицы объема)) называется отношение электрического дипольного момента малого объема DV диэлектрика к величине этого объема:
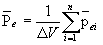
где Pei- электрический дипольный моментi-й молекулы;
n- общее число молекул в объемеDV.
Этот объем должен быть настолько малым, чтобы внутри него электрическое поле можно было считать однородным. Одновременно число n молекул в объеме DV должно быть достаточно велико для того, чтобы можно было применять статистические методы исследования.
Для однородного
неполярного диэлектрика, находящегося
в однородном электрическом поле: 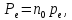 гдеn0 — число молекул в
единице объема, Рe-
дипольный момент одной молекулы.
гдеn0 — число молекул в
единице объема, Рe-
дипольный момент одной молекулы.
11. Теорема Гаусса для электростатического поля в диэлектрической среде. Вектор электрического смещения. Теорема Гаусса для электрического смещения
Для поля в
веществе электростатическая теорема
Гаусса может быть записана иначе —
через поток вектора электрического
смещения. При этом формулировка теоремы
выглядит следующим образом: поток
вектора электрического смещения через
замкнутую поверхность пропорционален
заключённому внутри этой поверхности
электрическому заряду: 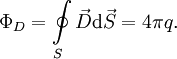
Если же рассматривать теорему для напряженности поля в веществе, то в качестве заряда qнеобходимо брать сумму заряда, находящегося внутри поверхности и поляризационного заряда диэлектрика: Потенциал внутри замкнутого проводника, помещенного в электрическое поле, постоянен.
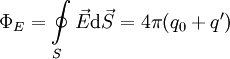
Где,
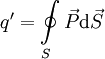
P— вектор поляризации диэлектрика.
Для удобства описания поля в диэлектрике вводят вспомогательный вектор — вектор электрического смещения:
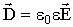 .
.
11. Потенциал электрического поля
Электростатическое поле точечного заряда – центральное, поэтому оно потенциально. В силу принципа суперпозиции потенциально любое электростатическое поле.
Потенциальная энергия заряда в электростатическом поле (Wp) – физическая величина, равная работе электростатического поля при перемещении заряда из его положения на нулевой уровень. Как правило, в электростатике принимается, что нулевой уровень находится на бесконечности.
Работа перемещения заряда в электростатическом поле равна изменению потенциальной энергии заряда, взятому с противоположным знаком: A = – (Wp2 – Wp1).
Потенциал электростатического поля () – физическая величина, равная отношению потенциальной энергии заряда в поле к его значению.
Потенциал – величина скалярная. За его единицу в системе СИ принимается вольт (1 В = 1 Дж/Кл).
Принцип суперпозиции для потенциала. Потенциал электростатического поля, одновременно создаваемого в некоторой точке пространства несколькими зарядами, равна сумме потенциалов электростатических полей, которые создавались бы в этой же точке каждым из зарядов по отдельности = 1 + 2 + … .
Эквипотенциальная поверхность – поверхность, во всех точках которой потенциал имеет одинаковые значения. Для поля точечного заряда эквипотенциальными поверхностями являются сферы с центром в точке расположения заряда.
Работа
электрического поля на криволинейном
участке траектории 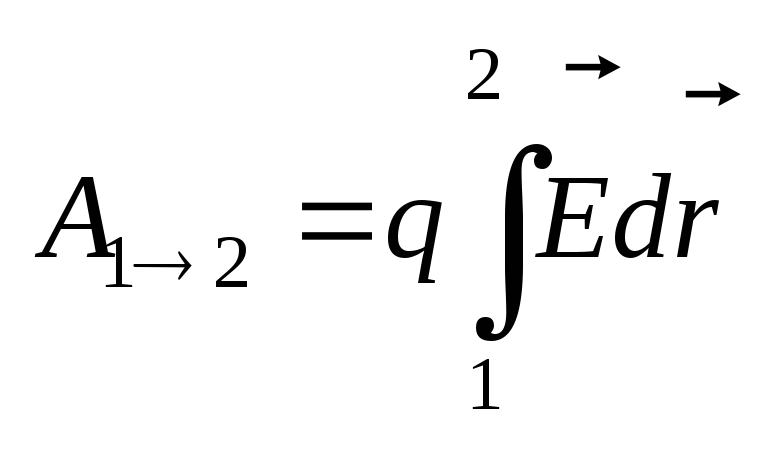 .
Циркуляция электростатического поля
на замкнутой траектории
.
Циркуляция электростатического поля
на замкнутой траектории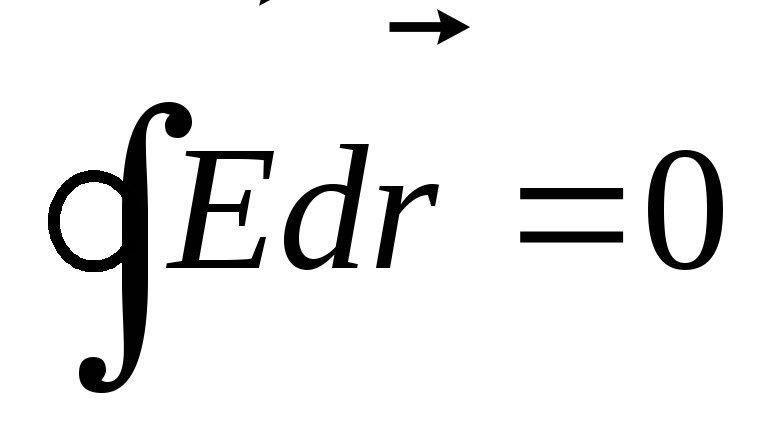 .
Потенциал электростатического поля
точечного заряда
.
Потенциал электростатического поля
точечного заряда 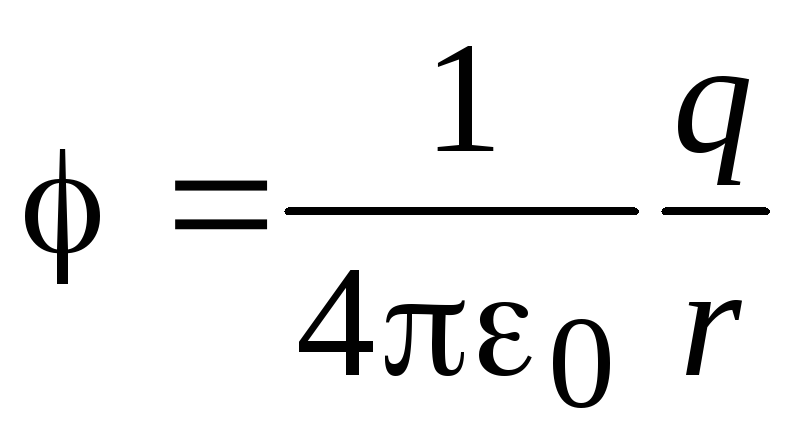 .
Потенциальная энергия взаимодействия
двух зарядов
.
Потенциальная энергия взаимодействия
двух зарядов 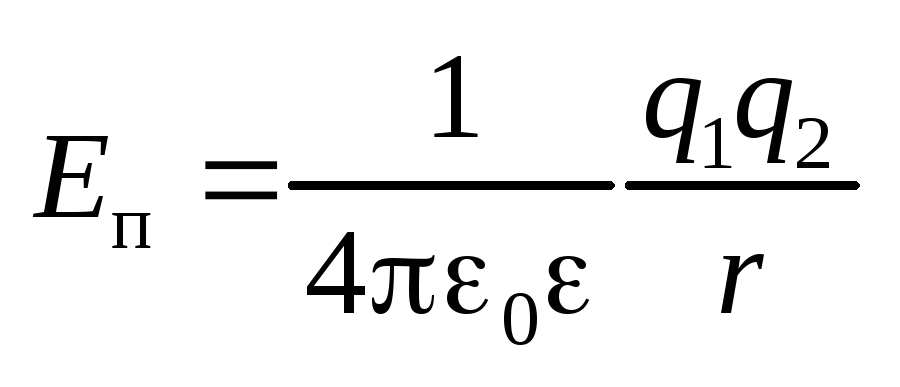 .
Потенциал электростатического поля
(определение)
.
Потенциал электростатического поля
(определение) .
Связь работы электростатического поля
с разностью потенциалов
.
Связь работы электростатического поля
с разностью потенциалов .
Выражение потенциала поля через работу
пробного заряда
.
Выражение потенциала поля через работу
пробного заряда .
Расчет потенциала по распределению
напряженности поля
.
Расчет потенциала по распределению
напряженности поля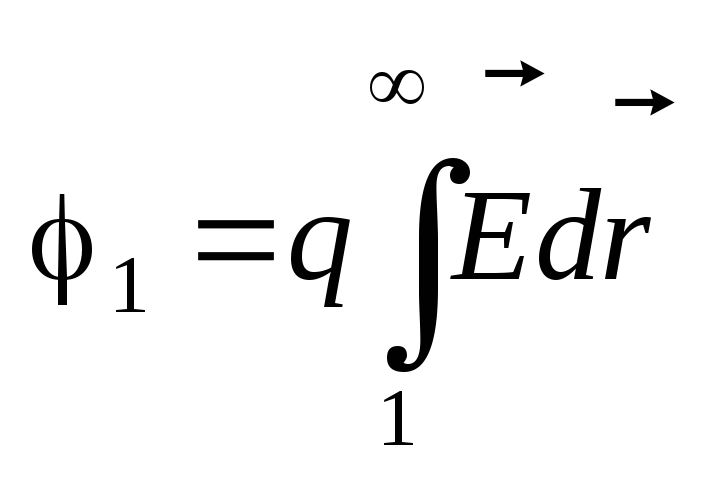 .
Расчет напряженности поля по распределению
потенциала
.
Расчет напряженности поля по распределению
потенциала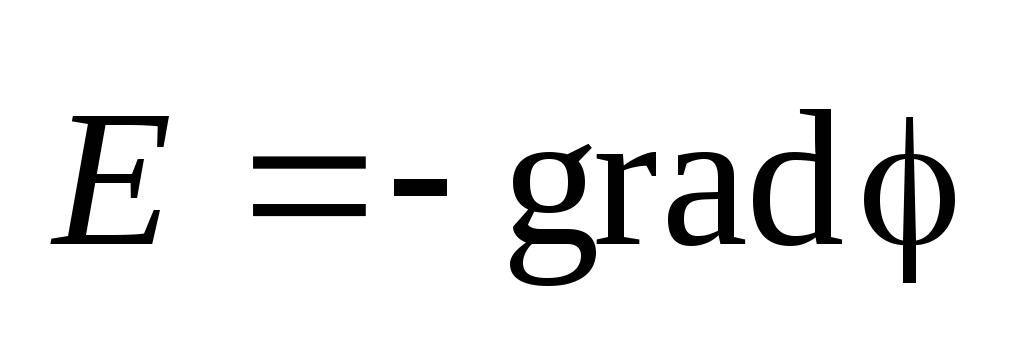 .
Связь между напряжением и напряженностью
для однородного поля
.
Связь между напряжением и напряженностью
для однородного поля 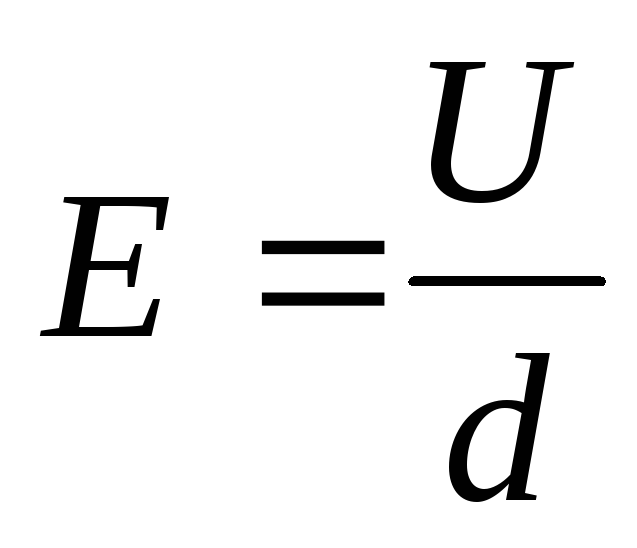 .
Дипольный момент электрического диполя
.
Дипольный момент электрического диполя  .
Момент сил, действующих на электрический
диполь в электрическом поле
.
Момент сил, действующих на электрический
диполь в электрическом поле 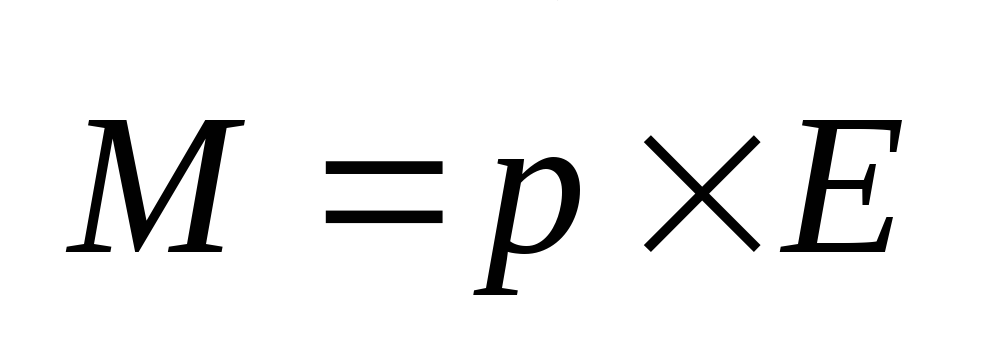 ;
;  .
Потенциальная энергия электрического
диполя во внешнем электрическом поле
.
Потенциальная энергия электрического
диполя во внешнем электрическом поле 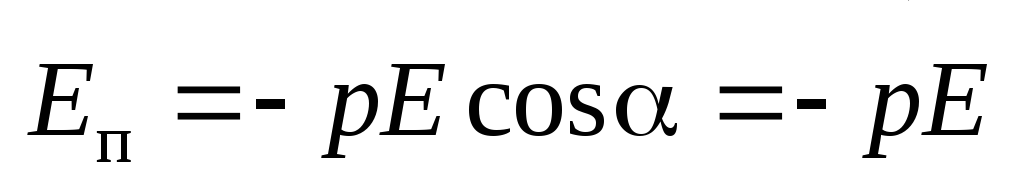 .
.
12. Проводник в электростатическом поле
Проводники – вещества, в которых имеются свободные заряды, способные перемещаться под действием электрического поля.
Электростатическая индукция – явление разделения разноименных зарядов в проводнике, помещенном в электрическое поле.
Свободные заряды в проводнике, находящемся во внешнем электростатическом поле, перераспределяются так, что создаваемое ими собственное поле компенсирует внешнее, в результате чего напряженность результирующего поля в проводнике становится равной нулю. На этом явлении основана электростатическая защита – защита чувствительных к электрическому полю приборов с помощью замкнутой металлической оболочки, т. к. внутри нее электрическое поле отсутствует.
Конденсатор – устройство для накопления значительных по величине разноименных электрических зарядов. Конденсатор состоит из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.
Электроемкость конденсатора – физическая величина, равная отношению заряда одной из пластин конденсатора (по модулю) к напряжению между его обкладками.
Свойства
электростатического поля внутри
проводника  .
Свойства электростатического поля вне
проводника около его поверхности
.
Свойства электростатического поля вне
проводника около его поверхности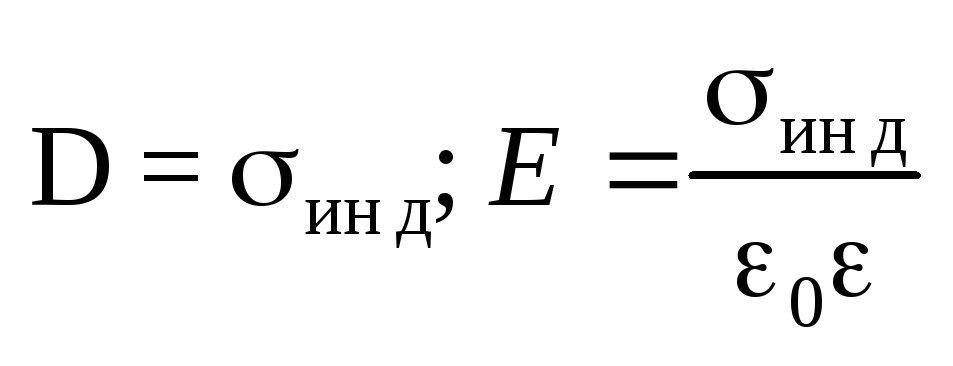 .
Электроемкость уединенного проводника
(определение)
.
Электроемкость уединенного проводника
(определение)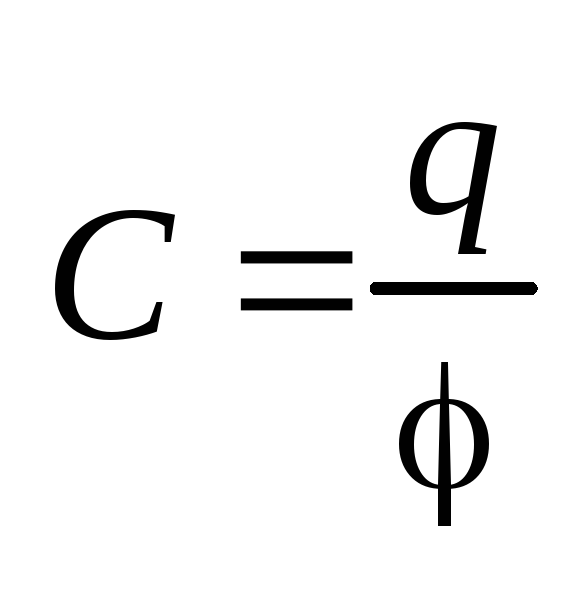 .
Электроемкость шара
.
Электроемкость шара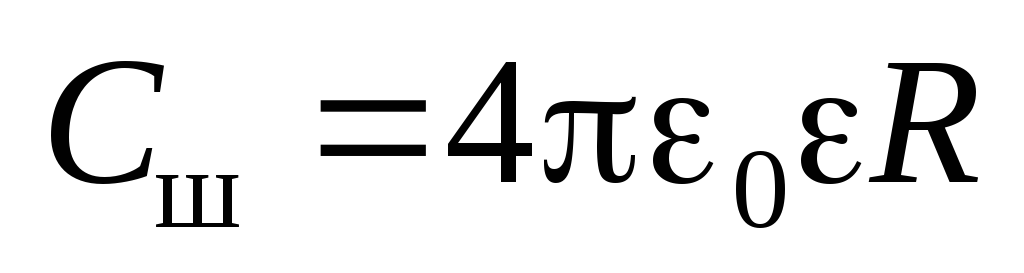 .
Электроемкость конденсатора (определение)
.
Электроемкость конденсатора (определение)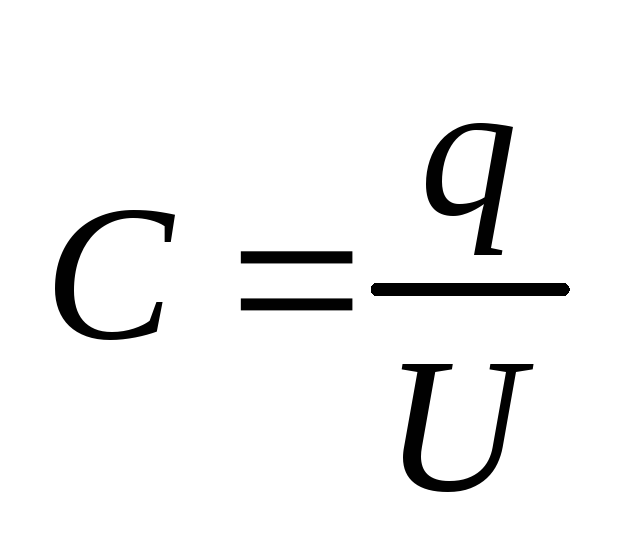 .
Электроемкость плоского конденсатора
.
Электроемкость плоского конденсатора 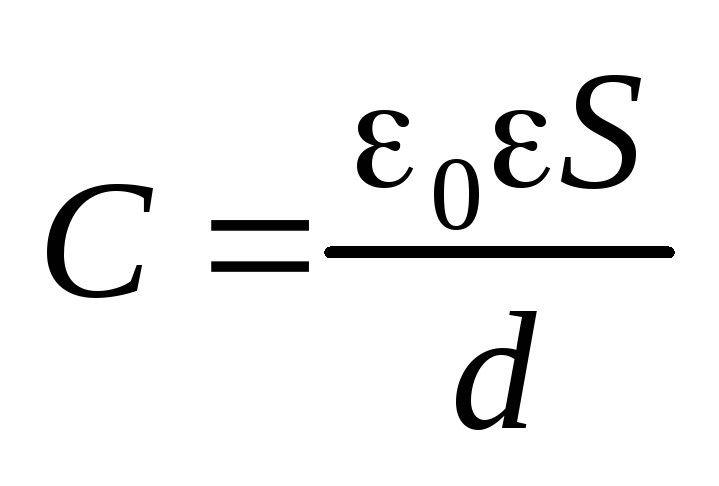 .
Электроемкость цилиндрического
конденсатора
.
Электроемкость цилиндрического
конденсатора 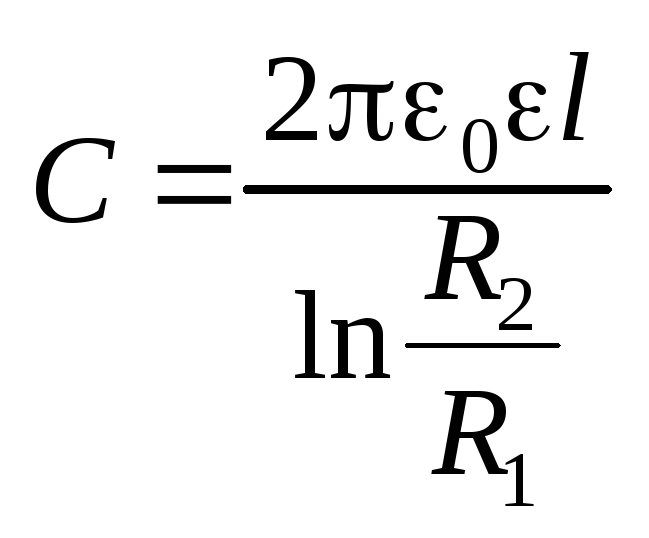 .
Электроемкость сферического конденсатора
.
Электроемкость сферического конденсатора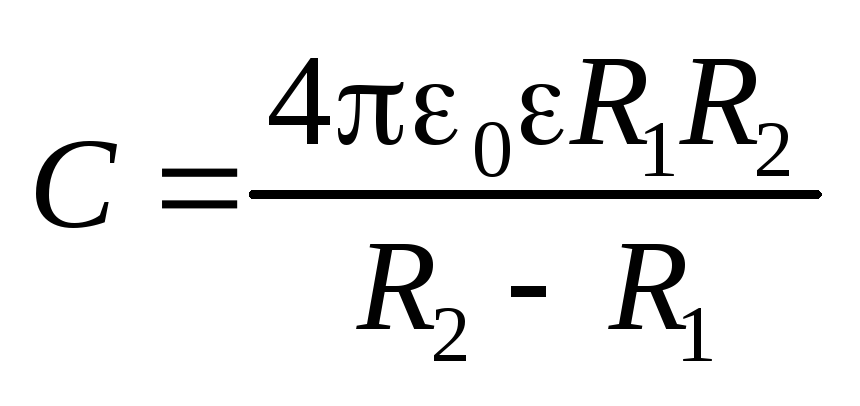 .
Электроемкость параллельно соединенных
конденсаторов
.
Электроемкость параллельно соединенных
конденсаторов .
Электроемкость последовательно
соединенных конденсаторов
.
Электроемкость последовательно
соединенных конденсаторов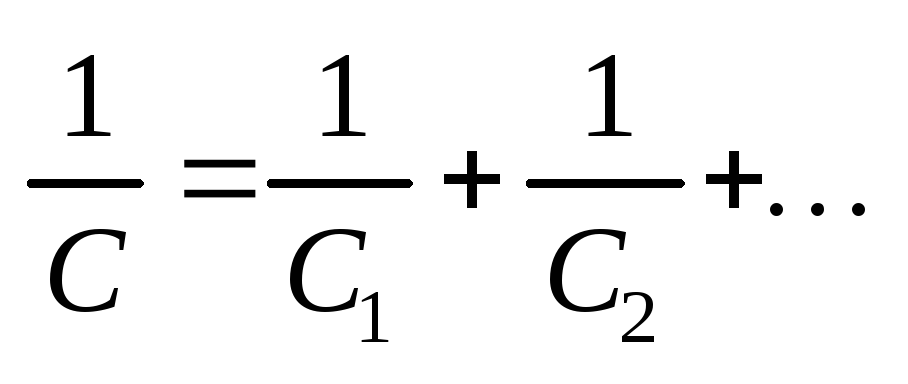 .
Потенциальная энергия системы
электрических зарядов
.
Потенциальная энергия системы
электрических зарядов .
Потенциальная энергия уединенного
проводника
.
Потенциальная энергия уединенного
проводника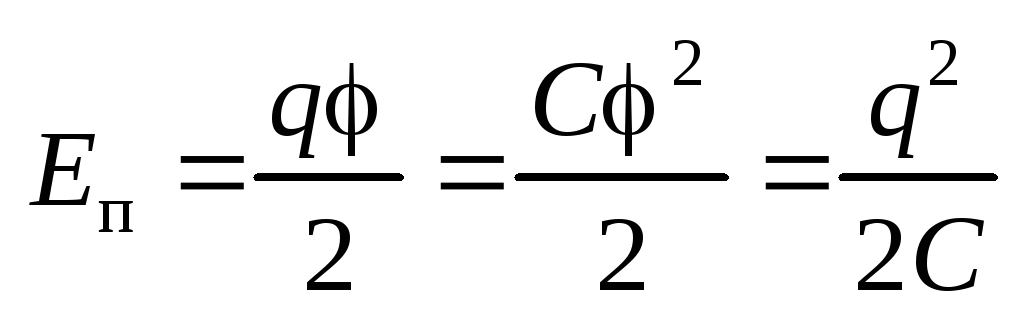 .
Потенциальная энергия конденсатора
.
Потенциальная энергия конденсатора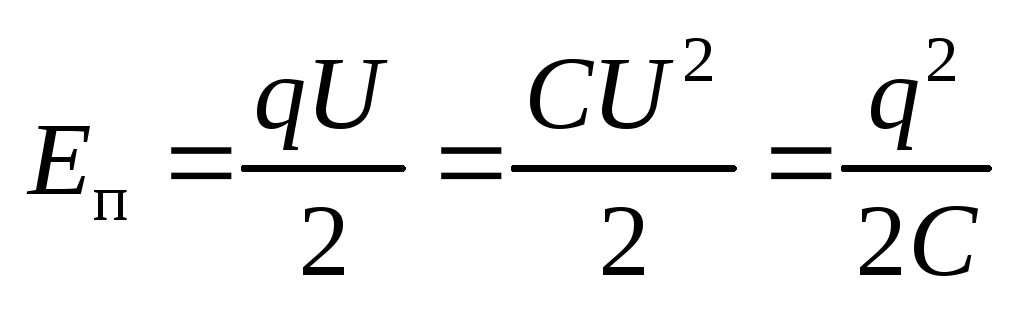 .
Объемная плотность энергии электрического
поля
.
Объемная плотность энергии электрического
поля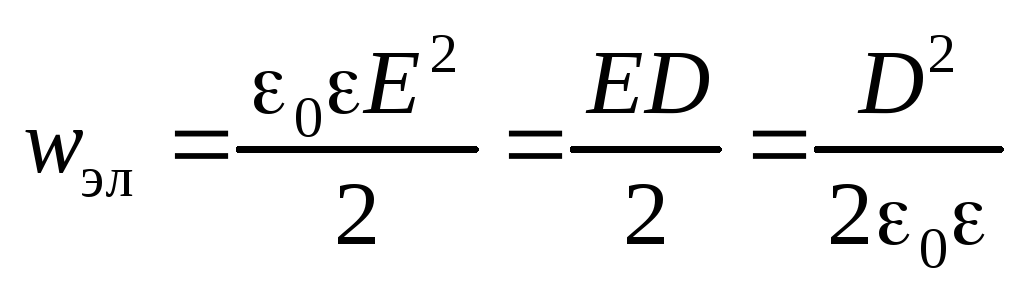 .
Условия на границе раздела двух
диэлектриков
.
Условия на границе раздела двух
диэлектриков ;
;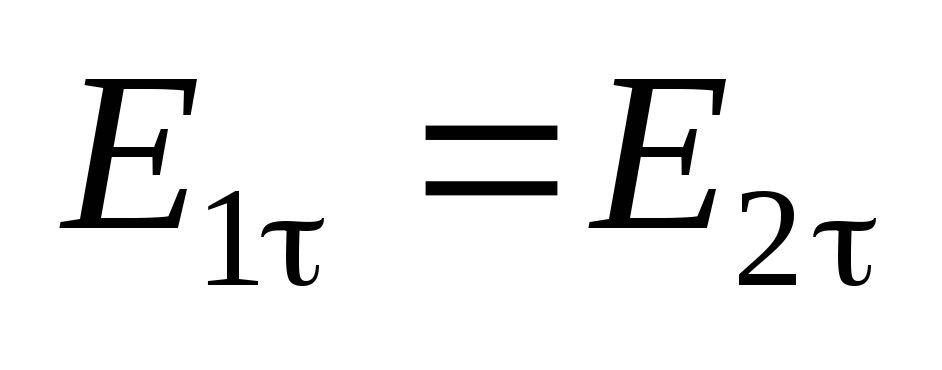 .
.
|
|
|
Плоский конденсатор | Параллельное соединение | Последовательное соединение |
Потенциал, работа электростатического поля. Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы
Тестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Аналогично Тогда энергия взаимодействия двух точечных зарядов
Энергия взаимодействия n зарядов