Постройте график зависимости емкостного сопротивления от частоты: 5. Постройте график зависимости емкостного сопротивления конденсатора от частоты. Как изменится емкостное сопротивление при увеличении частоты в 2,5 раза? — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Урок 45. Лабораторная работа № 11. Исследование зависимости силы тока от электроемкости конденсатора в цепи переменного тока

Лабораторная работа №11

Исследование зависимости силы тока от электроёмкости конденсатора в цепи переменного тока

Цель работы: изучить влияние электроёмкости на силу переменного тока.

Оборудование: набор неполярных конденсаторов известной ёмкости, регулируемый источник переменного тока ЛАТР, миллиамперметр с пределом измерения до 100 мА переменного тока, вольтметр с пределом измерения до 75 В переменного напряжения, соединительные провода.

Теория

Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Если же включить конденсатор в цепь переменного тока, то заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течёт переменный ток.

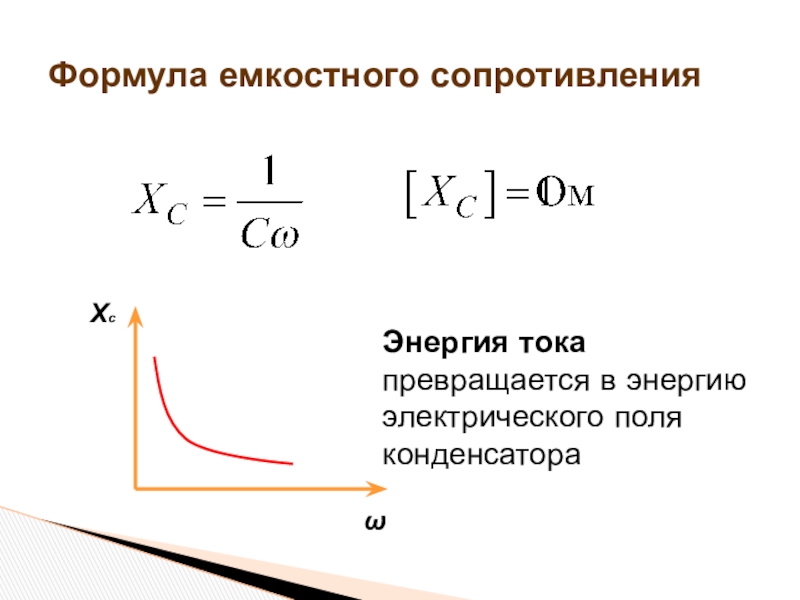
Сила тока тем больше, чем больше ёмкость конденсатора и чем чаще происходит его перезарядка, т.е. чем больше частота переменного тока.

Сопротивление, обусловленное наличием электрической ёмкости в цепи переменного тока, называют ёмкостным сопротивлением X_C. Оно обратно пропорционально ёмкости С и круговой частоте ω:

или, с учётом, что ω=2πν, где ν- частота переменного тока, (1).

Из закона Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление, действующее значение тока в цепи равно: (2).

Из формулы (2) следует, что в цепи с конденсатором переменный ток изменяется прямо пропорционально изменению ёмкости конденсатора при неизменной частоте тока.

Графически зависимость силы тока от электроёмкости конденсатора в цепи переменного тока изображается прямой линией (рис.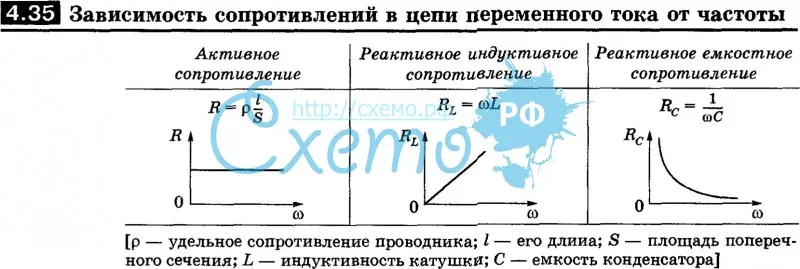 1).

В этом и предстоит убедиться опытным путём в данной работе.

Ход работы.

1. Собрать электрическую схему согласно рисунка 2 и перечертить её в тетрадь:

2. Подготовить таблицу для результатов измерений и вычислений:

Частота тока ν, Гц	Напряжение на конденсаторе U, В	Ёмкость конденсатора С, мкФ	Ток в цепи I, мА	Ёмкостное сопротивление , Ом
Частота тока ν, Гц	Напряжение на конденсаторе U, В	Ёмкость конденсатора С, мкФ	Ток в цепи I, мА	измеренное	вычисленное
50	50

Для каждого конденсатора из набора измерить силу тока при напряжении 50 В.

4. В каждом опыте рассчитать ёмкостное сопротивление по закону Ома для участка цепи переменного тока: , здесь I — действующее значение тока в мА, U=50 В — действующее значение напряжения.

5. В каждом опыте вычислите ёмкостное сопротивление по заданным значениям частоты переменного тока ν=50Гц и ёмкости конденсатора С: , здесь С — ёмкость в мкФ.

6. Сравните результаты расчётов в п.4 и в п.5 и сделайте вывод о выполнимости закона Ома для участка цепи переменного тока содержащего электроёмкость с учётом погрешности измерений.

7. Постройте график зависимости силы тока от электроёмкости конденсатора в цепи переменного тока:

8. Запишите вывод по результатам опытов и ответьте на контрольные вопросы.

Контрольные вопросы.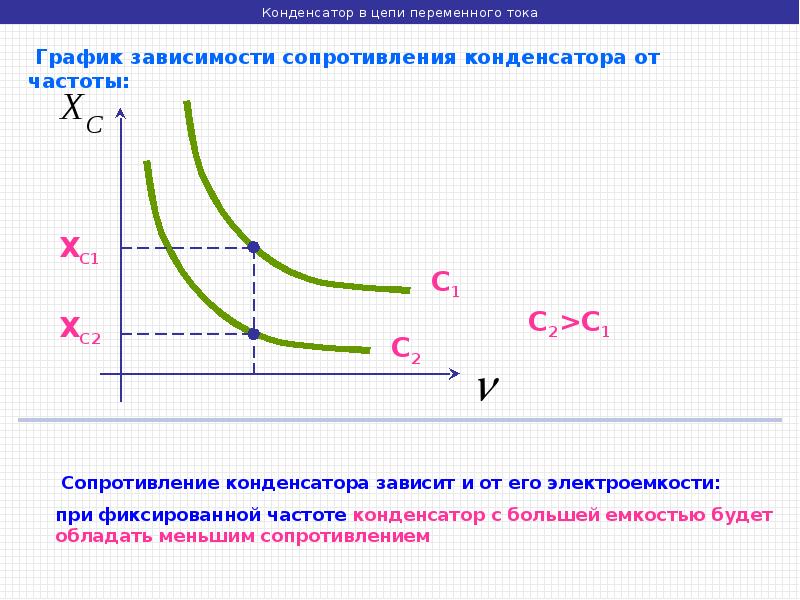

1. Почему постоянный ток не проходит через конденсатор?

2. Какое сопротивление называется ёмкостным? Почему оно является реактивным сопротивлением?

3. От чего и как зависит ёмкостное сопротивление?

4. Выполняется ли закон Ома для участка цепи переменного тока, содержащего ёмкостное сопротивление?

5. Напряжение на конденсаторе изменяется по закону . Запишите уравнение переменного тока в цепи с конденсатором.

Упражнения. Емкостная нагрузка в цепи переменного тока

Емкостная нагрузка в цепи переменного тока

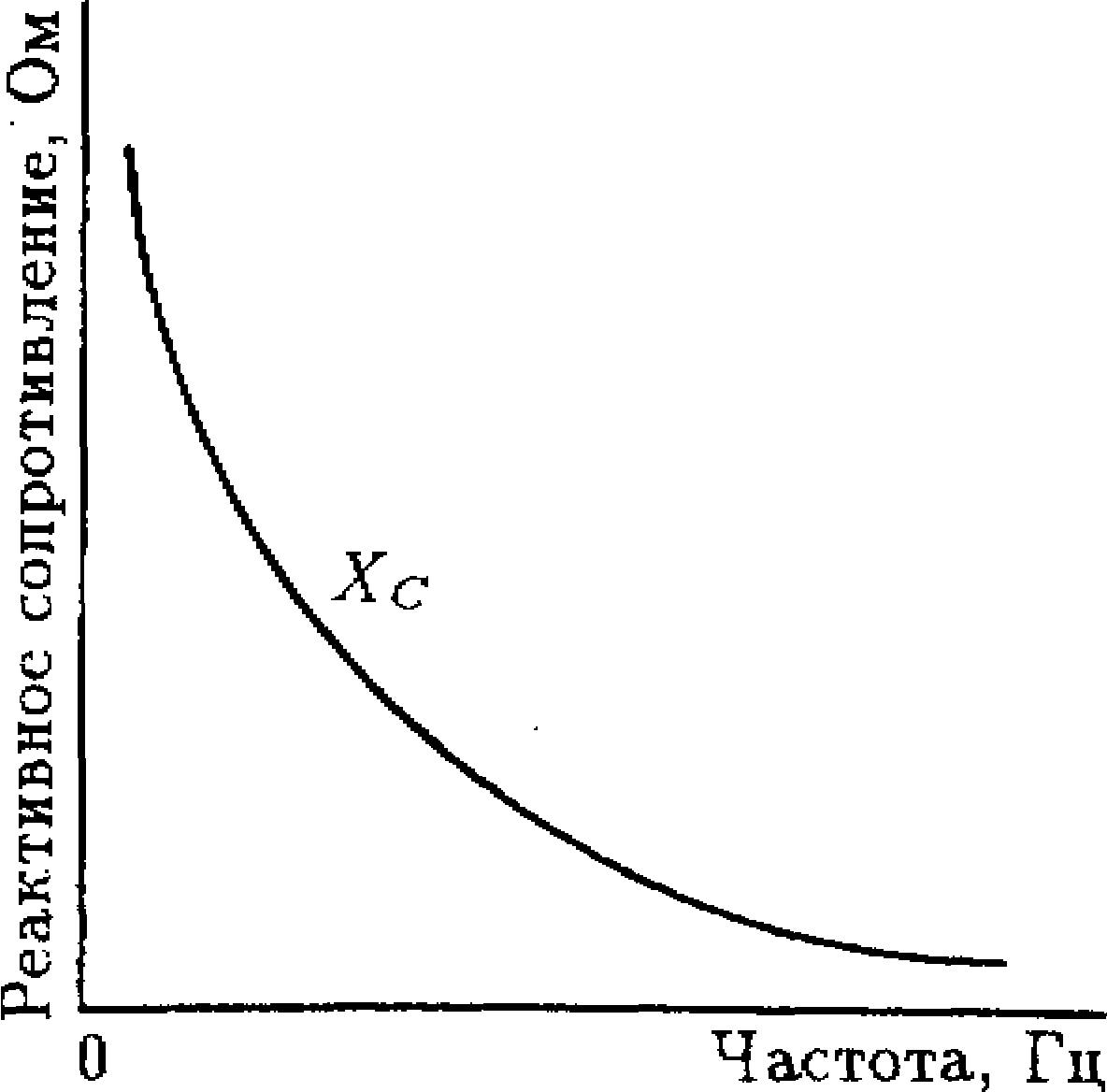
1. Рассчитайте сопротивление конденсатора емкостью С = 0,1 мкФ переменному току, если частота тока а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости емкостного сопротивления от частоты переменного тока.

2. К городской сети переменного тока с напряжением U_эф = 127 В присоединен конденсатор емкостью С = 40 мкФ. Определите амплитудное значение тока в цепи.

3. К зажимам генератора присоединен конденсатор емкостью С = 0,1 мкФ. Определите амплитуду напряжения на зажимах генератора, если амплитуда тока I_max = 2,2 А, а частота тока n = 5 кГц.

4. Найдите емкость конденсатора, если амплитуда переменного напряжения на нем U₀ =120 В, действующее значение тока I = 0,86 А, частота тока n = 50 Гц.

Индуктивная нагрузка в цепи переменного тока

1. Индуктивность катушки L = 0,5 мГн. Рассчитайте сопротивление катушки переменному току, если его частота а) 50 Гц; б) 1000 Гц; в) 10 кГц. Постройте график зависимости индуктивного сопротивления от частоты переменного тока. Катушка идеальная.

2. Найдите индуктивность катушки, если амплитуда переменного напряжения на ее концах U_мах = 160 В, амплитуда тока в ней I_мах = 10 А и частота тока 50 Гц. Катушка идеальная.

3. Индуктивное сопротивление катушки Х_L = 500 Ом, эффективное напряжение в сети, в которую включена катушка, U_эф = 100 В, частота тока 1000 Гц. Определите индуктивность катушки и амплитудное значение тока в цепи.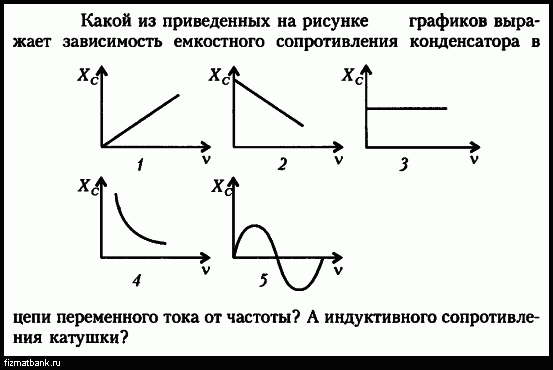 Активным сопротивлением катушки и подводящих проводов пренебречь.

Указания:

1. Помним, что для расчета емкостного или индуктивного сопротивления необходимо знать циклическую частоту w, а не обычную частоту n. Связь между ними w = 2pn.

2. Закон Ома для цепи с катушкой или конденсатором можно записать как для амплитудных, так и для действующих (эффективных) значений тока и напряжения.

Нельзя применять закон Ома, если значение одной из величин (тока или напряженяе) действующее, а значение другой величины амплитудное!!!

3. Действующие и амплитудные значения тока и напряжения связаны между собой следующим образом

Действующее и эффективное значение тока или напряжения – это одно и то же! Можно обозначать так, как Вам больше нравится – возможны три варианта:

7. Последовательное соединение R, L, C.

Рассмотрим реальный колебательный контур с источником синусоидальной ЭДС. Задача заключается в определении тока, протекающего по цепи.

Задачу можно решить двумя способами: алгебраически и геометрически. Обратимся сначала к алгебраическому решению. Запишем для контура второй закон Кирхгофа – сумма падений напряжений вдоль замкнутого контура равна сумме ЭДС, действующих в контуре:

С учетом того, что

уравнение перепишется в виде

Введем привычные обозначения . Тогда дифференциальное уравнение примет вид .

С подобным дифференциальным уравнением мы уже сталкивались, рассматривая вынужденные механические колебания под действием синусоидальной внешней вынуждающей силы. Тогда же мы показывали, что решение уравнения ищется в виде .

— решение однородного дифференциального уравнения имеет вид , где . С физической точки зрения это означает, что включение переменного тока сопровождается «звоном» собственных колебаний контура, затухающих с течением времени. Время затухания собственных колебаний будет порядка времени релаксации .

Если же мы, как обычно в электротехнике, интересуемся установившимися колебаниями при >> , то, как было уже показано ранее решение дифференциального уравнения ищется в виде . Физический смысл решения заключается в том, что под действием синусоидальной ЭДС в контуре будут происходить гармонические колебания с частотой внешней ЭДС. Очевидно, что мгновенные значения тока в контуре и напряжения на клеммах генератора сдвинуты по фазе, а это означает, что закон Ома для мгновенных значений тока и напряжения не выполняется.

В силу математической тождественности дифференциальных уравнений вынужденных механических и вынужденных электрических колебаний

мы можем воспользоваться уже готовым результатом, проведя замену механических величин на соответствующие электрические. Тогда

Ток к цепи равен , где

Амплитуда тока в контуре прямо пропорциональна амплитуде напряжения, то есть для амплитудных значений тока и напряжения выполняется закон Ома.

Величина играет роль сопротивления последовательной -цепи. Такое «сопротивление» принято называть импедансом.

Выше найден сдвиг фаз между зарядом и напряжением , а поскольку колебания тока опережают колебания заряда на , то сдвиг фаз между током и напряжением будет .

Итак, поставленная задача решена. Мы показали, что под действием синусоидальной ЭДС в колебательном контуре происходят гармонические колебания тока, нашли амплитуду тока и сдвиг по фазе между током и напряжением. Для последовательной -цепи можно пользоваться готовыми формулами. Однако, как правило, цепи переменного тока бывают не только последовательными. В этих случаях полученный нами результат не годится. В этих случаях гораздо проще рассчитать цепь графически, а не алгебраически. Покажем, как это делается.

При последовательном соединении сила тока одинакова во всех участках цепи, следовательно, . Если , то колебания напряжения на активной нагрузке совпадают по фазе с колебания ми силы тока .

На емкостной нагрузке колебания напряжения отстают от тока на : .

На индуктивной нагрузке напряжение опережает ток на : .

Мгновенное значение общего напряжения при последовательном соединении равно сумме напряжений на отдельных участках

Для сложения гармонических функций одинаковой частоты удобно воспользоваться методом векторных диаграмм. Каждое колебание изображается вектором, которому в полярных координатах соответствуют модуль (амплитуда) и полярный угол (фаза).

Изобразим вектор тока горизонтально. Напряжение на активной нагрузке синфазно току, соответственно откладываем вектор параллельно вектору тока. Напряжение опережает ток на , соответственно откладываем вектор перпендикулярно току с опережением по фазе. Напряжение отстает от тока на , откладываем вектор перпендикулярно току с отставанием по фазе.

На диаграмме, как правило, опускают индексы «max», чтобы не загромождать рисунок.

Сумма всех трех векторов напряжений даст вектор общего напряжения . Нетрудно видеть, что между током и напряжением существует сдвиг по фазе, это значит, что между мгновенными значениями тока и напряжения пропорциональность отсутствует. Для мгновенных значений тока и напряжения закон Ома не выполняется!

Сдвиг по фазе между напряжением и током

Амплитуда общего напряжения равна

Опять-таки обнаруживаем пропорциональность между амплитудными значениями тока и напряжения, это значит, что для них выполняется закон Ома.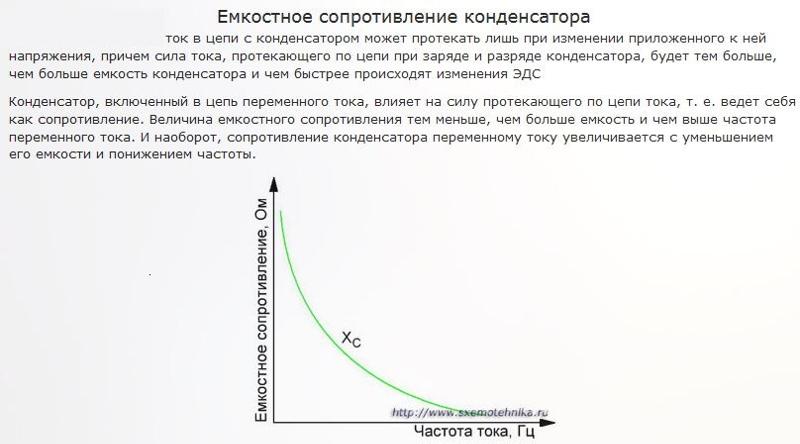

8. Резонанс напряжений (резонанс в последовательной -цепи)

Предположим, что при заданной амплитуде напряжения на клеммах генератора мы будем варьировать частоту внешней ЭДС. Очевидно, что амплитуда силы тока будет меняться, ибо индуктивное и емкостное сопротивления зависят от частоты .

Нетрудно видеть, что амплитуда тока примет максимальное значение при условии или . В этом случае наблюдается резонанс. При последовательном соединении элементов он называется резонансом напряжений. Векторная диаграмма при резонансе выглядит следующим образом

Напряжения на индуктивном и емкостном сопротивлениях равны по модулю и колеблются в противофазе, следовательно, они компенсируют друг друга. Общее напряжение становится равным падению напряжения на активной нагрузке.

Часто параметры контура подбираются таким образом, что >> . Тогда >> . При резонансе напряжений напряжения на отдельных участках цепи (на емкости и индуктивности) могут значительно превосходить напряжение на клеммах генератора.

Сдвиг по фазе между током и общим напряжением при резонансе обращается в ноль. При резонансе колебательный контур ведет себя как цепь исключительно с активной нагрузкой.

Частота тока, при которой наблюдается резонанс, может быть найдена следующим образом:

Как и следовало ожидать, резонанс наблюдается при совпадении частоты генератора с собственной частотой колебательного контура.

Резонансная кривая выглядит следующим образом

9. Резонанс токов

Рассмотрим параллельное соединение конденсатора с катушкой. Поскольку реальная катушка обладает активным сопротивлением, эквивалентная электрическая цепь будет выглядеть следующим образом:

Задача остается прежней – зная приложенное напряжение, рассчитать ток в цепи.

При параллельном соединении напряжения на ветвях, содержащих конденсатор и катушку, одинаковые . Ток в неразветвленной части (его мы и хотим определить) делится на два тока .

Для расчета этой цепи удобнее воспользоваться методом векторных диаграмм.

Начнем с ветви, содержащей индуктивность и активное сопротивление.

Напряжение на активной нагрузке совпадает по фазе с током – на векторной диаграмме вектор сонаправлен вектору .

Напряжение на индуктивной нагрузке опережает ток на — строим вектор перпендикулярно вектору тока с опережением по фазе. Общее напряжение находим по правилу параллелограмма. Оно опережает ток в -ветви на радиан.

Сопротивление -ветви равно . Амплитуда тока в этой ветви может быть найдена по закону Ома , а сдвиг по фазе определим по чертежу .

Разложим ток в -ветви на две составляющих – активную , параллельную вектору напряжения, и , перпендикулярную вектору напряжения:

Теперь перейдем к построению векторной диаграммы для всей цепи. Поскольку напряжение на отдельных ветвях одинаково, в основу диаграммы положим вектор общего напряжения , расположив его горизонтально.

Ток в ветви, содержащей емкость, найдем по закону Ома . Этот ток опережает напряжение по фазе на и колеблется в противофазе с .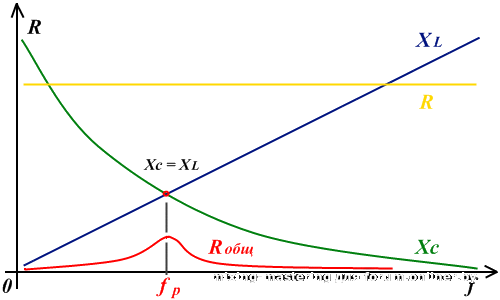 Ток в неразветвленной части цепи может быть найден по теореме Пифагора:

Нетрудно видеть, что при выполнении условия ток в неразветвленной части цепи принимает минимальное значение, равное . При этом токи в ветвях и могут оказаться намного больше тока в неразветвленной части цепи, при этом они колеблются практически в противофазе. В этом случае мы имеем дело с так называемым резонансом токов. Векторная диаграмма для резонанса токов выглядит следующим образом

При резонансе токов цепь ведет себя так, как будто в ней содержится только активная нагрузка. Аналогичная ситуация наблюдалась и при резонансе напряжений.

Найдем резонансную частоту

Тогда резонансная частота равна . Как правило, активное сопротивление катушки много меньше ее индуктивного сопротивления. В этом случае

т.е. резонанс токов наблюдается при совпадении частоты внешней ЭДС с собственной частотой колебательного контура.

Резонанс токов широко используется в радиотехнике, например, в приемном колебательном контуре антенны, в автогенераторе.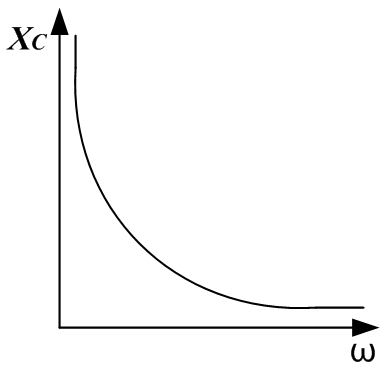 В электротехнике резонанс токов используется для повышения коэффициента мощности .

Лабораторная работа «Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов»

Лабораторная работа № 2

Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов.

Цель: изучить зависимость емкостного и индуктивного сопротивлений от частоты переменного тока и параметров элементов.

Краткое теоретическое описание

В цепи переменного тока кроме резисторов могут использоваться катушки индуктивности и конденсаторы. Для постоянного тока катушка индуктивности имеет только активное сопротивление, которое обычно невелико (если катушка не содержит большое количество витков). Конденсатор же в цепи постоянного тока представляет «разрыв» (очень большое активное сопротивление). Для переменного тока эти элементы обладают специфическим реактивным сопротивлением, которое зависит как от номиналов деталей, так и от частоты переменного тока, протекающего через катушку и конденсатор.

1.1. Катушка в цепи переменного тока.

Рассмотрим, что происходит в цепи, содержащей резистор и катушку индуктивности. Колебания силы тока, протекающего через катушку:

вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:

т.е. колебания напряжения опережают по фазе колебания силы тока на /2. Произведение LIm является амплитудой колебания напряжения:

Произведение циклической частоты на индуктивность называют индуктивным сопротивлением катушки:

(1)

поэтому связь между амплитудами напряжения и тока на катушке совпадает по форме с законом Ома для участка цепи постоянного тока:

(2)

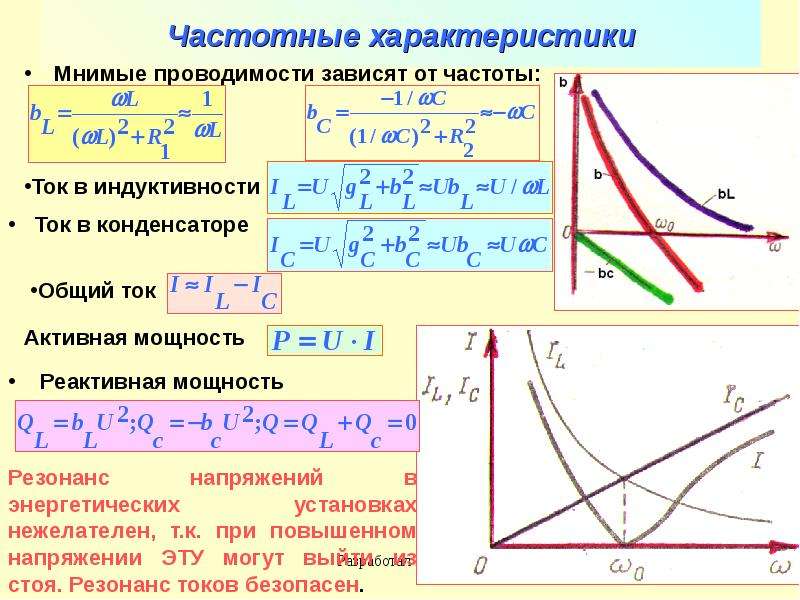
Как видно из выражения (1), индуктивное сопротивление не является постоянной величиной для данной катушки, а пропорционально частоте переменного тока через катушку. Поэтому амплитуда колебаний силы тока I_m в проводнике с индуктивностью L при постоянной амплитуде U_L напряжения убывает обратно пропорционально частоте переменного тока:

1.2. Конденсатор в цепи переменного тока.

При изменении напряжения на обкладках конденсатора по гармоническому закону: заряд q на его обкладках изменяется также по гармоническому закону:

Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:

Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на /2. Произведение CU_m является амплитудой колебаний силы тока:

Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:

(3)

Для конденсатора получаем соотношение, аналогичное закону Ома:

(4)

Формулы (2) и (4) справедливы и для эффективных значений тока и напряжения.

Порядок выполнения работы

Соберите цепь показанную на рисунке 1.

Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ), запишите показания вольтметров (напряжение на конденсаторе и на резисторе).

С, емкость,мкФ	5	10	15	20	25	30	35	40	45	50
U_конд
U_рез
I_эф
X_C

Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора (для этого надо напряжение на резисторе разделить на его сопротивление).

Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле (3).

Установите емкость конденсатора 10 мкФ. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока.

ω,частота,Гц	20	30	40	50	60	70	80	90	100
U_конд
U_рез
X_С

оберите цепь показанную на рисунке 2.

Рис.1.Рис.2.

Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Катушка — индуктивность 50 мГн;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн), запишите показания вольтметров (напряжение на катушке и на резисторе).

L,индукт,мГн	5	10	15	20	25	30	35	40	45	50
U_{катушки}
U_рез
I_эф
X_L

Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки (для этого надо напряжение на резисторе разделить на его сопротивление).

Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле (1).

Установите индуктивность катушки 100 мГн. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока.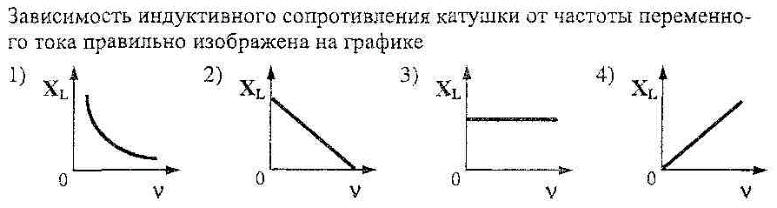

ω,частота,Гц	20	30	40	50	60	70	80	90	100
U_конд
U_рез
X_L

Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты переменного тока.

3. Контрольные вопросы.

3.1. Почему емкостное сопротивление уменьшается с увеличением частоты переменного ток а, индуктивное сопротивление – увеличивается?

3.2. Каковы разницы фаз между током и напряжением для катушки и конденсатора?

3.3. В каких единицах измеряются емкостное и индуктивное сопротивления?

3.4. Как записывается аналог закона Ома для максимальных (эффективных) значений тока и напряжения для реактивных элементов – конденсатора и катушки индуктивности?

Однофазные цепи переменного тока (страница 2)

Решение:
Полное сопротивление схемы

Полная мощность на входе схемы

Потери мощности в обмотке катушки

Активная мощность схемы

Коэффициент мощности схемы

Из таблиц тригонометрических величин .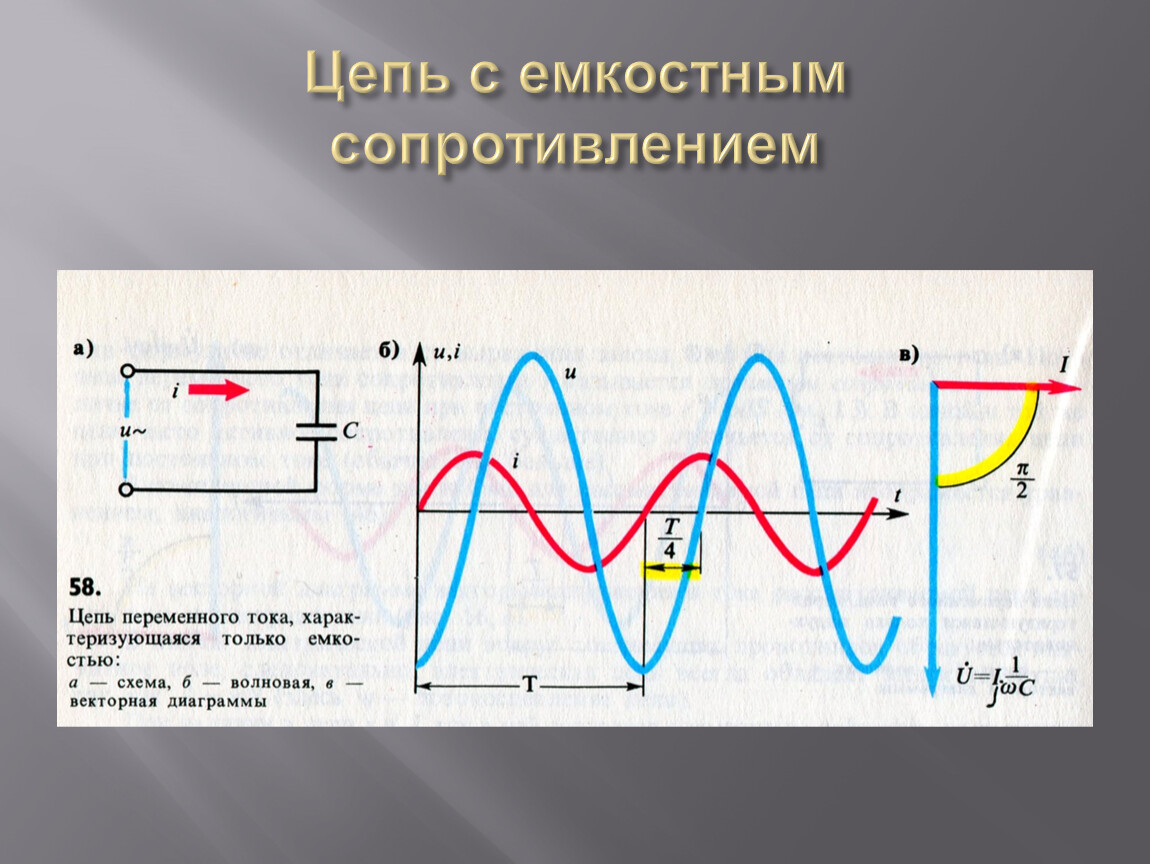
Активное сопротивление схемы

сопротивление дуги

Индуктивное сопротивление цепи представлено индуктивным сопротивлением катушки:

Эту же величину можно определить из треугольника сопротивлении (рис. 25, масштаб )

Искомая индуктивность катушки

Если бы вместо катушки был включен реостат, то сопротивление схемы имело бы ту же величину 6 Ом, но было бы чисто активным:

откуда

Потери мощности в катушке

Потери мощности в реостате

Отсюда ясно, что к. п. д. схемы выше при «погашении» избытка напряжения индуктивной катушкой. Действительно, к. п. д. при наличии катушки

к. п. д. при наличии реостата

Не следует забывать, что «погашение» избытка напряжения катушкой (или конденсатором) ухудшает коэффициент мощности (в данном примере при наличии катушки и при наличии реостата).

22. Последовательно с катушкой, параметры которой и L=15,92 мГн, включен реостат сопротивлением, .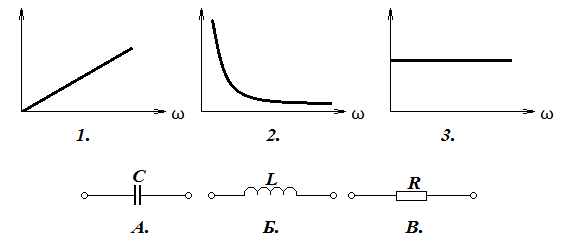 Цепь включена на напряжение U=130 В при частоте f=50 Гц.
Определить ток в цепи; напряжение на катушке и реостате; коэффициент мощности цепи и катушки.

Решение:
Индуктивное сопротивление катушки

Полное сопротивление катушки

Активное сопротивление цепи, состоящей из последовательно соединенных катушки и реостата,

Полное сопротивление цепи

На основании закона Ома ток в цепи

Напряжение на катушке

Напряжение на реостате

Арифметическая сумма много больше приложенного напряжения U=130 В. Коэффициент мощности цепи

Коэффициент мощности катушки

Следовательно, реостат увеличивает коэффициент мощности и сопротивление цепи, но уменьшает ток, увеличивает потребление энергии схемой.
Действительно, активная мощность катушки

активная мощность реостата

Так как цепь неразветвленная и ток один, то с него целесообразно начать построение векторной диаграммы (рис.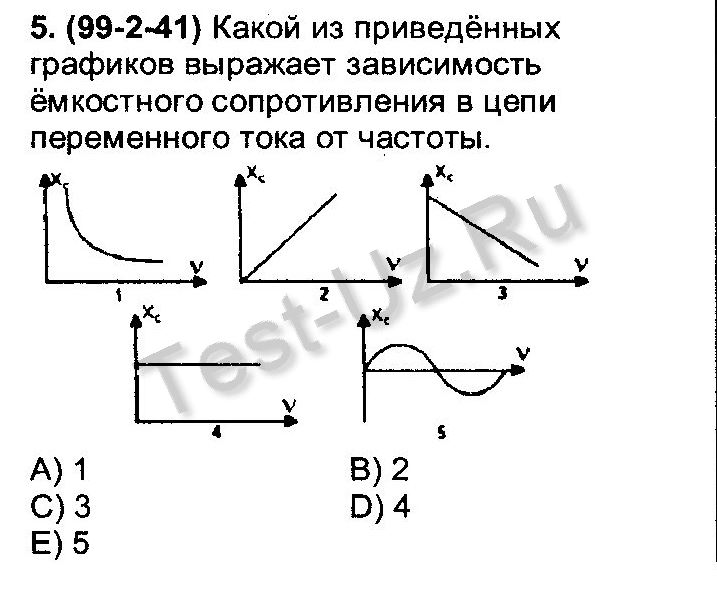

26).
Напряжение на реостате, представляющем собой чисто активное сопротивление, совпадает по фазе с током; на диаграмме вектор этого напряжения совпадает по направлению с вектором тока. Из конца вектора в сторону опережения вектора тока I, под углом в сторону, противоположную вращению стрелки часов, откладываем вектор напряжения на катушке . Векторы построены так с целью сложения по правилу многоугольника.

23. Неразветвленная цепь составлена из двух катушек: у первой катушки индуктивность и сопротивление , у второй катушки индуктивность и сопротивление .
Определить ток в цепи и напряжения на каждой катушке, а также построить в масштабе векторную диаграмму, если частота f=50 Гц и приложенное напряжение U=12,6 В.

Решение:
Индуктивное сопротивление первой катушки

т. е. оно численно равно активному сопротивлению , что обусловливает отставание тока по фазе от напряжения на 1/8 периода (на 45°).
Действительно, тангенс угла сдвига фаз

Индуктивное сопротивление второй катушки

Так как ее активное сопротивление то тангенс угла сдвига фаз

Построим в масштабе треугольник сопротивлений для рассматриваемой цепи. Для этого зададимся масштабом сопротивлений . Тогда на диаграмме сопротивление 1,57 Ом будет изображено отрезком 15,7 мм, сопротивление 2,7 Ом — отрезком 27 мм и т. д. На рис. 27 отрезок, изображающий активное сопротивление , отложен в горизонтальном направлении, а отрезок, изображающий индуктивное сопротивление , — в вертикальном направлении под прямым углом к .

Полное сопротивление первой катушки является гипотенузой прямоугольного треугольника. Из вершины с этого треугольника в горизонтальном направлении отложен отрезок, изображающий сопротивление , и под прямым углом к нему вверх — отрезок, изображающий сопротивление . Гипотенуза се прямоугольного треугольника означает полное сопротивление второй катушки.
Из рис. 27 видно, что отрезок ае, изображающий полное сопротивление z неразветвленной цепи из двух катушек, не равен сумме отрезков ас и се, т. е. . Чтобы определить полное сопротивление z рассматриваемой цепи, следует сложить отдельно активные (, отрезок аf) и индуктивные (, отрезок ef) сопротивления катушек.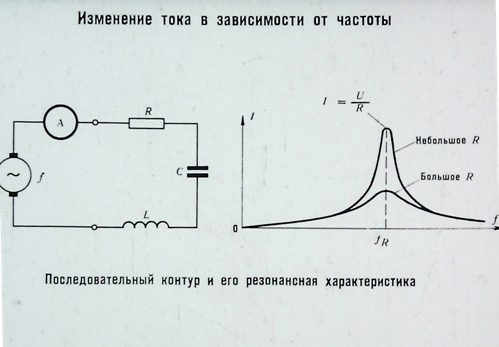
Гипотенуза ае, означающая полное сопротивление z цепи, определяется по теореме Пифагора:

Ток в цепи определяется по закону Ома:

Напряжение на первой катушке

Напряжение на второй катушке

Строим векторную диаграмму (рис. 28), приняв масштабы:
а) для тока ; тогда вектор тока изобразится отрезком длиной 25 мм;
б) для напряжения ; при этом вектор напряжения будет иметь длину 55,2 мм, вектор напряжения — длину 71 мм, а вектор приложенного напряжения — длину 126 мм.
Начало вектора совмещено с концом вектора для возможности сложения векторов напряжений но правилу многоугольника (напряжение, приложенное к неразветвленной цепи катушек, равно геометрической сумме напряжений отдельных катушек).

Методические указания для лабораторных работ по дисциплине «Электротехника и электроника»

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ВОЗДУШНОГО ТРАНСПОРТА

(РОСАВИАЦИЯ)

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ»

Хабаровский филиал СПбГУ ГА

ЭЛЕКТРОТЕХНИКА

КОМПЛЕКС практических РАБОТ

для студентов 1 курса очной формы обучения

Для специальности 23. 02.01

«Организация перевозок и управление на транспорте (по видам)

Для специальности 25.02.05

«Управление движением воздушного транспорта»

ХАБАРОВСК

2018

ОДОБРЕНА Учебно – методической комиссией циклов преподавателей гуманитарных и общепрофессиональных дисциплин (наименование комиссии) Протокол №__от «___»_______ 20___г.	Составлена в соответствии с требованиями к оценке качества освоения выпускниками программы подготовки специалистов среднего звена — по специальности 23.02.01 «Организация перевозок и управление на транспорте (воздушный транспорт)», 25.02.05 «Управление движением воздушного транспорта»
Председатель УМКЦ ___________________ Сорокин А. А.
СОГЛАСОВАНО
Зам директора по УР ____________________Казакова Е.Н.
	Рассмотрена и рекомендована методическим советом Филиала для выпускников, обучающихся по специальности 23.02.01 «Организация перевозок и управление на транспорте (воздушный транспорт)» 25.02.05 «Управление движением воздушного транспорта» Протокол №__от «___» _______20___г.

УДК 621.3.011.7

Практикум: методические указания по выполнению практических работ №1-7 по дисциплине «Электротехника и электроника» для студентов специальности 23.02.11 «Организация перевозок и управление на транспорте (по видам)», 25.02.05 «Управление движением воздушного транспорта» очной формы обучения /сост. А.А. Сорокин. – Хабаровск.

Разработаны в соответствии с программами курсов «Электротехника и электроника». Приведены краткие теоретические сведения по исследованию цепей постоянного и переменного тока. Даны общие правила расчетов, алгоритм расчетов и варианты заданий.

СОДЕРЖАНИЕ

Пояснительная записка ……………………………………………….5

Практическая работа №1: ……………………………………………6

Практическая работа №2: ……………………………………………9

Практическая работа №3:..…………………………………………..13

Практическая работа №4:……………………………………………16

Практическая работа №5:……………………………………………20

Практическая работа №6: ……………………………………………23

Практическая работа №7: ……………………………………………26

Приложение: ……………………………………….…………………29

Список литературы: ..………….…………………………………….32

Пояснительная записка

Сборник практических работ предназначен для студентов первого курса всех специальностей, изучающих электротехнику в рамках дисциплин Федерального Государственного образовательного стандарта среднего профессионального образования.

В соответствии с программой курса сборник содержит следующие разделы: электрические цепи постоянного тока, электрические измерения, электрические цепи переменного тока.

В каждом разделе даны краткие теоретические сведения и формулы, необходимые для последующего выполнения практических работ.

Целью данного сборника является закрепление теоретических знаний, а также на практике научится пользоваться электроизмерительными приборами.

В результате выполнения практических работ студенты должны:

Научится подбирать устройства электронной техники и электрические приборы с определенными параметрами и характеристиками.

Уметь читать и собирать электрические схемы.

Знать основные законы электротехники и уметь использовать их на практике.

ПРАКТИЧЕСКАЯ РАБОТА №1

Изучение зависимости сопротивления реальных проводников от их геометрических параметров и удельных сопротивлений материалов.

Цель: определить удельное сопротивление проводника и сравнить его с табличным значением.

Краткое теоретическое описание

Направленному движению электрических зарядов в любом проводнике препятствуют его молекулы и атомы. Поэтому как внешняя цепь, так и сам источник энергии оказывают препятствие прохождению тока. Величина, характеризующая противодействие электрической цепи прохождению электрического тока, называется электрическим сопротивлением.

Единицей измерения сопротивления является ом. При измерении больших сопротивлений используют единицы в тысячу и в миллион раз больше Ома. 1 кОм =1000 Ом; 1 МОм = 1 000 000 Ом.

Сопротивление проводника электрическому току зависит от материала, из которого он изготовлен и его геометрических размеров: длины и площади поперечного сечения. Если сравнить два проводника, изготовленных из одного и того же материала, то более длинный проводник имеет большее сопротивление при равных площадях поперечных сечений, а проводник с большим поперечным сечением имеет меньшее сопротивление при равных длинах. Также если сравнивать два проводника изготовленных из разных материалов, но имеющих одинаковую длину и площадь поперечного сечения, то их сопротивление будет раззным.

Для оценки электрических свойств материала проводника служит удельное сопротивление — это сопротивление проводника длиной в 1 м и площадью поперечного сечения в 1 мм2. Удельное сопротивление обозначается буквой p.

Также сопротивление проводников зависит от температуры, причем сопротивление металлических проводников с повышением температуры увеличивается. Для каждого металла существует определенный, так называемый температурный, коэффициент сопротивления, который выражает прирост сопротивления проводника при измнении температуры на 10 С отнесенный к 1 ом начального сопротивления.

2. Порядок выполнения работы

2.1. Соберите на монтажном столе электрическую схему, показанную на рисунке:

2. 2. В соответствии с вариантом выберете материал проводника, установите длину и площадь поперечного сечения:

Вариант

Материал проводника

Длина проводника, L (м)

Площадь поперечного сечения проводника, S

Напряжение батарейки, В

Никель

100

0,2

Медь

200

0,1

Нихром

100

0,1

100

Алюминий

150

0,2

Олово

250

0,5

Вольфрам

100

0,3

Золото

300

0,2

Латунь

250

0,1

190

Свинец

300

0,3

150

Серебро

400

0,3

Цинк

200

0,1

120

Платина

400

0,2

160

Молибден

250

0,3

Железо

200

0,1

170

2. 3. Определите при помощью мультиметра напряжение на проводнике.

Для этого необходимо нажать на кнопку получить мультиметр и подключить его

параллельно проводнику, при этом соблюдая полярность. Установите его в режим измерения постоянного напряжения в диапазоне 200 В.

Запишите показания в таблицу 1.

2.4. Определите при помощью мультиметра силу тока в цепи.

Для этого необходимо еще раз нажать на кнопку получить мультиметр

Второй мультиметр необходимо подключить в цепь последовательно как показано на рисунке 1, при этом соблюдая полярность. Установите мультиметр в режим измерения постоянного така. Запишите показания мультиметра в таблицу 1

2.5. Рассчитайте сопротивление проводника по формуле (1).

2.6. Расчитайте удельное сопротивление проводника по формуле (2).

2.7. Проделайте пункты 2. 3 – 2.6. изменяя длину. Площадь померечного сечения и материал проводника оставте при этом неизменным.

2.8. Результаты измерений занесите в таблицу 1:

2.9. Сравните полученное удельное сопротивление с табличным значением.

2.10. Измерьте сопротивление проводника непосредственно при помощи мультиметра. Для этого необходимо подключить мультиметр параллельно проводнику и установить его в режим измерения сопротивления в диапазоне 2000 Ом. Источник питания при этом необходимо отключить от цепи.

Таблица 1

опыта

Длина, м

Напряжение, В

Сила тока, А

Сопротивление, Ом

расчетное

Сопротивление, Ом

измеренное

Удельное сопротивление

1 1

2 2

3 3

4 4

5 5

Сформулируйте выводы по проделанной работе.

ПРАКТИЧЕСКАЯ РАБОТА №2

Исследование сопротивлений проводников при параллейном и последовательном соединение.

Цель: Изучить законы протекания тока через последовательно и параллельно соединённые проводники и проверить формулы расчета сопротивлений при различном соединении.

Краткое теоретическое описание

Проводники в схемах могут соединяться последовательно (Рис 1.) и параллельно(Рис.2.).

Рассмотрим схему последовательного соединения проводников, изображенную на Рис. 1.

Напряжение на концах всей цепи складывается из напряжений на каждом проводнике:

Uобщ = U1+U2+U3

При последовательном соединении проводников их общее сопротивление равно сумме электрических сопротивлений каждого проводника.

Rобщ = R1+R2+R3,

Сила тока протекающая через последовательно соединённые резисторы будет одинаковой на всех резисторах:

Iобщ = I1=I2=I3

Рассмотрим теперь схему параллельного соединения проводников, изображенную на Рис. 2.

При параллейном соединении резисторов напряжение будет одинаковым для всех резисторов:

Uобщ = U1=U2=U3

Сила тока при параллейном соединении резисторов будет равна сумме сил токов протекающих через каждый резистор:

Iобщ = I₁ + I₂ + I₃.

При параллельном соединении проводников величина, обратная сопротивлению цепи, равна сумме обратных величин сопротивлений всех параллельно соединенных проводников.

2. Порядок выполнения работы.

2.1. Соберите на монтажном столе электрическую схему, показанную на рисунке:

Рис 3.

Выберите номиналы сопротивлений в соответствии с вариантом. Значения сопротивлений в таблице указаны в Ом. Мощность на всех резисторах необходимо выставить 100Вт.

Вариант

U батареи, В

2. 2. Рассчитайте теоретические значения сопротивлений между всеми участками цепи.

Запишите эти вычисления.

2.3. Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между всеми участками цепи. Запишите измерения и сравните значения с расчетными.

2.4. Замкните ключ и измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора.

2.4. Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.

2.5. Измерьте с помощью мультиметра (в режиме измерения тока) токи, текущие через каждое сопротивление. Запишите показания прибора.

2.6. Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.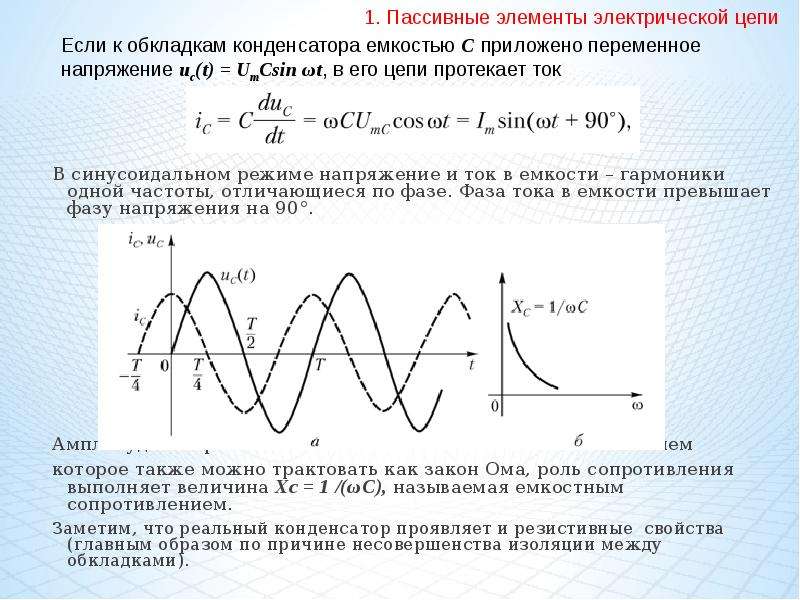

2.7. Зная напряжение на батарее рассчитайте значения напряжения и тока на каждом резисторе и сравните эти значения с измеренными.

ПРАКТИЧЕСКАЯ РАБОТА №3

ЭДС и внутреннее сопротивление источников постоянного тока. Закон Ома для полной цепи.

Цель: определить внутреннее сопротивление источника тока и его ЭДС.

Краткое теоретическое описание

Электрический ток в проводниках вызывают тока. Силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля, называются сторонними силами. Отношение работы «А», совершаемой сторонними силами по перемещению заряда «q» вдоль цепи, к значению этого заряда называется электродвижущей силой «Е» источника или сокращенно ЭДС:

Е = В (1)

Электродвижущая сила также ка и напряжение выражается в Вольтах.

Работа – эта мера превращения энергии из одного вида в другой. Следовательно, в источнике сторонняя энергия преобразуется в электрическую энергию.

Любой источник постоянного тока имеет внутреннее сопротивление. Согласно закону Ома для полной цепи: сила тока в цепи равна отношению электродвижущей силы источника к сумме сопротивлений внешнего и внутреннего участков цепи.

(2)

Отсюда ЭДС:

Е = I * (R+r) (3)

Для определения внутреннего сопротивления необходимо измерить два значения сил токов текущих через резистор и два значения напряжений на резисторе (см. рис.1). Подставив их в формулу (3) получим внутреннее сопротивление:

(4)

Порядок выполнения работы

Рис. 1

Соберите цепь по схеме, изображенной на рисунке 1. Установите сопротивление резистора, ЭДС батарейки и внутреннее сопротивление батарейки в соответствии с вариантом. На резисторе установите мощность 100Вт. Внутреннее сопротивление батарейки в программе обозначено как рабочая мощность.

Вариант

U батареи, В

2. 2. При помощи мультиметра определите напряжение на батарейке при разомкнутом ключе.

2.3. Замкните ключ и измерьте силу тока и напряжение на резисторе. Запишите показания приборов.

2.4. Измените сопротивление резистора и запишите другие значения силы тока и напряжения.

2.5. Повторите измерения силы тока и напряжения для 15 различных значений резистора и запишите полученные значения в таблицу.

опыта

2. 6. Рассчитайте внутреннее сопротивление по формуле (4).

2.7. Рассчитайте ЭДС батарейки по формуле (3).

ПРАКТИЧЕСКАЯ РАБОТА №4

Емкостное сопротивление. Зависимость емкостного сопротивления от частоты переменного тока и параметров элементов

Цель: изучить зависимость емкостного сопротивления от частоты переменного тока и параметров элементов.

Краткое теоретическое описание

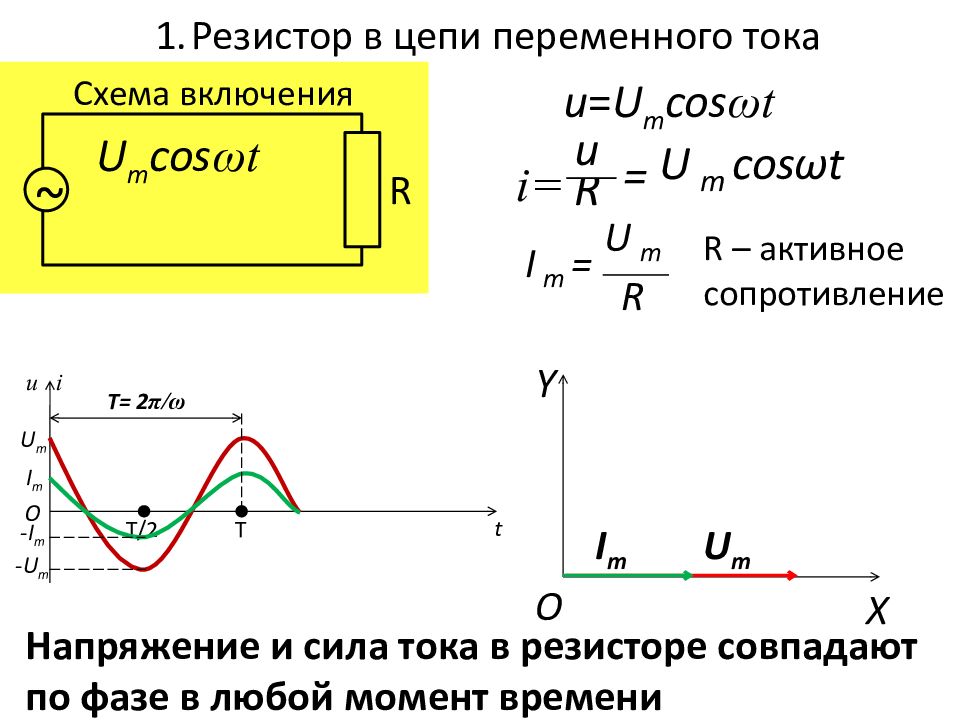
Выясним, от чего зависит сила тока в цепи с емкостью. Обозначим сопротивление цепи Хс и назовем его емкостным сопротивлением. Тогда закон Ома для цепи с емкостью можно выразить так:

Известно, что сила тока в цепи определяется количеством электрических зарядов, проходящих через поперечное сечение проводника в единицу времени:

Если в единицу времени по проводам протекает большое количество зарядов, то сила тока будет большой, и наоборот, когда по проводам в каждую секунду протекает малое количество зарядов, то сила тока оказывается незначительной.

Допустим, что частота переменного тока, вырабатываемого генератором, большая. В этом случае в каждую секунду конденсатор много раз (часто) заряжается и разряжается. В проводах, идущих от генератора к пластинам конденсатора, будет перемещаться в каждую секунду большое количество электрических зарядов. Поэтому можно сказать, что в рассматриваемой цепи возникает большая сила тока и в данном случае, согласно закону Ома, емкостное сопротивление цепи Хс оказывается малой величиной.

Если же частота переменного тока генератора будет мала, то конденсатор в каждую секунду зарядится и разрядится меньшее количество раз: В связи с этим по проводам цепи в каждую секунду пройдет незначительное количество зарядов и сила тока будет мала, а следовательно, емкостное сопротивление цепи, наоборот, будет большим.

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально частоте переменного тока.

Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь.

Допустим, что в цепь включен конденсатор большой емкости. Количество электричества, которое накапливает конденсатор при заряде и отдает при разряде, прямо пропорционально его емкости:

Чем больше емкость конденсатора, включенного в цепь переменного тока, тем большее количество электричества переместится при заряде и разряде, по проводам, идущим от генератора к его пластинам. Поэтому в проводах возникает ток большой силы и в данном случае, согласно закону Ома, емкостное сопротивление цепи Хc будет мало. Если же включенная в цепь емкость мала, то при заряде и разряде по проводам пройдет меньшее количество электрических зарядов и сила тока будет незначительной, следовательно, емкостное сопротивление цепи, наоборот, будет большим.

Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости.

Таким образом емкостное сопротивление:

Если включенная емкость измеряется в микрофарадах, то емкостное сопротивление:

2. Порядок выполнения работы

2.1. Соберите цепь показанную на рисунке 1.

Рис.1

2.2. Установите следующие значения параметров в соответствии с вариантом:

Генератор – напряжение (эффективное) 100 В, частота:

Вариант

Частота генератора

100 Гц

110 Гц

120 Гц

130 Гц

140 Гц

150 Гц

160 Гц

170 Гц

180 Гц

190 Гц

200 Гц

210 Гц

220 Гц

230 Гц

Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.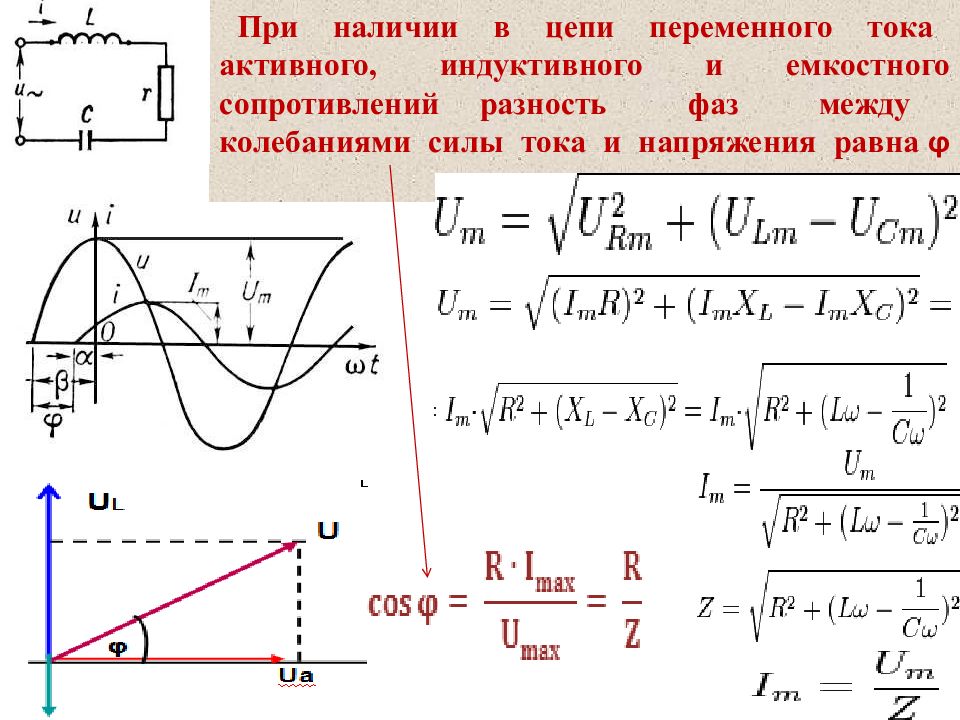

2.3 Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ), запишите показания вольтметров (напряжение на конденсаторе и на резисторе).

2.4. Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора (для этого надо напряжение на резисторе разделить на его сопротивление).

2.5. Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле (2).

2.6. Установите емкость конденсатора в соответствии с вариантом. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока.

Вариант

Емкость конденсатора

10 мкФ

20 мкФ

30 мкФ

40 мкФ

50 мкФ

60 мкФ

70 мкФ

80 мкФ

90 мкФ

100 мкФ

110 мкФ

120 мкФ

130 мкФ

140 мкФ

2. 7. Постройте график зависимости емкостного сопротивления от частоты переменного тока.

ПРАКТИЧЕСКАЯ РАБОТА №5

Индуктивное сопротивление. Зависимость индуктивного сопротивления от частоты переменного тока и параметров элементов

Цель: изучить зависимость индуктивного сопротивления от частоты переменного тока и параметров элементов.

Краткое теоретическое описание

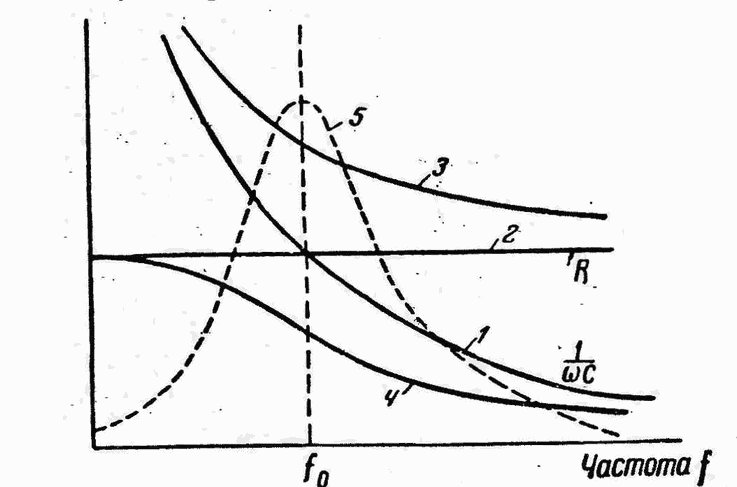
Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Под действием Э.Д.С. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции.

Электродвижущая сила самоиндукции, согласно правилу Ленца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э.д.с. генератора, то она препятствует прохождению переменного тока. При расчетах это учитывается по индуктивному сопротивлению, которое обозначается ХL и измеряется в Омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э.д. с. самоиндукции, зависит от скорости изменения тока в катушке (от частоты) и от индуктивности катушки L:

2.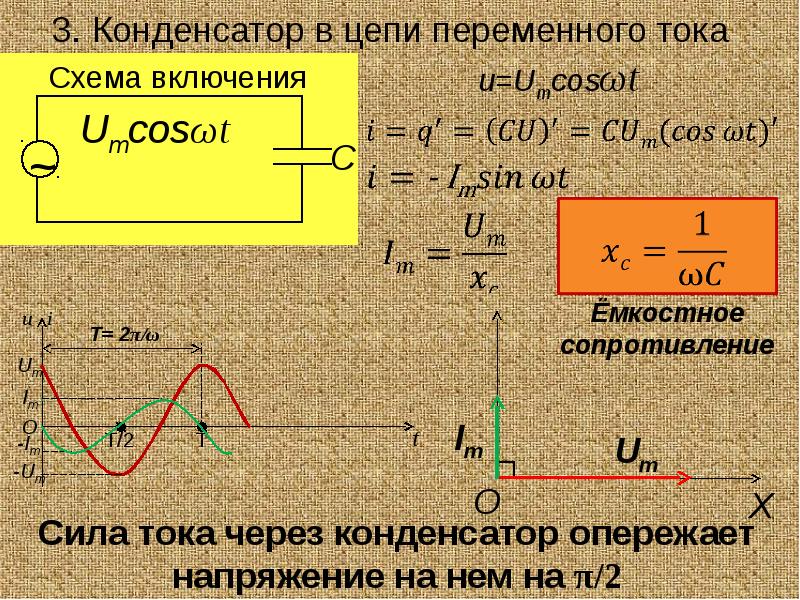 Порядок выполнения работы

2.1 Соберите цепь показанную на рисунке 1.

Рис. 1

2.2 Установите следующие значения параметров в соответствие с вариантом:

Генератор – напряжение (эффективное) 100 В, частота:

Вариант

Частота генератора

100 Гц

110 Гц

120 Гц

130 Гц

140 Гц

150 Гц

160 Гц

170 Гц

180 Гц

190 Гц

200 Гц

210 Гц

220 Гц

230 Гц

Катушка — индуктивность 50 мГн;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.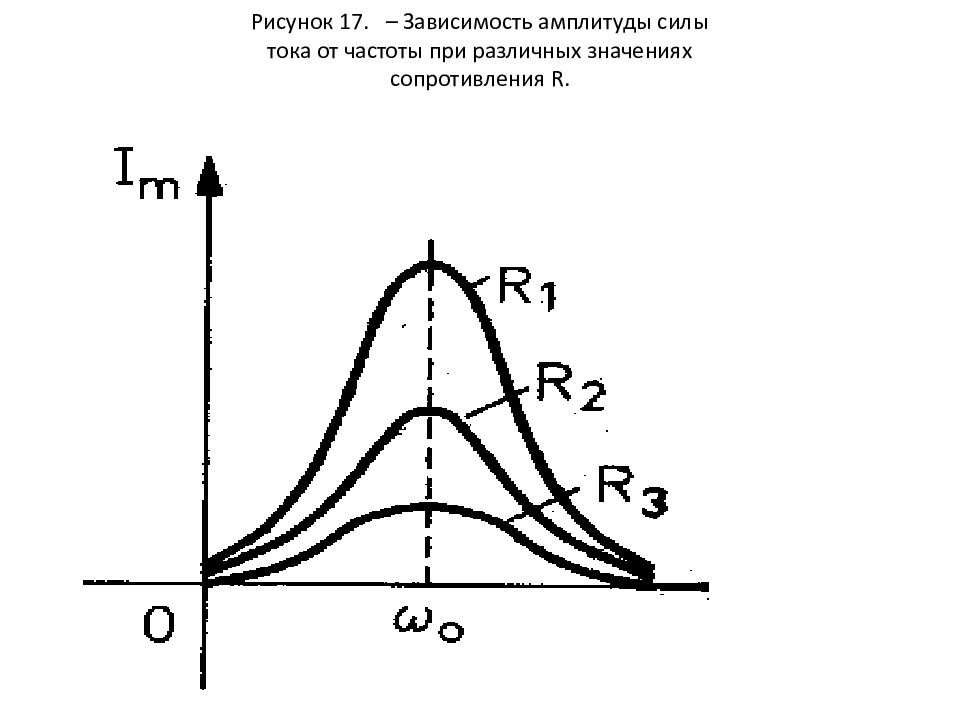

2.3 Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн), запишите показания вольтметров (напряжение на катушке и на резисторе).

2.4. Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки (для этого надо напряжение на резисторе разделить на его сопротивление).

2.5. Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле (1).

2.6 Установите индуктивность катушки в соответствии с вариантом. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока.

Вариант

Индуктивность катушки

100 мГн

110 мГн

120 мГн

130 мГн

140 мГн

150 мГн

160 мГн

170 мГн

180 мГн

190 мГн

200 мГн

210 мГн

220 мГн

230 мГн

2. 7. Постройте графики зависимостей индуктивного сопротивлений от частоты переменного тока.

ПРАКТИЧЕСКАЯ РАБОТА №6

Явление резонанса в цепи переменного тока

Цель: изучение установившихся вынужденных колебаний в цепях переменного тока. Исследование явления резонанса.

Краткое теоретическое описание

В цепи переменного тока с активным, индуктивным и емкостными сопротивлениями, соединенными последовательно (рис. 1), может возникнуть резонанс напряжений.

Рис. 1

При резонансе напряжения на зажимах индуктивного и емкостного сопротивлений могут стать значительно больше чем напряжение на зажимах цепи.

Резонанс напряжений наступает в том случае, если индуктивное сопротивление ХL и емкостное сопротивление ХC равны между собой, т. е.

Допустим, что подбором индуктивности и емкости или изменением частоты создано условие, при котором ХL=ХС. Когда цепь не настроена в резонанс, то ее полное сопротивление:

а в рассматриваемой цепи при резонансе (когда ХL=ХC) ее полное; сопротивление:

Таким образом, полное сопротивление цепи при резонансе оказывается равным активному сопротивлению.

Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении

Напряжение на индуктивности определяется согласно закону Ома произведением силы тока на величину индуктивного сопротивления/ Так как в цепи увеличилась сила тока, то напряжение возросло.

Напряжение на емкости также определяется произведением тока на величину емкостного сопротивления. Поэтому напряжение на емкости возросло.

В связи с тем, что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление ХL равно емкостному сопротивлению Хс, напряжение на индуктивности и напряжение на емкости равны:

Если одновременно увеличить оба реактивных сопротивления ХL и Хс, не нарушая при этом условия резонанса ХL=Хс, то соответственно возрастут оба частичных напряжения UL и Uс, а сила тока в цепи при этом не изменится. Таким путем можно получить UL и Uс во много раз большие, чем напряжение U на зажимах цепи.

2. Порядок выполнения работы.

2.1. Соберите на монтажном столе схему, показанную на рис. 1 предварительно выбрав значения параметров элементов соответствующие варианту:

Вариант

Uэф, В

R, Ом

С, мкФ

L, Гн

генератора, Гц

100

200

110

220

120

240

130

260

140

280

150

300

180

100

200

110

220

120

240

130

260

140

280

150

300

180

2. 2. Изменяя частоту генератора на 10 Гц, с помощью вольтметров измерьте напряжения на катушке, конденсаторе, резисторе и занесите измеренные значения в таблицу 1. В наборе конструктора имеется лишь два мультиметра, поэтому придется изменяя частоту генератора, провести измерения дважды – сначала подключив вольтметры к катушке и конденсатору, а второй раз – подключив вольтметр к резистору.

f генератора, Гц

2.3. Постройте графики зависимости напряжений на резисторе, конденсаторе и катушке в зависимости от частоты генератора.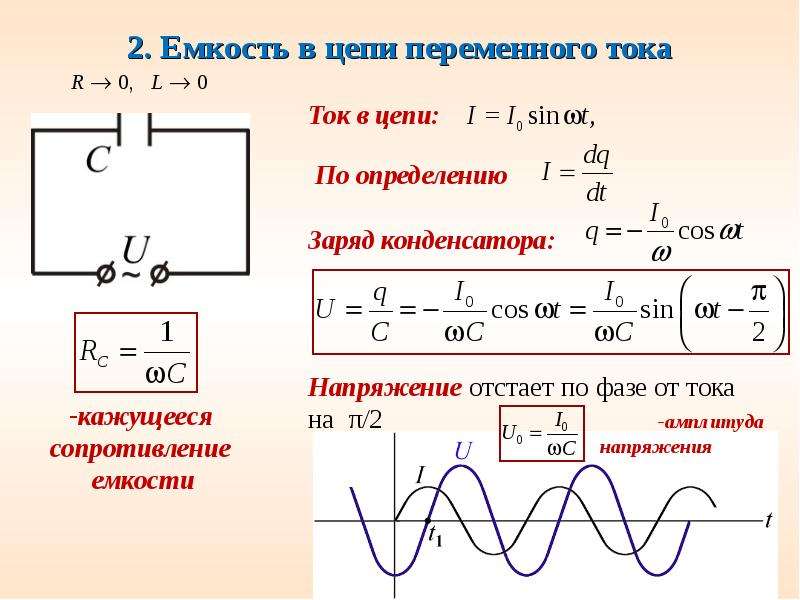

2.4. Измените параметры элементов и повторите измерения и расчеты.

2.5. Попытайтесь объяснить экспериментальные графики зависимости напряжений на элементах от частоты переменного тока в цепи.

ПРАКТИЧЕСКАЯ РАБОТА №7

Принципы работы плавких предохранителей в электрических цепях

Цель: рассчитать предохранители для защиты электрической сети с напряжением 220 В, питающей осветительные и электронагревательные приборы.

Краткое теоретическое описание.

Электрические цепи всегда рассчитаны на определенную силу тока. Если по той или иной причине сила тока в цепи становится больше допустимой, то провода могут значительно нагреться, а покрывающая их изоляция – воспламениться.

Причиной значительного увеличения силы тока в сети может быть или одновременное включение мощных потребителей тока, например электрических плиток, или короткое замыкание. Коротким замыкание называют соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.

Сопротивление цепи при коротком замыкании незначительно, поэтому в цепи возникает большая сила тока, провода при этом могут сильно накалиться и стать причиной пожара. Чтобы избежать этого, в сеть включают предохранители.

Назначение предохранителей – сразу отключить линию, если сила тока вдруг окажется больше допустимой нормы. Рассмотрим устройство предохранителей, применяемых в квартирной проводке. Главная часть предохранителя — проволока из легкоплавкого металла (например, из свинца), проходящая внутри фарфоровой пробки. Пробка имеет винтовую нарезку и центральный контакт. Нарезка соединена с центральным контактом свинцовой проволокой. Пробку ввинчивают в патрон, находящийся внутри фарфоровой коробки.

Свинцовая проволока представляет, таким образом, часть общей цепи.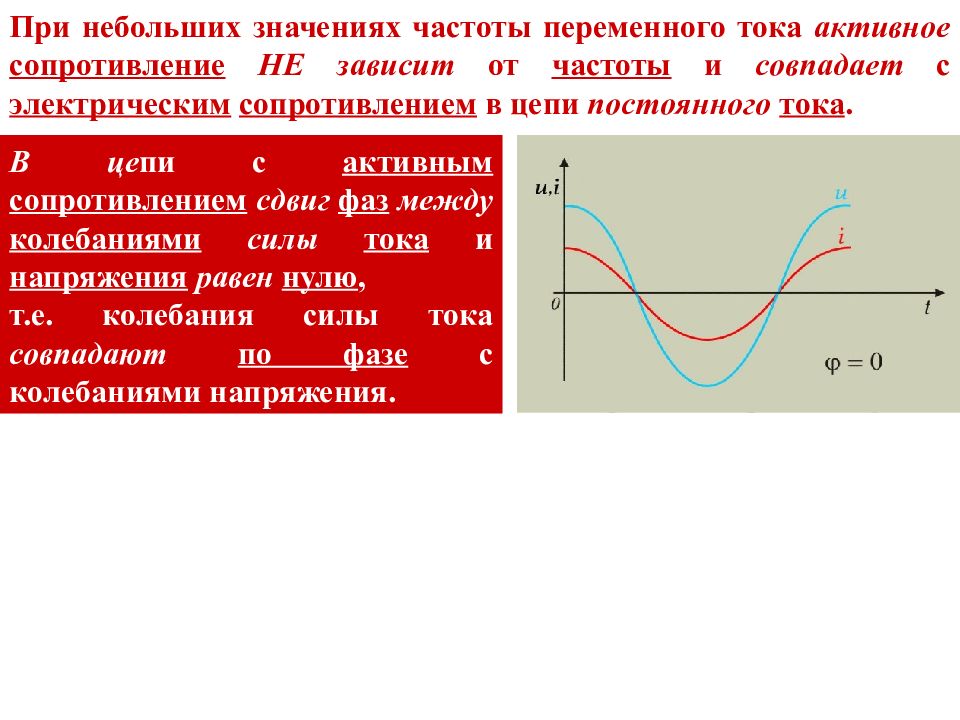 Толщина свинцовых проволок рассчитана так, что они выдерживают определенную силу тока. Если сила тока превысит допустимое значение, то свинцовая проволока расплавится и цепь окажется разомкнутой.

Предохранители с плавящимся проводником называют плавким предохранителем.

Плавкие предохранители должны обеспечивать нормальную работу электроприемников при длительном прохождении по ним номинального тока и немедленно отключать их при перегрузках и коротких замыканиях. Поэтому предохранители выбирают с учетом следующих обстоятельств:

Номинальный ток плавкой вставки должен удовлетворять требованию Iвст. = Iр,

где Iр – расчетный ток на защищенном участке цепи;

Каждый предохранитель должен срабатывать лишь тогда, когда произойдет короткое замыкание на участке цепи, который он защищает, т.е. предохранители должны работать избирательно (селективно).

Порядок выполнения работы.
1. Соберите электрическую цепь, изображенную на рисунке 1:

Рис.1.

1. Выберите напряжение генератора сети равным 220 В, мощности электрических лампочек и электронагревательных приборов выбрать в соответствие с вариантом. Рабочее напряжение для всех приборов установить 240В.

варианта

Мощность Пл1 (Вт)

Мощность Пл2 (Вт)

Мощность Лп1 (Вт)

Мощность Лп2 (Вт)

Мощность Лп3 (Вт)

1000

1800

260

300

600

1900

240

350

800

2000

300

310

900

1700

275

330

500

1600

230

340

700

1500

350

360

750

1650

100

240

400

650

1750

110

120

380

850

1550

120

210

370

950

1850

130

280

450

1050

1950

140

270

500

550

2050

150

300

220

1100

2100

160

200

420

1150

2200

170

250

510

1. Определите расчетный ток для каждого электроприемника по формуле . Результаты занесите в работу.
2. Рассчитайте номинальные значения токов плавких предохранителей, защищающих отдельно электроосветительную сеть (Пр.3 и Пр.4) и сеть, питающую электронагревательные приборы (Пр.2), а также ток для общего предохранителя (Пр.1), защищающего все электрические приборы.
3. Замкните ключи К1 и К6. Убедитесь, что лампа загорелась, а предохранители Пр.1 и Пр.4 не перегорают.
4. Замкните ключи К4 и К5. Убедитесь, что лампы загорелись, а предохранители Пр.1 и Пр.3 не перегорают.
5. Замкните ключи К2 и К3. Убедитесь, что все электроприборы включились, а все предохранители не перегорают.

Приложение:

В программе, а так же в быту, большинство измерительных приборов заменяет мультиметр. Мультиметр – это универсальный прибор для измерений. Измерений напряжения, тока, сопротивления, а так же проверки провода на обрыв.

Для того, чтобы измерить ту или иную величину необходимо с помощью переключателя выбрать определенный режим на мультиметре, а также выбрать предел измерения. Предел измерения- это максимальное значение измеряемой величины. Чем меньше предел измерения, тем точнее будут измерения. Но не стоит забывать, что если измеряемая величина в цепи превысит значение предела измерения, то прибор может выйти из строя. В большинство приборов встроена защита от перегрузок при неправильном выборе предела или режима измерений, однако не стоит проводить эксперименты.

Например, если постоянное напряжение цепи 12 В, необходимо установить мультиметр в режим измерения постоянного напряжения и выбрать предел измерения 20В. Можно установить предел измерений и большего значения, 200 или 1000 В., но тогда измерение будет не таким точным, а иногда десятые или сотые Вольта играют значительную роль. Тоже самое и с другими режимами. При работе с электронными компонентами ток в ним может достигать несколько десятков мА, а иногда и мкА. Если при таких токах установить предел измерений 10 А, то прибор не сможет измерить такие маленькие велечины и на дисплее вы увидите 0. У разных моделей мультиметров пределы измерений могут отличатся. Также существуют мультиметры с автоматическим подбором пределов измерений.

Мультиметр установлен в режим измерения постоянного напряжения. Предел измерения выбран 20 В.

Мультиметр установлен в режим измерения постоянного тока. Предел измерения выбран 200 мА.

Мультиметр установлен в режим измерения сопротивления. Предел измерений 20 кОм.

Список литературы:

Волынский В.А. и др. Электротехника /Б.А. Волынский, Е.Н. Зейн, В.Е. Шатерников: Учеб. пособие для вузов. – М.: Энергоатомиздат, 2001. – 528 с., ил.

Касаткин А.С., Немцов М.В. Электротехника: Учеб. пособие для вузов. – 4-е изд., перераб. – М.: Энергоатомиздат, 2003. – 440 с., ил.

Основы промышленной электроники: Учебник для неэлектротехн. спец. вузов /В.Г. Герасимов, О М. Князьков, А Е. Краснопольский, В.В. Сухоруков; под ред. В.Г. Герасимова. – 3-е изд., перераб. и доп. – М.: Высш. шк., 2006. – 336 с., ил.

Электротехника и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.1. Электрические и магнитные цепи. – М.: Высшая шк. – 1996 г.

Электротехника и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.2. Электромагнитные устройства и электрические машины. – М.: Высшая шк. – 1997 г.

ЛР №7

Лабораторная работа № 7

Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов

Краткое теоретическое описание

1.1. Катушка в цепи переменного тока.

вызывают падение напряжения на концах катушки в соответствии с законом самоиндукции и правилом Ленца:

т.е. колебания напряжения опережают по фазе колебания силы тока на  /2. Произведение  LI_m является амплитудой колебания напряжения:

Произведение циклической частоты на индуктивность называют индуктивным сопротивлением катушки:

(1)

(2)

1.2. Конденсатор в цепи переменного тока.

При изменении напряжения на обкладках конденсатора по гармоническому закону:

заряд q на его обкладках изменяется также по гармоническому закону:

Видно, что колебания напряжения на конденсаторе отстают по фазе от колебаний силы тока на  /2. Произведение  CU_m является амплитудой колебаний силы тока:

Аналогично тому, как было сделано с индуктивностью, введем понятие емкостного сопротивления конденсатора:

(3)

Для конденсатора получаем соотношение, аналогичное закону Ома:

(4)

Формулы (2) и (4) справедливы и для эффективных значений тока и напряжения.

Порядок выполнения работы:
1. Соберите цепь показанную на рисунке 1.
2. Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Конденсатор – рабочее напряжение 400 В, емкость 10 мкФ;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя емкость конденсатора от 5 до 50 мкФ (через 5 мкФ), запишите показания вольтметров (напряжение на конденсаторе и на резисторе).
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения емкости конденсатора (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите значения емкостных сопротивлений конденсатора для соответствующих значений его емкости и сравните их с рассчитанными по формуле (3).
Установите емкость конденсатора 10 мкФ. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты емкостного сопротивления в зависимости от частоты переменного тока.
Соберите цепь показанную на рисунке 2.

Рис.1. Рис.2.

Установите следующие значения параметров:

Генератор – напряжение (эффективное) 100 В, частота 100 Гц;

Катушка — индуктивность 50 мГн;

Резистор – рабочая мощность 500 Вт, сопротивление 100 Ом.

Изменяя индуктивность катушки от 50 до 500 мГн (через 50 мГн), запишите показания вольтметров (напряжение на катушке и на резисторе).
Рассчитайте эффективное значение токов, текущих в цепи, в зависимости от значения индуктивности катушки (для этого надо напряжение на резисторе разделить на его сопротивление).
Определите индуктивные сопротивления катушки для соответствующих значений ее индуктивности и сравните их с рассчитанными по формуле (1).
Установите индуктивность катушки 100 мГн. Изменяя частоту генератора от 20 до 100 Гц через 10 Гц, повторите измерения и расчеты индуктивного сопротивления в зависимости от частоты переменного тока..

Постройте графики зависимостей индуктивного и емкостного сопротивлений от частоты переменного тока.

Вывод: Изучил зависимость емкостного и индуктивного сопротивлений от частоты переменного тока и параметров элементов

3. Контрольные вопросы.

3.2. Каковы разницы фаз между током и напряжением для катушки и конденсатора?

3.3. В каких единицах измеряются емкостное и индуктивное сопротивления?

Ответы:

3.1 Чем больше частота, тем больше энергии участвует на перазарядке обкладок конденсатора, раз энергии идет больше, это эквивалентно уменьшению его реактивного сопротивления. Реактивное сопротивление означает, что энергия перезаряда не расходуется, а переодически возвращается в источник, т. е с той же частотой.

3.2 Разность фаз между напряжением и силой тока ф=arctg (w*L-1/w*C) / R

3.3

3.4 I₀ = U₀ / XC I₀ = U₀ / XL

Определение индуктивности катушки и ее активного сопротивления методом резонанса

Данченко О.П., учитель физики (гимназия №2 г. Хабаровск)

Принадлежности: звуковой генератор, катушка индуктивности, емкостная батарея (известной емкости), вольтметр, миллиамперметр.

Целью работы является: исследования зависимости полного сопротивления (импеданса) в цепи переменного тока от частоты, построение резонансной кривой и нахождение по ней резонансной частоты, активного сопротивления цепи и индуктивности катушки.

ТЕОРИЯ: При последовательном подключении в цепь с переменным электрическим током катушки индуктивности (реальная катушка всегда имеет активное сопротивление) и емкости получается последовательно соединенная R-L-C цепь. При последовательном соединении постоянным параметром цепи будет электрический ток. Напряжение на емкости и индуктивности будут сдвинуты относительно тока UL=IwLcos(wt+p¤2), UC=I/wC*cos(wt-p¤2). Этот сдвиг фаз удобно рассматривать на векторной диаграмме, представленной на рисунке. Из рисунка видно, что сдвиг фаз между током и напряжением на активном сопротивлении катушки R составляет 0, на индуктивности L +p¤2, а на емкости С -p¤2. Из графика видно, что сдвиг фаз между напряжениями на индуктивности UL и емкости UC составляет p, то есть, находится в противофазе. Результирующее напряжение определяется разностью: UL-UC и при равенстве этих напряжений по модулю общее напряжение на реактивных сопротивлениях равно нулю. В этом случае все падение напряжения источника тока приходится на активное сопротивление R (напряжение на индуктивности и емкости могут быть в этом случае во много раз больше, но их сумма равна нулю). Такое состояние системы называют резонансом. При резонансе сопротивление схемы минимально и равно активному сопротивлению катушки. График зависимости полного сопротивления цепи Z от частоты представлен на графике. Значения сопротивления определяют по формуле Ома Z=U/I . Так как при резонансе реактивные сопротивления равны, значения индуктивности можно выразить из формулы 1/wс=wL; L =1/w2C, где w резонансная частота, определенная из графика. ОПИСАНИЕ УСТАНОВКИ: Установку собирают согласно предложенной схеме (катушка представлена в виде активного и индуктивного сопротивления). Последовательно катушки подключают известную емкость. Измерительные приборы представлены вольтметром и миллиамперметром. Звуковой генератор должен иметь диапазон от 20 до 20000 гц и напряжение выхода порядка 20в.

Задание.

Соберите установку, согласно чертежу.

Заполните предложенную таблицу:

По данным таблицы постройте график зависимости полного сопротивления цепи от циклической частоты колебания. По графику определите:

Резонансную частоту. (При необходимости повторите измерения в точках, близких к резонансу.)

Активное сопротивление катушки.

Индуктивность катушки.

Напишите вывод.

Electronic — График зависимости емкости от частоты керамических конденсаторов — iTecTec

Каждый компонент имеет индуктивность (эквивалентную последовательную индуктивность или ESL), значение определяется площадью контура, через которую должен пройти ток. Он включает в себя монтажную индуктивность на печатной плате, переходные отверстия, дорожки и т. Д. Пример:

Это чисто механическое. Емкость конденсатора не имеет значения, она будет работать одинаково с резистором, даже с 0R или куском провода.

Колпачок имеет ESL и ESR, поэтому его импеданс равен:

\ $ Z = \ frac {1} {j \ omega C} + R + j \ omega L \ $

(без учета диэлектрического поглощения, утечки и т. Д. )

Конденсаторы одинакового физического размера (например, все 0805), как правило, имеют одинаковую индуктивность.Итак, если мы построим график их сопротивления в зависимости от частоты:

Низкочастотная часть показывает ожидаемое значение \ $ \ frac {1} {j \ omega C} \ $. На высокой частоте доминирует \ $ j \ omega L \ $. Поскольку все они одного размера, все они имеют одинаковый ВЧ-импеданс.

Провал — это резонансная частота. В его центре Z = R. Низкое СОЭ дает более глубокое падение.

На высоких частотах это индуктор: вы не можете измерить его емкость, потому что C не влияет на импеданс, в котором преобладает L.Вот почему кривая емкости на вашем листе данных останавливается. Его цель — показать, что емкость остается стабильной и хорошо работает на низких частотах, где это важно.

Теперь меньшие пакеты имеют более низкий ESL:

Итак, причина, по которой вы часто видите 10 нФ // 100 нФ, не в том, что ограничение 10 нФ «быстрее», а в том, что вы можете получить его в пакете 0201, таким образом он имеет меньшую индуктивность. Если оба конденсатора равны 0805, то 10 нФ бесполезны, а один 1 мкФ будет работать лучше.

РЕДАКТИРОВАТЬ: при параллельном соединении крышек вы строите резервуар LC, и он может звонить.Распараллеливание MLCC с низким ESR разных значений может вызвать неприятности. Вот почему для простых вещей (таких как логический вентиль или микроконтроллер) не беспокойтесь о 10n // 100n, это на самом деле будет хуже. Одно значение менее рискованно, 100n или 1µ. Также следы питания индуктивные, это еще один LC бак, ферритовые кольца с крышками тоже … специя помогает!

Теперь ваши колпачки сложены из керамики:

Вы можете сразу догадаться по их конструкции и тому факту, что они расположены над печатной платой, что у них будет намного больше ESL, чем у конденсаторов SMD.Наверное, больше на электролитический. Однако эти колпачки керамические, поэтому они выдерживают очень высокие температуры, а также имеют очень низкое ESR, что может быть преимуществом (также может вызывать сильный звон).

Итак, для коммутатора 500 кГц они не являются правильным выбором, если у вас нет экстремальных температур или другой причины для их использования. Электролитик, вероятно, будет дешевле и будет иметь немного СОЭ, чтобы предотвратить звон.

Чтобы отфильтровать шум 500 кГц, вам понадобится конденсатор с низким импедансом на этой частоте и выше.Итак, вам нужны небольшие MLCC, если вы паяете вручную, с 1-10 мкФ 0805 легко работать. Вы можете установить несколько параллельно, чтобы снизить индуктивность, и позаботьтесь о компоновке, потому что важна общая индуктивность, включая переходы к заземляющей плоскости и дорожки.

Если вам нужна помощь в выборе конденсатора, вам нужно указать, какой ток будет выдерживать DC-DC, его топологию (понижающий, повышающий …), напряжение, частоту и т. Д.

График Боде и Найквиста — PalmSens Коррозия

В этой главе представлены два основных способа визуализации спектров электрохимического импеданса (EIS), график Найквиста и Боде, и объясняется, как различные EIS простых электронных схем будут отображены на графике Боде и Найквиста.Это демонстрирует преимущества и недостатки двух графиков, а также служит основой для понимания анализа EIS с использованием эквивалентных схем.

Как упоминалось в предыдущей главе, есть два основных способа построить спектр импеданса. Один — участок Боде . Этот сюжет фактически представляет собой два сюжета в одном. По оси абсцисс отложена логарифмическая шкала частоты, по одной ординате — логарифм импеданса Z, а по второй ординате — фазовый сдвиг Φ.

Преимущество этого графика в том, что вся информация хорошо видна. Конденсатор, подключенный параллельно резистору, который является важной схемой для спектроскопии электрохимического импеданса, виден в этом спектре как пик фазового сдвига. Отдельные компоненты можно легче понять на графике Боде.

График Найквиста сложнее для понимания, но по практическим причинам он более популярен в электрохимии. Одна из причин заключается в том, что сюжет Найквиста очень чувствителен к изменениям.Другой заключается в том, что для наиболее распространенных схем некоторые параметры могут быть считаны непосредственно с графика. Чтобы получить график Найквиста, отрицательный мнимый импеданс –Z ’’ отображается в зависимости от действительной части импеданса Z ’.

В следующих параграфах будут показаны эффекты некоторых простых компонентов на графике Боде и графике Найквиста. Это полезно, потому что обычно создают электронную схему, которая представляет исследуемую электрохимическую систему. Подгонка спектра на основе этой эквивалентной схемы выполняется для определения вклада отдельных компонентов.

Самым простым компонентом является резистор, который следует закону Ома:

Уравнение 6.1 | Закон Ома

Это верно для постоянного и переменного тока. В результате отсутствует фазовый сдвиг (Φ = 0 °), а полное сопротивление Z, равное R в этом случае, не зависит от частоты переменного тока. Это видно на графике Боде двумя постоянными параллелями оси абсцисс (см. Рисунок 6.3). На графике Найквиста видна одна точка с Z ’’ = 0 и Z = R (см. Рисунок 6.3).

Рисунок 6.3 EIS резистора на схематическом графике Боде и Найквиста

Еще одним очень распространенным элементом, который часто встречается в реальных экспериментах, является конденсатор. Конденсаторы хранят заряд. Простой конденсатор — пластинчатый конденсатор. Он состоит из двух проводящих параллельных пластин, которые не соприкасаются друг с другом. Если к пластинам подключен источник питания, течет ток, который экспоненциально затухает, пока не станет незначительным.

А ток течет, потому что одна пластина заряжена отрицательно, а другая — положительно.Разделение зарядов означает протекание тока. В какой-то момент пластины не могут хранить больше заряда, и ток перестает течь. В соответствии с

сила тока со временем спадает.

Уравнение 6.2

E ^C — зарядный потенциал или напряжение, I ⁰ — пусковой ток, R — сопротивление цепи вокруг конденсатора, t время и C — емкость конденсатора. Емкость является свойством конденсатора и определяется как заряд Q, который может храниться на приложенный потенциал E или как уравнение

Уравнение 6.3

Обычно U используется для обозначения напряжения, но поскольку эти уравнения необходимо перенести в электрохимические эксперименты, полезно начинать с потенциала E вместо напряжения U. Эти два понятия не являются синонимами, но в данном контексте можно их поменять местами. .

Если предположить, что двойной электрохимический слой ведет себя точно так же, как пластинчатый конденсатор, два приведенных выше уравнения показывают три важных факта:

Емкостной ток экспоненциально спадает со временем t.Чем выше сопротивление R и емкость C, тем медленнее он будет распадаться. Произведение сопротивления R и емкости C часто называют постоянной времени τ.
Заряд Q, который может храниться, пропорционален приложенному потенциалу. Каждый раз, когда заряд Q, который может быть сохранен, изменяется, течет ток I, пока заряд Q не будет отрегулирован. Заряд Q, который может быть сохранен, изменяется, если изменяется потенциал E. Это выражается в уравнении:

Уравнение 6.4

В определении C неявно показано, а в приведенном выше уравнении явно показано, что чем выше емкость C, тем больше будет протекать емкостной ток при изменении потенциала.

Эти идеи были получены при рассмотрении системы постоянного тока, но они могут быть перенесены в систему переменного тока. Последнее уравнение показывает, что изменение потенциала на более высоких частотах приведет к протеканию более высоких токов, что означает низкое сопротивление Z. Уменьшение частоты переменного напряжения приведет к увеличению Z. Это означает, что на очень высокой частоте конденсатор не влияет на Z, а на очень низких частотах Z стремится к бесконечности. Фазовый сдвиг Φ идеального конденсатора составляет 90 °, а полное сопротивление Z рассчитывается согласно

Уравнение 6.5

В результате график Боде показывает постоянную Φ, равную 90 °, и линейную кривую с отрицательным наклоном, а график Найквиста показывает прямую линию вдоль ординаты (см. Рисунок 6.4). Из этого примера ясно, что на графике Найквиста частота, с которой было записано значение, не видна.

Рисунок 6.4 EIS конденсатора на схематическом графике Боде и Найквиста

Конденсаторы легко образуются в электрохимическом эксперименте. Ионы перед электродом и электроны (или их недостаток) в электроде образуют конденсатор (двойной электрохимический слой), оказывающий огромное влияние на электрохимические измерения.

К сожалению, параллельные кабели, зажимы типа «крокодил» и другие электронные компоненты также могут образовывать конденсатор. Это происходит на высокой частоте и приводит к паразитной емкости. PalmSens4 нейтрализует влияние конденсаторов, образующихся между кабелями в кабеле ячейки и экраном кабеля ячейки, за счет использования активного экрана. Тем не менее, желательно, чтобы кабели не были параллельны на небольшом расстоянии друг от друга.

A Конденсатор и резистор можно комбинировать по-разному, с разными эффектами.Если соединение последовательное, которое напоминает идеальное покрытие, как будет обсуждаться позже, импеданс Z не может быть меньше R. Удар конденсатора уменьшается с увеличением частоты. Полученные графики Найквиста и Боде можно увидеть на рис. 6.5.

Рисунок 6.5 EIS последовательного резистора и конденсатора на схематической диаграмме Боде и Найквиста

Более интересный эффект наблюдается, когда резистор и конденсатор включены параллельно. Ток выбирает путь с наименьшим импедансом, независимо от того, переменный он или постоянный.Как уже говорилось, импеданс конденсатора зависит от частоты, что означает, что путь, по которому выбирается ток, изменится.

На высоких частотах сопротивление конденсатора будет очень низким, и большая часть тока будет проходить через конденсатор. С уменьшением частоты сопротивление конденсатора увеличивается, и большая часть тока проходит через резистор. Когда большая часть тока протекает через резистор, полное мнимое сопротивление Z ’’ будет падать по мере увеличения действительной части Z ’.

Эти процессы приводят на графике Найквиста к полукругу (см. Рис. 6.6). Обратите внимание, что график Найквиста представляет собой комплексную плоскость, и каждое значение представляет собой комплексное число, поэтому оси должны иметь одинаковый масштаб. В этом случае идеальный конденсатор, подключенный параллельно резистору, образует полукруг.

Рисунок 6.6 EIS параллельного резистора и конденсатора на схематическом графике Боде и Найквиста

Эта схема уже довольно близка к реальной системе. Конденсатор представляет собой двойной электрохимический слой C _dl, который может только накапливать заряд.Резистор представляет собой сопротивление передачи заряда R _ct. Это сопротивление электрона изменению фазы, например от электрода в раствор или, если быть более точным, до вещества, растворенного в растворе. Это происходит во время каждой электрохимической реакции.

Это два пути прохождения тока через поверхность раздела электрод-раствор. Весь ток должен проходить через раствор, который действует как омический резистор R _sol. Полученная схема представлена на рисунке 6.7 и называется упрощенной схемой Рэндлса.

Рисунок 6.7 Упрощенная схема Рэндлса

В результате EIS выглядит примерно так, как показано на рисунке 6.6. Он отличается только аналогично, так как рисунок 6.5 отличается от рисунка 6.4, плюс то, что фазовый сдвиг Φ будет иметь пик. Φ начнется с 0 °, затем увеличится до 90 ° и снова упадет до 0 °. Интерактивный EIS схемы Randles Circuit можно загрузить вместе с бесплатным Wolfram Alpha Player здесь. К сожалению, реальные живые примеры не так хороши, как идеальные компоненты, представленные в этой главе.В следующей главе будут рассмотрены модели для реальных измерений.

Однако схема Рэндлса также хорошо показывает, почему сюжет Найквиста так популярен. На высоких частотах C _dl близок к 0, и основной вклад вносит R _sol. Итак, начало полукруга — рэндов. На низких частотах C _dl имеет очень высокий импеданс, и весь ток проходит через R _ct. Таким образом, вклад импеданса в точке, где правый конец полукруга будет касаться 0 оси y, равен R _sol + R _et.Таким образом, R _sol и R _et можно легко оценить, просто взглянув на полукруг. Кроме того, C _dl можно рассчитать по частоте в наивысшей точке полукруга (максимум Z ’’) f _max с использованием уравнения 6.6.

Уравнение 6.6

Емкостное реактивное сопротивление — обзор

Символ реактивного сопротивления.

X _C

Символ емкостного реактивного сопротивления.

X _L

Символ индуктивного реактивного сопротивления.

Демодуляция X и Z

Система демодуляции цветного ТВ, в которой два повторно вставленных сигнала поднесущей 3,58 МГц отличаются примерно на 60 °, а не на обычные 90 °. Напряжения R-Y, B-Y и G-Y выводятся из демодулированных сигналов, и эти напряжения управляют тремя пушками кинескопа. Важным преимуществом этой системы является то, что схема приемника проще, чем требуется при I- и Q-демодуляции.

Ось X

1. Референтная ось в кристалле кварца. 2. Горизонтальная ось в системе прямоугольных координат. 3. Направление по горизонтали или слева направо в двумерной системе координат. X-X означает одно направление, в котором следует метод пошагового повторения.

Диапазон X

Радиочастотный диапазон от 5200 до 11000 МГц с длинами волн от 5,77 до 2,75 см.

X-образный стержень

Прямоугольный кристаллический стержень, обычно вырезанный из Z-образного сечения, вытянутый параллельно X и с краями, параллельными X, Y и Z.

X-конденсатор

Конденсатор для подавления радиопомех, предназначенный для приложений, в которых отказ конденсатора не приведет к опасности поражения электрическим током.

Х-образный кристалл

Кристалл, вырезанный так, что его основные поверхности перпендикулярны электрической оси (X) исходного кристалла кварца.

ксенон

Инертный газ, используемый в некоторых тиратронах и других газовых трубках.

ксеноновая импульсная лампа

Источник некогерентного белого света высокой интенсивности; он работает, разряжая конденсатор через трубку с газом ксеноном. Такое устройство часто используется в качестве источника излучения накачки для различных лазеров с оптическим возбуждением.

ксерографический принтер

Устройство для печати оптического изображения на бумаге; светлые и темные области представлены электростатически заряженными и незаряженными участками на бумаге.Порошковые чернила, присыпанные пылью на бумаге, прилипают к заряженным участкам и затем плавятся в бумаге под воздействием тепла.

ксерографическая запись

Запись, полученная с помощью ксерографии.

ксерография

1. Раздел электростатической электрофотографии, в котором изображения формируются на фотопроводящей изолирующей среде с помощью инфракрасного, видимого или ультрафиолетового излучения. Затем среду присыпают порошком, который прилипает только к электростатически заряженному изображению.Затем применяется тепло, чтобы сплавить порошок в постоянное изображение. 2. Процесс печати электростатической электрофотографии, в котором используется фотопроводящая изолирующая среда в сочетании с инфракрасным, видимым или ультрафиолетовым излучением для создания структур скрытого электростатического заряда для достижения наблюдаемой записи.

xeroprinting

Эта ветвь электростатической электрофотографии, в которой узор из изоляционного материала на проводящей среде используется для формирования структур электростатического заряда для использования при копировании.

ксерорадиография

Процесс печати электростатической электрофотографии, в котором используется светопроводящая изолирующая среда в сочетании с рентгеновскими или гамма-лучами для создания структур скрытого электростатического заряда для получения наблюдаемого рисунка.

ксерорадиографическое оборудование

Оборудование, использующее принципы электростатики и фотопроводимости для записи рентгеновских изображений на сенсибилизированную пластину через короткое время после экспонирования.

xfmr

Сокращенное обозначение трансформатора.

xistor

Сокращенное обозначение транзистора.

Разъем XLR

Экранированный трехжильный микрофонный штекер или розетка с фиксатором для разблокировки пальцем для предотвращения случайного извлечения. Стандартный разъем для профессиональных пользователей микрофонов.

xmitter

Сокращенное обозначение передатчика.Также сокращенно trans или xmtr.

xmsn

Сокращенное обозначение передачи.

xmtr

Аббревиатура передатчика. Также сокращенно транс или xmitter.

X-off

Передатчик выключен.

X-on

Датчик включен.

Х-частица

Частица, имеющая такой же отрицательный заряд, что и электрон, но масса между электроном и протоном.Он создается космическим излучением, падающим на молекулы газа или фактически составляющим часть космических лучей.

Рентгеновский аппарат

Рентгеновская трубка и принадлежности к ней, включая рентгеновский аппарат.

Рентгеновская кристаллография

1. Использование рентгеновских лучей для изучения расположения атомов в кристалле. 2. Изучение структуры кристаллических материалов с использованием взаимодействия рентгеновских лучей и электронной плотности кристалла (дифракции).

Устройство для обнаружения рентгеновских лучей

Устройство, обнаруживающее неоднородности поверхности и объема твердых тел с помощью рентгеновских лучей.

Камера для дифракции рентгеновских лучей

Камера, которая направляет пучок рентгеновских лучей на образец неизвестного материала и позволяет полученным дифрагированным лучам воздействовать на полосу пленки.

Картина дифракции рентгеновских лучей

Картина, полученная на пленке, экспонированной с помощью рентгеновской дифракционной камеры.Он состоит из частей кругов с разным расстоянием между ними в зависимости от исследуемого материала.

Рентгеновский гониометр

Прибор, который определяет положение электрических осей кристалла кварца путем отражения рентгеновских лучей от атомных плоскостей кристалла.

Рентгеновские лучи

Также называются рентгеновскими лучами. Проникающее излучение, подобное свету, но имеющее гораздо более короткие длины волн (от 10 ^–7 до 10 ^–10 см).Обычно они генерируются при бомбардировке металлической мишени потоком высокоскоростных электронов.

Рентгеновский спектрограф

Прибор, который используется для построения диаграмм дифракции рентгеновских лучей, такой как рентгеновский спектрометр с фотографическими или другими регистрирующими устройствами.

Рентгеновский спектрометр

1. Прибор для получения спектра рентгеновского излучения и измерения длин волн его компонентов. 2. Прибор, предназначенный для получения рентгеновского спектра материала для помощи в его идентификации.Этот метод особенно полезен, когда материал не может быть физически разрушен.

Спектр рентгеновского излучения

Расположение пучка рентгеновских лучей в порядке длины волны.

Рентгеновский толщиномер

Бесконтактный толщиномер, используемый для измерения и индикации толщины движущегося холоднокатаного стального листа в процессе прокатки. Рентгеновский луч, направленный через лист, поглощается пропорционально толщине материала и его атомному номеру, и измерение количества поглощения дает непрерывное указание толщины листа.

Рентгеновская трубка

Вакуумная трубка, в которой рентгеновские лучи производятся путем бомбардировки мишени высокоскоростными электронами, ускоренными электростатическим полем.

Мишень для рентгеновской трубки

Также известен как антикатод. Электрод или электродная секция, на которую фокусируется электронный луч и который излучает рентгеновские лучи.

xso

Аббревиатура для кварцевого стабилизатора.

xtal

Аббревиатура кристалла.

X-волна

Одна из двух составляющих, на которые магнитное поле Земли делит радиоволну в ионосфере. Другой компонент — обыкновенная, или О-, волна.

Кристалл XY-огранки

Кристалл, ограненный таким образом, что его характеристики находятся между кристаллами X- и Y-огранки.

XY плоттер

1.Устройство, используемое вместе с компьютером для построения координатных точек в виде графика. 2. Компьютерное устройство вывода, которое реагирует на цифровые сигналы предварительно записанных и / или обработанных данных путем распечатки линейных сегментов. Эти данные, которые могут включать буквенно-цифровые символы, диаграммы, таблицы или рисунки, загружаются из памяти компьютера со скоростью, достаточной для работы плоттера. XY-плоттер нельзя использовать для прямой записи аналоговых сигналов без дигитайзеров.

Регистратор XY

1.Регистратор, который отслеживает на диаграмме отношения между двумя переменными, ни одна из которых не является временем. Иногда диаграмма перемещается, и одна из переменных контролируется так, что взаимосвязь увеличивается пропорционально времени. 2. Регистратор, в котором два сигнала одновременно записываются одним пером, которое приводится в движение в одном направлении (ось X) одним сигналом, а в другом направлении (ось Y) — вторым сигналом. 3. Регистратор данных, который используется для записи изменения одного параметра по отношению к другому.Например, изменение давления в зависимости от температуры. Для этих записывающих устройств доступен широкий спектр преобразователей для преобразования физических параметров в электрические сигналы, используемые в самописце. Датчики давления, термопары, тензодатчики и акселерометры — вот несколько примеров. 4. Тип регистратора, который реагирует на поступающие аналоговые сигналы по мере их появления. Сигналы печатаются на графике заранее определенного размера, который может охватывать тестовые периоды от нескольких секунд до целого года. XY-рекордер записывает непрерывные линии.Кроме того, скорость отклика прибора важна для точности записи.

Переключатель XY

Переключатель с дистанционным управлением, расположенный так, что дворники перемещаются вперед и назад по горизонтали.

Повышение точности моделирования при использовании пассивных компонентов

Лучшая модель IC может повысить точность моделирования PSpice, но другие компоненты, такие как пассивные компоненты, могут влиять на точность моделирования так же, как и модели IC.В этом примечании к применению будут рассмотрены различные примеры для описания влияния частоты и температуры на поведение выбранных общих пассивных компонентов.

Частотные эффекты

В этом разделе рассматривается влияние частоты на поведение следующих выбранных моделей:

Модели резисторов
Керамический конденсатор модели
Другие общие компоненты

Модели резисторов

Резистор, который работает просто, может изменить свое поведение по отношению к рабочей частоте в цепи постоянного тока.В зависимости от своего значения и частоты срабатывания резистор может вести себя резистивным, емкостным или индуктивным образом.

Рисунок 1: Схема модели резистора

На рисунке 1 вы можете видеть, что три основных элемента связаны со стандартным углеродным или металлическим пленочным резистором мощностью 0,25 Вт. Первый — это сам резистор, второй и третий — два основных паразитных элемента, которые входят в состав каждого резистора.Один — паразитный конденсатор, образованный поперек резистора; этот конденсатор снижает сопротивление резистора на высокой частоте. Другой — паразитная свинцовая индуктивность; эта индуктивность увеличивает сопротивление с увеличением частоты.

Небольшой резистор не показывает большой емкости шунта, но его полное сопротивление увеличивается с частотой из-за последовательной индуктивности. В случае больших резисторов емкость снижает импеданс при увеличении частоты, в то время как индуктивность незначительна.

Рисунок 2: Импеданс в зависимости от частоты

На рисунке 2 показан график зависимости полного сопротивления от частоты для нескольких номиналов резистора. Этот график ясно показывает, что значение сопротивления оказывает огромное влияние на поведение резистора на более высоких частотах.

Керамический конденсатор модели

Многослойные керамические конденсаторы имеют почти те же паразитные элементы, что и резистор, но немного изменены.На рис. 3 показано поведение частотно-зависимой модели для керамического конденсатора с основными выводами, где показано зависимость импеданса от частоты для нескольких типичных значений компонентов. Эквивалентное последовательное сопротивление (ESR) ограничивает добротность конденсатора; паразитная индуктивность и значение емкости задают частоту собственного резонанса.

Рисунок 3: Поведение модели керамического конденсатора

Все конденсаторы самостоятельно резонируют на некоторой частоте, после чего сопротивление начинает индуктивно расти.

Другие общие компоненты

Резисторы и конденсаторы — это только часть проблемы при точном моделировании PSpice. Проводники (дорожки на печатной плате и провода) и катушки индуктивности также отклоняются от идеальных при увеличении частоты.

Проводники

Проводник, который выглядит как небольшой резистор при постоянном токе, имеет увеличивающийся импеданс с частотой, которая зависит от физических размеров проводника.Его индуктивность можно приблизительно измерить с помощью катушки индуктивности примерно 20 нГн на дюйм длины, включенной последовательно с сопротивлением постоянному току. Таким образом, проводник выглядит индуктивным на частотах от 10 кГц до длины, составляющей примерно четверть длины волны. На большей длине проводник подвергается многополюсным и нулевым резонансам, как антенна. Частоту, при которой проводник перестает выглядеть индуктивным и начинает действовать как антенна, можно найти по формуле

F = 2850 / л

, где L — четверть длины волны в дюймах, а F — в МГц.Таким образом, проводник длиной 10 дюймов будет вести себя как антенна при частоте 285 МГц или выше. Большинство дорожек на печатной плате недостаточно длинные, чтобы действовать как антенны, но ленточные кабели могут быть такими. На печатных платах с контролируемым импедансом следы выглядят как линии передачи.

Даже плоскости питания и заземления, используемые в конструкции печатной платы, не избегают частотных эффектов. Импеданс заземляющего слоя не выглядит индуктивным на более высоких частотах; выглядит с потерями . На более высоких частотах скин-эффект плоскости начинает преобладать и увеличивает импеданс плоскостей.Скин-эффект пропорционален квадратному корню из частоты, поэтому он не нарастает так быстро, как у провода, который ведет себя индуктивно.

Катушки индуктивности

Индукторы сильно различаются по форме и размеру в зависимости от конкретной работы, которую они должны выполнять. Силовые индукторы, подобные тем, которые используются в выходных фильтрах импульсных источников питания, обычно представляют собой большие конструкции, которые могут саморезонировать на частотах от 500 кГц до 75 МГц. Эти силовые индукторы иногда проектируются с учетом низких потерь, поэтому они могут иметь большую добротность при резонансе.Высокая добротность вызывает довольно узкий резкий резонанс. Выше резонансной частоты преобладает шунтирующая емкость индуктора. Шунтирующая емкость обычно велика для индуктора большой мощности из-за емкостной связи между множеством используемых витков. При моделировании силовых индукторов резонансная частота зависит от размера сердечника. Как правило, чем больше размер сердечника, тем ниже собственная резонансная частота.

Ферритовые шарики, используемые для контроля электромагнитных помех, находятся на другом конце спектра.Бусины предназначены для работы с потерями и имеют очень низкие значения добротности при относительно низкой индуктивности. Пик собственного резонанса низкий и очень широкий, простирающийся на несколько октав частоты. Лучше всего моделировать шарики в виде индуктора с небольшим шунтирующим сопротивлением порядка 50-100 Ом и низкой шунтирующей емкостью 1-5 пФ или меньше.

Температурные эффекты

Окружающий

Значения пассивных компонентов могут подвергаться температурным воздействиям, которые зависят от рабочей температуры цепи.Чтобы учесть эти эффекты при моделировании, каждому соответствующему компоненту необходим оператор .MODEL, определяющий, как значение конкретного компонента изменяется в зависимости от температуры. Встроенные модели PSpice для резисторов, конденсаторов и катушек индуктивности имеют два члена температурного воздействия: линейный и квадратичный. Эти условия могут соответствовать фактическим температурным характеристикам компонента.

Резисторы — не единственные компоненты, подверженные температурным воздействиям; большинство конденсаторов, особенно керамических, имеют очень четкие температурные кривые в зависимости от диэлектрика, используемого в их конструкции.Однако односклонной температурной кривой недостаточно для моделирования наиболее распространенных типов конденсаторов, используемых в аналоговых схемах. Следовательно, как линейный, так и квадратичный температурные коэффициенты должны быть указаны в их операторах PSpice .MODEL, например,

.MODEL X7R CAP (C = 1, TC1 = 5.75E-5, TC2 = -1.285E-5)
.MODEL Z5U CAP (C = 1, TC1 = 2.38E-3, TC2 = -1.48E -4)

Примечание: Резисторы имеют дополнительный экспоненциальный температурный коэффициент, который можно использовать вместо линейных и квадратичных коэффициентов.

По компоненту

В PSpice пассивные компоненты также могут быть охарактеризованы для температурных эффектов, которые отменяют рабочую температуру схемы и температуру TNOM , при которой параметры модели считаются измеренными. Температурные режимы отдельных устройств можно настроить, указав параметр T_ABS, T_REL_GLOBAL или T_REL_LOCAL в операторе .MODEL. Новую температуру измерения также можно определить, задав параметр модели T_MEASURED .

Вы смоделируете схему, показанную на рисунке 4, чтобы понять влияние температуры на пассивные компоненты.

Рисунок 4: Схема для понимания температурного воздействия на пассивные компоненты

Предположим, что множитель сопротивления резистора равен единице при измерении при 0 ^ο C. Чтобы обозначить это, T_MEASURED может быть указано в соответствующем операторе .MODEL резистора как

.МОДЕЛЬ RMOD RES (R = 1, TC1 = 0,0001, T_MEASURED = 0)

Когда цепь работает при 0 ^ο C, R оценивается как 1. При 100 ^ο C, R оценивается как 1,01, что является множителем сопротивления (R = 1) плюс влияние рабочей температуры первого порядка (TC1 * (TEMPT_ MEASURED)).

T_ABS позволяет указать абсолютную температуру устройства. Если T_ABS задано как T_ABS = 25 , модель поддерживается на уровне 25 ^ο C независимо от рабочей температуры контура.Добавление T_ABS = 25 к определению модели приводит к тому, что R всегда будет оценивать значение 1,0025, даже если рабочая температура изменяется в рамках параметрического анализа или анализа с разверткой постоянного тока.

T_REL_GLOBAL используется для указания температуры устройства, которая связана с рабочей температурой цепи. Например, силовой резистор может рассеивать мощность и быть теплее окружающей среды на 10 ^ο C. Это может быть указано в заявлении .MODEL как

.МОДЕЛЬ Rbreak RES (R = 1, TC1 = 0,001, T_REL_GLOBAL = 10)

T_REL_LOCAL используется в инструкции AKO («своего рода») .MODEL . Модель AKO ссылается на существующую модель, таким образом наследуя определения параметров существующей модели. Значения параметров можно переопределить или добавить, указав их в операторе AKO .MODEL . Используя этот метод, температура устройства, определенная в новой модели, может быть рассчитана относительно абсолютной температуры устройства, указанной в базовой модели.Базовая модель должна определять абсолютную температуру устройства с помощью параметра T_ABS . Модель AKO должна определять относительное изменение температуры T_ABS с помощью параметра T_REL_LOCAL .

Например, модель RMOD, , температура устройства которой на 117 ^ο C выше, чем указанная в заявлении модели RBASE , может быть определена как

* Базовая модель
.МОДЕЛЬ RBASE RES (R = 1, TC1 = 0.001, T_ABS = 10)
* AKO Модель
.МОДЕЛЬ RMOD AKO: RBASE RES (T_REL_LOCAL = 117)

RBASE устанавливает абсолютную температуру резистора на 10 ^ο C. RMOD оценивает как 127 ^ο C.

Результаты моделирования PSpice схемы, которая имеет пассивные компоненты с операторами .MODEL, можно увидеть на рисунке 5.

Рисунок 5: Результаты моделирования пассивных компонентов с.Заявления MODEL

© Copyright 2016 Cadence Design Systems, Inc. Все права защищены. Cadence, логотип Cadence и Spectre являются зарегистрированными товарными знаками Cadence Design Systems, Inc. Все остальные являются собственностью соответствующих владельцев.

Как извлечь паразитные значения из таблицы данных конденсатора

В предыдущей статье «Улучшение результатов тестирования ЭМС с помощью реалистичного моделирования фильтров ЭМП» мы обсуждали важность включения паразитных элементов в модели анализа ЭМП.Здесь мы покажем вам, как извлечь эти паразитные значения из таблицы компонентов, используя в качестве примера конденсатор

Это действительно очень просто.

Модель конденсатора

Реальные конденсаторы имеют индуктивность и сопротивление последовательно с емкостью и индуктивность рассеяния параллельно. Значения эквивалентной последовательной индуктивности (ESL), эквивалентного последовательного сопротивления (ESR) и сопротивления утечки зависят от типа, номинала и размера конденсатора.

Когда емкостное и индуктивное сопротивление равны, конденсатор саморезонирует.На частотах ниже его собственной резонансной частоты преобладает емкость, и сопротивление реального конденсатора уменьшается с увеличением частоты. Выше собственной резонансной частоты преобладает ESL, и импеданс увеличивается. На собственной резонансной частоте импеданс равен ESR.

Лист данных Импеданс

Большинство технических паспортов конденсаторов содержат график зависимости полного сопротивления конденсатора от частоты. Часто сопротивление конденсаторов разной величины отображается на одном графике.

В таблице и графике ниже из таблицы данных по многослойной керамике AVX показаны свойства конденсаторов и импеданс для конденсаторов в диапазоне значений от 2,2 нФ до 47 нФ.

Извлечение элементов

Выделим значения элементов конденсатора 10 нФ.

Емкость

Это просто. Это 10 нФ, красная линия на графике выше.

Ниже 100 МГц полное сопротивление конденсатора определяется в первую очередь значением емкости.Остальные паразитические элементы мало влияют.

ESL — эквивалентная последовательная индуктивность

Выше 300 МГц импеданс конденсатора определяется его ESL. Извлечь ESL очень просто. Из прямой части графика над собственной резонансной частотой мы можем оценить, что полное сопротивление составляет 1,5 мОм на частоте 3 ГГц. ESL определяется следующим уравнением.

ESR — эквивалентное последовательное сопротивление

На собственной резонансной частоте конденсатора, нижней точке его кривой импеданса, его импеданс равен его ESR.Для конденсатора 10 нФ минимальный импеданс составляет около 200 МГц, где его значение составляет 60 мОм. Таким образом, СОЭ составляет 60 мОм.

Сопротивление утечке

Устойчивость к утечкам обычно указывается в технических характеристиках. Здесь оно указано как сопротивление изоляции, 1000 МОм.

Проверить результаты

EMI Analyst имеет встроенные модели для реальных компонентов. Модель конденсатора показана ниже.

Используя полученные выше значения, график импеданса конденсатора хорошо согласуется с таблицей данных, подтверждая правильность паразитных элементов, извлеченных из таблицы.

Улучшенный анализ ЭМС

Использование реалистичной модели конденсатора повышает точность анализа ЭМС, не только расчетов фильтра электромагнитных помех, но также расчетов выбросов и восприимчивости, когда конденсатор является частью цепи.

Для получения дополнительной информации ознакомьтесь со следующими полезными ссылками:

Улучшение результатов испытаний на ЭМС с помощью реалистичного моделирования фильтра ЭМП
Вносимые потери в фильтре ЭМП: как сопротивление цепи влияет на характеристики фильтра ЭМП
Анализ ЭМС: как рассчитать вносимые потери в фильтре
http: // www.avx.com/docs/techinfo/CeramicCapacitors/parasitc.pdf

Лаборатория 4 — Зарядка и разрядка конденсатора

Введение

Конденсаторы — это устройства, которые могут накапливать электрический заряд и энергию. Конденсаторы имеют несколько применений, например, в качестве фильтров в источниках питания постоянного тока и в качестве аккумуляторов энергии для импульсных лазеров. Конденсаторы пропускают переменный ток, но не постоянный, поэтому они используются для блокировки постоянной составляющей сигнала, чтобы можно было измерить переменную составляющую.Физика плазмы использует способность конденсаторов накапливать энергию. В физике плазмы часто требуются короткие импульсы энергии при чрезвычайно высоких напряжениях и токах. Конденсатор можно медленно заряжать до необходимого напряжения, а затем быстро разряжать для обеспечения необходимой энергии. Можно даже зарядить несколько конденсаторов до определенного напряжения, а затем разрядить их таким образом, чтобы получить от системы большее напряжение (но не больше энергии), чем было вложено. В этом эксперименте используется схема RC , которая является одной из простейших схем, в которой используется конденсатор.Вы изучите эту схему и способы изменения ее эффективной емкости, комбинируя конденсаторы последовательно и параллельно.

Обсуждение принципов

Конденсатор состоит из двух проводов, разделенных небольшим расстоянием. Когда проводники подключены к зарядному устройству (например, к батарее), заряд передается от одного проводника к другому до тех пор, пока разность потенциалов между проводниками из-за их равного, но противоположного заряда не станет равной разности потенциалов между клеммами. зарядного устройства.Количество заряда, накопленного на любом проводнике, прямо пропорционально напряжению, а константа пропорциональности известна как емкость . Это записывается алгебраически как Заряд C измеряется в единицах кулонов (C), напряжение

ΔV

в вольт (В) и емкость C в единицах фарад (F). Конденсаторы — физические устройства; Емкость является собственностью устройства.

Зарядка и разрядка

В простой RC-цепи резистор и конденсатор соединены последовательно с батареей и переключателем. См. Рис.1.

Рисунок 1 : Простая RC-цепь

Когда переключатель находится в положении 1, как показано на рис. 1 (а), заряд на проводниках через некоторое время достигает максимального значения. Когда переключатель переведен в положение 2, как показано на рис. 1 (b), аккумулятор больше не является частью цепи и, следовательно, заряд конденсатора не может быть восполнен.В результате конденсатор разряжается через резистор. Если мы хотим исследовать зарядку и разрядку конденсатора, нас интересует, что происходит сразу, после того, как переключатель перемещается в положение 1 или положение 2, а не дальнейшее поведение схемы в ее установившемся состоянии. Для схемы, показанной на рис. 1 (а), уравнение петли Кирхгофа можно записать как Решение уравнения. (2) — это

(3)

Q = Q _f

1 — e ^{(−t / RC)}

где

Q _f

представляет собой окончательный заряд на конденсаторе, который накапливается через бесконечный промежуток времени, R — сопротивление цепи, а C — емкость конденсатора.Из этого выражения вы можете видеть, что заряд растет экспоненциально во время процесса зарядки. См. Рис. 2 (а). Когда переключатель перемещается в положение 2, для схемы, показанной на рис. 1 (b), уравнение петли Кирхгофа теперь имеет вид Решение уравнения. (4) является

(5)

Q = Q ₀ e ^{(−t / RC)}

где

Q ₀

представляет начальный заряд на конденсаторе в начале разряда, то есть при

t = 0.

Из этого выражения видно, что заряд экспоненциально спадает при разряде конденсатора и что для полной разрядки требуется бесконечное количество времени. См. Рис. 2 (b).

Рисунок 2 : График изменения во времени

Постоянная времени

τ Произведение

(имеющее единицы времени) имеет особое значение; это называется постоянной времени цепи. Постоянная времени — это время, необходимое для повышения заряда зарядного конденсатора до 63% от его конечного значения.Другими словами, когда

t = RC,

(6)

Q = Q _f

1 — e ⁻¹

а также

(7)

1 — e ⁻¹ = 0,632.

Другой способ описать постоянную времени — сказать, что это количество секунд, необходимое для того, чтобы заряд на разряжающемся конденсаторе упал до 36,8%

(e ^-1 = 0,368)

от своего начального значения.Мы можем использовать определение

(I = dQ / dt)

тока через резистор и уравнение. (3) Q = Q _f

1 — e ^{(−t / RC)}

и уравнение. (5)

Q = Q ₀ e ^{(−t / RC)}

, чтобы получить выражение для тока во время процессов зарядки и разрядки.

(8)

зарядка: I = + I ₀ e ^{−t / RC}

(9)

разгрузка: I = −I ₀ e ^{−t / RC}

где в формуле.(8)

зарядка: I = + I ₀ e ^{−t / RC}

и уравнение. (9)

разряд: I = −I ₀ e ^{−t / RC}

— максимальный ток в цепи в момент времени t = 0. Тогда разность потенциалов на резисторе будет выражена следующим образом.

(10)

зарядка: ΔV = + ΔV _f e ^{−t / RC}

(11)

нагнетание: ΔV = — ΔV ₀ e ^{−t / RC}

Обратите внимание, что во время процесса разрядки ток будет течь через резистор в обратном направлении.Следовательно, I и

ΔV

в уравнении. (9)

разряд: I = −I ₀ e ^{−t / RC}

и уравнение. (11)

разряд: ΔV = — ΔV ₀ e ^{−t / RC}

отрицательны. Это напряжение как функция времени показано на рис.3.

Рисунок 3 : Напряжение на резисторе как функция времени

Полезно описывать зарядку и разрядку в терминах разности потенциалов между проводниками (т.е.е., «напряжение на конденсаторе»), поскольку напряжение на конденсаторе можно измерить непосредственно в лаборатории. Используя соотношение

Q = C ΔV,

Eq. (3) Q = Q _f

1 — e ^{(−t / RC)}

и уравнение. (5)

Q = Q ₀ e ^{(−t / RC)}

, которые описывают зарядку и разрядку конденсатора, можно переписать в терминах напряжения. Просто разделите оба уравнения на

, и отношения станут следующими.

(12)

зарядка: ΔV = ΔV _f

1 — e ^{(−t / RC)}

(13)

нагнетание: ΔV = ΔV ₀ e ^{(−t / RC)}

Обратите внимание, что эти два уравнения похожи по форме на формулу. (3) Q = Q _f

1 — e ^{(−t / RC)}

и уравнение. 5

Q = Q ₀ e ^{(−t / RC)}

.График зависимости напряжения на конденсаторе от времени показан на рисунке 4 ниже.

Рисунок 4 : Напряжение на конденсаторе как функция времени

Переставив уравнение. (12) зарядка: ΔV = ΔV _f

1 — e ^{(−t / RC)}

получаем Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить

(15)

−ln

График зависимости

−ln ((ΔV _f — ΔV) / ΔV _f)

от времени даст прямолинейный график с наклоном 1/ RC . Точно так же для процесса разряда уравнение. 13

разрядка: ΔV = ΔV ₀ e ^{(−t / RC)}

можно переписать, чтобы получить Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить

(17)

−ln

График зависимости

−ln (ΔV) / ΔV ₀)

от времени даст прямолинейный график с наклоном 1/ RC .

Использование прямоугольной волны для имитации роли переключателя

В этом эксперименте вместо переключателя мы будем использовать генератор сигналов, который может генерировать периодические волновые формы различной формы, такие как синусоидальная волна, треугольная волна и прямоугольная волна. Также можно регулировать как частоту, так и амплитуду формы волны. Здесь мы будем использовать генератор сигналов для создания изменяющегося во времени напряжения прямоугольной формы на конденсаторе, аналогичного показанному на рис.5.

Рисунок 5 : Прямоугольная волна с периодом Τ

Выходное напряжение генератора сигналов изменяется назад и вперед от постоянного положительного значения до постоянного нуля вольт через равные интервалы времени t . Время

T = 2t

— это период прямоугольной волны. В течение первой половины цикла, когда напряжение положительное, это похоже на то, что переключатель находится в положении 1. Во второй половине цикла, когда напряжение равно нулю, это то же самое, что переключатель находится в положении 2. .Таким образом, прямоугольная волна, представляющая собой напряжение постоянного тока, которое периодически включается и выключается, служит одновременно аккумулятором и переключателем в схеме, показанной на рис.1. Генератор сигналов позволяет выполнять это переключение многократно, и можно оптимизировать сбор данных, регулируя частоту повторения. Эта частота будет зависеть от постоянной времени RC-цепи. Когда время t больше постоянной времени τ RC-цепи, у конденсатора будет достаточно времени для зарядки и разрядки, и напряжение на конденсаторе будет таким, как показано на рис.4.

Объектив

В этом эксперименте (смоделированный компьютером) осциллограф будет использоваться для отслеживания разности потенциалов и, таким образом, косвенно, заряда конденсатора. Измерения напряжения будут использоваться двумя разными способами для вычисления постоянной времени цепи. Наконец, конденсаторы будут подключены параллельно, чтобы проверить их эквивалентную емкость цепи.

Оборудование

Печатная плата PASCO
Сигнальный интерфейс с выходной мощностью
Соединительные провода
Программное обеспечение Capstone

Процедура

Распечатайте лист для этой лабораторной работы.Этот лист понадобится вам для записи ваших данных.

Настройка RC-цепи

Печатная плата RLC, которую вы будете использовать, среди других элементов состоит из трех резисторов и двух конденсаторов. См. Рис. 6 ниже. Теоретически вы можете использовать разные комбинации резисторов и конденсаторов. В этом эксперименте вы будете использовать резисторы 33 и 100 Ом и два конденсатора.

Рисунок 6 : Печатная плата RLC

Подключите крайнюю правую выходную клемму сигнального интерфейса к резистору 33 Ом в точке 2.

Чтобы обойти индуктор, подключите провод от точки 8 к точке 9.

Подключите точку 6 ко второй выходной клемме сигнального интерфейса, чтобы замкнуть цепь.

Подключите пробник напряжения к аналоговому каналу A.

Чтобы измерить напряжение на конденсаторе, подключите черный провод датчика напряжения к точке 6, а красный провод — к точке 9. Убедитесь, что земля интерфейса (вывод «-») подключена к той же стороне конденсатора, что и земля генератора сигналов (выход мощности).Подключение вашей схемы должно выглядеть так, как показано на рис.7.

Рисунок 7 : Принципиальная схема

Контрольная точка 1:
Попросите своего технического специалиста проверить соединения вашей цепи.

Процедура A: Постоянная времени контура

В этом эксперименте мы будем использовать компьютер для эмуляции осциллографа.

Откройте файл Capstone, связанный с этой лабораторной работой.Отобразится экран, аналогичный показанному на рис. 8.

Рисунок 8 : Начальный экран файла Capstone

Настройте генератор сигналов на создание положительной прямоугольной волны, выбрав положительную прямоугольную волну в окне генератора сигналов, как показано на рисунке 9 ниже.

Рисунок 9 : Окно генератора сигналов

Если это еще не было установлено при открытии файла Capstone, настройте генератор сигналов на создание прямоугольной волны амплитудой 5 В с частотой 20 Гц и установите смещение напряжения на 5 В.

Включите генератор сигналов, щелкнув ON в окне генератора сигналов.

Чтобы контролировать сигнал, нажмите кнопку START в главном окне. Потребуется отрегулировать шкалы времени и напряжения, чтобы получить кривую сигнала, подобную показанной на рис. 10. Это позволит вам наблюдать, как напряжение на конденсаторе изменяется как функция времени. Для этого установите курсор на любое значение вдоль оси, которую вы хотите увеличить, и переместите курсор влево-вправо или вверх-вниз по мере необходимости.При правильном увеличении у вас будет только одна длина волны на графике, как на кривой на рис.10.

Рисунок 10 : Трасса сигнала

Если в любой момент вы захотите удалить записанный набор данных, нажмите кнопку Удалить последний прогон под графиком.

Нажмите кнопку Показать координаты из кнопок над графиком. См. Рис.11.

Рисунок 11 : Показать координаты

Когда активна функция отображения координат, показания напряжения и времени отображаются, куда бы вы их ни перетащили, как на рис.11. Используя этот инструмент, определите и запишите время начала (то есть, когда кривая начиналась от 0 вольт) на рабочем листе.

Вычислите 63,2% максимального напряжения,

ΔV _f,

(которое должно быть 5 В), настройку амплитуды генератора сигналов. Используя Показать координаты , определите и запишите время начала (то есть, когда кривая начиналась вверх с 0 вольт) на рабочем листе.

Из этих двух значений времени определите и запишите время, необходимое для перехода сигнала от Δ V = 0 до Δ V = 0.632

ΔV _f.

Это ваше экспериментальное значение для RC .

В рабочем листе введите принятые значения сопротивления и емкости, которые напечатаны на печатной плате.

Вычислите экспериментальное значение емкости, используя свое экспериментальное значение для RC и принятое значение R . Запишите это на листе.

Вычислите ошибку в процентах, используя два значения емкости.См. Приложение Б.

Контрольная точка 2:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.

Процедура B: Расчет емкости графическими методами

Запишите максимальное напряжение на листе.

Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, когда Δ V = 1, 2, 3 и 4 вольта на восходящей части кривой.Запишите эту информацию в Таблицу данных 1 на рабочем листе. Примечание : Возможно, вам придется сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента.

Выполните необходимые вычисления, чтобы заполнить Таблицу данных 1.

Используя Excel, постройте график

−ln ((ΔV _f — ΔV) / ΔV _f)

в зависимости от времени. См. Приложение G.

Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.См. Приложение H.

По значению крутизны определите постоянную времени и емкость. Запишите эти значения на листе.

Вычислите ошибку в процентах между этим значением емкости и принятым значением.

Контрольная точка 3:
Попросите своего технического специалиста проверить ваши данные, график и расчеты, прежде чем продолжить.

Процедура C: Измерение эффективной емкости

Емкость увеличивается непосредственно при параллельном подключении конденсаторов и в обратном порядке при последовательном подключении.Это противоположно правилу для резисторов. Для конденсаторов, подключенных параллельно, эффективная емкость определяется выражением

(18)

C _eff = C ₁ + C ₂ + C ₃ +. . .

а для конденсаторов, включенных последовательно, эффективная емкость равна

Подключите второй конденсатор (330 мк Ф) параллельно конденсатору, используемому в процедуре A, подключив провод от точки 6 к точке 7.

Переключите резистор на резистор 10 Ом, переместив соединение из точки 2 в точку 1.

Запишите другой набор данных, щелкнув START в главном окне. После того, как вы записали второй набор данных, вы можете захотеть отобразить только эти данные на графике и удалить набор данных 1. Для этого удалите первый прогон (см. Примечание к шагу 10). На графике вы будете видеть только одну длину волны.

В этой части эксперимента вы будете рассматривать разрядную часть кривой. Теперь начальное напряжение

ΔV ₀

будет наивысшим значением пика перед тем, как график начнет спадать.Запишите это значение на листе.

Из записанных данных с помощью интеллектуального инструмента найдите моменты времени, когда Δ V = 1, 2, 3 и 4 вольта на спадающей части кривой. ( Примечание : вам может потребоваться сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента). Запишите эту информацию в Таблицу данных 2 на рабочем листе.

Выполните необходимые вычисления, чтобы заполнить Таблицу данных 2.

Используя Excel, постройте график зависимости

−ln (ΔV) / ΔV ₀)

от времени.

Используйте параметр линии тренда в Excel, чтобы нарисовать линию, наиболее подходящую для ваших данных, определить наклон линии и записать это значение на листе.

По значению наклона определите постоянную времени и запишите это значение в рабочий лист.

Вычислите

C _eff,

эффективную емкость параллельной комбинации, используя принятое значение для R .

Сравните это экспериментальное значение с тем, что вы получили из уравнения.18

C _eff = C ₁ + C ₂ + C ₃ +. . .

и принятые значения емкости путем вычисления ошибки в процентах между двумя значениями.

Контрольная точка 4:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.

RF Modeler — CDE

Cornell Dubilier RF Mica Modeler

Перейти к CDE RF Mica Modeler

Новинка! Корнелл Дубильер RF Mica Modeler

Обзор

Программа RF Mica Modeler

Cornell Dubilier представляет собой интерактивную консоль, которая помогает инженеру-электрику выбрать лучший слюдяной конденсатор в диапазоне емкости 0.От 5 до 91 000 пФ и диапазон напряжений от 100 до 4 000 вольт для приложений в диапазоне частот от 1 кГц до 4 ГГц.

Выбор конденсатора

Составитель моделей приводит оценки высокочастотных электрических характеристик для трех основных классов слюдяных конденсаторов, установленных на нашей печатной плате: (1) слюдяные конденсаторы с выводами, используемые в конструкциях печатных плат со сквозными отверстиями, (2) слюда / PTFE в металлическом корпусе для поверхностного монтажа конденсаторы типа MIN02 (квадрат 5 мм) и MCM01 (10 мм × 12 мм) для работы с большими токами и высокой мощностью, и (3) конденсаторы для слюдяных кристаллов SMT типоразмеров 0805, 1210, 1812, 2220 и 3838.

После выбора одного из трех вышеупомянутых стилей упаковки в раскрывающемся списке «Стиль упаковки» в поле выбора «Номер детали CDE» предоставляется полный список стандартных каталожных номеров деталей в порядке увеличения емкости. Как только номер детали выбран, отображается контурный чертеж и отображаются физические размеры.

Подключение к испытательной цепи S-параметров: последовательное / шунтирующее управление

S-параметры могут быть смоделированы для конденсатора, установленного на линии передачи испытательной схемы, в последовательной или параллельной конфигурации, как выбирается в раскрывающемся списке в нижнем левом углу средства моделирования.Для графиков S-параметров параметры рассеяния конденсатора нанесены на график, извлеченные из выводов конденсатора в виде двух опорных плоскостей, максимально приближенных к местам, в которых выводы конденсатора обычно припаиваются к дорожкам на печатной плате на отрезке передачи. линия с волновым сопротивлением 50 Ом. При конфигурации в качестве испытательной схемы для конденсатора такая линия будет управляться от первого порта на одном конце линии от источника синусоидальной энергии с чисто резистивным сопротивлением источника 50 Ом, с конденсатором, установленным в физическом центре линия.Другой, невозбужденный конец линии — это второй тестовый порт, который имеет чисто резистивное сопротивление нагрузки 50 Ом для предотвращения отражений. Конденсатор на такой линии передачи может быть установлен последовательно с одним прерывистым проводом на линии, известный как последовательное соединение, или он может быть установлен поперек линии, что будет шунтирующим соединением. В обеих схемах подключения, поскольку предполагается, что конденсатор установлен симметрично и на равном расстоянии от двух портов (известная как «взаимная» схема монтажа), S21 точно равен S12, а S11 точно равен S22.

Индуктивность цепи (нГн): регулятор индуктивности

Если имеется дополнительная индуктивность цепи последовательно с подключением конденсатора, такая как дополнительный вывод или длина трассы, которую вы хотите включить в модель для конденсатора, вы включаете ее влияние на отображаемые и смоделированные параметрические кривые с помощью параметра «Индуктивность цепи. »Ползунок. Эта дополнительная индуктивность добавляется к внутренней индуктивности конденсатора (ESL) и влияет на резонансную частоту, а также на графики импеданса и S-параметров.Это также влияет на выходные файлы, если они сгенерированы (обсуждается ниже в разделе «Создание выходных данных модели»), и это значение индуктивности — если оно не равно нулю — указано в поле заголовка выходного файла для целей документации. Это не влияет на график максимального среднеквадратичного тока.

Ползунок радиатора Theta

Только для металлического корпуса мы предоставляем ползунок непосредственно над таблицей номинальных значений тока, чтобы можно было указать значение теплового сопротивления радиатора окружающей среде, поскольку эти конденсаторы предназначены для присоединения к радиатору или пайки к нему. медный теплораспределитель.Это обсуждается в следующем разделе диаграмм, которые строит разработчик моделей.

Интерактивные диаграммы

Разработчик модели создает шесть диаграмм для выбранного конденсатора. Точную частоту и значение параметра можно увидеть, наведя указатель мыши на кривую. Когда две или более кривых находятся в непосредственной близости от интересующей точки, обратите внимание, что прямоугольная рамка вокруг отображаемых координат принимает цвет легенды серии, на которую вы указываете.

В левом столбце на верхнем графике представлена расчетная типичная зависимость емкости от частоты для трех температур. Номинальная емкость при соответствующей испытательной частоте используется в качестве значения базовой емкости; очевидно, что допуск устройства применим к реальным конденсаторам. Температурный и частотный коэффициенты, принятые разработчиком модели, являются типичными значениями, но не гарантируются.

Под диаграммой емкости показаны типичная величина импеданса и последовательное сопротивление.На резонансной частоте устройства вершина кривой фактической величины импеданса всегда будет касаться кривой ESR. Обратите внимание, что из-за ограниченного числа точек данных на графике разработчика моделей для таких конденсаторов с высокой добротностью, как слюда, этот контакт иногда не может быть точно определен на диаграмме импеданса и ESR.

На нижнем левом графике изображена добротность конденсатора, которая представляет собой отношение реактивного сопротивления к сопротивлению. Q — это мультипликативная величина, обратная D, коэффициенту рассеяния, который можно визуализировать из логарифмической диаграммы Q, мысленно отразив ее относительно горизонтальной линии со значением ординаты Q = D = 1.

В правом столбце на верхнем графике показана оценка максимального ожидаемого действующего значения допустимого тока при трех температурах окружающей среды, предполагая, что конденсатор установлен на типовой печатной плате, которая также имеет температуру окружающей среды при естественной конвекции. В реальных приложениях мы рекомендуем снизить номинальный ток и испытать конденсатор в наихудших условиях для целей аттестации.

На более низких частотах график номинального тока обычно будет иметь линейный участок, который прямо пропорционален частоте, возникающий из предела среднеквадратичного напряжения конденсатора, которое на низких частотах является пределом напряженности электрического поля, а не пределом джоулей нагрева.

Для корпусов других типов, кроме металлического корпуса SMT, эти номинальные значения среднеквадратичного тока рассчитываются на основе расчетного ESR и максимального нагрева сердечника 60 ° C, ограниченного максимальной температурой ядра 125 ° C при установке на печатную плату в естественной свободной конвекции.

Для стилей SMT с металлическим корпусом расчет максимального действующего значения допустимого тока основан на предполагаемом максимально допустимом превышении температуры над окружающей средой 120 ° C, также ограниченном максимальной внутренней температурой 185 ° C.Тепловое сопротивление по умолчанию 50 ° C / Вт предназначено для естественной конвекции без радиатора или большого радиатора. Ползунок «Тепловое сопротивление радиатора к окружающей среде» можно перетащить влево, чтобы выбрать гораздо более низкое тепловое сопротивление радиатора к окружающей среде, даже такое низкое, как 1 ° C / Вт, что подразумевает использование экзотического радиатора, такого как медь с жидкостным охлаждением. Агрессивный радиатор, такой как менее 10 ° C / Вт, сильно повлияет на способность выдерживать ток с ограничением джоулевого нагрева на более высоких частотах. Из-за ограничений допустимой токовой нагрузки язычков устройства, ток во всех случаях ограничен среднеквадратичным значением 25 ампер.

Средняя диаграмма в правом столбце представляет собой график действительной и мнимой составляющих S-параметра S11, который идентичен S22 из-за предполагаемой симметричной схемы монтажа конденсатора. Последняя диаграмма в правом нижнем углу представляет собой график реальной и мнимой составляющих S-параметра S21, который идентичен S12.

Ограничения диапазона частот

Нижний диапазон частот выбирается для охвата частоты, на которой проверяются пределы емкости и ESR, которая составляет 1 кГц для конденсаторов номиналом 1000 пФ и выше и 1 МГц для конденсаторов номиналом менее 1000 пФ.Поскольку иногда конденсаторы номиналом до 10 пФ используются на частотах ниже 1 МГц, в диапазоне от 10 до 999 пФ самая низкая частота на графике составляет 100 кГц вместо 1 МГц.

Верхний частотный диапазон выбран так, чтобы покрывать меньшую из 6 ГГц и малое целое кратное первой резонансной частоты. Кратность ограничена электрическим размером конденсатора, а также возможностью циркуляции токов из-за дисбаланса геометрии проводника внутри конденсатора.Имейте в виду, что выше максимальной частоты на графике могут быть зазубрины на величине импеданса и скачки последовательного сопротивления вверх из-за циркулирующих внутри токов. Для наших свинцовых слюдяных конденсаторов номера деталей, начинающиеся с CMR, как правило, будут иметь лучшие характеристики в этом отношении. Если вы не можете найти конденсатор, охватывающий ваш частотный диапазон, обратитесь в отдел проектирования слюды Cornell Dubilier, так как мы можем создать конденсатор с более высокими характеристиками для более эффективного решения необходимого диапазона частот.

Кнопка вывода модели

Вы можете сгенерировать выходной сигнал модели в виде списка частот со значениями Z-параметра или S-параметра, выбрав нужный выходной формат в раскрывающемся списке «Формат вывода», включая температуру сердечника конденсатора, а затем нажав кнопку «Создать модель». Кнопка вывода. Обратите внимание, что выходной формат во всплывающем окне будет в формате Touchstone с разделителями-пробелами в соответствии со стандартом версии 1.0. Выход S-параметров — 2-портовый.s2p с опорным сопротивлением 50 Ом. Для Z-параметров формат по-прежнему соответствует стандарту Touchstone 1.0, но является однопортовым с эталонным импедансом, установленным на 1 Ом, так что сопротивление и реактивное сопротивление в Ом указаны без необходимости применения коэффициента 50. .

Список данных появляется во всплывающем окне, поэтому блокировщики всплывающих окон необходимо отключить. Само окно по умолчанию не сохраняется на вашем жестком диске или в облачном хранилище, и мы обнаружили, что лучший способ сохранить его в виде текста или.s2p — просто щелкнуть в любом месте всплывающего окна, Ctrl-A, чтобы выделить весь текст, затем Ctrl-C, чтобы скопировать, и Ctrl-V, чтобы вставить его в Блокнот или другой текстовый редактор. Затем вы можете сохранить этот файл в текстовом редакторе в текстовом формате с желаемым именем и расширением, что позволит импортировать его в выбранный вами разработчик радиочастотного моделирования или даже отобразить его в электронной таблице и т. Д. Данные такие же, как и те, что вы видите в соответствующие диаграммы разработчика моделей, отражающие логарифмический интервал частот в 100 точек на декаду, что составляет 2.Приращение частоты между двумя точками составляет 4%.

Чтобы вставить выходные данные в электронную таблицу, вы можете выделить весь текст во всплывающем окне вывода с помощью Ctrl-A, скопировать его с помощью Ctrl-C и вставить в электронную таблицу с помощью Ctrl-V. В Excel для разбора данных на отдельные столбцы вы можете выбрать ячейки в одном столбце, содержащем частоту и данные, затем перейти на вкладку «Данные» Excel, а в разделе «Инструменты для работы с данными» нажать «Текст в столбцы» и указать, что этот диапазон разделен (Далее ) с (флажком) пробелом, и данные будут разбиты на отдельные столбцы.

JavaScript

Согласно закону Этвуда, Cornell Dubilier RF Mica Modeler реализован на JavaScript. Поэтому в вашем браузере должен быть включен JavaScript. Реализация JavaScript немного отличается от браузера к браузеру, но апплет RF Mica Modeler был протестирован в последних выпусках самых популярных браузеров: Chrome, Firefox, Opera и Edge. Небольшие различия от одного браузера к другому обычно проявляются во внешнем виде апплета (например,g., размеры шрифтов и текстовых полей) и не должны приводить к другим кривым производительности или другим данным. Также может потребоваться отключить любой блокировщик всплывающих окон, чтобы открылось всплывающее текстовое окно результатов вывода модели.

Подсказок:

Эффективное использование апплета

При необходимости используйте Ctrl-колесо мыши для увеличения. Качество графики автоматически масштабируется, обеспечивая выдающееся качество снимков экрана.

Всплывающие подсказки отображают много полезной информации при перемещении курсора по соответствующим полям формы.Всплывающие подсказки также отображают координаты на различных сериях диаграмм и отображают любые метрические измерения на английском языке.

Ограничения и предостережения для средства моделирования: Этот разработчик моделей ВЧ основан на математических моделях физической конструкции конденсаторов, проверенных с помощью ограниченного количества данных векторного анализатора цепей при комнатной температуре.

Урок 45. Лабораторная работа № 11. Исследование зависимости силы тока от электроемкости конденсатора в цепи переменного тока

Упражнения. Емкостная нагрузка в цепи переменного тока

Лабораторная работа «Элементы цепей переменного тока. Емкостное и индуктивное сопротивления, их зависимость от частоты переменного тока и параметров элементов»

Однофазные цепи переменного тока (страница 2)

Методические указания для лабораторных работ по дисциплине «Электротехника и электроника»

ЛР №7

Определение индуктивности катушки и ее активного сопротивления методом резонанса

Electronic — График зависимости емкости от частоты керамических конденсаторов — iTecTec

График Боде и Найквиста — PalmSens Коррозия

Емкостное реактивное сопротивление — обзор

Повышение точности моделирования при использовании пассивных компонентов

Частотные эффекты

Керамический конденсатор модели

Другие общие компоненты

Проводники

Катушки индуктивности

Температурные эффекты

Окружающий

По компоненту

Как извлечь паразитные значения из таблицы данных конденсатора

Лаборатория 4 — Зарядка и разрядка конденсатора

Введение

Обсуждение принципов

Зарядка и разрядка

Постоянная времени

Использование прямоугольной волны для имитации роли переключателя

Объектив

Оборудование

Процедура

Настройка RC-цепи

Процедура A: Постоянная времени контура

Процедура B: Расчет емкости графическими методами

Процедура C: Измерение эффективной емкости

RF Modeler — CDE

alexxlab

Добавить комментарий Отменить ответ

Рубрики