Построение таблиц истинности для логических выражений

Похожие презентации:

Основы логики. Таблица истинности. Равносильные логические выражения

Алгебра высказываний. Определение высказывания. Таблица истинности для высказываний. Логические тождества. (Лекция 2)

Построение таблиц истинности сложных высказываний

Логика высказываний

Логические основы ЭВМ. Алгоритмы логики. Построение таблиц истинности

Логика высказываний. Таблицы истинности

Логическое высказывание. Виды сложных высказываний

Построение таблиц истинности. 8 класс

Логическая модель. Логика высказываний. Основы логики высказываний

Формулы алгебры высказываний

Тема урока:
«Построение таблиц истинности для
логических выражений»
Цель: Формирование навыков применения технологии
построения таблиц истинности для составных логических
выражений.

2. Построение таблицы истинности

Таблица истинности – это таблица, показывающая
истинность сложного высказывания при всех возможных
значениях входящих переменных.
Последовательность действий:
1. Определить количество строк в таблице:
• количество строк = 2n+1,
где n – количество
логических переменных, 1 – строка заголовков
2. Определить количество столбцов в таблице:
• количество столбцов = количеству логических
переменных + количество логических операций
3. Расставить приоритеты действий:
• приоритеты: ( ), ¬, &, V, импликация, эквиваленция;
4. Заполнить столбцы входных переменных наборами
значений.
5. Заполнить таблицу истинности, выполняя логические
операции в соответствии с приоритетами действий.

3. В составных высказываниях логические операции выполняются в следующем порядке:

1.
2.
3.
4.
5.
6.
В составных высказываниях логические
операции выполняются в следующем
порядке:
Действия в скобках
Отрицание (не)
Конъюнкция (и)
Дизъюнкция (или)
Импликация
Эквиваленция

4. Заполнение таблицы истинности

22+1=5
¬( A&B)
A
B
A&B
¬( A&B)
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
0
2+2=4
Наборы входных переменных, во избежание ошибок,
рекомендуют вводить следующим образом:
1) разделить столбец значений первой переменной
пополам и заполнить верхнюю часть колонки нулями, а
нижнюю — единицами;
2) разделить столбец значений второй переменной на
четыре части и заполнить четверти чередующимися
группами нулей и единиц, начиная с группы нулей;
3) продолжать деление столбцов значений последующих
переменных на 8, 16 и т. д. частей и заполнение их
группами нулей или единиц до тех пор, пока группа нулей
(единиц) не будет состоять из одного символа.

6. например:

Построить таблицу истинности для выражения:
F=(A
А
В
0
0
0
А
В
B)&(A
B)
А
В
А
В
0
1
1
1
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
F

7. РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, у которых
таблицы истинности совпадают,
называют равносильными.

8. Доказать, что логические выражения: А & В и А В, равносильны

Доказать, что логические выражения:
А & В и А В, равносильны
Таблица истинности для А&В
Таблица истинности для А v В
А
В
А
В
А & В
А
В
А
В
А
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
1
1
0
Таблицы истинности совпадают, следовательно, логические
выражения равносильны.
В
Построим таблицу истинности для логического выражения A v А & В.
В нём две переменные, две операции, причём сначала выполняется
конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре

столбца:
Наборы входных переменных — это целые числа от 0 до 3
представленные в двухразрядном двоичном коде: 00, 01, 10, 11.
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со
столбцом А. В таком случае говорят, что логическое выражение A v А& В
равносильно логической переменной А.
Таблица Для 3 переменных
(А В С)
А
В
С
С
В С
А В С (А В С)
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
1
0
1
1
1
0
0
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
1
0
1
1
1
0
0
1
0
Свойства логических операций
Законы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
VĀ
=B
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(B
A&
VC)=
0=0;(A&B)
A &1V =(A&C)
A
V 0 ==A;(AA
V1=1
AVA
(B&C)
VB)&(A
VC)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B

English     Русский Правила

Задание 2 ЕГЭ по информатике 2023

За правильное выполненное задание получишь 1 балл.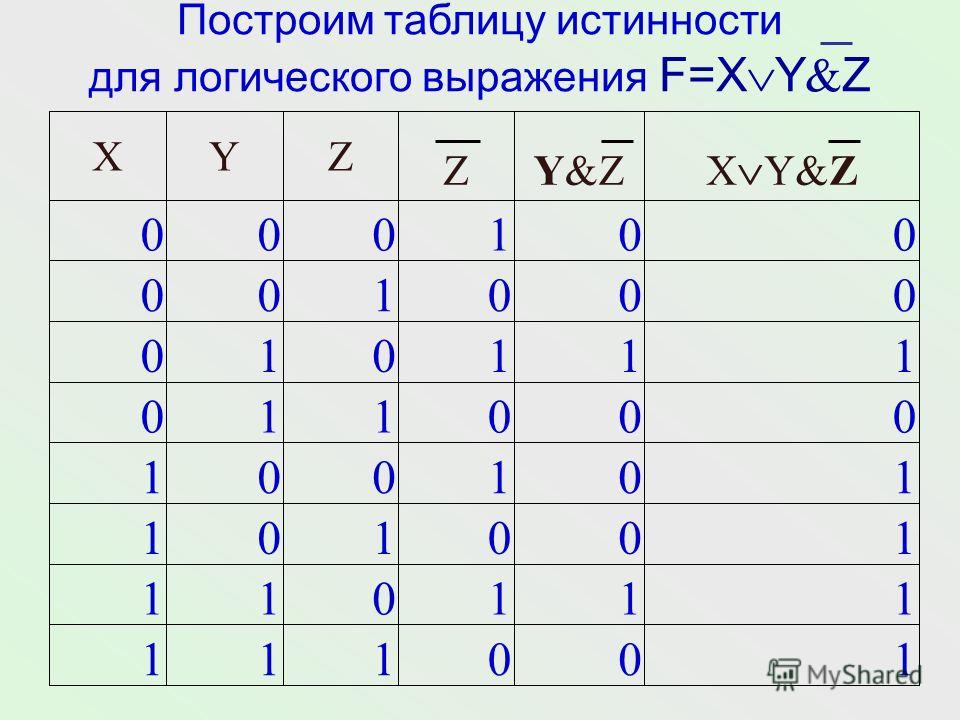 На решение отводится примерно 3 минуты.

Обозначения логических операций

\lnot A, не A — отрицание, инверсия
A \land B, A и B — логическое умножение, конъюнкция
A \lor B, A или B — логическое сложение, дизъюнкция
A \to B -импликация, следование
A \equiv B — эквивалентность, равносильность

Приоритет выполнения логических операций (если нет скобок)

Приоритет	Операция		Обозначение
1. Высший	НЕ	NOT	¬,¯
2. Высокий	И	AND	&,*,Λ
3. Средний	ИЛИ	OR	V, +
4. Низкий	Следование	IMP	→
5. Низший	Эквивалентность	EQU	≡,↔

 

Таблица логических операций

A	B	¬A	A Λ B	A V B	A → B	A ≡ B
0	0	1	0	0	1	1
0	1	1	0	1	1	0
1	0	0	0	1	0	0
1	1	0	1	1	1	1

Could not load xLike class!

Логическая функция F задаётся выражением (\lnot B \lor A \lor \lnot C) \land C. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.

?	?	?	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.

Обсуждение

Логическая функция F задаётся выражением (\lnot A \land B) \lor C \lor B . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.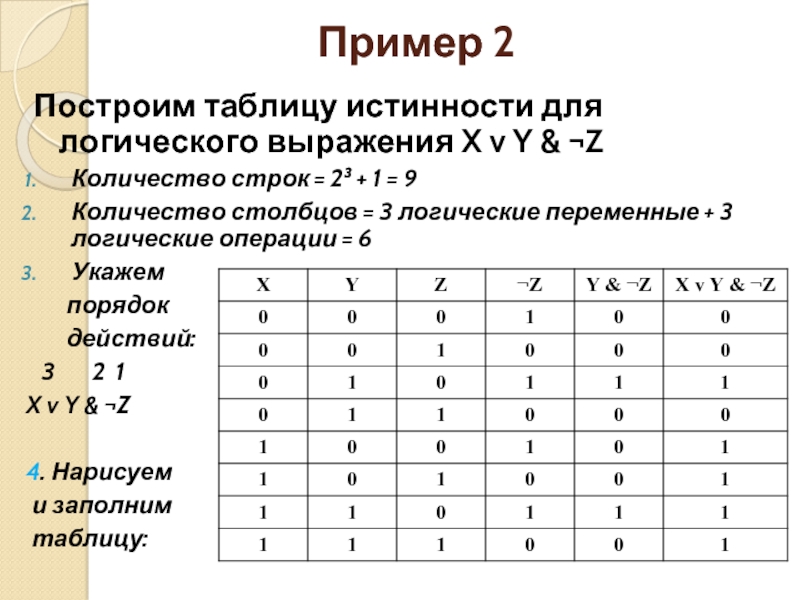

?	?	?	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.

Обсуждение

Логическая функция F задаётся выражением (\lnot C \land A) \lor B \lor \lnot C . Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.

?	?	?	F
0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.

Обсуждение

Логическая функция F задаётся выражением (\lnot C \land A) \lor (C \land B \land A). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.

?	?	?	F
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.

Обсуждение

Логическая функция F задаётся выражением C \to (A \land (B \lor C)). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных A, B, C.

?	?	?	F
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	1

В ответе напишите буквы A, B, C в том порядке, в котором идут соответствующие им столбцы.

Обсуждение

Начать

Что такое таблица истинности и как ею пользоваться?

Таблица истинности — это математический инструмент, используемый для определения того, является ли утверждение истинным или ложным. Он используется для проверки обоснованности аргумента, показывая все возможные результаты этого аргумента. Вы можете использовать генератор таблиц истинности, чтобы найти комбинации различных операторов. В этом блоге мы покажем вам, что такое таблица истинности и как ее использовать.

Что такое таблица истинности?

Таблица истинности — это математическая таблица, используемая для определения истинности логического выражения. Истинностное значение выражения либо истинно, либо ложно. В таблице истинности перечислены все возможные комбинации значений истинности для переменных в выражении и показано результирующее значение истинности для всего выражения.

Как используется таблица истинности?

Таблица истинности — это математическая таблица, используемая для определения того, является ли утверждение истинным или ложным. Таблицы истинности можно использовать для оценки составных утверждений, логических эквивалентностей и тавтологий.

Каковы преимущества использования таблицы истинности?

Таблица истинности — это математическая таблица, используемая для определения истинности логического выражения. Значение истинности выражения — это значение, которое оценивается выражением, когда всем переменным в выражении присваиваются определенные значения. Основное преимущество использования таблицы истинности заключается в том, что она позволяет вам увидеть все возможные комбинации входных и выходных значений для данного логического выражения. Это может быть полезно для понимания того, как работает выражение, и для поиска ошибок в выражении. Кроме того, таблицы истинности можно использовать для упрощения сложных выражений путем определения эквивалентных выражений с меньшим количеством переменных.

Как создать таблицу истинности

Таблица истинности — это математическая таблица, используемая для определения значения истинности логического выражения. Таблицы истинности можно использовать для проверки правильности аргумента или для вычисления выходных данных логической схемы.

Чтобы создать таблицу истинности, перечислите все возможные комбинации входных значений для переменных в выражении. Для каждой комбинации определите значение выражения. Результирующая таблица будет иметь по одному столбцу для каждой переменной в выражении и по одной строке для каждой комбинации входных значений.

Примеры таблиц истинности

Таблица истинности является удобным инструментом для определения выходных данных логической схемы. При заданном входе в таблице истинности перечислены все возможные выходы схемы. Другими словами, он показывает, как схема будет вести себя при различных обстоятельствах.

Таблицы истинности особенно полезны для устранения неполадок в цепях. Глядя на таблицу истинности, вы можете быстро увидеть, каким должен быть выход схемы при различных условиях. Если фактический результат не соответствует ожидаемому результату, то вы знаете, что есть проблема со схемой.

Допустим, у нас есть простой логический элемент И с двумя входами (A и B) и одним выходом (C). Таблица истинности для этого вентиля будет выглядеть так:

A | Б | С

—+—+—

0 | 0 | 0

0 | 1 | 0

1 | 0 | 0

1 | 1 | 1

Как видите, когда на обоих входах низкий уровень (0), на выходе всегда низкий уровень (0). Когда на обоих входах высокий уровень (1), на выходе также высокий уровень (1). Однако, когда один вход высокий, а другой низкий, выход всегда низкий (0). Так ведет себя логический вентиль И.

Заключение

Таблица истинности — это математическая таблица, используемая для определения того, является ли утверждение истинным или ложным. Таблицы истинности можно использовать для проверки достоверности аргументов и для вычисления результатов булевых функций. Булевы функции используются в цифровых схемах, таких как компьютерные процессоры, и в таких языках программирования, как C++ и Java. Если вы хотите узнать больше о том, как использовать таблицы истинности, есть много ресурсов, доступных в Интернете и в печати.

Приложение Noon — идеальный способ узнать о других предметах. Доступно более 10 000 лекций, и вы можете учиться из любой точки мира. Вы также можете учиться у учителей по всему миру. С приложением Noon вы можете начать учиться из любой точки земного шара!

Булева логика в JavaScript.

Часть 1: Булевы операторы и правда… | by Nick Gard

Часть 1. Булевы операторы и таблицы истинности

7 мин чтения

·

23 июля 2018 г.

Это часть серии статей. Прочтите части 2, 3 и 4.

Я не компьютерщик — у меня нет степени в области компьютерных наук. Но я математик, и эти знания и навыки были бесценны для меня, когда я учусь и занимаюсь программированием. В конечном итоге я ежедневно использую не статистику или расчеты, а мое глубокое понимание булевой логики. Много раз мне удавалось превратить сложную комбинацию амперсандов, вертикальной черты, восклицательных знаков и знаков равенства во что-то гораздо более простое и читабельное. Я хотел бы поделиться некоторыми из этих знаний, поэтому я начал писать эту статью. Получилось на самом деле длинный, поэтому я разбил его на несколько частей: операторы и таблицы истинности (эта статья), правила замены, универсальные и экзистенциальные утверждения и, наконец, перевод с английского на логику. Я надеюсь, что это так же полезно для вас, как и для меня. Наслаждаться!

Истинные и ложные значения в JavaScript

Прежде чем мы начнем рассматривать логические выражения, которые полагаются на истинность утверждений для получения достоверности выражения, мы должны хорошо понимать, что такое

.0077 правдивый в JavaScript. Так как JavaScript имеет свободную типизацию, значения могут быть преобразованы в логические значения для оценки логических выражений. если условия , && , || и часть троичного оператора, предшествующая вопросительному знаку ( _?_:_ ), все преобразуют свои оцениваемые значения в логические значения. (Обратите внимание, что это не означает, что они обязательно возвращают логическое значение из операции.) Быстрый способ узнать, что является правдой, — это знать, что существует только шесть false values ​​— false , null , undefined , NaN , 0 , и '' — и все остальное правда у . Это означает, что [] и {} оба правдивы, что обычно сбивает людей с толку.

Логические операторы

В формальной логике высказываний имеется всего несколько операторов: отрицание, конъюнкция, дизъюнкция, импликация и биусловие. У каждого из них есть эквиваленты JavaScript: ! , && , || , if (/* условие */) { /* then следствие */} и === соответственно. Все остальные логические операторы могут быть построены из них, включая операторы исключающих или (исключающее ИЛИ) и операторов if-then-else (троичных). Мы вернемся к ним во второй части.

Во-первых, давайте посмотрим на

таблицы истинности для каждого из наших основных операторов. Таблицы истинности говорят нам, что истинность выражения основан на правдивости его частей . Например, первую строку в таблице истинности отрицания (ниже) следует читать так: «если утверждение А истинно, то выражение !А ложно». Таблицы истинности важны, потому что если два выражения порождают одну и ту же таблицу истинности, то эти выражения эквивалентны и могут заменять друг друга .

Таблица Negation очень проста. Отрицание — единственный унарный логический оператор, то есть он действует на один вход. Это означает, что

!А || B не следует рассматривать как !(A || B) . Скобки действуют как группирующие обозначения, подобные тем, что вы найдете в математике.

Отрицать простое утверждение несложно; отрицание «идет дождь» — это «, а не идет дождь», а отрицание примитива JavaScript true — это, конечно, false . Однако отрицание сложных утверждений или выражений не так просто. Что такое отрицание «это всегда дождь” или isFoo && isBar ? Мы рассмотрим отрицание этих и подобных им выражений в следующей статье.

Таблица Conjunction показывает, что выражение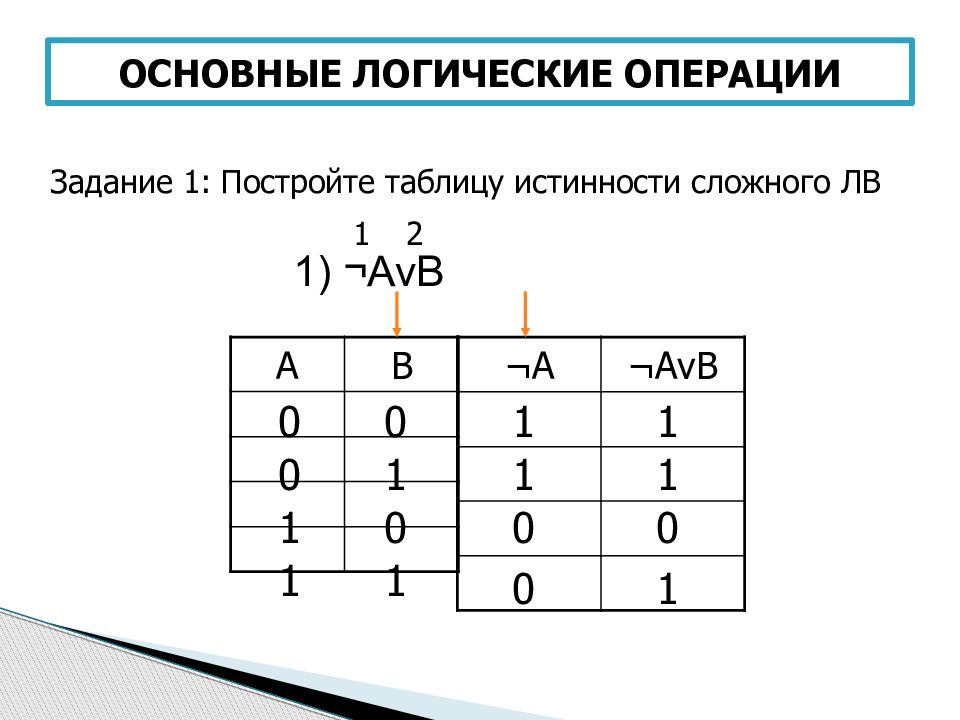

A && B истинно, только если и A и B истинны. Это должно быть хорошо знакомо вам по написанию JavaScript.

Таблица Disjunction также должна быть очень знакома. Дизъюнкция (логическое ИЛИ) истинно, если либо , либо оба из A и B верно.

Таблица Значение не так знакома. Поскольку A подразумевает B, истинность A подразумевает истинность B. Однако B может быть истинным по причинам, отличным от A, поэтому последние две строки таблицы верны. Единственный раз, когда импликация ложна, это когда A истинно, а B ложно, потому что тогда A не подразумевает B.

Хотя операторы if используются для импликаций в JavaScript, не все операторы if работают таким образом. Обычно мы используем вместо в качестве контроля потока, а не проверки достоверности, когда последствия также имеют значение при проверке. Вот архетипичная импликация if утверждение:

 импликация функции (A, B) { 
 if (A) { 
 return B; 
 } else { 
 /* если A ложно, импликация верна */ 
 return true; 
 } 
 } 

Не беспокойтесь, это несколько неудобно.