2 — Таблицы истинности логической функции
1. Логическая функция Fзадаётся выражением F = (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции Fсоответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
2. Логическая функция Fзадаётся выражением F = a ∧ b ∨ a ∧ (¬c). Определите, какому столбцу таблицы истинности функции Fсоответствует каждая из переменных a, b, c? В ответе напишите буквы a, b, c без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
3. Логическая функция Fзадаётся выражением F = ¬x ∧ y ∧ z ∨ ¬x ∧ ¬z. На рисунке приведены все строки таблицы истинности, в которых функция равна 1. Определите, какому столбцу соответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
4. Логическая функция Fзадаётся выражением F = x ∧ (y ∧ z ∨ y ∧ ¬w ∨ ¬w ∧ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 1. , y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
5. Логическая функция Fзадаётся выражением F = (¬x ∨ y ∨ z) ∧ (¬x ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, z без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
6. Логическая функция Fзадаётся выражением F = (¬x ∨ z) ∧ (¬x ∨ ¬y ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z? В ответе напишите буквы x, y, zбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
7. Логическая функция Fзадаётся выражением F = x ∨ ¬w ∨ y ∧ ¬z. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. , y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
8. Логическая функция Fзадаётся выражением F = x ∨ (¬y ∨ z ∨ ¬w) ∧ (y ∨ ¬z). На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, w без пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
9. Логическая функция Fзадаётся выражением F = ¬x ∨ ¬y ∧ ¬z ∨ ¬z ∧ ¬w ∨ ¬y ∧ w. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
10. Логическая функция Fзадаётся выражением F = ¬x ∨ y ∧ z ∨ y ∧ ¬w ∨ ¬z ∧ ¬w. На рисунке приведены все строки таблицы истинности, в которых функция равна 0. Определите, какому столбцу соответствует каждая из переменных x, y, z, w? В ответе напишите буквы x, y, z, wбез пробелов в том порядке, в котором идут соответствующие им столбцы. |
| Ответ: |
Таблицы истинности
Таблицы истинности
|
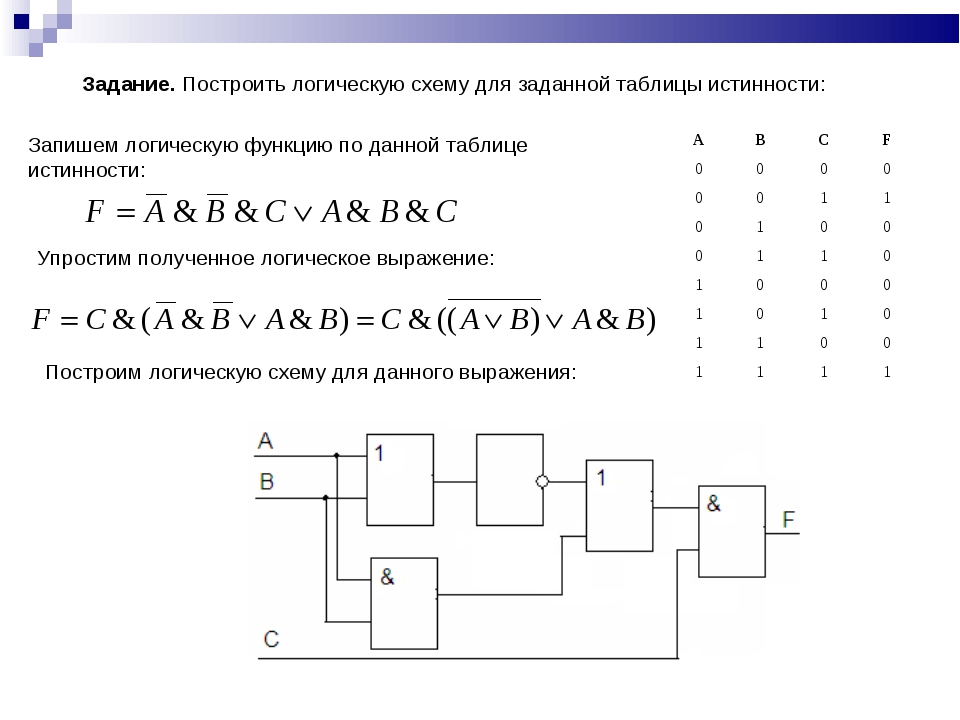
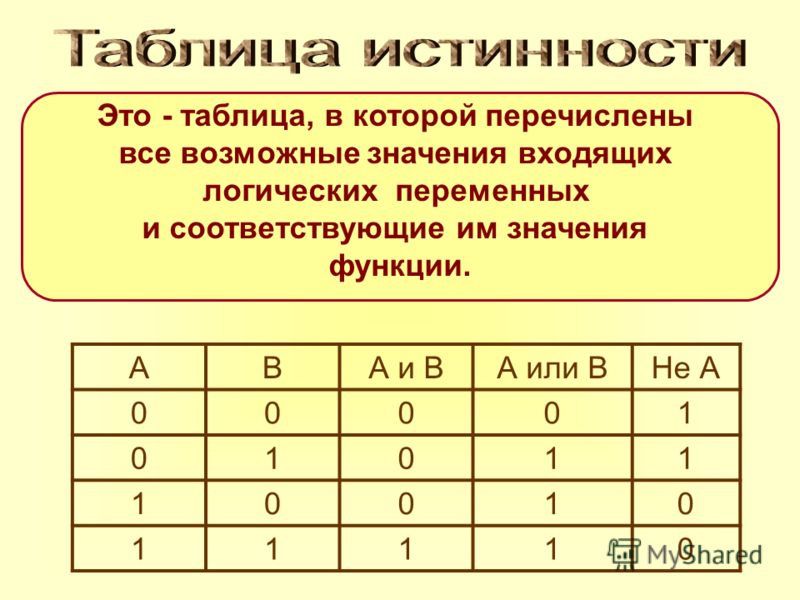
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения. |
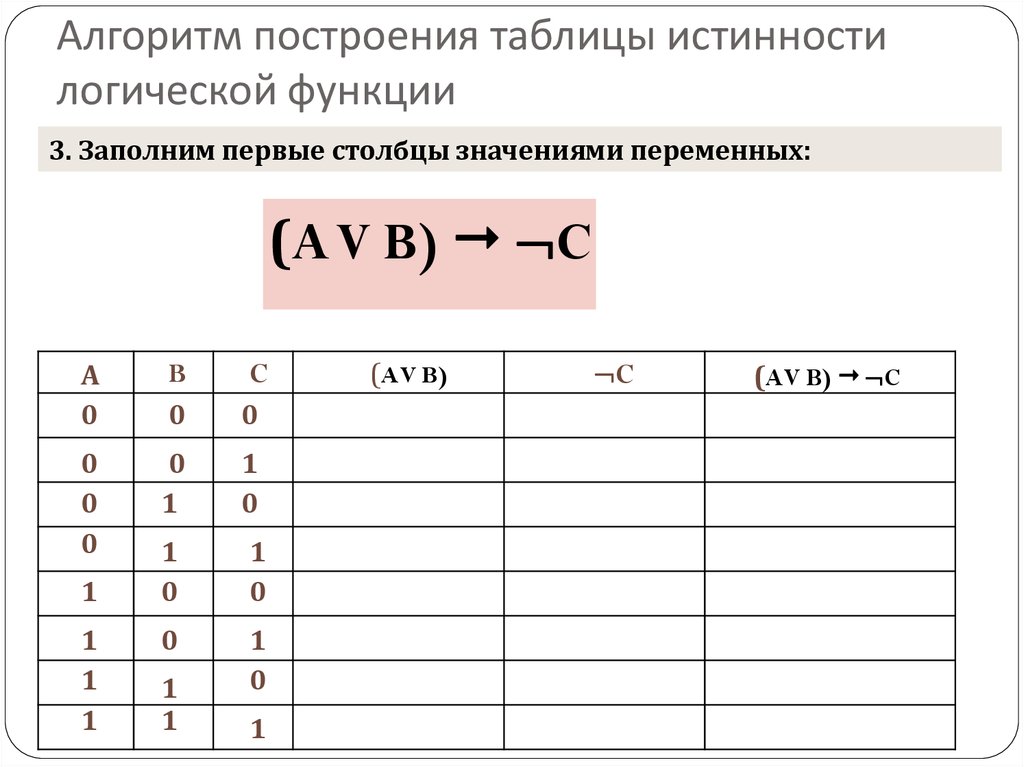
Для того чтобы построить таблицу истинности логического выражения, достаточно:
1) определить число строк таблицы m = 2n, где n — число переменных в логическом выражении;
2) определить число столбцов таблицы как сумму чисел логических переменных и логических операций в логическом выражении;
3) установить последовательность выполнения логических операций с учётом скобок и приоритетов операций;
4) заполнить строку с заголовками столбцов таблицы истинности, занеся в неё имена логических переменных и номера выполняемых логических операций;
5) выписать наборы входных переменных с учётом того, что они представляют собой ряд целых n-разрядных двоичных чисел от 0 до 2
6) провести заполнение таблицы истинности по столбцам, выполняя логические операции.
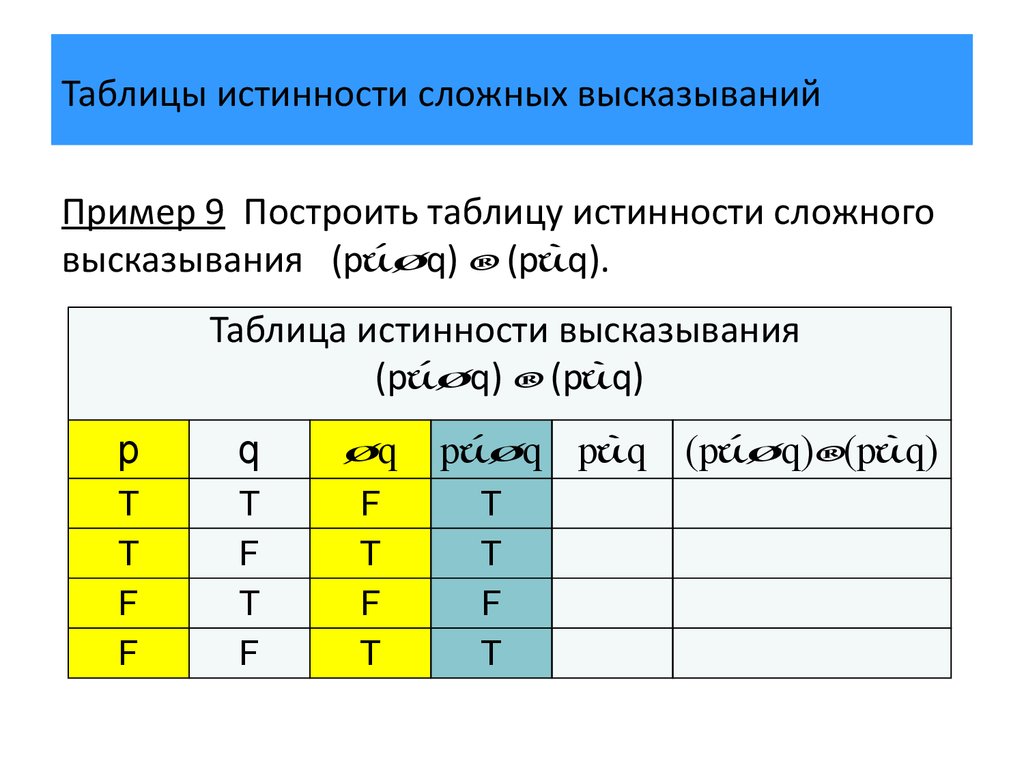
Пример 1. Построим таблицу истинности для логического выражения
В этом выражении две логические переменные и пять логических операций. Всего в таблице истинности будет пять строк (22 плюс строка заголовков) и 7 столбцов.
Начнём заполнять таблицу истинности с учётом следующего порядка выполнения логических операций: сначала выполняются операции отрицания (в порядке следования), затем операции конъюнкции (в порядке следования), последней выполняется дизъюнкция.
Обратите внимание на последний столбец, содержащий конечный результат. Какой из рассмотренных логических операций он соответствует?
|
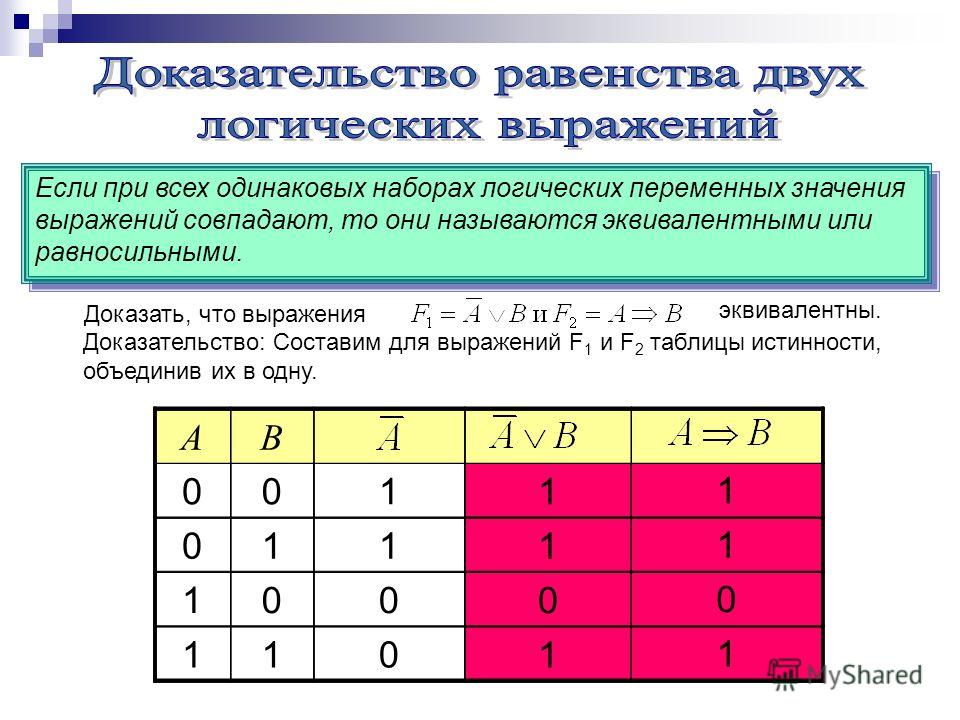
Логические выражения, зависящие от одних и тех же логических переменных, называются равносильными или эквивалентными, если для всех наборов входящих в них переменных значения выражений в таблицах истинности совпадают. |
Таблица истинности, построенная в предыдущем примере, доказывает равносильность выражений и А ↔ B.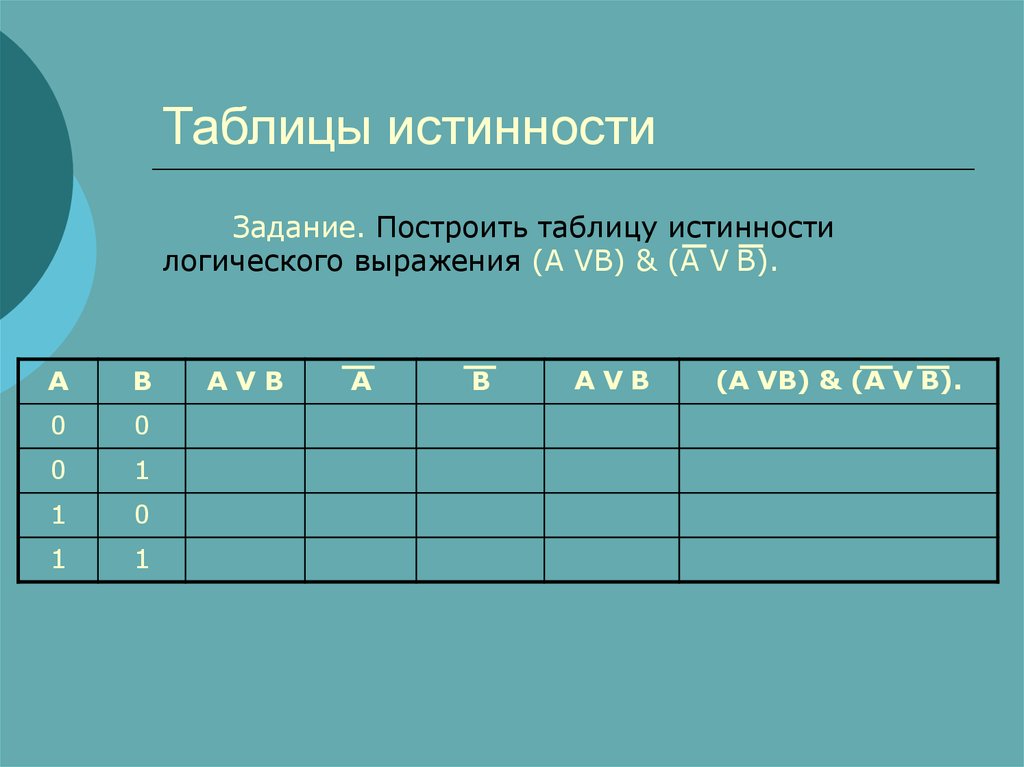
Можно записать:
С помощью таблиц истинности докажите равносильность выражений А ↔ В и
|
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции. |
Рассмотрим несколько примеров.
Пример 2. Известен фрагмент таблицы истинности для логического выражения F, содержащего логические переменные А, В и С.
Сколько из приведённых ниже логических выражений соответствуют этому фрагменту?
Ответить на поставленный вопрос можно, вычислив значение каждого логического выражения на каждом заданном наборе переменных и сравнив его с имеющимся значением F.
1) Логическое выражение соответствует данному фрагменту таблицы истинности:
2) Логическое выражение не соответствует данному фрагменту таблицы истинности, т.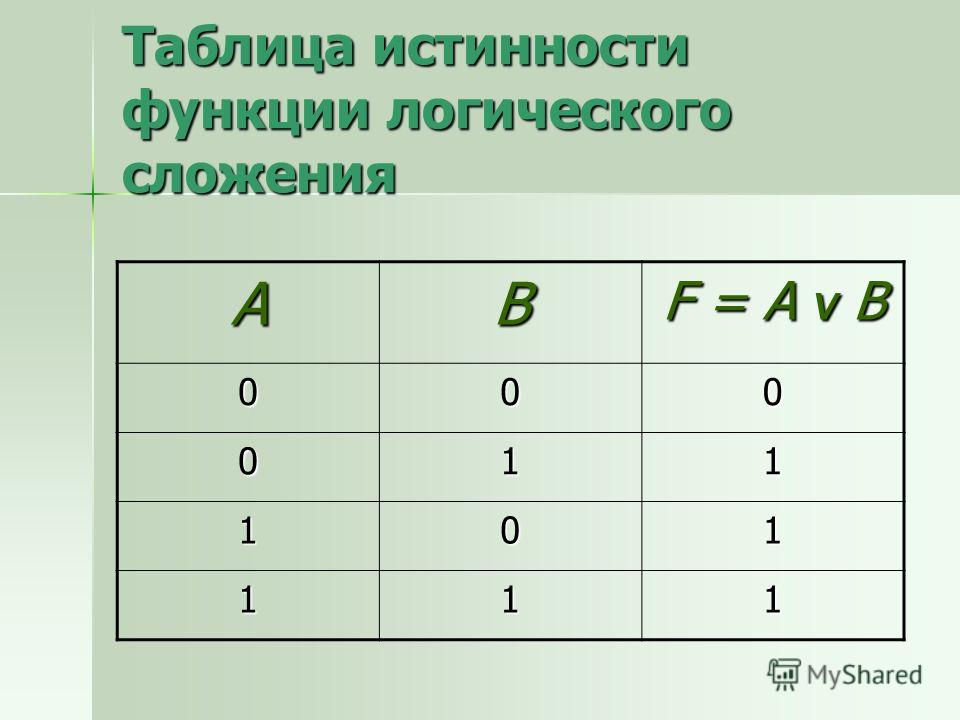 к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
к. уже на первом наборе значение рассматриваемого логического выражения не совпадает со значением F. Проведение дальнейших вычислений не имеет смысла.
3) Логическое выражение не соответствует данному фрагменту таблицы истинности:
4) Логическое выражение
Итак, имеется два логических выражения, соответствующих заданному фрагменту таблицы истинности.
Можно ли утверждать, что в результате решения задачи мы нашли логическое выражение F?
Пример 3. Логическая функция F задаётся выражением:
Ниже приведён фрагмент таблицы истинности, содержащий все наборы переменных, на которых F истинна.
Определим, какому столбцу таблицы истинности функции F соответствует каждая из переменных х, у, z.
В исходном логическом выражении задействовано три логические переменные. Полная таблица истинности для этого выражения должна состоять из 8 (2
Наборам переменных, на которых логическое выражение истинно, соответствуют десятичные числа 0, 2, 3, 4 и 7.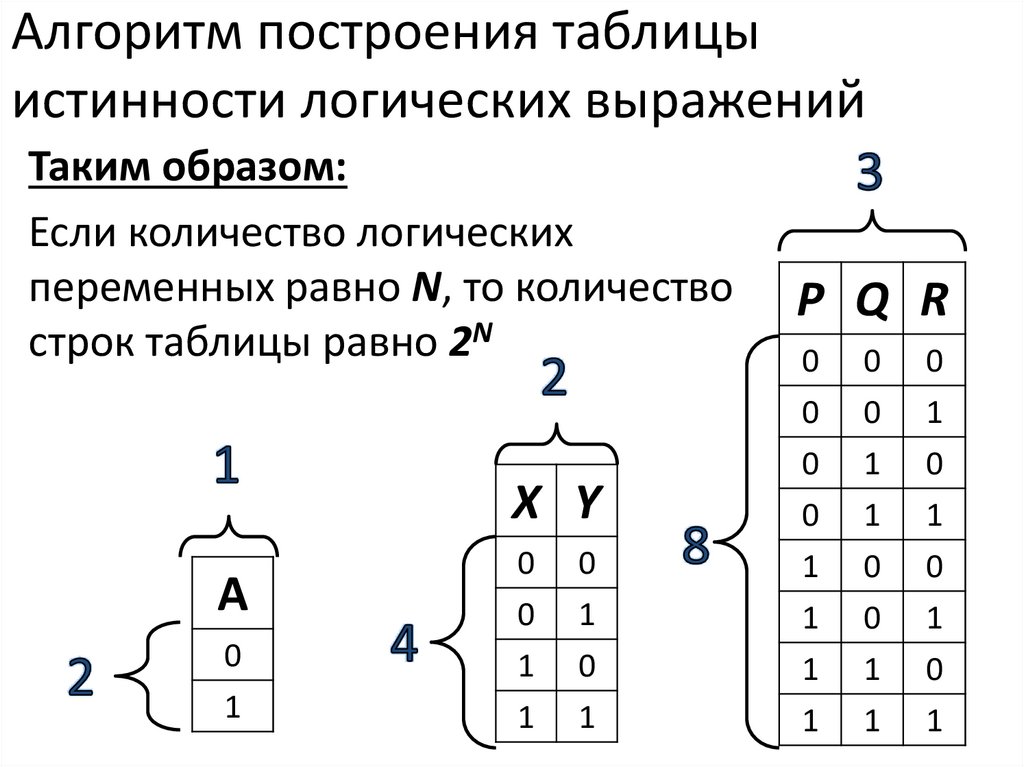
Следовательно, наборам переменных, на которых логическое выражение ложно, должны соответствовать десятичные числа 1, 5 и 6 (их двоичные коды 001, 101 и 110). Построим по этим данным вторую часть таблицы истинности:
Теперь выясним, при каких значениях х, у, z логическое выражение ложно: Логическое произведение ложно, если хотя бы один из операндов равен нулю. Таким образом, мы имеем две дизъюнкции, каждая из которых должна быть ложной. Это возможно только в случае равенства нулю каждого из операндов, входящих в дизъюнкцию. Подберём подходящие значения х, у и z, заполняя следующую таблицу:
Первая дизъюнкция равна нулю на наборе 011. Для равенства нулю второй дизъюнкции требуется, чтобы х = 1, у = 0, a z может быть и 0, и 1.
Сравним эту таблицу с восстановленным нами фрагментом исходной таблицы истинности, предварительно подсчитав, сколько раз каждая переменная принимает единичное значение.
Переменная у принимает единичное значение только один раз. Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Следовательно, ей соответствует второй столбец исходной таблицы. Из таблицы со значениями х, у и z следует, что при у = 1: х = 0, a z = 1. Следовательно, переменной z соответствует первый столбец, а переменной х — третий столбец исходной таблицы.
Убедиться в правильности полученного ответа можно, полностью заполнив следующую таблицу:
Самое главное
Таблицу значений, которые принимает логическое выражение при всех сочетаниях значений (наборах) входящих в него переменных, называют таблицей истинности логического выражения.
Истинность логического выражения можно доказать путём построения его таблицы истинности.
Функцию от n переменных, аргументы которой и сама функция принимают только два значения — 0 и 1, называют логической функцией. Таблица истинности может рассматриваться как способ задания логической функции.
1
Первый слайд презентации
Построение таблиц истинности для сложных логических выражений
Порядок выполнения действий:
Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
1) инверсия;
2) конъюнкция;
3) дизъюнкция;
Для изменения указанного порядка выполнения логических операций используются круглые скобки.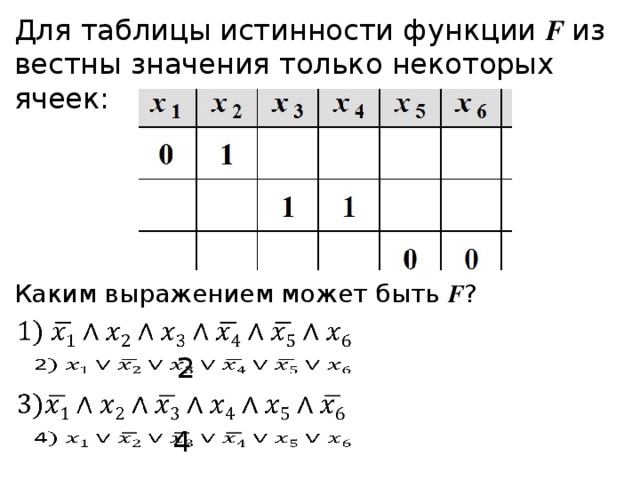
Изображение слайда
2
Слайд 2
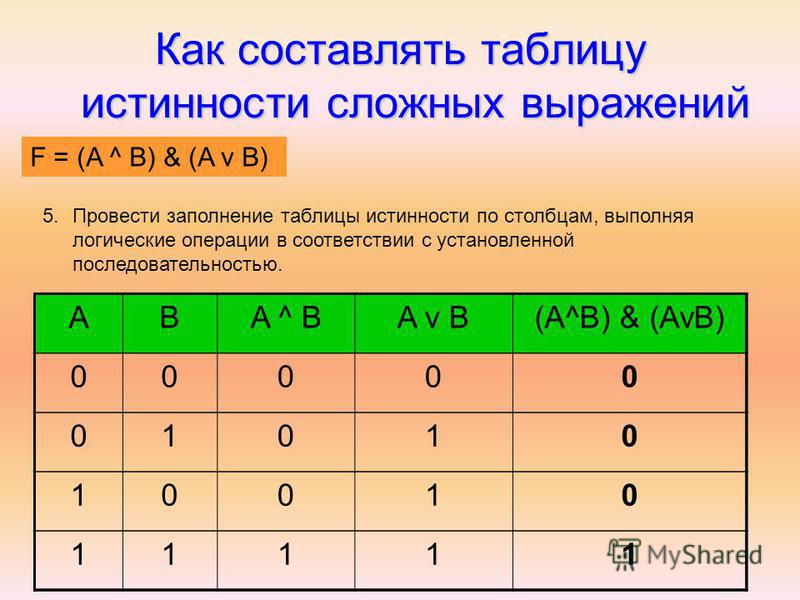
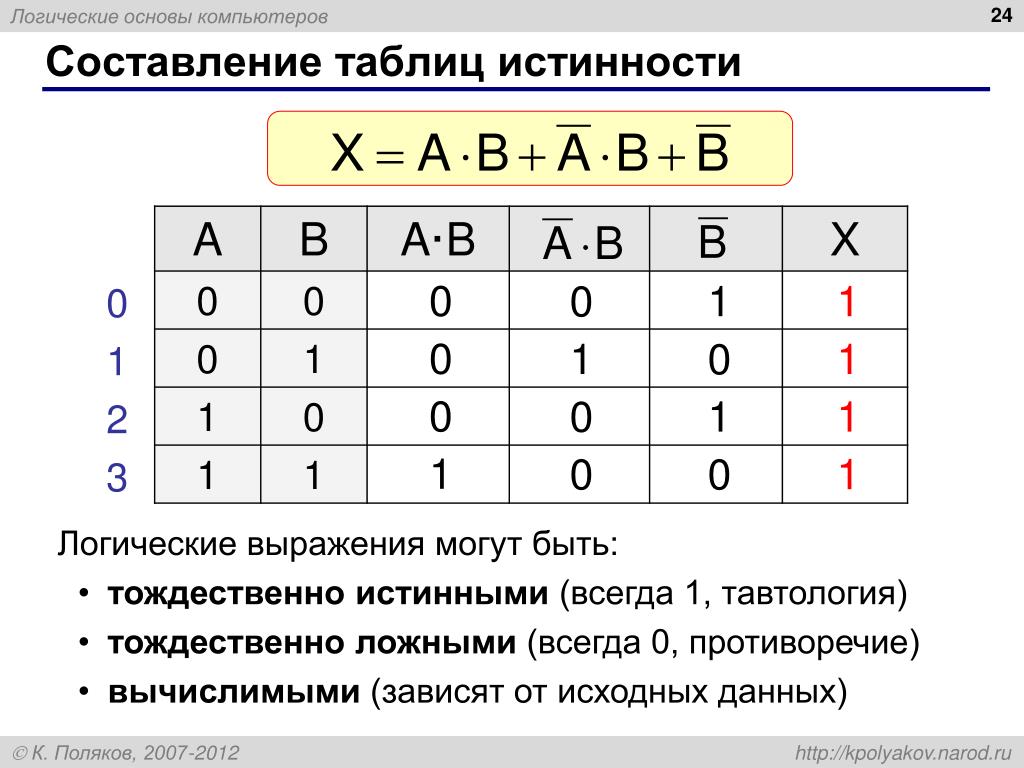
Алгоритм построения таблицы истинности 1) Определить количество строк таблицы по формуле: Q = 2 n, где n — количество входных переменных. 2) Определить количество столбцов: количество переменных плюс количество операций. 5) Внести в таблицу все наборы входных переменных. 3) Построить таблицу истинности с указанным количеством строк и столбцов. 4) Ввести названия столбцов таблицы в соответствии с последовательностью логических операций с учетом скобок и приоритета. 6) Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Изображение слайда
3
Слайд 3
Построить таблицу истинности логического выражения
F=A (B C)
1) Определить количество строк таблицы по формуле: Q = 2 n, где n — количество входных переменных.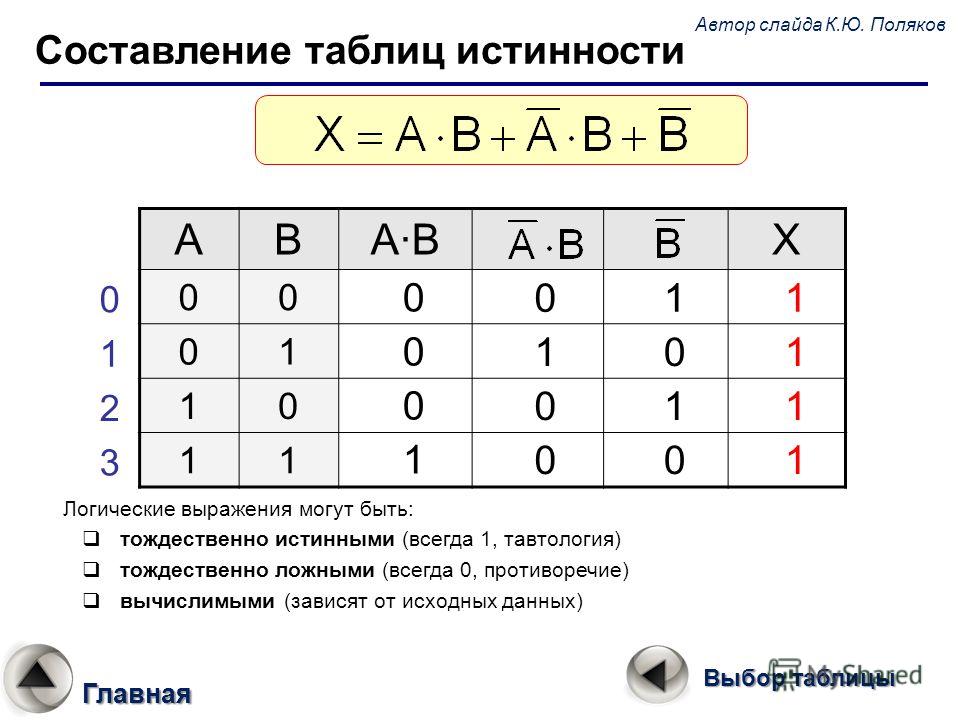 Q =2 3 =8
Значит в таблице 8 строк
Q =2 3 =8
Значит в таблице 8 строк
Изображение слайда
4
Слайд 4
Построить таблицу истинности логического выражения F=A (B C) 2) Определить количество столбцов: количество переменных плюс количество операций. Количество переменных — 3 Количество операций — 3 Значит строк в таблице 6
Изображение слайда
5
Слайд 5
Построить таблицу истинности логического выражения F=A (B C) 3) Построить таблицу истинности с указанным количеством строк и столбцов.
6
Слайд 6
Построить таблицу истинности логического выражения
F=A (B C)
4) Ввести названия столбцов таблицы в соответствии с последовательностью логических операций с учетом скобок и приоритета.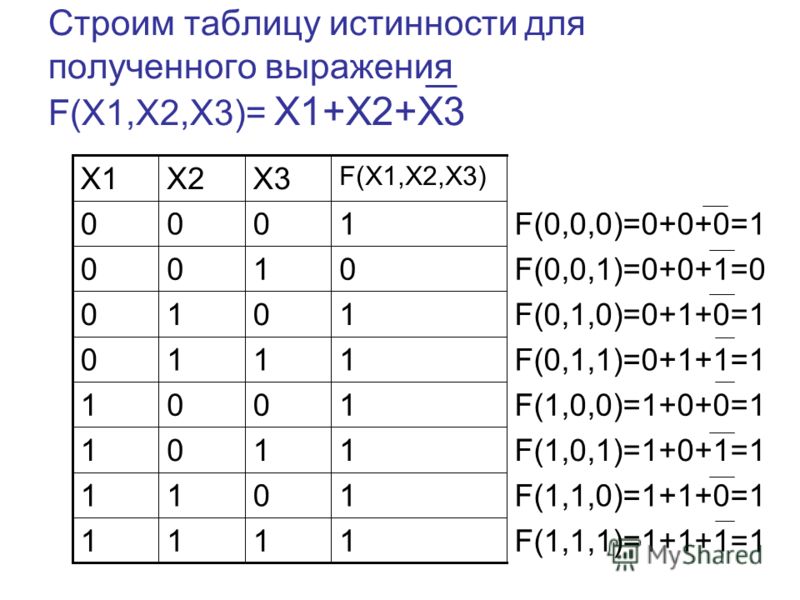 А В С А В С F
А В С А В С F
Изображение слайда
7
Слайд 7
Построить таблицу истинности логического выражения F=A (B C) 5) Внести в таблицу все наборы входных переменных. A B C A В С F 0 0 1 1 0 0 1 1 0 0 0 0 1 1 1 1 0 1 0 1 0 1 0 1
Изображение слайда
8
Слайд 8
Построить таблицу истинности логического выражения F=A (B C) 6) Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью. A B C A В С F 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0
Изображение слайда
9
Слайд 9
Построить таблицу истинности логического выражения
F=A (B C)
6) Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью. A B C A В С F
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
1
1
1
A B C A В С F
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
1
1
1
Изображение слайда
10
Слайд 10
Построить таблицу истинности логического выражения F=A (B C) 6) Заполнить таблицу истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью. 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 A B C A В С F 0 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0
Изображение слайда
11
Слайд 11
Постройте таблицы истин для следующих логических выражений B ВА A(A В С) A(B BC) A(B C) A В С переход переход переход переход переход
Изображение слайда
12
Слайд 12
Постройте таблицы истин для следующих логических выражений B ВА А В ВА В ВА 0 0 1 1 0 0 0 1 0 1 0 1
Изображение слайда
13
Слайд 13
Постройте таблицы истин для следующих логических выражений B ВА А В ВА В ВА 0 0 1 1 0 1 0 1 0 0 0 1 0 1 0 1 назад
Изображение слайда
14
Слайд 14
Постройте таблицы истин для следующих логических выражений 2) А(А В С) А В С А В А В С А(А В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 1
Изображение слайда
15
Слайд 15
Постройте таблицы истин для следующих логических выражений 2) А(А В С) А В С А В А В С А(А В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1
Изображение слайда
16
Слайд 16
Постройте таблицы истин для следующих логических выражений 2) А(А В С) А В С А В А В С А(А В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 назад
Изображение слайда
17
Слайд 17
Постройте таблицы истин для следующих логических выражений 3) А(В ВС) А В С В ВС В ВС А(В ВС) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0
Изображение слайда
18
Слайд 18
Постройте таблицы истин для следующих логических выражений 3) А(В ВС) А В С В ВС В ВС А(В ВС) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1
Изображение слайда
19
Слайд 19
Постройте таблицы истин для следующих логических выражений 3) А(В ВС) А В С В ВС В ВС А(В ВС) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 1 0 1 1 1 0 1
Изображение слайда
20
Слайд 20
Постройте таблицы истин для следующих логических выражений 3) А(В ВС) А В С В ВС В ВС А(В ВС) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 1 0 1 1 1 0 1 0 0 0 0 1 1 0 1 назад
Изображение слайда
21
Слайд 21
Постройте таблицы истин для следующих логических выражений 4) А(В С) А В С А С В С А(В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0
Изображение слайда
22
Слайд 22
Постройте таблицы истин для следующих логических выражений 4) А(В С) А В С А С В С А(В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0
Изображение слайда
23
Слайд 23
Постройте таблицы истин для следующих логических выражений 4) А(В С) А В С А С В С А(В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1
Изображение слайда
24
Слайд 24
Постройте таблицы истин для следующих логических выражений 4) А(В С) А В С А С В С А(В С) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 0 0 0 1 0 1 1 назад
Изображение слайда
25
Последний слайд презентации: Построение таблиц истинности для сложных логических выражений Порядок
Постройте таблицы истин для следующих логических выражений 5) А В С А В С С А В А В С А В С 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 1 0 1 0 1 0 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 0 0 0 0 0 0 назад
Изображение слайда
примеров таблицы истинности
пример таблицы истинностиПримеры таблиц истинности
Примеры булевой алгебры Двоичный/булев основной индекс
[Примеры таблиц истинности] [Упрощение логических выражений] [Примеры логических вентилей]
Таблицы истинности для основных операций:
|
|
| ||||||||||||||||||||||||||||||||||||||||||||
 Вот несколько:
Вот несколько:
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
поведение программы в зависимости от результатов тестов.
 Вот что это
глава о.
Вот что это
глава о.5.1. Логические значения и выражения
Логическое значение может быть либо истинным, либо ложным. Он назван в честь британского математика Джорджа Буля, впервые сформулировавшего логическое значение алгебра — некоторые правила рассуждений и комбинирования этих значений. Это основа всей современной компьютерной логики.
В Python два логических значения — True и False (значение заглавные буквы должны быть именно такими, как показано), а тип Python — bool .
>>> тип (правда) <класс 'буль'> >>> тип(правда) Traceback (последний последний вызов): Файл "<интерактивный ввод>", строка 1, в <модуль> NameError: имя «истина» не определено
A Логическое выражение — это выражение, которое вычисляется для получения результата, который логическое значение. Например, оператор == проверяет, равны ли два значения. Он производит (или дает ) логическое значение:
>>> 5 == (3 + 2) # Пятерка равна 5 результату 3 + 2? Истинный >>> 5 == 6 ЛОЖЬ >>> j = "хел" >>> j + "lo" == "привет" Истинный
В первом операторе два операнда оцениваются как равные значения, поэтому выражение вычисляется
на Истина; во втором утверждении 5 не равно 6, поэтому получаем False.
Оператор == является одним из шести общих операторов сравнения , которые все производят логический результат; вот все шесть:
x == y # Выдать True, если ... x равно y x != y # ... x не равно y x > y # ... x больше y x < y # ... x меньше y x >= y # ... x больше или равно y x <= y # ... x меньше или равно y
Хотя эти операции, вероятно, знакомы, символы Python отличается от математических символов. Распространенной ошибкой является использование одного знак равенства (=) вместо двойного знака равенства (==). Помните, что = — оператор присваивания, а == — оператор сравнения. Кроме того, есть нет такой вещи, как =< или =>.
Как и любые другие типы, которые мы видели до сих пор, логические значения могут быть присвоены переменные, печатные и т. д.
>>> возраст = 18 >>> old_enough_to_get_driving_licence = возраст >= 17 >>> print(old_enough_to_get_driving_licence) Истинный >>> type(old_enough_to_get_driving_licence) <класс 'буль'>
5.
 2. Логические операторы
2. Логические операторыИмеется три логических операторов , и, или, и не, которые позволяют нам строить более сложные Логические выражения из более простых логических выражений. семантика (значение) этих операторов аналогична их значению в английском языке. Например, x > 0 и x < 10 дают True, только если x больше 0 и в то же время x меньше 10.
n % 2 == 0 или n % 3 == 0 истинно, если либо условий истинно, то есть, если число n делится на 2 или , оно делится на 3. (Что делать как вы думаете, бывает, если n делится и на 2, и на 3 одновременно? Выдаст ли выражение True или False? Попробуйте это в своем интерпретаторе Python.)
Наконец, оператор not инвертирует логическое значение, поэтому not (x > y) истинно, если (x > y) равно False, то есть если x меньше или равно у.
Выражение слева от оператора или вычисляется первым: если результат True,
Python не выполняет (и не должен) вычислять выражение справа — это называется кратким вычислением .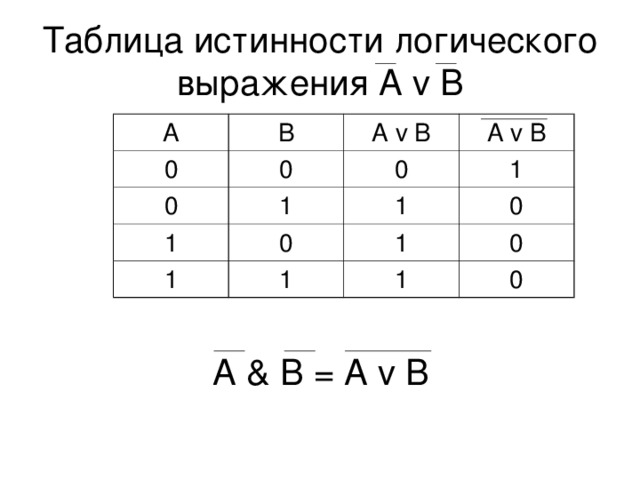 Точно так же для оператора and, если выражение слева дает False, Python не
оцените выражение справа.
Точно так же для оператора and, если выражение слева дает False, Python не
оцените выражение справа.
Чтобы не было лишних вычислений.
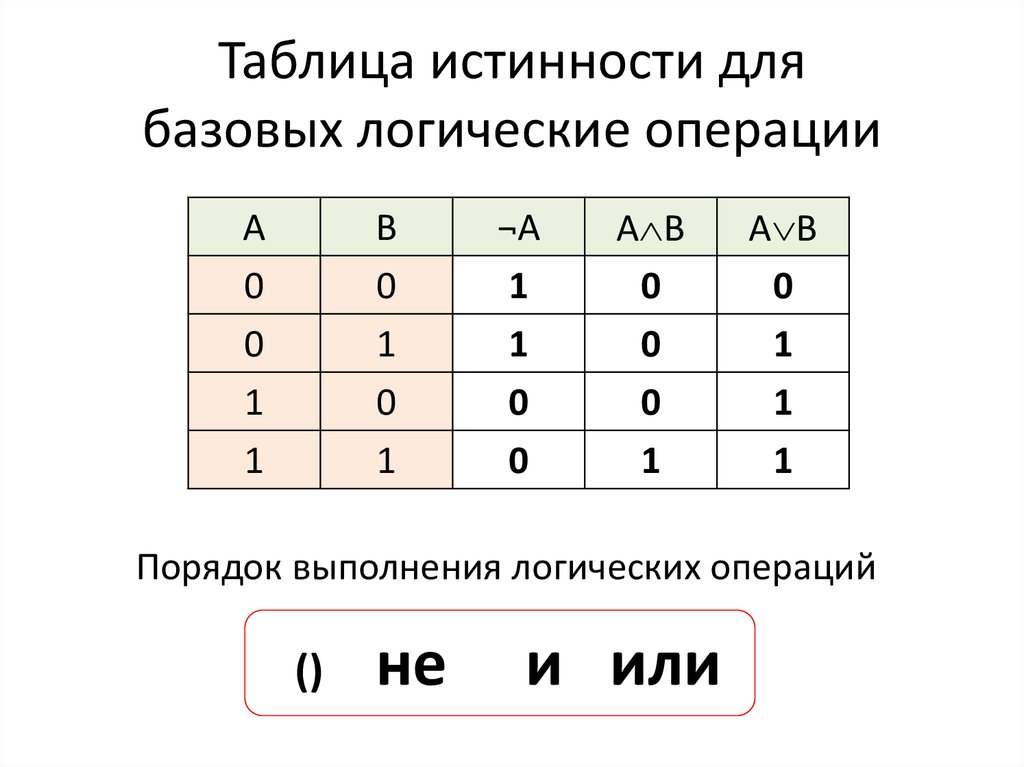
5.3. Таблицы истинности
Таблица истинности — это небольшая таблица, которая позволяет нам перечислить все возможные входные данные, и дать результаты для логических операторов. Потому что и и или каждый оператор имеет два операнда, в таблице истинности всего четыре строки, которые описывает семантику и.
и б а и б Ложь Ложь Ложь Ложь Правда Ложь Правда Ложь Ложь Правда Правда Правда
В таблице истинности мы иногда используем T и F как сокращение для двух Логические значения: вот таблица истинности, описывающая или:
и б а или б Ф Ф Ф Ф Т Т Т Ф Т Т Т Т
Третий логический оператор not принимает только один операнд, поэтому его таблица истинности имеет только две строки:
и не Ф Т Т Ф
5.
 4. Упрощение логических выражений
4. Упрощение логических выраженийНабор правил для упрощения и преобразования выражений называется алгеброй . Например, всем нам знакомы школьные правила алгебры, такие как:
п * 0 == 0
Здесь мы видим другую алгебру — булеву алгебру — который предоставляет правила для работы с булевыми значениями.
Во-первых, оператор и:
х и Ложь == Ложь Ложь и x == Ложь у и х == х и у х и правда == х Правда и х == х х и х == х
Вот некоторые соответствующие правила для оператора or:
х или Ложь == х Ложь или х == х у или х == х или у х или Истина == Истина Истина или х == Истина х или х == х
Два оператора not отменяют друг друга:
не (не х) == х
5.5. Условное выполнение
Чтобы писать полезные программы, почти всегда нужна возможность проверки
условия и соответствующим образом изменить поведение программы. Условный
операторы дают нам эту возможность. Самая простая форма - , если выписка:
Условный
операторы дают нам эту возможность. Самая простая форма - , если выписка:
если x % 2 == 0: print(x, "четно.") print("Знаете ли вы, что 2 - единственное простое четное число?") еще: print(x, " нечетно.") print("Знаете ли вы, что умножение двух нечетных чисел " + "всегда дает странный результат?")
Логическое выражение после оператора if называется условием . Если это правда, то выполняются все операторы с отступом. Если нет, то все операторы с отступом в предложении else выполняются.
Синтаксис оператора if выглядит следующим образом:
если БУЛЕВОЕ ВЫРАЖЕНИЕ: STATEMENTS_1 # Выполняется, если условие оценивается как True еще: STATEMENTS_2 # Выполняется, если условие оценивается как False
Аналогично определению функции из предыдущей главы и другим составным
операторы вроде for, оператор if состоит из строки заголовка и тела.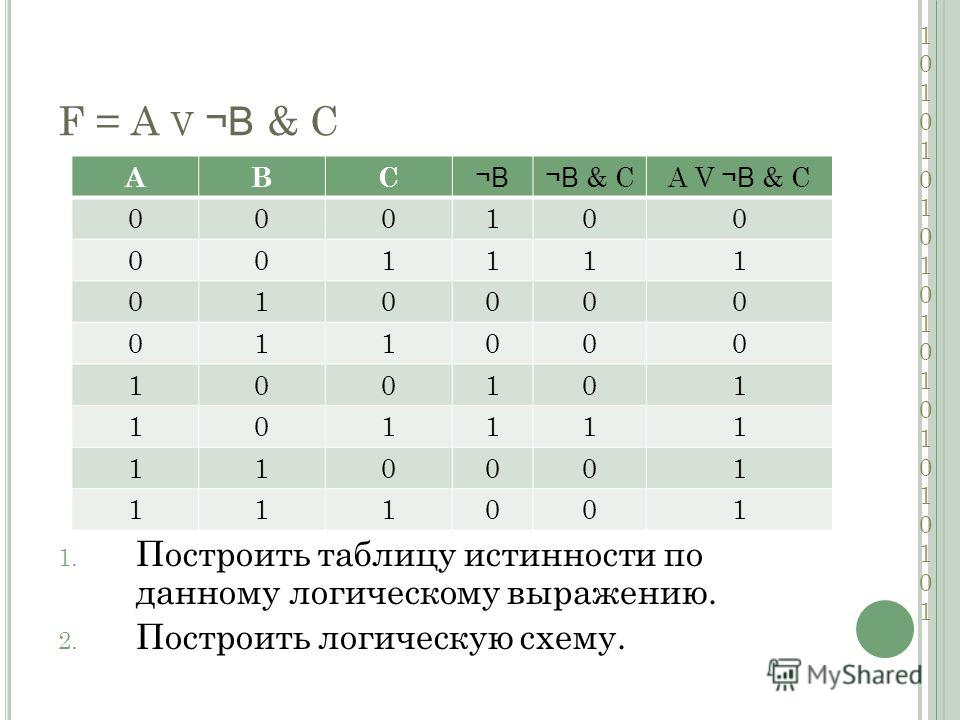 Заголовок
строка начинается с ключевого слова, если за ним следует логическое выражение и заканчивается
двоеточие (:).
Заголовок
строка начинается с ключевого слова, если за ним следует логическое выражение и заканчивается
двоеточие (:).
Следующие операторы с отступом называются блоком . Первый оператор без отступа отмечает конец блока.
Каждый из операторов внутри первого блока операторов выполняется в том порядке, в котором выражение оценивается как True. Весь первый блок утверждений пропускается, если логическое выражение оценивается как False, и вместо этого все операторы с отступом в предложении else выполняются.
Нет ограничений на количество утверждений, которые могут появляться в двух пунктах одного if, но в каждом блоке должно быть хотя бы одно выражение. Иногда полезно иметь раздел без заявлений (обычно в качестве хранителя места или подмостей, для кода, который мы еще не написали). В этом случае мы можем использовать оператор pass, который ничего не делает, кроме как выступает в качестве заполнителя.
если True: # Это всегда True, pass # так что это всегда выполняется, но ничего не делает еще: проходить
5.
 6. Пропуск предложения else
6. Пропуск предложения elseДругой формой оператора if является та, в которой предложение else полностью опущено. В этом случае, когда условие оценивается как True, операторы выполняется, в противном случае поток выполнения переходит к оператору после if.
если х < 0: print("Отрицательное число ", x, " здесь недопустимо.") х = 42 print("Вместо этого я решил использовать число 42.") print("Квадратный корень из ", x, "is", math.sqrt(x))
В этом случае функция печати, которая выводит квадратный корень, находится после if — not потому что мы оставили пустую строку, а из-за отступа кода. Обратите внимание, что вызов функции math.sqrt(x) выдаст ошибку, если у нас нет математического оператора импорта, обычно размещается в верхней части нашего скрипта.
Терминология Python
Документация Python иногда использует термин набор операторов для обозначения того, что мы
позвонили в блок здесь.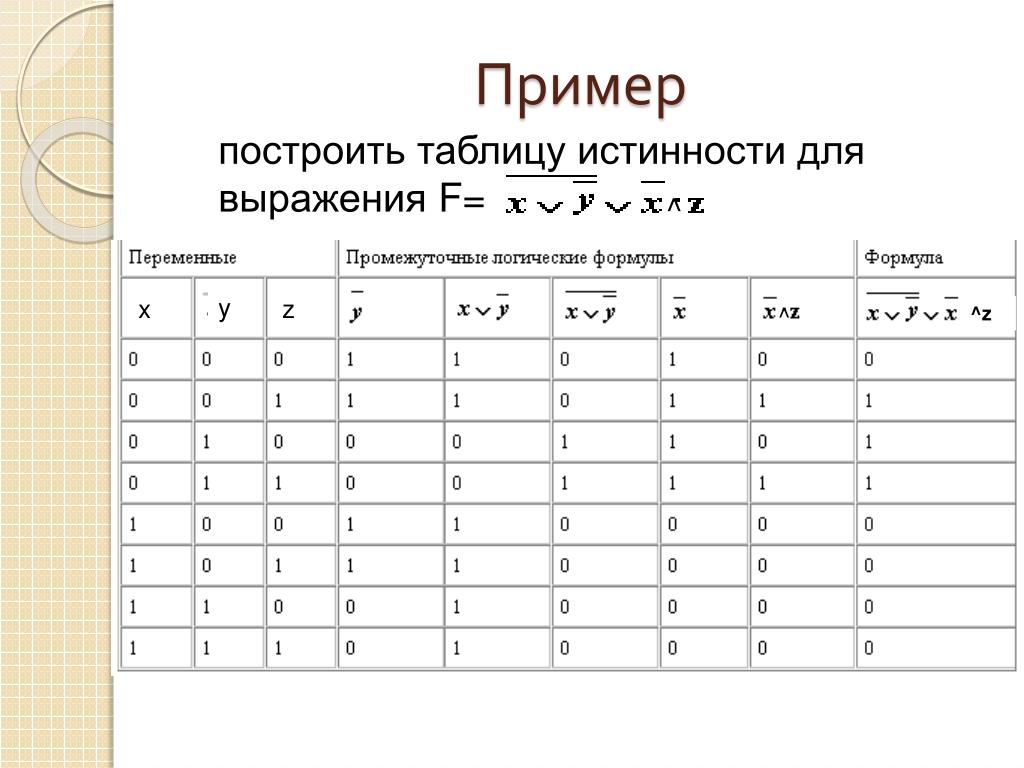 Они означают одно и то же, и поскольку большинство других языков и
Компьютерщики используют слово блок , мы будем придерживаться его.
Они означают одно и то же, и поскольку большинство других языков и
Компьютерщики используют слово блок , мы будем придерживаться его.
Также обратите внимание, что else не является оператором. Оператор if имеет два предложения , одно из которых является (необязательным) предложением else.
5.7. Связанные условные операторы
Иногда существует более двух возможностей, и нам нужно более двух ветви. Один из способов выразить такое вычисление — цепочка . условное :
если x < y: STATEMENTS_A Элиф х > у: STATEMENTS_B еще: STATEMENTS_C
Блок-схема этого связанного условного оператора
elif является сокращением от else if. Опять же, ровно одна ветвь будет казнен. Количество операторов elif не ограничено, а только один (и необязательный) оператор final else разрешен, и он должен быть последним ветка в заявлении:
если выбор == "a": функция_один() Элиф выбор == "b": функция_два() Элиф выбор == "с": функция_три() еще: print("Неверный выбор")
Каждое условие проверяется по порядку. Если первое ложно, проверяется следующее,
и так далее. Если одно из них истинно, выполняется соответствующая ветвь, и
заявление заканчивается. Даже если верно несколько условий, верно только первое
филиал выполняет.
Если первое ложно, проверяется следующее,
и так далее. Если одно из них истинно, выполняется соответствующая ветвь, и
заявление заканчивается. Даже если верно несколько условий, верно только первое
филиал выполняет.
5.8. Вложенные условные операторы
Одно условное выражение также может быть вложенным в другое. (это одна и та же тема опять-таки компонуемость!) Мы могли бы написать предыдущий пример выглядит следующим образом:
Блок-схема этого вложенного условного оператора
если x < y: STATEMENTS_A еще: если х > у: STATEMENTS_B еще: STATEMENTS_C
Внешнее условное предложение содержит две ветви. Вторая ветвь содержит еще один оператор if, который имеет две собственные ветви. Эти две ветви могут содержать также условные операторы.
Хотя отступ операторов делает структуру очевидной, вложенные
условные выражения очень быстро становятся трудными для чтения. В общем, это хорошо
Идея избегать их, когда мы можем.
В общем, это хорошо
Идея избегать их, когда мы можем.
Логические операторы часто позволяют упростить вложенные условные операторы. заявления. Например, мы можем переписать следующий код, используя один условно:
if 0 < x: # Предположим, что x здесь является целым числом если х < 10: print("x - положительная цифра")
Функция печати вызывается только в том случае, условные выражения, поэтому вместо приведенного выше, в котором используются два оператора if, каждый с простое условие, мы могли бы сделать более сложное условие, используя оператор и. Теперь мы только нужен один оператор if:
, если 0 < x и x < 10: print("x - положительная цифра")
5.10. Логические противоположности
Каждый из шести операторов отношения имеет логическую противоположность: например,
предположим, что мы можем получить водительские права, когда наш возраст больше или равен 17,
мы можем , а не получить водительские права, когда нам меньше 17 лет.
Обратите внимание, что вместо >= используется <.
оператор логическая противоположность == != != == < >= <= > > <= >= <
Понимание этих логических противоположностей позволяет иногда избавиться от не операторы. не операторы часто довольно трудно читать в компьютерном коде, и наши намерения обычно становятся яснее, если мы можем их устранить.
Например, если мы написали это Python:
если нет (возраст >= 17): print("Эй, ты слишком молод, чтобы получить водительские права!")
было бы понятнее использовать законы упрощения, и вместо этого напишите:
если возраст < 17 лет: print("Эй, ты слишком молод, чтобы получить водительские права!")
Два мощных закона упрощения (называемых законами де Моргана), которые часто полезны при работе со сложными булевыми выражениями:
не (х и у) == (не х) или (не у) не (x или y) == (не x) и (не y)
Например, предположим, что мы можем убить дракона, только если наша магия
световой меч заряжен до 90% или выше,
и у нас в защитном щите 100 и более единиц энергии.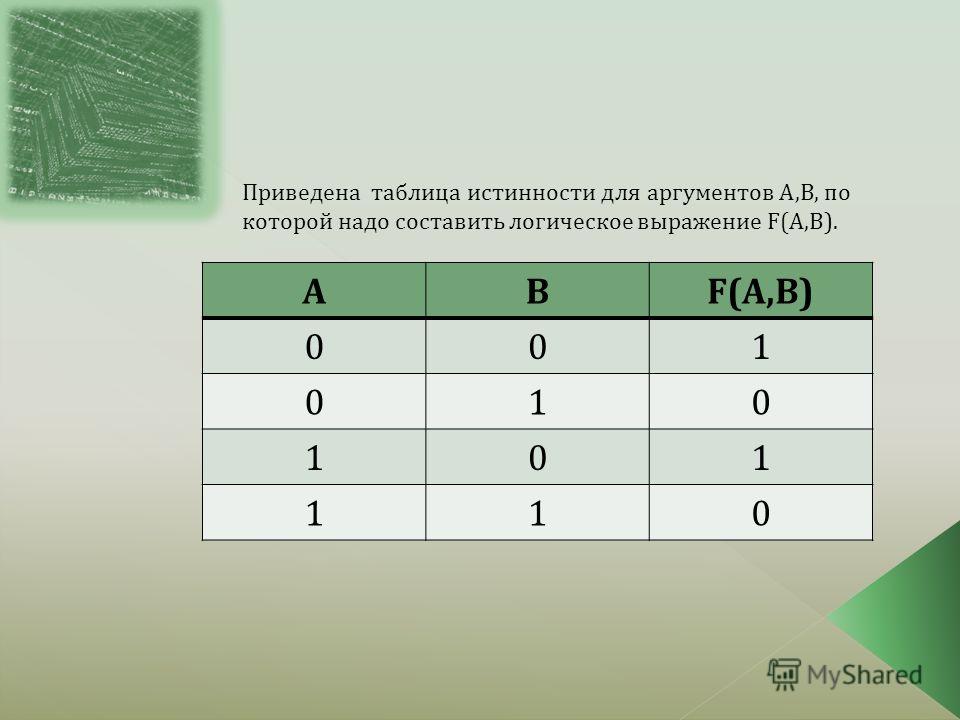 Находим этот фрагмент кода Python в игре:
Находим этот фрагмент кода Python в игре:
если нет ((sword_charge >= 0.90) и (shield_energy >= 100)): print("Ваша атака не имеет никакого эффекта, дракон поджарит вас до хрустящей корочки!") еще: print("Дракон сваливается в кучу. Вы спасаете великолепную принцессу!")
Законы де Моргана вместе с логическими противоположностями позволили бы нам переработайте условие в (возможно) более понятном виде:
если (sword_charge < 0,90) или (shield_energy < 100): print("Ваша атака не имеет никакого эффекта, дракон поджарит вас до хрустящей корочки!") еще: print("Дракон сваливается в кучу. Вы спасаете великолепную принцессу!")
Мы также можем избавиться от not, поменяв местами then и else части условного предложения. Итак, вот третья версия, тоже эквивалентная:
.
если (sword_charge >= 0.90) и (shield_energy >= 100): print("Дракон сваливается в кучу. Вы спасаете великолепную принцессу!") еще: print("Ваша атака не имеет никакого эффекта, дракон поджарит вас до хрустящей корочки!")
Эта версия, вероятно, лучшая из трех, потому что она очень точно соответствует начальное английское заявление. Ясность нашего кода (для других людей), и сделать так, чтобы код всегда делал то, что ожидалось. иметь высокий приоритет.
По мере развития наших навыков программирования мы обнаружим, что у нас есть
более чем один способ решения любой проблемы. Итак, хорошие программы разработаны .
Мы делаем выбор в пользу ясности, простоты и элегантности. Работа
название архитектор программного обеспечения многое говорит о том, что мы делаем — мы архитекторы которые разрабатывают наши продукты, чтобы сбалансировать красоту, функциональность, простоту и
ясность в наших творениях.
Подсказка
Как только наша программа заработает, мы должны немного поиграться, пытаясь отшлифовать ее. Пишите хорошие комментарии. Подумайте, будет ли код понятнее с разные имена переменных. Могли ли мы сделать это более элегантно? Должен мы скорее используем функцию? Можем ли мы упростить условные операторы?
Мы считаем наш код своим творением, своим произведением искусства! Мы делаем это здорово.
5.11. Преобразование типов
Мы впервые рассмотрели это в предыдущей главе. Пересмотреть еще раз не помешает!
Многие типы Python поставляются со встроенной функцией, которая пытается преобразовать значения другого типа в свой собственный тип. Функция int, например, принимает любое значение и преобразует его в целое число, если это возможно, или жалуется иначе:
>>> целое ("32")
32
>>> int("Привет")
ValueError: недопустимый литерал для int() с основанием 10: «Привет»
int также может преобразовывать значения с плавающей запятой в целые числа, но помните что он усекает дробную часть:
>>> целое (-2.3) -2 >>> целое(3.99999) 3 >>> интервал("42") 42 >>> целое (1.0) 1
Функция float преобразует целые числа и строки в числа с плавающей запятой. номера:
>>> с плавающей запятой(32)
32,0
>>> с плавающей запятой ("3.14159")
3.14159
>>> с плавающей запятой(1)
1,0
Может показаться странным, что Python различает целочисленное значение 1 от значение с плавающей запятой 1.0. Они могут представлять одно и то же число, но они относятся к разным типам. Причина в том, что они представлены по-разному. внутри компьютера.
Функция str преобразует любой переданный ей аргумент в тип строка:
>>> ул(32) '32' >>> ул(3.14149) «3.14149» >>> ул(правда) 'Истинный' >>> ул(правда) Traceback (последний последний вызов): Файл "<интерактивный ввод>", строка 1, в <модуль> NameError: имя «истина» не определено
str будет работать с любым значением и преобразовывать его в строку. В качестве
упоминалось ранее, True — это логическое значение; true — это обычное имя переменной,
и здесь не определено, поэтому мы получаем ошибку.
5.12. Гистограмма черепахи
Черепаха обладает гораздо большей силой, чем мы видели до сих пор. Полный документацию можно найти на http://docs.python.org/py3k/library/turtle.html или в PyScripter используйте Справка и найдите модуль черепахи.
Вот несколько новых трюков для наших черепах:
- Мы можем заставить черепаху отображать текст на холсте в текущей позиции черепахи. Способ сделать это alex.write("Привет").
- Мы можем заполнить форму (круг, полукруг, треугольник и т. д.) цветом. Это двухэтапный процесс. Сначала мы вызываем метод alex.begin_fill(), затем рисуем фигуру, затем вызываем alex.end_fill().
- Ранее мы установили цвет нашей черепахи — теперь мы также можем задать цвет ее заливки, что необязательно. быть таким же, как черепаха и цвет пера. Мы используем alex.color("blue","red"), чтобы установить черепаху рисовать синим цветом и заполнять красным.
Итак, мы можем заставить Тесс нарисовать гистограмму? Давайте начнем с некоторых данных, которые нужно нанести на карту:
xs = [48, 117, 200, 240, 160, 260, 220]
В соответствии с каждым измерением данных мы нарисуем простой прямоугольник такой высоты с фиксированная ширина.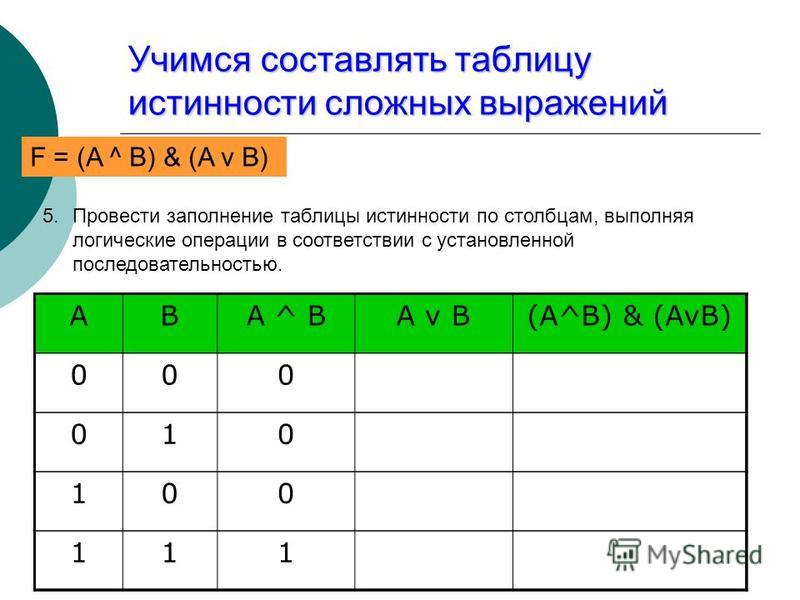
def draw_bar(t, height): """ Заставьте черепаху t нарисовать одну полосу высотой. """ т.левый(90) t.forward(height) # Нарисуйте левую сторону т.право(90) t.forward(40) # Ширина полосы по верху т.право(90) t.forward(height) # И снова вниз! t.left(90) # Поместите черепаху лицом туда, где мы ее нашли. t.forward(10) # Оставляем небольшой промежуток после каждого бара ... for v in xs: # Предположим, что xs и tess готовы draw_bar (тесс, v)
Ладно, не фантастично, но начало хорошее! Главное здесь было мысленное разбиение на части, или как мы разбили проблему на более мелкие части. Наш кусок состоит в том, чтобы нарисовать одну полосу, и мы написали для этого функцию. Тогда для всего chart мы неоднократно вызывали нашу функцию.
Далее в верхней части каждого столбца мы напечатаем значение данных.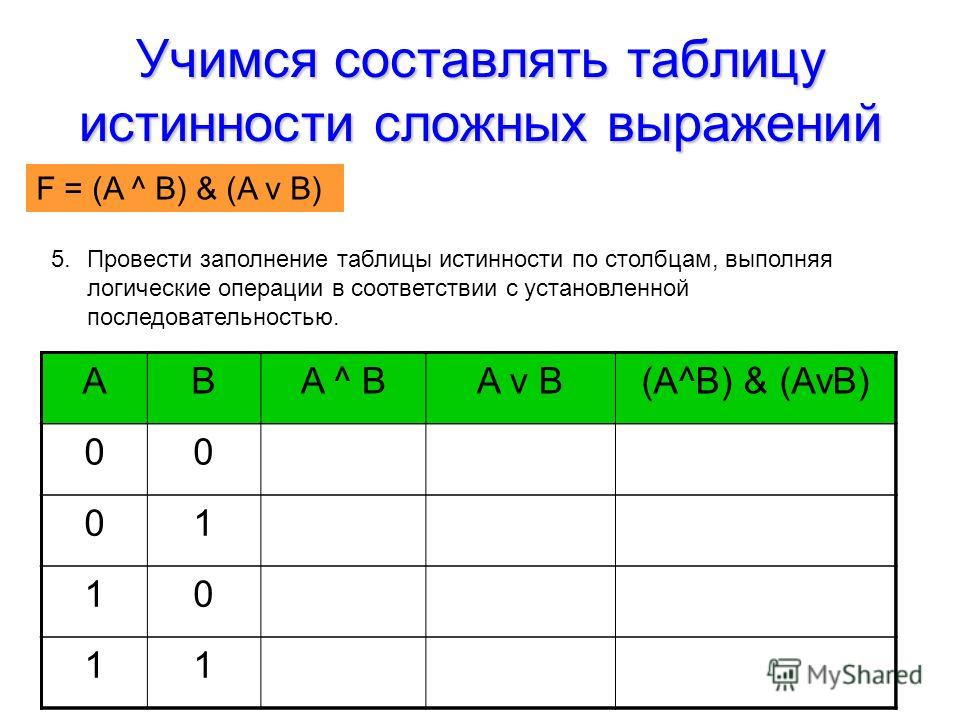 Мы сделаем это в теле draw_bar, добавив t.write(' ' + str(height))
как новая третья линия тела.
Мы поставили небольшой пробел перед номером и повернули
число в строку. Без этого дополнительного пространства мы склонны
чтобы неловко прижать наш текст к полосе слева.
Теперь результат выглядит намного лучше:
Мы сделаем это в теле draw_bar, добавив t.write(' ' + str(height))
как новая третья линия тела.
Мы поставили небольшой пробел перед номером и повернули
число в строку. Без этого дополнительного пространства мы склонны
чтобы неловко прижать наш текст к полосе слева.
Теперь результат выглядит намного лучше:
А теперь добавим по две строки для заполнения каждой полосы. Наша окончательная программа теперь выглядит так:
def draw_bar(t, height): """ Заставьте черепаху t нарисовать одну полосу высотой. """ t.begin_fill() # Добавлена эта строка т.левый(90) t.вперед(высота) t.write(" "+ ул(высота)) т.право(90) т.вперед(40) т.право(90) t.вперед(высота) т.левый(90) t.end_fill() # Добавлена эта строка т.вперед(10) wn = черепаха.Screen() # Настраиваем окно и его атрибуты wn.bgcolor("светло-зеленый") tess = черепаха.Turtle() # Создаем tess и устанавливаем некоторые атрибуты tess.color ("синий", "красный") tess.pensize (3) xs = [48 117 200 240 160 260 220] для а в xs: draw_bar (тесс, а) wn.mainloop()
Он производит следующее, что больше удовлетворяет:
Ммм. Возможно, бруски не должны стыковаться друг с другом внизу. Нам нужно будет взять ручку, делая зазор между стержнями. Мы оставим это в качестве упражнения для вас!
5.13. Глоссарий
- блок
- Группа последовательных операторов с одинаковым отступом.
- корпус
- Блок операторов в составном операторе, следующий за заголовок.
- Булева алгебра
- Некоторые правила перестановки и рассуждений о логических выражениях.
- Логическое выражение
- Выражение, которое либо истинно, либо ложно.
- Логическое значение
- Имеется ровно два логических значения: True и False.
 логический
значения получаются, когда логическое выражение оценивается Python
переводчик. Они имеют тип bool.
логический
значения получаются, когда логическое выражение оценивается Python
переводчик. Они имеют тип bool. - филиал
- Один из возможных путей потока исполнения, определяемый условное исполнение.
- связанное условие
- Условная ветвь с более чем двумя возможными потоками выполнения. В Связанные в цепочку условные операторы Python записываются с помощью if ... elif ... else заявления.
- оператор сравнения
- Один из шести операторов, сравнивающих два значения: ==, !=, >, <, >= и <=.
- состояние
- Логическое выражение в условном операторе, определяющее, какой ветка выполнена.
- условное выражение
- Оператор, управляющий потоком выполнения в зависимости от некоторых условие. В Python ключевые слова if, elif и else используется для условных операторов.
- логический оператор
- Один из операторов, объединяющий логические выражения: и, или, и нет.
- вложение
- Одна структура программы внутри другой, например условный оператор
внутри ветви другого условного оператора.

- подсказка
- Визуальный сигнал, сообщающий пользователю, что система готова к приему входных данных.
- таблица истинности
- Краткая таблица логических значений, которая может описать семантику оператора.
- преобразование типа
- Явный вызов функции, которая принимает значение одного типа и вычисляет соответствующее значение другого типа.
- код переноса в функцию
- Процесс добавления заголовка функции и параметров к последовательности операторов программы часто называют «обертыванием кода в функция". Этот процесс очень полезен всякий раз, когда программа рассматриваемые утверждения будут использоваться несколько раз. это еще полезнее, когда это позволяет программисту выражать свои мыслительные фрагментирование и то, как они разбили сложную проблему на части.
5.14. Упражнения
Предположим, дни недели пронумерованы 0,1,2,3,4,5,6 с воскресенья по субботу. Напишите функцию, которой дан номер дня, и она возвращает название дня (строку).

Вы отправляетесь в чудесный отпуск (возможно, в тюрьму, если вам не нравятся веселые упражнения) выезд в день номер 3 (среда). Вы возвращаетесь домой после 137 ночей. Напишите общую версию программы, которая запрашивает номер начального дня и продолжительность вашего пребывания, и он сообщит вам название дня недели, в который вы вернетесь.
Укажите логические противоположности этих условий
- а > б
- а >= б
- a >= 18 и день == 3
- a >= 18 и день != 3
Что оценивают эти выражения?
- 3 == 3
- 3 != 3
- 3 >= 4
- нет (3 < 4)
Заполните эту таблицу истинности:
р
q
р
(не (p и q)) или r
Ф
Ф
Ф
?
Ф
Ф
Т
?
Ф
Т
Ф
?
Ф
Т
Т
?
Т
Ф
Ф
?
Т
Ф
Т
?
Т
Т
Ф
?
Т
Т
Т
?
Напишите функцию, которая получает экзаменационную оценку и возвращает строку — оценка за эту марку — по этой схеме:
Знак
Марка
>= 75
Первый
[70-75)
Верхняя секунда
[60-70)
Второй
[50-60)
Третий
[45-50)
Приложение F1
[40-45)
Ф2
< 40
Ф3
Квадратные и круглые скобки обозначают закрытые и открытые интервалы.
 Закрытый интервал включает число, а открытый интервал исключает его. Таким образом, 39,99999 дает оценку F3, а 40 — оценку F2.
Предположим,
Закрытый интервал включает число, а открытый интервал исключает его. Таким образом, 39,99999 дает оценку F3, а 40 — оценку F2.
Предположим,xs = [83, 75, 74,9, 70, 69,9, 65, 60, 59,9, 55, 50, 49,9, 45, 44,9, 40, 39,9, 2, 0]Проверьте свою функцию, напечатав оценку и оценку для всех элементов в этом списке.
Измените программу гистограммы черепахи таким образом, чтобы перо было направлено вверх для небольших промежутков между столбцами.
Измените программу гистограммы черепахи, чтобы полоса для любого значения 200 или более закрашены красным цветом, значения между [100 и 200) закрашены желтым цветом, а столбцы, представляющие значения меньше 100, окрашены зеленым цветом.
В программе черепашьей гистограммы, что вы ожидаете, если один или несколько значений данных в списке является отрицательным? Попробуйте. Изменить программа так, что когда она печатает текстовое значение для отрицательных баров, она помещает текст под нижней частью панели.

Напишите функцию find_hypot, которая по заданным длинам двух сторон прямоугольного треугольника возвращает длина гипотенузы. (Подсказка: x ** 0,5 вернет квадратный корень.)
Напишите функцию is_rightangled, которая, учитывая длину трех сторон треугольника, определит, является ли треугольник прямоугольным. Предположим, что третий аргумент функция всегда является самой длинной стороной. Он вернет True, если треугольник прямоугольный или False в противном случае.
Подсказка: арифметика с плавающей запятой не всегда точна, поэтому небезопасно проверять числа с плавающей запятой на равенство. Если хороший программист хочет знать, x равен или достаточно близок к y, они, вероятно, закодировали бы его как:
if abs(x-y) < 0.000001: # Если x приблизительно равен y ...Расширьте приведенную выше программу, чтобы стороны могли быть переданы функции в любом порядке.
Если вас интересует, почему арифметические операции с плавающей запятой иногда бывают неточными, на кусочке бумаги, разделите 10 на 3 и запишите десятичный результат.
 Вы обнаружите, что это не прекращается,
поэтому вам понадобится бесконечно длинный лист бумаги. Представление чисел в компьютере
память или на вашем калькуляторе имеют аналогичные проблемы: память конечна, и некоторые цифры, возможно, придется отбросить. Настолько мал
закрадываются неточности. Попробуйте этот скрипт:
Вы обнаружите, что это не прекращается,
поэтому вам понадобится бесконечно длинный лист бумаги. Представление чисел в компьютере
память или на вашем калькуляторе имеют аналогичные проблемы: память конечна, и некоторые цифры, возможно, придется отбросить. Настолько мал
закрадываются неточности. Попробуйте этот скрипт:
Логические операторы Swift: разработка iOS для начинающих
В Swift есть три логических оператора: && , || и ! .
Вот таблица с описанием этих операторов:
| Оператор | Имя | Описание | Пример |
|---|---|---|---|
| && | Логический оператор И. | Тогда и только тогда, когда оба операнда истина , условие истина .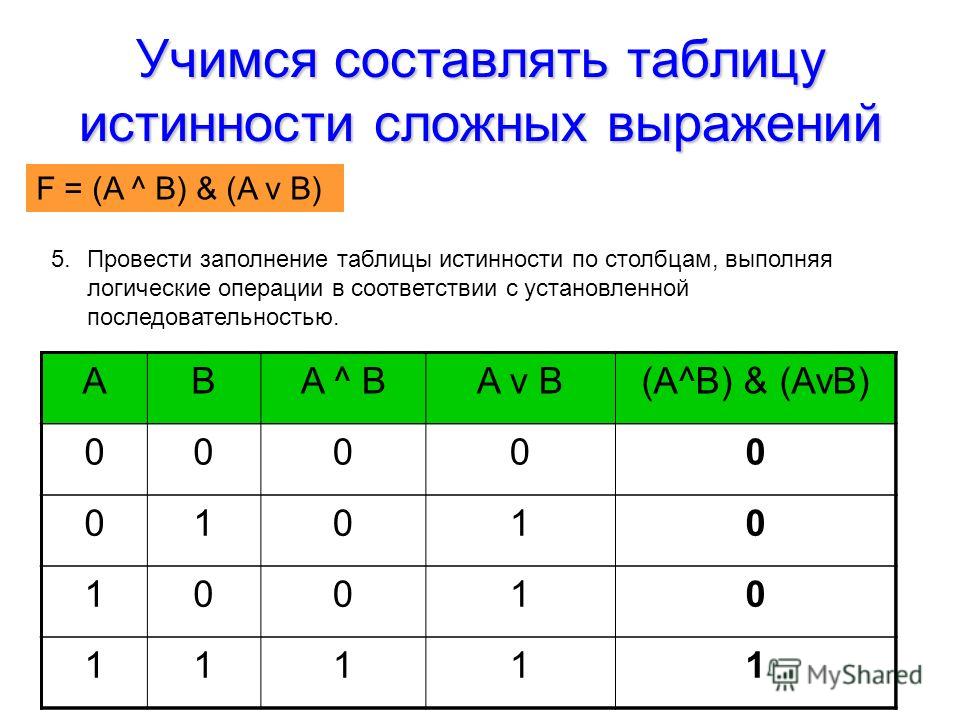 | истина && ложь = ложь |
| || | Логический оператор ИЛИ. | Если любой из двух операндов истина , условие истина . | верно || ложь = правда |
| ! | Логический оператор НЕ. | Инвертирует логическое состояние операнда. Если условие истинно , логическое НЕ делает его ложным . | !true = false |
Логические операторы используются для соединения значений истинности.
Они чрезвычайно полезны в программировании, и вы будете часто использовать их на протяжении всей своей карьеры разработчика программного обеспечения.
В этом руководстве вы узнаете, что такое логические операторы и логические выражения.
В самой следующей главе вы будете использовать их, поэтому убедитесь, что понимаете, как они работают и почему они полезны.
Эта глава является частью совершенно бесплатного руководства по Swift для начинающих. Прежде чем читать эту, убедитесь, что вы прошли все главы с самого начала.
Отказ от ответственности : Чтобы изучить Swift, вы должны повторить все, что вы видите в этом руководстве и в следующих руководствах. Если вы только читаете руководства, вы ничему не научитесь!
Логические операторы
Логические операторы используются в повседневной жизни.
Например, взгляните на это предложение: «Если сегодня жаркий и солнечный день, пойдем на пляж».
В этом самом предложении используется логический оператор «и» для объединения двух логических выражений.
Чтобы понять, что это значит, давайте перепишем предложение:
«Если сегодня солнечный день и если жаркий день, пойдем на пляж».
Теперь давайте разделим соответствующие части предложения на три части:
- Солнечный день
- И
- Жаркий день
Первая часть «Солнечный день» является логическим выражением. Другими словами, оно может быть истинным или ложным.
Другими словами, оно может быть истинным или ложным.
Слово «и» является логическим оператором. Он связывает первое логическое выражение со вторым.
Вторая часть предложения «Жаркий день» является вторым логическим выражением. Оно также может быть либо истинным, либо ложным.
Только если оба этих логических выражения верны, мы идем на пляж. Если одно или оба из них ложны, мы не пойдем на пляж.
Логические операторы в Swift
Когда вы разговариваете с компьютером, вы не можете просто сказать слово «и».
Вместо этого вы должны использовать логический оператор, понятный компьютеру.
В Swift логические операторы:
- && для AND
- || для ИЛИ
- ! вместо НЕ
Теперь вернемся к примеру с пляжем: «Если сегодня жаркий и солнечный день, пойдем на пляж».
В Swift вы можете переформулировать предложение, например, следующим образом:
var isSunny = true вар исхот = ложь var beachTime = солнечно && жарко print(beachTime)
Вывод:
false
Как видите, теперь эта программа может принять решение, идти вам на пляж или нет. Все, что вам нужно сделать, это указать истинные значения переменных — это солнечный , а — это горячий .
Все, что вам нужно сделать, это указать истинные значения переменных — это солнечный , а — это горячий .
Далее поговорим подробнее о логических операторах и таблицах истинности, которые помогут вам наглядно представить, как они работают.
Логические операторы и таблицы истинности
В предыдущем разделе вы видели пример использования оператора AND ( && ) для проверки истинности двух логических выражений.
Теперь давайте рассмотрим предложение: «Если сегодня жаркий и солнечный день, пойдем на пляж».
Возможны 4 сценария:
- Не солнечно и не жарко --> нет пляжа .
- Не солнечно, но жарко --> нет пляжа .
- Солнечно, но не жарко –> нет пляжа .
- Солнечно и жарко –> пляжное время .
Более формальным способом представления этих сценариев было бы построение таблицы истинности следующим образом:
| Солнечно | Жарко | Солнечно и жарко (пляжное время) | 6 0011 false | false | false |
|---|---|---|---|---|---|
| false | true | false | |||
| true | false | false | |||
| true | true | true |
Эта таблица истинности учитывает все возможные комбинации типов погоды.
В данном случае их четыре.
Крайний правый столбец в таблице истинности — это столбец результатов для двух логических выражений. В нашем примере приведенная выше таблица истинности показывает сценарии, в которых вам следует или не следует идти на пляж.
Вот как использовать таблицу истинности:
- Проверьте прогноз погоды, чтобы определить значения истинности для «Солнечно» и «Жарко».
- Используйте таблицу истинности, чтобы найти строку, которая соответствует истинным значениям из отчета о погоде.
- В соответствующей правой колонке указано, пора ли сейчас на пляж или нет.
Круто, не так ли?
Теперь, когда вы понимаете, что такое таблица истинности, давайте посмотрим на общие таблицы истинности логических операторов в Swift.
&& Таблица истинности
Имея два логических выражения A и B , которые могут быть либо истинными, либо ложными, вот таблица истинности для оператора И ( && ):
| 0 A | 0 | A && B | ||
|---|---|---|---|---|
| FALSE | ЛОЖЬ | ЛОЖЬ | ||
| ЛЕСС | TRUE | FALES0015| FALSE | FALSE | |
| TRUE | TRUE | TRUE |
только для того, чтобы взять домой, и это, и это, и RELECT and Poperator ( && 99999999999999 гг. выражения истинны .
выражения истинны .
|| Таблица истинности
Имея два логических выражения A и B , которые могут быть либо истинными, либо ложными, вот таблица истинности для ИЛИ ( || ) оператор:
| A | B | A || B |
|---|---|---|
| false | false | false |
| false | true | true |
| true | false | true |
| true | true | true |
Чтобы забрать домой, результат оператора ИЛИ может быть только ложно если ни одно из логических выражений не является истинным .
! Таблица истинности
Для данного единственного логического выражения A , которое может быть либо истинным, либо ложным, вот таблица истинности для оператора НЕ ( ! ).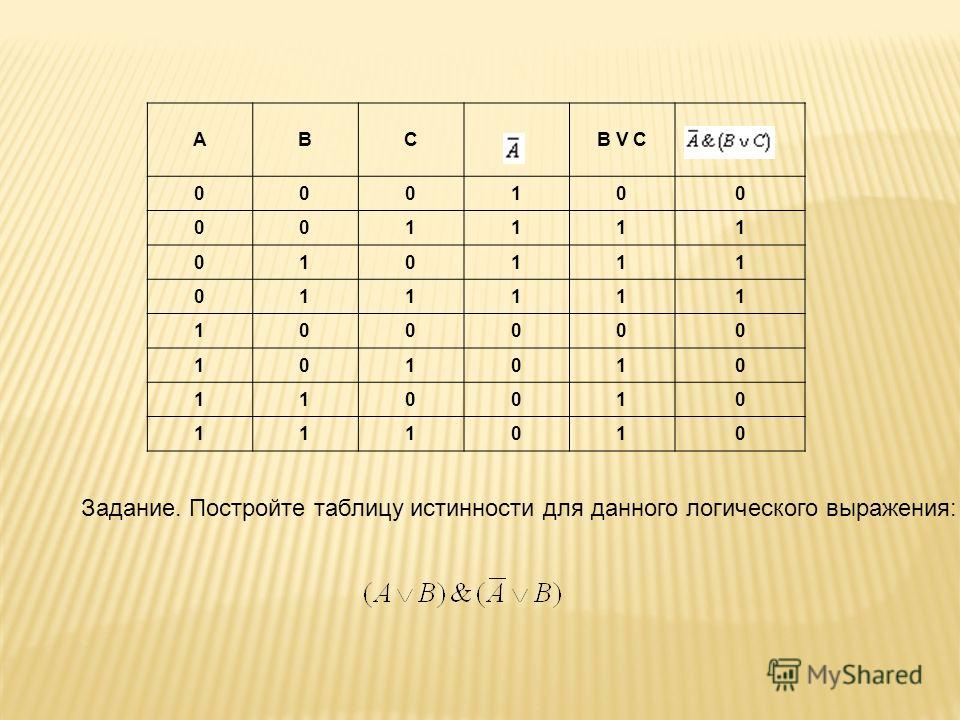
| A | !A |
|---|---|
| false | true |
| true | false |
In other words, the NOT operator ( ! ) превращает истинных в ложных и наоборот.
И последнее, но не менее важное: давайте рассмотрим несколько примеров с логическими операторами в Swift.
Примеры с логическими операторами в Swift
Давайте рассмотрим несколько полезных примеров логических выражений в Swift.
Ранее в этой главе вы уже видели пример оператора AND (&&) в задаче о посетителях пляжа.
Давайте посмотрим, как использовать ИЛИ ( || ) и НЕ ( ! ).
Например, давайте создадим два логических значения isStudying и isWorking, и определим занят человек или нет:
var isStudying = true вар isWorking = ложь var isBusy = isStudying || работает print(isBusy)
Вывод:
true
В этом примере человеку достаточно либо работать, либо учиться, чтобы быть занятым.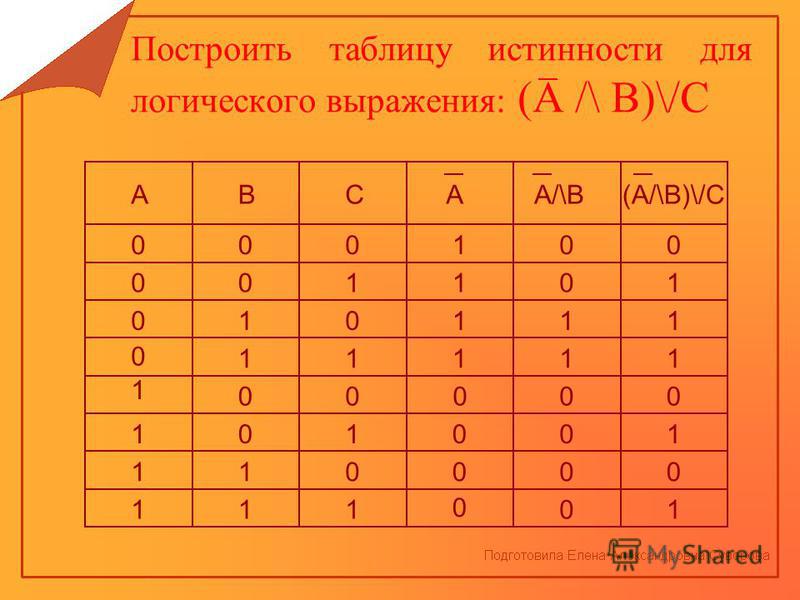 Человек не занят только тогда, когда он не учится и не работает.
Человек не занят только тогда, когда он не учится и не работает.
Наконец, давайте также рассмотрим пример использования оператора NOT.
переменная isSunny = истина var notSunny = !isSunny print(notSunny)
Вывод:
false
Здесь оператор НЕ переворачивает значение логического значения isSunny . Если это true , оператор NOT превращает его false и наоборот.
Следующая глава: Операторы If-Else в Swift
Заключение
Сегодня вы узнали, как использовать логические операторы в Swift.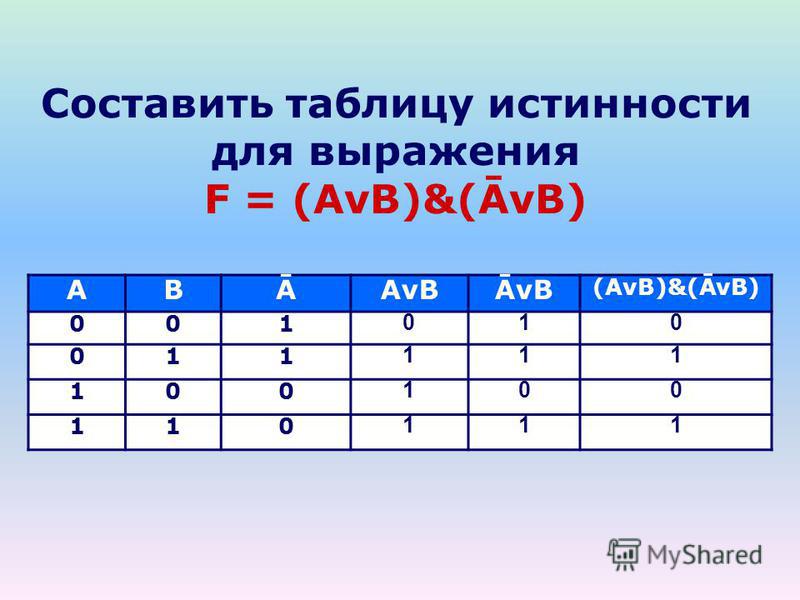



 Определите, какому столбцу соответствует каждая из переменных
Определите, какому столбцу соответствует каждая из переменных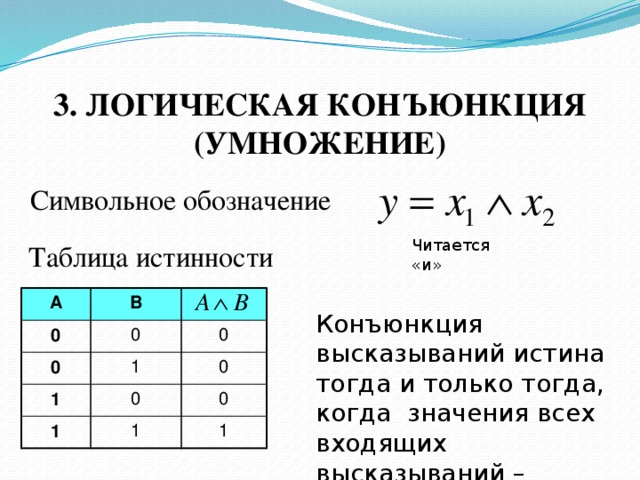
 Определите, какому столбцу соответствует каждая из переменных
Определите, какому столбцу соответствует каждая из переменных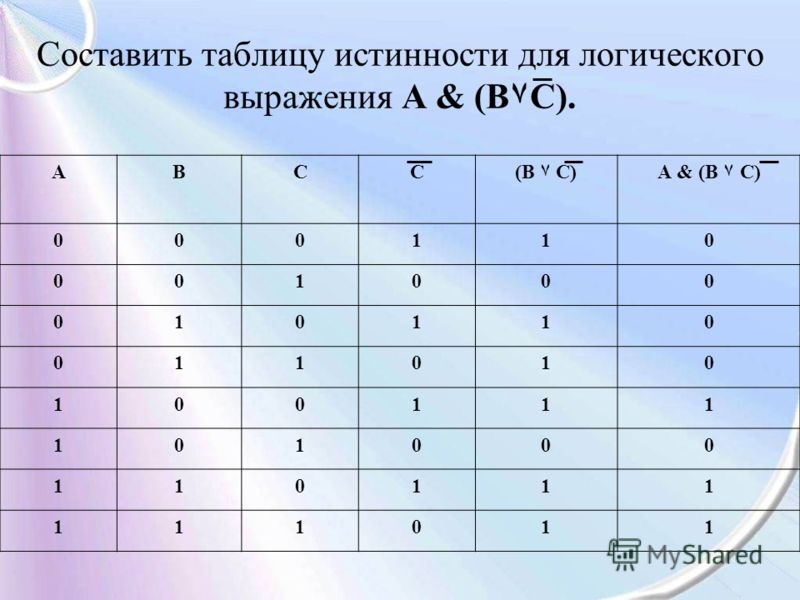


 3)
-2
>>> целое(3.99999)
3
>>> интервал("42")
42
>>> целое (1.0)
1
3)
-2
>>> целое(3.99999)
3
>>> интервал("42")
42
>>> целое (1.0)
1
 bgcolor("светло-зеленый")
tess = черепаха.Turtle() # Создаем tess и устанавливаем некоторые атрибуты
tess.color ("синий", "красный")
tess.pensize (3)
xs = [48 117 200 240 160 260 220]
для а в xs:
draw_bar (тесс, а)
wn.mainloop()
bgcolor("светло-зеленый")
tess = черепаха.Turtle() # Создаем tess и устанавливаем некоторые атрибуты
tess.color ("синий", "красный")
tess.pensize (3)
xs = [48 117 200 240 160 260 220]
для а в xs:
draw_bar (тесс, а)
wn.mainloop()
 логический
значения получаются, когда логическое выражение оценивается Python
переводчик. Они имеют тип bool.
логический
значения получаются, когда логическое выражение оценивается Python
переводчик. Они имеют тип bool.
 Закрытый интервал включает число, а открытый интервал исключает его. Таким образом, 39,99999 дает оценку F3, а 40 — оценку F2.
Предположим,
Закрытый интервал включает число, а открытый интервал исключает его. Таким образом, 39,99999 дает оценку F3, а 40 — оценку F2.
Предположим,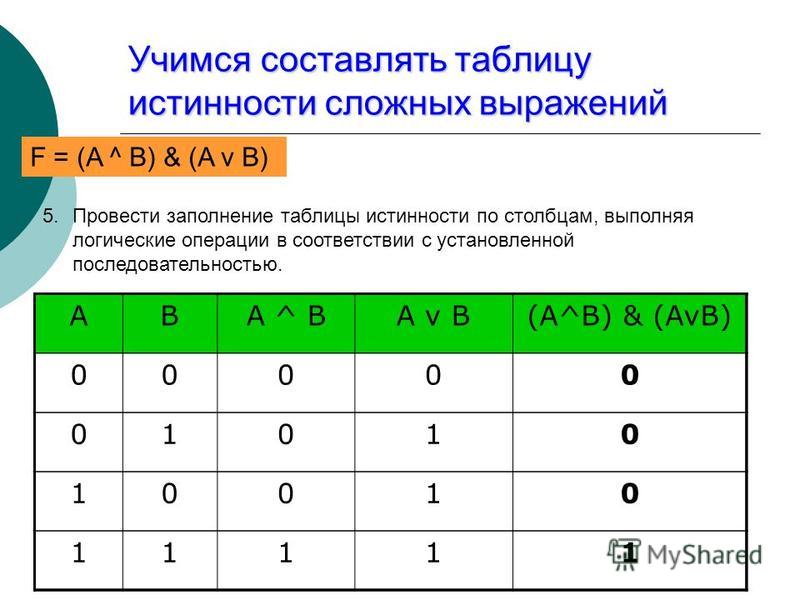
 Вы обнаружите, что это не прекращается,
поэтому вам понадобится бесконечно длинный лист бумаги. Представление чисел в компьютере
память или на вашем калькуляторе имеют аналогичные проблемы: память конечна, и некоторые цифры, возможно, придется отбросить. Настолько мал
закрадываются неточности. Попробуйте этот скрипт:
Вы обнаружите, что это не прекращается,
поэтому вам понадобится бесконечно длинный лист бумаги. Представление чисел в компьютере
память или на вашем калькуляторе имеют аналогичные проблемы: память конечна, и некоторые цифры, возможно, придется отбросить. Настолько мал
закрадываются неточности. Попробуйте этот скрипт: