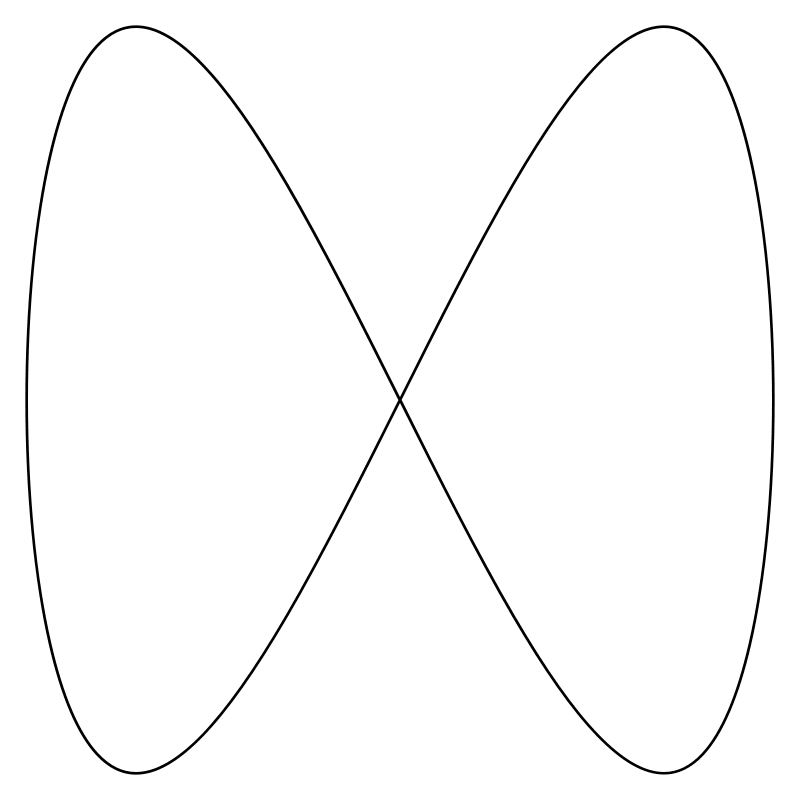
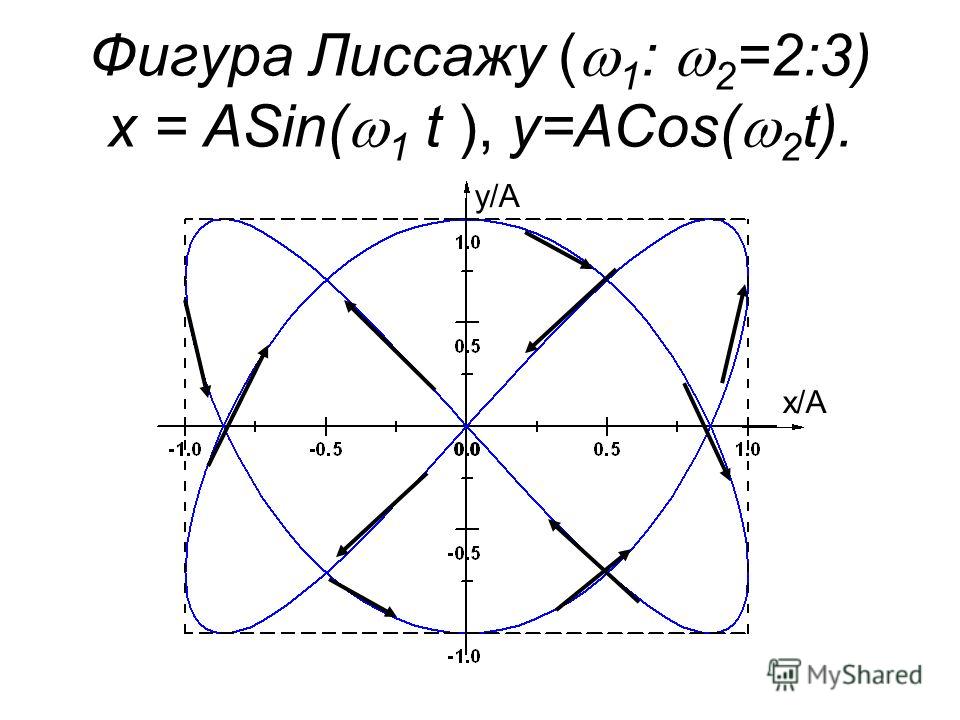
Моделирование фигур Лиссажу
Содержание
Введение.
Глава 1.Исследование гармонических колебаний с помощью фигур Лиссажу
1.1 Гармонические колебания.
1.2 Фигуры Лиссажу.
Глава 2.Моделирование фигур Лиссажу в среде MS Excel
2.1 Анализ среды MS Excel
2.2 Построение фигур Лиссажу средствами MS Excel
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Заключение
Список использованной литературы
Тема данной исследовательской работы: Моделирование фигур Лиссажу.
Настоящее исследование посвящено актуальной проблеме изучения фигур Лиссажу в курсах физики и математики.
Фигуры Лиссажу используют для сравнения гармонических колебаний, которые изучаются в курсе физики. Но в реальности провести опыты, в которых можно наблюдать и изучать колебательный процесс и его характеристики сложно. В ходе математического и компьютерного моделирования фигур Лиссажу можно исследовать соотношение между частотами и фазами гармонических колебаний.
Цель работы: показать возможности применения математических функций среды MS Excel для моделирования некоторых физических явлений.
Достижение поставленной цели предполагает решение следующих задач:
1.Проанализировать литературу по теме исследования.
2.Раскрыть понятие фигуры Лиссажу.
3.Рассмотреть способы построения графиков в среде MS Excel.
4.Разработать модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
Объектом исследования являются Фигуры Лиссажу. Предмет исследования: наглядное построение фигур Лиссажу. Методы исследования: для решения поставленных задач в работе используется теоретические и эмпирические методы.
1.1. Гармонические колебания
Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.
Гармоническое колебание, как математическая модель участвует в множестве физических процессов, которые можно использовать для передачи информации.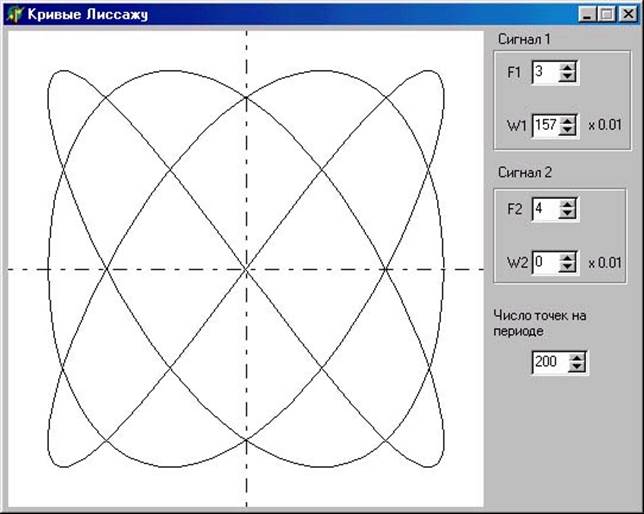 Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.
Многие системы совершают движение по гармоническому закону вполне естественным образом. В пример можно привести обычное раскачивание на качелях, ритмичные движения ног продолжали незатухающие колебания механического маятника, которым и являются качели.
Способы представления гармонических колебаний:[1;82-84]
- Аналитическая форма (формула):
2. Графическое представление (построение): Этот способ наглядно может показать вид и свойства данного явления.
- Гармоническое колебание изменяется во времени периодически. Период каждого совершённого колебания равен .
- Амплитуда (наибольшее значение) равна . Скорость изменения колебания во времени определяется круговой частотой , которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. — начальная фаза колебательного процесса. При совершении единичного гармонического колебания фаза особой роли не играет, а когда совершается несколько подобных колебаний, то даёт понять о местонахождении колебаний на оси времени друг относительно друга.
 Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
3. Векторное представление (делает очень наглядным фазовые и амплитудные соотношения между ними):
Эта формула выводится, если известна начальная фаза и амплитуда, т.е. значения при
Возьмём за гипотенузу прямоугольного треугольника, тогда будет в качестве его катета. Можно сказать, что сейчас гармоническому колебанию дали геометрическое представление. Такое представление гармонического колебания называют векторной диаграммой.
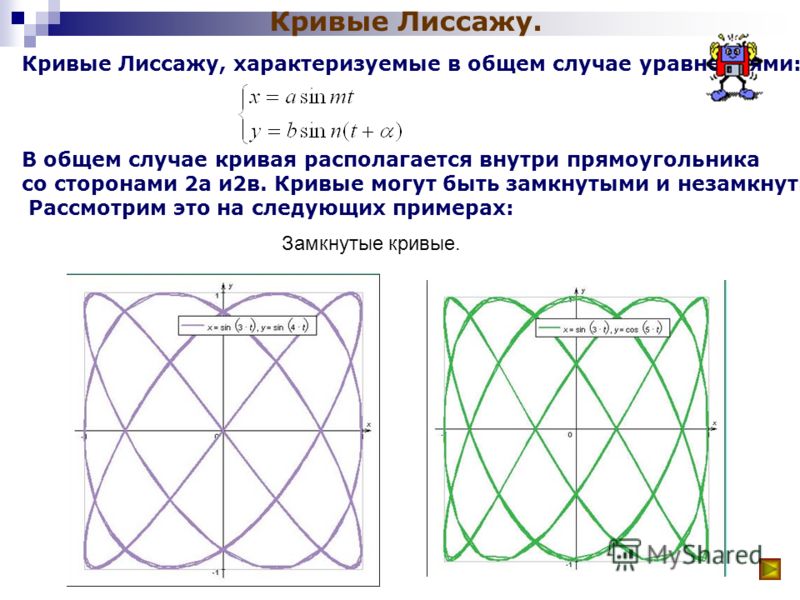
1.2 Фигуры Лиссажу
Фигуры Лиссажу — траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Эти фигуры, впервые изученные французским учёным Жюлем Антуаном Лиссажу.
Устройство для построения фигур Лиссажу — осциллограф. Изобретение относится к радиоизмерительной технике и может быть использовано для исследования параметров электрических сигналов.
Известные способы регистрации фигур Лиссажу с помощью двух координатных регистрирующих устройств позволяют производить измерения в ограниченном диапазоне частот и при отсутствии помех. Целью изобретения является создание способа регистрации фигур Лиссажу в широком диапазоне частот и при наличии помех.
Эти фигуры используют для осциллографического метода сравнения частот.
Осциллографический метод сравнениячастот:[2;97-98]
В качестве устройства сравнения частот используется осциллограф с отключённой разверткой (Развертка— это линия, которую чертит луч на экране при отсутствии исследуемого сигнала в результате действия только одного развертывающего напряжения.), таким образом информацию получают с экрана осциллографа по изображению интерференционных фигур (фигур Лиссажу).
Измеряемый сигнал подают на вход КВО (канал вертикального отклонения), а сигнал образцового генератора известной частоты — на вход КГО (канал горизонтального отклонения).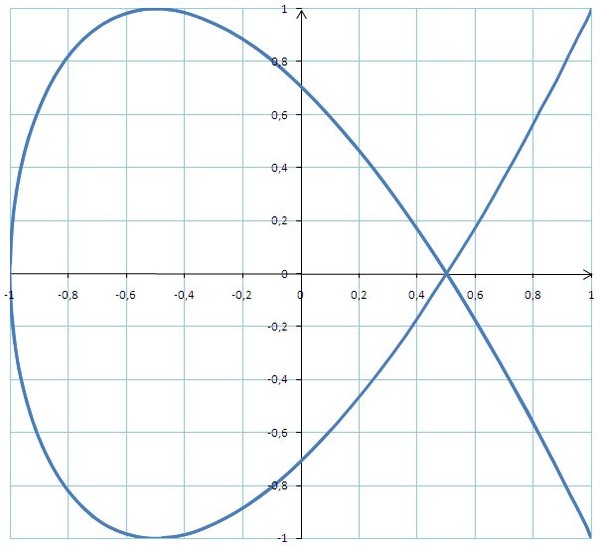 Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.
Плавным изменением частоты добиваются устойчивого изображения на экране осциллографа фигур Лиссажу. В этом методе отношение частот сравниваемых сигналов определяют путём подсчета числа пересечений фигуры Лиссажу с вертикальной осью и горизонтальной осью на экране осциллографа.
Из этой формулы можно вывести измеряемую частоту,
Закон гармонического осциллятора: [3;19]
Если закон дифференцировать по времени, то найдём закон изменения скорости при гармонических колебаниях:
Так же если повторить предыдущее действие, то найдём изменения ускорения при гармонических колебаниях:
После двух дифференцирований мы получим исходное выражение:
Перенеся слагаемые в одну сторону, то получим уравнение гармонического осциллографа:
Это уравнение встречается во всех разделах физики без исключения. Это уравнение описывает эволюцию малых отклонений динамических переменных от их устойчивых значений. Но для математика это обыкновенное уравнение 2-ого порядка с постоянными коэффициентами, в это уравнение входит функция со второй производной. Решением данного уравнения являются гармонические колебания.
Решением данного уравнения являются гармонические колебания.
1.2. Анализ среды MS Excel
Microsoft Office Excel – это программа, предназначенная для работы с электронными таблицами, которая позволяет хранить, организовывать и анализировать информацию.
Excel – это универсальная программа, которая позволяет работать с различными форматами данных. В Excel можно вести домашний бюджет, производить как простые, так и очень сложные расчеты, хранить данные, организовывать различные дневники, составлять отчеты, строить графики, диаграммы и многое-многое другое.
Функции MS Excel:
1.Работа с числовыми данными. Например, составление самых различных бюджетов, начиная от домашнего, как самого простого, и, заканчивая бюджетом крупной организации.
2.Работа с текстом. Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.
Разнообразный набор инструментов для работы с текстовыми данными дает возможность представить даже самые сложные текстовые отчеты.
3.Создание графиков и диаграмм. Большое количество инструментов позволяет создавать самые различные варианты диаграмм, что дает возможность представить ваши данные наиболее ярко и выразительно.
4.Организация списков и баз данных. В Microsoft Office Excel изначально была заложена структура строк и столбцов, поэтому организовать работу со списками или создать базу данных является для Excel элементарной задачей..
2.2. Построение фигур Лиссажу средствами MS Excel
В рамках данного исследования продемонстрируем построение фигур Лиссажу в табличном процессоре MS Excel, для этого понадобятся формула:
Уравнение гармонического колебания физической величины X с циклической частотой W и амплитудой А можно записать в виде формулы:,
где F-начальная фаза. Вместо W может быть использовано 2Пи/T ,где Т-период колебаний.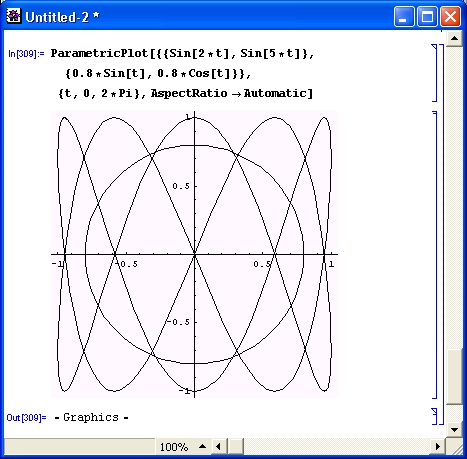
Для построения фигур Лиссажу средствами MS Excel:
1.Необходимо подготовить следующую таблицу:
- Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.
- Циклическая частота – скалярная величина, мера частоты вращательного или колебательного движения.
- Начальная фаза – место, откуда начинается колебательный процесс в определённый момент времени (начало отсчёта).
- Время колебаний – это время колебания системы.
- Колебание Х – это колебание системы по оси OX.
- Колебание Y – это колебание системы по оси OY.
2.Столбец F начиная с ячейки F5 и далее заполнить значениями от 0,01 до 10 с шагом 0,01
(используя функцию автозаполнения)
3.В столбец G начиная с ячейки G5 и далее ввести формулу для колебания X:
4.В столбец H начиная с ячейки H5 и далее ввести формулу для колебания Y:
5.Должна получиться вот такая таблица с данными:
6. Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.
Теперь необходимо построить диаграмму по этим данным. Для этого нужно выделить два столбца со значениями колебаний X и Y. После этого нажимаем на пиктограмму мастера построения диаграмм.
7.Тип диаграммы выбираем «СТАНДАРТНЫЕ» — «ТОЧЕЧНАЯ» — «Точечная диаграмма со значениями, соединенными сглаживающими линиями без маркеров» Нажимаем «Далее». Переходим на вкладку «РЯД» и называем «Ряд 1» — Колебание X ,а «Ряд 2» — Колебание Y. Нажимаем «Далее» теперь надо подписать название диаграммы «Фигуры Лиссажу». Нажимаем «Далее» и выбираем расположение диаграммы в текущем листе.
8.Должно получиться следующее:
2.3 Описание применения фигур Лиссажу для сравнения гармонических колебаний
Анализ литературы показал, что фигуры Лиссажу применяются: в радиотехнике для сравнения частот, в осциллографе. Если подать на входы «X» и «Y» осциллографа сигналы близких частот, то на экране можно увидеть фигуры Лиссажу. Этот метод широко используется для сравнения частот двух источников сигналов и для подстройки одного источника под частоту другого.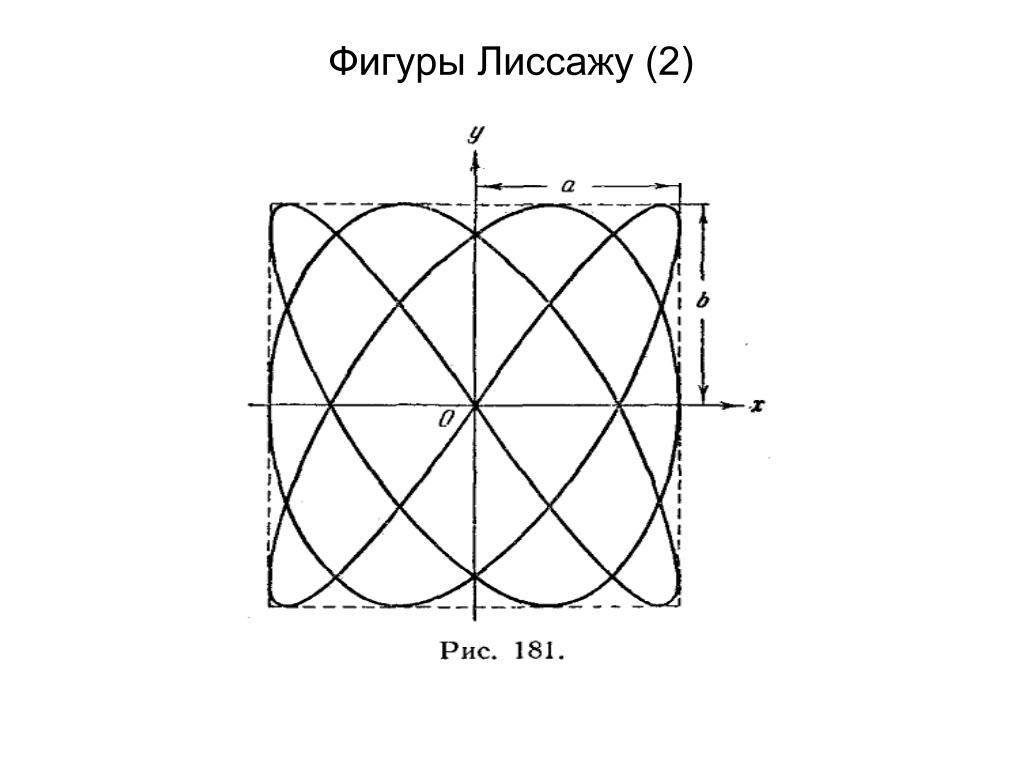 Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Когда частоты близки, но не равны друг другу, фигура на экране вращается, причём период цикла вращения является величиной, обратной разности частот, например, при периоде оборота равен 2с. разница в частотах сигналов равна 0,5 Гц. При равенстве частот фигура застывает неподвижно, в любой фазе, однако на практике, за счёт кратковременных нестабильностей сигналов, фигура на экране осциллографа обычно чуть-чуть подрагивает. Использовать для сравнения можно не только одинаковые частоты, но и находящиеся в кратном отношении, например, если образцовый источник может выдавать частоту только 5 МГц, а настраиваемый источник — 2,5 МГц.
Целью данной работы являлось рассказать и наглядно показать моделирование фигур Лиссажу.
В рамках исследования были решены следующие задачи:
1.Проанализированна литература по теме «Моделирование фигур Лиссажу»
2.Было раскрыты понятия: фигуры Лиссажу, гармоническое колебание, векторная диаграмма, развертка, Microsoft Office Excel, амплитуда колебаний, циклическая частота,
3. Рассмотрели способы построения графиков в среде MS Excel.
Рассмотрели способы построения графиков в среде MS Excel.
4.Разработали модель фигур Лиссажу в MS Excel для исследования гармонических колебаний.
В рамках исследования можно считать цель достигнутой.
- Мусин, Ю. Р. Физика: колебания, оптика, квантовая физика : учебное пособие для среднего профессионального образования / Ю. Р. Мусин. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2020. — 329 с.
- Аминев, А. В. Основы радиоэлектроники: измерения в телекоммуникационных системах : учебное пособие для среднего профессионального образования / А. В. Аминев, А. В. Блохин ; под общей редакцией А. В. Блохина. — Москва : Издательство Юрайт, 2019. — 223 с. URL: https://urait.ru/bcode/442543 .(97-98 стр.)
- Штыков, В. В. Введение в радиоэлектронику : учебник и практикум для среднего профессионального образования / В. В. Штыков. — 2-е изд., испр. и доп. — Москва : Издательство Юрайт, 2019. — 228 с. URL: https://urait.ru/bcode/437093 .(82-84 стр.
 )URL: https://urait.ru/bcode/449189 .( 19 стр.)
)URL: https://urait.ru/bcode/449189 .( 19 стр.)
Построение графика функции, заданной параметрически
Функция x: ?
Функция y: ?
Примеры
Параметр:
от до
Введите график функции
Важно a должно быть меньше b, иначе график не сможет построиться
Построим график параметрической функции x=x(t) и y=y(t), которая задаёт прямую или кривую линию,
где параметр t лежит в промежутке [a, b],
и вы можете указать свои границы.
Задайте также функции x и y, зависящих от параметра.
Поверхность параметрически заданную вы можете построить по
ссылке.
Производная параметрически заданная.
Подробнее про Параметрическое представление
.
Примеры кривых
| Название кривой | Уравнение |
|---|---|
| Окружность | x = sin(t) y = cos(t) t в [0, 2*pi] |
| Спираль | x = t*sin(t) y = t*cos(t) t в [0, 5*pi] |
| Дельтоида | x = 2*cos(t) + cos(2*t) y = 2*sin(t) - sin(2*t) t в [0, 2*pi] |
| Астроида | x = 2*sin(t)^3 y = 2*cos(t)^3 t в [0, 2*pi] |
| Гипоциклоиды | x = 20*(cos(t) + cos(5*t)/5) y = 20*(sin(t) - sin(5*t)/5) t в [0, 2*pi] |
x = 22/5*(cos(t) + 10*cos(11/10*t)/11) y = 22/5*(sin(t) - 10*sin(11/10*t)/11) t в [0, 20*pi] | |
x = 24. |
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Лаборатория Лиссажу
Лаборатория Лиссажу| Лаборатория Лиссажу |
| Для работы:
Нажмите кнопки Preset слева, чтобы увидеть образцы шаблонов.
Чтобы сделать свои собственные шаблоны, используйте цифровые показания на
право. Нажмите в верхней части цифры, чтобы увеличить ее значение; нажмите внизу, чтобы
уменьшить его значение. (Пользователи AOL: Этот проект может привести к сбою вашего браузера! Скопируйте и вставьте URL-адрес в Internet Explorer или Netscape. |
| Пояснение считываемых значений | |
| xчастота | количество горизонтальных циклов для каждого кадра графика. |
| yFreq | количество вертикальных циклов для каждого кадра графика. |
| hueFreq | Это количество циклов оттенка для каждого кадра графика. Каждый цикл оттенков представляет собой полный спектр цветов. |
| Образцы | Это количество сегментов линии, которые будут использоваться для рисования каждого кадра графика.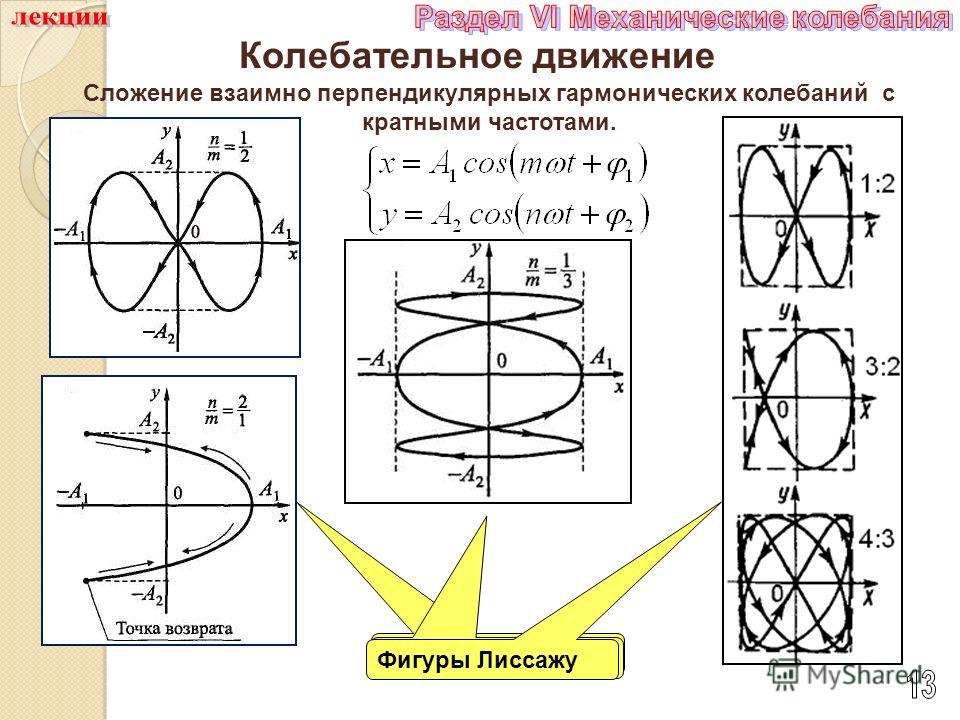 Увеличение этого числа сделает кривые более плавными. Уменьшение
это число усугубит алиасинг в сюжете (заставляя его выглядеть более
больше похоже на стринг-арт, чем на математическую кривую). Увеличение этого числа сделает кривые более плавными. Уменьшение
это число усугубит алиасинг в сюжете (заставляя его выглядеть более
больше похоже на стринг-арт, чем на математическую кривую). |
До появления цифровых частотомеров и контуров фазовой автоподстройки числа Лиссажу использовались для
определить частоты звуков или радиосигналов. Сигнал известной частоты подавался на
горизонтальной оси осциллографа, а измеряемый сигнал подавался на вертикальную ось. Фигуры Лиссажу часто использовались в качестве реквизита в научно-фантастических фильмах, снятых в 1950-х годах. Один из лучших примеры можно найти во вступительной последовательности Внешние пределы Телесериал. («Не пытайтесь настроить ваше изображение — мы управляем передачей».) Рисунок перекрещивающихся линий на самом деле является Лиссажу фигура. Лаборатория Лиссажу предоставляет вам виртуальный осциллограф, который вы можете использовать для создания этих шаблонов. ( |
| Лаборатория Лиссажу и описание были созданы Эдом Хоббсом. Он любезно разрешает репостить свою лабораторию Лиссажу. (Мы сожалеем, что его домашняя страница, кажется, недавно исчезла из Интернета, поэтому мы больше не можем найти его или дать ссылку на него!!) Copyright 1997-2000 Edward R. 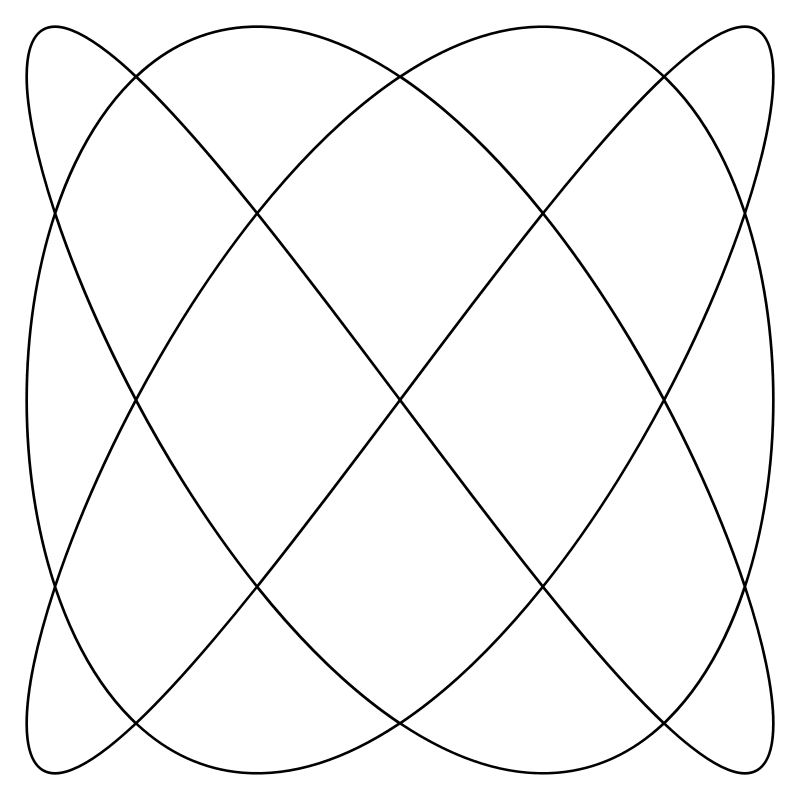 Hobbs Hobbs |
Визуализация стереоинформации с использованием фигур Лиссажу
БЕСПЛАТНЫЙ ВЕБИНАР — Знакомство со звуком Мастер-класс
Если вы хотите изучать Pro Audio онлайн, с поддержкой преподавателя и оцениваемыми практическими заданиями, Audio Masterclass — это то, что вам нужно. На этом вебинаре директор курса Дэвид Меллор проведет вас через наш самый популярный курс.
Зарегистрируйтесь сейчас
Хорошо иметь возможность визуализировать звук, а также слышать его, часто для выявления любых потенциальных дефектов. В одном интересном методе используются фигуры Лиссажу.
Мы должны поблагодарить Жюля Антуана Лиссажу из La Belle France за этот интересный способ визуализации стереоинформации. По сути, вы можете представить себе экран осциллографа с ярким пятном в центре. Примените левый канал стереосигнала, чтобы пятно двигалось горизонтально. Примените правый канал стереосигнала, чтобы пятно двигалось вертикально.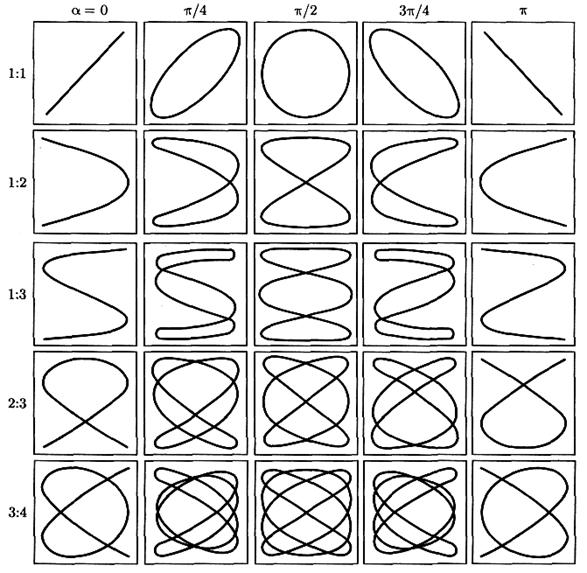
К сожалению, старый бедняга Жюль Антуан умер примерно за пятьдесят лет до того, как кто-либо смог увидеть его фантазии на экране осциллографа, хотя он изобрел способ проецировать на стену простые узоры, которые мы теперь знаем как фигуры Лиссажу. Теперь, конечно, мы можем использовать программное обеспечение для просмотра созданных паттернов — в данном случае это Spectre от Audiofile Engineering. Давайте перейдем непосредственно к стереозаписи ударных…
Стерео
Помните, что левый канал стереосигнала заставляет дорожку двигаться горизонтально, а правый канал заставляет ее двигаться вертикально. Таким образом, монофонический сигнал будет перемещать обе дорожки одинаково под углом 45 градусов с наклоном вверх вправо.
Наиболее отчетливо это видно на ударах малого и большого барабана, которые в миксе сильно монофонические. Там, где тарелки плещутся по комнате в оверхеды, разница между каналами и больше стереоконтента больше. Вы увидите, как шарик трассировки превращается в более толстый эллипс, снова наклоненный вверх вправо, а иногда и в круг.
Там, где тарелки плещутся по комнате в оверхеды, разница между каналами и больше стереоконтента больше. Вы увидите, как шарик трассировки превращается в более толстый эллипс, снова наклоненный вверх вправо, а иногда и в круг.
Это именно то, что вы ожидаете от стереосигнала. Однако вы не хотите, чтобы эллипс формировался с наклоном в противоположном направлении, поскольку это указывало бы на противофазный сигнал.
Моно
Для сравнения, вот моно запись ударных, сделанная с помощью одного микрофона перед установкой…
Как видите, стерео информации нет, а есть только линия наклонены вверх вправо. Но что, если что-то пошло не так, и сигнал был не в фазе?
Не в фазе
Чтобы продемонстрировать это, здесь придумана несовпадающая по фазе запись. На самом деле это продублированная предыдущая запись, один канал инвертирован, а затем преобразован в стерео. Он показывает эффект очень четко, и вы должны услышать, почему вы никогда не хотите, чтобы ваш звук был не в фазе…
Он показывает эффект очень четко, и вы должны услышать, почему вы никогда не хотите, чтобы ваш звук был не в фазе…
Семплы ударных
В качестве последнего примера у меня есть запись семплов ударных, сделанная особенно изобретательным студентом Audio Masterclass. (Если вы хотите нанять его, дайте мне знать, и я свяжусь с вами, но я не думаю, что подобное творчество будет стоить дешево.)
В этом примере вы можете услышать и увидеть, что запись находится в фазе, имеет полезный объем стереоконтента, и примерно на 12-секундной отметке вы можете увидеть крошечные монофонические удары тарелок, которые вообще не имеют стереоконтента. Обратите внимание, что они перемещают кривую по горизонтали или вертикали в зависимости от того, появляются ли они в левом или правом канале.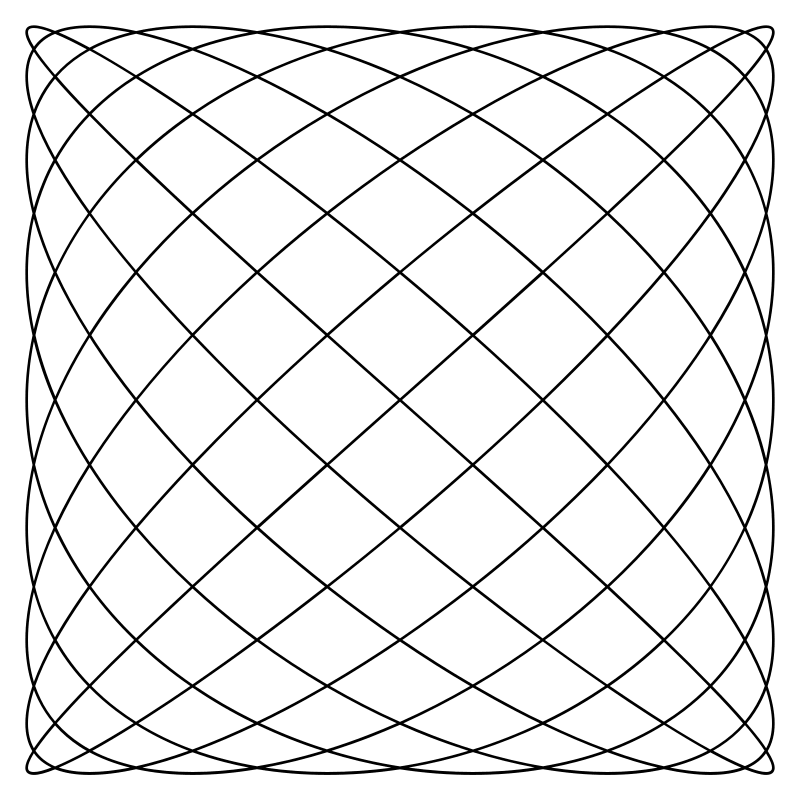


 Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная.
Если >0, то второе колебание сдвинуто влево, т.е. опережает первое, а если <0, то ситуация обратная. )URL: https://urait.ru/bcode/449189 .( 19 стр.)
)URL: https://urait.ru/bcode/449189 .( 19 стр.)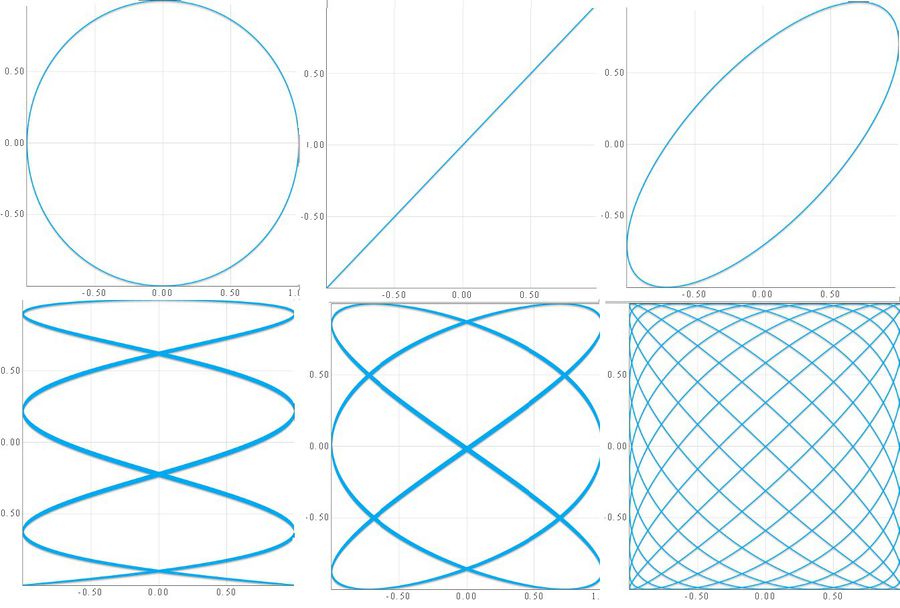 3
y = 13*cos(t) - 5*cos(2*t) - 2*cos(3*t) - cos(4*t)
t в [0, 2*pi]
3
y = 13*cos(t) - 5*cos(2*t) - 2*cos(3*t) - cos(4*t)
t в [0, 2*pi]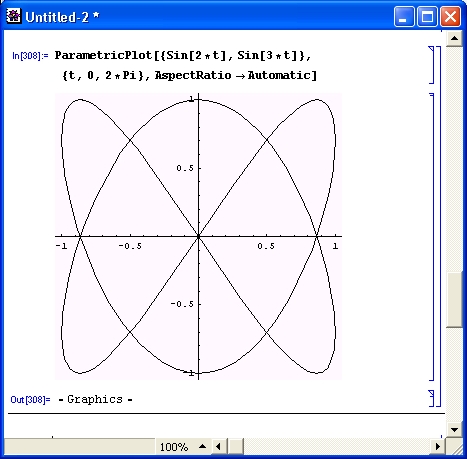 3
3 14159..
14159..