Как работает RC-цепь – RxTx.su
RC-цепь — это простая схема, которая содержит резистор R и конденсатор C. Она является распространенным элементом в электронных устройствах и играет важную роль в передаче электрических сигналов. RC-схемы используются в качестве аудиофильтров, электронных таймеров, генераторов и многого другого в широком спектре электронных проектов.
Принцип работы RC-цепи
Конденсатор может накапливать энергию, а резистор, включенный последовательно с ним, будет контролировать скорость, с которой он заряжается или разряжается. Это дает характерную временную зависимость и важный параметр, описывающий скорость заряда и разряда конденсатора:
\[T_C=R\times C\]
- TC : Постоянная времени RC цепи (заряда/разряда конденсатора) (в секундах)
- R : Сопротивление резистора в цепи (в Омах)
- C : Емкость конденсатора в цепи (в Фарадах)
Взгляните на схему ниже:
Когда переключатель замкнут, ток I будет течь к конденсатору через резистор R1. По мере повышения напряжения на конденсаторе UC1, разница в напряжении между конденсатором и батареей UBAT-UC1 уменьшается, поэтому ток зарядки конденсатора I будет постепенно уменьшается. Когда напряжение на конденсаторе достигнет напряжения батареи UBAT=UC1, зарядка конденсатора заканчивается.
По мере повышения напряжения на конденсаторе UC1, разница в напряжении между конденсатором и батареей UBAT-UC1 уменьшается, поэтому ток зарядки конденсатора I будет постепенно уменьшается. Когда напряжение на конденсаторе достигнет напряжения батареи UBAT=UC1, зарядка конденсатора заканчивается.
Зарядка конденсатора в RC-цепи
Скорость заряда и разряда конденсатора в RC-цепи описывается постоянной времени TC. Постоянная времени определяется как время, за которое напряжение на конденсаторе достигает
Разрядка конденсатора
Если бы конденсатор в приведенной выше схеме был замкнут на землю с помощью перемычки, напряжение на конденсаторе уменьшилось бы по кривой, подобной этой:
Зависимость напряжения на конденсаторе от постоянной времени при разрядеНапряжение на конденсаторе при разряде достигает 36,8% от напряжения питания U за время равное постоянной TC.
Как рассчитать постоянную времени RC-цепи
В качестве примера мы рассчитаем время, необходимое конденсатору емкостью
\[T_C=1000 \text{ мкФ}\times 100\text{ кОм}=0,001 \text{ Ф}\times 100000\text{ Ом}=100\text{ секунд.}\]
Таким образом, для зарядки конденсатора потребуется 100 секунд.
Надеюсь, эта статья помогла вам лучше узнать RC-цепи. Оставляйте комментарии ниже, если у вас есть вопросы.
Компоненты
- Набор резисторов
- 2-х ваттные резисторы
- Электролитические конденсаторы (0.5 кг)
- Набор керамических конденсаторов (18 номиналов по 10 штук)
Постоянная времени RC-цепи — что это такое?
Термин: Постоянная времени RC-цепи
τ – постоянная времени RC-цепи – это временна́я характеристика простой электрической цепи, в которой происходит изменение заряда конденсатора С за счёт его разряда через сопротивление R. Постоянная времени вычисляется как τ=R*C [Ф*Ом], что эквивалентно размерности «секунда» [c].
Постоянная времени вычисляется как τ=R*C [Ф*Ом], что эквивалентно размерности «секунда» [c].
Как показано на рисунке, постоянная времени τ входит в аналитическую функцию описания процесса изменения напряжения на конденсаторе U(t) при его заряде от источника напряжения через сопротивление R. На рисунке U(0) – это начальное напряжение на конденсаторе (в момент времени t=0), а U(∞) – это напряжение источника напряжения, к которому асимтотически стремится U(t).
За время, равное τ, напряжение на конденсаторе изменяется от U(0) до U(∞) + [U(0) — U(∞)]/e, где e=2,718. .
Экспоненциальный заряд конденсатора происходит для случая U(∞) > U(0), а экспоненциальный разряд – для случая U(∞) -t/τ ) в моменты времени t от t=0,001τ до t=10τ протекания экспоненциального процесса.
| Время процесса в единицах τ=RC | Доля неустановившейся величины напряжения e -t/τ | |
| *100, % | *10 6 , ppm | |
| 0,001τ | ≈99,9% | ≈999000 |
| 0,01τ | ≈99% | ≈990000 |
| 0,1τ | ≈90% | ≈900000 |
| 0,5τ | ≈61% | ≈610000 |
| τ | ≈37% | ≈370000 |
| 2τ | ≈14% | ≈140000 |
| 3τ | ≈5,0% | ≈50000 |
| 4τ | ≈1,8% | ≈1800 |
| 5τ | ≈0,67% | ≈6700 |
| 6τ | ≈0,25% | ≈2500 |
| 7τ | ≈0,091% | ≈910 |
| 8τ | ≈0,034% | ≈340 |
| 9τ | ≈0,012% | ≈120 |
| 10τ | ≈0,0045% | ≈45 |
Понятие постоянной времени RC-цепи помогает оценить время протекания процесса при анализе эквивалентных электрических схем, содержащих RC-цепи. Заметим только, что понятие постоянной времени не применимо для частного случая заряда-разряда конденсатора постоянным током, где закон изменения напряжения и заряда на конденсаторе имеет линейный характер, а не экспоненциальный.
Заметим только, что понятие постоянной времени не применимо для частного случая заряда-разряда конденсатора постоянным током, где закон изменения напряжения и заряда на конденсаторе имеет линейный характер, а не экспоненциальный.
Постоянные времени RC-цепей (в качестве величин с прозрачным физическим смыслом) участвуют в аналитических решениях дифференциальных уравнений, описывающих не только экспоненциальные процессы в электрических схемах, содержащих RC-цепи (например, пассивные и активные RC-фильтры).
Источник
Примеры [ править ]
Постоянные времени в электрических цепях [ править ]
Переходная характеристика напряжения конденсатора. Отклик на скачок напряжения индуктора.
В цепи RL, состоящей из одного резистора и катушки индуктивности, постоянная времени (в секундах ) равна τ {\displaystyle \tau }
τ = L R {\displaystyle \tau ={L \over R}}
где R
— сопротивление (в омах ), а
L
— индуктивность (в Генри ).
Точно так же в RC-цепи, состоящей из одного резистора и конденсатора, постоянная времени (в секундах) равна: τ {\displaystyle \tau }
τ = R C {\displaystyle \tau =RC}
где R
— сопротивление (в омах ), а
C
— емкость (в фарадах ).
Электрические схемы часто более сложны, чем эти примеры, и могут иметь несколько постоянных времени (см. Некоторые примеры в разделе « Переходная характеристика» и « Разделение полюсов»). В случае наличия обратной связи в системе могут наблюдаться нестабильные возрастающие колебания. Вдобавок физические электрические цепи редко являются действительно линейными системами, за исключением возбуждений с очень низкой амплитудой; однако широко используется приближение линейности.
В цифровых электронных схемах часто используется другая мера, FO4 . Это можно преобразовать в единицы постоянной времени с помощью уравнения . [4] 5 τ = FO4 {\displaystyle 5\tau ={\text{FO4}}}
Тепловая постоянная времени [ править ]
Постоянные времени — это характеристика сосредоточенного системного анализа (метод анализа сосредоточенной мощности) для тепловых систем, который используется, когда объекты равномерно охлаждают или нагреваются под влиянием конвективного охлаждения или нагревания .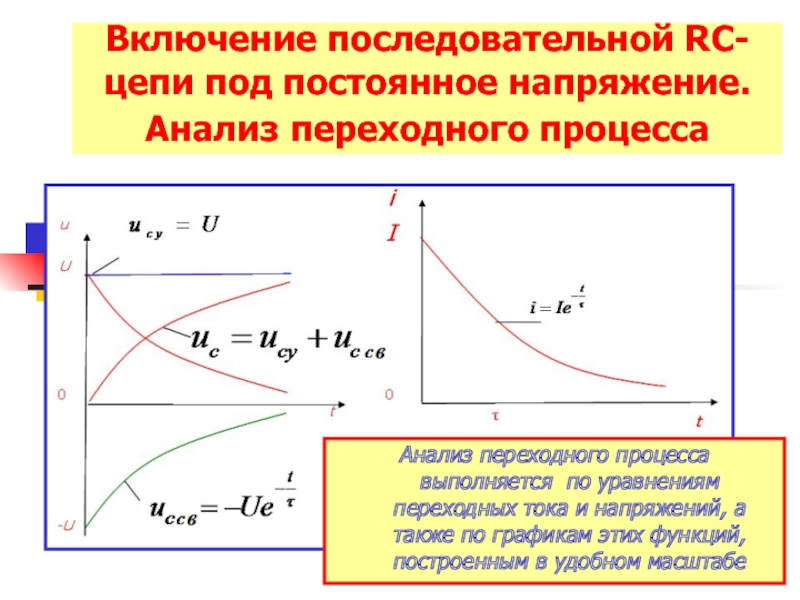 В этом случае передача тепла от тела к окружающей среде в данный момент времени пропорциональна разнице температур между телом и окружающей средой: [5]
В этом случае передача тепла от тела к окружающей среде в данный момент времени пропорциональна разнице температур между телом и окружающей средой: [5]
F = h A s ( T ( t ) − T a ) , {\displaystyle F=hA_{s}\left(T(t)-T_{a}\right),}
где h
— коэффициент теплопередачи ,
A
s — площадь поверхности,
T (t)
= температура тела в момент времени
t
, а
T
a — постоянная температура окружающей среды. Положительный знак указывает на то, что
F
является положительным, когда тепло выходит
из
тела, потому что его температура выше, чем температура окружающей среды (
F
— поток наружу). Если тепло теряется в окружающую среду, эта теплопередача приводит к падению температуры тела, определяемому по формуле [5]
ρ c p V d T d t = − F , {\displaystyle \rho c_{p}V{\frac {dT}{dt}}=-F,}
где ρ = плотность, с
р = удельная теплоемкость и
V
представляет собой объем тела. Отрицательный знак указывает на падение температуры при передаче тепла
Отрицательный знак указывает на падение температуры при передаче тепла
наружу
от тела (то есть, когда
F
> 0). Приравнивая эти два выражения для теплопередачи,
ρ c p V d T d t = − h A s ( T ( t ) − T a ) . {\displaystyle \rho c_{p}V{\frac {dT}{dt}}=-hA_{s}\left(T(t)-T_{a}\right).}
Очевидно, это LTI-система первого порядка, которую можно представить в виде:
d T d t + 1 τ T = 1 τ T a , {\displaystyle {\frac {dT}{dt}}+{\frac {1}{\tau }}T={\frac {1}{\tau }}T_{a},}
с
τ = ρ c p V h A s . {\displaystyle \tau ={\frac {\rho c_{p}V}{hA_{s}}}.}
Другими словами, постоянная времени говорит о том, что большие массы ρV
и большая теплоемкость
c
p приводят к более медленным изменениям температуры, в то время как большие площади поверхности
A
s и лучшая теплопередача
h
приводят к более быстрым изменениям температуры.
Сравнение с вводным дифференциальным уравнением предполагает возможное обобщение на изменяющуюся во времени температуру окружающей среды T
a .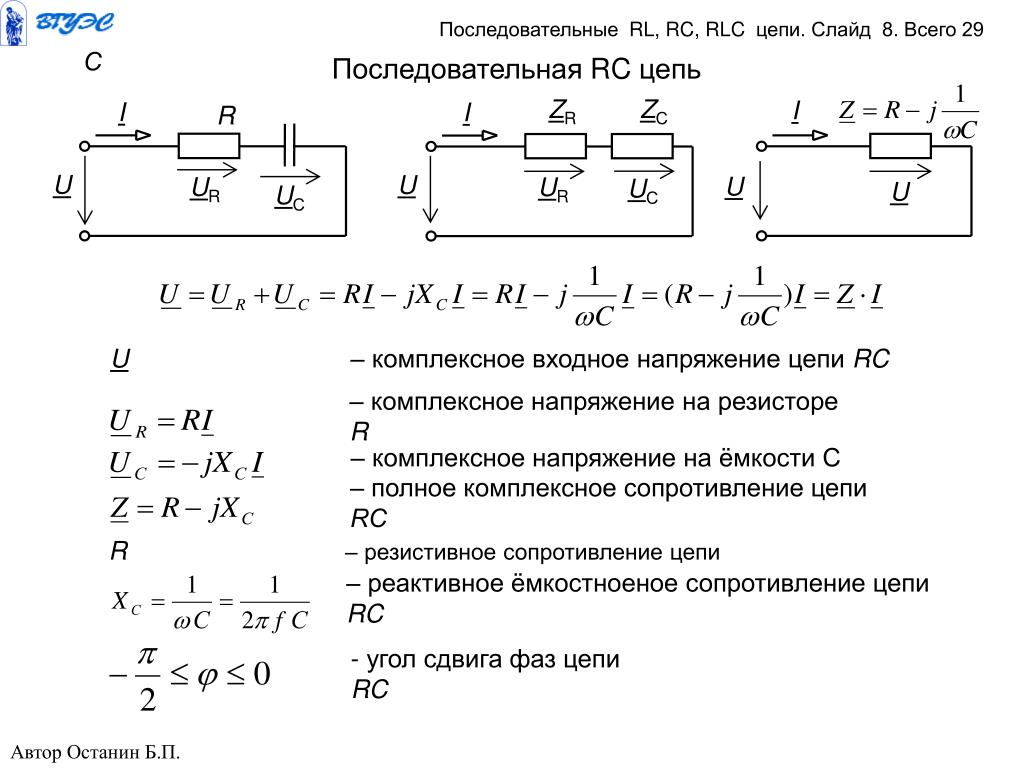 {-t/\tau }}
{-t/\tau }}
где напряжение в милливольтах, время в секундах и секундах. τ {\displaystyle \tau }
V max определяется как максимальное изменение напряжения от потенциала покоя , где
V max = r m I {\displaystyle V_{\textrm {max}}=r_{m}I}
где r
m — сопротивление через мембрану,
I
— ток через мембрану.
Настройка для t
= для повышения устанавливает
V
(
t
) равным 0,63
В
макс . Это означает , что постоянная времени является время , прошедшее после того, как 63%
V
макс было достигнуто
τ {\displaystyle \tau }
Установка для т
= для падения множеств
V
(
т
) , равное 0,37
V
макс , а это означает , что постоянная времени это время , прошедшее после того, как она упала до 37% от
V
макс .
τ {\displaystyle \tau }
Чем больше постоянная времени, тем медленнее растет или падает потенциал нейрона.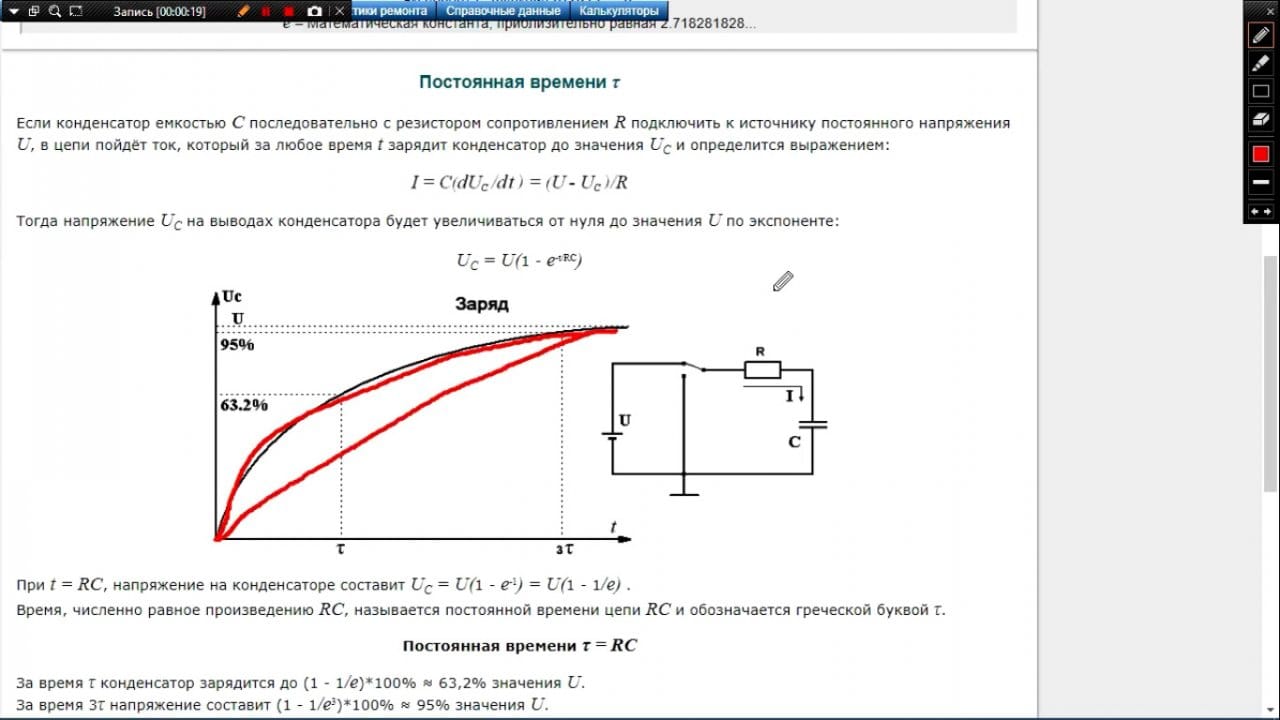 Длительная постоянная времени может привести к временному суммированию или алгебраическому суммированию повторяющихся потенциалов. Короткая постоянная времени, скорее, дает детектор совпадений посредством пространственного суммирования .
Длительная постоянная времени может привести к временному суммированию или алгебраическому суммированию повторяющихся потенциалов. Короткая постоянная времени, скорее, дает детектор совпадений посредством пространственного суммирования .
Экспоненциальный спад [ править ]
Дополнительная информация: Экспоненциальный спад
При экспоненциальном распаде , например, радиоактивного изотопа, постоянная времени может интерпретироваться как среднее время жизни . Полураспада Т
HL
связана с экспоненциальной постоянной времени путем τ {\displaystyle \tau }
T H L = τ ⋅ l n 2. {\displaystyle T_{HL}=\tau \cdot \mathrm {ln} \,2.}
Обратная величина постоянной времени называется постоянной затухания и обозначается λ = 1 / τ . {\displaystyle \lambda =1/\tau .}
Метеорологические датчики [ править ]
Постоянная времени
— это количество времени, которое требуется метеорологическому датчику, чтобы отреагировать на быстрое изменение измеряемой величины, пока он не будет измерять значения в пределах допуска точности, обычно ожидаемого от датчика.
Чаще всего это относится к измерениям температуры, температуры точки росы, влажности и давления воздуха. Особенно страдают радиозонды из-за их быстрого увеличения высоты.
Определение постоянной времени. Переходные процессы в R-L-C-цепи.
Переходные процессы в цепи с одним накопителем энергии и произвольным числом резисторов
Как отмечалось в предыдущей лекции, линейная цепь охвачена единым переходным процессом. Поэтому в рассматриваемых цепях с одним накопителем энергии (катушкой индуктивности или конденсатором) – цепях первого порядка – постоянная времени будет одной и той же для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение.
Общий подход к расчету переходных процессов в таких цепях основан на применении теоремы об активном двухполюснике: ветвь, содержащую накопитель, выделяют из цепи, а оставшуюся часть схемы рассматривают как активный двухполюсник А (эквивалентный генератор) (см. рис. 1, а) со схемой замещения на рис. 1,б.
1, а) со схемой замещения на рис. 1,б.
Совершенно очевидно, что постоянная времени здесь для цепей с индуктивным элементом определяется, как:
и с емкостным, как:
где — входное сопротивление цепи по отношению к зажимам 1-2 подключения ветви, содержащей накопитель энергии.
Например, для напряжения на конденсаторе в цепи на рис. 2 можно записать
где в соответствии с вышесказанным
Переходные процессы при подключении последовательной R-L-C-цепи к источнику напряжения
Рассмотрим два случая:
Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать
Тогда для первого случая принужденная составляющая этого напряжения
Характеристическое уравнение цепи
решая которое, получаем
В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:
1. или , где — критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.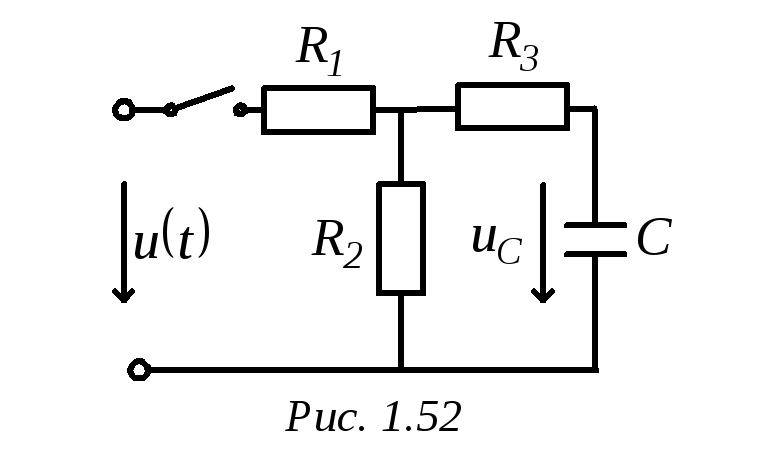
В этом случае
2. — предельный случай апериодического режима.
В этом случае и
3. — периодический (колебательный) характер переходного процесса.
В этом случае и
где — коэффициент затухания; — угловая частота собственных колебаний; — период собственных колебаний.
Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать
Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации , запишем для t=0 два уравнения:
решая которые, получим
Тогда ток в цепи
и напряжение на катушке индуктивности
На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .
Для критического режима на основании (2) и (4) можно записать
Для колебательного переходного процесса в соответствии с (2) и (5) имеем
Для нахождения постоянных интегрирования запишем
На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .
При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым
Здесь также возможны три режима:
| 1. ; | 2. | 3. |
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 — ; 2 — ; 3 — , — которые представлены на рис. 6,а…6,в соответственно.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов.
 –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
–7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- Как можно определить постоянную времени в цепи с одним накопителем энергии по осциллограмме тока или напряжения в какой-либо ветви?
- Определить, какой процесс: заряд или разряд конденсатора в цепи на рис. 2 – будет происходить быстрее?
- Влияет ли на постоянную времени цепи тип питающего устройства: источник напряжения или источник тока?
- В цепи на рис. 2 , С=10 мкФ. Чему должна быть равна индуктивность L катушки, устанавливаемой на место конденсатора, чтобы постоянная времени не изменилась?
- Как влияет на характер переходного процесса в R-L-C-контуре величина сопротивления R и почему?
- Определить ток через катушку индуктивности в цепи на рис.
 7, если ; ; ; ; .
7, если ; ; ; ; .
Определить ток в ветви с конденсатором в цепи на рис. 8, если ; ; ; .Источник
Переходные процессы в RC- и RL- цепях
Переходными, в электрической цепи, принято называть процессы возникающие в результате различных воздействий (например: включений или отключений цепи от источника питания, обрывах или коротких замыканиях, импульсных возмущающих воздействий и так далее) и переводящих её из одного стационарного (установившегося) состояния в новое (другое) стационарное состояние.
Рассмотрим переходный процесс в RC-цепи (рисунок 1), в состав которой входят резистор R, конденсатор С, ключ К и источник питания, на зажимах которого поддерживается постоянное напряжение E=U.
Рисунок 1. Схема RC-цепи.
Если установить ключ К в положение ”1” (рисунок 1), то начнётся процесс заряда конденсатора С через резистор R (рисунок 2,a). Для образовавшейся цепи будет справедливо соотношение :
Так как на конденсаторе напряжение скачком изменяться не может, то в момент (t=0) подключения цепи к источнику питания всё напряжение источника окажется на резисторе R, то есть uR = U, uc = 0.
В начальный момент времени заряда конденсатора, ток в RC-цепи будет иметь наибольшее значение: i=U/R. Конденсатор начнёт заряжаться, напряжение на нём “постепенно” повышается, что, в свою очередь, приведёт к уменьшению падения напряжения на резисторе uR = U — uC, а следовательно и уменьшению тока в RC-цепи, вплоть до его ”полного” прекращения. Напряжение на конденсаторе, во время заряда, нарастает по экспоненциальной зависимости согласно формуле:
где t – любой момент времени, τ – постоянная времени заряда конденсатора в секундах:
Значения напряжения на резисторе и общего тока RC-цепи уменьшаются также по экспоненциальному закону:
Рисунок 2. Переходные процессы в RC-цепи. (а – при подключении к источнику; б –при замыкании цепи)
Из приведенных выше математических выражений, а также изображений на рис.2,а можно сделать вывод что, величина τ характеризует скорость заряда конденсатора или скорость затухания переходного процеесса. Через время t= τ , после подключения RC-цепи к источнику постоянного напряжения, напряжение на конденсаторе достигнет значения
, а напряжение на резисторе уменьшится до значения . Процесс заряда конденсатора будет продолжаться до тех пор, пока напряжения на его выводах не достигнет значения равного напряжению источника питания U. Когда заряд конденсатора закончится — ток в RC-цепи становится равным нулю. Теоретически, для “полного” заряда конденсатора, потребуется бесконечно большое время.
Процесс заряда конденсатора будет продолжаться до тех пор, пока напряжения на его выводах не достигнет значения равного напряжению источника питания U. Когда заряд конденсатора закончится — ток в RC-цепи становится равным нулю. Теоретически, для “полного” заряда конденсатора, потребуется бесконечно большое время.
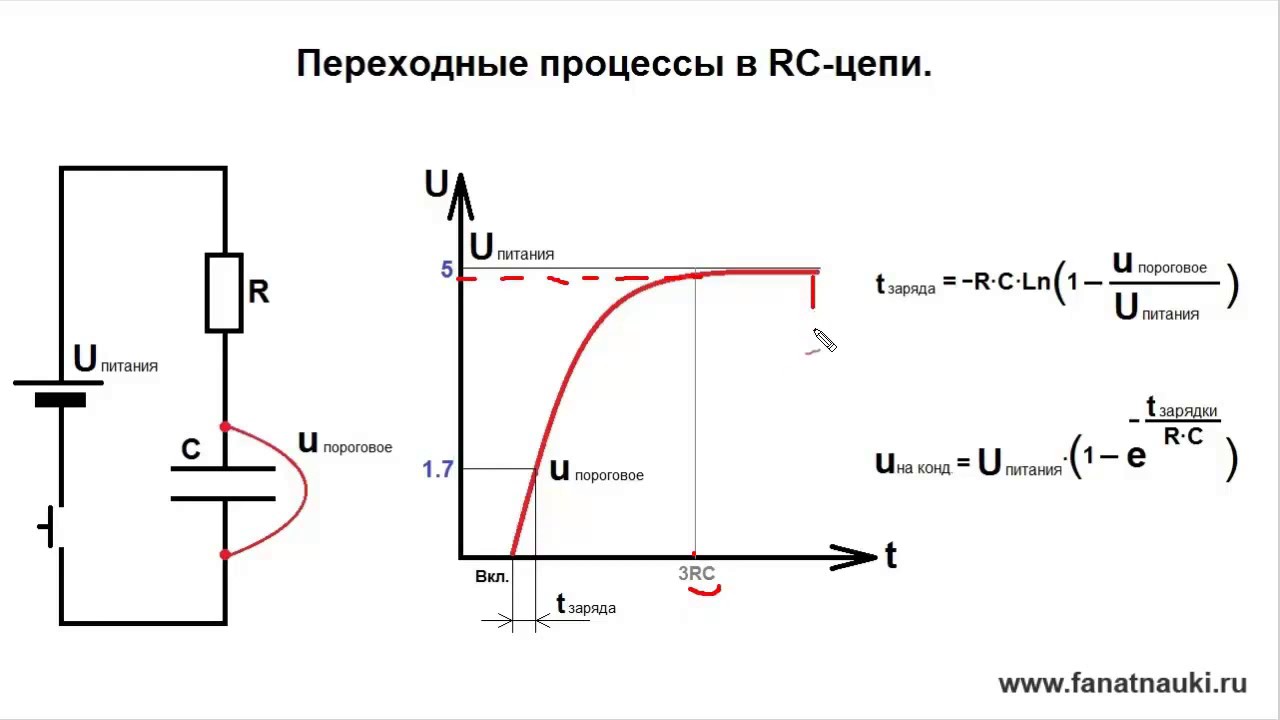
Поэтому, принято считать, что процесс заряда конденсатора заканчивается, когда напряжение на нём достигает значений 90,95 или 99% величины напряжения источника питания U=E.
В подавляющем большинстве случаев, как на практике, так и в теоретических расчётах, время t в течение которого конденсатор считается полностью заряженным, принимают равным 3τ. Также это можно отнести ко всем электрическим цепям, где токи меняются по экспоненциальному закону.
Если установить ключ К в положение ”2” (рисунок 1) то начнётся новый переходный процесс — разряд конденсатора С через резистор R (рисунок 2,a). В этом случае предварительно заряженный конденсатор становится фактическим источником напряжения, т. к. источник внешнего напряжения E=U перестаёт действовать и для любого момента времени становится действительным соотношение uC + uR = 0, то есть uC = -uR.
к. источник внешнего напряжения E=U перестаёт действовать и для любого момента времени становится действительным соотношение uC + uR = 0, то есть uC = -uR.
Ток в начальный момент ( t=0) разряда конденсатора будет иметь максимальное значение:
Но по мере разряда конденсатора (превращения накопленной в его электрическом поле энергии в тепловую на резисторе R ) напряжение на нём будет уменьшаться и, как следствие, будут уменьшаться по экспоненциальному закону ток в цепи и напряжение на резисторе:
Через некоторое время, например t=3τ (см. приведенную выше табл.), на конденсаторе останется примерно 5% напряжения от начального значения, что условно можно считать окончанием переходного процесса и возвратом схемы в исходное состояние когда: uC = 0, uR = 0, i = 0.
Теперь рассмотрим переходной процесс в RL-цепи (рис.3), в состав которой входят резистор R, катушка индуктивности L, ключ К и источник питания, на зажимах которого поддерживается постоянное напряжение E=U.
Рисунок 3. Схема RL-цепи.
Схема RL-цепи.
При подключении к источнику E=U, переводом ключа “K” в положение 1, ток в RL-цепи не сразу достигнет значения i=U/R, а будет нарастать по экспоненциальному закону (см.рис.4,а). Это связано с тем, что кроме источника E=U, в цепи с индуктивностью L начинает действовать ЭДС самоиндукции eL, препятствующая нарастанию тока. В момент включения, когда t=0, ЭДС самоиндукции максимальна и принимает значение eL = -U, при этом все напряжения выделяются на катушке индуктивности L :
, так как при t=0 ток в цепи i=0, следовательно iR = 0. С течением времени напряжение на катушке uL уменьшается, а ток i и напряжение на резисторе uR экспоненциально возрастают:
Постоянная времени RC — RC time constant
Постоянная времени RC
, также называемая тау, постоянная времени (в секундах ) RC-цепи , равна произведению сопротивления цепи (в омах ) на емкость цепи (в фарадах ), т. Е.
τ знак равно р C [секунды]
Это время, необходимое для зарядки конденсатора через резистор от начального напряжения заряда, равного нулю, до примерно 63,2% от значения приложенного напряжения постоянного тока или для разряда конденсатора через тот же резистор примерно до 36,8% от его начального значения.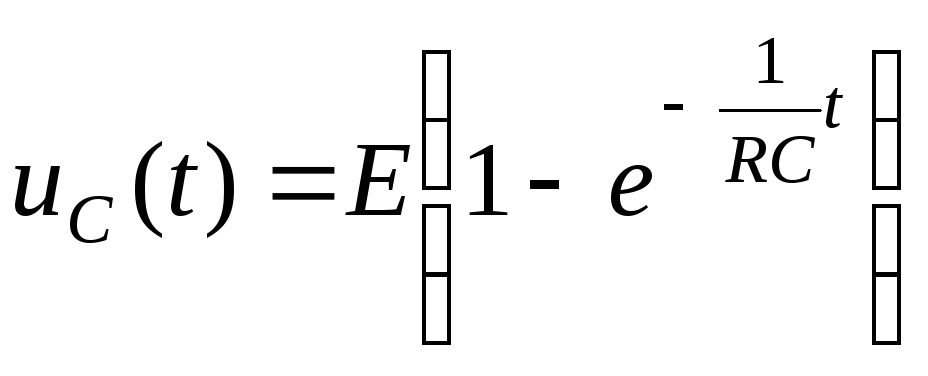 напряжение заряда. (Эти значения получены из математической константы e
напряжение заряда. (Эти значения получены из математической константы e
: и .) Следующие формулы используют ее, принимая постоянное напряжение, приложенное последовательно к конденсатору и резистору, для определения напряжения на конденсаторе в зависимости от времени: 63,2 % знак равно 1 — е — 1 >
Помехоподавляющая RC-цепочка в реле (сетевой снаббер)
Помехоподавляющая RC-цепочка (сетевой снаббер, сетевой демпфер, RC SNUBBER NETWORKS, RC element) – это устройство, используемое для подавления выбросов напряжения (Surge suppressors) в электрических цепях, устройство гашения импульсных перенапряжений.
Применение RC-цепочек сглаживает и ограничивает коммутационные перенапряжения на элементах схем релейного управления, снижает искрообразование на контактах управляющего реле и тем самым увеличивает его коммутационный ресурс. Предотвращение или сведение к минимуму искрения в контактах реле снижает интенсивность электромагнитного излучения, генерируемого в моменты коммутации, что обеспечивает необходимую помехоустойчивость при работе чувствительных электронных схем.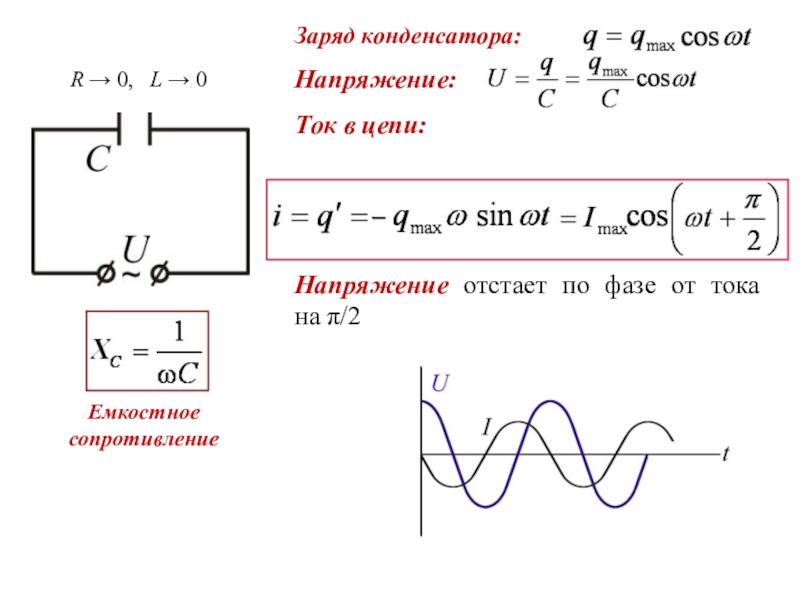
Дугогасящая RC-цепочка работает в момент размыкания контактов, отключающих катушку, поглощает и подавляет энергию дуги, замыкает выброс напряжения на себя, позволяя паразитной энергии обойти управляющий контакт.
RC-цепочка состоит из соединенных последовательно конденсатора и резистора. Конденсатор должен поглощать энергию импульсов тока и напряжения и обеспечивать защиту от потенциалов, генерируемых индуктивностью в процессе отключения и дребезга контактов. Диэлектрик конденсатора, используемого в снабберной цепи должен выдерживать величину перенапряжения. Резистор должен быть безындуктивного типа для обеспечения высокого быстродействия снаббера и проведения тока импульсной помехи. Искровые разряды и индуцированные шумы, возникающие при коммутации, должны эффективно поглощаться RC-цепочкой.
При управлении электромагнитными устройствами, имеющими значительную индуктивность (например, соленоиды электромагнитных клапанов, катушки электромагнитных пускателей, реле и контакторов), рекомендуется применять помехоподавляющие RC-цепочки в соответствии со схемой, приведенной на рис. 1.
1.
Рис. 1. Включение помехоподавляющей RC-цепи в схему управления контакторами. а) схема без RC-цепочки; б) схема с подключенной RC-цепочкой
Подробные осциллограммы, снятые в схеме управления реального АВР приведены ниже на рисунках.
На рис. 2 приведена осциллограмма напряжения 220 В на катушке управляющего реле в схеме без помехоподавляющей RC-цепи, в соответствии с рис. 1а. В схеме использован контактор АВВ ESB 20-11 Выброс напряжения при отключении контактов управляющего реле составил +2200 В (1 дел.=1000 В).
Рис. 2. Оосциллограмма напряжения на катушке управляющего реле в схеме без помехоподавляющей RC-цепи.
На рис. 3 приведена осциллограмма напряжения 220 В на катушке управляющего реле в схеме с установленной помехоподавляющей RC-цепочкой, в соответствии с рис. 1б. В схеме использован контактор АВВ ESB 20-11 Выброс напряжения при отключении контактов управляющего реле отсутствует (1 дел.=1000 В).
Рис. 3. Осциллограмма напряжения на катушке управляющего реле в схеме с установленной помехоподавляющей RC-цепочкой.
Рис. 4. Способ подключения RC-цепи к контактору
Примечание. Применение помехоподавляющей RC-цепочки с указанными параметрами приводит к незначительному увеличению времени отключения контактора/магнитного пускателя. Эта задержка составляет от 0,05 до 0,015 с, в зависимости от типа контактора. В большинстве применений увеличением задержки можно пренебречь.
Неправильный подбор параметров помехоподавляющей RC-цепи на катушке приводит к замедлению работы контактора в определенных режимах работы и еще большему дребезгу его силовых контактов.
RC цепочки:
Источник
Постоянная времени RC-цепи с несколькими конденсаторами и резисторами
Процесс довольно прост. Но результаты имеют нюансы.
Обозначим первый узел как \$v_x\$, а второй — как \$v_y\$. Тогда у вас есть два уравнения во временной области KCL:
$$\begin{align*} \ frac {v_x} {R_1} + \ frac {v_x} {R_2} + \ frac {\ text {d} \, v_x} {\ text {d} t} C_1 & = \ frac {v_ {_ \ text { CC}}}{R_1}+\frac{v_y}{R_2} \\\\ \ frac {v_y} {R_2} + \ frac {v_y} {R_3} + \ frac {\ text {d} \, v_y} {\ text {d} t} C_2 & = \ frac {v_x} {R_2} \end{выравнивание*}$$
То же самое в области Лапласа:
$$\begin{align*} \mathcal{L}\left\{v_x\right\}\left(\frac{1}{R_1\,C_1}+\frac{1}{R_2\,C_1}\right)+s\mathcal{L} \left\{v_x\right\} &= \frac{\mathcal{L}\left\{v_{_\text{CC}}\right\}}{R_1\,C_1}+\mathcal{L}\ влево\{v_y\вправо\}\frac{1}{R_2\,C_1} \\\\ \mathcal{L}\left\{v_y\right\}\left(\frac{1}{R_2\,C_2}+\frac{1}{R_3\,C_2}\right)+s\mathcal{L} \left\{v_y\right\}&=\mathcal{L}\left\{v_x\right\}\frac{1}{R_2\,C_2} \end{align*}$$
Или,
$$\begin{выравнивание*} V_x\left(\frac{1}{R_1\,C_1}+\frac{1}{R_2\,C_1}\right)+s\,V_x &= \frac{V_{_\text{CC}}} {R_1\,C_1}+V_y\frac{1}{R_2\,C_1} \\\\ V_y\left(\frac{1}{R_2\,C_2}+\frac{1}{R_3\,C_2}\right)+s\,V_y&=V_x\frac{1}{R_2\,C_2} \end{align*}$$
(где \$V_x=\mathcal{L}\left\{v_x\right\}\$ и \$V_y=\mathcal{L}\left\{v_y\right\ }\$. )
)
Это решаемо (в области Лапласа) с использованием SymPy как:
var( 'r1 r2 r3 c1 c2 vx vy vcc s' ) eqvx = Eq( vx*( 1/r1/c1 + 1/r2/c1) + s*vx, vcc/r1/c1 + vy/r2/c1) eqvy = Eq( vy*( 1/r2/c2 + 1/r3/c2) + s*vy, vx/r2/c2) ans = решить( [eqvx, eqvy], [vx, vy])
Так как я написал небольшую функцию для решения передаточных функций 2-го порядка (задокументировано в другом месте на этом сайте), я могу использовать \$V_{_\text{CC}}\$ в качестве «входа» и найти:
для y в ответе: tf2 (ответ [y]/vcc)
{омега: sqrt(r1 + r2 + r3)/(sqrt(c1)*sqrt(c2)*sqrt(r1)*sqrt(r2)*sqrt(r3)),
дзета: (c1*r1*r2/2 + c1*r1*r3/2 + c2*r1*r3/2 + c2*r2*r3/2)/(sqrt(c1)*sqrt(c2)*sqrt(r1 )*sqrt(r2)*sqrt(r3)*sqrt(r1 + r2 + r3)),
P: [{A: c2*r2*r3/(c1*r1*r2 + c1*r1*r3 + c2*r1*r3 + c2*r2*r3), N: 1},
{A: (r2 + r3)/(r1 + r2 + r3), N: 0}]}
{омега: sqrt(r1 + r2 + r3)/(sqrt(c1)*sqrt(c2)*sqrt(r1)*sqrt(r2)*sqrt(r3)),
дзета: (c1*r1*r2/2 + c1*r1*r3/2 + c2*r1*r3/2 + c2*r2*r3/2)/(sqrt(c1)*sqrt(c2)*sqrt(r1 )*sqrt(r2)*sqrt(r3)*sqrt(r1 + r2 + r3)),
P: [{A: r3/(r1 + r2 + r3), N: 0}]}
Это все еще символическая форма, но она показывает вам некоторые детали. Один из них заключается в том, что оба узла имеют одинаковые \$\omega_{_0}\$ и \$\zeta\$ (или \$Q\$). Другой заключается в том, что \$V_x\$ представляет собой комбинацию полосы пропускания и фильтр нижних частот, а \$V_y\$ просто фильтр нижних частот.
Один из них заключается в том, что оба узла имеют одинаковые \$\omega_{_0}\$ и \$\zeta\$ (или \$Q\$). Другой заключается в том, что \$V_x\$ представляет собой комбинацию полосы пропускания и фильтр нижних частот, а \$V_y\$ просто фильтр нижних частот.
Давайте посмотрим числовые результаты:
для y в ответах: tf2((ans[y]/vcc).subs({r1:200,r2:500,r3:300,vcc:100,c1:1e-3 ,c2:1e-3}))
{омега: 5.77350269189626,
дзета: 1.06809799800081,
Р: [{А: 0,405405405405405, Н: 1}, {А: 0,800000000000000, Н: 0}]}
{омега: 5.77350269189626,
дзета: 1.06809799800081,
П: [{А: 0,300000000000000, Н: 0}]}
Так \$\omega_{_0}\приблизительно 5,7735\:\frac{\text{рад}}{\text{s}}\$ (\$f_{_0}\приблизительно 918,86\:\text{мГц} \$) и \$\дзета\приблизительно 1,0681\$. Ни один из узлов не имеет недостаточного демпфирования (на самом деле они не могут быть в этой конфигурации независимо от номиналов деталей), поэтому узлы не должны демонстрировать звон во временной области при подаче источника напряжения.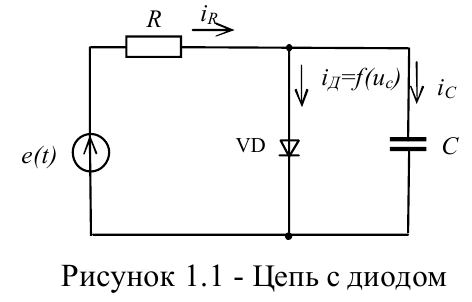
Вышеизложенное можно представить в стандартной форме (читая сверху, что \$K_{x_1}\приблизительно 0,450451\$, \$K_{x_0}=0,8\$ и \$K_{y_0}=0,3\ $): 92+37с+100\$. Это решение состоит из двух частей: \$\left(a_1 s — a_0\right)\cdot\left(b_1 s — b_0\right)\$. Это означает, что \$a_1\cdot b_1=3\$. Присвоим \$a_1=3\$ и \$b_1=1\$. Мы также знаем, что \$-a_1\cdot b_0-b_1\cdot a_0=-3\cdot b_0-a_0=37\$ и что \$a_0\cdot b_0=100\$. Эти два уравнения решаются как \$a_0=-25\$ и \$b_0=-4\$. Следовательно, \$\left(3 s — 25\right)\cdot\left( s — 4\right)=3\cdot\left(s — \frac{25}{3}\right)\cdot\left( с — 4\справа)\$. И есть две необходимые нам константы, \$-4\$ (соответствует \$250\:\text{ms}\$) и \$-\frac{25}{3}\$ (соответствует \$120\ :\text{ms}\$), чтобы использовать две степени \$e\$. 92-4\,\cdot\, 3\,\cdot\, 100}}{2\,\cdot\, 3}=\frac{-37\pm\sqrt{1369-1200}}{6}=\ frac{-37\pm\sqrt{169}}{6}=\frac{-37\pm 13}{6}\$ и здесь вы получите \$-\frac{25}{3}\$ и \$ -4\$ для корней.
Вы также можете использовать технику Verbal Kint, ФАКТЫ проиллюстрированы здесь, чтобы найти и суммируйте два основных \$\tau\$s, чтобы получить коэффициент для \$s\$ (из 37, это получается из суммы двух \$\tau\$, один из \$160\:\text{ms}\$ и другой из \$210\:\text{ms}\$.
2\$.
Множество путей. (Почти слишком много.)
Учитывая \$f_{_0}\приблизительно 918,86\:\text{мГц}\$ из приведенного выше, вы должны ожидать, что все в значительной степени уляжется примерно через \$2\:\text{s} \$.
RC естественный отклик — вывод
Резисторно-конденсаторная схема $(\text{RC})$ — одна из первых интересных схем, которые мы можем создать. Понимание этой схемы необходимо для понимания электронных систем.
Для точного понимания $\text{RC}$ требуются методы исчисления. Мы используем производные для описания поведения схемы $\text{RC}$.
Автор Вилли Макаллистер.
Содержание
- Стратегия
- Модель компонентов
- Модель схемы
- Решить схему
- Предложить решение
- Подставить в дифференциальное уравнение
- Характеристическое уравнение
- Общий раствор
- Проверка концепции: тестирование общего решения
- Частное решение: используйте начальные условия
- Постоянная времени
- Пример 1
- Практическое правило — $37\%$
- Имитационная модель
- Пример 2
- Другое эмпирическое правило — константы времени $3$
- Приложение — Еще один способ решения этого ОДУ
- Приложение — $e$ — специальный номер
- Приложение — Экспоненты случаются в природе
Куда мы движемся
Естественная характеристика резисторно-конденсаторной цепи — затухающая экспонента, 9{-t/\tau}$
Наша цель состоит в том, чтобы получить точное уравнение для естественного отклика этой цепи,
Мы придаем схеме некоторую начальную энергию, помещая заряд $q$ на конденсатор . Это вызывает появление напряжения на конденсаторе в соответствии с $q = \text C\,v$. Затем мы делаем шаг назад и наблюдаем за тем, что напряжение делает «естественно». Что бы ни происходило, это называется естественной реакцией . Естественная реакция — это то, что делает схема, когда у нее есть некоторая начальная энергия, но ничто извне не управляет схемой.
Это вызывает появление напряжения на конденсаторе в соответствии с $q = \text C\,v$. Затем мы делаем шаг назад и наблюдаем за тем, что напряжение делает «естественно». Что бы ни происходило, это называется естественной реакцией . Естественная реакция — это то, что делает схема, когда у нее есть некоторая начальная энергия, но ничто извне не управляет схемой.
«Найти ответ» означает найти $\goldD v$ и $\blueD i$ как функцию времени.
Стратегия
Вот стратегия, которую мы используем для моделирования схемы с помощью дифференциального уравнения и последующего ее решения. Если это ваше первое дифференциальное уравнение, не волнуйтесь, мы рассмотрим каждый шаг.
- Моделирование компонентов $\text R$ и $\text C$ с их уравнениями $i$-$v$
- Смоделируйте цепь, используя закон тока Кирхгофа (KCL)
- KCL дает нам дифференциальное уравнение
- Шаг за шагом решить дифференциальное уравнение
- Угадайте решение с регулируемыми константами
- Подставьте решение к дифференциальному уравнению
- Соберите одинаковые коэффициенты и определите характеристическое уравнение
- Найдите корень $s$ характеристического уравнения
- Найдите постоянную амплитуды $K$, используя начальное условие $\text V_0$
- Предположение подтверждается, если вы можете найти значение для $K$ и оно действительно является постоянным (не меняется со временем)
- Собрать результат
Смоделируйте компоненты
Для начала мы определим две отдельные текущие стрелки, $i_\text R$ и $i_\text C$.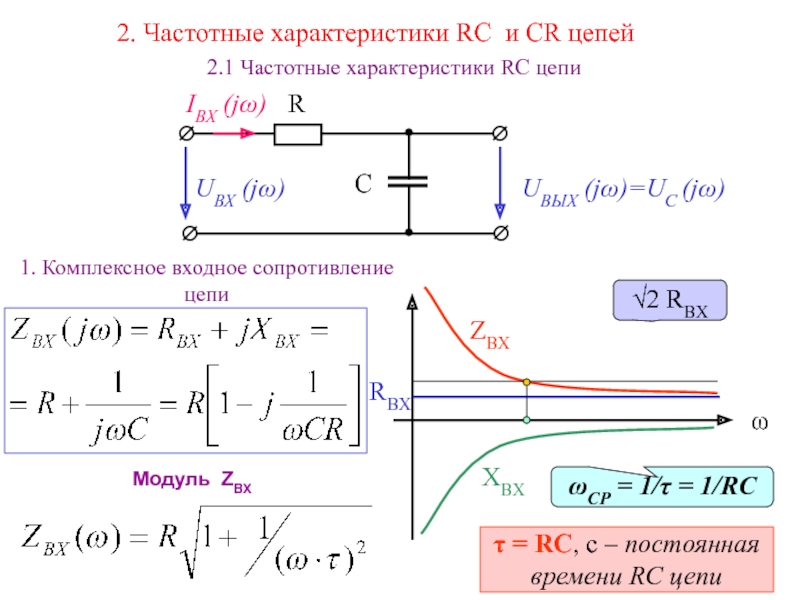 С помощью двух стрелок мы соблюдаем соглашение о знаках для пассивных компонентов как для $\text R$, так и для $\text C$.
С помощью двух стрелок мы соблюдаем соглашение о знаках для пассивных компонентов как для $\text R$, так и для $\text C$.
$i_\text R$ поступает в положительный вывод напряжения $\text R$. $i_\text C$ впадает в положительный вывод напряжения $\text C$. Это означает, что уравнения $i$-$v$, которые мы пишем для $\text R$ и $\text C$, не нуждаются в отрицательном знаке.
$\text R$ и $\text C$ описываются своими уравнениями напряжения-тока.
Резистор описывается законом Ома,
$i_{\text R} = \dfrac{v}{\text R}$
Соответствующее отношение $i$-$v$ для конденсатора:
$i_{\text C} = \text C\,\dfrac{dv}{dt}$
Откуда взялось это уравнение?Начнем с зависимости заряда конденсатора от напряжения,
$q=\текст C\,v$
Возьмите производную по времени от обеих сторон,
$\dfrac {dq} {dt} = \text C \,\dfrac {dv} {dt}$
Левая сторона ${dq}/{dt}$. Это представляет собой изменение заряда за изменение времени или перемещение заряда.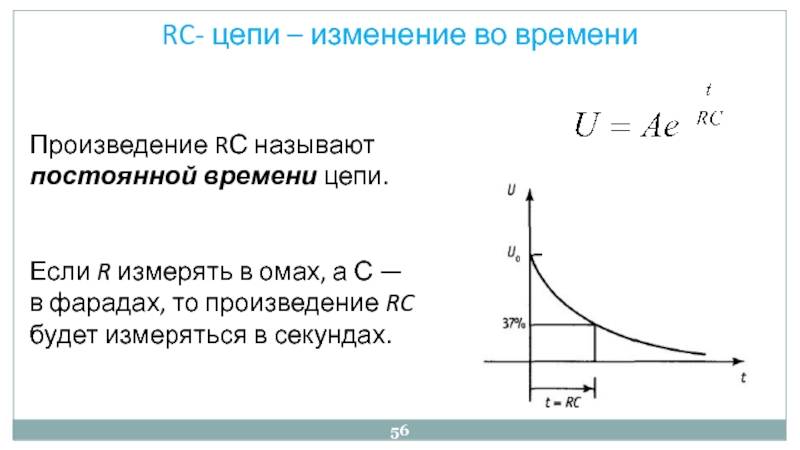 Движущийся заряд эл. тока!
Движущийся заряд эл. тока!
Термин «электрический ток» впервые употребил Андре-Мари Ампер. Символ, который мы используем для текущего, — ‘$i$’. Оно происходит от первой буквы французской фразы intensité du courant électrique .
Если мы заменим ${dq}/{dt}$ на $i$, мы получим соотношение ток-напряжение для конденсатора,
$i = \text C \,\dfrac{dv}{dt}$
Смоделируйте цепь
Затем мы напишем уравнение, используя закон тока Кирхгофа (KCL) с формой KCL, которая гласит: «токи, вытекающие из узла, составляют до $0$».
$i_\text C + i_\text R = 0$
Подставить в двух соотношениях $i$-$v$
$\text C\,\dfrac{dv}{dt} + \dfrac 1 {\text R} \, {v} = 0$
У этого уравнения причудливое название. Это обыкновенных дифференциальных уравнений первого порядка (ОДЭ).
Что означают эти термины?Это дифференциальное уравнение, потому что оно содержит производные $dv/dt$.
Это первого порядка , потому что старшей производной является первая производная $dv/dt$.
Это обычное , потому что есть только одна независимая переменная $t$ (в отличие от частных производных нескольких независимых переменных).
Удивительно, как схематические символы представляют фрагменты дифференциальных уравнений. Простые символы, сложные идеи.
Решить схему
Будем решать это уравнение вместе шаг за шагом,
$\text C\,\dfrac{dv}{dt} + \dfrac 1 {\text R} \, {v} = 0 \qquad$ (дифференциальное уравнение)
Когда вы решаете дифференциальное уравнение, вы должны найти функцию, в нашем случае, функцию напряжения относительно времени, $v(t)$, где подставляя функцию в дифференциальное уравнение делает уравнение верным. В качестве дополнительной задачи решение должно быть верным в каждый момент времени.
Откуда берутся решения? Один из способов — угадать решение и опробовать его — не какое-то дикое предположение, а обоснованное предположение. Если в вашем учебнике сказано что-то вроде «предположим решение вида…», это то же самое, что и предположение.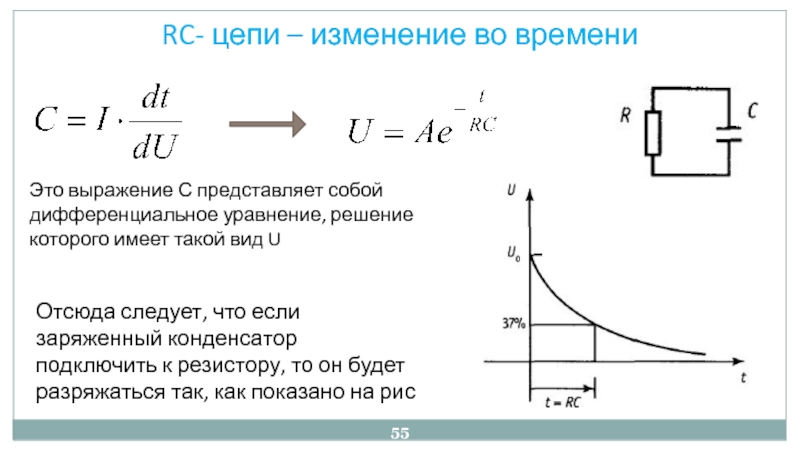
Глядя на дифференциальное уравнение, загляните в глубины своей памяти, где вы храните все, что знаете о функциях. Расслабься и следуй дальше…
Два члена в уравнении в сумме дают ноль. Это предполагает, что первая производная функции $dv/dt$ должна иметь ту же форму, что и сама функция $v$. Поищите в памяти любую функцию, первая производная которой выглядит точно так же, как она сама. Хм… 9{\ displaystyle \ alpha t} $
(Эту производную стоит запомнить. Вы можете просмотреть ее или получить полное доказательство.)
Чтобы решить наше дифференциальное уравнение, мы
- делаем смелое предложение относительно формы решения. . (Это требует мужества.)
- подставьте наше решение в уравнение и вычислите некоторые константы. (Это требует математики.)
Если все работает и дифференциальное уравнение оказывается верным, то наша предложенная функция является победителем.
9{\displaystyle st}$- $t$ — это время.
- $v(t)$ — зависимость напряжения от времени.

- $K$ и $s$ — константы, которые нам нужно вычислить.
- $K$ — коэффициент амплитуды, увеличивающий или уменьшающий напряжение.
- $s$ находится в показателе степени.
- Поскольку показатели степени не могут иметь размерности, единицами измерения $s$ должны быть $1/t$.
- $1/t$ — это единица частоты, поэтому $s$ называется собственной частотой . 9{-\infty}$ полностью вымирает. Это говорит нам о том, что через бесконечность времени конденсатор полностью разряжен. Это интересно, но не говорит нам о том, что произойдет в ближайшее время.
Более наводящее на размышления решение приходит из третьего варианта,
$s\text C + \dfrac 1 {\text R} = 0$
}$ схема.
Характеристическое уравнение верно, если
$s = -\dfrac{1}{\text{RC}}$
магический момент 9{-t/\text{RC}}$. Семейство функций, которые делают дифференциальное уравнение верным. Неизвестный коэффициент $K$ будет определен при рассмотрении начальных условий.
Проверка концепции: проверка общего решения
Проверка общего решения путем подстановки его в дифференциальное уравнение.
показать ответ
Пожалуйста, пожалуйста, попробуйте сами, прежде чем смотреть.Дифференциальное уравнение естественной реакции:
$\dfrac{dv}{dt} + \dfrac{1}{\text{RC}} \, {v} = 0$ 9{-t/\text{RC}} \stackrel{?}{=} 0$
Как мы это сделали?
$0 \stackrel{\checkmark}{=} 0$
Предложенное решение делает дифференциальное уравнение верным для любого значения $K$.
Частное решение: использовать начальные условия
Почти готово. Нам нужно найти значение для $K$, которое учитывает начальных условий — начальное напряжение на конденсаторе. Когда мы разрешаем произвольную константу $K$, мы нашли частных 90$
$\text V_0 = K \cdot 1$
$K = \text V_0$
$K$ — константа, не зависящая от $t$. Это подтверждает, что наша первоначальная догадка — экспоненциальное напряжение — была правильным выбором.
 (Если мы не смогли найти $K$ или если $K$ не было постоянным (если оказалось, что оно зависит от времени), то наша догадка не удалась, и нам пришлось начать с новой догадки.)
(Если мы не смогли найти $K$ или если $K$ не было постоянным (если оказалось, что оно зависит от времени), то наша догадка не удалась, и нам пришлось начать с новой догадки.)Один раз значение для $K$ определено, мы переходим от общего решения к частному решению, выбранному из миллиона возможных $v(t)$. Частным решением являются функции «одна из миллиона» от $v$, для которых начальным напряжением является точно $\text V_0$. Это единственный. 9{-t/\text{RC}}}$
где $\text V_0$ — пусковое напряжение на конденсаторе.
$v(t)$ — одна частная кривая, выбранная из всех возможных кривых, представленных общим решением. Вот как выглядит $v(t)$:
Кривая касается оси напряжения в точке $\text V_0$. Крутизна спада напряжения определяется произведением $\text{RC}$ в показателе степени. Через долгое время напряжение приближается к $0$.
Постоянная времени
Давайте заглянем внутрь естественного отклика $\text{RC}$ и сделаем некоторые наблюдения.
 {-t/\tau}$ 9{-1} = 1/e = 1/2,718…$, или около $0,37$
{-t/\tau}$ 9{-1} = 1/e = 1/2,718…$, или около $0,37$По прошествии одной постоянной времени напряжение падает до $37\%$ своего начального значения.
$v(\tau) = \text V_0 \cdot 0.37$
Пример 1
Пусть $\text R = 3 \,\text k\Omega$, $\text C = 1 \,\mu\text F$ и $v(0) = 1,4 \,\text V$.
а. Напишите выражение для $v(t)$.
б. Найдите $v(t)$, когда $t = \text{RC}$.
в. Постройте $v(t)$.а. Напишите выражение для $v(t)$. 9{-1}$
$v(3\,\text{ms}) = 1,4 \cdot 0,37$
$v(3\,\text{ms}) = 0,51 \,\text{volts}$
г. Постройте $v(t)$.
Нажмите Start, чтобы проследить временную характеристику.
Штриховыми линиями показан ответ из части б, $v(t) = 0,51 \,\text V$, когда $t=\text{RC} =$ одна постоянная времени $= 3 \,\text{ms}$ .
Эмпирическое правило — $37\%$
Когда время равно постоянной времени, $\text{RC}$, напряжение уменьшается по сравнению с первоначальным значением в $1/e = 1/2,71828… = 0,36787… $, или примерно до $37\%$ от начальной стоимости.
 Это верно для любое начальное напряжение и любое произведение $\text{RC}$.
Это верно для любое начальное напряжение и любое произведение $\text{RC}$.Имитационная модель
Имитационная модель примера 1. Нажмите TRAN для выполнения анализа переходных процессов. (Примечание: МОП-транзистор работает как переключатель. Они очень широкие, $\text W = 10{,}000$, поэтому их сопротивление очень мало при высоком напряжении на затворе.)
Пример 2
Пусть $ \text R = 1\,\text{k}\Omega$, $\text C = 1\,\text{pF}$ и $\text V_0 = 1.0\,\text V$.
9{-9} = 1\,\text{nsec}$При постоянной времени $1\,\text{наносекунд}$ это довольно быстрая схема.
в. Постройте $v(t)$.
Нажмите Start, чтобы проследить временную характеристику.
д. Сколько раз требуется, чтобы напряжение упало ниже $95\%$ от его начального значения?
$95\%$ ниже $\text V_0$ составляет $1,0 — (0,95 \х1,0) = 0,05$ вольт. Глядя на график, мы видим, что это происходит примерно при $3\,\text{nsec}$.
 Это соответствует $3$ постоянной времени. Эта точка отмечена черными пунктирными линиями на графике в части 9.0362 с.
Это соответствует $3$ постоянной времени. Эта точка отмечена черными пунктирными линиями на графике в части 9.0362 с. Анимация дает вам мысленный образ скорости экспоненциальной ступенчатой функции. Точка движется с постоянной скоростью слева направо. Обратите внимание, как быстро снижается напряжение в течение первой постоянной времени. Через некоторое время скорость изменения напряжения замедляется. После $3$ постоянных времени — $3\,\text{nsec}$ — шаг практически завершен. Почти ничего не происходит, и становится довольно скучно.
Еще одно эмпирическое правило — $3$ постоянных времени
Любой переходный процесс $\text{RC}$ практически заканчивается после $3$ постоянных времени. Удивительно, но это верно для 9{-t/\text{RC}}$
Где $\text V_0$ — напряжение в момент времени $t=0$.
Постоянная времени для схемы $\text{RC}$ равна $\tau = \text{RC}$.
Цепь $\text{RC}$ можно найти везде в электронике. Иногда вы создаете его специально.
случайно? В других случаях она появляется случайно, и вам приходится с ней бороться.
В других случаях она появляется случайно, и вам приходится с ней бороться.В реальной цепи провода всегда окружены другими проводящими элементами, например, другими проводами или металлическим корпусом. Два проводника, разделенные изолятором, — это конденсатор. Эти конденсаторы (обычно маленькие, обычно нежелательные) подключаются к нужному проводу. Много раз вы можете игнорировать эти так называемые паразитные емкости , но иногда они играют важную роль в работе схемы.
Приложение — Другой способ решения этого ОДУ
Мы использовали метод угадывания, чтобы решить ОДУ для этой схемы. Оказывается, это ОДУ представляет собой 90 136 разделимых 90 137 дифференциальных уравнений. Мы могли бы решить ее без догадок, используя метод разделимых дифференциальных уравнений. Это один из первых методов формального изучения дифференциальных уравнений. Приложение в конце естественного ответа RL показывает пример. Этот метод требует от вас навыков интеграции, но при этом не требуется никаких догадок.



 –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
–7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.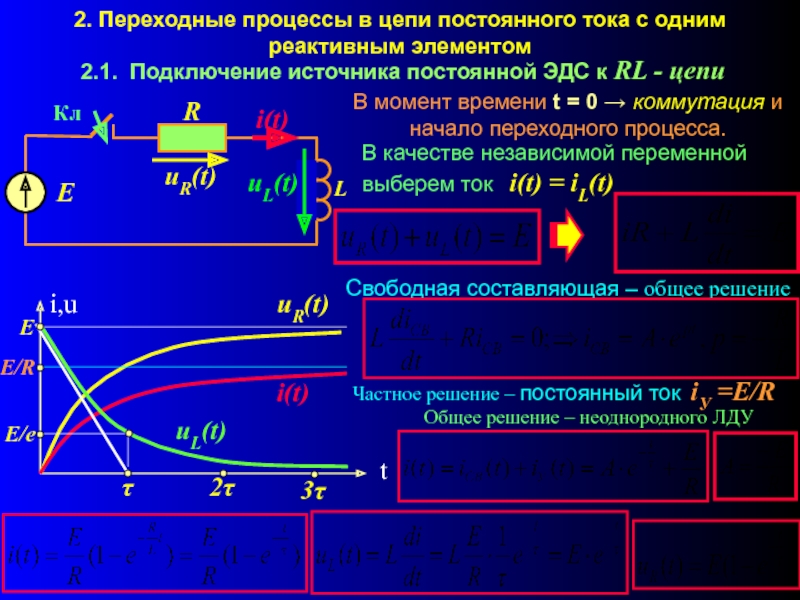 7, если ; ; ; ; .
7, если ; ; ; ; .


 (Если мы не смогли найти $K$ или если $K$ не было постоянным (если оказалось, что оно зависит от времени), то наша догадка не удалась, и нам пришлось начать с новой догадки.)
(Если мы не смогли найти $K$ или если $K$ не было постоянным (если оказалось, что оно зависит от времени), то наша догадка не удалась, и нам пришлось начать с новой догадки.) {-t/\tau}$ 9{-1} = 1/e = 1/2,718…$, или около $0,37$
{-t/\tau}$ 9{-1} = 1/e = 1/2,718…$, или около $0,37$ Это верно для любое начальное напряжение и любое произведение $\text{RC}$.
Это верно для любое начальное напряжение и любое произведение $\text{RC}$. Это соответствует $3$ постоянной времени. Эта точка отмечена черными пунктирными линиями на графике в части 9.0362 с.
Это соответствует $3$ постоянной времени. Эта точка отмечена черными пунктирными линиями на графике в части 9.0362 с.  В других случаях она появляется случайно, и вам приходится с ней бороться.
В других случаях она появляется случайно, и вам приходится с ней бороться.