Nach oben

Информация

• Контактное лицо
• Условия сотрудничества
• Декларация о конфиденциальности
• Вводные данные

Обслуживание

• Краткий обзор услуг
• Скачать
• Каталоги
• Вебинары и Видео
• Связаться со службой поддержки клиентов

Компания

• О нас
• Качественная политика
• Безопасность в классе

Please note

* Prices subject to VAT.

We only supply companies, institutions and educational facilities. No sales to private individuals.

Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.

Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина.
Сохраненные корзины вы можете найти в разделе My Account.

Название корзины

Холла эффект — Физическая энциклопедия

ХОЛЛА ЭФФЕКТ — возникновение в твёрдом проводнике с током плотностью j, помещённом в магн. поле Н, элек-трич. поля в направлении, перпендикулярном j и

Здесь a — угол между векторами Н и j (a<180°). Если H | j, то поле Холла Е_Н максимально: E_H = RHj. Коэф. R, наз. п о с т о я н н о й Х о л л а (к о э ф. Х о л л а), является основной количеств. характеристикой X. э. Знак R положителен, если j, Н, Е_H

X. э. открыт Э. Г. Холлом (Е. Н. Hall) в 1879 в тонких пластинках Аu. Для наблюдения X. э. прямоуг. пластины из исследуемых веществ длиной l, значительно большей ширины b и толщины d, вдоль к-рых течёт ток I=jbd, помещают в магн. поле Н, перпендикулярное плоскости пластинки (рис.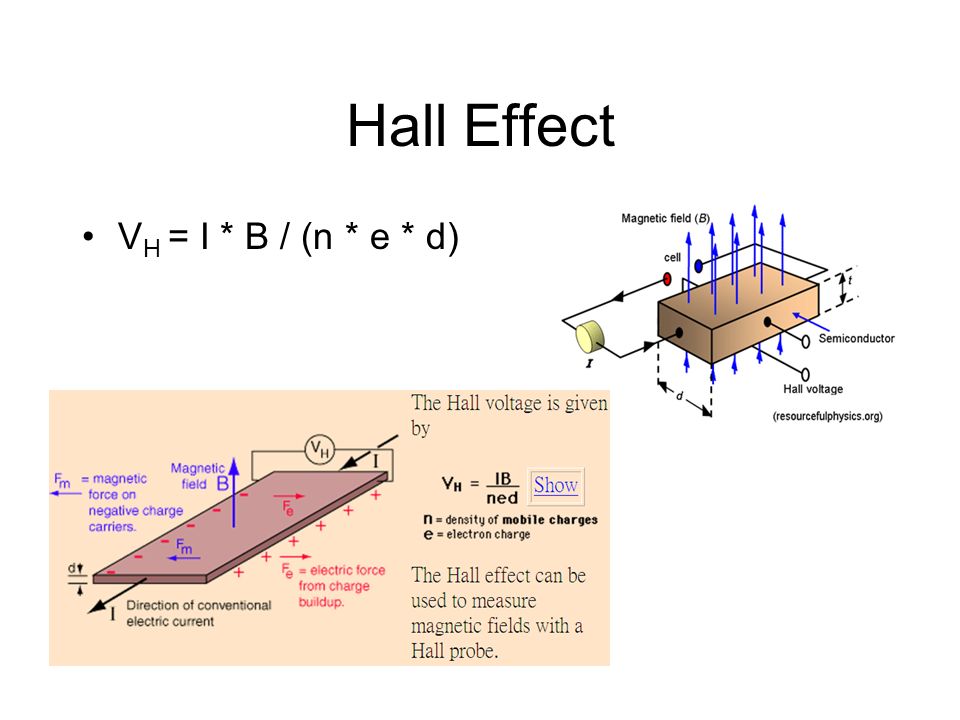 ). На середине боковых граней перпендикулярно току расположены электроды, между к-рыми измеряется эдс Холла

X. э. объясняется взаимодействием носителей заряда (электронов проводимости и дырок) с магн. полем. В магн. поле на электроны действует Лоренца сила F=e[Hu](u = =j/пе-ср. скорость направленного движения носителей в электрич. поле, п — концентрация носителей, е — их заряд), под действием к-рой частицы отклоняются в направлении, перпендикулярном j и Н. В результате на боковой грани пластины происходит накопление зарядов и возникает поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. При равновесии

Знак R совпадает со знаком носителей заряда. Для металлов, у к-рых n~10²² см^-3, R~10^-3 см³/Кл, у полупроводников R~1010⁵ см³/Кл.

Коэф. Холла может быть выражен через подвижность носителей заряда m = u_др/E (дрейфовая скорость носителей u_др= -eEt/m, где т — эффективная масса

Сказанное справедливо для изотропных проводников, в частности для поликристаллов .Для анизотропных кристаллов R = r/en, где коэф. r — величина, близкая к 1, зависящая от направления Н относительно кристаллографич. осей. В области сильных магн. полей r=1. Критерий сильного поля w_сt>1, где w_с — циклотронная частота носителей.

В полупроводниках в электропроводимости участвуют одновременно электроны проводимости и дырки. При этом постоянная Холла выражается через парциальные проводимости электронов s_э и дырок s_д и их концентрации п_э и n_д. В случае слабых полей

Для сильных полей

При п_э = п_д для всех значений магнитного поля R = = (1/еn)(s_э-s_д)/(s_э + s_д), а знак R соответствует знаку осн. носителей.

Для металлов величина R зависит от зонной структуры, т. е. формы

X. э.- один из наиболее эфф. методов изучения энерге-тич. спектра носителей заряда в металлах и полупроводниках. Зная R, можно определить знак носителей заряда и оценить их концентрацию, что позволяет сделать заключение о кол-ве примесей в полупроводниках. Линейная зависимость R от Н используется для измерения напряжённости магн. поля (см. Магнитометры ),а также для усиления пост. токов, в аналоговых вычислит. машинах, в измерит. технике и др. (Холла датчик).

При изучении X. э. в двумерном электронном газе кремниевого полевого транзистора, помещённого в квантующее магн. поле, К. фон Клитцинг (К. von Klitzing) в 1980 обнаружил, что холловское сопротивление (R_H=V_H/I), к-рое в условиях обычного X. э. , как следует из ф-л (2) и (3), обратно пропорционально п, при изменении п то остаётся постоянным, то резко изменяется, переходя с одного уровня на другой. Вместо монотонного убывания в зависимости R_H(n)наблюдались «ступеньки». При этом высота ступенек определяется такими фундам. константами, как постоянная Планка и заряд электрона, и не зависит от свойств вещества. Это явление получило назв. квантового Холла эффекта. Ю. П. Гайдуков.

При описании X. э. в магнетиках следует вместо поля Н рассматривать магн. индукцию В=Н+4pМ, где М— намагниченность .Поле Холла в поликристаллич. ферромагнетиках может быть записано в виде

Здесь x, у, z — координатные оси. Первое слагаемое описывает нормальный X. э. Вклад в поле Холла, пропорциональный намагниченности М, наз. ферромагнитным, спонтанным или аномальным X. э. Т. к. этот вклад существует в ферро-, ферри- и антиферромагн. металлах и полупроводниках, парамагнетиках и др., то термин «а н о м а л ь н ы й X. э.» является наиб. общим. Коэф. R_s в ферромагнетиках на 1-2 порядка больше R и обладает сильной (по сравнению с R)зависимостью от темп-ры. В сплавах величина и знак R_s зависят от концентрации компонент, причём в общем случае знак R_s может не совпадать со знаком R. В монокристаллах R_s также является тензорной величиной. Роль внеш. магн. поля в создании аномального X. э. сводится только к намагничиванию образца, в частности в однодоменных образцах аномальный X. э. наблюдается и без поля.

Аномальный X. э. обусловлен спин-орбитальным взаимодействием, к-рое пропорц. намагниченности и создаёт асимметрию рассеяния. носителей заряда, приводящую к холловскому «закручиванию» в отсутствие поля.

А. Б. Грановский.

Лит. см. при статьях Гальвано магнитные явления, Квантовый Холла эффект. Магнетизм.

      Предметный указатель      >>   

Изменение постоянной Холла при легировании магния » Строительно-информационный портал

Описанное электронное строение магния недавно было подтверждено Шиндлером и Салковитцем, изучившими зависимость постоянной Холла от состава некоторых магниевых сплавов.

Известно, что если через проводник в виде пластины пропустить электрический ток в направлении, перпендикулярном приложенному магнитному полю, то на концах проводника, перпендикулярных направлениям тока и магнитного поля, возникнет некоторая разность потенциалов. Указанное явление носит название эффекта Холла и постоянную Холла Rh можно определить из выражения

где E — электродвижущая сила; t — толщина образца в направлении приложенного магнитного поля; H — напряженность магнитного ноля и I — ток, проходящий через образец.

Если электроны проводимости в проводнике рассматривать как свободные, то можно показать, что постоянная Холла

где с — скорость распространения света; е — заряд электрона; N — число электронов в единице объема. Поскольку заряд электрона отрицателен, знак Rh для электронов также отрицателен. Так, постоянная Холла для натрия равна — 25,5*10в-4.

Во многих случаях, однако, нельзя рассматривать электроны как свободные; например, для почти заполненной зоны Бриллюэна имеются строгие ограничения направления распространения волновой функции, изображающей движущийся электрон; и можно показать, что в этих условиях электроны проводимости ведут себя так, как если бы они обладали отрицательной массой.

В почти заполненной зоне между искаженной поверхностью Ферми и граничными плоскостями зоны существуют «дырки». Волновое уравнение для электрона в почти заполненной зоне можно заменить соответствующим уравнением для дырок зоны. Эти дырки можно рассматривать как положительные частицы, и можно считать, что проводимость металлов и сплавов с почти заполненной зоной объясняется движением этих дырок. Постоянная Холла в этом случае

где N — число положительных дырок в единице объема, и знак Rh здесь уже положителен (так, например, для сурьмы +12000*10в-4).

В общем случае для структур, в которых благодаря перекрытию зон носителями зарядов могут быть одновременно электроны и дырки, можно написать:

где Nа — число атомов в единице объема; n1 — число электронов на атом, n2 — число положительных дырок на атом; a1 и а2 — соответственно подвижности электронов и дырок.

Если принять описанную электронную конфигурацию магния, то процесс проводимости следует считать двухзонным. Электроны, перекрывающие зону в направлении, перпендикулярном гексагональной оси, относительно свободны и могут быть носителями зарядов, как и имеющиеся в зоне Бриллюэна дырки. Постоянная Холла для чистого магния отрицательна; это указывает, что преобладает электронная проводимость. Однако следует ожидать, что при легировании магния относительное число электронов и дырок будет изменяться, что вызовет закономерное изменение постоянной Холла.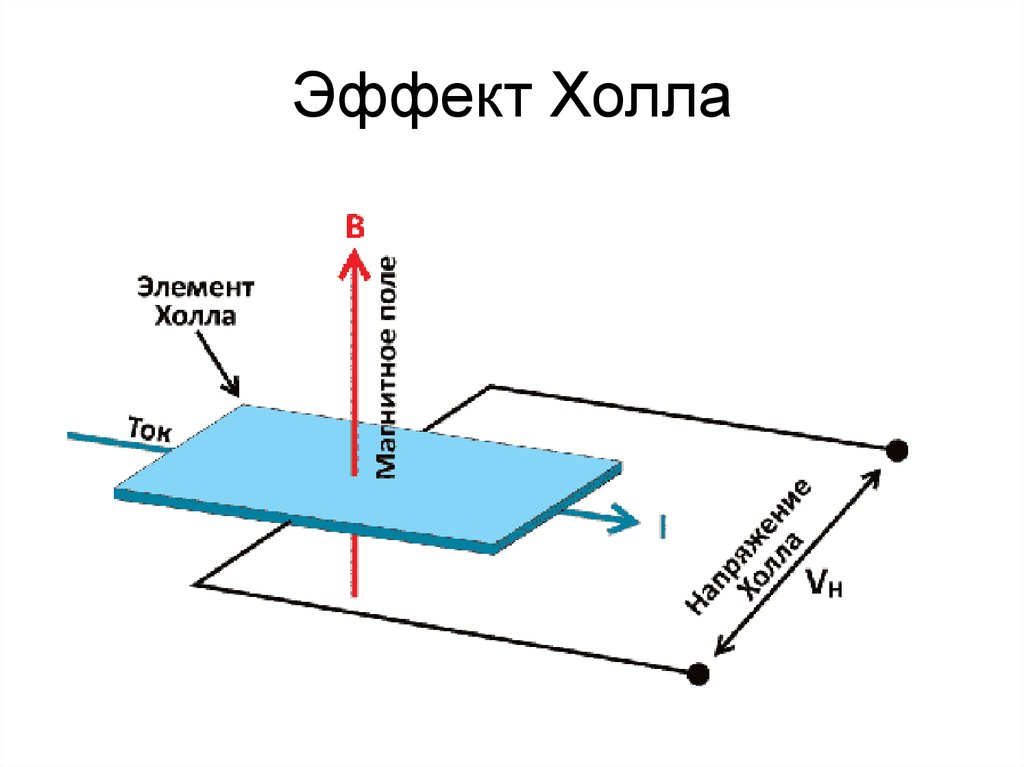 Ясно, что величина и направление изменения будут зависеть от подвижности a1 и а2 электронов и дырок, поэтому для количественных расчетов постоянной Холла необходимо знать эти величины. При перекрытии зон в направлении гексагональной оси можно ожидать значительного изменения постоянной Холла вследствие изменения относительного числа перекрывающихся электронов и дырок, остающихся в первой зоне.

Согласно данным Шиндлера и Салковитца, при добавлении серебра к магнию понижается численное значение отрицательной постоянной Холла. Это понижение линейно связано с атомным составом; 0,1 % (атомн.) Ag изменяет численное значение на 5%. Легирование серебром должно уменьшить число перекрывающихся электронов и увеличить число дырок, так что изменение постоянной Холла в сторону большей положительности вполне понятно. Ясно, что электронное строение магния существенно изменяется при образовании твердого раствора с серебром. Добавка к магнию алюминия должна привести к увеличению числа перекрывающихся электронов и к уменьшению числа положительных дырок.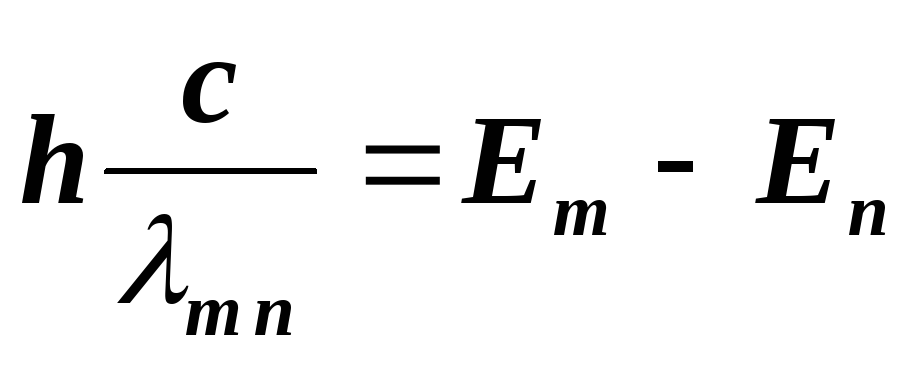

Экспериментально показано, что при введении в магний небольшого количества алюминия численное значение постоянной Холла уменьшается, однако не так быстро, как при введении серебра. Таким образом, в согласии с общими принципами, тенденция к увеличению положительности RH для алюминия значительно меньше заметна.

Данные об изменении периодов решетки магниевых сплавов подтверждают теоретический вывод о том, что перекрытие в направлении, параллельном гексагональной оси, происходит, когда число электронов на атом приблизительно достигает значения 2,0075. При этом вследствие увеличения числа отрицательных носителей заряда следует ожидать увеличения отрицательного значения постоянной Холла. Результаты, полученные Шиндлером и Салковитцем, полностью подтверждают это; при критическом содержании алюминия отрицательная величина RН (рис. 21) перестает уменьшаться и при дальнейшем увеличении содержания алюминия наблюдается некоторый рост RН. На рисунке видно, что перекрытие в направлении гексагональной оси начинается при содержании алюминия, приблизительно равном 1% (атомн.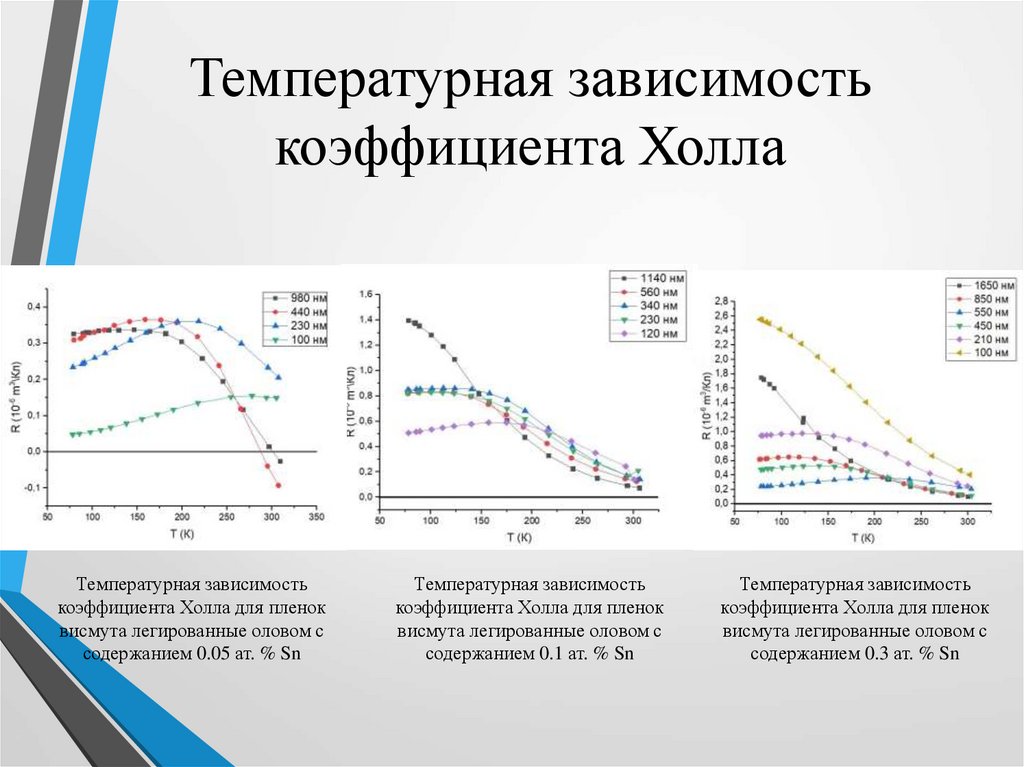 ). Это значение несколько больше значения, полученного из рентгеновских данных, но в общем согласие удовлетворительное.

Таким образом, прямое изучение электрических свойств магния и его сплавов подтверждает данные об электронной конфигурации магния, полученные более косвенными методами.

2.1.3 Эффект Холла

	Сравнительно легко рассчитать величину напряжения Холла U Холла , индуцированного магнитным полем Б .
		Сначала отметим, что мы также должны иметь электрическое поле E , параллельное j , потому что это движущая сила течения.
		Во-вторых, мы знаем, что магнитное поле под прямым углом к ​​току воздействует на движущиеся носители силой, так называемый Лоренц сила F L , то есть
		F L  =  q · ( v D × B )
		Мы должны взять дрейф скорость v D носителей, потому что другие скорости (и силы, вызванные этими компоненты) сокращаются до нуля в среднем. Векторное произведение гарантирует, что F L перпендикулярно v D и Б .
		Обратите внимание, что вместо обычного слова «электрон» используется нейтральный термин носитель , потому что в принципе электрический ток также может переноситься заряженными частицами, отличными от электронов, например. положительно заряженные ионы. Запомните простую, но важную картинку, приведенную ранее!
	Для приведенной выше геометрии сила Лоренца Ж Л есть только компонент в y — направление и мы можем использовать для него скалярное уравнение. F у есть дано
		F y  =  – q · v D,x · Б г
		Мы должны быть немного осторожны: Мы знаем, что сила находится в y -направлении, но мы больше не знаем знака.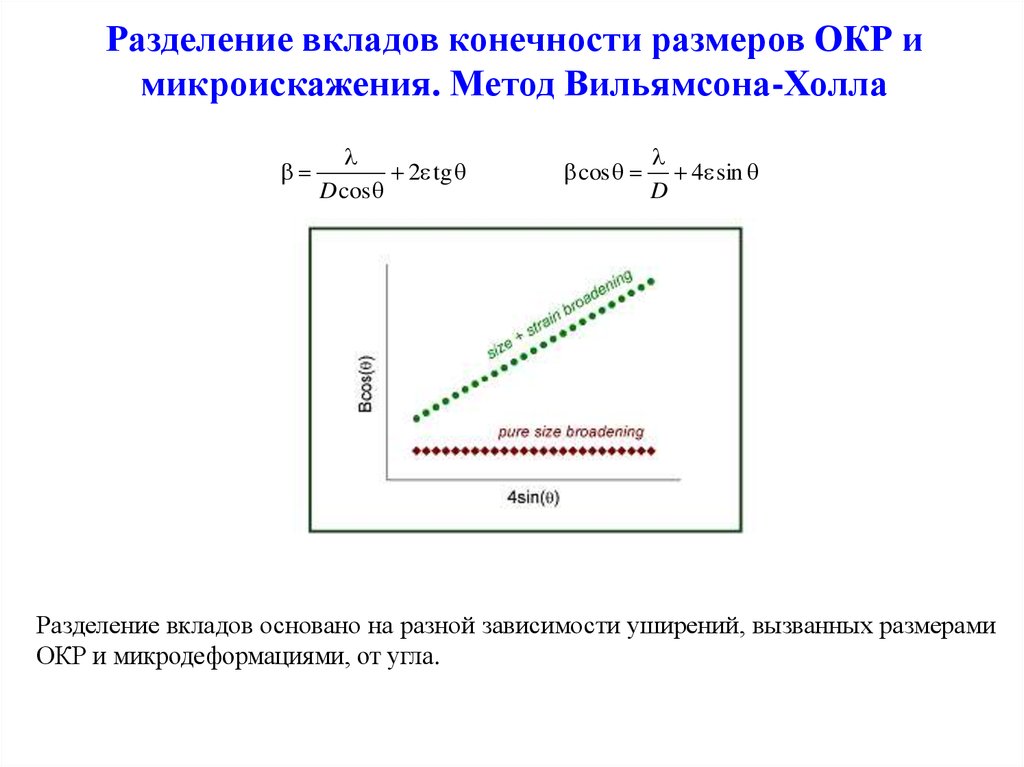 Он меняется, если либо q , v D или B z меняет направление, и мы должны знать что.
		Однако важно обратите внимание, что при фиксированной плотности тока j x направление силы Лоренца не зависит от знак носителей заряда – знак заряда и знак дрейфовой скорости просто компенсируют друг друга Другой.
	С в Д = µ · E и µ = подвижность носителей, получаем довольно простое уравнение для силы
		F y  =  – | q | · м · E x · B z
	Токи носителей отклонится от прямой в y -направлении.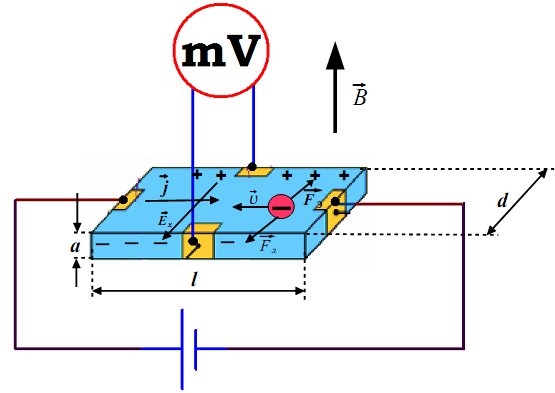 Другими словами, существует компонент скорость в y -направление и поверхности, перпендикулярные y -направлению, станут заряжается, как только ток (или магнитное поле) включается. Линии потока носителей будут иметь вид это:
		Зарядка поверхностей неизбежно, потому что некоторые из носителей в конечном итоге окажутся на поверхности, где они «застряли».
		Обратите внимание, что знак заряда для данного поверхности зависит от знака заряда носителей. Отрицательно заряженные электроны ( e — в рисунок) оказываются на поверхности, противоположной положительно заряженным носителям (обозначены на рисунке h + ).
		Обратите также внимание, что направление силы Ф y одинакова для обоих типов носителей просто потому, что и q , и v D поменять знаки в формуле силы
	затем поверхностный заряд индуцирует электрическое поле сила Лоренца; он пытается переместить носителей обратно.
		В равновесии сила Лоренца F y и сила электрического поля E y in y -направление (которое, конечно, просто q · E y ) должно быть равно противоположные знаки. Таким образом, мы получаем
		– q · E y  =  – | q | · м · E x · B z       E y  =  sgn( q ) · µ · E x · B z
	Напряжение Холла U Hall теперь просто поле в y -направление умноженное на размерность д у в у -направление.
		Тогда ясно, что (легко измеряемое) напряжение Холла является прямой мерой µ подвижности участвующих носителей, и что его знак или полярность изменится, если изменится знак протекающих зарядов.
	Принято определять зал коэффициент R Холла для данного материала.
		Это можно сделать разными, но эквивалентные способы. В ссылке мы смотрим на определение, которое особенно подходит для измерений. Здесь мы используем следующее определение:
		R Hall  =  E y B z · j x
	In other words, мы ожидаем что напряжение Холла E y · d y (с д г = размерность в y -направление) пропорциональна току(плотности) j и магнитному полю прочности B , которые, в конце концов, являются основными экспериментальными параметрами (помимо тривиальных размеров образец):
		E y  =  R Hall · B Z · J x
	Коэффициент. материальный параметр, действительно, потому что мы получим разные числа для R Холла , если мы это сделаем эксперименты с одинаковыми магнитными полями и плотностью тока, но с разными материалами. Коэффициент Холла, как упоминалось ранее, имеет интересные свойства:
		R Зал изменит свой знак, если изменится знак перевозчиков, потому что тогда E y тоже меняет знак. Таким образом, он указывает самым недвусмысленным образом, какой только можно вообразить, если он положителен. или отрицательные заряды несут ток.
		R Холл позволяет получить мобильность µ носителей, как мы сразу увидит.
	R Холл легко вычисляется: Используя уравнение для E y сверху, и основное уравнение j x = s · E x , мы получаем для отрицательно платные перевозчики:
		R Холл   =  – µ · E x · B z s · E x · B z  =  –   µ s   =   – µ | q | · n · µ =   – 1 | q | · n
	Синяя часть соответствует вывод указан в ссылке; n (очевидно) концентрация носителей.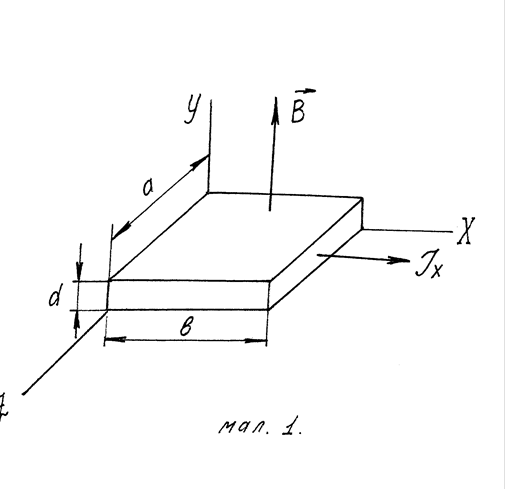
		Если известен коэффициент Холла или концентрация носителей, эффект Холла можно использовать для измерения напряженности магнитного поля B (иначе не так просто сделать!).
	Измерения коэффициента Холла материалов с известным проводимость (что-то легко измеримое), таким образом, дает нам напрямую мобильность носители, ответственные за проводимость.
		Знак минус выше получается для электронов , т.е. отрицательных зарядов.
		Если будут задействованы положительно заряженные носители, Постоянная Холла будет положительной .
		Обратите внимание, что не всегда легко измерить числовое значение напряжения Холла и, таким образом, R с хорошей точностью, это самое простое в мир для измерения полярности напряжения.
	Давайте посмотрим на несколько экспериментальных данных:
		Material Li Cu Ag Au Al Be In Полупроводники (например, Si , G e , GaAs , InP ,. ..) R (× 10 –24 ) cgs units –1,89 –0,6 –1,0 –0,8 +1,136 +2,7 +1,774 положительный или отрицательных значений в зависимости от «допинга» Комментарии: 1. положительных значений для металлы измерялись в несколько особых условиях (низкие температуры, монокристаллы с особой ориентацией), для других условий также могут быть получены отрицательные значения. 2. Единицы в данном случае не важны, но умножение на   9 · 10 13 дает значение в м 3 / кулон

Калькулятор коэффициента Холла | Действия по нахождению коэффициента Холла

Используйте Калькулятор коэффициента Холла, чтобы найти коэффициент Холла, определяющий природу носителей заряда в проводнике. Вы должны ввести данные о напряжении, толщине, токе и магнитном поле в предусмотренных полях ввода калькулятора. Нажмите кнопку расчета, чтобы проверить результат за короткий промежуток времени.

Выберите расчет

Найти коэффициент Холла | Заданное напряжение, толщина, ток, магнитное поле Найти напряжение | Учитывая Коэффициент Холла,Толщину,Ток,Магнитное поле Найти толщину | Заданное напряжение, коэффициент Холла, ток, магнитное поле Найти ток | Заданное напряжение, толщина, коэффициент Холла, магнитное поле Найти магнитное поле | Заданное напряжение, толщина, ток, коэффициент Холла

Напряжение:

ВмВкВМВ

Толщина:

mmmcmkminydftmi

Ток:

AmAµA

Магнитное поле:

TmTµT

Коэффициент Холла:

m ³ /C

Калькулятор коэффициента Холла: Определите природу электронов в проводнике с помощью удобного инструмента, представленного здесь. Узнайте, что такое эффект Холла, его применение и формулы коэффициента Холла из следующих разделов. Кроме того, получите простые ручные шаги для вычисления коэффициента Холла и примеры вопросов по нему.

Подробный пошаговый процесс получения коэффициента Холла для электронов в проводнике. Следуйте этим правилам и проверьте вывод на наличие ваших чисел.

• Получите необходимые данные, такие как напряжение, ток, толщина и магнитное поле.
• Умножьте напряжение на толщину проводника.
• Разделите результат на произведение тока и магнитного поля, чтобы проверить значение коэффициента Холла.

Эффект Холла заключается в том, что когда проводник с током помещается в перпендикулярное магнитное поле, напряжение можно определить под прямым углом к ​​току. Этот процесс получения измеримого напряжения называется эффектом Холла. Он был открыт Эдвином Гербертом Холлом в 1879 году.

Коэффициент Холла используется для измерения силы эффекта Холла. Математически это представляется как

RH = Vt/(IB)

Напряжение V = RH x I x B/t

Толщина t = RH x I x B/V

Ток I = Vt/(RH x B)

B = Vt/(RH x I)

Где

RH — коэффициент Холла

В — наблюдаемая разность напряжений

t — толщина проводника

I — ток, протекающий через проводник

B — магнитное поле

Коэффициент Холла определяет природу носителей заряда и их концентрацию в проводнике проводник. Его формула:

RH = -1/(nq)

Где

n — концентрация носителей

q — заряд одного носителя

Пример

Вопрос: Найдите коэффициент Холла для 5 x 10 ²⁸ атом/м ³ в медном блоке.

Решение:

, учитывая, что

NQ = 5 x 10 ²⁸ Atom/M ³

Коэффициент зала Rh = -1/(nq)

. ²⁸ )

= -0,125 x 10 ^-9 м ³ /C

Следовательно, коэффициент Холла равен -0,125 x 10 ^-9 м ³ /C

Если вы хотите решать задачи по физике без ручки и бумаги, зайдите на наш сайт Physicscalc. Com и нажмите на ссылку нужного калькулятора, чтобы мгновенно получить точный результат.

1. Для чего используется коэффициент Холла?

Коэффициент Холла используется для определения силы эффекта Холла. Возникновение разности потенциалов из-за магнитного поля называется эффектом холла.

2. Каковы применения эффекта Холла?

Применение эффекта Холла: трансформаторы тока, клавишные переключатели, определение скорости, аксессуары для Galaxy S4, датчики положения и другие.

3. По какой формуле рассчитывается коэффициент Холла?

Формула коэффициента Холла: RH = Vt/(IB). Здесь Rh — коэффициент Холла, V — наблюдаемая разность напряжений, I — ток, B — магнитное поле.

4. Может ли коэффициент Холла быть равен нулю?

Коэффициент Холла зависит от концентрации электронов и подвижности носителей. Если зазор между зоной проводимости и зоной дисперсии велик, то проводимость в изоляторе равна нулю. Нулевая проводимость означает нулевую подвижность, тогда коэффициент Холла также равен нулю.

Удельное сопротивление, постоянная Холла и коэффициент Зеебека CsAu (журнальная статья)

перейти к основному содержанию

• Полная запись
• Другие родственные исследования

Измерения удельного сопротивления, постоянной Холла и коэффициента Зеебека установили, что CsAu является полупроводником n-типа с концентрацией носителей 10/sup 18/— 10/sup 19/см/суп -3/. Концентрация носителей практически не зависит от температуры в диапазоне 4,2—300 град К, а подвижность составляет 30—60 см/суп 2/об/суп-1/с/суп-1/.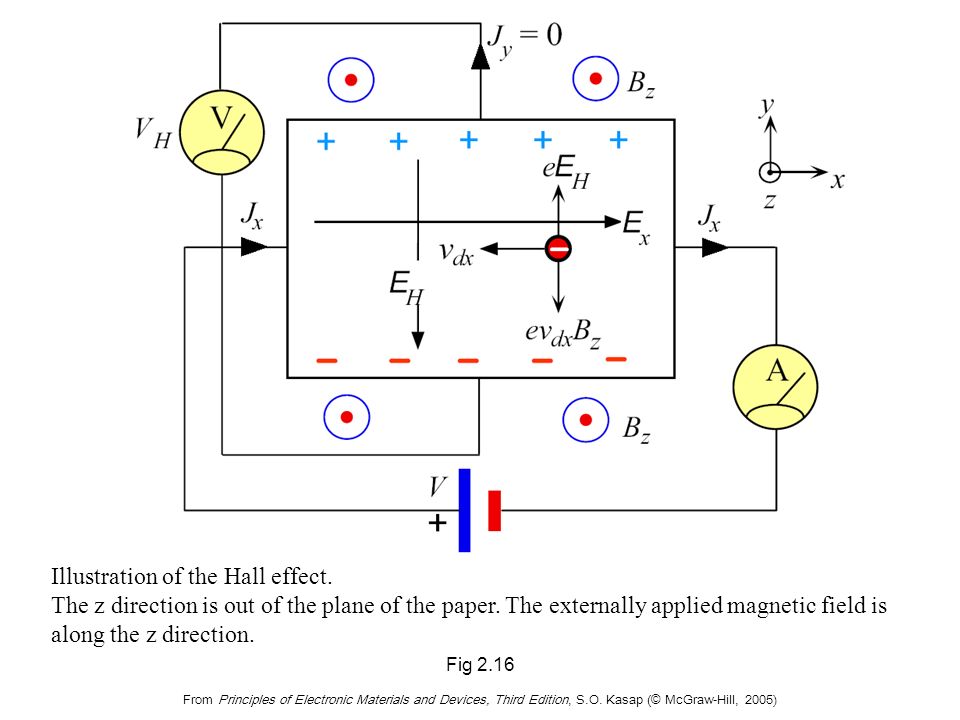 Предполагается, что избыток цезия вносит примесную зону, перекрывающуюся с зоной проводимости. Коэффициент Зеебека (-0,023 мВ/градус К при 300 градусах К) показывает, что уровень Ферми лежит примерно на 0,02 эв выше зоны проводимости, исходя из оптического рассеяния на решетке. (авт.)

Авторов:

Вутен, Ф; Кондас, Г. А.

Дата публикации:

15.07.1963

Исследовательская организация:

Унив. Калифорния, Ливермор

Идентификатор ОСТИ:

4696049

Номер(а) отчета:

UCRL-7236
Идентификатор журнала: PHRVA; 0031-899X

Номер АНБ:

НСА-17-027872

Тип ресурса:

Журнальная статья

Название журнала:

Physical Review (США) Частично заменен Phys. Ред. А, физ. Ред. B: твердое тело, физ. Rev. C и Phys. Ред. D

Дополнительная информация журнала:

Объем журнала: Том: 131; Другая информация: UCRL-7236. Ориг. Дата получения: 31-DEC-63

Страна публикации:

США

Язык:

Английский

Тема:

МЕТАЛЛЫ, КЕРАМИКА И ДРУГИЕ МАТЕРИАЛЫ; ЦЕЗИЙ; СПЛАВЫ ЦЕЗИЯ; ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ; ЗОЛОТЫЕ СПЛАВЫ; ЭФФЕКТ ХОЛЛА; ПРИМЕСИ; ИНТЕРМЕТАЛЛИЧЕСКИЕ СОЕДИНЕНИЯ; РЕШЕТКИ; ИЗМЕРЕННЫЕ ЗНАЧЕНИЯ; ОПТИКА; РАССЕЯНИЕ; ЭФФЕКТ Зеебека; ПОЛУПРОВОДНИКИ; ТЕМПЕРАТУРА; ТЕРМОЭЛЕКТРИЧЕСТВО

Форматы цитирования

• MLA
• АПА
• Чикаго
• БибТекс

Вутен, Ф. , и Кондас, Г.А. США: Н. П., 1963. Веб. doi: 10.1103/PhysRev.131.657.

Копировать в буфер обмена

Вутен, Ф., и Кондас, Г.А. Соединенные Штаты. https://doi.org/10.1103/PhysRev.131.657

Копировать в буфер обмена

Вутен Ф. и Кондас Г. А., 1963 г. «СОПРОТИВЛЕНИЕ, ПОСТОЯННАЯ ХОЛЛА И КОЭФФИЦИЕНТ Зеебека CsAu». Соединенные Штаты. https://doi.org/10.1103/PhysRev.131.657.

Копировать в буфер обмена

@статья{osti_4696049,
title = {СОЕДИНИТЕЛЬНОЕ СОПРОТИВЛЕНИЕ, ПОСТОЯННАЯ ХОЛЛА И КОЭФФИЦИЕНТ Зеебека CsAu},
автор = {Вутен, Ф. и Кондас, Г.А.},
abstractNote = {Измерения удельного сопротивления, постоянной Холла и коэффициента Зеебека установили, что CsAu является полупроводником n-типа с концентрацией носителей 10/sup 18/-- 10/sup 19/см/sup -3/. Концентрация носителей практически не зависит от температуры в диапазоне 4,2—300 град К, а подвижность составляет 30—60 см/суп 2/об/суп-1/с/суп-1/. Предполагается, что избыток цезия вносит примесную зону, перекрывающуюся с зоной проводимости. Коэффициент Зеебека (-0,023 мВ/градус К при 300 градусах К) показывает, что уровень Ферми лежит примерно на 0,02 эв выше зоны проводимости, исходя из оптического рассеяния на решетке. (авт.)},
doi = {10.1103/PhysRev.131.657},
URL = {https://www.osti.gov/biblio/4696049}, Journal = {Physical Review (США) Частично заменен Phys. Ред. А, физ. Ред. B: твердое тело, физ. Rev. C и Phys. Ред. D},
номер = ,
объем = объем: 131,
место = {США},
год = {1963},
месяц = ​​{7}
}

Копировать в буфер обмена

https://doi.org/10.1103/PhysRev.131.657

Найти в Google Scholar

Поиск в WorldCat, чтобы найти библиотеки, в которых может храниться этот журнал Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.

Аналогичных записей в сборниках OSTI.GOV:

• Аналогичные записи

Эффект Холла — эффект Холла в проводнике, полупроводнике N-типа и полупроводнике P-типа

Эффект Холла определение

Когда а магнитное поле приложено к проводнику с током в направление, перпендикулярное направлению тока, потенциал создается разностное или поперечное электрическое поле через проводник. Это явление известно как эффект Холла.

Холл Эффект был открыт Эдвином Холлом в 1879 году.

напряжение или электрическое поле, создаваемое из-за приложения магнитное поле также называют напряжением Холла или напряжением Холла. поле.

Что такое зал Эффект?

Мы знаю, что p-тип полупроводниковые и n-типа полупроводник — это два типа полупроводников.

В полупроводник n-типа, свободный электроны являются основными носителями, а дырки — неосновными носителями. Что означает, что большая часть тока в полупроводнике n-типа проводится свободными электронами.

В полупроводник p-типа, дырки являются основными носителями и свободные электроны являются неосновными носителями. Это означает, что большая часть ток в полупроводнике p-типа проводится дырками.

Сейчас мы получаем представление о полупроводниках p-типа и n-типа. Но как мы можем определить, является ли полупроводник p-типа или н-тип.

Бесплатно электроны а дырки — это очень маленькие частицы. Поэтому мы их не видим прямо нашими глазами. Но с помощью эффекта Холла мы можем легко определить, относится ли полупроводник к p-типу или n-типу.

Когда напряжение приложено к проводнику или полупроводнику, электрическому через него начинает течь ток. В проводниках электрические ток проводится свободными электронами, тогда как в полупроводниках электрический ток проводится как свободными электроны и дырки.

свободные электроны в полупроводнике или проводнике всегда пытаются течь по прямому пути. Однако из-за непрерывного столкновения с атомами, свободные электроны немного меняют свое направление. Но если приложенное напряжение достаточно велико, свободные электроны решительно следовать прямому пути. Это происходит только в том случае, если нет другие силы приложены к нему в другом направлении.

Если мы приложим силу в другое направление с помощью магнитного поля, свободного электроны в проводнике или полупроводнике меняют свое направление.

Учитывать материал, полупроводник или проводник, как показано на рисунок ниже. При подаче напряжения электрический ток начинает течь в положительном x-направлении (слева на Правильно).

Если к этому проводнику с током приложено магнитное поле или полупроводника в направлении, перпендикулярном направлению течение тока (то есть направление z), электрическое поле произведенный в нем, который оказывает силу в отрицательном направлении y (вниз). Это явление известно как эффект Холла. Зал Эффект назван в честь американского физика Эдвина Холла. открыл это явление в 1879 г..

Эффект Холла в проводник

электрическое поле, создаваемое в материале, отталкивает заряд носители вниз. Если материал является проводником, электрическое поле толкает свободные электроны вниз (т. отрицательное направление Y). В результате большое количество зарядов носители (свободные электроны) скапливаются на дне поверхность проводника.

Потому что этого большого скопления отрицательных зарядов (свободных электроны) на нижней поверхности и дефицит отрицательных заряды (свободные электроны) на верхней поверхности, на нижней поверхность заряжена отрицательно, а верхняя поверхность положительно заряжен.

Как результат, электрическая разность или разность потенциалов развивается между верхней поверхностью и нижней поверхностью проводник. Эта разность потенциалов известна как напряжение Холла. В проводнике электрическое поле создается за счет отрицательно заряженные свободные электроны. Итак, напряжение холла в проводнике отрицательна.

Эффект Холла в полупроводник n-типа

Если магнитное поле приложено к полупроводнику n-типа, оба свободные электроны и дырки вытесняются вниз поверхность полупроводника n-типа. Так как отверстия пренебрежимо мал в полупроводнике n-типа, поэтому свободные электроны в основном скапливается на нижней поверхности n-типа полупроводник.

Это производит отрицательный заряд на нижней поверхности с равным количеством положительного заряда на верхней поверхности. Итак, в n-типе полупроводник, нижняя поверхность которого заряжена отрицательно и верхняя поверхность заряжена положительно.

Как в результате возникает разность потенциалов между верхняя и нижняя поверхности полупроводника n-типа. в Полупроводник n-типа, электрическое поле в основном создается за счет отрицательно заряженных свободных электронов. Итак, зал напряжение, создаваемое в полупроводнике n-типа, отрицательно.

Эффект Холла в полупроводник p-типа

Если магнитное поле приложено к полупроводнику p-типа, мажоритарные носители (дырки) и неосновные носители (свободные электроны) отталкиваются к нижней поверхности полупроводник р-типа. В полупроводнике р-типа свободный электроны пренебрежимо малы. Так отверстия в основном скапливаются на нижней поверхности полупроводник р-типа.

Итак в полупроводнике p-типа нижняя поверхность положительно заряжены, а верхняя поверхность заряжена отрицательно.

Как в результате возникает разность потенциалов между верхняя и нижняя поверхности полупроводника р-типа. в Полупроводник p-типа, электрическое поле в основном создается за счет положительно заряженных дырок. Итак, напряжение холла в полупроводнике р-типа положителен. Это приводит к факт, что создаваемое электрическое поле имеет направление в положительное направление Y.

Эффект Холла помогает определить тип материала

Мы можно легко определить, относится ли полупроводник к р-типу или n-типа с использованием эффекта Холла. Если создаваемое напряжение равно положительный, то говорят, что материал p-типа, а если генерируемое напряжение отрицательно, то говорят, что материал н-тип.

Напряжение Холла прямо пропорционально протекающему току через материал и напряженность магнитного поля, и это обратно пропорциональна количеству мобильных зарядов в материала и толщины материала. Итак, чтобы для получения большого напряжения Холла нам нужно использовать тонкий материал с небольшими мобильными зарядами на единицу объема.

Математический выражение для напряжения Холла дается как

Где,

V _H = напряжение Холла
I = ток, протекающий через материал
B = напряженность магнитного поля
д = заряд
n = количество подвижных носителей заряда на единицу объема
d = толщина материала

Применение эффекта Холла

• Эффект Холла используется, чтобы определить, относится ли полупроводник к N-типу или P-типу.
• Эффект Холла используется для определения концентрации носителей.
• Эффект Холла используется для расчета подвижности носителей заряда (свободный электроны и дырки).
• Холл Эффект используется для измерения проводимости.
• Эффект Холла используется для измерения переменного тока. мощность и сила магнитного поля поле.
• Эффект Холла используется в приборе, называемом множителем на эффекте Холла, который дает выход, пропорциональный произведению двух входных сигналы.

Добро пожаловать в Экспериментальную лабораторию физики 111 B Дональда А. Глейзера

 

Профессор Дональд А.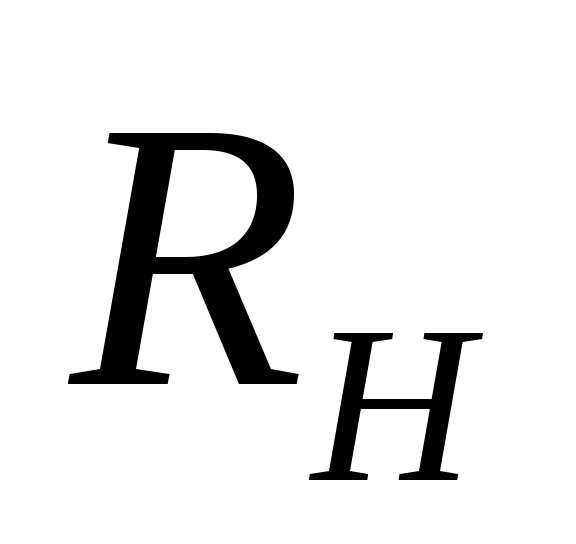 Глейзер на протяжении всей своей карьеры был мастером экспериментальных наук. Он родился в Кливленде и получил образование в Технологическом институте Кейса, получил докторскую степень в Калифорнийском технологическом институте и преподавал в Мичиганском университете, а затем в 1919 году занял пост в Калифорнийском университете в Беркли.59. В начале своей карьеры д-р Глейзер экспериментировал со способами сделать работу субатомных частиц видимой. За свое последующее изобретение пузырьковой камеры он был удостоен Нобелевской премии по физике 1960 года. Затем он начал исследовать новую область молекулярной биологии, совершенствуя методы работы с бактериальными фагами, бактериями и клетками млекопитающих. Разработав оборудование для автоматизации своих экспериментов и масштабирования их, он мог одновременно проводить тысячи экспериментов, генерируя достаточно данных для продвижения науки вперед. Осознавая последствия для медицины, доктор Глейзер и двое его друзей создали новаторскую биотехнологическую компанию Cetus Corporation в 1919 году. 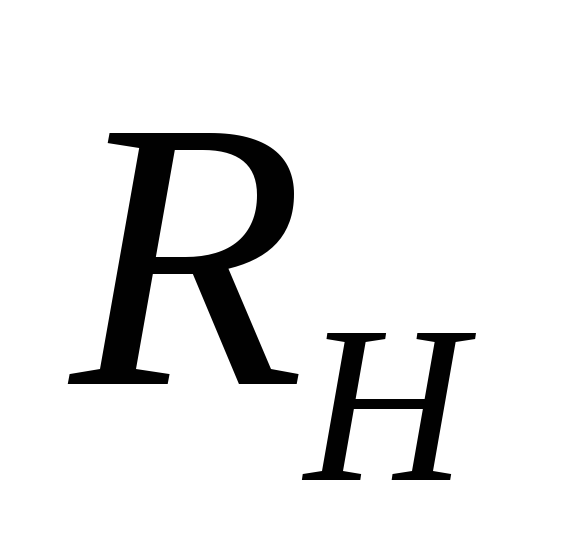71, тем самым запустив индустрию генной инженерии.

Позднее в своей карьере доктор Глейзер продолжил свои экспериментальные исследования, разрабатывая математические модели для понимания фундаментальных процессов человеческого зрения. На протяжении всей своей жизни он сочетал научную работу с не менее страстным интересом к классической музыке, играя на альте в камерных ансамблях, где бы он ни был. Чрезвычайно любопытный, новаторский и преданный продвижению научных знаний, доктор Глейзер был очень востребованным консультантом и советником до своей смерти в 2013 году.

Экспериментальная лаборатория Physics 111 — это интенсивный лабораторный курс из 3-х частей для студентов-физиков 3-го и 4-го курсов Калифорнийского университета в Беркли. Он следует за Физикой 111A Приборной лаборатории , которая знакомит студентов с электроникой, методами измерения, обработкой сигналов, компьютеризированным сбором данных и управлением. С помощью этих инструментов учащиеся экспериментальной лаборатории раздела Physics 111 проводят четыре эксперимента, на выполнение каждого из которых уходит около 2 недель. Студенты выбирают эти эксперименты из 19или около того эксперименты, постоянно установленные в 111-лаборатории. Они представляют широкий круг тем и методов, используемых в экспериментальной физике. Многие из экспериментов повторяют исследования, получившие Нобелевскую премию, и все они предназначены для развития навыков, необходимых для проведения исследований.

Содержимое Что делать в первую очередь Физика 111 Углубленная лабораторная программа и сроки сдачи Справочный центр библиотеки Physics 111-Lab Об этом расширенном сайте Для студентов, обучающихся в настоящее время на курсе Для остальных посетителей Пожертвования Благодарности Полезные инструменты

---

Что делать в первую очередь Перед тем, как прийти в лабораторию Physics 111

• список доступных экспериментов для этого требования. Регистрация оборудования).
• Все учащиеся входят в систему bCourses, заполняют карточку подписи и отправляют ее онлайн, прежде чем прийти в лабораторию. Вы должны выполнить это, прежде чем начинать что-либо в лаборатории.
• Все учащиеся приходят на вводное собрание в 251 LeConte Hall в первый учебный день в 14:10.
• Каждый студент должен иметь свою фотографию на сайте Калифорнийского университета в Беркли на сайте bCourses. Если НЕТ, вы должны сдать ФОТО НА ПАСПОРТ (не паспорт, а настоящую фотографию паспортного типа) в первый день Лаборатории в целях безопасности.
• Все учащиеся экспериментальной лаборатории физики 111B должны выполнить упражнение по анализу ошибок , назначенное в течение первой недели (см. сроки выполнения).
• Подготовьтесь к одному обязательному устному отчету с профессором. Это может быть первый, второй или третий эксперимент.
• При доступе к компьютерам 111B-Lab, если вы НЕ можете войти в систему, выполните следующие действия:
  Перейдите в Calnet Active Directory и синхронизируйте свое имя CalNet.

 

Внимание: В Лаборатории 111 НЕЛЬЗЯ есть или пить нигде, кроме на скамейках с СИНЕЙ полосой вокруг в комнатах 282 и 286 LeConte . Об этом сайте0983   Лаборатория . Каждая ссылка в меню «Экспериментальные лабораторные эксперименты» вверху ведет на страницы, содержащие руководство по эксперименту, которое включает предварительные и промежуточные вопросы, справочные материалы, теорию и инструкции.

Вернуться к началу

Для студентов, которые в настоящее время зачислены на этот курс

Вы можете просматривать и распечатывать любые страницы на этом сайте Experimentation Laboratory без учетной записи или входа в систему.

Если вы видите ошибки в описаниях лабораторных работ или места, которые нуждаются в улучшении, поговорите со своими инструкторами или Уинтропом Уильямсом . Они могут быстро редактировать страницы, внося небольшие изменения, чтобы следующий учащийся получил улучшенную версию. Если вы видите необходимость значительных изменений, распечатайте страницу и напишите свои предложения, чтобы передать их инструктору. Вы также можете оставить комментарии в оценочном опросе в нижней части статьи, и мы внесем изменения по мере необходимости, если они предложат какие-то полезные улучшения. Мы очень ценим вклад студентов, чтобы сделать лабораторные работы лучше.

Наверх

Для других посетителей  

Этот сайт открыт для просмотра, но не для редактирования или комментирования. Авторские права принадлежат Калифорнийскому университету Риджентс. Тем не менее, мы с радостью предоставляем контент другим школам для некоммерческого использования в образовательных целях. Некоторые ссылки на справочные материалы и программное обеспечение, защищенные авторским правом, недоступны никому без аутентификации в качестве студента или сотрудника Physics 111.

Вернуться к началу

Вернуться к началу

Благодарности

Этот сайт был разработан Доном Орландо и Студентами Сегре. Стажер Сегре , Натан Белмор провел большую часть июля 2014 года, переводя лабораторные описания из Wiki в Drupal, разрабатывая новый веб-сайт и преобразовывая все коды. Уинтроп Уильямс в настоящее время управляет веб-страницами. Преподавательский состав и Уинтроп Уильямс занимаются редактированием и обслуживанием.

Сотрудники лаборатории:

• Заведующий лабораторией и инженер-исследователь 3: Уинтроп Уильямс  (510) 685-1164; Электронная почта: [email protected]

• Дон Орландо ушел на пенсию

Наверх

Домашняя страница физического факультета

Текущие достижения: постоянная тонкой структуры

Константы Темы: Значения Энергия Эквиваленты Доступный для поиска Библиография Фон Константы Библиография Константы, Единицы и Неопределенность домашняя страница

Введение в константы для неспециалистов Введение 1900 — 1920 1920 — 1940 1940 — 1960 Текущий (индекс) Текущие достижения: постоянная тонкой структуры и квантовый эффект Холла Постоянная тонкой структуры α имеет размерность 1 (т. е. просто число) и почти равна 1/137. Это «константа связи» или мера силы электромагнитного взаимодействия, которая определяет, насколько электрически заряжены элементарные частицы (например, электрон, мюон) и свет (фотоны) взаимодействуют. В настоящее время значение α с наименьшей неопределенностью получается из сравнения теоретического выражения a e (theor) и экспериментального значения a e (expt) аномального магнитного момента электрона a e . Начиная с В 1980-х годах новый и совершенно другой подход к измерению с использованием квантового эффекта Холла (КЭХ) вызвал волнение, поскольку значение α , полученное из него независимо, подтверждает значение α по аномалии магнитного момента электрона. Значение QHE α не имеет такой малой неопределенности, как значение магнитного момента электрона, но дает существенное независимое подтверждение этого значения. Величина α была введена в физику А. Зоммерфельдом в 1916 г. и в прошлом часто называлась постоянной тонкой структуры Зоммерфельда. Чтобы объяснить наблюдаемое расщепление или тонкую структуру энергетических уровней атома водорода, Зоммерфельд расширил теорию Бора, включив в нее эллиптические орбиты и релятивистскую зависимость массы от скорости. Количество α, , что равно отношению v 1 / c , где v 1 — скорость электрона на первой круговой боровской орбите, а c — скорость света в вакууме. , появились естественным образом в анализе Зоммерфельда и определили размер расщепления или тонкую структуру водородных спектральных линий. Теория Зоммерфельда имела некоторый ранний успех в объяснении экспериментальных наблюдений, но не могла приспособиться к открытию спина электрона. Хотя релятивистская теория электрона Дирака, введенная в 1928 решает основные аспекты проблемы тонкая структура водорода, α , по-прежнему определяет его размер, как и в теории Зоммерфельда. Следовательно, название константы «тонкой структуры» для нижеследующей группы констант осталось: ,

, где e — заряд элемента, = ч /2π, где ч — постоянная Планка, ε 0 = 1/ µ 0 c 2 — электрическая постоянная (диэлектрическая проницаемость вакуума) и µ 0 — магнитная постоянная (проницаемость вакуума). В Международной системе единиц (СИ) c , ε 0 и µ 0 являются точно известными константами. Наш взгляд на постоянную тонкой структуры заметно изменился с тех пор, как Зоммерфельд ввел ее более 80 лет назад. Теперь мы рассматриваем α как константу связи для электромагнитной силы, аналогичную константам для трех других известных фундаментальных сил или взаимодействий в природе: гравитационное взаимодействие, слабое ядерное взаимодействие и сильное ядерное взаимодействие. Далее, с α пропорционально e 2 , оно рассматривается как квадрат эффективного заряда, «экранированного поляризацией вакуума и видимого с бесконечного расстояния». Согласно квантовой электродинамике (КЭД), релятивистской квантовой теории поля взаимодействия заряженных частиц и фотонов, электрон может излучать виртуальные фотоны, которые затем могут излучать виртуальные электрон-позитронные пары (e + , e — ). Виртуальные позитроны притягиваются к исходным или «голым» электрон, в то время как виртуальные электроны отталкиваются от него. Таким образом, голый электрон экранируется из-за этой поляризации. Обычная постоянная тонкой структуры α определяется как квадрат полностью экранированного заряда, то есть величина, наблюдаемая на бесконечном расстоянии или в пределе нулевой передачи импульса. короче расстояния, соответствующие более высоким энергетическим процессам или зондам (большие передачи импульса), происходит частичное пробитие экрана и увеличивается сила электромагнитного взаимодействия, поскольку увеличивается эффективный заряд. Таким образом, α зависит от энергии, при которой оно измеряется, увеличиваясь с увеличением энергии, и считается эффективной или текущей константой связи. Действительно, благодаря e + e — и другие процессы поляризации вакуума, при энергии, соответствующей массе W-бозона (примерно 81 ГэВ, что эквивалентно расстоянию примерно 2 x 10 -17 м), α ( m Вт ) составляет примерно 1/128 по сравнению с его значением нулевой энергии примерно 1/137. Таким образом, известное число 1/137 не является уникальным или особенно фундаментальным. Как указано выше, значение альфа из квантового эффекта Холла (КЭХ) подтвердило значение из аномалии магнитного момента электрона а е . КЭХ характерен для полностью квантованного двумерного электронного газа. Такой газ может быть реализован в высокомобильном полупроводниковом приборе, таком как полевой транзистор металл-оксид-полупроводник кремния (MOSFET) или GaAsAl x Ga 1- x В качестве гетероперехода стандартного стержня Холла геометрия в приложенном магнитном потоке B порядка 10 Тл и охлаждении примерно до 1 К. Для фиксированного тока I (обычно от 10 мкА до 50 мкА) через устройство, на кривой зависимости напряжения Холла U H от напряжения затвора для МОП-транзистора или U H от B для гетеропереход, где U H остается постоянным при изменении либо напряжения затвора, либо B . Эти области постоянных U H называются плато Холла. В пределе нулевого рассеяния (нулевого падения напряжения) в направлении протекания тока отношение напряжения Холла к току равно U H ( i )/ I или сопротивление Холла R H ( i ) из i -го плато (мы рассматриваем только целое плато, где i QHE), is quantized and given by R H ( i ) = U H ( i )/ I = R K / i where R K – постоянная фон Клитцинга (по имени первооткрывателя КЭХ). Теория прогнозирования QHE и экспериментально наблюдаемая универсальность R H ( I ) = U H ( I ) / I = R K /7 I = R K /77 I = R K / 77. i согласуется с предсказанием, что R K = h / e 2 = µ 0 c 4 9,0502 /2 Так как в СИ µ 0 = 4π x 10 -7 N/A 2 точно, и c = 299 792 458 м/с точно в результате переопределения метра в терминах скорости света в 1983 году, измерения R K в Единицы СИ (т. е. омы) с заданной неопределенностью дадут значение постоянной тонкой структуры α с той же неопределенностью. На практике R K измеряется с точки зрения лабораторного эталона сопротивления. Таким образом, сопротивление эталона должно быть определено в единицах СИ в омах в отдельном эксперименте с использованием прибора, известного как вычисляемый перекрестный конденсатор, в котором неизвестное сопротивление эталонного резистора сравнивается с известным импедансом конденсатора. 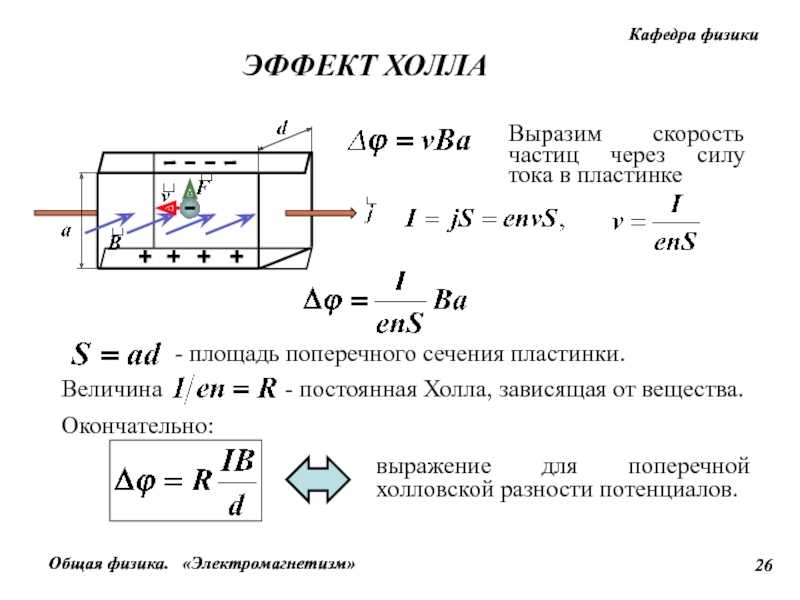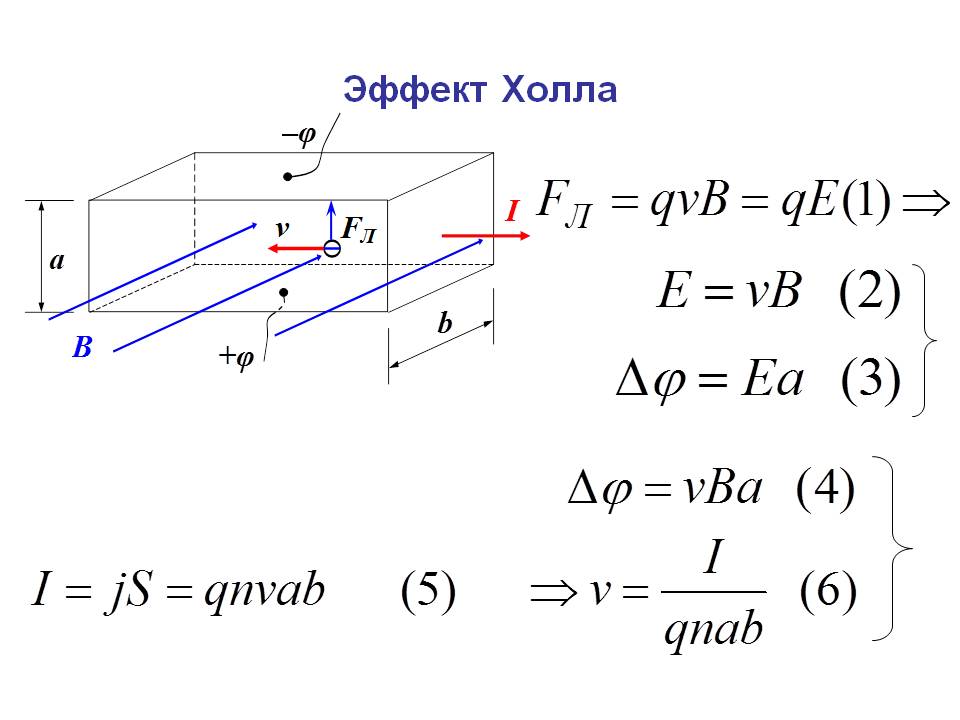Изменение емкости такого конденсатора, а следовательно, и его импеданса, легко вычислить, так как это изменение зависит только от положения подвижного экранного электрода, смещение которого можно измерить с помощью лазерного интерферометра. В версии эксперимента NIST известное изменение емкости расчетного перекрестного конденсатора NIST на 0,5 пФ используется для измерения емкости эталонных конденсаторов емкостью 10 пФ. Затем они и мост 10:1 используются в два этапа для измерения емкости двух конденсаторов емкостью 1000 пФ, которые, в свою очередь, используются в качестве двух ветвей специального частотно-зависимого моста для измерения импеданса двух резисторов по 100 кОм. Последние затем сравниваются с помощью моста 100:1 с переносным резистором на 1000 Ом, который, в свою очередь, сравнивается с помощью методов постоянного тока с эталоном сопротивления, относительно которого R K измерено. Разность сопротивлений переменного и постоянного тока резистора на 1000 Ом определяется с помощью специального коаксиального резистора на 1000 Ом с незначительной разностью сопротивлений переменного и постоянного тока. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника