ХОЛЛА ЭФФЕКТ • Большая российская энциклопедия

Авторы: О. А. Котельникова

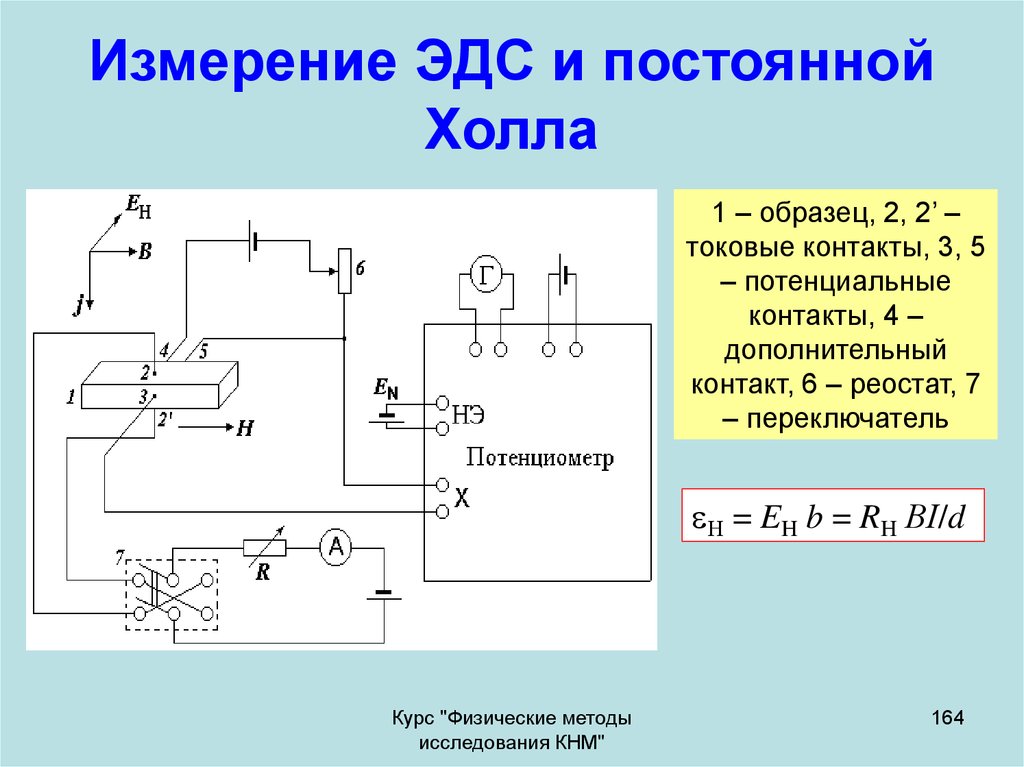
ХО́ЛЛА ЭФФЕ́КТ, воз­ник­но­ве­ние в твёр­дом про­вод­ни­ке с плот­но­стью то­ка $\boldsymbol j$, поме­щён­ном в маг­нит­ное по­ле на­пря­жён­но­стью $\boldsymbol H$, элек­трич. по­ля на­пря­жён­но­стью $\boldsymbol E_H$ в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном $\boldsymbol H$ и $\boldsymbol j$. От­крыт Э. Г. Хол­лом в 1879 в тон­ких пла­стин­ках зо­ло­та. Ве­ли­чи­на на­пря­жён­но­сти элек­трич. по­ля (по­ля Хол­ла) $E_H=RHj\sin α$, где $α$ – угол ме­ж­ду $\boldsymbol H$ и $\boldsymbol j$ ($α < 180°$). Ес­ли $\boldsymbol H⊥\boldsymbol j$, то $E_H$ мак­си­маль­но: $E_H=RHj$. Ко­эф. $R$ на­зы­ва­ет­ся по­сто­ян­ной Хол­ла, ко­то­рая пол­но­стью ха­рак­те­ри­зу­ет Х. э. Знак $R$ по­ло­жи­те­лен, ес­ли $\boldsymbol j$, $\boldsymbol H$ и $\boldsymbol E_H$ об­ра­зу­ют пра­во­вин­то­вую сис­те­му ко­ор­ди­нат. Эдс Хол­ла $U_H=E_Hb=RHI/d$ из­ме­ря­ют ме­ж­ду элек­тро­да­ми, рас­по­ло­жен­ны­ми на бо­ко­вых гра­нях об­раз­ца в ви­де пря­мо­уголь­ной пла­сти­ны ($b$ – ши­ри­на, $d$ – тол­щи­на, ко­то­рые на­мно­го мень­ше дли­ны пла­сти­ны), пер­пен­ди­ку­ляр­но то­ку $I=jbd$.

Воз­ник­но­ве­ние эдс Хол­ла обу­слов­ле­но взаи­мо­дей­ст­ви­ем но­си­те­лей то­ка (элек­тро­нов и ды­рок) с внеш­ним маг­нит­ным по­лем. Си­ла Ло­рен­ца $\boldsymbol F=q[\boldsymbol v \boldsymbol H]$, дей­ствую­щая со сто­ро­ны маг­нит­но­го по­ля на дви­жу­щие­ся за­ря­ды ($q$ – за­ряд, $\boldsymbol v=\boldsymbol j/nq$ – ср. ско­рость на­прав­лен­но­го дви­же­ния но­си­те­лей за­ря­да, $n$ – их кон­цен­тра­ция), при­во­дит к от­кло­не­нию но­си­те­лей в на­прав­ле­нии, пер­пен­ди­ку­ляр­ном $\boldsymbol H$ и $\boldsymbol j$, или к «за­кру­чи­ва­нию» их тра­ек­то­рии. В ре­зуль­та­те воз­ни­ка­ет по­ле Хол­ла, ко­то­рое дей­ст­ву­ет на за­ря­ды и урав­но­ве­ши­ва­ет си­лу Ло­рен­ца: $qE_H=qvH$, и, сле­до­ва­тель­но, $R=1/nq$. Знак $R$ со­в­па­да­ет со зна­ком но­си­те­лей за­ря­да. В ме­тал­лах, где $n$≈10²⁸ м^—3, R име­ет по­ря­док ве­ли­чи­ны 10^—9 м³/Кл, в по­лу­про­вод­ни­ках $R$≈10^—5-10^—1 м³/Кл. Для ме­тал­лов ве­ли­чи­на $R$ за­ви­сит от зон­ной струк­ту­ры, сте­пе­ни чис­то­ты об­раз­ца, его ори­ен­та­ции от­но­си­тель­но кри­стал­ло­гра­фич. осей, ве­ли­чи­ны маг­нит­но­го по­ля и темп-ры.

При опи­са­нии Х. э. в маг­не­ти­ках сле­ду­ет учи­ты­вать на­ли­чие в них собств. мо­ле­ку­ляр­но­го по­ля, соз­да­вае­мо­го упо­ря­до­чен­ны­ми маг­нит­ны­ми мо­мен­та­ми. То­гда по­ле Хол­ла име­ет вид: $E_y=RB_zj_x+R_s4πM_zj_x$ (ин­дек­сы $x$, $y$, $z$ ука­зы­ва­ют со­от­вет­ст­вую­щую про­ек­цию на ко­ор­ди­нат­ную ось; $\boldsymbol B$, $\boldsymbol M$ – ин­дук­ция маг­нит­но­го по­ля и на­маг­ни­чен­ность маг­не­ти­ка со­от­вет­ст­вен­но; $R_s$ – по­сто­ян­ная ано­маль­но­го эф­фек­та Хол­ла). Вклад в по­ле Хол­ла, про­пор­цио­наль­ный $M$, на­зы­ва­ют спон­тан­ным или ано­маль­ным Х. э., по­сколь­ку он реа­ли­зу­ет­ся в фер­ро-, ан­ти­фер­ро- и фер­ри­маг­нит­ных про­вод­ни­ках и по­лу­про­вод­ни­ках. В фер­ро­маг­не­ти­ках $R_s$ мо­жет на по­ря­док пре­вы­шать ве­ли­чи­ну $R$. По­сто­ян­ная $R_s$ име­ет слож­ную тем­пе­ра­тур­ную за­ви­си­мость, при­чём зна­ки $R$ и $R_s$ мо­гут не сов­па­дать. За воз­ник­но­ве­ние ано­маль­но­го Х. э. от­вет­ст­вен­но спин-ор­би­таль­ное взаи­мо­дей­ст­вие, ко­то­рое при­во­дит к асим­мет­рич­но­му рас­сея­нию но­си­те­лей за­ря­да в маг­не­ти­ках. В силь­ных маг­нит­ных по­лях в пло­ских про­вод­ни­ках (ква­зид­ву­мер­ных сис­те­мах) про­яв­ля­ют­ся кван­то­вые осо­бен­но­сти по­ве­де­ния но­си­те­лей за­ря­да (ква­зид­ву­мер­но­го элек­трон­но­го га­за) – воз­ни­ка­ет кван­то­вый эф­фект Хол­ла. При даль­ней­шем уве­ли­че­нии маг­нит­но­го по­ля пе­ре­строй­ка элек­трон­ной сис­те­мы ста­но­вит­ся столь силь­ной, что при­во­дит к т. н. дроб­но­му кван­то­во­му эф­фек­ту Хол­ла.

Ли­ней­ную за­ви­си­мость по­ля Хол­ла от $H$ ис­поль­зу­ют для из­ме­ре­ния на­пря­жён­но­сти маг­нит­но­го по­ля (дат­чи­ки Хол­ла). Х. э. при­ме­ня­ет­ся для ум­но­же­ния по­сто­ян­ных то­ков в ана­ло­го­вых вы­чис­лит. ма­ши­нах, в из­ме­рит.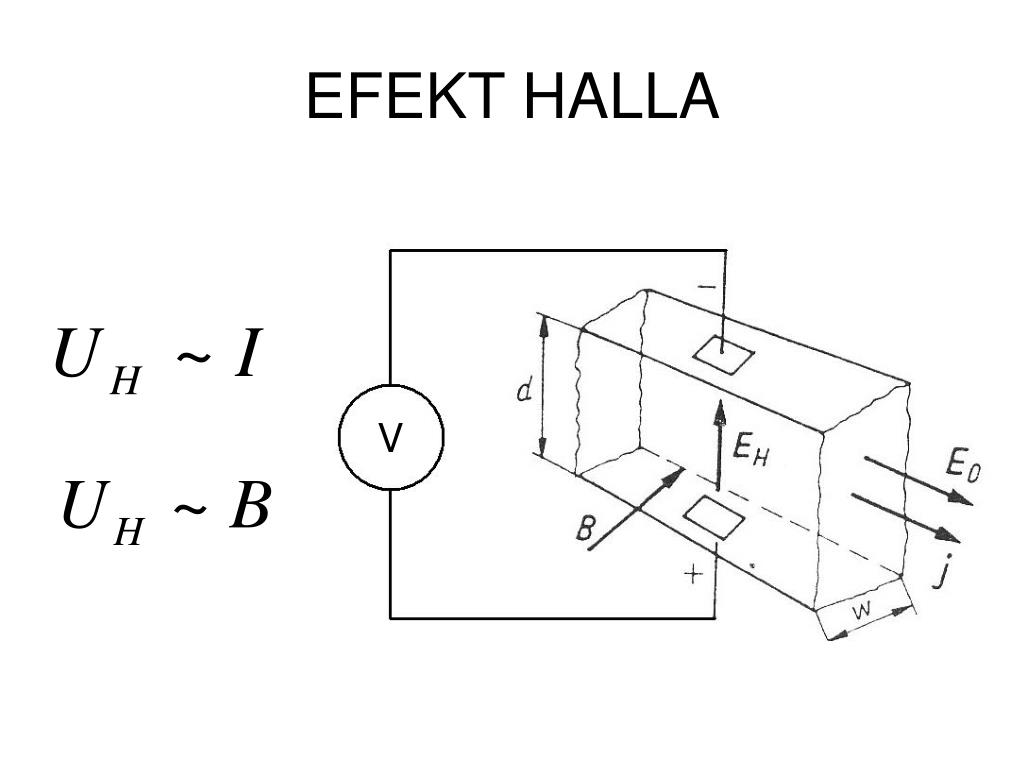 тех­ни­ке и др.

8.5. Эффект Холла

Эффектом Холла называется возникновение поперечного электрического поля в проводнике или полупроводнике с током при помещении его в магнитное поле. Это явление обусловлено влиянием силы Лоренца на движение носителей тока.

Рис. 8.7

Металлическая пластинка с током плотностью помещается в магнитное поле , перпендикулярное . Электроны испытывают действие силы Лоренца , направление которой задается правилом левой руки. Таким образом, у верхнего края пластинки возникнет повышенная концентрация электронов (зарядится отрицательно), а у нижнего их недостаток (зарядится положительно). В результате этого между краями пластинки возникнет дополнительное поперечное электрическое поле , направленное снизу вверх (рис. 8.7). Отклонение носителей тока в поперечном направлении происходит до тех пор, пока действие поперечного электрического поля не уравновесит силу Лоренца.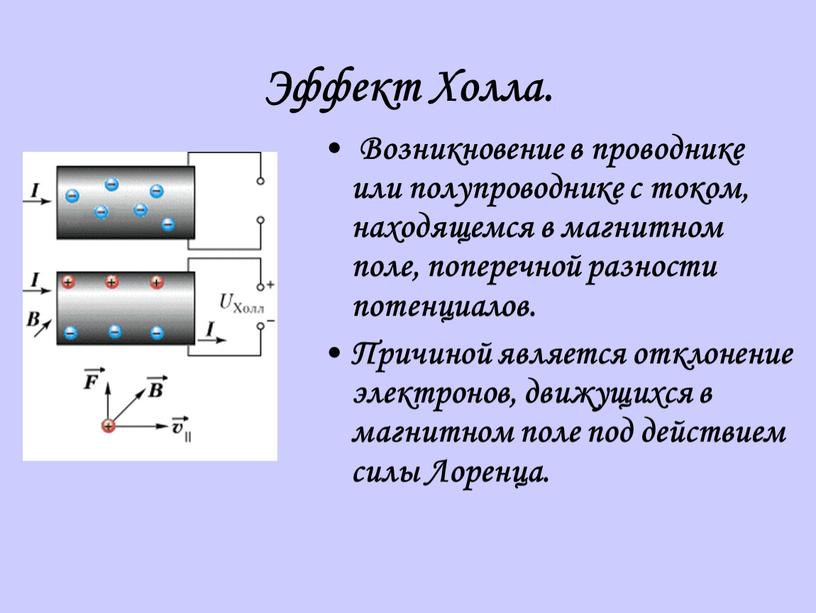

Тогда:

, (13)

где а – ширина пластинки, – поперечная (холловская) разность потенциалов.

Учитывая, что сила тока

,

( – площадь поперечного сечения пластинки толщиной , n – концентрация электронов, – средняя скорость упорядоченного движения электронов, равная ) получим выражение для холловской разности потенциалов:

. (14)

Холловская разность потенциалов пропорциональна магнитной индукции , силе тока I и обратно пропорциональна толщине пластинки

d.

Постоянная Холла зависит от вещества

.

По измеренному значению постоянной Холла можно: а) определить концентрацию носителей тока в проводнике; б) судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда носителей тока: в случае электронной проводимости (n — типа) , , а в случае дырочной проводимости (p — типа) , ; в) использовать для измерения индукции магнитного поля .

Таким образом, эффект Холла – метод изучения энергетического спектра носителей тока в металлах и полупроводниках.

1. Сформулируйте и запишите закон Ампера. Сформулируйте правило левой руки.

2. В каких единицах измеряются индукция и напряженность магнитного поля?

3. Определите числовое значение магнитной постоянной.

4. Какую силу называют силой Лоренца? Как определить величину и направление этой силы?

5. Изменяется ли величина скорости заряженной частицы под действием силы Лоренца? Чему равна работа этой силы?

6. Какова траектория движения заряженной частицы в магнитном поле, если скорость частицы направлена: а) вдоль линий индукции ; б) перпендикулярно линиям индукции ; в) под острым углом к вектору индукции .

7. Когда заряженная частица движется в магнитном поле по спирали? От чего зависит шаг спирали? Ответ подтвердите выводами формул.

8. Заряженная частица движется в магнитном поле по окружности. Выведите формулу для радиуса окружности и периода обращения. Зависит ли период обращения частицы от ее скорости? Что называется удельным зарядом частицы?

9. Что такое ускорители заряженных частиц? Какие они бывают и чем характеризуются.

10. В чем заключается эффект Холла? Выведите формулу для холловской разности потенциалов. От чего зависит постоянная Холла?

11. Как на основе эффекта Холла определить a) концентрацию носителей заряда? б) тип проводимости данного материала?

2.1.3 Эффект Холла

	Сравнительно легко рассчитать величину напряжения Холла U Холла , индуцированного магнитным полем Б .
		Сначала отметим, что мы также должны иметь электрическое поле E , параллельное j , потому что это движущая сила течения.
		Во-вторых, мы знаем, что магнитное поле под прямым углом к ​​току воздействует на движущиеся носители силой, так называемый Лоренц сила F L , то есть
		F L  =  q · ( v D × B )
		Мы должны взять дрейф скорость v D носителей, потому что другие скорости (и силы, вызванные этими компоненты) сокращаются до нуля в среднем. Векторное произведение гарантирует, что F L перпендикулярно v D и Б .
		Обратите внимание, что вместо обычного слова «электрон» используется нейтральный термин носитель , потому что в принципе электрический ток также может переноситься заряженными частицами, отличными от электронов, например. положительно заряженные ионы. Запомните простую, но важную картинку, приведенную ранее!
	Для приведенной выше геометрии сила Лоренца Ж Л есть только компонент в y — направление и мы можем использовать для него скалярное уравнение. F у есть дано
		F y  =  – q · v D,x · Б г
		Мы должны быть немного осторожны: Мы знаем, что сила находится в y -направлении, но мы больше не знаем знака. Он меняется, если либо q , v D или B z меняет направление, и мы должны знать о что.
		Однако важно обратите внимание, что при фиксированной плотности тока j x направление силы Лоренца не зависит от знак носителей заряда – знак заряда и знак дрейфовой скорости просто компенсируют друг друга другой.
	С в Д = µ · E и µ = подвижность носителей, получаем довольно простое уравнение для силы
		F y  =  – | q | · м · E x · B z
	Токи носителей отклонится от прямой в y -направлении. Другими словами, существует компонент скорость в y -направление и поверхности, перпендикулярные y -направлению, станут заряжается, как только ток (или магнитное поле) включается. Линии потока носителей будут иметь вид это:
		Зарядка поверхностей неизбежно, потому что некоторые из носителей в конечном итоге окажутся на поверхности, где они «застряли».
		Обратите внимание, что знак заряда для данного поверхности зависит от знака заряда носителей. Отрицательно заряженные электроны ( e — в рисунок) оказываются на поверхности, противоположной положительно заряженным носителям (обозначены на рисунке h + ).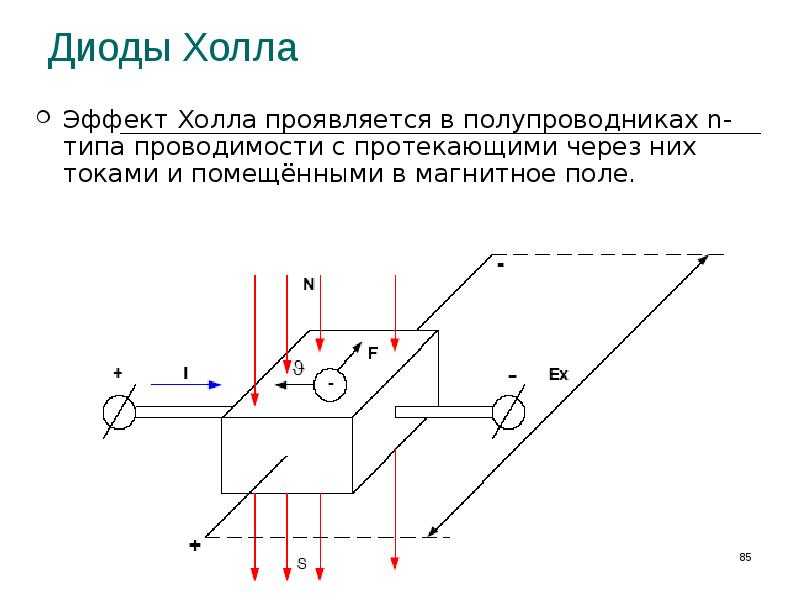
		Обратите также внимание, что направление силы Ф y одинакова для обоих типов носителей просто потому, что и q , и v D поменять знаки в формуле силы
	затем поверхностный заряд индуцирует электрическое поле сила Лоренца; он пытается переместить носителей обратно.
		В равновесии сила Лоренца F y и сила электрического поля E y in y -направление (которое, конечно, просто q · E y ) должно быть равно противоположные знаки. Таким образом, мы получаем
		– q · E y  =  – | q | · м · E x · B z       E y  =  sgn( q ) · µ · E x · B z
	Напряжение Холла U Hall теперь просто поле в y -направление умноженное на размерность д у в у -направление.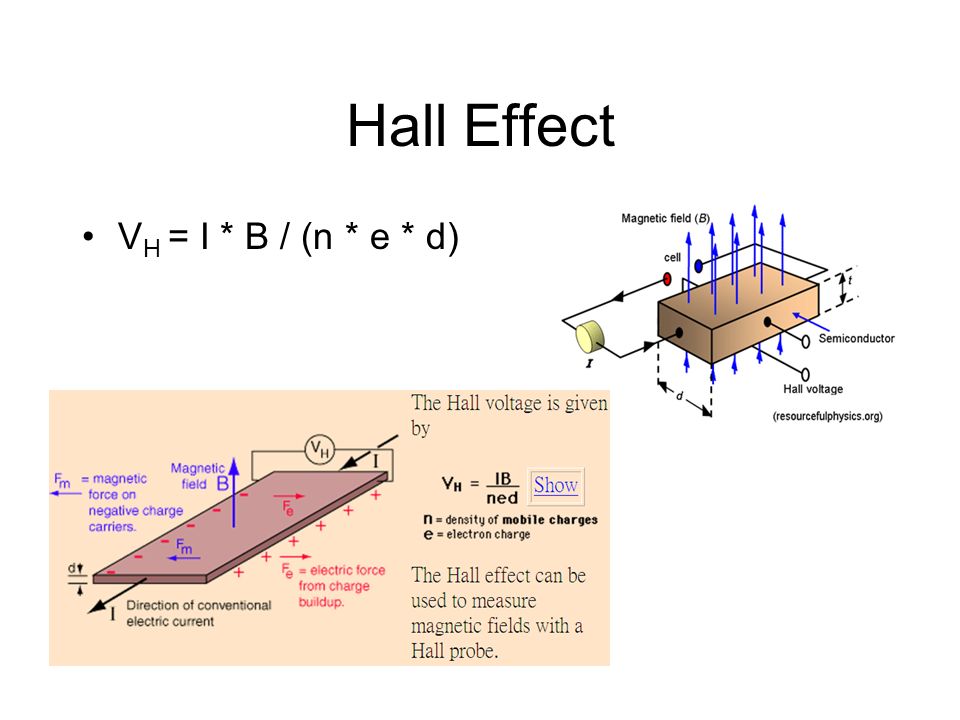
		Тогда ясно, что (легко измеряемое) напряжение Холла является прямой мерой µ подвижности участвующих носителей, и что его знак или полярность изменится, если изменится знак протекающих зарядов.
	Принято определять зал коэффициент R Холла для данного материала.
		Это можно сделать разными, но эквивалентные способы. В ссылке мы смотрим на определение, которое особенно подходит для измерений. Здесь мы используем следующее определение:
		R Hall  =  E y B z · j x
	In other words, мы ожидаем что напряжение Холла E y · d y (с д г = размерность в y -направление) пропорциональна току(плотности) j и магнитному полю прочности B , которые, в конце концов, являются основными экспериментальными параметрами (помимо тривиальных размеров образец):
		E y  =  R Hall · B Z · J X
	Коэффициент. материальный параметр, действительно, потому что мы получим разные числа для R Холла , если мы это сделаем эксперименты с одинаковыми магнитными полями и плотностью тока, но с разными материалами. Коэффициент Холла, как упоминалось ранее, имеет интересные свойства:
		R Зал изменит свой знак, если изменится знак перевозчиков, потому что тогда E y тоже меняет знак. Таким образом, он указывает самым недвусмысленным образом, какой только можно вообразить, если он положителен. или отрицательные заряды несут ток.
		R Холл позволяет получить мобильность µ носителей, как мы сразу увидит.
	R Холл легко вычисляется: Используя уравнение для E y сверху, и основное уравнение j x = s · E x , получаем для отрицательно платные перевозчики:
		R Холл   =  – µ · E x · B z s · E x · B z  =  –   µ s   =   – µ | q | · n · µ =   – 1 | q | · n
	Синяя часть соответствует вывод указан в ссылке; n (очевидно) концентрация носителей.
		Если известен коэффициент Холла или концентрация носителей, эффект Холла можно использовать для измерения напряженности магнитного поля B (иначе не так просто сделать!).
	Измерения коэффициента Холла материалов с известным проводимость (что-то легко измеримое), таким образом, дает нам напрямую мобильность носители, ответственные за проводимость.
		Знак минус выше получается для электронов , т.е. отрицательных зарядов.
		Если будут задействованы положительно заряженные носители, Постоянная Холла будет положительной .
		Обратите внимание, что не всегда легко измерить числовое значение напряжения Холла и, таким образом, R с хорошей точностью, это самое простое в мир для измерения полярности напряжения.
	Давайте посмотрим на несколько экспериментальных данных:
		Material Li Cu Ag Au Al Be In Полупроводники (например, Si , G e , GaAs , InP ,. ..) R (× 10 –24 ) cgs units –1,89 –0,6 –1,0 –0,8 +1,136 +2,7 +1,774 положительный или отрицательных значений в зависимости от «допинга» Комментарии: 1. положительных значений для металлы измерялись в несколько особых условиях (низкие температуры, монокристаллы с особой ориентацией), для других условий также могут быть получены отрицательные значения. 2. Единицы в данном случае не важны, но умножение на   9 · 10 13 дает значение в м 3 / кулон

Эффект Холла – принцип, теория, формула, области применения и часто задаваемые вопросы

Эффект Холла – это процесс, при котором в твердом материале возникает поперечное электрическое поле, когда материал, по которому течет электрический ток, помещается в магнитное поле то есть перпендикулярно току. Эффект Холла был открыт Эдвином Гербертом Холлом в 1879 году. В этой статье мы подробно узнаем об эффекте Холла.

Принцип эффекта Холла

Принцип эффекта Холла гласит, что когда проводник с током или полупроводник помещается в перпендикулярное магнитное поле, напряжение может быть измерено под прямым углом к ​​пути тока. Этот эффект получения измеримого напряжения известен как эффект Холла.

Теория

Когда проводящая пластина подключается к цепи с батареей, начинает течь ток. Носители заряда будут следовать по линейному пути от одного конца пластины к другому концу. Движение носителей заряда приводит к возникновению магнитных полей. При помещении магнита вблизи пластины магнитное поле носителей заряда искажается. Это нарушает прямолинейный поток носителей заряда. Сила, которая изменяет направление потока носителей заряда, известна как сила Лоренца.

Из-за искажения магнитного поля носителей заряда отрицательно заряженные электроны будут отклоняться в одну сторону пластины, а положительно заряженные дырки — в другую.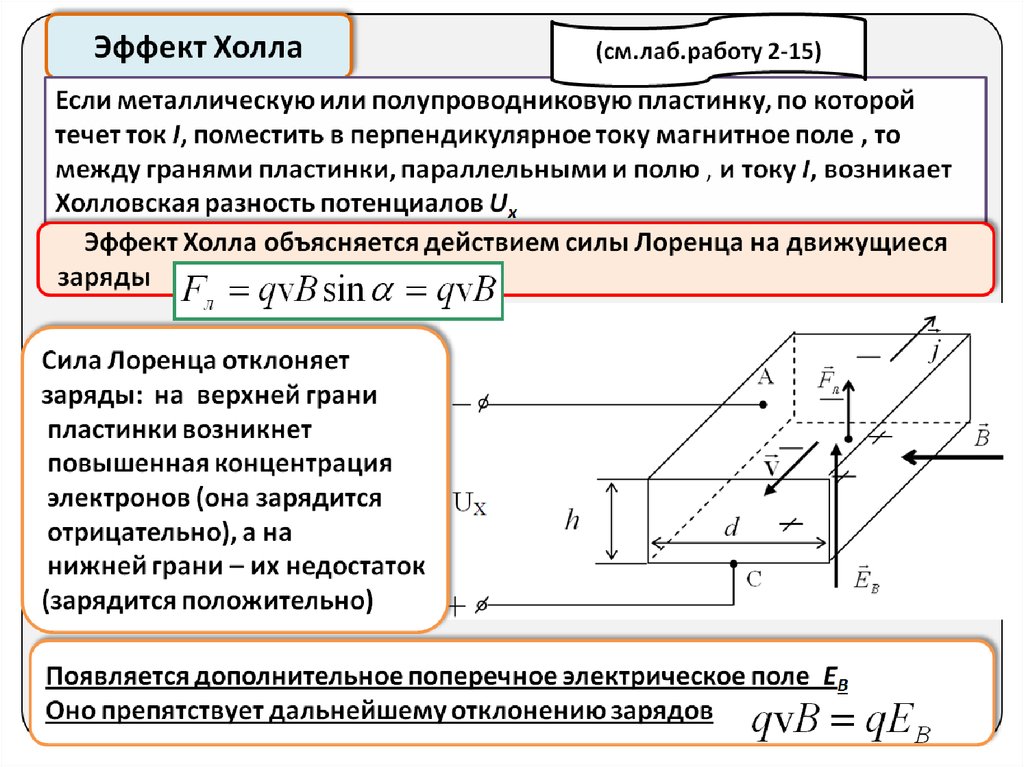 Между обеими сторонами пластины будет создаваться разность потенциалов, известная как напряжение Холла, которую можно измерить с помощью измерителя.

Напряжение Холла, представленное как V _H , определяется по формуле:

\(\begin{массив}{l}V_H=\frac{IB}{qnd}\end{массив} \)

Здесь,

I — ток, протекающий через датчик

B — напряженность магнитного поля

q это заряд

n — количество носителей заряда в единице объема

d — толщина сенсора.

Аналогичное чтение:

Коэффициент Холла

Коэффициент Холла R _H математически выражается как

\(\begin{array}{l}R_H=\frac{E}{jB}\end{array} \)

Где j — плотность тока электрона-носителя, Ey — индуцированное электрическое поле, а B — напряженность магнитного поля. Коэффициент Холла положителен, если положительных зарядов больше, чем отрицательных. Точно так же он отрицателен, когда электронов больше, чем дырок.

Применение эффекта Холла

Принцип эффекта Холла используется в следующих случаях:

• Оборудование для измерения магнитного поля
• Для измерения постоянного тока используется тестер клещей на эффекте Холла.
• Используется для измерения фазового угла
• Датчики приближения
• Датчики и преобразователи на эффекте Холла
• Датчики линейного или углового смещения
• Для определения скорости вращения колес и, соответственно, помощи антиблокировочной тормозной системе.

Следите за новостями BYJU’S и Влюбитесь в обучение!

Часто задаваемые вопросы – Часто задаваемые вопросы

Назовите одно практическое применение эффекта Холла.

Эффект Холла используется для определения того, является ли вещество полупроводником или изолятором. Природа носителей заряда может быть измерена.

Как развивается потенциал Холла?

Когда проводник с током находится в присутствии поперечного магнитного поля, магнитное поле оказывает отклоняющую силу в направлении, перпендикулярном как магнитному полю, так и скорости дрейфа.