Эквивалентное последовательное сопротивление esr. Эквивалентное последовательное сопротивление конденсатора

Собственно, как я уже когда-то очень давно обещал, расскажу про простейший измеритель ESR. В дальнейшем буду писать не ESR, а ЭПС(эквивалентное последовательное сопротивление), поскольку лень переключать раскладку. И так, кратко, что же такое ЭПС.

ЭПС можно представить в виде резистора, включенного последовательно с кондесатором.
На данной картинке — R. Собственно, у исправного конденсатора этот показатель измеряется долями Ома, для конденсаторов малой емкости (до 100мкф) может достигать 2-3 Ом. Более подробно значения ЭПС для исправных конденсаторов можно найти в справочных данных производителей. Со временем, из-за испарения электролита, это сопротивление увеличивается, что приводит к повышению мощности потерь. Как результат конденсатор сильнее нагревается, что еще сильнее ускоряет процесс испарения электролита и приводит к потере емкости.
На практике ремонта точное измерение ЭПС не нужно. Достаточно считать любой конденсатор с ЭПС выше 1-2 Ом неисправным. Можно считать это спорным утверждением, в интернете достаточно легко найти целые таблицы с значениями ЭПС для конденсаторов различной емкости. Однако я убеждался неоднократно, что приблизительной оценки вполне достаточно. Не говоря уже о том, что результаты измерения ЭПС одних и тех же конденсаторов(новых), одного и того же производителя сильно разнятся в зависимости от партии, времени года и фазы луны.

Я использую простой измеритель на копеечной микросхеме. Разработал его Manfred Mornhinweg .

Конструкция довольно простая, но привлекательна своей нетребовательностью к трансформатору. Из недостатков — шкала получается «широкая», в моем случае 0-20ом. Соответственно, нужна большая измерительная головка, т.н. «магнитофонные» (из индикаторов уровня магнитофонов), не подойдут — будет неудобно работать.

В качестве трансформатора автор намотал две обмотки 400 и 20 витков на ферритном кольце 19х16х5мм 2000НМ. Однако можно поступить значительно проще — использовать трансформатор дежурки из любого ATX блока питания. Достаточно заменить R8 на подстроечный многооборотный резистор 3296W сопротивлением 51к. При помощи этого резистора можно будет увеличить коэффициент усиления измерительного усилителя и компенсировать недостаточный коэффициент трансформации. LM7805 необходимо заменить на LM1117-5, это снизит потребляемый ток, плюс нижний порог напряжения питания опустится примерно до 6.5В. Стабилизатор обязателен, иначе шкала будет плавать в зависимости от напряжения питания. Для питания я использовал обычную «Крону». Саму микросхему обязательно поставьте в панельку!
Настройка прибора сводится к установке «нуля» и калибровке шкалы. Для калибровки шкалы используются низкоомные резисторы с допусками 0.5% и сопротивлениями от 0 до 2-5 Ом. Калибровка производится следующим образом — снимаем защитное стекло с индикаторной головки. Включаем прибор и измеряем сопротивление эталонных резисторов. Смотрим, куда отклоняется стрелка и ставим в этом месте на шкале метку с соответствующим сопротивлением. Так размечаем шкалу.
Измеряемые низковольтные конденсаторы(до 50-80 вольт без проблем) разряжаются резисторами R5, R6 и первичной обмоткой трансформатора. «Сетевые» емкости(те, которые после диодного моста в импульсных БП) я предварительно разряжаю приспособой, сделанной из резистора 510 Ом/1Вт, иглы от шприца, крокодила и корпуса гелевой ручки. В теории цепочка R5-R6 должна разрядить и такие емкости, но на практике, выбивает TL062:) Именно поэтому ее надо ставить в панельку -чтобы быстро заменить. Но надежнее — предварительно разрядить «сетевую» емкость.
В целом — очень удачный прибор — дешев, прост, не требователен к трансформатору.

Equivalent Series Resistance (Эквивалентное Последовательное Сопротивление — ЭПС), как один из значимых паразитных параметров электролитических конденсаторов, в последние годы приобрёл широкую популярность среди ремонтников электронной аппаратуры. Измерители и пробники ESR для многих мастеров стали прибором первой необходимости наряду с тестером или мультиметром.
Увеличение ESR конденсатора на несколько Ом, а иногда на несколько десятых долей Ома, может являться причиной неработоспособности устройства, в котором он установлен, что иногда невозможно выявить существующими измерителями ёмкости, не способными учитывать другие параметры конденсатора.

Обычно в ремонтной практике не требуется особой точности в измерении ESR, поэтому ощутимая погрешность пробников чаще не вызывает неудобств в отыскании неисправных элементов, а определение состояния конденсатора пробником может упрощаться до оценки его качества по принципу – годен или не годен для работы в конкретном узле устройства.
Но, следует отметить, для конденсаторов, работающих при больших импульсных токах, например, в фильтрах преобразователей, иногда требуется более объективная оценка качества, а погрешность в десятые и даже сотые доли Ома может иметь существенное значение.

Большинство популярных и применяемых в ремонтной практике приборов и пробников ESR основаны на измерении полного сопротивления переменному току на частоте 40 — 100 кГц. На частотах этого порядка для электролитических конденсаторов больших номиналов такие приборы покажут значения, максимально близкие к величине ESR, которая составит основную часть импеданса на этих частотах.
Недостатком такого способа является значительная погрешность при измерении малых номиналов ёмкостей (менее 10 uF), когда реактивное сопротивление конденсатора на данной частоте соизмеримо и может превышать ESR.

Тогда прибор покажет значение импеданса, а реальное значение ESR может быть в несколько раз меньше.

Одним из требований в плане практичности использования ESR-пробников является возможность производить замеры без выпаивания конденсатора из платы. Следовательно, процесс измерения должен происходить при достаточно низком падении напряжения на проверяемом конденсаторе, исключая отпирание переходов полупроводниковых элементов схемы.

В большинстве случаев такие нехитрые измерители импеданса мастера собирают самостоятельно по схемам, широко распространённым в интернете, но кто-то применяет и свои разработки с учётом личных предпочтений в плане удобства пользования или точности измерений.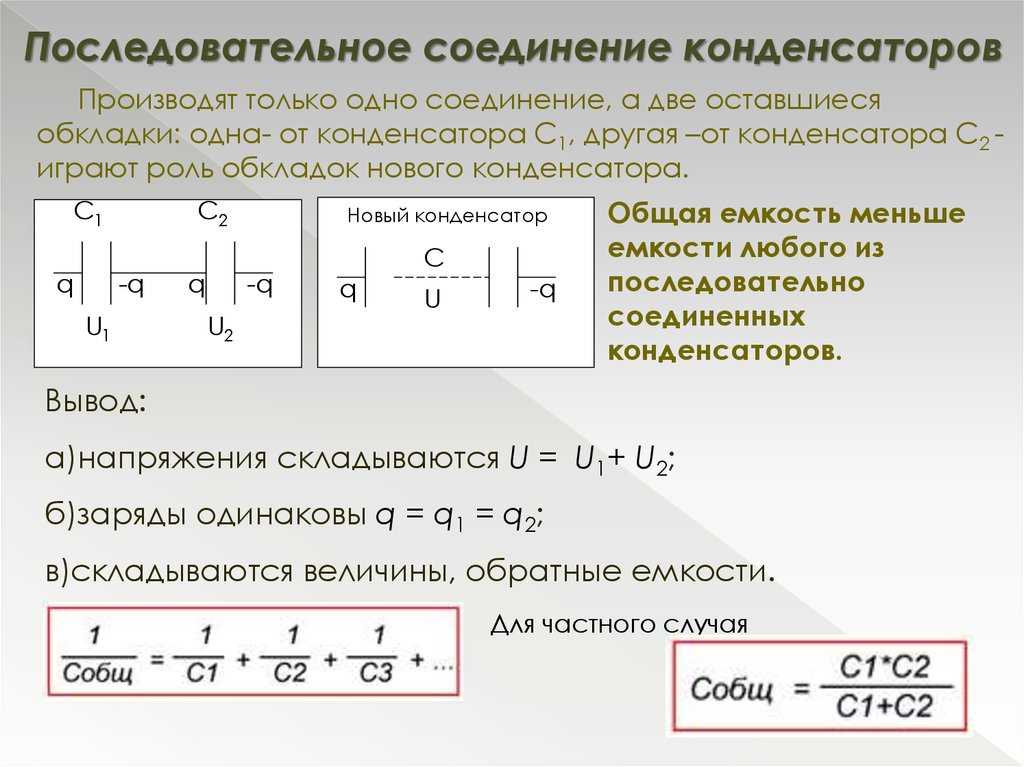

В продаже существуют как простые пробники со светодиодной или стрелочной индикацией, так и измерители с цифровой шкалой различной степени сложности.

Подробно останавливаться на принципах и методах измерения импеданса нет необходимости, таких обсуждений и описаний существует достаточно много и их нетрудно найти в интернете. Но некоторые особенности отдельных конструкций всё же могут заслуживать внимания.

В этой статье предлагается рассмотреть один из способов измерения ESR и ёмкости, как отдельных параметров конденсатора.

Достаточно точный и несложный метод, который используется во многих любительских и промышленных приборах, реализован в измерителе Micro, популярном среди мастеров – участников ремонтных форумов monitor.net.ru и monitor.espec.ws.

Если испытываемый конденсатор ёмкостью C заряжать от источника постоянного тока I , напряжение на его выводах будет линейно нарастать от значения U R по закону:

C dU/dt = I = const .

U R – падение напряжения на активном сопротивлении конденсатора (ESR).

В таком случае ёмкость конденсатора будет определяться выражением:

Посчитать U R для вычисления ESR можно несколькими способами, например, составив уравнение прямой по двум точкам и найти координату Y для нулевого значения X, либо геометрически, исходя из соотношения сторон подобных треугольников…

Активное сопротивление конденсатора (ESR) в таком случае составит:

Для реализации такого метода нет необходимости в применении АЦП, пороговые значения напряжений для управления таймером устанавливаются компараторами, а математические вычисления ёмкости и ESR производятся микроконтроллером с выводом информации на ЖК дисплей.

В некоторых подобных конструкциях для измерения ESR используется более простой, но менее точный способ.
Производится измерение уровня напряжения

U R посредством АЦП в начальный момент времени.
Несмотря на то, что измерительный импульс достаточно короткий (1-2 uS), конденсаторы меньшей ёмкости успевают зарядиться до большего значения, чем конденсаторы большой ёмкости, что создаёт некоторую погрешность в измерении ESR разных номиналов конденсаторов.

Следует учитывать, что ESR, измеренный постоянным током, является относительным показателем качества электролитического конденсатора.
Значимой составляющей ESR являются диэлектрические потери, которые существенно меняются с изменением частоты переменного тока.

Существуют более сложные и точные методики и способы измерений, основанные на анализе сдвига фаз в конденсаторе. В этом случае ESR определится произведением импеданса и тангенса угла потерь.

Замечания и предложения принимаются и приветствуются!

Какой главный параметр для оценки исправности конденсаторов? Конечно их ёмкость. Но по мере распространения импульсной высоковольтной техники, стало очевидно, что надо обратить внимание на ещё один параметр, от которого зависит надёжность и качество работы импульсных преобразователей — это эквивалентное последовательное сопротивление (ЭПС, по англ.

ESR — equivalent series resistance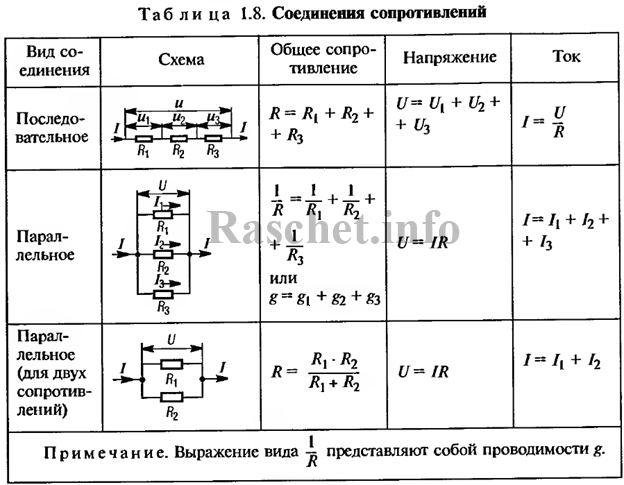

). Применение конденсаторов с увеличенным значением ЭПС приводит к росту пульсаций выходного напряжения по сравнению с расчётными значениями, и бстрому выходу их из строя из-за повышенного нагрева за счёт выделения тепла на ЭПС, нередки даже случаи закипания электролита, деформация корпуса, а также взрывы конденсаторов. Особая выраженность негативного влияния ЭПС именно в силовых импульсных преобразователях вызвана, работой на больших токах заряда-разряда, а также тем, что с ростом рабочей частоты ЭПС возрастает. Наличие ESR объясняется конструкцией оксидного конденсатора и обусловлена сопротивлением обкладок, сопротивлением выводов, переходным сопротивлением контактов между обкладками и выводами, а также потерями в материале диэлектрика. С течением времени ESR конденсатора возрастает, что совсем не хорошо.

ESR конденсаторов разных типов

Естественно, проконтролировать обычным Омметром эквивалентное последовательное сопротивление конденсатора невозможно — тут нужен специальный прибор. В интернете есть несколько простых конструкций ESR-метров , но при желании, можно собрать более точный и удобный измеритель на микроконтроллере. Например из журнала Радио 7-2010.

Схема измерителя ESR конденсаторов на
Attiny2313

Все необходимые файлы и прошивки — в архиве . После сборки и включения крутим регулятор контрастности до появления на экране LCD надписи в две строки. Если её нет — проверяем монтаж и правильность прошивки МК ATtiny2313. Если всё ОК — нажимаем кнопку «Калибровка» — в прошивку внесётся поправка на скорость срабатывания входной части измерителя. Далее понадобится несколько новых электролитических конденсаторов высокого качества ёмкостью 220…470 мкФ разных партий, лучше всего — на разные напряжения. Подключаем любой из них к входным гнёздам прибора и начинаем подбирать резистор R2 в пределах 100…470 ом (у меня получилось 300 ом; можно применить временно цепочку постоянный+подстроечный) так, чтобы значение ёмкости на экране ЖКИ примерно было похоже на номинал конденсатора. К большой точности пока что стремиться не стОит — ещё будет корректироваться; затем проверить и с другими конденсаторами.

Для настройки измерителя ESR нужна таблица с типовыми значениями этого параметра для разных конденсаторов. Эту табличку рекомендуется приклеить на корпус прибора под дисплеем.

В следующей табличке указаны максимальные значения эквивалентного последовательного сопротивления для электролитических конденсаторов. Если у измеряемого конденсатора оно будет выше, то его уже нельзя использовать для работы в сглаживающем фильтре выпрямителя:

Подключаем конденсатор 220 мкФ и, незначительным подбором сопротивления резисторов R6, R9, R10 (на схеме и на моём сборочном чертеже обозначены со звёздочками), добиваемся показаний Esr, близких к указанным в таблице. Проверяем на всех имеющихся заготовленных эталонных конденсаторах, в т.ч. уже можно использовать и конденсаторы от 1 до 100 мкФ.

Так как для измерения ёмкости конденсаторов от 150 мкФ и для измерителя ESR применяется один и тот же участок схемы, после подбора сопротивления этих резисторов несколько изменится точность показаний измерителя ёмкости. Теперь можно подстроить ещё сопротивление резистора R2, чтобы эти показания стали точнее. Другими словами, нужно подбирая сопротивление R2 — уточнить показания измерителя ёмкости, подстраивая резисторы в делителе компараторов — уточнить показания ESR-метра. Причём, приоритет надо отдавать измерителю внутреннего сопротивления.

Теперь надо настроить измеритель ёмкости конденсаторов диапазона 0,1…150 мкФ. Так как для этого в схеме предусмотрен отдельный источник тока, измерение ёмкости таких конденсаторов можно сделать очень точным. Подключаем конденсаторы малой ёмкости к входным гнёздам прибора и, подбором сопротивления R1 в пределах 3,3…6,8 кОм добиваемся максимально точных показаний. Этого можно достичь, если в качестве эталонных применить не электролитические, а высокоточные конденсаторы К71-1 ёмкостью 0,15 мкФ с гарантированным отклонением 0,5 или 1%.

Когда собрал данный измеритель ESR — схема завелась сразу, понадобилась только калибровка. Этот измеритель много раз помогал при ремонте БП, так что устройство рекомендуется к сборке. Схему разработал — DesAlex , собрал и испытал: sterc .

Обсудить статью ИЗМЕРИТЕЛЬ ESR НА МИКРОКОНТРОЛЛЕРЕ

Что такое ESR?

Теория

ESR — Equivalent Series Resistance — один из параметров конденсатора, характеризующий его активные потери в цепи переменного тока. В эквиваленте его можно представить, как включенный последовательно с конденсатором резистор, сопротивление которого определяется, главным образом, диэлектрическими потерями, а так же сопротивлением обкладок, внутренних контактных соединений и выводов конденсатора. В русскоязычной аббревиатуре — Эквивалентное Последовательное Сопротивление — ЭПС .

Потери в диэлектрике, обусловленные особенностями его поляризации, составляют основную часть потерь в конденсаторе и определяются материалом, а так же толщиной слоя диэлектрика. В электролитических конденсаторах значимой частью ESR является сопротивление жидкого электролита, который используется в качестве составляющей одной из обкладок для обеспечения максимальной площади соприкосновения с диэлектриком. Если сопротивление электролита в конденсаторе рассмотреть как проводник с поперечным сечением, равным площади одной из обкладок и длиной проводника, приблизительно равной толщине пропитанной бумаги, можно предположить, что эта величина будет относительно небольшой. В реальных конденсаторах средних размеров типовое значение составит 0.01Ом при 20°C. Но, следует учитывать, что для конденсаторов большой ёмкости, используемых в фильтрах выпрямителей ИИП на рабочей частоте порядка 100кГц, когда его реактивное сопротивление измеряется тысячными долями Ома, эта величина будет составлять достаточно большие потери. Величина диэлектрических потерь на таких частотах в электролитических конденсаторах фильтров ИИП обычно в несколько раз больше, и лишь в самых лучших случаях может быть примерно равна и даже меньше потерь в электролите.

Сопротивление электролита существенно зависит от температуры по причине изменения степени его вязкости и подвижности ионов. В процессе работы происходит нагрев диэлектрика и электролита переменным током, в связи с чем может существенно уменьшаться сопротивление электролита, тогда ESR конденсатора будет определяться, главным образом, его диэлектрическими потерями. В случаях разогрева до температуры кипения, электролит утрачивает свои первоначальные свойства и при последующем охлаждении становится более вязким, что значительно повышает его сопротивление. Дальнейшая эксплуатация будет вызывать ещё больший разогрев и ухудшение качества электролита, что в последствии приведёт к непригодности конденсатора для дальнейшей работы в устройстве. Обычно неисправные электролитические конденсаторы, в которых кипел электролит, определяются визуально по вздувшемуся и разгерметизированному корпусу.

Для надёжности работы электролитических конденсаторов очень важен правильный выбор его типа, номинала и максимального напряжения в зависимости от режимов. Для фильтров преобразователей, работающих на частотах десятков килогерц, производители выпускают специальные конденсаторы с малым ESR и указывают полное сопротивление переменному току (импеданс Z) для всех номиналов в таблицах. Тип таких конденсаторов сопровождается пометкой в технической документации — Low impedance или Low ESR .

Практика

Электролитические конденсаторы это навереное единственные электронные элементы, которые страдают от высыхания. Если у вас есть любые электронные устройства, которые на протяжении многих лет работали, но вдруг перестали исправно функционировать, имеются хорошие шансы, что один или несколько электролитических конденсаторов внутри него деградировали и стали причиной проблемы. Электролитические конденсаторы выходят из строя несколькими способами: они могут стать электрически проводящие, вызывая постоянный ток через них, что может даже их взорвать. Они могут уменьшаться в величине емкости. Но наиболее часто увеличивается их эквивалентное последовательное сопротивление, которое является очень нежелательным.

ESR электролитического конденсатора обычно составляет доли Ом для конденсаторов низкого напряжения (таких как 1000µF, 16V), и может быть два или три Ома для малой емкости и высокого рабочего напряжения (1uF, 450V). Когда конденсатор стареет, это сопротивление возрастает, и часто из-за этого оборудование полностью прекращает функционировать. Очень часто конденсаторы увеличивают сопротивление ESR до 100 раз от их нормального сопротивления, в то время как их емкость остается хорошей! На измерении емкости они покажут близкое к правильному значение, но они уже не годные! Для анализа состояния конденсатора применяются измерители и пробники ESR. ESR-метр может проверить конденсаторы, даже когда они находятся в цепи. Соединенные параллельно с ним другие детали будут иметь минимальное влияние на измерение. Сколько примерно должен иметь сопротивления тот или иной исправный конденсатор — смотрите в таблице . Таковы особенности, которые делают ESR-метр незаменимым прибором для диагностики и ремонта электронного оборудования.

Наиболее слабым местом в любой радиосхеме являются электролитические конденсаторы, которые подвержены постоянному высыханию. И чем большие токи проходят через них — тем этот процесс быстрее. Обычным омметром определить плохой конденсатор не получится, поэтому необходим спецприбор — esr измеритель.

Схема электрическая esr измерителя конденсаторов

Печатные платы — рисунок

В типичной схеме, может быть 10 или даже 100 конденсаторов. Выпаивать каждый для тестирования очень утомительно и существует большой риск повреждения платы. Этот тестер использует низкое напряжение (250 мВ) высокой частоты (150 кГц), и он способен мерять ESR конденсаторов прямо в схеме. Напряжение выбрано достаточно низкими, чтобы другие окружающие радиоэлементы схемы не влияли на результаты замеров. А если вам случайно доведется испытать заряженный конденсатор — не беда. Этот измеритель выдерживает до 400В заряда на конденсаторе. Опыт показал, что ЭПС метр выявляет около 95% конденсаторов с потенциальными проблемами.

Особенности работы прибора

• Тест электролитических конденсаторов > 1 мкФ.
• Полярность не важна для тестирования.
• Переносит заряд конденсаторов до 400В.
• Низкий ток потребления от батареи — около 25 мА.
• Легко читать данные аналогового измерителя.
• Меряет ЭПС в диапазоне от 0-75 Ом по расширенной шкале с помощью омметра.

Будьте осторожны, если вы тестируете высоковольтные конденсаторы. Имейте в виду, что высоковольтные конденсаторы могут нести сильный заряд в течение нескольких дней, в зависимости от схемы.

Как использовать ESR метр

Включаете прибор. Убедитесь, что проверяемая схема находится не под напряжением. Разрядите конденсатор перед тестированием — ЭПС метр не делает этого автоматически. Замкните выводы конденсатора и удерживайте их так в течение нескольких секунд. С помощью вольтметра убедитесь, что конденсатор полностью разряжен. Вольтметр должен показывать нулевое значение. Прикоснитесь щупами ESR метра к конденсатору. Определите сопростивление ESR. Является ли значение ESR приемлемым узнаём путем сравнения измеренного ESR с эталонными данными. Посмотреть эту таблицу

Определение эквивалентного последовательного сопротивления (ESR) конденсаторов

Добавлено 12 декабря 2019 в 07:16

Рассмотрим подробнее важность ESR (эквивалентного последовательного сопротивления) конденсатора, как его измерить, и какие факторы могут повлиять на ваши измерения.

По мере того, как рабочие частоты увеличиваются, а электронные системы становятся все сложнее и меньше, разработчики должны уделять пристальное внимание ESR (эквивалентному последовательному сопротивлению) конденсатора, поскольку оно влияет на энергопотребление и эффективность.

Знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.

Некоторые производители указывают ESR при конкретных частоте и рабочих условиях, некоторые просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния.

Эквивалентное последовательное сопротивление (ESR) является одной из характеристик неидеального конденсатора, которая может вызывать различные проблемы производительности в электронных схемах. Высокое значение ESR ухудшает производительность из-за потерь I²R, шума и более высокого падения напряжения.

В некоторых случаях тепло, выделяемое благодаря ESR, невелико и может не вызывать проблем.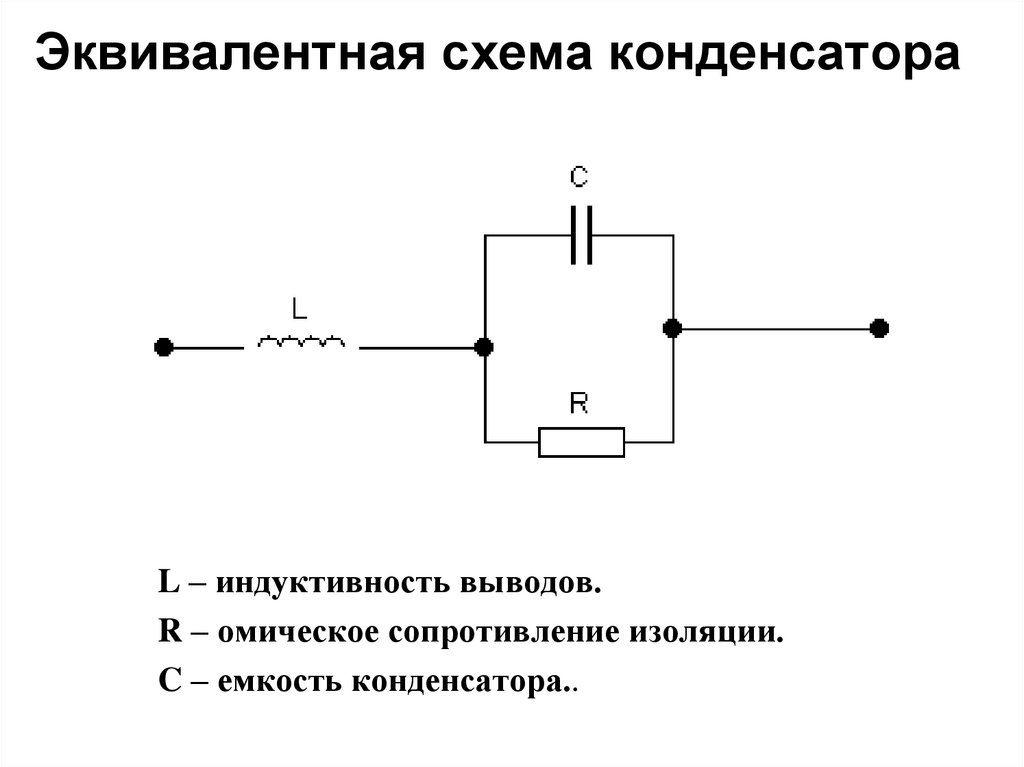 Однако в некоторых схемах, особенно в приложениях с большим током, рассеиваемое тепло может вызвать значительное повышение температуры, повлиять на работу схемы и вызвать деградирование конденсатора. Кроме того, на сопротивлении происходит значительное падение напряжения, что снижает долю полезной энергии в приложении.

Таким образом, при выборе конденсатора для таких применений, как ВЧ, аккумулирование энергии, схемы фильтров и другие чувствительные схемы, требуется учет и других характеристик, помимо значений емкости и напряжения.

Связанная информация

• Особенности конденсаторов
• Практические аспекты применения конденсаторов
• Чистое питание для каждой микросхемы, часть 2: Выбор и использование блокировочных конденсаторов

Влияние ESR на радиочастотные схемы и схемы аккумулирования энергии

Несмотря на то, что ESR у керамических конденсаторов очень мало, порядка миллиом, это сопротивление может существенно повлиять на такие схемы, как радиочастотные схемы и схемы с низким энергопотреблением.

В переносных радиочастотных передатчиках конденсаторы с высоким ESR в схемах связи или обхода источника питания усилителя потребляют и расходуют больше энергии аккумулятора из-за более высоких потерь I²ESR. Это уменьшает эффективность, выходную мощность и срок службы батареи.

Кроме того, большинство радиочастотных полупроводниковых устройств, изготовленных для согласующих каскадов, построены с очень низким входным сопротивлением. Таким образом, согласующий конденсатор, такой как многослойный керамический чип-конденсатор (MLCC) с высоким ESR, будет представлять собой значительную долю от общего полного сопротивления цепи. Например, если входной импеданс устройства составляет 1 Ом, согласующий конденсатор с ESR 0,8 Ом будет рассеивать около 40 процентов общей мощности, таким образом, уменьшая выходную мощность и эффективность схемы.

Конденсаторы в приложениях по аккумулированию энергии выполняют более важную роль – накапливают заряд от низковольтных источников энергии и быстро и эффективно разряжают эту накопленную энергию для питания нагрузки.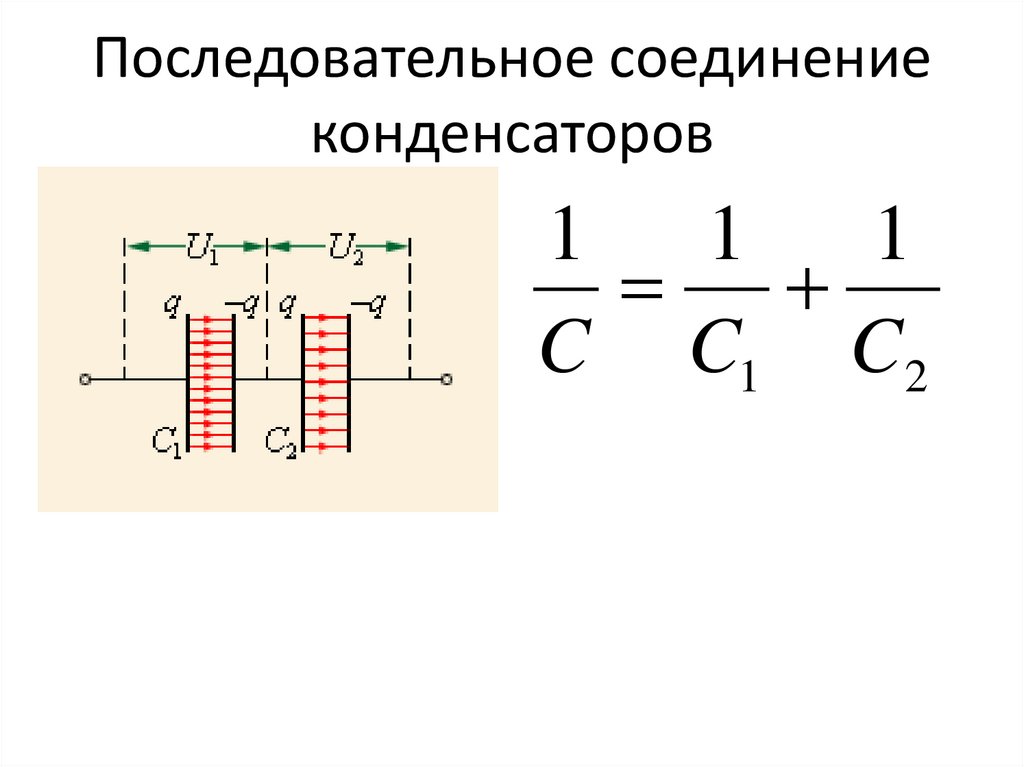 Следовательно, конденсаторы и другие компоненты в цепях аккумулирования энергии должны во время работы потреблять очень мало энергии.

Конденсатор с высоким ESR будет иметь бо́льшие потери I²ESR, поэтому часть полученной энергии в конечном итоге будет потрачена впустую в виде тепла, что приведет к уменьшению выходной энергии конденсатора. Однако разработчики могут предпочесть суперконденсаторы (несмотря на их более высокие ESR и утечку), потому что они предлагают более высокую плотность энергии.

Определение эквивалентного последовательного сопротивления с помощью измерителя ESR

Измеритель ESR является умеренно точным прибором, который доступен и удобен в использовании, особенно при измерении нескольких конденсаторов, когда они находятся в схеме. На конденсатор в схеме делителя напряжения подается переменное напряжение. Частота подаваемого переменного напряжения обычно равна значению, при котором реактивное сопротивление конденсатора незначительно.

Рисунок 1 – Простая модель измерения ESR

Во время теста с использованием измерителя ESR ток пропускается через конденсатор в течение очень короткого времени, поэтому конденсатор не заряжается полностью. Ток создает напряжение на конденсаторе. Это напряжение будет равно произведению тока на ESR конденсатора, плюс незначительное напряжение из-за небольшого заряда в конденсаторе.

Поскольку ток известен, значение ESR рассчитывается путем деления измеренного напряжения на ток. Результаты затем отображаются на показаниях измерителя.

Измерения ESR могут выполняться, когда конденсатор находится и в схеме, и вне схемы. Для конденсаторов, подключенных параллельно, измерение дает в результате общее сопротивление. Если необходимо определить отдельно ESR у конкретных конденсаторов, они должны быть извлечены из схемы. Однако при наличии сотен конденсаторов утомительно вынимать каждый из них, а также существует повышенный риск повреждения конденсаторов или печатной платы во время удаления.

Типовой измеритель ESR использует низкое напряжение около 250 мВ или менее с частотой около 100 кГц. Низкое напряжение является недостаточным для смещения и активации полупроводниковых устройств в окружающих цепях, что гарантирует, что импеданс соседних компонентов не влияет на показания ESR.

Перед проведением измерения конденсатор должен быть разряжен. Некоторые измерители ESR имеют встроенный механизм разряда. Однако может быть важно разрядить конденсатор вручную, особенно если это высоковольтный конденсатор, заряд которого может повредить измеритель ESR.

Несмотря на то, что измеритель ESR может удобно тестировать конденсаторы внутри схемы, он имеет ограничения по частоте, а также по самому низкому уровню сопротивления, который он может точно измерить.

Измерение с помощью коаксиальной резонансной трубы для сверхнизких сопротивлений на высоких частотах

Поскольку значение ESR зависит от рабочей частоты, измерение сверхнизких значений ESR на очень высоких частотах становится проблемой при использовании обычных измерителей ESR.

Для керамических конденсаторов наиболее точным методом определения ESR на высоких частотах (от 100 МГц до 1,3 ГГц) является метод коаксиальной резонансной линии. Этот метод основан на стандартной модели Boonton 34A и используется вместе с генератором высокочастотных сигналов и высокочастотным вольтметром.

Рисунок 2 – Блок-схема измерителя ESR на коаксиальной резонансной трубке

Линия коаксиального резонатора выполнена из медной трубки со сплошным медным стержнем в качестве центрального проводника. Тестируемый конденсатор устанавливается последовательно между центральным проводником и проводником экрана.

Перед выполнением измерения ESR конденсатора необходимо определить характеристики ненагруженной линии резонатора. ВЧ возбуждение закороченной коаксиальной линии помогает определить ширину полосы λ/4 и 3λ/4, тогда как ширина полосы λ/2 и λ определяется, когда линия разомкнута (λ – это длина волны; дополнительную информацию см. в этой статье). Эти данные характеризуют резонансную частоту, добротность (Q) ненагруженной резонансной линии и сопротивление крепежного элемента.

Затем тестируемый конденсатор помещается в секцию DUT (device under test, тестируемое устройство), и генератор сигналов настраивается на пиковое резонансное напряжение. Конденсатор вызывает изменение резонансной частоты и добротности, значения которых теперь отличаются от значений ненагруженной коаксиальной линии. Затем используются расчеты линии передачи, и значение ESR определяется на основе взаимосвязи между новой частотой и добротностью, а также частотой и добротностью исходного состояния без нагрузки.

Рисунок 3 – Полоса пропускания нагруженной и незагруженной линии передачи

В настоящее время обычной практикой является использование векторного анализатора цепей для замены как генератора сигналов, так и высокочастотного вольтметра. При использовании векторного анализатора цепей резонансная частота считывается с дисплея. Некоторые модели векторных анализаторов могут экспортировать результаты непосредственно в программу расчета и отображать окончательное значение ESR.

Длина трубки рассчитана на работу в диапазоне частот от 100 МГц до 1,5 ГГц; однако для частот, выходящих за пределы этого диапазона, трубка может быть выполнена произвольной длины.

Факторы, которые влияют на измерения ESR

Ошибки измерения ESR могут возникать в результате проблем с техникой, способа выполнения контакта с конденсатором или отсутствия калибровки измерительного оборудования.

Должны быть приняты во внимание сопротивления, самоиндукция и емкость измерительного прибора и его выводов, особенно на высоких частотах измерения.

Сопротивление и индуктивность измерительных проводов

Сопротивление измерительных проводов является распространенным источником ошибок при измерениях низких сопротивлений. Это сопротивление добавляется к сопротивлению тестируемого устройства.

Кроме того, следует избегать измерительных проводов со спиральной намоткой, поскольку источником ошибки может стать их индуктивность.

Помехи от соседнего оборудования

Измерение следует проводить в местах, удаленных или экранированных от источников значительных электромагнитных помех. В противном случае измерительные провода могут ловить помехи, и это может повлиять на показания.

Заключение

ESR варьируется в зависимости от типа конденсатора и условий эксплуатации, таких как частота и температура. Некоторые производители указывают ESR на определенной частоте и при определенных условиях работы, другие просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния. Тем не менее, знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.

Тип метода, используемого для определения ESR, зависит от таких факторов, как тип конденсатора, рабочая частота и требуемая точность. В то время как измеритель ESR и другие самодельные измерители подходят для ряда применений на частотах примерно до 100 кГц, они не могут точно определить очень низкие значения ESR на очень высоких частотах. Метод коаксиальной резонансной линии часто является предпочтительным при определении сверхнизких значений ESR на частотах между приблизительно 100 МГц и 1,3 ГГц.

По мере того, как рабочие частоты увеличиваются, а электронные системы становятся меньше и сложнее, необходимо уделять пристальное внимание таким параметрам, как ESR, которые напрямую влияют на характеристики схемы и эффективность энергопотребления.

Оригинал статьи:

• Amos Kingatua. Determining the Equivalent Series Resistance (ESR) of Capacitors

Теги

ESR (эквивалентное последовательное сопротивление)ИзмерениеКерамический конденсаторКонденсаторЭквивалентная схемаЭлектролитический конденсатор

Конденсатор (электронный компонент) | это.

.. Что такое Конденсатор (электронный компонент)?

Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик

Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические.

Различные конденсаторы для объёмного монтажа

Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Содержание 1 История 2 Свойства конденсатора 3 Обозначение конденсаторов на схемах 4 Характеристики конденсаторов 4.1 Основные параметры 4.1.1 Ёмкость 4. 1.2 Удельная ёмкость 4.1.3 Номинальное напряжение 4.1.4 Полярность 4.2 Паразитные параметры 4.2.1 Электрическое сопротивление изоляции конденсатора — r 4.2.2 Эквивалентное последовательное сопротивление — R 4.2.3 Эквивалентная последовательная индуктивность — L 4.2.4 Тангенс угла потерь 4.2.5 Температурный коэффициент ёмкости (ТКЕ) 4.2.6 Диэлектрическое поглощение 5 Классификация конденсаторов 6 Применение конденсаторов 7 Внешние ссылки 8 Смотри также 9 Ссылки

История

В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку».

Свойства конденсатора

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течет, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора.

В терминах метода комплексных амплитуд конденсатор обладает комплексным импедансом

,

где — мнимая единица, — частота^[1] протекающего синусоидального тока, — ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).

При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью , собственной индуктивностью и сопротивлением потерь .

Резонансная частота конденсатора равна

При конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:

где — напряжение (разность потенциалов), до которого заряжен конденсатор.

Обозначение конденсаторов на схемах

В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74^[2] либо международному стандарту IEEE 315-1975:

Обозначение по ГОСТ 2.728-74	Описание
	Конденсатор постоянной ёмкости
	Поляризованный конденсатор
	Подстроечный конденсатор переменной ёмкости

На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 10⁶ пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 – 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, т.е. на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.

Характеристики конденсаторов

Основные параметры

Ёмкость

Основной характеристикой конденсатора является его ёмкость. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад.

Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью каждая, расположенных на расстоянии друг от друга, в системе СИ выражается формулой: , где — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда много меньше линейных размеров пластин).

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

или

Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.

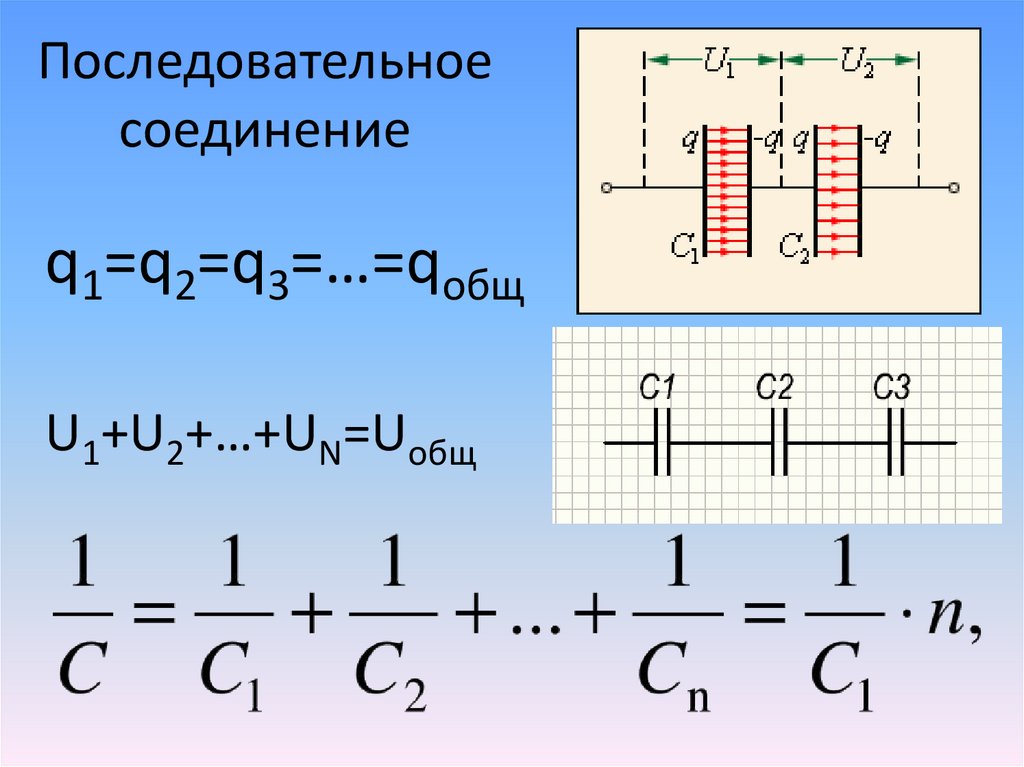
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы. Общая ёмкость батареи последовательно соединённых конденсаторов равна

или

Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.

Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.

Удельная ёмкость

Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.

Номинальное напряжение

Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.

Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается.

Полярность

Конденсаторы, разрушившиеся без взрыва из-за температуры и напряжения, не соответствующих рабочим.

Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.

Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков.

Паразитные параметры

Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:

— собственная ёмкость конденсатора; — сопротивление изоляции конденсатора; — эквивалентное последовательное сопротивление; — эквивалентная последовательная индуктивность.

Электрическое сопротивление изоляции конденсатора —

r

Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением r = U / I_ут , где U — напряжение, приложенное к конденсатору, I_ут — ток утечки.

Эквивалентное последовательное сопротивление —

R

Эквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор.

В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр., Capacitor plague(англ.)).

Эквивалентная последовательная индуктивность —

L

Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности.

Тангенс угла потерь

Тангенс угла потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости.

Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол , где — угол диэлектрических потерь. При отсутствии потерь . Тангенс угла потерь определяется отношением активной мощности P_а к реактивной P_р при синусоидальном напряжении определённой частоты. Величина, обратная , называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.

Температурный коэффициент ёмкости (ТКЕ)

ТКЕ — относительное изменению емкости при изменении температуры окружающей среды на один градус Цельсия (Кельвина). Таким образом значение ёмкости от температуры представляется линейной формулой:

,

где ΔT — увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость емкости от температуры, и конденсаторы с большими уходами емкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение емкости в рабочем диапазоне температур.

Диэлектрическое поглощение

Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками. Наименьшим диэлектрическим поглощением обладают конденсаторы с органическими диэлектриками: тефлон (фторопласт), полистирол, полиэтилентерефталат, поликарбонат.

Классификация конденсаторов

Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др.

По виду диэлектрика различают:

• Конденсаторы вакуумные (обкладки без диэлектрика находятся в вакууме).
• Конденсаторы с газообразным диэлектриком.
• Конденсаторы с жидким диэлектриком.
• Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические, стеклоплёночные), слюдяные, керамические, тонкослойные из неорганических плёнок.
• Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.
• Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах) или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги или спеченного порошка.

Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:

• Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости (кроме как в течение срока службы).
• Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости в процессе функционирования аппаратуры. Управление ёмкостью может осуществляться механически, электрическим напряжением (вариконды, варикапы) и температурой (термо­конденсаторы). Применяются, например, в радиоприемниках для перестройки частоты резонансного контура.
• Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных ёмкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение ёмкости.

В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения.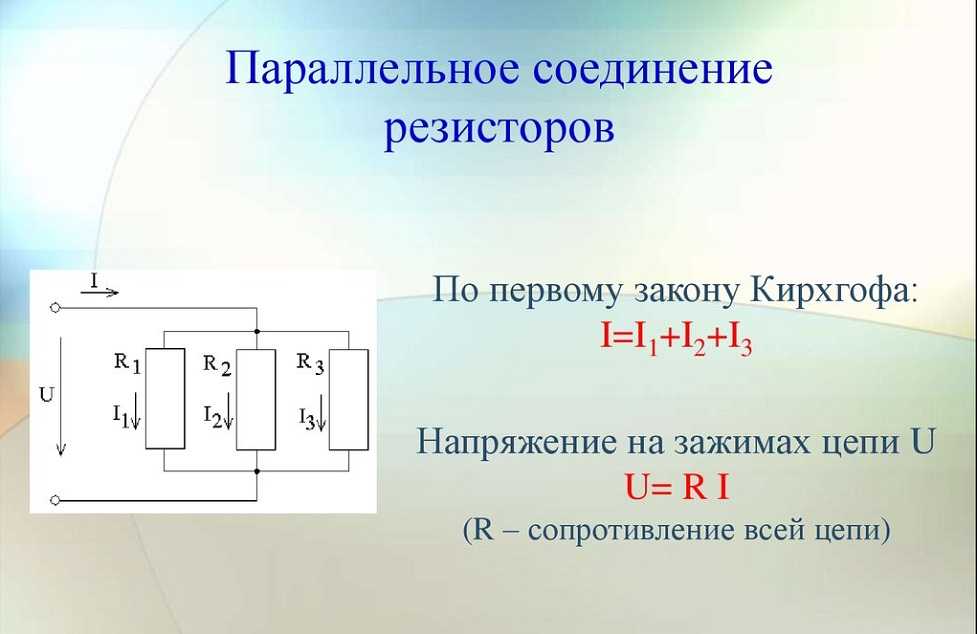 Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляюшие, дозиметрические, пусковые и другие конденсаторы.

Применение конденсаторов

Конденсаторы находят применение практически во всех областях электротехники.

• Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п..

• При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, импульсных лазерах с оптической накачкой, генераторах Маркса, (ГИН; ГИТ), генераторах Кокрофта-Уолтона и т. п.

• Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.

• В промышленной электротехнике конденсаторы используются для компенсации реактивной мощности и в фильтрах высших гармоник.

• Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора.
• ИП влажности воздуха (изменение состава диэлектрика приводит к изменению емкости)
• ИП влажности древесины

• В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит. В частности, в схеме работы АПВ использование конденсатора позволяет обеспечить требуемую кратность срабатывания защиты.

Внешние ссылки

• Описание работы конденсатора и емкости на аналогии с водопроводом.
• Статические конденсаторы для компенсации реактивной мощности
• Программа для расчёта реактивного сопротивления конденсатора

Смотри также

• Электрический импеданс
• Ионистор
• Переходный процесс
• Схемы на переключаемых конденсаторах

Ссылки

1. ↑ Частота в радианах в секунду.
2. ↑ ГОСТ 2.728-74 (2002)

Что такое конденсатор. Его параметры

Приветствую, друзья!

В первой части статьи мы рассмотрели, как устроен конденсатор.

Вы уже знаете, в каких единицах измеряется его ёмкость, как конденсаторы обозначаются в электрических схемах.

Вы уже знаете, где и как используются конденсаторы в компьютерной технике.

Конденсатор, как и любой компьютерный «кирпичик», обладает параметрами, которые характеризуют его работу.

Давайте углубим наши знания и посмотрим

Какими ещё параметрами характеризуются конденсаторы?

Вообще говоря, таких параметров много. У нас тут не нобелевская лекция, поэтому ограничимся только необходимым минимумом, который пригодится в практической деятельности.

Номинальное рабочее напряжение. Конденсатор может использоваться в режимах, когда напряжение на нём не превышает рабочего.

Использовать, например, электролитический конденсатор с рабочим напряжением 10 В в цепях +5 В или +3 В можно.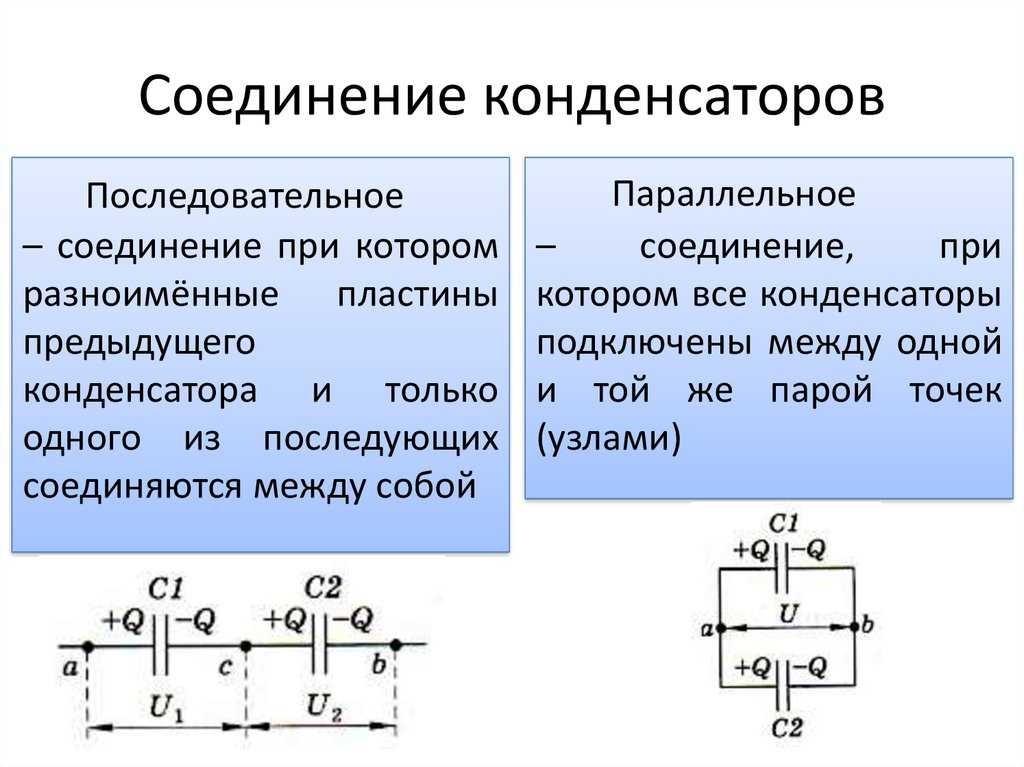

Чем больше рабочее напряжение электролитического конденсатора при равной ёмкости, тем больше его габариты.

Рабочее напряжение на керамических и других конденсаторах может явно не указываться или не указываться вообще — особенно, если конденсатор имеет маленькие размеры.

Полная информация о всех параметрах конденсатора имеется в соответствующем даташите (справочных данных), который имеется на сайте фирмы — производителя.

ESR (Equivalent Series Resistance) — эквивалентное последовательное сопротивление. Выводы конденсатора и их контакты с обкладками имеет не нулевое, хотя и очень небольшое сопротивление. Это сопротивление активное, поэтому, в соответствии с законами Ома и Джоуля-Ленца, при протекании тока на этом сопротивление будет рассеиваться тепло.

Это приведет к нагреву конденсатора.

Поэтому на электролитических конденсаторах обычно указывает максимальную рабочую температуру.

В компьютерных блоках питания и материнских платах используются специальные конденсаторы — с пониженным ESR.

Величина ESR может для таких конденсаторов быть в пределах от сотых до десятых долей Ома.

Что будет, если вместо конденсатора с пониженным ESR при ремонте блоков питания или материнских плат поставить обычный? Некоторое время он поработает. Но так как его ESR больше, то через цепь такого конденсатора будет протекать больший ток, который вызовет ускоренную деградацию конденсатора. Поэтому он быстро выйдет из строя.

Величиной ESR можно узнать по специальной маркировке (чаще всего 2 латинских буквы) на корпусе конденсатора. Соответствие этих букв реальным значениям ESR указывается в даташите.

Параллельное соединение конденсаторов

Несколько конденсаторов могут включаться последовательно или параллельно. При параллельном соединении ёмкости всех конденсаторов суммируются. При последовательном соединении общая ёмкость батареи конденсаторов меньше самой маленькой, так как складываются величины, обратные емкости. Но зато напряжение, при котором можно работать такая батарея, будет больше рабочего напряжения одного конденсатора.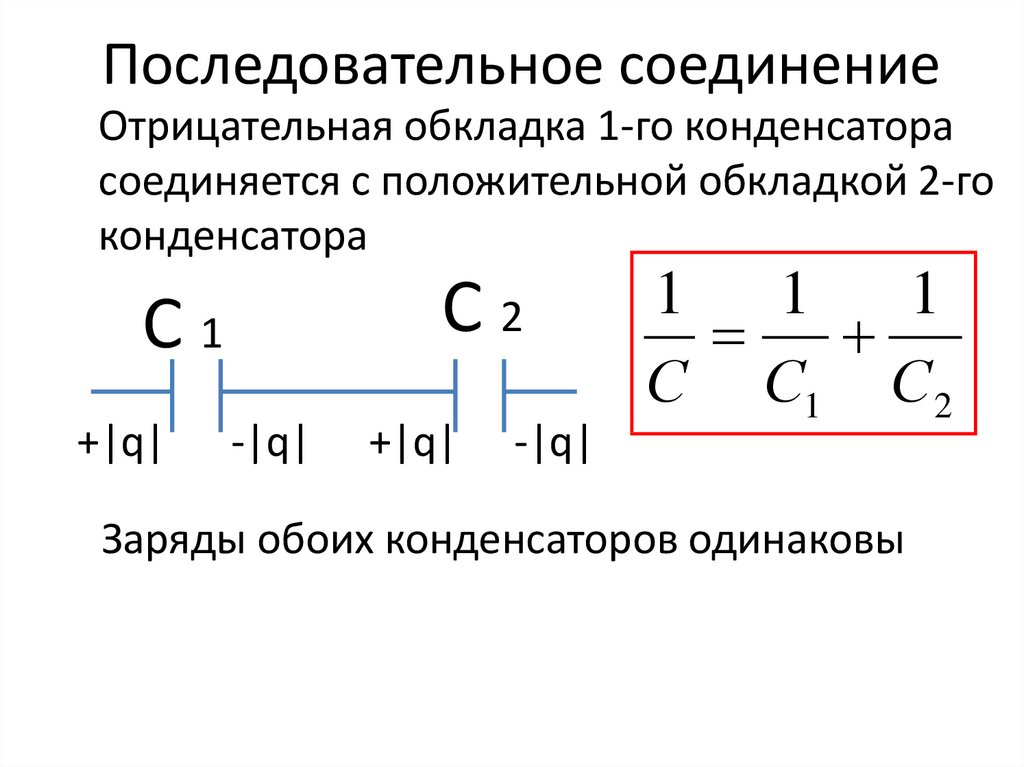

На материнских платах в цепи низковольтного источника напряжения, питающего ядро процессора, используется несколько однотипных конденсаторов, соединенных параллельно.

Интересный вопрос: почему бы не поставить один конденсатор емкостью, эквивалентной емкости батареи конденсаторов?

Дело в том, что у параллельно соединенных конденсаторов суммарное ESR будет гораздо меньше, чем ESR одного конденсатора. Потому что при параллельном соединении сопротивлений общее сопротивление уменьшается.

Что будет, если перепутать полярность конденсатора?

Если ошибиться с полярностью электролитического конденсатора – он обязательно выйдет из строя!

Сопротивление конденсатора при обратной полярности небольшое, поэтому через его цепь потечет значительный ток.

Это вызовет быстрый перегрев, закипание электролита, пары которого разорвут  корпус.

Такой же эффект вызовет и увеличение рабочего напряжения выше указанного на корпусе.

Чтобы исключить нехорошие последствия, верхняя крышка корпуса делается профилированной, с канавками-углублениями на верхней крышке.

При повышенном давлении внутри крышка расходится по этим канавкам, выпуская пары наружу.

Следует отметить, что электролитические конденсаторы,  использующиеся в компьютерных блоках питания и материнских платах, могут выйти из строя после нескольких лет эксплуатации в нормальном рабочем режиме.

Дело в том, что в конденсаторах из-за наличия электролита постоянно протекают электрохимические процессы, усугубляющиеся тяжелым режимом работы и повышенной температурой.

Как правильно заменить неисправные конденсаторы при  ремонте материнской платы компьютера можно прочитать здесь.

Как измерить ёмкость и ESR конденсатора?

Ёмкость конденсатора можно измерить с помощью обычного цифрового мультиметра.

Большинство цифровых мультиметров могут измерять не только ток, напряжение или сопротивление, но и ёмкость.

При измерении емкости надо с помощью переключателя выбрать необходимый поддиапазон и использовать отдельные гнёзда с маркировкой «F».

Однако большинство мультиметров измеряет емкость не более 20 микрофарад.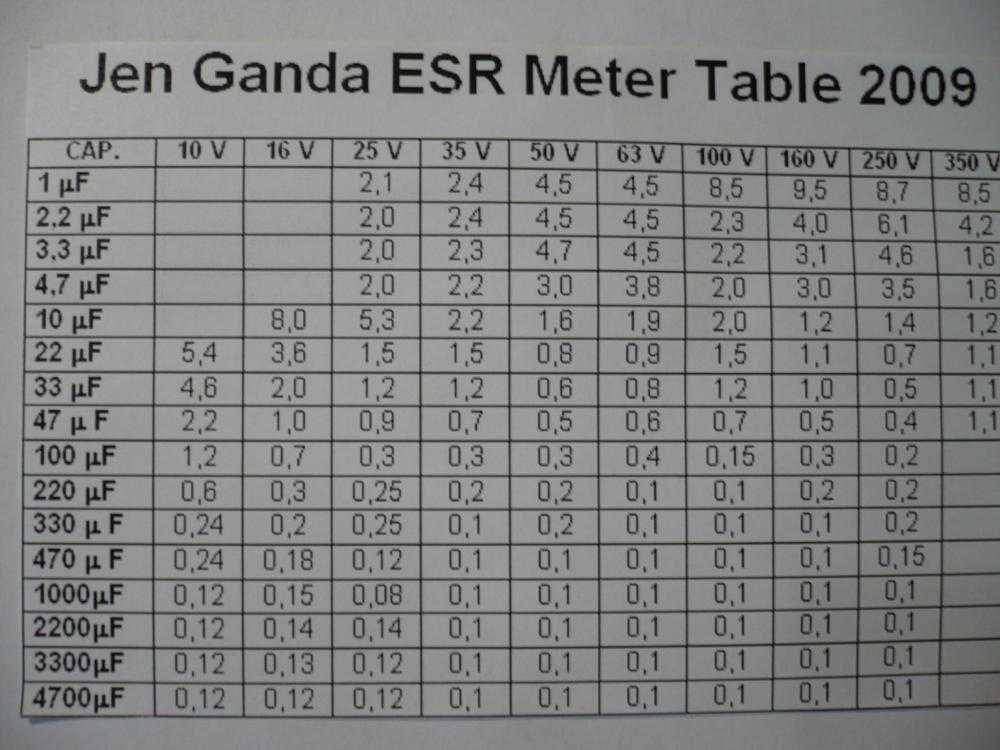 А если надо измерить ёмкость в несколько тысяч микрофарад?

В этом случае необходимо использовать комбинированные приборы — измерители ёмкости и ESR. Существует множество разновидностей таких приборов и приборчиков.

Автор использует в своей практике мультитестер с АлиЭкспресс.

Кроме измерения ESR и ёмкости, им можно проверять полупроводниковые приборы, сопротивления и индуктивности.

Удобная штука, доложу я вам!

Если проверять вздутые электролитические конденсаторы — выяснится, что у них повышенное ESR и сниженная емкость.

Иногда тестер вообще дают ошибку, не опознавая конденсатор как конденсатор. Может быть и так, что конденсатор по внешнему виду абсолютно нормальный, но имеет повышенное ESR (хотя и достаточную емкость).

Поэтому в блоке питания он нормально работать не будет!

Заканчивая, отметим, что конденсаторы небольшой ёмкости, использующиеся в «дежурке» компьютерного блока питания, имеют очень небольшие габариты. Электролита у них внутри немного, поэтому у них «не хватает силы» вздуться.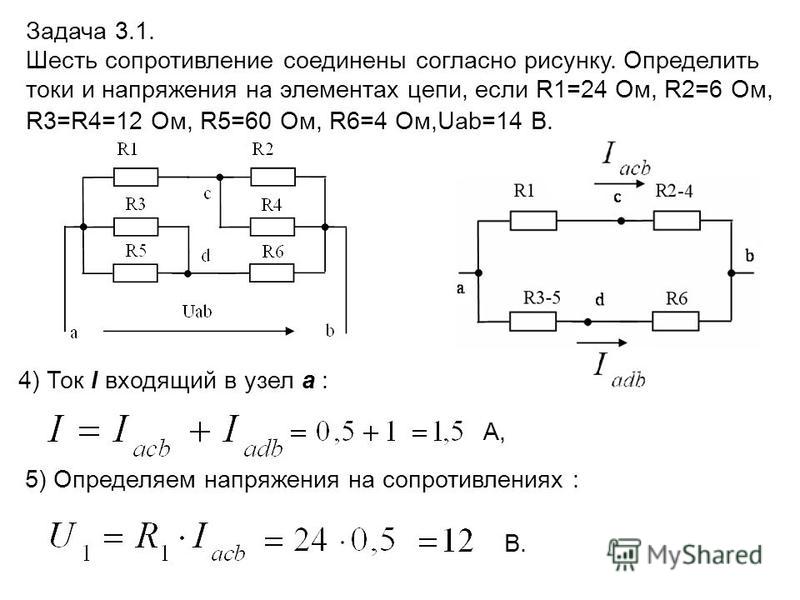

До встречи на блоге!

Роль конденсатора в аудиосистеме | журнал АвтоЗвук

Любая аудиосистема без источника питания — ничто, поэтому начинается она в автомобиле с аккумулятора. Однако возможности аккумулятора не безграничны, поэтому, начиная с некоторого момента, увеличение громкости приводит не только к миганию фар в такт музыке, но и к заметному искажению звучания. Применение силовой проводки большого сечения или специальных аккумуляторов только оттягивает этот момент, но полностью не исключает. Вот тут (или даже раньше) понадобится конденсатор.

Происхождение этого термина окутано тайной. Лингвисты эту загадку пока игнорируют. С легкой руки радиолюбителей этот «узкоспециальный» термин распространился и среди поклонников car audio.

Любой источник напряжения (в том числе, и аккумулятор, и генератор) обладает определенным внутренним сопротивлением, в результате чего напряжение на его выходе зависит от нагрузки. Чем больше внутреннее сопротивление, тем сильнее снижается выходное напряжение с увеличением тока нагрузки. Обладают сопротивлением и провода питания, и кузов.

Схема питания аудиосистемы приведена на рисунке. Для простоты «чисто автомобильные» цепи не показаны, а сопротивление кузова приведено к сопротивлению линий связи. Внутреннее сопротивление компонентов обозначено как r_i, сопротивление линий связи — как r_s.

Внутреннее сопротивление генератора достаточно велико, но его выходное напряжение поддерживается реле-регулятором. К сожалению, «таблетка» контролирует напряжение на клеммах встроенного выпрямителя (в точке A), а не на клеммах аккумулятора (точка B), и это еще один повод содержать генератор и проводку от него до аккумулятора в порядке.

Выходное сопротивление исправного заряженного аккумулятора мало (тысячные доли ома). На этом, кстати, основан контроль аккумуляторов нагрузочной вилкой — просто и наглядно. Ток в сотни ампер аккумуляторы разных типов переносят по-разному, но при нагрузке до нескольких десятков ампер снижение напряжения малозаметно.

Однако низкое внутреннее сопротивление свойственно аккумуляторам только при постоянной или медленно изменяющейся нагрузке. Ток, потребляемый мощными усилителями класса AB, быстро изменяется в достаточно широком диапазоне, и аккумулятор просто не успевает отдать нужный ток. Время реакции зависит от скорости ионных процессов (то есть от типа и состояния аккумулятора), и составляет у штатных батарей до нескольких десятых долей секунды. У специальных «аудиофильских» аккумуляторов этот показатель заметно меньше.

Однако даже сотые доли секунды — это много. За это время усилитель, оставшись «на голодном пайке», ограничивает сигнал. Вот в этот момент и нужна помощь конденсатора. Хотя накопленная им энергия не идет ни в какое сравнение с запасенной в аккумуляторе, именно эти сотые доли секунды определяют правильность воспроизведения импульсных сигналов, из которых и состоит музыка.

Кроме того, не надо забывать и о сопротивлении проводов. Чтобы полностью использовать все преимущества, которые дает конденсатор, он должен быть установлен как можно ближе к основному потребителю энергии (то есть усилителю). Если усилителей несколько, лучше для каждого из них использовать отдельный конденсатор. Необходимая емкость конденсаторов определена эмпирическим путем и составляет примерно 0,5—1,0 Ф на каждый киловатт выходной мощности усилителя.

Подобно аккумуляторной батарее, конденсатор накапливает энергию. Но в то время как аккумулятор накапливает и отдает энергию в результате электрохимических реакций, конденсатор накапливает энергию в виде электростатического заряда. Именно различие в принципе действия делает конденсатор полезным компонентом аудиосистемы.

Простейший конденсатор состоит из двух пластин (обкладок), разделенных изолятором. Когда конденсатор присоединен к источнику напряжения, одна обкладка теряет электроны и приобретает положительный заряд, вторая получает электроны и приобретает отрицательный заряд. В итоге конденсатор накапливает электростатический заряд. Когда конденсатор разряжают, происходит обратный процесс. В обоих случаях ток течет во внешней цепи, поскольку обкладки разделены изолятором.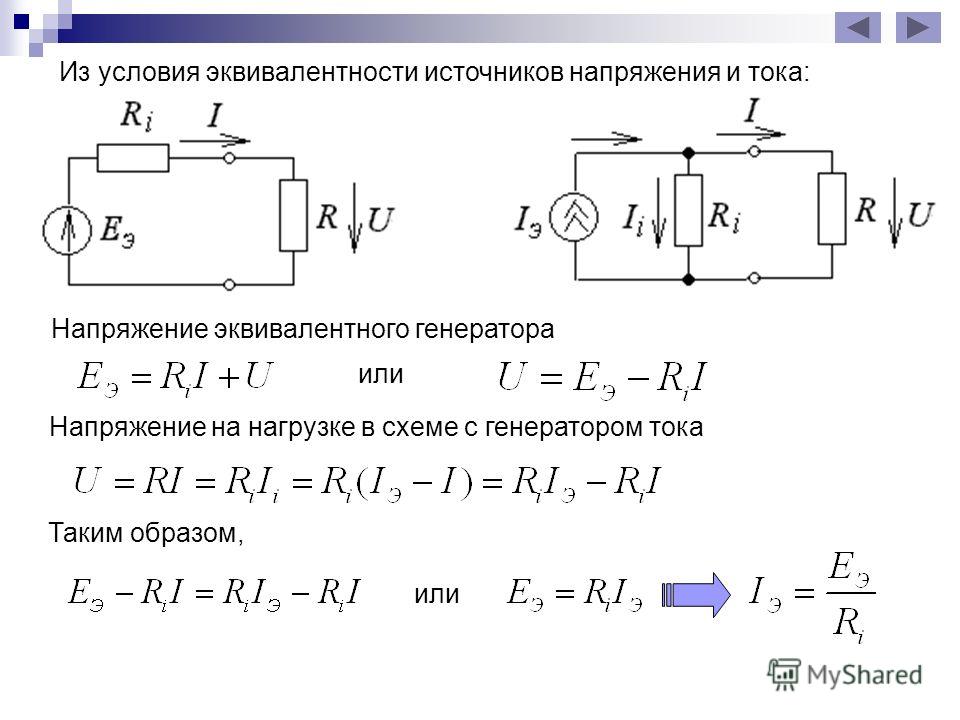

Накопленная конденсатором энергия измеряется в джоулях и описывается следующей формулой:

V — напряжение в вольтах, C — емкость в фарадах.

Таким образом, заряд пропорционален квадрату напряжения и емкости конденсатора. Емкость конденсатора определяет количество запасенной энергии, с другой стороны энергия определяется произведением мощности на время работы. Здесь можно провести параллель с емкостью аккумулятора в ампер-часах.

Емкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между ними. Вследствие этого конденсаторы большой емкости должны иметь обкладки значительной площади, разделенные очень тонким промежутком.

Электролитические конденсаторы

Электролитические (оксидные) конденсаторы стали первыми конденсаторами большой емкости. Их конструкция за последние семьдесят лет не претерпела значительных изменений. Обкладки выполнены из тонкой алюминиевой фольги, покрытой оксидным слоем, и разделены слоем электролита. Для увеличения рабочей поверхности фольга скатана в рулон, поэтому большинство конденсаторов имеет цилиндрическую форму и относительно небольшой объем.

Электрохимические конденсаторы

В последние годы в развитии конденсаторов произошел гигантский скачок. Появились двухслойные электрохимические конденсаторы (Electrochemical Double Layer Capacitors, сокращенно EDLC). В печати также используют термины суперконденсатор (supercap) или ультраконденсатор (ultracap). В отечественной практике используется термин ионистор, отражающий другую особенность этих приборов — участие ионов в формировании заряда.

Новые конденсаторы используют принцип, открытый еще в 50-е годы прошлого века. Для увеличения площади обкладок используются пористые угольные электроды, разделенные сепаратором (рис.1). Суммарная площадь пор может достигать площади футбольного поля. Поэтому запасаемая энергия в среднем в 300 раз больше, чем у электролитических конденсаторов тех же габаритов.

Напряжение пробоя ионисторов не превосходит нескольких вольт, поэтому для получения нужных рабочих напряжений используется последовательное соединение отдельных конденсаторов.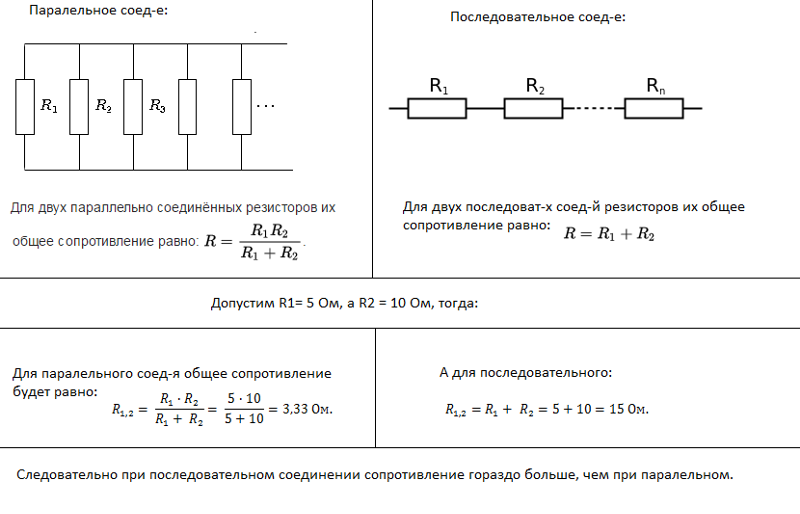 Обычно в цепочке 6-8 элементов. Чтобы уравнять напряжения на отдельных элементах этой батареи, каждый из них шунтируется резистором. Такая батарея создает некоторую нагрузку на аккумулятор и может привести к его разряду при длительных перерывах в работе. Поэтому во многих конденсаторах предусмотрена схема управления включением.

Потери в конденсаторах

Теоретически в конденсаторе два источника потерь: эквивалентное последовательное сопротивление (Equivalent Sereis Resistance, ESR) и эквивалентная последовательная индуктивность (Equivalent Sereis Inductance, ESL). Обычно вместо двух отдельных параметров используют обобщенный — эквивалентное реактивное сопротивление потерь (Equivalent Sereis Reactance, ESR). Именно этот фактор является ограничивающим в тех случаях, когда от конденсатора требуется получить продолжительный разряд.

Идеальный конденсатор не имеет сопротивления, поэтому при коротком замыкании заряженного конденсатора ток достигнет бесконечного значения в течение ничтожно малого промежутка времени.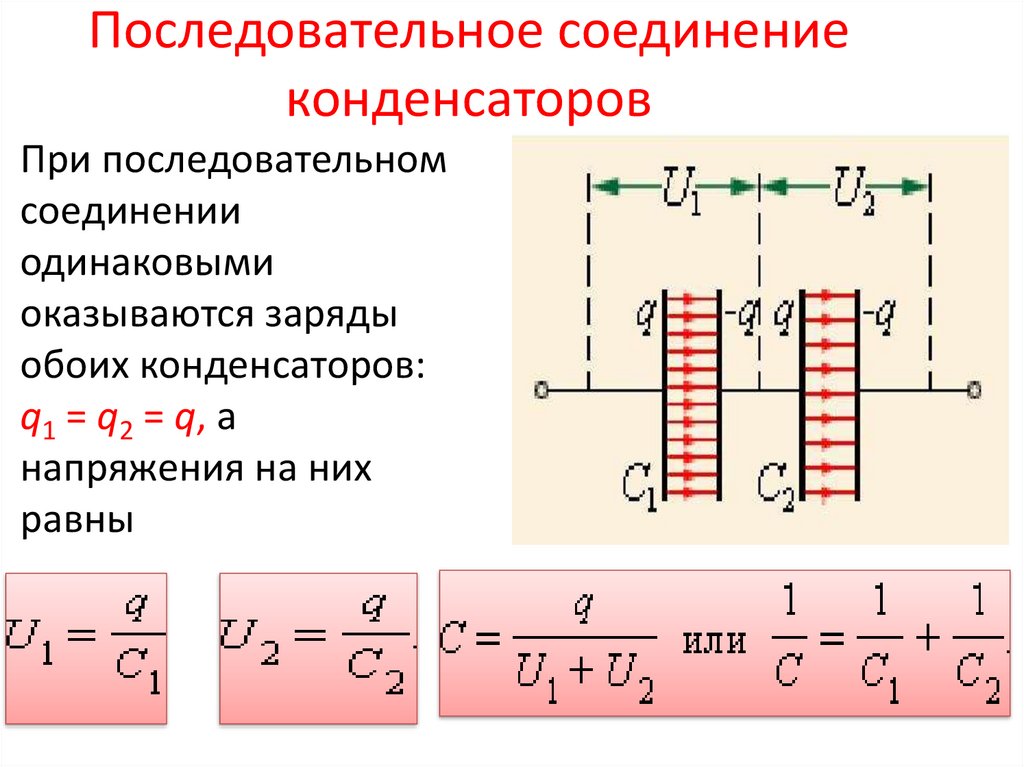 В реальном конденсаторе ток короткого замыкания ограничивается эквивалентным сопротивлением потерь в полном соответствии с законом Ома:

Например, конденсатор, имеющий сопротивление потерь 0,01 Ом, заряженный до напряжения 14 вольт, в состоянии отдать ток до 1400 А. В действительности мы не устраиваем короткое замыкание, поэтому отдаваемый ток зависит от разности двух напряжений — напряжения бортовой сети без нагрузки и этого же напряжения под нагрузкой. Тот же конденсатор при разряде до напряжения 11 вольт отдаст ток (14‑11)/0,01=300 А. Значение имеют также и другие параметры, прежде всего время переходного процесса (нарастания тока нагрузки).

Рулон фольги в традиционных электролитических конденсаторах обладает заметной индуктивностью. Ее можно снизить при смешанном соединении электродов или использовать бифилярную намотку (в чередующихся направлениях). Ионисторы и без этих ухищрений имеют относительно низкое эквивалентное реактивное сопротивление потерь.
Приводимые далее результаты исследований помогут разобраться, в каких случаях конденсатор окажет реальную помощь, а каких его применение не даст ощутимого эффекта. Материал позаимствован из журнала Car Audio & Electronics за ноябрь 2002 г. (Robert Zeff, «Stiffing Capasitors«). В роли подопытных кроликов выступили конденсаторы, выпускаемые ведущими производителями аудиотехники: Alumapro, Phoenix Gold, Xstatic.

От переводчика:

Сокращённый перевод не является буквальным изложением статьи, оставлены только технические подробности, без излишней патетики. Попытка полностью сохранить стиль оригинала заставила бы предположить, что читатели обучались в школе для детей, мягко скажем, не совсем обычных, где обучение заканчивается на началах арифметики, а названия физических величин вызывают буйный восторг. Ерничать по этому поводу уже поздно — наше образование за прошедшие двадцать лет успешно приблизилось к американскому…

Характеристики при постоянной нагрузке

В тесте, имитирующем соревнования по SPL, измерялась мощность и искажения сигнала. Хотя мощность была далека от той, которая используется на реальных соревнованиях, результаты будут аналогичными.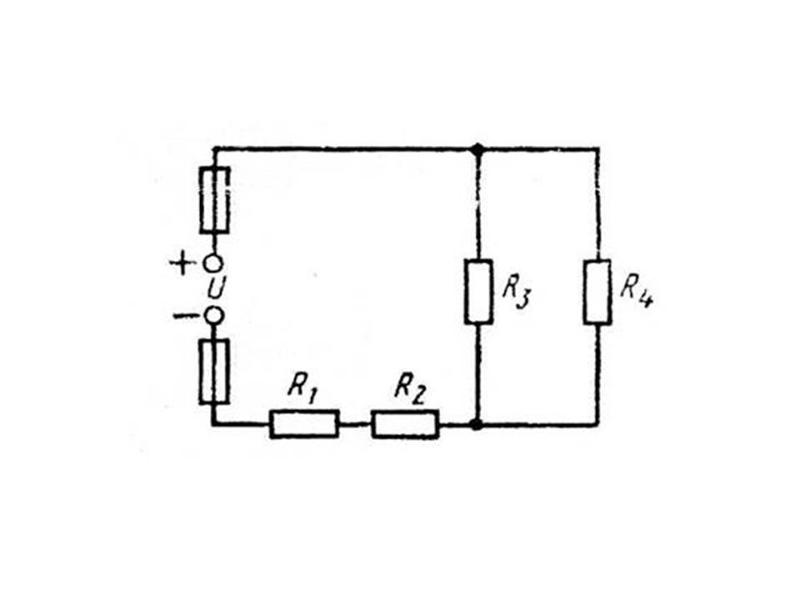 Использовался синусоидальный сигнал частотой 50 Гц, усилитель доводился до заметного клиппирования. Измерения проводились с буферным конденсатором емкостью 50 фарад и без него.

В результате оказалось, что напряжение питания в обоих случаях снижается на 1,4 В. Запасенная конденсатором энергия некоторое время поддерживает напряжение батареи, но этого времени явно недостаточно, чтобы существенно повлиять на выходную мощность. Добавление конденсатора увеличивает мощность всего на три ватта, меньше, чем на один процент.

Измерялся также уровень пульсаций напряжения питания и выходная мощность при гармонических искажениях 20%. Прибавка мощности с конденсатором составила всего несколько ватт.

Результат станет понятным, если обратиться к формуле, описывающей время заряда или разряда конденсатора:

Например, при разряде током 50 А напряжение на конденсаторе емкостью 50 Ф снижается со скоростью 1 вольт в секунду. Если ток разряда возрастет до 500 А, напряжение на конденсаторе снизится на 1 вольт уже за 1/10секунды.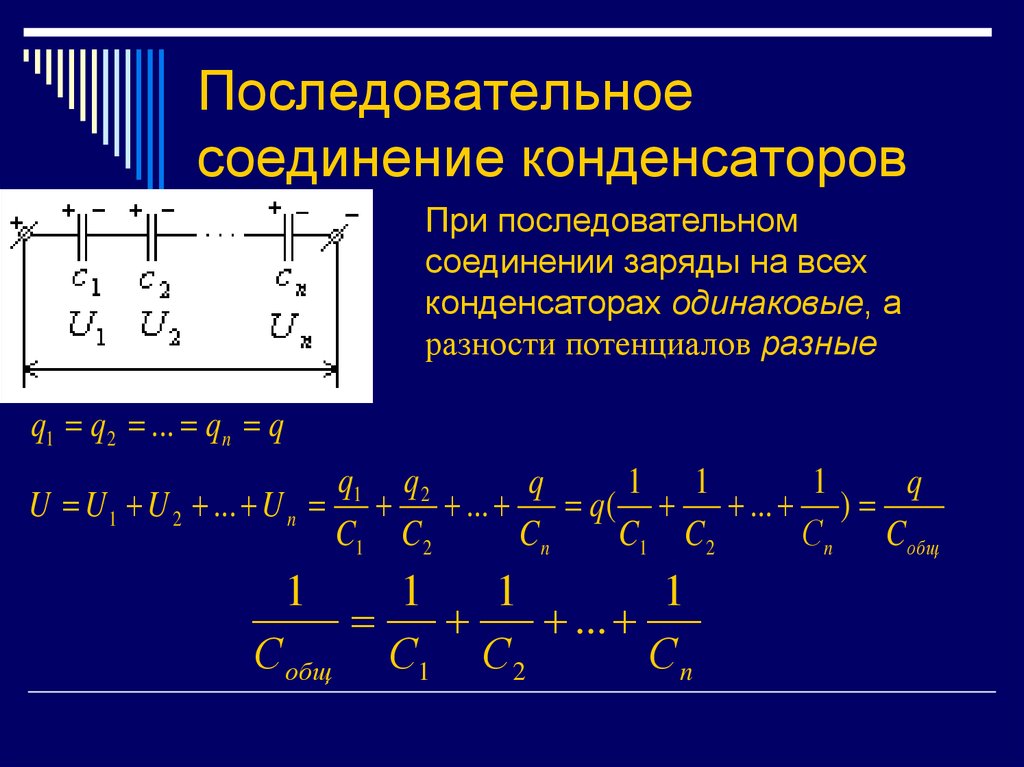 Таким образом, заметно улучшить характеристики аккумулятора при разрядке большим током могут только гиперконденсаторы емкостью в сотни фарад.

С другой стороны, в усилителе уже есть несколько накопителей энергии — входные и выходные фильтры питания, в составе которых есть дроссели и конденсаторы. В случае использования усилителя со стабилизированным источником питания эффект от внешних фильтров будет еще меньше. Поскольку запасенная энергия пропорциональна квадрату напряжения, внутренние буферные конденсаторы в цепях вторичного (повышенного) напряжения гораздо эффективнее. В чем же тогда польза буферных конденсаторов в цепи первичного напряжения?

Характеристики при импульсной нагрузке

В этом тесте усилитель воспроизводил импульсный сигнал, длительность пачки импульсов составляла 300 миллисекунд. Видно, что просадка напряжения с конденсатором вдвое меньше.

Поскольку аккумулятор запасает намного больше энергии, чем конденсатор, его последовательное сопротивление потерь также намного выше. Как и в случае конденсатора, оно ограничивает максимальный ток батареи. Конденсатор берет на себя часть нагрузки, продлевая тем самым жизнь батарее.

Стабилизация напряжения бортовой сети

Приведенные выше результаты получены при работе от аккумулятора, без участия генератора и системы зарядки, то есть при напряжении около 12 вольт. Что же произойдет, если идет зарядка батареи: генератор работает и напряжение в системе более 14 вольт?

Внутреннее сопротивление батареи во время зарядки сильно возрастает. Ее номинальное напряжение составляет 12 вольт, именно при нем она обеспечивает номинальный ток нагрузки. У свежезаряженной батареи напряжение несколько выше, но быстро снижается до 12 вольт под нагрузкой. Кроме того, батарея не может отдать большой ток, пока напряжение не снизится до 12 вольт.

В те моменты, когда усилитель потребляет большой ток, напряжение бортовой сети моментально снижается до 12 вольт. Это вызвано тем, что встроенный в генератор регулятор напряжения не успевает отслеживать быстрые изменения тока нагрузки. Легко заметить, что зарядный ток в эти моменты отсутствует, более того — энергию для потребителей поставляет в основном аккумулятор.

В остальные периоды времени внутреннее сопротивление бортовой сети складывается из выходного сопротивления генератора и сопротивления проводки. Подключение конденсатора заметно снижает колебания напряжения.

Таким образом, суперконденсатор выступает в роли стабилизатора напряжения. Кроме того, он снижает уровень помех. Особенно это актуально в тех случаях, когда усилитель установлен в багажнике. Протекающие по длинным проводам питания импульсы тока могут вызвать наводки в несимметричных RCA-кабелях, что приведет к росту гармонических искажений на низких частотах. В некоторых случаях искажения возрастают до 0,5%. Если установить конденсатор непосредственно возле усилителя, это уменьшит импульсный ток, протекающий в цепях его питания, и снизит искажения.

ВЫВОДЫ

Буферные конденсаторы вряд ли окажут существенную помощь участникам — SPL-состязаний, хотя и стабилизируют напряжение питания головных устройств и сигнальных процессоров. Однако они расширяют возможности батареи и обеспечивают неискаженную передачу импульсных сигналов, снижают коэффициент гармоник на низких частотах и будут весьма полезны поклонникам чистого звучания.

Теги: конденсаторсуперконденсатор

Частотные характеристики конденсаторов. Импеданс и ESR

   Частотные характеристики конденсаторов являются важными параметрами, которые необходимы для разработки схем. Понимание частотных характеристик конденсатора позволит вам определить, например, какие шумы может подавлять конденсатор или какие флуктуации напряжения цепи питания он может контролировать. Эта статья описывает два типа частотных характеристик: |Z| (импеданс или полное сопротивление) и ESR (эквивалентное последовательное сопротивление конденсатора).

   Импеданс Z идеального конденсатора определяется формулой 1, где ω — угловая частота, а C — емкость конденсатора.

Рисунок 1. Идеальный конденсатор

(1)

   Из формулы 1 видно, что с увеличением частоты импеданс конденсатора уменьшается.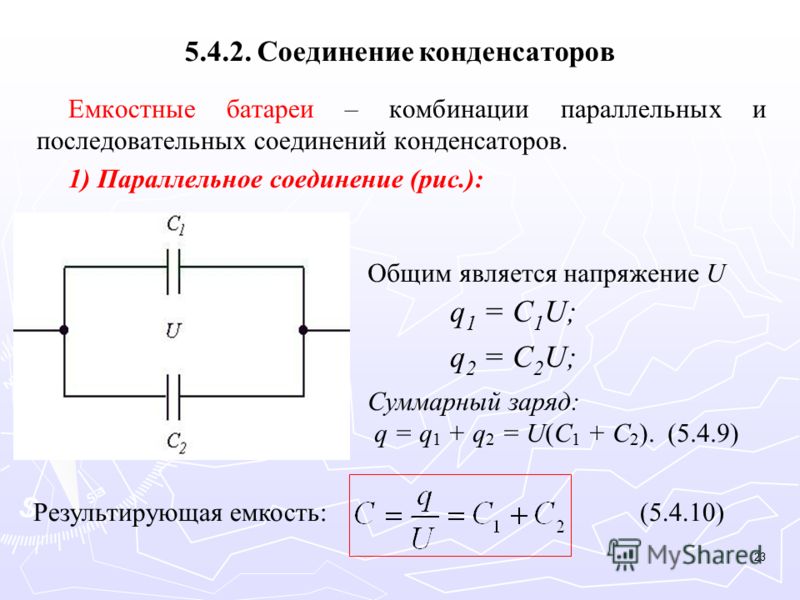 Это показано на рисунке 1. В идеальном конденсаторе нет потерь и эквивалентное последовательное сопротивление (ESR) равно нулю.

Рисунок 2. Частотная характеристика идеального конденсатора

   В реальном конденсаторе (рис. 3) существует некоторое сопротивление (ESR), вызванное диэлектрическими потерями, потерями на сопротивлении обкладок конденсатора и потерями связанные с сопротивлением утечки, а также паразитная индуктивность (ESL) выводов и обкладок конденсатора. В результате частотная характеристика импеданса принимает V образную форму (или U образную в зависимости от типа конденсатора), как показано на рисунке 4.Также на рисунке показана частотная характеристика ESR.

Рисунок 3. Реальный конденсатор

Рисунок 4. Пример частотной характеристики реального конденсатора

   Причина, по которой графики |Z| и ESR имеют такой вид как на рисунке 4, можно объяснить следующим образом.

Низкочастотная область

   |Z| в этой области уменьшается обратно пропорционально частоте, как и в идеальном конденсаторе.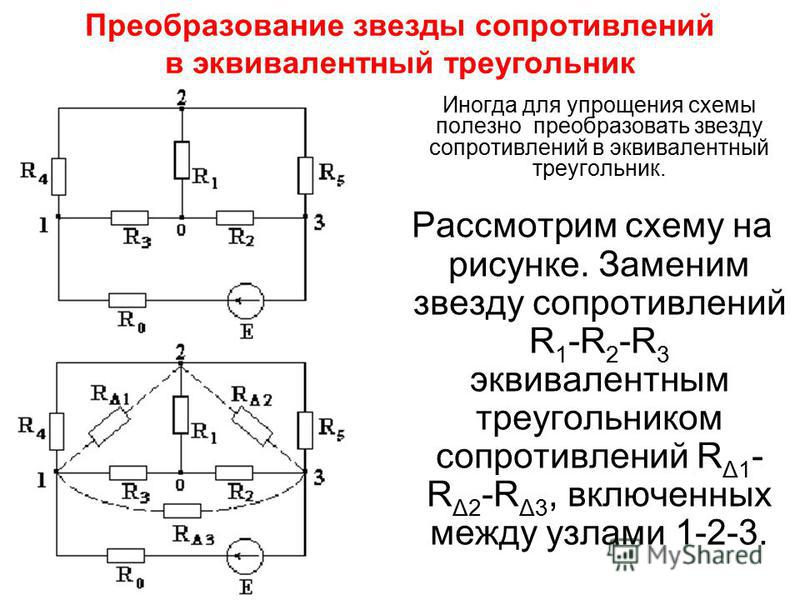 Значение ESR определяется диэлектрическими потерями в конденсаторе.

Область резонанса

   При повышении частоты ESR, в результате паразитной индуктивности, сопротивления электродов и других факторов, вызывает отклонение |Z| от идеальной характеристики (красная пунктирная линия) и достигает минимального значения. Частота, на которой |Z| достигает минимума, называется собственной резонансной частотой и на этой частоте |Z| = ESR. После превышения собственной частоты резонанса, характеристика элемента меняется с емкостной на индуктивную и |Z| начинает повышаться. Область ниже собственной резонансной частоты называется емкостной областью, а область выше — индуктивной.
   В области резонанса к диэлектрическим потерям добавляются потери на электродах.

Высокочастотная область

   При дальнейшем увеличении частоты характеристика |Z| определяется паразитной индуктивностью конденсатора. В высокочастотной области |Z| увеличивается пропорционально частоте, согласно формуле 2.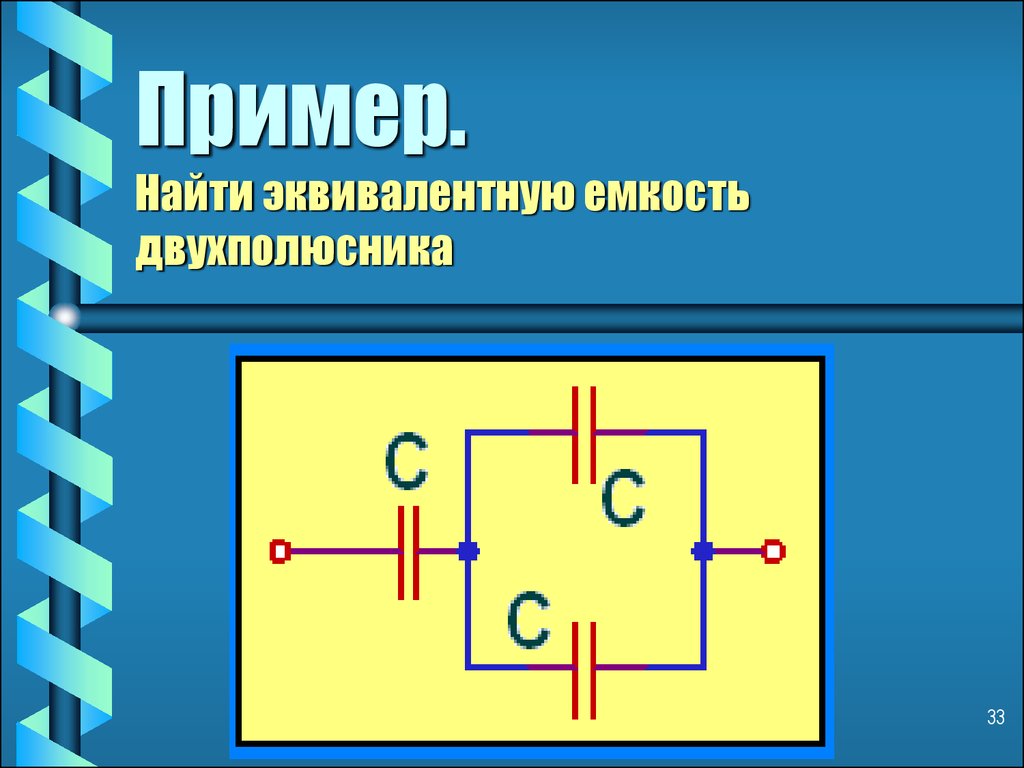 Что касается ESR, в этой области начинают проявляться скин-эффект , эффект близости и другие.

(2)

   Итак, мы рассмотрели частотную характеристику реального конденсатора. Здесь важно запомнить, что c повышением частоты ESR и ESL уже нельзя игнорировать. Поскольку существуют большое количество приложений, в которых конденсаторы используются на высоких частотах, ESR и ESL становятся важными параметрами, характеризующими конденсатор помимо значения его емкости.

   Паразитные составляющие реальных конденсаторов имеют различное значение в зависимости от их типа. Давайте посмотрим на частотные характеристики разных конденсаторов. На рисунке 5 показаны графики |Z| и ESR для конденсаторов емкостью 10 мкФ. Все конденсаторы, кроме пленочных, планарные (SMD).

Рисунок 5. Частотные характеристики конденсаторов разных типов.

   Для всех типов конденсаторов |Z| ведет себя одинаково до частоты 1 кГц. После 1 кГц импеданс увеличивается сильнее в алюминиевых и танталовых электролитических конденсаторах, чем в монолитных керамических и пленочных конденсаторах.
   Это происходит из-за того, что алюминиевые и танталовые конденсаторы имеют высокое удельное сопротивление электролита и большое ESR. В пленочных и монолитных керамических конденсаторах используются металлические материалы для электродов и, следовательно, они обладают очень маленьким ESR.
   Монолитные керамические конденсаторы и пленочные показывают примерно одинаковые характеристики до точки собственного резонанса, но у монолитных керамических конденсаторов резонансная частота выше, а |Z| в индуктивной области ниже.
   Эти результаты показывают, что импеданс монолитных керамических конденсаторов SMD типа в широком диапазоне частот имеет небольшое значение. Это делает их наиболее подходящими для высокочастотных приложений.

   Существует также несколько типов монолитных керамических конденсаторов, изготовленных из различных материалов и имеющих различную форму. Давайте посмотрим, как эти факторы влияют на частотные характеристики.

ESR

   ESR в емкостной области зависит от диэлектрических потерь, вызванных материалом диэлектрика. 2-й класс диэлектрических материалов на основе сегнетоэлектриков имеет высокую диэлектрическую постоянную и, как правило, высокое ESR. 1-ый класс материалов — температурно-компенсированные материалы на основе параэлектриков — имеют низкие диэлектрические потери и низкое ESR.
На высоких частотах в области резонанса и индуктивной области, в дополнение к сопротивлению материала электродов, их форме и количеству слоев, ESR зависит от скин-эффекта и эффекта близости. Электроды часто делают из Ni, но для дешевых конденсаторов иногда применяют Cu, который тоже имеет низкое сопротивление.

ESL

   ESL монолитных керамических конденсаторов сильно зависит от внутренней структуры электродов. Если размеры внутренних электродов задаются длиной, шириной и толщиной, то индуктивность ESL может быть определена математически. Значение ESL уменьшается, когда электроды конденсатора короче, шире и тоньше.
   На рисунке 6 показана связь между номинальной емкостью и резонансной частотой различных типов монолитных керамических конденсаторов.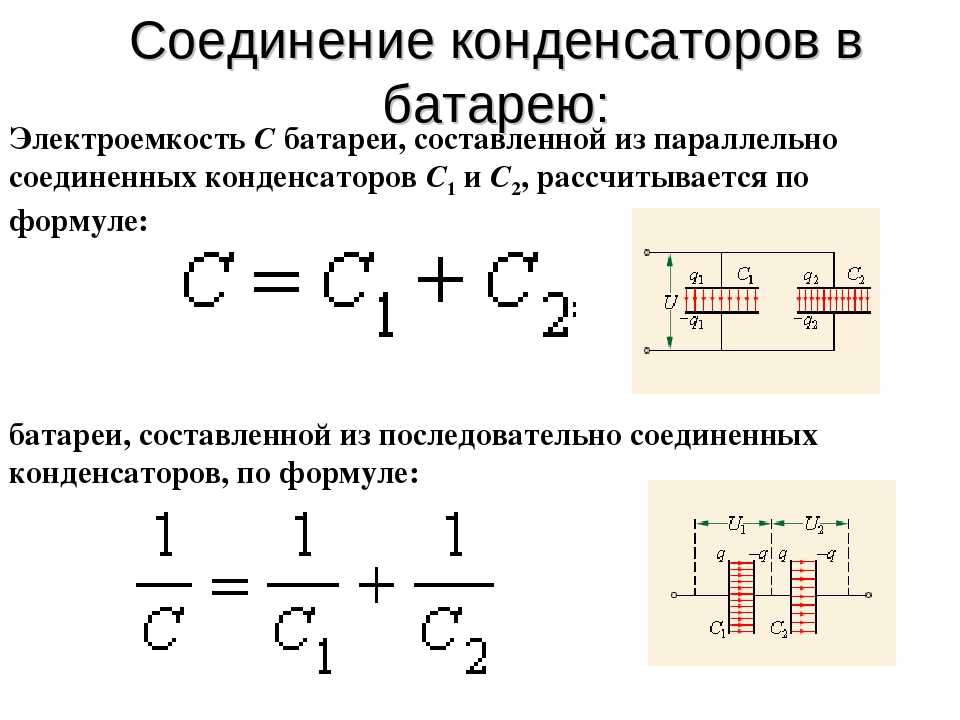 Вы можете видеть, что при уменьшении размеров конденсатора собственная резонансная частота увеличивается, а ESL уменьшается для одинаковых значений емкости. Это означает, что небольшие конденсаторы короткой длины лучше подходят для высокочастотных приложений.

Рисунок 6.

   На рисунке 7 показан обратный LW конденсатор с короткой длиной L и большой шириной W. Из частотных характеристик, показанных на рисунке 8, можно увидеть, что LW конденсатор имеет меньший импеданс и лучшие характеристики, чем обычный конденсатор такой же емкости. С помощью LW конденсаторов можно достичь тех же характеристик, как у обычных конденсаторов, но меньшим числом компонентов. Уменьшение числа компонентов, позволяет сократить расходы и уменьшить монтажное пространство. 

Рисунок 7. Внешний вид обратного LW конденсатора.

Рисунок 8. |Z| и ESR обратного LW конденсатора и конденсатора общего назначения

По материалам фирмы Murata. 
Вольный перевод ChipEnable. Ru

Эквивалентные схемы и имитационные модели

Современное измерительное оборудование, такое как анализатор импеданса HP4195A и аналогичные приборы, позволяет компьютеризировать создание эквивалентных схем и их оптимизацию. Постоянные параметры индуктивности L, емкости C и сопротивления R необходимы для моделирования электронных схем. Неправильный подход к определению схемы замещения приводит к ошибочным или некорректным результатам моделирования.

Эквивалентные параметры схемы никоим образом не являются юридически обязывающими, точными наблюдаемыми характеристиками, но показывают пользователю примерное положение основных допусков. Тот факт, что эти данные ранее были недоступны, во многом связан с традициями тестирования и маркетинга, которые в будущем должны быть заменены усилиями по обеспечению удобства для пользователя.

Электронные компоненты, резисторы, конденсаторы, катушки индуктивности, проводники, приближенные к ферритовым материалам и изоляционным материалам могут быть адекватно охарактеризованы параметрами переменного тока. Условием является то, что их свойства не изменяются заметно при различных уровнях высокого напряжения и тока или чтобы они работали в малом диапазоне сигналов. Затем говорят о линейных компонентах, а не о нелинейных компонентах, таких как варисторы, диоды, транзисторы и т. д. Другой. Проводники генерируют магнитные поля за счет протекания тока и обладают частичной индуктивностью благодаря энергии, запасенной в этих магнитных полях. Конечная проводимость меди, серебра и т. д. или проводимость многослойных резисторов
, генерируемые локально, приводят к частичному сопротивлению. Параллельные проводники также можно рассматривать как участки высокочастотных линий на высоких частотах, обладающие волновым сопротивлением, временем прохождения сигнала и, возможно, затуханием сигнала.

Реальность вообще чрезвычайно сложна. Если бы кто-то захотел нарисовать или даже рассчитать микроскопически тонкую схему со всеми парциальными сопротивлениями, емкостями или индуктивностями, он был бы обречен на неудачу. К счастью для пользователя, можно легко найти точные эквивалентные схемы для конденсаторов и катушек индуктивности без железных или ферритовых сердечников. Также хорошо описываются аппроксимации других индуктивных составляющих, усредненные параметры которых намного лучше неизвестных характеристик. Реальные значения измерений в виде кривых сравниваются с моделями эквивалентных схем, чтобы продемонстрировать пользователю получение этих значений. Это особенно относится к ферритам ЭМС, с которыми подавляются помехи, но не формируется точная схема.

2.1 Наиболее важные типы эквивалентных схем

Конденсаторы → серии резонанс

Рис. 1.39: серии резонансной цепи и импедант на частоту

индуктивность выводов L _s (порядка нескольких нГн) и сопротивление дорожек R _s (тип. порядка 20 мОм…100 мОм, для конденсаторов с холодным электролитом до 1 Ом). На низких частотах преобладает емкостная составляющая, на собственной резонансной частоте

сопротивление пути можно измерить.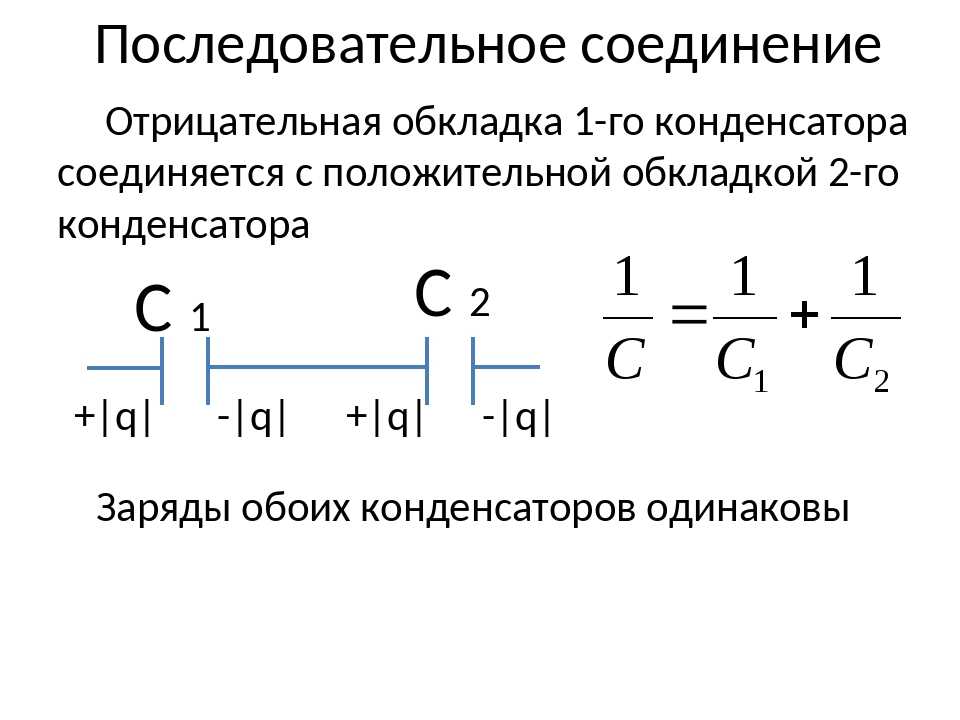 Выше последовательного резонанса преобладает индуктивная составляющая, на которую в некоторой степени может влиять наличие коротких соединительных длин. Фазовая кривая изменяется от ≈ –90° до ≈ +90° в области резонанса. Таким образом, фазовая точка 0° точно определяет точку резонансной частоты, часто гораздо точнее, чем это возможно с помощью измерения амплитуды. Фазовая кривая также служит для компьютерного определения схемы замещения (1-е приближение).

Индуктивность → Параллельный резонанс

Рис. 1.40: Параллельная цепь и импеданс на частоту

Идеальное индуктивное индуктивное давление L _P влияет на недоировку для верожественного веруния. потерь (материал сердечника, потери в обмотках). Для катушек индуктивности желательно бесконечно большое параллельное сопротивление R _p , для ЭМС ферритов наоборот очень малое и широкополосное сопротивление R _p – желаемый параметр. Индуктивность L _p играет меньшую роль и является ключом к преобразованию резистивных потерь в линию.

Это означает, что в модели на месте феррита ЭМС разрезана линия и вставлена ​​эквивалентная схема. Компонент точно описывается только всеми тремя параметрами L, C и R. Одного параметра недостаточно, хотя для известных конфигураций можно предсказать другие свойства.

Представьте себе трехмерную систему координат с осями R _стр. , L _стр. , С _стр. ; компонент представляет собой точку в этом пространстве, а его поле допуска представляет собой прямоугольное тело. Различные компоненты расположены в этом пространстве допусков как разные точки.

Рис. 1.41: Пространство допусков

Эта математическая обработка последовательного и параллельного резонанса может быть резюмирована следующим образом: во все значения L, C и R включены. Стандартизированная расстройка унифицирует параметры добротности и резонансной частоты f _РЕС . Это облегчает описание поведения резонансных систем в их частотном диапазоне

(Δf … отклонение частоты от резонансной частоты)

Последовательные резонансные контуры:

Рис. 1.42: 1 + jΩ (величина и фаза) в зависимости от Ом

Параллельные резонансные контуры:

0003

Параллельный резонанс

Резонансные условия:

для серии резонанса:

Для параллельного резонанса:

Нормализованный резонанс:

для серии резонанс:

для параллелизации:

. обозначает, насколько резонансный контур расстроен по сравнению с навязанными колебаниями. Вкратце: Мера отклонения частоты (контура) от резонансной частоты (контура).

Нормализованные кривые представлены на рисунках 1.42 и 1.43 для R = 1 (верхняя амплитуда, нижняя фаза).

Выбрав подходящие операнды (нормализация), можно изобразить все характеристики в виде двух стандартных кривых. Они служат для обеспечения общего понимания, в то время как в приложениях оцениваются измеренные резонансные кривые или в компьютерном моделировании численные значения L, R и C.

Вывод простых эквивалентных схем кривые, полученные с HP 4195 анализируются. Однако в принципе не имеет значения, с помощью какого измерительного прибора или конфигурации получаются кривые.
Анализ основан на фундаментальных концепциях теоретического моделирования.

Рис. 1.44: Кривая полного сопротивления катушки с 6 витками на керамическом каркасе ∅ 6 мм

На рисунке 1.44 показано полное сопротивление небольшой воздушной катушки диаметром 6 мм и 6 витками обмотки. Простая оценка индуктивности по значениям на частотах 10 МГц и 100 МГц дала L 63,7 нГн. Поскольку фаза Θ находится в пределах 85°–90°, можно принять чистую индуктивность и получить из |Z| = 4 Ом на частоте 10 МГц и |Z| = 40 Ом на частоте 100 МГц.

Анализатор измеряет L = 58 нГн благодаря более точно сохраненным значениям, чем отображаемые. На рис. 1.44 различимы только две кривые: толстая кривая измерения и одна, построенная анализатором в результате измерения эквивалентной схемы. На самом деле он включает калькулятор эквивалентной схемы. Он вычисляет эквивалентную схему, изображенную на рис. 1.44, и записывает рассчитанные значения |Z| и Θ рядом с кривой измерения. Без компьютера пришлось бы довольствоваться лишь грубым расчетом.

В вопросах ЭМС требуются многомерные меры; точность не имеет первостепенного значения.

Рис. 1.45: Кривая полного сопротивления керамического конденсатора емкостью 10 нФ с прибл. Соединительные ножки длиной 5 мм

На рис. 1.45 показана кривая импеданса керамического дискового конденсатора с номинальной емкостью 10 нФ и прибл. Соединительные ножки длиной 5 мм. Читая кривые измерения и вычисляя, можно найти C = 11,37 нФ и L = 9,55 нГн. Из |Z| кривая при Θ = –90° можно рассчитать емкость

, а при Θ = + 90° можно рассчитать индуктивную составляющую

.

|З| _{200 кГц} = 70 Ом, |Z| _{4 МГц} ≈ 3,5 Ом, C = 11,37 нФ, |Z| _{40 МГц} ≈ 2 Ом,
|Z| _{200 МГц} = 12 Ом и L = 9,55 нГн.

Последовательное сопротивление согласно измерениям составило 33,8 мОм. При правильно выбранной схеме замещения (рис. 1.45) анализатор измерил R = 33,7 мОм, C = 11,2 нФ и L = 9 нГн, и совпадающая с ней кривая показала, что никаких дополнительных паразитных параметров схемы замещения, имеющих какое-либо значение, не было. В то время как катушка на рис. 1.45 по-прежнему полезна на частоте 200 МГц, конденсатор
применим только до 30 МГц.

Отсюда видно, насколько важно учитывать линейные индуктивности в связи с блокирующими процессами. Это иллюстрирует пример на рис. 1.46.

Рис. 1.46: Влияние треугольного импульса, возникающего во время фронта переключения в логических схемах, на конденсатор с линейными индуктивностями

Если треугольный импульс достигает «голого» конденсатора без индуктивности, снижение на 25 мВ происходит за 10 нс со скругленным задним фронтом. Индуктивность линии 9Только nH добавляет биполярный импульс с крутым фронтом ±90 мВ, эффект, который наблюдал каждый, кто смотрел на свою линию питания с помощью осциллографа. Мало толку заменить 10 нФ на 1 мкФ; если индуктивность остается, шумовое напряжение остается. Чистое изменение заряда конденсатора емкостью 10 нФ за счет треугольного импульса приводит к изменению напряжения ΔU на конденсаторе.

Края тока ΔI/Δt всего при 9 нГн создают биполярный сдвиг напряжения

Рис. 1.47: Кривая импеданса и эквивалентная схема резонансного контура

В качестве примера на Рисунке 1.47 показан резонансный контур, состоящий из катушки и конденсатора, соединенных параллельно с резистором 1 кОм. Анализатор с выбранной структурой A побеждает в эквивалентной схеме. Другие структуры приводят к плохим или бесполезным приближениям. Анализатор в первую очередь пытается приблизиться к фазовой кривой. Можно вручную улучшить параметры и получить новые приближения.

В этом случае индуктивность можно определить по кривой измерения. Емкость может быть найдена только в ограниченной степени. |З| _{3 МГц} = 4 Ом, |Z| _{57,6 МГц} = 969 Ом, |Z| _{200 МГц} = 24 Ом, L _p = 207 нГн, R _p = 989 Ом, C _p = 36,4 пФ.

Тогда помогает условие резонанса:

Результаты анализатора подтверждают расчетные значения.

Рис. 1.48: Эквивалентные типы цепей от HP4195A

Рис. 1.49: Кривые импеданса при параллельном соединении двух разнородных конденсаторов (Легенда об эффективной блокировке по ВЧ)

На рис. 1.49 показана кривая импеданса при параллельном соединении двух разнородных конденсаторов. Большой конденсатор емкостью 150 нФ был дополнен небольшим конденсатором емкостью 150 пФ для улучшения блокировки по ВЧ. Он должен «сбалансировать» недостаток более длинной линии конденсатора с нагрузкой. Результатом является резонансный пик на частоте 61,57 МГц с Z 59.0 Ом (без нагрузки). Каждый крутой фронт импульса обязательно вызовет длительные затухающие колебания и значительно снизит полезность блокировки.

Получение эквивалентной схемы из |Z| кривых происходит в несколько этапов. Фазовая кривая Q сигнализирует о емкости до 2 МГц (зона I). Последовательный резонанс на частоте 2 МГц является следствием прибл. Ножки подключения конденсатора 150 пФ длиной 4 см. Схема индуктивная в зоне II для создания параллельного резонанса с 590 Ом на 60 МГц, где уже нельзя говорить о блокировке. В диапазоне от 30 МГц до 100 МГц (зона III) импеданс превышает 100 Ом и крайне вреден для внутренней связи сигнала. Конденсатор емкостью 150 пФ начинает играть роль за пределами параллельного резонанса и влияет на последовательный резонанс на частоте 154 МГц. Фазовая кривая Q наблюдается в зоне IV.

Расчетные значения
в зоне I |Z| _{600 кГц} = 2 Ом ∩ 133 нФ,
в зоне II |Z| _{20 МГц} = 6,5 Ом ∩ 52 нГн,
в зоне III резонанс 61,6 МГц C _b = 1/ω ² · L = 128,6 пФ,
в зоне IV резонанс 154,6 МГц L – 1/ω ² · C _b = 8,25 нГн

3 Эквивалент Схема получена

Рис. 1.50: Эквивалентная схема двух параллельных подключенных конденсаторов

---

ABC CLR: Глава L Индукторы

Эквивалентные циркуиты и модели симуляции — Цепь

Эк. 0002 Контент по лицензии EPCI от: Würth Elektronik eiSos, Trilogy of Magnetics, распечатки руководств можно заказать здесь.

Содержание этой страницы находится под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.

см. предыдущую страницу: Функции трансформатора

< Страница 7 >

Конденсаторы последовательно и параллельно

Конденсаторы последовательно и параллельно
Далее: Энергия, накопленная конденсаторами Вверх: Емкость Предыдущий: Диэлектрики Конденсаторы являются одним из стандартных компонентов электронных схем. Кроме того, часто встречаются сложные комбинации конденсаторов. в практических схемах. Это, поэтому полезно иметь набор правил для нахождения эквивалентной емкости некоторого общего расположения конденсаторов. Оказывается, всегда можно найти эквивалентная емкость повторным применение двух простых правил. Эти правила касаются конденсаторов, подключенных последовательно и параллельно.

Рисунок 15: Два конденсатора соединены параллельно.

Рассмотрим два конденсатора , соединенных параллельно : т.е. , с положительно заряженные пластины, соединенные с общим «входным» проводом, а отрицательно заряженные пластины, присоединенные к общему «выходному» проводу — см. рис. 15. Чему равна эквивалентная емкость между входным и выходным проводами? В этом случае потенциал разница между двумя конденсаторами одинакова и равна разность потенциалов между входным и выходным проводами. Общий заряд , однако, хранящийся в двух конденсаторах, делится между конденсаторы, так как он должен распределяться так, чтобы напряжение на два одинаковые. Так как конденсаторы могут иметь разную емкость, и , заряды и тоже могут быть разными. Эквивалентная емкость пары конденсаторов — это просто отношение , где это общий накопленный заряд. Это следует из того

(113)

давать

(114)

Здесь мы использовали тот факт, что напряжение является общим для всех трех конденсаторы. Таким образом, правило такое:

Эквивалентная емкость двух конденсаторов, соединенных параллельно представляет собой сумму отдельных емкостей.

Для конденсаторов, соединенных параллельно, уравнение (114) обобщается на .

Рисунок 16: Два последовательно соединенных конденсатора.

Рассмотрим два конденсатора , соединенных последовательно : , т. е. , в линию так, что положительная пластина одного прикреплена к отрицательной пластине другого — см. Рис. 16. В самом деле, предположим, что положительная пластина конденсатора 1 соединена к «входному» проводу минусовая пластина конденсатора 1 подключена к положительная пластина конденсатора 2 и отрицательная пластина конденсатора 2 подключен к «выходному» проводу. Какова эквивалентная емкость между входным и выходным проводами? В этом случае важно понимать, что заряд, хранящийся в два конденсатора одинаковые. Это легче всего увидеть, рассмотрев «внутренние» пластины: т.е. , отрицательная пластина конденсатора 1, и положительная пластина конденсатора 2. Эти пластины физически разъединены от остальной цепи, поэтому общий заряд на них должен Остаются неизменными. Предположим, что кажется разумным, что эти пластины несут нулевой заряд. когда к двум конденсаторам приложена нулевая разность потенциалов, следует что при наличии ненулевой разности потенциалов заряд на положительном пластина конденсатора 2 должна быть уравновешена равным и противоположным зарядом на отрицательной пластине конденсатора 1. Так как отрицательная пластина конденсатора конденсатор 1 несет заряд, положительная пластина должна нести заряд. Аналогично, поскольку положительная пластина конденсатора 2 несет заряд отрицательная пластина должна нести заряд. В результате оба конденсатора обладают одинаковым запасенным зарядом. Потенциал падает, а через два конденсатора, в общем, разные. Однако сумма этих падения равняется общему падению потенциала, приложенному к входу и выходу провода: т.е. , . Эквивалентная емкость пары конденсаторы снова . Таким образом,

(115)

давать

(116)

Здесь мы воспользовались тем, что заряд общий для всех трех конденсаторы. Отсюда правило:

Обратная величина эквивалентной емкости двух конденсаторов, соединенных в ряд представляет собой сумму обратных величин отдельных емкостей.

Для конденсаторов, соединенных последовательно, уравнение (116) обобщается на

---

Далее: Энергия, накопленная конденсаторами Вверх: Емкость Предыдущий: Диэлектрики

Ричард Фицпатрик 2007-07-14

Достижение любого сопротивления/емкости с помощью подручных компонентов

Это не просто еще один калькулятор последовательного/параллельного эквивалентного сопротивления! Эта программа рассчитывает, как комбинировать резисторы / конденсаторы, которые у вас есть в настоящее время, для достижения целевого значения сопротивления / емкости, которое вам нужно.

Вам когда-нибудь понадобился определенный резистор или конденсатор, которого у вас нет или который не существует? Не бойся! Вероятно, вы можете получить это конкретное значение сопротивления или емкости, используя уже имеющиеся у вас компоненты. Используйте эту программу вместо того, чтобы решать огромную задачу многомерной оптимизации с миллионами различных комбинаций!

Просто выберите резистор или конденсатор, введите целевое значение, введите максимальное количество компонентов, которые вы хотели бы использовать, введите список значений компонентов, которые у вас есть, и нажмите «Рассчитать»! Программа подскажет, какие компоненты использовать и как их соединить, чтобы достичь целевого значения.

Чтобы попробовать калькулятор, посетите это веб-приложение.

Чтобы просмотреть исходный код, посетите этот репозиторий Github.

Пожалуйста, дайте мне знать, если у вас есть какие-либо предложения по дальнейшему улучшению удобства использования этого инструмента дизайна!

Шаг 1: Исходная информация

Это веб-приложение было разработано по необходимости. Я конструирую множество различных схем, для которых требуются очень специфические резисторы или конденсаторы. Часто у меня нет резистора или конденсатора с таким номиналом. Иногда они даже не делают компонент с такой уникальной ценностью! Вместо того, чтобы сдаться или согласиться на что-то далекое от идеала, я решил написать программу, которая просматривает все возможные комбинации резисторов (каждое возможное значение и независимо от того, включены ли они последовательно или параллельно) и возвращает наилучшую комбинацию.

При проектировании схемы моего органа в рамках проекта «Битва оркестров» мне пришлось вручную рассчитать наилучшую комбинацию конденсаторов для достижения определенной частоты. Этот процесс был невероятно утомительным, и в конце концов я просто сдался и перешел к комбинациям конденсаторов, которые давали любую слышимую частоту. Теперь с помощью этого веб-приложения я могу настроить свой орган на определенную частоту и настроить его на ноты на клавиатуре! Приведенное ниже уравнение используется для расчета конкретной частоты и обсуждается в другом учебном проекте.

f = 1 / (0,693×C×(R1 + 2×R2))

Используя это уравнение, где R1 = 100 кОм и R2 = 10 кОм, я подсчитал, что конденсатор емкостью 27,33 нФ будет воспроизводить ноту A4 (частота 440). Гц). Используя мою программу, я смог рассчитать эквивалентное значение емкости в пределах 0,001 нФ (намного меньше, чем допуск для стандартного конденсатора), которое я могу создать, используя конденсаторы, которые у меня уже были. Полученный результат и конфигурация описаны ниже. Теперь я могу гораздо более эффективно и действенно настраивать свой орган на точные частоты стандартных нот. Хотел бы я сделать это с самого начала. Моя демо-песня на органе, наверное, звучала бы намного лучше.

Ближайшее значение: 27,329 нФ

Разница: 0,001 нФ

Конфигурация конденсатора: C0=0,068 нФ || C1=30 нФ + C2=300 нФ

Уравнения эквивалентности резистора и конденсатора

Для справки ниже приведены уравнения эквивалентности для объединения резисторов и конденсаторов в цепи.

• Резисторы, соединенные последовательно (R1 + R2): Необх. = R1 + R2
• Резисторы, соединенные параллельно (R1 || R2): Необх. = 1 / (1/R1 + 1/R2)
• C2): Ceq = 1 / (1/C1 + 1/C2)
• Параллельное подключение конденсаторов (C1 || C2): Ceq = C1 + C2

Шаг 2: Входы

Необходимо указать 4 входа:

• Если вы вычисляете значение для резистора или конденсатор.
• Целевое значение сопротивления или емкости и единицы измерения.
• Максимальное количество компонентов, которые вы хотели бы использовать для достижения целевого значения (т. е. я не хотел бы использовать более 3 резисторов для достижения целевого значения сопротивления).
• Список номиналов резисторов/конденсаторов, которые у вас есть. Эти значения должны быть в тех же единицах, что и ваше целевое значение (т. е. если ваше целевое значение было 110 нФ, все ваши значения должны быть указаны в нФ).

Шаг 3: Результат

Вы получите 3 выхода для вашего результата:

• Ближайшее значение — ближайшее значение сопротивления/емкости, которое вы смогли получить с вашими параметрами.
• Разница — насколько далеко ваше ближайшее значение от целевого значения.
• Конфигурация резисторов/конденсаторов — список номиналов используемых резисторов/конденсаторов и их конфигурация.

Шаг 4: понимание результата

В выходных данных конфигурации используются стандартные обозначения. «+» означает, что компоненты включены последовательно, а «||» означает, что компоненты параллельны. Операторы имеют одинаковый приоритет и ассоциативны слева направо, что означает, что вы группируете термины вместе, начиная слева и двигаясь вправо.

Например, взгляните на следующий результат:

Конфигурация резистора: R0=15 Ом + R1=470 Ом || R2=3300 Ом + R3=15000 Ом

Если вы будете следовать приведенным выше рекомендациям, вы увидите, что это эквивалентно следующему уравнению и изображению выше.

((R0+R1)||R2)+R3

Другие проекты

Чтобы увидеть больше проектов, посетите мои страницы:

• https://dargen.io
• https://github.com /mjdargen
• https://www.hackster.io/mjdargen
• https://www.buymeacoffee.com/mjdargen

Series and Parallel — AP Physics 1

All AP Physics 1 Ресурсы

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

AP Physics 1 Справка » Электричество и волны » Электричество » Схемы » Последовательная и параллельная

Цепь имеет резистор с сопротивлением  , за которым следуют три параллельных ответвления, каждое из которых содержит резистор с сопротивлением  . Чему равно полное эквивалентное сопротивление цепи?

Возможные ответы:

Правильный ответ:

Объяснение:

Во-первых, нам нужно рассчитать эквивалентное сопротивление трех параллельно соединенных резисторов. Для этого воспользуемся следующим уравнением:

Теперь, чтобы получить общее эквивалентное сопротивление, мы можем просто сложить два оставшихся значения, так как они идут последовательно:

Сообщить об ошибке

Рассмотрим данную цепь:

К точкам A и B приложено напряжение, так что ток течет от A к R2 и к B. Каково значение этого напряжения, если ток через R2 равен 4 А?

Возможные ответы:

Правильный ответ:

Объяснение:

Во-первых, нам нужно рассчитать ток, протекающий через резистор R2 без дополнительного напряжения. Нам нужно будет рассчитать полное эквивалентное сопротивление цепи. Поскольку два резистора включены последовательно, мы можем просто добавить их.

Затем мы можем использовать закон Ома для расчета тока в цепи:

Теперь, когда у нас есть ток, мы можем рассчитать дополнительный ток, который вносит новое напряжение:

2

На пути нового напряжения есть только один резистор (R2), поэтому мы можем рассчитать, каким должно быть это напряжение, чтобы обеспечить новый ток:

Сообщить об ошибке

Каково эффективное сопротивление этой цепи постоянного тока?

Возможные ответы:

Ни один другой ответ Объяснение:

Во-первых, давайте напомним себе, что эффективное сопротивление последовательно соединенных резисторов равно  и эффективное сопротивление параллельно подключенных резисторов равно .

Начните эту задачу с определения эффективного сопротивления резисторов 2, 3 и 4:

 (Это потому, что эти три резистора соединены последовательно. )

Теперь схему можно упростить до следующего:

 

Далее нам нужно определить эффективное сопротивление резисторов  и 6:

Опять же, схему можно упростить:

Отсюда можно определить эффективное сопротивление цепи постоянного тока, вычислив эффективное сопротивление резисторов , 1 и 5:

Сообщить об ошибке

Две лампочки, одна с классом  и одна с классом  подключены последовательно к батарее. Какой из них будет ярче? А если их подключить параллельно?

Возможные ответы:

Не хватает информации, чтобы выполнить эту проблему

Серия:

Параллель:

Серия:

Параллель:

Серия:

Параллель:

Series:

:

:

Series:

:

:

.

Ряд: 

Параллельный: 

Правильный ответ:

Ряд:

Параллельный: 

Объяснение:

Первый шаг к решению этой проблемы — выяснить, как сопротивление лампочки соотносится с номинальной мощностью. Для резистора рассеиваемая мощность равна:

Таким образом, существует обратная зависимость между сопротивлением лампочки и номинальной мощностью.

Вторым шагом является рассмотрение элементов схемы, соединенных последовательно и параллельно. Последовательно они имеют один и тот же ток; параллельно они делят одно и то же напряжение. Таким образом, для двух последовательно соединенных лампочек ярче будет та, у которой больше сопротивление (меньшая мощность), а для параллельной конфигурации ярче будет лампочка с меньшим сопротивлением (больше мощность).

Сообщить об ошибке

Если у нас есть 3 последовательно соединенных резистора, причем резистор 1 имеет сопротивление , резистор 2 имеет сопротивление , а резистор 3 имеет сопротивление , каково эквивалентное сопротивление серии?

Возможные ответы:

Правильный ответ:

Пояснение:

Общее сопротивление последовательно соединенных резисторов равно сумме их индивидуальных сопротивлений. В этом случае

Сообщить об ошибке

Вам представлены три резистора, каждый размер . В чем разница между общим сопротивлением резисторов, соединенных последовательно, и полным сопротивлением резисторов, соединенных параллельно?

Возможные ответы:

Правильный ответ:

Объяснение:

Резисторы последовательно:

Параллельные резисторы:

Сообщить об ошибке

Каково общее сопротивление трех резисторов, , , и , включенных параллельно?

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение эквивалентного сопротивления для нескольких резисторов, включенных параллельно:

Подставьте известные значения и решите.

Обратите внимание, что для параллельных резисторов общее сопротивление никогда не превышает сопротивления наименьшего элемента.

Сообщить об ошибке

Цепь создается с использованием батареи и 3-х одинаковых резисторов, как показано на рисунке. Каждый из резисторов имеет сопротивление . Если резистор удалить из цепи, как это повлияет на ток через резистор?

Возможные ответы:

Проходной ток увеличится в два раза

Проходной ток останется прежним

Проходной ток уменьшится

Проходной ток увеличится в четыре раза

Невозможно определить, не зная удельного сопротивления провода

Правильный ответ:

Ток через  уменьшится

Объяснение:

Поскольку резисторы и образуют параллельную сеть, удаление из цепи увеличивает сопротивление этой части цепи. Поскольку новая схема представляет собой последовательную комбинацию и , увеличенное сопротивление приводит к снижению тока в каждом из этих резисторов.

Сообщить об ошибке

Определите общий заряд, хранящийся в цепи с двумя одинаковыми плоскопараллельными конденсаторами, соединенными параллельно, с площадью и расстоянием между параллельными пластинами. Предположим, что пространство между параллельными пластинами представляет собой вакуум. Схема показывает разницу напряжений 10 В.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы определить общий накопленный заряд, нам нужно сложить емкость каждого конденсатора (поскольку они соединены параллельно) и умножить на разницу напряжений. Напомним, что для конденсаторов

Для конденсаторов с параллельными пластинами:

Здесь, , которая представляет собой диэлектрическую проницаемость пустого пространства,  является диэлектрической проницаемостью, которая из-за присутствия только вакуума, , которая представляет собой площадь параллельных пластин, и , что является расстоянием между пластинами.

Подставьте известные значения для определения емкости.

Каждый из двух конденсаторов имеет емкость

Поскольку конденсаторы подключены параллельно, общая емкость представляет собой сумму емкостей каждого из них. Общая емкость в цепи определяется как:

Подставьте это значение в наше первое уравнение и найдите общий накопленный заряд.

, где — общий заряд, хранящийся в конденсаторе. Начиная с

Сообщить об ошибке

Каков общий ток, протекающий через систему с 2 параллельными резисторами с сопротивлением и и аккумулятором с разностью напряжений 10 В?

Возможные ответы:

Правильный ответ:

Объяснение:

Сначала нам нужно определить общее сопротивление цепи, прежде чем мы узнаем, какой ток протекает через нее. Поскольку резисторы подключены параллельно, их сопротивления складываются обратно:

, где — общее сопротивление цепи.

Теперь, когда мы решили для , мы знаем, что ток, протекающий через цепь, можно найти с помощью закона Ома:

Сообщить об ошибке

← Предыдущий 1 2 Далее →

Уведомление об авторских правах

Все ресурсы AP Physics 1

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Learn by Concept

Лекция 8

Лекция 8 Резюме

• Закон Ома
• Электроэнергия
• Правила Кирхгофа

• Письменная викторина Гл. 20

---

Конец материала экзамена I

---



• Цепи с конденсаторами
• Конденсаторы, включенные последовательно и параллельно
Пример #1
Пример #2


• Зарядка и разрядка в цепях RC апплет
• Незаряженный конденсатор похож на провод
• Заряженный конденсатор подобен разомкнутой цепи


• Апплет схемы для схемы лампы-вспышки (проблема 21. 80)
Пример #3
Пример #4

• Результаты обучения по лекциям
  Студент, освоивший темы данной лекции, сможет:
• расчет эквивалентной емкости конденсаторов, соединенных последовательно или параллельно
• используют характеристики незаряженных и заряженных конденсаторов для прогнозирования поведения простых резисторно-конденсаторных цепей как сразу после подключения батареи, так и спустя долгое время после подключения батареи
• [Мы не будем изучать постоянную времени RC или зависящее от времени экспоненциальное поведение резисторно-конденсаторных цепей.]

Практика:
Попробуйте эти дополнительные примеры

Пример #5

Пример #6

Пример #7

Подготовить:
Прочитать раздел 22-1 учебника перед следующей лекцией

ТП4 20.49
Два конденсатора по 25 мк F и 5 µ F соединены параллельно по 100 В на каждом. Какова полная запасенная энергия?
А. 150 мкм J
Б. 0,150 Дж
С. 150 Дж
D. 150 кДж
Ответ

POP4 20.49
Два конденсатора 25 мк Ф и 5 мк Ф соединены последовательно. Какое Δ V требуется для накопления 0,150 Дж?
А. 22,8 В
Б. 100 В
С. 137 В
Д. 268 В
Ответ

клм Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен. Если ℰ = 6,00 В, R  = 10,0 Ом и C  = 72,0 мк F, какой ток протекает через батарею сразу после замыкания ключа?
симулятор цепи

А. 0,432 мА
Б. 0,600 А
С. 0,900 А
Д. 1.20 А
Ответ

клм Walker5e CnEx 21-19
Переключатель на рисунке ниже изначально разомкнут, а конденсатор не заряжен. Если ℰ = 6,00 В, R  = 10,0 Ом и C  = 72,0 мк F, какой ток протекает через батарею спустя долгое время после замыкания ключа?

А. 0,432 мА
Б. 0,600 А
С. 0,900 А
Д. 1.20 А
Ответ

клм Walker5e Ex 21-17
Если C  = 24,0 µ F в схеме ниже, какова эквивалентная емкость всей цепи?

А. 8.00 мкм F
Б. 16.0 мкм F
С. 36.0 мкм F
D. 72.0 µ F
Ответ

Уокер5е 21,61
Два конденсатора, C ₁ = C и C ₂  = 2 C , подключены к аккумулятору. Конденсатор _____ накапливает больше энергии, когда они соединены с батареей последовательно, а конденсатор _____ накапливает больше энергии, когда они соединены параллельно с батареей.
А. С ₁ … С ₁
Б. С ₂ … С ₁
С. С ₁ … С ₂
D. C ₂ … C ₂
Ответ

sj6 28,33
Аккумулятор был подключен к цепи ниже в течение длительного времени. Какое напряжение на конденсаторе?
А. 2,00 В
Б. 4,00 В
С. 6,00 В
Д. 8.00 В
Ответ

 

Б. 0,150 Дж

 

Д. 268 В

 

Д. 1,20 А

Сразу после замыкания ключа конденсатор разряжается и ведет себя как провод. Батарея на 6,00 В пропускает ток 0,600 А через каждый из резисторов 10,0 Ом (или, если хотите, два параллельных резистора имеют эквивалентное сопротивление 5,00 Ом), в результате чего через батарею протекает 1,20 А.

 

Б. 0,600 А

Через долгое время после замыкания переключателя конденсатор полностью заряжен и ведет себя как разомкнутая цепь. Батарея на 6,00 В пропускает ток 0,600 А через левый резистор 10,0 Ом.

 

C. 36,0 µ F

Два последовательно соединенных конденсатора имеют эквивалентную емкость ½ C и подключены параллельно с третьим идентичным конденсатором. Следовательно, мы добавляем две емкости, чтобы получить эквивалентную емкость 1,50·9. 0024 C , или 1,50 × 24,0 мк F = 36,0 мк F.

 

C. C ₁ … C ₂

При последовательном соединении два конденсатора имеют одинаковый заряд. Отметив, что U  = ½ Q ²/ C , вы можете увидеть, что меньший конденсатор C ₁ хранит больше всего энергии. (Убедитесь сами, что при напряжении батареи 6,0 В и С = 10,0 мк F, C ₁ запасы 80  µ Дж и C ₂ запасы 40  µ Дж.)
При параллельном соединении два конденсатора имеют одинаковое напряжение. Отметив, что U  = ½ CV ², вы можете увидеть, что больший конденсатор C ₂ хранит больше всего энергии. (Убедитесь сами, что при напряжении батареи 6,0 В и С = 10,0 мк F, С ₁ сохраняет 180 мк Дж и С ₂ хранит 360 мк Дж. )

 

С. 6,00 В

Левая сторона конденсатора имеет более высокий потенциал.

19.6 Конденсаторы, соединенные последовательно и параллельно – College Physics

Глава 19 Электрический потенциал и электрическое поле

Резюме

• Получите выражения для полной емкости при последовательном и параллельном подключении.
• Определите последовательное и параллельное соединение конденсаторов.
• Рассчитайте эффективную емкость при последовательном и параллельном подключении по отдельным емкостям.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от того, как они соединены. Существует два простых и распространенных типа соединений, называемых сериями , , , и 9. 0024 параллельно , для которых мы можем легко рассчитать общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного соединения.

На рис. 1(а) показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением соотношением [latex]{C = \frac{Q}{V}}[/latex].

Обратите внимание на рис. 1, что противоположные заряды величиной [латекс]{Q}[/латекс] текут по обеим сторонам первоначально незаряженной комбинации конденсаторов при приложении напряжения [латекс]{В}[/латекс]. Сохранение заряда требует, чтобы на пластинах отдельных конденсаторов создавались заряды равной величины, поскольку в этих изначально нейтральных устройствах заряд только разделяется. Конечным результатом является то, что комбинация напоминает один конденсатор с эффективным расстоянием между пластинами больше, чем у отдельных конденсаторов по отдельности. (См. рис. 1(b).) Большее расстояние между пластинами означает меньшую емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рисунок 1. (а) Конденсаторы, соединенные последовательно. Величина заряда на каждой пластине равна Q . (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d . Последовательные соединения дают общую емкость меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассматривая напряжение на отдельных конденсаторах, показанных на рисунке 1. Решение [латекс]{С = \frac{Q}{V}}[/латекс] для [латекс]{В} [/latex] дает [latex]{V = \frac{Q}{C}}[/latex]. Таким образом, напряжения на отдельных конденсаторах равны [латекс]{V_1 = \frac{Q}{C_1}}[/latex], [латекс]{V_2 = \frac{Q}{C_2}}[/latex] и [ латекс]{V_3 = \frac{Q}{C_3}}[/латекс]. Общее напряжение представляет собой сумму отдельных напряжений:

[латекс] {V = V_1 + V_2 + V_3}. [/латекс]

Теперь, называя общую емкость [латекс]{C_S}[/латекс] последовательной емкостью, считайте, что

[латекс] {V =} [/латекс] [латекс] {\ гидроразрыва {Q} {C_S}} [/ латекс] [латекс] { = V_1 + V_2 + V_3}. [/латекс]

Введя выражения для [латекс]{V_1}[/латекс], [латекс]{V_2}[/латекс] и [латекс]{V_3}[/латекс], мы получим

[латекс] {\ гидроразрыва {Q} {C_S} = \ гидроразрыва {Q} {C_1} + \ гидроразрыва {Q} {C_2} + \ гидроразрыва {Q} {C_3}}. [/латекс]

Отменяя [латекс]{Q}[/латекс], мы получаем уравнение для полной емкости последовательно [латекс]{C_S}[/латекс] равной

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+ } [/латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1} {C_3}} [/латекс] [ латекс]{+ \cdots},[/латекс]

, где «…» указывает, что выражение справедливо для любого количества последовательно соединенных конденсаторов. Выражение этой формы всегда приводит к тому, что общая емкость [латекс]{C_S}[/латекс] меньше любой из отдельных емкостей [латекс]{С_1}[/латекс], [латекс]{С_2}[/латекс]. ], …, как показано в следующем примере.

Полная последовательная емкость,

C _с

Полная последовательная емкость: [латекс] {\ frac {1} {C_S} = \ frac {1} {C_1} + \ frac {1} {C_2} + \frac{1}{C_3} + \cdots}[/latex]

Пример 1: Что такое последовательная емкость?

Найдите общую емкость трех последовательно соединенных конденсаторов, если их индивидуальные емкости равны 1000, 5000 и 8000 [латекс]\mu \textbf{F}[/латекс].

Стратегия

Имея данную информацию, общую емкость можно найти, используя уравнение для последовательной емкости.

Решение

Ввод данных емкостей в выражение для [латекс]{\ гидроразрыва {1} {C_S}} [/латекс] дает [латекс] {\ гидроразрыва {1} {C_S} = \ гидроразрыва {1 {C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex].

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ мю \ textbf {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{1}{5.000 \;\textbf{F}}}[/латекс] [латекс]{+}[/латекс] [ латекс] {\ гидроразрыва {1} {8.000 \; \ mu \ textbf {F}}} [/ латекс]  [латекс] {=} [/латекс] [латекс] {\ гидроразрыва {1,325} {\ му \ textbf { F}}}[/латекс]

Инвертирование для нахождения [латекс]{C_S}[/латекс] дает [латекс]{C_S = \frac{\mu \textbf{F}}{1,325} = 0,755 \;\mu \textbf{F}}[/ латекс].

Обсуждение

Суммарная последовательная емкость [латекс]{C_s}[/латекс] меньше наименьшей индивидуальной емкости, как и было обещано. При последовательном соединении конденсаторов сумма меньше частей. На самом деле, это меньше, чем любой человек. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в этом случае (показывая только вычисления целых чисел) равен 40. Таким образом,

[латекс] {\ гидроразрыва {1} {C_S}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {40} {40 \; \ mu \ textbf {F}} }[/латекс] [латекс]{+}[/латекс] [латекс]{\гидроразрыва{8}{40 \;\mu \textbf{F}}}[/латекс] [латекс]{+}[/латекс ] [латекс] {\ гидроразрыва {5} {40 \; \ mu \ textbf {F}}} [/ латекс] [латекс] {=} [/ латекс] [латекс] {\ гидроразрыва {53} {40 \; \mu \textbf{F}}},[/latex]

, так что

[latex]{C_S =}[/latex] [latex]{\frac{40 \;\mu \textbf{F}}{ 53}}[/латекс] [латекс]{= 0,755 \; \mu \textbf{F}}.[/latex]

На рис. 2(а) показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти проще, чем в последовательном случае. Чтобы найти эквивалентную общую емкость [латекс]{\текст{С}_{\текстбф{р}}}[/латекс], сначала отметим, что напряжение на каждом конденсаторе равно [латекс]{В}[/латекс], такие же, как и у источника, так как они подключены непосредственно к нему через проводник. (Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения. ) Таким образом, конденсаторы имеют на себе такие же заряды, как если бы они были подключены к источнику напряжения по отдельности. Общий заряд [латекс]{Q}[/латекс] представляет собой сумму отдельных сборов:

[латекс] {Q = Q_1 + Q_2 + Q_3}.[/латекс]

Рисунок 2. (a) Параллельное подключение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был один, и поэтому общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и, следовательно, может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение [латекс]{Q = CV}[/латекс], мы видим, что общий заряд равен [латекс]{Q = C_{\textbf{p}}V}[/латекс], а отдельные заряды равны [латекс]{Q_1 = C_1 V}[/латекс] ,  [латекс]{Q_2 = C_2 V}[/латекс] , и [латекс]{Q_3 = C_3 V}[/латекс]. Ввод их в предыдущее уравнение дает

[латекс] {C_{\textbf{p}} V = C_1 V + C_2 V + C_3 V}. [/latex]

Исключая [латекс]{V}[/латекс] из уравнения, мы получаем уравнение для полной емкости параллельно [латекс]{С_{\текстбф{р}}}[/латекс]:

[латекс]{C_{\textbf{p}} = C_1 + C_2 + C_3 \cdots}[/латекс] .

Общая емкость при параллельном подключении представляет собой просто сумму отдельных емкостей. (Опять « … ” указывает, что выражение справедливо для любого количества конденсаторов, соединенных параллельно.) Так, например, если бы конденсаторы в приведенном выше примере были соединены параллельно, их емкость была бы

[латекс]{C_{\textbf{p}} = 1,000 \;\mu \textbf{F} + 5,000 \;\mu \textbf{F} + 8,000 \;\mu \textbf{F} = 14,000 \; \mu \textbf{F}}.[/latex]

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рис. 2(b).

Суммарная емкость при параллельном подключении,

C _p [латекс] {C_{\textbf{p}}}[/latex]

Суммарная емкость при параллельном подключении [латекс]{C_{\textbf{p}} = C_1 + C_2 + C_3 + \cdots}[/латекс]

Более сложные соединения конденсаторов иногда могут представлять собой комбинации последовательного и параллельного соединения. (См. рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую емкость.

Рис. 3. (а) Эта схема содержит как последовательное, так и параллельное соединение конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ расположены последовательно; их эквивалентная емкость C _S меньше любого из них. (c) Обратите внимание, что C _S находится параллельно с C ₃ . Таким образом, общая емкость равна сумме C _S и C ₃ .

Смесь последовательных и параллельных емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех знаков после запятой ([latex]{C_1 = 1,000 \;\mu\textbf {F}}[/латекс], [латекс]{C_2 = 5. 000 \;\mu \textbf{F}}[/латекс] и [латекс]{C_3 = 8.000 \;\mu \textbf{F}}[ /latex]) и округлить ответ до трех знаков после запятой.

Стратегия

Чтобы найти общую емкость, мы сначала определяем, какие конденсаторы соединены последовательно, а какие — параллельно. Конденсаторы [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] включены последовательно. Их комбинация, обозначенная на рисунке [латекс]{C_S}[/латекс], параллельна [латекс]{С_3}[/латекс].

Решение

Поскольку [латекс]{C_1}[/латекс] и [латекс]{С_2}[/латекс] соединены последовательно, их общая емкость определяется как [латекс]{\ гидроразрыва {1} {C_S } = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}}[/latex]. Ввод их значений в уравнение дает

[латекс] {\ гидроразрыва {1} {C_1}} [/ латекс] [латекс] {+} [/ латекс] [латекс] {\ гидроразрыва {1} {C_2}} [/ латекс] [латекс] { =} [/латекс] [латекс] {\ гидроразрыва {1} {1,000 \; \ mu \ textbf {F}}} [/ латекс] [латекс] {+} [/латекс] [латекс] {\ гидроразрыва {1 }{5.