Определение эквивалентного последовательного сопротивления (ESR) конденсаторов
Добавлено 12 декабря 2019 в 07:16
Сохранить или поделиться
Рассмотрим подробнее важность ESR (эквивалентного последовательного сопротивления) конденсатора, как его измерить, и какие факторы могут повлиять на ваши измерения.
По мере того, как рабочие частоты увеличиваются, а электронные системы становятся все сложнее и меньше, разработчики должны уделять пристальное внимание ESR (эквивалентному последовательному сопротивлению) конденсатора, поскольку оно влияет на энергопотребление и эффективность.
Знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.
Некоторые производители указывают ESR при конкретных частоте и рабочих условиях, некоторые просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния.
Эквивалентное последовательное сопротивление (ESR) является одной из характеристик неидеального конденсатора, которая может вызывать различные проблемы производительности в электронных схемах. Высокое значение ESR ухудшает производительность из-за потерь I
В некоторых случаях тепло, выделяемое благодаря ESR, невелико и может не вызывать проблем. Однако в некоторых схемах, особенно в приложениях с большим током, рассеиваемое тепло может вызвать значительное повышение температуры, повлиять на работу схемы и вызвать деградирование конденсатора. Кроме того, на сопротивлении происходит значительное падение напряжения, что снижает долю полезной энергии в приложении.
Таким образом, при выборе конденсатора для таких применений, как ВЧ, аккумулирование энергии, схемы фильтров и другие чувствительные схемы, требуется учет и других характеристик, помимо значений емкости и напряжения.
Связанная информация
Влияние ESR на радиочастотные схемы и схемы аккумулирования энергии
Несмотря на то, что ESR у керамических конденсаторов очень мало, порядка миллиом, это сопротивление может существенно повлиять на такие схемы, как радиочастотные схемы и схемы с низким энергопотреблением.
В переносных радиочастотных передатчиках конденсаторы с высоким ESR в схемах связи или обхода источника питания усилителя потребляют и расходуют больше энергии аккумулятора из-за более высоких потерь I2ESR. Это уменьшает эффективность, выходную мощность и срок службы батареи.
Кроме того, большинство радиочастотных полупроводниковых устройств, изготовленных для согласующих каскадов, построены с очень низким входным сопротивлением. Таким образом, согласующий конденсатор, такой как многослойный керамический чип-конденсатор (MLCC) с высоким ESR, будет представлять собой значительную долю от общего полного сопротивления цепи. Например, если входной импеданс устройства составляет 1 Ом, согласующий конденсатор с ESR 0,8 Ом будет рассеивать около 40 процентов общей мощности, таким образом, уменьшая выходную мощность и эффективность схемы.
Конденсаторы в приложениях по аккумулированию энергии выполняют более важную роль – накапливают заряд от низковольтных источников энергии и быстро и эффективно разряжают эту накопленную энергию для питания нагрузки. Следовательно, конденсаторы и другие компоненты в цепях аккумулирования энергии должны во время работы потреблять очень мало энергии.
Конденсатор с высоким ESR будет иметь бо́льшие потери I2ESR, поэтому часть полученной энергии в конечном итоге будет потрачена впустую в виде тепла, что приведет к уменьшению выходной энергии конденсатора. Однако разработчики могут предпочесть суперконденсаторы (несмотря на их более высокие ESR и утечку), потому что они предлагают более высокую плотность энергии.
Определение эквивалентного последовательного сопротивления с помощью измерителя ESR
Измеритель ESR является умеренно точным прибором, который доступен и удобен в использовании, особенно при измерении нескольких конденсаторов, когда они находятся в схеме. На конденсатор в схеме делителя напряжения подается переменное напряжение. Частота подаваемого переменного напряжения обычно равна значению, при котором реактивное сопротивление конденсатора незначительно.
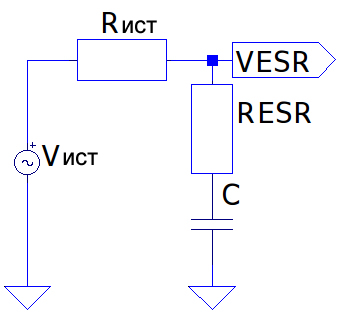 Рисунок 1 – Простая модель измерения ESR
Рисунок 1 – Простая модель измерения ESRВо время теста с использованием измерителя ESR ток пропускается через конденсатор в течение очень короткого времени, поэтому конденсатор не заряжается полностью. Ток создает напряжение на конденсаторе. Это напряжение будет равно произведению тока на ESR конденсатора, плюс незначительное напряжение из-за небольшого заряда в конденсаторе.
Поскольку ток известен, значение ESR рассчитывается путем деления измеренного напряжения на ток. Результаты затем отображаются на показаниях измерителя.
Измерения ESR могут выполняться, когда конденсатор находится и в схеме, и вне схемы. Для конденсаторов, подключенных параллельно, измерение дает в результате общее сопротивление. Если необходимо определить отдельно ESR у конкретных конденсаторов, они должны быть извлечены из схемы. Однако при наличии сотен конденсаторов утомительно вынимать каждый из них, а также существует повышенный риск повреждения конденсаторов или печатной платы во время удаления.
Типовой измеритель ESR использует низкое напряжение около 250 мВ или менее с частотой около 100 кГц. Низкое напряжение является недостаточным для смещения и активации полупроводниковых устройств в окружающих цепях, что гарантирует, что импеданс соседних компонентов не влияет на показания ESR.
Перед проведением измерения конденсатор должен быть разряжен. Некоторые измерители ESR имеют встроенный механизм разряда. Однако может быть важно разрядить конденсатор вручную, особенно если это высоковольтный конденсатор, заряд которого может повредить измеритель ESR.
Несмотря на то, что измеритель ESR может удобно тестировать конденсаторы внутри схемы, он имеет ограничения по частоте, а также по самому низкому уровню сопротивления, который он может точно измерить.
Измерение с помощью коаксиальной резонансной трубы для сверхнизких сопротивлений на высоких частотах
Поскольку значение ESR зависит от рабочей частоты, измерение сверхнизких значений ESR на очень высоких частотах становится проблемой при использовании обычных измерителей ESR.
Для керамических конденсаторов наиболее точным методом определения ESR на высоких частотах (от 100 МГц до 1,3 ГГц) является метод коаксиальной резонансной линии. Этот метод основан на стандартной модели Boonton 34A и используется вместе с генератором высокочастотных сигналов и высокочастотным вольтметром.
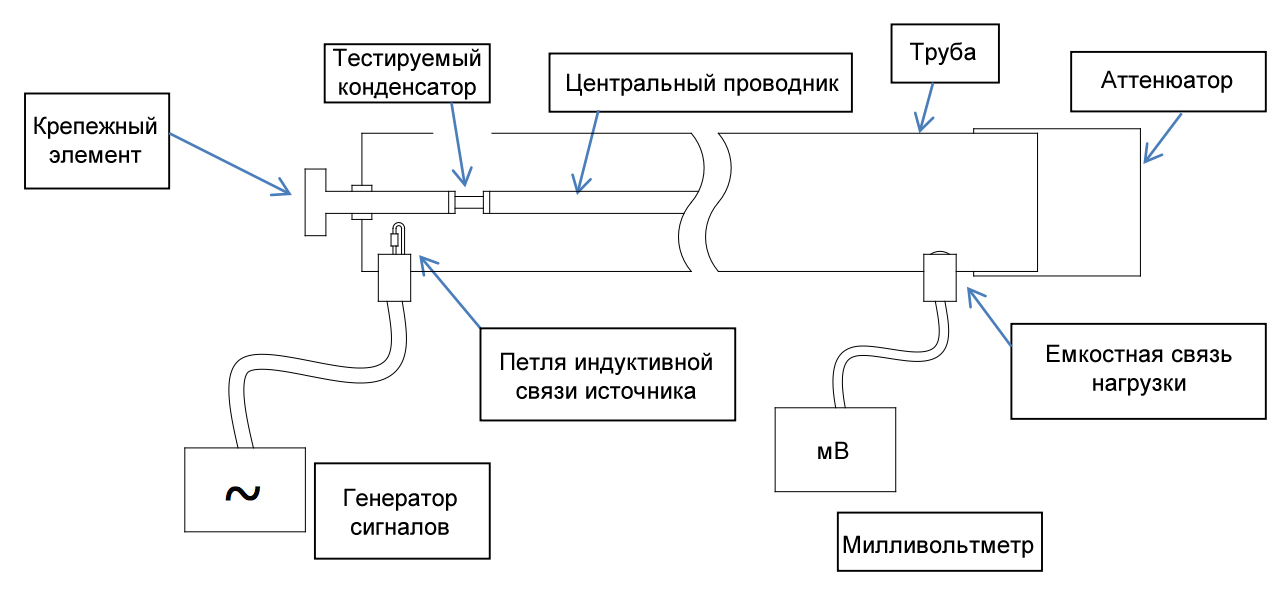 Рисунок 2 – Блок-схема измерителя ESR на коаксиальной резонансной трубке
Рисунок 2 – Блок-схема измерителя ESR на коаксиальной резонансной трубкеЛиния коаксиального резонатора выполнена из медной трубки со сплошным медным стержнем в качестве центрального проводника. Тестируемый конденсатор устанавливается последовательно между центральным проводником и проводником экрана.
Перед выполнением измерения ESR конденсатора необходимо определить характеристики ненагруженной линии резонатора. ВЧ возбуждение закороченной коаксиальной линии помогает определить ширину полосы λ/4 и 3λ/4, тогда как ширина полосы λ/2 и λ определяется, когда линия разомкнута (λ – это длина волны; дополнительную информацию см. в этой статье). Эти данные характеризуют резонансную частоту, добротность (Q) ненагруженной резонансной линии и сопротивление крепежного элемента.
Затем тестируемый конденсатор помещается в секцию DUT (device under test, тестируемое устройство), и генератор сигналов настраивается на пиковое резонансное напряжение. Конденсатор вызывает изменение резонансной частоты и добротности, значения которых теперь отличаются от значений ненагруженной коаксиальной линии. Затем используются расчеты линии передачи, и значение ESR определяется на основе взаимосвязи между новой частотой и добротностью, а также частотой и добротностью исходного состояния без нагрузки.
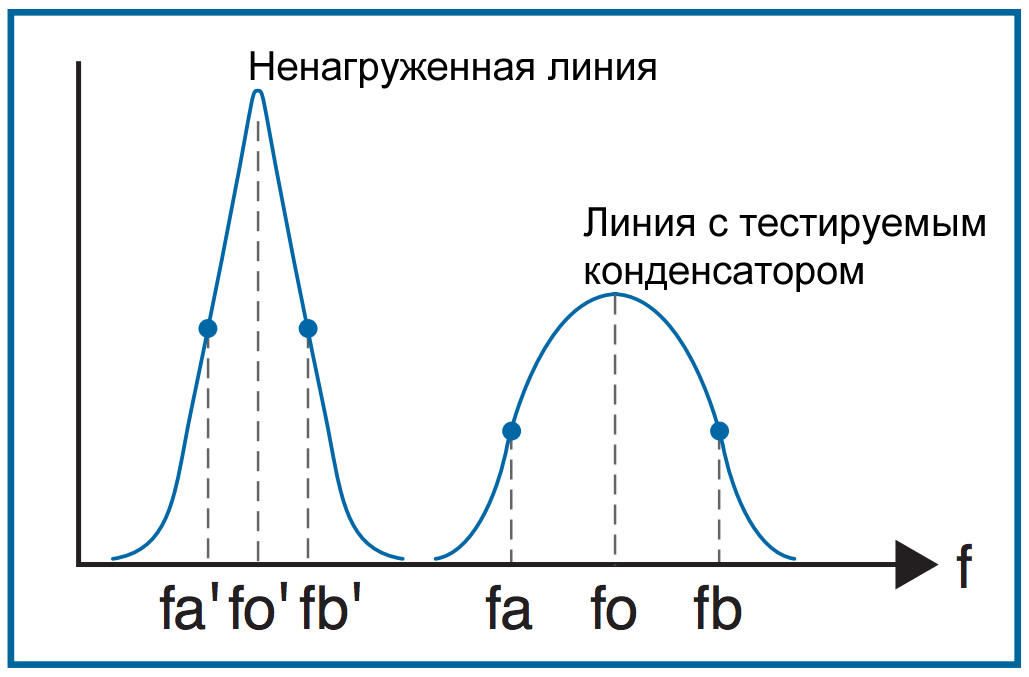 Рисунок 3 – Полоса пропускания нагруженной и незагруженной линии передачи
Рисунок 3 – Полоса пропускания нагруженной и незагруженной линии передачиВ настоящее время обычной практикой является использование векторного анализатора цепей для замены как генератора сигналов, так и высокочастотного вольтметра. При использовании векторного анализатора цепей резонансная частота считывается с дисплея. Некоторые модели векторных анализаторов могут экспортировать результаты непосредственно в программу расчета и отображать окончательное значение ESR.
Длина трубки рассчитана на работу в диапазоне частот от 100 МГц до 1,5 ГГц; однако для частот, выходящих за пределы этого диапазона, трубка может быть выполнена произвольной длины.
Факторы, которые влияют на измерения ESR
Ошибки измерения ESR могут возникать в результате проблем с техникой, способа выполнения контакта с конденсатором или отсутствия калибровки измерительного оборудования.
Должны быть приняты во внимание сопротивления, самоиндукция и емкость измерительного прибора и его выводов, особенно на высоких частотах измерения.
Сопротивление и индуктивность измерительных проводов
Сопротивление измерительных проводов является распространенным источником ошибок при измерениях низких сопротивлений. Это сопротивление добавляется к сопротивлению тестируемого устройства.
Кроме того, следует избегать измерительных проводов со спиральной намоткой, поскольку источником ошибки может стать их индуктивность.
Помехи от соседнего оборудования
Измерение следует проводить в местах, удаленных или экранированных от источников значительных электромагнитных помех. В противном случае измерительные провода могут ловить помехи, и это может повлиять на показания.
Заключение
ESR варьируется в зависимости от типа конденсатора и условий эксплуатации, таких как частота и температура. Некоторые производители указывают ESR на определенной частоте и при определенных условиях работы, другие просто указывают коэффициент рассеяния, а другие не предоставляют ни ESR, ни коэффициента рассеяния. Тем не менее, знание значения ESR в ожидаемых условиях работы может очень помочь в определении пригодности конкретного конденсатора для выполнения заданной функции.
Тип метода, используемого для определения ESR, зависит от таких факторов, как тип конденсатора, рабочая частота и требуемая точность. В то время как измеритель ESR и другие самодельные измерители подходят для ряда применений на частотах примерно до 100 кГц, они не могут точно определить очень низкие значения ESR на очень высоких частотах. Метод коаксиальной резонансной линии часто является предпочтительным при определении сверхнизких значений ESR на частотах между приблизительно 100 МГц и 1,3 ГГц.
По мере того, как рабочие частоты увеличиваются, а электронные системы становятся меньше и сложнее, необходимо уделять пристальное внимание таким параметрам, как ESR, которые напрямую влияют на характеристики схемы и эффективность энергопотребления.
Оригинал статьи:
Теги
ESR (эквивалентное последовательное сопротивление)ИзмерениеКерамический конденсаторКонденсаторЭквивалентная схемаЭлектролитический конденсаторСохранить или поделиться
Эквивалентная ёмкость конденсаторов
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ. Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
Удачи в расчетах!
- Эквивалентное сопротивление онлайн >>
Конденсатор — это… Что такое Конденсатор?

Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик

Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические.

Различные конденсаторы для объёмного монтажа
Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых
История
В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку».
Свойства конденсатора
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течет, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора.
В терминах метода комплексных амплитуд конденсатор обладает комплексным импедансом
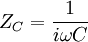 ,
,
где 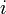 — мнимая единица,
— мнимая единица, 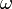 — частота[1] протекающего синусоидального тока,
— частота[1] протекающего синусоидального тока, 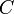
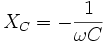 . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
. Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью 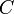
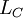 и сопротивлением потерь
и сопротивлением потерь 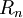 .
.Резонансная частота конденсатора равна
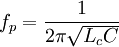
При 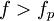
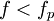 , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.
, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
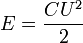
где 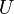 — напряжение (разность потенциалов), до которого заряжен конденсатор.
— напряжение (разность потенциалов), до которого заряжен конденсатор.
Обозначение конденсаторов на схемах
В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74[2] либо международному стандарту IEEE 315-1975:
| Обозначение по ГОСТ 2.728-74 | Описание |
|---|---|
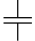 | Конденсатор постоянной ёмкости |
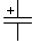 | Поляризованный конденсатор |
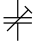 | Подстроечный конденсатор переменной ёмкости |
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 106 пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 – 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, т.е. на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.
Характеристики конденсаторов
Основные параметры
Ёмкость
Основной характеристикой конденсатора является его ёмкость. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью  каждая, расположенных на расстоянии
каждая, расположенных на расстоянии 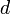 друг от друга, в системе СИ выражается формулой:
друг от друга, в системе СИ выражается формулой: 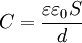 , где
, где  — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда
— относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда 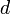 много меньше линейных размеров пластин).
много меньше линейных размеров пластин).
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
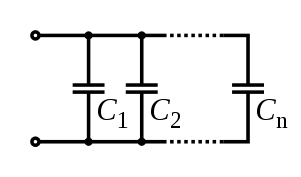
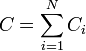 или
или 
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы. Общая ёмкость батареи последовательно соединённых конденсаторов равна
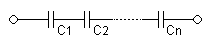
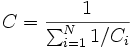 или
или 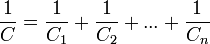
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Номинальное напряжение
Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.
Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается.
Полярность

Конденсаторы, разрушившиеся без взрыва из-за температуры и напряжения, не соответствующих рабочим.
Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.
Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков.
Паразитные параметры
Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:
Электрическое сопротивление изоляции конденсатора — r
Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением r = U / Iут , где U — напряжение, приложенное к конденсатору, Iут — ток утечки.
Эквивалентное последовательное сопротивление — R
Эквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор.
В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр., Capacitor plague(англ.)).
Эквивалентная последовательная индуктивность — L
Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности.
Тангенс угла потерь
Тангенс угла потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости. 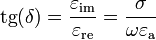
Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол 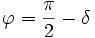 , где
, где 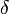 — угол диэлектрических потерь. При отсутствии потерь
— угол диэлектрических потерь. При отсутствии потерь 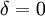 . Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная
. Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная 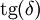 , называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
, называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
Температурный коэффициент ёмкости (ТКЕ)
ТКЕ — относительное изменению емкости при изменении температуры окружающей среды на один градус Цельсия (Кельвина). Таким образом значение ёмкости от температуры представляется линейной формулой:
 ,
,
где ΔT — увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость емкости от температуры, и конденсаторы с большими уходами емкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение емкости в рабочем диапазоне температур.
Диэлектрическое поглощение
Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками. Наименьшим диэлектрическим поглощением обладают конденсаторы с органическими диэлектриками: тефлон (фторопласт), полистирол, полиэтилентерефталат, поликарбонат.
Классификация конденсаторов
Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др.
По виду диэлектрика различают:
- Конденсаторы вакуумные (обкладки без диэлектрика находятся в вакууме).
- Конденсаторы с газообразным диэлектриком.
- Конденсаторы с жидким диэлектриком.
- Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические, стеклоплёночные), слюдяные, керамические, тонкослойные из неорганических плёнок.
- Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.
- Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах) или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги или спеченного порошка.
Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:
- Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости (кроме как в течение срока службы).
- Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости в процессе функционирования аппаратуры. Управление ёмкостью может осуществляться механически, электрическим напряжением (вариконды, варикапы) и температурой (термоконденсаторы). Применяются, например, в радиоприемниках для перестройки частоты резонансного контура.
- Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных ёмкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение ёмкости.
В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляюшие, дозиметрические, пусковые и другие конденсаторы.
Применение конденсаторов
Конденсаторы находят применение практически во всех областях электротехники.
- Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
- Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора.
- ИП влажности воздуха (изменение состава диэлектрика приводит к изменению емкости)
- ИП влажности древесины
- В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит. В частности, в схеме работы АПВ использование конденсатора позволяет обеспечить требуемую кратность срабатывания защиты.
Внешние ссылки
Смотри также
Ссылки
- ↑ Частота в радианах в секунду.
- ↑ ГОСТ 2.728-74 (2002)
Эквивалентное последовательное сопротивление (ESR)
Какой главный параметр для оценки исправности конденсаторов? Конечно их ёмкость. Но по мере распространения импульсной высоковольтной техники, стало очевидно, что надо обратить внимание на ещё один параметр, от которого зависит надёжность и качество работы импульсных преобразователей — это эквивалентное последовательное сопротивление (ЭПС, по англ. ESR — equivalent series resistance ). Применение конденсаторов с увеличенным значением ЭПС приводит к росту пульсаций выходного напряжения по сравнению с расчётными значениями, и бстрому выходу их из строя из-за повышенного нагрева за счёт выделения тепла на ЭПС, нередки даже случаи закипания электролита, деформация корпуса, а также взрывы конденсаторов. Особая выраженность негативного влияния ЭПС именно в силовых импульсных преобразователях вызвана, работой на больших токах заряда-разряда, а также тем, что с ростом рабочей частоты ЭПС возрастает. Наличие ESR объясняется конструкцией оксидного конденсатора и обусловлена сопротивлением обкладок, сопротивлением выводов, переходным сопротивлением контактов между обкладками и выводами, а также потерями в материале диэлектрика. С течением времени ESR конденсатора возрастает, что совсем не хорошо.ESR конденсаторов разных типов
Естественно, проконтролировать обычным Омметром эквивалентное последовательное сопротивление конденсатора невозможно — тут нужен специальный прибор. В интернете есть несколько простых конструкций ESR-метров , но при желании, можно собрать более точный и удобный измеритель на микроконтроллере. Например из журнала Радио 7-2010.
Схема измерителя ESR конденсаторов на
Attiny2313
Все необходимые файлы и прошивки — в архиве . После сборки и включения крутим регулятор контрастности до появления на экране LCD надписи в две строки. Если её нет — проверяем монтаж и правильность прошивки МК ATtiny2313. Если всё ОК — нажимаем кнопку «Калибровка» — в прошивку внесётся поправка на скорость срабатывания входной части измерителя. Далее понадобится несколько новых электролитических конденсаторов высокого качества ёмкостью 220…470 мкФ разных партий, лучше всего — на разные напряжения. Подключаем любой из них к входным гнёздам прибора и начинаем подбирать резистор R2 в пределах 100…470 ом (у меня получилось 300 ом; можно применить временно цепочку постоянный+подстроечный) так, чтобы значение ёмкости на экране ЖКИ примерно было похоже на номинал конденсатора. К большой точности пока что стремиться не стОит — ещё будет корректироваться; затем проверить и с другими конденсаторами.
Для настройки измерителя ESR нужна таблица с типовыми значениями этого параметра для разных конденсаторов. Эту табличку рекомендуется приклеить на корпус прибора под дисплеем.
В следующей табличке указаны максимальные значения эквивалентного последовательного сопротивления для электролитических конденсаторов. Если у измеряемого конденсатора оно будет выше, то его уже нельзя использовать для работы в сглаживающем фильтре выпрямителя:
Подключаем конденсатор 220 мкФ и, незначительным подбором сопротивления резисторов R6, R9, R10 (на схеме и на моём сборочном чертеже обозначены со звёздочками), добиваемся показаний Esr, близких к указанным в таблице. Проверяем на всех имеющихся заготовленных эталонных конденсаторах, в т.ч. уже можно использовать и конденсаторы от 1 до 100 мкФ.
Так как для измерения ёмкости конденсаторов от 150 мкФ и для измерителя ESR применяется один и тот же участок схемы, после подбора сопротивления этих резисторов несколько изменится точность показаний измерителя ёмкости. Теперь можно подстроить ещё сопротивление резистора R2, чтобы эти показания стали точнее. Другими словами, нужно подбирая сопротивление R2 — уточнить показания измерителя ёмкости, подстраивая резисторы в делителе компараторов — уточнить показания ESR-метра. Причём, приоритет надо отдавать измерителю внутреннего сопротивления.
Теперь надо настроить измеритель ёмкости конденсаторов диапазона 0,1…150 мкФ. Так как для этого в схеме предусмотрен отдельный источник тока, измерение ёмкости таких конденсаторов можно сделать очень точным. Подключаем конденсаторы малой ёмкости к входным гнёздам прибора и, подбором сопротивления R1 в пределах 3,3…6,8 кОм добиваемся максимально точных показаний. Этого можно достичь, если в качестве эталонных применить не электролитические, а высокоточные конденсаторы К71-1 ёмкостью 0,15 мкФ с гарантированным отклонением 0,5 или 1%.
Когда собрал данный измеритель ESR — схема завелась сразу, понадобилась только калибровка. Этот измеритель много раз помогал при ремонте БП, так что устройство рекомендуется к сборке. Схему разрабо
Конденсатор — это… Что такое Конденсатор?

Основа конструкции конденсатора — две токопроводящие обкладки, между которыми находится диэлектрик

Слева — конденсаторы для поверхностного монтажа; справа — конденсаторы для объёмного монтажа; сверху — керамические; снизу — электролитические.

Различные конденсаторы для объёмного монтажа
Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
История
В 1745 году в Лейдене немецкий физик Эвальд Юрген фон Клейст и голландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку».
Свойства конденсатора
Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течет, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора.
В терминах метода комплексных амплитуд конденсатор обладает комплексным импедансом
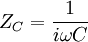 ,
,
где 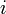 — мнимая единица,
— мнимая единица, 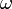 — частота[1] протекающего синусоидального тока,
— частота[1] протекающего синусоидального тока, 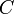 — ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно:
— ёмкость конденсатора. Отсюда также следует, что реактивное сопротивление конденсатора равно: 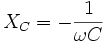 . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
. Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).
При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью 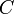 , собственной индуктивностью
, собственной индуктивностью 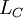 и сопротивлением потерь
и сопротивлением потерь 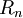 .
.
Резонансная частота конденсатора равна
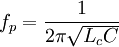
При 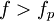 конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах
конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах 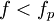 , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.
, на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.
Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:
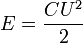
где 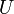 — напряжение (разность потенциалов), до которого заряжен конденсатор.
— напряжение (разность потенциалов), до которого заряжен конденсатор.
Обозначение конденсаторов на схемах
В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.728-74[2] либо международному стандарту IEEE 315-1975:
| Обозначение по ГОСТ 2.728-74 | Описание |
|---|---|
 | Конденсатор постоянной ёмкости |
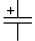 | Поляризованный конденсатор |
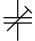 | Подстроечный конденсатор переменной ёмкости |
На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 106 пФ) и пикофарадах, но нередко и в нанофарадах. При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, т.е. постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения (пикоФарад). Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мк x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 – 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятичнологарифмических рядов значений Е3, Е6, Е12, Е24, т.е. на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.
Характеристики конденсаторов
Основные параметры
Ёмкость
Основной характеристикой конденсатора является его ёмкость. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до сотен микрофарад. Однако существуют конденсаторы с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью 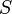 каждая, расположенных на расстоянии
каждая, расположенных на расстоянии 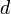 друг от друга, в системе СИ выражается формулой:
друг от друга, в системе СИ выражается формулой: 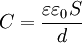 , где
, где  — относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда
— относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (эта формула справедлива, лишь когда  много меньше линейных размеров пластин).
много меньше линейных размеров пластин).
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
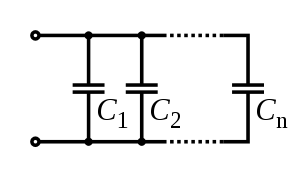
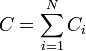 или
или 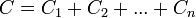
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы. Общая ёмкость батареи последовательно соединённых конденсаторов равна
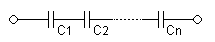
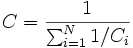 или
или 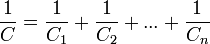
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
Удельная ёмкость
Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
Номинальное напряжение
Другой, не менее важной характеристикой конденсаторов является номинальное напряжение — значение напряжения, обозначенное на конденсаторе, при котором он может работать в заданных условиях в течение срока службы с сохранением параметров в допустимых пределах.
Номинальное напряжение зависит от конструкции конденсатора и свойств применяемых материалов. При эксплуатации напряжение на конденсаторе не должно превышать номинального. Для многих типов конденсаторов с увеличением температуры допустимое напряжение снижается.
Полярность

Конденсаторы, разрушившиеся без взрыва из-за температуры и напряжения, не соответствующих рабочим.
Многие конденсаторы с оксидным диэлектриком (электролитические) функционируют только при корректной полярности напряжения из-за химических особенностей взаимодействия электролита с диэлектриком. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.
Взрывы электролитических конденсаторов — довольно распространённое явление. Основной причиной взрывов является перегрев конденсатора, вызываемый в большинстве случаев утечкой или повышением эквивалентного последовательного сопротивления вследствие старения (актуально для импульсных устройств). Для уменьшения повреждений других деталей и травматизма персонала в современных конденсаторах большой ёмкости устанавливают клапан или выполняют насечку на корпусе (часто можно заметить её в форме буквы X, K или Т на торце). При повышении внутреннего давления открывается клапан или корпус разрушается по насечке, испарившийся электролит выходит в виде едкого газа, и давление спадает без взрыва и осколков.
Паразитные параметры
Реальные конденсаторы, помимо ёмкости, обладают также собственными сопротивлением и индуктивностью. С высокой степенью точности, эквивалентную схему реального конденсатора можно представить следующим образом:
Электрическое сопротивление изоляции конденсатора — r
Сопротивление изоляции — это сопротивление конденсатора постоянному току, определяемое соотношением r = U / Iут , где U — напряжение, приложенное к конденсатору, Iут — ток утечки.
Эквивалентное последовательное сопротивление — R
Эквивалентное последовательное сопротивление (ЭПС, англ. ESR) обусловлено главным образом электрическим сопротивлением материала обкладок и выводов конденсатора и контакта(-ов) между ними, а также потерями в диэлектрике. Обычно ЭПС возрастает с увеличением частоты тока, протекающего через конденсатор.
В большинстве случаев этим параметром можно пренебречь, но иногда (напр., в случае использования электролитических конденсаторов в фильтрах импульсных блоков питания) достаточно малое его значение может быть жизненно важным для надёжности устройства (см., напр., Capacitor plague(англ.)).
Эквивалентная последовательная индуктивность — L
Эквивалентная последовательная индуктивность обусловлена, в основном, собственной индуктивностью обкладок и выводов конденсатора. На низких частотах (до единиц килогерц) обычно не учитывается в силу своей незначительности.
Тангенс угла потерь
Тангенс угла потерь — отношение мнимой и вещественной части комплексной диэлектрической проницаемости. 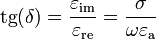
Потери энергии в конденсаторе определяются потерями в диэлектрике и обкладках. При протекании переменного тока через конденсатор векторы напряжения и тока сдвинуты на угол 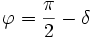 , где
, где 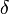 — угол диэлектрических потерь. При отсутствии потерь
— угол диэлектрических потерь. При отсутствии потерь 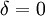 . Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная
. Тангенс угла потерь определяется отношением активной мощности Pа к реактивной Pр при синусоидальном напряжении определённой частоты. Величина, обратная 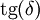 , называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
, называется добротностью конденсатора. Термины добротности и тангенса угла потерь применяются также для катушек индуктивности и трансформаторов.
Температурный коэффициент ёмкости (ТКЕ)
ТКЕ — относительное изменению емкости при изменении температуры окружающей среды на один градус Цельсия (Кельвина). Таким образом значение ёмкости от температуры представляется линейной формулой:
 ,
,
где ΔT — увеличение температуры в °C или °К относительно нормальных условий, при которых специфицировано значение ёмкости. TKE применяется для характеристики конденсаторов со значительной линейной зависимостью ёмкости от температуры. Однако ТКЕ определяется не для всех типов конденсаторов. Конденсаторы, имеющие нелинейную зависимость емкости от температуры, и конденсаторы с большими уходами емкости от воздействия температуры окружающей среды в обозначении имеют указание на относительное изменение емкости в рабочем диапазоне температур.
Диэлектрическое поглощение
Если заряженный конденсатор быстро разрядить до нулевого напряжения путём подключения низкоомной нагрузки, а затем снять нагрузку и наблюдать за напряжением на выводах конденсатора, то мы увидим, что напряжение медленно повышается. Это явление получило название диэлектрическое поглощение или адсорбция электрического заряда. Конденсатор ведёт себя так, словно параллельно ему подключено множество последовательных RC-цепочек с различной постоянной времени. Интенсивность проявления этого эффекта зависит в основном от свойств диэлектрика конденсатора. Подобный эффект можно наблюдать и на большинстве электролитических конденсаторов, но в них он является следствием химических реакций между электролитом и обкладками. Наименьшим диэлектрическим поглощением обладают конденсаторы с органическими диэлектриками: тефлон (фторопласт), полистирол, полиэтилентерефталат, поликарбонат.
Классификация конденсаторов
Основная классификация конденсаторов проводится по типу диэлектрика в конденсаторе. Тип диэлектрика определяет основные электрические параметры конденсаторов: сопротивление изоляции, стабильность ёмкости, величину потерь и др.
По виду диэлектрика различают:
- Конденсаторы вакуумные (обкладки без диэлектрика находятся в вакууме).
- Конденсаторы с газообразным диэлектриком.
- Конденсаторы с жидким диэлектриком.
- Конденсаторы с твёрдым неорганическим диэлектриком: стеклянные (стеклоэмалевые, стеклокерамические, стеклоплёночные), слюдяные, керамические, тонкослойные из неорганических плёнок.
- Конденсаторы с твёрдым органическим диэлектриком: бумажные, металлобумажные, плёночные, комбинированные — бумажноплёночные, тонкослойные из органических синтетических плёнок.
- Электролитические и оксидно-полупроводниковые конденсаторы. Такие конденсаторы отличаются от всех прочих типов прежде всего своей огромной удельной ёмкостью. В качестве диэлектрика используется оксидный слой на металлическом аноде. Вторая обкладка (катод) — это или электролит (в электролитических конденсаторах) или слой полупроводника (в оксидно-полупроводниковых), нанесённый непосредственно на оксидный слой. Анод изготовляется, в зависимости от типа конденсатора, из алюминиевой, ниобиевой или танталовой фольги или спеченного порошка.
Кроме того, конденсаторы различаются по возможности изменения своей ёмкости:
- Постоянные конденсаторы — основной класс конденсаторов, не меняющие своей ёмкости (кроме как в течение срока службы).
- Переменные конденсаторы — конденсаторы, которые допускают изменение ёмкости в процессе функционирования аппаратуры. Управление ёмкостью может осуществляться механически, электрическим напряжением (вариконды, варикапы) и температурой (термоконденсаторы). Применяются, например, в радиоприемниках для перестройки частоты резонансного контура.
- Подстроечные конденсаторы — конденсаторы, ёмкость которых изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры. Их используют для подстройки и выравнивания начальных ёмкостей сопрягаемых контуров, для периодической подстройки и регулировки цепей схем, где требуется незначительное изменение ёмкости.
В зависимости от назначения можно условно разделить конденсаторы на конденсаторы общего и специального назначения. Конденсаторы общего назначения используются практически в большинстве видов и классов аппаратуры. Традиционно к ним относят наиболее распространённые низковольтные конденсаторы, к которым не предъявляются особые требования. Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляюшие, дозиметрические, пусковые и другие конденсаторы.
Применение конденсаторов
Конденсаторы находят применение практически во всех областях электротехники.
- Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
- Измерительный преобразователь (ИП) малых перемещений: малое изменение расстояния между обкладками очень заметно сказывается на ёмкости конденсатора.
- ИП влажности воздуха (изменение состава диэлектрика приводит к изменению емкости)
- ИП влажности древесины
- В схемах РЗиА конденсаторы используются для реализации логики работы некоторых защит. В частности, в схеме работы АПВ использование конденсатора позволяет обеспечить требуемую кратность срабатывания защиты.
Внешние ссылки
Смотри также
Ссылки
- ↑ Частота в радианах в секунду.
- ↑ ГОСТ 2.728-74 (2002)


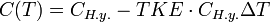 ,
,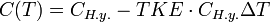 ,
,