Полусумматор | это… Что такое Полусумматор?
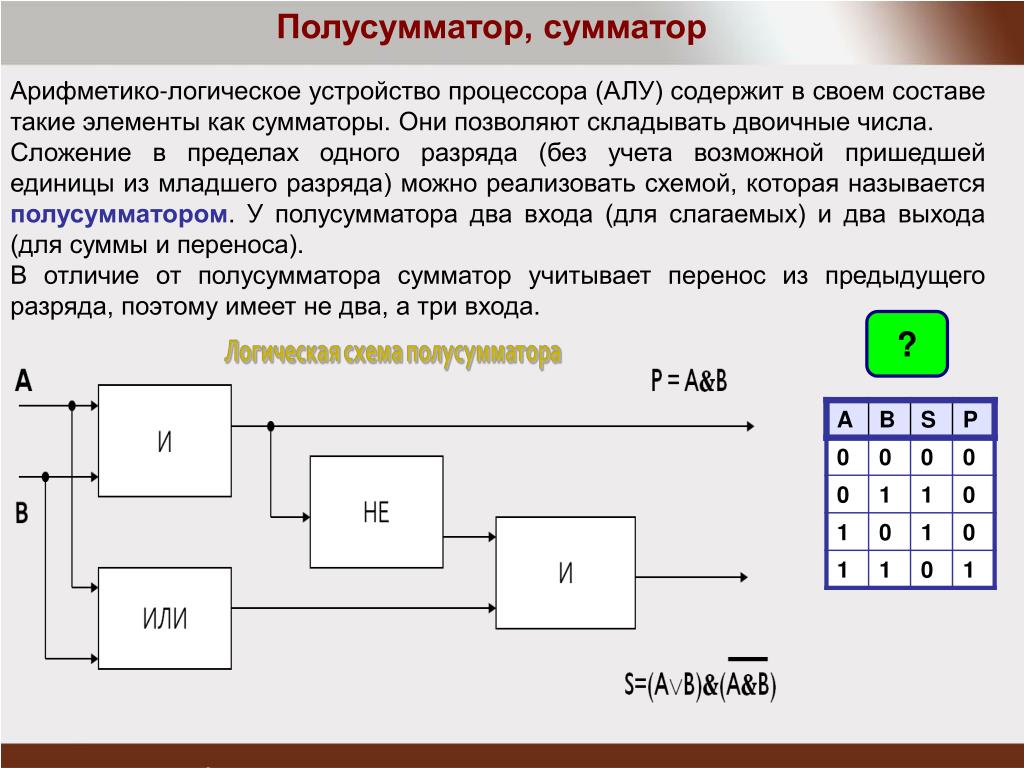
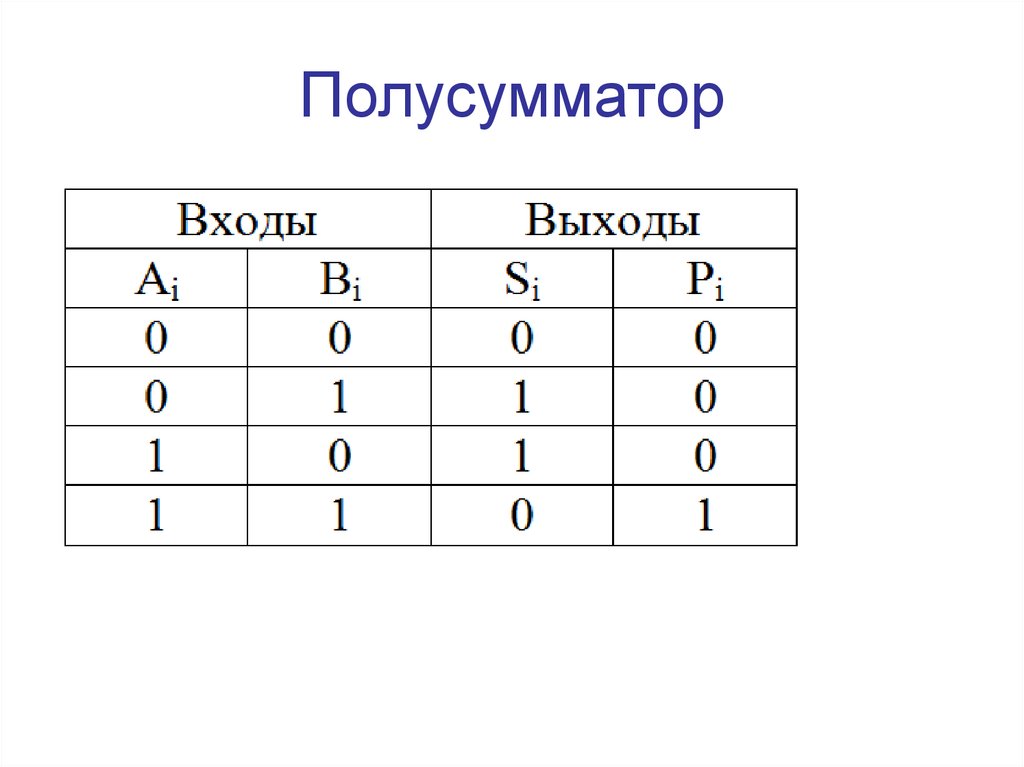
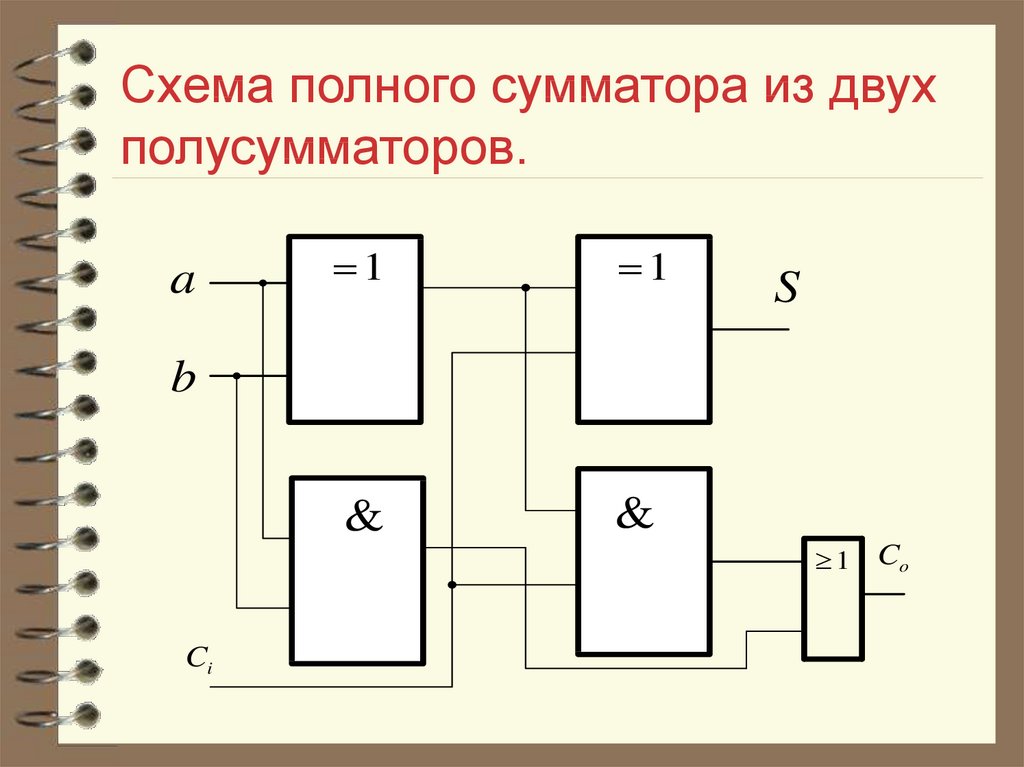
Полусумматор — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, трёхступенчатая разновидность которого состоит из двух полусумматоров и логического элемента 2ИЛИ.
Содержание
|
История
- 1939 год — Джордж Штибиц (Georg Stibits) из компании Bell Laboratories создал первый двоичный полусумматор «Model K Аdder» на двух электромеханических реле [1].
- 1958 год — в МГУ (мехмат) Н. П. Брусенцов построил первую электронную троичную ЭВМ «Сетунь» с первым электронным троичным полусумматором[2].
Двоичный полусумматор может быть определён тремя способами:
1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.
Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.
Двоичный полусумматор
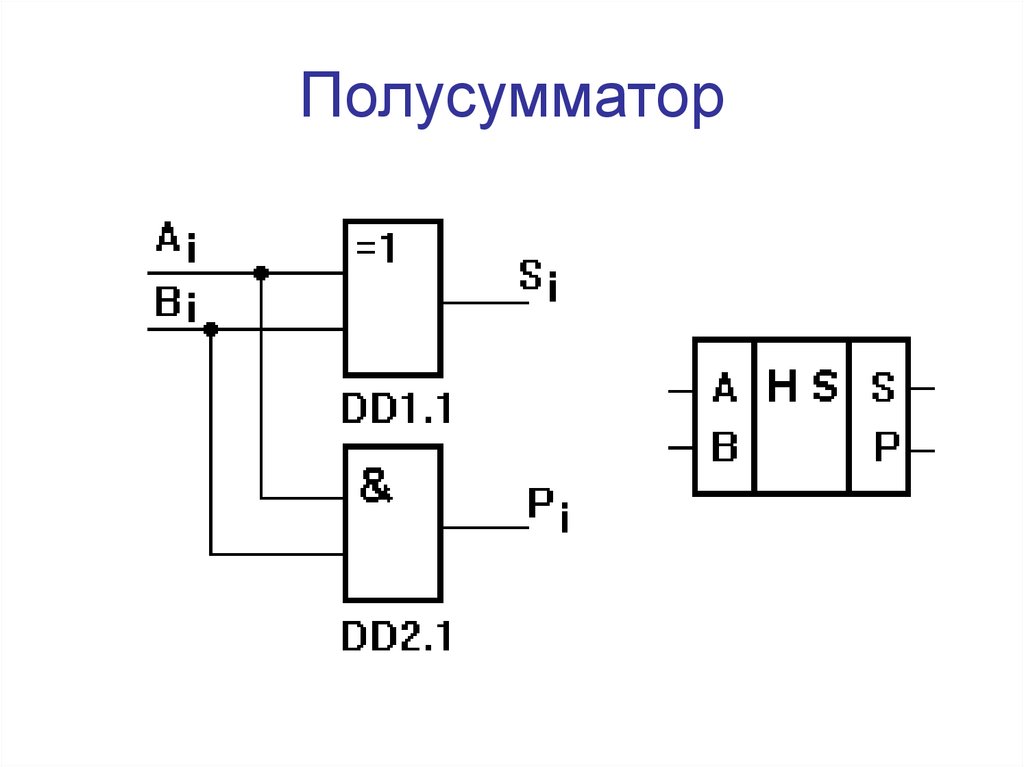
Двоичный полусумматор представляет собой объединение двух бинарных (двухоперандных) двоичных логических функций: сумма по модулю два — S и разряд переноса при двоичном сложении — C.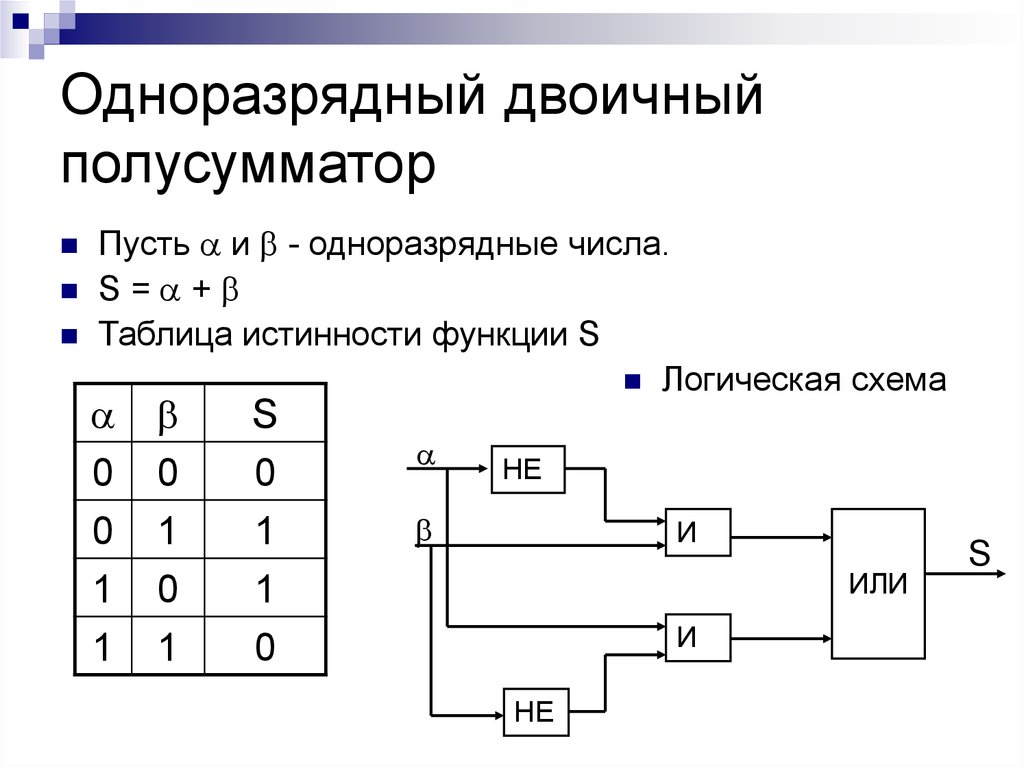
| x0=A | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | Название действия (функции) | Номер функции |
| S | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F2,6 |
| C | 1 | 0 | 0 | 0 | Бит переноса | F2,8 |
Ненулевой перенос образуется в 1-м случае из 4-х.
СДНФ суммы по модулю 2:
СДНФ бита переноса:
Полусумматор Штибица «Model K Аdder»
Полусумматор Штибица «Model K Аdder» состоит: из двух последовательно соединённых гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (S) и бита переноса (C)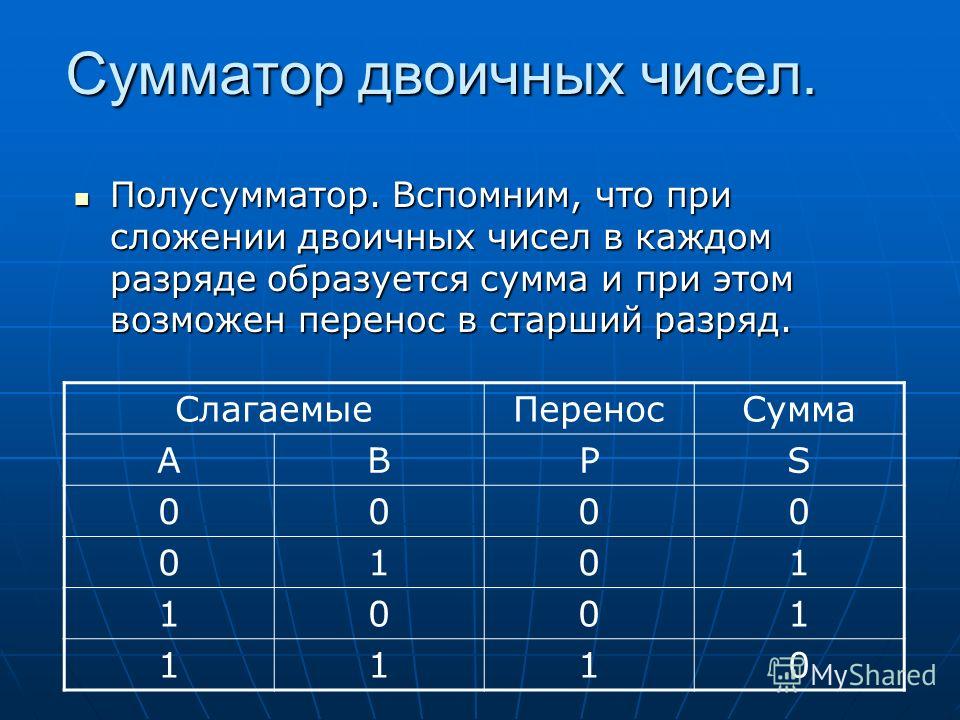
Так как существуют две троичных системы счисления — несимметричная, в которой в разряде переноса не бывает значения больше «1» и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем — трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.
Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «сложение по модулю 3» и «разряд переноса при троичном сложении».
| x1=x | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | Название действия (функции) | Номер функции |
| S | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Трит суммы по модулю 3 | |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Трит переноса |
Троичный полусумматор в симметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «младший разряд (трит) суммы (разности)» и «старший разряд (трит) суммы (разности) (разряд переноса при сложении в троичной симметричной системе счисления)».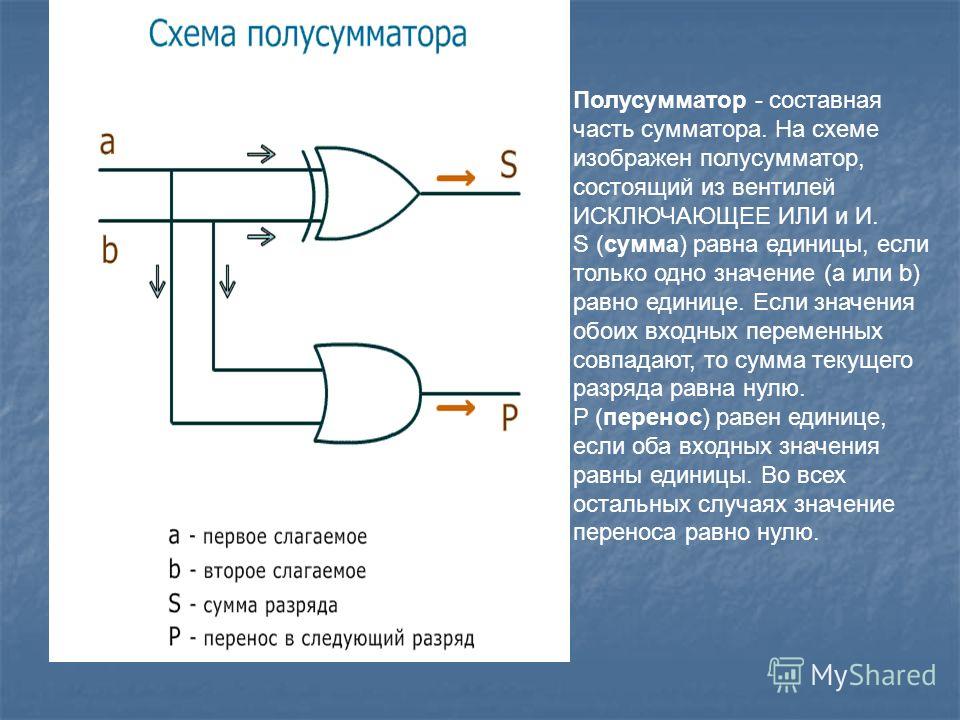
| x | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | Название действия (функции) | Номер функции |
| S | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | Младший трит суммы | F710107071=F-4160 |
| C | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | Старший трит суммы (трит переноса) | F100000007=F6560 |
«7» обозначает «-1»
Ненулевой перенос образуется в 2-х случаях из 9-ти.
Троичный трёхуровневый полусумматор описан в [3].
Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный (BCT) полусумматор, работающий в несимметричной троичной системе счисления приведён в [4], в разделе BCT Addition, в подразделе (f) Circuit diagram и, с ошибочным названием «двухразрядный BCT сумматор», в [5] на рис.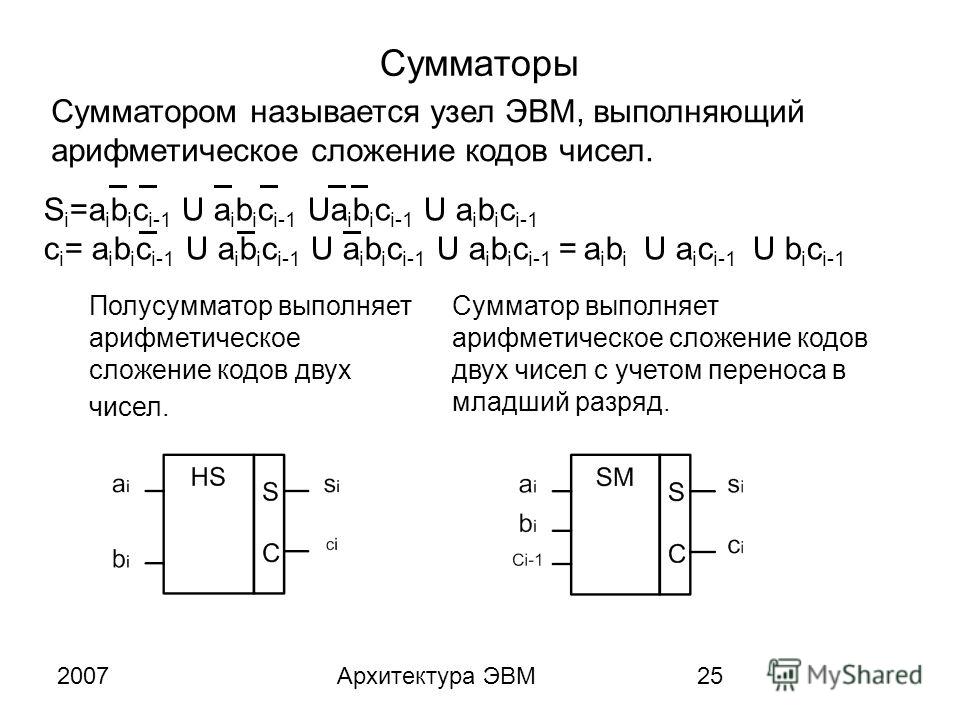 3.
3.
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов, описанного в
Троичный зеркально-симметричный одноразрядный полусумматор описан в [8].
См. также
- Сумматор
Ссылки
- ↑ 1 2 http://www.computerhistory.org/collections/accession/XD127.80 Computer History Museum
- ↑ http://www.computer-museum.ru/histussr/setun2.htm Малая автоматическая цифровая машина “Сетунь”. Н. П. Брусенцов, Е. А. Жоголев, В. В. Веригин, С. П. Маслов, А. М. Тишулина
- ↑ http://spanderashvili.narod.ru/PA.pdf Астраханский Государственный Технический Университет, Кафедра «Автоматизированные системы обработки информации и управления», Курсовая работа по дисциплине «Объектно-ориентированное проограммирование» по специальности 220200 «Автоматизированные системы обработки информации и управления», Выполнили Морозов А.

- ↑ http://www.dcs.gla.ac.uk/~simon/teaching/CS1Q-students/systems/tutorials/tut3sol.pdf CS1Q Computer Systems
- ↑ http://314159.ru/kushnerov/kushnerov1.pdf Троичная цифровая техника. Ретроспектива и современность
- ↑ Троичный бинарный сумматор в троичной несимметричной системе счисления в трёхбитной системе троичных логических элементов. А.Куликов
- ↑ http://andserkul.narod2.ru/troichnie_summatori/ А.С.Куликов. Троичные сумматоры
- ↑ Компьютеры Фибоначчи. Троичное зеркально-симметричное сложение и вычитание
Полусумматор | это… Что такое Полусумматор?
Полусумматор — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а
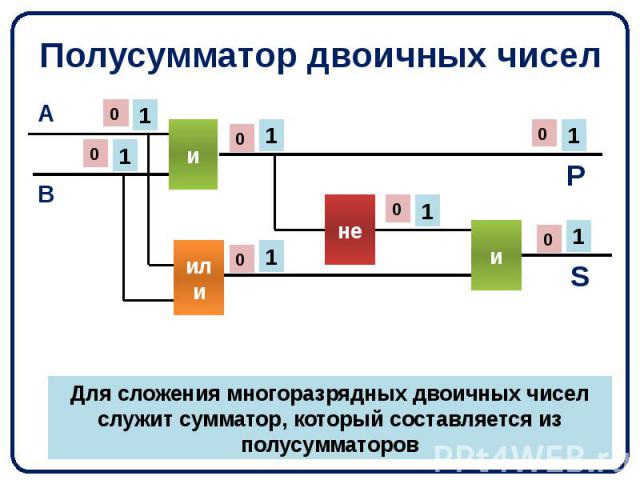 Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, трёхступенчатая разновидность которого состоит из двух полусумматоров и логического элемента 2ИЛИ.
Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, трёхступенчатая разновидность которого состоит из двух полусумматоров и логического элемента 2ИЛИ.Содержание
|
История
- 1939 год — Джордж Штибиц (Georg Stibits) из компании Bell Laboratories создал первый двоичный полусумматор «Model K Аdder» на двух электромеханических реле [1].
- 1958 год — в МГУ (мехмат) Н. П. Брусенцов построил первую электронную троичную ЭВМ «Сетунь» с первым электронным троичным полусумматором[2].

Двоичный полусумматор может быть определён тремя способами:
1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.
Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.
Двоичный полусумматор
Двоичный полусумматор представляет собой объединение двух бинарных (двухоперандных) двоичных логических функций: сумма по модулю два — S и разряд переноса при двоичном сложении — C.
| x0=A | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | Название действия (функции) | Номер функции |
| S | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F2,6 |
| C | 1 | 0 | 0 | 0 | Бит переноса | F2,8 |
Ненулевой перенос образуется в 1-м случае из 4-х.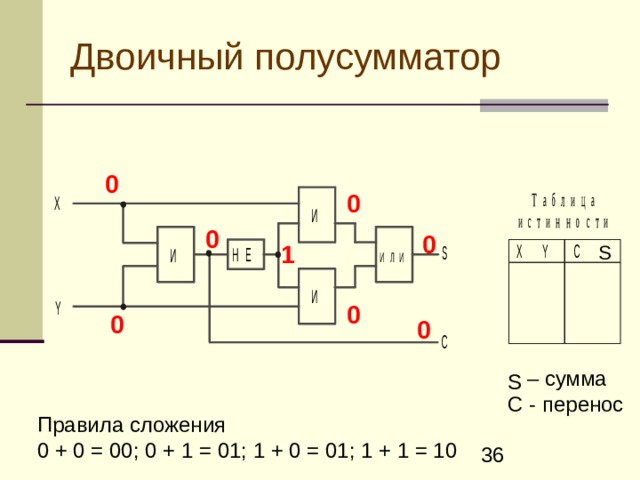
СДНФ суммы по модулю 2:
СДНФ бита переноса:
Полусумматор Штибица «Model K Аdder»
Полусумматор Штибица «Model K Аdder» состоит: из двух последовательно соединённых гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (S) и бита переноса (C)[1].
Так как существуют две троичных системы счисления — несимметричная, в которой в разряде переноса не бывает значения больше «1» и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем — трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.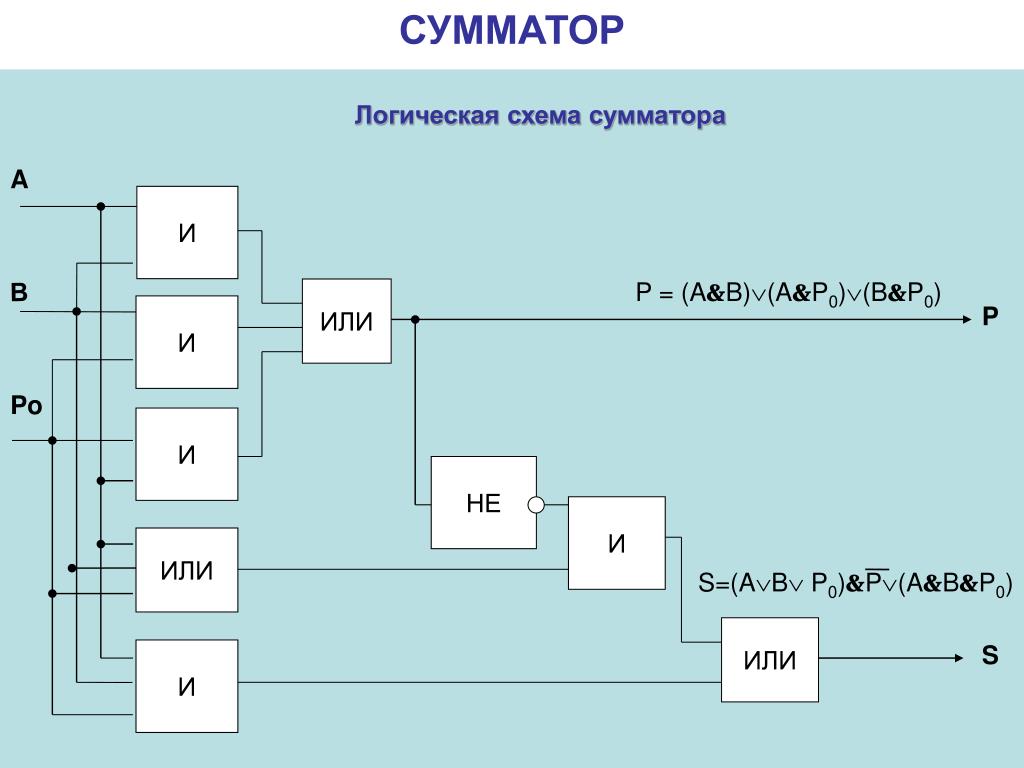
Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «сложение по модулю 3» и «разряд переноса при троичном сложении».
| x1=x | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | Название действия (функции) | Номер функции |
| S | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | Трит суммы по модулю 3 | |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | Трит переноса |
Троичный полусумматор в симметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «младший разряд (трит) суммы (разности)» и «старший разряд (трит) суммы (разности) (разряд переноса при сложении в троичной симметричной системе счисления)».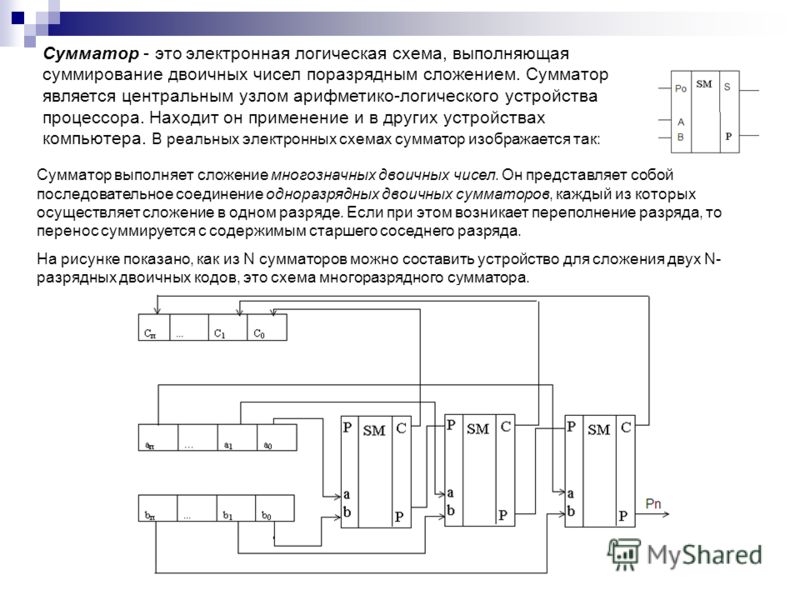
| x1=x | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0=y | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | Название действия (функции) | Номер функции |
| S | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | Младший трит суммы | F710107071=F-4160 |
| C | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | Старший трит суммы (трит переноса) | F100000007=F6560 |
«7» обозначает «-1»
Ненулевой перенос образуется в 2-х случаях из 9-ти.
Троичный трёхуровневый полусумматор описан в [3].
Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный (BCT) полусумматор, работающий в несимметричной троичной системе счисления приведён в [4], в разделе BCT Addition, в подразделе (f) Circuit diagram и, с ошибочным названием «двухразрядный BCT сумматор», в [5] на рис.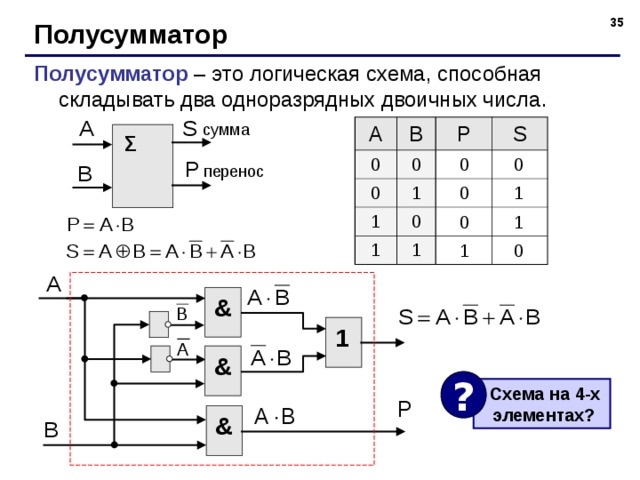 3.
3.
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов, описанного в [6][7].
Троичный зеркально-симметричный одноразрядный полусумматор описан в [8].
См. также
- Сумматор
Ссылки
- ↑ 1 2 http://www.computerhistory.org/collections/accession/XD127.80 Computer History Museum
- ↑ http://www.computer-museum.ru/histussr/setun2.htm Малая автоматическая цифровая машина “Сетунь”. Н. П. Брусенцов, Е. А. Жоголев, В. В. Веригин, С. П. Маслов, А. М. Тишулина
- ↑ http://spanderashvili.narod.ru/PA.pdf Астраханский Государственный Технический Университет, Кафедра «Автоматизированные системы обработки информации и управления», Курсовая работа по дисциплине «Объектно-ориентированное проограммирование» по специальности 220200 «Автоматизированные системы обработки информации и управления», Выполнили Морозов А.
 В., Спандерашвили Д.В., Алтуфьев М.Ю., Проверил к.т.н., доц. Лаптев В.В., Гл.XXIV Троичный полусумматор. Астрахань-2001 г.
В., Спандерашвили Д.В., Алтуфьев М.Ю., Проверил к.т.н., доц. Лаптев В.В., Гл.XXIV Троичный полусумматор. Астрахань-2001 г. - ↑ http://www.dcs.gla.ac.uk/~simon/teaching/CS1Q-students/systems/tutorials/tut3sol.pdf CS1Q Computer Systems
- ↑ http://314159.ru/kushnerov/kushnerov1.pdf Троичная цифровая техника. Ретроспектива и современность
- ↑ Троичный бинарный сумматор в троичной несимметричной системе счисления в трёхбитной системе троичных логических элементов. А.Куликов
- ↑ http://andserkul.narod2.ru/troichnie_summatori/ А.С.Куликов. Троичные сумматоры
- ↑ Компьютеры Фибоначчи. Троичное зеркально-симметричное сложение и вычитание
Разница между полусуммером и полным сумматором
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 21 июн, 2022
Улучшить статью
Сохранить статью
1.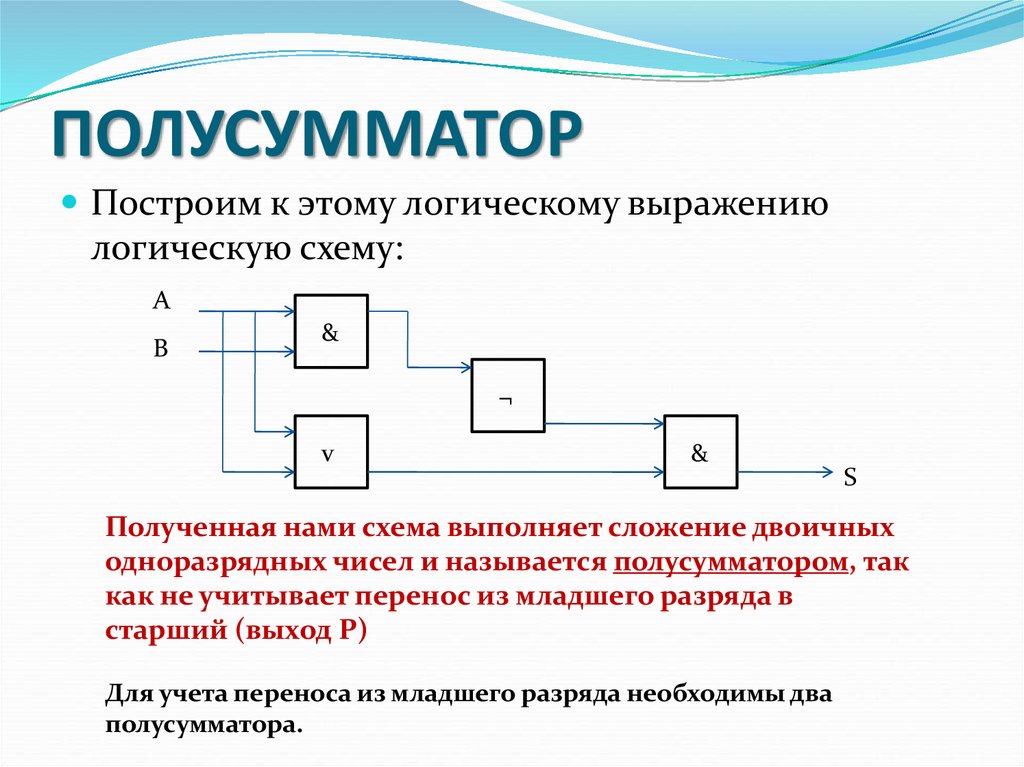 Полусумматор : Полусумматор представляет собой комбинационную логическую схему, которая разработана путем соединения одного элемента EX-OR и одного элемента AND. Схема полусумматора имеет два входа: A и B, которые добавляют две входные цифры и генерируют перенос и сумму.
Полусумматор : Полусумматор представляет собой комбинационную логическую схему, которая разработана путем соединения одного элемента EX-OR и одного элемента AND. Схема полусумматора имеет два входа: A и B, которые добавляют две входные цифры и генерируют перенос и сумму.
Выход, полученный с помощью логического элемента EX-OR, представляет собой сумму двух чисел, а результат, полученный с помощью логического элемента AND, представляет собой перенос. Не будет переадресации добавления переноса, потому что нет логического элемента для его обработки. Таким образом, это называется схемой полусумматора.
Логическое выражение:
Сумма = XOR B Carry = A AND B
Таблица истинности:
2. Полный сумматор : Полный сумматор — это схема, состоящая из двух вентилей EX-OR, двух вентилей AND и двух вентилей AND.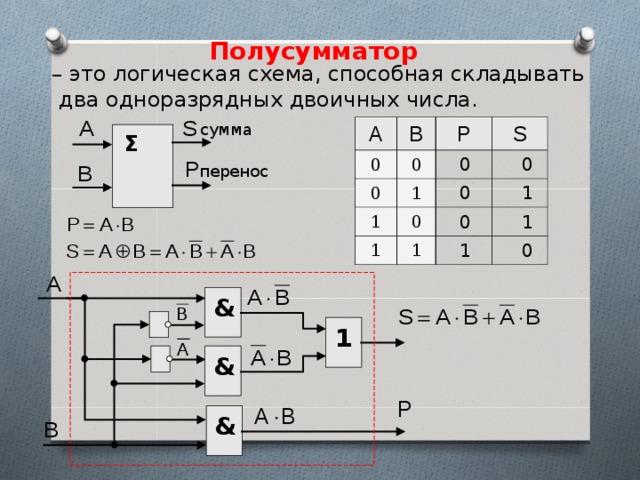 Полный сумматор — это сумматор, который добавляет три входа и производит два выхода, которые состоят из двух вентилей EX-OR, двух вентилей AND и одного вентиля ИЛИ. Первые два входа — это A и B, а третий вход — входной перенос как C-IN. Выходной перенос обозначается как C-OUT, а нормальный выход обозначается как S, что является СУММОЙ.
Полный сумматор — это сумматор, который добавляет три входа и производит два выхода, которые состоят из двух вентилей EX-OR, двух вентилей AND и одного вентиля ИЛИ. Первые два входа — это A и B, а третий вход — входной перенос как C-IN. Выходной перенос обозначается как C-OUT, а нормальный выход обозначается как S, что является СУММОЙ.
Уравнение, полученное вентилем EX-OR, представляет собой сумму двоичных цифр. В то время как выход, полученный логическим элементом И, является переносом, полученным путем сложения.
Таблица истинности:
Логическое выражение:
СУММ = (A XOR B) XOR Cin = (A ⊕ B) ⊕ Cin ВЫПОЛНЕНИЕ = A AND B ИЛИ Cin(A XOR B) = A.B + Cin(A ⊕ B)
Разница между полусумматорами и полными сумматорами:
| S.No. | Параметры | Полусумматор | Полный сумматор |
|---|---|---|---|
| 1. | Описание | Полусумматор представляет собой комбинационную логическую схему, которая складывает две однобитовые цифры.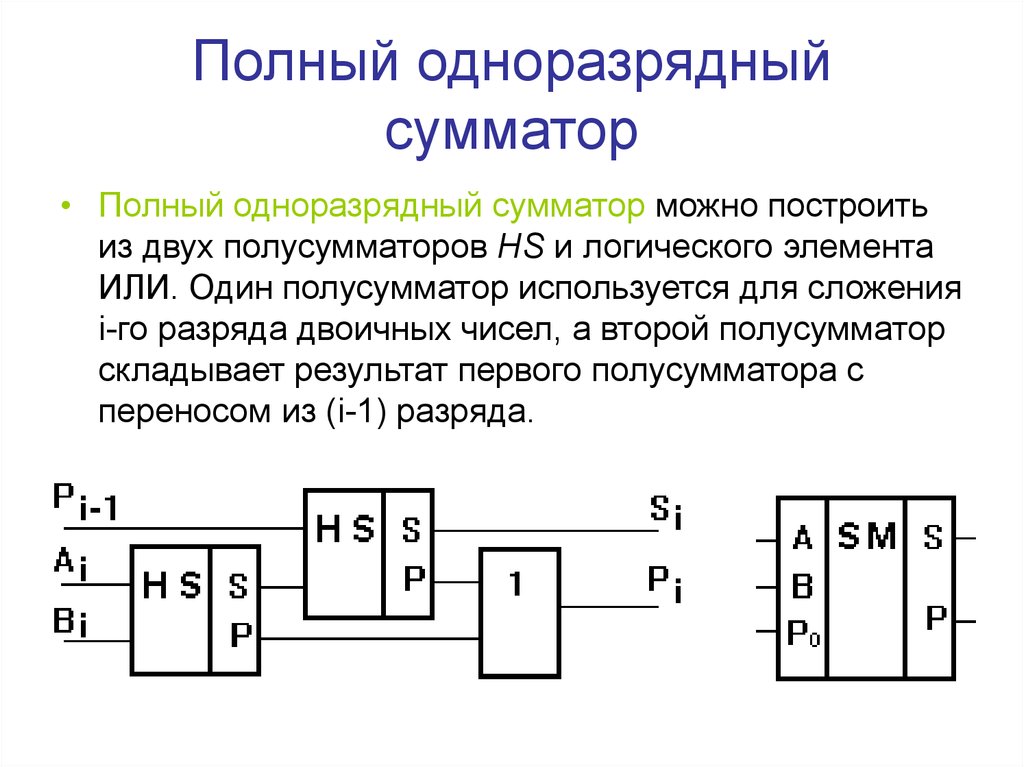 Полусумматор производит сумму двух входов. Полусумматор производит сумму двух входов. | Полный сумматор — это комбинационная логическая схема, выполняющая операцию сложения трех однобитовых двоичных чисел. Полный сумматор производит сумму трех входов и значения переноса. |
| 2. | Предыдущий перенос | Предыдущий перенос не используется. | Используется предыдущий перенос. |
| 3. | Входы | Полусумматор имеет два входных бита (A, B). | В полном сумматоре имеется три входных бита (A, B, C-in). |
| 4. | Выходы | Сгенерированный вывод состоит из двух битов — сумма и перенос из 2-битного входа. | Сгенерированный вывод состоит из двух битов — сумма и перенос из 3-битного ввода. |
| 5. | Используется как | Схема полусумматора не может использоваться так же, как схема полного сумматора. | Полную схему сумматора можно использовать вместо схемы половинного сумматора.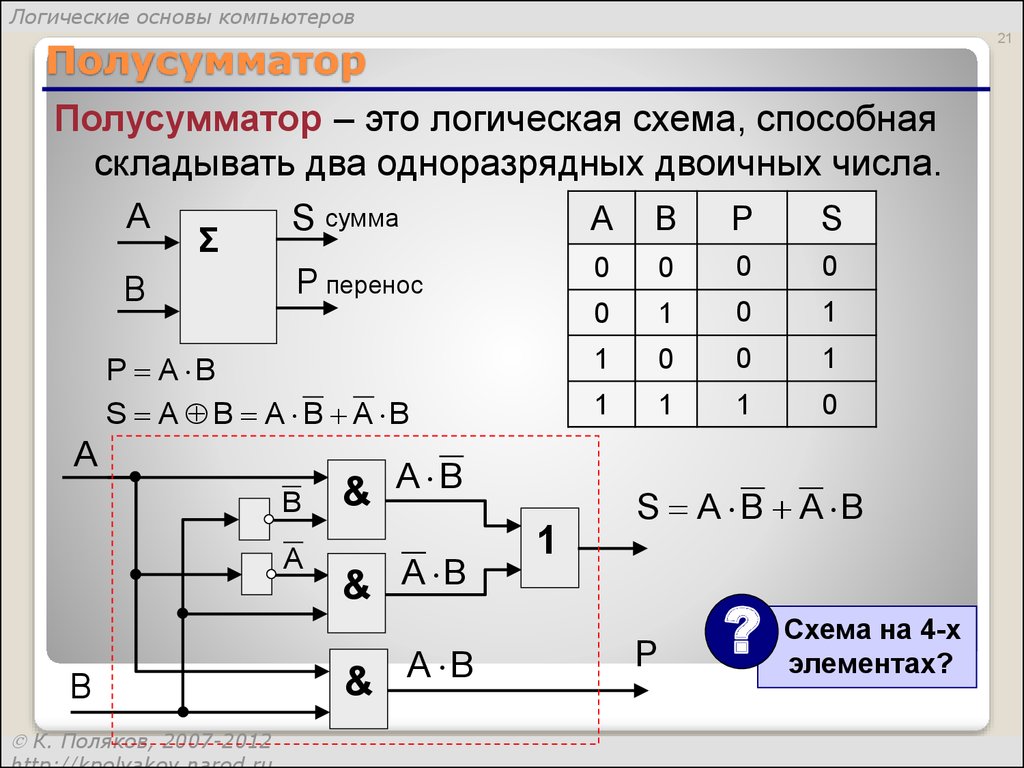 |
| 6. | Характеристика | Простота и удобство реализации | Конструкция полного сумматора не так проста, как половинного сумматора. |
| 7. | Логическое выражение | Логическое выражение для полусумматора: S=a⊕b ; С=а*б. | Логическое выражение для полного сумматора: S=a⊕b⊕Cin; Cout=(a*b)+(Cin*(a⊕b)). |
| 8. | Логические элементы | Состоит из одного вентиля EX-OR и одного вентиля AND. | Он состоит из двух логических элементов «ИСКЛЮЧАЮЩЕЕ ИЛИ», двух вентилей «И» и одного вентиля «ИЛИ». |
| 6 | Приложения | Используется в калькуляторах, компьютерах, цифровых измерительных устройствах и т. д. | Используется в многоразрядном сложении, цифровых процессорах и т. д.0174 |
Half Adder — Javatpoint
следующий → ← предыдущая Полусумматор — это базовый строительный блок для сложения двух чисел в качестве двух входных данных и получения двух выходных данных. Блок-схемаТаблица истинностиВ приведенной выше таблице
Форма SOP суммы и переноса следующая: Сумма = x’y+xy’ На блок-схеме мы видели, что она содержит два входа и два выхода. augent и addent биты являются входными состояниями, а переносят и сумма являются выходными состояниями полусумматора. Полусумматор построен с помощью следующих двух логических элементов:
1. Логический элемент исключающего ИЛИ с 2 входами или вентильный элемент исключающего ИЛИБит Sum генерируется с помощью Exclusive-OR или Ex-OR Ворота. Это символ ворот EX-OR . На приведенной выше диаграмме «A» и «B» — это входные данные, а «SUMOUT» — это окончательный результат после выполнения операции XOR для обоих чисел. Таблица истинности ворот EX-OR выглядит следующим образом: Из приведенной выше таблицы видно, что вентиль XOR дает результат 1, когда оба входа различны. Когда оба входа одинаковы, XOR дает результат 0. Чтобы узнать больше о вентиле XOR, нажмите здесь. 2. 2-входовой вентиль И: Логический элемент XOR не может сгенерировать бит переноса. Для этой цели мы используем другой вентиль под названием AND Gate. Логический элемент И дает правильный результат переноса. |


 также
также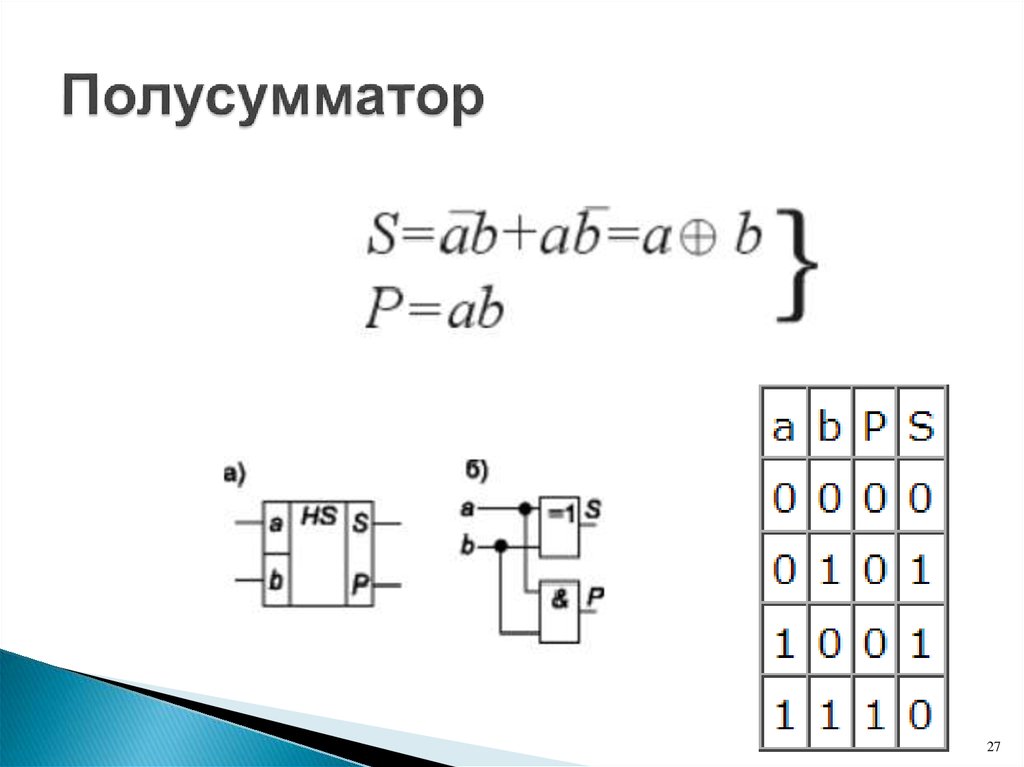
 В., Спандерашвили Д.В., Алтуфьев М.Ю., Проверил к.т.н., доц. Лаптев В.В., Гл.XXIV Троичный полусумматор. Астрахань-2001 г.
В., Спандерашвили Д.В., Алтуфьев М.Ю., Проверил к.т.н., доц. Лаптев В.В., Гл.XXIV Троичный полусумматор. Астрахань-2001 г.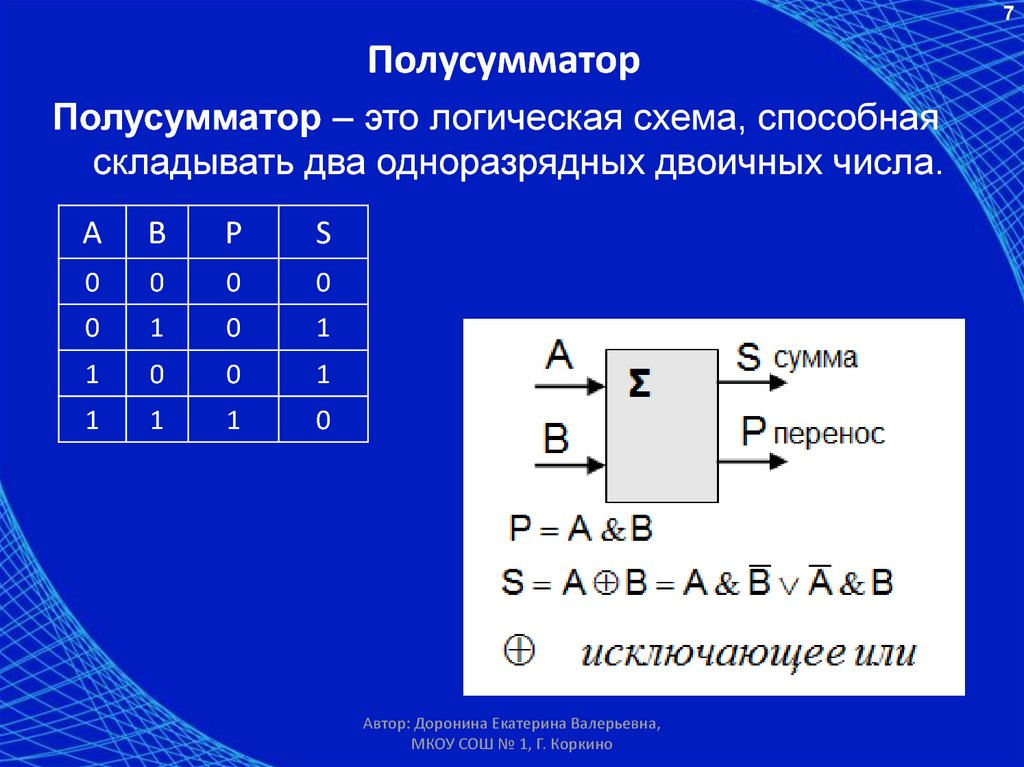 Сумматор используется для выполнения операции ИЛИ над двумя однобитными двоичными числами. Биты augent и addent являются двумя входными состояниями, а ‘перенос ‘ и ‘сумма ‘ являются двумя выходными состояниями полусумматора.
Сумматор используется для выполнения операции ИЛИ над двумя однобитными двоичными числами. Биты augent и addent являются двумя входными состояниями, а ‘перенос ‘ и ‘сумма ‘ являются двумя выходными состояниями полусумматора.