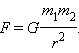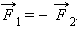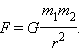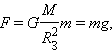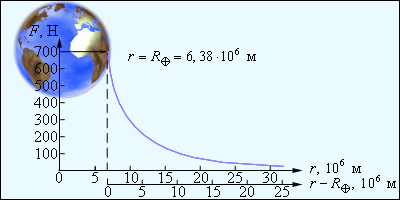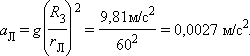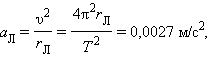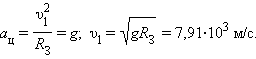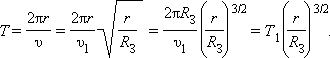Учебник. Закон всемирного тяготения. Движение тел под действием силы тяжести
По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.
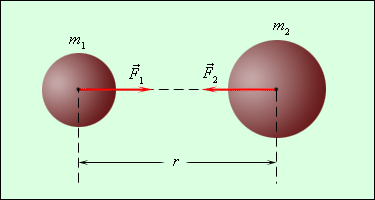
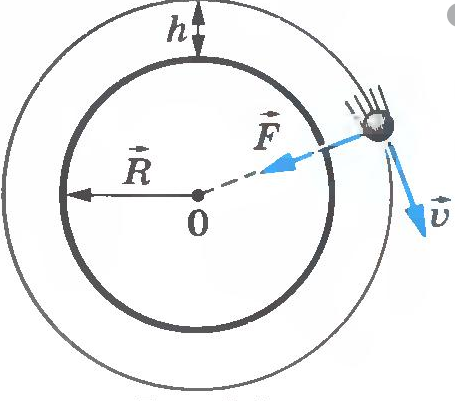
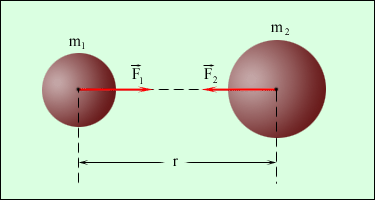
Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в § 1.23. У тела в виде однородного шара центр масс совпадает с центром шара.
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет (см. §1.24), открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
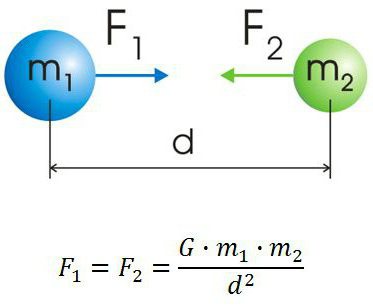
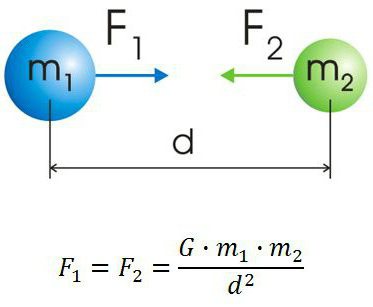
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними: F=G m 1 m 2 r 2 .
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной G = 6,67ċ10–11 Нċм2/кг2 (СИ).
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все они находят объяснение на основе закона всемирного тяготения и законов динамики.
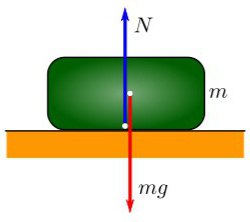
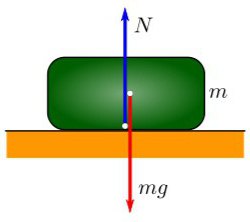
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38ċ106 м), можно вычислить массу Земли М: M= g R З 2 G =5,98ċ 10 24 кг.
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84ċ106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет a Л =g ( R 3 r Л ) 2 = 9,81м/ с 2 60 2 =0,0027 м/ с 2 .
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения (см. §1.6): a Л = υ 2 r Л = 4 π 2 r Л T 2 =0,0027 м/ с 2 , где
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением: g Л =G M Л R Л 2 =G M З T З 2 3,7 2 81 =0,17 g=1,66м/ с 2 .
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.
Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной. Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения, получим: a n = υ 1 2 R З =g; υ 1 = g R З =7,91ċ 10 3 м/с.
Двигаясь с такой скоростью, спутник облетал бы Землю за время T 1 = 2π R 3 υ 1 =84 мин 12 с.
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия υ 2 r =g R З 2 r 2 , υ= g R З R З r = υ 1 R З r .
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период T обращения такого спутника равен T= 2πr υ = 2πr υ l r R З = 2π R З υ 1 ( r R З ) 3/2 = T 1 ( r R З ) 3/2 .
Здесь T1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6 RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6 RЗ называется геостационарной.
Гравитационные силы. Закон всемирного тяготения. 🐲 СПАДИЛО.РУ
Все тела взаимодействуют друг с другом. Так, две материальные точки, обладающие массой, притягиваются друг к другу с некоторой силой, которую называют гравитационной, или силой всемирного тяготения.
Сила всемирного тяготения — сила, с которой все тела притягиваются друг к другу.
Закон всемирного тяготенияСила взаимного притяжения двух тел прямо пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними.
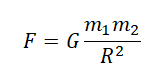
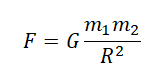
F — сила всемирного тяготения, m1 и m2 — массы двух притягивающихся друг к другу тел, R — расстояние между этими телами, G — гравитационная постоянная (G = 6,67∙10–11 Н ∙ м2/кг2).
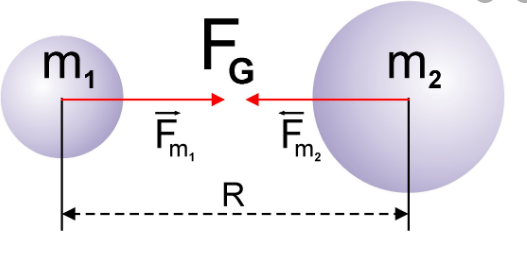

Сила всемирного тяготения направлена по линии, соединяющей центры двух тел.
Гравитационная постоянная численно равна силе притяжения между двумя точечными телами массой 1 кг каждое, если расстояние между ними равно 1 м. Если R = 1 м, m1 = 1 кг и m2 = 1 кг, то F = G.
G = 6,67∙10–11 Н ∙ м2/кг2.
Сила тяжести
Согласно закону всемирного тяготения, все тела притягиваются между собой. Так, Земля притягивает к себе падающий на нее мяч, а мяч притягивает к себе Землю.
Сила тяжести — сила, с которой Земля притягивает к себе тела.
Сила тяжести действует на все тела, находящиеся в поле притяжения Земли. Она всегда направлена к центру нашей планеты.


Силу тяжести можно рассчитать с помощью закона всемирного тяготения. Тогда одна из масс будет равна массе земли. Обозначим ее большой буквой M. Вторая масса будет принадлежать телу, притягивающемуся к Земли. Обозначим его m. В качестве R будет служить радиус Земли. В таком случае сила тяжести будет определяться формулой:
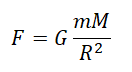
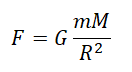
Вывод формулы ускорения свободного падения
Согласно второму закону Ньютона, сила, которая действует на тело, сообщает ему ускорение. Поэтому силу тяжести также можно выразить через это ускорение. Обозначим его g — ускорение свободного падения.


Пример №1. Мальчик массой 50 кг прыгнул под углом 45 градусов к горизонту. Найти силу тяжести, действующую на него во время прыжка.
Сила тяжести зависит только от массы тела и ускорения свободного падения. Направлена она всегда к центру Земли, и от характера движения тела не зависит. Поэтому:
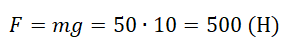
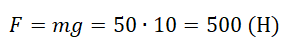
Мы получили две формулы для вычисления силы тяжести: одну — исходя из закона всемирного тяготения, вторую — исходя из второго закона Ньютона. Приравняем правые части формул и получим:


Отсюда:
Формула расчета ускорения свободного падения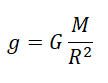
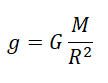
Пример №2. Рассчитать ускорение свободного падения на Луне. Считать, что радиус Луны равен 1736 км, а ее масса — 7,35∙1022 кг.
Переведем километры в метры: 1736 км = 1736000 м.
Первая космическая скорость
Исаак Ньютон смог доказать, что причиной падения тел на Землю, движения Луны вокруг Земли и движения Земли вокруг Солнца является сила тяготения. Если камень бросить в горизонтальном направлении, его траектория будет отклонена от прямой линии под действием земной силы тяжести. Если же придать этому камню большую скорость, камень приземлится на большем расстоянии. Значит, существует такая скорость, при которой камень не приземлится, а начнет бесконечно вращаться вокруг Земли.


Вывод формулы первой космической скорости
Когда тело массой m вращается на некоторой высоте h, расстояние между ним и центром Земли равно сумме этой высоты и радиуса Земли. Поэтому сила тяготения между этим телом и Землей будет равна:


Движение тела вокруг планеты — частный случай движения тела по окружности с постоянной по модулю скоростью. Мы уже знаем, что такое тело движется с центростремительным ускорением, направленным к центру окружности. В данном случае центростремительное ускорение будет направлено к центру Земли. Это ускорение сообщает телу сила тяготения.

Так как тело движется на некоторой высоте h от поверхности Земли, центростремительное ускорение будет определяться формулой:
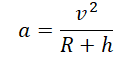
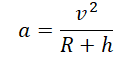
Подставив это ускорение в формулу второго закона Ньютона, получим силу, с которой Земля притягивает к себе тело массой m:
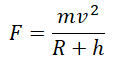
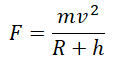
Приравняем правые части формул, следующих из закона всемирного тяготения и второго закона Ньютона, и получим:
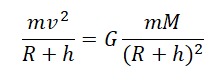
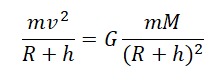
Отсюда скорость, с которой должно тело массой m бесконечно вращаться вокруг Земли на высоте h, равна:


Скорость бесконечно вращающегося вокруг Земли тела не зависит от его массы. Она зависит только от высоты, на которой оно находится. Чем выше высота, тем меньше скорость его вращения.
Тело, вращающееся вокруг планеты, называется ее спутником. Чтобы любое тело стало спутником Земли, нужно сообщить ему некоторую скорость на поверхности планеты в горизонтальном направлении. Высота h в этом случае равна 0. Тогда эта скорость будет равна:
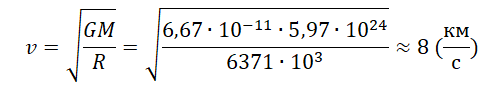
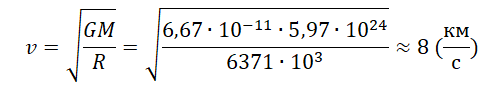
8 км/с — первая космическая скорость Земли.
Пример №3. Рассчитать первую космическую скорость для Венеры. Считать, что масса Венеры равна 4,87∙1024 кг, а ее радиус равен 6052 км.
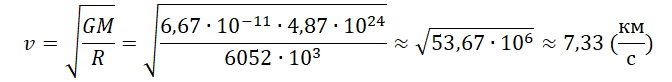
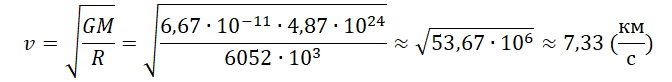
Закон всемирного тяготения. Движение тел под действием силы тяжести — Студопедия
По второму закону Ньютона причиной изменения движения, т. е. причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.
Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). Понятие центра масс тела будет строго определено в § 1.23. У тела в виде однородного шара центр масс совпадает с центром шара.
|
Рисунок 1.10.1.
Гравитационные силы притяжения между телами. 
|
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет (см. §1.24), открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
|
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
| G = 6,67·10–11 Н·м2/кг2 (СИ). |
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики.
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если М – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна
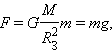
|
где g – ускорение свободного падения у поверхности Земли:

|
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения (см. §1.5). Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли М:
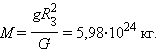
|
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
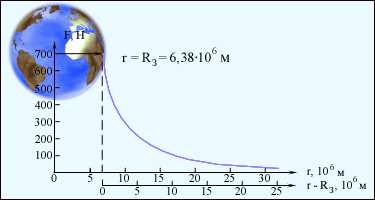
|
| Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли. |
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
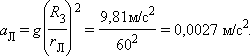
|
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения (см. §1.6):
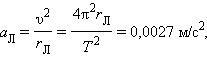
|
где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением:
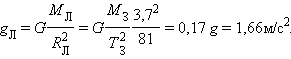
|
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.
Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной (см. §1.24). Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения (см. §1.6), получим:
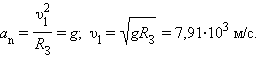
|
Двигаясь с такой скоростью, спутник облетал бы Землю за время 
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия
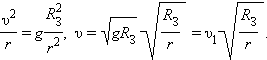
|
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период T обращения такого спутника равен
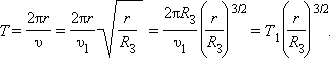
|
Здесь T1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Движение тела под действием силы тяжести: определение, формулы
Движение тела под действием силы тяжести является одной из центральных тем в динамической физике. О том, что раздел динамики базируется на трех законах Ньютона, знает даже обычный школьник. Давайте постараемся разобрать эту тему досконально, а статья, подробно описывающая каждый пример, поможет нам сделать изучение движения тела под действием силы тяжести максимально полезным.
Немного истории
Испокон веков люди с любопытством наблюдали за различными явлениями, происходящими в нашей жизни. Человечество долгое время не могло понять принципы и устройство многих систем, однако длительный путь изучения окружающего мира привел наших предков к научному перевороту. В наши дни, когда технологии развиваются с неимоверной скоростью, люди почти не задумываются о том, каким образом работают те или иные механизмы.

А между тем наши предки всегда интересовались загадками природных процессов и устройством мира, искали ответы на самые сложные вопросы и не переставали изучать, пока не находили на них ответы. Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.

Тот факт, что закономерности движения тел, описанные более 500 лет назад, актуальны и по сей день, означает, что наша планета подчиняется неизменным законам. Современному человеку необходимо хотя бы поверхностно изучить основные принципы обустройства мира.
Основные и вспомогательные понятия динамики
Для того чтобы полностью понять принципы подобного движения, следует сначала ознакомиться с некоторыми понятиями. Итак, самые необходимые теоретические термины:
- Взаимодействие — это воздействие тел друг на друга, при котором происходит изменение или начало их движения относительно друг друга. Различают четыре вида взаимодействия: электромагнитное, слабое, сильное и гравитационное.
- Скорость — это физическая величина, обозначающая быстроту, с которой двигается тело. Скорость является вектором, то есть имеет не только значение, но также и направление.
- Ускорение — та величина, которая показывает нам быстроту изменения скорости тела в промежуток времени. Она также является векторной величиной.
- Траектория пути — это кривая, а иногда — прямая линия, которую очерчивает тело при движении. При равномерном прямолинейном движении траектория может совпадать со значением перемещения.
- Путь — это длина траектории, то есть ровно столько, сколько прошло тело за определенное количество времени.
- Инерциальная система отсчета — это среда, в которой выполняется первый закон Ньютона, то есть тело сохраняет свою инерцию, при условии, что полностью отсутствуют все внешние силы.
Вышеуказанных понятий вполне достаточно для того, чтобы грамотно начертить или представить в голове моделирование движения тела под действием силы тяжести.

Что значит сила?
Давайте перейдем к основному понятию нашей темы. Итак, сила — это величина, смысл которой заключается в воздействии или влиянии одного тела на другое количественно. А сила тяжести — это та сила, которая действует абсолютно на каждое тело, находящееся на поверхности или вблизи нашей планеты. Возникает вопрос: откуда же берется эта самая сила? Ответ заключается в законе всемирного тяготения.
А что такое сила тяжести?
На любое тело со стороны Земли оказывает влияние гравитационная сила, которая сообщает ему некоторое ускорение. Сила тяжести всегда имеет вертикальное направление вниз, к центру планеты. Иначе говоря, сила тяжести притягивает предметы к Земле, вот почему предметы всегда падают вниз. Получается, что сила тяжести — это частный случай силы всемирного тяготения. Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m1 х m2) / R2.
Чему равно ускорение свободного падения?
Тело, которое отпустили с некоторой высоты, всегда летит вниз под действием силы притяжения. Движение тела под действием силы тяжести вертикально вверх и вниз можно описать уравнениями, где основной константой будет являться значение ускорения «g». Эта величина обусловлена исключительно действием силы притяжения, и ее значение приблизительно равно 9,8 м/с2. Получается, что тело, брошенное с высоты без начальной скорости, будет двигаться вниз с ускорением равным значению «g».
Движение тела под действием силы тяжести: формулы для решения задач
Основная формула нахождения силы тяжести выглядит следующим образом: Fтяжести = m х g, где m — это масса тела, на которое действует сила, а «g» — ускорение свободного падения (для упрощения задач его принято считать равным 10 м/с2).
Есть еще несколько формул, используемых для нахождения того или иного неизвестного при свободном движении тела. Так, например, для того чтобы вычислить пройденный телом путь, необходимо подставить известные значения в эту формулу: S = V0 х t + a х t2 / 2 (путь равен сумме произведений начальной скорости умноженной на время и ускорения на квадрат времени, деленной на 2).
Уравнения для описания вертикального движения тела
Движение тела под действием силы тяжести по вертикали можно описать уравнением, которое выглядит так: x = x0 + v0 х t + a х t2 / 2. Используя данное выражение, можно найти координаты тела в известный момент времени. Необходимо просто подставить известные в задаче величины: начальное местоположение, начальную скорость (если тело не просто отпустили, а толкнули с некоторой силой) и ускорение, в нашем случае оно будет равно ускорению g.
Таким же образом можно найти и скорость тела, которое движется под действием силы притяжения. Выражение для нахождения неизвестной величины в любой момент времени: v = v0 + g х t (значение начальной скорости может быть равным нулю, тогда скорость будет равна произведению ускорения свободного падения на значение времени, за которое тело совершает движение).
Движение тел под действием силы тяжести: задачи и способы их решений
При решении многих задач, связанных с силой тяжести, рекомендуем воспользоваться следующим планом:
- Определить для себя удобную инерциальную систему отсчета, обычно принято выбирать Землю, потому как она отвечает многим требованиям к ИСО.
- Нарисовать небольшой чертеж или рисунок, на котором изображены основные силы, действующие на тело. Движение тела под действием силы тяжести подразумевает набросок или схему, на которой указано, в каком направлении движется тело, если на него действует ускорение, равное g.
- Затем следует выбрать направление для проецирования сил и полученных ускорений.
- Записать неизвестные величины и определить их направление.
- И наконец, используя указанные выше формулы для решения задач, вычислить все неизвестные величины, подставив данные в уравнения для нахождения ускорения или пройденного пути.
Готовое решение легкой задачи
Когда речь идет о таком явлении, как движение тела под действием силы тяжести, определение того, каким способом практичнее решать поставленную задачу, может быть затруднительным. Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.
Некоторое тело отпустили с высоты 20 м без начальной скорости. Определить, за какое количество времени оно достигнет поверхности земли.
Решение: нам известен путь, пройденный телом, известно, что начальная скорость была равна 0. Также можем определить, что на тело действует только сила тяжести, получается, что это движение тела под действием силы тяжести, и поэтому следует воспользоваться этой формулой: S = V0 х t + a х t2/2. Так как в нашем случае a = g, то после некоторых преобразований получаем следующее уравнение: S = g х t2 / 2. Теперь осталось только выразить время через эту формулу, получаем, что t2 = 2S / g. Подставим известные величины (при этом считаем, что g = 10 м/с2) t2 = 2 х 20 / 10 = 4. Следовательно, t = 2 с.
Итак, наш ответ: тело упадет на землю за 2 секунды.
Трюк, позволяющий быстро решить задачу, состоит в следующем: можно заметить, что описанное движение тела в приведенной задаче происходит в одном направлении (вертикально вниз). Оно весьма схоже с равноускоренным движением, так как на тело не действует никакая сила, кроме силы тяжести (силой сопротивления воздуха пренебрегаем). Благодаря этому можно воспользоваться легкой формулой для нахождения пути при равноускоренном движении, минуя изображения чертежей с расстановкой действующих на тело сил.
Пример решения более сложной задачи
А теперь давайте посмотрим, как лучше решать задачи на движение тела под действием силы тяжести, если тело движется не вертикально, а имеет более сложный характер перемещения.
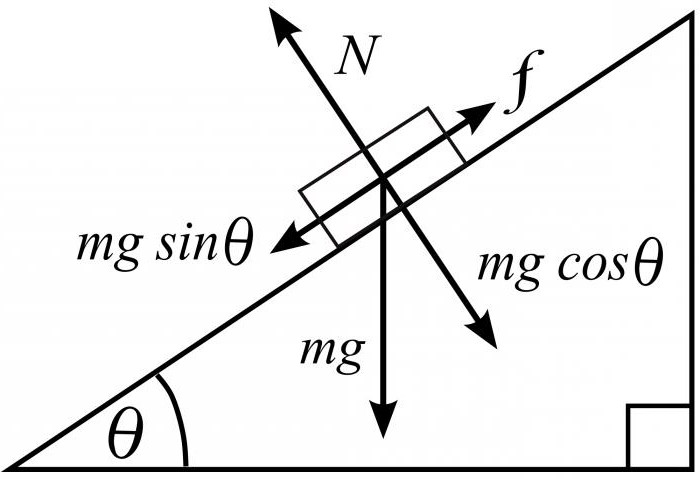
Например, следующая задача. Некоторый предмет массой m движется с неизвестным ускорением вниз по наклонной плоскости, коэффициент трения которой равен k. Определить значение ускорения, которое имеется при движении данного тела, если угол наклона α известен.
Решение: Следует воспользоваться планом, который описан выше. В первую очередь начертить рисунок наклонной плоскости с изображением тела и всех действующих на него сил. Получится, что на него действуют три составляющие: сила тяжести, трения и сила реакции опоры. Выглядит общее уравнение равнодействующих сил так: Fтрения + N + mg = ma.
Главной изюминкой задачи является условие наклонности под углом α. При проецировании сил на ось ox и ось oy необходимо учесть данное условие, тогда у нас получится следующее выражение: mg х sin α — Fтрения = ma (для оси ох) и N — mg х cos α = Fтрения (для оси oy).
Fтрения легко вычислить по формуле нахождения силы трения, она равна k х mg (коэффициент трения, умноженный на произведение массы тела и ускорения свободного падения). После всех вычислений остается только подставить найденные значения в формулу, получится упрощенное уравнение для вычисления ускорения, с которым движется тело вдоль наклонной плоскости.
Урок физики по теме «Движение тел в гравитационном поле»
Цели урока:
Образовательные:
- изучить движение тел в гравитационном поле;
- выработать умения воспринимать и излагать новый материал;
- научить использовать знания, полученные на уроках информатики при решении задач по физике;
- показать практическую значимость изученного материала.
Развивающие:
- развивать умения выделять главное, анализировать, делать выводы;
- развивать внимание, память, творческие способности учащихся;
- развивать познавательную, информационно-коммуникативную компетенции.
Воспитательные:
- формировать интерес учащихся к изучению физики;
- воспитывать чувство патриотизма и гордости за свою Родину.
Формы и методы обучения: рассказ учителя с элементами беседы, самостоятельная работа, практическая работа, компьютерная презентация.
Оборудование: компьютерный класс, мультимедийный проектор, презентация урока, презентации учащихся, табличный процессор Excel, диск Microsoft Office в школе.
План урока.
1.Организационный момент. Объявление темы урока, порядка работы на уроке. – 1мин.
2.Проверка домашнего задания: компьютерный тест. – 6мин.
3.Обьяснение нового материала. Вывод первой космической скорости. – 12мин.
Вывод второй космической скорости. Работа с учебником. – 6мин.
4. Презентации учащихся — 10мин.
5.Закрепление изученного материала. Решение задачи.- 8мин.
6.Подведение итогов. Домашнее задание. – 2мин.
“Мы — дети Галактики,
Но самое главное –
Мы дети твои, дорогая Земля!”
Р. Рождественский.
I.Организационный момент.
Объявление темы урока, порядка работы на уроке.
II.Учащиеся выполняют компьютерный тест.
Тест составлен с помощью диска Microsoft Office в школе, создание тестов.
III.Объяснение нового материала.
Слайд №1
Сегодня на уроке мы выясним, как двигается тело, находящееся в гравитационном поле. Выведем формулу первой и второй космической скорости.
Рассмотрим, для чего используются искусственные спутники Земли.
Внимание на экран. Слайд №2
Траектория тел движущихся с малой скоростью.
У нас имеется тело, которое находится в гравитационном поле Земли на высоте Н над поверхностью.
Скажите, какая сила действует на это тело?
Как будет двигаться тело под действием силы тяжести, если его скорость равна 0?
Что представляет собой траектория движения тела?
Если этому телу сообщить небольшую скорость направленную горизонтально, как в этом случае будет двигаться тело? По какой траектории?
С увеличением скорости увеличивается дальность полета. Слайд №3
При определенной скорости тело будет настолько приближаться к поверхности Земли, насколько поверхность будет удаляться из-за кривизны Земли. Оно не упадет, а будет двигаться вокруг Земли по круговой орбите. Такая скорость называется первой космической. Тело становится искусственным спутником Земли. Слайд №4
Минимальная скорость, которую надо сообщить телу у поверхности Земли (или небесного тела), чтобы тело могло двигаться вокруг Земли (или небесного тела) по круговой орбите – называется первой космической скоростью.
Вывод формулы первой космической скорости.
Как направлена скорость тела в любой точке круговой траектории?
Как направлено ускорение этого тела?
На тело действует только сила тяжести. Запишем формулу закона всемирного тяготения для тела и Земли. Слайд №5
F= G
ускорение тела найдем по формуле а=
По II закону Ньютона F= ma
Приравниваем выражения m= G
Выразим скорость =
При H0 = .
Проанализируем формулу. От каких величин зависит ?
Учитывая, что g = G
Получим =
Рассчитаем численное значение первой космической скорости. Слайд №6
Обладая такой скоростью, спутник будет двигаться сколь угодно долго по орбите, не падая на Землю при условии отсутствия помех его движению. В противном случае он пойдет по спирали с убывающим радиусом, войдет в атмосферу и сгорит.
С такой скоростью в нашей стране впервые был запущен I искусственный спутник Земли.
IV. Презентация 1 учащегося
о первом ИСЗ, полете Ю.А. Гагарина. Слайд №7,8(Первый искусственный спутник Земли запущен 4 октября 1957 года в СССР. Масса 83,6 кг. Период обращения 96 мин. На орбите находился 3 месяца).
Если > то тело будет двигаться по эллипсу. Чем больше скорость, тем более вытянутый будет эллипс. Слайд №9. Слайд №10
Минимальная скорость, которую надо сообщить телу у поверхности Земли (или небесного тела) для того чтобы, оно преодолело гравитационное притяжение Земли (или небесного тела), называется второй космической скоростью .
можно вывести из закона сохранения механической энергии.
Учащиеся работают с учебником. Выводят формулу второй космической скорости.
При запуске потенциальная энергия тела E = — mgR, а кинетическая E =
При удалении от Земли на бесконечно большое расстояние E p = 0 и E k = 0. Запишем закон сохранения механической энергии — mgR= 0 отсюда =
Сравнить с = = 11,2 км/с
При такой скорости тело становится искусственным спутником Солнца.
Что представляет собой траектория движения такого тела? (парабола)
Если учитывать и направление движения Земли, то корабль лучше запускать с запада на восток, тогда к скорости корабля добавится линейная скорость точек поверхности Земли.
Впервые вторая космическая скорость была достигнута тоже в нашей стране. Это произошло 2 января 1959 года.
Если скорость тела будет 16,7 км/с, то траектория движения тела станет гиперболической. Слайд №11
Минимальная скорость, которую надо сообщить телу у поверхности Земли для того, чтобы оно преодолело гравитационное притяжение Солнца, называется третьей космической скоростью.
= 16,7 км/с.
Автоматические станции, запущенные с такой скоростью покидают пределы Солнечной системы. Величина третьей космической скорости зависит от направления запуска космического корабля. При запуске в направлении орбитального движения Земли вокруг Солнца она равна = 16,7 км/с.
Если же запускать корабль в сторону, противоположную движению Земли вокруг Солнца, то третья космическая скорость возрастет до 73 км/с.
Презентация 2 учащегося о космическом аппарате Вояджер-2 с посланием к другим цивилизациям. Слайд №12, 13, 14.
(Космический аппарат Вояджер-2 в1977году, пройдя мимо всех больших планет, аппарат вышел в 1989 году за пределы Солнечной системы. Сейчас он двигается к галактике “Туманность Андромеды” с посланием к другим цивилизациям. На борту находится видиодиск с важнейшими научными данными, виды Земли, изображение человека, звуки: шепот, плач ребенка, голоса птиц и зверей, шум ветра, речь человека.)
Изучение движения тела в гравитационном поле имеет большое практическое значение для запуска спутников связи, научно-исследовательских спутников в геодезии, метеоспутников. Для изучения других планет космического пространства на орбите сейчас находятся целые научно-исследовательские лаборатории.
Сделаем вывод.
Как меняется траектория движения тела находящегося в гравитационном поле с увеличением скорости? Слайд №15
При =0 прямая линия;
< парабола;
= окружность;
>> эллипс;
парабола;
гипербола.
V. Закрепление.
Слайд №16
Учащиеся выполняют практическую работу, используя программу MS Excel.
На экране дана таблица. Выбрав свой вариант, учащийся должен рассчитать первую космическую скорость для данной планеты.
1.Занести данные в таблицу MS Excel.
2.Ввести формулу первой космической скорости.
3.Расчитать первую космическую скорость.
4.Вывести отчет на печать.
| Название планеты | R м | M кг | G | м/с |
| Меркурий | 2,4Е6 | 3,3Е23 | 6,67Е-11 | ? |
| Венера | 6,05Е6 | 4,87Е24 | 6,67Е-11 | ? |
| Земля | 6,4Е6 | 6Е24 | 6,67Е-11 | 7,9Е3 |
| Марс | 3,4Е6 | 6,4Е23 | 6,67Е-11 | ? |
| Юпитер | 6,99Е7 | 1,9Е27 | 6,67Е-11 | ? |
| Сатурн | 6Е7 | 5,7Е26 | 6,67Е-11 | ? |
VI. Итоги урока.
Домашнее задание-§37 стр. 168 зад.№4 подготовить сообщение об использовании ИСЗ.
Литература:
- В.А. Касьянов “Физика 10 класс” М. Дрофа. 2003.
- Энциклопедия для детей. Т.8. Астрономия / глав.ред.М.Д. Аксенова.– М. Аванта 97
- И.Л. Касаткина “ Репетитор по физике” Ростов-на-Дону. Феникс.2003.
Презентация
Приложение
1.10. Закон всемирного тяготения. Движение тел под действием силы тяжести
Силы в природе
По второму закону Ньютона причиной изменения движения, то есть причиной ускорения тел, является сила. В механике рассматриваются силы различной физической природы. Многие механические явления и процессы определяются действием сил тяготения.
Закон всемирного тяготения был открыт И. Ньютоном в 1682 году. Еще в 1665 году 23-летний Ньютон высказал предположение, что силы, удерживающие Луну на ее орбите, той же природы, что и силы, заставляющие яблоко падать на Землю. По его гипотезе между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии, соединяющей центры масс (рис. 1.10.1). У тела в виде однородного шара центр масс совпадает с центром шара.
1 |
Рисунок 1.10.1. Гравитационные
силы притяжения между телами. |
В последующие годы Ньютон пытался найти физическое объяснение законам движения планет, открытых астрономом И. Кеплером в начале XVII века, и дать количественное выражение для гравитационных сил. Зная как движутся планеты, Ньютон хотел определить, какие силы на них действуют. Такой путь носит название обратной задачи механики. Если основной задачей механики является определение координат тела известной массы и его скорости в любой момент времени по известным силам, действующим на тело, и заданным начальным условиям (прямая задача механики), то при решении обратной задачи необходимо определить действующие на тело силы, если известно, как оно движется. Решение этой задачи и привело Ньютона к открытию закона всемирного тяготения.
Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними:
|
Коэффициент пропорциональности G одинаков для всех тел в природе. Его называют гравитационной постоянной
G = 6,67·10–11 Н·м2/кг2 (СИ). |
Многие явления в природе объясняются действием сил всемирного тяготения. Движение планет в Солнечной системе, движение искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все эти явления находят объяснение на основе закона всемирного тяготения и законов динамики.
Одним из проявлений силы всемирного тяготения является сила тяжести. Так принято называть силу притяжения тел к Земле вблизи ее поверхности. Если M – масса Земли, RЗ – ее радиус, m – масса данного тела, то сила тяжести равна
|
где g – ускорение свободного падения у поверхности Земли:
|
Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю с ускорением свободного падения. Среднее значение ускорения свободного падения для различных точек поверхности Земли равно 9,81 м/с2. Зная ускорение свободного падения и радиус Земли (RЗ = 6,38·106 м), можно вычислить массу Земли M:
|
При удалении от поверхности Земли сила земного тяготения и ускорение свободного падения изменяются обратно пропорционально квадрату расстояния r до центра Земли. Рис. 1.10.2 иллюстрирует изменение силы тяготения, действующей на космонавта в космическом корабле при его удалении от Земли. Сила, с которой космонавт притягивается к Земле вблизи ее поверхности, принята равной 700 Н.
2 |
Рисунок 1.10.2. Изменение силы тяготения, действующей на космонавта при удалении от Земли. |
Примером системы двух взаимодействующих тел может служить система Земля–Луна. Луна находится от Земли на расстоянии rЛ = 3,84·106 м. Это расстояние приблизительно в 60 раз превышает радиус Земли RЗ. Следовательно, ускорение свободного падения aЛ, обусловленное земным притяжением, на орбите Луны составляет
|
С таким ускорением, направленным к центру Земли, Луна движется по орбите. Следовательно, это ускорение является центростремительным ускорением. Его можно рассчитать по кинематической формуле для центростремительного ускорения (см. §1.6):
|
где T = 27,3 сут – период обращения Луны вокруг Земли. Совпадение результатов расчетов, выполненных разными способами, подтверждает предположение Ньютона о единой природе силы, удерживающей Луну на орбите, и силы тяжести.
Собственное гравитационное поле Луны определяет ускорение свободного падения gЛ на ее поверхности. Масса Луны в 81 раз меньше массы Земли, а ее радиус приблизительно в 3,7 раза меньше радиуса Земли. Поэтому ускорение gЛ определится выражением:
|
В условиях такой слабой гравитации оказались космонавты, высадившиеся на Луне. Человек в таких условиях может совершать гигантские прыжки. Например, если человек в земных условиях подпрыгивает на высоту 1 м, то на Луне он мог бы подпрыгнуть на высоту более 6 м.
Рассмотрим теперь вопрос об искусственных спутниках Земли. Искусственные спутники движутся за пределами земной атмосферы, и на них действуют только силы тяготения со стороны Земли. В зависимости от начальной скорости траектория космического тела может быть различной (см. §1.24). Мы рассмотрим здесь только случай движения искусственного спутника по круговой околоземной орбите. Такие спутники летают на высотах порядка 200–300 км, и можно приближенно принять расстояние до центра Земли равным ее радиусу RЗ. Тогда центростремительное ускорение спутника, сообщаемое ему силами тяготения, приблизительно равно ускорению свободного падения g. Обозначим скорость спутника на околоземной орбите через υ1. Эту скорость называют первой космической скоростью. Используя кинематическую формулу для центростремительного ускорения (см. §1.6), получим:
|
Двигаясь с такой скоростью, спутник
облетал бы Землю за время 
На самом деле период обращения спутника по круговой орбите вблизи поверхности Земли несколько превышает указанное значение из-за отличия между радиусом реальной орбиты и радиусом Земли.
Движение спутника можно рассматривать как свободное падение, подобное движению снарядов или баллистических ракет. Различие заключается только в том, что скорость спутника настолько велика, что радиус кривизны его траектории равен радиусу Земли.
Для спутников, движущихся по круговым траекториям на значительном удалении от Земли, земное притяжение ослабевает обратно пропорционально квадрату радиуса r траектории. Скорость спутника υ находится из условия
|
Таким образом, на высоких орбитах скорость движения спутников меньше, чем на околоземной орбите.
Период T обращения такого спутника равен
|
Здесь T1 – период обращения спутника на околоземной орбите. Период обращения спутника растет с увеличением радиуса орбиты. Нетрудно подсчитать, что при радиусе r орбиты, равном приблизительно 6,6RЗ, период обращения спутника окажется равным 24 часам. Спутник с таким периодом обращения, запущенный в плоскости экватора, будет неподвижно висеть над некоторой точкой земной поверхности. Такие спутники используются в системах космической радиосвязи. Орбита с радиусом r = 6,6R3 называется геостационарной.
Движение тел под действием гравитационных сил. Движение тел под действием силы тяжести
Движение тела под действием силы тяжести является одной из центральных тем в динамической физике. О том, что раздел динамики базируется на трех знает даже обычный школьник. Давайте постараемся разобрать эту тему досконально, а статья, подробно описывающая каждый пример, поможет нам сделать изучение движения тела под действием силы тяжести максимально полезным.
Немного истории
Люди с любопытством наблюдали за различными явлениями, происходящими в нашей жизни. Человечество долгое время не могло понять принципы и устройство многих систем, однако длительный путь изучения окружающего мира привел наших предков к научному перевороту. В наши дни, когда технологии развиваются с неимоверной скоростью, люди почти не задумываются о том, каким образом работают те или иные механизмы.
А между тем наши предки всегда интересовались загадками природных процессов и устройством мира, искали ответы на самые сложные вопросы и не переставали изучать, пока не находили на них ответы. Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.

Тот факт, что закономерности движения тел, описанные более 500 лет назад, актуальны и по сей день, означает, что наша планета подчиняется неизменным законам. Современному человеку необходимо хотя бы поверхностно изучить основные принципы обустройства мира.
Основные и вспомогательные понятия динамики
Для того чтобы полностью понять принципы подобного движения, следует сначала ознакомиться с некоторыми понятиями. Итак, самые необходимые теоретические термины:
- Взаимодействие — это воздействие тел друг на друга, при котором происходит изменение или начало их движения относительно друг друга. Различают четыре вида взаимодействия: электромагнитное, слабое, сильное и гравитационное.
- Скорость — это физическая величина, обозначающая быстроту, с которой двигается тело. Скорость является вектором, то есть имеет не только значение, но также и направление.
- Ускорение — та величина, которая показывает нам быстроту изменения скорости тела в промежуток времени. Она также является
- Траектория пути — это кривая, а иногда — прямая линия, которую очерчивает тело при движении. При равномерном прямолинейном движении траектория может совпадать со значением перемещения.
- Путь — это длина траектории, то есть ровно столько, сколько прошло тело за определенное количество времени.
- Инерциальная система отсчета — это среда, в которой выполняется первый закон Ньютона, то есть тело сохраняет свою инерцию, при условии, что полностью отсутствуют все внешние силы.
Вышеуказанных понятий вполне достаточно для того, чтобы грамотно начертить или представить в голове моделирование движения тела под действием силы тяжести.

Что значит сила?
Давайте перейдем к основному понятию нашей темы. Итак, сила — это величина, смысл которой заключается в воздействии или влиянии одного тела на другое количественно. А сила тяжести — это та сила, которая действует абсолютно на каждое тело, находящееся на поверхности или вблизи нашей планеты. Возникает вопрос: откуда же берется эта самая сила? Ответ заключается в законе всемирного тяготения.
А что такое сила тяжести?
На любое тело со стороны Земли оказывает влияние гравитационная сила, которая сообщает ему некоторое ускорение. Сила тяжести всегда имеет вертикальное направление вниз, к центру планеты. Иначе говоря, сила тяжести притягивает предметы к Земле, вот почему предметы всегда падают вниз. Получается, что сила тяжести — это частный случай силы всемирного тяготения. Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m 1 х m 2) / R 2 .
Чему равно ускорение свободного падения?
Тело, которое отпустили с некоторой высоты, всегда летит вниз под действием силы притяжения. Движение тела под действием силы тяжести вертикально вверх и вниз можно описать уравнениями, где основной константой будет являться значение ускорения «g». Эта величина обусловлена исключительно действием силы притяжения, и ее значение приблизительно равно 9,8 м/с 2 . Получается, что тело, брошенное с высоты без начальной скорости, будет двигаться вниз с ускорением равным значению «g».
Движение тела под действием силы тяжести: формулы для решения задач
Основная формула нахождения силы тяжести выглядит следующим образом: F тяжести = m х g, где m — это масса тела, на которое действует сила, а «g» — ускорение свободного падения (для упрощения задач его принято считать равным 10 м/с 2).
Есть еще несколько формул, используемых для нахождения того или иного неизвестного при свободном движении тела. Так, например, для того чтобы вычислить пройденный телом путь, необходимо подставить известные значения в эту формулу: S = V 0 х t + a х t 2 / 2 (путь равен сумме произведений начальной скорости умноженной на время и ускорения на квадрат времени, деленной на 2).
Уравнения для описания вертикального движения тела
Движение тела под действием силы тяжести по вертикали можно описать уравнением, которое выглядит так: x = x 0 + v 0 х t + a х t 2 / 2. Используя данное выражение, можно найти координаты тела в известный момент времени. Необходимо просто подставить известные в задаче величины: начальное местоположение, начальную скорость (если тело не просто отпустили, а толкнули с некоторой силой) и ускорение, в нашем случае оно будет равно ускорению g.
Таким же образом можно найти и скорость тела, которое движется под действием силы притяжения. Выражение для нахождения неизвестной величины в любой момент времени: v = v 0 + g х t (значение начальной скорости может быть равным нулю, тогда скорость будет равна произведению ускорения свободного падения на значение времени, за которое тело совершает движение).
Движение тел под действием силы тяжести: задачи и способы их решений
При решении многих задач, связанных с силой тяжести, рекомендуем воспользоваться следующим планом:
- Определить для себя удобную инерциальную систему отсчета, обычно принято выбирать Землю, потому как она отвечает многим требованиям к ИСО.
- Нарисовать небольшой чертеж или рисунок, на котором изображены основные силы, действующие на тело. Движение тела под действием силы тяжести подразумевает набросок или схему, на которой указано, в каком направлении движется тело, если на него действует ускорение, равное g.
- Затем следует выбрать направление для проецирования сил и полученных ускорений.
- Записать неизвестные величины и определить их направление.
- И наконец, используя указанные выше формулы для решения задач, вычислить все неизвестные величины, подставив данные в уравнения для нахождения ускорения или пройденного пути.
Готовое решение легкой задачи
Когда речь идет о таком явлении, как движение тела под действием того, каким способом практичнее решать поставленную задачу, может быть затруднительным. Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.
Некоторое тело отпустили с высоты 20 м без начальной скорости. Определить, за какое количество времени оно достигнет поверхности земли.
Решение: нам известен путь, пройденный телом, известно, что начальная с
5. СИЛА И ДВИЖЕНИЕ — 1
5. СИЛА И ДВИЖЕНИЕ — 1Когда объект внезапно меняет свою скорость и / или направление, мы можем всегда находите взаимодействие между этим объектом и его окружением, которое несет ответственность за это изменение. Мы утверждаем, что окружающая среда оказывает давление на изучаемый объект. Под действием силы объект будет ускоряться. Законы силы позволяют рассчитать силу, действующую на тело, исходя из свойства тела и окружающей его среды. законы движения являются впоследствии используется для расчета ускорения объекта под воздействием силы.
В этом курсе мы будем обсуждать законы движения, полученные Ньютоном. Это называется Ньютоновская механика . Следует понимать, что Механика Ньютона не всегда дает правильные ответы. Если скорость вовлеченные объекты составляют значительную часть скорости света, мы должны заменить ньютоновскую механику специальной теорией относительности Эйнштейна.Для проблемы в масштабе атомной структуры мы должны заменить ньютоновскую механику квантовой механикой.
Вокруг нас мы наблюдаем, что все движущиеся объекты рано или поздно остановятся, если мы не применим к ним силу. Нам нужно продолжать крутить педали, если мы хотим сохранить велосипед движется с постоянной скоростью, нам нужно, чтобы наш двигатель работал, если мы хотите продолжать движение со скоростью 55 миль / час. Во всех этих случаях трение в конечном итоге остановит любой движущийся объект, если только сила трения не отменяется силой, создаваемой нашими ногами, нашим двигателем и т. д.Если мы уменьшим трение, движущемуся объекту потребуется больше времени для замедления, а необходимая сила для преодоления силы трения будет меньше. В пределе отсутствия трения наши объект будет продолжать двигаться с постоянной скоростью, и сила не требуется приложенное. Этот вывод резюмирован в первом законе Ньютона :
. « Рассмотрим тело, на которое не действует чистая сила. Если тело покоится, оно останется в покое. Если тело движется с постоянной скоростью, оно будет продолжать делать это. «
Первый закон Ньютона — это действительно утверждение о системе отсчета в том смысле, что он определяет виды систем отсчета, в которых законы механики Ньютона держать. Системы отсчета, в которых применяется первый закон Ньютона, называются инерциальных системы отсчета .
Один из способов проверить, является ли система отсчета инерциальной системой отсчета, — это положить испытательное тело в покой и расположить вещи так, чтобы в нем не действовала никакая сила. Если система отсчета является инерциальной системой отсчета, тело останется в покое; если тело не остается в покое, система отсчета не является инерциальной.Если поставить шар для боулинга на карусель, никакие видимые силы воздействуют на мяч, но он не остается в покое. Вращающийся эталон кадры не являются инерциальными опорными кадрами. Собственно говоря, земля следовательно, также не инерциальная система отсчета, однако, только если мы рассматриваем крупномасштабные движение, такое как ветер и океанское течение, нужно ли нам учитывать не инерционный характер вращающейся земли.
Если мы приложим одну и ту же силу к нескольким объектам с разной массой, мы будем наблюдать разные ускорения.Например, можно бросить бейсбольный мяч значительно дальше (и быстрее), чем шар такого же размера, сделанный из свинца. Единицей силы является Ньютон (Н), а сила в 1 Н определяется как сила что при применении к объекту массой 1 кг вызывает ускорение 1 м / с 2 . Если приложить силу, равную 2 Н, соответствующее ускорение 2 м / с 2 .
Эксперименты показали, что сила — вектор. Это может быть показано демонстрируя, что сила имеет величину и направление.Предположим, мы приложить силу 3 Н к нашему стандартному объекту (масса 1 кг). Сила приложена таким образом, чтобы результирующее ускорение 3 м / с 2 было направлено вверх (положительное Y-направление). Кроме того, мы прикладываем силу 4 Н в горизонтальном направлении. (эта сила приложена так, что стандартный объект будет ускоряться с ускорение 4 м / с 2 в направлении положительной оси x, если это единственная приложенная сила). Ситуация проиллюстрирована на рисунке 5.1. Если обе силы действуют на стандартную массу одновременно, ускорение объекта составляет 5 м / с 2 , а направление движения ускорение совпадает с направлением векторной суммы двух сил. Полная сила равна 5 Н и равна величине вектора суммы две силы (если предположить, что направление силы равно направление ускорения). Делаем вывод, что сила действительно вектор и что сила и соответствующее ускорение имеют одинаковые направление.
Рисунок 5.1. Ускорение стандартного тела под воздействием двух сил.
Ускорение, создаваемое определенной силой, зависит от массы предмет. Ускорение объекта, масса которого вдвое превышает стандартную. масса под действием определенной силы вдвое меньше ускорения стандартная масса за счет той же силы. Следующий список суммирует то, что мы узнали пока о силах:
1.Сила — это вектор.
2. Сила, действующая на объект, вызывает ускорение. Направление ускорение совпадает с направлением приложенной силы.
3. Для данной силы результирующее ускорение тела с массой в два раза стандартной массы, вдвое меньше ускорения стандартной масса под действием той же силы.
Выводы обобщены во втором законе Ньютона : ‘
где [Sigma] F — векторная сумма всех сил, действующих на объект с масса m, а — результирующее ускорение (примечание: сумма включает только внешние силы).Если мы разложим и силу, и ускорение на их индивидуальные компонент по осям x, y и z, получаем следующие соотношения:
Второй закон Ньютона включает формальную формулировку первого закона Ньютона: если на объект не действует действующая сила ([Sigma] F = 0 Н), ускорение равна нулю (и скорость объекта постоянна).
Пример задачи 5-1
Студент толкает нагруженные санки массой 240 кг на расстояние 2,3 м. по поверхности замерзшего озера без трения. Он оказывает горизонтальную силу равна 130 Н. Если сани трогаются с места, какова его конечная скорость?
Рисунок 5.2. Пример системы координат Задача 5-1.
Это одномерная проблема. Система координат определяется такое, что начало координат совпадает с положением салазок в момент времени t = 0 с, и сила прилагается в положительном направлении (см. рисунок 5.2). Поскольку сила постоянна, результирующее ускорение a также постоянно и может быть вычислено с применением второго закона Ньютона:
Постоянное ускорение применяется только на расстоянии d (= 2,3 м). В выбранной системе координат уравнение движения можно записать в виде следует:
Из этого уравнения, время, за которое сани преодолели расстояние d можно рассчитать:
а скорость саней в это время равна
Пример задачи 5-2
В двухмерной перетягивании каната Алекс, Бетти и Чарльз тянут веревки которые привязаны к автомобильной шине.Канаты образуют углы, как показано на рисунке. 5.3, вид сверху. Алексей тянет с силой F A = 220 Н и Чарльз с силой F C = 170 Н. С какой силой должна Бетти тянуть, чтобы шина оставалась неподвижной?
Поскольку шина неподвижна, результирующая сила, действующая на шину, должна быть равна нулю. это также означает, что чистая сила в направлении x и y должна быть равна нулю:
Подставляя известные значения для F A , F C и [theta] в первом уравнении, мы можем вычислить [phi]:
Подставляя это значение для [phi] во второе уравнение, мы можем рассчитать F B :
Рисунок 5.3. Пример задачи силовой диаграммы 5-2.
Если молоток воздействует на гвоздь, гвоздь оказывает равное, но противоположное направленное усилие на молот. В целом это верно и описывается Третий закон Ньютона : ‘
«Предположим, что тело A действует на тело B с силой (F BA ). Эксперименты показывают, что в этом случае тело B оказывает на тело A силу (F AB ). две силы равны по величине и противоположно направлены:
«
Примечание: Поскольку два члена пары действие-противодействие всегда действуют на разные тела, они не могут отменять друг друга.
Масса тела и вес тела — совершенно разные свойства. Масса м тела — скаляр; его единица СИ — килограмм. Масса тело можно определить, сравнив его со стандартным килограммом. Масса — это внутреннее свойство тела; то же самое и на земной поверхности, в на орбите спутника, на Марсе или в межзвездном пространстве. Вес тела — вектор; его единица СИ в Ньютоне.Вес тела с масса m определяется как:
где g — ускорение свободного падения в месте нахождения тела. Поскольку ускорение свободного падения меняется от точки к точке, вес объект зависит от своего местоположения и, следовательно, не является внутренним свойство тела.
5.4.1. Измерение массы
Масса тела может быть определена путем сравнения с эталоном. масса.Для этого предназначены равноплечные весы (см. Рисунок 5.4). Равновесие уравновешивается, если сила слева равна силе на справа:
Рисунок 5.4. Равновесие на руках.
Эти две силы — силы тяжести . действует на m 1 и m 2 и легко вычисляется:
Если ускорение свободного падения постоянно в месте расположения баланса, можно сделать вывод, что если рычаги уравновешены:
м 1 = м 2
Следовательно, равноправный баланс определяет относительная масса двух объектов путем сравнения их веса.
5.4.2. Измерение веса
Измерение веса объекта можно производить с помощью пружинная шкала (см. рисунок 5.5). Весы с пружинами используют пружину для измерения вес объекта. Существует взаимно однозначное отношение между отрезками пружина и приложенная сила (отвечающая за растяжение). В основном, пружинные весы откалиброваны и показывают массу объекта. Однако это Следует подчеркнуть, что масса объекта получается из измеренных веса, и при этом предполагается, что ускорение свободного падения равно 9.8 м / с 2 . Следовательно, пружинная шкала укажет только правильной массы, если он используется в месте, в котором ускорение свободного падения равным таковому на месте калибровки (примечание: пружинная шкала будет неправильно определить массу объекта, если он используется на Луне или в ускоряющий лифт).
Рисунок 5.5. Весенняя шкала.
Пример задачи 5-7
На рис. 5.6 показан блок массой m = 15 кг, подвешенный на трех тросах.Что напряжение в этих шнурах?
На массу m действует сила тяжести, равная mg. Поскольку масса равна в состоянии покоя шнур C должен обеспечивать противодействующую силу, равную mg. Применение Ньютона В соответствии с третьим законом, мы заключаем, что шнур C действует на узел с силой, величина которой равно mg (и указано в направлении, показанном на рисунке 5.6). Поскольку система в состоянии покоя, чистая сила на узле должна быть равна нулю:
Это векторное уравнение можно переписать в терминах его составляющих вдоль по оси X и Y, используя следующую информацию:
Рисунок 5.6. Пример задачи 5-7.
Используя эти выражения, мы можем записать уравнения для x и y-компоненты чистой силы:
Первое выражение может использоваться для выражения T A через Т В :
Подставляя это выражение в уравнение для [Sigma] F y получаем:
из которого мы можем рассчитать T B :
Зная T B , теперь мы можем рассчитать T A :
В случае примера задачи 5-6 натяжение шнуров составляет:
T A = 100 Н
T B = 140 Н
T C = 150 Н
Проблема
Рисунок 5.7 показан блок массой m на плоскости без трения под наклоном на угол [тета]. Какое ускорение блока?
Рисунок 5.7. Масса м на наклонной плоскости.
Чтобы определить ускорение блока, мы должны определить суммарная сила, действующая на блок по наклонной плоскости. Две силы действуют на блок: сила тяжести, оказываемая землей на блок, и сила, называемая нормальной силой , прилагаемой плоскостью к блоку (см. Рисунок 5.8). Эта сила должна присутствовать, поскольку в ее отсутствие масса m будет испытать свободное падение (вместо скольжения). Поскольку нормальная сила равна перпендикулярно наклонной плоскости, вдоль нее нет компонента. Составляющая силы тяжести вдоль наклонной плоскости равна
Ускорение, создаваемое этой силой, можно определить по формуле Ньютона. второй закон
Рисунок 5.8. Силы, действующие на массу m.
Пример задачи 5-8
На рис. 5.9 показан блок массой m, удерживаемый шнуром на плоскости без трения. наклонен на угол [тета]. Какое натяжение шнура? Какая сила самолет прикладывают к блоку?
Рисунок 5.9. Пример задачи 5-8.
Эту проблему легко решить, если выбрать систему координат осторожно. Наилучший выбор системы координат показан на рисунке 5.10. Поскольку блок находится в состоянии покоя, результирующая сила, действующая на него, должна быть равна нулю:
Из-за выбора системы координат и N, и T имеют только компоненты по оси y и оси x соответственно:
Масса останется в покое, если все компоненты чистой силы ноль:
Из этих уравнений можно получить N и T:
Рисунок 5.10. Система координат №1, использованная в примере задачи 5-8.
Рисунок 5.11. Система координат №2, использованная в примере задачи 5-8.
Стандартный выбор системы координат с совпадающей осью x с горизонтальным направлением и осью y, совпадающей с вертикальной направление (см. рис. 5.11) сделало бы проблему значительно более сложной. трудно. В этой системе координат N и T имеют компонент вдоль обоих x и направление y:
В этом случае N и T можно получить, решив следующие уравнения:
Конечно, решения для N и T идентичны полученным ранее, но вывод сложнее.
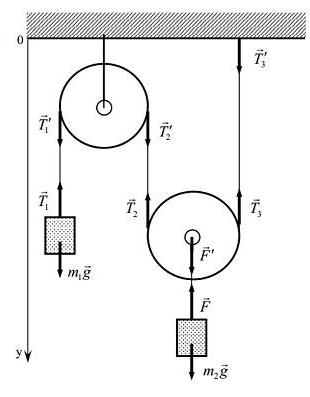
Пример задачи 5-10
Два блока соединены шнуром, который проходит над (невесомым) шкивом (см. Рисунок 5.12). Найдите натяжение шнура и (общее) ускорение.
Блоки движутся с постоянным ускорением. Поскольку шнур предполагается к жесткому, ускорение массы m должно быть равно ускорению масса M. Однако, поскольку шкив меняет направление движения, направление ускорения массы m противоположно направлению движения ускорение массы М.Для каждой из масс можно записать следующее уравнения силы:
Первое уравнение можно использовать для выражения T через a:
Подставляя это выражение для T во второе уравнение, мы получить:
Рисунок 5.12. Пример установки задачи 5-10.
Теперь можно рассчитать ускорение a:
Обратите внимание, что a положительно, когда M> m, и отрицательно, когда M Проблема Блок массой m 1 на гладкой наклонной плоскости
угол [тета] соединен шнуром через небольшой шкив без трения с
второй блок массой m 2 висит вертикально (см. рисунок 5.13).
массой шнура и шкива можно пренебречь. а) Какое ускорение у каждого блока? б) Какое натяжение у шнура? Рисунок 5.13. Наклонный самолет и шкив. Чтобы определить ускорение и натяжение, мы должны определить
все силы действуют на обе массы. На m 1 действуют следующие силы.
(см. рисунок 5.14): В общем, чистая сила, действующая на 1 м, будет отличной от нуля и
m 1 будет иметь ненулевое ускорение.Ускорение будет
вдоль оси x (см. рисунок 5.14) и определяется как положительное, если
ускорение идет в том же направлении, что и натяжение T. Составляющие
полезная сила, действующая на м 1 определяется по (1) (2) Рисунок 5.14. Силы, действующие на м 1 . Рисунок 5.15. Силы, действующие на м 2 . На м 2 (см. Рисунок 5.15) действуют следующие силы: Чистая сила на 2 m будет отличной от нуля, и масса будет ускоряться.
Поскольку m 1 и m 2 соединены шнуром, они будут иметь
такое же ускорение. Если направление ускорения м 1 вдоль Т, направление разгона на 2 м будет по
W 2 (см. Рисунок 5.15). Ни одна из сил, действующих на м 2 имеет компонент вдоль оси x, поэтому мы будем рассматривать только сетку
сила по оси Y: (3) Уравнения (1) и (3) представляют собой два уравнения с двумя неизвестными (T и a), и
можно решить.Уравнение (3) можно переписать как (4) Подставляя уравнение (4) для T в уравнение (1), мы можем определить a: (5) Подставляя уравнение (5) в уравнение (4), получаем натяжение T: (6) Куратор: Piet Hut Гравитационное Моделирование N-тел , то есть численные решения уравнений
движений для N частиц, взаимодействующих гравитационно, широко
использованные инструменты в астрофизике, с приложениями от нескольких тел или Солнца
системы, подобные системам, вплоть до галактических и космологических
Весы. В этой статье мы представляем сводный обзор отрасли
выделение основных методов моделирования N-тела и
астрофизический контекст, в котором они обычно применяются. Основная динамика, важная в астрофизическом контексте для
система из N частиц, взаимодействующих гравитационно, обычно
Закон Ньютона плюс, в случае, внешнее потенциальное поле (см.
ниже для обсуждения моделирования N-тел в целом
относительность). Сила \ (\ vec {F} _i \), действующая на частицу
\ (i \) массы \ (m_i \) составляет: \ [\ tag {1}
\ vec {F} _i = — \ sum_ {j \ ne i} G \ frac {m_i m_j (\ vec {r} _i- \ vec {r} _j)} {| \ vec {r_i} — \ vec {r_j } | ^ 3} — \ vec {\ nabla} \ cdot \ phi_ {ext} (\ vec {r} _i),
\] Если задан набор начальных условий (например, начальное
позиции \ (\ vec {r} _i \) и скорости \ (\ vec {v} _i \ Equiv
\ partial \ vec {r} _i / \ partial t \) всех частиц) существует
уникальное решение, аналитическое только для двух тел, в то время как больше N
требуют численного интегрирования (например, см. Press et al. 2007). тем не мение
необходимо соблюдать особую осторожность, чтобы гарантировать точность и
эффективность. Фактически, гравитационная сила
(Экв.(1) представляет особенность, когда расстояние
две частицы стремятся к 0, что может привести к сколь угодно большим
относительные скорости. Кроме того, учитывая нелинейный характер
уравнения, особенности подвижны, т. е. зависят от
конкретный выбор начальных условий. Напротив, все особенности
в линейных обыкновенных дифференциальных уравнениях не зависят от начальных
условия и, следовательно, легче лечить. Поэтому постоянный временной шаг
методы не могут гарантировать заданную точность в
случай гравитационной динамики и приводят к нефизическим ускорениям
во время близких встреч, которые, в свою очередь, могут создавать несвязанные звезды.
общая адаптивная схема временного шага может правильно следовать за близким
встречи, но цена оплачивается с точки зрения эффективности, поскольку все
другие частицы системы эволюционируют в масштабе времени
встречи, которая может быть на несколько порядков меньше, чем
глобальном масштабе времени, что приводит к замораживанию
система. Сингулярности можно избежать, введя длину смягчения в
Eq. (1) (например, см. Aarseth 1963), то есть путем изменения гравитационного
взаимодействие в малых масштабах.{3/2}},
\] где \ (\ epsilon> 0 \) — длина размягчения, т.е.
типичное расстояние, ниже которого гравитационное взаимодействие
подавлено. Чтобы свести к минимуму ошибки силы и глобальное влияние
смягчение для расстояний больше, чем конечный размер \ (\ epsilon \, \)
ядра, обеспечивающие непрерывные производные силы, могут быть
заняты (например, см. Dehnen 2001). Эта стратегия эффективно
подавляет бинарное образование и сильные гравитационные взаимодействия, но
ценой изменения динамики системы.7 \. \) Произвольно большой динамический диапазон в несмягченной динамике и
дорогостоящая оценка силы привела к разработке
большое количество численных методов, направленных на получение надежного
численное решение с минимальным количеством вычислительных ресурсов,
в зависимости от интересующей астрофизической проблемы. Здесь мы начинаем с
обсуждение различных астрофизических контекстов, в которых N-тела
моделирование обычно используется, и затем мы представляем состояние
художественные методы решения этих проблем. Моделирование N-тела применяется к широкому спектру различных
астрофизические проблемы, так что наиболее подходящий метод для использования
зависит от конкретного контекста и, в частности, от шкалы времени
и коллизия проблемы. Система из N частиц, гравитационно взаимодействующих с полной массой M
и справочный размер R (например, радиус, содержащий половину
общая масса) достигает состояния динамического равновесия в масштабе времени
сопоставимо с типичным временем \ (T_ {cr} \), которое требуется частице для того, чтобы
пересечь систему \ ((T_ {cr} \ приблизительно 1 / \ sqrt {GM / R ^ 3}) \.2 \, \] и W — его потенциал
энергия \ [W = — 1/2 \ sum_ {i \ ne j} G m_i m_j
/ | \ vec {r} _i- \ vec {r} _j | \] (при условии отсутствия внешнего поля). Если система изначально находится вне равновесия,
это достигается за счет перемешивания в фазовом пространстве за счет флуктуаций
гравитационный потенциал, процесс, называемый насильственным
релаксация (Lynden-Bell 1967). Когда система находится в динамическом равновесии, долгосрочная эволюция
возможно, движимое расслаблением двух тел. Медленно обменивается энергией
между частицами и системой стремится к термодинамической
равновесие и равнораспределение энергии.Шкала времени \ (T_ {rel} \) для этого процесса
зависит от количества частиц и геометрии системы \ [T_ {rel} \ propto N / log (0.11 N) T_ {cr} \] (например, см. Spitzer
1987). Системы N тел, такие как галактики и гало темной материи, имеют
время релаксации намного больше, чем время жизни Вселенной, и поэтому
рассматриваются бесстолкновительные системы. Меньшие системы, такие как
шаровые и рассеянные скопления являются столкновительными, поскольку релаксация
время короче их возраста. Также подавляется расслабление двух тел
когда одна частица в системе доминирует над гравитационным потенциалом,
например, в случае динамики Солнечной системы, когда планеты
по сути, квазитестовые частицы. Близкие столкновения трех или более частиц не только вносят свой вклад
к энергообмену, но также может приводить к образованию связанных
подсистемы (в основном двоичные). Формирование и эволюция двойной
популяцию лучше всего отслеживать с помощью прямого, несглаженного, N-тела
методы. Самогравитирующая система N-тел, состоящая из одиночных частиц, имеет
отрицательная удельная теплоемкость, то есть увеличивает свою кинетическую энергию как
результат потерь энергии (Lynden-Bell & Wood 1968). Это следствие
теорема вириала и качественно аналогична
ускорение искусственного спутника Земли при наличии
атмосферное сопротивление.Система с отрицательной теплоемкостью термодинамически нестабильна и
шкала времени релаксации двух тел эволюционирует в сторону гравотермической
коллапс, создавая структуру ядро-гало, где ядро постепенно
увеличивает его концентрацию, вызывая общее расширение ореола.
коллапс в конечном итоге останавливается, как только три взаимодействия тел приводят к
формирование двоичных файлов. Так называемое «ядро коллапсировало глобулярное»
кластеры »считаются образованными в результате этого механизма. Система из N частиц, гравитационно взаимодействующих, определяет 6N + 1
размерное фазовое пространство, заданное N векторами положения и скорости
связанный с каждой частицей в каждый момент времени t.Решение N-тела
Задача определяет траекторию в этом фазовом пространстве. Если количество
частицы достаточно велики, то есть если время релаксации двух тел
долго по сравнению с интересующим вас периодом времени, тогда
возможно статистическое описание проблемы. Это позволяет нам перейти от измерения 6N + 1 к измерению 6 + 1.
фазовое пространство. Идея состоит в том, чтобы построить среднее поле
описание динамической системы в терминах одной частицы
функция распределения \ (f (\ vec {x}, \ vec {v}, t) \, \) где
\ (f (\ vec {x}, \ vec {v}, t) d ^ 3x d ^ 3v \) пропорционально
вероятность нахождения частицы в 6D элементе объема \ (
d ^ 3x d ^ 3v \) с центром в позиции \ (\ vec {r} \) и
скорость \ (\ vec {v} \) в момент времени t.В этой упрощенной структуре
знание функции распределения однозначно определяет все
свойства системы. Динамика описывается
бесстолкновительное уравнение Больцмана, которое по существу выводится из
Теорема Лиувилля: \ [
\ frac {D f} {D t} = \ frac {\ partial f} {\ partial t} + \ vec {v} \ cdot \ frac {\ partial f} {\ partial \ vec {x}} — \ frac {\ partial \ phi_T} {\ partial \ vec {x}} \ cdot \ frac {\ partial f} {\ partial \ vec {v}} = 0,
\] , где полное потенциальное поле \ (\ phi_T = \ phi_ {ext} (\ vec {x}, t) +
\ phi (\ vec {x}, t) \) — это сумма внешнего потенциала плюс
самосогласованное поле \ (\ phi (\ vec {x}, t) \), определенное из
саму функцию распределения через решение пуассоновского
уравнение: \ [
\ nabla ^ 2 \ phi (\ vec {x}, t) = 4 \ pi G \ rho (\ vec {r}, t),
\] где \ (\ rho (\ vec {r}, t) = \ int f (\ vec {x}, \ vec {v}, t) d ^ 3v \.\) Благодаря высокой размерности (6 + 1) бесстолкновительный Больцман
уравнение обычно решается путем выборки начального распределения
функции, а затем путем развития полученной системы N-тел с помощью
численный метод подавления взаимодействия двух тел при малых
Весы. Взаимодействие смягчается не только для
вычислительное удобство для ограничения максимальной относительной скорости
во время близких контактов, но особенно для предотвращения искусственного образования
двоичных файлов. Это потому, что симуляционная частица в бесстолкновительном
run представляет собой ансамбль реальных частиц (например,9] \)). Однако обратите внимание, что расслабление двух тел
движется как близкими, так и отдаленными встречами, поэтому смягчение
не подавляйте это. В принципе, любой численный метод, имеющий небольшой
смягчение масштаба подходит для отслеживания бесстолкновительной динамики. Описание среднего поля для системы N-тела возможно также для
столкновительных систем, то есть когда время релаксации сравнимо с
или короче интересующего вас периода. В этом случае
бесстолкновительное уравнение Больцмана модифицируется введением
оператор столкновения \ (C [f] \) в правой части: \ [
\ frac {D f} {D t} = \ frac {\ partial f} {\ partial t} + \ vec {v} \ cdot \ frac {\ partial f} {\ partial \ vec {x}} — \ frac {\ partial \ phi_T} {\ partial \ vec {x}} \ cdot \ frac {\ partial f} {\ partial \ vec {v}} = C [f].\] В этой структуре оператор \ (C [f] \) описывает
вероятность для частиц войти / покинуть элемент фазового пространства как
результат гравитационных столкновений. Оператор столкновения
C обычно строится в предположении, что столкновения (i) марковские
процессы, то есть C зависит только от текущего состояния системы,
(ii) локальный, то есть изменяется только скорость частиц и
не их положения и (iii) слабая, это типичная скорость
изменение намного меньше, чем сама скорость.Под этими
допущения Методы Монте-Карло доступны для решения динамики
систему (см. следующий раздел). Приложения оператора столкновения
включают динамику шаровых скоплений и самовзаимодействующих темных
иметь значение. Моменты скорости уравнения Больцмана определяют набор
уравнения, известные как уравнения Джинса (например, Бинни и Тремейн
2007). Первые три уравнения системы формально идентичны
уравнения Навье-Стокса для самогравитирующего газа и, как в
аналогия гидродинамики, выражает сохранение массы, импульса
и энергия.Поэтому численные алгоритмы, разработанные с учетом
динамика систем N-тел находит широкое применение также в контексте
гидродинамики, одним из важных примеров является сглаженная
Метод гидродинамики частиц (SPH) (Gingold & Monaghan 1977).
принципиальное различие между двумя корпусами в том, что джинсы
уравнения выводятся в пределе бесстолкновительной системы, а уравнения
Уравнения Навье-Стокса предполагают систему с высокой степенью столкновений с
длина свободного пробега частицы приближается к нулю.Для жидкостей это приводит к
определение уравнения состояния, которое замыкает Навье-Стокса
уравнения. Вместо этого уравнения Джинса представляют собой бесконечное открытое множество, где
n-й момент скорости зависит от момента n-го + 1. На основе предыдущих соображений о столкновении и
шкалы времени, четыре основных астрофизических области для моделирования N-тел могут
быть идентифицированным, каждый из которых требует различных численных методов для
гарантировать максимальную производительность и точность: Небесная механика (солнечные и внесолнечные планетные системы).Вот
одно тело доминирует над гравитационным полем, а все остальные
объекты движутся почти как пробные частицы, подверженные взаимному
возмущения. В этой структуре требуется очень высокая точность, чтобы
правильно оценивать пертурбативные термины и избегать доминирования
числовым шумом, например ошибками дискретизации по времени и округлениями. Плотные звездные системы , такие как рассеянные скопления и шаровые
кластеры. Эти системы столкновения, состоящие из компонентов примерно
равная масса представляет собой богатую динамику с множеством близких столкновений
звезды.Эволюция требует прослеживания в шкале времени релаксации.
с правильным описанием короткодействующих взаимодействий. Сфера влияния массивной ЧД в центре звезды.
система. Сфера влияния ЧД — это объем, в котором
гравитация ЧД преобладает над гравитацией других частиц.
ситуация напоминает динамику солнечной системы, но здесь, учитывая
очень высокая плотность звезд часты встречи двух тел, из-за чего
проблема сложный гибрид между двумя предыдущими случаями.В
кроме того, может потребоваться включение постньютоновской физики, если
точность требуется в непосредственной близости от ЧД. Динамика и космология галактик . Галактики и особенно темные
ореолы материи состоят из очень большого количества частиц, поэтому
что их динамика может быть хорошо описана в терминах среднего
поле. Близкие контакты не важны, и обычно
используются в этих моделированиях N-тел, чтобы избежать нефизического образования двойных систем. Особо следует упомянуть самовзаимодействующие частицы темной материи в этом классе: если ореолы темной материи
из Слабо взаимодействующих массивных частиц, то их динамика может
изменяться негравитационным самовзаимодействием, особенно эффективным в центре
острых темных ореолов.Динамика такой системы описывается
Столкновительное уравнение Больцмана, которое может быть приближенно решено с помощью Fokker-Plank
методы. История моделирования N-тел начинается с новаторской попытки
Холмберг (1941), который следил за эволюцией системы из 37 частиц,
где сила рассчитывалась с помощью лампочек и гальванометров
(используя то же масштабирование \ (r ^ {- 2} \)
электромагнитное и гравитационное взаимодействия).Компьютерное моделирование
началось в начале шестидесятых с использованием до 100 частиц (например, см. von
Hoerner 1960 и Aarseth 1963) и расцвели в
восьмидесятых годов с развитием быстрых и эффективных
алгоритмы для работы с бесстолкновительными системами, такими как сетка частиц
коды (см. Hockney & Eastwood 1988 и ссылки в них) и
метод дерева (Barnes & Hut 1986). В то же время методы регуляризации
были разработаны, чтобы иметь дело с близкими встречами и бинарной динамикой в случае
прямое моделирование системы столкновений (например,6 \) можно проследить за сотни динамических времен (например, Ричардсон и др., 2000). В ближайшем будущем также ожидаются крупные прорывы.
будущее благодаря GRAPE-DR следующего поколения и удвоению
прецизионные графические процессоры, обеспечивающие чрезвычайно высокую стоимость
конкурентоспособные высокопроизводительные вычислительные возможности. Прямые методы не вводят приближений в решение
уравнения движения и, таким образом, обеспечивают высочайшую точность на
цена самого длительного времени расчета, порядка
\ (O (N ^ 2) \) за временной шаг.Интеграция осуществляется с помощью адаптивного
(индивидуальные) временные шаги и обычно Эрмит четвертого порядка
интегратора. Точно обрабатываются близкие встречи и связанные подсистемы.
в терминах преобразований Кустаанхеймо-Штейфеля. По сути, они состоят в преобразованиях координат с помощью пертурбативного
подход над аналитическим двухчастичным решением. Если больше двух
частицы сильно взаимодействуют между собой, стратегия регуляризации цепи
(Mikkola 1990), который заключается в переработке проблемы в
с точки зрения серии отдельных взаимодействий Кустаанхеймо-Штейфеля.8 \) часов процессора. Алгоритм можно распараллелить, но в
практика дисбаланса нагрузки может преуменьшить выигрыш в эффективности,
поэтому некоторые из наиболее требовательных к процессору симуляций были выполнены специально
аппаратное обеспечение, такое как GRAPE, где архитектура чипа была
оптимизирован для вычисления гравитационных взаимодействий, таким образом обеспечивая
Производительность в терафлопсах. Метод древовидного кода (Barnes & Hut 1986) обеспечивает быстрое и общее
интегратор для бесстолкновительных систем, когда близкие встречи не
важно и где сила вкладов из очень далеких
частицы не нужно вычислять с очень высокой точностью.По факту,
с помощью древовидного кода обычно смягчаются мелкомасштабные сильные взаимодействия (но см. McMillan & Aarseth 1993), в то время как
потенциалы удаленных групп частиц аппроксимируются формулой
мультипольные разложения о групповых центрах масс. Результирующий
время вычислений масштабируется как \ (O (N log (N)) \), но приближения вносят небольшие ошибки силы. Погрешности дальнодействующей силы контролируются одним
параметр (угол раскрытия), определяющий, насколько малый и дальний
группа частиц должна использовать приближение.Эта стратегия
хорошо работает, чтобы сохранить низкую среднюю ошибку силы, но в худшем случае
анализ сценария показывает, что несвязанные ошибки могут возникать в редких,
но астрофизически разумные конфигурации, такие как конфигурация
классическая «взрывающаяся галактика» (Salmon & Warren 1994). Кроме того, сила
ошибки из кода дерева могут привести к нарушению импульса
сохранение. Типичные реализации древовидного кода расширяют
потенциалов до квадрупольного порядка и построить древовидную иерархию
частицы, использующие рекурсивный алгоритм двоичного разделения.Дерево делает
не нужно пересчитывать с нуля на каждом временном шаге, экономя
значительное время процессора. Системы с несколькими сотнями тысяч
Бесстолкновительные частицы можно легко смоделировать на GFlops
рабочую станцию для времени Хаббла, используя этот метод. Стандартная реализация древовидного кода не использует преимущества
тот факт, что близлежащие частицы будут подвергаться аналогичному ускорению
из-за удаленных групп частиц. Быстрый мультипольный метод
(Greengard & Rokhlin 1987) эксплуатируют эту идею и используют мультипольный
расширение для вычисления силы от удаленной исходной ячейки в пределах
раковина.Это дополнительное приближение гравитационного взаимодействия
утверждалось, что снижает сложность с \ (O (N log (N)) \) до
\ (O (N) \, \), но точное масштабирование кажется реализацией
зависимы и обсуждались в литературе (например, см. Dehnen 2000
и ссылки там). Одним из преимуществ метода быстрого мультиполя является
что симметрия при обработке ячеек стока и источника с
относительно мультипольного разложения может гарантировать точное сохранение
импульса. Недавние успешные реализации быстрого мультиполя
коды или гибриды со схемой древовидных кодов, включая декартову систему Денена
схема расширения (код GyrfalcON — Dehnen 2000) и PKDGRAV (Stadel 2001). Метод частиц сетки представляет собой еще один путь к ускорению прямого
оценка силы для бесстолкновительных систем. В этом случае
гравитационный потенциал системы построен на сетке
начиная с поля плотности и решая ассоциированную пуассоновскую
уравнение. Частицы не взаимодействуют напрямую между собой, а
только через среднее поле. Метод существенно смягчает
гравитационные взаимодействия в малых масштабах, то есть ниже ячейки
длина.Поле плотности построено с использованием ядра для разделения
масса частиц в ячейках сетки вокруг частицы
позиция. Самый простой выбор — назначить всю массу одному
ячейке, но это приводит к значительным колебаниям силы, которые могут
уменьшено с помощью облака в ячейке (8 баллов) или облака треугольной формы
(27 баллов) ядро. Уравнение Пуассона обычно решается с помощью быстрого
Преобразование Фурье, но также могут быть использованы другие сеточные методы, такие как последовательное чрезмерное расслабление, напримерсм. Bodenheimer et al. (2007). Движущая сила, определенная на сетке, тогда
обратно к частицам с использованием того же ядра, что и для
построение поля плотности, чтобы избежать ложного
силы. Метод достигает линейной сложности по количеству
частиц и (\ (O (N_g log (N_g) \)) в количестве сетки
ячеек (последнее масштабирование относится к методу БПФ). Цена до
Оплата с точки зрения точности на коротких дистанциях, так как сила плохая
аппроксимация закона Ньютона с точностью до нескольких шагов сетки
расстояние. Динамический диапазон кодов сетки частиц может быть увеличен с помощью
адаптивная, а не статическая сетка для решения уравнения Пуассона. В
Метод адаптивного уточнения сетки (AMR) элементы сетки
сосредоточены там, где требуется более высокое разрешение, например, вокруг
регионы с самой высокой плотностью. Одна возможность получить адаптивную
разрешение состоит в том, чтобы сначала построить решение с низким разрешением
Уравнение Пуассона, а затем постепенно уточнять области, где
локальная ошибка усечения (оценивается по методу Ричардсона
экстраполяция) наиболее высока.Многосеточная структура должна учитывать
проблемы с учетными записями, такие как сопоставление решения на интерфейсах сетки.
Коды AMR хорошо подходят для космологического моделирования (например, см. Код ENZO, Bryan & Norman
1998). Вариантом кода Particle Mesh является расширение плотности
и потенциал системы с точки зрения основы ортогональных
собственные функции. Клаттон-Брок (1972) был одним из первых, кто применил
эта идея в звездной динамике, а современная реализация
Hernquist & Ostriker (1992).Этот метод гарантирует фиксированное
вычислительных ресурсов более высокая точность, чем древовидный код и
алгоритмы сетки частиц при условии, что набор базисных функций
правильно выбранный. Это ограничивает на практике общее применение
метода, который, однако, остается очень конкурентоспособным для изучения
динамическая устойчивость бесстолкновительных систем, построенных из
модели функций распределений. Для увеличения разрешающей способности сетки частиц кодирует
было предложено связать описание среднего поля в больших масштабах
с прямым, смягченным, рассмотрением гравитационных взаимодействий
на расстояниях порядка нескольких шагов сетки или меньше (например,3M \)
коды имеют вычислительную стоимость, которая масштабируется как \ (O (N
log (N)) \, \) как в древовидном коде. Наконец, еще одна возможность —
использовать древовидный код для оценки силы ближнего действия, приводящей к
гибридная схема PM-Tree. Эти методы обычно очень хороши.
подходит для космологического моделирования, например, см. Gadget2 (Springel 2005). Вычислительная небесная механика относится к серии методов
ориентирована на изучение динамики малых N систем (\ (N
\ lesssim 20 \)).Наименьшее нетривиальное N равно N = 3, то есть
проблема трех тел, которая имеет множество приложений, начиная с космоса
полет к планетам движения спутников и двойным одиночным звездам
встречи. Небесная механика требует чрезвычайно высокой точности
учитывая хаотический характер проблемы N тел. Численные методы
основана на использовании локальной системы координат, для борьбы с округлением
ошибки в системах с широким динамическим диапазоном, например при исследовании
звезда-планета-спутник, а также на вариационные
формализм уравнений и теории возмущений, чтобы воспользоваться преимуществами
аналитическое невозмущенное движение планет в гравитационном поле
своей звезды (e.грамм. см. Beutler 2005). В этом контексте широко используются симплектические интеграторы (например, см. Wisdom & Holman 1991; Leimkuhler & Reich 2005). В качестве альтернативы методам N-тел на основе частиц, динамика
система частиц, взаимодействующих гравитационно, может сопровождаться
решение зависящего от времени уравнения Больцмана в сочетании с
самосогласованное уравнение Пуассона. Этот подход может использовать стандартные вычислительные методы.
разработан для решения уравнений в частных производных, таких как последовательные
методы сверхрелаксации и сопряженных градиентов.Однако это требует
решить многомерную (6D + время) нелинейную систему частичных
дифференциальные уравнения. В общем, узкое место, таким образом,
необходим большой объем памяти (например, терабиты, чтобы иметь
сетка среднего разрешения по 100 элементов в каждом измерении). тем не мение
этот метод конкурентоспособен, если интересующая астрофизическая задача
представляет симметрии, которые уменьшают количество измерений, необходимых в
модель. Например, в случае динамики шаровых скоплений очень
хорошее приближение может быть получено с помощью трехмерной модели:
предполагая сферическую симметрию в пространстве позиций (1D) и радиальную
анизотропия в пространстве скоростей (2D). Эти методы решают столкновительное уравнение Больцмана, начиная с
заданной функции распределения и проследив за пробными частицами в шести
размерное фазовое пространство положение-скорость. На каждом временном шаге
скорость частиц возмущается случайными колебаниями
согласно принятому виду оператора столкновения \ (
C [f] \, \), который зависит от вычисленных сечений для двух, трех и
встречи с четырьмя телами. Сложность кодов Монте-Карло линейна.
с количеством частиц и, следовательно, с реалистичным количеством частиц
можно использовать для моделирования столкновительных систем с \ (N> 10 ^ 5
\) с серийным кодом.Метод идеален для
исследование сеток начальных условий после надлежащей проверки
путем сравнения с прямой интеграцией (например, см. Heggie et al. 2006). При наличии сильного гравитационного поля, например, в
близость горизонта событий черной дыры, моделирование N тел
не может основываться на ньютоновской физике, но должен учитывать
учитывать основы общей теории относительности. Как численное решение
Уравнение Эйнштейна чрезвычайно сложное, постньютоновское
приближения используются, когда гравитационное поле не
слишком сильно отклоняться от ньютоновского случая.Постньютоновские поправки
обычно достаточно хороши для решения большинства астрофизических проблем
динамика звезд вокруг черной дыры. Полная общая теория относительности
каркас требуется только для изучения слияния и гравитационного
излучение волн двух черных дыр (например, см. Baker et al. 2006). Альтернативный подход к повышению эффективности численного
Решение проблемы N-тела заключается в оптимизации оборудования. Для прямого
моделирования этот подход может быть очень эффективным, благодаря тому, что
что узкое место вычислений — это просто оценка
гравитационная сила, которая имеет очень простое выражение.3
\. \) Это оборудование специального назначения может быть затем сопряжено с
компьютер общего назначения, который заботится обо всех остальных числовых
операции, необходимые для решения уравнений движения. С
GRAPE-6, крупнейшее опубликованное моделирование во временной шкале столкновений
на сегодняшний день имеет N = 131028 (Baumgardt & Makino 2003). Еще одна многообещающая разработка оборудования в последнее время — возможность
использовать графические карты (GPU) для выполнения интенсивной работы процессора
оценка. Производительность графических процессоров текущего поколения кажется
быть лучше (по соотношению флоп / $), чем у серии GRAPE6
(Portegies-Zwart et al.2007). В дополнение к доступности автономных кодов было создано несколько программных сред, которые содержат различные инструменты для настройки начальных условий, запуска моделирования, а также анализа и визуализации их результатов. Некоторые примеры: NEMO, Starlab, ACS, MUSE. Внутренние ссылки Книги Обзорные статьи Веб-материалы Открытые исходные коды Фотографии и видео из моделирования тела N Вычислительная небесная механика, теория КАМ, задача трех тел, вычислительная астрофизика, вычислительная космология
* Сила тяжести W 1 = m 1 г.Эта сила
направленным вниз в вертикальном направлении.
* Нормальная сила N. Эта сила прилагается поверхностью наклонной
плоскости на массе и направлена в направлении, перпендикулярном наклонному
Это.
* Натяжение T. Шнур оказывает эту силу на массу. Его направление
параллельно наклонной плоскости.
* Сила тяжести W 2 = m 2 г. Эта сила
направленный вниз по вертикали.
* Натяжение T. Шнур оказывает эту силу на массу. Эта сила
направленный вверх по вертикали. Натяжение шнура одинаковое при
каждой точке, и поэтому величина этой силы равна
действует на m 1 , хотя и указывает в другом направлении.
Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса., симуляций N-тел (гравитационные) — Scholarpedia
Действия после публикации Введение
где \ (G = 6.2 = \ vec {F} _i / m_i \) с положением всех
частицы в системе. Астрофизические области и шкалы времени
Временные рамки, равновесие и столкновения
Метод среднего поля: уравнение Больцмана
Подход среднего поля: аналогии и различия с гидродинамикой
Астрофизические области
Ньютоновская гравитация: методы
Прямые методы
Коды деревьев
Быстрые многополюсные методы
Коды сетки частиц
Метод адаптивного уточнения сетки
Самосогласованные методы поля
Коды P3M и PM-Tree
Коды небесной механики
Методы среднего поля
Решатели для бесстолкновительного уравнения Больцмана на основе сеток
Методы Фоккера-Планка и Монте-Карло
За пределами Ньютона: сильные гравитационные поля
Оборудование
Среда моделирования
Список литературы
Рекомендуемая литература
Внешние ссылки
См. Также