Полное сопротивление катушки формула
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока
В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0 о и 180 о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока
Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L= 0 ö и I L= -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.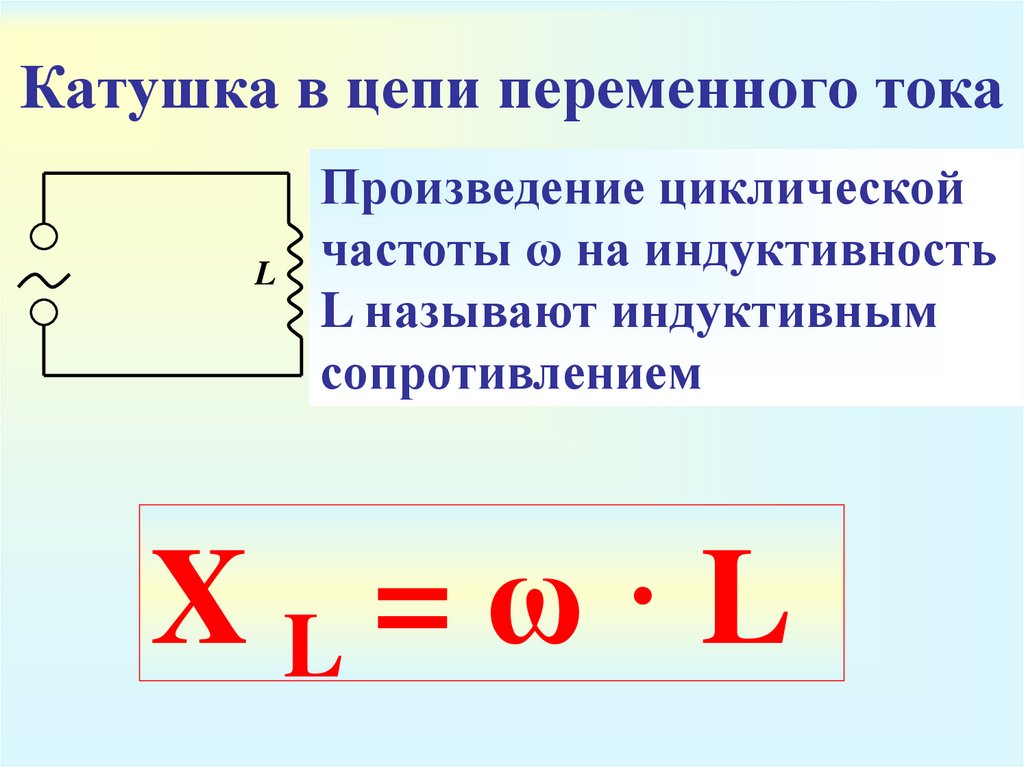
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты
Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V Rи V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V Rи V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.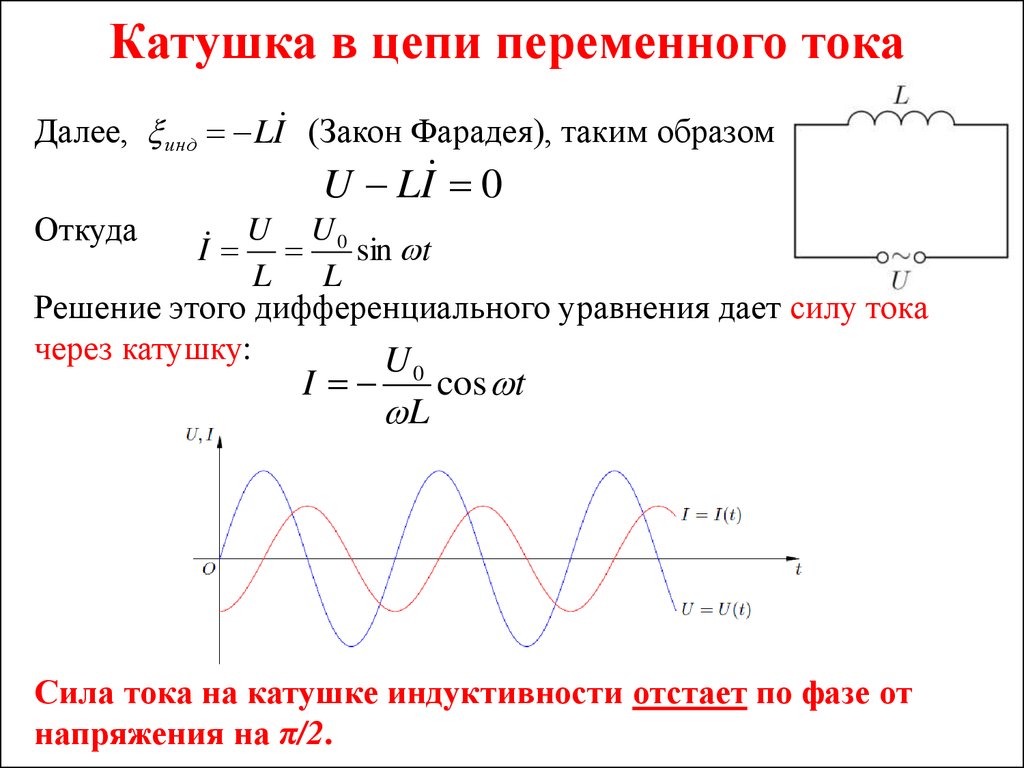
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR
На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
Треугольник сопротивления
В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.
Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
В данной статье мы подробно поговорим про индуктивное сопротивление, реактивное сопротивление и треугольники напряжения, сопротивления и силы.
Введение
Итак, мы рассмотрели поведение индукторов, подключенных к источникам постоянного тока, и, надеюсь, теперь мы знаем, что когда на индуктор подается постоянное напряжение, рост тока через него происходит не мгновенно, а определяется индуктором, индуцированным самим индуктором или обратным значением ЭДС.
Также мы видели, что ток индукторов продолжает расти, пока не достигнет своего максимального установившегося состояния после пяти постоянных времени. Максимальный ток, текущий через индукционную катушку ограничиваются только резистивной частью катушек обмотки в омах, и как мы знаем из закона Ома, это определяется отношением напряжения к току V / R .
Когда переменное напряжение подается на катушку индуктивности, поток тока через него ведет себя совершенно иначе, чем при приложении постоянного напряжения. Эффект синусоидального питания приводит к разности фаз между напряжением и формами тока. Теперь в цепи переменного тока противодействие току, протекающему через обмотки катушек, зависит не только от индуктивности катушки, но и от частоты сигнала переменного тока.
Сопротивление току, протекающему через катушку в цепи переменного тока, определяется сопротивлением переменного тока, более известным как полное сопротивление (Z) цепи. Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянного тока от сопротивления переменного тока, обычно используется термин «реактивное сопротивление» .
Как и сопротивление, значение реактивного сопротивления также измеряется в омах, но ему присваивается символ X (заглавная буква «X»), чтобы отличить его от чисто резистивного значения.
Поскольку интересующий нас компонент является индуктором, реактивное сопротивление индуктора поэтому называется «Индуктивное реактивное сопротивление». Другими словами, электрическое сопротивление индуктивности при использовании в цепи переменного тока называется индуктивным сопротивлением .
Индуктивное сопротивление, которому дается символ X L , является свойством в цепи переменного тока, которое противодействует изменению тока. В наших уроках о конденсаторах в цепях переменного тока мы видели, что в чисто емкостной цепи ток I C «опережает» напряжение на 90 o . В чисто индуктивной цепи переменного тока верно обратное: ток I L отстает от напряжения на 90 o или (π / 2 рад).
Схема индуктивности переменного тока
В приведенной выше чисто индуктивной цепи индуктор подключен непосредственно через напряжение питания переменного тока. Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Когда напряжение питания увеличивается и уменьшается с частотой, самоиндуцированная обратная ЭДС также увеличивается и уменьшается в катушке по отношению к этому изменению.
Мы знаем, что эта самоиндуцированная ЭДС прямо пропорциональна скорости изменения тока через катушку и имеет наибольшее значение при переходе напряжения питания от положительного полупериода к отрицательному полупериоду или наоборот в точках 0 о и 180 о вдоль синусоиды.
Следовательно, минимальная скорость изменения напряжения возникает, когда синусоида переменного тока пересекается при своем максимальном или минимальном пиковом уровне напряжения. В этих положениях в цикле максимальный или минимальный токи протекают через цепь индуктора, и это показано ниже.
Векторная диаграмма индуктора переменного тока
Эти формы напряжения и тока показывают, что для чисто индуктивной цепи ток отстает от напряжения на 90 o . Также можно сказать, что напряжение опережает ток на 90 o . В любом случае общее выражение заключается в том, что ток отстает, как показано на векторной диаграмме. Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Здесь вектор тока и вектор напряжения показаны смещенными на 90 o . Ток отстает от напряжения .
Мы можем также написать это заявление как, V L= 0 ö и I L= -90 о по отношению к напряжению, V L . Если форма волны напряжения классифицируется как синусоида, то ток I L можно классифицировать как отрицательный косинус, и мы можем определить значение тока в любой момент времени как:
Поскольку ток всегда отстает от напряжения на 90 o в чисто индуктивной цепи, мы можем найти фазу тока, зная фазу напряжения или наоборот. Так что если мы знаем значение V L , то I L должно отставать на 90 o . Аналогичным образом, если мы знаем значение I L, то V L, следовательно, должно опережать на 90 o . Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Затем это отношение напряжения к току в индуктивном контуре будет производить уравнение, определяющее индуктивное сопротивление Х L катушки.
Мы можем переписать уравнение для индуктивного сопротивления в более привычную форму, которая использует обычную частоту питания вместо угловой частоты в радианах ω и это будет выглядеть так:
Из приведенного выше уравнения для индуктивного реактивного сопротивления можно видеть, что, если увеличить частоту, либо индуктивность, общее значение индуктивного реактивного сопротивления также увеличится. Когда частота приближается к бесконечности, реактивное сопротивление индукторов также увеличивается до бесконечности, действуя как разомкнутая цепь.
Однако, когда частота приближается к нулю или постоянному току, реактивное сопротивление индукторов будет уменьшаться до нуля, действуя как короткое замыкание. Это означает, что индуктивное сопротивление «пропорционально» частоте.
Другими словами, индуктивное реактивное сопротивление увеличивается с частотой, в результате чего X L будет небольшим на низких частотах, а X L будет высоким на высоких частотах, что продемонстрировано на графике ниже.
Индуктивное сопротивление от частоты
Затем мы видим, что при постоянном токе индуктор имеет нулевое реактивное сопротивление (короткое замыкание), на высоких частотах индуктор имеет бесконечное реактивное сопротивление (разомкнутая цепь).
Питание от сети переменного тока серии LR
До сих пор мы рассматривали чисто индуктивную катушку, но невозможно иметь чистую индуктивность, поскольку все катушки, реле или соленоиды будут иметь определенное сопротивление, независимо от того, насколько мало связано с витками используемого провода. Тогда мы можем рассматривать нашу простую катушку как последовательное сопротивление с индуктивностью (LR).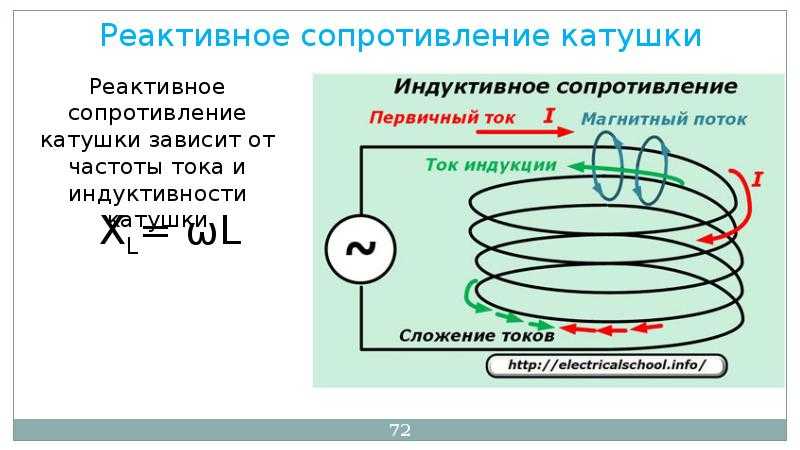
В цепи переменного тока, которая содержит как индуктивность L и сопротивление R, напряжение V будет векторная сумма двух компонентов напряжения, V Rи V L . Это означает, что ток, протекающий через катушку еще будет отставать от напряжения, но на величину меньше чем 90 ö в зависимости от значений V Rи V L .
Новый фазовый угол между напряжением и током известен как фазовый угол цепи и обозначается греческим символом фи, Φ .
Чтобы получить векторную диаграмму зависимости между напряжением и током, необходимо найти эталонный или общий компонент. В последовательно соединенной цепи RL ток является общим, так как один и тот же ток течет через каждый компонент. Вектор этой эталонной величины обычно рисуется горизонтально слева направо.
Из наших руководств о резисторах и конденсаторах, мы знаем, что ток и напряжение в цепи переменного резистивного тока, оба «в фазе» и, следовательно, вектор V R рисуется с наложением на текущую или контрольную линию.
Из вышесказанного также известно, что ток «отстает» от напряжения в чисто индуктивной цепи и, следовательно, вектор V L отображается на 90 o перед опорным током и в том же масштабе, что и V R, это показано ниже.
Цепь переменного тока серии LR
На приведенной выше векторной диаграмме видно, что луч OB представляет текущую опорную линию, луч OA — это напряжение резистивного компонента, которое в фазе с током, луч OC показывает индуктивное напряжение, которое составляет 90 o перед током, поэтому видно, что ток отстает от напряжения на 90 o , луч OD дает нам результирующее или питающее напряжение в цепи. Треугольник напряжения выводится из теоремы Пифагора и имеет вид:
Треугольник сопротивления
В цепи постоянного тока отношение напряжения к току называется сопротивлением. Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Однако в цепи переменного тока это отношение известно как полное сопротивление Z с единицами измерения в омах. Полное сопротивление — это полное сопротивление току в «цепи переменного тока», содержащее как сопротивление, так и индуктивное сопротивление.
Если мы разделим стороны треугольника напряжения выше на ток, получим еще один треугольник, стороны которого представляют сопротивление, реактивное сопротивление и полное сопротивление катушки. Этот новый треугольник называется «Треугольник сопротивления».
Силовой треугольник индуктора переменного тока
Существует еще один тип конфигурации треугольника, который мы можем использовать для индуктивной цепи, и это «силовой треугольник». Мощность в индуктивной цепи называется реактивной мощностью или вольт-амперной реактивной, символ Var, который измеряется в вольт-амперах. В цепи переменного тока серии RL ток отстает от напряжения питания на угол Φ o .
В чисто индуктивной цепи переменного тока ток будет сдвинут по фазе на 90 o к напряжению питания. Таким образом, общая реактивная мощность, потребляемая катушкой, будет равна нулю, так как любая потребляемая мощность компенсируется генерируемой самоиндуцированной ЭДС-мощностью. Другими словами, полезная мощность в ваттах, потребляемая чистым индуктором в конце одного полного цикла, равна нулю, так как энергия берется из источника и возвращается к нему.
Реактивная мощность ( Q ) катушки может быть задана как: I 2 x X L (аналогично I 2 R в цепи постоянного тока). Затем три стороны силового треугольника в цепи переменного тока представлены кажущейся мощностью ( S ), реальной мощностью ( P ) и реактивной мощностью ( Q ), как показано.
Обратите внимание, что данный индуктор или катушка будет потреблять мощность в ваттах из — за сопротивления обмоток, создающих сопротивление Z.
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Рассматривая цепь переменного тока, содержащую только индуктивное сопротивление (смотрите статью «Катушка индуктивности в цепи переменного тока»), мы предполагали равным нулю активное сопротивление этой цепи.
Однако в действительности как провод самой катушки, так и соединительные провода обладают хотя и небольшим, но активным сопротивлением, поэтому цепь неизбежно потребляет энергию источника тока.
Поэтому при определении общего сопротивления внешней цепи нужно складывать ее реактивное и активное сопротивления. Но складывать эти два различных по своему характеру сопротивления нельзя.
В этом случае полное сопротивление цепи переменному току находят путем геометрического сложения.
Строят прямоугольный треугольник (см. рисунок 1) одной стороной которого служит величина индуктивного сопротивления, а другой — величина активного сопротивления.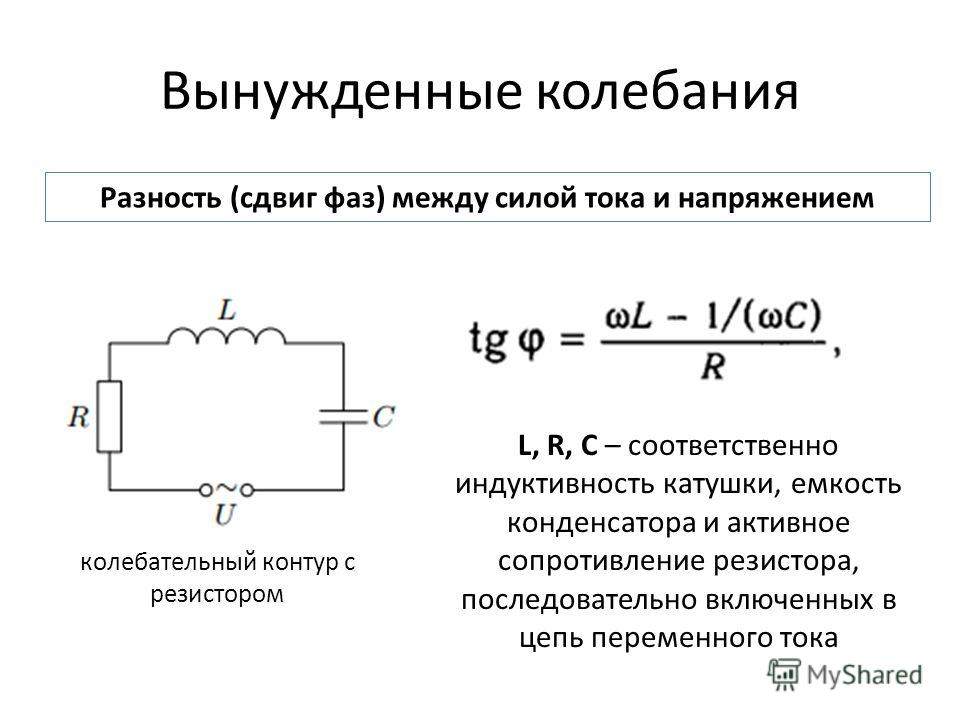 Искомое полное сопротивление цепи определится третьей стороной треугольника.
Искомое полное сопротивление цепи определится третьей стороной треугольника.
Рисунок 1. Определение полного сопротивления цепи, содержащей индуктивное и активное сопротивление
Полное сопротивление цепи обозначается латинской буквой Z и измеряется в омах. Из построения видно, что полное сопротивление всегда больше индуктивного и активного сопротивлений, отдельно взятых.
Алгебраическое выражение полного сопротивления цепи имеет вид:
где Z — общее сопротивление, R — активное сопротивление, X L — индуктивное сопротивление цепи.
Таким образом, полное сопротивление цепи переменному току, состоящей из активного и индуктивною сопротивлений, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений этой цепи.
Закон Ома для такой цепи выразится формулой I = U / Z , где Z — общее сопротивление цепи.
Разберем теперь, какое будет напряжение, если цепь, кроме и и сдвиг фаз между током и на индуктивности, обладает также сравнительно большим активным сопротивлением. На практике такой цепью может служить, например, цепь, содержащая катушку индуктивности без железного сердечника, намотанную из тонкой проволоки (дроссель высокой частоты).
На практике такой цепью может служить, например, цепь, содержащая катушку индуктивности без железного сердечника, намотанную из тонкой проволоки (дроссель высокой частоты).
В этом случае сдвиг фаз между током и напряжением составит уже не четверть периода (как это было в цепи только с индуктивным сопротивлением), а значительно меньше; причем чем больше будет активное сопротивление, тем меньший получится сдвиг фаз.
Рисунок 2. Ток и напряжение в цепи, содержащей R и L
Теперь и сама ЭДС самоиндукции не находится в противофазе с напряжением источника тока, так как сдвинута относительно напряжения уже не на половину периода, а меньше. Кроме того, напряжение, создаваемое источником тока на зажимах катушки, не равно ЭДС самоиндукции, а больше нее на величину падения напряжения в активном сопротивлении провода катушки. Иначе говоря, напряжение на катушке состоит как бы из двух слагающих:
uL— реактивной слагающей напряжения, уравновешивающей действие ЭДС самоиндукции,
uR — активной слагающей напряжения, идущей на преодоление активного сопротивления цепи.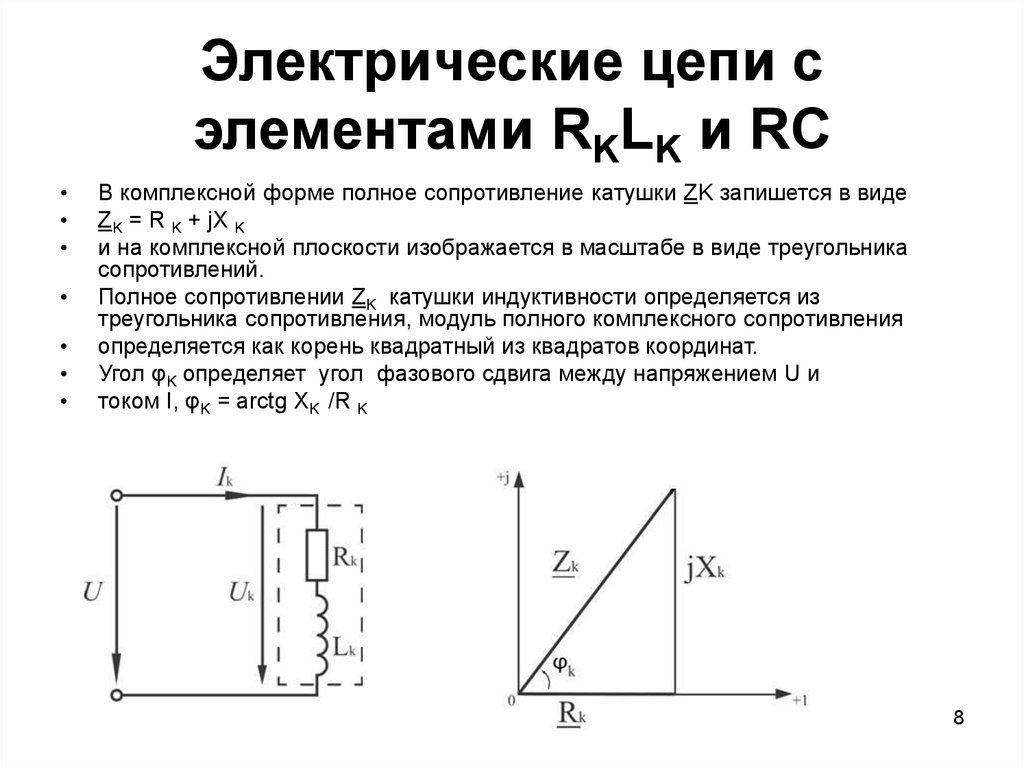
Если бы мы включили в цепь последовательно с катушкой большое активное сопротивление, то сдвиг фаз настолько бы уменьшился, что синусоида тока почти догнала бы синусоиду напряжения и разность фаз между ними была бы едва заметна. В этом случае амплитуда слагающей и, была бы больше амплитуды слагающей.
Точно так же можно уменьшить сдвиг фаз и даже совсем свести его к нулю, если уменьшить каким-либо способом частоте генератора. Уменьшение частоты приведет к уменьшению ЭДС самоиндукции, а следовательно, и к уменьшению вызываемого ею сдвига фаз между током и напряжением в цепи.
Мощность цепи переменного тока, содержащей катушку индуктивности
Цепь переменного тока, содержащая катушку, не потребляет энергии источника тока и что в цепи происходит процесс обмена энергией между генератором и цепью.
Разберем теперь, как будет обстоять дело с мощностью, потребляемой такой цепью.
Мощность, потребляемая в цепи переменного тока, равна произведению тока на напряжение, но так как ток и напряжение есть переменные величины, то и мощность будет также переменной. При этом значение мощности для каждого момента времени мы сможем определить, если умножим величину тока на величину напряжения, соответствующую данному моменту времени.
При этом значение мощности для каждого момента времени мы сможем определить, если умножим величину тока на величину напряжения, соответствующую данному моменту времени.
Чтобы получить график мощности, мы должны перемножить величины отрезков прямых линий, определяющие ток и напряжение в различные моменты времени. Такое построение и приведено на рис. 3, а. Пунктирная волнообразная кривая р показывает нам, как изменяется мощность в цепи переменного тока, содержащей только индуктивное сопротивление.
При построении этой кривой использовалось следующее правило алгебраического умножения : при умножении положительной величины на отрицательную получается отрицательная величина, а при перемножении двух отрицательных или двух положительных — положительная величина.
Рисунок 3. Графики мощности: а — в цепи содержащей индуктивное сопротивление, б — тоже, активное сопротивление
Рисунок 4. График мощности для цепи, содержащей R и L
Кривая мощности в этом случае расположена выше оси времени. Это значит, что обмена энергией между генератором и цепью не происходит, а следовательно, мощность, отдаваемая генератором в цепь, полностью потребляется цепью.
Это значит, что обмена энергией между генератором и цепью не происходит, а следовательно, мощность, отдаваемая генератором в цепь, полностью потребляется цепью.
На рис. 4 изображен график мощности для цепи, содержащей в себе одновременно индуктивное и активное сопротивления. В этом случае также происходит обратный переход энергии из цепи к источнику тока, однако в значительно меньшей степени, чем в цепи с одним индуктивным сопротивлением.
Рассмотрев приведенные выше графики мощности, мы приходим к выводу, что только сдвиг фаз между током и напряжением в цепи создает «отрицательную» мощность. При этом, чем больше будет сдвиг фаз между током и напряжением в цепи тем потребляемая цепью мощность будет меньше, и, наоборот, чем меньше сдвиг фаз, тем потребляемая цепью мощность будет больше.
Как вычислить полное сопротивление катушки если известны ее активное сопротивление индуктивность
Активное сопротивление и катушка индуктивности в цепи переменного тока
Рассматривая цепь переменного тока, содержащую только индуктивное сопротивление (смотрите статью «Катушка индуктивности в цепи переменного тока»), мы предполагали равным нулю активное сопротивление этой цепи.
Однако в действительности как провод самой катушки, так и соединительные провода обладают хотя и небольшим, но активным сопротивлением, поэтому цепь неизбежно потребляет энергию источника тока.
Поэтому при определении общего сопротивления внешней цепи нужно складывать ее реактивное и активное сопротивления. Но складывать эти два различных по своему характеру сопротивления нельзя.
В этом случае полное сопротивление цепи переменному току находят путем геометрического сложения.
Строят прямоугольный треугольник (см. рисунок 1) одной стороной которого служит величина индуктивного сопротивления, а другой — величина активного сопротивления. Искомое полное сопротивление цепи определится третьей стороной треугольника.
Рисунок 1. Определение полного сопротивления цепи, содержащей индуктивное и активное сопротивление
Полное сопротивление цепи обозначается латинской буквой Z и измеряется в омах. Из построения видно, что полное сопротивление всегда больше индуктивного и активного сопротивлений, отдельно взятых.
Алгебраическое выражение полного сопротивления цепи имеет вид:
где Z — общее сопротивление, R — активное сопротивление, X L — индуктивное сопротивление цепи.
Таким образом, полное сопротивление цепи переменному току, состоящей из активного и индуктивною сопротивлений, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений этой цепи.
Закон Ома для такой цепи выразится формулой I = U / Z , где Z — общее сопротивление цепи.
Разберем теперь, какое будет напряжение, если цепь, кроме и и сдвиг фаз между током и на индуктивности, обладает также сравнительно большим активным сопротивлением. На практике такой цепью может служить, например, цепь, содержащая катушку индуктивности без железного сердечника, намотанную из тонкой проволоки (дроссель высокой частоты).
В этом случае сдвиг фаз между током и напряжением составит уже не четверть периода (как это было в цепи только с индуктивным сопротивлением), а значительно меньше; причем чем больше будет активное сопротивление, тем меньший получится сдвиг фаз.
Рисунок 2. Ток и напряжение в цепи, содержащей R и L
Теперь и сама ЭДС самоиндукции не находится в противофазе с напряжением источника тока, так как сдвинута относительно напряжения уже не на половину периода, а меньше. Кроме того, напряжение, создаваемое источником тока на зажимах катушки, не равно ЭДС самоиндукции, а больше нее на величину падения напряжения в активном сопротивлении провода катушки. Иначе говоря, напряжение на катушке состоит как бы из двух слагающих:
uL— реактивной слагающей напряжения, уравновешивающей действие ЭДС самоиндукции,
uR — активной слагающей напряжения, идущей на преодоление активного сопротивления цепи.
Если бы мы включили в цепь последовательно с катушкой большое активное сопротивление, то сдвиг фаз настолько бы уменьшился, что синусоида тока почти догнала бы синусоиду напряжения и разность фаз между ними была бы едва заметна. В этом случае амплитуда слагающей и, была бы больше амплитуды слагающей.
Точно так же можно уменьшить сдвиг фаз и даже совсем свести его к нулю, если уменьшить каким-либо способом частоте генератора. Уменьшение частоты приведет к уменьшению ЭДС самоиндукции, а следовательно, и к уменьшению вызываемого ею сдвига фаз между током и напряжением в цепи.
Уменьшение частоты приведет к уменьшению ЭДС самоиндукции, а следовательно, и к уменьшению вызываемого ею сдвига фаз между током и напряжением в цепи.
Мощность цепи переменного тока, содержащей катушку индуктивности
Цепь переменного тока, содержащая катушку, не потребляет энергии источника тока и что в цепи происходит процесс обмена энергией между генератором и цепью.
Разберем теперь, как будет обстоять дело с мощностью, потребляемой такой цепью.
Мощность, потребляемая в цепи переменного тока, равна произведению тока на напряжение, но так как ток и напряжение есть переменные величины, то и мощность будет также переменной. При этом значение мощности для каждого момента времени мы сможем определить, если умножим величину тока на величину напряжения, соответствующую данному моменту времени.
Чтобы получить график мощности, мы должны перемножить величины отрезков прямых линий, определяющие ток и напряжение в различные моменты времени. Такое построение и приведено на рис. 3, а. Пунктирная волнообразная кривая р показывает нам, как изменяется мощность в цепи переменного тока, содержащей только индуктивное сопротивление.
3, а. Пунктирная волнообразная кривая р показывает нам, как изменяется мощность в цепи переменного тока, содержащей только индуктивное сопротивление.
При построении этой кривой использовалось следующее правило алгебраического умножения : при умножении положительной величины на отрицательную получается отрицательная величина, а при перемножении двух отрицательных или двух положительных — положительная величина.
Рисунок 3. Графики мощности: а — в цепи содержащей индуктивное сопротивление, б — тоже, активное сопротивление
Рисунок 4. График мощности для цепи, содержащей R и L
Кривая мощности в этом случае расположена выше оси времени. Это значит, что обмена энергией между генератором и цепью не происходит, а следовательно, мощность, отдаваемая генератором в цепь, полностью потребляется цепью.
На рис. 4 изображен график мощности для цепи, содержащей в себе одновременно индуктивное и активное сопротивления. В этом случае также происходит обратный переход энергии из цепи к источнику тока, однако в значительно меньшей степени, чем в цепи с одним индуктивным сопротивлением.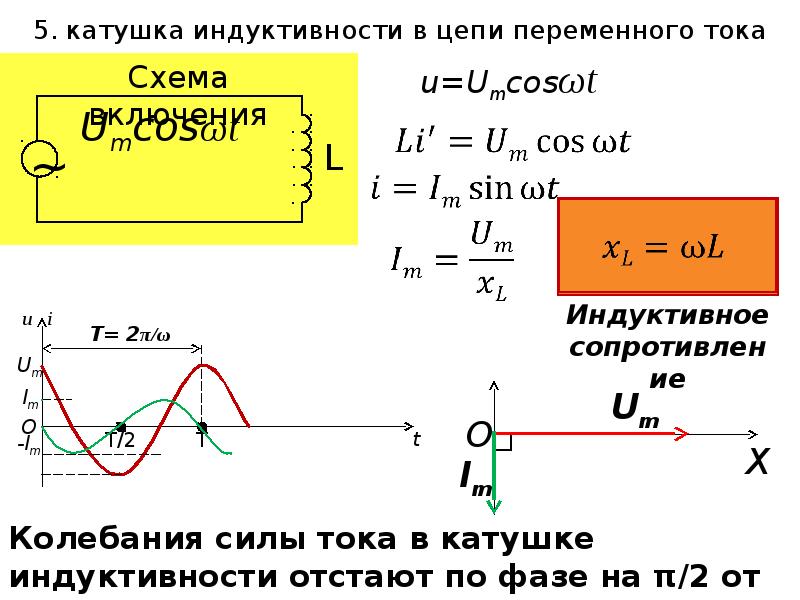
Рассмотрев приведенные выше графики мощности, мы приходим к выводу, что только сдвиг фаз между током и напряжением в цепи создает «отрицательную» мощность. При этом, чем больше будет сдвиг фаз между током и напряжением в цепи тем потребляемая цепью мощность будет меньше, и, наоборот, чем меньше сдвиг фаз, тем потребляемая цепью мощность будет больше.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Определение индуктивности катушки
Полное сопротивление катушки индуктивности переменному току (Z) складывается из индуктивного ( ) и активного (R) сопротивлений. Величина полного сопротивления определяется формулой:
Активное сопротивление катушки индуктивности — это сопротивление проводника, из которого сделана катушка. Оно, естественно, зависит от геометрических размеров, материала и температуры проводника. Наличие активного сопротивления приводит к потерям энергии при протекании тока по проводнику или, иными словами, превращению некоторой части электрической энергии во внутреннюю энергию проводника.
Индуктивное сопротивление обусловлено взаимодействием протекающего по катушке тока с магнитным полем, созданным этим током внутри катушки. Если катушка подключена к источнику переменного тока, то на стадии роста напряжения источника (первая четверть периода колебаний) явление самоиндукции сдерживает нарастание тока в цепи. Энергия, отбираемая при этом от источника питания, переходит в энергию магнитного поля катушки. Стадия нарастания напряжения источника питания продолжается ограниченное время, и ток не успевает достигнуть предельного значения, определяемого активным сопротивлением катушки. Далее наступает стадия уменьшения напряжения источника питания (следующая четверть периода), на которой явление самоиндукции проявляется в отставании спада тока от уменьшения напряжения, а энергия, запасенная в магнитном поле, возвращается в электрическую цепь. Таким образом, катушка индуктивности препятствует протеканию тока в цепи, не внося в систему энергетических потерь.
Индуктивное сопротивление XLзависит от частоты изменения внешнего напряжения v и индуктивности катушки L следующим образом: .
Чтобы подчеркнуть, что индуктивное сопротивление не связано с преобразованием электромагнитной энергии в другие виды энергии, такое сопротивление в отличии от активного называют реактивным.
В сети переменного тока с частотой 50 Гц индуктивное сопротивление катушки, содержащей несколько сотен витков медного провода большого сечения, как правило, значительно превосходит ее активное сопротивление. В этом случае активным сопротивлением катушки можно пренебречь и считать, что ее полное сопротивление совпадает с индуктивным: . На этом основан метод определения индуктивности, применяемый в данной работе.
Согласно закону Ома ток в цепи равен: , откуда следует, что: . Поскольку в нашем случае индуктивное сопротивление практически совпадает с полным сопротивлением, можно записать: . С другой стороны, как было записано выше, индуктивное сопротивление катушки равно: .
Исключая из двух последних соотношений, получаем:
Следовательно, для измерения индуктивности катушки ее необходимо подключить к источнику переменного тока известной частоты и измерить напряжение на катушке и силу тока в ней.
Схема электрической цепи, применяемой для определения индуктивного сопротивления, приведена на рис. 3.10. Кроме дросселя L, индуктивность которого надо определить, в cхему включен резистор . Величина его известна, поэтому, измерив напряжение на нем, можно рассчитать силу тока в цепи, как и в предыдущем упражнении.
Что такое активное сопротивление катушки
Одной из наиболее важных радиотехнических деталей является катушка индуктивности. Статья раскроет тему, что такое активное сопротивление катушки. Также будет дана информация о назначении и принципе действия этого элемента, приведена формула расчета сопротивления.
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).

- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.
Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.

- Универсальная, может совмещать сразу несколько вариантов обмотки.
Независимо от конструкции, все катушки работают по одному и тому же принципу.
Принцип работы
Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.
Элементами формулы являются:
- «Ф» — величина магнитного потока.
- «L» — индукция.
- «I» — величина тока.
Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.
В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.
Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.
- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Активное сопротивление
Катушка индуктивности, не подключенная к электрической цепи, имеет только активное сопротивление.
Оно создается медным проводом и зависит от его длины, сечения. Активное сопротивление способно нарастать только после подключения в цепь. В этом случае процессы, протекающие внутри элемента, зависят от типа тока.
Постоянный ток
В подключенной к постоянному току катушке индуктивности создается магнитное поле. Его величина зависит от числа витков на сердечнике. При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.
При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.
За счет образования ЭДС, возникает эффект занижения нарастания тока в этой цепи. Ток, имея определенную силу, не способен нарасти мгновенно, так как на него действует сопротивление катушки. Постепенно преодолевая ограничение, ток плавно нарастает и достигает нормальных значений. Скорость такого переходного процесса рассчитывается с использованием следующих значений:
- «L» — индуктивность, генри;
- «R» — сопротивление электрической цепи, ом. Берется значение всей схемы с катушкой;
- «t» — время переходного процесса, сек.
Формула расчета выглядит следующим образом: t=L/R. В этой формуле также используется число витков элемента. Например, t=5×0.7/70=0.05 секунд, где 5 — число витков.
Для катушек индуктивности с первичной и вторичной обмоткой, ЭДС индуктивности протекает немного иным способом. Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
В трансформаторах первичная обмотка создает эффект сильного увеличения напряжения на контактах выхода. Этого удается достичь за счет изменения силы тока на первичной обмотке. Учитывая мгновенно изменение силы тока (одномоментное размыкание), во вторичной обмотке наводится импульс э.д.с амплитудой в десятки киловольт. Примером такого явления является катушка зажигания автомобиля. Ее магнитное поле позволяет достичь напряжения в тысячи вольт, несмотря на то, что сама она работает от аккумулятора с напряжением 12 вольт.
Переменный ток
Переменный ток сильно отличается от постоянного. Поэтому и его влияние на катушку индуктивности так же будет сильно отличаться. Помимо активного сопротивления, катушка подключенная к источнику переменному току, обладает еще и индуктивным.
Активное сопротивление не подключенной в цепь катушки зависит только от марки провода, его длины и сечения.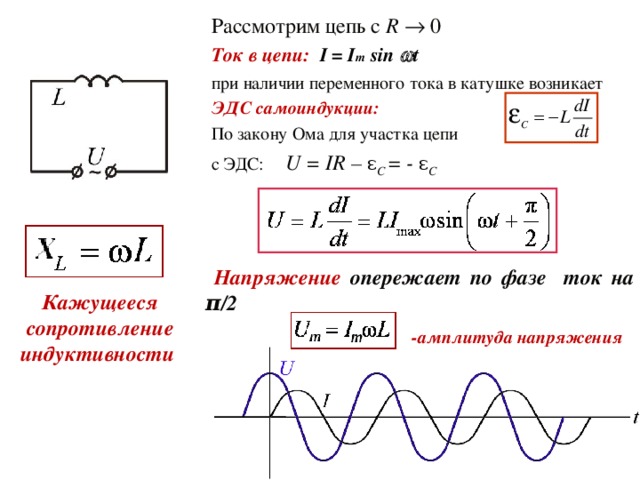 При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.
При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.
Индуктивное сопротивление возникает только после подключения катушки в цепь переменного тока. Оно зависит от частоты тока и числа витков. Индуктивное сопротивление можно определить, используя простую формулу: XL=2×π×f×L. В данном выражении:
- «XL» — индуктивное сопротивление.
- «π» — число «пи», равное 3.14.
- «f» — частотная характеристика тока.
- «L» — индуктивность.
При прохождении переменного тока по виткам катушки, создается эффект вытеснения магнитными потоками доли токов. Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Данный эффект увеличивается в зависимости от сечения провода, его проводимости и температуры. Эффект близости, сильно влияющий на увеличение активного сопротивления, снижают за счет подбора сечения обмоточного провода. Снижение эффекта близости недопустимо за счет увеличения расстояния между витками. Такой подход влияет на реактивное сопротивление и мощность магнитного поля.
В итоге активное сопротивление при подключении катушки к источнику переменного тока обладает следующими свойствами:
- Взаимодействует с параметрами индуктивного сопротивления.
- Способно занижать скорость магнитного потока.
- Создает сдвиг фаз напряжения и тока.
- При работе в условиях больших токов, активное сопротивление катушки увеличивает температуру самого компонента и всей цепи в целом.
 Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
В электротехнике существует ряд разновидностей экранированных катушек индуктивности. Такие экран часто делают из стали или алюминия. Они необходимы для снижения воздействия магнитного поля на ближайшие элементы схемы. У экранов есть и обратная функция. С помощью них катушка защищает себя от воздействия смежных компонентов схемы. Таким образом производители могут уменьшить определенную часть помех. Воздействие магнитного поля неэкранированной катушки можно услышать, например, если поднести элемент к включенному радиоприемнику. У экрана есть и один существенный недостаток. Он сильно увеличивает активное сопротивление самой детали.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.

- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.
При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Заключение
Расчет активного сопротивления катушки несет в себе большую практическую пользу. Радиолюбители и инженеры могут определить наименьший коэффициент сопротивляемости элемента, что помогает настроить частотные характеристики электронной аппаратуры.
Реактивное сопротивление в электротехнике
Содержание
Реактивное сопротивление катушки индуктивности
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.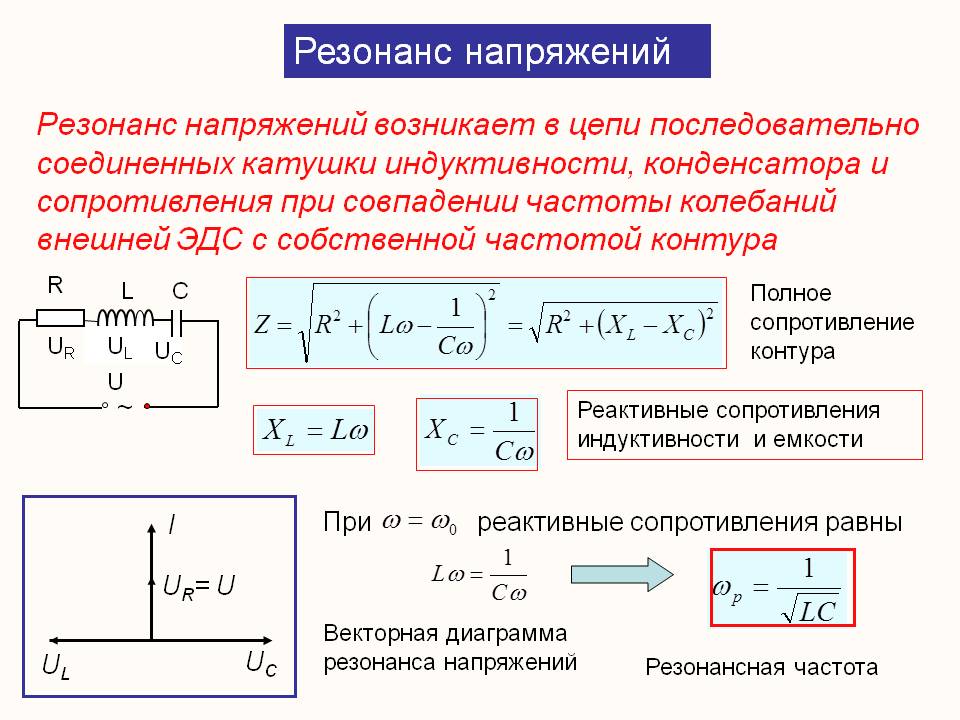
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.

Таблицы максимальных значений емкости конденсаторов.
Действие индуктивного сопротивления кабельных линий
Полное сопротивление электрической цепи разделяется на активное и индуктивное сопротивление. Из них последнее является составной частью реактивного сопротивления, возникающего во время прохождения переменного тока через элементы, относящиеся к реактивным. Индуктивность считается основной характеристикой катушек, не учитывая активное сопротивление их обмоток. Как правило, реактивное сопротивление возникает под влиянием ЭДС самоиндукции. При ее росте, в зависимости от частоты тока, происходит одновременное увеличение сопротивления.
Таким образом, активное и реактивное сопротивление кабелей образуют полное сопротивление, которое есть ни что иное, как сумма квадратов каждой составляющей. Графически это отображается в виде прямоугольного треугольника, в котором гипотенуза является полным сопротивлением, а катеты – его составными элементами.
Очень быстро вычислить активное и индуктивное сопротивление кабелей помогает таблица, в которой отражаются основные характеристики наиболее распространенных проводников. Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.
Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.
В свою очередь Х определяется по другой формуле X = 0,145lg * (2Dср/d) + 0,0157 μт, в которой 2Dср является средним расстоянием между проводниками или центрами кабельных жил, d – диаметр этих проводников или жил, μт – отражает относительную магнитную проницаемость металла проводника. Таким образом, при увеличении сечения проводника реактивное сопротивление Х будет незначительно уменьшаться.
Формула индуктивного сопротивления
Активное и реактивное сопротивление
Сопротивление медного провода
Таблица перевода сечения кабеля AWG и GA в дюймы и миллиметры
Активная реактивная и полная мощность
Удельное сопротивление алюминия
Аналогия с электрическим сопротивлением проводника на примере резистора
Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.
Активное сопротивление
Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Резисторы – источники активного сопротивления
Реактивное сопротивление
К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.
Индуктивная нагрузка
Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:
R=U/I=0/I=0.
Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.
Катушка индуктивности
Емкостная нагрузка
При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.
Детали, обладающие емкостью
Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами
Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.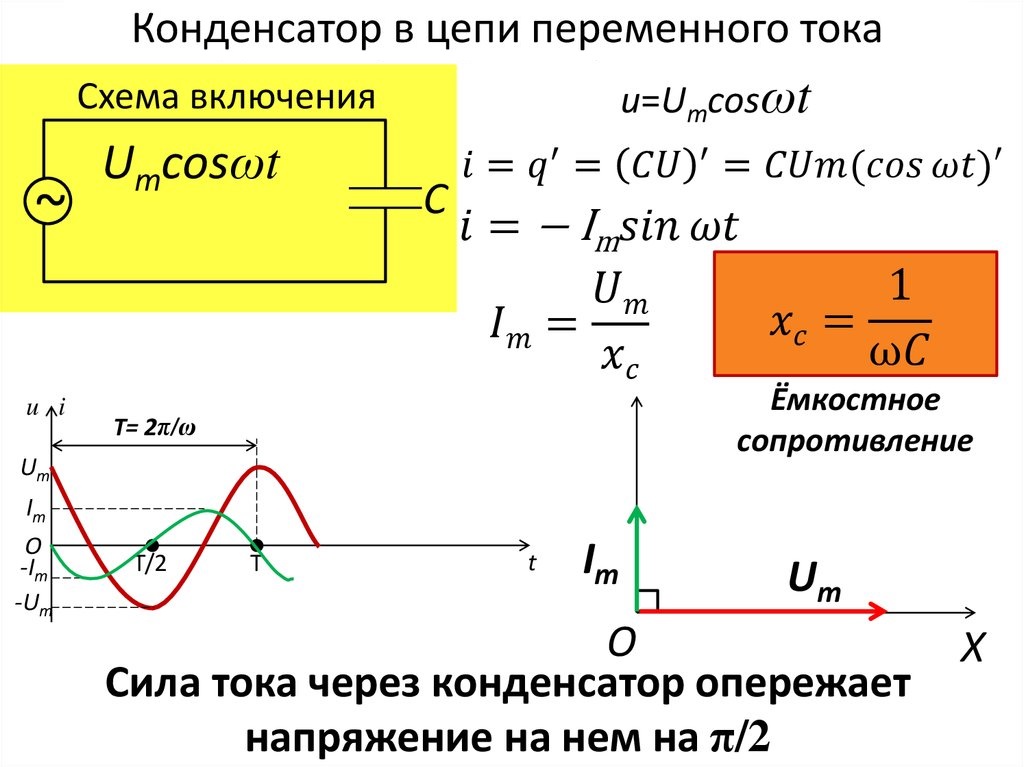
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.
Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение
Емкостная проводимость
Одним из эксплуатационных показателей остается данный параметр, обозначающий емкость между проводниками и землей, а также аналогичный показатель между самими токопроводниками.
Для его определения в трехфазной линии воздушных передач применяется выражение:
Можно увидеть прямую зависимость рабочей емкости от уменьшения расстояния между кабелями и их сечения. Следовательно, для линий низкого напряжения данная величина всегда будет больше, чем для высокого.
Проводимость подобного вида в воздушных линиях одноцепной конструкции рассчитывается так:Токи емкостного происхождения существенно влияют на работу линий с рабочими характеристиками напряжения лот 110 кВ и более, а также в магистралях уложенными кабелями с идентичными параметрами выше 10 кВ.
Попытка применить именно подобный способ для самостоятельного выполнения будет весьма непростой задачей, ведь в нем применяются и различные конструктивные нюансы типа геометрических характеристик, и диэлектрическая проницаемость изоляционного слоя, и многие другие вводные. Следовательно, оптимальным решением будет информация из таблиц, составленных производителями для конкретной марки кабеля. В каталогах все данные приведены с учетом номинального напряжения для каждой модификации.
Для начала линии, когда мы имеем дело с холостым ходом, емкостный ток определяется так:
Данный показатель будет объективным только при полностью обесточенных приемниках электричества.
Большое значение обозначенная емкость в любой рассматриваемой конструкции имеет для точного выполнения предварительных расчетов для устройств компонентов защиты и элементов заземления.
Для воздушной линии действительна такая формула:
Для кабельных магистралей:
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Свойства ёмкостей.
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
Расчет сопротивления.
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Вычисление Xc
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
График, отображающий эту величину конденсатора при непостоянном токе цепи, имеет форму гиперболы
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку
Его электросопротивляемость является безваттной, реактивной.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Импеданс элемента.
Реактивное сопротивление конденсатора
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt) запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений .
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора называют ёмкостным.
Что такое реактивное сопротивление
Согласно известному закону Ома, достаточно приложить к концам электрической цепи различные напряжения, и под таким воздействием по проводникам будет протекать ток, сила которого будет зависеть от сопротивления сердечника.
Катушка
От источников напряжения переменный ток поступает к собранной схеме, повторяя очертания синусоиды. Когда цепь не работает на изменение направления потока электронов, и вектор, согласно фазе, соответствует приложенному напряжению, то на данном участке резистором создается активное чистое сопротивление. Если же отмечаются отличительные черты во вращении векторов, то такое сопротивление именуется реактивным.
Реактивное сопротивление у катушки индуктивности может возникнуть, если присоединить источник переменного напряжения и участок изолированной проволоки. Последняя подключается к генератору и на концы магнитопровода, используемого для улучшения поступления магнитных потоков. При замерах тока в обоих случаях отмечается, что его величина значительно снижена, а по фазе имеется отставание на заданный угол.
Генератор
Важно! Это явление отмечается при возникновении противодействующих индукционных сил, которые проявляются под воздействием закона Ленца
Электрический импеданс
Полное сопротивление цепи переменного тока или импеданс есть отражение трансформирующейся во времени величины тока. В электротехнической литературе обозначается латинской буквой Z. Импеданс является двумерной (векторной) величиной, включающей в себя две независимые скалярные одномерные характеристики: активное и реактивное противодействие переменному электротоку. Проще говоря, полное сопротивление — это активное и реактивное в сумме.
В электротехнической литературе обозначается латинской буквой Z. Импеданс является двумерной (векторной) величиной, включающей в себя две независимые скалярные одномерные характеристики: активное и реактивное противодействие переменному электротоку. Проще говоря, полное сопротивление — это активное и реактивное в сумме.
Активный компонент импеданса, обозначаемый буквой R, является критерием уровня, с которым материал противодействует потоку отрицательно заряженных частиц среди своих атомов. Низкоомными материалами принято считать:
- золото;
- серебро;
- медь.
Высокоомные материалы называют диэлектриками или изоляторами. К перечню таких материалов можно отнести:
- полиэтилен;
- слюду;
- оргстекло.
Вещества с промежуточной степенью противодействия относят к группе полупроводников. В эту группу входят:
- окисды металлов;
- сернистые соединения;
- соединения с селеном;
- химические элементы (мышьяк, германий, фосфор, кремний, сера, теллур, углерод, гален и др.
 ).
).
Полное сопротивление вычисляется по формуле: Z = √ R2 +(XL — XC)2, где: R — активное электросопротивление; XL — индуктивное сопротивление, единица измерения Ом; XC — емкостное противодействие, единица измерения Ом. Полное противодействие рассчитывается пошагово. Вначале рисуют схему, потом вычисляют равнозначные противодействия индивидуально для активного, индуктивного и емкостного компонентов нагрузки и вычисляется полное противодействие электрической цепи.
Характеристики потерь
При подсчете мощностного значения на компоненте цепи всегда принимаются во внимание потери, возникающие в сопротивлениях. Мощностные потери, характерные для активных сопротивлений, связаны с характеристиками проводниковых компонентов и качествами изоляционного покрытия
Реактивные потери в сети связаны с индуктивными противодействиями проводов, а также особенностями задействованных емкостных и катушечных элементов.
Чтобы суметь правильно рассчитать требуемые характеристики элементов сети, нужно знать, на какие составляющие делится сопротивление. Активная компонента связана с необратимым переходом энергии из одной формы в другую.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т
, равновеликого площади, ограниченной кривой р(t)
и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = S p
выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности P m.
В этом случае часть площади Sp
, находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I 2 R = U 2 R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) .
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным , а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные .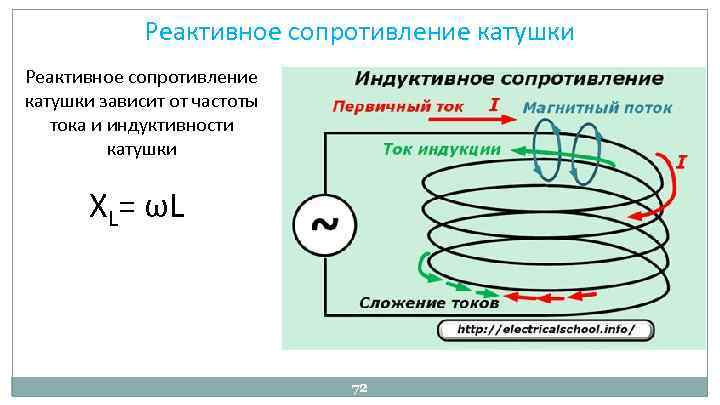
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току — Z
, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
Помогла ли вам статья?
Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях
Что такое импеданс индуктора? (с картинками)
`;
Жан-Мари Аста
Полное сопротивление индуктора, также известное как индуктивное реактивное сопротивление, представляет собой обобщенное понятие сопротивления индуктора постоянному току (DC) и переменному току (AC). Пассивный компонент, индуктор, предназначен для сопротивления изменениям тока. Материалы и конструкция индуктора определяют импеданс индуктора. Математическая формула может быть использована для расчета значения импеданса конкретной катушки индуктивности.
Математическая формула может быть использована для расчета значения импеданса конкретной катушки индуктивности.
Способность сопротивляться изменению тока в сочетании со способностью накапливать энергию в магнитном поле — вот некоторые из наиболее полезных свойств индуктора. Когда ток протекает через определенный индуктор, он создает изменяющееся магнитное поле, которое может индуцировать напряжение, противодействующее создаваемому току. Затем индуцированное напряжение пропорционально скорости изменения тока и значению индуктивности.
Катушка индуктивности может быть изготовлена разными способами и из различных материалов.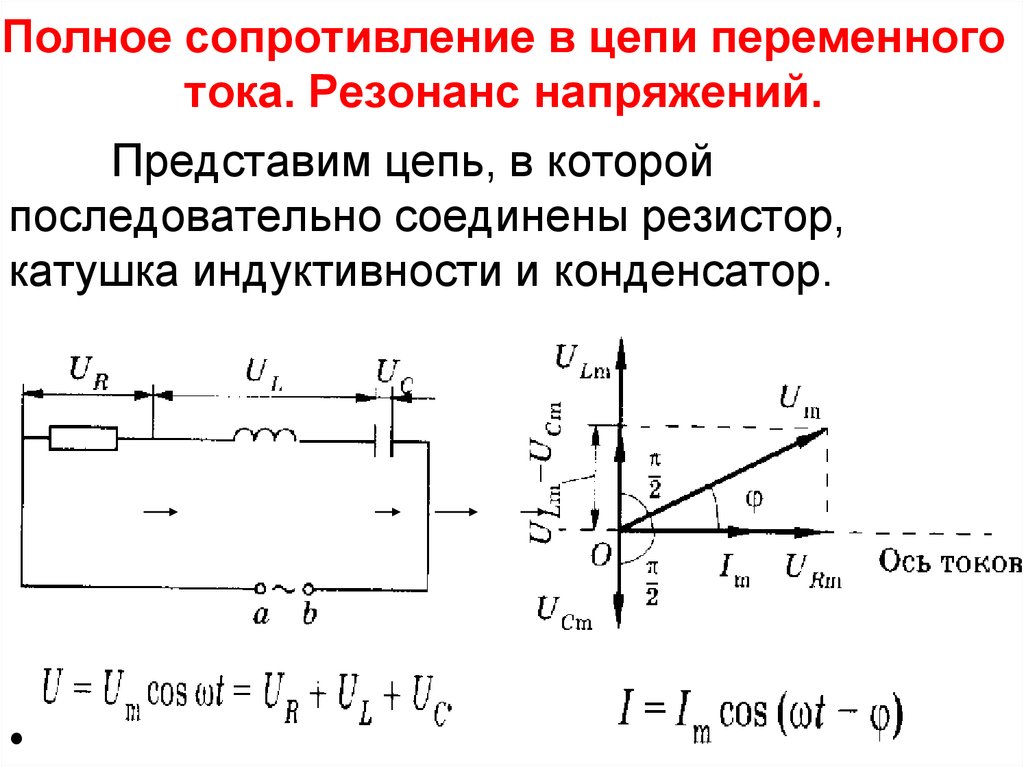
Импеданс может быть разным и зависеть от материалов, из которых изготовлен индуктор. Например, катушка индуктивности может иметь две цепи, которые связаны и отрегулированы таким образом, что выходное сопротивление одной цепи эквивалентно входному сопротивлению противоположной цепи. Это называется согласованным импедансом и является выгодным, поскольку в результате такой схемы индуктивности возникают минимальные потери мощности.
Например, катушка индуктивности может иметь две цепи, которые связаны и отрегулированы таким образом, что выходное сопротивление одной цепи эквивалентно входному сопротивлению противоположной цепи. Это называется согласованным импедансом и является выгодным, поскольку в результате такой схемы индуктивности возникают минимальные потери мощности.
Импеданс индуктора можно решить с помощью математического уравнения, используя угловую частоту и индуктивность. Импеданс зависит от частоты длины волны; чем выше частота длины волны, тем выше импеданс. Кроме того, чем выше значение индуктивности, тем выше импеданс индуктора.

Сопротивление блокировки громкоговорителя: метод конечных элементов Magnetics
Полное сопротивление блокировки громкоговорителя
Дэвид Микер
dmeeker@ieee. org
org
01 ноября 2015 г.
Введение
Определение «заблокированного импеданса» [1] привода звуковой катушки является ключевой частью понимания его частотно-зависимого поведения. Цель этой страницы — описать, как FEMM можно использовать для анализа драйвера громкоговорителя с заблокированным импедансом. С помощью FEMM эффекты вихревых токов и/или короткозамыкающих колец могут быть включены в модель слабого сигнала.
Пример геометрии громкоговорителя
Подробный пример геометрии сабвуфера SSF-082 описан в [2]. После публикации [2] сабвуфер теперь производится Lavoce Italiana, и доступно техническое описание громкоговорителя с параметрами Тиле/Смолла. Рисунки 1 и 2 взяты из [2], показывая геометрию прототипа вуфера «SSF-082». Синие области на рис. 1 обозначают участки, которые можно использовать для замыкания колец.
После публикации [2] сабвуфер теперь производится Lavoce Italiana, и доступно техническое описание громкоговорителя с параметрами Тиле/Смолла. Рисунки 1 и 2 взяты из [2], показывая геометрию прототипа вуфера «SSF-082». Синие области на рис. 1 обозначают участки, которые можно использовать для замыкания колец.
Рис. 1: Геометрия низкочастотного динамика SSF-082 из [2].
Рис. 2: Фрагмент геометрии звуковой катушки низкочастотного динамика SSF-082 из [2].
Тезис утверждает, что материал магнита — феррит Y30. Здесь магнит моделируется с использованием определения «Ceramic 5» из библиотеки материалов FEMM, материала, эквивалентного Y30. Определение FEMM для керамики 5 по существу совпадает с кривой 20 o C, показанной на рисунке 3 ниже.
Рис. 3: Кривые размагничивания для магнитного материала Ceramic 5 / Y30.
Магнитопровод указан в [2] как «низкоуглеродистая сталь». Модель стали 1018 из библиотеки материалов FEMM была выбрана в качестве конкретного и репрезентативного сорта низкоуглеродистой стали для целей этого примера.
Материал провода, указанный в [2], представляет собой магнитопровод 25 AWG, 15% плакированный медью алюминий (CCA) с одинарной изоляцией. Новые сборки FEMM имеют типы проводов CCA 10% и 15%, что позволяет рассчитывать потери близости и скин-эффекта в обмотках объемного CCA. Проводимость этого материала должна быть указана как средняя проводимость при интересующей температуре. В частности, при 20°C средняя проводимость проволоки с 15%-ным углеродным волокном составляет (0,15*58 МС/м + 0,85*35,09 МС/м) = 38,5265 МС/м. (Обратите внимание, что при получении характеристик типа проволоки CCA предполагалась проводимость 60,5% IACS для алюминия).
Руководство по моделированию
Создание сетки
Поскольку целью данной задачи является определение импеданса переменного тока, необходимо руководство по выбору размера сетки для железных деталей, подвергающихся воздействию вихревых токов.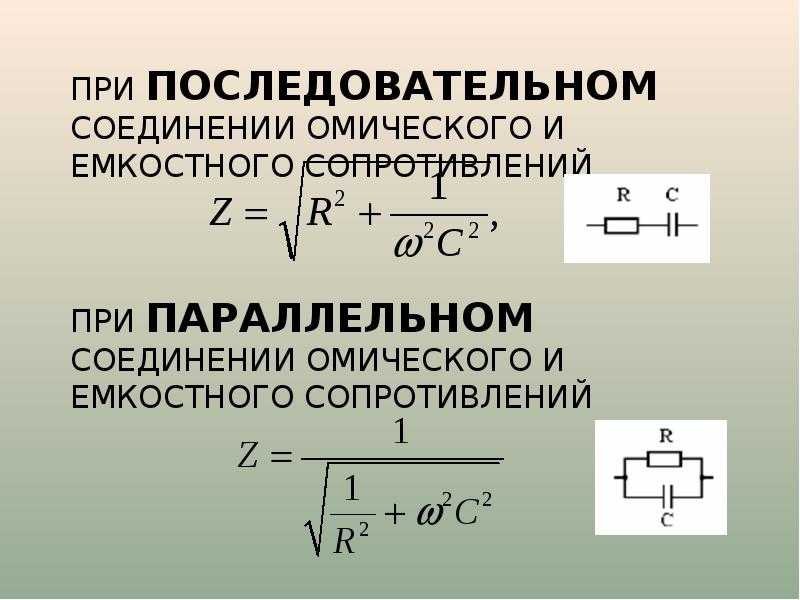 Чтобы обеспечить это руководство, необходимо сначала рассчитать глубину скин-слоя. Для определения глубины скин-слоя необходимо знать магнитную проницаемость железа (\(\mu_r\)) и электропроводность (\(\omega\)). Затем глубину скин-слоя \(\delta\) можно рассчитать с помощью: 9{-7}\) Гн/м), а \(\omega\) — частота в радианах/секунду.
Чтобы обеспечить это руководство, необходимо сначала рассчитать глубину скин-слоя. Для определения глубины скин-слоя необходимо знать магнитную проницаемость железа (\(\mu_r\)) и электропроводность (\(\omega\)). Затем глубину скин-слоя \(\delta\) можно рассчитать с помощью: 9{-7}\) Гн/м), а \(\omega\) — частота в радианах/секунду.
Многие громкоговорители изготовлены из низкоуглеродистой стали для прохождения потока. Низкоуглеродистая сталь обычно имеет максимальную относительную проницаемость порядка 1000. Однако максимальная проницаемость, как правило, достигается при довольно низкой плотности потока — относительная проницаемость 500, вероятно, более характерна для средней проницаемости.
Типичная проводимость низкоуглеродистой стали при комнатной температуре составляет ранее предполагаемую величину 5,8 МС/м (такая же, как проводимость 10 % по IACS).
При проблемах со звуком обычно интересуют частоты от 20 до 20 000 Гц. Предельным случаем для выбора размера сетки является 20 кГц. Для указанных выше свойств материала глубина скин-слоя на частоте 20 кГц составляет 0,066 мм.
Для указанных выше свойств материала глубина скин-слоя на частоте 20 кГц составляет 0,066 мм.
Для точного расчета импеданса по переменному току должно быть несколько элементов по толщине области глубины скин-слоя. Чтобы получить адекватную сетку, размер ячейки 0,0125 мм может быть определен на поверхности всех деталей из низкоуглеродистой стали.
Моделирование катушки
Для удобства перемещения звуковой катушки предлагается пометить все объекты в звуковой катушке как члены группы 1. Достаточно смоделировать катушку как «объемную» область намотки, в которой каждый виток не моделируется. Модель магнитной проволоки в FEMM автоматически включает потери от близости и скин-эффекта.
Анализ
Сценарий анализа был создан для анализа кривой BL динамика и частотно-зависимой индуктивности звуковой катушки при различных смещениях. Обе версии скрипта для Mathematica и Matlab доступны ниже в разделе «Файлы» вместе с моделью громкоговорителя . FEM. Скрипт сохраняет DC и AC версии динамика. При каждом смещении версия постоянного тока анализируется, чтобы получить рабочую точку постоянного тока. Затем выполняется ряд прогонов переменного тока, чтобы получить частотную зависимость возмущений относительно рабочей точки постоянного тока.
FEM. Скрипт сохраняет DC и AC версии динамика. При каждом смещении версия постоянного тока анализируется, чтобы получить рабочую точку постоянного тока. Затем выполняется ряд прогонов переменного тока, чтобы получить частотную зависимость возмущений относительно рабочей точки постоянного тока.
Чтобы получить достаточно высокую плотность сетки для точного разрешения эффектов вихревых токов в верхней части звукового спектра, потребовалась сетка из почти 200 000 узлов. В одном тесте каждая итерация AC занимает около минуты, а весь набор смещений и частот требует около 2 часов. Время решения может быть значительно сокращено за счет меньшего количества точек на десятилетие частоты; учитывая меньший частотный диапазон (Здесь рассматривался частотный диапазон 1 Гц-10 кГц, но 10 Гц-1 кГц больше соответствует рабочему диапазону низкочастотного динамика. При максимальной частоте 1 кГц будет достаточно грубой поверхностной сетки 0,04.)
Кривая BL, рассчитанная с помощью FEMM, показана на рисунке 4. Этот результат практически идентичен рассчитанной кривой, показанной на рисунке 3.20 в [2].
Этот результат практически идентичен рассчитанной кривой, показанной на рисунке 3.20 в [2].
Рис. 4: График рассчитанной кривой Bl для громкоговорителя SSF-082.
Кривые зависимости импеданса и индуктивности от частоты при различных положениях катушки показаны на рисунках 5 и 6. На рисунке 7 альтернативно показана индуктивность, разбитая на эффективную индуктивность с действительным знаком (L eff ) и эффективное активное сопротивление (R эфф ). Эти графики показывают, что существует значительная зависимость этих величин от положения, даже несмотря на то, что единственным механизмом частотной зависимости являются вихревые токи в низкоуглеродистой стали (в настоящем примере не моделируются замыкающие кольца). Эта зависимость от положения, в конечном счете, способствует искажению выходного сигнала громкоговорителя.
Рис. 5: Импеданс заблокированной катушки в зависимости от частоты при различных смещениях катушки.
Рис.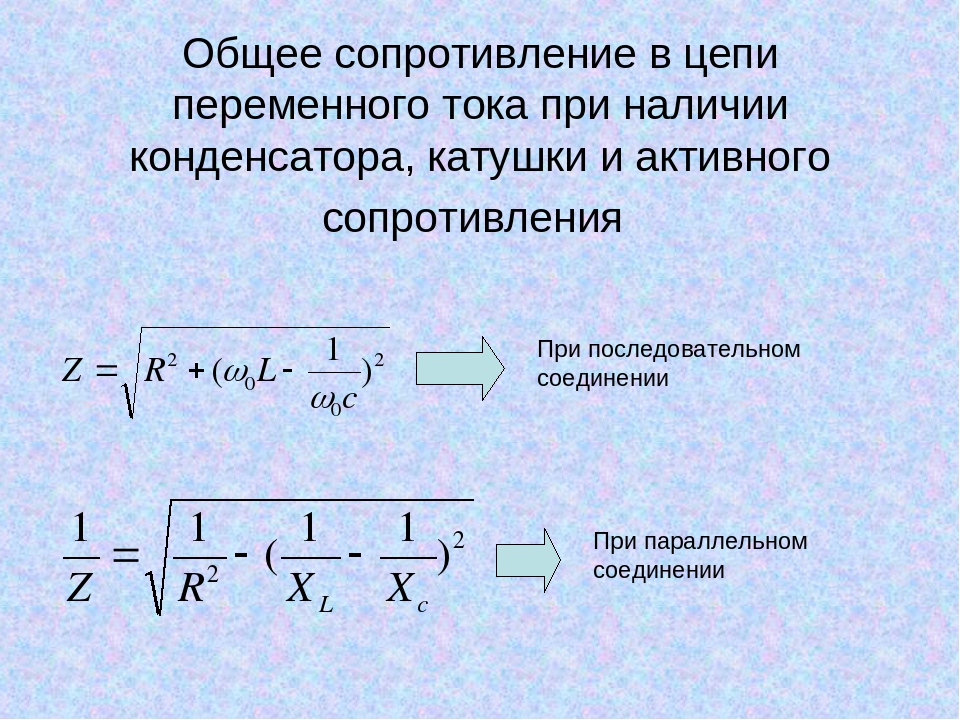 6: Зависимость индуктивности заблокированной катушки от частоты при различных смещениях катушки.
6: Зависимость индуктивности заблокированной катушки от частоты при различных смещениях катушки.
Рис. 7. Заблокированная катушка L eff и R eff в зависимости от частоты при различных смещениях катушки.
Выводы
Смысл этого примера в том, чтобы просто показать, как можно рассчитать импеданс в зависимости от частоты и положения, используя новую инкрементальную формулу переменного тока, которая теперь включена в FEMM. Эта формулировка оценивает отклик переменного тока относительно рабочей точки постоянного тока, здесь установленной постоянным магнитом.
Дальнейшие примеры также могут расширить настоящую работу, чтобы показать, как динамическая модель характеристик динамика во временной области, которая включает зависящие от положения и частоты изменения индуктивности, может быть регрессирована из анализа, выполненного в настоящем примере. См. TransientLoudspeaker.
Будущие примеры (или версии настоящего примера) могут включать влияние различных закорачивающих колец на импеданс блокировки.
Файлы
Ссылки
[1] М. Додд, В. Клиппель и Дж. Окли-Браун, «Импеданс звуковой катушки как функция частоты и смещения», Конвенция 117 Общества звукоинженеров, октябрь 2004 г.
[2] Л. Борто, Оптимизация колец демодуляции в профессиональных громкоговорителях , магистерская диссертация, Университет Падуи, 2012.
[3] Лист данных LaVoce SSF082.00L.
Как рассчитать импеданс катушки?
Противодействие току, протекающему через катушку в цепи переменного тока, определяется сопротивлением цепи переменному току , более известным как импеданс (Z). Но сопротивление всегда связано с цепями постоянного тока, поэтому, чтобы отличить сопротивление постоянному току от сопротивления переменному току, обычно используется термин реактивное сопротивление.
Что такое импеданс?
электрический импеданс, мера полного сопротивления, которое цепь или часть цепи оказывает электрическому току . Импеданс включает в себя как сопротивление, так и реактивное сопротивление (qq. v.). … Полное сопротивление сводится к сопротивлению в цепях с постоянным постоянным током.
Импеданс включает в себя как сопротивление, так и реактивное сопротивление (qq. v.). … Полное сопротивление сводится к сопротивлению в цепях с постоянным постоянным током.
Как рассчитать импеданс?
В цепях переменного тока закон Ома принимает более общую форму: E = I⋅Z , где E — напряжение, а I — ток, как и раньше. Новый термин, Z, представляет собой импеданс, векторную комбинацию: сопротивления, R (в омах), с падением напряжения в фазе с током.
Что такое импеданс в цепи переменного тока?
Полное сопротивление переменному току равно 90 139 показателю сопротивления, которое цепь представляет току каждый раз, когда подается напряжение 90 140 . В более количественном смысле это отношение напряжения к току в пределах переменного тока. Импеданс можно расширить до идеи сопротивления цепи переменного тока и включить как фазу, так и величину. 23 декабря 2018 г.
В более количественном смысле это отношение напряжения к току в пределах переменного тока. Импеданс можно расширить до идеи сопротивления цепи переменного тока и включить как фазу, так и величину. 23 декабря 2018 г.
Импеданс равен сопротивлению?
Импеданс расширяет понятие сопротивления цепям переменного тока (AC) и обладает как величиной, так и фазой, в отличие от сопротивления, которое имеет только величину. Импеданс представляет собой комплексное число с теми же единицами, что и сопротивление , для которого единицей СИ является ом (Ом).
Связанные
Что такое низкий импеданс?
Низкий импеданс находится в диапазоне приблизительно от 4 до 16 Ом . Динамики с низким импедансом используются в различных звуковых системах, таких как бытовая стереосистема и автомобильная аудиосистема. Под высоким импедансом обычно понимается импеданс от нескольких сотен до нескольких кОм. 26 мая 2011 г.
Динамики с низким импедансом используются в различных звуковых системах, таких как бытовая стереосистема и автомобильная аудиосистема. Под высоким импедансом обычно понимается импеданс от нескольких сотен до нескольких кОм. 26 мая 2011 г.
Что такое РЧ импеданс?
В электротехнике импеданс равен отношение напряжения к току с учетом фазового угла. … В ВЧ идея согласования импеданса заключается в выравнивании импеданса источника и нагрузки для максимальной передачи мощности. Импеданс представлен как Z и является сложным, чем просто сопротивление сети. 15 апреля 2017 г.
Что такое мнимое сопротивление?
Мнимая часть импеданса называется реактивным сопротивлением. В общем Z = R + jX , где X — реактивное сопротивление, а Z — импеданс. При увеличении частоты сигнала емкостное сопротивление XC уменьшается, а индуктивное сопротивление XL увеличивается. Это приводит к изменению полного импеданса в зависимости от частоты.
Это приводит к изменению полного импеданса в зависимости от частоты.
Связанные
Что такое импеданс и как он измеряется?
Импеданс рассчитывается путем деления напряжения в такой цепи на ее ток . Короче говоря, импеданс можно описать как ограничение протекания тока в цепи переменного тока. Импеданс обозначается символом «Z» и измеряется в омах (Ом), той же единице измерения, которая используется для измерения сопротивления постоянному току.
Связанные
Что такое импеданс конденсатора?
Полное сопротивление емкостного элемента; это измеряется в омах и является мерой того, насколько емкостной элемент «контролирует или препятствует» уровню тока в сети.
Родственный
Что такое эффективное сопротивление?
Насколько я понимаю ваш вопрос, эффективный импеданс равен сопротивлению цепи, состоящей из RLC при заданной рабочей частоте (сопротивление Ls и Cs изменяется с частотой).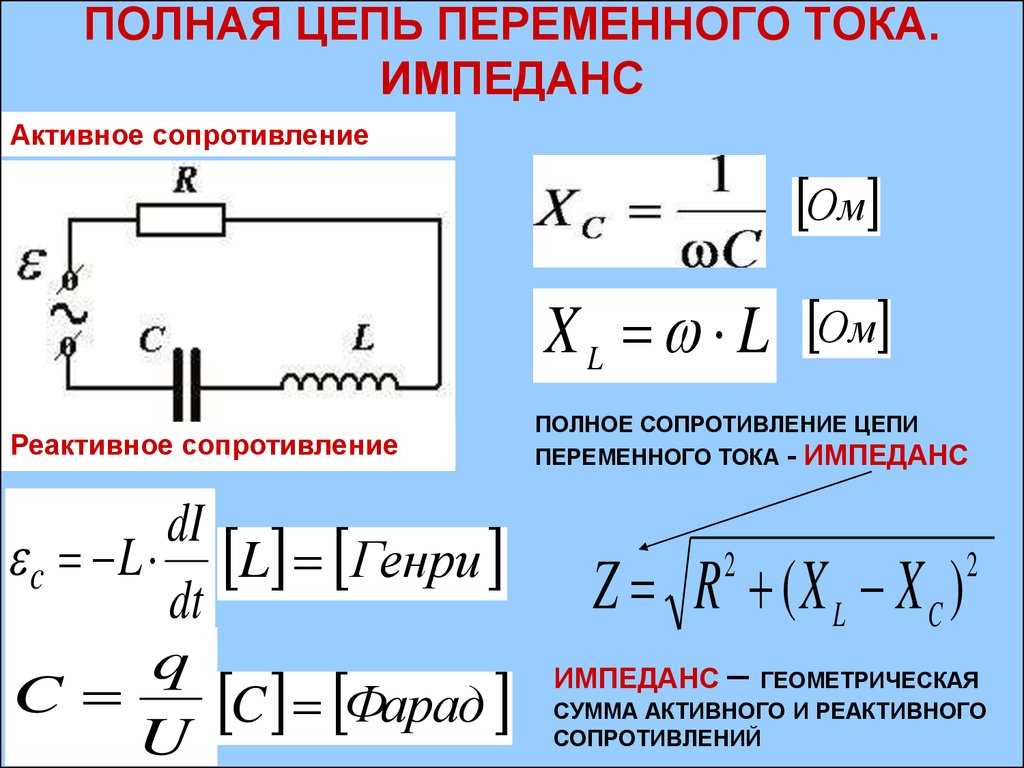 Возьмите каждый L и C в цепи и рассчитайте их сопротивление на заданной частоте.
Возьмите каждый L и C в цепи и рассчитайте их сопротивление на заданной частоте.
Связанные
Что такое добротность катушки?
«Q» означает «фактор качества». Катушки легко пропускают постоянный ток, но действуют как резистор для переменного тока. … Отношение между составляющими сопротивления и частотно-зависимой индуктивностью (R/2πf L) называется коэффициентом потерь, а его обратное число — значением добротности (Q=2πf L/R) .
Связанные
Что такое импеданс цепи переменного тока класса 12?
Импеданс (символ Z) — это мера полного сопротивления цепи току или того, насколько она препятствует потоку заряда . Это похоже на сопротивление, но также учитывает емкость и индуктивность. Ом – это единица измерения импеданса (Ом).
Связанные
Как рассчитать импеданс цепи?
К вычислить полное сопротивление , рассчитайте сопротивление и реактивное сопротивление цепи , затем обозначьте сопротивление как R и реактивное сопротивление как X.
 Возведите в квадрат R и X и сложите два произведения вместе. Возьмите квадратный корень из суммы квадратов R и X, чтобы получить импеданс .
Возведите в квадрат R и X и сложите два произведения вместе. Возьмите квадратный корень из суммы квадратов R и X, чтобы получить импеданс .
Связанные
Что такое импеданс в электрических цепях и каково его значение?
Электрический импеданс, мера полного сопротивления цепи или ее части электрическому току. Импеданс включает как сопротивление , так и реактивное сопротивление (qqv). Составляющая сопротивления возникает из-за столкновений проводящих ток заряженных частиц с внутренней структурой проводника.
Связанные
Что понимается под импедансом в цепи?
В электротехнике электрический импеданс является мерой сопротивления, которое цепь оказывает току при приложении напряжения. Количественно импеданс элемента схемы с двумя выводами представляет собой отношение комплексного представления синусоидального напряжения между его выводами к комплексному представлению тока, протекающего через него.





 Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.

 ).
). Возведите в квадрат R и X и сложите два произведения вместе. Возьмите квадратный корень из суммы квадратов R и X, чтобы получить импеданс .
Возведите в квадрат R и X и сложите два произведения вместе. Возьмите квадратный корень из суммы квадратов R и X, чтобы получить импеданс .