Вопрос 3. В чем заключается явление резонанса напряжений и при каких условиях оно возникает?
Ответ 3.1: В данной цепи при равенстве индуктивного и емкостного сопротивлений полное сопротивление цепи будет минимальным и чисто активным Z=R, а ток – максимальным .
Падения напряжения на индуктивном и емкостном элементах рассчитываются по закону Ома: , и т.к.величина напряжения на идеальной индуктивности ULравнанапряжению на емкости UC. , но фазы напряженийULи UC противоположны (сдвинуты на 180°).
Режим работы цепи c последовательным соединением R,L,C элементов при котором и (или )называют резонансом напряжений.
Сумма
комплексов напряжений ŪLи ŪC равна нулю,
следовательно и модуль суммы будет
равен нулю. Вольтметр, измеряющий падение
напряжения
Вольтметр, измеряющий падение
напряжения
При резонансе напряжения на емкости и на индуктивности могут значительно превышать подводимое напряжение U, если изначительно превышают R:
, .
Физическая
причина возникновения повышенных
напряжений – это колебания значительной
энергии, запасаемой попеременно в
электрическом поле емкостного и
магнитном поле индуктивного элементов.
При резонансе напряжений малые количества
энергии, поступающей от источника и
компенсирующие потери энергии в активном
элементе – сопротивлении R,
достаточны для поддержания незатухающих
колебаний в системе относительно больших
количеств энергии электрического и
магнитного полей.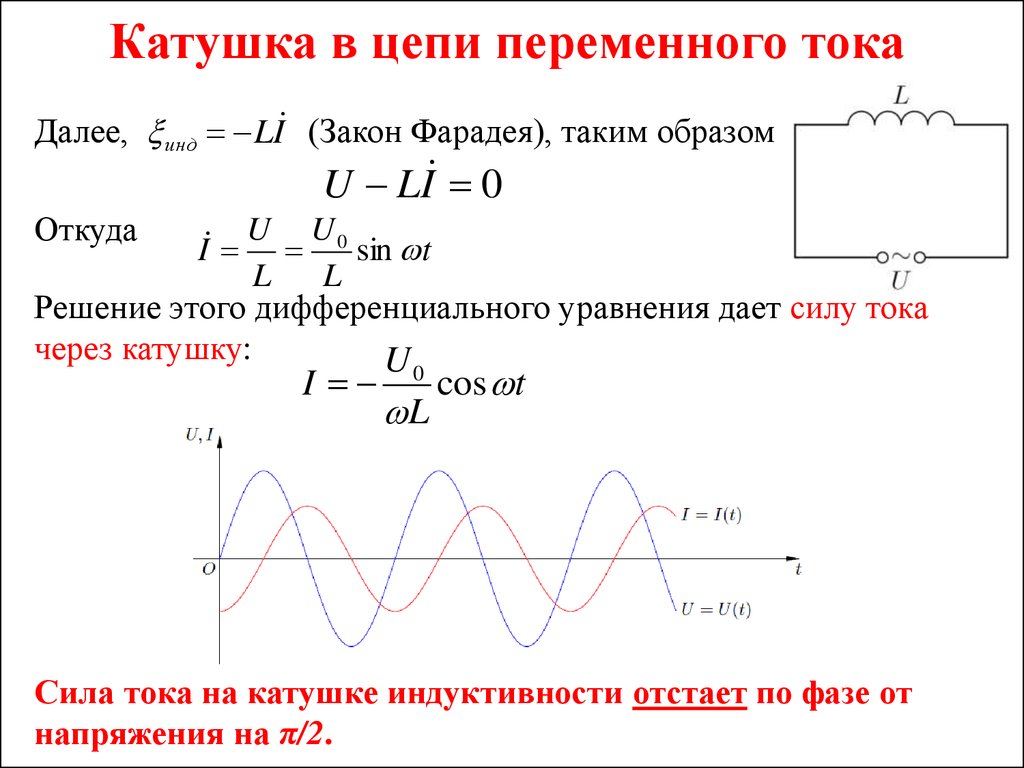
Резонанс напряжений в промышленных электрических установках нежелательное и опасное явление, так как оно может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или пробою изоляции.
**) Для мощных двигателей отношение сопротивлений обмоток XL/R на промышленной частоте составляет несколько десятков. Напряжение питания двигателей обычно <380В. Поэтому в случае резонанса, напряжение на обмотке UL превысит напряжение питания в деcятки раз (UL>>3800В).
В
тоже время резонанс напряжений в
электрических цепях переменного тока
широко используется в радиотехнике в
различных приборах и устройствах,
основанных на резонансных явлениях.
Вопрос 4. Изменением каких параметров электрической цепи (см. Рис.1) можно получить резонанс напряжений ?
Ответ 4: При резонансе напряжений выравниваются реактивные сопротивления ХL=XC.
Т.к. ХL=ω·L , а XC=1/ωС , то равенства сопротивлений можно добиться тремя способами:
при постоянных ω и L изменяя величину емкости С;
при постоянных ω и С изменяя величину индуктивности L;
при постоянных L и С изменяя частоту ω. При резонансе .
Вопрос 5. С помощью каких приборов и по какому признаку можно судить о возникновении резонанса напряжений в электрической цепи?
Ответ
5: 1) В данной
лабораторной установке опыты проводятся
при постоянных величинах ω и L.
По мере увеличения емкости от минимального
до резонансного значения С0=1/ωXL,
полное сопротивление цепи
будет уменьшаться, при этом ток в цепи
согласно формуле для тока
будет расти. При резонансе он достигнет
максимального значения .
При резонансе он достигнет
максимального значения .
Вывод 1
1: Амперметр покажет максимальное значение тока.
2)
Т.к. UL=I·X
Вывод 2:
1)Вольтметр PVК также покажет максимальное значение

Т.к . ток в цепи один , а величины сопротивлений ХL, XC при резонансе одинаковы, то и напряжения одинаковы UL =UС. При этом Uвх = UR. При резонансе =.Следовательно показания вольтметров PVК и PVCбудут разными. Очевидно, что UК > UC.
Вывод 3: при резонансе показания вольтметра PVК
4) Ваттметр PW измеряет активную мощность потребляемую цепью. Т.к. при резонансе ток максимальный, а активная мощность Р = I2·R, то и мощность P будет максимальной.
Вывод
4: Ваттметр
покажет максимальное значение Рмакс = I02·R= U2вх / R.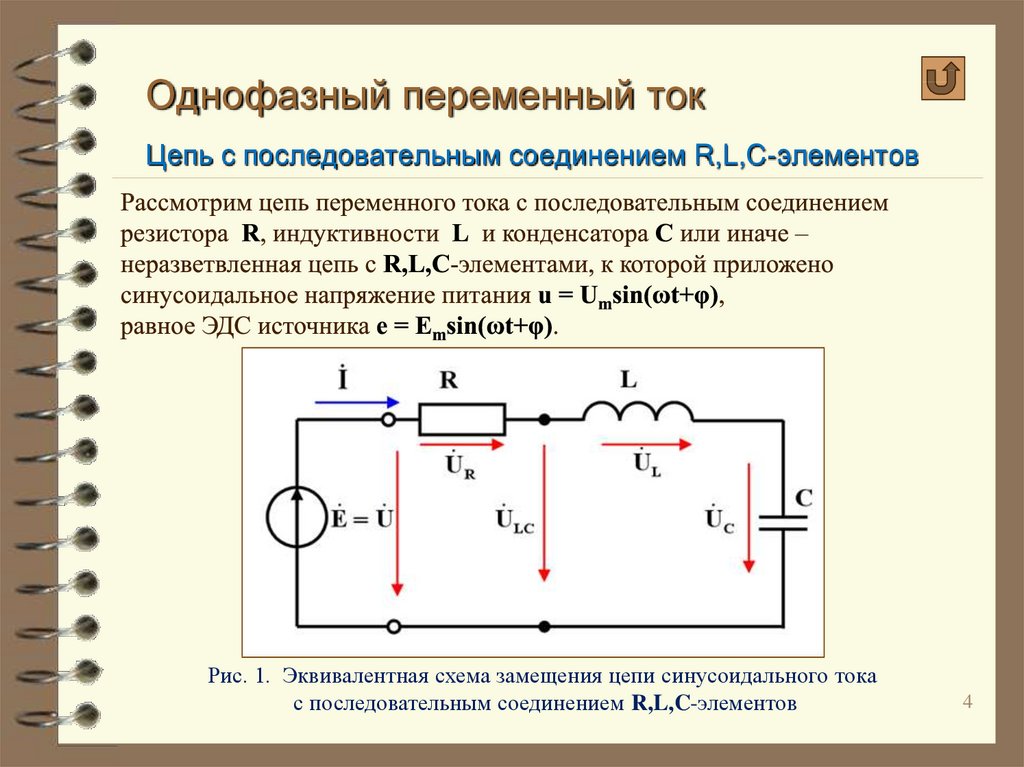
Резонанс напряжений, что это такое, когда возникает
Содержание:
Резонанс – что это такое
Резонанс в физике – это частотно-избирательный отклик системы колебаний на внешние силы, которые периодически воздействуют на систему. Проявляется это воздействие в резком увеличении амплитуды движений этих колебаний, когда частота внешней воздействующей силы совпадает с некоторыми, характерными для данной колебательной системы, частотами.
Важно! Суть резонирования заключается в резком увеличении амплитуды колебаний при совпадении значения частоты силы, воздействующей на систему извне, с собственной частотой колебаний этой системы.
Тупое и острое резонирование
Чтобы далее говорить о явлении резонирования, следует понять, что такое колебания и частота. Колебания – это процесс изменения состояний колебательной системы, который повторяется через определенные промежутки времени и происходит вокруг точки равновесия. В пример можно привести раскачивание на качелях. Произойти резонирование частот может только там, где есть колебательные движения. Причем совсем неважно, к какому именно виду относятся колебания: электрические, звука, механические.
Произойти резонирование частот может только там, где есть колебательные движения. Причем совсем неважно, к какому именно виду относятся колебания: электрические, звука, механические.
Виды колебательных движений
Процесс колебаний характеризуют частота и амплитуда. Простыми словами, на примере качели можно сказать, что амплитуда – это высшая точка, которую они достигают. Частота колебаний отвечает за скорость достижения качелями этой точки.
Возвращаясь к примеру с качелями, можно сказать, что когда они раскачиваются, система колебаний совершает вынужденные колебания. Увеличить амплитуду этих колебаний можно путем воздействия на эту систему определенным образом. То есть, если толкать качели с определенной силой и в определенное время, то можно сильно раскачать их без применения больших усилий.
Это явление и будет называться резонансом: частота воздействий извне будет совпадать с частотой колебаний в системе, и вследствие этого будет увеличиваться амплитуда.
Резонирование напряжений в электроцепи
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Рис. 1. Резонанс в электрической цепи
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления.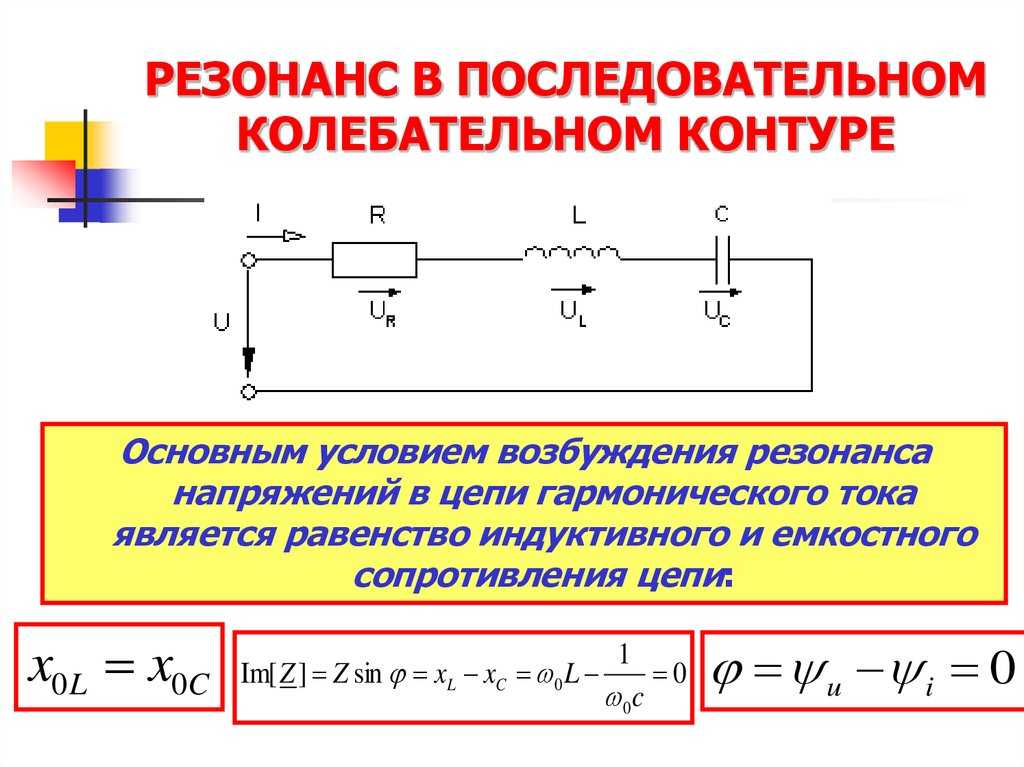 То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
Рис. 3. Последовательный колебательный контур
Рис. 4. Параллельный колебательный контур
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.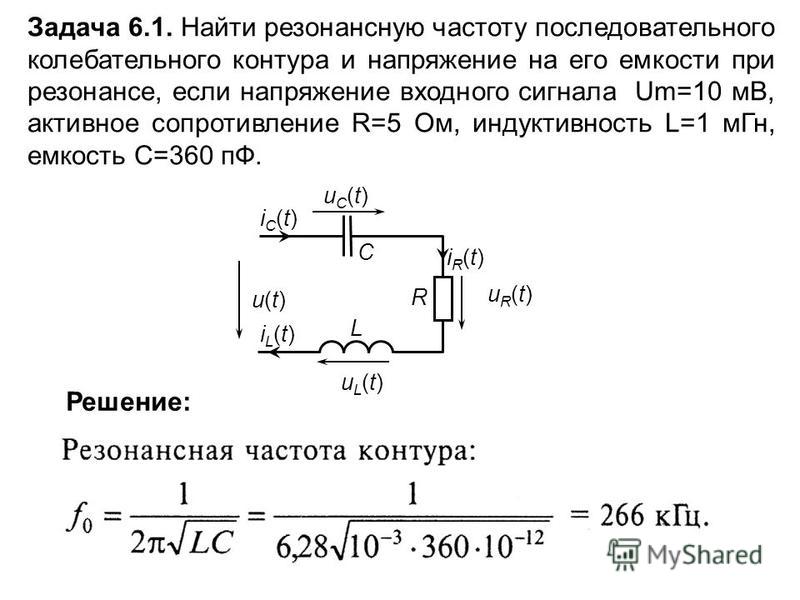
Явление резонанса в цепях переменною тока
Цель работы. Изучить явление резонанса в цепях переменною тока. Определить резонансные частоты и параметры цепей для различных типов соединений.
1. Изучение резонанса напряжений в цепях переменного тока
Резонанс напряжений возникает при определенных условиях в цепи переменного тока с последовательно соединенным активным сопротивлением R, соленоидом индуктивностью L и конденсатором емкостью С (рис. 1).
Пусть цепь подключена к источнику синусоидального напряжения U, которое изменяется с циклической частотой
. По закону Кирхгофа для данной цепи
или
Дифференциальное уравнение (2) можно решить различными методами, используем для ею решения метод векторных диаграмм.
Эту же задачу можно решить методом векторных диаграмм. Этот метод основан на том, что синусоидально изменяющуюся со временем величину (например,
графически можно предоставить в виде проекции на вертикальную ось вращающегося вектора, длина которого равна максимальному (амплитудному) значению
. Угловая скорость вращения вектора равна циклической частоте
Угловая скорость вращения вектора равна циклической частоте
а угол, образованный вектором с горизонтальной осью в начальный момент времени, равен начальной фазе
синусоидальной величины (рис. 2).
Пользуясь методом векторных диаграмм, можно алгебраическое сложение мгновенных значений синусоидально изменяющихся со временем величин одинаковой частоты заменить геометрическим сложением векторов их представляющих. Тогда длина результирующего вектора даст амплитуду результирующей синусоиды, а угол, образованный им с горизонтальной осью – ее начальную фазу.
Возможно вам будут полезны данные страницы:
| Мощность цепи синусоидального тока |
| Коэффициент мощности и его экономическое значение |
| Характерные особенности резонанса напряжений |
| Трехфазные цепи |
Построим векторную диаграмму напряжений нашей цепи. Для этого заметим, что если источник в цепи создает синусоидальное напряжение и, изменяющееся с частотой
, то ток в цепи будет также синусоидальным с той же частотой.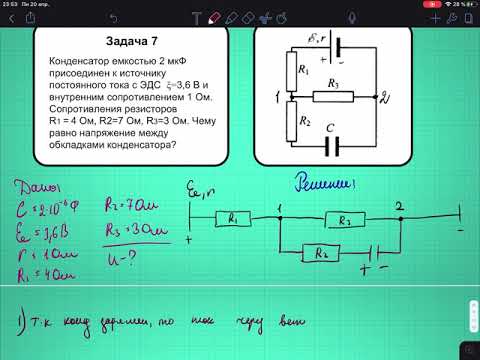 Поскольку ток в последовательной цепи на всех участках одинаков, то удобнее принять начальную фазу тока равной нулю, а напряжения на участках цепи рассчитать при этом условии.
Поскольку ток в последовательной цепи на всех участках одинаков, то удобнее принять начальную фазу тока равной нулю, а напряжения на участках цепи рассчитать при этом условии.
где
– амплитуда тока. Тогда мгновенное значение напряжения на активном сопротивлении
т.е. совпадает по фазе с силой тока, где
– амплитуда напряжения на активном сопротивлении R.
Мгновенное значение напряжения на индуктивности
т.е. опережает но фазе силу тока на
, где
– амплитуда напряжения на катушке индуктивности L.
Мгновенное значение напряжения на емкости
т.е. отстает по фазе от силы тока на
, где
– амплитуда напряжения на емкости С.
При построении векторной диаграммы вектор тока откладывается горизонтально, поскольку он одинаков во всех последовательно соединенных элементах цепи R. L и С. Вектора, соответствующие напряжениям, представляются с учетом соответствующего сдвига фаз относительно тока (рис. 3).
Первый из них совпадает с направлением вектора, соответствующего току, а второй и третий повернуты на углы
. относительно тока. При сложении этих векторов получается результирующий вектор, длина которого дает амплитуду приложенного напряжения
относительно тока. При сложении этих векторов получается результирующий вектор, длина которого дает амплитуду приложенного напряжения
, а угол
– разность фаз напряжения и тока.
Отсюда получим выражение для силы тока
Величина
называется полным сопротивлением (импедансом) цепи,
– индуктивным сопротивлением.
– емкостным сопротивлением, а
– реактивным сопротивлением цепи. Это выражение представляет собой закон Ома для данной цени, поскольку связывает амплитудные значения тока и напряжения постоянным коэффициентом Z (при постоянных R, L, С и
).
Сдвиг фаз между током и напряжением также определяется из векторной диаграммы:
Анализ выражений (9) и (10) показывает, что частоту
(при постоянных значениях L и С) можно подобрать так, чтобы индуктивное и емкостное сопротивления были одинаковыми:
При этом реактивное сопротивление X цепи обращается в нуль, полное сопротивление Z минимально и равно только активному сопротивлению (Z = R), сила тока и напряжение совпадают по фазе
, амплитуда силы тока
достигает максимальной величины:
При этих условиях амплитудные значения напряжений на емкости и индуктивности противоположны по фазе и равны по величине
и, поэтому это явление называется резонансом напряжений (на индуктивности и емкости), а частота
при которой достигается резонанс-резонансной частотой. Она находится из соотношения (11):
Она находится из соотношения (11):
Период колебаний тока и напряжений при резонансе
Поскольку напряжения на индуктивности и емкости изменяются в противоположных фазах, то суммарное напряжение на участке индуктивность-емкость равно нулю, хотя напряжения на индуктивности и емкости по отдельности могут быть весьма значительными и даже большими, чем напряжение на концах всей цепи.
Действительно, если
то, как следует из выражения (11),
, что может быть опасным для цепи.
Условие резонанса может быть достигнуто разными способами:
1) подбором частоты
при постоянных значениях L и С;
2) подбором индуктивности L при постоянных значениях
и С;
3) подбором емкости С при постоянных значениях
и L.
Зависимость амплитуды силы тока
от частоты
графически изображена на рис. 4. Представленные кривые называются резонансными. Чем меньше активное сопротивление R, тем круче и острее кривая, а чем больше R, тем кривая более пологая.
Зависимость сдвига фаз
от частоты
графически изображена на рис. 5, где приведены две кривые для разных значений активного сопротивления R. При частотах
сдвиг фаз
, т.е. в цени преобладает емкостное сопротивление. При
сдвиг фаз
, и в цепи преобладает индуктивное сопротивление. При резонансе
величина
Все рассмотренные соотношения справедливы и для действующих значений
и U, так как последние отличаются от амплитудных только постоянным множителем. Например, для гармонически изменяющихся величин
Резонанс токов и напряжений
Механический резонанс
Параллельный контур используют, чтобы создать резонанс тока. Для выполнения отмеченных выше условий выбирают равные значения реактивных проводимостей (BL и Bc). По мере увеличения частоты общее сопротивление контура возрастает, что сопровождается уменьшением силы тока.
График изменения тока и проводимости, формулы для расчетов
В последовательном резонансном контуре устанавливают аналогичные функциональные компоненты. Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.
Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.
Резонанс напряжений в цепи переменного тока: график, электрическая схема и формула расчета
Для чего используется резонанс
Как явление, резонанс напряжений часто используется в различных фильтрах электрического типа. Например, если есть необходимость устранения из сигнала передачи некоторой составляющей тока определенной частоты, то к приемнику параллельно подключают катушку и конденсатор, которые по отношению друг к другу соединены последовательно. В результате подобных действий электроток определенной резонансной частоты замкнется через цепочку дроссель-конденсатор и не попадет на приемник.
Колебательный контур
Важно! Сам по себе резонанс напряженности в электричестве — явление негативное, так как он способствует появлению перенапряжений на некоторых участках соединения и выводит из строя приборы.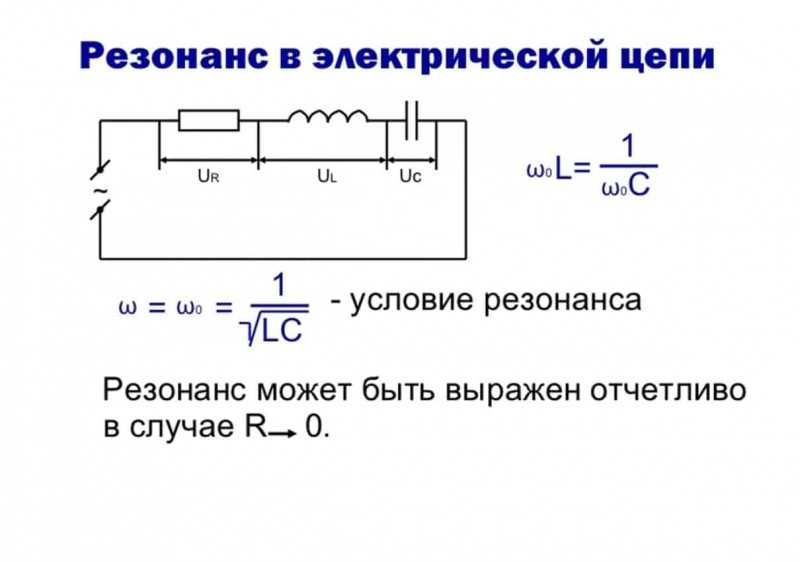
Принцип работы резонанса
Если сопротивление емкости и индуктивности подключить последовательно, то они вызовут в переменной цепи гораздо меньший сдвиг фаз, чем при отдельном включении. Говоря иначе, одновременное воздействие индуктивности и емкости создает компенсационные силы сдвига фаз. Полностью сдвиг компенсируется лишь в том случае уравнивания индуктивного и емкостного сопротивления, когда ωL = 1 / ωС.
Обратите внимание! Такая схема будет полностью характеризоваться активным R, то есть вести себя так, как будто в нее не подключены дроссель и конденсатор. Эта сопротивляемость будет равна сумме всех активных характеристик катушки и проводов соединения.
Вместе с этим рабочие напряжения дросселя и конденсатора будут равными и максимальными для данных условий. Если при маленьком активном сопротивлении данные характеристики значительно превысят общую напряженность цепи, то напряжения начнут резонировать.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Они используются для настройки фильтров или для управления токами в отдельных узлах.
Катушки индуктивности
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Использование резонанса напряжений для передачи радиосигнала
Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.
Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.
Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:
- Lп=1/w2*C;
- Сп=1/w2*L;
- Wп=1/√L*C.
Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.
Последовательный контур с графиками
На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.
Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:
- Добротность – Q=p/R;
- Затухание – 1/Q.
Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.
Амплитудно-частотная характеристика (АЧХ) и полоса пропускания
Последовательный колебательный контур
В колебательном контуре можно получить незатухающие колебания, если подключить его к источнику переменного тока.
Если источник подключен последовательно с катушкой L и конденсатором С , то такая цепь называется последовательным колебательным контуром (рис.3).
При подключении внешнего источника к контуру в нем возникают не собственные (свободные) колебания контура, которые определяются значениями L и C, а с частотой напряжения источника U=Um∙sinω∙t.
Такие колебания контура называются вынужденными.
При вынужденных колебаниях элементы контура L, C будут иметь, в зависимости от частоты источника, определенные индуктивное XL и емкостное Xc сопротивления и соответствующие падения напряжения UL, Uc на них.
Но контур имеет не только реактивные сопротивления, а еще и активное cопротивление потерь R, которое в основном равно сопротивлению провода катушки.
Так как в катушке и конденсаторе напряжения сдвинуты относительно тока на разные фазовые углы, то более наглядно их можно показать на векторных диаграммах (рис.4)
Напряжение на индуктивном сопротивлении UL опережает ток на 90°, а напряжение на емкостном сопротивлении Uc отстает от тока на такой же угол 90° И получается, что векторы UL и Uc сдвинуты между собой на 180°, т. е. находятся в противофазе.
е. находятся в противофазе.
Вектор напряжения на источнике U будет равен геометрической сумме напряжения вектора UR и вектора разницы напряжений реактивных сопротивлений UL-Uc.
Как видно из диаграммы рис.4а при UL > Uc напряжение внешнего источника опережает ток в колебательном контуре на угол φ<90° и находится выше оси абcцисс в зоне напряжений индуктивности. Значит в данном случае контур имеет сопротивление индуктивного характера.
При UL < Uc (рис.4b) вектор источника уже будет отставать от вектора тока на угол φ<90° и контур будет иметь емкостное сопротивление.
Полное сопротивление контура Z будет равно:
Амплитудное значение тока Im определяется по формуле:
где Um – амплитудное напряжение источника, а ω -его угловая частота.
При выполнении равенства:
Параллельный колебательный контур
В параллельном колебательном контуре источник сигнала соединен с катушкой индуктивности и конденсатором параллельно (рис. 11).
11).
При подаче переменного напряжения на контур происходит обмен энергиями между конденсатором и катушкой, но только в цепи внутри контура.
Для возникновения резонанса в нем, как и в последовательном контуре, необходимыми условиями являются равенство емкостного Хс и индуктивного ХL сопротивлений, а так же равенство частоты собственных колебаний контура и частоты колебаний источника тока.
Только резонанс в параллельном колебательном контуром, в отличии от резонанса в последовательном контуре, называют резонансом тока.
В идеальном параллельном контуре (без потерь) вектора индуктивного Ic и емкостного тока IL (при ХL=Xc) при резонансе будут направлены в противоположные стороны и
суммарный ток будет обращаться в нуль (рис.14a). А это значит, что сопротивление контура будет стремится к бесконечности.
Но в реальном параллельном контуре существует сопротивление потерь R которое сосредоточено в основном в индуктивности (рис 14b) и поэтому, даже при резонансе ток в контуре уже не равен нулю, а равен активной составляющей тока в цепи катушки – Iк=IL+IR.
Значит полное сопротивление контура Z будет уже не бесконечно, а равно:
Z=L/CR.
На рис.15 показан график характеристик зависимости тока Iк и полного сопротивления Z параллельного контура от частоты.
Можно сделать вывод: в цепи параллельного контура существуют два тока – ток от источника I протекающий через активное сопротивление потерь катушки и реактивный ток контура Iк .
Внутри контура протекают реактивный ток довольно таки большой величины:
Iк=IQ,
но он потребляет малый ток от источника, который необходим лишь для компенсации потерь в контуре:
I=U/Z.
Добротность Q параллельного контура, в отличии от последовательного контура, показывает во сколько раз ток в элементах контура больше потребления тока источника:
Q ≈ Iк/I.
На рис.16 дан конкретный пример параллельного колебательного контура, где видно, что ток контура больше тока источника в Q раз.
В радиоприемниках так же применяется непосредственная связь колебательного контура с антенной, т. е. контур включен параллельно источнику сигнала (рис.17).
е. контур включен параллельно источнику сигнала (рис.17).
Переменным конденсатором настраиваем контур на частоту сигнала нужной радиостанции. При резонансе контурный ток, вызванный нужной радиостанцией, становится относительно большим, а сопротивление контура тоже большим.Поэтому между точками а и b получается значительное напряжение.
Для других станций контур представляет малое сопротивление и сигнал радиостанции уходит в “землю”.
Польза и вред резонанса
Для того чтобы сделать некий вывод о плюсах и минусах резонанса, необходимо рассмотреть, в каких случаях он может проявляться наиболее активно и заметно для человеческой деятельности.
Положительный эффект
Явление отклика широко используется в науке и технике. Например, работа многих радиотехнических схем и устройств основывается на этом явлении.
Двухтактный двигатель. Глушитель двухтактного двигателя имеет особую форму, рассчитанную на создание резонансного явления. Оно улучшает работу двигателя засчет снижения потребления и загрязнения. Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.
Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.- Музыкальные инструменты. В случае струнных и духовых инструментов звуковое производство происходит в основном при возбуждении колебательной системы (струны, колонны воздуха) до возникновения явления резонанса.
- Радиоприемники. Каждая радиостанция излучает электромагнитную волну с четко определенной частотой. Для его захвата цепь RLC принудительно подвергается вибрации с помощью антенны, которая захватывает все электромагнитные волны, достигающие ее. Для прослушивания одной станции собственная частота RLC-схемы должна быть настроена на частоту требуемого передатчика, изменяя емкость переменного конденсатора (операция выполняется при нажатии кнопки поиска станции). Все системы радиосвязи, будь то передатчики или приемники, используют резонаторы для «фильтрации» частот сигналов, которые они обрабатывают.
- Магнитно-резонансная томография (МРТ). В 1946 году два американца Феликс Блох и Эдвард Миллс Перселл самостоятельно обнаружили явление ядерного магнитного резонанса, также называемое ЯМР, которое принесло им Нобелевскую премию по физике.

Отрицательное воздействие
Однако не всегда явление полезно. Часто можно встретить ссылки на случаи, когда навесные мосты ломались при прохождении по ним солдат «в ногу». При этом ссылаются на проявление резонансного эффекта воздействия резонанса, и борьба с ним приобретает масштабный характер.
Автотранспорт. Автомобилисты часто раздражаются шумом, который появляется при определенной скорости движения транспортного средства или в результате работы двигателя. Некоторые слабо закругленные части корпуса вступают в резонанс и излучают звуковые колебания. Сам автомобиль с его системой подвески представляет собой осциллятор, оснащенный эффективными амортизаторами, которые препятствуют возникновению острого резонанса.- Мосты. Мост может выполнять вертикальные и поперечные колебания. Каждый из этих типов колебаний имеет свой период. Если стропы подвешены, система имеет очень разную резонансную частоту.

- Здания. Высокие здания чувствительны к землетрясениям. Некоторые пассивные устройства позволяют защитить их: они являются осцилляторами, чья собственная частота близка к частоте самого здания. Таким образом, энергия полностью поглощается маятником, препятствующим разрушению здания.
Следующая
РазноеЧто такое активная мощность?
2020 Учебное пособие высшего класса: E5A — Резонанс и добротность: характеристики резонансных цепей; последовательный и параллельный резонанс; Вопрос; полоса пропускания половинной мощности; фазовые соотношения в реактивных цепях
Что ж, пришло время снова… время для обновления Руководства по изучению лицензии высшего класса! Вот первый раздел первой главы. Комментарии приветствуются!
Резонанс — одна из самых крутых вещей в электронике. Резонансные схемы — это то, что делает возможным радио в том виде, в каком мы его знаем.
Что такое резонанс? Итак, цепь называется резонансной, когда индуктивное сопротивление и емкостное сопротивление равны друг другу. То есть, когда
2πfL = 1/(2πfC)
, где L — индуктивность в генри, а C — емкость в фарадах.
Для данного L и данного C это происходит только на одной частоте:
f = 1/(2π√(LC))
Эта частота называется резонансной частотой.
ВОПРОС: Что такое резонанс в цепи LC или RLC? (Е5А02)
ОТВЕТ: Частота, при которой емкостное сопротивление равно индуктивному сопротивлению
Рассчитаем несколько резонансных частот, используя в качестве примеров вопросы из набора дополнительных вопросов:
ВОПРОС: Какова резонансная частота RLC-цепи, если R 22 Ом, L 50 микрогенри и C 40 пикофарад? (E5A14)
ОТВЕТ: 3,56 МГц
f = 1/(2π√(LC)) = 1/(6,28 × √(50×10-6 × 40×10-12)) = 1/(2,8 × 10-7) = 3,56 МГц
Обратите внимание, что значение сопротивления на самом деле не имеет значения.
ВОПРОС: Какова резонансная частота цепи RLC, если R равно 33 Ом, L равно 50 микрогенри и C равно 10 пикофарадам? (E5A16)
ОТВЕТ: 7,12 МГц
f = 1/(2π√(LC)) = 1/(6,28×√(50×10-6×10×10-12)) = 1/(1,4× 10-7) = 7,12 МГц
Когда катушка индуктивности и конденсатор соединены последовательно, импеданс последовательной цепи на резонансной частоте равен нулю, поскольку реактивные сопротивления равны и противоположны на этой частоте. Если в цепи есть резистор, то только этот резистор влияет на импеданс. Следовательно, величина импеданса последовательного RLC-контура в резонансе примерно равна сопротивлению контура.
ВОПРОС: Какова величина импеданса последовательной цепи RLC при резонансе? (E5A03)
ОТВЕТ: Приблизительно равно сопротивлению цепи. фактически открытая цепь. Следовательно, величина импеданса цепи с резистором, катушкой индуктивности и конденсатором, соединенными параллельно, при резонансе примерно равна сопротивлению цепи.
ВОПРОС: Какова величина импеданса параллельной цепи RLC при резонансе? (E5A04)
ОТВЕТ: Приблизительно равно сопротивлению цепи
ВОПРОС: Какова величина тока на входе параллельного RLC-контура при резонансе? (E5A07)
ОТВЕТ: Минимум
И наоборот, величина циркулирующего тока в компонентах параллельного LC-контура при резонансе высока, потому что контур внутри контура фактически является последовательным резонансным контуром.
ВОПРОС: Какова величина циркулирующего тока в компонентах параллельного LC-контура при резонансе? (E5A06)
ОТВЕТ: Максимальное значение
Высокие токи, циркулирующие в резонансной цепи, могут привести к тому, что напряжение на последовательно включенных реактивных сопротивлениях будет больше, чем приложенное к ним напряжение.
ВОПРОС: Что может привести к тому, что напряжение на реактивных сопротивлениях в последовательной RLC-цепи будет выше, чем напряжение, приложенное ко всей цепи? (E5A01)
ОТВЕТ: Резонанс
Еще одно последствие того, что индуктивное и емкостное сопротивления компенсируют друг друга в том, что фазовый сдвиг на резонансной частоте отсутствует.
ВОПРОС: Каково фазовое соотношение между током и напряжением последовательного резонансного контура при резонансе? (E5A08)
ОТВЕТ: Напряжение и ток совпадают по фазе
В идеале последовательная LC-цепь должна иметь нулевое полное сопротивление на резонансной частоте, тогда как параллельная LC-цепь будет иметь бесконечное полное сопротивление на резонансной частоте. В реальном мире, конечно, резонансные схемы так не работают. И катушки индуктивности, и конденсаторы имеют последовательное сопротивление, которое необходимо учитывать. Чтобы описать, насколько схема ведет себя подобно идеальному резонансному контуру, мы используем добротность, или Q. Поскольку индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению на резонансной частоте, Q параллельного RLC-контура представляет собой сопротивление, деленное либо на индуктивное, либо на емкостное реактивное сопротивление, или Q = R/XL или R/XC.
Поскольку индуктивное реактивное сопротивление равно емкостному реактивному сопротивлению на резонансной частоте, Q параллельного RLC-контура представляет собой сопротивление, деленное либо на индуктивное, либо на емкостное реактивное сопротивление, или Q = R/XL или R/XC.
ВОПРОС: Как рассчитывается добротность параллельного резонансного контура RLC? (E5A09)
ОТВЕТ: Сопротивление, деленное на реактивное сопротивление либо индуктивности, либо емкости
Добротность резонансного контура серии RLC представляет собой индуктивное реактивное сопротивление или емкостное реактивное сопротивление, деленное на сопротивление, или Q = XL/R или XC /Р.
ВОПРОС: Как рассчитывается добротность резонансного контура серии RLC? (E5A10)
ОТВЕТ: Реактивное сопротивление индуктивности или емкости, деленное на сопротивление
В принципе, чем выше добротность, тем больше резонансный контур ведет себя как идеальный резонансный контур, и чем выше добротность, тем меньше резистивные потери в контуре.
ВОПРОС: Что из следующего увеличивает добротность катушек индуктивности и конденсаторов? (E5A15)
ОТВЕТ: Меньшие потери
Но увеличение Q имеет и свои недостатки. Увеличение Q в резонансном контуре приведет к увеличению внутренних напряжений и циркулирующих токов, и резонансный контур должен быть изготовлен из компонентов, способных выдерживать эти более высокие напряжения и токи.
ВОПРОС: Каков эффект увеличения добротности в последовательном резонансном контуре? (E5A13)
ОТВЕТ: Увеличение внутренних напряжений
Параметр резонансного контура, связанный с добротностью, представляет собой полосу пропускания по половинной мощности. Полоса пропускания половинной мощности — это полоса пропускания, в которой последовательный резонансный контур пропускает половину мощности входного сигнала и в которой параллельный резонансный контур подавляет половину мощности входного сигнала.
Мы можем использовать добротность цепи для расчета полосы пропускания половинной мощности:
BW = f/Q
Рассмотрим пару примеров:
ВОПРОС: Какова полоса пропускания по половинной мощности резонансного контура с резонансной частотой 7,1 МГц и добротностью 150? (E5A11)
ОТВЕТ: 47,3 кГц
BW = f/Q = (7,1 × 10 6) /150 = 47,3 × 10 3 = 47,3 кГц
резонансный контур с резонансной частотой 3,7 МГц и добротностью 118? (E5A12)
ОТВЕТ: 31,4 кГц
BW = f/Q = (3,7 × 10 6) /118 = 31,4 × 10 3 = 31,4 кГц
Резонансные схемы часто используются в качестве схем согласования импеданса. Поскольку BW = f/Q, увеличение добротности резонансного контура, используемого для этого приложения, приводит к уменьшению диапазона частот или полосы пропускания, в которой он может согласовать импеданс между двумя контурами или между передатчиком и антенной.
Поскольку BW = f/Q, увеличение добротности резонансного контура, используемого для этого приложения, приводит к уменьшению диапазона частот или полосы пропускания, в которой он может согласовать импеданс между двумя контурами или между передатчиком и антенной.
ВОПРОС: Каков результат увеличения добротности схемы согласования импеданса? (Е5А05) https://remove-image-background.com E5A01 Что может привести к тому, что напряжение на последовательно соединенных реактивных сопротивлениях будет больше, чем приложенное к ним напряжение? E5A02 Что такое резонанс в электрической цепи? E5A03 Какова величина импеданса последовательной цепи RLC при резонансе? E5A04 Какова величина импеданса цепи с резистором, катушкой индуктивности и конденсатором, соединенными параллельно, в резонансе? E5A05 Какова величина тока на входе последовательной цепи RLC, когда частота проходит через резонанс? E5A06 Какова величина циркулирующего тока в компонентах параллельной LC-цепи при резонансе? E5A07 Какова величина тока на входе параллельной RLC-цепи при резонансе? E5A08 Каково фазовое соотношение между током и напряжением в последовательном резонансном контуре при резонансе? (C) E5A09 Каково фазовое соотношение между током и напряжением в параллельном резонансном контуре при резонансе? E5A10 Какова полоса пропускания при половинной мощности параллельного резонансного контура с резонансной частотой 1,8 МГц и добротностью 95? E5A11 Какова полоса пропускания по половинной мощности параллельного резонансного контура с резонансной частотой 7,1 МГц и добротностью 150? E5A12 Какова полоса пропускания по половинной мощности параллельного резонансного контура с резонансной частотой 3,7 МГц и добротностью 118? E5A13 Какова полоса пропускания по половинной мощности параллельного резонансного контура с резонансной частотой 14,25 МГц и добротностью 187? E5A14 Какова резонансная частота последовательной цепи RLC, если сопротивление R равно 22 Ом, L равно 50 микрогенри и C равно 40 пикофарадам? E5A15 Какова резонансная частота последовательной цепи RLC, если сопротивление R равно 56 Ом, L равно 40 микрогенри и C равно 200 пикофарад? E5A16 Какова резонансная частота параллельной цепи RLC, если сопротивление R равно 33 Ом, L равно 50 микрогенри и C равно 10 пикофарадам? E5A17 Какова резонансная частота параллельной RLC-цепи, если R равно 47 Ом, L равно 25 микрогенри и C равно 10 пикофарадам? E5B01 Какое время требуется, чтобы конденсатор в RC-цепи зарядился до 63,2 % приложенного напряжения? E5B02 Как называется время, за которое заряженный конденсатор в RC-цепи разрядится до 36,8 % начального напряжения? E5B03 Конденсатор в RC-цепи разряжается до какого процента от пускового напряжения после двух постоянных времени? E5B04 Какова постоянная времени цепи с двумя конденсаторами по 220 мкФ и двумя резисторами по 1 МОм, включенными параллельно? E5B05 Сколько времени требуется, чтобы начальный заряд 20 В постоянного тока уменьшился до 7,36 В постоянного тока в конденсаторе емкостью 0,01 мкФ, когда к нему подключен резистор сопротивлением 2 МОм? t = RC = (2 x 106) x (0,01 x 10-6) = 0,02 секунды E5B06 Сколько времени требуется, чтобы начальный заряд 800 В постоянного тока уменьшился до 294 В постоянного тока в конденсаторе емкостью 450 мкФ, когда к нему подключен резистор сопротивлением 1 МОм? t = R C = (1 x 10 6 ) x (450 x 10 -6 ) = 450 секунд E5B07 Каков фазовый угол между напряжением и током в последовательной цепи RLC, если сопротивление XC равно 500 Ом, R равно 1 кОм и XL равно 250 Ом? E5B08 Каков фазовый угол между напряжением на проводе и током в последовательной цепи RLC, если сопротивление XC равно 100 Ом, R равно 100 Ом, а XL равно 75 Ом? E5B09 Какая связь между током через конденсатор и напряжением на конденсаторе? E5B10 Какая связь между током через индуктор и напряжением на индукторе? E5B11 Каков фазовый угол между напряжением и током в последовательной цепи RLC, если сопротивление XC равно 25 Ом, R равно 100 Ом, а XL равно 50 Ом? E5B12 Каков угол сдвига фаз между напряжением и током в последовательной RLC-цепи, если сопротивление XC равно 75 Ом, R равно 100 Ом, а XL равно 50 Ом? E5B13 Каков угол сдвига фаз между напряжением на проводе и током в последовательной цепи RLC, если сопротивление XC равно 250 Ом, R равно 1 кОм, а XL равно 500 Ом? E5C01 Чему равен в полярных координатах импеданс сети, состоящей из катушки индуктивности с реактивным сопротивлением 100 Ом, последовательно соединенной с резистором 100 Ом? E5C02 В полярных координатах каково полное сопротивление цепи, состоящей из катушки индуктивности с сопротивлением 100 Ом, конденсатора с сопротивлением 100 Ом и резистора с сопротивлением 100 Ом, соединенных последовательно? E5C03 В полярных координатах каково полное сопротивление сети, состоящей из последовательно соединенных конденсатора с реактивным сопротивлением 300 Ом, катушки индуктивности с реактивным сопротивлением 600 Ом и резистора с сопротивлением 400 Ом? E5C04 Чему равен в полярных координатах импеданс сети, состоящей из последовательно включенного конденсатора с реактивным сопротивлением 400 Ом и резистора сопротивлением 300 Ом? E5C05 Чему равен в полярных координатах импеданс сети, состоящей из индуктора с реактивным сопротивлением 400 Ом, включенного параллельно с резистором 300 Ом? E5C06 Чему равен в полярных координатах импеданс сети, состоящей из конденсатора с реактивным сопротивлением 100 Ом, последовательно соединенного с резистором 100 Ом? E5C07 Каково в полярных координатах полное сопротивление сети, состоящей из конденсатора с реактивным сопротивлением 100 Ом, соединенного параллельно с резистором 100 Ом? E5C08 Каково в полярных координатах полное сопротивление сети, состоящей из катушки индуктивности с реактивным сопротивлением 300 Ом, последовательно соединенной с резистором 400 Ом? E5C09 При использовании прямоугольных координат для построения графика импеданса цепи, что представляет собой горизонтальная ось? E5C10 Что представляет собой вертикальная ось при использовании прямоугольных координат для построения графика импеданса цепи?
ОТВЕТ: Полоса пропускания уменьшена
Главная
Получить приложение
Создать
A. Резонанс
B. Емкость
C. Проводимость
D. Сопротивление В реальных схемах он может быть в 10 или 100 раз больше. Как это может быть? Причина в том, что конденсатор и катушка индуктивности накапливают подведенную энергию, рассеивая небольшое ее количество на резистивные потери. Приложенное напряжение «накачивает» резонансный контур, накапливая энергию в каждом компоненте.
В реальных схемах он может быть в 10 или 100 раз больше. Как это может быть? Причина в том, что конденсатор и катушка индуктивности накапливают подведенную энергию, рассеивая небольшое ее количество на резистивные потери. Приложенное напряжение «накачивает» резонансный контур, накапливая энергию в каждом компоненте.
A. Самая высокая частота, при которой будет проходить ток
B. Самая низкая частота, при которой будет проходить ток
C. Частота, при которой емкостное сопротивление равно индуктивному сопротивлению
D. Частота, при которой реактивное сопротивление равно резистивному сопротивлению
A. Высокое по сравнению с сопротивлением цепи
B. Приблизительно равно емкостному сопротивлению
C. Приблизительно равно индуктивному сопротивлению
Приблизительно равно индуктивному сопротивлению
D. Приблизительно равно сопротивлению цепи
A. Примерно равно сопротивлению цепи
B. Примерно равно индуктивному сопротивлению
C. Низкое по сравнению с сопротивлением цепи
D. Примерно равно емкостному сопротивлению
A. Минимум
Минимум
B. Максимум
C. R/L
D. L/R
A. Минимум
B. Максимум
C. Равно 1, деленное на количество, умноженное на 2 Pi, умноженное на корень квадратный из индуктивности L, умноженной на емкость C
D. Равно 2, умноженное на Pi, умноженное на частоту «F», умноженное на индуктивность «L»
A. Минимум
Минимум
B. Максимум
C. R/L
D. L/R
A. Напряжение опережает ток на 90 градусов
B. Ток опережает напряжение на 90 градусов
C. Напряжение и ток совпадают по фазе
D. Напряжение и ток не совпадают по фазе на 180 градусов
A. Напряжение опережает ток на 90 градусов
B. Ток опережает напряжение на 90 градусов
C. Напряжение и ток совпадают по фазе
D.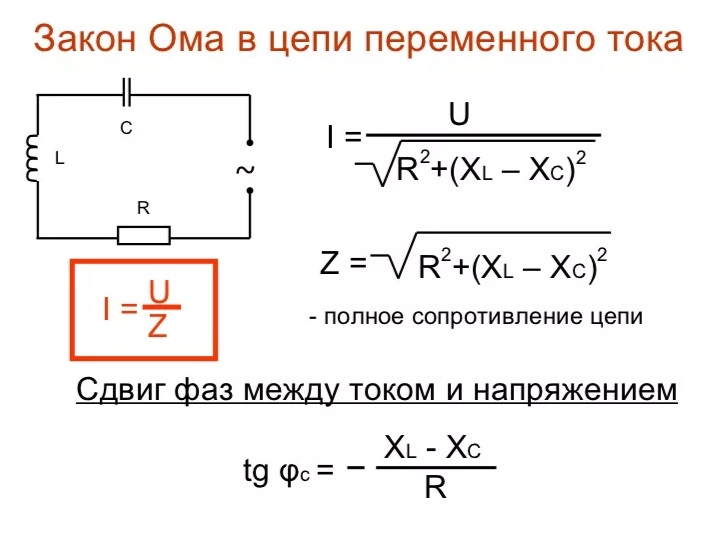 Напряжение и ток не совпадают по фазе на 180 градусов
Напряжение и ток не совпадают по фазе на 180 градусов
A. 18,9 кГц
B. 1,89 кГц
C. 94,5 кГц
D. 9,45 кГц
A. 157,8 Гц
B. 315,6 Гц
C. 47,3 кГц
D. 23,67 кГц
A. 436,6 кГц
436,6 кГц
B. 218,3 кГц
C. 31,4 кГц
D. 15,7 кГц
A. 38,1 кГц
B. 76,2 кГц
C. 1,332 кГц
D. 2,665 кГц
A. 44,72 МГц
B. 22,36 МГц
C. 3,56 МГц
D. 1,78 МГц
А. 3,76 МГц
В. 1,78 МГц
C. 11,18 МГц
D. 22,36 МГц
A. 23,5 МГц
23,5 МГц
B. 23,5 кГц
C. 7,12 кГц
D. 7,12 МГц
A. 10,1 МГц
B. 63,2 МГц
C. 10,1 кГц
D. 63,2 кГц
A. Экспоненциальная скорость, равная единице
B. Одна постоянная времени
C. Один экспоненциальный период
D. Коэффициент времени, равный единице
A. Один период разряда
B. Экспоненциальная скорость разряда один
C. Коэффициент разряда один
D. Одна постоянная времени
A. 86,5%
B. 63,2%
C. 36,8%
D. 13,5% На графике разряда показан результат
На графике разряда показан результат
A. 55 секунд
B. 110 секунд
C. 440 секунд
D. 220 секунд
A. 0,02 секунды
B. 0,04 секунды
C. 20 секунд
D. 40 секунд Постоянная времени для этой схемы:
Постоянная времени для этой схемы:
A. 4,50 секунды
B. 9 секунд
C. 450 секунд
D. 900 секунд
A. 68,2 градуса с опережением напряжения над током
B. 14,0 градуса с опережением напряжения над током
14,0 градуса с опережением напряжения над током
C. 14,0 градуса с отставанием напряжения от тока
D. 68,2 градуса с отставанием напряжения от тока
A. 14 градусов с отставанием напряжения от тока
B. 14 градусов с опережением напряжения над током
C. 76 градусов с опережением напряжения над током
76 градусов с опережением напряжения над током
D. 76 градусов с отставанием напряжения от тока
A. Напряжение и ток совпадают по фазе
B. Напряжение и ток не совпадают по фазе на 180 градусов
C. Напряжение опережает ток на 90 градусов
D. Ток опережает напряжение на 90 градусов Для чистого реактивного сопротивления (без сопротивления) фазовый угол составляет 90 °.
Для чистого реактивного сопротивления (без сопротивления) фазовый угол составляет 90 °.
А. Напряжение опережает ток на 90 градусов
B. Ток опережает напряжение на 90 градусов
C. Напряжение и ток сдвинуты по фазе на 180 градусов
D. Напряжение и ток совпадают по фазе
A. 14 градусов с отставанием напряжения от тока
14 градусов с отставанием напряжения от тока
B. 14 градусов с опережением напряжения над током
C. 76 градусов с отставанием напряжения от тока
D. 76 градусов с опережением напряжения над током
А. 76 градусов с отставанием напряжения от тока
B. 14 градусов, когда напряжение опережает ток
C. 14 градусов, когда напряжение отстает от тока
14 градусов, когда напряжение отстает от тока
D. 76 градусов, когда напряжение опережает ток
A. 81,47 градуса с отставанием напряжения от тока
B. 81,47 градуса с опережением напряжения по току
C. 14,04 градуса с отставанием напряжения от тока
D. 14,04 градуса с опережением напряжения по току Фазовый угол между напряжением и током:
Фазовый угол между напряжением и током:
А. 121 Ом под углом 35 градусов
B. 141 Ом под углом 45 градусов
C. 161 Ом под углом 55 градусов
D. 181 Ом под углом 65 градусов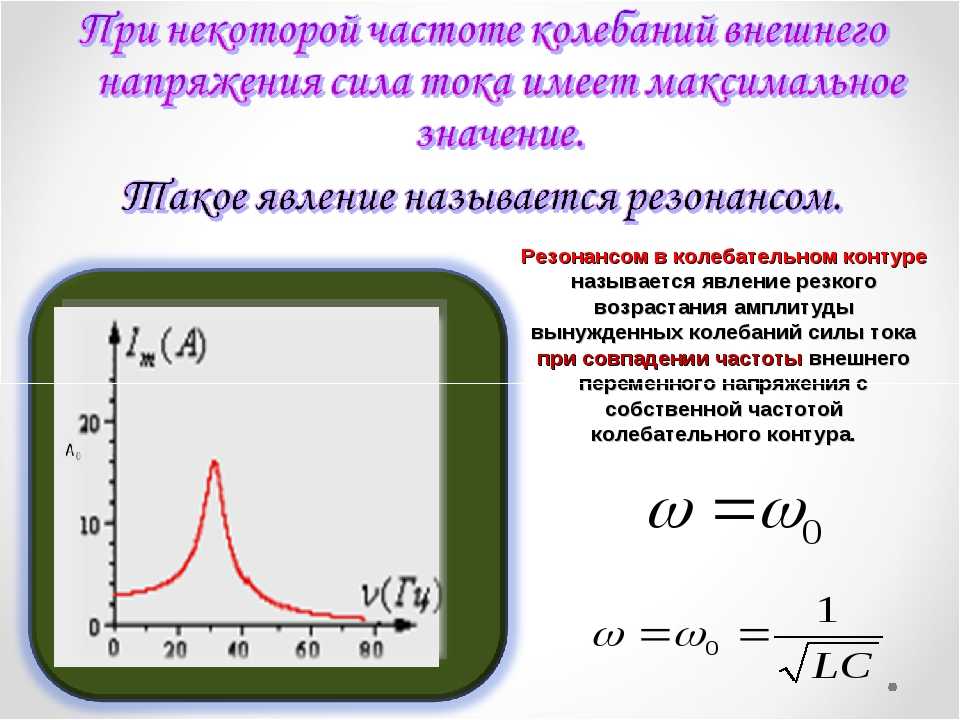 Вы можете рассчитать их по сопротивлению (R) и реактивному сопротивлению (X), используя следующие формулы, в которых вертикальные полосы вокруг Z обозначают «величину» без учета фазового угла.
Вы можете рассчитать их по сопротивлению (R) и реактивному сопротивлению (X), используя следующие формулы, в которых вертикальные полосы вокруг Z обозначают «величину» без учета фазового угла.
A. 100 Ом под углом 90 градусов
B. 10 Ом под углом 0 градусов
C. 10 Ом под углом 90 градусов
D. 100 Ом под углом 0 градусов
A. 500 Ом под углом 37 градусов
500 Ом под углом 37 градусов
B. 900 Ом под углом 53 градуса
C. 400 Ом под углом 0 градусов
D. 1300 Ом под углом 180 градусов
A. 240 Ом под углом 36,9 град
B. 240 Ом под углом -36,9 град
C. 500 Ом под углом 53,1 град
D. 500 Ом под углом -53,1 град
A. 240 Ом под углом 36,9 град
240 Ом под углом 36,9 град
B. 240 Ом под углом -36,9 град
C. 500 Ом под углом 53,1 град
D. 500 Ом под углом -53,1 град
A. 121 Ом под углом -25 градусов
B. 191 Ом под углом -85 градусов
C. 161 Ом под углом -65 градусов
D. 141 Ом под углом -45 градусов
A. 31 Ом под углом -15 градусов
B. 51 Ом под углом -25 градусов
C. 71 Ом под углом -45 градусов
Д. 91 Ом под углом -65 градусов
A. 400 Ом под углом 27 градусов
400 Ом под углом 27 градусов
B. 500 Ом под углом 37 градусов
C. 500 Ом под углом 47 градусов
D. 700 Ом под углом 57 градусов
A. Резистивная составляющая
B. Реактивная составляющая
C. Сумма реактивной и резистивной составляющих
D. Разница между резистивной и реактивной составляющими
A. Резистивная составляющая
B. Реактивная составляющая
C. Сумма реактивной и резистивной составляющих
D. Разница между резистивной и реактивной составляющими


 Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.
Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.
