Делители для измерения постоянного и переменного напряжений

Страница 37 из 41

Приборы для непосредственного измерения напряжений в сотни киловольт являются громоздкими и дорогими. Поэтому в настоящее время при измерении высоких напряжений широко применяются делители напряжений.
Делители напряжения состоят из цепочки последовательно соединенных активных сопротивлений или емкостей, а иногда из их комбинаций и включаются между проводом, находящимся под высоким напряжением, и землей. Трансформатор напряжения является по существу индуктивным делителем напряжения.
Принципиальная схема делителя напряжения представлена на рис. 5-34. Делитель состоит из N секций; напряжение снимается с п секций и измеряется прибором. Часть делителя (п секций), параллельно которой включается измерительный прибор, называют низковольтным плечом, а остальную часть — высоковольтным плечом делителя.
Если обозначить через U1 высокое напряжение, прикладываемое к делителю, а через U2— напряжение, измеряемое прибором, то отношение

Практически выполненные делители напряжения неполностью удовлетворяют комплексу вышеуказанных требований.

Чтобы учесть дополнительные погрешности, которые вносит делитель при измерении высокого напряжения, надо знать зависимости коэффициента деления от амплитуды называется коэффициентом деления делителя. Если в делитель включены секции с одинаковыми сопротивлениями и напряжение равномерно распределяется -по секциям, то
(5-41)
Для обеспечения необходимой точности измерения сопротивление измерительного прибора должно быть во много раз больше сопротивления низковольтного плеча делителя. Измеренная прибором величина напряжения, умноженная на коэффициент деления, дает полное измеряемое напряжение

К делителям напряжения предъявляются следующие основные требования:

1. Подключение делителя не должно влиять на амплитуду и форму измеряемого напряжения.
2. Напряжение, снимаемое с низковольтного плеча, должно по форме повторять измеряемое напряжение, для чего коэффициент деления делителя не должен зависеть от частоты и амплитуды измеряемого напряжения в рабочем интервале изменения этих величин.
3. Коэффициент деления не должен зависеть от атмосферных условий (давление, температура).
4. Энергия, рассеиваемая в делителе, при принятой системе охлаждения не должна вызывать заметного изменения его коэффициента деления.
5. В делителе должны отсутствовать корона и утечки по изоляции или их влияние на коэффициент деления должно быть незначительным.

Рис. 5-34. Принципиальная схема делителя напряжения.

 На рис. 5-35 представлена упрощенная электрическая схема замещения делителя напряжения.

При измерении высоких постоянных напряжений применяют активные делители. Для активных делителей используют проволоку из сплавов высокого сопротивления (константан, манганин, нихром и др.), а также непроволочные сопротивления различных типов, широко применяемые в радиотехнике.

Большинство высоковольтных источников постоянного напряжения, применяемых в лабораториях, имеют ограниченную выходную мощность, и токи от этих источников редко превышают несколько миллиампер. Делитель постоянного напряжения должен иметь высокое сопротивление, чтобы потребляемая им энергия от источника напряжения была сравнительно небольшой. С другой стороны, величина активного сопротивления делителя не должна быть слишком большой, так как в этом случае увеличивается погрешность в коэффициенте деления за счет короны· и утечек по изоляции.

Рис. 5-35. Электрическая схема замещения делителя напряжения.

Исходя из этих требований, сопротивление делителя принимается таким, чтобы ток, протекающий через делитель, находился в пределах от десятков до 1—2 мА.
Погружение сопротивлений делителя в масло значительно повышает теплоемкость делителя, улучшает его общую изоляцию и увеличивает электрическую прочность в отношении короны.
С помощью двух блоков делителя постоянного напряжения с проволочными сопротивлениями, соединенных последовательно, измерялись постоянные напряжения до 300 кВ с точностью ±0,3%. Блок сопротивлений величиной 80 Мом собирался из отдельных секций и помещался в бакелитовый цилиндр диаметром 27 см и высотой 46 см, заполненный маслом. При напряжении 125 кВ блок рассеивал мощность 200 Вт, при этом температура масла поднималась до 40° С, что соответствовало температуре кожуха блока 25° С. Осуществлялась естественная циркуляция масла, причем устройство секций и их расположение содействовали благоприятным условиям циркуляции масла. Сопротивление утечки через масло и кожух составляло 3·1012 Ом, что оказывало незначительное влияние на точность измерений. Для уменьшения коронирования на фланцах каждого блока делителя монтировались металлические экраны с закругленными краями.
В качестве сопротивлений секций блока делителя использовалась нихромовая проволока диаметром 0,051

мм, которая вплотную, виток к витку, наматывалась на узкую полоску из прессшпана с поперечным сечением 1,78X0,25 мм2. Эта полоска затем наматывалась спиралью на вторую полоску из прессшпана с поперечным сечением 6,4X0,43 мм2 и расстоянием между соседними витками спирали, равным 0,51 мм. Пленка окиси на поверхности проволоки была достаточной, чтобы обеспечить изоляции: между витками спирали, даже когда они касались дру1 друга. Сопротивление 1 м такой спирали составляв 0,2 Мом. Наконец, спираль наматывалась на изолирующие каркасы в виде дисков, которые образовывали секции а последние — блок сопротивлений.
Температурный коэффициент сопротивления нихрома составлял 9,8х10-5 град-1 в пределах от 20 до 500° С и при необходимости вводилась поправка на температуру. Таких образом, для изготовления делителя высокого постоянной напряжения требуются сотни километров проволоки с боль шим удельным сопротивлением и малым температурных коэффициентом сопротивления.

Когда не требуется большой точности в измерении напряжения и не оправдываются затраты на изготовление делителей из проволочных сопротивлений, применяются непроволочные сопротивлeния.

Различают непроволочные сопротивления поверхностного и композиционного типов. В сопротивлениях поверхностного типа проводящий слой образован пленкой углерода или тонкой пленкой металлических сплавов, осажденных на поверхность керамического стержня или трубки. Сопротивления композиционного типа состоят из плохо проводящих искусственных материалов на основе смесей проводника со связующим его диэлектриком. Сопротивления композиционного типа выполняются как в виде массивного проводящего тела — объемная конструкция, так и в виде проводящих слоев на изолирующем основании—пленочная конструкция.
Сопротивления поверхностного типа отличаются от пленочных композиционных сопротивлений не только отсутствием связующего диэлектрика в проводящей пленке, но и значительно меньшей толщиной проводящей пленки.
Температурный коэффициент непроволочных сопротивлений по абсолютной величине обычно больше, чем у проволочных сопротивлений, и для большинства типов непроволочных сопротивлений является отрицательным.
Кроме того, непроволочные сопротивления изменяют свою величину в зависимости от приложенного напряжения даже в том случае, когда проходящий через них ток не вызывает их существенного нагрева, могущего изменить величину сопротивления в соответствии с температурным коэффициентом. Величина сопротивления, начиная с некоторого значения напряжения, уменьшается с повышением напряжения. Сопротивление в этой области будет нелинейным. Степень нелинейности характеризуется коэффициентом напряжения, выражающим относительное изменение величины сопротивления при изменении напряжения на нем:
(5-42)
где R2 и R1— величины сопротивлений при U2 и U1, причем U2>U1.
Практически kн определяется при напряжении U2, равном наибольшему рабочему напряжению, и U1= 0,1U2

.

Величина коэффициента напряжения для хороших сопротивлений поверхностного типа не превышает 1—2%, для композиционных сопротивлений kH может достигать 10—20%.
Следует также учитывать, что в непроволочных сопротивлениях с течением времени происходят необратимые изменения—процесс старения сопротивления. При этом в большинстве случаев сопротивление увеличивает свою величину. Старение сопротивлений имеет сложный характер, зависящий как от типа сопротивления, так и от условий, в которых оно находится. Особенно интенсивно процесс старения сопротивлений протекает при их -перегрузке, а также при работе во влажной среде.

В практике для делителей напряжения часто используются обычные радиотехнические непроволочные сопротивления различных типов. Отметим, что отечественной промышленностью выпускаются и специальные высоковольтные непроволочные сопротивления композиционного типа, предназначенные для делителей напряжения, для разряда конденсаторов фильтров выпрямителей и других целей.
В табл. 5-11 приводятся основные параметры сопротивлений композиционного типа, выпускаемых отечественной промышленностью.

Таблица 5-11
Основные параметры сопротивлений типа КЛВ

Эти сопротивления изготовляются на основе проводящих лакопленочных композиций, нанесенных спиралью на фарфоровый стержень. Края спирали покрываются низкоомным контактным клеем, на них насаживаются металлические колпачки. Сопротивления защищены эмалевым покрытием. Сопротивления типа КЛВ изготовляются I с допусками до 15% к номиналу. Коэффициент напряжения не превышает 15%, температурный коэффициент сопротивления в среднем не превышает —25· 10-4 град-1,

вольтметр или микроамперметр. Для удобства приборы непосредственно отградуированы в киловольтах измеряемого напряжения. При измерении напряжения с помощью микроамперметра было установлено, что необходимо ограничивать ток, «протекающий через микроамперметр, до 0,1 тока, протекающего через делитель, чтобы сохранить точность измерения в пределах ±1,5%.
На рис. 5-36 показано устройство делителя постоянного напряжения на 500 кВ, обеспечивающего точность измерения около ± 1,5%. Делитель состоит из цепочки последовательно соединенных углеродистых сопротивлений, каждое величиной 5 Мом и мощностью 1 вт. Температурный коэффициент сопротивления — 60х10-4 град-1 в интервале температур 10—30° С, коэффициент напряжения — около 11%. Сопротивления 1 смонтированы на изолирующей опоре 2 в зигзагообразном виде и помещались в маслонаполненный бакелитовый цилиндр 3 с двойными стенками.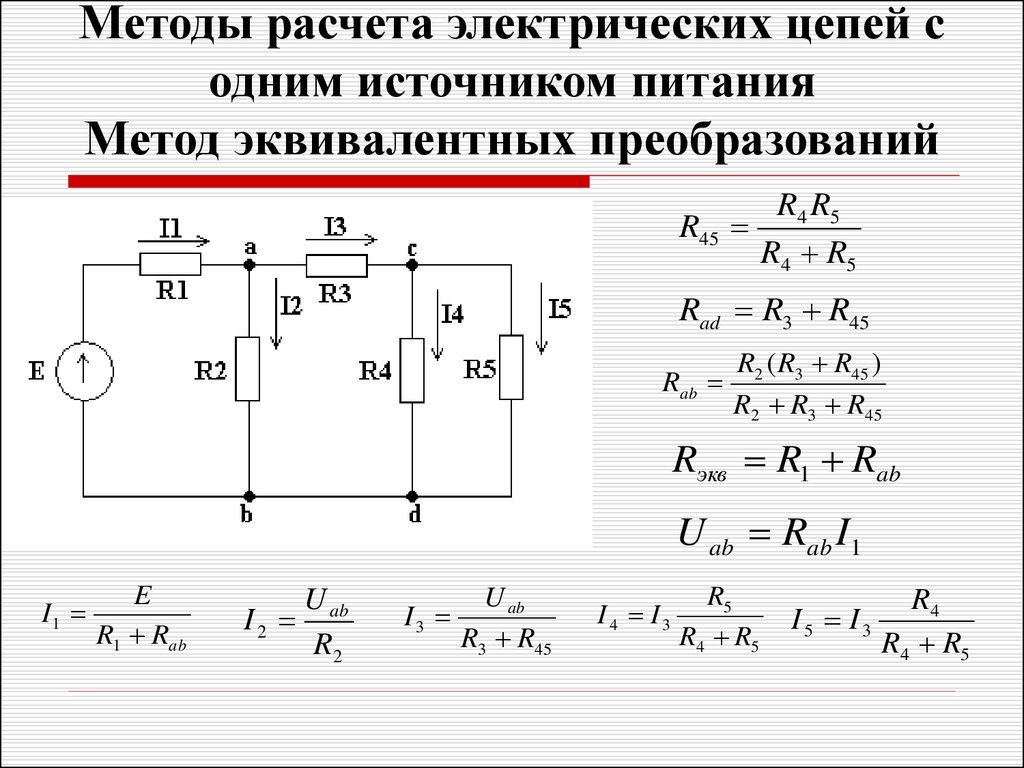 Естественная циркуляция масла осуществлялась так, что нагретое сопротивлениями масло проходило близ внутренней стенки наружного цилиндра и тем самым лучше охлаждалось. Для уменьшения коронирования на кожух цилиндра установлены алюминиевые экраны. Делители такой конструкции на напряжения 100 и 500 кВ имеют наружные кожухи одинакового диаметра, равного 17 см и высоты 56 см и 124 см соответственно.

Рис. 5-36. Делитель постоянного напряжения на 500 кВ, собранный из непроволочных сопротивлений.

1 — непроволочные сопротивления; 2       —изолирующая опора; 3 — наружный и внутренний кожух и делителя; 4- металлические экраны; 5 — вывод для подключения измерительного прибора. Стрелки указывают направление потоков масла.

При измерении напряжения параллельно низковольтному плечу делителя подключался электростатический ток.
При необходимости учитывался и температурный коэффициент этого сопротивления.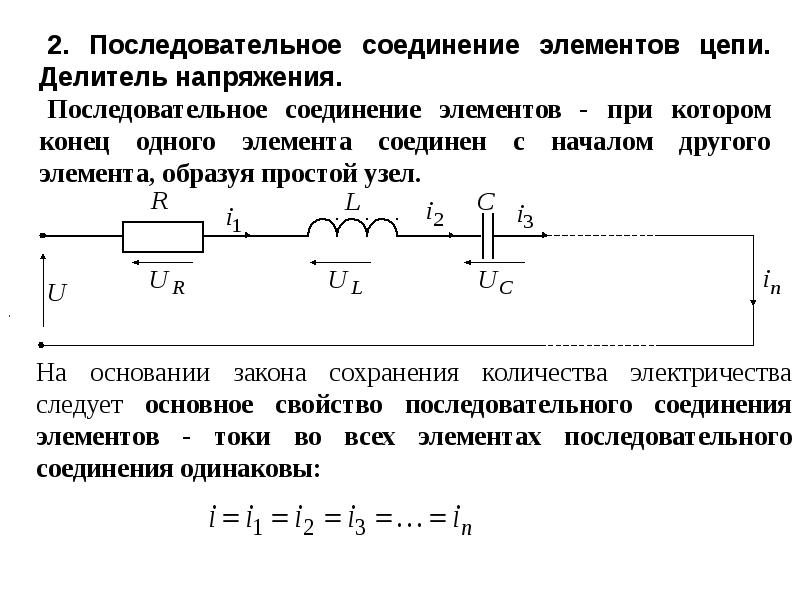
Иногда микроамперметр включается последовательно с делителем напряжения между концом низкого напряжения делителя и землей. В этом случае делитель напряжения выполняет роль дополнительного сопротивления.
Активные делители постоянного напряжения изготовляются на напряжения порядка 1000—2 000 кВ. Делитель постоянного напряжения на 1250 кВ состоял из 2 000 непроволочных сопротивлений по 0,75 Мом каждое с общим сопротивлением величиной 1 500 Мом. Сопротивления погружались в масло. Напряжение на низковольтном плече измерялось с помощью электростатического вольтметра.
Упомянем коротко о делителе постоянного напряжения на 50 кВ, предназначенном для прецизионных измерений постоянных напряжений с точностью ±0,01%. Такая большая точность была достигнута за счет того, что имелась возможность определять коэффициент деления делителя при включенном высоком напряжении. Проволочные сопротивления из манганина 200 ком, мощностью 30 Вт собирались в блоки, а последние соединялись в мостовую схему.
Чтобы избежать влияния токов утечки, использовалась система экранов, которым сообщались потенциалы от вспомогательного делителя напряжения, включенного параллельно основному делителю.
При измерении высоких напряжений промышленной частоты применяют емкостные и реже активные делители. Применение активных делителей переменного напряжения сопряжено с установкой громоздких и дорогостоящих сопротивлений на высокие напряжения. Емкостные делители по сравнению с активными имеют меньшие размеры и стоимость их ниже.
При измерении переменных напряжений с помощью активных делителей возникают ошибки, связанные с наличием емкостных токов, протекающих через емкости элементов делителя на землю Сз и емкости относительно провода Сп. Основные ошибки вносятся емкостями Сз. Если принять, что емкость Сз равномерно распределена вдоль высоковольтного плеча делителя с активным со
противлением R1, то при приложении к активному делителю синусоидального напряжения с угловой частотой ω=2πf полное сопротивление Z1 высоковольтного плеча делителя определяется выражением
(5 43)
Таким образом, емкость Сз вызывает угловую погрешность первого порядка, равную:

и погрешность второго порядка в величине полного сопротивления, равную:
Из (5-43) видно, что погрешность при измерениях с помощью активного делителя напряжения возрастает с увеличением сопротивления высоковольтного плеча R1, емкости элементов делителя по отношению к земле С3 и с увеличением частоты f измеряемого напряжения.
С ростом измеряемого переменного напряжения приходится увеличивать величину сопротивления R1, чтобы ток, протекающий через активный делитель, был в допустимых пределах. При этом увеличивается и емкость элементов делителя по отношению к земле.
Для уменьшения ошибок, связанных с наличием емкостных токов, применяют плоские дисковые экраны, присоединенные к высоковольтному концу делителей. Экран образует с поверхностью земли плоский конденсатор, поле которого достаточно равномерно, если диаметр экрана превышает высоту делителя.
Действие экрана равносильно компенсации емкостей делителя на землю. Такие экраны просты по устройству, но не всегда достаточно эффективны там, где требуется большая точность измерений. В этих случаях иногда сопротивления делителя делят на несколько секций, помещая каждую из них в отдельный металлический экран с потенциалом, равным среднему потенциалу каждой секции. Напряжение на экраны обычно подается от вспомогательного делителя напряжения, подсоединенного параллельно с главным. Таким образом, можно добиться хорошей компенсации влияния емкостей делителя на землю и значительно уменьшить его коронирование. В построенном делителе переменного напряжения промышленной частоты на 100 кВ. с использованием таких экранов угловая погрешность составляла не более 0,0002 рад. Эти делители имеют большие габариты и стоимость.
В случаях, где не требуется большой точности в измерениях, в качестве делителей переменного напряжения иногда применяют непроволочные сопротивления.
Начиная с напряжения 100 кВ и выше, погрешности активных делителей переменного напряжения достигают значительной величины и быстро увеличиваются с ростом напряжений, поэтому рациональным пределом для таких делителей является напряжение 100 кВ при частоте f=50 Гц.
Для измерения высоких переменных напряжений большое распространение получили емкостные делители, состоящие из ряда последовательно включенных емкостей. В емкостном делителе напряжения емкость Сз не имеет существенного значения, так как добавление ее к собственной емкости делителя не изменит зависимости от частоты, если пренебречь собственной индуктивностью делителя. Емкостные делители имеют и то преимущество, что они практически не потребляют активной энергии и могут быть использованы при высоких напряжениях промышленной частоты порядка нескольких миллионов вольт, а также при высоких частотах. Они используются и при измерениях импульсных напряжений. В качестве емкостей делителя широкое применение получили конденсаторы с керамическими диэлектриками, имеющими большую диэлектрическую проницаемость и высокую электрическую прочность. Такой делитель использовался для измерения напряжения трансформаторного каскада на 2 250 кВ. Делитель состоит из последовательно-параллельно соединенных конденсаторов в виде колонок. Центральная измерительная колонка окружена коленками конденсаторов, служащих экранами. Вместо керамических часто применяют конденсаторы с бумажно-масляной изоляцией.

Рис. 5-37. Конденсатор под давлением на 900 кВ.
В измерениях в качестве делителей переменного напряжения используются также конденсаторы с газообразным диэлектриком и концентрическими цилиндрическими электродами, изготовленными так, чтобы избежать коронирования.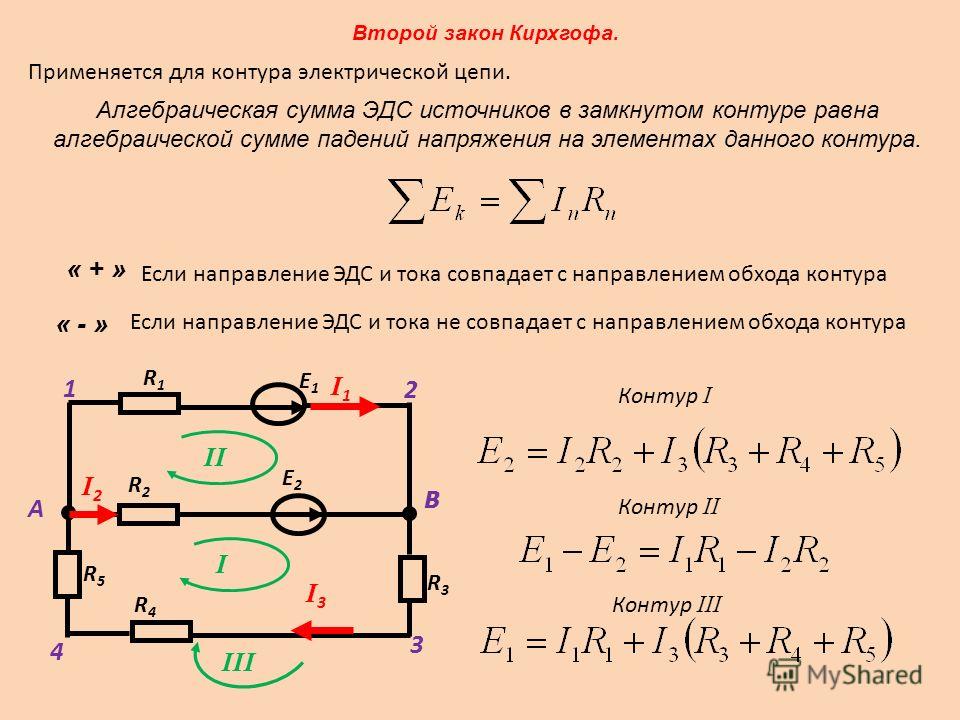 В таких конденсаторах в атмосфере сухого воздуха при нормальной плотности может быть допущена напряженность поля между электродами около 10 кВ/см без перекрытия. Конденсаторы этого типа используются при напряжениях до 300 кВ.

Емкость таких конденсаторов может быть рассчитана с точностью до 0,01%, их угловая погрешность составляет менее 10-5 рад.
Так как электрическая прочность газа увеличивается с его плотностью, размер конденсатора при данном напряжении может быть значительно уменьшен помещением электродов в бак под давлением. Это также защищает электроды от атмосферных загрязнений. На рис. 5-37 показано устройство конденсатора под давлением на 900 кВ с электродами в виде коаксиальных цилиндров. В качестве диэлектрика использовался азот или углекислый газ под давлением 14 ат. Бакелитовый кожух конденсатора одновременно служит и в качестве высоковольтного изолятора. Для низковольтного плеча делителя могут быть применены слюдяные конденсаторы хорошего качества.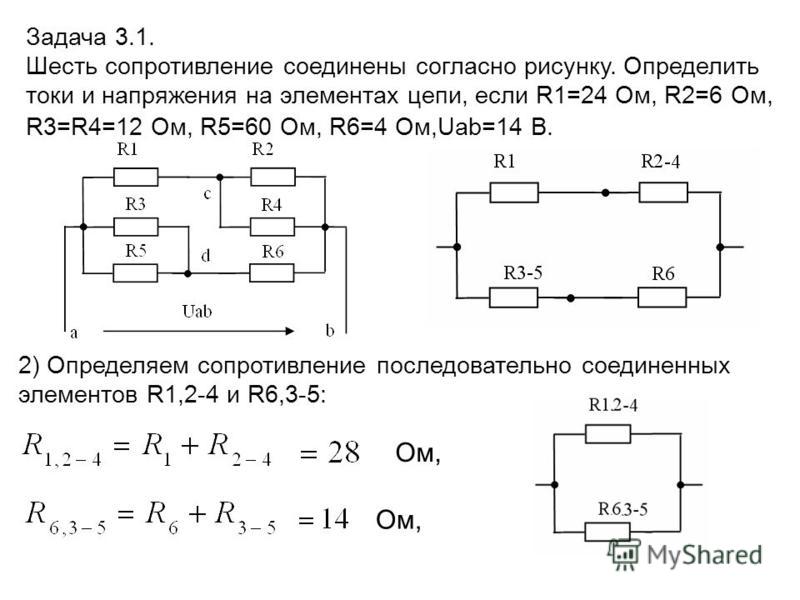
Конденсаторы под давлением стоят дороже цепочки керамических или бумажных конденсаторов на одно и то же напряжение. Но последние имеют большую индуктивность и потери энергии. Поэтому конденсаторы под давлением обычно применяют при необходимости измерения напряжений с большой точностью.
1 — электрод низкого напряжения; 2—электрод высокого напряжения; 3— бакелитовый цилиндр; 4 — вывод для измерительной цепи; 5 — заземленное основание.

Рис. 5-38. Схема измерительного устройства с емкостным делителем напряжения.
При измерении переменных напряжений промышленной частоты в высоковольтных электрических сетях обычно используют измерительные трансформаторы напряжения. Однако при напряжениях 110 кВ и выше размеры трансформаторов напряжения становятся большими, и стоимость их сильно возрастает. Поэтому в практике измерений иногда используют и другие способы измерения напряжений. Значительное распространение в подобных случаях получили делители напряжения.

Удобным способом измерения переменных напряжений является использование в качестве емкостного делителя напряжения конденсаторных вводов выключателей и силовых трансформаторов. Л. М. Залесский и Н. А. Погарский указывают на возможность применения трансформаторов тока с конденсаторной изоляцией в качестве комбинированных трансформаторов тока и напряжения. Очевидно, что использование емкости конденсаторной изоляции трансформаторов тока для измерения напряжения 110 кВ и выше может дать значительную экономию средств. В практически выполненных устройствах для измерения напряжения с использованием вводов конденсаторного типа обычно имеется ряд вспомогательных элементов для обеспечения удобства и повышения точности измерений.

Изоляция вводов конденсаторного типа разделена на ряд слоев с помощью концентрических цилиндров из металлической фольги. Таким образом, образуется ряд заключенных друг в друга цилиндрических конденсаторов, соединенных последовательно. Измерительный прибор (электростатический или катодный вольтметр) включается параллельно последнему конденсатору и измеряется падение напряжения на нем, обычно равное 4—6 кВ.
В последнее время в связи с развитием в энергосистемах высокочастотной связи в качестве емкостных делителей напряжения используют также конденсаторы высокочастотной связи. С помощью упомянутых выше емкостных делителей напряжения можно измерять высокие напряжения порядка нескольких сотен киловольт.
Принципиальная схема такого устройства с емкостным делителем напряжения показана на рис. 5-38. Напряжение на емкости С2 составляет часть измеряемого напряжения и может быть дальше понижено до удобной для измерения величины с помощью трансформатора напряжения Тр. Для обеспечения наибольшей точности измерения в измерительную цепь включается регулируемая индуктивность L. Величина индуктивности L устанавливается такой, чтобы образовать резонансный контур с питающей емкостью С2.

Рис. 5-39. Эквивалентная Т-образная схема измерительного устройства, представленного на рис. 5-38.

При коротком замыкании в цепи измерительного трансформатора напряжение на реакторе L и емкости С2 может достигнуть недопустимой величины. Для предупреждения подобных перенапряжений служит разрядник Р.
Принимая трансформатор напряжения Тр за нагрузку, делитель напряжения вместе с реактором L можно представить в виде эквивалентной Т-образной схемы, которая показана на рис. 5-39.

Для повышения точности измерения надо уменьшить активное сопротивление r реактора. Это достигается путем применения реактора со стальным сердечником и небольшим воздушным зазором.
Измерительные устройства, использующие вводы конденсаторного типа, по сравнению с трансформаторами напряжения. обладают меньшей точностью измерения и имеют малую мощность. Однако в ряде случаев эти устройства в связи с их низкой стоимостью с успехом заменяют трансформаторы напряжения.
Погрешность емкостного делителя напряжения зависит от температуры, влажности изоляции, отбираемой измерительным устройством мощности и других причин. Мощность емкостного делителя зависит  емкости применяемых вводов конденсаторного типа и увеличивается с ростом измеряемого напряжения. Существующие делители этого типа при напряжении 110 кВ имеют мощность 15 ва, при напряжении 220 кВ — 35 ва. Поэтому такие приспособления целесообразно применять при измерении напряжений 110 кВ и выше. Применение емкостных делителей в виде независимых аппаратов, не связанных с вводами конденсаторного типа, позволяет значительно увеличить их мощность.

• Назад
• Вперёд

Параллельное включение резисторов. Параллельное соединение резисторов, а также последовательное

Автор Vic На чтение 18 мин Просмотров 9.4к. Опубликовано 25.04.2021

Содержание

1. Что такое резистор и для чего он нужен
2. Понятие параллельного подключения резисторов
3. Типы проводников
4. Последовательное подключение
5. Теоретическая часть
6. Примеры расчета
7. Общее сопротивление Rобщ
8. Смешанное подключение
9. Что ещё нужно учитывать при подключении резисторов
10. Общее сопротивление Rобщ
11. Схема параллельного соединения
12. Как высчитывать сопротивление составных резисторов
13. Какая мощность тока при последовательном и параллельном соединении
14. Мощность при параллельном соединении
15. Мощность при последовательном соединении
16. Параллельное соединение проводников
17. Сопротивление при параллельном соединении проводников
18. Напряжение при параллельном соединении проводников
19. Сила тока при параллельном соединении проводников
20. Зависимость сопротивления
21. Электрические величины
22. Тип и геометрические параметры
23. Температурные показатели
24. Свойства резисторов при параллельном подключении
25. Формула для вычисления напряжения
26. Отличия между двумя видами подключений
27. Как рассчитать сложные схемы соединения резисторов

Что такое резистор и для чего он нужен

Резистор – пассивный элемент электрической цепи, который поглощает энергию тока и преобразовывает её в тепло за счет сопротивления потоку электронов в цепи.

Зависимость тока от сопротивления описывается законом Ома и рассчитывается по формуле I = U/R.

Свойство резисторов ограничивать ток и снижать напряжение используется во многих электронных устройствах и бытовых приборах.

Справка: Резисторы бывают двух видов – постоянные и переменные, во втором случае сопротивление проводника изменяется механическим путем (вручную).

Последовательное и параллельное соединение резисторов – основные способы соединения резистивных элементов.

Внимание! Резистор не имеет полярности, длина выводов с обоих концов одинакова, поэтому для лучшего понимания сути соединения предлагается называть выводы:

1. С правого края – правый.
2. С левого края – левый.

Понятие параллельного подключения резисторов

При параллельном подключении правые выводы всех резисторов соединяются в один узел, левые – во второй узел.

При параллельном включении резисторов ток в цепь разветвляется по отдельным ветвям, протекая через каждый элемент – по закону Ома величина тока обратно пропорциональна сопротивлению, напряжение на всех элементах одинаковое.

Справка: Ветвь – фрагмент электрической цепи, содержащий один или несколько последовательно соединенных компонентов от узла до узла.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Последовательное подключение

При последовательном соединении резисторы нужно подключить в цепь друг за другом – правый вывод одного резистора к левому второго, правый второго – к левому третьего и так далее в зависимости от количества соединяемых элементов.

При последовательном соединении ток, не изменяя своей величины, течет через все резистивные элементы.

Теоретическая часть

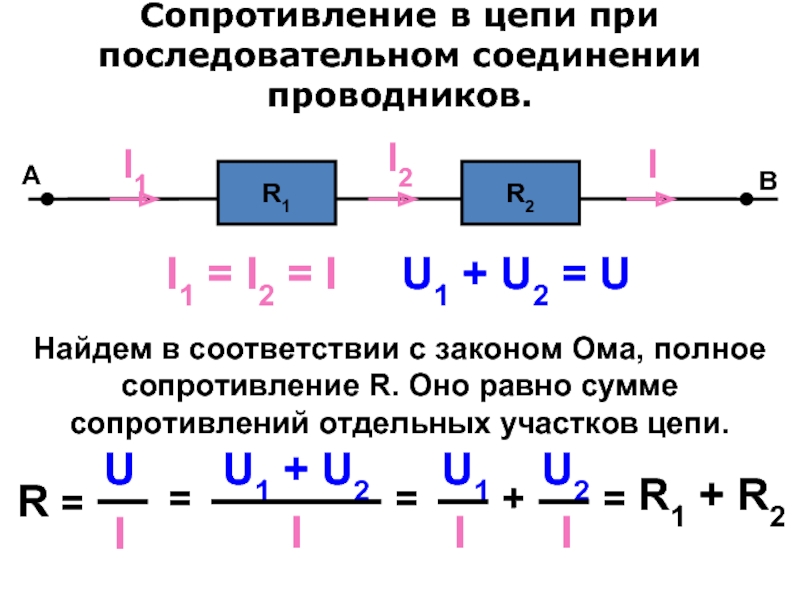
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2). Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых. Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.

Последовательное подключение.

Примеры расчета

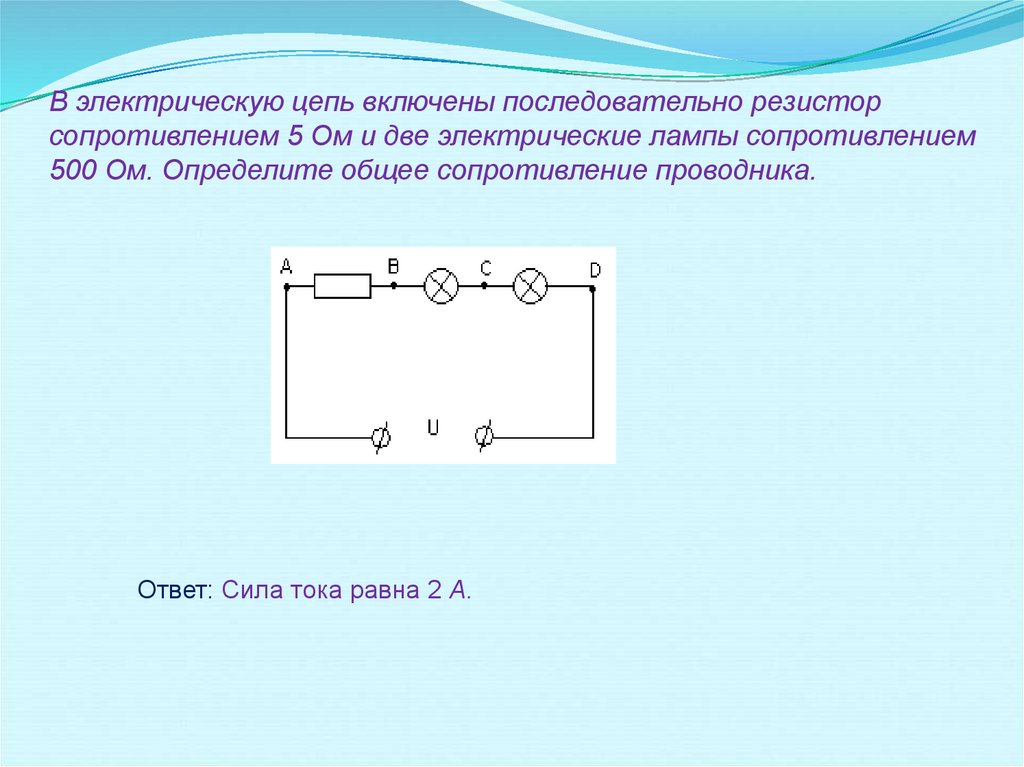
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:

• U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
• U2 = R2 * I = 800 Ом * 2А = 1600 В.

Будет интересно➡  SMD резисторы: что это такое и для чего используются?

Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток.   R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.

Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2  А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.

А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором  — 1600 В.  При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ

При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.

Смешанное подключение

При смешанном подключении в одной схеме сочетаются несколько видов соединений – последовательное, параллельное соединение резисторов и их комбинации. Самую сложную электрическую схему, состоящую из источников питания, диодов, транзисторов, конденсаторов и других радиоэлектронных элементов можно заменить резисторами и источниками напряжения, параметры которых изменяются в каждый момент времени.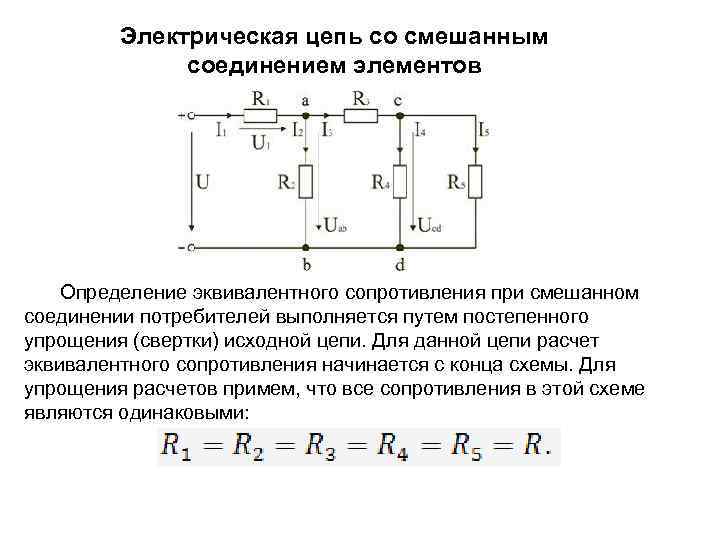 О параллельном соединении резистора и конденсатора читайте тут.

Смешанная схема делится на фрагменты, ток и напряжение рассчитывается для каждого отдельно в зависимости от того, как они соединены на выбранном сегменте электрической схемы.

Важно! Для расчета сопротивления резистора в схеме применяют отдельные формулы для каждого конкретного элемента в зависимости от вида соединения.

Что ещё нужно учитывать при подключении резисторов

Важный показатель в работе резистивного элемента мощность рассеивания – переход электрической энергии в тепловую, вызывающую нагрев элемента.

При превышении допустимой мощности рассеивания резисторы будут сильно греться и могут сгореть, поэтому при расчете схем соединения надо учитывать этот параметр – важно знать насколько изменится мощность резистивных элементов при включении в электрическую цепь.

Общее сопротивление Rобщ

При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается. Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.

То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков». То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи. В случае с параллельным соединением резисторов — от их номинала.

Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.

Схема параллельного соединения

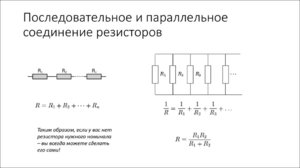
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна. Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно. Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.

Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.

Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом. Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала. Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.

Как высчитывать сопротивление составных резисторов

Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.

Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом.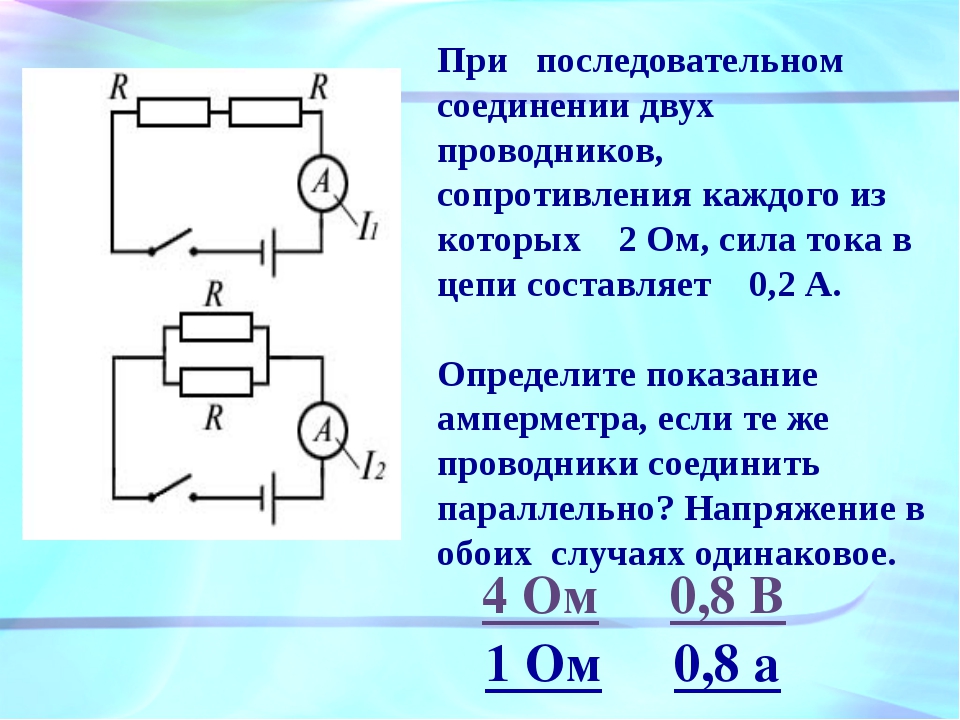 Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.

Какая мощность тока при последовательном и параллельном соединении

Определение мощности отдельного резистивного элемента производится по формуле

P = U²/R или P = I²R , которую можно вывести из формулы расчета мощности электрической цепи P = UI по закону Ома.

Мощность при параллельном соединении

Рассчитав сопротивление каждого элемента в отдельности, считаем мощность каждого по формуле P = I²R, где

• R – не номинальное сопротивление резистивного элемента, а рассчитанное для данной цепи;
• I – сила тока в цепи.

При параллельном соединении через меньший резистор протекает больший ток – мощность рассеивания на этом резистивном элементе будет больше, чем на остальных.

Важно! При расчете параллельной цепи следует учитывать мощность сопротивления с самым маленьким номиналом.

Мощность при последовательном соединении

Вычислив сопротивление каждого резистивного элемента по отдельности, рассчитываем мощность каждого по формуле P = U²/R, где

• R – рассчитанное нами сопротивление для определенной схемы;
• U – падение напряжения на данном резистивном элементе.

Справка: Полную мощность цепи при последовательном и параллельном соединении можно найти, сложив вычисленные мощности отдельных элементов, входящих в цепь Pобщ = P1+P2+P3+…+Pn.

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет.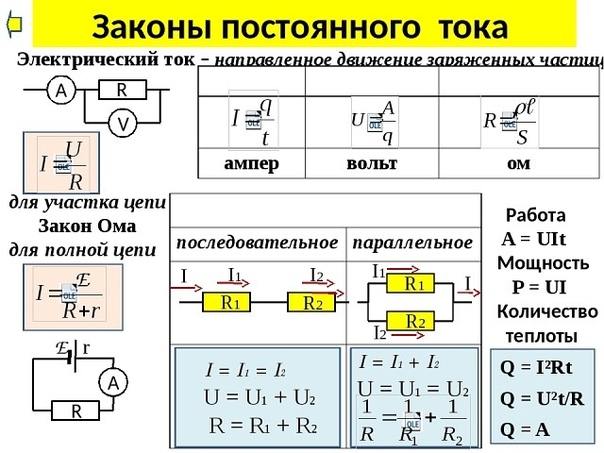 Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

I1 = U/R1

I2 = U/R2

I3 = U/R3

Если бы у нас еще были резисторы, соединенные параллельно, то для них

In = U/Rn

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.

I1 = U/R1

I2 = U/R2

I3 = U/R3

Если бы у нас еще были резисторы, соединенные параллельно, то для них

In = U/Rn

Следовательно,

I1 = U/R1 = 10/2=5 Ампер

I2 = U/R2 = 10/5=2 Ампера

I3 = U/R3 = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I1 + I2 + I3 = 5+2+1=8 Ампер

2-ой способ найти I

I=U/Rобщее

Чтобы найти Rобщее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.

I=U/Rобщее = 10/1,25=8 Ампер.

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Свойства резисторов при параллельном подключении

При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи. При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.

Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.

Стандартная формула напряжения

Формула для вычисления напряжения

При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.

При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.

Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:

U = U1 = U2 = … = Uобщ.

Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.

Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.

Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп

В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.

Отличия между двумя видами подключений

Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.

Пример подключения с предохранителем

Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.

Как рассчитать сложные схемы соединения резисторов

Если соединять большее количество элементов, надо в рассмотренные формулы добавить необходимое количество слагаемых.

Исходные данные:

• источник постоянного тока 12V;
• сопротивление параллельных резисторов, Ом: 10, 40, 60, 80.

Расчет:

• основная формула: 1/Rэкв = 1/R1 + 1/R2 + 1/R3 + 1/R4;
• подставив исходные данные, вычисляют проводимость: G = 1/Rэкв =1/10 + 1/40 + 1/60 +1/80 = 0,1 + 0,025 + 0,0166 +0,0125 = 0,1541;
• эквивалентное сопротивление: Rэкв = 1/0,1541 ≈ 6,5 Ом;
• ток в цепи: Iобщ = Uип/ Rэкв = 12/ 6,5 ≈ 1,85 А.

Сложные схемы

По аналогичной технологии делают расчеты более сложных цепей. На рисунке обозначены номиналы сопротивлений. В обоих случаях применяется одинаковый источник питания с Uип = 12V.

Расчет 1 (последовательное и параллельное соединение):

• для каждого параллельного участка можно использовать формулу: Rобщ = 1/ (1/R1 + 1/R2) = R1*R2/R1 + R2;
• эквивалентное сопротивление первой части: Rэкв1 = (2*4)/ (2+4) = 1,3 Ом;
• второй: Rэкв2 = (15*5)/ (15+5) = 3,75 Ом;
• общее: Rэкв = 1,3 + 10 + 3,75 = 15,05 Ом;
• Iобщ = Uип/ Rэкв = 12/ 15,05 ≈ 0,8 А.

Расчет 2 (сложное параллельное соединение):

• в этом варианте сначала вычисляют проводимость части (R3, R4, R5) по формуле: G345 = 1/5 + 1/10 + 1/ 20 =7/20 = 0,35 сим;
• Rэкв (345) = 1/0,35 ≈ 2,857 Ом;
• суммарное значение для цепи: R1 + R2 = 20 Ом;
• по аналогии с предыдущим способом определяют: G12345 = 0,4 сим и Rэкв(12345) = (20*2,857)/ 20 + 2,857) ≈ 2,5 Ом;
• после добавления последнего элемента (R6=7,5 Ом) получают итоговый результат: Rэкв = 2,5 + 7,5 = 10 Ом;
• делением определяют силу тока в нагрузке, подключенной к источнику тока 12 V: I = 12/10 = 1,2 А.

В последнем примере применен дополнительный компонент цепи (R6). Соответственно, для этой схемы не будет выполняться рассмотренная выше пропорция равенства напряжений (источника и на подключенной нагрузке).

В этом случае разница потенциалов на шестом резисторе составит:

U6 = I *R6 = 1,2 * 7,5 = 9 В.

Соответственно, изменится напряжение между контрольными точками:

Uав = I * Rэкв(12345) = 1,2*2,5 = 12-9 =3V.

Вторая часть формулы демонстрирует проверку вычитанием напряжений (Uип — U6).

Источники

• https://onlineelektrik.ru/eoborudovanie/kondensatori/parallelnoe-soedinenie-rezistorov-a-takzhe-posledovatelnoe.html
• https://rusenergetics.ru/praktika/raschet-soprotivleniya-rezistorov
• https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
• https://www.RusElectronic.com/serial-and-parallel/
• https://rusenergetics.ru/polezno-znat/parallelnoe-soedinenie
• https://amperof.ru/teoriya/parallelnoe-soedinenie-rezistorov.html

Что такое правило делителя напряжения?

Вы когда-нибудь задавались вопросом, как определить напряжение между двумя резисторами, соединенными последовательно? Не ищите ничего, кроме надежного правила делителя напряжения! Обладая фундаментальными знаниями алгебры, вы можете применить это простое правило для расчета спада напряжения на двух последовательно соединенных резисторах. Готовы углубиться в правило делителя напряжения? Тогда продолжайте читать!

Что такое делитель напряжения?

Для регулирования электрического тока и напряжения в делителе напряжения используются два резистора или другие типы пассивных компонентов, соединенных последовательно. Определив соотношение между напряжениями в каждом узле, мы можем легко рассчитать выходное напряжение этого делителя. Согласно правилу делителя напряжения (VDR), выходное напряжение делителя эквивалентно входному напряжению, умноженному на отношение двух резисторов.

В простейшем случае, когда два резистора соединены последовательно, общее напряжение источника питания пропорционально разделяется в соответствии с их индивидуальными отношениями сопротивлений. Используя закон Ома (V=IR), можно определить, какой ток будет потреблять каждый компонент и какая разница потенциалов между ними существует. Рассчитав разность потенциалов, мы можем измерить и определить выходное напряжение этого делителя — важный шаг для любой успешной электрической цепи. [1]

Что такое правило делителя напряжения?

Если вы хотите определить выходное напряжение цепи, содержащей два резистора, вам может помочь это уравнение! Согласно правилу, в последовательной цепи отношение номиналов резисторов определяет, какое напряжение создается на каждом компоненте. Например, если у вас есть цепь с двумя резисторами (R1 и R2), в которой сопротивление R1 в два раза больше сопротивления R2, ​​то потери напряжения через R1 будут в два раза больше, чем через аналог. Чтобы найти общее падение напряжения на обоих резисторах, вы просто используете закон Ома V = IR, где I — ток через оба резистора, а R — их суммарное значение сопротивления. Математически это можно выразить следующим образом:

Vout = Vin *(R2/(R1 + R2))

Правило делителя напряжения полезно во многих приложениях, поскольку оно позволяет инженерам точно рассчитать падение напряжения на широком диапазоне компонентов. Например, если инженер пытается разработать схему с двумя резисторами, которые должны обеспечить 12 В, он может легко рассчитать требуемые значения резисторов, используя уравнение VDR. Это делает простым и эффективным проектирование цепей с несколькими компонентами, требующими определенных падений напряжения.

Правило делителя напряжения можно использовать не только для расчета точных значений при построении цепей, но и для измерения неизвестных уровней сопротивления. Соединив два известных резистора последовательно и измерив выходное напряжение, вы можете использовать закон Ома и уравнение VDR для определения R1 или R2. [2]

Когда использовать правило делителя напряжения?

Используйте правило делителя напряжения, чтобы снизить величину напряжения, подаваемого в электрическую цепь. Это особенно полезно при работе со схемами, требующими разных наборов напряжений, поскольку его можно использовать для регулировки входного напряжения, чтобы каждый компонент получал желаемый уровень.

Основная цель использования правила делителя напряжения заключается в согласовании импедансов, что гарантирует, что компоненты в цепи получают именно то количество напряжения, которое необходимо для оптимальной работы.

Он обычно используется в радиочастотных (РЧ) приложениях, таких как усилители, антенны и фильтры, а также во многих других типах электронных проектов.

Также может потребоваться использование правила делителя напряжения при работе с несколькими источниками в одной цепи. Снижая напряжение, подаваемое на определенные компоненты, вы можете оптимизировать мощность, поступающую на каждую часть. Это может быть необходимо, например, если один компонент требует меньшего напряжения, чем другой, или если определенный набор компонентов должен использовать один источник питания.

Правило делителя напряжения также можно использовать при построении простых цепей со стандартными резисторами и конденсаторами. В этом сценарии важно отрегулировать напряжение так, чтобы через каждый компонент проходило правильное количество тока — слишком маленький ток, и ваша схема не будет работать так эффективно, как должна; слишком большой ток, и это может привести к повреждению. Поняв основные принципы, лежащие в основе правила, вы сможете быстро регулировать напряжения в любой электронной схеме. [3]

Формула делителя напряжения

Это простое уравнение, используемое в электронике для расчета выходного напряжения цепи. Он основан на законе Ома, который гласит, что сила тока в цепи равна напряжению, деленному на сопротивление. Деление напряжения происходит, когда два резистора соединены последовательно с источником напряжения, таким как источник питания переменного или постоянного тока .

Соотношение между этими двумя резисторами определяет, какая часть входного напряжения сможет пройти через них и достичь выходной стороны схемы. Это известно как «деление напряжения» и может быть рассчитано по формуле Vвых = (R1 / R1 + R2) * Vin, где Vвых — выходное напряжение с делителя, Vin — входное напряжение, приложенное к обоим резисторам, R1 — сопротивление первого резистора, а R2 — сопротивление второго резистора.

Правило делителя напряжения можно использовать для разработки схем с определенным выходным напряжением или для измерения неизвестного напряжения источника с использованием двух известных сопротивлений. Его также можно использовать для создания источника питания с регулируемыми выходными напряжениями и токами. Понимание этой базовой формулы и ее приложений поможет инженерам разрабатывать эффективные схемы для своих проектов.

Примеры делителя напряжения

Правило делителя напряжения — это электротехнический принцип, который можно использовать для расчета падения напряжения на резисторе в простой последовательной цепи. В нем говорится, что общее напряжение делится между всеми резисторами в соответствии с их относительными значениями. Это правило можно использовать для объяснения того, как в цепях возникают падения напряжения, а также для расчета напряжения в практических приложениях.

Давайте рассмотрим несколько примеров того, как работает правило делителя напряжения. Предположим, у нас есть цепь с двумя последовательно соединенными резисторами, каждый из которых имеет сопротивление R1 и R2 соответственно. Тогда общее сопротивление этой цепи будет равно R1 + R2. В соответствии с правилом делителя напряжения падение напряжения на каждом резисторе пропорционально сопротивлению:

V1 = (R1 / (R1 + R2)) * Vtotal
V2 = (R2 / (R1 + R2)) * Vtotal

В этом примере V1 будет представлять падение напряжения на резисторах R1 и V2 будет падение напряжения на резисторе R2.

Предположим, что в нашей схеме общее приложенное напряжение составляет 10 В , а два резистора равны по 5 Ом каждый. Затем мы можем рассчитать, сколько напряжения будет падать на каждом резисторе, используя правило делителя напряжения:

V1 = (5 / (5+5))*10 В = 5 В
V2 = (5 / (5+5))*10 В = 5 В

Итак, в этом примере мы видим, что Падение напряжения одинаково на обоих резисторах, так как они имеют одинаковое значение сопротивления.

Мы также можем использовать правило делителя напряжения, чтобы рассчитать, какой ток протекает через каждый резистор в нашей цепи. Поскольку ток — это просто скорость протекания заряда, и поскольку заряд должен сохраняться во всей последовательной цепи, общий ток в любой точке цепи должен оставаться постоянным. Следовательно, если I1 — это ток, протекающий через R1, а I2 — это ток, протекающий через R2, то:

I1 = I2

и

I1 = Vtotal / R1+R2

Теперь, используя приведенный выше пример, мы можем рассчитать ток, протекающий через каждый резистор:

900 07 I1 = 10 В / (5+5 ) = 1A
I2= 10V / (5+5) = 1A

Как видите, в этой цепи ток везде одинаковый и постоянный.

Проекты домашней автоматизации Arduino

В заключение, правило делителя напряжения является полезным инструментом для понимания падений напряжения в последовательных цепях и для расчета напряжений и токов. Это позволяет нам быстро определить, сколько напряжения будет падать на каждом резисторе в любой данной цепи. С практикой это может помочь нам разработать более эффективные системы, которые потребляют меньше энергии, но при этом обеспечивают максимальную производительность. [4]

Емкостные делители напряжения

Правило делителя напряжения описывает простую схему, в которой последовательно соединены два резистора, при этом выходное напряжение снимается с одного из резисторов. То же правило относится и к емкостным делителям, где два конденсатора соединены последовательно и выходное напряжение снимается на одном из них. В этом случае, поскольку конденсаторы препятствуют изменению напряжения, выходное напряжение будет меньше входного.

Базовый пример емкостного делителя напряжения состоит из двух одинаковых конденсаторов емкостью 100 нанофарад (нФ). Когда на эту схему подается входное напряжение, выходное напряжение будет выглядеть как Vout = Vin * C1/(C1+C2) = Vin * 0,5. Это означает, что если входное напряжение равно 10 вольт, выходное напряжение будет 5 вольт.

Емкостные делители напряжения обычно используются в системах связи и схемах генераторов. В системах связи их можно использовать для уменьшения шума или контроля уровня сигнала. В генераторах их можно использовать для управления амплитудой и частотой генерируемых сигналов. Они также полезны для согласования импедансов между каскадами в цепи, а также для развязки источников питания.

В заключение следует отметить, что схемы емкостных делителей напряжения позволяют снизить входное напряжение на определенный коэффициент, что делает их очень полезными для многих приложений, таких как системы связи, генераторы, согласование импеданса и развязка источников питания. Они имеют преимущества перед резистивными делителями благодаря широкому диапазону частот, низким потерям и высокой линейности. В результате емкостные делители напряжения являются важными компонентами современной электроники.

Индуктивные делители напряжения

IVD представляют собой тип электрической цепи, которая делит входное напряжение на два выхода.

Это делается путем последовательного соединения катушки индуктивности с резистором и последующего измерения напряжения в каждой точке соединения. Правило делителя напряжения (VDR) гласит, что отношение выходных напряжений равно отношению значений сопротивления, соединенных последовательно. Это простое правило можно использовать для расчета падения напряжения на резисторах, обеспечивая точные решения для сложных цепей.

Обладая этими знаниями, инженеры могут разрабатывать эффективные решения по питанию для любых приложений, от автомобильной электроники до микросхем. Кроме того, IVD также используются в системах управления беспилотными автомобилями и другими автономными транспортными средствами, где по соображениям безопасности необходим точный контроль над распределением мощности. Используя правило делителя напряжения, инженеры могут гарантировать, что все компоненты системы получат требуемое напряжение с минимальными потерями мощности. [5]

Примеры задач делителя напряжения

Схемы делителя напряжения могут использоваться для решения множества задач. Рассмотрим следующий пример:

Предположим, у нас есть 12-вольтовый источник питания постоянного тока , и мы хотим разделить его на два 6-вольтовых выхода. Для этого нам потребуется использовать ИВД с двумя резисторами — один сопротивлением R1, а другой сопротивлением R2.

Используя правило делителя напряжения, мы можем рассчитать, что R1 должно быть в два раза больше, чем R2, чтобы выходное напряжение было равным.

Другими словами, если R1 = 8 Ом и R2 = 4 Ом, , то оба выходных напряжения будут 6 вольт. Этот же принцип можно применить и к делителям переменного напряжения, где резисторы должны быть соединены параллельно с конденсатором, а не последовательно.

В конечном счете, понимание и применение правила делителя напряжения является важным навыком для любого инженера-электрика или техника, поскольку оно может помочь им точно рассчитать падение напряжения на различных компонентах. Используя это простое уравнение, инженеры могут разрабатывать эффективные решения по питанию для любых приложений — от автомобильной электроники до микросхем. Обладая этими знаниями, они могут продвигаться по карьерной лестнице и руководить успешными проектами, оказывающими огромное влияние на окружающий нас мир.

Точки отвода напряжения в сети делителей

Правило делителя напряжения — важный принцип электротехники, который можно применять к различным цепям. В нем указано, что напряжение в любой точке ответвления в последовательно соединенной сети резисторов будет равно отношению сопротивлений между этим конкретным узлом и землей, умноженному на напряжение питания. Это позволяет инженерам использовать правило делителя для расчета ожидаемых напряжений в каждом узле, чтобы определить, правильно ли они спроектировали свою схему.

Кроме того, это может помочь им устранить неполадки, когда во время тестирования обнаруживаются неправильные напряжения. Использование этого правила позволяет инженерам выполнять быстрые расчеты с минимальными усилиями и получать точные результаты. Кроме того, понимание того, как значения сопротивления влияют на точки отвода напряжения, дает ценную информацию о проектировании эффективных сетей для различных приложений.

Понимая основы правила делителя напряжения, инженеры могут принимать взвешенные решения при проектировании и устранении неисправностей электрических цепей. Это гарантирует, что их устройства будут работать должным образом и будут надежными для длительного использования.

Предположим, вы хотите разработать простую схему с двумя резисторами, соединенными последовательно между источником питания 5 В и землей. Если первый резистор имеет сопротивление 100 Ом, а второй резистор 200 Ом, , то напряжение в любой точке отвода в этой сети будет 4В (5В * (100/300)). Обладая этими знаниями, инженер может точно определить, какие уровни напряжения следует ожидать во всей конструкции, не тратя время на ручные расчеты или испытания.

Применение правила делителя напряжения

Правило делителя напряжения можно использовать для ряда приложений, таких как измерение напряжения в электрических цепях и управление током через определенные компоненты. Его также можно использовать для управления выходом цепи путем регулировки резисторов внутри нее.

Кроме того, это правило часто используется в низковольтных источниках питания, что позволяет инженерам и проектировщикам легко настраивать параметры своей конструкции. Наиболее важно то, что правило делителя напряжения необходимо при проектировании аналоговых схем с высоким импедансом, чувствительных к входным напряжениям. Используя эту полезную концепцию, инженеры и дизайнеры получают доступ к более точному управлению схемой, чем когда-либо прежде.

Правило делителя напряжения — это мощный инструмент, который был принят современным инженерным сообществом благодаря своей полезности и простоте. Поняв эту концепцию, инженеры и дизайнеры могут в полной мере воспользоваться огромными возможностями, которые она предоставляет при проектировании схем.

В заключение отметим, что правило делителя напряжения является фундаментальным инструментом, который широко используется в инженерии и проектировании. Его можно использовать для различных приложений, включая измерение напряжения в электрических цепях, контроль тока через компоненты, регулировку резисторов в цепи для управления ее выходом и разработку аналоговых цепей с высоким импедансом с точным контролем напряжения. Таким образом, это правило является неотъемлемой частью современных инженерных проектов. [6]

Часто задаваемые вопросы

Что утверждает правило делителя напряжения?

Правило делителя напряжения гласит, что напряжение в последовательной цепи равно сумме всех отдельных напряжений в цепи, деленной на общее сопротивление. Другими словами, в нем говорится, что общее напряжение в последовательной цепи можно рассчитать, используя закон Ома и разделив его на общее сопротивление. Математически это можно записать как V = V1 + V2 + … + VR / R, где V — общее напряжение в цепи, а R — полное сопротивление. Затем это уравнение можно использовать для расчета любых неизвестных значений для конкретной цепи.

Как можно применить это правило?

Правило делителя напряжения чаще всего применяется при разработке схем с несколькими последовательно соединенными резисторами. Используя закон Ома и уравнение делителя напряжения, можно рассчитать отдельные напряжения на всех резисторах в цепи. Это правило также можно использовать для точного измерения разности потенциалов между двумя точками цепи, подключив между ними известный резистор и измерив напряжение на нем. Кроме того, это правило полезно для расчета токов в сложных цепях с несколькими резисторами. Наконец, это правило можно использовать для анализа транзисторных схем и других нелинейных компонентов.

Каковы некоторые ограничения этого правила?

Правило делителя напряжения не принимает во внимание какие-либо дополнительные источники сопротивления или импеданса в цепи, такие как индуктивность или емкость. Кроме того, это уравнение не учитывает никаких изменений сопротивления цепи из-за температуры или других факторов окружающей среды. Наконец, это уравнение не включает каких-либо эффектов паразитных элементов, таких как резисторы или конденсаторы, которые могут присутствовать в цепи. В этих случаях необходимо использовать более сложные методы анализа для точного расчета разностей потенциалов и токов во всей цепи.

Что еще мне следует знать об этом правиле?

Вообще говоря, важно помнить, что уравнение делителя напряжения применимо только тогда, когда все компоненты в ряду имеют одинаковую температуру и постоянное сопротивление во всем рабочем диапазоне. Если какое-либо из этих условий не выполняется, то необходимо использовать более совершенные методы для точного расчета напряжений и токов в данной цепи. Кроме того, важно отметить, что это уравнение не учитывает никаких изменений сопротивления из-за нелинейных компонентов или факторов окружающей среды. Наконец, важно знать о потенциальных опасностях, связанных с работой с высоким напряжением и током – всегда соблюдайте надлежащие меры предосторожности.

Полезное видео: Что такое правило делителя напряжения и делителя тока | VDR и CDR с практическим экспериментом

Заключение

Правило делителя напряжения — мощный инструмент для понимания поведения электрических цепей. Используя это правило, можно быстро вычислить напряжение на любом резисторе в цепи без решения каких-либо сложных уравнений. Это может быть особенно полезно при анализе цепей с несколькими резисторами и определении того, как каждый компонент влияет на общую производительность системы. Благодаря последовательному применению он помогает упростить многие задачи и обеспечивает надежный метод расчета напряжений и токов в цепи.

В целом, правило делителя напряжения оказалось бесценным ресурсом, открывающим множество возможностей для понимания электричества и электрических компонентов. Это позволяет инженерам эффективно и точно анализировать схемы, чтобы они могли лучше понять, как работают их системы, и как лучше всего оптимизировать их для достижения максимальной производительности. С правилом делителя напряжения гораздо меньше неизвестных, с которыми нужно бороться, и больше уверенности в надежности результатов.

Поэтому всем, кто работает с электричеством или изучает его, стоит ознакомиться с этим простым, но действенным правилом. Понимание того, как это работает, может обеспечить ценную основу, которая окажется чрезвычайно полезной в любом электрическом проекте или исследовательской деятельности.

Ссылки

1. https://study.com/learn/lesson/voltage-divider-circuit-rule-bias-formula.html
2. https://www.elprocus.com/voltage-divider-rule -с-примерами/
3. https://www.seeedstudio.com/blog/2019/10/09/voltage-dividers-everything-you-need-to-know/
4. https://www.electronics-tutorials .ws/dccircuits/voltage-divider.html
5. https://www.electricalclassroom.com/voltage-division-rule-potential-divider-circuit/
6. https://electricalbaba.com/voltage-division-rule- объяснение-формула-вывод/

Как стать инженером-электронщиком?

Правило деления напряжения

Правило деления напряжения является одним из основных правил анализа цепей. Он применим ко всем последовательным и комбинированным резисторным схемам. Последовательное соединение резисторов всегда действует как делитель напряжения. При последовательном соединении через каждый резистор протекает одинаковый ток. Следовательно, падение напряжения на каждом из них пропорционально их омическому значению. Кроме того, ток, протекающий через них, должен быть пропорционален общему сопротивлению цепи.

Напряжение на каждом резисторе по закону Ома представляет собой ток, протекающий через цепь, умноженный на значение сопротивления. Рассмотрим цепь с числом резисторов, соединенных последовательно, и напряжением V, приложенным к ней.

Общее сопротивление, обеспечиваемое этим последовательным соединением резисторов потоку тока, будет равно сумме отдельных сопротивлений.

Треб = R ₁ + R ₂ + R ₃ + ………… + R _n

Полный ток, протекающий через резистор, должен быть: 

I = V / R _eq  —————————————— (i)

Напряжение на каждом резисторе R1 должно быть

В ₁  = I. R ₁  —————————- (ii)

Напряжение на каждом резисторе R1 должно составлять  —————— ———- (iii)

Напряжение на каждом резисторе R1 должно быть

В ₃ = I.R ₃  —————————- (iv)

Напряжение на каждом резисторе R1 должно быть

В _n = I.R _n —————————— (v)

Сравнение (i) и (ii),

В 9 0272 1 = V.R ₁ /R _eq

Сравнение (i) и (iii),

V ₂ = V.R ₂ /Req

Сравнение (i) и (iv),

V ₃ = V.R ₃ /R _eq

Сравнение (i) и (v),

V _n = V.R _n /R _eq

Где V _n — напряжение на n-м резисторе. В общем случае

Напряжение на любом резисторе при последовательном соединении резисторов должно быть равно отношению резистор, деленный на эквивалентное сопротивление цепи. Это называется правилом деления напряжения.

Для лучшего представления рассмотрим цепь с двумя последовательно соединенными резисторами R ₁ и R ₂ , к которым приложено напряжение V.

Общее сопротивление = R ₁ + R ₂

Пусть общий ток равен I.

Ток I = В/(R ₁ + R ₂ )

Напряжение на R ₁ , В ₁ = I.R ₁ = V.R ₁ / (R 9027 2 1 +R ₂ )

Напряжение между R ₂ , В ₂ = И.Р ₂ = В.Р ₂ / (Р ₁ +Р ₂ )

Примеры

1. Найти напряжение на резисторе R3 в цепи.

Общее сопротивление Rt = 5 + 5 + 5 = 15 Ом 5/15  = 1,67 В

2. Найти напряжение на резисторе R2 в цепи.

Общее сопротивление R _t = 5 + 4= 9 Ом

Напряжение на сопротивлении R ₂ = V.R ₂ /R _т = 5 . 4/9  = 2,22 В

3.