Закон Ома для участка цепи, не содержащего источника ЭДС. — Студопедия.Нет
Закон (правило) Ома для участка цепи, не содержащего источник ЭДС, устанавливает связь между током и напряжением на этом участке. Применительно к рис. 2.5
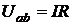
или
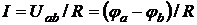 (2.4)
(2.4)
Закон Ома для участка цепи, содержащего источник ЭДС. Обобщенный закон Ома.
Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа — φс) на концах участка цепи и имеющейся на этом участке ЭДС Е. Так, по уравнению (2.2) для схемы рис. 2.6а
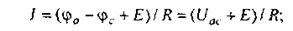
по уравнению (2.3) для схемы рис. 2.6
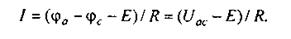
В общем случае
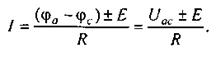 (2.5)
(2.5)
Уравнение (2.5) математически выражает закон Ома для участка цепи, содержащего источник ЭДС:
— знак плюс перед Е соответствует рис. 2.5а ;
— знак минус — рис. 2.5б.
В частном случае при E = 0 уравнение (2.5) переходит в уравнение (2.4).
Неразветвленные и разветвленные электрические цепи.
Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 2.6
Ветвь — участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами.
Узел — это точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рис. 2.6в), то в этом месте есть электрическое соединение двух линий, в противном случае (рис. 2.6
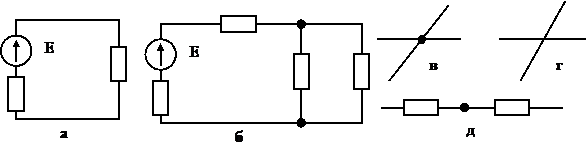
Рис.2.6
Кроме термина «узел» иногда используют термин «устранимый узел». Под устранимым узлом понимают точку, в которой соединены два последовательных сопротивления (рис. 2.6д). Этим понятием пользуются при введении данных в ЭВМ о значении и характере сопротивлений.
Последовательное соединение элементов —это соединение элементов, в которых протекает один и тот же ток (рис.2.6а).
Это соединение элементов можно заменить одним эквивалентным сопротивлением, вычисленным по формуле:
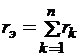
Эквивалентная проводимость определяется по формуле:
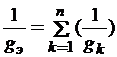 .
.
Параллельное соединение элементов – это соединение элементов, когда напряжение на каждом из элементов имеет одно и тоже значение.
Это соединение элементов можно заменить одним эквивалентным сопротивлением, вычисленным по формуле:
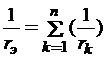
Эквивалентная проводимость определяется по формуле:
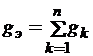 .
.
Смешанное соединение резистивных элементов
При наличии в цепи только одного источника ЭДС внешнюю по отношению к источнику часть электрической цепи можно в большинстве случаев рассматривать как смешанное (последовательно-параллельное) соединение элементов.
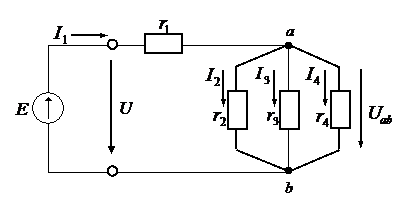
Рис.2.7.
В приведенной схеме (рис.2.7) несколько резистивных элементов, которые соединены параллельно.
Расчет смешанного соединения нужно начинать с определения эквивалентной проводимости
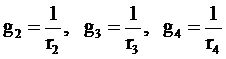 ;
;
эквивалентная проводимость равна:
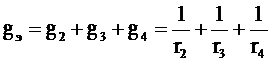 .
.
После замены параллельного соединения резистивных элементов эквивалентным резистивным элементом с сопротивлением  (рис.2.12) получается эквивалентная схема с последовательным соединением двух резистивных элементов r
(рис.2.12) получается эквивалентная схема с последовательным соединением двух резистивных элементов r
Электродвижущая сила. Закон Ома для полной цепи
Как вы знаете, для существования электрического тока, необходимо наличие электрического поля. Причем, это поле должно постоянно поддерживаться неким источником тока. Сегодня мы поговорим об основной характеристике источника тока, которая называется электродвижущей силой (или, сокращенно, ЭДС). Для начала рассмотрим простой опыт: возьмем два противоположно заряженных шарика и соединим их проводником. В этом случае, в проводнике возникнет электрический ток, но он будет очень кратковременным. Дело в том, что очень скоро произойдет перераспределение заряда, и потенциалы шариков уравняются. Значит, перестанет существовать электрическое поле.
Из этого можно сделать вывод, что для поддержания постоянного тока необходимо наличие неких сил неэлектрического происхождения, чтобы эти силы могли перемещать заряды против поля. Такие силы называются сторонними силами. То есть, сторонние силы — это любые силы, которые действуют на электрические заряды, но при этом не являются силами электрического происхождения. Например, это могут быть силы, действующие на заряды со стороны магнитного поля — это используется в генераторах.

В батареях или аккумуляторах работу по разделению электрических зарядов выполняют химические реакции.

Еще один аргумент, который мы можем привести — это то, что работа кулоновских сил при перемещении заряда по замкнутому контуру, равна нулю. А это значит, что какие-то другие силы должны обеспечивать ненулевую работу для поддержания разности потенциалов.
Устройство для поддержания электрического тока, называется источником тока.

Из формулы видно, что электродвижущая сила, как и напряжение, измеряется в вольтах:

Теперь, когда мы познакомились с ЭДС, мы можем перейти к изучению закона Ома для полной цепи. Полной цепью называется замкнутая цепь, включающая в себя источник тока. Для удобства, мы рассмотрим простейшую электрическую цепь, состоящую только из источника тока, резистора и соединительных проводов:

Как мы уже сказали, источник тока характеризуется ЭДС. Тем не менее, любой источник тока обладает определенным сопротивлением, которое называется

Как вы знаете, каждый участок цепи выделяет то или иное количество теплоты. По закону Джоуля-Ленца, это количество теплоты вычисляется по формуле:

Исходя из закона сохранения энергии, мы можем приравнять это количество теплоты к работе сторонних сил:

Закон Ома для полной цепи звучит так: сила тока в замкнутой цепи равна отношению ЭДС источника к полному сопротивлению цепи:

Вывести закон Ома для полной цепи можно, рассуждая несколько иначе. Как мы знаем, при последовательном соединении полное напряжение цепи равно сумме падений напряжений на всех участках цепи:

Мы видим, что произведение силы тока и сопротивления резистора есть не что иное, как напряжение на этом резисторе. А произведение силы тока и внутреннего сопротивления — это падение напряжения на самом источнике:

Надо сказать, что внутреннее сопротивление источника во многих случаях пренебрежимо мало по сравнению с сопротивлением внешней части цепи. В этом случае, мы можем считать, что напряжение на зажимах источника примерно равно ЭДС (то есть падение напряжения на источнике считается приблизительно равным нулю):

Тем не менее, именно внутренним сопротивлением определяется сила тока в цепи при коротком замыкании. Напомним, что при коротком замыкании, внешнее сопротивление становится почти нулевым, поэтому в цепи резко возрастает сила тока:

Рассмотрим теперь цепь, содержащую несколько последовательно соединенных источников тока.

В этом случае, ЭДС всей цепи равна алгебраической сумме ЭДС отдельных источников.
В таких случаях необходимо выбрать так называемое
«направление обхода тока». Это направление выбирается условно (в нашем случае —
против часовой стрелки). Тогда,  ,поскольку
они стремятся вызвать ток в направлении обхода.
,поскольку
они стремятся вызвать ток в направлении обхода.
А ,поскольку
они стремятся вызвать ток в направлении, противоположном направлению обхода.
Отрицательная ЭДС означает, что сторонние силы внутри источника совершают отрицательную
работу. Таким образом, ЭДС нашей цепи будет равна:
,поскольку
они стремятся вызвать ток в направлении, противоположном направлению обхода.
Отрицательная ЭДС означает, что сторонние силы внутри источника совершают отрицательную
работу. Таким образом, ЭДС нашей цепи будет равна:

В соответствии с правилами последовательного соединения, суммарное сопротивление цепи равно сумме внешнего сопротивления и внутренних сопротивлений всех источников тока:

Пример решения задачи.
Задача. К источнику тока с внутренним сопротивлением 1 Ом подключили резистор с сопротивлением 15 Ом. После этого в цепь включили амперметр, который показал, что сила тока равна 5 А. Найдите работу сторонних сил внутри источника, совершенную за 2 минуты.

Закон Ома для активного и пассивного участка линейной электрической цепи
Закон Ома для пассивного участка электрической цепи.
При протекании электрического тока через сопротивление R, напряжение U и ток I на этом участке связаны между собою согласно закону Ома:
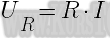
Сопротивление R — это коэффициент пропорциональности между током и напряжением. Чтобы найти сопротивление, нужно напряжение на участке электрической цепи разделить на ток, протекающий на этом же участке.
Закон Ома можно записать через разность потенциалов:
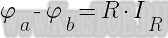
Закон Ома для активного участка электрической цепи.
Закон Ома для активного участка цепи между точками а и в имеет вид:
Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.
Пример составления уравнения по закону Ома
Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.
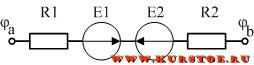
Пусть в данной электрической цепи направление тока будет из точки «a» в точку «b». Напряжение Uab Направляется всегда из первой буквы («a») к последней («b»).
Согласно правилу составления уравнения по закону Ома источник ЭДС E1 берем со знаком «плюс», т.к. его направление (направление стрелочки) совпадает с направлением протекающего тока.
Источник ЭДС E2 берем со знаком «минус», т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.
Напряжение Uab или разность потенциалов φa — φb берем со знаком «плюс», т.к. его направление совпадает с направление протекающего тока.
Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.
В результате составленное уравнение по закону Ома будет иметь вид:
Пусть потенциал в данной задаче потенциал точки «а» равен 10 вольт, потенциал точки «b» = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:
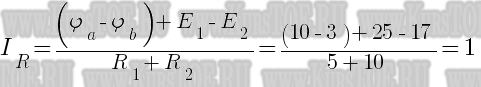
Полученный ток равен 1 Ампер.
Обобщенный закон Ома.
Закон
Ома выражаемый формулой ,
определяет зависимость между током и
напряжением на пассивном участке
электрической цепи.
,
определяет зависимость между током и
напряжением на пассивном участке
электрической цепи.
Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).
Из формулы 15 следует:
a-b=I(R1+R2)- E1+E2 (16)
На положительное напряжение на участке a – b Uab=a-b
Следовательно, Uab= I(R1+R2)- E1+E2 (17)
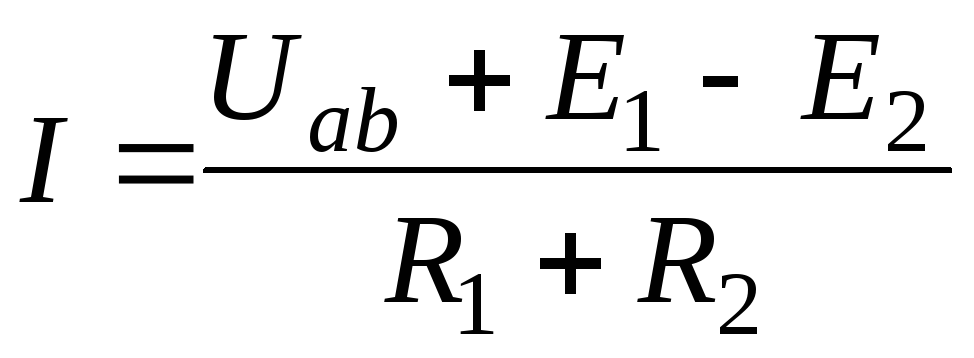 (18)
(18)
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.
Из формулы видно, что если ток, напряжение и э.д.с. совпадают по направлению, то в выражение закона Ома они входят с одинаковыми знаками. Если э.д.с. действует в сторону, противоположную положительному направлению тока, то в выражении ставится знак «-».
Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.
Пример № 1 построения потенциальной диаграммы:
Построить потенциальную диаграмму для одноконтурной схемы:
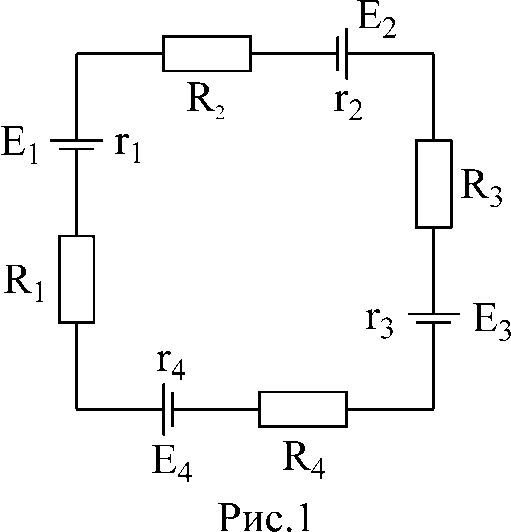
E1=25В; E2=5В; E3=20В; E4=35В,
R1=8 Ом; R2=24 Ом; R3=40 Ом; R4=4 Ом,
r1=2 Ом; r2=6 Ом; r3=2 Ом; r4=4 Ом.
Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1— r4) за их пределы; обозначим точки контура.
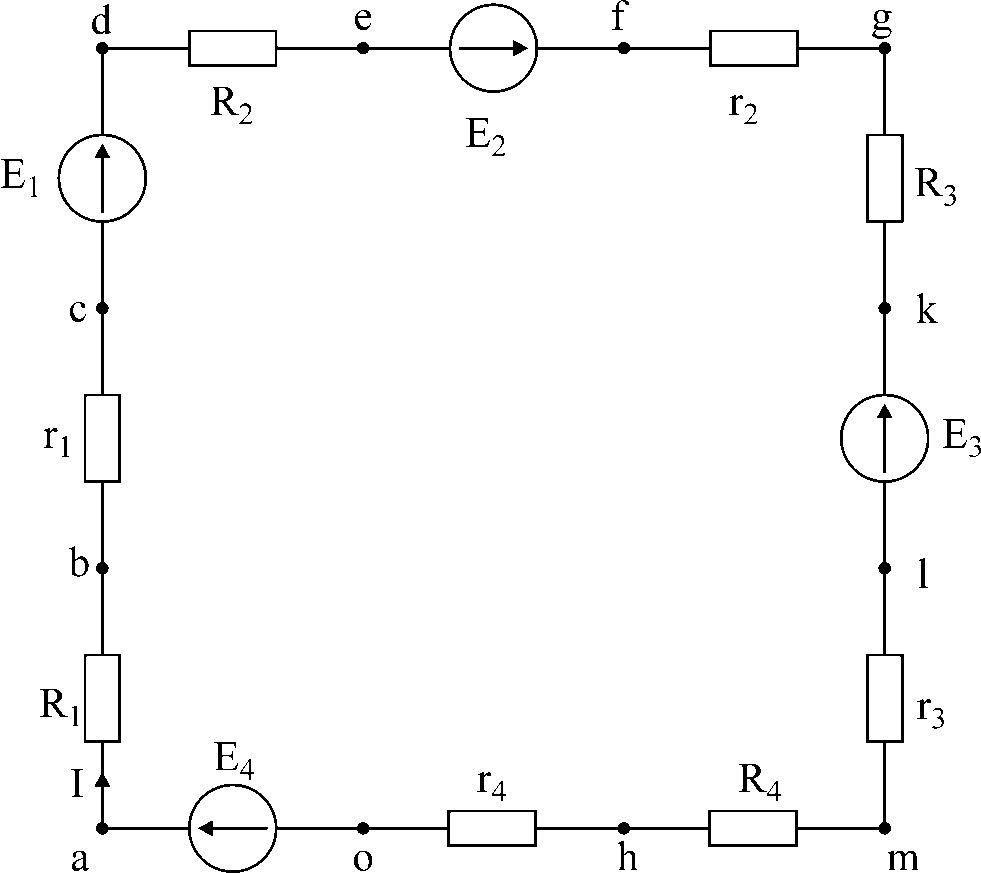
Рис.2
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:
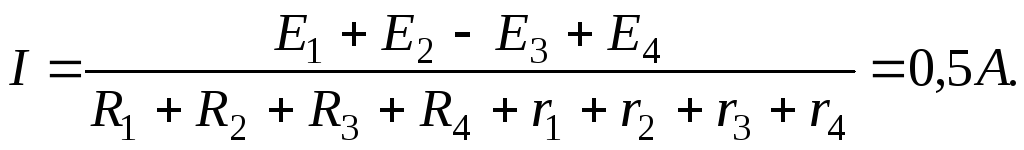
3. За базисную точку примем точку a. Найдем потенциалы остальных точек:
b= a– IR1 = — 4В e= d– IR2 = 8В
c= b– Ir1 = — 5В f= e+ E2 = 13В
d= c+ E1 = 20В q= f– Ir2 = 10В
k= q– IR3 = — 10В n= m– IR4 = — 33В
e = k – E3 = — 30В o = n – Ir4 = — 35В
m = e – Ir3 = — 31В a = o + E4 = 0
4. В системе координат строим потенциальную диаграмму:
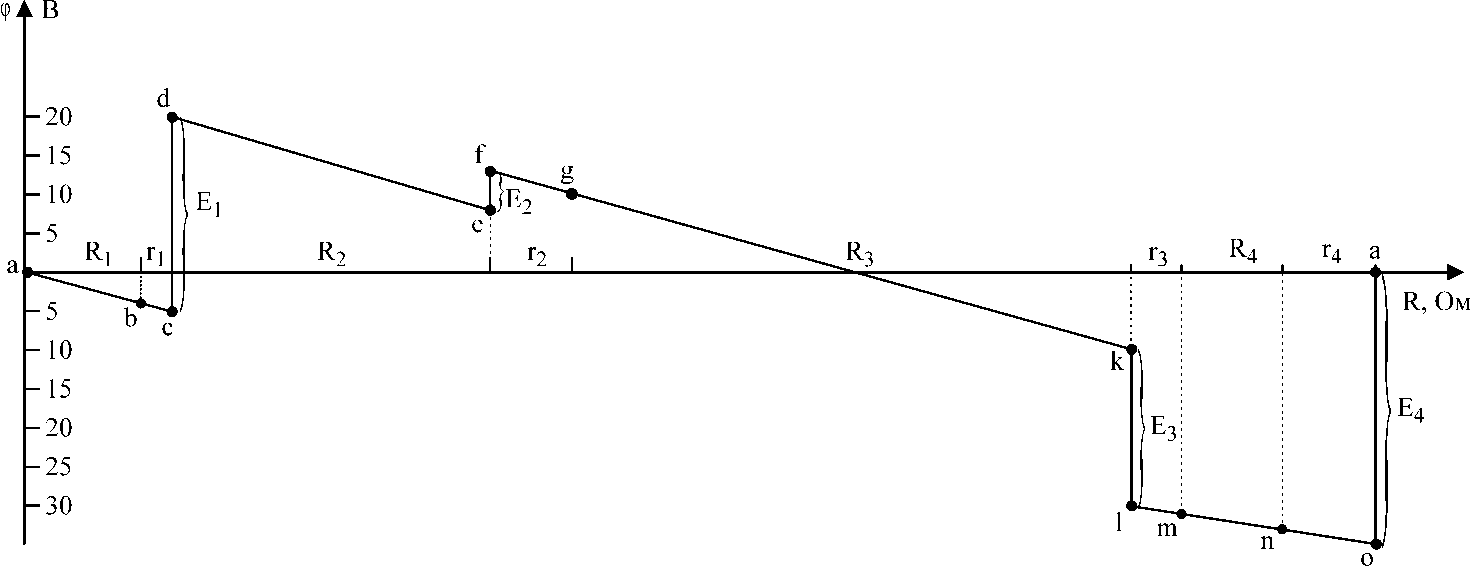
Законы Кирхгофа.
Распределение токов по ветвям электрической цепи подчиняется первому закону Кирхгофа, а распределение напряжений по участкам цепи подчиняется второму закону Кирхгофа.
Законы Кирхгофа наряду с законом Ома являются основными в теории электрических цепей.
Первый закон Кирхгофа:
Алгебраическая сумма токов в узле равна нулю:
i = 0 (19)
Где i — число ветвей, сходящихся в данном узле.
Т.е., суммирование распространяется на токи в ветвях, которые сходятся в рассматриваемом узле.

Рис.17. Иллюстрация к первому закону Кирхгофа.
Число уравнений, составляемых по первому закону Кирхгофа, определяется формулой:
Nуp = Nу – 1,
Где Nу – число узлов в рассматриваемой цепи.
Знаки токов в уравнении берутся с учетом выбранного положительного направления. Знаки у токов одинаковы, если токи одинаково ориентированы относительно данного узла.
Например, для узла, представленного на рис.17: припишем токам, подтекающим к узлу знаки «+», а к токам, оттекающим от узла – знаки «-».
Тогда уравнение по первому закону Кирхгофа запишется так:
I1 – I2 + I3 – I4 = 0.
Уравнения, составленные по первому закону Кирхгофа, называются узловыми.
Этот закон выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Второй закон Кирхгофа:
Алгебраическая сумма э.д.с. в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура:
Ui = Ei
IiRi=Ei(20)
Где i – номер элемента(сопротивления или источника напряжения) в рассматриваемом контуре.
**Число уравнений, составляемых по второму закону Кирхгофа, определяется формулой:
Nуp = Nb – Nу + 1 – Nэ.д.с.
Где Nb – число ветвей электрической цепи;
Nу — число узлов;
Nэ.д.с. — число идеальных источников э.д.с.
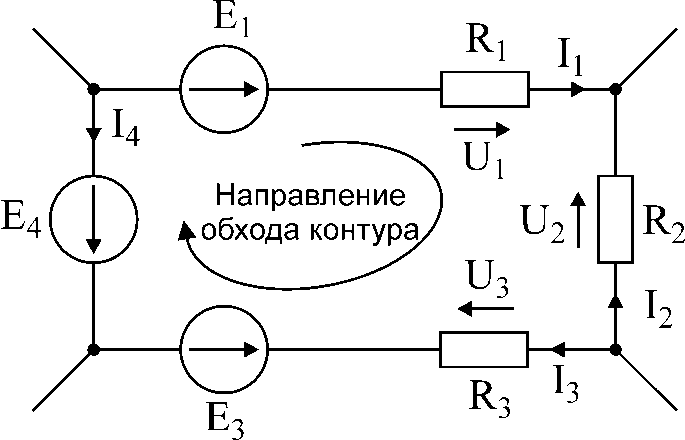
Рис.18. Иллюстрация ко второму закону Кирхгофа.
Для того, чтобы правильно записать второй закон Кирхгофа для заданного контура, следует выполнять следующие правила:
произвольно выбрать направление обхода контура, например, по часовой стрелке (рис.18).
э.д.с. и падения напряжения, которые совпадают по направлению с выбранным направлением обхода, записываются в выражении со знаком «+»; если э.д.с. и падения напряжения не совпадают с направлением обхода контура, то перед ними ставится знак «-».
Например, для контура рис.18, второй закон Кирхгофа запишется следующим образом:
U1 – U2 + U3 = E1 – E3 – E4 (21)
Уравнение (20) можно переписать в виде:
(Ui – Ei) = 0 (22)
Где (U – E) – напряжение на ветви.
Следовательно, второй закон Кирхгофа можно сформулировать следующим образом:
Алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Потенциальная диаграмма, рассмотренная ранее, служит графической интерпретацией второго закона Кирхгофа.
Задача №1.
В схеме рис.1 заданы токи I1 и I3, сопротивления и э.д.с. Определить токи I4, I5, I6 ; напряжение между точками a и b, если I1 = 10мA, I3 = -20 мA, R4 = 5kОм, E5 = 20B, R5 = 3kОм, E6 = 40B, R6 = 2kОм.
.
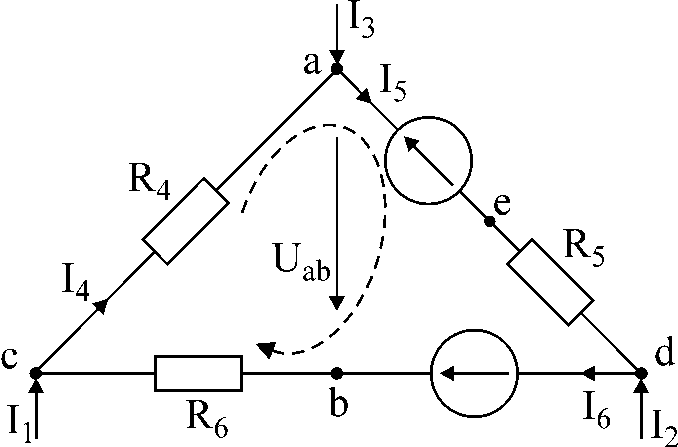
Рис.1
Решение:
Для заданного контура составим два уравнения по первому закону Кирхгофа и одно – по второму. Направление обхода контура указано стрелкой.
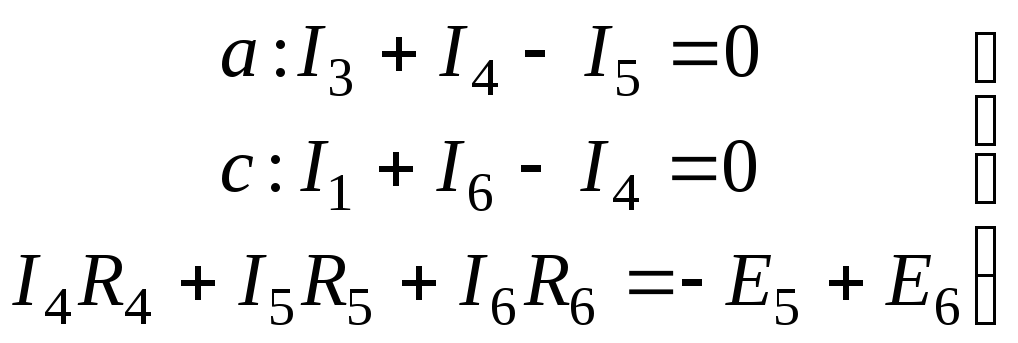
В результате решения получаем: I6 = 0; I4 = 10мA; I5 = -10мA
зададим направление напряжения между точками a и b от точки «a» к точке «b» — Uab. Это напряжение найдем из уравнения по второму закону Кирхгофа:
I4R4 + Uab + I6R6 = 0
Uab = — 50B.
Задача №2.
Для схемы рис.2 составить уравнения по законам Кирхгофа и определить неизвестные точки.
Дано: I1 = 20мA; I2 = 10мA
R1 = 5kОм, R3 = 4kОм, R4 = 6kОм, R5 = 2kОм, R6 = 4kОм.
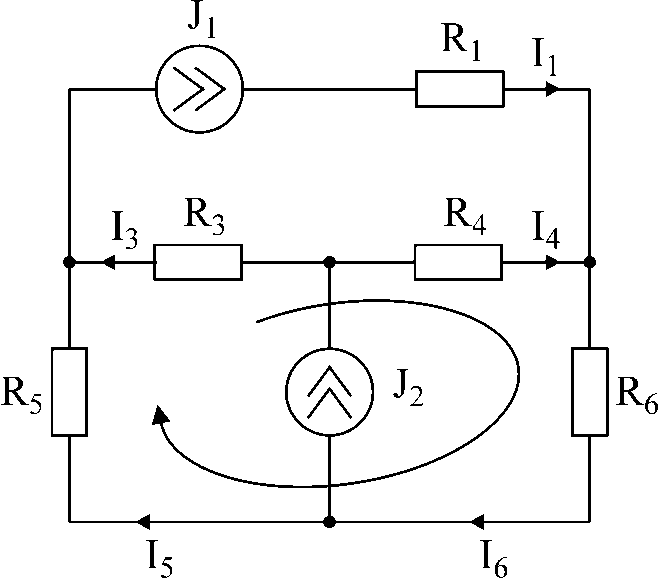
Рис.2
Решение:
Число узловых уравнений – 3, число контурных уравнений – 1.
Запомнить! При составлении уравнения по второму закону Кирхгофа выбираем контур, в который не входят источники тока. Направление контура указано на рисунке.
В данной цепи известны токи ветвей I1 и I2. Неизвестные токи I3, I4, I5, I6.
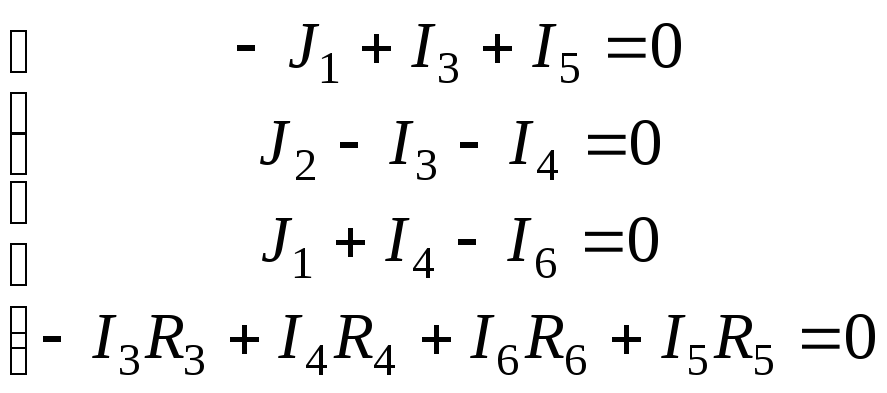
Решая систему, получаем: I3 = 13,75 мA; I4 = -3,75мA; I5 = 6,25мA; I6 = 16,25мA.
BILET_dlya_1_kursa_6_8_7
Закон Ома для участка цепи без ЭДС. Сопротивление проводника. Падение напряжения. Потеря напряжения.
Закон Ома был установлен экспериментально.
Для участка, который не содержит источника тока, и, следовательно, сторонние силы отсутствуют, и перемещение носителей происходит только под действием кулоновских сил, закон формулируется следующим образом.
Сила тока на однородном участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
С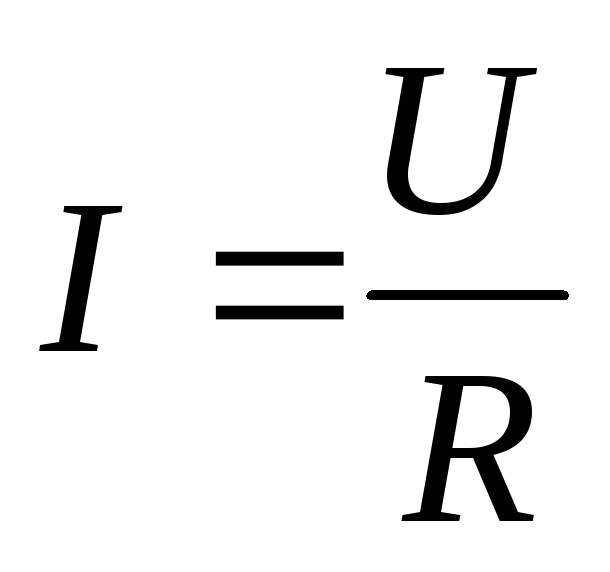 ила
тока – скалярная физическая величина, равная
отношению заряда q,
прошедшего через поперечное сечение
проводника за промежуток времени t,
к этому промежутку.
ила
тока – скалярная физическая величина, равная
отношению заряда q,
прошедшего через поперечное сечение
проводника за промежуток времени t,
к этому промежутку.
Е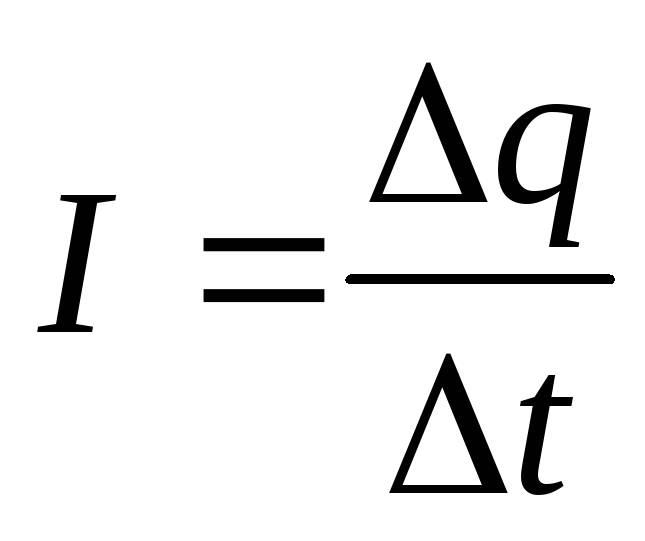 диница
измерения силы тока – 1 А. Это
сила такого неизменяющегося тока,
который, проходя по двум бесконечно
длинным прямолинейным параллельным
проводникам очень малого сечения,
расположенным на расстоянии 1 м друг от
друга в вакууме, вызывает силу
взаимодействия между ними 2 10-7 Н на каждый метр проводников.
диница
измерения силы тока – 1 А. Это
сила такого неизменяющегося тока,
который, проходя по двум бесконечно
длинным прямолинейным параллельным
проводникам очень малого сечения,
расположенным на расстоянии 1 м друг от
друга в вакууме, вызывает силу
взаимодействия между ними 2 10-7 Н на каждый метр проводников.
Н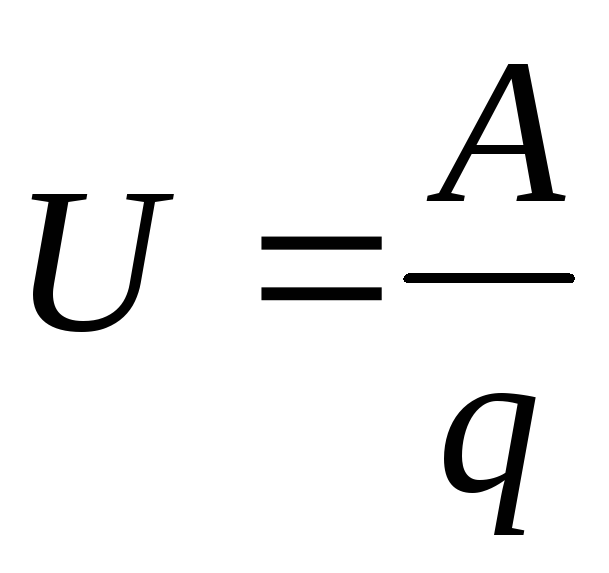 апряжением на участке
цепи называется скалярная физическая
величина, численно равная полной работе
А, которая совершается кулоновскими и
сторонними силами по перемещению вдоль
участка цепи единичного положительного
заряда.
апряжением на участке
цепи называется скалярная физическая
величина, численно равная полной работе
А, которая совершается кулоновскими и
сторонними силами по перемещению вдоль
участка цепи единичного положительного
заряда.
Е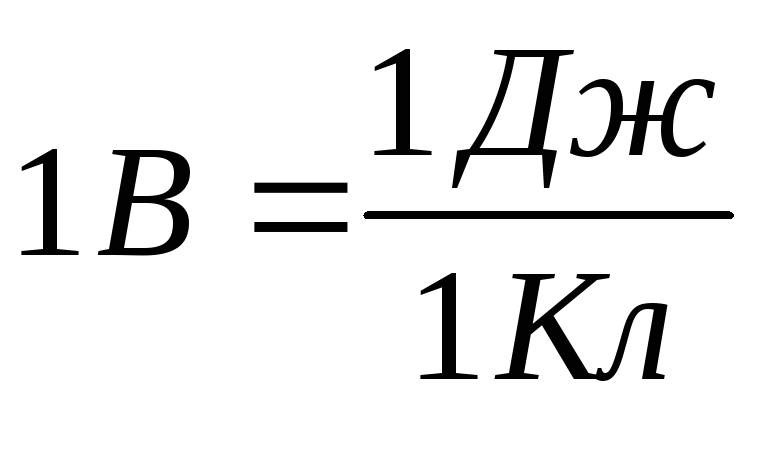 диница
измерения напряжения – 1 В.
диница
измерения напряжения – 1 В.
Электрическое сопротивление – физическая величина, характеризующая свойство проводника уменьшать скорость упорядоченного движения свободных носителей заряда в проводнике.
Сопротивление металла связано с рассеянием электронов проводимости на ионах кристаллической решётки и структурных неоднородностях (дефектах и примесях решётки).
Единица измерения сопротивления – 1 Ом. Проводник имеет сопротивление 1 Ом, если при напряжении 1 В сила тока в нём 1 А.
С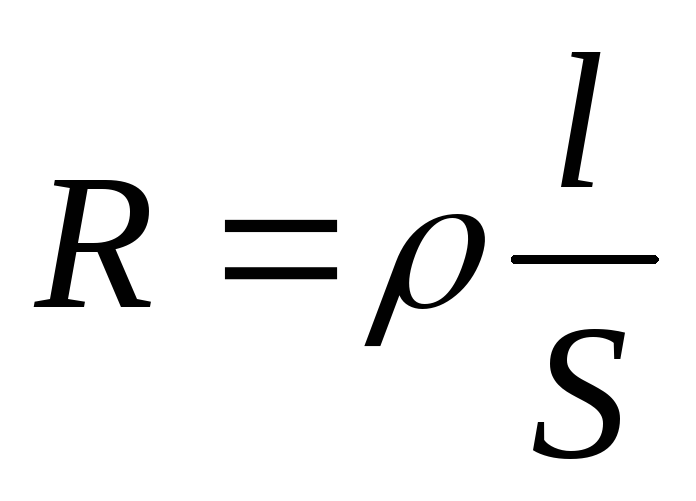 опротивление
зависит от рода вещества проводника,
его геометрических размеров и формы.
опротивление
зависит от рода вещества проводника,
его геометрических размеров и формы.
Где — удельное сопротивление проводника, l – длина проводника, S – сечение проводника.
Удельное сопротивление проводника зависит от вещества и температуры
г де
0 – удельное сопротивление проводника
при 00С,
— удельное сопротивление проводника
при t0C,
-температурный коэффициент сопротивления,
для чистых металлов он равен 1/273.
де
0 – удельное сопротивление проводника
при 00С,
— удельное сопротивление проводника
при t0C,
-температурный коэффициент сопротивления,
для чистых металлов он равен 1/273.
Сопротивление проводника определяет вид зависимости тока от напряжения.
Зависимость силы тока от напряжения называется вольт-амперной характеристикой. Для металлов это линейная зависимость.
Падением напряжения на резисторе называется напряжение, которое должно быть приложено к проводнику сопротивлением R, чтобы по нему протекал ток I. Оно равно
U=IR
Для однородного участка цепи падение напряжения равно напряжению.
Потерями напряжения называется падение напряжения на подводящих проводах.
БИЛЕТ 8
Работа и мощность электрического тока. Тепловое действие электрического тока. Закон Джоуля-Ленца.
Электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. При напряжении U между точками цепи работа электрического поля определяется выражением
A=qU
где q – переносимый заряд.
При постоянном токе q=It, где I – сила тока в проводнике, t — время прохождения тока. Тогда А=IUt
Работа тока на участке цепи равна произведению силы тока на напряжение на этом участке и на время прохождения тока.
Единица измерения работы тока – 1 Дж=1 В 1А 1 с
Е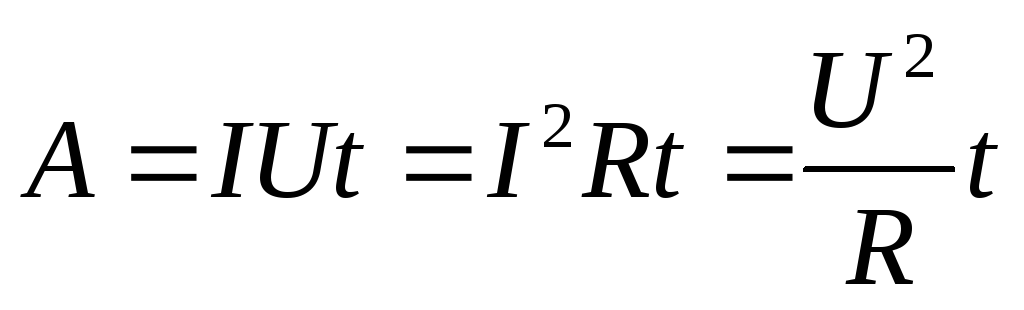 сли
ток протекает по однородному участку
цепи сопротивлением R,
то на основании закона Ома для однородного
участка цепи, можно получить следующие
формулы для расчёта работы тока
сли
ток протекает по однородному участку
цепи сопротивлением R,
то на основании закона Ома для однородного
участка цепи, можно получить следующие
формулы для расчёта работы тока
М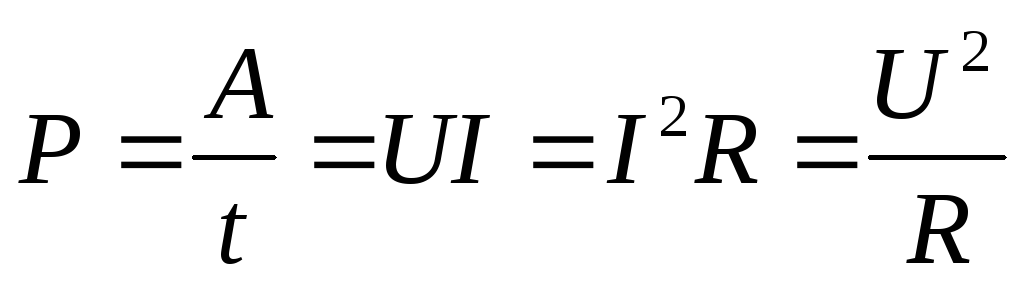 ощность
электрического тока равна работе, которая совершается током
за единицу времени
ощность
электрического тока равна работе, которая совершается током
за единицу времени
Единица измерения мощности – 1 Вт=1 Дж/1 с.
Внесистемная единица измерения работы тока – 1 киловатт-час. 1кВт ч=1000 Дж3600 с=3,6 106 Дж.
Под действием электрического поля электроны приобретают дополнительную кинетическую энергию. При соударении электрона с ионом решётки эта энергия полностью передаётся решётке и идёт на увеличение внутренней энергии проводника, т.е. проводник нагревается.
Количество теплоты, которое выделяется в проводнике при прохождении электрического тока, определяется законом Джоуля-Ленца.
Количество теплоты, выделяющееся в проводнике при прохождении электрического тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока.
Q=I2Rt
Если на участке цепи не совершается механическая работа и ток не производит химического действия, то вся работа тока затрачивается на нагревание проводника Q=А.
Е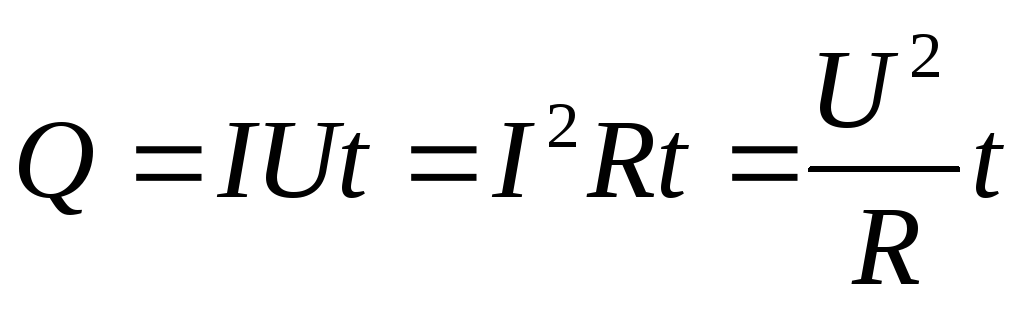 сли
участок цепи однородный, то на основании
закона Ома для однородного участка цепи
можно записать
сли
участок цепи однородный, то на основании
закона Ома для однородного участка цепи
можно записать
Если два проводника сопротивлениями R1 и R2 соединены последовательно, то
К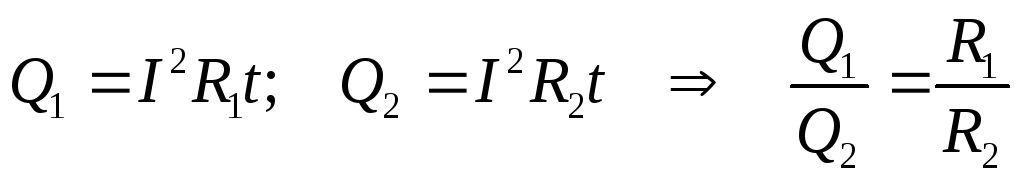 оличество
теплоты, выделяемое током на последовательно
соединённых проводниках, пропорционально
сопротивлениям этих проводников.
оличество
теплоты, выделяемое током на последовательно
соединённых проводниках, пропорционально
сопротивлениям этих проводников.
Если два проводника сопротивлениями R1 и R2 соединены параллельно, то
К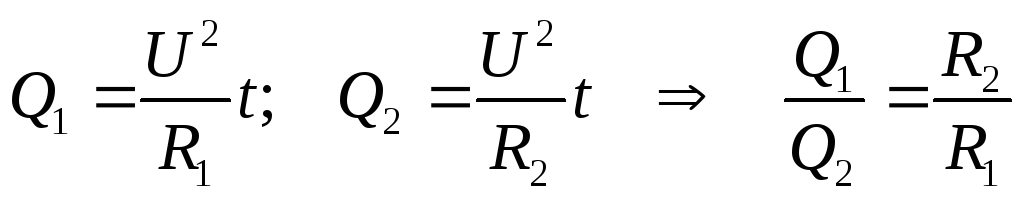 оличество
теплоты, выделяемое током на параллельно
соединённых проводниках, обратно
пропорционально сопротивлениям этих
проводников.
оличество
теплоты, выделяемое током на параллельно
соединённых проводниках, обратно
пропорционально сопротивлениям этих
проводников.
На законе Джоуля-Ленца основано действие многих электронагревательных приборов.
БИЛЕТ 7
Внешний и внутренний участки цепи. Закон Ома для замкнутой цепи с одной ЭДС.
Для существования постоянного тока в цепи необходимо поддерживать неизменную разность потенциалов на её концах. Эту функцию выполняет устройство, которое называется источником тока. Внутри источника тока за счёт сил неэлектростатической природы, так называемых сторонних сил, происходит перенос положительного заряда от меньшего потенциала к большему, т.е. происходит разделение зарядов, в результате которого на одном из полюсов источника накапливается положительный заряд, а на другом – отрицательный, т.е. поддерживается разность потенциалов между полюсами источника тока.
Характеристикой действия сторонних сил является электродвижущая сила – ЭДС.
ЭДС численно равна работе сторонних сил по перемещению единичного положительного заряда по замкнутой цепи.
Е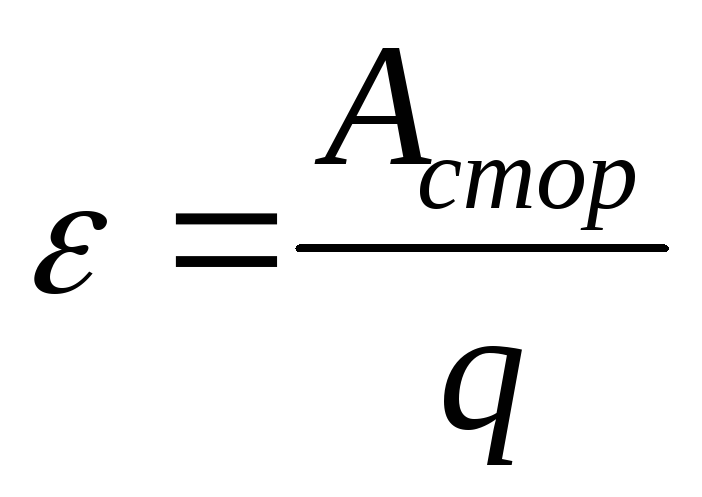 диница
измерения ЭДС – 1 В.
диница
измерения ЭДС – 1 В.
Замкнутая цепь состоит из внутренней и внешней частей. Внутренняя часть цепи представляет собой источник тока, обладающий внутренним сопротивлением r; внешняя – различные потребители, соединительные провода, приборы и т.д. с общим сопротивлением R.
Работа сторонних сил по перемещению по замкнутой цепи заряда q равна
Аст=q
Если в цепи не совершается механическая работа и ток не производит химического действия, то вся работа затрачивается на нагревание проводника.
По закону Джоуля-Ленца
Q=I2Rt+I2rt=I2(R+r)t
Т ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
Сила тока в замкнутой цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна полному сопротивлению цепи.
Если сопротивление внешней цепи стремится к нулю, то в цепи возникает максимально возможный ток, который называется током короткого замыкания.
З акон
Ома можно записать в следующем виде
акон
Ома можно записать в следующем виде
= IR+ I r=U+Ir
Это значит, что ЭДС источника равна сумме падений напряжений на внешнем и внутреннем участках замкнутой цепи.
Полная мощность источника
Р= I= I2(R+r)
Мощность, выделяемая на внешнем участке цепи, называется полезной мощностью
М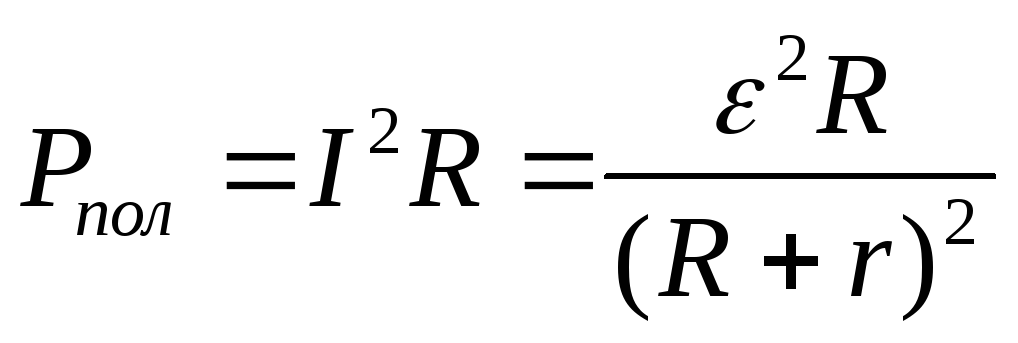 ощность,
выделяемая на внутреннем сопротивлении
в источнике тока, называется теряемой
мощностью
ощность,
выделяемая на внутреннем сопротивлении
в источнике тока, называется теряемой
мощностью
К
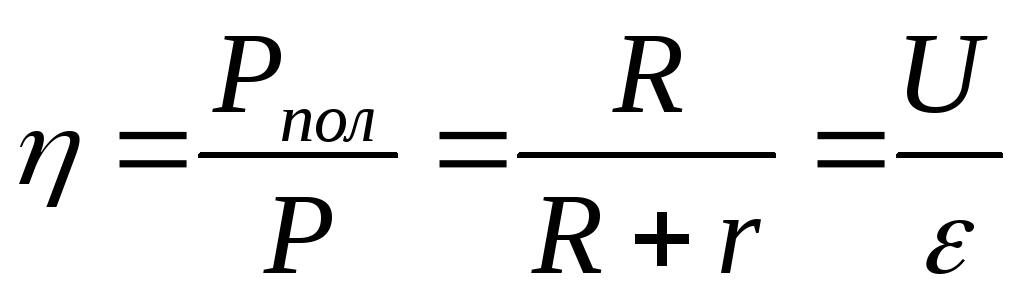 оэффициент
полезного действия источника тока
равен отношению полезной мощности Рпол к полной мощности Р
оэффициент
полезного действия источника тока
равен отношению полезной мощности Рпол к полной мощности Р


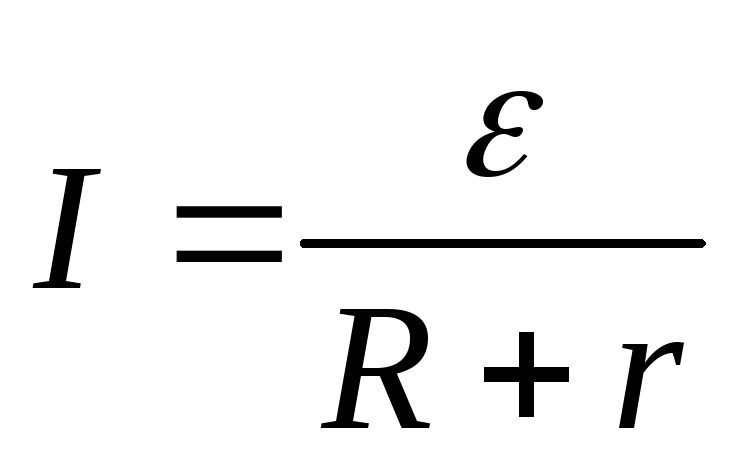 ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи
ак
как Аст= Q, то q=
It=
I2(R+r)t
и =
I(R+r). Отсюда получаем закон Ома для
замкнутой цепи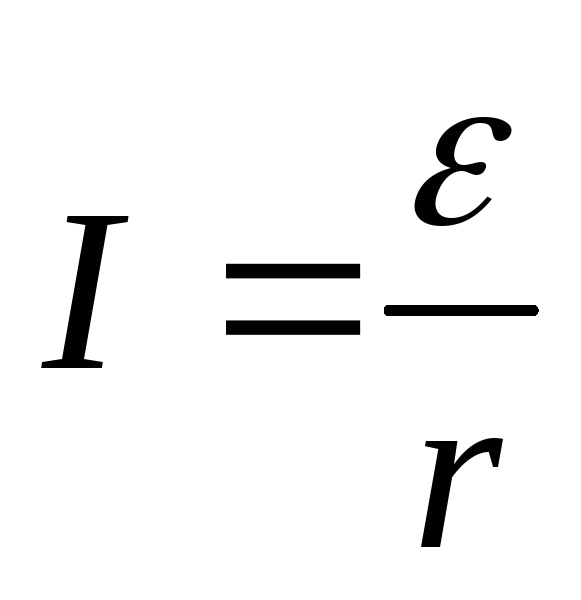 акон
Ома можно записать в следующем виде
акон
Ома можно записать в следующем виде