как рассчитать по току и напряжению, формула
Содержание:
-
Что такое плоские конденсаторы
- Описание и технические характеристики
-
Как найти его емкость, формулы
- Способы расчета по току и напряжению
Содержание
-
Что такое плоские конденсаторы
- Описание и технические характеристики
-
Как найти его емкость, формулы
- Способы расчета по току и напряжению
Что такое плоские конденсаторы
Определение
Конденсатор — это устройство для накопления заряда и энергии электрического поля.
Определение
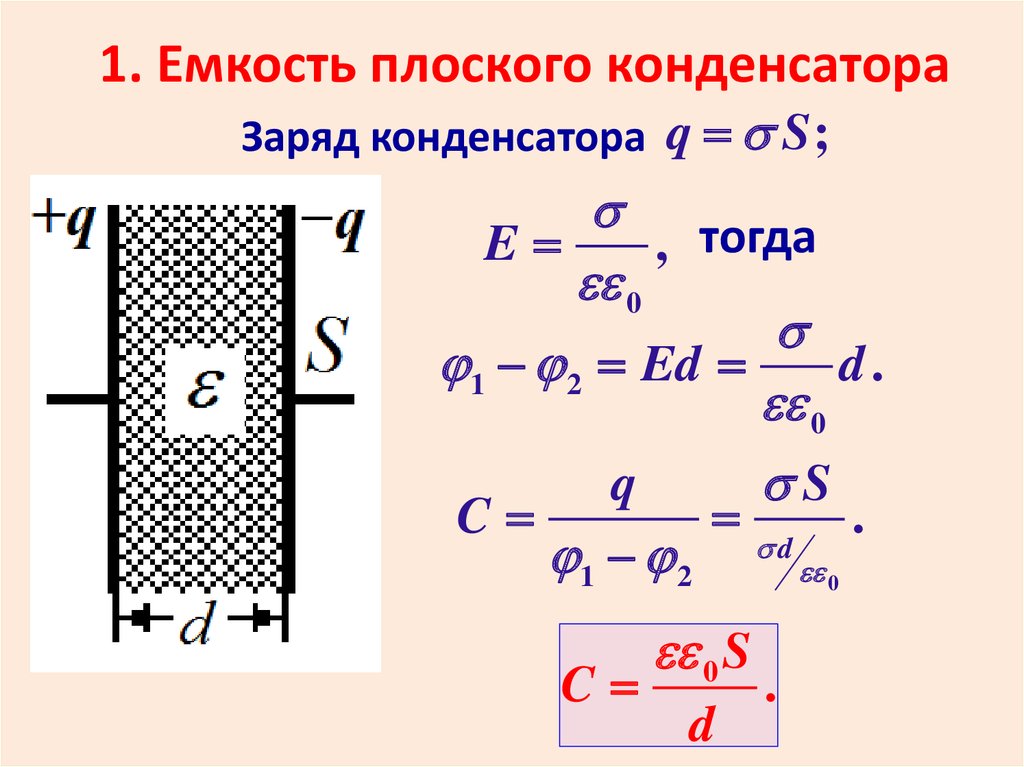
Плоский конденсатор — конденсатор, который представляет собой две параллельные проводящие плоскости (обкладки), которые разделяет небольшой промежуток, заполненный диэлектриком. На обкладках сосредоточены равные по модулю и противоположные по знаку заряды.
Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.
Описание и технические характеристики
Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.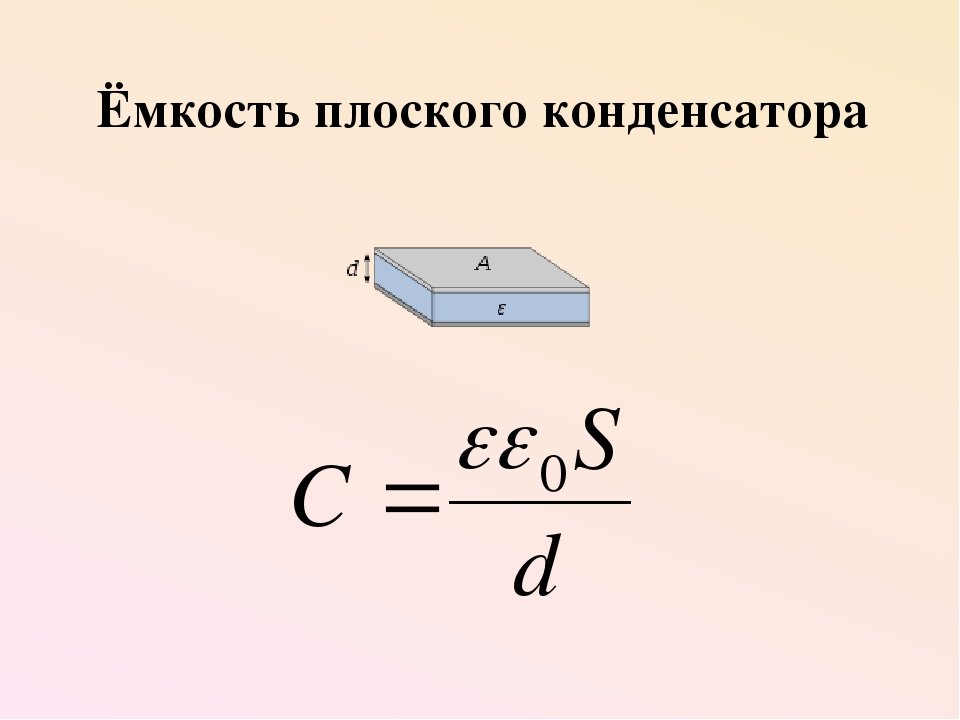
Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд.
Конденсатор обладает следующими техническими параметрами:
- номинальной и реальной емкостью — заявленной и фактической способностью накапливать заряд;
- удельной емкостью — отношением емкости к массе или объему диэлектрика;
- плотностью энергии;
- номинальным напряжением;
- полярностью — электролитические конденсаторы требуют корректной полярности напряжения для безопасной работы;
- электрическим сопротивлением изоляции диэлектрика;
- временем самостоятельной потери заряда;
- эквивалентным последовательным сопротивлением — внутренним электрическим сопротивлением диэлектрика, материала обкладок, выводов, контактов;
- эквивалентной последовательной индуктивностью и собственной частотой резонанса;
- температурным коэффициентом емкости — относительным изменением емкости при изменении температуры окружающей среды;
- диэлектрической абсорбцией — поглощением и сохранением части заряда при быстрой разрядке;
- пьезоэффектом — генерацией напряжения на обкладках при механических деформациях.
 {-12}\;\frac Фм\).
{-12}\;\frac Фм\).Таким образом, емкость плоского конденсатора легко изменить, погрузив его в жидкость или иную среду с нужной диэлектрической проницаемостью.
Способы расчета по току и напряжению
Конденсатор — это два проводящих тела, которые разделены диэлектриком. Они несут равные по величине и противоположные по знаку заряды \(q_1\) и \(q_2 \) имеют потенциалы \(\varphi_1\) и \(\varphi_2\).
Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника \(\varphi.\) Их зависимость выражается формулой:\(С\;=\;\frac qU\)
Где U — разность потенциалов тел, т. е. обкладок конденсатора, или напряжение на конденсаторе.
Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Оно вычисляется по формуле:
\( U\;=\;\varphi2\;-\;\varphi_1\)
Заряд измеряется в
 Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:\(q\;=\;I\;\times\;t\)
Когда конденсатор включен в колебательный контур, то, зная период электромагнитных колебаний T и индуктивность катушки контура L, можно вычислить емкость, воспользовавшись формулой Томсона:
\(T\;=\;2\mathrm\pi\sqrt{\mathrm{LC}}\)
При решении задач часто требуется вычислить емкости каждого конденсатора в цепи
При параллельном соединении:\({\mathrm С}_{\mathrm{общ}\;}\;=\;{\mathrm С}_1\;+\;{\mathrm С}_2\;+\;{\mathrm С}_{3\;}+\;…\;+\;{\mathrm С}_{\mathrm n}\)
При последовательном:
\(\frac{1\;}{{\mathrm С}_{\mathrm{общ}\;}}=\;\frac1{{\mathrm С}_1}\;+\;\frac1{{\mathrm С}_2}\;+\;\frac1{{\mathrm С}_{3\;}}+\;.

Примечание
Эти формулы справедливы для любого конденсатора, не только для плоского.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)Буховцев Б.Б., Климонтович Ю.Л., Мякишев Г.Я. Физика. 9 класс. Учебник. — 6-е изд. — М.: Просвещение, 1982. — 272 с.
В учебнике на современном уровне изложены фундаментальные вопросы школьной программы, представлены основные технические применения законов физики, рассмотрены методы решения задач.
 Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз.
Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз.
Оглавление
ТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКА
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ. РАЗМЕРЫ МОЛЕКУЛ
2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО
3. БРОУНОВСКОЕ ДВИЖЕНИЕ.
4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ
5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ
6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ
7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ I
Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ
8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА
9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ
10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
12. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ
14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ III
Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
16. РАБОТА В ТЕРМОДИНАМИКЕ
17. КОЛИЧЕСТВО ТЕПЛОТЫ
18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ
20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ
21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ IV
Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ
23. НАСЫЩЕННЫЙ ПАР
24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА
25. ВЛАЖНОСТЬ ВОЗДУХА
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ V
Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ
27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ VI
Глава VII. ТВЕРДЫЕ ТЕЛА
29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА
30. АМОРФНЫЕ ТЕЛА
31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ
32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ
33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ VII
ОСНОВЫ ЭЛЕКТРОДИНАМИКИ
34. ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?
Глава VIII. ЭЛЕКТРОСТАТИКА
35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ
37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА
39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ
41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ
43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ
46. ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ
48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ
50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА
51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ
52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
53. ЭЛЕКТРОЕМКОСТЬ. ЕДИНИЦЫ ЭЛЕКТРОЕМКОСТИ
54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА
55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ X
Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА
57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА
58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ
59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ
60. СВЕРХПРОВОДИМОСТЬ
61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ
63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА
65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ IX
Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ
66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ
67. ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ
68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ
69. ЗАКОН ЭЛЕКТРОЛИЗА
70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ
71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ
72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ
73. ПЛАЗМА
74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ
75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД
76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА
77. ЭЛЕКТРИЧЕСКИЙ ТОК В ПОЛУПРОВОДНИКАХ
78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ
79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ
80. ПОЛУПРОВОДНИКОВЫЙ ДИОД
ПОЛУПРОВОДНИКОВЫЙ ДИОД
81. ТРАНЗИСТОР
82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ
КРАТКИЕ ИТОГИ ГЛАВЫ X
Глава XI. МАГНИТНОЕ ПОЛЕ
83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ
84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ
85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ
86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК
88. ЗАКОН АМПЕРА
89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД. СИЛА ЛОРЕНЦА
90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ XI
Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА
93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ
96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ
97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
КРАТКИЕ ИТОГИ ГЛАВЫ XII
ЗАКЛЮЧЕНИЕ
ЛАБОРАТОРНЫЕ РАБОТЫ
ОТВЕТЫ К УПРАЖНЕНИЯМ
электростатика — Почему свернутые конденсаторы можно моделировать как плоские параллельные пластины?
спросил
Изменено 2 года, 7 месяцев назад
Просмотрено 4к раз
$\begingroup$
Если у вас есть две параллельные пластины противоположного заряда с диэлектриком между ними, то
Емкость $$ C = \dfrac{A \epsilon_{0}}{d} K$$ Где $K$ — диэлектрическая проницаемость.

Используется для расчета емкости конденсатора. Однако настоящий конденсатор на самом деле представляет собой две пластины, скрученные много раз. Разве электрическое поле $ \vec{E} $ не будет другим?
Так почему уравнение для емкости все еще верно?
- электростатика
- емкость
$\endgroup$
0
$\begingroup$
Вы по-прежнему можете использовать эту формулу, если параллельные пластины прокатываются достаточное количество раз, так что кривизна пластин минимальна. Следовательно, эта формула по-прежнему верна. Помните, что эта формула даже в случае реальных параллельных пластин требует, чтобы $A >> d$. Значит, это не точно. Существует также краевая проблема: близкая к границе конденсатора $\vec{E}$ не перпендикулярна обкладкам.
Все это говорит о том, что это уравнение является приблизительным.
 Насколько это хорошее приближение? Это инженерный вопрос. В лаборатории $C$ зависит от отношения $\frac{A}{d}$, величины V и, да, от кривизны пластин, если они свернуты.
Насколько это хорошее приближение? Это инженерный вопрос. В лаборатории $C$ зависит от отношения $\frac{A}{d}$, величины V и, да, от кривизны пластин, если они свернуты.$\endgroup$
2
$\begingroup$
Я думаю, что емкость свернутого конденсатора в два раза больше емкости плоского конденсатора с равной площадью поверхности — это основано на том факте, что после скручивания каждый слой имеет две поверхности, обращенные к противоположно заряженной поверхности (той, которая находится выше и один ниже). Таким образом, будут + — — + + — — + + и т. д. слои.
Не знаю, помогло ли это, но стоит моих пяти центов…
$\endgroup$
$\begingroup$
Ответ на вопрос заключается в том, что они не используют эту формулу для расчета емкости скрученных конденсаторов.
 Определение емкости проводника – это количество заряда, необходимого для приведения проводника к электрическому потенциалу, $V$, пропорциональному потенциалу: $$Q = CV,$$, а константа пропорциональности – это емкость. Например, изолированная проводящая сфера радиуса $R$ имеет емкость: $C = 4\pi R \epsilon_0$. Вы можете сделать аналогичный расчет, чтобы показать, что емкость на единицу длины бесконечно длинного цилиндра с радиусом $a$ внутри заземленного цилиндра с радиусом $b$ равна: $$\frac{C}{L} = \frac{ 2\pi\epsilon_0}{\ln\left(\frac{b}{a}\right)}.$$
Определение емкости проводника – это количество заряда, необходимого для приведения проводника к электрическому потенциалу, $V$, пропорциональному потенциалу: $$Q = CV,$$, а константа пропорциональности – это емкость. Например, изолированная проводящая сфера радиуса $R$ имеет емкость: $C = 4\pi R \epsilon_0$. Вы можете сделать аналогичный расчет, чтобы показать, что емкость на единицу длины бесконечно длинного цилиндра с радиусом $a$ внутри заземленного цилиндра с радиусом $b$ равна: $$\frac{C}{L} = \frac{ 2\pi\epsilon_0}{\ln\left(\frac{b}{a}\right)}.$$Таким образом, скрученный конденсатор с двумя переплетенными спиралями будет иметь несколько сложное выражение для емкости, которое, вероятно, может быть рассчитано только численно, если требуется предсказание заданной формы. На практике я могу предположить, что фирмы, ответственные за изготовление этих устройств, имеют эмпирические измерения емкости для свернутых геометрий в зависимости от таких факторов, как натяжение обмотки, длина цилиндра и т.
 д.
д.Хотя выражение для цилиндра простое превратиться в приближение, сводящееся к $C = \epsilon_0 A/d$, если использовать $b=d + a$ и $d \ll a$. Итак, пока расстояние между спиралями намного меньше, чем все из:
- ширина пластин,
- длина спиралей, а
- радиус кривизны спирали для всей кривой,
приближение параллельной пластины должно работать. Несоблюдение этих условий приводит к отклонению от приближения, но не от основного определения емкости, $Q = CV$.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электростатики — Емкость одной заряженной пластины?
Ответ Тома полностью правильный, но я хотел добавить к нему некоторые детали.
Во-первых, почему ваша логика не работает? Ответ заключается в том, что известная формула для емкости двух параллельных пластин основана на приближении, что электрическое поле между двумя пластинами полностью однородно. В таком случае имеем $E = V/d$ и $E = Q/\epsilon_0 A$; приравняв два выражения друг к другу и решив $C = Q/V$, мы получим известную формулу для емкости пары параллельных пластин.
Однако, если мы возьмем две пластины и начнем их раздвигать, то в какой-то момент наши предположения об электрическом поле перестанут работать; электрическое поле перестанет быть однородным и уж точно не будет связано с зарядом на обкладках указанным выше образом. Обычно это приближение действительно начинает давать сбои, когда $d$ становится значительной долей размера пластин; как только это произойдет, формула параллельных пластин будет плохим приближением.
 Иными словами, известная формула емкости с параллельными пластинами была получена в предположении, что $d \ll \sqrt{A}$, и, следовательно, вы не можете принять ее предел как $d \to \infty$ и при этом ожидать его держать.
Иными словами, известная формула емкости с параллельными пластинами была получена в предположении, что $d \ll \sqrt{A}$, и, следовательно, вы не можете принять ее предел как $d \to \infty$ и при этом ожидать его держать.Итак, представьте, что два диска перемещаются на большое расстояние друг от друга. В какой-то момент они окажутся достаточно далеко друг от друга, чтобы больше не «чувствовать» друг друга, и в этот момент каждая пластина будет действовать как независимый заряженный проводник, одиноко стоящий в пространстве. Но между каждым проводником и бесконечностью все еще будет разность потенциалов, и в этот момент мы можем определить емкость этого одинокого проводника и другого «электрода в бесконечности». Поскольку мы обычно определяем $V = 0$ на бесконечности, нам просто нужно вычислить потенциал проводника, когда он несет заряд $Q$, и снова взять отношение $Q/V$. Это процесс, описанный @tom в его ответе.
Теперь, для проводника произвольной формы у вас возникнут проблемы с получением точного результата для $C$.



 {-12}\;\frac Фм\).
{-12}\;\frac Фм\).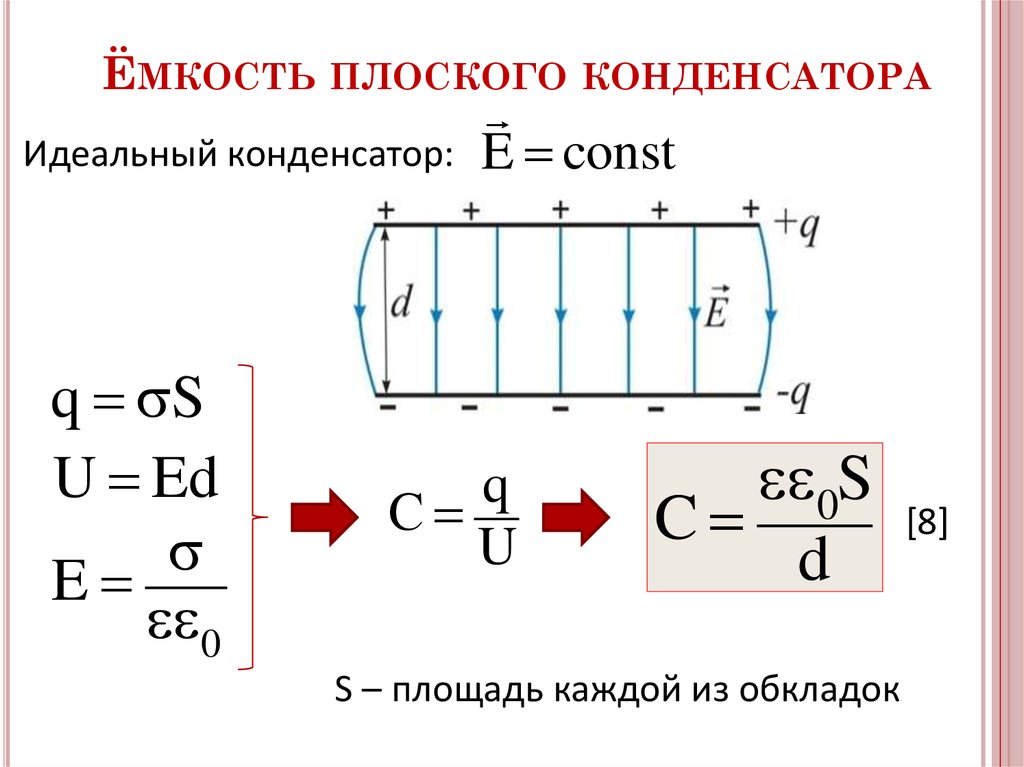 Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
Таким образом, зная силу тока и время зарядки конденсатора в секундах, можно произвести вычисление по формуле:
 Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз.
Книга адресована учащимся средних школ, слушателям и преподавателям подготовительных отделений вузов, а также читателям, занимающимся самообразованием и готовящимся к поступлению в вуз.
 УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ
УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ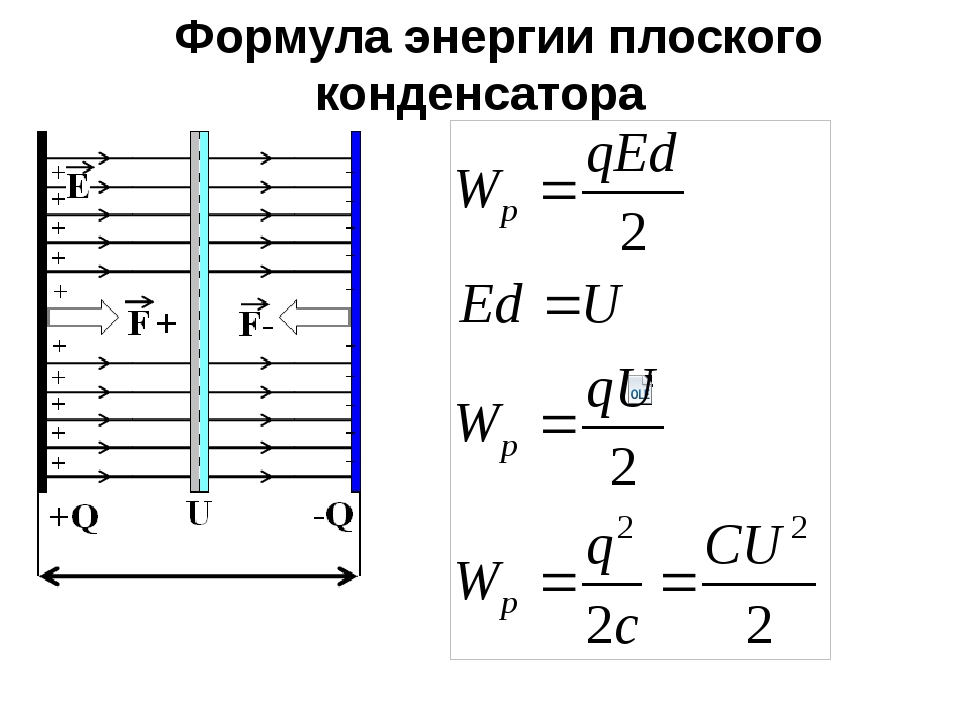 СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ
ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ. ДВА ВИДА ДИЭЛЕКТРИКОВ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ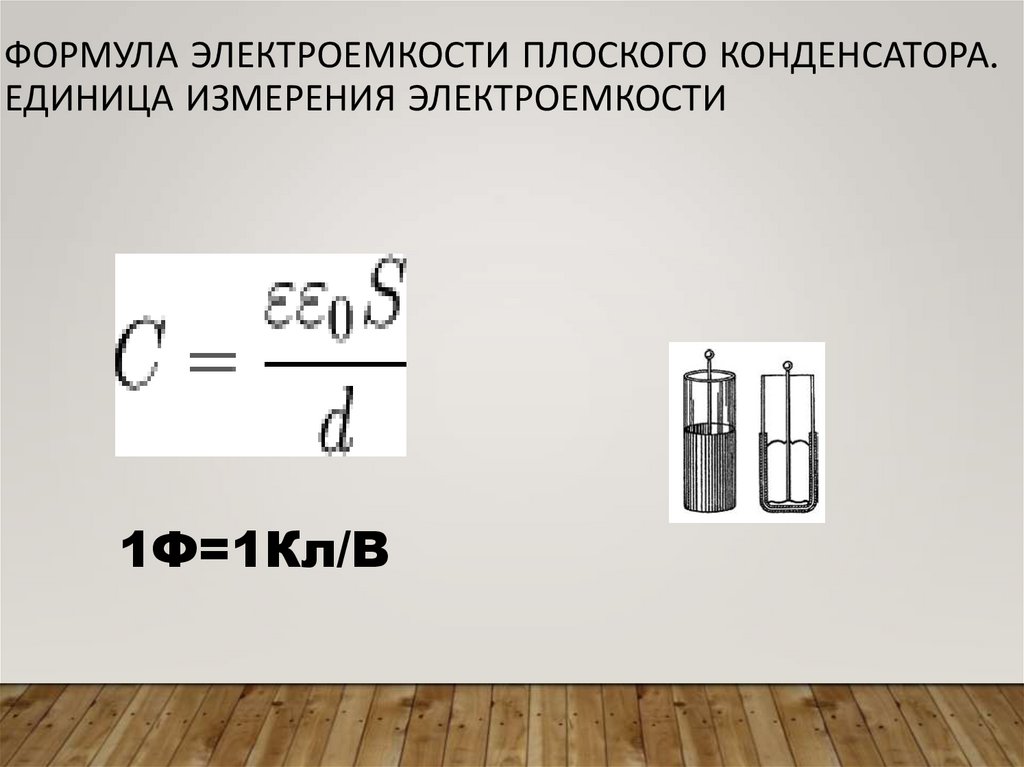 ПОЛУПРОВОДНИКОВЫЙ ДИОД
ПОЛУПРОВОДНИКОВЫЙ ДИОД
 Насколько это хорошее приближение? Это инженерный вопрос. В лаборатории $C$ зависит от отношения $\frac{A}{d}$, величины V и, да, от кривизны пластин, если они свернуты.
Насколько это хорошее приближение? Это инженерный вопрос. В лаборатории $C$ зависит от отношения $\frac{A}{d}$, величины V и, да, от кривизны пластин, если они свернуты. Определение емкости проводника – это количество заряда, необходимого для приведения проводника к электрическому потенциалу, $V$, пропорциональному потенциалу: $$Q = CV,$$, а константа пропорциональности – это емкость. Например, изолированная проводящая сфера радиуса $R$ имеет емкость: $C = 4\pi R \epsilon_0$. Вы можете сделать аналогичный расчет, чтобы показать, что емкость на единицу длины бесконечно длинного цилиндра с радиусом $a$ внутри заземленного цилиндра с радиусом $b$ равна: $$\frac{C}{L} = \frac{ 2\pi\epsilon_0}{\ln\left(\frac{b}{a}\right)}.$$
Определение емкости проводника – это количество заряда, необходимого для приведения проводника к электрическому потенциалу, $V$, пропорциональному потенциалу: $$Q = CV,$$, а константа пропорциональности – это емкость. Например, изолированная проводящая сфера радиуса $R$ имеет емкость: $C = 4\pi R \epsilon_0$. Вы можете сделать аналогичный расчет, чтобы показать, что емкость на единицу длины бесконечно длинного цилиндра с радиусом $a$ внутри заземленного цилиндра с радиусом $b$ равна: $$\frac{C}{L} = \frac{ 2\pi\epsilon_0}{\ln\left(\frac{b}{a}\right)}.$$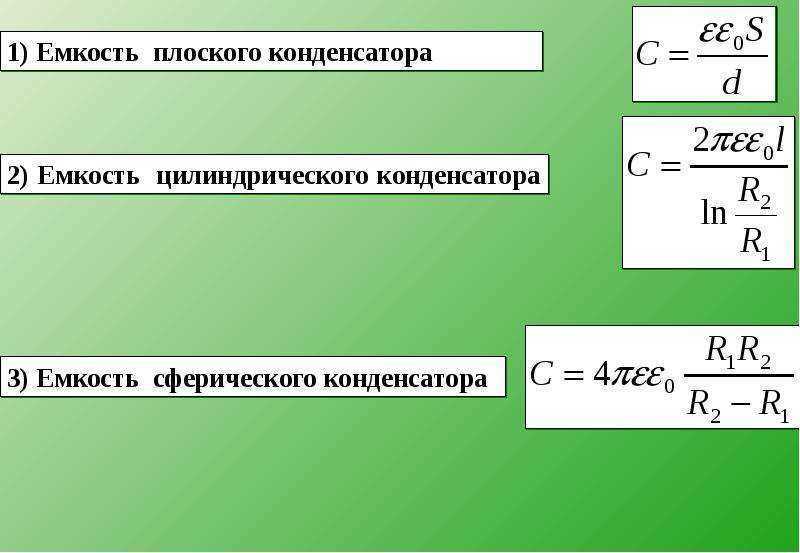 д.
д.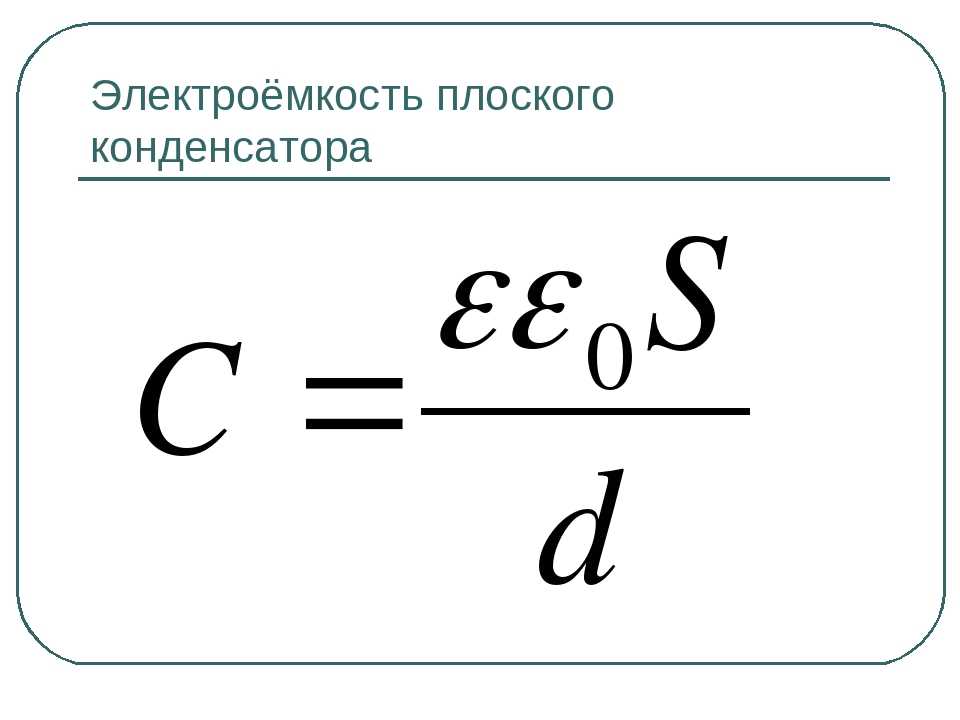
 Иными словами, известная формула емкости с параллельными пластинами была получена в предположении, что $d \ll \sqrt{A}$, и, следовательно, вы не можете принять ее предел как $d \to \infty$ и при этом ожидать его держать.
Иными словами, известная формула емкости с параллельными пластинами была получена в предположении, что $d \ll \sqrt{A}$, и, следовательно, вы не можете принять ее предел как $d \to \infty$ и при этом ожидать его держать.