12.1. Первое уравнение Максвелла
Оно является обобщением закона электромагнитной индукции ,
и в интегральной форме имеет следующий вид (5)
и утверждает.что с переменным магнитным полем неразрывно связано вихревое электрическое поле, которое не зависит оттого находятся в нем проводники или нет. Из (3) следует, что . (6)
Из сравнения (5) и (6) находим, что (7)
Это и есть первое уравнение Максвелла в дифференциальной форме.
12.2. Ток смещения. Второе уравнение Максвелла
Максвелл обобщил закон полного тока предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитного поля. Для количественной характеристики «магнитного действия» переменного электрического поля Максвелл ввел понятие

По теореме Гаусса — Остроградского поток электрического смещения сквозь замкнутую поверхность
Продифференцировав это выражение по времени, получим для неподвижной и недеформирусмой поверхности S (8)
Левая часть этой формулы имеет размерность тока, который, как известно, выражается через вектор плотности тока . (9)
Из сравнения (8) и (9) следует, что имеет размерность плотности тока: А /м2.Максвелл предложил назвать плотностью тока смещения:
. (10)
Ток смещения . (11)
Из
всех физических свойств, присущих
действительному току (току проводимости),
связанному с переносом зарядов, ток
смещения обладает лишь одним: способностью
создавать магнитное поле. При
«протекании» тока смещения в
вакууме или диэлектрике не выделяется
тепло. Примером тока смещения может
служить переменный ток через конденсатор.
В
общем случае токи проводимости и
смещения не разделены в пространстве
и можно говорить о полном токе, равном
сумме токов проводимости и смещения:
При
«протекании» тока смещения в
вакууме или диэлектрике не выделяется
тепло. Примером тока смещения может
служить переменный ток через конденсатор.
В
общем случае токи проводимости и
смещения не разделены в пространстве
и можно говорить о полном токе, равном
сумме токов проводимости и смещения:
С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смещения . (13)
Итак, второе уравнение Максвелла в интегральной форме имеет вид:
. (14)
Из (3) следует, что . (15)
Из
сравнения
(14)
и
(15)
находим, что
. (16)
(16)
Это и есть второе уравнение Максвелла в дифференциальной форме.
12.3. Третье и четвертое уравнения Максвелла
Максвелл обобщил теорему Гаусса — Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид: . (I7)или
где — объемная плотность свободных зарядов, [] = Кл / м3
Из (1) следует, что . (19)
Из сравнения (18) и (19) находим,что . (20)
Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет
следующий
вид: ,(21)
. (22)
(22)
Уравнения Максвелла в дифференциальной форме
; (2.5)
; (2.6)
; (2.7)
. (2.8)
Первое уравнение Максвелла в дифференциальной форме (2.5) показывает, что вихревое магнитное поле создается как плотностью тока проводимости, так и тока смещения.
Второе уравнение Максвелла в дифференциальной
Третье и четвертое уравнения Максвелла в дифференциальной форме отражают наличие носителей у электрического поля (2.7) и отсутствие носителей у магнитного поля (2.8).
Уравнением непрерывности называют дифференциальную форму закона сохранения заряда
. (2.9)
(2.9)
Из (2.9) следует, что в точках, являющихся
Уравнения Максвелла в комплексной форме. В радиотехнике часто используются гармонические колебания. В линейных системах удобно использовать метод комплексных амплитуд. В этом случае от реального сигнала cos (t+z) с помощью добавления мнимой составляющей isin (t+z) по формуле Л. Эйлера переходят к комплексному представлению
Когда анализ завершен, для получения окончательного ответа из комплексного результата достаточно выделить действительную часть.
В комплексной форме операции интегрирования и дифференцирования по времени существенно упрощаются
;
;. (2.10)
(2.10)
Комплексную амплитуду (кроме амплитуды в нее входит и начальная фаза) будем обозначать точкой сверху. В комплексной форме уравнения (2.5) и (2.6) будут иметь вид
; (2.12)
, . (2.13)
Введение делает уравнения (2.11) и (2.12) похожими.
. (2.14)
Тангенс угла диэлектрических потерь. Для оценки соотношения между током проводимости и током смещения удобно ввести величину тангенс угла диэлектрических потерь
==. (2.15)
В зависимости от значения tg среды можно классифицировать так:
– диэлектрик;
– полупроводящая среда;
– проводник.
(2.16)
Из
уравнения (2.15) следует, что tg зависит
от частоты. Это значит, что одно и то же
вещество может на НЧ вести себя как
проводник, а на ВЧ – как диэлектрик.
Например, морская вода с параметрами = 1 См/м и = 80 на частотах менее 23 МГц проявляет себя как проводник, а на частотах более 2,3 ГГц – как диэлектрик. Следует отметить, что такие типичные диэлектрики, как фарфор, эбонит, слюда, из-за очень малой проводимости ( <10–12 См/м) даже на очень низких частотах остаются диэлектриками, а металлы из-за очень высокой проводимости ( >106 См/м) остаются проводниками на высоких частотах вплоть до диапазона КВЧ.
При измерениях на высоких частотах tg обычно оказывается больше, чем результаты по уравнению (2.15). Это происходит в основном из-за влияния поляризационных потерь [1, 11], которые суммируются с tg (2.15). Для типичных радиодиэлектриков на высоких частотах именно данный вид потерь является преобладающим [2], поэтому более точным будет определение tg как отношения активной части плотности полного тока смещения к реактивной [1, 2]
, (2. 17)
17)
где Э – угол запаздывания по фазе от[1, 2].
Система уравнений Максвелла с учетом сторонних источников. В задачах электродинамики к сторонним источникам относят такие источники ЭМП, которые возбуждают это поле, но сами от него не зависят, так как их поддерживают сторонние по отношению к исследуемому ЭМП физические явления [11]. Например, при определении ЭМП вокруг проволочной антенны целесообразно исключить из анализа ЭМП генератор и линию передачи, которые вместе с антенной образуют единую электродинамическую систему, а влияние происходящих в них процессов учесть введением в систему плотности стороннего тока, что существенно упрощает решение задачи [11].
Таким образом, сторонние величины (jст, ст и т. п.) суммируются (или вычитаются, в
зависимости от направления взаимодействия
токов или полярностей зарядов) с
соответствующими величинами системы
уравнений Максвелла.
; ; (2.18)
; . (2.19)
В комплексной форме уравнения (2.18)–(2.19) будут иметь вид
; ; (2.20)
; . (2.21)
Индексы (м) указывают источники магнитного типа. Введение эквивалентных (физически фиктивных) магнитных зарядов и токов может упростить решение некоторых электродинамических задач.
Список рекомендуемой литературы: [1, гл. 3, с. 17–23; 2, с. 28–39; 3, гл. 1–2, с. 16–21; 4, с. 16–21; 5, с. 8–13, 17–18; 6, с. 7–41, 119–121; 7, с. 34–49; 8, с. 5–7; 9, с. 30–38, 51–56; 10, с. 19–38, 51–56; 11, с. 16–42, 48–52; 12, с. 26–37, 46–54; 13, с. 8–29, 36–39, 123–128; 15, с. 199–207; 31].
{\ left \ vert i + 2 \ right \ vert} \ Wedge dt $ $и, таким образом,
$ $ \ text {d} F = \ left (\ dfrac {\ partial E_ {y}} {\ partial x }-\dfrac{\partial E_{x}}{\partial y}+\dfrac{\partial B_{z}}{\partial t}\right)dx\клин dy\клин dt+\left(\dfrac{\ частичное E_ {z}} {\ парциальное y} — \ dfrac {\ парциальное E_ {y}} {\ парциальное z} + \ dfrac {\ парциальное B_ {x}} {\ парциальное t} \ справа) dy \ клин dz \ клин dt + \ left (\ dfrac {\ partial E_ {x}} {\ partial z} — \ dfrac {\ partial E_ {z}} {\ partial x} + \ dfrac {\ partial B_ {y}} { \partial t}\right)dz\клин dx\клин dt+\mathbf{\nabla\cdot B}\text{vol}^{3}$$ 9{я}$$
если хочешь. Самое смешное, что, конечно, любая замена $G\rightarrow G+d\phi$ ($\phi$ — 2-форма) не переопределит заряд $j=dG\rightarrow d\left(G+d\phi \справа)=dG$.
Самое смешное, что, конечно, любая замена $G\rightarrow G+d\phi$ ($\phi$ — 2-форма) не переопределит заряд $j=dG\rightarrow d\left(G+d\phi \справа)=dG$.
Уравнения Максвелла
Уравнения МаксвеллаУравнения Максвелла представляют собой один из самых элегантных и лаконичных способов изложения основ электричества и магнетизма. Из них можно развить большинство рабочих отношений в этой области. Из-за их сжатого изложения они воплощают высокий уровень математической сложности и поэтому обычно не вводятся во вводное рассмотрение предмета, за исключением, возможно, сводных соотношений. Эти основные уравнения электричества и магнетизма можно использовать в качестве отправной точки для продвинутых курсов, но обычно они впервые встречаются как объединяющие уравнения после изучения электрических и магнитных явлений.
| Индекс Концепции уравнений Максвелла | ||||||||||||||||
| Назад | ||||||||||||||||
Интегральная форма в отсутствие магнитных или поляризуемых сред:
| Индекс Концепции уравнений Максвелла | ||||||||||||||||||||||||
|


 Закон Гаусса для электричества
Закон Гаусса для электричества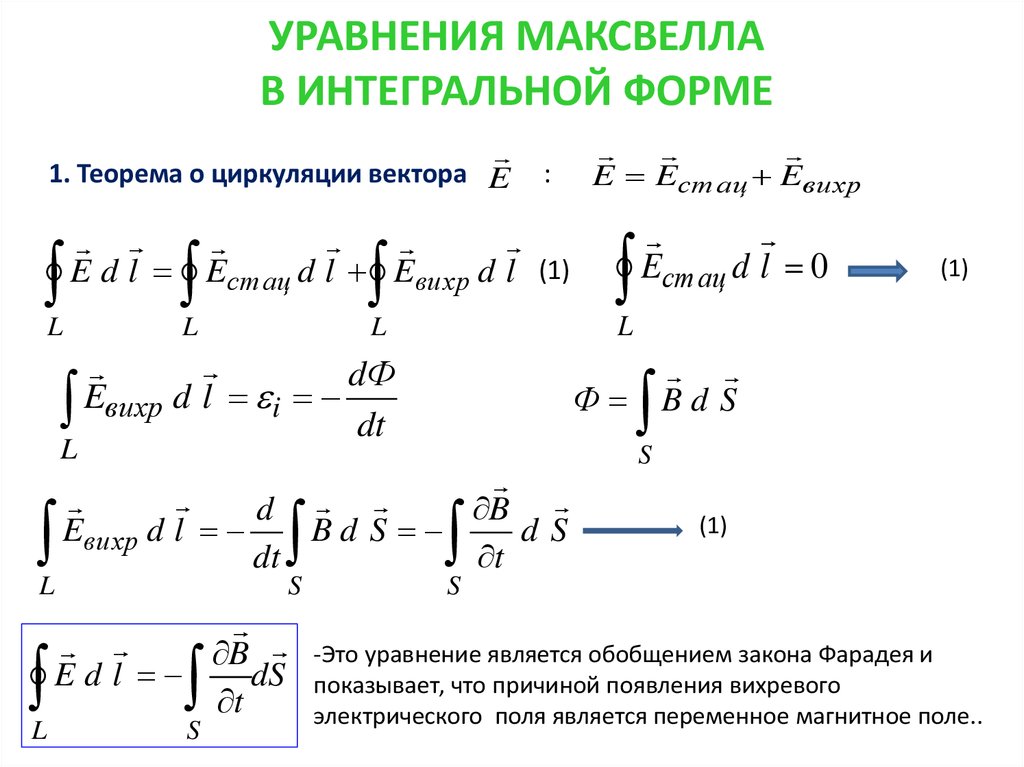 Закон индукции Фарадея
Закон индукции Фарадея