Разработка и исследование микрополосковых фильтров низких частот с высокой крутизной склона АЧХ и влияние электромагнитного окружения на основные параметры фильтров
Ю.А. Ламанов, Т.О. Кудрявцева, Н.Б. Дроботун
Введение
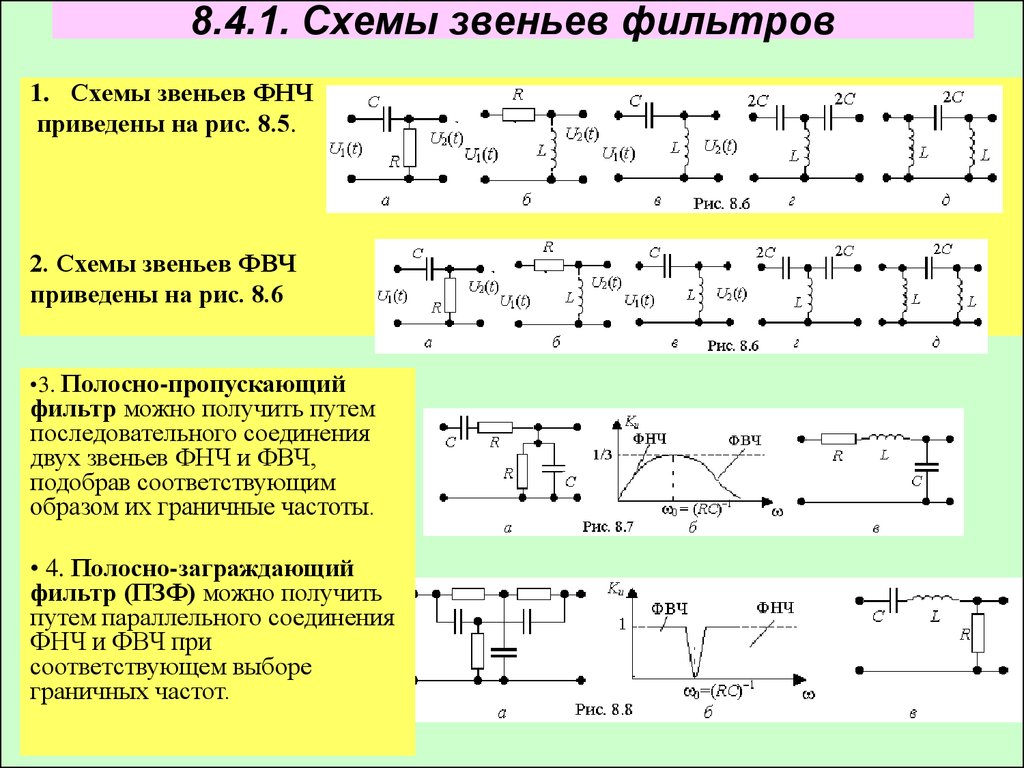
Частотно-селективные устройства СВЧ-диапазона, в частности полосно-пропускающие фильтры (ППФ) и фильтры низких частот (ФНЧ), в последнее время являются наиболее востребованными устройствами среди разработчиков радиоаппаратуры различного назначения. Они применяются при разработке систем связи, радиолокационных и радионавигационных устройств, а также в различной измерительной и специальной радиоаппаратуре. Стремительное развитие современных средств связи делает крайне актуальной разработку ППФ с широкой полосой и высокой крутизной, однако в решении задач подавления зеркальной частоты в высокочастотном тракте приемников и измерительной аппаратуре (векторные анализаторы цепей) активно применяются ФНЧ [1,2]. Их повсеместное использование обусловлено высокой избирательностью, малыми потерями в полосе пропускания и технологичностью производства при низкой стоимости.
Их повсеместное использование обусловлено высокой избирательностью, малыми потерями в полосе пропускания и технологичностью производства при низкой стоимости.
В последние годы активно разрабатываются и исследуются разнообразные конструкции ФНЧ в микрополосковом исполнении [3–6]. Для улучшения их характеристик, как правило, используется большой набор различных резонаторов, который формирует полосу пропускания и полосу заграждения, а также позволяет увеличить крутизну склона АЧХ и расширить диапазон полосы заграждения и пропускания.
На сегодняшний день среди множества топологий фильтров ФНЧ с распределенными параметрами являются наиболее простыми как в расчете, так и в производстве. Примером такого фильтра является гребешковый и полосковый фильтр [7, 8]. Несмотря на вышеперечисленные достоинства у таких фильтров существует ряд существенных недостатков, например, сравнительно низкая собственная добротность и, как следствие, высокие потери в полосе пропускания.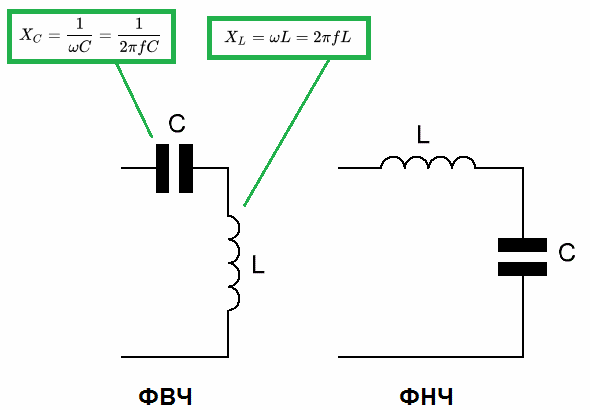

Расчет фильтра на основе чередующихся резонаторов с низким и высоким сопротивлением
Исходя из требований технического задания по обеспечению равномерной АЧХ в полосе пропускания, в качестве фильтра прототипа использовался фильтр Баттерворта 16-ого порядка с максимально плоской характеристикой. При аппроксимации с помощью гладкой кривой частотная характеристика фильтра-прототипа НЧ описывается формулой (1)
Производные функции LБ начиная от первой и кончая (2N − 1)-ой равны нулю при x = 0. Таким образом, функция LБ является максимально плоской при x = 0 [12].
На рисунке 1 приведена схема нормированного фильтра прототипа нижних частот с сосредоточенными параметрами для нечетного числа элементов.
Рис.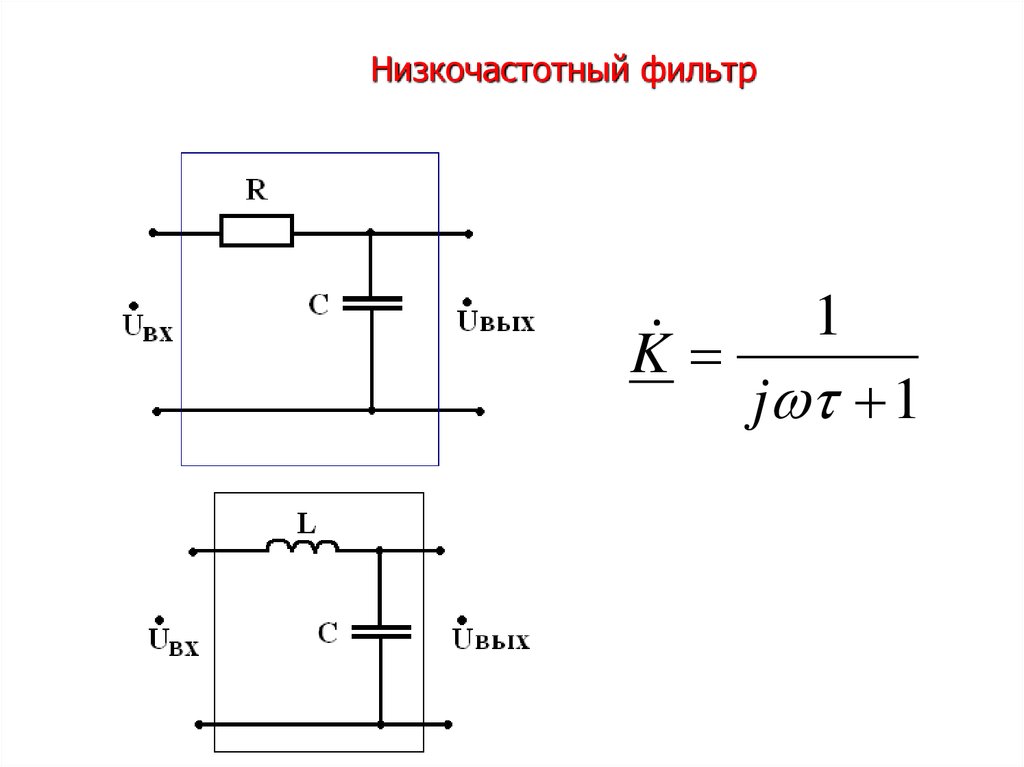 1. Схема нормированного фильтра прототипа нижних частот
1. Схема нормированного фильтра прототипа нижних частот
Количество элементов в схеме показывает степень N в функции LБ. Для обеспечения низкого уровня подавления установлен большой порядок фильтра, число элементов в нем равно 33.
Коэффициент передачи, соответствующий максимально плоской частотной характеристики фильтра прототипа, может быть реализован с помощью схемы, изображенной на рисунке 1, при определенном подборе ее нормированных параметров g.
Значения параметров g определяется по формуле Беннета (2) [12]:
В таблице 1 приведены значения для фильтра НЧ Баттерворта с 33-мя элементами.
Таблица 1
Значение парметров g фильтра Баттерворта
|
g |
значение | gk | значение | gk | значение |
| g1 |
0.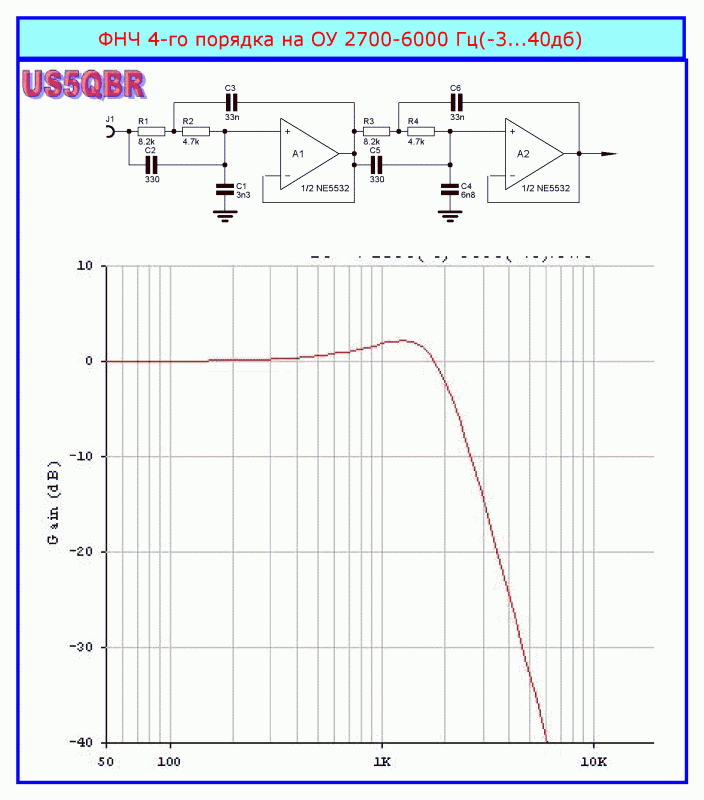 095 095
|
g12 | 1.778 | g23 | 1.683 |
| g2 | 0.285 | g13 | 1.857 | g24 | 1.572 |
| g3 | 0.472 | g14 | 1.919 | g25 | 1.447 |
| g4 | 0.654 | g15 | 1.964 | g26 | 1.31 |
| g5 | 0.831 | g16 | 1.991 | g27 |  16 16
|
| g6 | 1 | g17 | 2 | g28 | 1 |
| g7 | 1.16 | g18 | 1.991 | g29 | 0.831 |
| g8 | 1.31 | g19 | 1.964 | 0.654 | |
| g9 | 1.447 | g20 | 1.919 | g31 | 0.472 |
| g10 | 1.572 | g21 |
1.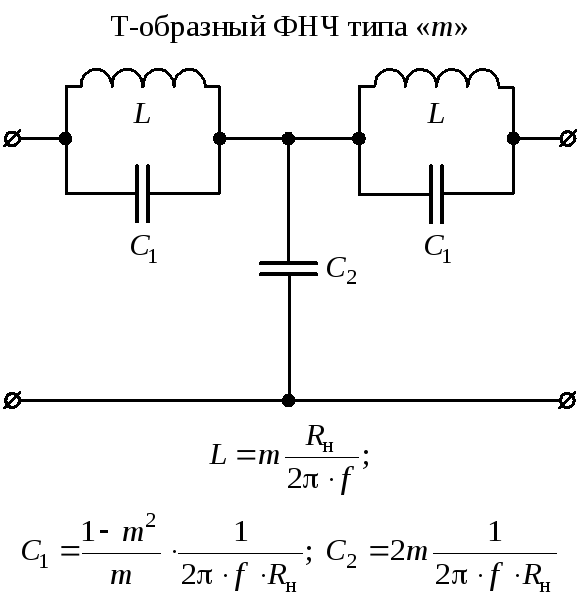 857 857
|
g32 | 0.285 |
| g11 | 1.683 | g22 | 1.778 | g33 | 0.095 |
Для перехода от схемы фильтра-прототипа к эквивалентной схеме проектируемого фильтра, представленной на рисунке 2, были рассчитаны значения элементов при заданных ωс = 2πf, частоте среза f = 6 ГГц, волновом сопротивлении Zв= 50 по формулам (3) (для k-нечетных) и (4) (для k-нечетных) [12]:
Рис. 2. Эквивалентная схема ФНЧ
Рассчитанные значения сосредоточенных элементов L и C показаны в таблице 2.
Значение схемы ФНЧ
| k | Элементы | |
| Индуктивность L, нГн | Емкость C, пФ | |
| 1 | - |
0. 05049 05049
|
| 2 | 0.3775 | - |
| 3 | - | 0.2501 |
| 4 | 0.8676 | - |
| 5 | - | 0.4408 |
| 6 | 1.326 | - |
| 7 | - | 0.6155 |
| 8 | 1.737 | - |
| 9 | - | 0.7679 |
| 10 | 2.085 | - |
| 11 | - |
0. 8926 8926
|
| 12 | 2.358 | - |
| 13 | - | 0.985 |
| 14 | 2.545 | - |
| 15 | - | 1.042 |
| 16 | 2.641 | - |
| 17 | - | 1.061 |
| 18 | 2.641 | - |
| 19 | - | 1.042 |
| 20 | 2.545 | - |
| 21 | - |
0. 985 985
|
| 22 | 2.358 | - |
| 23 | - | 0.8926 |
| 24 | 2.085 | - |
| 25 | - | 0.7679 |
| 26 | 1.737 | - |
| 27 | - | 0.6155 |
| 28 | 1.326 | - |
| 29 | - | 0.4408 |
| 30 | 0.8676 | - |
| 31 | - |
0. 2501 2501
|
| 32 | 0.3775 | - |
| 33 | - | 0.05049 |
Далее были найдены длины и ширины отрезков линий, реализующих индуктивности и емкости. Длина волны в линии λg. = λgL = λgC (формула 5) [13].
Были рассчитаны волновые сопротивления несимметричной полосковой линии (рисунок 3).
Рис. 3. Несимметричная полосковая линия передачи
Параметры индуктивности технологически были ограничены шириной, она не должна быть меньше 20 мкм. Также ширина не должна превышать 200 мкм, так как это значение близко к значению регулярной линии передач. Диапазон ширин составляет от 40 мкм до 180 мкм.
Ширины, выбранные для расчета, представлены в таблице 3.
Таблица 3
Ширины отрезков линий, реализующих индуктивные элементы
| № | b, мкм |
| 1 | 40 |
| 2 | 60 |
| 3 | 80 |
| 4 | 100 |
| 5 | 120 |
| 6 | 140 |
| 7 | 160 |
| 8 | 180 |
Волновое сопротивление индуктивности рассчитано по формуле (6), при b/d < 2 [14]:
где d = 254 мкм; t = 3 мкм.
Для обеспечения так называемого «скачка сопротивлений» при переходе от индуктивного элемента к емкостному было необходимо обеспечить разницу волновых сопротивлений этих элементов не менее чем в 3 раза.
После того, как были найдены средние значения волновых сопротивлений, были рассчитаны длины отрезков, реализующих индуктивности и емкости, по приведённым формулам 7-8 [13].
Таблица 4
Значения длин отрезков линий, реализующих индуктивности и емкости
| Индуктивность L, нГн | Длина lL, мм | Емкость C, пФ | Длина lC, мм |
| 0.3775 | 0.518 | 0.05049 |
0. 109 109
|
| 0.8676 | 1.233 | 0.2501 | 0.542 |
| 1.326 | 2.026 | 0.4408 | 0.972 |
| 1.737 | 3.149 | 0.6155 | 1.396 |
| 2.085 | 4.114 | 0.7679 | 1.807 |
| 2.358 | 4.318 | 0.8926 | 2.195 |
| 2.545 | 4.448 | 0.985 | 2.539 |
| 2.641 |
4. 511 511
|
1.042 | 2.796 |
| 1.061 | 2.896 |
Из диапазона 40-180 мкм было выбрано среднее значение ширины индуктивного элемента. Ширина емкостного элемента была рассчитана по формуле (9), при b/d > 2 [14].
В таблицы 5 представлены расчётные значения длин отрезков микрополосковых линий.
Таблица 5
Средние значения длин микрополосковых линий, реализующих индуктивные и емкостные элементы
| Индуктивность | Емкость | |
| Среднее значения волнового сопротивления, Ом | 69 | 23 |
| Среднее значение длин отрезков, мм | 2,64 | 1,695 |
| Среднее значение ширин отрезков, мм | 0,110 | 1,64 |
По данным из таблицы 5 в САПР Advanced Design System (ADS) была реализована модель ФНЧ с двумерной конструкцией (рисунок 4), в которой реализуется дополнительная электромагнитная связь между несмежными резонаторами. Такая перекрестная связь позволяет существенно увеличить крутизну склона АЧХ [15].
Такая перекрестная связь позволяет существенно увеличить крутизну склона АЧХ [15].
Рис. 4. Топология фильтра нижних частот
Синтез топологии фильтра в САПР
Согласно требованиям технического задания разрабатываемый фильтр планируется применять как дополнительное частотно-селективное звено совместно с ППФ диапазона 5…6 ГГц для подавления побочных полос пропускания ППФ. Таким образом, было принято решение оптимизировать предложенную топологию под требуемый частотный диапазон. В качестве целей оптимизации были установлены: возвратные потери в полосе частот 5…6 ГГц не хуже −20 дБ, потери в полосе не более −3 дБ. Сама оптимизация проводилась в несколько этапов. На первом этапе были получены желаемые характеристики в полосе. Целью второго этапа было увеличение крутизны частоты среза. Для этого потребовалось увеличить перекрёстную связь между звеньями фильтра, что было достигнуто за счёт добавления в топологию коротких меандровых элементов.
В качестве материала подложки был выбран поликор. Фильтр 16-го порядка был расположен на подложке с диэлектрической проницаемостью ε = 10,3 и толщиной d = 0,25 мм. Рассматриваемая топология симметрична относительно центрального емкостного элемента. Финальный рисунок топологии фильтра после программной оптимизации представлен на рисунке 5.
Рис. 5. Топология измененного ФНЧ с двумерной конструкцией
Рис. 6. Амплитудно-частотные характеристики фильтра нижних частот с двумерной конструкцией. Сплошная – FEM, точки – Momentum Microware
На рисунке 6 представлены результаты моделирования в САПР ADS двумя методами расчета (Momentum Microware и FEM): АЧХ прямых потерь S21 и возвратных потерь S11 фильтра нижних частот с полосой пропускания 5…6 ГГц и полосой затухания 7…8 ГГц.
Зависимости на рисунке 6 показывают высокую крутизну склона АЧХ. Однако видно, что при расчете разными методами, характеристика смещается, в данном случае на 0,3 ГГц.
Однако видно, что при расчете разными методами, характеристика смещается, в данном случае на 0,3 ГГц.
Исследование изготовленных опытных образцов фильтров
Для проведения исследований топологии в коаксиальном тракте разработанный фильтр 16-го порядка на подложке из поликора устанавливался на печатную плату с помощью токопроводящего клея EPO-TEK (рисунок 7). Размеры подложки — 36 × 7,1 мм. Подводящие отрезки на печатной плате выполнены в виде копланарных линий с волновым сопротивлением 50 Ом.
Рис. 7. Конструкция фильтра нижних частот
На рисунке 8 показано сравнение расчетных данных с экспериментальными. По результатам измерения видно, что подавление в полосе заграждения, по сравнению с расчетным, выше на 20 дБ, крутизна склона по экспериментальным данным увеличилась.
Рис. 8. Амплитудно-частотные характеристики измеренного фильтра нижних частот. Сплошная – измеренные, точки – Momentum Microware, пунктир – FEM
Сплошная – измеренные, точки – Momentum Microware, пунктир – FEM
Для проверки параметров фильтра в условиях, приближенных к реальным (фильтры предполагается устанавливать во фрезерованный паз глубиной 3 мм и накрывать сверху крышкой) на него была установлена конструкция, имитирующая указанное реальное электромагнитное окружение (рисунок 9). Другими словами, фильтр находился в прямоугольном волноводе, широкая стенка а которого равна 10 мм, узкая b — 3 мм. Расстояние от платы до крышки составило 3 мм. Помимо конструктивных особенностей данная сборка обеспечивает ЭМС фильтра с другими элементами системы, в которой данный фильтр будет использован.
Однако данная конструкция не должна оказывать существенного влияния на характеристики фильтра. Для этого не должно выполняться условие (10), при котором длина волны в волноводе меньше критической. Критическая длина волны волновода, рассчитанная по формуле (11) на основном типе волны H10, равна 20 мм, тогда как длина волны на частоте среза равна 50 мм. Следовательно, условие не выполняется, волновод не работает в диапазоне частот 5…6 ГГц и никак не влияет на работу фильтра нижних частот [14].
Следовательно, условие не выполняется, волновод не работает в диапазоне частот 5…6 ГГц и никак не влияет на работу фильтра нижних частот [14].
Рис. 9. Конструкция фильтра нижних частот с крышкой
На рисунке 10 сравниваются АЧХ фильтра с крышкой и без. С крышкой возвратные потери увеличиваются, это происходит из-за переотражения волн. Данная проблема решается с помощью поглотителя ЗИПСИЛ КЛ РПМ-01 ТУ 2541-004-24624998-2014, графики сравнения представлены на рисунке 11.
Рис. 10. Амплитудно-частотные характеристики измеренного фильтра нижних частот. Сплошная – без крышки, точки – с крышкой
Рис. 11. Амплитудно-частотные характеристики измеренного фильтра нижних частот. Сплошная – без крышки, точки – с крышкой, пунктир – с крышкой и поглотителем ЗИПСИЛ
Благодаря простоте изготовления и высоким частотно-селективным свойствам, фильтры такого типа весьма перспективны для применения в СВЧ-устройствах. В качестве продолжения эксперимента по предложенной методике был рассчитан, изготовлен и измерен фильтр аналогичной конструкции, но оптимизированный для полосы пропускания 6-7 ГГц. Конструкция фильтра и его характеристики представлены на рисунке 12.
В качестве продолжения эксперимента по предложенной методике был рассчитан, изготовлен и измерен фильтр аналогичной конструкции, но оптимизированный для полосы пропускания 6-7 ГГц. Конструкция фильтра и его характеристики представлены на рисунке 12.
Рис.12. Фильтр нижних частот (6…7 ГГц)
Рис. 13. Амплитудно-частотные характеристики фильтра нижних частот (6-7 ГГц) с двумерной конструкцией. Сплошная – S21, точки – S11. Сверху фото образца фильтра
Заключение
Изготовленная конструкция на микрополосковых резонаторах обладает большой крутизной и высокими амплитудно-частотными характеристиками. Благодаря свернутой форме образуются дополнительные связи, с помощью которых существенно увеличивается крутизна склона АЧХ. Такой фильтр прост в изготовлении, а установка на плате существенно экономит место в приборе. При этом численный электродинамический расчет хорошо согласуется с экспериментом, что позволяет без кардинальных изменений проводить синтез устройств с заданными характеристиками.
В ходе работы было экспериментально исследовано влияние электромагнитного окружения (фрезерованный канал и заполнение его поглощающим материалом) на топологию фильтра.
Литература
1. Morgan M. A. Reflectionless Filters. In: Artech House Microwave Library. Boston; L., 2017. 258 p.
2. Hunter I. C. Theory and Design of Microwave Filters. IET Electromagnetic Waves Series. Cambridge: Cambridge Univ. Press, 2006. V. 48. 353 p.
3. Li K., Zhao M., Fan Yo., Zhu Z., Cui W. With Parallel Open-Ended Stubusing Novel Double-Folded SCMRC Structurecompact Lowpass Filter with Wide Stopband // Progress in Electromagn. Res. Lett. 2013. V. 36. P. 77–86.
4. Hayati M., Shama F. A Compact Lowpass Filter with Ultra Wide Stopband Using Stepped Impedance Resonator // Radioengineering. 2017. V. 26. № 1. P. 269– 274.
5. Kumarand D., De A. Compact Ultra Wide Band Filter Using Triangular Patch Resonators // Radioelectronics and Communs Syst. 2015. V. 58. № 4. P. 151–156.
2015. V. 58. № 4. P. 151–156.
6. Hayati M., Asadbeigi H., Sheikhi A. Microstrip Lowpass Flter with High and Wide Rejection Band // Electronics Lett. 2012. V. 48. № 19. P. 1217–1219.
7. Arfiya K., Pramod K., Kumaraswamy H., Jayaraj N. Design and Simulation of Printed micro strip Low pass Filter based on the Electromagnetic models 18GHz printed microstrip Lowpass Filter using x-models // International Journal of Research in Engineering and Technology. 2014. № 3. P. 312–318.
8. Hong J., Liu Y., Wang B., Mei K. A Novel Differential Equation Model for a Microstrip Lowpass Filter // Microwave and Optical Technology Letters. 2002. V. 35. № 5. P. 368–370.
9. Беляев Б. А., Ходенков С. А., Галеев Р. Г., Шабанов В. Ф. Фильтр нижних частот на двумерном микрополосковом электромагнитном кристалле // Доклады академии наук. 2019. Т. 485. № 1. С. 27–32.
10. Беляев Б.А., Сержантов А.М., Лексиков Ан. А., Бальва Я.Ф., Грушевский Е.О., Ходенков С.А. Высокоселективный полосковый фильтр нижних частот с уровнем заграждения более 100 dB в широкой полосе // Письма в ЖТФ. 2020. Т. 46. № 8. С. 10–13.
А., Бальва Я.Ф., Грушевский Е.О., Ходенков С.А. Высокоселективный полосковый фильтр нижних частот с уровнем заграждения более 100 dB в широкой полосе // Письма в ЖТФ. 2020. Т. 46. № 8. С. 10–13.
11. Abid A., Zhirun H. Sharp cut-off, Miniaturized Metamaterial Binomial Microstrip Low-pass Filter // Microwave and Optical Technology Letters. 2007. V/ 49. № 10. P. 2406–2409.
12. Неганов В.А., Клюев Д.С., Табаков Д.П. Устройства СВЧ и антенны Ч.1 // Под ред. В.А. Неганова. Изд. Стереотип. М.: ЛЕНАНД, 2016 – 608 с.
13. Вольман А.А., Муравцова А.Д. СВЧ цепи Анализ и автоматизированное проектирование // пер. с англ. Под ред. В.И. Вольмана – М.: Радио и связь, 1990. 288 с.
14. Гошин Г.Г. Антенны и фидеры. Сборник задач с формулами и решениями // Учебное пособие. – Томск, ТУСУР, 2012. – 236 с.
15. Belyaev B. A., Serzhantov A. M., Bal’va Y.F., Tyurnev V. V., Leksikov A. A., Galeev R. G. Implementations of Cross Couplings in Microwave Bandpass Filters // Microwave and Optical Technol. Lett. 2014. V. 56. № 9. P. 2021–2025.
Lett. 2014. V. 56. № 9. P. 2021–2025.
Фильтр нижних частот.
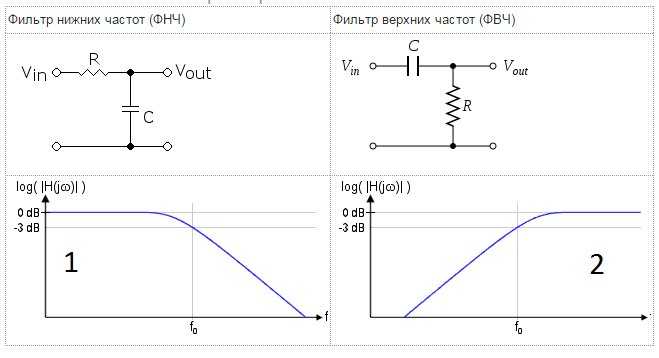
Фильтр нижних частот первого порядка на ОУ и его АЧХ. Если объединить схему инвертирующего усилителя со схемой интегратора, образуется схема фильтра нижних частот первого порядка, которая показана ниже. Амплитудно-частотная характеристика – зависимость амплитуды сигнала на выходе устройства от частоты при постоянной амплитуде на входе этого устройства – представлена ниже.
Такой фильтр представляет собой инвертирующий усилитель, обладающий постоянным коэффициентом усиления в полосе прозрачности от постоянного тока до граничной частоты fср. Частотную характеристику такого фильтра можно охарактеризовать формулой (0 ≤ f ≤ fср).
Видно, что в пределах
полосы пропускания, пока емкостное
сопротивление конденсатора достаточно
велико, коэффициент усиления схемы
совпадает с коэффициентом усиления
инвертирующего усилителя (см. выражение
(1)).
выражение
(1)).
Частота среза этого фильтра определяется элементами цепи обратной связи в соответствии с выражением (2).
В полосе затухания выше частоты среза fср усиление уменьшается с интенсивностью 20 дБ/декада (или 6 дБ/октава), что означает уменьшение коэффициента усиления по напряжению в 10 раз при увеличении частоты также в 10 раз или уменьшение коэффициента усиления в два раза при каждом удвоении частоты.
Фильтр нижних частот второго порядка на ОУ. Если такой крутизны наклона амплитудно-частотной характеристики в полосе затухания недостаточно, можно использовать фильтр нижних частот второго порядка, схема которого показана ниже.
Коэффициент усиления фильтра нижних частот второго порядка такой же, как у фильтра первого порядка, в связи с тем, что суммарное сопротивление резисторов в цепи инверсного входа, как и ранее, выражается согласно формуле (1).
АЧХ этого фильтра
отличается повышенной крутизной наклона,
которая составляет 12 дБ/октава. Таким
образом, в полосе затухания при увеличении
частоты вдвое напряжение сигнала на
выходе фильтра уменьшается в четыре
раза.
Таким
образом, в полосе затухания при увеличении
частоты вдвое напряжение сигнала на
выходе фильтра уменьшается в четыре
раза.
4. Описание и классификация активных фильтров. Фильтр верхних частот. Описание и классификация активных фильтров.
Активный фильтр – аналоговый электронный фильтр, в котором присутствует один или несколько активных компонентов.
При использовании в качестве элемента схемы фильтра операционного усилителя (ОУ) можно синтезировать характеристику любого LC-фильтра без применения катушек индуктивности. В отличие от пассивных RC-фильтров, активные обеспечивают более качественное разделение полос пропускания и затухания. В схемы активных фильтров помимо пассивных компонентов (резисторов, конденсаторов и катушек индуктивности) входят такие активные изделия, как транзисторы или интегральные микросхемы.
Активные
резисторно-конденсаторные фильтры
имеют огромное преимущество перед их
пассивными аналогами, особенно на
частотах ниже 10 кГц.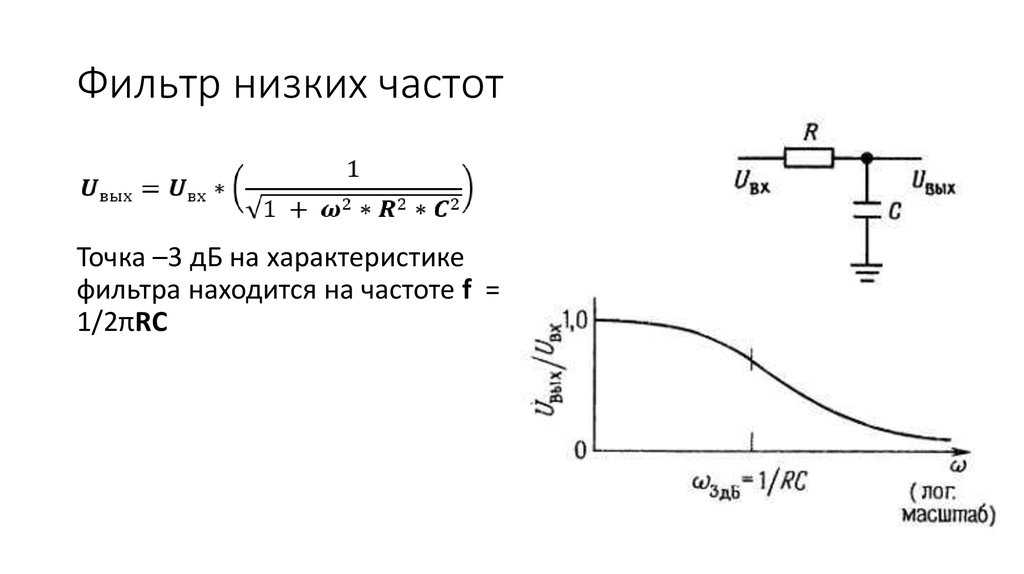 Пассивные фильтры
для низких частот должны содержать
катушки большой индуктивности и
конденсаторы большой емкости. Поэтому
они получаются громоздкими, дорогостоящими,
а их характеристики оказываются далеко
не идеальными.
Пассивные фильтры
для низких частот должны содержать
катушки большой индуктивности и
конденсаторы большой емкости. Поэтому
они получаются громоздкими, дорогостоящими,
а их характеристики оказываются далеко
не идеальными.
Схемы дифференциатора (см. рис. а) и интегратора (см. рис. б), построенные с применением операционных усилителей, представляют собой простейшие активные фильтры. При выборе элементов схемы в определенной зависимости от частоты дифференциатор становится фильтром верхних частот, а интегратор — фильтром нижних частот.
Активные фильтры можно разделить на группы по различным признакам: назначению, полосе пропускаемых частот, типу усилительных элементов, виду обратных связей и др. По полосе пропускаемых частот фильтры делятся на четыре основные группы: нижних частот, верхних частот, полосовые и заграждающие.
По назначению фильтры
делятся на сглаживающие фильтры
источников питания, заграждающие фильтры
помех, фильтры для селективных усилителей
низкой или высокой частоты и др.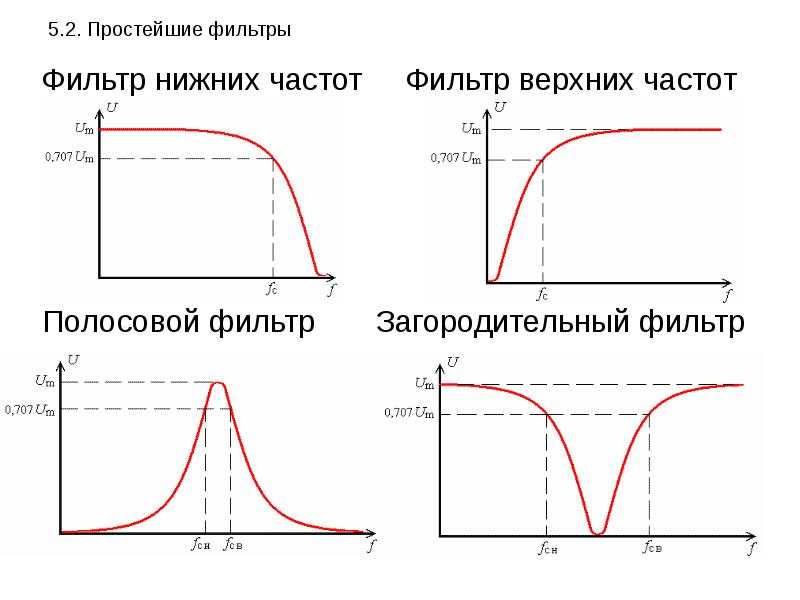
По типу усилительных элементов можно выделить транзисторные фильтры, фильтры на усилителях с ограниченным усилением, на операционных усилителях, на повторителях напряжения и др. Все рассмотренные фильтры могут иметь одну цепь обратной связи или несколько. В связи с этим различают фильтры с одноконтурной и с многоконтурной обратной связью. Кроме этого, различают фильтры по числу полюсов на частотной характеристике – фильтры первого порядка, второго и более высоких порядков. Фильтры высоких порядков имеют более крутые границы полос пропускания и затухания и более плоскую характеристику в области полосы пропускания, что естественно улучшает качество фильтра.
Широкие возможности
активных RC-фильтров связаны с
использованием в них активных элементов.
Цепи, содержащие только сопротивления
и емкости, имеют полюсы передаточной
функции на отрицательной действительной
полуоси комплексной плоскости p=σ+iω,
что ограничивает возможности создания
фильтров. В отличие от пассивных, активные RC-фильтры (ARС-фильтры) могут
иметь полюсы в любой части комплексной
плоскости. Однако схемы с полюсами в
правой полуплоскости неустойчивы,
поэтому в активных фильтрах используются
только те схемы, полюсы передаточной
функции которых располагаются в левой
полуплоскости или на оси jω.
Однако схемы с полюсами в
правой полуплоскости неустойчивы,
поэтому в активных фильтрах используются
только те схемы, полюсы передаточной
функции которых располагаются в левой
полуплоскости или на оси jω.
При проектировании активных фильтров фильтр заданного порядка разбивается на звенья первого и второго порядка. Результирующая АЧХ получится перемножением характеристик всех звеньев. Применение активных элементов (транзисторов, операционных усилителей) позволяет исключить влияние звеньев друг на друга и проектировать их независимо. Это обстоятельство значительно упрощает и удешевляет проектирование и настройку активных фильтров.
Фильтры нижних и верхних частот
Фильтры нижних и верхних частотNext: Полосовые и задерживающие фильтры Up: Таксономия фильтров Предыдущий: Таксономия фильтров Содержимое Индекс
На сегодняшний день наиболее частой целью использования фильтра является извлечение либо
низкочастотная или высокочастотная часть звукового сигнала, ослабляющая
остальные.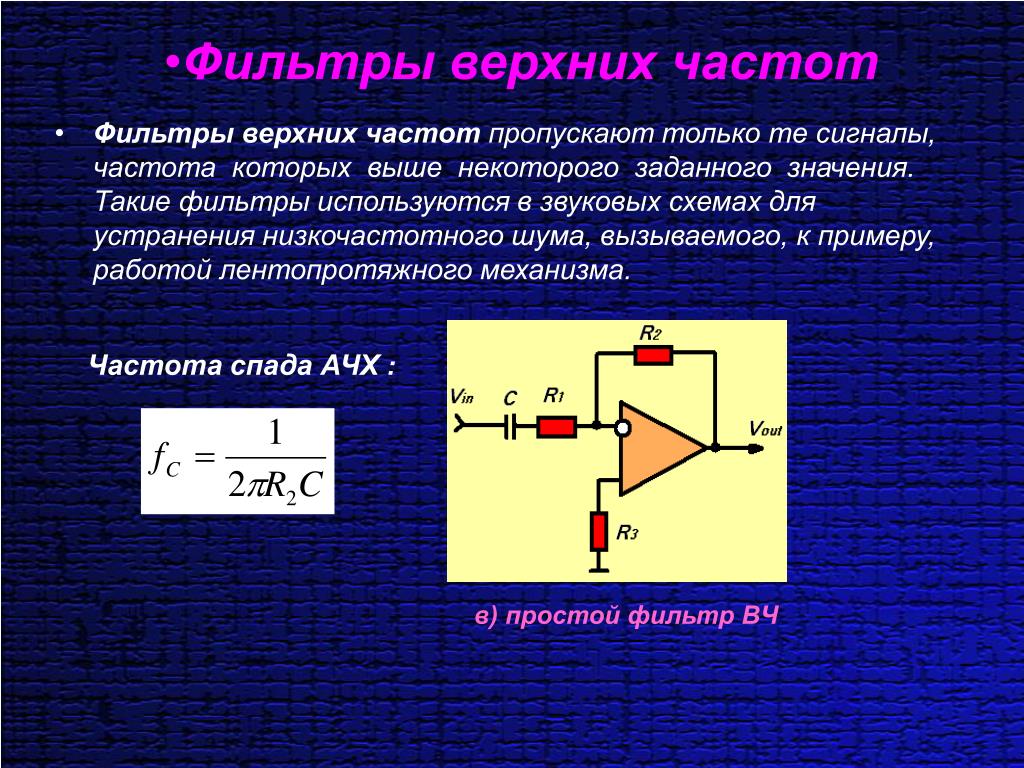 Это достигается с помощью низкочастотный или высокочастотный фильтр.
Это достигается с помощью низкочастотный или высокочастотный фильтр.
В идеале фильтр нижних или верхних частот должен иметь частотную характеристику 1 до (или до) указанной частоты среза и ноль после нее; но такие фильтры не могут быть реализованы на практике. Вместо этого мы пытаемся найти возможные приближения к этому идеальному отклику. Чем больше дизайнерских усилий и время вычислений, которое мы вкладываем в это, тем ближе мы можем добраться.
На рис. 8.2 показана частотная характеристика фильтра нижних частот.
фильтр. Спектр частот разделен на три полосы, обозначенные на
Горизонтальная ось. полоса пропускания это область (полоса частот), через которую фильтр должен пропускать входной сигнал.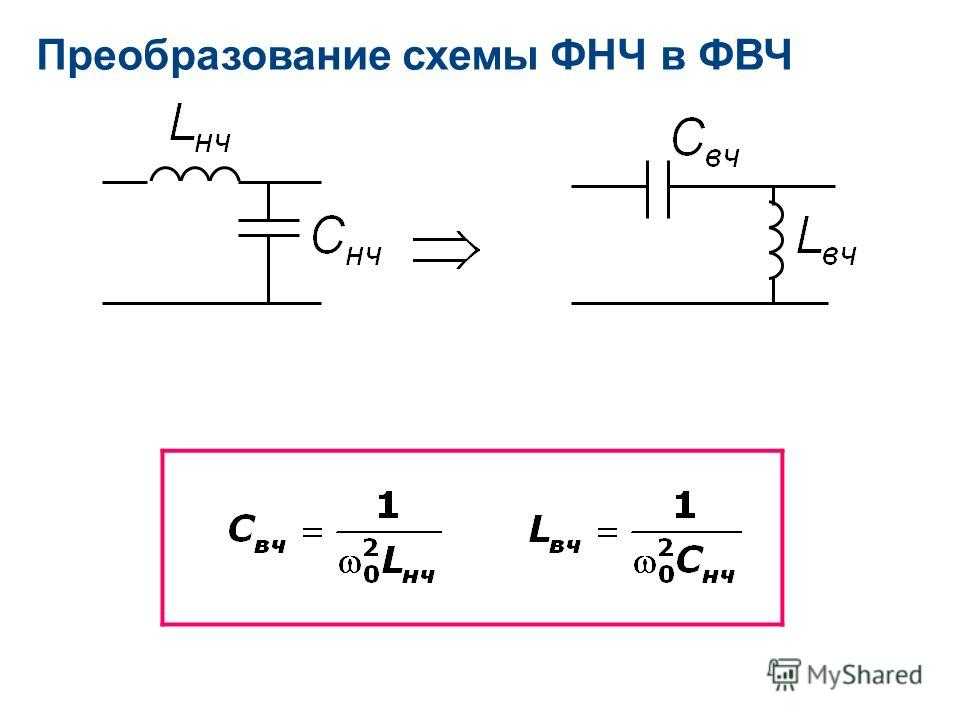 на его выходе с единичным коэффициентом усиления.
Для фильтра нижних частот (как показано) полоса пропускания достигает частоты
ноль до определенного предела частоты. Для фильтра верхних частот полоса пропускания
появится в правой части графика и будет простираться от
ограничение частоты до максимально возможной частоты. Любой
полоса пропускания реализуемого фильтра будет лишь приблизительно плоской;
отклонение от плоскостности называется пульсация ,
и часто определяется путем предоставления отношения между самым высоким и самым низким усилением
в полосе пропускания, выраженное в децибелах. Идеальный фильтр нижних или верхних частот
будет иметь пульсацию 0 дБ.
на его выходе с единичным коэффициентом усиления.
Для фильтра нижних частот (как показано) полоса пропускания достигает частоты
ноль до определенного предела частоты. Для фильтра верхних частот полоса пропускания
появится в правой части графика и будет простираться от
ограничение частоты до максимально возможной частоты. Любой
полоса пропускания реализуемого фильтра будет лишь приблизительно плоской;
отклонение от плоскостности называется пульсация ,
и часто определяется путем предоставления отношения между самым высоким и самым низким усилением
в полосе пропускания, выраженное в децибелах. Идеальный фильтр нижних или верхних частот
будет иметь пульсацию 0 дБ.
полоса задерживания фильтра нижних или верхних частот – это область спектра (частота
диапазон), в котором фильтр не предназначен для передачи входных данных. затухание в полосе задерживания это разница в децибелах между самым низким коэффициентом усиления в полосе пропускания
и максимальное усиление в полосе задерживания. В идеале это было бы
быть бесконечным; чем выше, тем лучше.
В идеале это было бы
быть бесконечным; чем выше, тем лучше.
Наконец, реализуемый фильтр, частотная характеристика которого всегда непрерывная функция частоты, всегда нуждается в области или частоте полоса, в которой усиление падает от усиления в полосе пропускания до полосы задержания прирост; это называется переходная полоса . Чем тоньше можно сделать эту полосу, тем более идеальным будет фильтр.
Next: Полосовые и задерживающие фильтры Up: Таксономия фильтров Предыдущий: Таксономия фильтров Содержание Индекс Миллер Пакетт 2006-03-03
Фильтры нижних частот, фильтры миллиметрового диапазона | Knowles Precision Devices
Используйте отдельно или в качестве дополнения к полосовому фильтру для дополнительного подавления гармоник. Пользовательские версии могут быть адаптированы для поддержки более высоких требований по отбраковке или других потребностей. Фильтры нижних частот проходят от постоянного тока к нужному частотному диапазону и подавляют остальную часть нежелательного спектра. Диапазон частот от постоянного тока до 67 ГГц
Фильтры нижних частот проходят от постоянного тока к нужному частотному диапазону и подавляют остальную часть нежелательного спектра. Диапазон частот от постоянного тока до 67 ГГц
- Термостабильность: от -55 до 125 градусов C
- Уменьшение размера фильтра: до 20 раз при использовании материала CG, 10 раз при использовании CF, 3 раза при использовании PG по сравнению с типичным PWB
- Высокая воспроизводимость — производство тонких пленок обеспечивает точные производственные характеристики; без тюнинга
- Устройство для поверхностного монтажа со встроенным экраном; нет необходимости в укрытии или канализации
Пользовательские версии
Не нашли то, что искали ниже? Свяжитесь с нами
Фильтры нижних частот, микрополосковые
| Номер детали | Частота среза 3 дБ (ГГц) | FL (ГГц) | FH (ГГц | IL (дБ, при 25)ºC | Д x Ш x В, дюймы (мм) | Лист данных | Вспомогательные файлы |
|---|---|---|---|---|---|---|---|
Л050СФ9С | 5 | DC | 4 | 1,0 дБ | 0,220 (5,588) х 0,180 (4,572) х 0,103 (2,616) | Л050СФ9С | Л050СФ9С |
Л065СГ9В | 6,5 | DC | 6 | 1,3 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,118 (2,997) | Л065СГ9В | Л065СГ9В |
Л065СГ9С | 6,5 | DC | 6 | 1,3 дБ | 0,220 (5,588) х 0,180 (4,572) х 0,103 (2,616) | Л065СГ9С | Л065СГ9С |
Л095СГ9С | 9,5 | DC | 9 | 1,3 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,103 (2,616) | Л095СГ9С | Л095СГ9С |
Л117Сх5С | 11,7 | DC | 11 | 1,0 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,103 (2,616) | Л117Сх5С | Л117Сх5С |
Л128Сх5С | 12,8 | DC | 12 | 1,2 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,103 (2,616) | Л128Сх5С | Л128Х5С |
Л117Сх5В | 11,7 | DC | 12,6 | 2,0 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,113 (2,87) | Л117Сх5В | Л117Сх5В |
Л157СГ3С | 15,7 | DC | 15 | 2,2 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,103 (2,616) | Л157СГ3С | Л157СГ3С |
Л185СФ4С | 18,5 | DC | 18 | 2,2 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,098 (2,489) | Л185СФ4С | Л185СФ4С |
Л185СФ4В | 18,5 | DC | 18 | 2,0 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,113 (2,87) | Л185СФ4В | Л185СФ4В |
Л204СФ4С | 20,4 | DC | 20 | 1,8 дБ | 0,220 (5,588) х 0,140 (3,556) х 0,098 (2. |


