Понятие передаточной функции фильтра верхних частот первого порядка

Добавлено 27 декабря 2019 в 01:55

Сохранить или поделиться

Данная статья продолжает наше обсуждение передаточных функций в s-области и их роль в разработке и анализе аналоговых фильтров.

Если вы читали предыдущие статьи этой серии (о передаточных функциях фильтров нижних частот и полюсах и нулях), вы уже знакомы с различными важными понятиями, относящимися к анализу в s-области и к теории аналоговых фильтров. Давайте кратко пройдемся по ним:

• Мы можем создать выражение для поведения фильтра нижних частот при передаче сигнала от входа к выходу, проанализировав схему в s-области.
• Выражение V_вых/V_вх схемы является передаточной функцией фильтра, и если мы сравним это выражение с нормированной формой, мы сможем быстро определить два критических параметра, а именно частоту среза и максимальный коэффициент усиления (коэффициент передачи).
• Передаточная функция может быть записана в виде полинома числителя, деленного на полином знаменателя. Корни полинома числителя – это нули передаточной функции, а корни полинома знаменателя – полюсы передаточной функции. Другой способ сказать это: нули передаточной функции приводят к T(s) = 0, а полюсы передаточной функции приводят к T(s) → ∞.
• Полюсы приводят к тому, что наклон логарифмической амплитудно-частотной характеристики системы уменьшается на 20 дБ/декада; нули приводят к увеличению наклона на 20 дБ/декада.
• Полюсы дают сдвиг фазы -90°, а нули дают сдвиг фазы +90°.

Передаточная функция фильтра верхних частот

Схема RC фильтра верхних частот первого порядка реализована следующим образом:

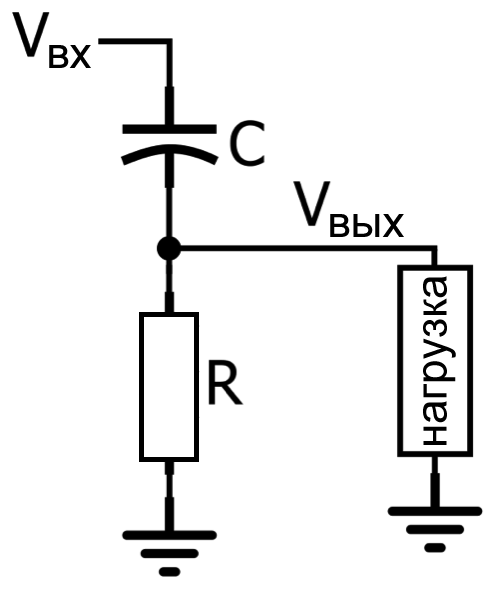Рисунок 1 – RC фильтр верхних частот – частотно-зависимый делитель напряжения

\[\frac{V_{вых}}{V_{вх}}=\frac{R}{\frac{1}{sC}+R}=\frac{sRC}{1+sRC}=\frac{s}{s+\frac{1}{RC}}\]

Поведение фильтра верхних частот первого порядка при передаче сигнала от входа к выходу можно описать с помощью следующей нормированной передаточной функции:

\[T(s)_{ФВЧ}=\frac{a_{1}s}{s+\omega _{0}}\]

Давайте сравним это с соответствующим выражением для фильтра нижних частот:

\[T(s)_{ФНЧ}=\frac{a_{0}}{s+\omega _{0}}\]

Как видите, знаменатели одинаковы. В обоих случаях мы имеем полюс при s = –ω₀, что означает, что и фильтр нижних частот, и фильтр верхних частот будут иметь следующие характеристики:

• уровень амплитудно-частотной характеристики при ω₀ будет на 3 дБ ниже максимального уровня АЧХ; для пассивного фильтра максимальный уровень АЧХ равен единице (0 дБ), а в случае при ω₀ значение составляет –3 дБ;
• абсолютное значение сдвига фазы цепи при ω₀ будет 45°.

Таким образом, выходной уровень при ω₀ в этих двух цепях очень похож. Однако на уровень АЧХ на частотах выше и ниже ω₀ влияет числитель T(s), и различие между этими двумя числителями в том, что делает фильтр нижних частот очень отличным от фильтра верхних частот.

Влияние числителя

Числитель T(s) фильтра верхних частот говорит нам о двух вещах: начальный наклон АЧХ будет равен +20 дБ/декада, а максимальный уровень АЧХ будет равен a₁. Давайте подробнее рассмотрим эти две характеристики.

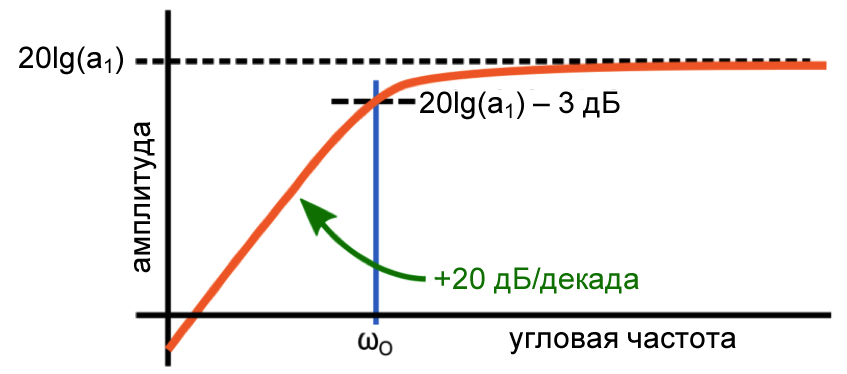Рисунок 2 – Амплитудно-частотная характеристика фильтра верхних частот

Начальный наклон

Поскольку теперь в числителе есть переменная s, у нас будет передаточная функция, равная нулю при любом значении s, при котором числитель будет равен нулю. В случае фильтра верхних частот первого порядка весь числитель умножается на s, поэтому ноль находится при s = 0.

Как ноль при s = 0 влияет на амплитудно-частотную и фазо-частотную характеристики реальной цепи? Во-первых, давайте рассмотрим АЧХ. Мы знаем, что ноль приведет к увеличению наклона кривой АЧХ на 20 дБ/декада. Однако это увеличение происходит при ω = 0 рад/с (или ƒ = 0 Гц), и здесь кроется ловушка: горизонтальная ось логарифмической амплитудно-частотной характеристики (диаграммы Боде) никогда не достигает 0 Гц. Это логарифмическая шкала, что означает, что частота уменьшается с 10 Гц до 1 Гц, до 0,1 Гц, до 0,01 Гц и так далее. Она никогда не достигает 0 Гц. Следовательно, мы никогда не видим угловую частоту нуля при ω = 0 рад/с.

Вместо этого кривая АЧХ просто начинается с наклона +20 дБ/декада. Выходной уровень продолжает увеличиваться до частоты полюса; полюс уменьшает наклон на 20 дБ/декада, в результате чего график АЧХ становится плоским (то есть наклон = 0 дБ/декада) и остается плоским при увеличении ω до бесконечности.

Максимальный коэффициент усиления

Всё, что нам нужно, это немного математических манипуляций, чтобы увидеть, что максимальный коэффициент усиления фильтра верхних частот будет равен a₁. Из общей формы амплитудно-частотной характеристики фильтра верхних частот мы знаем, что коэффициент усиления не может уменьшаться по мере увеличения ω до бесконечности. Таким образом, мы можем найти максимальный коэффициент усиления, определив T(s) при s → ∞. В знаменателе мы получаем s + ω₀. При добавлении чего-то к бесконечности мы получаем бесконечность, поэтому в этом случае мы можем упростить T(s) следующим образом:

\[T(s→∞)=\frac{a_{1}s}{s}\]

s в числителе и s в знаменателе сокращаются, поэтому

\[T(s→∞)=a_{1}\]

Фазо-частотная характеристика фильтра верхних частот

Как упоминалось ранее, ноль вносит в фазо-частотную характеристику системы сдвиг фазы +90°, при сдвиге фазы +45° на частоте нуля. Сдвиг фазы достигает +90° на частоте, которая на одну декаду выше частоты нуля, но фильтр верхних частот имеет ноль при ω = 0 рад/с, и вы не можете указать частоту, которая на одну декаду выше 0 рад/с – опять же, здесь мы имеем дело с логарифмической шкалой, которая означает, что горизонтальная ось никогда не достигнет 0 рад/с, и при этом она никогда не достигнет частоты, которая на одну декаду выше 0 рад/с (такая частота на самом деле не существует: 0 рад/с × 10 = 0 рад/с).

Результатом всего этого является то, что фазо-частотная характеристика фильтра верхних частот имеет начальное значение +90°. Другими словами, все низкочастотные входные сигналы будут смещены на +90°, а затем, по мере приближения частоты входного сигнала к частоте полюса, сдвиг фазы начинает уменьшаться:

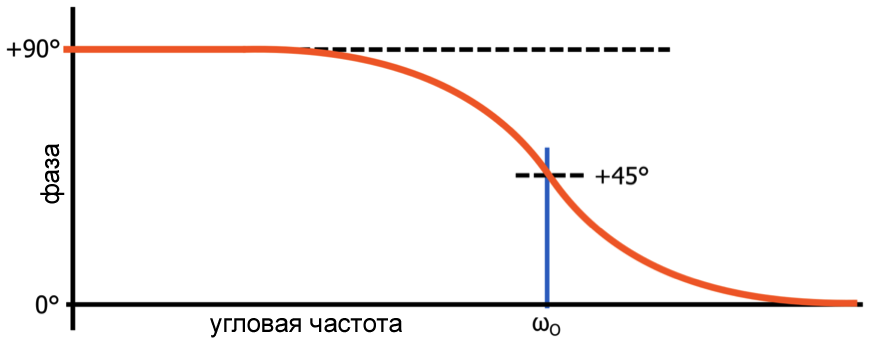Рисунок 3 – Фазо-частотная характеристика фильтра верхних частот

Заключение

Мы рассмотрели стандартную передаточную функцию для фильтра верхних частот первого порядка и увидели, как эта передаточная функция приводит к амплитудно-частотной и фазо-частотной характеристикам.

В следующей статье мы увидим, что передаточную функцию фильтра нижних частот и передаточную функцию фильтра верхних частот можно объединить в общую передаточную функцию первого порядка, а также кратко рассмотрим полосовой фильтр первого порядка.

Оригинал статьи:

Теги

s-областьАЧХ (амплитудно-частотная характеристика)Передаточная функцияСдвиг фазыФВЧ (фильтр верхних частот)ФЧХ (фазо-частотная характеристика)Частота среза

Сохранить или поделиться

Понятие передаточных функций фильтров нижних частот

Добавлено 21 декабря 2019 в 07:01

Сохранить или поделиться

Данная статья дает некоторое представление о взаимосвязи между передаточной функцией в s-области и поведением фильтра нижних частот первого порядка.

В последнее время я довольно много пишу на тему фильтров, и хотя я сосредоточился на практических соображениях, я чувствую необходимость объяснить некоторые важные теоретические концепции в пользу тех, кто хотел бы более подробно понять и проанализировать поведение аналоговых фильтров. В настоящее время каждый имеет доступ к программным инструментам, которые делают сложное проектирование фильтров относительно безболезненным, но я не думаю, что было бы разумно полностью игнорировать математические основы просто потому, что они не являются строго необходимыми для выполнения многих реальных задач проектирования.

s-область

Отклик фильтра может быть выражен передаточной функцией в s-области; переменная s появляется из преобразования Лапласа и представляет комплексную частоту. Например:

\[T(s) = \frac{K}{1+ \left( \frac{s}{\omega_0} \right) }\]

Эта передаточная функция является математическим описанием поведения фильтра нижних частот первого порядка в частотной области. Выражение в s-области эффективно передает общие характеристики, и если мы хотим вычислить конкретную информацию об амплитуде и фазе, всё, что нам нужно сделать, это заменить s на jω, а затем вычислить выражение при заданной угловой частоте.

Вам может быть интересно, откуда берутся K и ω₀ – вы, вероятно, никогда не видели принципиальной схемы, в которой значения компонентов были выражены в значениях K и ω₀. Идея в том, что K и ω₀ подобны частям шаблона, и в следующем разделе мы рассмотрим взаимосвязь между этим шаблоном и принципиальной схемой.

Анализ схем в s-области

RC фильтр нижних частот является частотно-зависимым делителем напряжения. При анализе в s-области импеданс резистора равен R, а импеданс конденсатора равен \(\frac{1}{sC}\).

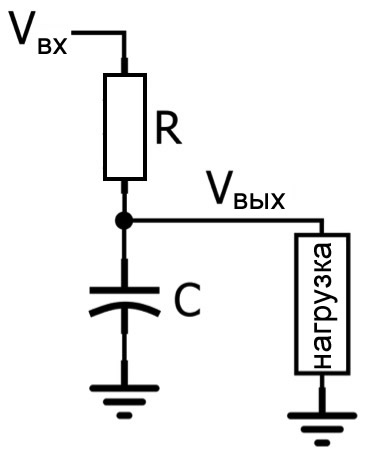Рисунок 1 – RC фильтр нижних частот является частотно-зависимым делителем напряжения

\[\frac{V_{вых}}{V_{вх}} = {\frac{1}{sC} \over \frac{1}{sC} + R} = \frac{1}{1+sRC}\]

Если мы сравним это выражение с нормированной передаточной функцией, то увидим, что K = 1 и \(\omega_0 = \frac{1}{RC}\). Удобство использования нормированной формы становится понятным, как только вы узнаете, что представляют собой K и ω₀: K – это коэффициент усиления схемы при постоянном напряжении, а ω₀ – это частота среза. Таким образом, сравнивая передаточную функцию схемы с нормированной передаточной функцией, вы можете сразу же сформулировать выражения для двух определяющих характеристик фильтра нижних частот первого порядка, а именно для коэффициента усиления при постоянном напряжении и частоты среза.

Другой нормированной формой передаточной функции фильтра нижних частот первого порядка является следующее:

\[T(s)=\frac{a_0}{s+\omega_0}\]

Мы можем встроить передаточную функцию схемы в этот шаблон, если разделим числитель и знаменатель на RC:

\[T(s)= \frac{1}{1+sRC} \rightarrow { \frac{1}{RC} \over s + \frac{1}{RC} } \]

Таким образом, \(a_0=\frac{1}{RC}\), и \(\omega_0 = \frac{1}{RC}\). Эта форма напрямую не дает нам коэффициент усиления по постоянному напряжению, но если мы вычислим нормированное выражение для s = 0, то получим

\[T(s=0) = \frac{a_0}{\omega_0}\]

Это означает, что коэффициент усиления по постоянному напряжению нашего RC-фильтра равен

\[\left( \frac{1}{RC} \right) / \left( \frac{1}{RC} \right) = 1\]

А коэффициент усиления по постоянному напряжению, равный единице, – это именно то, что мы ожидаем от пассивного фильтра нижних частот.

Понятие частоты среза

Мы видели, что ω₀ в стандартной передаточной функции представляет частоту среза, но каково математическое основание этого факта?

Во-первых, давайте, преобразуем стандартную передаточную функцию в s-области в эквивалентную передаточную функцию jω.

\[T(s) = \frac{K}{1 + \frac{s}{\omega_0}} \rightarrow T(j\omega) = \frac{K}{1 + j\frac{\omega}{\omega_0}}\]

Теперь давайте вычислим выражение при частоте среза.

\[T(j\omega = j\omega_0) = \frac{K}{1 + j\frac{\omega_0}{\omega_0}}= \frac{K}{1+j}\]

Знаменатель является комплексным числом, поэтому модуль будет равен

\[|T(j\omega = j\omega_0)|= \frac{K}{\sqrt{1^2+1^2}} = \frac{K}{\sqrt{2}}\]

Поскольку K – это коэффициент усиления по постоянному напряжению, очень низкочастотный входной сигнал с амплитудой в один вольт приведет к выходному сигналу с амплитудой в K вольт. Если входная частота увеличивается до ω₀ радиан в секунду, выходная амплитуда будет равна \(\frac{K}{\sqrt{2}}\). Коэффициент \(\frac{1}{\sqrt{2}}\) соответствует –3 дБ, и, как вы, вероятно, знаете, другое название частоты среза – это частота –3 дБ.

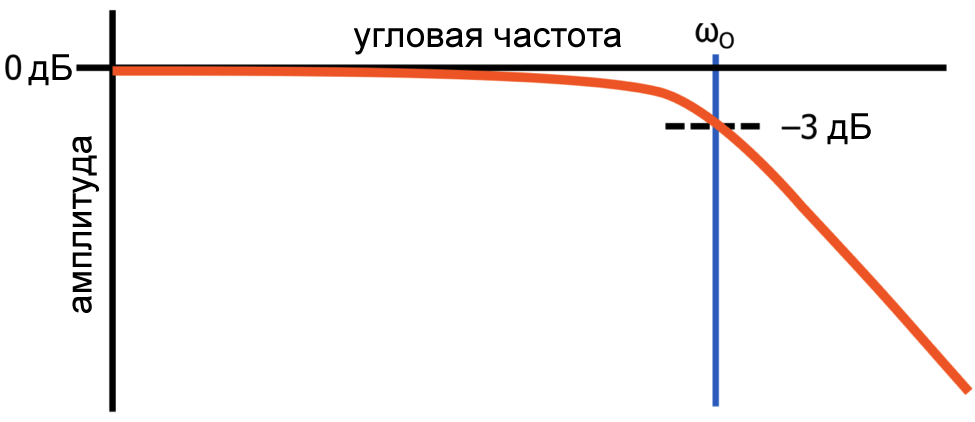Рисунок 2 – Амплитудно-частотная характеристика пассивного фильтра нижних частот первого порядка (амплитуда откладывается в дБ в зависимости от частоты в логарифмическом масштабе)

Этот простой анализ передаточной функции ясно продемонстрировал, что частота среза – это просто частота, на которой амплитудно-частотная характеристика фильтра снижается на 3 дБ относительно выходного уровня на очень низкой частоте.

Частота среза и сдвиг фазы

Частота среза фильтра нижних частот имеет особое значение также в отношении фазо-частотной характеристики схемы. Если мы напишем комплексное число в форме x + jy, мы рассчитаем фазу следующим образом:

\[\theta=\text{arctg}\left( \frac{y}{x} \right)\]

Таким образом, общая фазо-частотная характеристика нашего RC фильтра низких частот следующей:

\[\theta(\omega)= -\text{arctg}\left( \frac{\frac{\omega}{\omega_0}}{1} \right)= -\text{arctg}\left( \frac{\omega}{\omega_0} \right)\]

Если мы вычислим это выражение при ω = ω₀, сдвиг фазы будет равен

\[-\text{arctg}\left( \frac{\omega_0}{\omega_0} \right) = -\text{arctg}\left( 1 \right) = -45^\circ\]

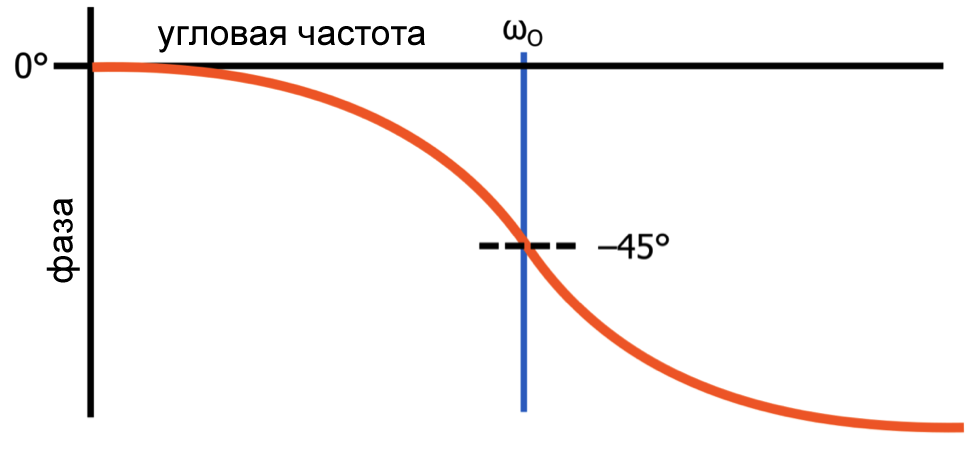Рисунок 3 – Фазо-частотная характеристика пассивного фильтра нижних частот первого порядка (фаза откладывается в зависимости от частоты в логарифмическом масштабе)

Максимальный сдвиг фазы, создаваемый фильтром нижних частот первого порядка, составляет 90°, поэтому этот анализ говорит нам, что частота среза является «центром» фазо-частотной характеристики схемы – другими словами, это частота, на которой фильтр создает половину своего максимального сдвига фазы.

Заключение

Я надеюсь, что вам понравилось это краткое введение в концепции s-области и анализ передаточных функций. Поначалу математические основы схем аналоговых фильтров могут быть немного пугающими, но я думаю, что стоит потратить некоторое время на то, чтобы получить некоторое представление об этих темах. Я продолжу исследовать эту тему в будущих статьях.

Оригинал статьи:

Теги

s-областьАЧХ (амплитудно-частотная характеристика)Комплексные числаПередаточная функцияПреобразование ЛапласаСдвиг фазыФНЧ (фильтр нижних частот)ФЧХ (фазо-частотная характеристика)Частота среза

Сохранить или поделиться

Фильтр с бесконечной импульсной характеристикой — Википедия

Фильтр с бесконечной импульсной характеристикой (Рекурсивный фильтр, БИХ-фильтр) или IIR-фильтр (IIR сокр. от infinite impulse response — бесконечная импульсная характеристика) — линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть образующий обратную связь. Основным свойством таких фильтров является то, что их импульсная переходная характеристика имеет бесконечную длину во временной области, а передаточная функция имеет дробно-рациональный вид. Такие фильтры могут быть как аналоговыми, так и цифровыми.

Примерами БИХ-фильтров являются фильтр Чебышёва, фильтр Баттерворта, Фильтр Калмана и фильтр Бесселя.

Динамические характеристики[править | править код]

Разностное уравнение, описывающее дискретный БИХ-фильтр, устанавливает связь между входным и выходным сигналами во временной области:

y(n)=b0x(n)+b1x(n−1)+⋯+bPx(n−P)−a1y(n−1)−a2y(n−2)−⋯−aQy(n−Q){\displaystyle y(n)=b_{0}x(n)+b_{1}x(n-1)+\cdots +b_{P}x(n-P)-a_{1}y(n-1)-a_{2}y(n-2)-\cdots -a_{Q}y(n-Q)}

где P{\displaystyle P} порядок входного сигнала, bi{\displaystyle b_{i}} — коэффициенты входного сигнала, Q{\displaystyle Q} — порядок обратной связи, ai{\displaystyle a_{i}} — коэффициенты обратной связи, x(n){\displaystyle x(n)} — входной, а y(n){\displaystyle y(n)} — выходной сигналы.

Более компактная запись разностного уравнения:

y(n)=∑i=0Pbix(n−i)−∑k=1Qaky(n−k){\displaystyle y(n)=\sum _{i=0}^{P}b_{i}x(n-i)-\sum _{k=1}^{Q}a_{k}y(n-k)}

Для того, чтобы найти ядро фильтра, положим

x(n)=δ(n){\displaystyle x(n)=\delta (n)}

где δ(n){\displaystyle \delta (n)} — дельта-функция.

Тогда импульсная переходная функция (ядро фильтра) записывается как

h(n)=∑i=0Pbiδ(n−i)−∑k=1Qakh(n−k){\displaystyle h(n)=\sum _{i=0}^{P}b_{i}\delta (n-i)-\sum _{k=1}^{Q}a_{k}h(n-k)}

Z-преобразование импульсной переходной функции даёт передаточную функцию БИХ-фильтра:

H(z)=∑i=0Pbiz−i1+∑k=1Qakz−k{\displaystyle H(z)={\frac {\sum _{i=0}^{P}b_{i}z^{-i}}{1+\sum _{k=1}^{Q}a_{k}z^{-k}}}}

Об устойчивости фильтра с бесконечной импульсной характеристикой судят по его передаточной функции. Для дискретного фильтра необходимо и достаточно, чтобы все полюса его передаточной функции по модулю были меньше единицы (т.е. лежали внутри единичного круга на z-плоскости). Все критерии устойчивости, применимые в теории линейных стационарных систем, например критерий устойчивости Найквиста или критерий устойчивости Рауса применимы и в случае БИХ-фильтров.

В отличие от КИХ-фильтров, БИХ-фильтры не всегда являются устойчивыми.

Если рассматривается передаточная функция вида:

H(z)=Y(z)X(z)=∑k=0Mbkz−k1+∑k=1Nakz−k=B(z)A(z),{\displaystyle H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{k=0}^{M}b_{k}z^{-k}}{1+\sum _{k=1}^{N}a_{k}z^{-k}}}={\frac {B(z)}{A(z)}},}

то соотношение между входом и выходом такой системы должно удовлетворять разностному уравнению:

y(n)=−∑k=1Na(k)y(n−k)+∑k=0Mb(k)x(n−k){\displaystyle y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+\sum _{k=0}^{M}b(k)x(n-k)}

Это уравнение может быть записано непосредственно из выражения для передаточной функции, таким образом форму построения цепи, соответствующей этому уравнению, называют прямой формой 1.

Прямая реализация типа 1 БИХ фильтра

При построении БИХ фильтра для простоты можно принять, что M=N. БИХ фильтры могут быть реализованы с использованием трех элементов или основных операций: умножитель, сумматор и блок задержки. Этих элементов достаточно для всех возможных цифровых фильтров. Вариант, показанный на рисунке есть прямая реализация БИХ-фильтров типа 1.

Поскольку совокупности коэффициентов b(k) и a(k) соответствуют полиномам числителя B(z) и знаменателя A(z) передаточной функции Н(z), то прямую форму БИХ-фильтра, показанную на рисунке, можно трактовать как каскадное соединение двух цепей. Первая из них реализует нули и имеет передаточную функцию B(z), а вторая — полюсы, и имеет передаточную функцию 1/A(z). Обозначив выходной сигнал первой системы w(n), разностное уравнение можно заменить системой уравнений:

y(n)=−∑k=1Na(k)y(n−k)+w(n),{\displaystyle y(n)=-\sum _{k=1}^{N}a(k)y(n-k)+w(n),}

w(n)=∑k=0Mb(k)x(n−k){\displaystyle w(n)=\sum _{k=0}^{M}b(k)x(n-k)}

которая и реализована структурой, показанной на рисунке.

В дискретных системах с постоянными параметрами соотношение между входом и выходом не зависит от порядка каскадного соединения блоков. Из этого свойства вытекает вторая прямая форма построения БИХ-фильтра. Если сначала реализовать полюсы H(z) соответствующие правой части структурной схемы верхнего рисунка, которая имеет передаточную функцию 1/A(z), а после — нули передаточной функцией B(z), то получим структуру, показанную на рисунке 2, которая соответствует системе уравнений:

w(n)=−∑k=1Na(k)w(n−k)+x(n),{\displaystyle w(n)=-\sum _{k=1}^{N}a(k)w(n-k)+x(n),}

y(n)=∑k=0Mb(k)w(n−k).{\displaystyle y(n)=\sum _{k=0}^{M}b(k)w(n-k).}

Прямая реализация типа 2 БИХ фильтра (неканоническая)

Объединив линии задержки в структуре, показанной на верхнем рисунке, получим прямую каноническую форму БИХ-фильтра:

Прямая реализация типа 2 БИХ фильтра (каноническая)

В некоторых случаях, с точки зрения шумовых характеристик, фильтр, реализованный в прямой форме, лучше, чем в канонической.

Передаточная функция — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 мая 2019; проверки требует 1 правка.

Переда́точная фу́нкция — один из способов математического описания динамической системы. Используется в основном в теории управления, связи и цифровой обработке сигналов. Представляет собой дифференциальный оператор, выражающий связь между входом и выходом линейной стационарной системы. Зная входной сигнал системы и передаточную функцию, можно восстановить выходной сигнал.

В теории управления передаточная функция непрерывной системы представляет собой отношение преобразования Лапласа выходного сигнала к преобразованию Лапласа входного сигнала при нулевых начальных условиях.

Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета САР сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных объектов управления. Передаточная функция является дробно-рациональной функцией комплексной переменной для разных систем.

Пусть u(t){\displaystyle u(t)} — входной сигнал линейной стационарной системы, а y(t){\displaystyle y(t)} — её выходной сигнал. Тогда передаточная функция W(s){\displaystyle W(s)} такой системы записывается в виде:

W(s)=Y(s)U(s){\displaystyle W(s)={\frac {Y(s)}{U(s)}}}, где s = jω [рад/с] — оператор передаточной функции, U(s){\displaystyle U(s)} и Y(s){\displaystyle Y(s)} — преобразования Лапласа для сигналов u(t){\displaystyle u(t)} и y(t){\displaystyle y(t)} соответственно

U(s)=L{u(t)}≡∫0+∞u(t)e−stdt{\displaystyle U(s)={\mathcal {L}}\left\{u(t)\right\}\equiv \int \limits _{0}^{+\infty }u(t)e^{-st}\,dt},

Y(s)=L{y(t)}≡∫0+∞y(t)e−stdt{\displaystyle Y(s)={\mathcal {L}}\left\{y(t)\right\}\equiv \int \limits _{0}^{+\infty }y(t)e^{-st}\,dt}.

Для дискретных и дискретно-непрерывных систем вводится понятие дискретной передаточной функции. Пусть u(k){\displaystyle u(k)} — входной дискретный сигнал такой системы, а y(k){\displaystyle y(k)} — её дискретный выходной сигнал, k=0,1,2,…{\displaystyle k=0,1,2,\dots }. Тогда передаточная функция W(z){\displaystyle W(z)} такой системы записывается в виде:

W(z)=Y(z)U(z){\displaystyle W(z)={\frac {Y(z)}{U(z)}}},

где U(z){\displaystyle U(z)} и Y(z){\displaystyle Y(z)} — z-преобразования для сигналов u(k){\displaystyle u(k)} и y(k){\displaystyle y(k)} соответственно:

U(z)=Z{u(k)}≡∑k=0∞u(k)z−k{\displaystyle U(z)={\mathcal {Z}}\left\{u(k)\right\}\equiv \sum _{k=0}^{\infty }u(k)z^{-k}},

Y(z)=Z{y(k)}≡∑k=0∞y(k)z−k{\displaystyle Y(z)={\mathcal {Z}}\left\{y(k)\right\}\equiv \sum _{k=0}^{\infty }y(k)z^{-k}}.

Связь с другими динамическими характеристиками[править | править код]

• АФЧХ системы можно получить из передаточной функции с помощью формальной замены комплексной переменной s{\displaystyle s} на jω{\displaystyle j\omega }:

W(jω)≡W(s),s=jω{\displaystyle W(j\omega )\equiv W(s),s=j\omega }.

Свойства передаточной функции, полюсы и нули передаточной функции[править | править код]

1. Для стационарных систем (т.е систем неизменяемыми параметрами компонентов) и с сосредоточенными параметрами передаточная функция — это дробно-рациональная функция комплексной переменной s{\displaystyle s}:

W(s)=R(s)Q(s)=b0sm+b1sm−1+⋯+bma0sn+a1sn−1+⋯+an{\displaystyle W(s)={\frac {R(s)}{Q(s)}}={\frac {b_{0}s^{m}+b_{1}s^{m-1}+\dots +b_{m}}{a_{0}s^{n}+a_{1}s^{n-1}+\dots +a_{n}}}}.

2. Знаменатель и числитель передаточной функции — это характеристические полиномы дифференциального уравнения движения линейной системы. Полюсами передаточной функции называют корни характеристического полинома знаменателя, нули — корни характеристического полинома числителя.

3. В физически реализуемых системах порядок полинома числителя передаточной функции m{\displaystyle m} не может превышать порядка полинома её знаменателя n{\displaystyle n}, то есть m≤n{\displaystyle m\leq n}

4. Импульсная переходная функция представляет собой оригинал (преобразования Лапласа) для передаточной функции.

5. При формальной замене s=jω{\displaystyle s=j\omega } в W(s){\displaystyle W(s)} получается комплексная передаточная функция системы, описывающая одновременно амплитудно-частотную (в виде модуля этой функции) и фазо-частотную характеристики системы как аргумент её.

Для MIMO-систем вводится понятие матричной передаточной функции. Матричная передаточная функция от вектора входа системы U(t){\displaystyle U(t)} до вектора выхода Y(t){\displaystyle Y(t)} — это матрица W={wi,j}{\displaystyle W=\{w_{i,j}\}}, элемент i{\displaystyle i}-й строки j{\displaystyle j}-го столбца представляет собой передаточную функцию системы от i{\displaystyle i}-й координаты вектора входа системы до j{\displaystyle j}-й координаты вектора выхода.

Фильтр с конечной импульсной характеристикой — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2014; проверки требуют 8 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2014; проверки требуют 8 правок.

Фильтр с конечной импульсной характеристикой (Нерекурсивный фильтр, КИХ-фильтр) или FIR-фильтр (FIR сокр. от finite impulse response — конечная импульсная характеристика) — один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени его импульсной характеристики (с какого-то момента времени она становится точно равной нулю). Такой фильтр называют ещё нерекурсивным из-за отсутствия обратной связи. Знаменатель передаточной функции такого фильтра — константа.

Разностное уравнение, описывающее связь между входным и выходным сигналами фильтра:

y(n)=b0x(n)+b1x(n−1)+…+bPx(n−P){\displaystyle y\left(n\right)=b_{0}x\left(n\right)+b_{1}x\left(n-1\right)+…+b_{P}x\left(n-P\right)}

где P{\displaystyle P} — порядок фильтра, x(n){\displaystyle x(n)} — входной сигнал, y(n){\displaystyle y(n)} — выходной сигнал, а bi{\displaystyle b_{i}} — коэффициенты фильтра.

Иными словами, значение любого отсчета выходного сигнала определяется суммой масштабированных значений P{\displaystyle P} предыдущих отсчетов в силу свойства линейности. Можно сказать иначе: значение выхода фильтра в любой момент времени есть значение отклика на мгновенное значение входа и сумма всех постепенно затухающих откликов P{\displaystyle P} предыдущих отсчетов сигнала, которые всё ещё оказывают влияние на выход (после P{\displaystyle P} отсчетов импульсная переходная функция становится равной нулю, поэтому все члены после P{\displaystyle P}-го тоже станут равными нулю). Запишем предыдущее уравнение в более ёмком виде:

y(n)=∑i=0Pbix(n−i){\displaystyle y\left(n\right)=\sum _{i=0}^{P}b_{i}x\left(n-i\right)}

Для того, чтобы найти ядро фильтра, положим

x(n)=δ(n){\displaystyle x(n)=\delta (n)}

где δ(n){\displaystyle \delta (n)} — дельта-функция. Тогда импульсная характеристика КИХ-фильтра может быть записана как:

h(n)=∑i=0Pbiδ(n−i){\displaystyle h\left(n\right)=\sum _{i=0}^{P}b_{i}\delta \left(n-i\right)}

Z-преобразование импульсной характеристики даёт нам передаточную функцию КИХ-фильтра:

H(z)=∑i=0Pbiz−i{\displaystyle H\left(z\right)=\sum _{i=0}^{P}b_{i}z^{-i}}

КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр. Вот некоторые из них:

• КИХ-фильтры устойчивы.
• КИХ-фильтры при реализации не требуют наличия обратной связи.
• Фаза КИХ-фильтров может быть сделана линейной

КИХ-фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.

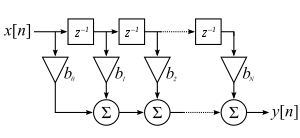Реализация прямой формы КИХ-фильтра

Представление передаточной функции фильтра. Реализация фильтров высоких порядков.

Передаточная функция это отношение изображения по Лапласу выходной величины изображению по Лапласу входной величины фильтра.

В общем случае фильтр можно рассматривать как четырехполюсник с передаточной функцией:

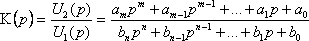
где 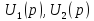– входное и выходное напряжение четырехполюсника в операторной форме; 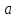и – вещественные постоянные величины; 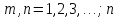– определяет порядок фильтра. Для установившейся частоты 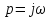и передаточную функцию можно привести к виду:

Чем выше порядок фильтра, тем точнее он аппроксимирует идеальную характеристику с резкими границами. Однока, с повышением пордяка фильтра возрастае его сложность, размеры и стоимость.

Проектирование таких фильтров состоит из двух этапов:

Определение трубемой математической передаточной функции;

Проектирование схемы для реализации найденнной математической функции.

Переход от передаточной функции к построению схемы.

Используем многкоскадные фильтры. Этот способ основывается на разложение передаточной функции на сомножители первого и второго порядков. Передаточную функцию каждого из полученных сомножителей можно реализовать по отдетльности каскадами первого или второго порядков, причем их взаимное влияние исключается.

Пусть задана передачтоная функция:

Разложим её на линейные и квадратичные сомножители:

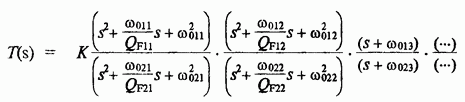
19. Реализация звеньев фнч и фвч первого и второго порядка.

Широкораспространенны фильтры на ОУ, поэтому мы и будем использовать их в наших дальнейших записях/рассуждениях.

ФНЧ

ФНЧ — предназначен для выделения сигналов, частота которых ниже некоторой заданной частоты, называемой частотой среза фильтра. ФНЧ практически без ослабления пропускает сигналы в полосе частот от постоянного напряжения до частоты среза и ослабляет сигналы, частота которых выше частоты среза.

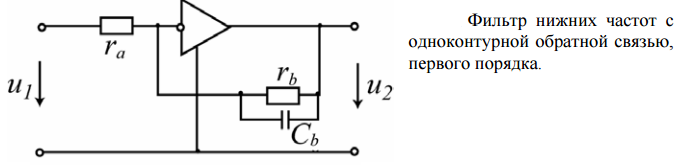
У ОУ показан один вход из-за принятого обозначения, это означает что неинвентирующий вход заземлён.

Коэффициент передачи ФНЧ по напряжению:

где 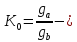коэффициент передачи фильтра на постоянном напряжении, – частота среза фильтра, при этом http://stu.alnam.ru/book_ane-28

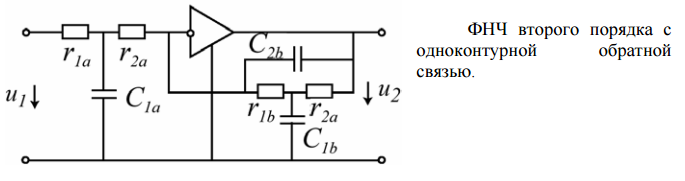
Коэффициент передачи ФНЧ по напряжению:

где 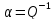— затухание фильтра, — его добротность. Выражение имеет два полюса:

В данном случае частота среза определяется выражением:

А коэффициент передачи на постоянном напряжении:

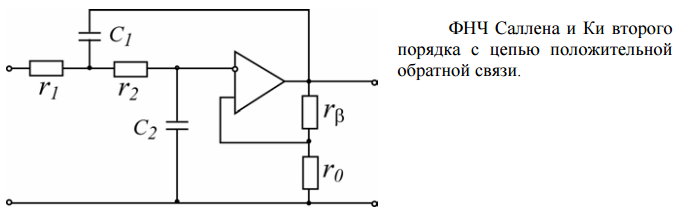
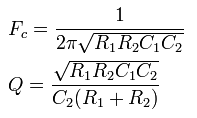
Другой способ реализации. Наилучшая избирательность при этом достигается за счёт того, что одно из звеньев 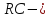цепи входит в цепь положительной обратной связи. Такая структура была предложена Салленом и Ки. Его операторный коэффициент передачи при этом имеет вид:

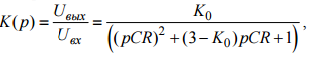
При значении параметров 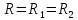и , при этом, если , то передаточная функция имеет единственный полюс кратности 2, что соответсвует спаду АЧХ у граница среза фильтра в -12 Дб/окт. В этом случае он эквивалентен

– фильтру нижних частот.

ФВЧ

ФВЧ предназначен для выделения сигналов, частота которых, выше некоторой заданной частоты – частоты среза.

Для построения данного фильтра достаточно выбрать: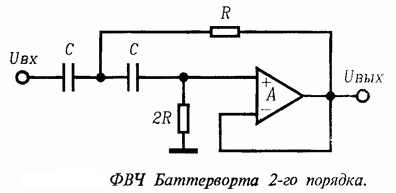

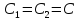
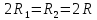
Данный фильтр представляет собой филтр Саллена и Ки путём заменой резисторов на конденсаторы и наоборот. Метод расчёта аналогичный с соответствующими заменами.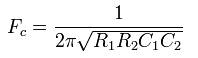

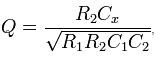
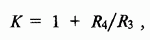
Параметры схемы:

1) Коэффициент передачи:

а) инвертирующий: 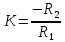б) неинвертирующий вариант: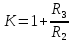

2) Частота полюса: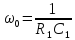

Классификация фильтров по передаточным функциям

Рассмотрим эту классификацию на примере фильтров низкой частоты. На практике широко используются фильтры, отличающиеся характерными особенностями амплитудно-частотных характеристик. Это фильтры Баттерворта, Чебышева, Бесселя (Томсона) (рис. 6).

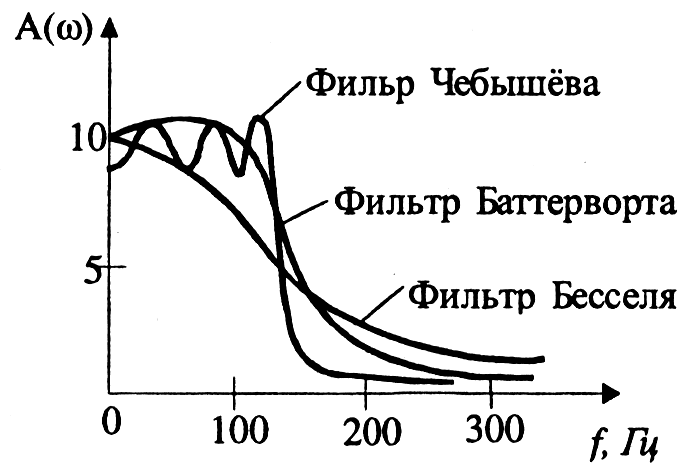
Рис. 6. Амплитудно-частотные характеристики фильтров

Фильтры Баттерворта характеризуются наиболее плоской амплитудно-частотной характеристикой в полосе пропускания. Это их достоинство. Но в переходной полосе указанные характеристики спадают плавно, недостаточно резко.

Фильтры Чебышева отличаются резким спадом амплитудно-частотных характеристик в переходной полосе, но в полосе пропускания эти характеристики не являются плоскими.

Фильтры Бесселя характеризуются очень пологим участками амплитудно-частотных характеристик в переходной полосе, еще более пологими, чем у фильтров Баттерворта. Их фазочастотные характеристики достаточно близки к идеальным, соответствующим постоянному времени замедления, поэтому такие фильтры мало искажают форму входного сигнала, содержащего несколько гармоник.

Активные фильтры

Приведем в качестве примера две схемы фильтров второго порядка. Схема фильтра нижних частот приведена на рис.7. Можно отметить, что на низких частотах (и на постоянном токе) фильтр имеет коэффициент усиления, который описывается следующим выражением:

,

где К – величина, определяющая сопротивление в цепи обратной связи (К-1)·R (рис. 7).

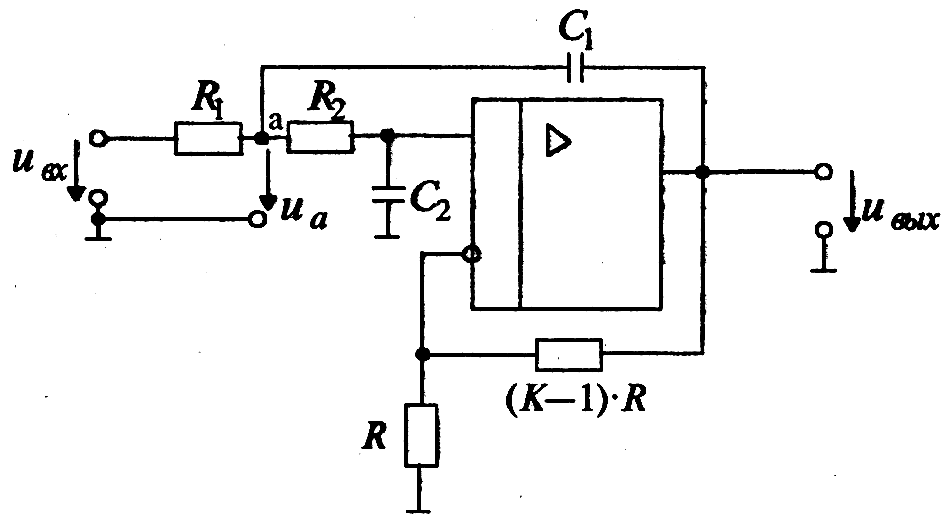
Рис. 7. Активный фильтр нижних частот

Приведенное выражение соответствует неинвертирующему усилителю. При увеличении частоты входного сигнала напряжение на выходе уменьшается во-первых, в связи с уменьшением напряжения на неинвертирующем входе (т.е. на емкости С₂) из-за уменьшения модуля комплексного сопротивления емкости С₂. Во-вторых, уменьшается напряжение u_а из-за того, что модуль комплексного сопротивления емкости С₁ уменьшается и через эту емкость с выхода усилителя в точку «а» подается ток, который значительно сдвинут по фазе относительно напряжения

u_вх.

Фильтр верхних частот представлен на рис. 8. На высоких частотах коэффициент усиления фильтра равен К. В зависимости от параметров резисторов R₁ и R₂ и конденсаторов С₁ и С₂ схема реализует фильтры Баттерворта, Чебышева или Бесселя.

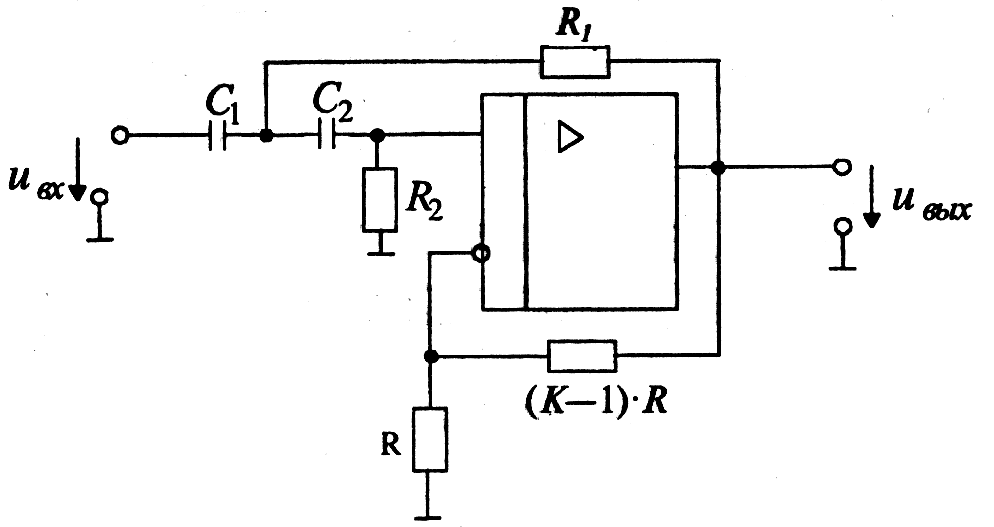
Рис. 8. Активный фильтр верхних частот

Силовой трансформатор.

Трансформатором называется статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток и предназначенное для преобразования посредством электромагнитной индукции одной или нескольких систем переменного тока в одну или нескольких систем переменного тока в одну или несколько других систем переменного тока. Различают двухобмоточные трансформаторы, имеющие две гальванически не связанные обмотки, и трех- и многообмоточные трансформаторы, имеющие три и более гальванически не связанных обмоток. Передача энергии из первичной цепи трансформатора во вторичную цепь происходит посредством магнитного поля.

Трансформатор называется силовым, если он применяется для преобразования электрической энергии в электрических сетях и в установках, предназначенных для приема и использования электрической энергии. К силовым трансформаторам относятся трансформаторы трехфазные и многофазные мощностью 6,3 кВ*А и более, однофазные мощностью 5 кВ*А и более. При меньших мощностях трансформаторы называются трансформаторами малой мощности. Различаю силовые трансформаторы общего назначения, предназначенные для включения в сети, не отличающихся особыми условиями работы, или для непосредственного питания приемников электрической энергии, если эти сети или приемники отличаются особыми условиями работы, характером нагрузки или режимом работы. К числу таких сетей и приемников электрической энергии относятся, например, подземных рудничные и шахтные сети и установки, выпрямительные установки, электрические печи и т.п.

Номинальной мощностью обмотки трансформатора называется указанное на паспортной табличке значение мощности на основном ответвлении обмотки, гарантированное изготовителем в номинальных условиях места установки и охлаждающей среды при номинальной частоте и номинальном напряжении обмотки. Номинальной мощностью двухобмоточного трансформатора является номинальная мощность каждой из его обмоток, в трехобмоточном трансформаторе – наибольшая из его номинальных мощностей трех его обмоток. Номинальный ток обмотки трансформатора определяется по его номинальным мощности и напряжению. При наличии в обмотке регулировочных ответвлений для каждого ответвления устанавливаются свои номинальные мощность, напряжение и ток. Номинальной мощностью автотрансформатора является номинальная мощность обмоток, имеющих общую часть, т.е. проходная мощность.

Основными частями трансформатора являются магнитная система (магнитопровод), обмотки и система охлаждени

Магнитная система (магнитопровод) трансформатора представляет собой комплект пластин или других элементов электротехнической стали или иного ферромагнитного материала, собранных в определенной геометрической форме, предназначенных для локализации в нем основного магнитного поля трансформатора. Магнитная система в полностью собранном виде совместно со всеми узлами и деталями, служащими для скрепления отдельных частей в единую конструкцию, называется остовом трансформатора.

Основным элементом обмотки является виток, т.е. деталь из электрического проводника, или ряд параллельно соединенных таких деталей, однократно обхватывающий часть магнитной системы трансформатора, электрический ток которой совместно с токами других таких деталей и других частей трансформатора создает магнитное поле трансформатора и которой под действием этого магнитного поля наводится электродвижущая сила.

Обмоткой называется совокупность витков, образующих электрическую цепь, в которой суммируются ЭДС, наведенные в витках с целью получения высшего, среднего или низшего напряжения трансформатора или с другой целью. В трехфазном трансформаторе под обмоткой обычно подразумевают совокупность соединяемых между собой обмоток одного напряжения трех фаз.

Основными называются обмотки трансформатора, к которым подводится энергия преобразуемого или от которых отводится энергия преобразованного переменного тока. Кроме основных трансформатор может иметь вспомогательные обмотки, предназначенные, например, для компенсации третей гармонической магнитного поля, подмагничивания магнитной системы постоянным током, питания сети собственных нужд с мощностью существенно меньшей, чем номинальная мощность трансформатора, и т.п.

Обмотки, как правило, выполняются из медного или алюминиевого изолированного провода в виде круговых цилиндров. В двухобмоточном трансформаторе различают обмотку высшего напряжения (ВН), присоединяемую к сети более высокого напряжения, и обмотку низшего напряжения (НН), присоединяемую к сети более низкого напряжения. В трехобмоточном трансформаторе различают обмотки высшего (ВН), среднего (СН) и низшего (НН) напряжения.

Единая конструкция, включающая в собранном виде остов трансформатора, обмотки с их изоляцией, отводы, т.е. проводники, соединяющие обмотки между собой и с другими частями трансформа, части устройства регулирования напряжения, а также все детали служащие для их механического соединения, называется активной частью трансформатора.

Трансформаторы с естественным воздушным охлаждением (сухие трансформаторы) обычно не имеют специальной системы охлаждения. В масляных трансформаторах в систему охлаждения входят бак трансформатора, заливаемый маслом, а для мощных трансформаторов – также и охладители, вентиляторы, масляные насосы, теплообменники и т.п.