Параллельный колебательный контур — Студопедия
Если источник сигнала подключен параллельно элементам L и С, то контур называется параллельным.
При параллельном включении напряжение действующее на L и С одно и тоже, а токи протекающие в L и С разные.

В идеальном контуре без потерь в случае равенства ХС и ХL (ІС и ІL), суммарный ток обращается в 0, то есть сопротивление контура приближается к бесконечности.
Если же частота сигнала спадает, то ХС становится больше чем XL, следовательно IС < IL, то есть появляется ток отстающий на 90° от напряжения и следовательно сопротивление контура можно рассматривать как индуктивность.

В реальном контуре присутствуют потери сосредоточенные главным образом в катушке L. При наличии потерь сопротивление контура на резонансной частоте уже не бесконечно.

С учетом потерь, даже при резонансе (XL = ХС), ток в контуре не равен 0, а равен активной составляющей тока в цепи катушки (IK = IL + IR).

Если частоту сигнала изменить в сторону увеличения, то сопротивление XL возрастет, а ХС спадет. Следовательно  растет, a
растет, a 

Ток контура при этом тоже растет и приобретает емкостной характер (угол сдвига фаз φ между напряжением и током равен 0), общее сопротивление контура спадает, а реактивное увеличивается.
Если частоту уменьшать, то XL уменьшится, а ХС возрастет следовательно ІL возрастет, а ІС уменьшится. Ток общий и становится индуктивным (φ < 0). Резонансный ток растет, следовательно общее сопротивление (Z) контура уменьшается, а реактивное растет.

Если частоту сильно изменить, то X начинает убывать, так как при уменьшении частоты индуктивное сопротивление спадает, а при увеличении частоты емкостное сопротивление спадает. Таким образом на резонансной частоте контура сопротивление контура (Z) наибольшее и имеет активный характер (φ между напряжением и током равно 0), а при изменении частоты оно быстро уменьшается и приобретает комплексный характер.
В параллельном контуре как и в последовательном условием резонанса является равенства реактивных сопротивлений.
XL = ХC
Следовательно для параллельного контура остаются такие выражения для f

В отличии от последовательного контура в параллельном контуре добротность показывает во сколько раз ток в элементах контура больше тока потребляемого источника сигнала.
Математическое выражение для резонансного сопротивления параллельного контура (Z0) выводится из условия, что ток в индуктивной ветви IК определяется комплексным сопротивлением в этой ветви.



тогда  (так как
(так как 
 — резонансное сопротивление параллельного контура.
— резонансное сопротивление параллельного контура.
Так как резонансное сопротивление контура зависит от частоты, то его можно использовать для выделения сигнала нужных частот.
Кроме последовательного и параллельного контуров, называемых контурами 1-го вида, в радиотехнике часто применяют контуры П-го и Ш-го вида.
Особенностью контуров П-го вида является то, что у них есть две резонансные частоты f0посл и f0пар.

Например в контуре с двумя индуктивностями можно определить такую частоту (ωпосл), на которой L2 и С образуют последовательный колебательный контур, но на частотах ниже ωпосл общее реактивное сопротивление цепи L2C(x) имеет емкостной характер. Следовательно вместе с L1 цепь L2C образует параллельный колебательный контур. Частота последовательного резонанса определяется из условия:

параллельного резонанса из условия:


Аналогично в контуре с двумя конденсаторами в цепи: C2L наблюдается последовательный резонанс при условии ωL = 1/ωС2 и параллельный резонанс при условии  .
.
Эквивалентное сопротивление контуров П-го и Ш-го вида (R0e), при параллельном резонансе меньше, чем у контура 1-го вида с теми же элементами.
Например если в контуре П-го вида с двумя катушками L1 = L2 = L, то R0e для контура 1-го вида  , а для контура П-го вида будет
, а для контура П-го вида будет  , то есть в четыре раза меньше.
, то есть в четыре раза меньше.
Если обозначить отношение  — коэффициент включения, то получится:
— коэффициент включения, то получится:

где р ≤ 1 — коэффициент включения.
Это соотношение справедливо также для контура Ш-го вида с двумя конденсаторами только в этом случае:

Из выражения * видно что для контура П-го и Ш-го вида шунтирующее действие внешней нагрузки ослабляется в 1/р2 раз.
Подключение к параллельному контуру (либо к отдельному конденсатору или индуктивности) источника сигнала с внутренним сопротивлением Ri, либо другого внешнего сопротивления, уменьшит его сопротивление.
Например если к контуру с сопротивлением R0е = p2/r подключить источник сигнала с сопротивлением R (при
(при  )
)
Но это равносильно тому, что в контуре увеличилось сопротивление потерь r в два раза.
Следовательно между шунтирующим внешним сопротивлением и сопротивлением потерь существует обратно пропорциональная зависимость. Таким образом если к параллельному контуру подключено внешнее шунтирующее сопротивление Rш, то это равносильно включению дополнительного сопротивления последовательно с катушкой индуктивности, ухудшающего добротность контура.


Например есть контур у которого:
ρ = ХL =ХC =100 Ом, на частоте 1000кГц, и r =1Ом.
Тогда Q = ρ/2 =100, П = 2Δf = f0/Q =1000/100 =10Кгц
R0e = ρ2/r = 10 кОм.
Если к этому контуру подключить источник сигнала (например антенну) с внутренним сопротивлением 1100 Ом, то это равносильно включению дополнительного сопротивления потерь.

Теперь 

Таким образом пропускание увеличилось в 10 раз. Если же теперь подключить антенну к отводу от 1/10 витков, то



При этом полоса почти не расширяется, но ослабляется входящий сигнал из-за падения напряжения на R
Связанные колебательные контуры
Контуры называются связанными, если энергия одного из них через элемент связи передается во второй. Элементом связи может быть, например магнитное поле, которое пересекает обороты катушки двух колебаний контуров, такая связь называется трансформаторной.

Если в первый контур подавать сигнал (U) с частотой равной резонансным частотам этих контуров, то в первом контуре возникнет ток І1 совпадающий с фазой U. Этот ток создает в катушке L1 магнитный поток Ф, который пересекает витки катушки L2 и вызовет в ней ЭДС взаимоиндукции U1,2:
 , т.к.
, т.к. 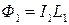 , то
, то  , где М – взаимоиндуктивность.
, где М – взаимоиндуктивность.
Эта ЭДС вызовет ток І2 совпадающий по фазе с U1,2 (при резонансе R – активное). Ток І2 вызовет ЭДС взаимоиндукции (U2,1) катушки L1.

Эта ЭДС направленная против U, поэтому суммарное напряжение и ток І1 уменьшается. Это равнозначно тому, что увеличилось сопротивление потерь Rn1 в первом контуре. Таким образом, второй контур как бы вносит сопротивление в первый, причем тем большее, чем больше взаимоиндукция (М). Если частота сигнала не отвечает резонансным частотам контуров, то вносимое сопротивление будет иметь активную и реактивную составляющие.

Если f сигнала < f0 контуров, то их сопротивление имеет емкостной характер. При этом токи в обоих контурах опережают напряжения .ЭДС U2,1 можно представить активной и реактивной составляющими. Действие активной составляющей (U2.1А)можно расценивать, как активное вносимое сопротивление. а реактивной (U2.1Р),как реактивное вносимое сопротивление.
Таким образом, реактивная составляющая направлена одинаково с ЭДС самоиндукции U, то они суммируются и это равносильно увеличению индуктивности, то есть увеличению индуктивного сопротивления катушки. Поэтому Хвнес – индуктивное.
Если fС > f0 контуров, то их сопротивление носит индуктивный характер, а токи в обоих контурах отстают от напряжений.

В этом случае ЭДС U2,1 также имеет активную (U2,1А) и реактивную (U2,1Р) составляющие, поэтому вносится активное и реактивное сопротивление. Причем реактивная составляющая направлена против ЭДС самоиндукции катушки L1, то есть уменьшит напряжение на ней, поэтому реактивное внесенное сопротивление имеет емкостной характер.

Кроме трансформаторной связи между контурами может быть автотрансформаторная связь, и связь за счет внутренней и внешней емкости.



При любом виде связи, связь осуществляется путем сопротивления связи.
При трансформаторной связи, сопротивление связи определяется взаимоиндуктивностью.

При индуктивной связи, сопротивление связи определяется катушкой связи.
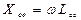
При индуктивной внутриемкостной связи, сопротивление связи зависит от емкости связи.

Аналогично, при зовніємнісному связи.

При любом виде связи, степень связи количественно оценивается коэффициентом связи.
 ,
,
где Хсв – реактивное сопротивление элемента связи. Х1, Х2 – реактивное сопротивление элементов контуров, которые имеют такой же характер, как и Хсв.
— Для трансформаторной связи:
 .
.
— Для автотрансформаторной связи:

— Для внутриемкостной связи:

— Для внешнеемкостной связи:

Чем больше степень связи между контурами (Ксв), тем больше вносимые сопротивления. Так как вносимое сопротивление имеет иной характер, чем сопротивление контура при расстройке (при f < f0, XK – носит емкостный характер, Хвнес – индуктивный и наоборот), то при увеличении Ксв на частотах отличных от резонансной, может выполняться условие Хвнес – ХК = 0, то есть возникает резонанс.
Таким образом, на частоте ниже f0, сопротивление контура несет в себе емкостной характер, а Хвнес – индуктивный и на некоторой частоте f1 возникает резонанс (нижняя частота связи). А на частоте выше f0,сопротивление контура несет в себе индуктивный характер, а вносимое – емкостный характер, и на f2 может возникнуть еще один резонанс (верхняя частота связи). При этом, если увеличивать Ксв, то увеличивается Хвнес и частоты связи изменяются (раздвигаются относительно f0), а если Ксв уменьшашать, то и Хвнес тоже уменьшается и тогда частоты связи сближаются к f0 .

При некотором Ксв < Ккритич частоты связи (резонансы) вообще не возникают, так как Хвнес < Хк.
При Ксв > Ккритич в форме АЧХ на fо появляется провал из-за того, что Rвнес возрастает и становится больше, чем Rвнес на частотах частотных резонансов. При К = Ккритич ,Rвнес= Rп1. Это условие выполняется и на частотах связи.
Качественные показатели связанных контуров определяются в зависимости от того, какие требования предъявляются к ним.
Чаще всего от связанных контуров требуется обеспечить определенную полосу пропускания при высокой крутизне АЧХ. В связанных контурах П (полоса) определяется не только через f0 и Q, а и через Ксв. При очень маленькой связи (Ксв < Ккритич) полоса связанных контуров меньше полосы одиночного контура почти в два раза. Псв=0,64 Под (при Ксв << Ккритич).
При увеличении Ксв полоса расширяется и при Ксв=0,68Ккритич она равна полосе одиночного контура Псв= Под (при Ксв=0,68Ккр).
При Ксв= Ксв, Псв= 1,41Под.
С увеличением Ксв ,П расширяется и при провале в АЧХ связанных контуров до уровня 0,707 Ксв= 2,41Ккр, а Псв= 3,1Под.
Следовательно в отличие от одиночных контуров в связанных колебательных контурах можно регулировать П изменением Ксв.
Еще одним достоинством связанных контуров является более высокая крутизна скатов АЧХ. Это обьясняется тем, что ток второго контура зависит не только от f источника сигнала, но и от тока первого контура, который тоже уменьшается с изменением f.
В зависимости от настройки контуров различают первый частичный, второй частичный, а также полный и сложный резонанс.
Первый частичный резонанс наблюдается, если частота настройки первого контура совпадает с f источника сигнала, а частота второго не совпадает. В этом случае при расстройке первого контура ток его (І1) уменьшается и потому уменьшается U1,2 и ток второго контура (І2) (f01 зависит от f02, так как зависит от Хвн, которое зависит от f02).

Второй частичный резонанс наблюдается, если f второго контура совпадает с f сигнала, a f первого не совпадает. Тогда при расстройке второго контура уменьшается І2, но и уменьшается и вносимое им сопротивление в первый контур, поэтому ток І1 увеличивается.

Чтобы получить полный резонанс необходимо каждый контур в отдельности настроить на f сигнала, при очень малой связи между ними, а затем можно увеличивать Ксв до Ксв=Ккр, при этом вносимые сопротивления будут незначительны и не появяются резонансы на частотах связи.
Только при полном резонансе можно добиться наибольшего КПД и наибольшей мощности во втором контуре. С увеличением Ксв увеличивается Rвн, поэтому ток І1 уменьшается.
С увеличением Ксв растает ЭДС взаимоиндукции U1,2, которая вызывает ток І2. Но при Ксв > Ккр ток І2 уменьшается т.к. ток І1 тоже уменьшается, a Rвнес из первого во второй контур увеличивается


Электрические фильтры и их классификация
Электрический фильтр – это устройство пропускающее сигналы определенных частот.
Электрические фильтры обычно используются для выделения требуемых гармонических составляющих из несинусоидальных сигналов.
Частоты, которые фильтры пропускают (должны пропускать) без заметного ослабления, составляют полосу пропускания фильтра.
Частоты, которые фильтры не пропускают составляют полосу задерживания фильтра.
Частота разделяющая полосу пропускания и полосу задерживания называется частотой среза.
В зависимости от того какие частоты пропускает фильтр, различают фильтры низких и верхних частот, а также полосовые и ре-электронные фильтры.

Любой фильтр можно характеризовать либо коэффициентом  , либо вносимым затуханием
, либо вносимым затуханием  .
.

Причем в полосе пропускания коэффициент передачи должен быть максимальным и постоянным, а в полосе задерживания – минимальным (нулевым).
Все реальные фильтры не обеспечивают нулевого коэффициента передачи в полосе задерживания и постоянного коэффициента передачи в полосе пропускания.

Существует несколько различных видов фильтров. Например: RC, LC, CL, кварцевые, пьезоэлектрические, электромеханические и др.
Параллельный колебательный контур — Студопедия
Параллельный колебательный контур – это частотно-избирательная цепь, образованная параллельным соединением индуктивности  и емкости
и емкости  . Активные потери контура учитываются сопротивлением
. Активные потери контура учитываются сопротивлением  , которое подключается последовательно или параллельно (рис. 5.4а,б). Контур широко используется как самостоятельно (полосовой фильтр), так и в составе различных радиотехнических устройств (автогенераторов, модуляторов, преобразователей частоты и др.).
, которое подключается последовательно или параллельно (рис. 5.4а,б). Контур широко используется как самостоятельно (полосовой фильтр), так и в составе различных радиотехнических устройств (автогенераторов, модуляторов, преобразователей частоты и др.).

Рис. 5.3. Фильтр нижних частот (а), АЧХ и ФЧХ фильтра (б)
Основные параметры контура и их математические выражения [4,7]:
1. Резонансная частота контура –  .
.
2. Добротность контура (рис. 5.4,а) –  , добротность контура (рис. 5.4,б) –
, добротность контура (рис. 5.4,б) –  .
.
3. Волновое сопротивление –  .
.
4. Затухание контура –  .
.

Рис. 5.4. Параллельный колебательный контур с последовательным (а) и
параллельным (б) включением сопротивления потерь
Для описания частотно-избирательных свойств параллельного контура применяют комплексное входное сопротивление  и частотные коэффициенты передачи по току
и частотные коэффициенты передачи по току  и напряжению
и напряжению  – резонансные характеристики контура.
– резонансные характеристики контура.
Комплексное входное сопротивление является основной характеристикой контура. Оно равно отношению комплексной амплитуды выходного напряжения к комплексной амплитуде тока в контуре. Определим эту характеристику для контура, изображенного на рис. 5.4,а.
 .
.
Полагаем, что потери в контуре малы. Это позволяет в области резонансной частоты считать, что  . Тогда
. Тогда
 .
.
Как видно из данной формулы, при резонансе, когда  , входное сопротивление контура носит резистивный характер. Оно называется резонансным сопротивлением и равно
, входное сопротивление контура носит резистивный характер. Оно называется резонансным сопротивлением и равно
 .
.
Продолжая преобразования формулы для  , получим
, получим
 ,
,
где  – частотная расстройка,
– частотная расстройка,  – обобщенная расстройка контура.
– обобщенная расстройка контура.
При малых расстройках в области частот, близких к резонансной  , можно записать
, можно записать
 .
.
Таким образом, комплексное входное сопротивление контура равно
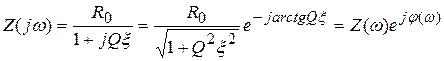 . (5.5)
. (5.5)
Здесь
 – модуль входного сопротивления контура. Зависимость модуля входного сопротивления контура от частоты является амплитудно-частотной характеристикой контура;
– модуль входного сопротивления контура. Зависимость модуля входного сопротивления контура от частоты является амплитудно-частотной характеристикой контура;
 – аргумент входного сопротивления контура. Зависимость аргумента входного сопротивления контура от частоты является фазо-частотной характеристикой контура.
– аргумент входного сопротивления контура. Зависимость аргумента входного сопротивления контура от частоты является фазо-частотной характеристикой контура.
Амплитудно-частотная и фазочастотная характеристики параллельного колебательного контура при различных значениях добротности приведены на рис. 5.5.

Рис. 5.5. АЧХ (а) и ФЧХ (б) параллельного колебательного контура
Определим полосу пропускания контура на уровне  :
:
 ;
;  ;
;  .
.
Отсюда следует  . Данное определение добротности предоставляет возможность ее экспериментального измерения.
. Данное определение добротности предоставляет возможность ее экспериментального измерения.
Колебательный контур — Википедия
Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном − параллельным[1].
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Резонансная частота контура определяется так называемой формулой Томсона:
- f 0 = 1 2 π L C . {\displaystyle f_{0}={1 \over 2\pi {\sqrt {LC}}}.}
Принцип действия
Пусть конденсатор ёмкостью C заряжен до напряжения U 0 {\displaystyle U_{0}} . Энергия, запасённая в конденсаторе, составляет
- E C = C U 0 2 2 . {\displaystyle E_{C}={\frac {CU_{0}^{2}}{2}}.}
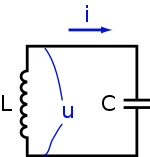 Параллельный колебательный контур
Осциллограмма LC-контура во время замыкания заряженного конденсатора на катушку индуктивности.
Параллельный колебательный контур
Осциллограмма LC-контура во время замыкания заряженного конденсатора на катушку индуктивности.С — 240 нФ (заряженный)
L — 360 нГн
F0 ≈ 542 кГц
При соединении конденсатора с катушкой индуктивности в цепи потечёт ток I {\displaystyle I} , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности), в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора E C = 0 {\displaystyle E_{C}=0} . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
- E L = L I 0 2 2 , {\displaystyle E_{L}={\frac {LI_{0}^{2}}{2}},}
где L {\displaystyle L} — индуктивность катушки, I 0 {\displaystyle I_{0}} — максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть зарядка конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор в этом случае снова будет заряжен до напряжения − U 0 {\displaystyle -U_{0}} .
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
Описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи больше тока, проходящего через весь контур, причём эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.
Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.
Математическое описание процессов
Напряжение на идеальной катушке индуктивности при изменении протекающего тока:
- u L = L d i L d t . {\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}
Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:
- i C = C d u C d t . {\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}
Из правил Кирхгофа, для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:
- u L + u C = 0 , {\displaystyle u_{L}+u_{C}=0,} — для напряжений,
и
- i C = i L {\displaystyle i_{C}=i_{L}} — для токов.
Совместно решая систему дифференциальных уравнений (дифференцируя одно из уравнений и подставляя результат в другое), получаем:
- d 2 q ( t ) d t 2 + 1 L C q ( t ) = 0. {\displaystyle {\frac {d^{2}q(t)}{dt^{2}}}+{\frac {1}{LC}}q(t)=0.}
Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ω = 1 L C {\displaystyle \omega ={\frac {1}{\sqrt {LC}}}} (она называется собственной частотой гармонического осциллятора).
Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:
- i ( t ) = I a sin ( ω t + φ ) , {\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi ),}
где I a {\displaystyle I_{a}} — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний, φ {\displaystyle \varphi } — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой.
Например, при начальных условиях φ = 0 {\displaystyle \varphi =0} и амплитуде начального тока I a {\displaystyle I_{a}} решение сведётся к:
- i ( t ) = I a sin ( ω t ) . {\displaystyle i(t)=I_{a}\sin({\omega }t).}
Решение может быть записано также в виде
- i ( t ) = I a 1 sin ( ω t ) + I a 2 cos ( ω t ) , {\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}
где I a 1 {\displaystyle I_{a1}} и I a 2 {\displaystyle I_{a2}} — некоторые константы, которые связаны с амплитудой I a {\displaystyle I_{a}} и фазой φ {\displaystyle \varphi } следующими тригонометрическими соотношениями:
- I a 1 = I a cos ( φ ) , {\displaystyle I_{a1}=I_{a}\cos {(\varphi )},}
- I a 2 = I a sin ( φ ) . {\displaystyle I_{a2}=I_{a}\sin {(\varphi )}.}
Комплексное сопротивление (импеданс) колебательного контура
Колебательный контур может быть рассмотрен как двухполюсник, представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как
- z ^ ( i ω ) = i ω L 1 − ω 2 L C , {\displaystyle {\hat {z}}(i\omega )\;={\frac {i\omega L}{1-\omega ^{2}LC}},}
где i — мнимая единица.
Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).
Эта частота равна
- ω h = 1 L C {\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}
и совпадает по значению с собственной частотой колебательного контура.
Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.
Для последовательного контура добротность растёт с увеличением L:
- Q = 1 R L C , {\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}
где R — активное сопротивление контура. Для параллельного контура:
- Q = R e C L , {\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}
где R e = L C R L + C {\displaystyle R_{e}={\frac {L}{CR_{L+C}}}} , ( R L + C {\displaystyle R_{L+C}} — сумма активных сопротивлений в цепи катушки и цепи конденсатора[2]).
Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение[3] и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении R e {\displaystyle R_{e}} , которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что R e {\displaystyle R_{e}} в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре R e {\displaystyle R_{e}} легко обретает физический смысл — это активное сопротивление провода катушки и проводников цепи.
Практическое применение
Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях, радиоприёмниках, а также в различных устройствах автоматики. Например, на самолётах Ил-62М, Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя[4].
См. также
Примечания
Литература
- Попов В. П. Основы теории цепей: Учеб. для вузов / В. П. Попов. — 4-е изд., испр. — М.: Высш. шк., 2003. — 575 с.
- Скрипников Ю. Ф. Колебательный контур — М.: Энергия, 1970—128 с.: ил. — (МРБ; Вып. 739)
- Изюмов Н. М., Линде Д. П. Основы радиотехники. — М.:Радио и связь, 1983
Варианты двухзвенных согласующих устройств.1) Устройство согласующее активную нагрузку и активное эквивалентное совпротивление выходного контура. Если необходимо повысить фильтрующие способности этого устройства, то между конденсатором и индуктивностью включается последовательный контур настроенный на эту же частоту.. Тогда получается автотрансформаторный вход передатчика. Реактивное сопротивление конденсатора здесь равно сумме сопротивлений согласующего устройства и кондесатора дополнительного последовательного контура. Если пна подключаемых концах антенны имеется какое-то реактивное сопротивление, то оно может быть нейтрализовано изменением емкости С согласующего устройства. Таким образом это устройство может согласовывать нагрузки, если она меньше эквивалентного сопротивления выходного каскада. Для варианта Для этого устройства целесообразно провести новый расчет Представим это выражение в виде Далее, при последовательном подключении реактивного сопротивление от катушки L1 получим Наконец, введя обозначения и подсоединяя паралелльно катушку XL2 получим Условие резонанаса сводится к равенству нулю мнимого второго члена, что возможно при Отсюда Отсюда следуют два предельных случая , при котором XL2=0 и XL1=0 . После подстановки сюда a и b получим Это очень примечательное выражение, ибо оно дает возможность вычислить сопротивление индуктивности по известному сопротивлению нагрузки и емкостному реактивному соппротивлению параллельного контура. Отсюда видно, что подключение нагрузки к параллельному контуру изменяет частоту резонанса. Расчет по новому выражению для П-контура, для приведенных выше условий, дает значения: с1=60,11 пкф, с2=232пкф, L=9,31мкгн. Как видно, различие в значениях, особенно с2, с ранее приведенным, весьма большое. Именно по этим данным такая настройка и проводится практически. То есть этот расчет показывает, что правильно рассчитанный П-контур действительно хорошо фильтрует сигнал и согласует входное сопротивление антенны в случае отсутствия в нем реактивной составляющей. Но он удобен только в случае лампового выходного каскада с высоким эквивалентным сопротивлением. Для выходного каскада на транзисторах, с низким выходным сопротивлением, расчетные значения конденсаторов оказываются очень большими и трудно выполнимыми практически. Поэтому здесь целесообразно использовать второй вариант комбинации двух Г- образных звеньев, когда они меняются местами и соединяются своими точками с высоким напряжением, а точки с низким напряжением соединяются с антенной и выходным каскадом с низким эквивалентным сопротивлением,. Впрочем, можно несколько изменить Т- контур заменив индуктивности на емкости и наоборот. Тогда будет новый вариант.Можно ли работать на нескольких диапазонах с одной антенной?Судя по рассмотренным выше особенностям П-контура, его применение как согласующего устройства для работы с одной антенной на разных диапазонах, возможно, для ламповых выходных каскадов, если дополнительно компенсировать реактивные сопротивления в самой антенне. Оно ограничено только возможным диапазоном изменения переменных конденсаторов и переменных индуктивностей с переключателями на различное число витков. Допустим очень трудно регулировать очень малые емкости или создавать большие индуктивности. Если антенна питается через коаксиальный кабель, то в принципе это ничего не меняет, ибо надо только рассчитать какой ток он может выдержать в узлах. Для транзисторных выходных каскадов более подходит, описанный выше Т- контур. Однако все зависит еще и от фактических входных параметров антенны на разных диапазонах. Вообще желание иметь одну антенну на все диапазоны вполне осуществимое дело. Надо только хорошо разбираться как это сделать. Трудно ли определить сопротивление излучения и реактивную составляющую антенны на разных диапазонах? Эти параметры также являются весьма завуалированными в различных описаниях, ибо отсутствуют простые способы их определения. Автор практически опробовал несколько вариантов таких устройств и подобрал наиболее удачную схему. Для ее реализации нет необходимости строить специальное сооружение в корпусе ибо в таком виде оно даже может исказить результаты. На первых порах достаточно иметь ГИР (Например, промышленный ГИР1) , микроамперметр на 50 мка с выпрямляющим мостом, два переменных конденсатора 15-500 пкф, две катушки индуктивности в 30 мкгн., с напаянными выводами для захвата крокодильчиками через 2-3 витка, размещенных на корпусах диаметром 60 мм с шагом укладки намотки в 3-1,5мм -для удобства напайки жестких отводов. Можно также использовать катушки со скользящими контактами. Кроме этого надо иметь набор проводов длиной по 10-15 см с крокодильчиками на концах для проведения временных соединений. Затраты на изготовление и приобретение всего названного с лихвой окупятся эмоциональностью лицезрения действия многих полезных функций создаваемого прибора. Полная схема его показана на рис 3: Рис 3. Схема прибора. . Микроамперметр присоединяется параллельно к клеммам 1 совместно с клеммами ВЧ напряжения от ГИРа. Если используется источник ВЧ напряжения с низким выходным сопротивлением, то подключение проводится через резистор. Падение напряжения на нем как раз и фиксируется в резонансе. Установив нужную частоту источника, постепенно увеличивается напряжение ВЧ и проверяется наличие отклонения стрелки прибора.. Теперь можно приступить к первому этапу работы- тарировке емкости конденсаторов по углу поворота и индуктивности по числу витков. Сначала надо добиться резонанса вращением конденсатора С1 в сторону максимума показания прибора. После этого следует увеличить ВЧ напряжение до максимальной точки шкалы. Подключая параллельно контуру различные постоянные конденсаторы и восстанавливая резонанс находится несколько контрольных точек, по которым определяется зависимость емкости конденсатора от угла поворота. Затем по показаниям емкости тарируется катушка индуктивности. Эти данные заносятся в таблицу и интерполируются на целые деления угла поворота через 10 градусов. Аналогичная процедура проводится и с парой С2 , После этого можно приступить к измерениям. Для несведущих напомним, что любая антенна ведет себя двояко. С одной стороны ее можно представить как последовательный контур, соединяющий индуктивность и емкость, и некоторое активное сопротивление называемое сопротивлением излучения. Если к концам 2 на рис 3 подключить активное сопротивление то вместе с L2 и C2 как раз и будет образован последовательный контур. С другой стороны та же самая антенна может работать как параллельный контур по типу L1, C1 с концами 1 замкнутыми сопротивлением излучения. Эти сопротивления, для одной и той же антенны, отличается на порядок. Почему именно так работает антенна никому неизвестно, хотя и есть обоснованные предположения. Но что это именно так, можно убедиться из последующих измерений. Чтобы определить сопротивление излучения при параллельном подключении антенны используется только L1 и C1. Включив ГИР необходимо подать переменное напряжение на одном из рабочих диапазонов добившись резонанса по максимуму отклонения стрелки микроамперметра. Затем необходимо определить емкость конденсатора по углу поворота. После этого к концам катушки L1 подключаются выводы антенны (Для антенны типа длинный провод одним концом является заземление.). После подключения показания прибора снизятся. Это произойдет ввиду наличия в антенне реактивного и активного сопротивления. Вращая ручку конденсатора следует вновь добиться резонанса по максимуму показаний и определить емкость конденсатора. Необходимо также записать новое показание прибора. Если емкость конденсатора увеличилась, то это значит, что антенна обладает дополнительным индуктивным сопротивлением Xa, которое подключаясь параллельно к индуктивному сопротивлению L1 уменьшая его значение. Для определения индуктивного сопротивления антенны, именно в этом случае, необходимо вычислить емкостное сопротивление конденсатора, которое было до подключения антенны и после подключения Xc, Xca, и провести вычисления по формулам X=Xc-Xca Xa=X*Xc/(Xc-X) . Далее по Xa следует вычислить величину индуктивности за зажимах антенны. Подключая затем вместо антенны переменное сопротивление и устанавливая резонанс необходимо добиться того же показания прибора, которое было при подключенной антенне. Это как раз и будет сопротивлением излучения. Если емкость при подключении антенны, в резонансе, уменьшится, то это значит, что антенна обладает дополнительным емкостным сопротивление. Величина изменения емкости конденсатора как раз и будет равна входной емкости антенны. . Работа по определению сопротивления излучению при последовательном резонансе проводится после подключения антенны к разъему 2. При этом устанавливается максимум показаний при вращении конденсатора 1 и минимум показаний при вращении конденсатора 2. Это достигается последовательно несколькими настройками. После этого записываются показания двух конденсаторов и прибора. Далее вместо антенны подключается переменное сопротивление и, повторяя всю процедуру устанавливая резонанс двумя конденсаторами и величину сопротивления так, чтобы добиться прежнего показания прибора. После этого вновь записывают показания двух конденсаторов и тестером измеряют величину переменного сопротивления. Она и будет равна сопротивлению излучения. Величина емкости С1 должна автоматически быть той же, что и при подключении антенны. По значению отклонения С2 с антенной и с активным сопротивлением можно найти величину реактивного сопротивления антенны. Если емкость с антенной была меньше, чем с активным сопротивлением, то это значит, что антенна имеет дополнительное индуктивное входное сопротивление, которое в приборе компенсируется уменьшением емкости. Это уменьшение и будет численно равно индуктивному сопротивлению. Если, наоборот, емкость с антенной больше, что означает уменьшение емкостного сопротивления, то следовательно антенна имеет дополнительное емкостное сопротивление- как раз то, на которое уменьшилось сопротивление конденсатора. Точка подключения к контуру L1, C1 определяется удобством измерений. В качестве примера ниже приведены результаты таких измерение для антенны типа LW длинный провод с заземлением имеющей собственную резонансную частоту в 5,94 мгц.
Что же дальше?После определения сопротивления излучения и реактивного сопротивления на всех диапазонах антенна была подключена к П- контуру передатчика с возможностью регулировки мощности в пределах 1-20 ватт и минимальным эквивалентным сопротивлением выходного каскада на лампе ГУ-50 равным 7500 ом. В результате оказалось, что на 28 мгц антенна работала в последовательном резонансе с добротностью порядка 11, что можно подсчитать разделив 7500 на сопротивление излучения в 75 ом и извлекая квадратный корень из по полученного значения. На 21 мгц антенна работала в параллельном резонансе. На 14 мгц удалось добиться согласования регулировкой конденсаторов контура, но антенна работала в параллельном резонансе- то есть конденсатор связи пришлось уменьшить почти до предела. Естественно большое сопротивление нагрузки привело к уменьшению добротности до 1,4. При этом естественно фильтрация гармоник практически отсутствовала ( для нормальной работы добротность должна быть не ниже 8). На 7 мгц антенна также работала в параллельном подключении с плохими фильтрующими свойствами. На частотах 3,5 и 1,84 мгц добиться хотя бы удовлетворительной работы не удалось. Далее были предприняты попытки применить дополнительные согласующие устройства. На частоте 28 мгц оказалось удобным подключить в разрыв антенны последовательный контур настроенный на эту же частоту переменным конденсатором из того же набора, что и в измерениях. Установка последовательного контура здесь играет двойную роль. Он, с одной стороны, компенсирует излишнее реактивное сопротивление антенны, и действует как фильтр-пробка для гармоник. Путем последующей подстройки контура на 28 мгц удалось несколько улучшить согласование, то есть анодный ток увеличился. На 21 мгц таким добавлением также несколько улучшилось согласование. На частоте 14 мгц добиться перехода в последовательный резонанс не удалось. Но за счет установки последовательного контура значительно увеличилась добротность и емкость конденсатора связи стала больше. То есть произошло смещение в сторону последовательного резонанса и добротность стала равной примерно 8. Отдаваемая мощность увеличилась примерно на 20 процентов.. Это же самое произошло и на частоте 7 мгц., где мощность увеличилась на 25-30 процентов. На частоте 3,5 мгц., с помощью последовательного контура удалось полностью компенсировать реактивное сопротивление и антенна хорошо работала в последовательном резонансе отдавая полную мощность при высокой добротности- около 20-ти. На частоте 1,84 мгц оказалось целесообразным подключить антенну к параллельному контуру и того же набора, что и при измерениях. Затем на 1/5 витков катушки был подключен выход передатчика, что снизило сопротивление нагрузки до 760 ом Далее настройкой П-контура и конденсатора параллельного контура весьма своеобразным способом удалось добиться полного согласования и отдачи мощности так, что этот диапазон стал доступным несмотря на 13-метровую антенну. Из параметров антенны должно быть ясным почему именно на этом диапазоне пришлось применить параллельный контур- ведь сопротивление излучения в параллельном резонансе, для этого диапазона, очень велико. Таким образом в данном конкретном случае удалось согласовать имеющуюся антенну для работы на всех диапазонах без каких-либо действий над самой антенной, а лишь только путем установки дополнительного последовательного контура.. Только в диапазоне 1,84 мгц был установлен дополнительный параллельный контур. Думаю, что таким же образом можно исследовать любую антенну и добиться удовлетворительной или даже хорошей ее работы не загрязняя эфир побочными излучениями. Характерной особенностью работы настроенной антенны является полное совпадения максимума мощности с максимумом тока и напряжением в антенне и максимумом анодного тока, а также максимума напряженности поля. Таким образом однозначно решается вопрос о способе определении точки полной настройки антенны- ее можно определять только по максимальному анодному току. КСВ-метр оказался лишним. Кстати он определяет только отношение мощности отраженной или возвращаемой мощности, ввиду несогласованности, к подводимой, но не раскрывает причину почему это происходит. При полном согласовании полностью пропадают признаки какого-либо самовозбуждения или наличия ВЧ на ключе, педали управления и наушниках. Более того практически исчезают помехи телевидению там, где ранее, как казалось, они были неизбежны. Приведенный пример послужит помощью тем, кто уже имеет передатчик с П- контуром. Для тех же, кто имеет импортную аппаратуру с фиксированным выходным эквивалентным сопротивлением, например в 50 ом, то здесь несколько сложней добиться именно такого входного сопротивления от антенны. Очевидно придется сделать специальное согласующее устройство использующее свойства Г- образного звена последовательного контура… Беспокоиться о фильтрации гармоник здесь не придется ибо на выходе, как правило, сигнал уже хорошо отфильтрован. Надо только избавиться от реактивной составляющей за счет дополнительного значения последовательного включения емкости или индуктивности. Для тех, кто занимается конструированием передающей аппаратуры на транзисторах придется решать задачу согласования при очень маленьком эквивалентным сопротивлении выходного каскада. Как отмечено выше это удобней сделать Т-контуром. Например, антенна, с приведенными выше параметрами, согласовывалась с транзисторным выходом трансивера мощностью 2 ватта, с эквивалентным выходным сопротивлением в 35 ом, на трех диапазонах 14, 7 и 3,5 мгц. В первом случае, ввиду отсутствия реактивной составляющей антенны, использовался Т-контур, в котором катушка индуктивности подключалась одним концом к массе, а ко второму концу подключался корпус двухсекционного переменного конденсатора, неподвижные и изолированные секции которого образовывали две ветви. К одной из них подключалась антенна, а ко второй -выход передатчика. Затем подбором витков и настройкой в резонанс по максимуму коллекторного тока устанавливалось полное согласование. Впрочем на этом же диапазоне хорошо работал просто последовательный контур, у которого катушка индуктивности подключалась к массе, а конденсатор- к выходу трансивера. Антенна присоединялась к части витков катушки индуктивности так, чтобы при резонансе ток был максимально допустимым. Кстати, этот вариант очень простой и удобный. Надо только соблюдать условия достаточности фильтрации сигнала устанавливая значения емкости и индуктивности соответствующие большой добротности . Добротность рассчитывается как корень квадратный из частного от деления сопротивления в точке соединения этих элементов на эквивалентное сопротивление выходного каскада. На диапазоне 7 мгц использовался только последовательный контур подключенный как описано выше. Поскольку на этом диапазоне антенна имеет дополнительное индуктивное сопротивление, то, при подключении ее к части витков индуктивности контура, уменьшает индуктивность той части катушки, к которой она присоединяется. Это уменьшение компенсируется подстройкой конденсатора. На диапазоне 3,5 мгц также использовался последовательный контур. При этом катушка индуктивности подключалась к массе, а антенна- к конденсатору. Выход от передатчика подключался к части витков катушки индуктивности. Поскольку на этом диапазоне антенна имеет емкостное сопротивление, то оно компенсируется увеличенной индуктивностью контура. Таким образом и в этом случае удается добиться хорошего согласования.ЗаключениеЗа долгую и славную эпоху существования радиолюбительского движения энтузиасты эфира внесли большой вклад в теорию и практику проведения связей и конструирования аппаратуры. Думаю, что появление этой статьи побудит новую волну многочисленных исследователей по раскрытию еще неизвестных закономерностей в области антенн. Мы просто должны преодолеть то, что нам еще неизвестно или в чем мы сомневаемся . Несмотря на появление специальных импортных Матч-боксов, в том числе и встроенных в трансивер, с автоматической подстройкой под любую антенну, которые как бы уже все решают, в основе их, все еще, просто механическая копировка известных решений без осмысленного применения. Основываясь на изложенных здесь принципах и при использовании компьютерных программ, можно быстро рассчитать любое устройство и, затем, с меньшими затратами провести опытную проверку с минимальной доработкой. Это дает также возможность внести изменения в существующие конструкции, где по разным причинам оказались скрытыми неучтенные возможности или погрешности в расчетах. |
Для простого параллельного контура (рис. 16.1 а) имеем  ,
,  . Отсюда для контура без потерь получаем
. Отсюда для контура без потерь получаем

где  – волновое или характеристическое сопротивление контура,
– волновое или характеристическое сопротивление контура,
 – резонансная частота,
– резонансная частота,  – относительная расстройка.
– относительная расстройка.
Частотные характеристики  приведены на рис. 16.2.
приведены на рис. 16.2.
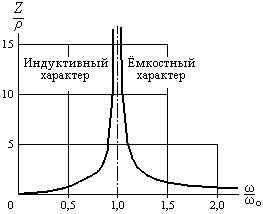
Рис. 16.2. Относительные частотные характеристики сопротивления простого идеального параллельного колебательного контура
В области частот вблизи резонансной для реальных контуров, имеющих потери, обычно выполняются условия
 и
и 
Поэтому в числителе выражения (16.1) можно пренебречь активными составляющими сопротивлений, а в знаменателе этого делать нельзя, так как вблизи резонансной частоты реактивная составляющая мала. С учётом сказанного получаем



где  – добротность контура,
– добротность контура,  – полное сопротивление потерь – сумма сопротивлений потерь ветвей при последовательном обходе параллельного контура,
– полное сопротивление потерь – сумма сопротивлений потерь ветвей при последовательном обходе параллельного контура,  – активная и
– активная и  – реактивная составляющие полного сопротивления параллельного контура.
– реактивная составляющие полного сопротивления параллельного контура.
Следовательно, сопротивление простого параллельного колебательного контура с потерями изменяется с частотой как ток в последовательном колебательном контуре (рис. 16.3).

Рис. 16.3. Относительные частотные характеристики сопротивления простого параллельного колебательного контура с потерями
Сопротивление контура на резонансной частоте  максимально и имеет величину
максимально и имеет величину

а ток в неразветвлённой части цепи минимален и равен

Сопротивления ветвей на резонансной частоте с учётом неравенств (16.4) можно считать чисто реактивными и по модулю равными друг другу

Следовательно, величины токов в ветвях на резонансной частоте будут одинаковыми

и в  раз больше тока в неразветвлённой части цепи. Поэтому резонанс в схеме параллельного колебательного контура называют резонансом токов, векторная диаграмма которого приведена на рис. 16.4.
раз больше тока в неразветвлённой части цепи. Поэтому резонанс в схеме параллельного колебательного контура называют резонансом токов, векторная диаграмма которого приведена на рис. 16.4.

Рис. 16.4. Векторная диаграмма токов и напряжений на резонансной частоте для простого параллельного колебательного контура с потерями
Рассмотрим проводимость параллельного контура вблизи резонансной частоты, используя формулу (16.5 а),


Следовательно, вблизи резонансной частоты контур может быть представлен эквивалентной схемой (рис. 16.5).
Коэффициент передачи цепи с простым параллельным колебательным контуром (рис. 16.6)


изменяется с частотой по закону, аналогичному закону изменения сопротивления контура.

Рис. 16.5. Эквивалентная схе- Рис. 16.6. Цепь с простым парал-
ма параллельного колебательного лельным колебательным контуром
контура
Здесь  – коэффициент передачи схемы на резонансе,
– коэффициент передачи схемы на резонансе,  – эквивалентная добротность контура.
– эквивалентная добротность контура.
Внутреннее сопротивление источника сигнала  весьма существенно влияет на АЧХ цепи, расширяя полосу пропускания и ухудшая избирательные свойства контура. Для уменьшения указанного влияния внутреннее сопротивление источника сигнала необходимо выбирать много большим, чем
весьма существенно влияет на АЧХ цепи, расширяя полосу пропускания и ухудшая избирательные свойства контура. Для уменьшения указанного влияния внутреннее сопротивление источника сигнала необходимо выбирать много большим, чем  (рис. 16.7). Однако увеличение
(рис. 16.7). Однако увеличение  уменьшает коэффициент передачи.
уменьшает коэффициент передачи.

Рис. 16.7. Влияние внутреннего сопротивления источника эдс на полосу пропускания простого параллельного колебательного контура
Параллельный колебательный контур с двумя емкостями
Параллельный колебательный контур с двумя индуктивностями
Простой параллельный колебательный контур
Основные понятия
Параллельный колебательный контур
ЛЕКЦИЯ 16
План лекции:
Параллельным колебательным контуром называют электрическую цепь с параллельным соединением  элементов. Различают простой и сложные (с двумя индуктивностями и двумя ёмкостями) параллельные колебательные контуры (рис. 16.1).
элементов. Различают простой и сложные (с двумя индуктивностями и двумя ёмкостями) параллельные колебательные контуры (рис. 16.1).
Параллельные колебательные контуры, которые характеризуются неполным включением индуктивности или ёмкости в ветвь, называют сложными. Коэффициентом включения называют отношение сопротивления ветви на резонансной частоте контура к резонансному сопротивлению всего контура.
Параллельные колебательные контуры применяют в тех случаях, когда требуется получить большое сопротивление на резонансной частоте.
Специально сопротивления  и
и  в схему не включают. Это – собственные потери индуктивных и емкостных элементов.
в схему не включают. Это – собственные потери индуктивных и емкостных элементов.
Входное сопротивление любого из трёх видов контуров может быть рассчитано по формуле


Рис. 16.1. Простой (а) и сложные (б, в) параллельные колебательные контуры
Для любого параллельного контура без потерь, когда  , его сопротивление является чисто реактивным
, его сопротивление является чисто реактивным

Выясним, как изменяется ток в цепи и напряжение на контуре при изменении частоты генератора, имея в виду, что внутреннее сопротивление генератора не зависит от частоты, а сопротивление контура зависит.
Если
внутреннее сопротивление генератора  значительно меньше
резонансного сопротивлений контура,
то падение напряжения на внутреннем
сопротивлении генератора мало, и им
можно пренебречь.
значительно меньше
резонансного сопротивлений контура,
то падение напряжения на внутреннем
сопротивлении генератора мало, и им
можно пренебречь.
Будем
считать, что  .
В этом случае напряжение на контуре не
зависит от частоты и всегда равно э. д.
с. генератора. Ток
.
В этом случае напряжение на контуре не
зависит от частоты и всегда равно э. д.
с. генератора. Ток в
общей цепи
в
общей цепи
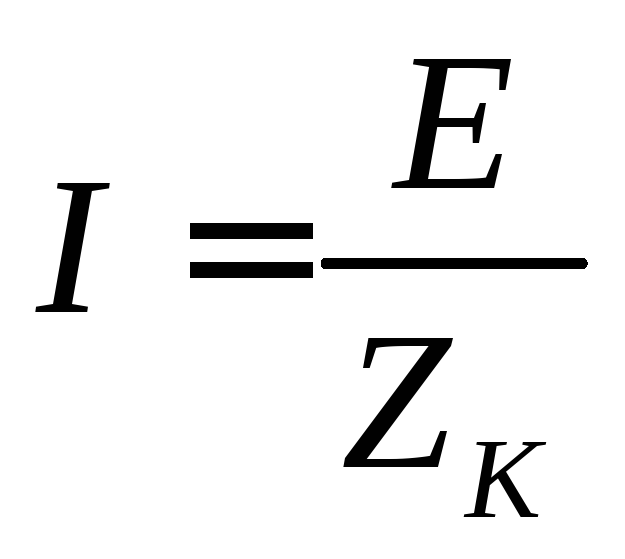 .
.
Необходимо
учитывать, что сопротивление  контура – комплексное,
т. е. состоит из активной и реактивной
составляющих. Зависимость напряжения
на контуре и тока
контура – комплексное,
т. е. состоит из активной и реактивной
составляющих. Зависимость напряжения
на контуре и тока  в общей цепи при
в общей цепи при показана на рис.18.
показана на рис.18.
Ток в цепи при резонансе имеет наименьшее значение, равное
 .
.
Кривая, показывающая зависимость тока в цепи от частоты генератора, называется резонансной кривой тока.

Рис.18.
Зависимость напряжения и тока параллельного
контура от частоты при  .
.
Говорить
о резонансной кривой напряжения при  не имеет смысла, так как напряжение на
контуре остается неизменным.
не имеет смысла, так как напряжение на
контуре остается неизменным.
Если
внутреннее сопротивление генератора
значительно больше резонансного
сопротивления контура ,
то полное сопротивление
цепи можно считать практически неизменным,
равным
,
то полное сопротивление
цепи можно считать практически неизменным,
равным  . Ток в общей цепи при
этом не зависит от частоты генератора
и равен
. Ток в общей цепи при
этом не зависит от частоты генератора
и равен
 ,
,
где  – электродвижущая сила генератора
как идеального генератора напряжения.
– электродвижущая сила генератора
как идеального генератора напряжения.
В этом случае не следует говорить о резонансной кривой тока, так как с изменением частоты генератора ток в цепи практически не изменяется (рис.19).

Рис.19.
Зависимость напряжения и тока параллельного
контура от частоты при 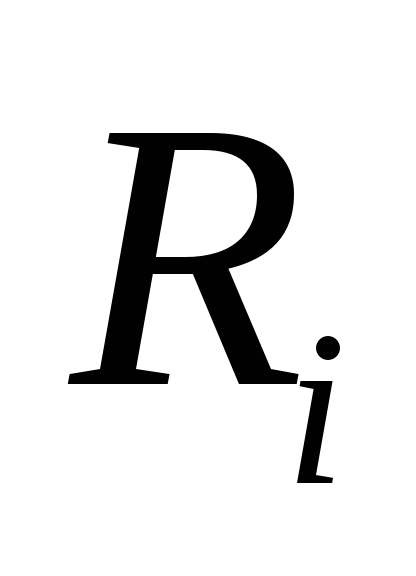 >>
>>
Напряжение на контуре при этом хотя и составляет небольшую часть э. д. с. генератора, но при изменении частоты генератора резко изменяется.


Рис.20.
Зависимости напряжения (а) и тока (б)
параллельного контура от частоты при
различных соотношениях между внутренним
сопротивлением генератора  и сопротивлением контура
и сопротивлением контура
Поведение резонансных характеристик параллельного контура при различных внутренних сопротивлениях генератора показано на рисунке 20, из которого следует, что:
(1)
форма резонансных кривых параллельного
контура зависит от соотношения между  и
и  ;
;
(2) резонансная кривая тока и резонансная кривая напряжения параллельного контура не подобны друг другу по форме.
Поэтому
для параллельного контура следует
различать полосу пропускания по току
и по напряжению. В общем случае, когда  и
и  соизмеримы
по величине, резонансные кривыетока и напряжения можно изобразить так,
как показано на рис. 20. Значения
полос пропускания по напряжениюи по токуне равны:
соизмеримы
по величине, резонансные кривыетока и напряжения можно изобразить так,
как показано на рис. 20. Значения
полос пропускания по напряжениюи по токуне равны:
 .
.
Полоса
пропускания контура по току – это полоса частот, в
пределах которой ток в цепи изменяетсяне более чем в  раз
по сравнению с током при резонансе.
раз
по сравнению с током при резонансе.
Соответственно полосой пропускания
по напряжению будем
называть полосу частот, в пределах
которой напряжение на контуре изменяется
не болеечем в раз по сравнению с напряжением при
резонансе.
раз по сравнению с напряжением при
резонансе.
Полоса пропускания
параллельного контура по току имеет наименьшее значение при
имеет наименьшее значение при ,
и в этом случае равна полосе пропускания
последовательного контура по току
,
и в этом случае равна полосе пропускания
последовательного контура по току с такими же параметрамиL, С,R. Величина
полосы пропускания определяется формулой
с такими же параметрамиL, С,R. Величина
полосы пропускания определяется формулой
 .
.
Расчеты
показывают, что при  полоса пропускания контура по току
увеличивается до значения
полоса пропускания контура по току
увеличивается до значения

При
дальнейшем увеличении  полоса пропускания
по току растет и при
полоса пропускания
по току растет и при  становится
бесконечно большой.
становится
бесконечно большой.
Полоса
пропускания параллельного контура по
напряжению  при
при  равна
полосе пропускания последовательного
контура по току
равна
полосе пропускания последовательного
контура по току  с такими же параметрами L, С, R и определяется формулой
с такими же параметрами L, С, R и определяется формулой
 .
.
Однако этот случай представляет чисто теоретический интерес, поскольку напряжение на контуре при этом бесконечно мало.
При  полоса пропускания параллельного
контура по напряжению
полоса пропускания параллельного
контура по напряжению в два раза больше полосы пропускания
последовательного контура по току
в два раза больше полосы пропускания
последовательного контура по току  с такими же параметрами:
с такими же параметрами:
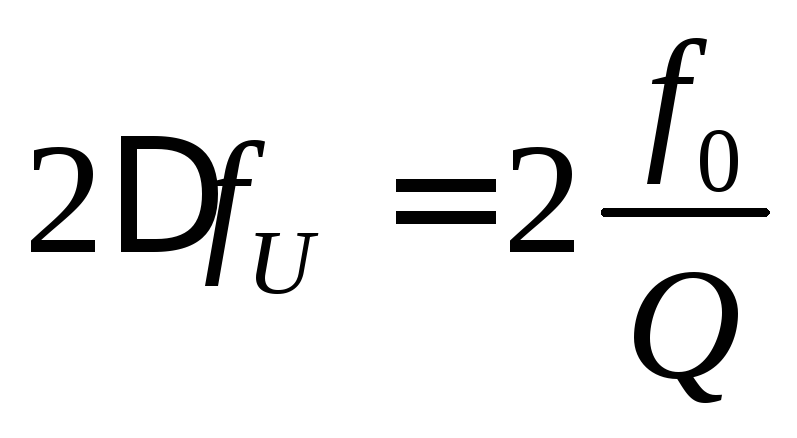 .
.
Принципиальное различие между последовательной и параллельной цепью существует в зависимости от ориентации компонентов в цепи. В последовательной схеме множество компонентов соединены каскадным образом, то есть хвостовая часть компонента соединена с головкой другого.
Находясь в параллельной цепи, несколько компонентов соединены в направлении головы к голове и хвоста к хвосту.
В этом разделе мы обсудим основные дифференцирующие факторы последовательных и параллельных цепей.Но перед этим давайте посмотрим, что содержится в этой статье.
Содержимое: серия против параллельной цепи
- Сравнительная таблица
- Определение
- Ключевые различия
- Заключение
Сравнительная таблица
| Основа для сравнения | СерияСхема | Параллельная цепь|
|---|---|---|
| Ориентация компонентов | Компоненты соединяются один за другим. | Здесь компоненты соединяются в направлении головы к голове и хвоста к хвосту. |
| Ток | Одинаковый ток протекает через все компоненты в цепи. | Различный ток протекает через каждый компонент в цепи. |
| Напряжение | Для каждого компонента существует разная разность потенциалов (напряжение). | Разность потенциалов (напряжение), существующая на различных компонентах в цепи, одинакова. |
| Количество путей | Один | Несколько (зависит от количества компонентов). |
| Ошибка | Ошибка в одном из компонентов схемы вызывает помехи в работе всей цепи. | Неисправность в одном компоненте не препятствует работе остальной цепи. |
| Устранение неисправностей | Сложно. | Довольно просто. |
| Эквивалентное сопротивление | Эквивалентное сопротивление всегда больше, чем самое высокое значение сопротивления в последовательном соединении. | Эквивалентное сопротивление всегда имеет меньшее значение, чем любой из отдельных резисторов, подключенных параллельно. |
Определение последовательной цепи
В последовательной схеме компоненты схемы соединены друг с другом или, можно сказать, каскадным способом.
Более конкретно, мы можем сказать, что последовательная схема обеспечивает соединение таким образом, что хвостовая часть одного компонента напрямую соединяется с головкой другого и т. Д., Что соответствует двум концам батареи.
На рисунке ниже показано последовательное соединение 4 резисторов в цепи:
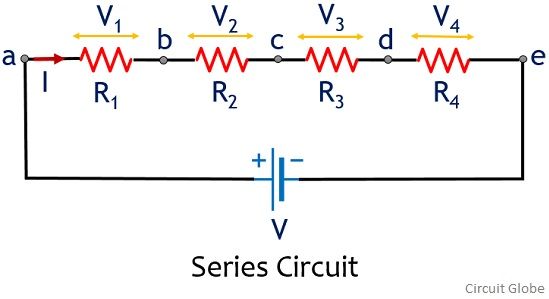
Как мы можем ясно видеть, что компоненты каскадируются в одну линию, таким образом, один и тот же ток, я буду протекать через все резисторы последовательной сети. При этом разная разность потенциалов существует между различными резисторами схемы.
Можно понять таким образом, что, если один и тот же ток течет среди всех резисторов, то падение на каждом резисторе будет зависеть от сопротивления, предлагаемого каждым резистором в цепи.
Таким образом, мы можем сказать, что в последовательной цепи из-за наличия одного пути, один и тот же ток течет через все компоненты. Таким образом, возникновение существования разной разности потенциалов (напряжения) на каждом компоненте.
Определение параллельной цепи
В параллельной цепи компоненты расположены таким образом, что головки каждого компонента соединены вместе с общей точкой. При этом хвосты связаны между собой еще одной общей точкой.Тем самым образуется множество параллельных ветвей в цепи.
На рисунке показано параллельное соединение 4 резисторов в цепи:
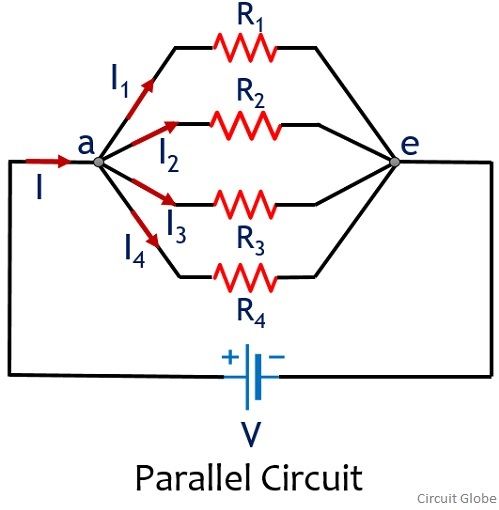
Как мы видим здесь, параллельная цепь имеет 4 ветви, и через каждую ветвь течет разный ток. Но поскольку ветви разделяют общие точки, таким образом, один и тот же потенциал существует в двух точках относительно двух концов потенциала батареи.
Можно также понять, что если на каждом резисторе цепи имеется одинаковая разность потенциалов.Тогда фактический ток, протекающий через каждую ветвь, будет автоматически зависеть от сопротивления, предлагаемого каждым резистором в цепи.
Таким образом, мы можем сказать, что из-за наличия нескольких цепей в цепи, общий ток от источника делится на несколько ветвей, так как напряжение на точках одинаково.
Ключевые различия между последовательным и параллельным контуром
- Компоненты в последовательной цепи расположены по по одному пути от одного конца источника питания до другого конца.Тем не менее, множество компонентов в параллельной схеме расположены в множественных трактов относительно двух концевых выводов батареи.
- В последовательной цепи общий ток протекает через все компоненты схемы. В параллельной цепи различное количество тока протекает через каждую параллельную ветвь цепи.
- В последовательной схеме различное напряжение существует для каждого компонента в цепи. В то время как в параллельной цепи одно и то же напряжение существует на нескольких компонентах схемы.
- Ошибка в одном из компонентов последовательной цепи вызывает помехи в работе всей цепи. В отличие от неисправности в одном компоненте в параллельной сети не препятствуют функционированию другой части схемы.
- Обнаружение ошибки в случае последовательной цепи является сложным, но это довольно легко в параллельных цепях.
- Эквивалентное сопротивление в случае последовательной цепи всегда больше, чем самое высокое значение сопротивления в последовательном соединении.При этом эквивалентное сопротивление в параллельной цепи всегда меньше, чем любое из отдельных сопротивлений в параллельной комбинации.
Заключение
Итак, из этого обсуждения мы можем сказать, что в последовательной цепи протекающий ток остается одинаковым в каждой части схемы. В параллельных цепях напряжение на двух конечных точках ответвлений такое же, как и подаваемое напряжение.
,Серияи параллельные цепи — learn.sparkfun.com
Избранные любимец 48 Серияи параллельные цепи
Простые схемы (с несколькими компонентами) обычно довольно просты для начинающих. Но вещи могут становиться липкими, когда другие компоненты приходят на вечеринку. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, отважный читатель.Ценная информация следует.
В этом руководстве мы сначала обсудим разницу между последовательными и параллельными цепями, используя схемы, содержащие самые основные компоненты — резисторы и батареи — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы объединяете различные типы компонентов, таких как конденсаторы и катушки индуктивности.
В этом уроке
- Как выглядят конфигурации последовательных и параллельных цепей
- Как действуют пассивные компоненты в этих конфигурациях
- Как источник напряжения будет действовать на пассивные компоненты в этих конфигурациях
Рекомендуемое Чтение
Возможно, вы захотите посетить эти учебные пособия по основным компонентам, прежде чем углубляться в построение схем в этом учебном пособии.
Видео
Схемы серии
узлов и ток
Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел . Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема смоделирована на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя одноцветными узлами.
Это полдела, чтобы понять разницу между сериями и параллелями. Нам также необходимо понять , как ток протекает через цепь . Ток течет от высокого напряжения к более низкому напряжению в цепи. Некоторое количество тока будет протекать через каждый путь, по которому можно добраться до точки наименьшего напряжения (обычно называемой заземлением). Используя приведенную выше схему в качестве примера, вот как будет течь ток при его прохождении от положительной клеммы аккумулятора к отрицательной:
Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же схеме, что и выше.Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R 1 и R 2 ) ток поступает так же, как и при выходе. В других узлах (в частности, в трехстороннем соединении между R 2 , R 3 и R 4 ) основной (синий) ток разделяется на два разных. Это ключевое различие между серией и параллелью!
Схемы серииопределены
Два компонента соединены последовательно, если они совместно используют общий узел и если через них протекает один и тот же ток , то .Вот пример схемы с тремя последовательными резисторами:
Есть только один способ протекания тока в вышеуказанной цепи. Начиная с положительного полюса аккумулятора, ток вначале встретится с R 1 . Оттуда ток протекает прямо к R 2 , затем к R 3 и, наконец, обратно к отрицательному выводу батареи. Обратите внимание, что существует только один путь для текущего. Эти компоненты в серии.
параллельных цепей
Определены параллельные цепи
Если компоненты совместно используют двух общих узлов, они расположены параллельно.Вот пример схемы трех резисторов параллельно с батареей:
От положительной клеммы аккумулятора ток течет до R 1 … и R 2 и R 3 . Узел, который соединяет батарею с R 1 , также соединен с другими резисторами. Другие концы этих резисторов аналогичным образом связаны друг с другом, а затем снова связаны с отрицательным выводом батареи. Есть три различных пути, по которым ток может пройти до возвращения в батарею, и связанные резисторы, как говорят, параллельны.
Если все последовательные компоненты проходят через одинаковые токи, параллельные компоненты имеют одинаковое падение напряжения на них — серия: ток :: параллель: напряжение.
Серияи параллельные цепи, работающие вместе
Оттуда мы можем смешивать и сочетать. На следующем рисунке мы снова видим три резистора и батарею. С положительной клеммы аккумулятора ток сначала сталкивается с R 1 . Но по другую сторону от R 1 узел разделяется, и ток может доходить до R 2 и R 3 .Токовые пути через R 2 и R 3 затем снова связываются вместе, и ток возвращается к отрицательной клемме батареи.
В этом примере R 2 и R 3 параллельны друг другу, а R 1 последовательно с параллельной комбинацией R 2 и R 3 .
Расчет эквивалентных сопротивлений в последовательных цепях
Вот некоторая информация, которая может быть вам более полезна.Когда мы соединяем резисторы вместе, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть 10 В на 10 кОм; резистор, закон Ома гласит, что у нас течет ток 1 мА.
Если мы тогда поставим еще 10 кОм; последовательно с первым резистором и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление удвоилось.
Другими словами, есть только один путь для прохождения тока, и мы только усложнили его для прохождения тока.Насколько сложнее? 10k & Ом; + 10кОм; = 20 кОм. И вот как мы рассчитываем резисторы последовательно — только добавляют их значения .
Чтобы сформулировать это уравнение более широко: общее сопротивление N — произвольное число резисторов — это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
А как насчет параллельных резисторов? Это немного сложнее, но не намного.Рассмотрим последний пример, где мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавим еще 10 кОм; параллельно вместо серии. Теперь есть два пути для тока. Так как напряжение питания не изменилось, закон Ома гласит, что первый резистор все еще будет потреблять 1 мА. Но, так же, как и второй резистор, и теперь у нас есть 2 мА от источника, удваивая первоначальный 1 мА. Это означает, что мы сократили общее сопротивление вдвое.
Пока можно сказать, что 10кОм; || 10k & Ом; = 5 кОм; («||» примерно означает «параллельно с»), у нас не всегда будет 2 одинаковых резистора.Что тогда?
Уравнение для добавления произвольного числа резисторов параллельно:
Если взаимные переходы не для вас, мы также можем использовать метод под названием «произведение на сумму», когда у нас есть два резистора параллельно:
Однако этот метод подходит только для двух резисторов в одном расчете. С помощью этого метода мы можем объединить более 2 резисторов, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (опять же как произведение на сумму), но обратный метод может быть менее трудоемким.
Время эксперимента — часть 1
Что вам нужно:
Давайте попробуем простой эксперимент, чтобы доказать, что эти вещи работают так, как мы говорим.
Во-первых, мы собираемся подключить около 10 кОм; резисторы в серии и смотреть, как они добавляются самым таинственным образом. Используя макет, поместите один 10 кОм; резистор, как указано на рисунке и измерьте с помощью мультиметра. Да, мы уже знаем, что это будет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Как только мы убедимся в том, что мир не сильно изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогичным образом, но с выводом от каждого резистора, электрически подключенного через макет, и проведите измерения снова. Теперь счетчик должен сказать что-то близкое к 20 кОм.
Вы можете заметить, что измеренное вами сопротивление может не совпадать с сопротивлением, которое, по словам резистора, должно быть. Резисторы имеют определенное значение с допуском , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10,01 кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читатель должен продолжать это упражнение до тех пор, пока не убедится, что он знает, каким будет результат, прежде чем делать это снова, или у него закончатся резисторы, чтобы прилипнуть к макету, в зависимости от того, что наступит раньше.
Время эксперимента — часть 2
Теперь давайте попробуем это с резисторами в параллельной конфигурации .Поместите один 10 кОм; резистор в макете, как и раньше (мы будем полагать, что читатель уже полагает, что один резистор 10 кОм будет измерять что-то близкое к 10 кОм на мультиметре). Теперь поместите вторую 10 кОм; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора были в электрически соединенных рядах. Но прежде, чем измерить комбинацию, рассчитайте с помощью суммирования по продукту или взаимных методов, каким должно быть новое значение (подсказка: оно будет 5 кОм).Тогда измерить. Это что-то близкое к 5 кОм? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.
Повторите упражнение сейчас с 3, 4 и 5 резисторами. Расчетные / измеренные значения должны составлять 3,33 кОм; 2,5 кОм; и 2кОм соответственно. Все получилось как запланировано? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Пойди попей молочный коктейль, прежде чем мы продолжим. Ты заслужил это.
Полезные правила для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать некоторых творческих комбинаций резисторов.Например, если мы пытаемся создать очень специфический источник опорного напряжения вы почти всегда необходимо очень специфическое соотношение резисторов, значения которых вряд ли будут «стандартные» значения. И хотя мы можем получить очень высокую степень точности значений резисторов, нам, возможно, не захочется ждать X дней, которые требуются для доставки чего-либо, или платить цену за нестандартные значения. Таким образом, в крайнем случае, мы всегда можем построить наши собственные значения резисторов.
Совет №: Равные резисторы в параллельном соединении
Если добавить резисторов N с одинаковым номиналом R параллельно, мы получим R / N Ом.Допустим, нам нужно 2,5 кОм; резистор, но все, что у нас есть, это ящик, заполненный 10 кОм. Параллельное объединение четырех из них дает нам 10 кОм / 4 = 2,5 кОм.
Совет №: допуск
Знай, какую толерантность ты можешь терпеть. Например, если вам нужно 3,2 кОм; резистор, можно было бы поставить 3 10 кОм; резисторы параллельно. Это даст вам 3,3 кОм, что примерно на 4% меньше допустимого значения. Но, если схема, которую вы строите, должна быть с допустимым отклонением более 4%, мы можем измерить наш тайник в 10 кОм, чтобы увидеть, какие значения являются самыми низкими, потому что они тоже имеют допуск.По идее если заначка 10кОм; все резисторы имеют допуск 1%, мы можем получить только до 3,3 кОм. Но производители деталей, как известно, допускают именно такие ошибки, поэтому стоит немного поковыряться.
Совет№ 3: Номинальная мощность в серии / параллельно
Этот вид последовательных и параллельных комбинаций резисторов также подходит для номинальной мощности. Допустим, нам нужно 100 Ом. резистор рассчитан на 2 Вт (Вт), но все, что мы получили, это группа 1 кОм; резисторы четверть ватта (¼W) (а сейчас 3 часа ночи, вся Mountain Dew ушла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 кОм; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень, но это поможет нам завершить проект и даже может дать нам дополнительные очки за способность думать на ногах.
Нам нужно быть немного более осторожными, когда мы объединяем резисторы разного значения параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Это должно быть совершенно очевидно для читателя, но …
Совет №: Различные резисторы параллельно
Совместное сопротивление двух резисторов разных значений всегда меньше, чем резистор наименьшего значения.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и достигает значения, которое находится на полпути между двумя резисторами (1 кОм; || 10 кОм; НЕ равняется чему-то около 5 кОм!). Общее параллельное сопротивление всегда будет перемещаться ближе к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет № 4 10 раз.
Совет №: Рассеяние мощности параллельно
Мощность, рассеиваемая в параллельной комбинации разнородных значений резисторов, не разделяется равномерно между резисторами, потому что токи не равны.Используя предыдущий пример (1k & ome; || 10k & ohm;), мы можем видеть, что 1 k & ohm; будет в 10 раз больше тока 10 кОм. Так как закон Ома гласит, что мощность = напряжение х ток, из этого следует, что 1 кОм; резистор рассеивает в 10 раз мощность 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем, когда параллельно объединяем резисторы разной величины. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.
серии и параллельные конденсаторы
Объединение конденсаторов похоже на объединение резисторов … только наоборот. Как бы странно это ни звучало, это абсолютно верно. С чего бы это?
Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.И если пластины раздвигаются дальше, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы разрядиться в друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для тока. Отсюда следует, что число электронов, которые разряжаются из крышки на дне, будет таким же, как число электронов, выходящих из крышки наверху.Значит, емкость не увеличилась?
На самом деле, это даже хуже, чем это. Размещая конденсаторы последовательно, мы эффективно расположили пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается вместе. Таким образом, у нас нет 20 мкФ или даже 10 мкФ. У нас есть 5 мкФ. В результате мы добавляем значения последовательных конденсаторов так же, как добавляем значения параллельных резисторов. Как суммируемый, так и взаимный методы действительны для последовательного добавления конденсаторов.
Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое больше напряжения (или номинальное напряжение). Как и батареи, когда мы последовательно соединяем конденсаторы, напряжение накапливается.
Параллельное добавление конденсаторов похоже на последовательное добавление резисторов: значения просто складываются, никаких хитростей. Почему это? Размещение их параллельно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Просто.
Время эксперимента — часть 3
Что вам нужно:
Давайте посмотрим, как работают последовательно и параллельно подключенные конденсаторы. Это будет немного сложнее, чем примеры с резисторами, потому что измерять емкость непосредственно с помощью мультиметра сложнее.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается от нуля вольт. Когда ток начинает идти в одном из выводов, равное количество тока выходит из другого.И если нет последовательного сопротивления с конденсатором, это может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, медленнее сбегает до тех пор, пока напряжения не станут равными, когда поток тока полностью прекратится.
Как указано выше, потребление тока может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). В этом эксперименте мы хотим иметь возможность следить за зарядом конденсатора, поэтому мы будем использовать 10 кОм; резистор последовательно, чтобы замедлить действие до точки, где мы можем легко его увидеть.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в Фарадах. Просто? Нет? Мы продемонстрируем на следующей странице.
Время эксперимента — часть 3, продолжение …
Для первой части этого эксперимента мы собираемся использовать один резистор 10 кОм и один 100 мкФ (что соответствует 0,0001 фарадам). Эти две части создают постоянную времени в 1 секунду:
При зарядке нашего конденсатора емкостью 100 мкФ через 10 кОм; Резистор, мы можем ожидать, что напряжение на крышке возрастет примерно до 63% от напряжения питания за 1 постоянную времени, что составляет 1 секунду.Через 5 временных констант (в данном случае 5 секунд) крышка заряжается примерно на 99% до напряжения питания, и она будет следовать кривой заряда, как показано на рисунке ниже.
Теперь, когда мы знаем этот материал, мы собираемся подключить схему на схеме (убедитесь, что полярность правильно установлена на этом конденсаторе!).
С нашим мультиметром, настроенным на измерение вольт, проверьте выходное напряжение блока при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5 В (это будет немного больше, если батареи новые). Теперь подключите цепь, следя за тем, чтобы выключатель аккумуляторного блока находился в положении «ВЫКЛ», прежде чем подключать его к макету. Также позаботьтесь о том, чтобы красный и черный провода шли в правильные места. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного развести эти ножки, чтобы было легче).
Как только мы убедимся, что схема выглядит правильно и наш прибор включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ON».Примерно через 5 секунд индикатор должен показывать значение, близкое к напряжению аккумуляторной батареи, что показывает, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще хорошо держит это напряжение, не так ли? Это потому, что нет пути для тока разрядить конденсатор; у нас есть разомкнутая цепь. Чтобы разрядить крышку, вы можете использовать другой резистор 10K параллельно. Примерно через 5 секунд он вернется почти к нулю.
Время эксперимента — часть 3, даже больше…
Теперь перейдем к интересным деталям, начиная с последовательного подключения двух конденсаторов. Помните, что мы сказали, что результат будет аналогичен соединению двух резисторов параллельно. Если это правда, мы можем ожидать (используя перерасход)
Что это будет делать с нашей постоянной времени?
Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает нулевое напряжение (или около того), и установите переключатель в положение «ON».Заряжалось ли примерно вдвое меньше времени, чтобы зарядиться до напряжения аккумуляторной батареи? Это потому, что емкость вдвое меньше. Электронный газовый баллон стал меньше, поэтому для его зарядки требуется меньше времени. Для этого эксперимента предлагается третий конденсатор, чтобы доказать это, но мы держим пари, что читатель увидит надпись на стене.
Теперь мы попробуем конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на последовательное добавление резисторов. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
Это означает, что теперь потребуется около 10 секунд, чтобы увидеть зарядку параллельных конденсаторов до напряжения питания 4.5V.
Для доказательства начните с нашей оригинальной схемы в 10 кОм; резистор и один конденсатор емкостью 100 мкФ последовательно, как показано на первой диаграмме для этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно через 5 секунд. Теперь добавьте второй конденсатор параллельно. Убедитесь, что показания счетчика близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и установите переключатель на батарейном блоке в положение «ON». Это займет много времени, не так ли? Конечно же, мы сделали электронный газовый баллон больше, и теперь для его заполнения требуется больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и наблюдать, как он заряжается в течение длительного времени.
Серияи параллельные индукторы
Серияи параллельные индукторы
Случаи, когда катушки индуктивности необходимо добавлять последовательно или параллельно, встречаются довольно редко, но не случайно. В любом случае, давайте обратимся к ним, чтобы быть полными.
Короче говоря, они добавляют так же, как и резисторы, то есть они добавляют со знаком плюс, когда в серии, и с перерасходом продукта, когда параллельно.Сложная часть возникает, когда они расположены близко друг к другу, чтобы иметь взаимодействующие магнитные поля, умышленно или нет. По этой причине предпочтительно иметь один компонент, а не два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они добавляют, как резисторы. Больше информации, чем то, что касается индукторов, выходит за рамки данного руководства.
Ресурсы и дальнейшее развитие
Теперь, когда вы знакомы с основами последовательных и параллельных цепей, почему бы не проверить некоторые из этих руководств?
- Делители напряжения
- . Делителем напряжения является одна из самых основных и повторяющихся цепей.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
- Что такое Arduino? — Теперь, когда вы ознакомились с основами микросхем, вы можете приступить непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino. Основы коммутатора
- . Мы говорили о некоторых элементах схемы в этом руководстве, но это не был один из них. Переключатели являются критически важным компонентом практически для каждого проекта в области электроники.Узнайте все о переключателях в этом уроке
- Шитье с проводящей нитью — цепи не обязательно должны быть макетами и проволокой. Электронный текстиль использует проводящую нить, чтобы шить огни и другую электронику в одежду или другую ткань.
О нет! Почему у вас не рождественские огни? О, вы подумали, что было бы забавно вытащить одну из лампочек, и теперь все облажалось! Если вы одна из тех несчастливых душ, которым удалось полностью отключить свет, не расстраивайтесь, вы не одиноки. Каждый год миллионы огней тускнеют по всему миру за один важный урок — чтобы вы узнали разницу между последовательными и параллельными цепями!
Во-первых, основы
Прежде чем мы углубимся в разницу между последовательными и параллельными цепями, давайте рассмотрим некоторые базовые термины, которые мы будем использовать.
- Ток. Электричество есть над чем работать, и когда электроны обтекают цепь, это ток на работе.
- Схема. Если это замкнутый, непрерывный путь, то электричество будет течь по нему. На этом пути электричество может сделать массу удивительных вещей, таких как питание вашего смартфона или отправить людей в космос!
- Сопротивление . Это то, с чем сталкивается электричество, когда оно течет вдоль физического материала, будь то медный провод или обычный старый резистор.Сопротивление ограничивает ток электрического тока.
Ниже вы найдете изображение простой схемы, которая включает в себя батарею, выключатель и лампочку.

Простейшая из цепей, питающая лампочку с аккумулятором.
Сезон Серии
Давайте вернемся к нашим рождественским огням, чтобы понять, как именно работает проводная серия. Скажем, у вас есть цепь огней, соединенных один за другим. Если бы вы видели это в цепи, это выглядело бы примерно так:

Ваши рождественские огни в серии, обратите внимание, что все огни подключены один за другим.(Источник изображения)
Когда мы подключим наш источник света к розетке, что будет делать ток? Давайте следовать за потоком:
- Включение. Когда мы подключаем наши рождественские огни, ток начинает течь из нашей розетки.
- течет вдоль. Затем он движется вдоль медного провода и сквозь наш рождественский свет, заставляя их ярко светить.
- Придя домой. Когда наш ток достигает конца нашей цепи огней, он направляется к земле, чтобы немного отдохнуть, и цикл продолжается.
Неважно, какие компоненты вы помещаете в последовательную цепь, вы можете смешивать и сочетать конденсаторы, резисторы, светодиоды и несколько рождественских огней вместе, и ток будет течь одинаково, от одной части к другой.
Теперь, когда рождественские огни имеют тенденцию падать. Что произойдет, если вы потянете одну из этих лампочек в своем огне? Если ваши огни похожи на наши, то все они выключены! Почему это? Подумайте об этом, если ток течет от света к свету, и вы нарушаете эту связь, то вы прерываете путь, по которому пытается течь электричество.Это называется разомкнутой цепи .
Ток и сопротивление в серии
Существует фундаментальный закон Вселенной, который нужно помнить о том, как ток и сопротивление работают в последовательной цепи:
Чем больше работа (сопротивление) последовательной цепи, тем больше уменьшается ее ток.
Имеет смысл, верно? По мере того, как вы добавляете больше сопротивления к цепи, например, к рождественским огням или даже к резистору, вам приходится выполнять больше работы для вашей схемы.Допустим, вы берете схему, которую мы представили в начале этого блога, в которой была одна лампочка. Теперь, что произойдет, если вы добавите еще один свет в эту схему? Будут ли обе лампочки светить ярче? Нет. Когда вы подключите эту вторую лампочку, обе станут одинаково тусклыми, потому что вы добавили больше сопротивления в свою цепь, что уменьшает ток.

Добавление еще одной лампочки в серии уменьшает ток , потому что у нашей батареи теперь еще много работы!
Но как узнать, какое сопротивление у вас в последовательной цепи? Вы просто складываете все различные значения сопротивления вместе.Например, в схеме ниже у нас есть два резистора, каждый по 10 кОм. Чтобы получить общее сопротивление в этой цепи, просто сложите все числа вместе. Это 10k + 10k, что составляет 20 кОм от общего сопротивления.

Объединить наши резисторы в последовательную цепь легко, просто сложите каждый из них вместе.
А что будет с вашим током в этой цепи на основе этого сопротивления? Вот как вы можете понять это. 
- Используя наш законный треугольник Ома, мы получаем уравнение, которое нам нужно использовать: I = V / R или ток = напряжение, деленное на сопротивление.
- Включая числа, которые мы знаем, мы получаем I = 10V / 20k. 0,5 миллиампер (мА) проходят через нашу цепь!
- Что, если мы вынули один из резисторов? Теперь наше уравнение равно I = 10 В / 10 кОм, и мы увеличили наш ток до 1 миллиампера (мА), уменьшив сопротивление.
Параллельная работа
А разве не было бы замечательно, если бы вы вытащили одну из лампочек на своей рождественской гирлянде, но остальные остались? Если бы ваши рождественские огни были подключены параллельно, то именно так они бы себя вели!
Представьте себе, что ваша параллельная цепь соединена вместе.Но вместо того, чтобы каждая лампочка была соединена одна за другой, все они были соединены отдельно, в своих цепях, как на рисунке ниже. Как видите, каждая лампочка имеет свою собственную мини-схему, которая отделена от другой, но все они работают вместе как часть большей цепи.

Ваши рождественские огни теперь параллельны, обратите внимание, что у каждого света есть своя собственная схема. (Источник изображения)
Но как протекает ток в такой цепи? Это не просто следовать одному пути; это следует за ними всеми одновременно! Вот почему это потрясающе — представьте, что вы вытаскиваете одну из лампочек в цепи такого типа.Вместо того, чтобы останавливать всю работу рождественского света, остальная часть цепи будет продолжать течь, потому что каждый источник света не зависит от источника света до или после него.
Ток и Сопротивление в Параллеле
Когда цепь подключена параллельно, ток и сопротивление начинают делать какие-то странные вещи, которые вы не можете ожидать, вот что вы хотите запомнить:
В параллельных цепях, когда вы увеличиваете сопротивление, вы также увеличиваете тока, но в результате ваше сопротивление уменьшается вдвое.
Подожди, что? Это звучит безумно! Но подумай об этом в отношении твоих рождественских огней. Когда вы добавляете больше разноцветных источников света в свою схему, вам нужно использовать больше тока для питания всех этих источников света, верно? Итак, волшебная вещь начинает происходить, чем больше света вы добавляете, тем выше ваш текущий подъем, но этот увеличенный ток оказывает противоположное влияние на ваше сопротивление.
Это может быть немного сложно, чтобы обдумать, так что давайте рассмотрим простой пример.Проверьте схему ниже:

Здесь у нас есть параллельная схема с двумя резисторами 10 кОм и батареей 10 В.
Здесь у нас есть аккумуляторная батарея на 10 В и два резистора на 10 кОм, которые соединены параллельно. Теперь, поскольку каждый резистор имеет свою собственную схему, нам нужно выяснить, какой ток будет использовать каждый:
- Возвращаясь к нашему Законному треугольнику Ома, мы знаем, что нам нужно использовать уравнение I = V / R, или ток равен напряжению, деленному на сопротивление.
- И подключив наши числа, мы получаем I = 10 В / 10 К, что составляет 1 мА.Но это только одна из двух цепей резисторов; Теперь нам нужно удвоить ток, чтобы получить общее значение для всей цепи, которое составляет 2 мА.
- Теперь, что происходит с нашим сопротивлением на двух усилителях? Мы можем использовать закон Ома, чтобы выяснить это с R = V / I, что составляет R = 10 В / 2 мА = 5 кОм. Из-за того, что мы удвоили наш ток, наши оригинальные резисторы 10 кОм теперь дают только половину сопротивления!
Да, все это становится довольно сумасшедшим, не так ли? Это всего лишь один из тех законов вселенной.
Как ваши рождественские огни действительно работают
Так как же эти твои рождественские огни действительно работают? Вот подсказка — они не 100% серии и не 100% параллели, они оба! Эти умные инженерные эльфы решили, что самый эффективный способ заставить ваши рождественские огни работать — это соединить несколько последовательных источников света параллельно. Проверьте изображение ниже, чтобы увидеть, что мы имеем в виду:

Вы найдете много современных рождественских огней, соединенных последовательно / параллельно.(Источник изображения)
Вот почему этот сериально-параллельный гибрид великолепен — если вы потянете один источник света, выключится только одна его часть, но не все. Это потому, что вы затронули только одну из последовательных цепей в вашей большой параллельной цепи. Но почему инженерные эльфы просто не включили все огни параллельно? Это потребовало бы тонны проводов, и Санта должен следить за его производственными затратами так же, как мы!
Но подождите, вы, возможно, помните тот год, когда у вас погас свет, но остальные огни продолжали работать, что там произошло? Вы можете поблагодарить этот маленький фокус на так называемом шунте .Это небольшое устройство позволяет току продолжать движение по цепи даже после того, как свет погаснет. Как так? Давайте внимательнее посмотрим на один из ваших рождественских огней ниже:

Шунтирующий провод сохраняет электричество даже после того, как погаснет свет. (Источник изображения)
Видите тот провод, который обернут вокруг нижней части света? Это шунт, и на нем есть покрытие, которое предотвращает прохождение электричества через него, пока свет работает правильно.Но когда провод наверху перегорает, повышение температуры растапливает покрытие шунтирующего провода, позволяя электричеству продолжать проходить от одного терминала к другому, и ваши рождественские огни продолжают работать!
Дар дарения
Это твой подарок на год! Теперь у вас есть некоторые новые знания о разнице между цепями, соединенными последовательно и параллельно, и о том, как они работают вместе, чтобы ваши рождественские огни ярко светили.
Схемы, соединенные последовательно, проще всего понять, когда ток течет в одном непрерывном плавном направлении.И чем больше работа у вас есть последовательная схема, тем больше ваш ток будет уменьшаться. Параллельные цепи немного сложнее, позволяя соединять несколько цепей, работая по отдельности как часть большей цепи. Из-за этого интересного соединения, когда вы увеличиваете сопротивление в параллельной цепи, вы также увеличиваете ток!
Если у вас все еще есть проблемы со всем этим, то вот отличное видео от Bozeman Science, которое облегчает понимание:
И если вы все еще потеряны, то, возможно, вы достигли своего предела в eggnog.Готовы создать свои собственные схемы сегодня? Попробуйте Autodesk EAGLE бесплатно!
,Последовательные и параллельные цепи — формула и примеры
СМОТРЕТЬ БОЛЬШЕ
Все электрические устройства нуждаются в цепях для бесперебойной и эффективной работы.Теперь, что это за схемы? Это просто электронные компоненты, собранные вместе и соединенные проводами? Ну, почти. Но схема это больше, чем просто. Представьте себе, что вы можете использовать схему для выполнения такой простой задачи, как зажигание лампочки, и таких масштабных задач, как запуск автомобиля. Расположение компонента в неправильной области или неправильном терминале или даже соединение неправильных концов может создать много проблем. Следовательно, мы должны знать все об основах схем, чтобы освоить торговлю.
В этой конкретной статье мы узнаем больше о различных типах цепей и о том, как их различия и сходства.Читай дальше, чтобы узнать больше.
Что такое схема?
Основная схема состоит из трех компонентов; это источник напряжения, нагрузка и проводящий путь.
Давайте узнаем больше об этом.
1. ИСТОЧНИК НАПРЯЖЕНИЯ
Источник напряжения обеспечивает цепь питанием или источником энергии. Это заставляет ток течь. Типичным примером источника напряжения является батарея.
2. ПРОВОДНОЙ ПУТЬ
Проводящий путь в основном обеспечивает маршрут для прохождения тока. Ток проходит через все компоненты прямо из начальной точки обратно в конечную точку, которая также является начальной точкой.Важно, чтобы проводящий путь образовывал правильную петлю, ведущую источник напряжения от отрицательной клеммы к положительной клемме.
3. НАГРУЗКА
Нагрузка — это электронный компонент, потребляющий энергию. Он делает всю работу в цепи. Говорят, что это сердце схемы, потому что без нагрузки нет смысла строить схему. Это практически бесполезно.
Типичным примером нагрузки является одиночная лампочка. Лампочки используются в простых цепях, тогда как в сложных больших цепях нагрузка может представлять собой комбинацию различных других электронных компонентов, таких как конденсаторы, резисторы, транзисторы и т. Д.
Существуют разные типы цепей; два основных — это последовательные и параллельные цепи.
(изображение будет загружено в ближайшее время)
ЦЕПЬ СЕРИИ
Говорят, что цепь соединена последовательно, когда один и тот же ток протекает через все компоненты, подключенные к цепи. Ток имеет только один путь. Например: если мы возьмем источник света, скажем, сказочные огни. Это в основном провод с несколькими крошечными лампочками, соединенными последовательно друг с другом. Если одна лампочка перегорает, ток останавливается у перегоревшей лампы, все лампочки после перегоревшей лампы не загораются.Причина в том, что схема подключена последовательно. Существует только один путь для электричества. Количество энергии одинаково во всех компонентах схемы. Скорость или скорость потока электричества никогда не будут колебаться по всей цепи. Сопротивление этой цепи является суммой всех отдельных сопротивлений. Чем больше число резисторов в цепи, тем выше сопротивление, и, следовательно, тем труднее протекать ток.
(изображение будет загружено в ближайшее время)
Говорят, что цепь соединена параллельно, если она имеет несколько путей прохождения электричества.Резисторы и источники будут подключены между двумя наборами электрически общих точек. Электричество может течь в разных направлениях, как горизонтальных, так и вертикальных. Компоненты, являющиеся частью параллельной цепи, будут иметь постоянное напряжение на всех концах. Потенциал, который несет цепь, также будет идентичным.
В параллельной цепи всегда имеется более одного резистора (колбы), и они расположены таким образом, что электричество может проходить по многим путям.Это означает, что электричество (электроны) может перемещаться от одного конца ячейки через множество ветвей к другому концу ячейки. .
для цепи серии
Общее сопротивление (R) = r1 (индивидуальное сопротивление) + r2 + r3
Для параллельной цепи
Общее сопротивление (R) = 1 / r1 + 1 / r2 + 1 / r3
2.Помимо различия в формуле, тот факт, что последовательная цепь отличается от параллельной цепи, заключается в том, что если один компонент в последовательной цепи обрывается, резистор перегорает, следовательно, цепь не будет полной. Принимая во внимание, что в параллельных цепях, однако, функционирование другого компонента
3. В последовательной цепи ток в любой точке цепи определяется одним из наиболее важных и фундаментальных законов электричества, известных как закон Ома. , Чтобы освежить вашу память, закон Ома гласит, что I = V / R, где I обозначает электрический ток, V — напряжение, подаваемое источником, а R — общее сопротивление или сопротивление потоку электрического тока в цепи.Принимая во внимание, что в параллельной цепи ток в каждой ветви цепи всегда обратно пропорционален сопротивлению, даваемому резистором в каждой ветви, а полный ток всегда равен сумме токов в каждой отдельной ветви.

