Параллельный колебательный контур — Спектральный анализ (Инженерия)
5. Параллельный колебательный контур
5.1. Схема параллельного колебательного контура
Параллельный колебательный контур представляет собой параллельное соединение катушки индуктивности и конденсатора , принципиальная схема которого показана на рис. 5.1а.
На рис. 5.1б показана эквивалентная схема параллельного колебательного контура, в которую включено сопротивление потерь катушки индуктивности, сопротивление потерь конденсатора в большинстве случаев можно не учитывать.
В ряде случаев применяется параллельная эквивалентная схема, показанная на рис. 5.1в, в этом случае сопротивление не является сопротивлением потерь контура, хотя и зависит от него. Параллельная модель рис. 5.1в удобна при расчете проводимости цепи.
Рис. 5.1
5.2. Входное сопротивление и проводимость
В дальнейшем в основном будем использовать модель параллельного колебательного контура вида рис. 5.1б. Ее комплексное сопротивление определяется выражением
5.1б. Ее комплексное сопротивление определяется выражением
108
. (5.1)
В окрестности частоты , равной
, (5.2)
пренебрегая в числителе (5.1) величиной , получим
. (5.3)
Как видно, целесообразно перейти к координатам обобщенной расстройки, рассмотренным в подразделе 3.6,
, (5.4)
— добротность параллельного колебательного контура, равная
, (5.5)
— характеристическое сопротивление контура,
109
. (5.6)
В результате из (5.3) получим выражение для комплексного сопротивления контура в координатах обобщенной расстройки
, (5.7)
из которого нетрудно найти модуль , аргумент , активную и реактивную составляющие,
, (5.8)
, (5. 9)
9)
, (5.10)
, (5.11)
(получите эти выражения самостоятельно). Графики этих функций показаны на рис. 5.2.
110
Рис.5.2
На частоте (5.2) сопротивление контура максимально, чисто активно и равно
, (5.12)
графики на рис. 5.2 построены при кОм (сравните с сопротивлением последовательного контура, которое минимально на этой частоте). При отклонении от частоты сопротивление резко падает, появляется реактивная компонента. При сопротивление контура имеет индуктивный характер, а при — емкостный, этот же результат вытекает и из анализа фазовой характеристики на рис. 5.2б.
Анализ проводимости контура, в том числе и для модели рис. 5.1в, проведите самостоятельно.
5.3. Напряжение и токи в контуре
Подключим к параллельному колебательному контуру идеальный источник тока с комплексной амплитудой , как показано на рис.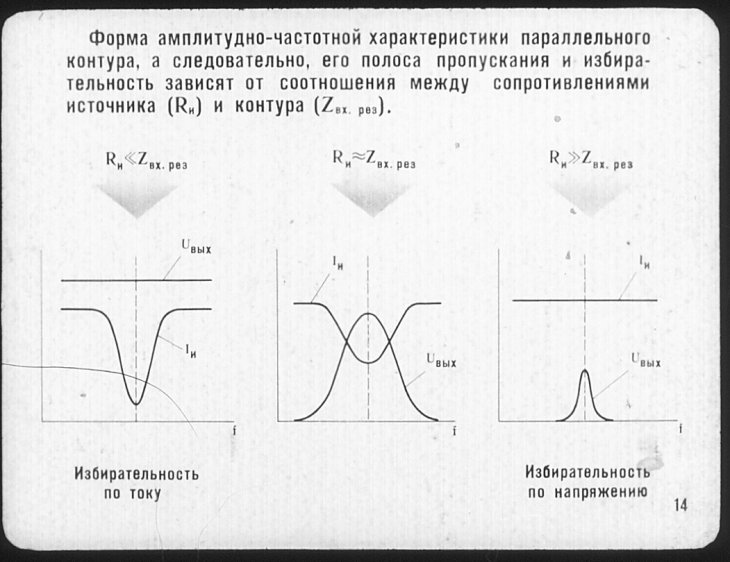 5.3, и определим напряжение на параллельных ветвях контура ,
5.3, и определим напряжение на параллельных ветвях контура ,
111
. (5.13)
Токи и в реактивных ветвях контура в окрестности частоты , то есть при условии , соответст-
Рис. 5.3 венно равны
, (5.14)
. (5.15)
Амплитуда и начальная фаза напряжения на контуре определяются выражениями
, (5.16)
, (5.17)
где — начальная фаза тока источника. Зависимости амплитуды напряжения и сдвига фаз между этим напряжением и током источника от обобщенной расстройки показаны на рис. 5.4 при кОм и мА.
Как видно, кривая имеет экстремальный характер,
112
однако резонанс напряжения в параллельном колебательном контуре отсутствует, так как напряжение на контуре всегда равно напряжению на источнике тока.
Рис.5.4
Токи и в реактивных ветвях контура определяются формулами (5.14) и (5.15), из которых следует
или . (5.18)
(5.18)
Эти равенства нарушают первый закон Кирхгофа
, (5.19)
то есть выражения (5.14) и (5.15) являются приближенными (как и все вычисления в координатах обобщенной расстройки).
Амплитуды этих токов одинаковы и равны
, (5.20)
а начальные фазы и определяются соотношениями
113
, (5.21)
, (5.22)
Как видно, токи в реактивных ветвях контура противофазны. Зависимости амплитуд токов в реактивных ветвях контура и сдвигов фаз и между токами в реактивных ветвях и током источника от обобщенной расстройки показаны на рис. 5.5 при мГн, нФ, Ом и мА.
Рис.5.5
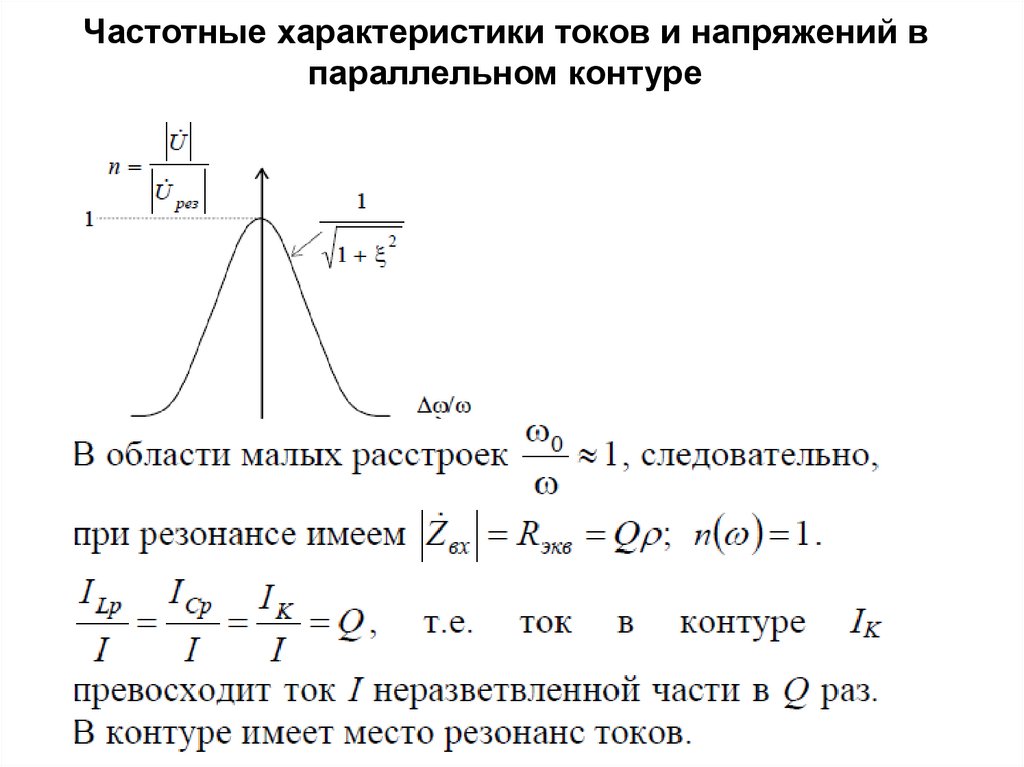
Как видно, токи и резко возрастают в окрестности точки (или частоты ) по сравнению с амплитудой тока источника, то есть в параллельном колебательном контуре имеет место резонанс токов в реактивных ветвях.
Частота (5.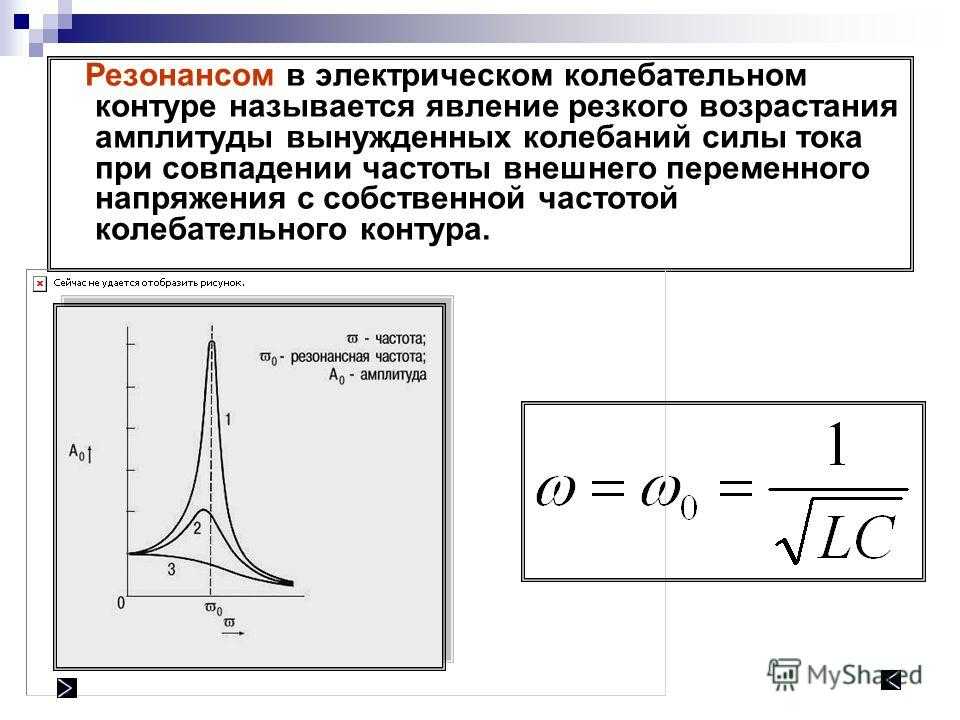 2) является резонансной частотой контура, на которой
2) является резонансной частотой контура, на которой
, (5.23)
114
то есть резонансный ток в реактивных ветвях контура в раз больше тока источника.
Так как токи и противофазны, то вводят в рассмотрение кольцевой замкнутый ток в контуре , как показано на рис. 5.6. Он совпадает по направлению с током и поэтому равен
. (5.24)
Рис. 5.6
Амплитуда контурного тока
равна (5.20), а начальная фаза (5.22), соответствующие графики показаны на рис. 5.5. Резонансный контурный ток в раз больше тока источника.
. (5.25)
5.4. Вторичные параметры колебательного контура
Параллельный колебательный контур (как и последовательный) полностью описывается своими первичными параметрами , и . На практике широко используются вторичные параметры:
— резонансная частота контура
(5. 26)
26)
или
; (5.27)
115
— характеристическое сопротивление контура
; (5.28)
— добротность контура
. (5.29)
5.5. Частотные характеристики
Частотные характеристики параллельного колебательного контура представляют собой зависимость от частоты характеристик комплексного коэффициента передачи по току
(5.30)
или
, (5.31)
где и — комплексные амплитуды токов реактивных ветвей контура, — комплексная амплитуда тока источника.
Рассмотрим комплексный коэффициент передачи тока емкости (аналогичный анализ проведите самостоятельно). Из (5.30) с учетом (5.14) получим
. (5.32)
116
Для АЧХ и ФЧХ контура получим
, (5.33)
, (5.34)
где обобщенная расстройка определяется выражением (3. 38)
38)
. (5.35)
Частотные характеристики параллельного колебательного контура в координатах вида (5.33) и (5.34) численно совпадают с аналогичными характеристиками для последовательного контура (3.42) и (3.43). Эти зависимости показаны на рис. 5.7 при .
Рис. 5.7
Те же графики в координатах абсолютной расстройки оказаны на рис. 5.8 при и рад/с.
117
Рис. 5.8.
Максимум АЧХ равен и достигается при , то есть на резонансной частоте . При отклонении частоты от коэффициент передачи резко падает, то есть параллельный колебательный контур может использоваться как узкополосный частотный фильтр.
Влияние параметров контура на форму частотных характеристик было рассмотрено при анализе последовательного колебательного контура (повторите его самостоятельно)
5.6. Полоса пропускания и коэффициент
прямоугольности
Так как выражение для АЧХ (5.33) параллельного колебательного контура совпадает с аналогичным выражением для последовательного контура, то формулы для полосы пропускания и коэффициента прямоугольности этих контуров совпадают (получите эти результаты еще раз самостоятельно),
, (5.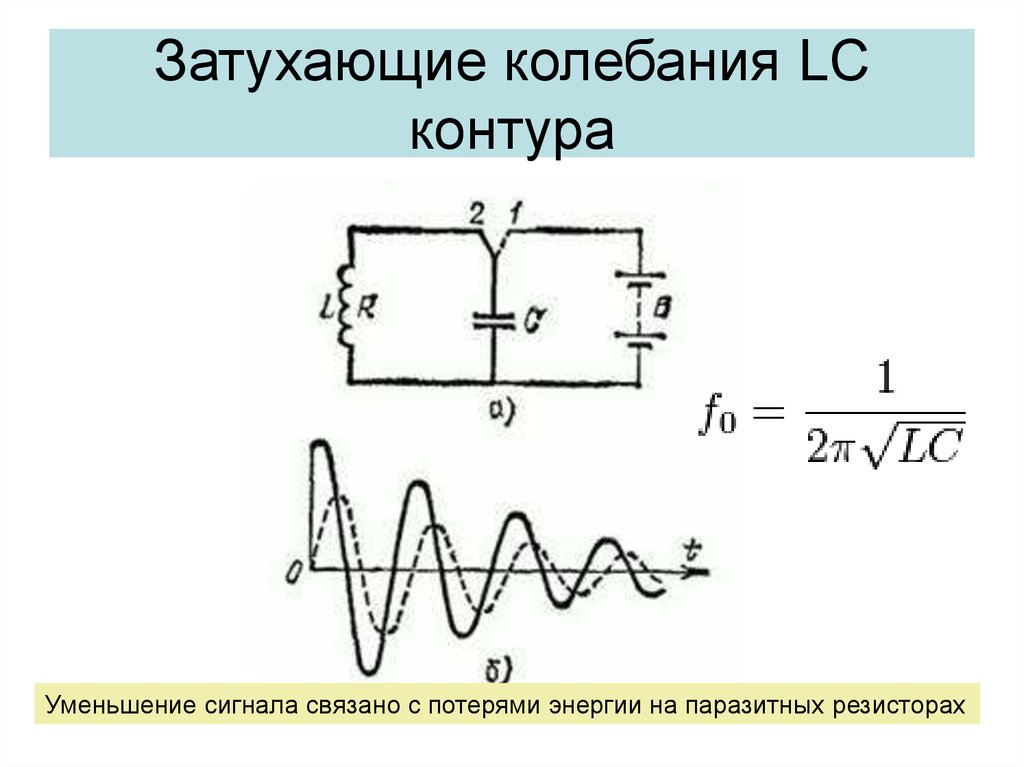 36)
36)
. (5.37)
118
5.7. Влияние сопротивления источника сигнала и
нагрузки на резонансные свойства контура
Рассмотрим параллельный колебательный контур на рис. 5.9а с реальным источником тока ( — внутреннее сопротивление источника) и параллельно подключенной нагрузкой .
Рис. 5.9
Параллельное соединение и заменяется эквивалентным сопротивлением , как показано на рис. 5.9б, а в этой схеме необходимо преобразовать параллельное соединение и ветви в эквивалентное последовательное соединение в окрестности резонансной частоты контура . Найдем сопротивление параллельного соединения,
, (5.38)
выделим его действительную и мнимую составляющие и приравняем их составляющим эквивалентного последовательного соединения элементов (рис. 5.9в) вида
. (5.39)
119
В результате получим
, (5.40)
. (5.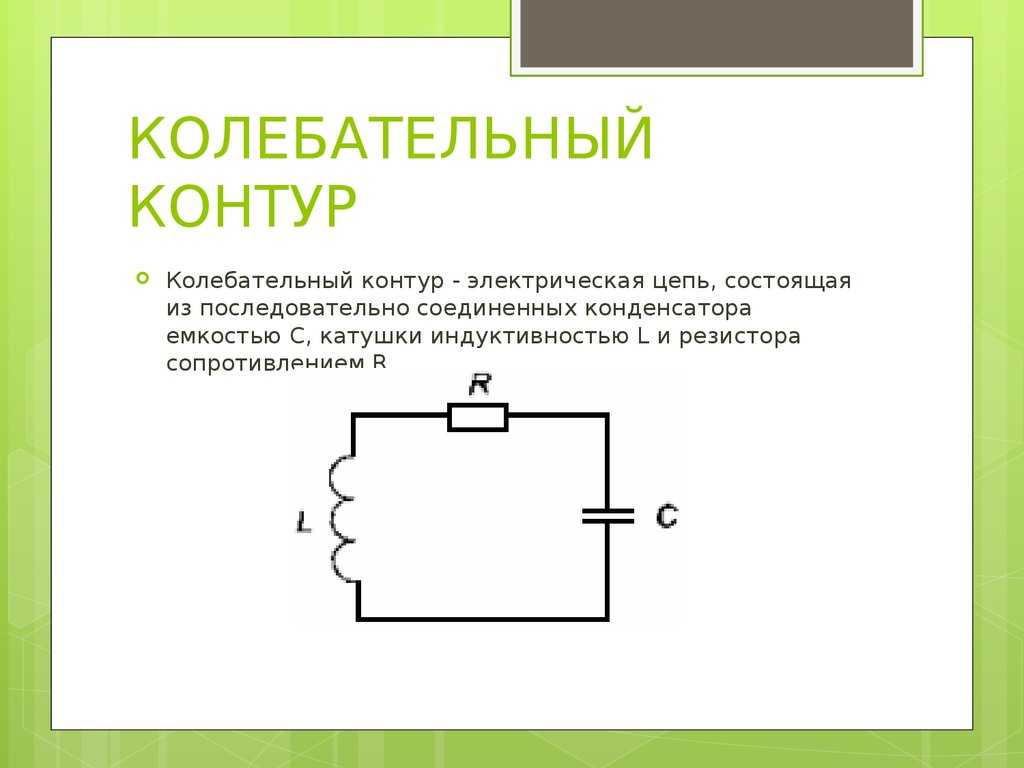 41)
41)
Допустим, что сопротивление много больше величин и , тогда в окрестности резонансной частоты можно записать
, (5.42)
(5.43)
(повторите эти преобразования самостоятельно).
Как видно из (5.42), подключение внутреннего сопротивления источника сигнала и нагрузки приводит к повышению эквивалентных потерь в контуре, эквивалентная добротность которого при этом равна
. (5.44)
Полученное выражение совпадает с аналогичной формулой, учитывающей влияние нагрузки в последовательном колебательном контуре (проверьте это самостоятельно).
120
Подключение реального источника сигнала и нагрузки снижает эквивалентную добротность контура. Чтобы добротность упала незначительно, необходимо выполнение условий
(5.45)
Например, если , то , то есть добротность значительно снижается, а если , то .
Реализовать условие (5.45) достаточно сложно, а часто и невозможно и требуются использование неполного включения контура к источнику сигнала и нагрузке, как показано на рис. 5.10. Можно показать, что эквивалентная добротность в этом случае равна
5.10. Можно показать, что эквивалентная добротность в этом случае равна
, (5.46)
где
и (5.47)
— коэффициенты включения в контур источника сигнала и нагрузки. Их значения выбираются достаточно малыми (например, 0,1), что существенно ослабляет влияние на добротности сопротивлений и ,.которые должны Рис. 5.10
удовлетворять условиям
121
(5.48)
что значительно проще реализовать, чем (5.45).
Колебательные контуры вида рис. 5.10 называют сложными параллельными колебательными контурами. Помимо резонанса токов на частоте , равной
, (5.49)
имеется резонанс напряжений в последовательном колебательном контуре на частоте
. (5.50)
Рабочим является интервал частот в окрестности , в котором сопротивление контура в точках подключения источника сигнала в координатах обобщенной расстройки равно
. (5.51)
(5.51)
5.8. Расчеты цепей с параллельными колебательными
контурами
Если в составе цепи имеется параллельный колебательный контур, то ее расчет целесообразно проводить в координатах обобщенной расстройки. Рассмотрим цепь, показанную на рис. 5.11 при Ом, мГн, нФ, кОм, в нее
122
включен источник гармонических колебаний с комплексной амплитудой В и частотой рад/с.
В состав цепи входит параллельный колебатель- Рис. 5.11
ный контур , его
резонансная частота , добротность и обобщенная расстройка соответственно равны
рад/с,
,
.
Вычислим комплексное сопротивление контура в координатах обобщенной расстройки,
кОм.
Тогда ток равен
мА,
а напряжение на емкости —
123
В.
Рассмотрим цепь со сложным параллельным колебательным контуром, показанную на рис. 5.12. приняв мГн, мГн и оставив остальные исходные данные теми же, что и для цепи на рис. 5.11. Коэффициент включения источника в контур равен
5.11. Коэффициент включения источника в контур равен
,
Рис. 5.12
а общая индуктивность контура соответственно мГн, при этом резонансная частота, добротность и обобщенная расстройка будут такими же, как и в предыдущей задаче.
Сопротивление контура в точках подключения источника определяется выражением
Ом,
ток равен
мА,
а напряжение на емкости соответственно
В.
124
5.9. Моделирование параллельного колебательного
контура
Проведем схемотехническое моделирование цепи, показанной на рис. 5.11 в пакете MicroCAP7, схема модели представлена на рис. 5.13, частота источника 157,6 кГц (рад/с).
Рис. 5.13
В верхней части рис. 5.14 показаны полученные в результате моделирования временные реализации напряжений в узлах 1 (пунктир) и 2, которые на рис 5.13 отмечены цифрами в кружках. В его нижней части показаны временные диаграммы токов в неразветвленной части контура — тока источника (кривая с маленькой амплитудой) и токов в емкостной (пунктир) и индуктивной ветвях контура.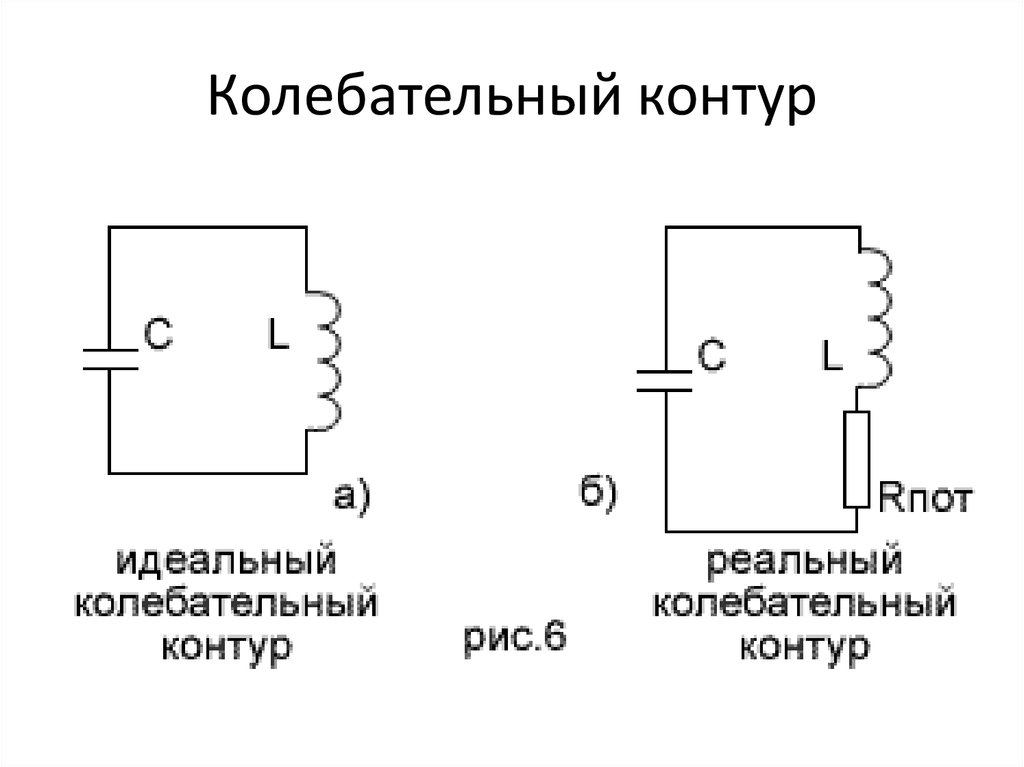 На начальном интервале времени 60 мкс (60u) наблюдается переходной процесс, а затем колебания устанавливаются и можно проводить измерения (убедитесь самостоятельно, что результаты расчета и моделирования совпадают).
На начальном интервале времени 60 мкс (60u) наблюдается переходной процесс, а затем колебания устанавливаются и можно проводить измерения (убедитесь самостоятельно, что результаты расчета и моделирования совпадают).
Как видно, токи в индуктивности и емкости противофазны, их амплитуды одинаковы и много больше амплитуды тока источника, то есть в параллельном колебательном контуре имеет место резонанс токов.
На рис. 5.15 приведены частотные характеристики цепи по передаче напряжения от узла 1 к узлу 2, по которым нетрудно определить напряжение на емкости (в узле 2).
125
126
127
5.10. Применение параллельного колебательного
контура
Параллельный колебательный контур чаще всего используется как элемент частотного фильтра аналогично последовательному контуру (пример будет рассмотрен далее), или как нагрузка активного элемента (транзистора) в резонансном усилителе сигнала. Пример схемы такого усилителя в моделирующем пакете MicroCAP7 показан на рис. 5.16.
5.16.
Рис. 5.16
В состав усилителя входит импортный биполярный транзистор типа 2N5190 (можно использовать отечественный аналог) с цепями питания по постоянному току от источника постоянного напряжения 15В, параллельный колебательный контур и источник гармонического входного сигнала с частотой 159,15 кГц.(рад/с), совпадающей с резонансной частотой контура, и амплитудой 4 мВ.
На рис. 5.17 показаны временные диаграммы напряжений источника (верхняя кривая), выходного напряжения на коллекторе транзистора в узле 4 (нижняя кривая) и там же постоянное напряжение питания.
128
129
На рис. 5.18 представлены частотные характеристики резонансного усилителя (верхняя кривая – АЧХ, нижняя – ФЧХ). Коэффициент усиления равен примерно 3000 на частоте 151,6 кГц, что следует и из кривых на рис 5.17: амплитуда входного сигнала равна 3 мВ, а выходного 8,36 В (максимум АЧХ на рис. 5.18 несколько выше измеренного по временным диаграммам, так как она моделируется при весьма слабом сигнале).
Рис. 5.18
Проведите моделирование рассмотренной цепи самостоятельно, изменяя ее параметры. Введите неполное включение транзистора к контуру, сравните результаты.
5.11. Задания для самостоятельного решения
Задание 5.1. Вычислите резонансное сопротивление параллельного колебательного контура при мГн, пФ, Ом.
130
Задание 5.2. Определите резонансную частоту контура
Ещё посмотрите лекцию «22 Основы протестантской культуры» по этой теме.
при кОм и С=1 нФ.
Задание 5.3. Найдите напряжение на емкости параллельного контура в цепи рис. 5.19 при мГн, пФ, Ом, В, кОм, рад/с. Расчет проведите в координатах обобщенной расстройки.
Рис. 5.19
Задание 5.5. Получите выражение для АЧХ цепи, показанной на рис. 5.20. Постройте график АЧХ при мГн, пФ, Ом, кОм. Проведите расчет в координатах обобщенной расстройки и абсолютной частоты, сравните результаты.
Coil32 — Параллельный LC колебательный контур
Параллельный колебательный контур в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного. Реальные элементы контура обладают потерями и при анализе цепи используется реалистичная модель из идеальных сосредоточенных элементов в которой потери учитываются с помощью «виртуальных» последовательных активных сопротивлений RL и RC.
Собственная паразитная емкость катушки обычно не учитывается, т. к. она просто суммируется с контурной. Программа Coil64 рассчитывает потери в проводе катушке RL без учета потерь в каркасе, экране, сердечнике и во всех предметах, с которыми взаимодействует окружающая катушку электромагнитная волна. Однако, учитывается скин-эффект и эффект близости. Эти же потери учитывает параметр «конструктивная добротность катушки» — QL. Это не добротность всего контура, а добротность катушки, которая связана с ее сопротивлением потерь следующим соотношением:
| [1] |
Потери в контурном конденсаторе на порядок меньше и характеризуются добротностью конденсатора. Поскольку потери конденсатора сосредоточены в основном в диэлектрике, можно считать, что его добротность QC и сопротивление потерь RC связаны с параметром, учитывающем потери в диэлектрике tgδ, следующим образом:
Поскольку потери конденсатора сосредоточены в основном в диэлектрике, можно считать, что его добротность QC и сопротивление потерь RC связаны с параметром, учитывающем потери в диэлектрике tgδ, следующим образом:
| [2] |
При анализе цепи часто ее преобразуют в эквивалентную параллельную RLC-цепь. В этом случае, заменяя сопротивления проводимостями, мы упрощаем анализ и получаем формулы идентичные формулам последовательного контура. Многие радиолюбители полагают, что последовательные R
Как видим активные сопротивления и реактивности при таком преобразовании «перепутались», поэтому для наглядности проведем анализ без использования проводимостей, прямо по исходной схеме. Входное сопротивление двухполюсника получается следующим:
Активная и реактивная (мнимая) составляющие:
При резонансе токи в реактивных элементах (IL, IC) в Q раз больше общего тока цепи (I), поэтому для параллельного контура явление носит название резонанса токов.
Резонансная частота параллельного колебательного контура — это частота, при которой реактивная составляющая входного сопротивления равна нулю, входное сопротивление чисто активно, и, соответственно, фазовый сдвиг между током и напряжением на входных зажимах цепи тоже равен нулю. Приравняв Xвх к нулю и проведя соответствующие преобразования получим следующую формулу для резонансной частоты параллельного колебательного контура:
| [3] |
Один из важнейших параметров контура — его характеристическое сопротивление:
| ρ = √L/C | [4] |
Формулу резонансной частоты можно представить иначе:
| [5] |
ω0 — резонансная частота последовательного колебательного контура.
Как видим резонансная частота параллельного колебательного контура равна резонансной частоте последовательного колебательного контура, составленного из тех же элементов, с добавкой поправочного коэффициента √[(L/C — RL^2)/(L/C — RC^2)]. На практике этот коэффициент всегда близок к единице и равен единице если RL=RC или RL=RC=0.
На практике этот коэффициент всегда близок к единице и равен единице если RL=RC или RL=RC=0.
Пример:
Имеем контур с индуктивностью 3μГн и емкостью 42пФ, сопротивление потерь катушки — RL=2 Ом, конденсатора — RC=0.1 Ом. По формуле Томпсона резонансная частота контура равна 14.178649 МГц, точно вычисляем по формуле [1] — 14.178253 МГц. Как видим, активные сопротивления потерь вносят в идеальный контур дополнительную реактивность и уводят его частоту вниз, в данном случае почти на 400 Гц.
Это совсем небольшое отклонение нужно иметь ввиду, но оно намного меньше отклонений, вносимых неучтенными паразитными емкостями. Поэтому при выполнении условий: RL<< ρ, RC<< ρ, что обычно бывает на практике, можно считать, что условия резонанса токов совпадают с условиями резонанса напряжений в последовательном контуре, составленном из тех же элементов L и C,
ω0 = 1/√LC или ƒ0 = 1/(2π√LC)
На этом «родственная схожесть» последовательного и параллельного контуров не заканчивается.
При выполнении тех же условий: RL<< ρ, RC<< ρ где Zвх.посл = (RL + RC) + j(ωL — 1 ⁄ ωC) – входное сопротивление последовательного контура, составленного из тех же элементов.
-
RΣ = RL + RC;
Как видим, можно считать, что сопротивления потерь катушки и конденсатора суммируются, поэтому общую добротность контура Q можно определить следующим выражением:
| [6] |
На резонансной частоте ω0:
| [7] |
Поскольку реактивные сопротивления взаимно компенсируются, контур на резонансной частоте имеет чисто активное сопротивление равное Rэ (эквивалентное или эффективное сопротивление контура).
Из последней формулы следует, что:
| [8] |
Т.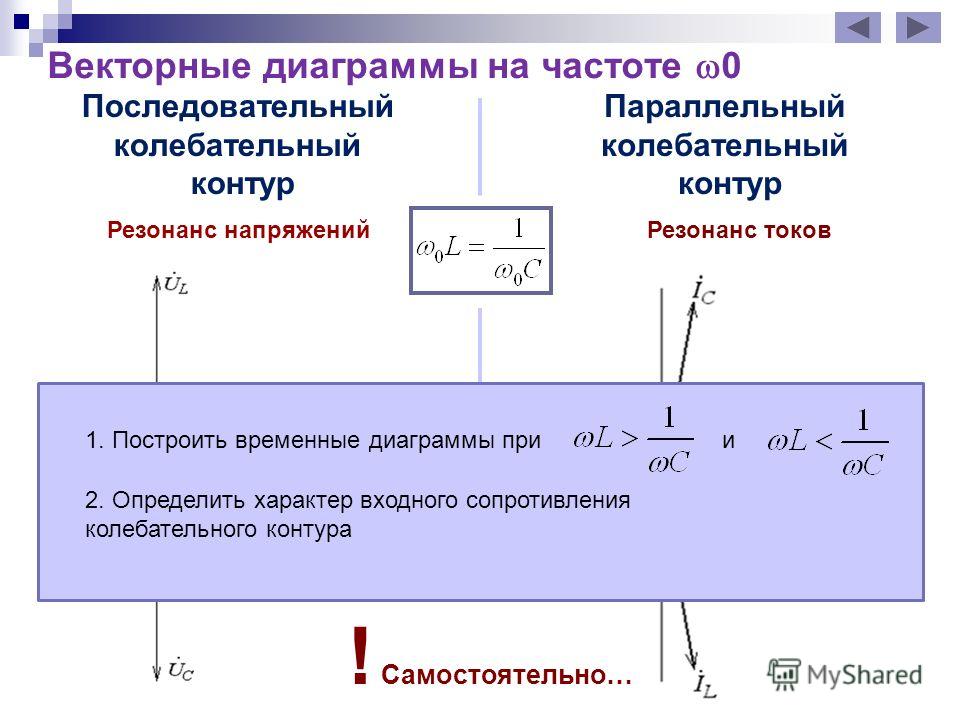 е. добротность контура равна отношению его характеристического сопротивления к сопротивлению потерь. Иначе говоря, на данной частоте более добротным будет контур с меньшей емкостью и большей индуктивностью. Как же тогда соотносится добротность контура с конструктивной добротностью катушки? Чтобы понять это, следует иметь ввиду, что характеристическое сопротивление контура численно равно модулю реактивного сопротивления индуктивности или емкости на резонансной частоте. Последние, как известно, в этом случае равны и отличаются лишь знаком. Если мы пренебрежем потерями в конденсаторе, тогда формула [8] сводится к формуле [1]. Ведь на резонансной частоте ρ = |XL|, а в сумме RΣ = RL + RC, последнее слагаемое мы не учитываем. Другими словами, если пренебречь потерями в конденсаторе, то добротность контура равна конструктивной добротности катушки. В итоге мы приходим к выводу, что формулы [1] и [8] в этом случае эквивалентны.
е. добротность контура равна отношению его характеристического сопротивления к сопротивлению потерь. Иначе говоря, на данной частоте более добротным будет контур с меньшей емкостью и большей индуктивностью. Как же тогда соотносится добротность контура с конструктивной добротностью катушки? Чтобы понять это, следует иметь ввиду, что характеристическое сопротивление контура численно равно модулю реактивного сопротивления индуктивности или емкости на резонансной частоте. Последние, как известно, в этом случае равны и отличаются лишь знаком. Если мы пренебрежем потерями в конденсаторе, тогда формула [8] сводится к формуле [1]. Ведь на резонансной частоте ρ = |XL|, а в сумме RΣ = RL + RC, последнее слагаемое мы не учитываем. Другими словами, если пренебречь потерями в конденсаторе, то добротность контура равна конструктивной добротности катушки. В итоге мы приходим к выводу, что формулы [1] и [8] в этом случае эквивалентны. Если же нам необходимо учесть потери в конденсаторе, то следует использовать формулу [6].
Если же нам необходимо учесть потери в конденсаторе, то следует использовать формулу [6].
Необходимо отметить два важных момента:
- Coil64 рассчитывает конструктивную добротность для «голой катушки в вакууме». Наличие экрана увеличивает распределенную емкость и уменьшает индуктивность. Характеристическое сопротивление контура падает, добротность уменьшается. Кроме этого добавляются потери на вихревые токи в экране. Каркас катушки также снижает ее добротность и добротность контура соответственно.
- Добротность катушки растет с ростом частоты только на «низких» частотах, далеких от частоты собственного резонанса катушки. При приближении к собственному резонансу добротность достигает максимума на частотах 60-85% от Fsrf и затем плавно снижается. Это происходит от того, что на этих частотах начинает проявляться зависимость индуктивности и собственной емкости катушки от частоты.
Амплитудно-частотная характеристика имеет такой же вид, как и резонансная кривая последовательного контура; ФЧХ представляет собой зеркальное отображение ФЧХ последовательного контура.
Важно понятие полоса пропускания контура Это частотный интервал в пределах которого импеданс Zвх не ниже
1 ⁄ √2 (или 0,707) от максимального на резонансной частоте. Справедлива следующая формула, которую можно использовать для измерения добротности:
| Q = f0/Δf | [9] |
В практике представляет интерес величина ослабления контуром нежелательных частот:
| [10] |
Для расстроек более трех полос пропускания формула упрощается:
где знак не учитывается.
В реальной схеме контур связан с источником колебаний и нагрузкой, которые вносят в него дополнительные потери, снижающие добротность. Эквивалентная добротность Q параллельного колебательного контура:
Q = Q
- Q0 — добротность ненагруженного контура
- Ri — входное сопротивление источника
- Rэ — эквивалентное сопротивление ненагруженного котура
Эту формулу можно использовать для учета влияния любых подключенных к контуру сопротивлений (например, нагрузки) на его добротность.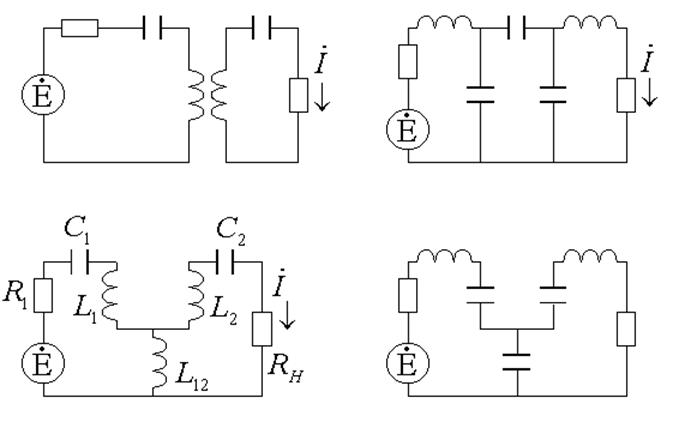
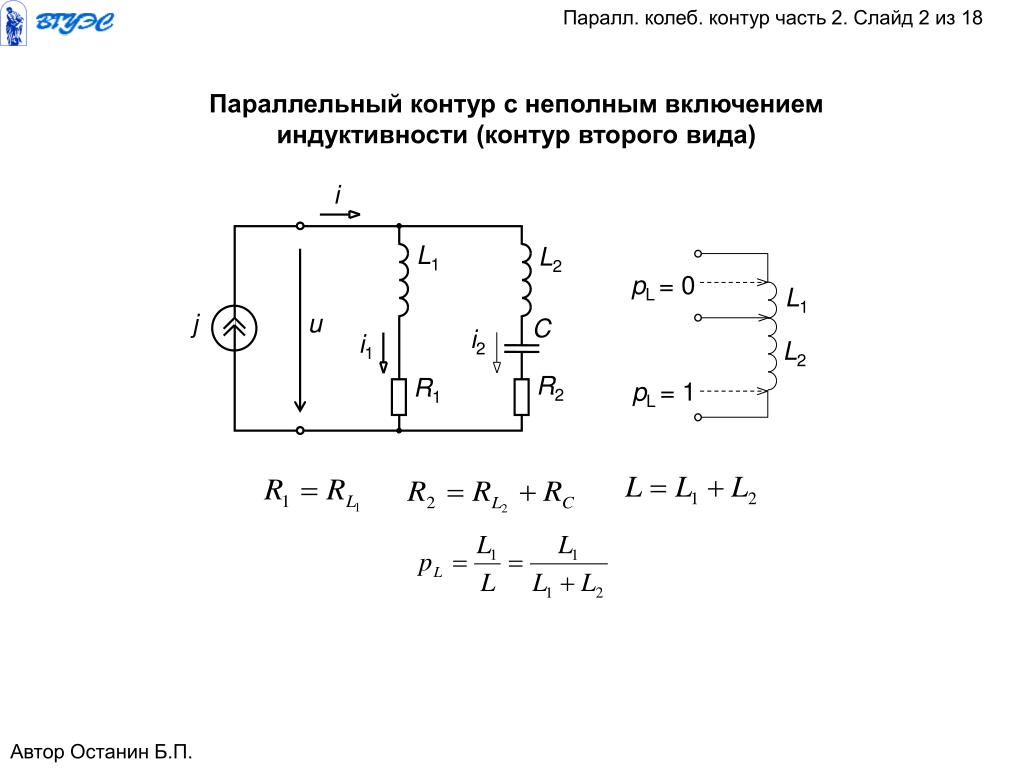
Для уменьшения влияния внешних цепей, а также для трансформации сопротивлений применяют частичное включение нагрузки в контур
Как видно из рисунка это можно сделать различными способами, отводом от катушки, с помощью катушки связи, емкостным делителем. Тогда выходное сопротивление контура:
где p –коэффициент связи. Для емкостного делителя:
p = C1 ⁄ (C1 + C2)
Для индуктивной связи:
p = M ⁄ L
где M — полная взаимоиндуктивность между Lc и L (это относится как к случаю с отводом катушки так и к случаю с катушкой связи). Следует отметить, что коэффициент связи не равен отношению числа витков, как в трансформаторе, поскольку каждый виток катушки Lc пересекается не всеми силовыми линиями катушки контура вследствие рассеяния магнитного поля.
При подключении внешней нагрузки к контуру с помощью частичного включения, результирующая добротность определяется:
Ru = p2Ri (Ri – внешняя нагрузка)
Следует отметить, что для максимального коэффициента передачи электромагнитной энергии, выходное сопротивление контура должно быть равно сопротивлению нагрузки.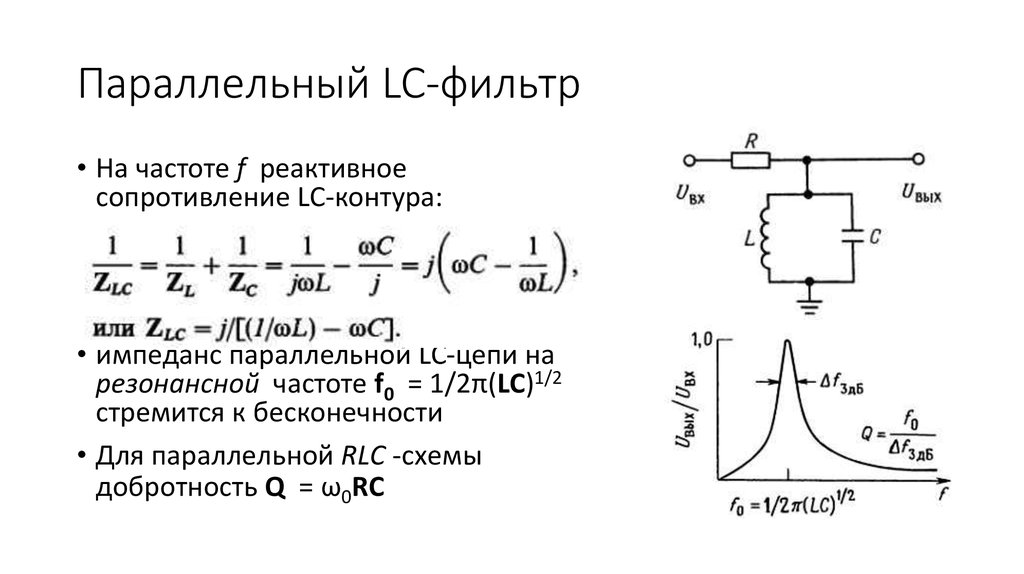 Все вышесказанное справедливо и в случае согласования контура с источником сигнала.
Все вышесказанное справедливо и в случае согласования контура с источником сигнала.
ПАРАЛЛЕЛЬНАЯ ЦЕПЬ определение | Кембриджский словарь английского языка
Примеры параллельного подключения
Параллельное подключение
Однако сейчас самое время взглянуть на разницу между последовательными и параллельными схемами.
Из проводного
Это прекратилось, когда лампа-ретранслятор вышла из строя, и параллельная схема вступила во владение.
Из проекта Гутенберг
В последовательной цепи с двумя лампочками и выключателем лампочки (ярче) (тусклее) (такие же), как когда они были в параллельный контурный .
Из проекта Гутенберг
Из проекта Гутенберг
Использовались две генераторные динамо-машины, которые были соединены в параллельную цепь , но таким образом, что разность потенциалов в обеих машинах все время оставалась одинаковой.
Из проекта Гутенберг
Без побочных эффектов синтез может получить высокопараллельные схемы из функционального описания, потому что он должен учитывать только прямые зависимости данных.
Из Кембриджского корпуса английского языка
Измеряемый ток протекал через обе катушки за параллельный контур , один представляет его количество, выражаемое в амперах, а другой — его потенциал, выражаемый в вольтах.
Из проекта Гутенберг
Эти сверхактивные параллельные цепи аналогичны цепям повторного входа в миокарде, которые часто вызывают аритмии.
Из Кембриджского корпуса английского языка
Две параллельные цепи составили эффективное короткое замыкание.
Из проекта Гутенберг
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Переводы parallel chain
на китайский (традиционный)
並聯電路…
Подробнее
на китайском (упрощенном)
并联电路…
Подробнее
на португальском языке
Circuito Paralelo…
Увидеть больше
на других языкахна польском
obwód równoległy…
Узнать больше
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится параллельная цепь ?
Обзор
помощник юриста
паралингвистический
параллакс
параллельно
параллельная цепь
параллельный запрос данных
параллельная экономика
параллельная эволюция БЕТА
параллельный импорт
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам
- {{randomImageQuizHook.
 copyright1}}
copyright1}} - {{randomImageQuizHook.copyright2}}
Авторы изображений
Пройди тест сейчас
Слово дня
педаль
Великобритания
Ваш браузер не поддерживает аудио HTML5
/ˈped.əl/
НАС
Ваш браузер не поддерживает аудио HTML5
/ˈped.əl/
небольшая часть машины или предмета, которую нажимают ногой для приведения в действие или перемещения машины или предмета
Об этом
Блог
Сохранение мира и оливковые ветви (идиомы для того, чтобы снова стать друзьями после ссоры)
Подробнее
Новые слова
грязное здоровье
Больше новых слов
добавлен в список
Наверх
Содержание
EnglishIntermediateExamplesTranslations
Что такое последовательно-параллельная цепь — электрическая…
В простых последовательных цепях все компоненты соединены встык, образуя только один путь для прохождения электронов по цепи:
В простой параллельной цепи В цепях все компоненты соединены между одними и теми же двумя наборами электрически общих точек, создавая множество путей для движения электронов от одного конца батареи к другому:
Для каждой из этих двух основных конфигураций схемы у нас есть определенные наборы правил, описывающих отношения между напряжением, током и сопротивлением.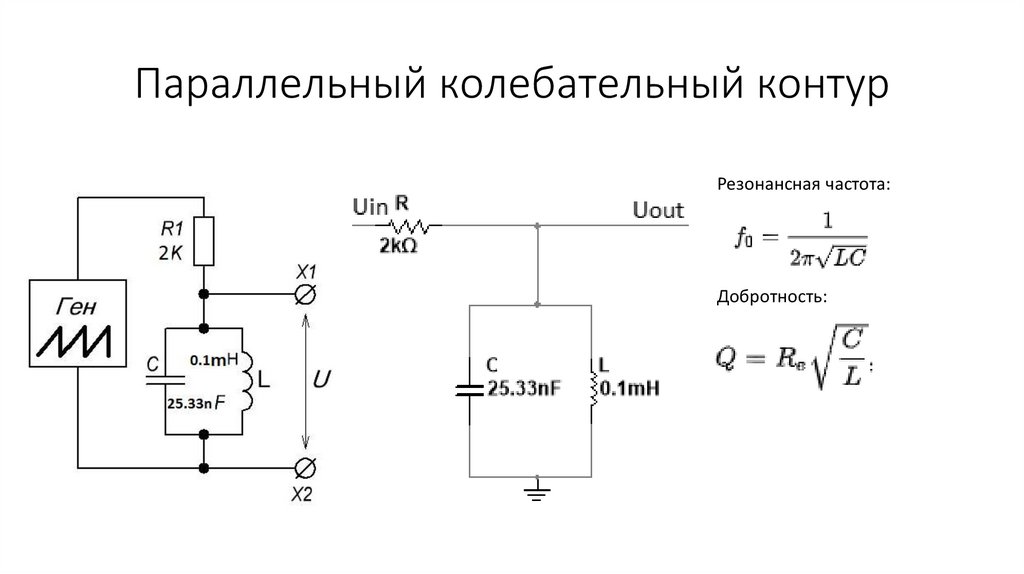
Цепи серии:
- Падение напряжения добавляется к общему напряжению.
- Все компоненты имеют одинаковый (равный) ток.
- Сопротивления добавляются к общему сопротивлению.
Параллельные цепи:
- Все компоненты имеют одинаковое (равное) напряжение.
- Токи ветвей добавляются к общему току.
- Сопротивление уменьшается до равного общему сопротивлению.
Однако, если компоненты схемы соединены последовательно в одних частях и параллельно в других, мы не сможем применить единый набор правил к каждой части этой цепи. Вместо этого нам нужно будет определить, какие части этой схемы являются последовательными, а какие параллельными, а затем выборочно применить правила последовательностей и параллельных последовательностей, необходимые для определения того, что происходит. Возьмем, к примеру, следующую схему:
Эта схема не является ни простой последовательной, ни простой параллельной. Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R 3 и R 4 , воссоединяется, затем снова разделяется, чтобы пройти через R 1 и R 2 , затем снова объединяется, чтобы вернуться к верхняя часть аккумулятора. Существует более одного пути прохождения тока (не последовательного), но в цепи имеется более двух наборов электрически общих точек (не параллельных).
Скорее, он содержит элементы обоих. Ток выходит из нижней части батареи, разделяется, чтобы пройти через R 3 и R 4 , воссоединяется, затем снова разделяется, чтобы пройти через R 1 и R 2 , затем снова объединяется, чтобы вернуться к верхняя часть аккумулятора. Существует более одного пути прохождения тока (не последовательного), но в цепи имеется более двух наборов электрически общих точек (не параллельных).
Поскольку цепь представляет собой комбинацию как последовательной, так и параллельной цепи, мы не можем применять правила для напряжения, тока и сопротивления «по всему столу», чтобы начать анализ, как мы могли бы, когда цепи были тем или иным образом. Например, если бы приведенная выше схема была простой последовательностью, мы могли бы просто сложить R 1 по R 4 , чтобы получить общее сопротивление, найти общий ток, а затем найти все падения напряжения. Точно так же, если бы приведенная выше схема была простой параллельной, мы могли бы просто найти токи ветвей, сложить токи ветвей, чтобы вычислить общий ток, а затем рассчитать общее сопротивление из общего напряжения и полного тока.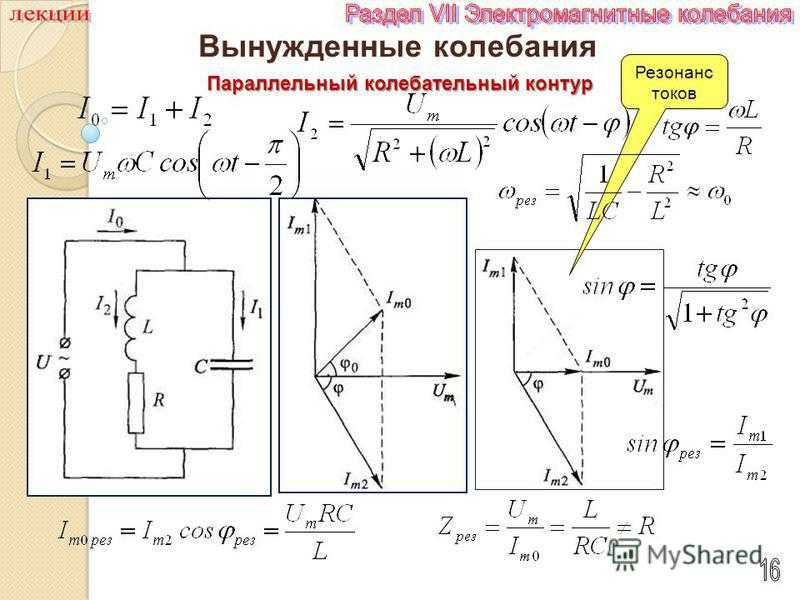


 copyright1}}
copyright1}}