Объяснение урока: Параллельные схемы | Нагва

В этом объяснении мы узнаем, как рассчитать разность потенциалов, ток и сопротивление в разных точках простых параллельных цепей.

На приведенной ниже схеме показана схема, состоящая из ячейки и резистора. Разность потенциалов, обеспечиваемая ячейкой, равна 𝑉, ток в цепи равно 𝐼, а сопротивление резистора равно 𝑅.

В приведенной выше схеме есть только один путь, по которому могут течь электроны, чтобы двигаться от одного конца ячейки к другому. Однако в приведенной ниже схеме есть два пути, по которым электроны могут течь, чтобы двигаться от одного конца ячейки к другому.

Путь между двумя терминалами ячейки разделяется на две ветви в точке A. Пути снова соединяются в точке B. На каждом пути есть резистор.

Когда существует несколько различных путей, по которым электроны могут пройти между выводами ячейки, как этот, мы говорим, что эта часть цепи параллельно . Если в цепи есть элементы, включенные последовательно и параллельно, то она называется комбинированной схемой. Когда все компоненты цепи соединены только параллельными соединениями, это называется параллельной цепью.

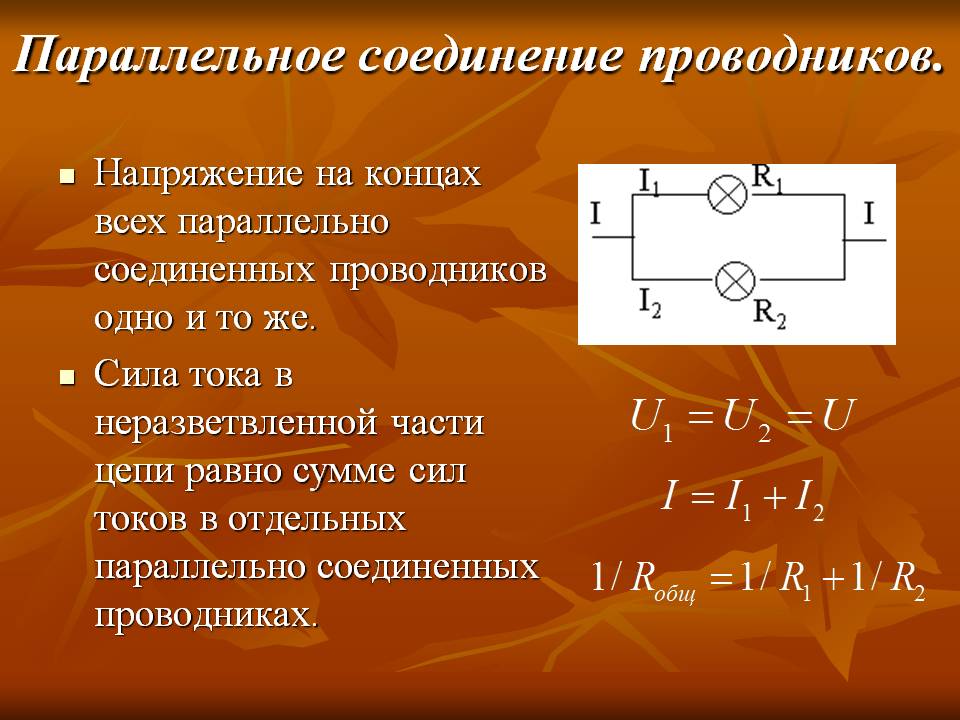
Давайте рассмотрим пример.

Пример 1: Идентификация компонентов, соединенных параллельно

На схеме показаны четыре цепи. Какая цепь содержит два резистора, включенных параллельно?

Ответ

Компоненты соединены параллельно , если они находятся на разных путях цепи.

В цепи а есть два резистора, но они находятся на одном пути, а не на разных. Электроны, идущие от одного конца клетки к другому, должны пройти через оба резистора. Следовательно, они последовательно, а не параллельно.

Схема b очень похожа на схему; единственное отличие состоит в том, что компоненты размещены на разных сторонах диаграммы. Это не влияет независимо от того, соединены ли компоненты последовательно или параллельно, эти компоненты также соединены последовательно.

В схеме d есть два возможных пути движения электронов между клеммами ячейки, но один путь проходит через лампочку, а другой — через лампочку. два резистора последовательно. Резисторы параллельны лампочке, но не друг другу.

В схеме c также есть два возможных пути движения электронов, каждый из которых содержит резистор. Эти резисторы включены параллельно.

Правильный ответ: схема c.

Определить, где именно начинается и где заканчивается параллельная цепь, может быть непросто. Рассмотрим следующие параллельные схемы.

Несмотря на то, что кажется, что они начинаются и заканчиваются в разных местах, эти схемы эквивалентны. Обведенная площадь обоих точно такая же: раскол, с 𝑅 на одном пути и 𝑅 на другом, то оба пути в конце сходятся.

Пока пути, по которым проходят токи, одинаковы, цепи эквивалентны. На схеме ниже есть еще две схемы, которые эквивалентны.

Ориентация компонентов не имеет значения, если схема может быть описана одинаково — в данном случае это разделение на два пути, один содержит 𝑅, а другой 𝑅, которые затем снова собираются вместе.

На приведенной ниже схеме показаны четыре полностью эквивалентные схемы с двумя резисторами и лампочкой.

Эти схемы эквивалентны, поскольку компоненты соединены параллельно. Все они могут быть описаны как раздвоение пути, одно из которых содержит два резистора, а другой содержит лампочку, а затем пути снова собираются вместе. На рисунке ниже это описание показано визуально с использованием двух схем.

Давайте рассмотрим пример.

Пример 2: определение эквивалентных схем цепей

На схеме показаны четыре цепи с компонентами, соединенными параллельно. Какие две схемы эквивалентны?

Ответ

Рассмотрим пути в этих цепях. Цепь а имеет разделение с резистором 10 Ом. на одном пути и лампочка и резистор 20 Ом на другом.

Цепь b имеет разделение с резистором 20 Ом на одном пути и лампочкой и Резистор 10 Ом с другой стороны.

Цепь c сначала имеет резистор 20 Ом, а затем разделяется на две цепи с лампочкой на одной и другой резистор 10 Ом с другой стороны. Примечательно, что это не настоящая параллельная схема, а скорее комбинированная схема, так как он имеет компоненты как последовательно, так и параллельно.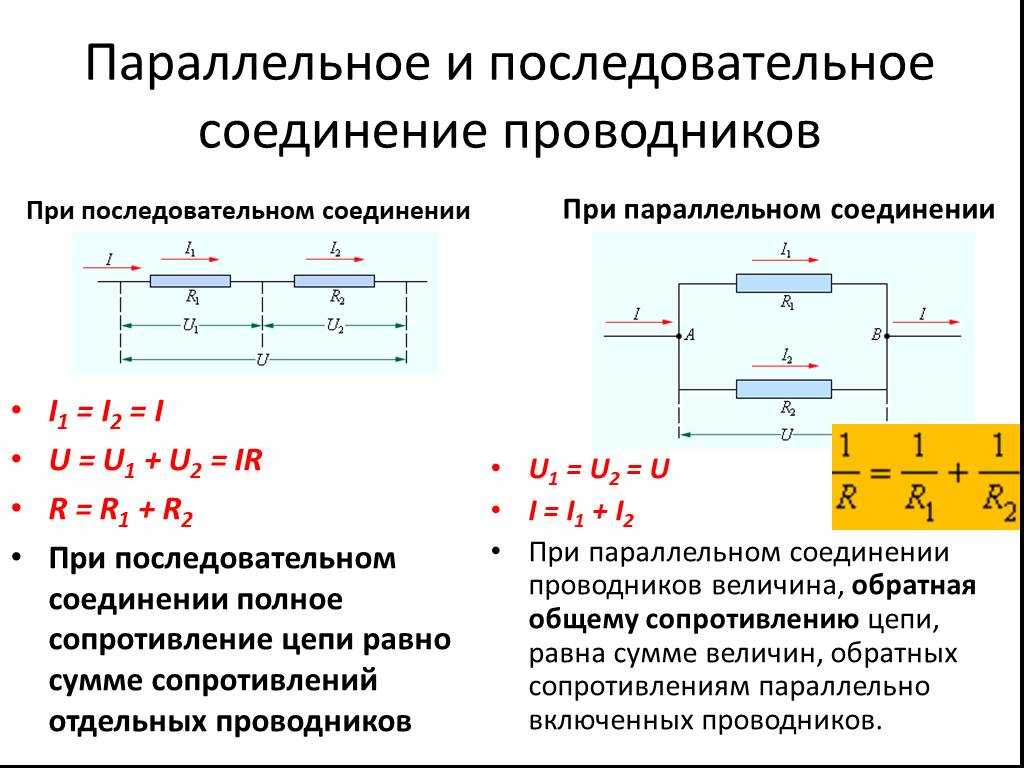

Цепь d разделена, с резистором 10 Ом на одном пути и лампочкой и резистор 20 Ом с другой стороны.

Если ток проходит по одному и тому же пути через одни и те же компоненты, цепи эквивалентны. Два, которые описываются одинаково, это a и d.

В параллельной цепи разность потенциалов на каждой параллельной ветви будет одинаковой. Независимо от значений сопротивления компонентов на этих путях, разность потенциалов на каждом из них будет одинаковой. На приведенной ниже диаграмме показаны два вольтметра, измеряющие разность потенциалов на двух резисторах.

Если 𝑅 равно 1 Ом и 𝑅 равно 1‎ ‎000 Ом, неважно. Разность потенциалов между ними составляет 20 В.

Правило: Разность потенциалов между компонентами, включенными параллельно

Разность потенциалов на каждой ветви параллельной цепи одинакова: 𝑉=𝑉=𝑉=….

Рассмотрим пример.

Пример 3: поиск потенциальных различий между компонентами, включенными параллельно

На схеме показаны два резистора, подключенных параллельно к ячейке.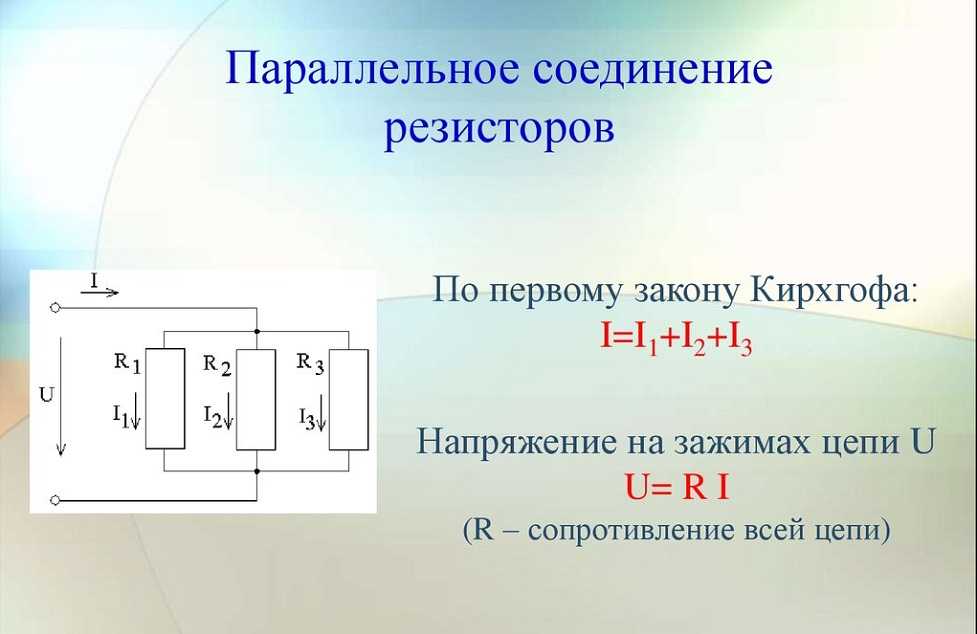 Если разность потенциалов на 3 Ом резистор 18 В, какова разность потенциалов на резистор 6 Ом?

Ответ

Разность потенциалов между параллельными компонентами определяется правилом 𝑉=𝑉=𝑉=….

Для этой схемы с двумя компонентами правило выглядит так 𝑉=𝑉.

Нам дано значение разности потенциалов на резисторе 3 Ом, 𝑉, быть 18 В. Разность потенциалов на резисторе 6 Ом тогда должно быть одинаково: 18 В.

В отличие от разности потенциалов на разных ветвях, которая одинакова для каждой ветви, ток в каждой ветви может быть разным.

Напомним, что сопротивление — это сопротивление потоку электрического заряда. Если одна ветвь имеет большее сопротивление, чем другая, заряду будет труднее течь по ней. и поэтому ток в нем будет слабее, а ток в другом ответвлении сильнее.

Однако все электроны из ячейки должны пройти по одной из ветвей. Следовательно, суммарный ток по всем ветвям будет равен к току до того, как путь цепи разделился.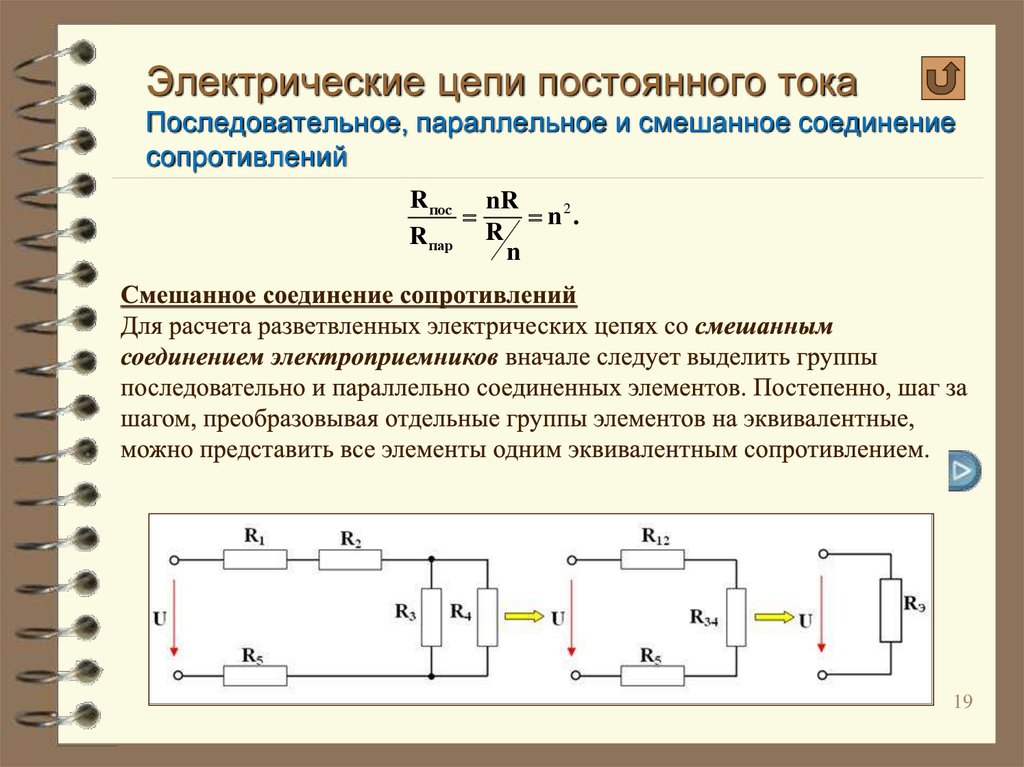

На приведенной ниже диаграмме общий ток 𝐼total равен сумме токов в отдельных ветвях, 𝐼 и 𝐼.

Правило: Суммарный ток в параллельных цепях цепи

Суммарный ток параллельных компонентов, 𝐼total, равен сумме токов в каждой цепи: 𝐼=𝐼+𝐼+𝐼+…, всего где 𝐼, 𝐼, 𝐼 и т. д. — токи на определенном пути.

Точный способ разделения тока зависит от сопротивления каждого пути. На приведенной ниже диаграмме показана цепь, которая разделена на три пути с током в каждом.

Нам дан общий ток 𝐼общий и ток в двух цепях вдоль резисторов 𝑅 и 𝑅. Мы можем использовать их, чтобы найти ток через крайний левый путь, 𝐼.

Суммарный ток в цепи равен 9 А. Средний путь можно назвать 𝐼, а крайний правый путь 𝐼, равный 5 A и 1 A соответственно. Мы можем использовать правило для полного тока вдоль параллельных путей, чтобы представить это как уравнение: 𝐼=𝐼+𝐼+𝐼.total

Подставляя наши известные значения тока, уравнение становится (9)=𝐼+(5)+(1)9=𝐼+6.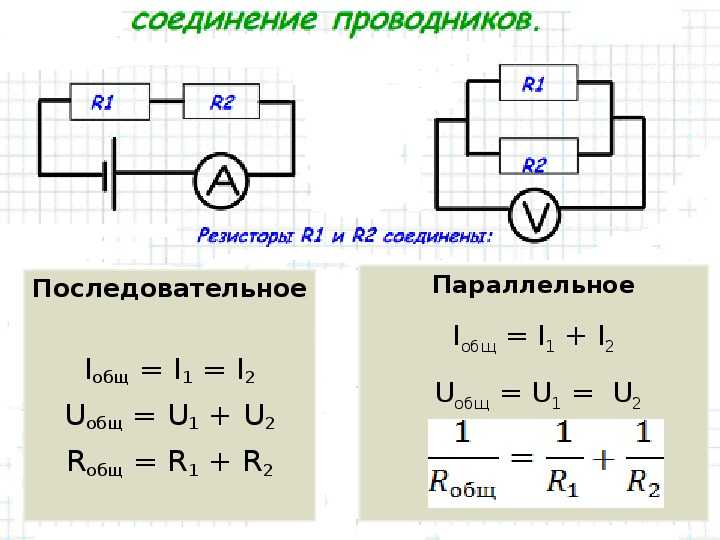 AAAAAA

Чтобы найти 𝐼, нам нужно вычесть 6 А с обеих сторон: 9−6=𝐼+6−63=𝐼.AAAAA

Итак, ток по крайнему левому пути, 𝐼, равен 3 А.

Предположим теперь, что нам не задан ток по пути, как в диаграмма ниже.

Мы можем определить, сколько тока проходит по каждому пути, сравнив значения сопротивления. На приведенной выше схеме резисторы имеют одинаковое значение сопротивления 𝑅. Это означает, что ток будет равномерно разделен между двумя путями: 𝐼=𝐼.

Итак, глядя на общий ток, 𝐼=𝐼+𝐼.total

Подстановка всех токов на 𝐼, поскольку они одинаковы, дает нам 𝐼=𝐼+(𝐼)𝐼=2𝐼.totaltotal

Чтобы найти 𝐼, мы просто делим обе части на 2: 𝐼2=2𝐼2𝐼2=𝐼.totaltotal

Таким образом, отдельные пути имеют половину общего тока. Суммарный ток равен 8 А, поэтому 𝐼2=4.totalA

Поскольку 𝐼 и 𝐼 равны друг другу, они оба равны 4 А.

Давайте рассмотрим несколько примеров вопросов.

Пример 4: Определение токов через компоненты, соединенные параллельно

Схема, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке.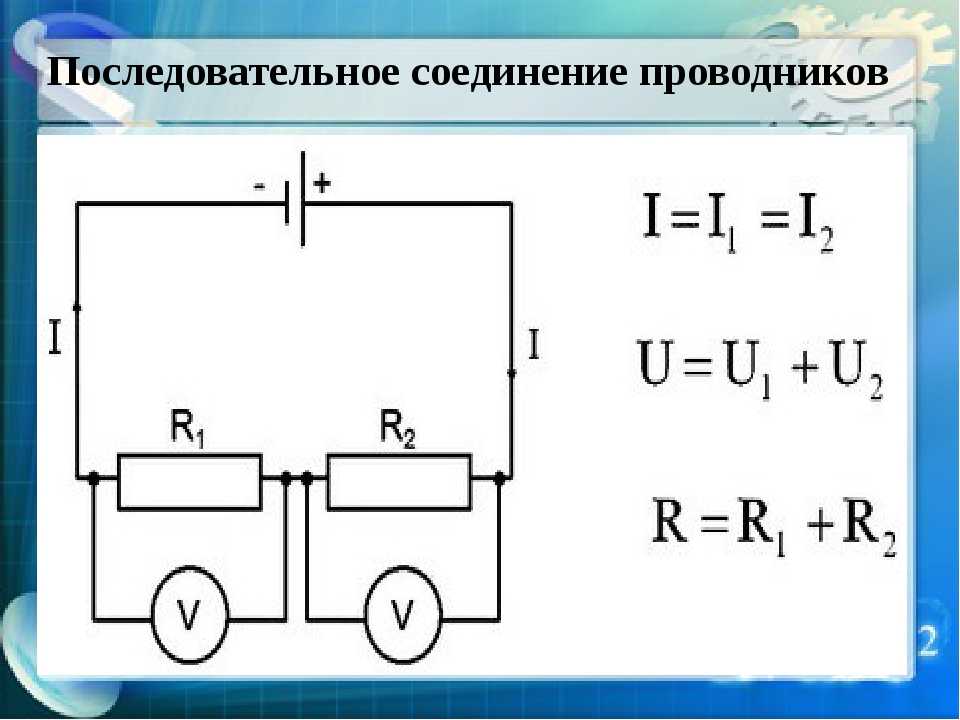 Значение 𝐼total равно до 30 А. Каково значение 𝐼?

Ответ

Суммарный ток в цепи с параллельными элементами определяется по правилу 𝐼=𝐼+𝐼+𝐼+….total

Всего для двух компонентов на разных путях это правило становится 𝐼=𝐼+𝐼.Всего

Два резистора на дорожках в этой цепи одинаковы, поэтому ток распределяется между ними поровну. Это означает, что текущий 𝐼 то же, что и 𝐼: 𝐼=𝐼.

Подстановка этого соотношения в правило для полного тока дает 𝐼=(𝐼)+𝐼𝐼=2𝐼.totaltotal

Теперь, чтобы найти 𝐼, разделим обе части на 2: 𝐼2=2𝐼2.total

Это приводит к тому, что 2 в правой части уравнения отменяется, оставляя 𝐼2=𝐼.всего

Суммарный ток равен 30 А. Подстановка этого значения дает значение 𝐼: (30)2=15.AA

Итак, значение 𝐼 равно 15 А.

Чтобы проследить, как ток изменяется в зависимости от сопротивления пути, мы должны сначала посмотреть, как найти общее сопротивление компонентов, включенных параллельно. .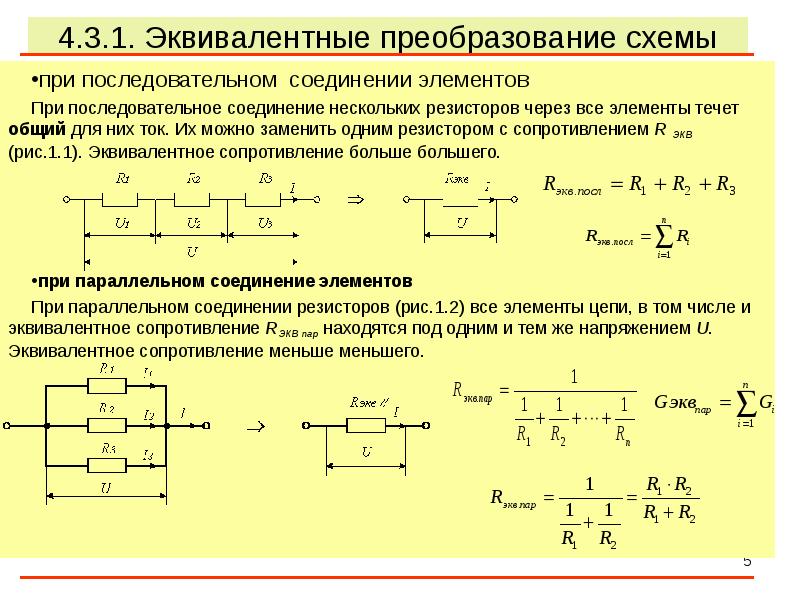

Правило: общее сопротивление компонентов, расположенных параллельно

Для ряда компонентов, расположенных параллельно, общее сопротивление 𝑅total равно 1𝑅=1𝑅+1𝑅+1𝑅+…, всего где 𝑅 — сопротивление первой составляющей, 𝑅 — второй и т. д.

Давайте используем это уравнение только с двумя резисторами, 𝑅 и 𝑅, чтобы продемонстрировать, как найти 𝑅общий сам по себе. Это делает уравнение 1𝑅=1𝑅+1𝑅.total

Мы можем взять обратное значение обеих частей, чтобы получить 𝑅total в левой части: 1=1+.total

Деление на дробь равносильно умножению на знаменатель, поэтому левая часть становится 1=1×𝑅1=𝑅.totaltotaltotal

Это делает уравнение 𝑅=1+.total

Теперь умножим обе части на 𝑅𝑅; поскольку это всего лишь один, он сохранит 𝑅полный член в левой части: 𝑅×𝑅𝑅=1+×𝑅𝑅.Всего

Дробь означает, что верх и низ будут распределяться поперек для дроби с правой стороны: 𝑅×1=1×𝑅𝑅+𝑅=𝑅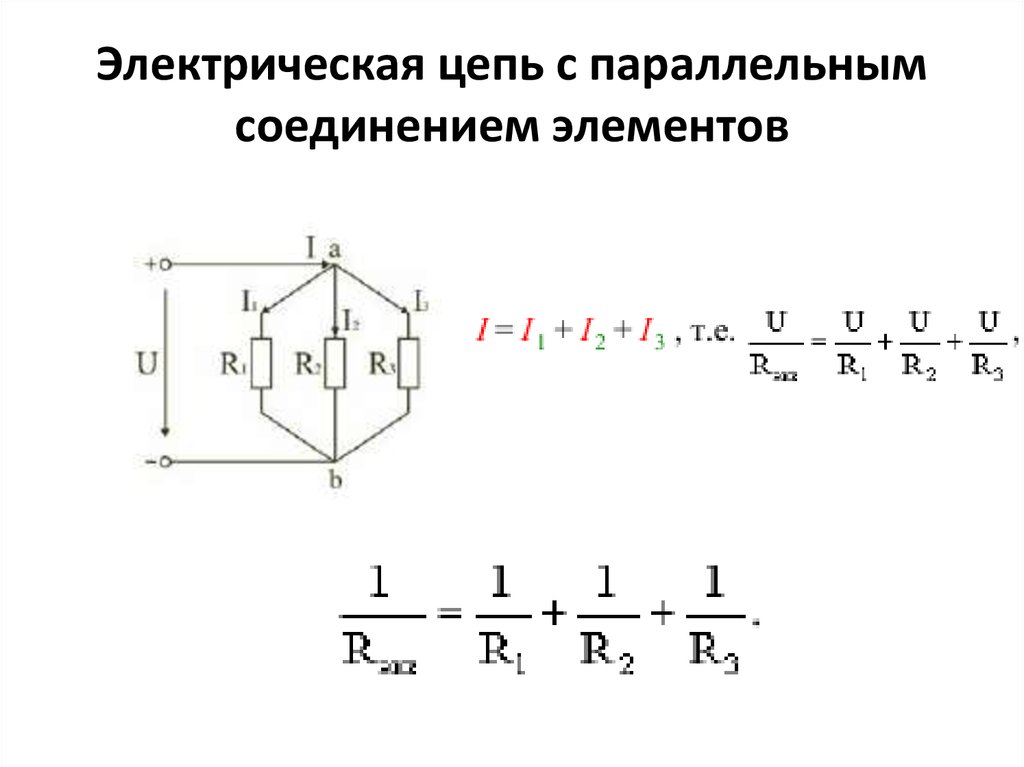+. totaltotal

𝑅 больше 𝑅, поэтому уравнение теперь равно единице 𝑅=𝑅1+.total

Теперь умножим обе части на 𝑅𝑅: 𝑅×𝑅𝑅=𝑅1+×𝑅𝑅.total

Умножая 𝑅 сверху и снизу для правой части, получаем 𝑅×1=𝑅×𝑅𝑅1+.total

𝑅 распределяется по знаменателю: 𝑅=𝑅𝑅𝑅+.total

𝑅𝑅 в знаменателе равно 1, что дает 𝑅=𝑅𝑅(𝑅+𝑅).total

Таким образом, при наличии двух резисторов это уравнение можно использовать для определения общего сопротивления цепи.

Правило: полное сопротивление двухкомпонентной параллельной цепи

Когда два компонента проходят параллельные пути, общее сопротивление 𝑅total равно 𝑅=𝑅𝑅(𝑅+𝑅), всего где 𝑅 — сопротивление первого компонента, а 𝑅 — сопротивление второго компонента.

В приведенной ниже схеме мы можем вычислить 𝑅total, используя это правило.

Примем 𝑅 за 5 Ом и 𝑅 за 20 Ом. Ввод этих значений в уравнение для полного сопротивления дает 𝑅=(5)(20)(5)+(20)=100(25).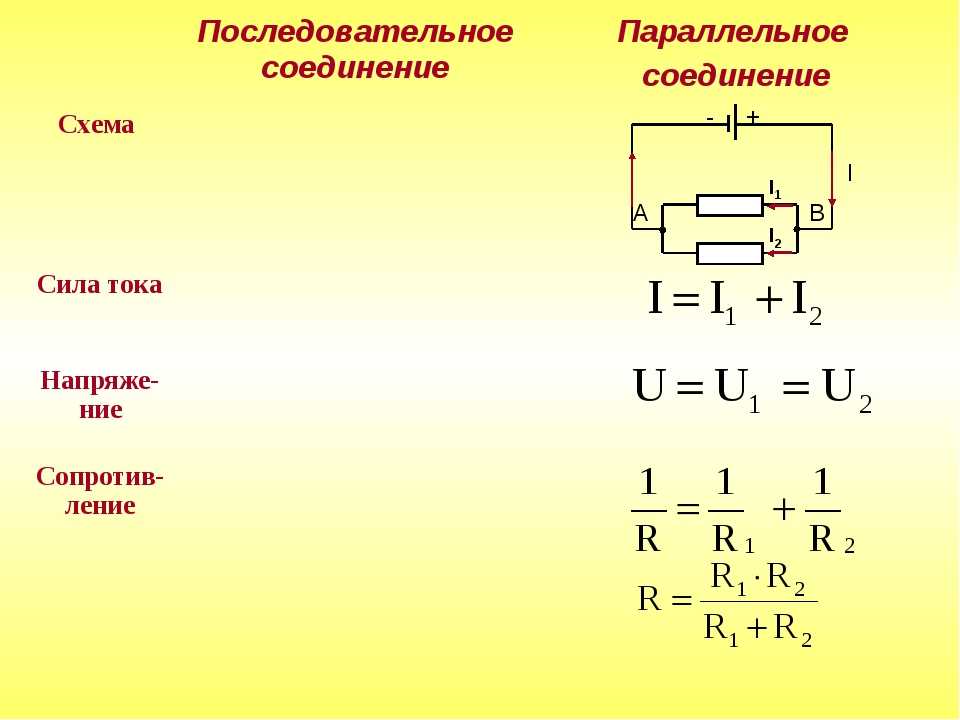 totalΩΩΩΩΩΩ

Деление на омы отменяет квадрат в омах член в числителе, дающий общее сопротивление как 100(25)=4.ΩΩΩ

Рассмотрим пример.

Пример 5. Определение того, как изменяется ток в зависимости от количества параллельных путей в цепи

Учащийся устанавливает схему, показанную на схеме. Изначально переключатель разомкнут. Когда ученик замкнет переключатель, будет ли ток течь через схема увеличения или уменьшения?

Ответ

Чтобы определить полный ток в цепи, закон Ома можно представить в терминах силы тока: 𝐼=𝑉𝑅.

Разность потенциалов в этой цепи фиксируется ячейкой, но сопротивление может изменяться, когда путь снизу закрыт. Назовем резисторы как 𝑅 и 𝑅 нравится так.

Первоначально, когда переключатель разомкнут, в нижней ветви этой цепи отсутствует ток. Все электроны из клетки будут проходить только через 𝑅. Таким образом, полное сопротивление можно описать как 𝑅=𝑅. total

Когда ключ замкнут, в ветвях, содержащих как 𝑅, так и 𝑅, будет ток. Напомним, что общая сопротивление в цепи с двумя параллельными резисторами определяется по уравнению 𝑅=𝑅𝑅(𝑅+𝑅).всего

Теперь, независимо от значения 𝑅, общее сопротивление будет уменьшаться. Это потому, что умножение 𝑅 на 𝑅, то деление на сумму всегда будет меньше, чем 𝑅 само по себе: 𝑅>𝑅𝑅(𝑅+𝑅).

Чтобы убедиться в этом, предположим, что 𝑅 равно 1 Ом, и проверим 𝑅 как 0,1 Ом и 1‎ ‎000 Ом: 𝑅=1.Ω

Заменив 0,1 Ω на 𝑅, общее сопротивление 𝑅total станет 𝑅𝑅(𝑅+𝑅)(1)(0,1)((0,1)+(1))=0,099.ΩΩΩΩΩΩΩ

Теперь давайте попробуем заменить 1‎ ‎000 Ом на 𝑅: (1)(1000)((1000)+(1))=0,999.ΩΩΩΩΩΩ

Мы видим, что в обоих этих случаях окончательный результат меньше, чем просто 𝑅.

Значит, если общее сопротивление уменьшается, то по закону Ома общий ток в цепи должен увеличиваться, так как ток обратно пропорционален к сопротивлению: 𝐼=𝑉𝑅.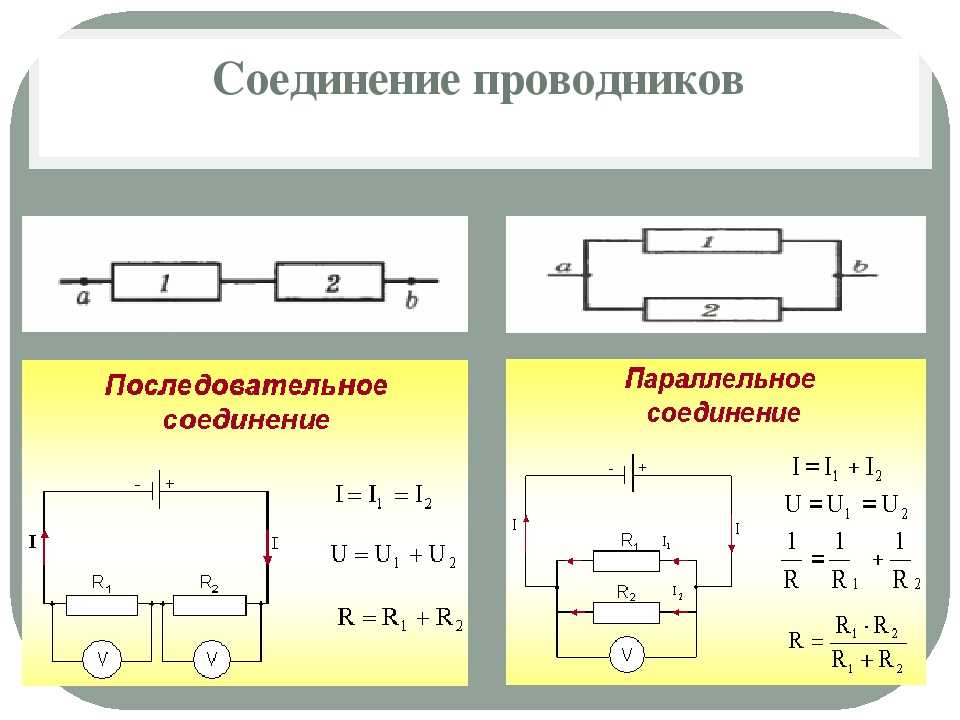

Правильный ответ: ток увеличивается при замыкании ключа.

Теперь, когда мы видим, как работают ток, сопротивление и разность потенциалов в параллельных цепях, мы можем использовать эти правила, чтобы найти нужные значения в цепи.

Давайте рассмотрим пример.

Пример 6: Определение значений разности потенциалов и тока для компонентов, соединенных параллельно

Схема, показанная на схеме, состоит из двух резисторов, подключенных параллельно к ячейке. Значение тока, даваемое вторым амперметром, 𝐼 равно 3 А. Каково значение 𝐼total?

Ответ

Мы знаем, что в параллельной цепи полный ток равен сумме всех токов в параллельных цепях. Таким образом, для этой цепи полный ток равен 𝐼=𝐼+𝐼.total

Это означает, что мы должны найти ток второго пути, 𝐼, поэтому мы можем добавить его к 𝐼 и найти общий ток. Мы можем сделать это, рассмотрев потенциальные различия на каждом пути.

Нам не известна разность потенциалов клетки, но мы знаем, что разность потенциалов одинакова на обоих путях: 𝑉=𝑉. 

Это дает возможность использовать закон Ома, чтобы связать два пути вместе. Однако прежде чем мы это сделаем, предположим, что резистор вдоль путь 𝐼 — это 𝑅, а путь 𝐼 — это 𝑅.

Разность потенциалов на первом пути, используя закон Ома, можно записать как 𝑉=𝐼𝑅 и второй путь как 𝑉=𝐼𝑅, но поскольку 𝑉=𝑉, мы можем связать эти уравнения как 𝐼𝑅=𝐼𝑅.

Теперь мы можем найти желаемое значение 𝐼, разделив обе части на 𝑅: 𝐼𝑅𝑅=𝐼𝑅𝑅.

Отмена с левой стороны дает 𝐼=𝐼𝑅𝑅.

𝐼 равно 3 А, 𝑅 равно 4 Ом, и 𝑅 равно 12 Ом. Подставляя эти значения в уравнение, получаем 𝐼=(3)(12)(4).AΩΩ

Теперь мы разделим единицы измерения омов, сократив их как в числителе, так и в знаменателе, что даст 𝐼=(3)(3)𝐼=9.AA

Теперь, когда у нас есть 𝐼, мы просто добавляем его вместе с 𝐼, чтобы получить общий ток: 𝐼=9+3𝐼=12.totaltotalAAA

Итак, общий ток 12 ампер.