Электричество и магнетизм
В этом разделе мы решим задачи о зарядке и разрядке конденсатора. Электрическая цепь показана на рис. 4.20. Переключатель S позволяет подсоединять и отсоединять источник тока.
|
Рис. 4.20. Цепь для зарядки и разрядки конденсатора Пусть сначала конденсатор емкостью С не заряжен, и мы перебрасываем выключатель в положение а. По цепи пойдет зависящий от времени ток I(t), переносящий положительный заряд на верхнюю пластину конденсатора. Отметим, что хотя ток зарядки и разрядки конденсатора не является постоянным, но рассматривается здесь, поскольку его изменение в данном случае можно считать медленным. Обозначим заряд на этой пластине в момент t через q(t). Напряжение на конденсаторе можно найти как разницу между ЭДС и падением напряжения на нагрузке, то есть либо как отношение заряда к емкости
Согласно закону сохранения заряда, изменение заряда q на обкладках конденсатора происходит только из-за наличия тока I. Поэтому второе уравнение процесса имеет вид
Подставим (4.37) в (4.36):
Мы видим, что у этого уравнения имеется стационарное решение (постоянный заряд на конденсаторе)
При таком заряде на конденсаторе напряжение на нем равно ЭДС источника тока, и ток по цепи не идет
Введем отклонение у заряда на конденсаторе от его стационарного значения
или
Подставляя это соотношение в (4.
Это уравнение легко интегрируется
откуда
Вычисляя интегралы. находим
или
где y0 — произвольная постоянная интегрирования (значение у в начальный момент времени). Отсюда находим заряд на конденсаторе
Нам осталось использовать начальное условие: в момент t = 0 конденсатор был не заряжен
Отсюда находим
и окончательно
Дифференцируя q(t) по времени, находим ток в цепи |
|
(4. |
Напряжение на конденсаторе U(t) = q(t)/C без труда получается из (4.39)
|
(4.41) |
Таким образом, по мере роста заряда и напряжения на конденсаторе ток в цепи уменьшается. При этом заряд конденсатора стремится к своему стационарному значению а напряжение на конденсаторе — к ЭДС источника тока. Величина имеет размерность времени и определяет характерное время процесса зарядки. За промежуток ток в цепи уменьшается
в е = 2,72 раза.
На рис. 4.21 показана зависимость заряда на конденсаторе и тока в цепи для конкретных значений R = 1,5 кОм, С = 2 мкФ, Характерное время процесса равно при этих значениях Из рисунков видно, что уже при временах порядка
конденсатор почти полностью заряжается.
Рис. 4.21. Графики зависимости напряжения на конденсаторе (слева) и тока в цепи (справа)
при зарядке конденсатора емкостью С = 2 мкФ через активное сопротивление R = 1,5 кОм от источника тока с ЭДС 12 В
Рассмотрим теперь процесс разрядки конденсатора. Зарядив его до какого-то заряда (или, что то же самое, до начального напряжения U0 = q0/C), мы перебрасываем переключатель в положение
|
|
(4. |
Все эти величины быстро уменьшаются с течением времени: за тот же характерный промежуток заряд конденсатора, напряжение на нем и ток в цепи падают в 2,72 раза. Отрицательный знак в выражении для тока означает, что ток при разрядке течет в направлении, обратном току при зарядке конденсатора.
Дополнительная информация
http://www.scorcher.ru/art/electronica/electronica1.php — зарядка — разрядка конденсатора.
5/9
Конденсаторные преобразователи напряжения
В статье рассматриваются преобразователи напряжения, построенные на цепях с переключаемыми конденсаторами. На взгляд автора, подобные топологии незаслуженно забыты и в настоящее время, с учетом наличия на рынке быстродействующих и экономичных силовых ключей, могут обрести «вторую молодость».
Конденсаторные, или как их еще называют, безындуктивные преобразователи напряжения используются относительно нечасто. На то есть свои причины – например, относительно небольшая выходная мощность и невысокий КПД.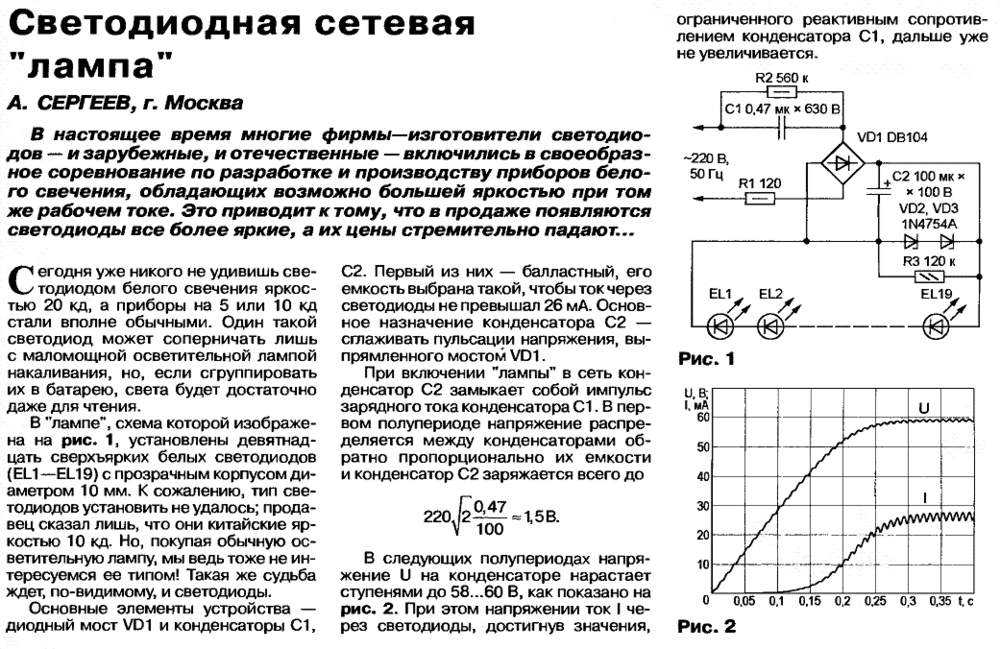 Однако в ряде случаев, когда требуется увеличить напряжение для небольшой нагрузки, а пульсации выходного напряжения не особенно критичны, использование подобных схем может оказаться весьма соблазнительной альтернативой.
Однако в ряде случаев, когда требуется увеличить напряжение для небольшой нагрузки, а пульсации выходного напряжения не особенно критичны, использование подобных схем может оказаться весьма соблазнительной альтернативой.
Схема одного из диодно–конденсаторных каскадов, который обеспечивает высокое выходное напряжение, приведена на рисунке 1а. Наиболее примечательным в этой схеме является то обстоятельство, что номинальные напряжения диодов и конденсаторов каждого каскада должны соответствовать напряжениям этого каскада, а не сумме напряжений всех предыдущих каскадов, хотя выходное напряжение цепочки каскадов (см. рис. 1б) равно именно суммарному напряжению всех каскадов, составляющих цепочку!
Приведенные на рисунке 1 схемы, наверное, знакомы каждому радиолюбителю, и все же в двух словах напомним их принцип действия. При отрицательной полуволне правая обкладка конденсатора С1 (см. рис. 1а) заряжается до пикового напряжения полуволны за вычетом напряжения на диоде D1. При положительной полуволне конденсатор С1 оказывается последовательно включенным с вторичной обмоткой трансформатора, поэтому конденсатор С2 заряжается удвоенным напряжением за вычетом напряжения на диодах D1 и D2.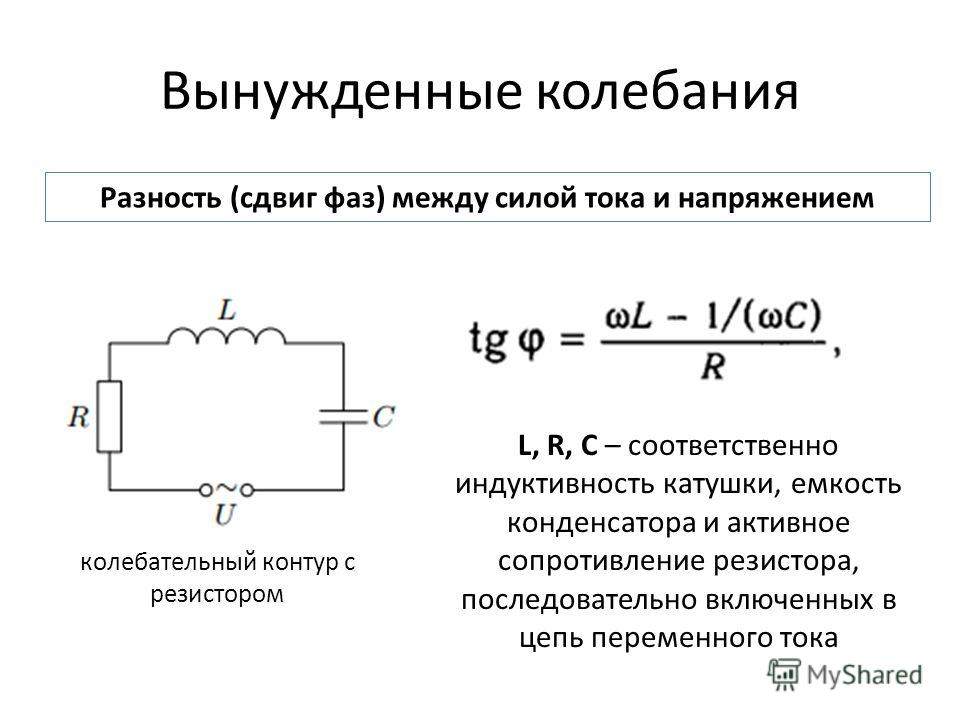 При последовательном соединении нескольких цепочек (см. рис. 1б) конденсаторы С2, С4 и С6 составляют последовательно соединенный стек конденсаторов, и напряжение всех конденсаторов суммируется.
При последовательном соединении нескольких цепочек (см. рис. 1б) конденсаторы С2, С4 и С6 составляют последовательно соединенный стек конденсаторов, и напряжение всех конденсаторов суммируется.
а) схема диодно-конденсаторного каскада;
б) цепочки диодно-конденсаторных каскадов
На основе описанной схемы появились разные модификации для работы с постоянным входным напряжением. Одна из таких схем – зарядный насос Диксона – показана на рисунке 2.
Рис. 2. Схема зарядного насоса Диксона с:а) диодными каскадами;
б) MOSFET
Похожая схема используется в ИС EEPROM и флэш-памяти для увеличения напряжения питания. Благодаря ей стало возможным уменьшить внешнее питание этих микросхем до 1,8 В. Выходное напряжение N‑каскадной схемы описывается уравнением (1):
VOUT = VIN(N+1) – (N+1)VF, (1)
где VF – прямое падение напряжения на диоде.
Для повышения выходного напряжения можно вместо диодов использовать MOSFET с низким сопротивлением канала в открытом состоянии, но при этом несколько возрастет стоимость решения. На рисунке 3 показан результат моделирования в LT-spice трехкаскадного зарядного насоса Диксона.
На рисунке 3 показан результат моделирования в LT-spice трехкаскадного зарядного насоса Диксона.
На рисунке 4 показана схема зарядовых насосов с плавающими или переключающимися конденсаторами. Такое название обусловлено тем, что при коммутации в некоторые моменты времени конденсаторы извлекаются из схемы и оба их конца «висят в воздухе». Необходимо, чтобы между коммутациями было мертвое время. Эту универсальную топологию можно использовать не только для усиления, но и для уменьшения, а также для инвертирования напряжения. Как правило, эту топологию компании производители применяют для построения безындуктивных DC/DC-преобразователей.
Рис. 4. Схема зарядового насоса с плавающими конденсаторамиВ фазе 1 ключи SW1 и SW2 замкнуты (см. рис. 4), а ключи SW3 и SW4 разомкнуты; при этом конденсаторы С1 и С2 соединены последовательно и подключены к источнику входного напряжения. Каждый конденсатор заряжается до половины входного напряжения. Во второй фазе картина меняется на противоположную: ключи SW1 и SW2 разомкнуты, а SW3 и SW4 – замкнуты. В этом случае конденсаторы С1 и С2 соединены параллельно и подключены к выходу схемы. Таким образом, входное напряжение уменьшается в два раза.
Каждый конденсатор заряжается до половины входного напряжения. Во второй фазе картина меняется на противоположную: ключи SW1 и SW2 разомкнуты, а SW3 и SW4 – замкнуты. В этом случае конденсаторы С1 и С2 соединены параллельно и подключены к выходу схемы. Таким образом, входное напряжение уменьшается в два раза.
Для уменьшения размера конденсаторов можно увеличить рабочую частоту; при этом, однако, возрастут коммутационные потери. Еще одним фактором, ограничивающим рабочую частоту, является постоянная времени заряда конденсаторов, которая ограничена выходным сопротивлением источника входного напряжения VIN, сопротивлением открытого канала ключей и эквивалентным последовательным сопротивлением (ESR) конденсаторов. В практической схеме, возможно, следует предусмотреть мягкий пуск, чтобы ограничить пусковой ток. В противном случае не исключено срабатывание защиты от максимального тока.
Примечательной особенностью этой схемы является ее обратимость. Если поменять местами входы и выходы и на выход VOUT подать входное напряжение, то на выводе VIN схемы появится удвоенное напряжение.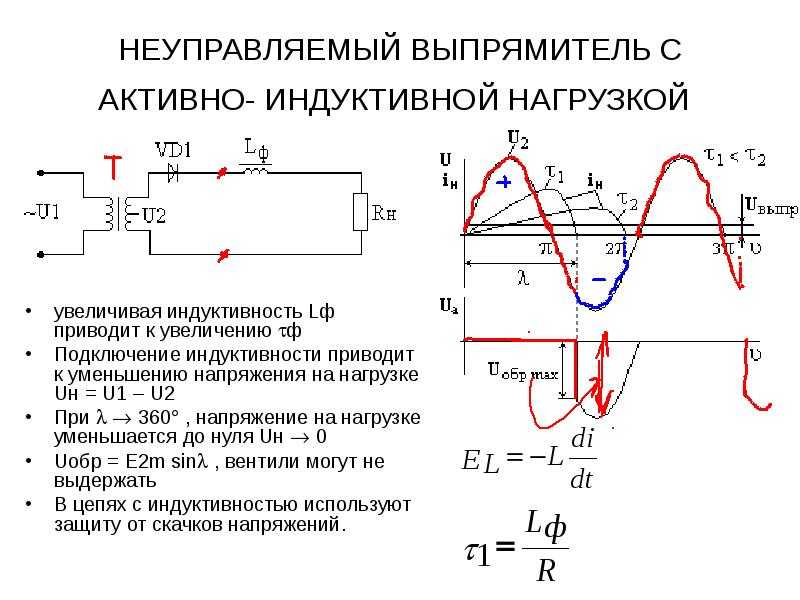 В этом случае заряжаются параллельно соединенные конденсаторы С1 и С2, а выходное напряжение снимается с последовательно соединенных конденсаторов. Заметим, что максимальный выходной ток в этом случае меньше, чем в случае понижения напряжения.
В этом случае заряжаются параллельно соединенные конденсаторы С1 и С2, а выходное напряжение снимается с последовательно соединенных конденсаторов. Заметим, что максимальный выходной ток в этом случае меньше, чем в случае понижения напряжения.
Для схемы, представленной на рисунке 4, при низком сопротивлении открытых каналов ключей SW1, SW2, SW3 и SW4 величина КПД достигает 90%. Следует учесть, что при использовании N‑канальных MOSFET для управления ключей высокой стороны понадобится большее напряжение, чем VIN. В этом случае придется использовать удвоитель напряжения (см. рис. 1). Меняя схему коммутации ключей, можно получить источник отрицательного напряжения, а с помощью дополнительных конденсаторов и ключей можно изменять коэффициент передачи напряжения.
При необходимости только инвертировать напряжение применяется простейшая схема, показанная на рисунке 5. Импульс тактирования заряжает конденсатор С1 через диод D2. В паузе между импульсами, когда потенциал на входном выводе близок к потенциалу земли, конденсатор С1 разряжается по цепи «С1 – вывод «Вход» – С2 – D1».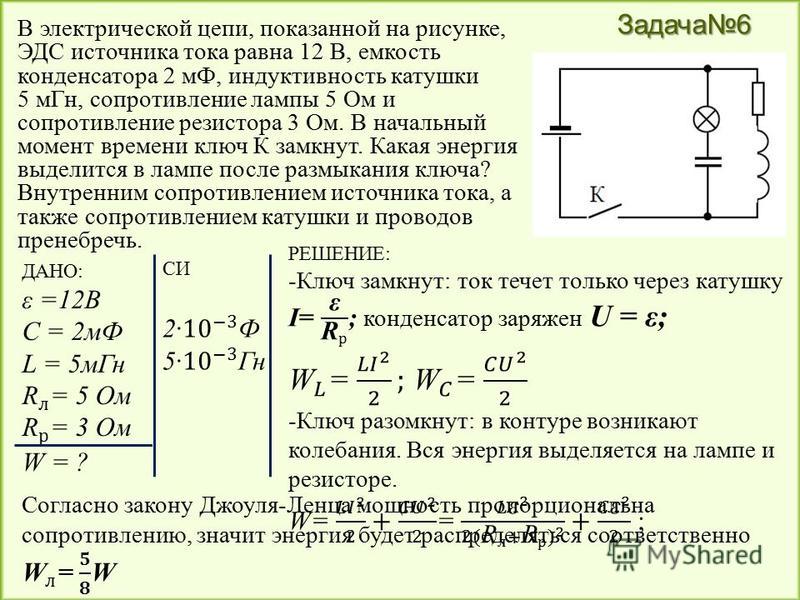 Таким образом, на верхней обкладке конденсатора, связанной с выходным электродом, появляется отрицательный заряд.
Таким образом, на верхней обкладке конденсатора, связанной с выходным электродом, появляется отрицательный заряд.
Существует еще одна интересная топология для получения высоковольтного отрицательного напряжения. Ее упрощенная схема показана на рисунке 6. Заметим, что в этой схеме ключ Q1 контроллера (для простоты контроллер не показан на схеме) жестко «привязан» к земле, в то время как в других подобных схемах его потенциал «плавает» между входным и выходным выводами. Соответственно, и выходное напряжение в таких схемах ограничено максимальным напряжением питания контроллера за вычетом входного напряжения. В схеме на рисунке 6 это ограничение отсутствует – она работает в режиме прерывистой проводимости.
Рис. 6. Упрощенная схема высоковольтного инвертирующего преобразователяРаботу схемы можно разделить на три интервала (см. рис. 7). В первом интервале d1 (см. рис. 7а) силовой MOSFET включен, ток через дроссель нарастает, и в нем запасается энергия.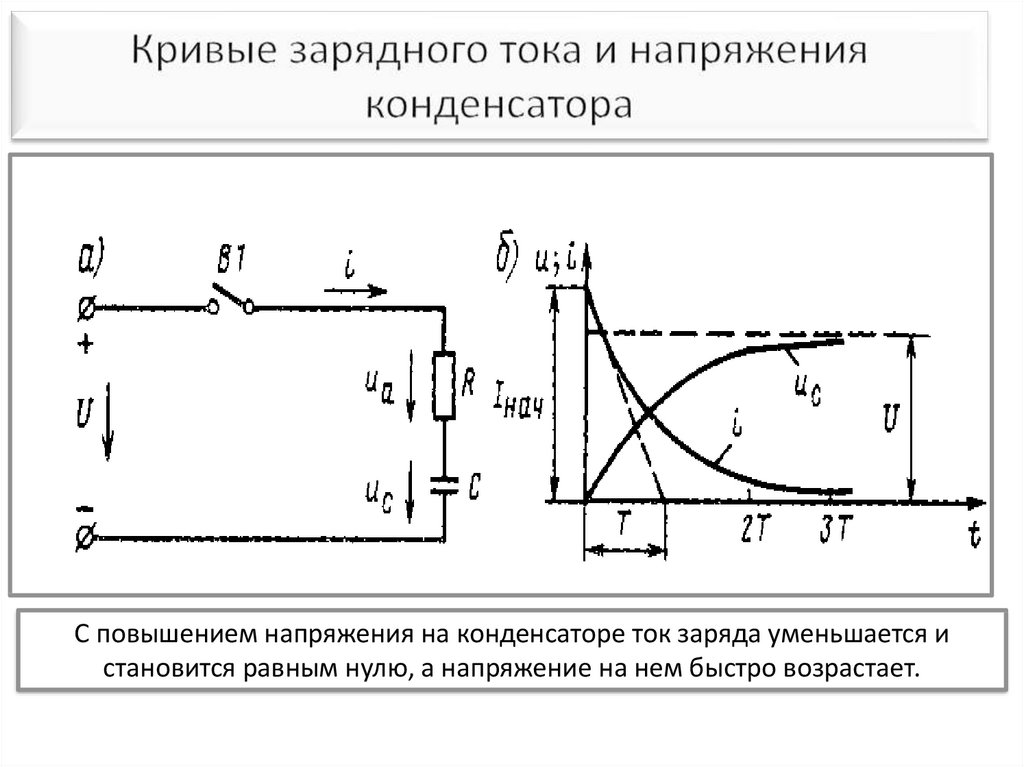 Конденсатор С2 отдает запасенную энергию в нагрузку. Поскольку схема рассматривается в установившемся режиме, мы полагаем конденсатор С1 заряженным, т. е. ток через него не течет.
Конденсатор С2 отдает запасенную энергию в нагрузку. Поскольку схема рассматривается в установившемся режиме, мы полагаем конденсатор С1 заряженным, т. е. ток через него не течет.
В следующем интервале времени d2 силовой MOSFET выключается, и ток дросселя начинает протекать через конденсатор С1 через диод D1. При выключении диода из-за восстановления его обратной проводимости ток в контуре меняет направление. И, наконец, в третьем интервале d3, когда конденсатор С1 заряжен током дросселя и его напряжение превышает выходное напряжение, энергия передается от конденсатора С1 к конденсатору С2. Ток протекает через диод D2, пока напряжения на конденсаторах С1 и С2 не сравняются. При этом ток дросселя продолжает протекать через внутренний диод силового ключа MOSFET. Подробная временная диаграмма рассмотренной выше схемы, показана на рисунке 8.
Рис. 8. Временная диаграмма схемы, показанной на рисунке 6Для режима с прерывистыми токами расчетные соотношения для схемы, приведенной на рисунке 6, следуют из формулы (2), оценивающей необходимый запас энергии в дросселе в течение интервала времени d1.
где: IPK – пиковый ток индуктивности; L – индуктивность дросселя; f – частота коммутации; K – КПД преобразователя; VOUT – выходное напряжение; RLOAD – сопротивление нагрузки.
Опуская ряд промежуточных алгебраических преобразований, приведем расчетные соотношения для выбора компонентов схемы. Длительность интервала времени d1 определяется из (3):
где: Т = 1/f – период цикла коммутации.
Длительность интервала времени d2 рассчитывается следующим образом:
Последний интервал времени d3 определяется из простого соотношения (5):
d3 = Т – (d1 + d2). (5)
В этом кратком обзоре мы хотели напомнить разработчикам о незаслуженно, на наш взгляд, забытых решениях, которые могут облегчить жизнь при проектировании систем питания для случаев, когда не требуется высокая стабильность выходного напряжения и минимальные значения линейных и нагрузочных регулировочных характеристик.
Включение сглаживающих конденсаторов при повышенном высоком напряжении |
Наконец-то наступает момент, когда можно приступить к рассмотрению законченных и имеющих практическое применение схем блоков высоковольтного и низковольтного источников питания. Так как к схеме предусилителя всегда предъявляются более жесткие требования, необходимо рассмотрение начать со схемы источника питания, предназначенного для предусилительных каскадов. После этого можно будет просто использовать уже рассмотренные в деталях блоки для применения в других низкочастотных каскадах. Однако, прежде чем начать рассмотрение конкретных схем, необходимо разобраться с техническими требованиями к источникам питания и их разумному выбору. Выбор высоковольтного напряжения Хотя параметры источника питания должны задаваться таким образом, чтобы соответствовать требованиям нагрузки (то есть
в нашем случае аудиоусилителя), предварительный расчет источника питания дает неплохую возможность оценить, как именно необходимо
его спроектировать, чтобы обеспечить необходимую величину питающего напряжения и при этом избежать ситуации, когда предъявляемые
к техническим характеристикам блока питания чрезмерные требования приведут к слишком большим расходам на этапе практического
воплощения его схемы. В современной аппаратуре, включая как бытовую технику, так и компьютеры, с целью снижения себестоимости, уменьшения массо-габаритных показателей, на сегодняшний день наиболее часто используются не линейные, а импульсные источники питания. В импульсных источниках питания сетевое напряжение выпрямляется непосредственно (без трансформации), на выходе выпрямителя используется накопительный конденсатор. В Европе напряжение сетевого питания варьируется от 220 до 240 В, что приводит к значению напряжения на выходе выпрямителя порядка 325 В постоянного тока. В силу этого конденсаторы, рассчитанные на рабочее напряжение 385 В и имеющие небольшую собственную индуктивность, оказываются вполне доступными как по их номенклатуре, так и по стоимости, что делает их применение оправданным. Благодаря этой причине, конденсаторы, рассчитанные именно на рабочее напряжение 385 В являются наиболее ходовыми из относительно высоковольтных. Итак, именно выбор рабочего напряжения сглаживающего накопительного конденсатора зачастую определяет верхний порог выбора
питающего анодного напряжения усилителя. Время от времени при проектировании усилителей возникает потребность применять более высокие значения питающего напряжения,
однако, это вызывает дорогостоящие последствия, что станет вполне очевидным из следующего раздела. В случаях, когда необходимо использовать более высокое значение высокого напряжения, например напряжения 430 В для пары ламп EL34, то сглаживающий конденсатор, рассчитанный на рабочее напряжение 450 В (такие конденсаторы также доступны в продаже), зачастую будет оказываться под более высоким напряжением в случае, если сетевое напряжение вдруг возрастет на 10% (значение, которое допускается существующими нормами на электросети). Существует два варианта избежать пробоя конденсатора: либо использовать конденсатор, рассчитанный на более высокие значения рабочего напряжения, который, как правило, будет бумажным или пленочным пластиковым типом конденсаторов, имеющих невысокое значение емкости, либо использовать последовательное включение одинаковых по емкости электролитических конденсаторов, чтобы получить необходимое значение результирующего рабочего напряжения такой конденсаторной батареи. В случае, когда два конденсатора включены последовательно, ток, протекающий по ним, будет одинаковым, а заряды, накопленные
на их обкладках, также будут равны (так как Q = It). К сожалению, даже если емкости конденсаторов будут равны, маловероятно, что значения токов утечки отдельно взятых электролитических конденсаторов окажутся равными, поэтому падения напряжения на конденсаторах также окажутся не равными друг другу. С целью выровнять падения напряжений и предохранить каждый конденсатор от превышения допустимого рабочего напряжения на нем, параллельно каждому конденсатору необходимо будет включить резистор (рис. 6.40), поэтому образующаяся цепь делителя напряжения заставит падения напряжения на конденсаторах быть равными. Рис. 6.40 Стабилизирующие резисторы выравнивают падения напряжения на конденсаторах Для того, чтобы гарантировать правильную работу, по цепи делителя напряжения должен будет протекать ток, величина которого
должна, по крайней мере, в десять раз превышать ожидаемое значение токов утечки конденсаторов. Гораздо более рациональным способом является использование двух раздельных высоковольтных обмоток трансформатора с соответствующими цепями выпрямления и сглаживания пульсаций, и последовательным включением результирующих плавающих выходных напряжений для получения необходимого значения высоковольтного напряжения (рис. 6.41). Этот способ гарантирует, что напряжение на каждом из конденсаторов не превысит допустимого рабочего значения, однако, конструкция силового трансформатора при этом заведомо усложнится. Необходимость разряда высоковольтных конденсаторов В обеих предыдущих схемах, используемых для получения составного высоковольтного конденсатора, предназначенного для работы
при напряжениях, превышающих значения рабочих напряжений каждого из отдельных конденсаторов, оказалось, что у одного из
конденсаторов его отрицательный
вывод будет отсоединен от шины с потенциалом земли. Рис. 6.41 Схема высоковольтного, превышающего значение 340 В, источника выпрямленного напряжения с электролитическими конденсаторами Высоковольтный источник питания представляет собой источник повышенной электрической опасности, поэтому необходимо, чтобы
всегда предпринимались меры для полного разряда накопительного и других сглаживающих конденсаторов после выключения питания
оборудования. Следовательно, в каждом высоковольтном источнике питания должна быть предусмотрена цепь с чисто омическим сопротивлением,
подключенная к точке с нулевым потенциалом и обеспечивающая стекание заряда с конденсаторов. |
|
Зависимость напряжения от разряда и заряда конденсатора
Присоединим цепь, состоящую из незаряженного конденсатора емкостью С и резистора с сопротивлением R, к источнику питания с постоянным напряжением U (рис. 16-4).
Так как в момент включения конденсатор еще не заряжен, то напряжение на нем Поэтому в цепи в начальный момент времени падение напряжения на сопротивлении R равно U и возникает ток, сила которого
Рис. 16-4. Зарядка конденсатора.
Прохождение тока i сопровождается постепенным накоплением заряда Q на конденсаторе, на нем появляется напряжение и падение напряжения на сопротивлении R уменьшается:
как и следует из второго закона Кирхгофа. Следовательно, сила тока
Следовательно, сила тока
уменьшается, уменьшается и скорость накопления заряда Q, так как ток в цепи
С течением времени конденсатор продолжает заряжаться, но заряд Q и напряжение на нем растут все медленнее (рис. 16-5), а сила тока в цепи постепенно уменьшается пропорционально разности – напряжений
Рис. 16-5. График изменения тока и напряжения при зарядке конденсатора.
Через достаточно большой интервал времени (теоретически бесконечно большой) напряжение на конденсаторе достигает величины, равной напряжению источника питания, а ток становится равным нулю — процесс зарядки конденсатора заканчивается.
Практически принято считать, что процесс зарядки закончился, когда ток уменьшился до 1% — начального значения или, – что то же, когда напряжение на конденсаторе достигло 99% напряжения источника питания
Процесс зарядки конденсатора тем продолжительней, чем больше сопротивление цепи R, ограничивающее силу тока, и чем больше емкость конденсатора С, так как при большой емкости должен накопиться больший заряд.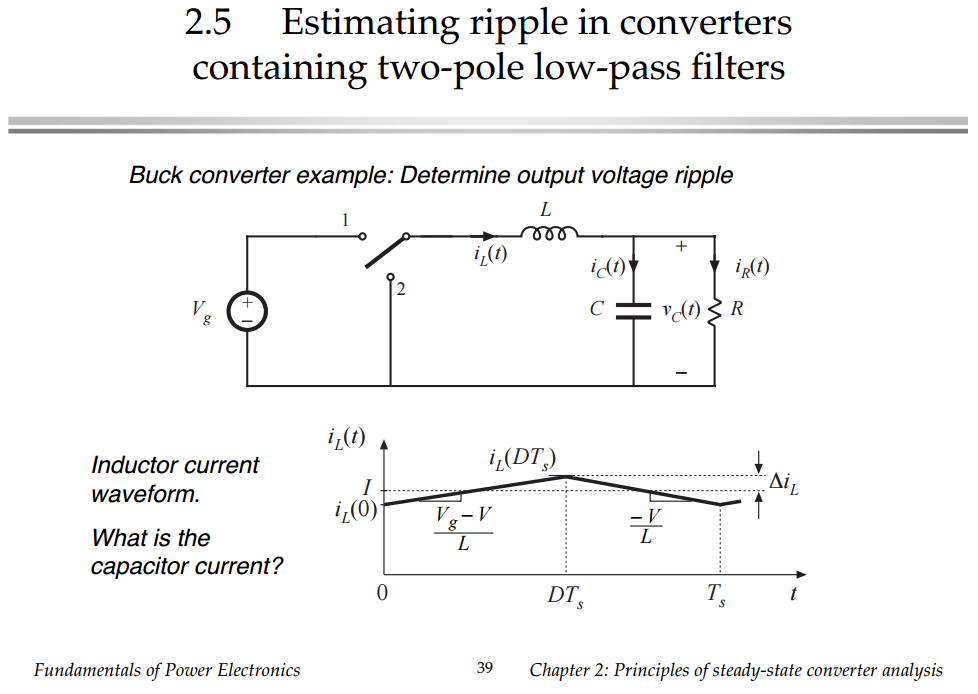 Скорость протекания процесса характеризуют постоянной времени цепи
Скорость протекания процесса характеризуют постоянной времени цепи
чем больше , тем медленнее процесс.
Постоянная времени цепи имеет размерность времени, так как
Через интервал времени с момента включения цепи, равный , напряжение на конденсаторе достигает примерно 63% напряжения источника питания, а через интервал процесс зарядки конденсатора можно считать закончившимся.
Напряжение на конденсаторе при зарядке
т. е. оно равно разности постоянного напряжения источника питания и свободного напряжения убывающего с течением времени по закону показательной функции от значения U до нуля (рис. 16-5).
Зарядный ток конденсатора
Ток от начального значения постепенно уменьшается по закону показательной функции (рис. 16-5).
б) Разряд конденсатора
Рассмотрим теперь процесс разряда конденсатора С, который был заряжен от источника питания до напряжения U через резистор с сопротивлением R (рис. 16-6, Где переключатель переводится из положения 1 в положение 2).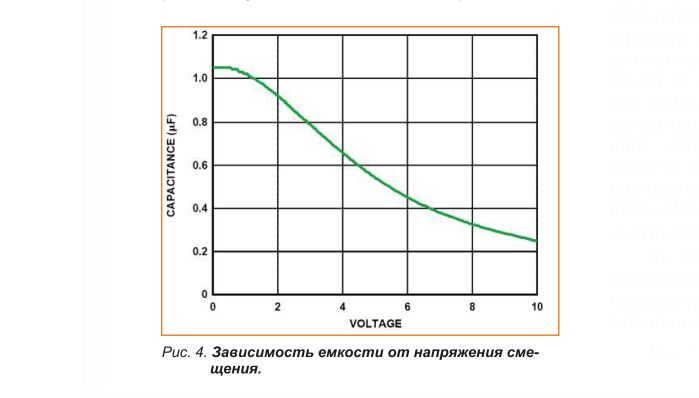
Рис. 16-6. Разряд конденсатора на резистор.
Рис. 16-7. График изменения тока и напряжения при разрядке конденсатора.
В начальный момент, в цепи возникнет ток и конденсатор начнет разряжаться, а напряжение на нем уменьшаться. По мере уменьшения напряжения будет уменьшаться и ток в цепи (рис. 16-7). Через интервал времени напряжение на конденсаторе и ток цепи уменьшатся при мерно до 1% начальных значений и процесс разряда конденсатора можно считать закончившимся.
Напряжение на конденсаторе при разряде
т. е. уменьшается по закону показательной функции (рис. 16-7).
Разрядный ток конденсатора
т. е. он, так же как и напряжение, уменьшается по тому же закону (рис. 6-7).
Вся энергия, запасенная при зарядке конденсатора в его электрическом поле, при разряде выделяется в виде тепла в сопротивлении R.
Электрическое поле заряженного конденсатора, отсоединенного от источника питания, не может долго сохраняться неизменным, так как диэлектрик конденсатора и изоляция между его зажимами обладают некоторой проводимостью.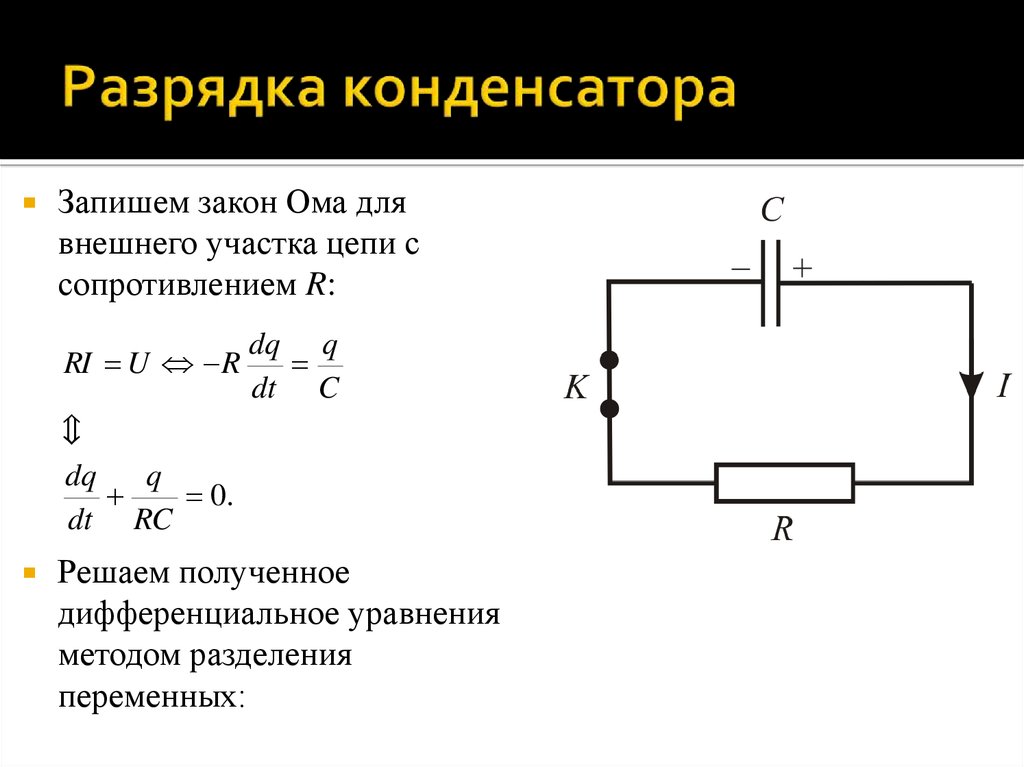
Разряд конденсатора, обусловленный несовершенством диэлектрика и изоляции, называется саморазрядом. Постоянная времени при саморазряде конденсатора не зависит от формы обкладок и расстояния между ними.
Процессы зарядки и разряда конденсатора называются переходными процессами.
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.
Заряд конденсатора от источника постоянной ЭДС
Разряд конденсатора через сопротивление
Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):
Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:
При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
Во время зарядки конденсатора, напряжение на нем изменяется по закону
где величину
называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:
Энергия, запасенная в конденсаторе:
Работа, выполненная источником ЭДС:
Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. 1 показана схема заряда конденсатора. Конденсатор С присоединен к зажимам генератора. При помощи ключа можно замкнуть или разомкнуть цепь. Рассмотрим подробно процесс заряда конденсатора.
Генератор обладает внутренним сопротивлением. При замыкании ключа конденсатор зарядится до напряжения между обкладками, равного э. д. с. генератора: Uс = Е. При этом обкладка, соединенная с положительным зажимом генератора, получает положительный заряд (+ q ), а вторая обкладка получает равный по величине отрицательный заряд ( -q ). Величина заряда q прямо пропорциональна емкости конденсатора С и напряжению на его обкладках: q = CUc
P ис. 1 . Схема заряда конденсатора
Для того чтобы обкладки конденсатора зарядились, необходимо, чтобы одна из них приобрела, а другая потеряла некоторое количество электронов. Перенос электронов от одной обкладки к другой совершается по внешней цепи электродвижущей силой генератора, а сам процесс перемещения зарядов по цепи есть не что иное, как электрический ток, называемый зарядным емкостным током I зар.
Зарядный ток в цени протекает обычно тысячные доли секунды до тех пор, пока напряжение на конденсаторе достигнет величины, равной э. д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.
д. с. генератора. График нарастания напряжения на обкладках конденсатора в процессе его заряда представлен на рис. 2,а, из которого видно, что напряжение Uc плавно увеличивается, сначала быстро, а затем все медленнее, пока не станет равным э. д. с. генератора Е. После этого напряжение на конденсаторе остается неизменным.
Рис. 2. Графики напряжения и тока при заряде конденсатора
Пока конденсатор заряжается, по цепи проходит зарядный ток. График зарядного тока показан на рис. 2,б. В начальный момент зарядный ток имеет наибольшую величину, потому что напряжение на конденсаторе еще равно нулю, и по закону Ома io зар = E/ R i , так как вся э. д. с. генератора приложена к сопротивлению R i.
По мере того как конденсатор заряжается, т. е. возрастает напряженно на нем, для зарядного тока уменьшается. Когда напряженно па конденсаторе уже имеется, падение напряжения на сопротивление будет равно разности между э. д. с. генератора и напряжением на конденсаторе, т. е. равно Е – U с.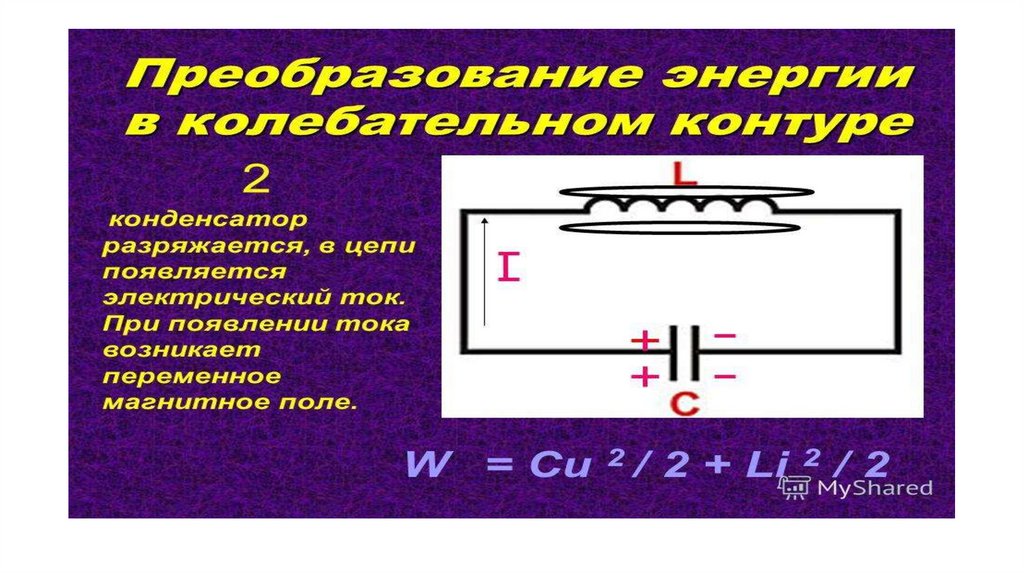 Поэтому i зар = (E-Uс)/R i
Поэтому i зар = (E-Uс)/R i
Отсюда видно, что с увеличением Uс уменьшается i зар и при Uс = E зарядный ток становится равным нулю.
Про закон Ома подробнее смотрите здесь: закон Ома для участка цепи
Продолжительность процесса заряда конденсатора зависит от двух величии:
1) от внутреннего сопротивления генератора R i ,
2) от емкости конденсатора С.
На рис. 2 показаны графики нарядных токов для конденсатора емкостью 10 мкф: кривая 1 соответствует процессу заряда от генератора с э. д. с. Е = 100 В и с внутренним сопротивлением R i = 10 Ом, кривая 2 соответствует процессу заряда от генератора с такой же э. д. с, но с меньшим внутренним сопротивлением: R i = 5 Ом.
Из сравнения этих кривых видно, что при меньшем внутреннем сопротивлении генератора сила нарядного тока в начальный момент больше, и поэтому процесс заряда происходит быстрее.
Рис. 2. Графики зарядных токов при разных сопротивлениях
На рис. 3 дается сравнение графиков зарядных токов при заряде от одного и того же генератора с э.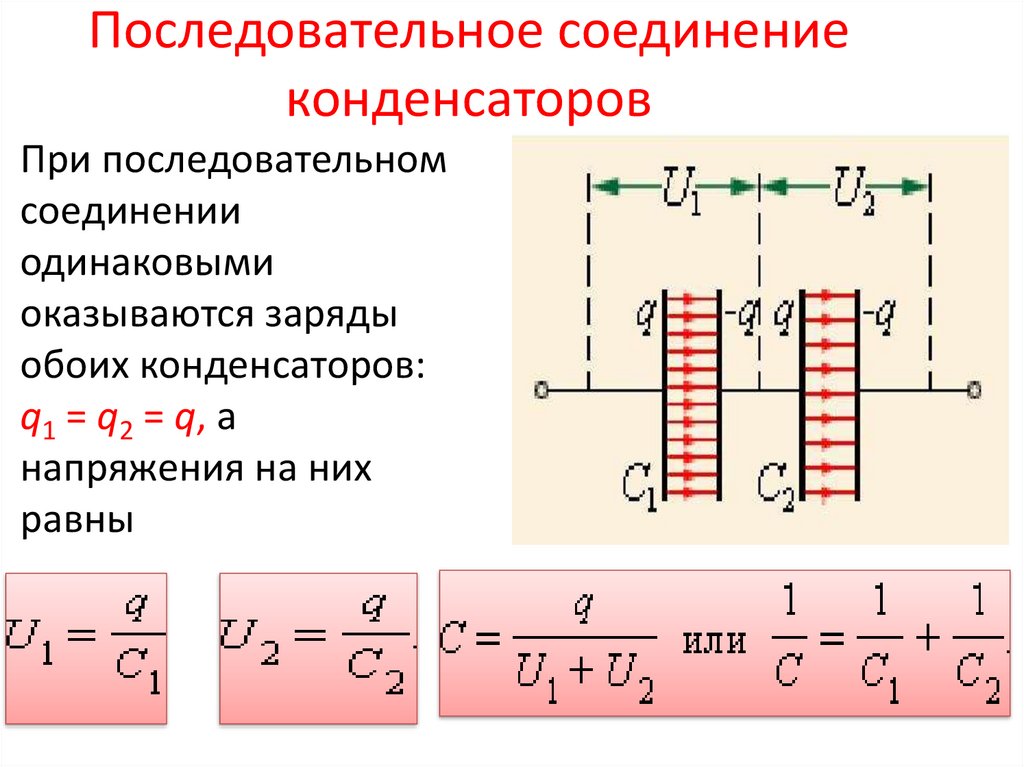 д. с. Е = 100 В и внутренним сопротивлением R i = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).
д. с. Е = 100 В и внутренним сопротивлением R i = 10 ом двух конденсаторов разной емкости: 10 мкф (кривая 1) и 20 мкф (кривая 2).
Величина начального зарядного тока io зар = Е/ Ri = 100/10 = 10 А одинакова для обоих конденсаторов, по так как конденсатор большей емкости накапливает большее количество электричества, то зарядный его ток должен проходить дольше, и процесс заряда получается более длительным.
Рис. 3. Графики зарядных токов при разных емкостях
Отключим заряженный конденсатор от генератора и присоединим к его обкладкам сопротивление.
На обкладках конденсатора имеется напряжение U с, поэтому в замкнутой электрической цепи потечет ток, называемый разрядным емкостным током i разр.
Ток идет от положительной обкладки конденсатора через сопротивление к отрицательной обкладке. Это соответствует переходу избыточных электронов с отрицательной обкладки на положительную, где их недостает. Процесс рам ряда происходит до тех пор, пока потенциалы обеих обкладок не сравняются, т.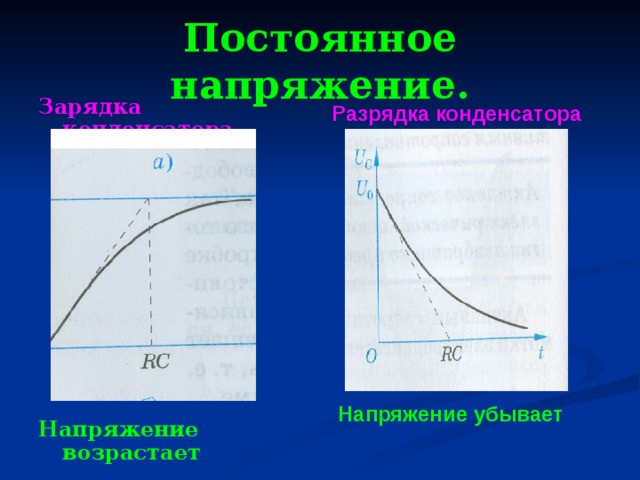 е. разность потенциалов между ними станет равном нулю: Uc=0 .
е. разность потенциалов между ними станет равном нулю: Uc=0 .
На рис. 4, а показан график уменьшения напряжения на конденсаторе при разряде от величины Uc о =100 В до нуля, причем напряжение уменьшается сначала быстро, а затем медленнее.
На рис. 4,б показан график изменения разрядного тока. Сила разрядного тока зависит от величины сопротивления R и по закону Ома i разр = Uc / R
Рис. 4. Графики напряжения и токов при разряде конденсатора
В начальный момент, когда напряжение па обкладках конденсатора наибольшее, сила разрядного тока также наибольшая, а с уменьшением Uc в процессе разряда уменьшается и разрядный ток. При Uc=0 разрядный ток прекращается.
Продолжительность разряда зависит:
1) от емкости конденсатора С
2) от величины сопротивления R , на которое конденсатор разряжается.
Чем больше сопротивление R , тем медленнее будет происходить разряд. Это объясняется тем, что при большом сопротивлении сила разрядного тока невелика и величина заряда на обкладках конденсатора уменьшается медленно.
Это можно показать на графиках разрядного тока одного и того же конденсатора, имеющего емкость 10 мкф и заряженного до напряжения 100 В, при двух разных величинах сопротивления (рис. 5): кривая 1 — при R = 40 Ом, i оразр = Uc о/ R = 100/40 = 2,5 А и кривая 2 – при 20 Ом i оразр = 100/20 = 5 А.
Рис. 5. Графики разрядных токов при разных сопротивлениях
Разряд происходит медленнее также тогда, когда емкость конденсатора велика. Получается это потому, что при большей емкости на обкладках конденсатора имеется большее количество электричества (больший заряд) и для стекания заряда потребуется больший промежуток времени. Это наглядно показывают графики разрядных токов для двух конденсаторов раиной емкости, заряженных до одного и того же напряжения 100 В и разряжающихся на сопротивление R =40 Ом (рис. 6 : кривая 1 — для конденсатора емкостью 10 мкф и кривая 2 — для конденсатора емкостью 20 мкф).
Рис. 6. Графики разрядных токов при разных емкостях
Из рассмотренных процессов можно сделать вывод, что в цепи с конденсатором ток проходит только в моменты заряда и разряда, когда напряжение на обкладках меняется.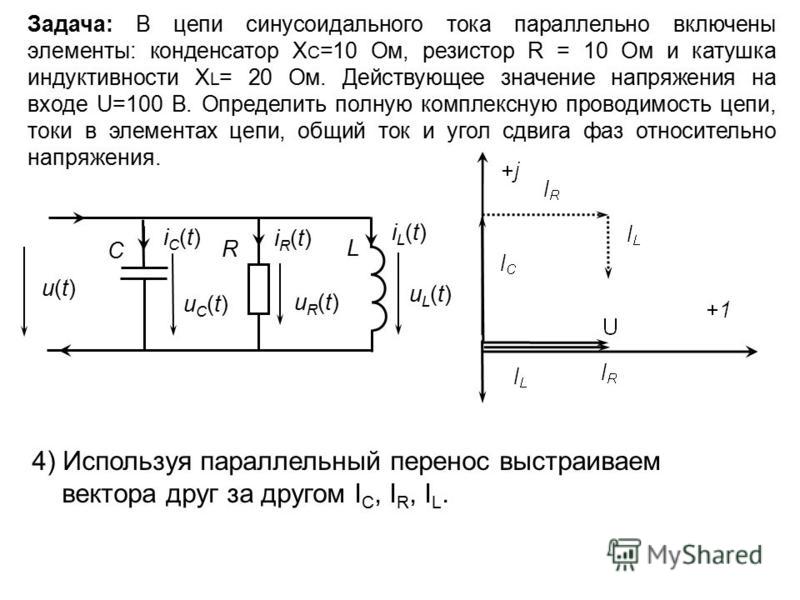
Объясняется это тем, что при изменении напряжения изменяется величина заряда на обкладках, а для этого требуется перемещение зарядов по цепи, т. е. по цепи должен проходить электрический ток. Заряженный конденсатор не пропускает постоянный ток, так как диэлектрик между его обкладками размыкает цепь.
В процессе заряда конденсатор накапливает энергию, получая ее от генератора. При разряде конденсатора вся энергия электрического поля переходит в тепловую энергию, т. е. идет на нагрев сопротивления, через которое разряжается конденсатор. Чем больше емкость конденсатора и напряжение на его обкладках, тем больше будет энергия электрического поля конденсатора. Величина энергии, которой обладает конденсатор емкостью С, заряженный до напряжения U, равна: W = W с = С U 2 /2
Пример. Конденсатор С=10 мкф заряжен до напряжении U в = 500 В. Определить энергию, которая выделится в вило тепла на сопротивлении, через которое разряжается конденсатор.
Решение. Пpи разряде вся энергия, запасенная конденсатором, перейдет в тепловую. Поэтому W = W с = С U 2 /2 = (10 х 10 -6 х 500)/2 = 1,25 дж.
Поэтому W = W с = С U 2 /2 = (10 х 10 -6 х 500)/2 = 1,25 дж.
Ускорители. — 1962 — Электронная библиотека «История Росатома»
Ускорители. — 1962 — Электронная библиотека «История Росатома»Главная → Указатель произведений
ЭлектроннаябиблиотекаИстория Росатома
Ничего не найдено.
Загрузка результатов…
Закладки
Обложка123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350351352353354355356357358359360361362363364365366367368369370371372373374375376377378379380381382383384385386387388389390391392393394395396397398399400401402403404405406407408409410411412413414415416417418419420421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454455456457458459460461462463464465466467468469470471472473474475476477478479480481482483484485486487488489490491492493494495496497498499500501502503504505506507508509510511512513514515516517518519520521522523524525526527528529530531532533534535536537538539540541542543544545546547548549550551552553554555556 пустая557558559560
Увеличить/уменьшить масштаб
По ширине страницы
По высоте страницы
Постранично/Разворот
Поворот страницы
Навигация по документу
Закладки
Поиск в издании
Структура документа
Скопировать текст страницы
(работает в Chrome 42+,
Microsoft Internet Explorer и Mozilla FireFox
c установленным Adobe Flash Player)
Добавить в закладки
Текущие страницы выделены рамкой.
Содержание
ОбложкаОбложка
1Титульные листы
3Яблоков Б. Н.
Предисловие к русскому переводу 5Балдингер Э.
Каскадные генераторы5[Введение]
6I. Теория простых выпрямительных схем
6A. Выпрямитель, работающий на фильтр с емкостным входом
19Б. Выпрямитель с конденсатором очень большой емкости
32B. Выпрямитель с индуктивностью на входе фильтра
37II. Каскадные генераторы
37A. Предварительные замечания
38Б. Постановка задачи
42B. Нагруженный каскадный генератор
61Г. Разновидности каскадного генератора
66III. Получение высокого напряжения с помощью лампового генератора
77IV. Заключительные замечания
79Литература
80Херб Р.
Ускорители Ван де Граафа80Введение
82A. Первые разработки
88Б. Конструкция электродов
93B. Зарядная система
101Г. Система крепления
104Д. Ускорительная трубка
113Е. Ионные источники и связанное с ними оборудование
117Ж. Измерение и стабилизация напряжения генератора
Измерение и стабилизация напряжения генератора
122З. Рабочие характеристики и возможности действующих генераторов
126И. Общие вопросы
131Литература
133Коуэн Б.
Циклотрон и фазотрон133Введение
136А. Теория
136I. Орбитальная устойчивость
136а) Магнитная фокусировка в циклотроне и фазотроне
143б) Магнитная фокусировка в циклотроне с азимутальной вариацией поля
149в) Влияние электрического поля
154II. Фазовое движение
154а) Начальная область
157б) Фазовое движение в циклотроне
163в) Фазовое движение в фазотроне
170Б. Основные узлы циклотронов
170а) Электромагнит
178б) Высокочастотная система
187в) Ионные источники
191г) Вакуумные системы
193д) Система вывода пучка
198е) Мишени
200ж) Опасность облучения и защита
204з) Управление и блокировка
205В. Разное
218Приложение. Вывод уравнения (5.13)
219Литература
221Вильсон Р.
Синхротрон2211. Введение
Введение
2222. Фазовая устойчивость в синхротроне
2243. Магниты синхротронов
2294. Инжекторы
2305. Влияние остаточного газа на работу синхротрона
2336. Электромагнитное излучение электронов
2387. Синхротронные колебания
2438. Бетатронные колебания
2479. Высокочастотная система
24910. Интенсивность
25211. Калибровка синхротрона
255Литература
257Керст Д.
Бетатрон257I. Принцип индукционного ускорения
258II. Теория орбит
275III. Практические схемы
291Литература
292Грин Г., Курант Э.
Синхрофазотрон292А. Введение
295Б. Синхрофазотрон с постоянным градиентом
295I. Орбиты частиц
310II. Общее описание
315III. Магнитные системы
343IV. Системы питания магнитов
354V. Вакуумная система
366VI. Инжекция
384VII. Высокочастотная система
414VIII. Работа синхрофазотрона
425В. Теория ускорителей со знакопеременным градиентом
453Г. Синхрофазотроны со знакопеременным градиентом
486Литература
489Смит Л.
489I. Введение
492II. Общие принципы
497III. Электронные ускорители
524IV. Ускорители ионов
554Литература
557Содержание
560Концевая страница
Обращаясь к сайту «История Росатома — Электронная библиотека»,
я соглашаюсь с условиями использования представленных там материалов.
Правила сайта (далее – Правила)
- Общие положения
- Настоящие правила определяют порядок и условия использования материалов, размещенных на сайте www.biblioatom.ru (далее именуется Сайт), а также правила использования материалов Сайтом и порядок взаимодействия с Администрацией Сайта.
- Любые материалы, размещенные на Сайте, являются объектами интеллектуальной собственности (объектами авторского права или смежных прав, а также прав на средства индивидуализации). Права Администрации
Сайта на указанные материалы охраняются законодательством о правах на результаты интеллектуальной деятельности.

- Использование материалов, размещенных на Сайте, допускается только с письменного согласия Администрации Сайта или иного правообладателя, прямо указанного на конкретном материале, размещенном на Сайте, или в непосредственной близости от указанного материала.
- Права на использование и разрешение использования материалов, размещенных на Сайте, принадлежащих иным правообладателям, нежели Администрация Сайта, допускается с разрешения таких правообладателей или в соответствии с условиями, установленными такими правообладателями. Никакое из положений настоящих Правил не дает прав третьим лицам на использование материалов правообладателей, прямо указанных на конкретном материале, размещенном на Сайте, или в непосредственной близости от указанного материала.
- Настоящие Правила распространяют свое действие на следующих пользователей: информационные агентства, электронные и печатные средства массовой информации, любые физические и юридические лица, а также
индивидуальные предприниматели (далее — «Пользователи»).

- Использование материалов. Виды использования
- Под использованием материалов Сайта понимается воспроизведение, распространение, публичный показ, сообщение в эфир, сообщение по кабелю, перевод, переработка, доведение до всеобщего сведения и иные способы использования, предусмотренные действующим законодательством Российской Федерации.
- Использование материалов Сайта без получения разрешения от Администрации Сайта не допустимо.
- Внесение каких-либо изменений и/или дополнений в материалы Сайта запрещено.
- Использование материалов Сайта осуществляется на основании договоров с Администрацией Сайта, заключенных в письменной форме, или на основании письменного разрешения, выданного Администрацией Сайта.
- Запрещается любое использование (бездоговорное/без разрешения) фото-, графических, видео-, аудио- и иных материалов, размещенных на Сайте, принадлежащих Администрации Сайта и иным правообладателям
(третьим лицам).

- Стоимость использования каждого конкретного материала или выдача разрешения на его использование согласуется Пользователем и Администрацией Сайта в каждом конкретном случае.
- В случае необходимости использования материалов Сайта, права на которые принадлежат третьим лицам (иным правообладателям, нежели Администрация Сайта, о чем прямо указано на таких материалах либо в непосредственной близости от них), Пользователи обязаны обращаться к правообладателям таких материалов для получения разрешения на использование материалов.
- Обязанности Пользователей при использовании материалов Сайта
- 3.1. При использовании материалов Сайта в любых целях при наличии разрешения Администрации Сайта, ссылка на Сайт обязательна и осуществляется в следующем виде:
- в печатных изданиях или в иных формах на материальных носителях Пользователи обязаны в каждом случае использования материалов указать источник – электронная библиотека «История Росатома»
(www.
 biblioatom.ru)
biblioatom.ru)
- в интернете или иных формах использования в электронном виде не на материальных носителях, Пользователи в каждом случае использования материалов обязаны разместить гиперссылку на Сайт — электронная библиотека «История Росатома» (www.biblioatom.ru), гиперссылка должна являться активной и прямой, при нажатии на которую Пользователь переходит на конкретную страницу Сайта, с которой заимствован материал.
- Ссылка на источник или гиперссылка, указанные в пп. 3.1.1 и 3.1.2. настоящих Правил, должны быть помещены Пользователем в начале используемого текстового материала, а также непосредственно под используемым аудио-, видео-, фотоматериалом, графическим материалом Администрации Сайта.
- в печатных изданиях или в иных формах на материальных носителях Пользователи обязаны в каждом случае использования материалов указать источник – электронная библиотека «История Росатома»
(www.
- Размеры шрифта ссылки на источник или гиперссылки не должны быть меньше размера шрифта текста, в котором используются материалы Сайта, либо размера шрифта текста Пользователя, сопровождающего аудио-,
видео-, фотоматериалы и графические материалы Сайта, а также цвет ссылки должен быть идентичен цветам ссылок на Сайте и должен быть видимым Пользователю.

- Использование материалов с Сайта, полученных из вторичных источников (от иных правообладателей, нежели Администрация Сайта, о чем прямо указано на таких материалах либо в непосредственной близости от них), возможно только со ссылкой на эти источники и, в случае необходимости, установленной такими источниками (правообладателями), — с их разрешения.
- Не допускается переработка оригинального материала (произведения), взятого с Сайта, в том числе сокращение материала, иная его переработка, в том числе приводящая к искажению его смысла.
- 3.1. При использовании материалов Сайта в любых целях при наличии разрешения Администрации Сайта, ссылка на Сайт обязательна и осуществляется в следующем виде:
- Права на материалы третьих лиц, урегулирование претензий
- Материалы, права на которые принадлежат третьим лицам, размещенные на Сайте, размещены либо с разрешения правообладателя, полученного Администрацией Сайта, либо, в случае, если таковое использование
прямо не запрещено правообладателем, в соответствии с Законодательством РФ в информационных целях с обязательным указанием имени автора, материал которого используется, и источника заимствования.

- В случае, если в обозначении авторства материалов в соответствии с п. 4.1. настоящих Правил содержится ошибка, или в случае использования материала с предполагаемым или реальным нарушением прав
третьих лиц, или в иных спорных случаях использования объектов интеллектуальной собственности, размещенных на Сайте, в том числе в случае, когда права третьего лица тем или иным образом нарушаются с
использованием Сайта, применяется следующая схема урегулирования претензий третьих лиц к Администрации Сайта:
- в адрес Администрации Сайта по электронной почте на адрес [email protected] направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
принадлежат
заявителю и который используется незаконно посредством Сайта или с нарушением правил использования, или иным образом права заявителя как обладателя исключительного права на объект интеллектуальной
собственности, размещенный на Сайте, нарушены посредством Сайта, с приложением документов, подтверждающих правомочия заявителя, данные о правообладателе и копия доверенности на действия от лица
правообладателя, если лицо, направляющее претензию, не является руководителем компании правообладателя или непосредственно физическим лицом — правообладателем.
 В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
- Администрация Сайта обязуется рассмотреть надлежаще оформленную претензию в срок не менее 5 (пяти) рабочих дней с даты ее получения по электронной почте. Администрация Сайта обязуется уведомить заявителя о результатах рассмотрения его заявления (претензии) посредством отправки письма по электронной почте на адрес, указанный заявителем, а также направить ответ в письменном виде на адрес, указанный заявителем (в случае неуказания такового адреса отправки, обязательство по предоставлению письменного ответа на претензию с Администрации Сайта снимается). В том числе, Администрация Сайта вправе запросить дополнительные документы, свидетельства, данные, подтверждающие законность предъявляемой претензии. В случае признания претензии правомерной, Администрация Сайта примет все возможные меры, необходимые для прекращения нарушения прав заявителя и урегулирования претензии;
- Администрация Сайта в любом случае предпринимает все возможные меры к скорейшему удовлетворению обоснованных претензий третьих лиц и стремиться к максимально скорому урегулированию всех
спорных
вопросов.

- в адрес Администрации Сайта по электронной почте на адрес [email protected] направляется претензия, содержащая информацию об объекте интеллектуальной собственности, права на который
принадлежат
заявителю и который используется незаконно посредством Сайта или с нарушением правил использования, или иным образом права заявителя как обладателя исключительного права на объект интеллектуальной
собственности, размещенный на Сайте, нарушены посредством Сайта, с приложением документов, подтверждающих правомочия заявителя, данные о правообладателе и копия доверенности на действия от лица
правообладателя, если лицо, направляющее претензию, не является руководителем компании правообладателя или непосредственно физическим лицом — правообладателем.
- Материалы, права на которые принадлежат третьим лицам, размещенные на Сайте, размещены либо с разрешения правообладателя, полученного Администрацией Сайта, либо, в случае, если таковое использование
прямо не запрещено правообладателем, в соответствии с Законодательством РФ в информационных целях с обязательным указанием имени автора, материал которого используется, и источника заимствования.
- Прочие условия
- Администрация Сайта оставляет за собой право изменять настоящие Правила в одностороннем порядке в любое время без уведомления Пользователей. Любые изменения будут размещены на Сайте. Изменения вступают в силу с момента их опубликования на Сайте.
- По всем вопросам использования материалов Сайта Пользователи могут обращаться к Администрации Сайта по следующим координатам: [email protected]
- Во всем, что не урегулировано настоящими Правилами в отношении вопросов использования материалов на Сайте, стороны руководствуются положениями Законодательства РФ.
СогласенНе согласен
Емкостной делитель напряжения
В схеме делителя напряжения, напряжение питания или напряжение схемы распределяется между всеми компонентами в цепи одинаково, в зависимости от емкости этих компонентов.
Сама схема емкостного делителя напряжения такая же, как и у схемы резистивного делителя напряжения.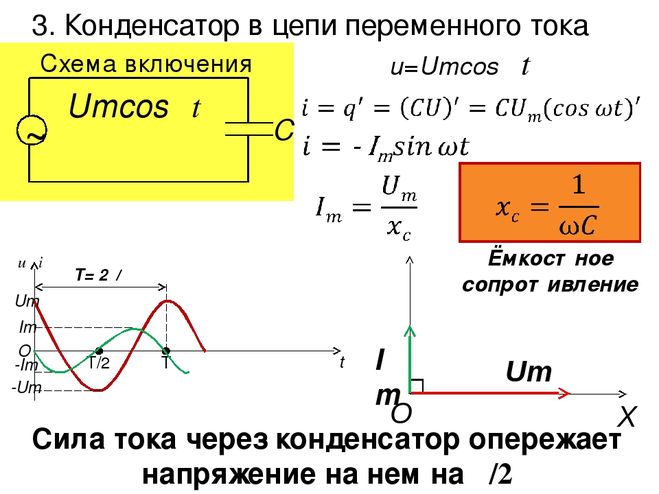 Но, как и резисторы, на схему емкостного делителя напряжения не влияют изменения частоты, даже если в ней используются реактивные элементы.
Но, как и резисторы, на схему емкостного делителя напряжения не влияют изменения частоты, даже если в ней используются реактивные элементы.
Конденсатор — это пассивный компонент, который накапливает электрическую энергию на металлических пластинах. Конденсатор состоит из двух пластин, и они разделены непроводящим или изолирующим материалом, так называемым «диэлектриком».
Здесь положительный заряд хранится на одной пластине, а отрицательный заряд — на другой пластине.
Когда на конденсатор подается постоянный ток, он полностью заряжается. Диэлектрический материал между пластинами действует как изолятор, а также препятствует прохождению тока через конденсатор.
Это сопротивление току, подаваемому через конденсатор, называется реактивным сопротивлением (XC) конденсатора. Реактивное сопротивление конденсатора также измеряется в омах.
Полностью заряженный конденсатор действует как источник энергии, т.к. конденсатор накапливает энергию и разряжает ее на компонентах схемы.
Если на конденсатор подается переменный ток, то конденсатор непрерывно заряжается и разряжает ток через свои пластины. В это время конденсатор также имеет реактивное сопротивление, которое изменяется в зависимости от частоты питания.
Мы знаем, что заряд, который хранится в конденсаторе, зависит от напряжения питания и емкости конденсатора. Таким же образом реактивное сопротивление также зависит от некоторых параметров.
Если конденсатор имеет меньшее значение емкости, то время, необходимое для зарядки конденсатора, меньше, т.е. требуется меньшая постоянная времени RC. Точно так же постоянная времени RC высока для большей емкости конденсаторов.
Получается, что конденсатор с большим значением емкости имеет меньшее значение реактивного сопротивления, тогда как меньшее значение емкости конденсатора имеет большее значение реактивного сопротивления, т.е. реактивное сопротивление конденсатора обратно пропорционально значению емкости конденсатора.
X C ∝ 1 / C
Если частота приложенного тока низкая, время зарядки конденсатора увеличивается. Это указывает на высокое значение реактивного сопротивления. Таким же образом, если частота приложенного тока высокая, то реактивное сопротивление конденсатора низкое.
Отсюда можно заметить, что реактивное сопротивление конденсатора обратно пропорционально частоте.
Наконец, мы можем сказать, что реактивное сопротивление (XC) любого конденсатора обратно пропорционально частоте (f) и значению емкости (C).
X C ∝ 1 / f
Формула емкостного реактивного сопротивления
Мы уже знаем, что емкостное реактивное сопротивление обратно пропорционально частоте и значению емкости конденсатора. Таким образом, формула реактивного сопротивления:
Х С = 1 / 2πfC
XC = реактивное сопротивление конденсатора в омах (Ом)
f = частота в герцах (Гц)
C = емкость конденсатора в фарадах (Ф)
π = числовая константа (22/7 = 3,142)
Распределение напряжения в последовательно соединенных конденсаторах
Если конденсаторы соединены последовательно, распределение напряжения рассчитывается между конденсаторами, т. к. конденсаторы имеют разные значения напряжения в зависимости от значений емкости при последовательном соединении.
к. конденсаторы имеют разные значения напряжения в зависимости от значений емкости при последовательном соединении.
Реактивное сопротивление конденсатора, препятствующего прохождению тока, зависит от значения емкости и частоты приложенного тока.
Итак, теперь давайте посмотрим, как реактивное сопротивление влияет на конденсаторы, вычислив значения частоты и емкости. На картинке ниже показана схема емкостного делителя напряжения, в которой последовательно соединены 2 конденсатора.
Емкостной делитель напряжения
Два последовательно соединенных конденсатора, имеют значения емкости 10 мкФ и 22 мкФ соответственно. В схеме, напряжение в цепи равно 10В, это напряжение распределяется между обоими конденсаторами.
При последовательном соединении все конденсаторы имеют одинаковый заряд (Q), но напряжение питания (VS) не одинаково для всех конденсаторов.
Напряжение цепи распределяется между конденсаторами в зависимости от значений емкости конденсаторов, т. е. в соотношении V = Q/C.
е. в соотношении V = Q/C.
По этим значениям мы должны рассчитать реактивное сопротивление (XC) каждого конденсатора, используя значения частоты и емкости конденсаторов.
Пример емкостного делителя напряжения №1
Теперь мы рассчитаем распределение напряжения на конденсаторы 10 мкФ и 22 мкФ, которые показаны на картинке выше, которые имеют напряжение питания 10 В с частотой 40 Гц.
Реактивное сопротивление конденсатора 10 мкФ,
X C1 = 1 / 2πfC1 = 1 / (2 * 3,142 * 40 * 10 * 10-6) = 400 Ом
Реактивное сопротивление конденсатора 22 мкФ,
X C\2 = 1 / 2πfC2 = 1 / (2 * 3,142 * 40 * 22 * 10-6) = 180 Ом
Общее емкостное реактивное сопротивление цепи составляет,
XC = X C1 + X C2 = 400 Ом + 180 Ом = 580 Ом
CT = C1C2 / (C1 + C2) = (10 * 22 * 10-12) / (32 * 10-6) = 6,88 мкФ
XCT = 1 / 2πfC T = 1 / (2 * 3,142 * 40 * 6,88 * 10-6) = 580 Ом
Ток в цепи равен,
I = V/X C = 10 В/580 Ом = 17,2 мА
Теперь падение напряжения на каждом конденсаторе составляет
V C1 = I * X C1 = 17,2 мА * 400 Ом = 6,9 В
V C2 = I * X C2 = 17,2 мА * 180 Ом = 3,1 В
Пример емкостного делителя напряжения №2
Теперь мы рассчитаем падение напряжения на конденсаторах 10 мкФ и 22 мкФ, которые подключены последовательно и работают с напряжением питания 10 В с частотой 4000 Гц (4 КГц).
Реактивное сопротивление конденсатора 10 мкФ,
X C1 = 1/2πfC1 = 1 / (2 * 3,142 * 4000 * 10 * 10-6) = 4 Ом
Реактивное сопротивление конденсатора 22 мкФ,
XC\2 = 1/2πfC2 = 1 / (2 * 3,142 * 4000 * 22 * 10-6) = 1,8 Ом
Общее емкостное реактивное сопротивление цепи составляет,
XC = XC1 + XC2 = 4 Ом + 1,8 Ом = 5,8 Ом
CT = C1C2/(C1 + C2) = (10 * 22 * 10-12) / (32 * 10-6) = 6,88 мкФ
XCT = 1/2πfC T = 1 / (2 * 3,142 * 4000 * 6,88 * 10-6) = 5,8 Ом
Ток в цепи равен,
I = V/XCT = 10 В / 5,8 Ом = 1,72 А
Теперь падение напряжения на каждом конденсаторе составляет
VC1 = I * X C1 = 1,72 A * 4 Ом = 6,9 В
VC2 = I * X C2 = 1,72 A * 1,8 Ом = 3,1 В
Из двух приведенных выше примеров мы можем сделать вывод, что конденсатор с более низким значением (10 мкФ) будет заряжаться до более высокого напряжения (6,9 В), а конденсатор с более высоким значением (22 мкФ) будет заряжаться до более низкого уровня напряжения (3,1 В).
Наконец, сумма двух значений падения напряжения на конденсаторах равна напряжению питания (т.е. 6,9 В + 3,1 В = 10 В). Эти значения напряжения одинаковы для всех значений частоты, поскольку падение напряжения не зависит от частоты.
Падение напряжения на двух конденсаторах одинаково в обоих примерах, где частота различается. Частота составляет 40 Гц или 40 кГц, падение напряжения на конденсаторах одинаково в обоих случаях.
Ток, протекающий по цепи, изменяется в зависимости от частоты. Ток будет увеличиваться с увеличением частоты, он составляет 17,2 мА для частоты 40 Гц, но 1,72 А для частоты 4KHZ, то есть ток увеличится почти в 100 раз при увеличении частоты с 4 Гц до 4 Гц.
Наконец, мы можем сказать, что ток, протекающий по цепи, прямо пропорционален частоте (I α f).
Итог
Противодействие протеканию тока в конденсаторе, называется реактивным сопротивлением (XC) конденсатора. На это емкостное реактивное сопротивление влияют такие параметры, как значение емкости, частота напряжения питания, а также эти значения обратно пропорциональны реактивному сопротивлению. Схема делителя переменного напряжения распределяет напряжение питания на все конденсаторы в зависимости от их емкости. Эти падения напряжения на конденсаторах одинаковы для любой частоты напряжения питания. т.е. падение напряжения на конденсаторах не зависит от частоты. Но текущий ток зависит от частоты, а также эти два значения прямо пропорциональны друг другу. Но в схемах делителя напряжения постоянного тока вычислить падение напряжения на конденсаторах — непростая задача, поскольку оно зависит от значения реактивного сопротивления, поскольку конденсаторы блокируют прохождение постоянного тока через него после полной зарядки.
Схема делителя переменного напряжения распределяет напряжение питания на все конденсаторы в зависимости от их емкости. Эти падения напряжения на конденсаторах одинаковы для любой частоты напряжения питания. т.е. падение напряжения на конденсаторах не зависит от частоты. Но текущий ток зависит от частоты, а также эти два значения прямо пропорциональны друг другу. Но в схемах делителя напряжения постоянного тока вычислить падение напряжения на конденсаторах — непростая задача, поскольку оно зависит от значения реактивного сопротивления, поскольку конденсаторы блокируют прохождение постоянного тока через него после полной зарядки.
Цепи емкостного делителя напряжения используются в крупных электронных устройствах. В основном они используются в емкостных чувствительных экранах, которые изменяют свое выходное напряжение при прикосновении пальца человека. А также используются в трансформаторах для увеличения падения напряжения, где обычно сетевой трансформатор содержит микросхемы и компоненты с низким падением напряжения. Наконец, нужно сказать, что в схеме делителя напряжения падение напряжения на конденсаторах одинаково для всех значений частоты.
Наконец, нужно сказать, что в схеме делителя напряжения падение напряжения на конденсаторах одинаково для всех значений частоты.
С Уважением, МониторБанк
Падение напряжения на конденсаторе — формула и понятия
Мир
Конденсатор является одним из важных компонентов в электрической цепи . Мы обсуждали конденсаторы и их комбинации в других статьях. Как и другие компоненты (резисторы, катушки индуктивности), конденсатор также оказывает сопротивление протекающему через него току (только постоянный ток). Из закона Ома получаем выражение для падения напряжения на резисторе. Теперь вопрос: « Есть ли падение напряжения на конденсаторе? «Ответ: « Да «. Но почему? Как рассчитать напряжение на конденсаторе ? В этой статье я собираюсь обсудить все эти вещи. Обратите внимание, что напряжение на конденсаторе и падение потенциала на конденсаторе — это одно и то же.
Обратите внимание, что напряжение на конденсаторе и падение потенциала на конденсаторе — это одно и то же.
См. также: Падение напряжения на катушке индуктивности в цепи переменного тока и Падение напряжения на резисторах
Почему на конденсаторе возникает падение напряжения?Падение напряжения на конденсаторе
Включите JavaScript
Падение напряжения на конденсаторе
Конденсатор — это просто нейтральный проводник в отсутствие внешнего источника напряжения (до зарядки). Но когда на конденсатор подается внешнее напряжение, он начинает накапливать внутри себя электрические заряды. Теперь напряжение на конденсаторе прямо пропорционально электрическому заряду на нем . Напряжение на конденсаторе изменяется из-за изменения заряда на нем. Так, во время заряда конденсатора напряжение на нем увеличивается. Когда конденсатор полностью заряжен, напряжение на конденсаторе становится постоянным. Теперь, если мы вытащим внешнюю батарею, начнется разрядка конденсатора. Во время разрядки конденсатора напряжение на нем уменьшается и через некоторое время его напряжение падает до нуля.
Теперь, если мы вытащим внешнюю батарею, начнется разрядка конденсатора. Во время разрядки конденсатора напряжение на нем уменьшается и через некоторое время его напряжение падает до нуля.
Здесь я собираюсь написать формулы падения напряжения на конденсаторе на разных этапах, например
- Когда конденсатор не заряжен.
- Во время зарядки конденсатора.
- Когда конденсатор полностью заряжен.
- При разрядке конденсатора.
Прочтите для них следующее.
Напряжение на незаряженном конденсатореПадение напряжения на незаряженном конденсаторе равно нулю. Потому что для незаряженного конденсатора Q=0 и, следовательно, напряжение V=0.
Напряжение на конденсаторе во время зарядкиВо время зарядки конденсатора переменного тока емкостью C с последовательным резистором R уравнение для напряжения на зарядном конденсаторе в любой момент времени t равно,
292
V(t) = V с (1 – e -t/τ ) ……. .(1)
.(1)Здесь τ = RC – постоянная времени в последовательной RC-цепи и В с максимальное напряжение внешней батареи.
Падение напряжения на полностью заряженном конденсатореПосле длительной зарядки конденсатор достигает состояния насыщения. В этом состоянии падение напряжения на нем становится максимальным. Максимальное напряжение на конденсаторе В с . Но практически напряжение на конденсаторе не может быть больше максимального напряжения батареи. Должно быть возможное напряжение В 0 . Если Q — максимальный заряд конденсатора, то формула для максимального напряжения на конденсаторе выглядит следующим образом: \small {\color{Blue} V_{0} = \frac{Q}{C}}…….(2)
Тогда получаем Q = CV 0 . Это популярная формула для напряжения на конденсаторе.
Теперь при удалении внешней батареи конденсатор переходит в режим разрядки и падение напряжения на конденсаторе начинает уменьшаться. Напряжение на разряжающемся конденсаторе примет вид0007
τ = RC – постоянная времени .
Как найти напряжение на конденсаторе?Приведенные выше уравнения полезны для определения напряжения на конденсаторе. Для разных ситуаций существуют разные формулы. Нам нужно использовать правильную формулу, чтобы найти напряжение на конденсаторе в соответствии с нашими требованиями.
- Шаг 1: Сначала определите ситуацию – заряжается ли конденсатор, разряжается или находится в состоянии насыщения.
- Шаг 2: Используйте правильную формулу или уравнение в соответствии с условием.
- Шаг 3: Поместите значения требуемых величин, таких как R, C, постоянная времени, напряжение батареи и заряда (Q) и т.
 д. в это уравнение.
д. в это уравнение. - Шаг 4: Рассчитайте значение напряжения по уравнению.
1. Аккумулятор переменного тока с пиковым напряжением 10 вольт подключен к цепи, состоящей из последовательно соединенных резистора сопротивлением 100 Ом и конденсатора переменного тока емкостью 0,01 фарад. Если конденсатор изначально не заряжен, то найти напряжение на конденсаторе через 2 с.
Ответ: В этом случае конденсатор переменного тока находится в режиме зарядки. Таким образом, падение напряжения на конденсаторе со временем увеличивается.
Постоянная времени, τ = RC = 1 , максимальное напряжение батареи, В с = 10 вольт и время, t = 2 секунд.
Теперь, используя уравнение для зарядки конденсатора, V(t) = V с (1 – e -t/τ ) , мы получаем напряжение на конденсаторе через 2 секунды, В = 8,65 вольт .
Это все из этой статьи о напряжении на конденсаторе по формуле . Если у вас есть какие-либо сомнения по этой теме, вы можете спросить меня в разделе комментариев.
Спасибо!
Похожие сообщения:
- Напряжение на катушке индуктивности в цепи переменного тока
- Формула для емкости конденсаторов различных типов0009 Энергия, хранящаяся в конденсаторе
- Падение напряжения на резисторах в последовательной и параллельной цепях
Решение «падений» напряжения на конденсаторе? — Обмен стека электротехники
спросил
Изменено 5 месяцев назад
Просмотрено 51к раз
\$\начало группы\$
У меня возникли проблемы с определением напряжения на конденсаторах в следующей цепи:
Поскольку это параллельная цепь, мы знаем, что напряжение на C3 должно быть 6 В.
Но как узнать напряжение на C1 и C2? Сохраняет ли C1 всю энергию и оставляет ли C2 без напряжения? Или это пропорционально?
Я попытался решить это в CircuitLab, и он вычисляет 6 В на C1 и 0 В на C2…
конденсатор
\$\конечная группа\$
\$\начало группы\$
Заряды C1 и C2 должны быть равны по закону сохранения заряда, поскольку узел между ними изолирован. Напряжение C1 и C2 в сумме должно быть 6В. Используйте q=CV и найдите напряжения.
Переработано RM:
Дубль 3:
Один и тот же ток течет в C1 и C2.
Поскольку заряд по определению пропорционален току (Q = I x t), то
заряд на С1 и С2 должен быть одинаковым.
Но также по определению заряд = емкость x напряжение (Q = C x V).
Или, переставляя, V = Q/C.
Итак, при одинаковых зарядах в каждом напряжение на конденсаторе будет обратно пропорционально емкости.
Суммарное напряжение C1 и C2 должно составлять 6 В. Используйте q=CV и найдите напряжения.
Обмотка
Возьмем 2:
Связь между зарядом Q, напряжением V и емкостью C определяется выражением
Q = C x V.
Перестановка, V = Q/C.
Заряд Q определяется как сумма тока во времени, т.е. Q = i x t
Поскольку через C1 и C2 должен течь одинаковый ток, они оба испытывают одинаковый ток x время, поэтому их заряды равны.
Но сверху Vcap = Q/C.
, т. е. при одинаковых зарядах напряжения на емкостях будут обратно пропорциональны размерам конденсаторов.
Таким образом, в этом примере напряжения на C1 и C2 будут обратно пропорциональны размерам конденсаторов, поэтому VC1 = 2 x VC2.
По осмотру, VC2 = 2, VC1 = 4.
\$\конечная группа\$
13
\$\начало группы\$
«Заряд на C1 и C2 должен быть равным» не объясняет этого. Почему они должны быть равны?
Почему они должны быть равны?
Думайте об этом как о делителе напряжения, но если для резисторов \$ V_{R2} = \dfrac{R2}{R1 + R2} V1 \$, то для конденсаторов: \$ V_{C2} = \dfrac{C1 {C1 + C2} V1 \$. Обратите внимание на разные индексы в числителе.
Доказательство
ПРЕДУПРЕЖДЕНИЕ. Уродливые уравнения впереди. Не волнуйтесь, если они выглядят слишком сложными; все, что вам нужно на практике, это приведенное выше уравнение.
.
.
.
.
.
.
.
\$ V_{C2} = \dfrac{Z_{C2}}{Z_{C1} + Z_{C2}}V1 = \dfrac{\dfrac{1}{j\omega C2}}{\dfrac{1 }{j \ omega C1} + \ dfrac {1} {j \ omega C2}} V1 = \ dfrac {\ dfrac {C1} {j \ omega C1 C2}} {\ dfrac {C2} {j \ omega C1 C2 } + \dfrac{C1}{j\omega C1 C2}} V1 = \dfrac{C1}{C1 + C2} V1 \$
Последний шаг разрешен только для \$\omega \ne 0\$. Для DC мы должны взять предел:
\$ V_{C2} = \displaystyle \lim_{\omega \to 0} \dfrac{\dfrac{C1}{j\omega C1 C2}}{\dfrac{C2 }{j\omega C1 C2} + \dfrac{C1}{j\omega C1 C2}} V1 = \dfrac{C1}{C1 + C2} V1 \$
Вам не нужно делать этот вывод каждый раз , просто помните, что это инверсия резисторного делителя.
\$\конечная группа\$
13
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Падение напряжения на конденсаторах и катушках индуктивности
Обсуждение падения напряжения в устройствах резистивного типа (включая провода) относительно просто, поскольку они не меняются со временем. Как только в цепь подается напряжение, начинает течь ток, и мощность рассеивается в устройствах, что приводит к устойчивым падениям напряжения. Но есть два типа устройств, которые со временем вызывают изменения: конденсаторы и катушки индуктивности. В этой статье обсуждается, как учитывать падение напряжения в этих особых случаях.
Рис. 1. Набор различных конденсаторов. Изображение Эрика Шредера. [CC BY-SA 2.0]
В электронике существуют три основные категории нагрузочных устройств. Как правило, чисто резистивные нагрузки первыми вводятся в курс или программу по электронике из-за их простоты. Пока к правильно сконструированной резистивной цепи приложено напряжение, ток немедленно протекает через цепь с постоянной скоростью. Это приводит к преобразованию энергии в каждом компоненте и, следовательно, к падению напряжения.
Это приводит к преобразованию энергии в каждом компоненте и, следовательно, к падению напряжения.
Основная характеристика резистивных нагрузок заключается в том, что они не изменяются независимо от того, как долго цепь активна. На самом деле небольшие изменения неизбежны — даже ток в устройстве меняет свою температуру, влияя на сопротивление. Таким образом, реальная схема не может оставаться точно такой же. Но можно предположить, что при резистивной нагрузке ток остается в основном одинаковым независимо от прошедшего времени.
Другие две категории нагрузочных устройств могут быть более сложными для обсуждения. Влияние каждого из них на схему меняется в зависимости от типа напряжения, т. Е. Применение постоянного или переменного тока. Этими компонентами являются конденсатор и катушка индуктивности.
Еще одно важное замечание, которое следует учитывать при работе с этими устройствами, заключается в том, что они никогда не действуют в цепи поодиночке. Некоторые цепи могут быть чисто резистивными, но никогда не будет чисто емкостной или индуктивной нагрузки. Оба они включают некоторый элемент сопротивления, даже если это значение сопротивления заключено в самом конденсаторе или катушке индуктивности.
Оба они включают некоторый элемент сопротивления, даже если это значение сопротивления заключено в самом конденсаторе или катушке индуктивности.
Падение напряжения на конденсаторе
Как обсуждалось в предыдущих статьях, падение напряжения определяется как разность потенциальной энергии, деленная на заряд, который пройдет через эти точки. Пока мы можем определить, как энергия изменяется при прохождении тока через нагрузочное устройство, мы можем затем определить падение напряжения или, по крайней мере, мы можем определить, как напряжение изменяется во времени.
Конденсатор — это любой компонент с двумя проводниками, разделенными изолятором. Иногда это нежелательный эффект, например, два провода рядом друг с другом в жгуте проводов. В других случаях устройство может быть тщательно сконструировано с использованием проводящих пластин и диэлектриков, чтобы максимально увеличить емкость.
Рис. 2. Высоковольтный вакуумный конденсатор.

Как только на цепь, содержащую конденсатор, подается напряжение, заряд начинает накапливаться на одном из проводников, поскольку он не может пройти через изоляционный слой. В этот же момент противоположный заряд начинает накапливаться на встречном проводнике. Другой способ думать об этом состоит в том, что в то время как отрицательный заряд начинает накапливаться на одной стороне, положительный заряд накапливается на противоположной, в результате чего отрицательный заряд продолжает путешествовать по цепи, как будто конденсатора там и не было.
Из этого начального описания сразу после подачи напряжения мы можем сделать вывод, что движение заряда «через» конденсатор чрезвычайно велико, и не требуется много энергии, чтобы притянуть заряд на противоположной стороне. Если энергия, необходимая для движения, невелика, а движение заряда велико, напряжение низкое:
Со временем, возможно, всего за несколько миллисекунд, противоположные заряды будут продолжать накапливаться на обоих проводниках. По мере увеличения этой разницы увеличивается и энергия, необходимая для поддержания заряда. По мере замедления скорости роста заряда движение заряда в цепи также будет замедляться. Это приводит к высокому напряжению:
По мере увеличения этой разницы увеличивается и энергия, необходимая для поддержания заряда. По мере замедления скорости роста заряда движение заряда в цепи также будет замедляться. Это приводит к высокому напряжению:
Возможно, точные значения компонентов в цепи могут помочь вычислить напряжения и токи, но, по крайней мере, из этих наблюдений мы можем дать первоначальную оценку. Когда напряжение впервые подается на разряженный конденсатор, ток будет высоким, а падение напряжения на конденсаторе низким. Со временем ток будет уменьшаться, а напряжение будет увеличиваться, пока мы не достигнем максимального напряжения (источника), после чего ток полностью прекратится.
Падение напряжения на катушке индуктивности
Катушки индуктивности обычно обсуждаются вместе с конденсаторами (так же, как и здесь, в этой статье), но будьте осторожны — принцип работы СОВЕРШЕННО отличается. Единственное сходство заключается в том, что индукторы действительно демонстрируют изменение напряжения и тока с течением времени, хотя и иначе, чем конденсаторы.
Катушка индуктивности представляет собой катушку из проволоки, обычно намотанную на металлический сердечник, состоящий из композитов железа. Это железо способно удерживать энергию в виде магнитного поля, хотя оно и непостоянно.
Рис. 3. Тороидальный индуктор. Изображение предоставлено Coilcraft.
Когда на эту катушку впервые подается напряжение, энергия в основном передается от заряда в цепи в магнитное поле железного сердечника. Таким образом, для создания этого магнитного поля требуется много энергии. В самом начале это будет отнимать больше всего энергии. Исходя из формулы для напряжения, эта разность энергий в катушке приведет к большому напряжению:
Со временем энергия, хранящаяся в магнитном поле, достигнет максимума, и больше энергии для строительства не требуется. Когда это произойдет, напряжение на катушке индуктивности упадет:
Изменения тока
Одним из важных различий между конденсаторами и катушками индуктивности является начальное движение заряда (ток) и изменение величины во времени. Катушка индуктивности представляет собой катушку из длинного тонкого провода, создающего измеримое сопротивление. Ток в чистом конденсаторе в начале может быть очень и очень большим при почти нулевом сопротивлении. Мы ожидаем такой же чрезвычайно высокий ток в катушке индуктивности через некоторое время, когда падение напряжения невелико. Однако внутреннее сопротивление катушки ограничивает ток.
Катушка индуктивности представляет собой катушку из длинного тонкого провода, создающего измеримое сопротивление. Ток в чистом конденсаторе в начале может быть очень и очень большим при почти нулевом сопротивлении. Мы ожидаем такой же чрезвычайно высокий ток в катушке индуктивности через некоторое время, когда падение напряжения невелико. Однако внутреннее сопротивление катушки ограничивает ток.
По этой причине мы никогда не увидим нагрузочное устройство, состоящее только из конденсатора. Тем не менее, мы могли бы ожидать индуктора в качестве нагрузки, поскольку он также имеет значительное собственное сопротивление. На самом деле реле, контакторы, соленоиды и даже двигатели состоят просто из катушек и являются индуктивными нагрузками, но у них все еще есть внутреннее сопротивление для ограничения тока.
RC-цепи
РЦ Цепи
Цепь RC
это просто схема с резистором и конденсатором. Эту комбинацию полезно изучать, потому что конденсаторы
можно использовать для хранения энергии и резистора, расположенного вдоль
с конденсатором может контролировать скорость, с которой энергия
освобождается от конденсатора.
Эту комбинацию полезно изучать, потому что конденсаторы
можно использовать для хранения энергии и резистора, расположенного вдоль
с конденсатором может контролировать скорость, с которой энергия
освобождается от конденсатора.
Мы будем Ограничим наши исследования следующим типом RC-цепи.
Переключатель может быть перемещены из позиции в в позиция б . Прежде чем мы пойдем далее, давайте рассмотрим некоторые факты о конденсаторах:
заряд на конденсаторе не может измениться мгновенно . С момента изменения в заряд D Q = I D t , там всегда должно быть ненулевое время перед зарядом может измениться на ненулевую сумму, если только не было бесконечный ток.

Есть отсутствует ток через конденсатор в установившемся режиме . Поскольку заряд накапливается на конденсаторе, а не протекая через него, ток может нарастать до тех пор, пока дело в том, что напряжение В=Q/C будет балансировать внешнее напряжение, толкающее заряд на конденсаторе.
При наличии конденсатора емкостью С последовательно с батареей напряжением В б и резистор сопротивления R , падение напряжения должно быть:
,
, который является заявлением
что напряжение, полученное на аккумуляторе, должно
равно падению напряжения на конденсаторе плюс
падение напряжения на резисторе. Уравнение, в котором
скорость изменения количества (D Q/ D t )
пропорционально количеству (D Q) всегда будет
имеют показательное решение. Рассмотрим два случая:
Уравнение, в котором
скорость изменения количества (D Q/ D t )
пропорционально количеству (D Q) всегда будет
имеют показательное решение. Рассмотрим два случая:
Разгрузка конденсатор : Конденсатор изначально подключен (переключатель в положении и ) долгое время, а затем отключается перенос переключателя на b в момент времени t = 0 . затем конденсатор разряжается, оставляя конденсатор без заряда или напряжения после длительного времени.
Зарядка конденсатор : Переключатель в положении b в течение длительного времени, что позволяет конденсатор не должен иметь заряда.
 В момент т
= 0 , переключатель меняется на a и конденсатор заряжается.
В момент т
= 0 , переключатель меняется на a и конденсатор заряжается.
| Разрядка | Зарядка | |
| Плата | ||
| Текущий | ||
| Напряжение |
Здесь, Q 0 , В 0 и I 0 ток и напряжение заряда,
конденсатор в тот момент, когда переключатель брошен. Время t — характерное время распада, т = РК . Когда
столкнувшись с проблемой RC , лучший
стратегия следующая:
Время t — характерное время распада, т = РК . Когда
столкнувшись с проблемой RC , лучший
стратегия следующая:
Решите, что заряд на конденсаторе был непосредственно перед переключатель был брошен. Так как заряд не может изменить мгновенно, это заряд сразу после переключатель брошен.
Решите, что заряд долго после того, как переключатель брошен.
Выберите экспоненциальная форма для заряда К(т) , чтобы удовлетворить правильный начальный и конечный обвинения.
Напряжение через конденсатор можно найти через, В = К/К .
 Напряжения на
другие элементы можно найти с помощью Кирхгофа
первый закон.
Напряжения на
другие элементы можно найти с помощью Кирхгофа
первый закон.Текущий через конденсатор всегда должен распадаться и заканчиваться на нуле, так как заряд не может течь непрерывно через конденсатор. Начальный ток может обычно определяют с помощью Ома закон, V=R I .
Характерное время t = RC сообщает, что зарядка/разрядка медленнее с большим резистором или конденсатор. Это имеет смысл, потому что больший резистор препятствует протеканию тока; тем самым замедляя зарядка/разрядка, а больший конденсатор вмещает больше обвинение; поэтому требуется больше времени для зарядки.
У всех должно быть хорошее самочувствие
для показательных функций. Ниже представлены эскизы
зарядка Q(t) для зарядки
и разрядка конденсаторов.
Ниже представлены эскизы
зарядка Q(t) для зарядки
и разрядка конденсаторов.
айглкайла
Примеры Кирхгофа законы / Указатель цепи RC
Подробные факты – Lambda Geeks
В этой статье разъясняется, что такое падение напряжения и как рассчитать падение напряжения в последовательной цепи. Всякий раз, когда напряжение встречает какой-либо резистивный элемент в цепи, значение уменьшается или «падает».
В последовательной цепи имеется несколько сопротивлений или импедансов. Каждый раз, когда через них проходит ток, напряжение уменьшается. Итак, нам нужно знать значение определенного сопротивления и тока, проходящего через него, чтобы вычислить падение напряжения на нем. Падение напряжения — это ток, умноженный на сопротивление.
Что такое падение напряжения? Предположим, мы соединяем батарею с резистором через провод. Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительного к отрицательному выводу.
Электроны имеют тенденцию течь от отрицательной стороны батареи к положительной. Это похоже на электрический заряд, идущий от положительного к отрицательному выводу.
Когда одна единица заряда сталкивается с резистором, он на некоторое время останавливается. Когда он проходит резистор, приходит другая единица заряда и останавливается. В любой момент времени заряд на конце резистора меньше, чем заряд на начале резистора. Это явление создает «падение потенциала или напряжения».
Подробнее…..Постоянно ли напряжение в последовательной цепи: полная информация и часто задаваемые вопросы
Как рассчитать общее падение напряжения в последовательной цепи?Полное падение напряжения в последовательной цепи представляет собой сумму всех отдельных падений напряжения, вызванных параметрами импеданса. Кроме того, сумма равна общему напряжению, подаваемому на цепь, или напряжению до любого «падения».
Рассмотрим явления с помощью схемы. В схеме ниже есть два резистора, R 1 на 100 Ом и R 2 на 200 Ом, подключенные к источнику питания V 30 вольт. Текущий [латекс] i = \frac {V} {R_{1} + R_{2}} = \frac {30} {100+200} = 0,1 \; [/латекс]. Поэтому падение напряжения на R 1 [Латекс] = i \times R_{1} = 0,1 \times 100 = 10 \; V [/Latex] и через R2 [Latex] = i \times R_{2} = 0,1 \times 200 = 20 \; В[/латекс].
В схеме ниже есть два резистора, R 1 на 100 Ом и R 2 на 200 Ом, подключенные к источнику питания V 30 вольт. Текущий [латекс] i = \frac {V} {R_{1} + R_{2}} = \frac {30} {100+200} = 0,1 \; [/латекс]. Поэтому падение напряжения на R 1 [Латекс] = i \times R_{1} = 0,1 \times 100 = 10 \; V [/Latex] и через R2 [Latex] = i \times R_{2} = 0,1 \times 200 = 20 \; В[/латекс].
Цепи переменного или переменного тока представляют собой электрические цепи с напряжением питания переменного тока. Последовательная цепь переменного тока состоит из любой комбинации резистора, катушки индуктивности и конденсатора, соединенных последовательно.
Точно так же, как и при постоянном токе, мы можем вычислить полное сопротивление последовательной цепи переменного тока, складывая их. Аналогичным образом можно найти и падение напряжения. Падение напряжения на любом элементе последовательной цепи переменного тока равно V = iZ, где Z — полное сопротивление цепи, а i — полный ток, протекающий через нее.
Подробнее о…..Как рассчитать напряжение в последовательной цепи: подробные факты
Падение напряжения в серии RLC цепь:Цепь RLC является частным случаем цепей переменного тока. Цепь RLC состоит из резисторов, конденсаторов и катушек индуктивности, соединенных последовательно. Давайте разберемся с падением напряжения в последовательной цепи RLC на примере.
Схема состоит из трех компонентов, изображенных ниже: резистор ом, индуктор L Генри и конденсатор C фарад. Ранее мы знали, что падение напряжения на любом из них = импеданс × ток. Итак,
Падение напряжения на резисторе = iR, индуктивность = iXL и конденсатор = iXC, где XL = 2πfL и XC = 1/2πfC
Q1. Три резистора соединены последовательно со значениями R 1 = 4 Ом, R 2 = 5 Ом и R 3 = 6 Ом. Цепь соединена с источником питания 15 В. Найдите падение напряжения на резисторах.
Цепь соединена с источником питания 15 В. Найдите падение напряжения на резисторах. Для расчета падения потенциала на R 1 , R 2 и R 3 нам сначала нужно получить ток в цепи. Мы знаем, [Latex] current = \frac {net \; напряжение} {эквивалентное \; сопротивление} [/Latex]
Эквивалентное сопротивление [Latex] R_{eq} = R_{1} + R_{2} + R_{3} = 4 + 5 + 6 = 15 \; \Omega [/Latex]
Следовательно, общий ток [Latex] = \frac { 15 \: V} {15 \: \Omega } = 1\: A [/Latex]
Теперь мы можем использовать закон Ома ( V = IR) для каждого резистора и найти падения напряжения на них.
Итак, [Латекс] V_{1} = I \times R_{1} = 1 \times 4 = 4 \; V [/Latex] ,
[Latex] V_{2} = I \times R_{2} = 1 \times 5 = 5 \; V [/Latex]
[Latex] V_{3} = I \times R_{3} = 1 \times 6 = 6 \; V[/Latex]
Q2. Для приведенной ниже схемы падение напряжения на резисторе 6 Ом составляет 12 В. Найдите другие падения напряжения и рассчитайте общее падение напряжения или напряжение питания.
Мы знаем, что падение напряжения на любом резисторе в последовательной цепи = сопротивление × общий ток
Если в цепи протекает ток i, падение напряжения на резисторе 6 Ом равно 6i.
6i = 12 или i = 2 ампера
Следовательно, падение напряжения на резисторе 2 Ом = 2 x 2 = 4 В
Падение напряжения на резисторе 4 Ом = 2 x 4 = 8 В
Таким образом, чистое напряжение падение напряжения питания = (12 + 4 + 8) = 24 В
Q3. На изображении ниже показана цепь серии RLC со следующими компонентами: Источник питания переменного тока 120 В, 50 Гц , Резистор 100 Ом , Конденсатор 20 мкФ , Катушка индуктивности 420 мГн. Рассчитать падение напряжения на всех трех импедансах. Раньше мы знали, как рассчитать падение напряжения для последовательной цепи RLC. Ток, умноженный на импеданс (R или X L или X C ), дает нам падение напряжения. Сначала найдем X L и X C .
Сначала найдем X L и X C .
X L = 2πfL (f — частота сети переменного тока)
9{\ круг} \; A [/Latex]Следовательно, [Latex] V_{R} = iR = 1,16\угол -15,22 \times 100\угол 0 = 116\угол -15,22\; V [/Latex]
Здесь ток опережает напряжение как X C > X L .
[Латекс] V_{C} = iX_{C} = 1,16\угол -15,22\умножить на 159,15\угол 90 = 184,61\угол 74,78\; V [/Latex]
[Latex] V_{L} = iX_{L} = 1,16\угол -15,22\умножить на 131,95\угол -90 = 153,06\угол -105,22\; V [/Latex]
Подробнее… Что такое напряжение в последовательной цепи: подробные факты
Основные вопросы и ответы по электротехнике для первокурсников
Этот набор основных вопросов и ответов по электротехнике для первокурсников посвящен «Распределению напряжения между последовательно включенными конденсаторами».
1. Общее падение напряжения на ряде конденсаторов __________
а) Падение напряжения на любом из конденсаторов
б) Сумма падений напряжения на каждом из конденсаторов
в) Произведение падения напряжения на каждом из конденсаторов
d) Ноль
Посмотреть ответ
Ответ: b
Объяснение: Общее падение напряжения на ряду конденсаторов равно сумме падений напряжения на каждом из конденсаторов, потому что при последовательном соединении конденсаторов напряжение падает на каждый конденсатор.
2. Конденсаторы С1, С2 и С3 имеют падение напряжения 2В, 3В и 5В соответственно. Вычислите полное напряжение в цепи.
а) 10В
б) 2В
в) 5В
г) 0В
Посмотреть ответ
Ответ: а
Объяснение: При последовательном соединении конденсаторов:
Vtotal=V12+V2+V3 = 2+3+5 = 10В.
3. Какое напряжение на конденсаторе 2F?
a) 240 В
b) 200 В
c) 220 В
d) 120 В
Посмотреть ответ
Ответ: d
Пояснение: Конденсаторы соединены последовательно.
1/C=1/2+1/4+1/6, следовательно, C=(12/11)F.
Q = C*V = 220*(12/11) = 240°С.
В на конденсаторе 2F = Q/C = 240/2 = 120В.
реклама
реклама
4. Какое напряжение на конденсаторе 4F?
a) 120 В
b) 60 В
c) 100 В
d) 220 В
Посмотреть ответ
Ответ: b
Пояснение: Конденсаторы соединены последовательно.
1/C=1/2+1/4+1/6, следовательно, C=(12/11)F.
Q = C*V = 220*(12/11) = 240°С.
В на конденсаторе 4F = Q/C = 240/4 = 60В.
5. Рассчитайте напряжение на конденсаторе 6F.
а) 120В
б) 60В
в) 40В
г) 220В
Посмотреть ответ
Ответ: в
Объяснение: Конденсаторы соединены последовательно.
1/C=1/2+1/4+1/6, следовательно, C=(12/11)F.
Q = C*V = 220*(12/11) = 240°С.
В на конденсаторе 6F = Q/C = 240/6 = 40В.
6. Какие из следующих правил применяются при последовательном соединении конденсаторов?
a) Делитель напряжения
b) Делитель тока
c) Делитель напряжения и делитель тока
d) Ни делитель напряжения, ни делитель тока
Просмотреть ответ
Ответ: a
последовательно, потому что когда конденсаторы соединены последовательно, напряжение на каждом конденсаторе различно.
7. Конденсатор не допускает резких изменений _________
а) Ток
б) Напряжение
в) Сопротивление
г) Индуктивность
Посмотреть Ответ
Ответ: б
Пояснение: Конденсатор не допускает резких изменений напряжения, потому что эти изменения происходят в нулевое время, что приводит к бесконечности тока, что невозможно.
объявление
8. Какое из следующих выражений верно относительно напряжения на последовательно включенных конденсаторах?
a) V1/V2=C2/C1
b) V2/V1=C2/C1
c) V1*V2=C1*C2
d) V1/C1=V2/C2
Посмотреть ответ
Ответ: a
Объяснение : когда конденсаторы соединены последовательно, заряд на каждом конденсаторе остается одинаковым, а напряжение на каждом из них меняется. При последовательном соединении двух конденсаторов:
Q=V1C1; Q=V2C2. Таким образом: V1/V2=C2/C1.
9. Два конденсатора 4F соединены последовательно, рассчитайте напряжение на каждом, если общее напряжение равно 20В.
а) 10В
б) 5В
c) 20 В
d) 0 В
Просмотреть ответ
Ответ: a
Объяснение: Два конденсатора имеют одинаковую емкость, поэтому напряжение делится поровну. В на каждом = общее напряжение/2 = 20/2 = 10 В.
объявление
10. Два конденсатора напряжением 2F и 4F соединены последовательно. Эта комбинация подключена к источнику питания 100 В, рассчитайте напряжение на конденсаторе 2F.
а) 66,67 В
б) 33,33 В
в) 100 В
г) 0 В
Посмотреть ответ
Ответ: a
Объяснение: C всего = 2*4/(2+4) = 4/3F
Q = CV = (4/3)*100 = 400/3 C.
В на конденсаторе 2F = Q/C = (400/3)/2 = 200/3 = 66,67F.
Sanfoundry Global Education & Learning Series – основы электротехники.
Чтобы попрактиковаться во всех областях базовой электротехники для первокурсников, здесь представлен полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .
Следующие шаги:
- Получите бесплатный сертификат о заслугах в области базовой электротехники
- Участие в конкурсе по базовой сертификации электротехники
- Стать лучшим специалистом в области базовой электротехники
- Пройти базовые тесты по электротехнике
- Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
реклама
реклама
Подпишитесь на наши информационные бюллетени (тематические).


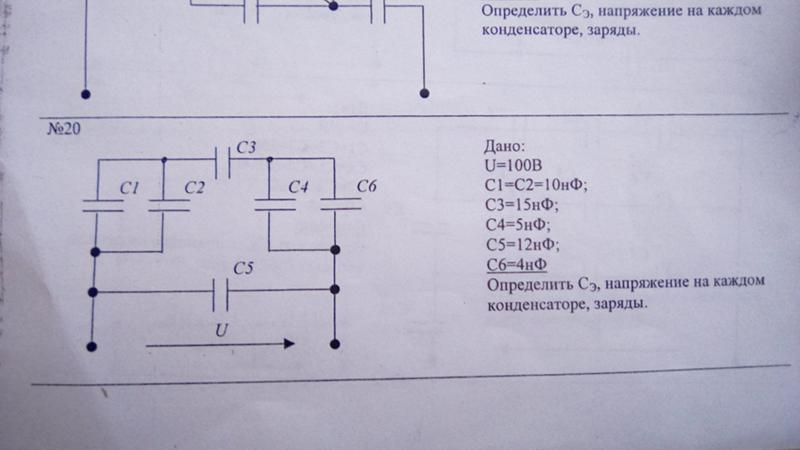 38), находим уравнение для функции
38), находим уравнение для функции  40)
40) 42)
42)
 Исходя из вышесказанного, на начальном этапе проектирования можно считать, что
в наличии есть выпрямленное напряжение 230 В на вторичной обмотке трансформатора и электролитический конденсатор на рабочее
напряжение 385 В (как наиболее доступный) постоянного тока в качестве накопительного. При таком выборе питающего напряжения,
вполне реализуема простейшая схема мостового выпрямления, нагруженная на один из сглаживающих фильтров, рассмотренных выше.
С учетом падения напряжения на стабилизаторах напряжения и развязывающих демпферах, установленных между отдельными каскадами,
можно предположить, что окончательное значение высоковольтного напряжения на лампах каждого каскада можно принять равным
примерно 285 В. Именно по этой причине большинство схем, рассчитывались исходя из значения высокого напряжения 285 В.
Исходя из вышесказанного, на начальном этапе проектирования можно считать, что
в наличии есть выпрямленное напряжение 230 В на вторичной обмотке трансформатора и электролитический конденсатор на рабочее
напряжение 385 В (как наиболее доступный) постоянного тока в качестве накопительного. При таком выборе питающего напряжения,
вполне реализуема простейшая схема мостового выпрямления, нагруженная на один из сглаживающих фильтров, рассмотренных выше.
С учетом падения напряжения на стабилизаторах напряжения и развязывающих демпферах, установленных между отдельными каскадами,
можно предположить, что окончательное значение высоковольтного напряжения на лампах каждого каскада можно принять равным
примерно 285 В. Именно по этой причине большинство схем, рассчитывались исходя из значения высокого напряжения 285 В.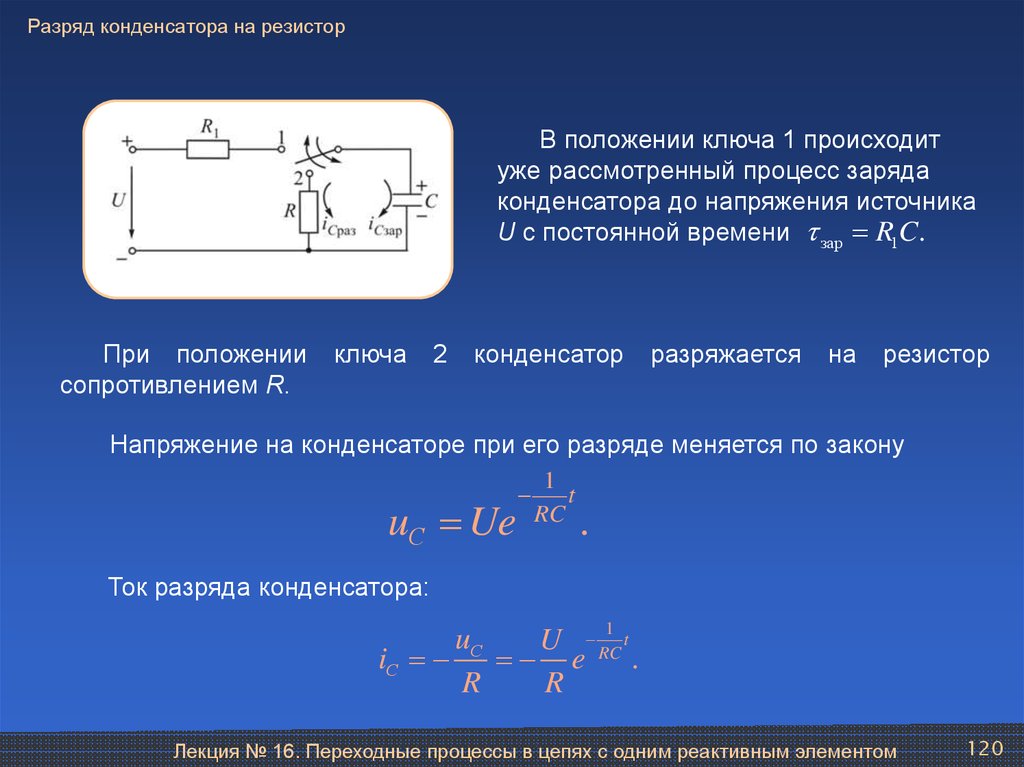
 Если значения емкости конденсаторов будут
равны, то будут равны и напряжения на них (Q = CV).
Если значения емкости конденсаторов будут
равны, то будут равны и напряжения на них (Q = CV). Для этих целей чаще всего
используются резисторы с сопротивлением 220 кОм. Исходя из этого, а также из требуемого тока делителя, необходимо рассчитать
требуемую мощность рассеяния резисторов. Разумеется, — рассеяние этих резисторов является бесполезными потерями энергии.
Для этих целей чаще всего
используются резисторы с сопротивлением 220 кОм. Исходя из этого, а также из требуемого тока делителя, необходимо рассчитать
требуемую мощность рассеяния резисторов. Разумеется, — рассеяние этих резисторов является бесполезными потерями энергии. Это обстоятельство имеет очень большое значение, так как потенциал металлического
корпуса электролитического конденсатора почти не отличается от потенциала его минусового вывода. Таким образом, корпуса при
повышенных напряжениях должны быть не только изолированы от земляной шины (или шасси), но так же должны быть изолированы
соответствующим образом, чтобы не допустить поражения электрическим током при случайном прикосновении к ним.
Это обстоятельство имеет очень большое значение, так как потенциал металлического
корпуса электролитического конденсатора почти не отличается от потенциала его минусового вывода. Таким образом, корпуса при
повышенных напряжениях должны быть не только изолированы от земляной шины (или шасси), но так же должны быть изолированы
соответствующим образом, чтобы не допустить поражения электрическим током при случайном прикосновении к ним. Наиболее простым способом осуществить
эту цель является подключение резистора с сопротивлением 220 Ом и мощностью рассеяния 2 Вт параллельно выводам накопительного
электролитического конденсатора (как это было сделано в предыдущем случае), который не только разряжает этот конденсатор,
но также разряжает последовательно включенные высоковольтные конденсаторы.
Наиболее простым способом осуществить
эту цель является подключение резистора с сопротивлением 220 Ом и мощностью рассеяния 2 Вт параллельно выводам накопительного
электролитического конденсатора (как это было сделано в предыдущем случае), который не только разряжает этот конденсатор,
но также разряжает последовательно включенные высоковольтные конденсаторы.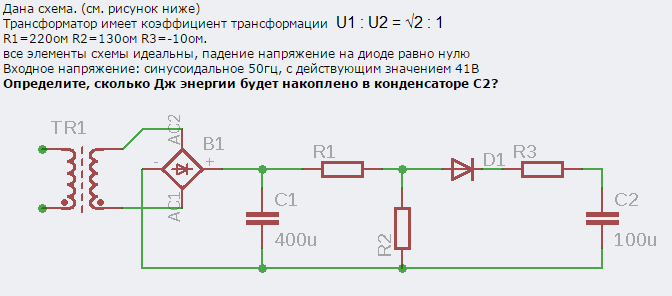
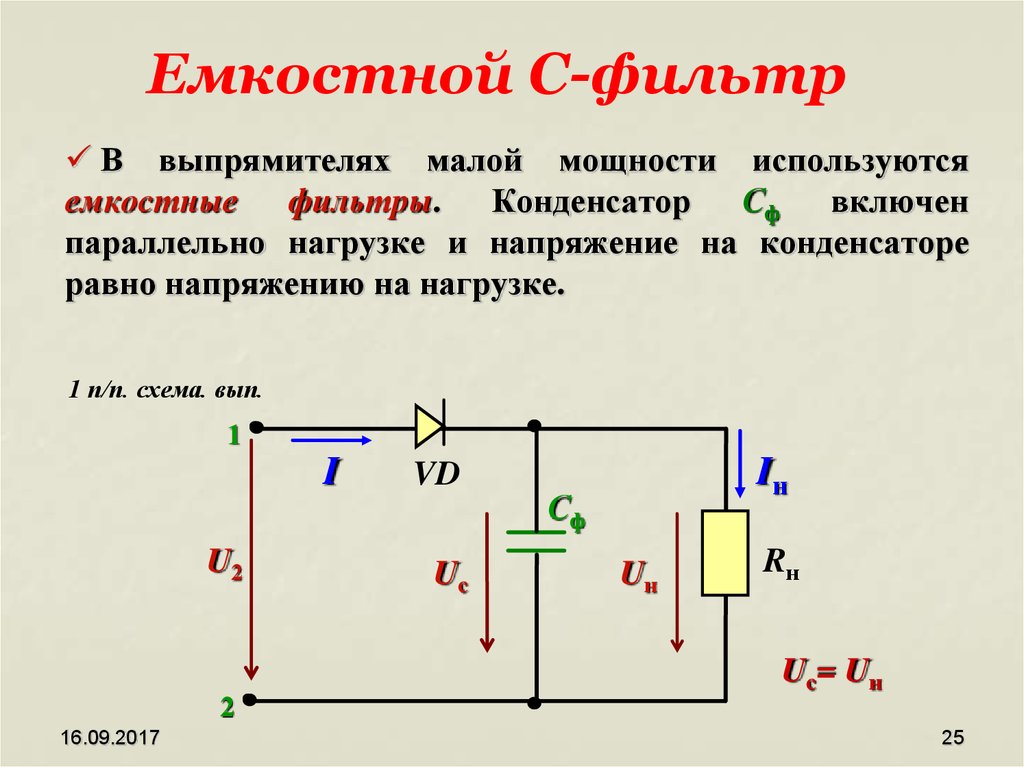
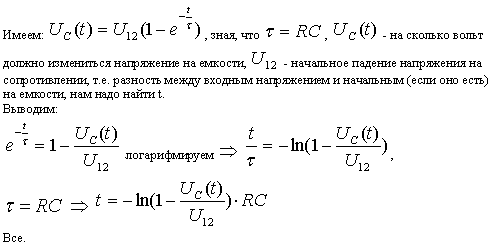
 biblioatom.ru)
biblioatom.ru)

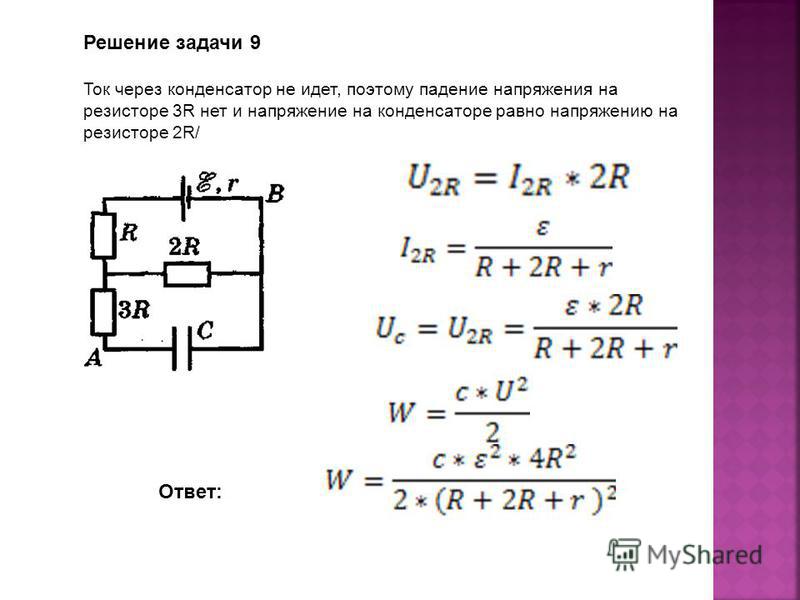
 В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
В претензии также указывается адрес
страницы
Сайта, которая содержит данные, нарушающие права, и излагается полное описание сути нарушения прав;
