Отрицательная катушка индуктивности

Как результат интерпретации по главному принципу относительности, может быть найдено, что явление противоположной самоиндукции вызвано изменением относительной величины потока между одинаковыми типами электрических зарядов. В качестве использования явления, было бы возможно произвести электроэнергию из пространства при уменьшении энтропии. Теперь я представлю основной элемент схемы, создающий это.

Ток проводимости это относительный поток между свободными электронами, несущими отрицательный заряд и ионами, несущими положительный заряд. Короче говоря, это относительный поток между различными видами зарядов. В этом случае, происходит нормальная самоиндукция. Чтобы производить противоположную самоиндукцию в токе проводимости, необходимо делать относительный поток между одинаковыми видами электрических зарядов. Чтобы сделать это, надо положительные ионы заменить на отрицательные ионы, или свободные электроны должны быть заменены на позитроны. Однако это невозможно, исходя из понимания материи. Также опыт, по переносу относительного потока между различными видами зарядов, заряжая проводник отрицательно, является нереалистичным. Причина — то, что необходимо концентрировать отрицательный заряд близко к проводнику contraly к силе Coulomb. Кроме того, большее количество отрицательных зарядов, чем положительных ионов в проводнике необходимо. Конечно, это невозможно.

 Сначала, давайте представим ток проводимости, который не вызвал бы самоиндукцию. Это означает ток без собственного магнитного поля, то есть двухсторонний ток. Это два вида токов, которые одинаковы по величине и противоположны по направлению, ток в двух параллельных электрических проводниках, магнитные поля их не проявляются, подавляемые друг другом. Представляя эти сдвоенные проводники, как одинарный проводник, с точки зрения положительных ионов, величина потока свободных электронов, текущих налево, равно потоку текущему направо. Соответственно, магнитное поле не появляется с точки зрения ионов. Следуя этому предположению, с точки зрения свободных электронов, текущих налево, половина всех свободных электронов, может быть представлена, как ионы текущие направо с двойной ионной скоростью. То есть величина потока свободных электронов равна величине потока ионов. Соответственно, магнитное поле не появляется, с точки зрения свободных электронов, текущих налево. С другой стороны, рассматривая ситуацию с точки зрения свободных электронов, текущих направо, половина из всех свободных электронов, как ионы текут налево с двойной ионной скоростью. То есть величина потока свободных электронов равна величине потока ионов. Соответственно, магнитное поле не появляется, с точки зрения свободных электронов, текущих направо.

Д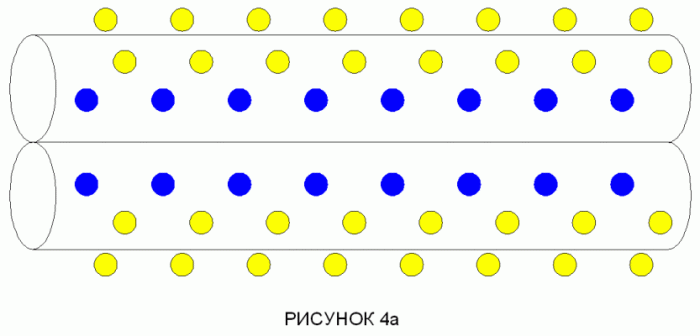иаг_04а.gif

ДИАГРАММА 4 относительный поток зарядов в бифилярных проводах ( магнитное поле отсутствует)

Диаг_04.gif

Предположим, что два тока одинаковой величины текут в противоположном направлении в двойных электрических проводах. Когда изменяется ток, происходит изменение величины потока положительных электрических зарядов всегда равное изменению величины потока отрицательных электрических зарядов, т.е. изменяется поток свободных электронов. Соответственно, изменяющаяся величина потока электрических зарядов, появляющегося на заднем плане (на подложке) из свободных электронов, не приводит к изменению магнитного поля. Без изменения магнитного поля, наведенное электрическое поле не может появляться. И относительная самоиндукция между потоком электронов и фоном не возникает.

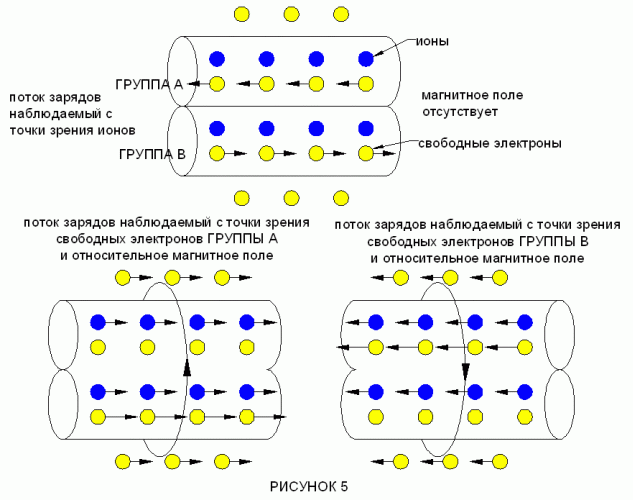
  Когда ток изменяется в условии, что фон (подложка) бифилярных проводов заряжен отрицательно, происходит относительное изменение величины потока между свободными электронами, текущими в проводниках и свободными электронами на заднем плане (в подложке). То есть возможность изменить относительную величину потока этого вида зарядов. В это время проявляется отрицательная самоиндукция с отрицательной энергией.

Диаг_05.gif

NGflow.gif

 ДИАГРАММА 5

Когда фон (подложка) под бифилярными проводами заряжен отрицательно, магнитные поля с отрицательной энергией, появляется с точки зрения свободных электронов в Группе А и Группе B отрицательной самоиндукцией.

  Двойные катушки могут быть сделаны, в два электрических провода с магнитным сердечником. После того, как мы зарядим магнитный сердечник отрицательно, относительно потока электрического тока в двойных катушках, именно тогда явление относительной противоположной самоиндукции появляется между свободными электронами, около магнитного сердечника и свободных электронов, текущих в двойных катушках. В результате этого, отрицательная энергия может быть запасена в среде, где появляется относительное магнитное поле. Мы вводим название отрицательная катушка индуктивности катушке индуктивности, которая состоит из магнитного сердечника, электрически заряженного отрицательно и двойных катушек (неиндуктивная катушка) в которых токи одинаковы и противоположно направлены.

Диаг_06.gif

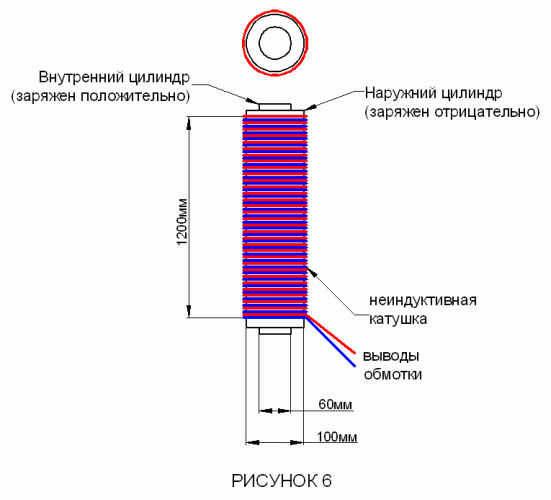
ДИАГРАММА 6 ОТРИЦАТЕЛЬНАЯ КАТУШКА ИНДУКТИВНОСТИ

ДИАГРАММА 6 — вариант самой простой отрицательной катушки индуктивности. Чтобы увеличивать электростатическую емкость магнитного сердечника, два алюминиевых цилиндра с различными диаметрами установлены коаксиально к магнитному сердечнику. Наматывая непосредственных на него два эмалированных провода плотно по внешнему цилиндру (в диаграмме, один провод обозначен с синим, другой с красным), одни концы проводов замкнуты а другие концы разомкнуты. Два разомкнутых конца являются выводами отрицательной катушки индуктивности. Чтобы генерировать относительное магнитное поле, которое наблюдается с точки зрения свободных электронов, текущих в катушке, и появляющееся в направлении, которое создает противоположная самоиндукция, необходимо зарядить внешний цилиндр отрицательно, а внутренний цилиндр положительно. Если цилиндры заряжены с противоположно рекомендации, в двойных катушках возникает положительная индуктивность.

К ДИАГРАММЕ 6, исходные условия:

а = 30 mm (диаметр – 60мм),

b = 50 mm (диаметр – 100мм),

c = 1200 mm, радиус проволоки (медь), создающей электрической катушку 0,1мм (диаметр – 0,2мм),

напряжение приложенное к магнитному сердечнику,

внутренний цилиндр заряжен положительно, а внешний цилиндр — отрицательно. И два близко расположенных вывода от катушки. При условии, что двойные катушки этой отрицательной катушки индуктивности имеют потенциал 500 В, электродвижущая сила противоположной самоиндукции — 15 В, в начальный момент времени.

  Направление электродвижущей силы противоположной самоиндукции в увеличивающемся токе равно направлению начального приложенного напряжения. Соответственно, в выше приведенном случае, при начальном напряжении 500 В, полное напряжение немедленно достигает 515 В. При этом, наводятся намного большие токи и электродвижущие силы в направлении, способствующем увеличению тока. С такой бесконечной индукцией, ток может легко достигать предельного физического значения в короткое время. И когда ток вызван уменьшением управляющего напряжения, наведенная электродвижущая сила в направлении, которое способствует уменьшению тока, после того, как ток достигает нуля немедленно, он начинает быстро увеличиваться в противоположном направлении.

  Отрицательная индуктивность отрицательной катушки индуктивности пропорциональна произведению скорости изменения относительных магнитных потоков, проникающих в катушку и числу витков катушки, подобно основной катушке индуктивности. При повышении напряжения, приложенного к магнитному сердечнику, общее число относительных магнитных потоков, проникающих в двойные катушки, может увеличиться.

В действующей схеме, с отрицательной катушкой индуктивности, необходимо минимизировать магнитные поля, чтобы полностью сохранить отрицательной индуктивность схемы.

Отрицательная катушка индуктивности хранит отрицательную энергию в пространстве, где проявляется относительное магнитное поле, и как противодействие, катушка индуктивности производит положительную энергию как электроэнергию. Свободные электроны, которые получили кинетическую энергию от пространства — как ускорение, возвращают кинетическую энергию пространству — как замедление. В нормальном проводнике, свободные электроны теряют кинетическую энергию, сталкиваясь с атомами. В этом случае, атомы, увеличивают энергию вибраций от столкновения со свободными электронами (повышают температуру). В электрическом проводе отрицательной катушки индуктивности, кинетическая энергия электронов входит и из пространства, так, чтобы электроны слабо влияли на атомы. По этой причине, свободные электроны работают на уменьшение тепловых колебаний атомов. То есть отрицательная катушка индуктивности, приведенная в действие, становится прохладной. То же самое явление происходит в отрицательном проводнике. Хотя свободные электроны в проводнике делают движения в случайном направлении при сталкивании с атомами, эти свободные электроны влияют на скорости друг друга так, что ток не проявляется макроскопически. Эта ситуация равна той, в которой эти два тока одинаковой величины в различных направлениях текут в неиндуктивных двойных катушках. При условии, что проводник заряжен отрицательно, каждый свободный электрон, имеющий тепловое движение может приносить противоположную самоиндукцию при ускорении или замедлении. Соответственно, проводник с отрицательным зарядом охлаждается, и поле отрицательной энергии появляется в пространстве. Таким образом, проводник, который стал отрицательно заряжен, может рассматриваться как работающий отрицательный проводник.

Наша перспективная задача состоят в том, чтобы развить вечный двигатель, используя отрицательную катушку индуктивности и изучить эффект антигравитации, созданный отрицательной катушкой индуктивности.

Диаг_07.gif

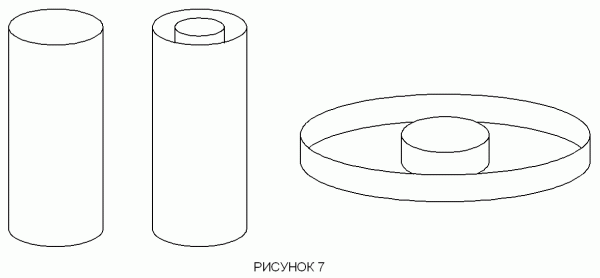
ДИАГРАММА 7 Отдельный цилиндр, заряженный отрицательно.

Коаксиальные цилиндры: внутренний цилиндр заражен положительно, а внешний цилиндр — отрицательно.

Образец магнитного сердечника, используемого в отрицательной катушке индуктивности, соленоидального типа. Двойные катушки наматывают вокруг цилиндра заряженного отрицательно.

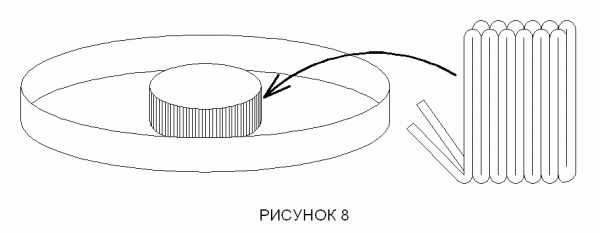
Диаг_08.gif

ДИАГРАММА 8

Магнитный сердечник, используемый в отрицательной катушке индуктивности, тороидального типа. Внутренний цилиндр заряжен в отрицательно, а внешний цилиндр заряжен положительно. Неиндуктивный электрический провод размещен на поверхности внутреннего цилиндра по окружности в направлении его оси. Неиндуктивный электрический провод не помещен на внешнем цилиндре. Для свободных электронов, текущих в направлении оси цилиндра, заряженные двойные цилиндры равны тороидальной катушке.

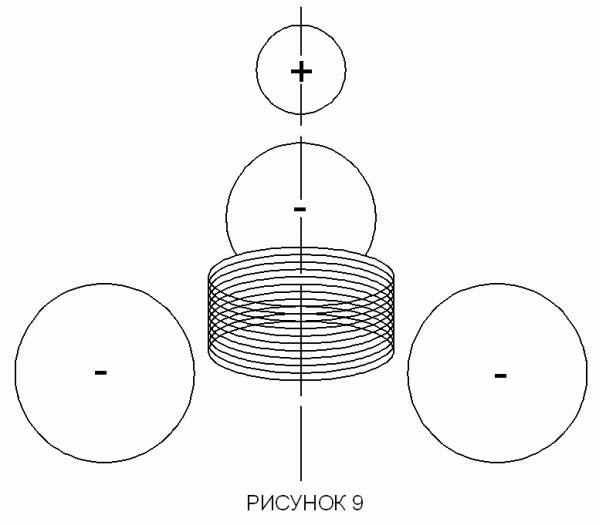
Диаг_09.gif

ДИАГРАММА 9

Установка с металлическими шарами, которые заряжены отрицательно, симметрично вокруг оси бифилярных катушек (неиндуктивная катушка). Установка другого меньшего металлического шара, который заряжен положительно, на оси, отдельно от катушки. Поскольку неиндуктивная катушка не производит магнитное поле, в точке зрения свободных электронов, текущих в намотанном проводе в круговом движении, есть только магнитное поле, вызванное заряженными шарами. Это относительное магнитное поле проникает в катушку, и стимулирует появление противоположной самоиндукции.

reactor.jpg

Самовозбуждаемый генератор

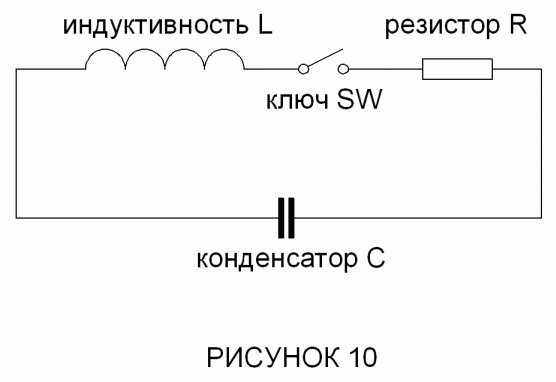
Диаг_010.gif

Популярная RLC схема для генерации электрических колебаний.

В этой схеме, переключатель подключает катушку к заряженному конденсатору, когда осциллирующий ток равен:

Начальные условия:

E — основа естественного логарифма, e = 2.7182

d- постоянная затухания, d = R/2L (постоянный и независимый от времени)

Ток с затухающим колебанием, показанным в ДИАГРАММА 11

ДИАГРАММА 11 затухающее колебание

 Когда сопротивление R = 0, постоянная затухания d = 0. В этой ситуации, ток становится незатухающим колебанием, показанным в ДИАГРАММА 12

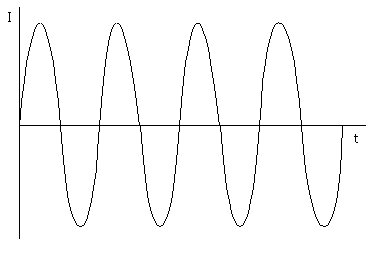
ДИАГРАММА 12 незатухающее колебание

Когда, в RLC схеме, созданы условия, что индуктивность L отрицательна, какой тогда потечет ток? Интересно, если d — отрицательная величина, то нарастающие колебания, показанные в ДИАГРАММА 13 происходят при удовлетворяющим колебания условии. В это время, согласно уравнению 1, т.к. величина синусоидального сигнала отрицательна, величина тока, становится мнимым числом. Другими словами, движения свободных электронов следуют за мнимым временем.

ДИАГРАММА 13 возрастающее колебание

Если это мнимый ток I(A) текущий в схеме в течение t секунд в режиме реального времени, которая имеет сопротивление R, величина работы H (J) производимой от схемы должна быть отрицательна согласно закону Джоуля.

В RLC схеме, где полная индуктивность отрицательна из-за отрицательной катушки индуктивности, мнимый ток увеличивает колебания. Из-за этого мнимого тока, схема остывает.

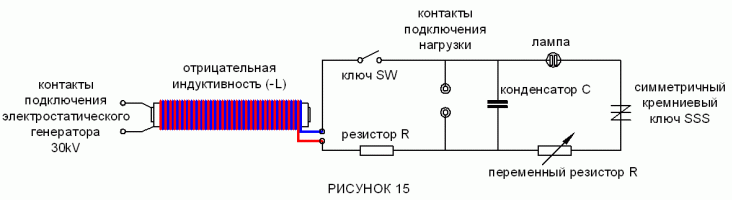
 Диаг_015.gif

ДИАГРАММА 15 — экспериментальная схема, для производства электроэнергии. Использование симметрического кремниевого выключателя (SSS), чье пробивное напряжение — приблизительно 60 V, защищает схему от высокого напряжения, электрическим пробоем с КЗ, и обеспечивает устойчивый выход.

Фактическая экспериментальная установка, упомянута в ДИАГРАММА 16.

genesis.gif

ДИАГРАММА 16 — САМОВОЗБУЖДЕННЫЙ ГЕНЕРАТОР

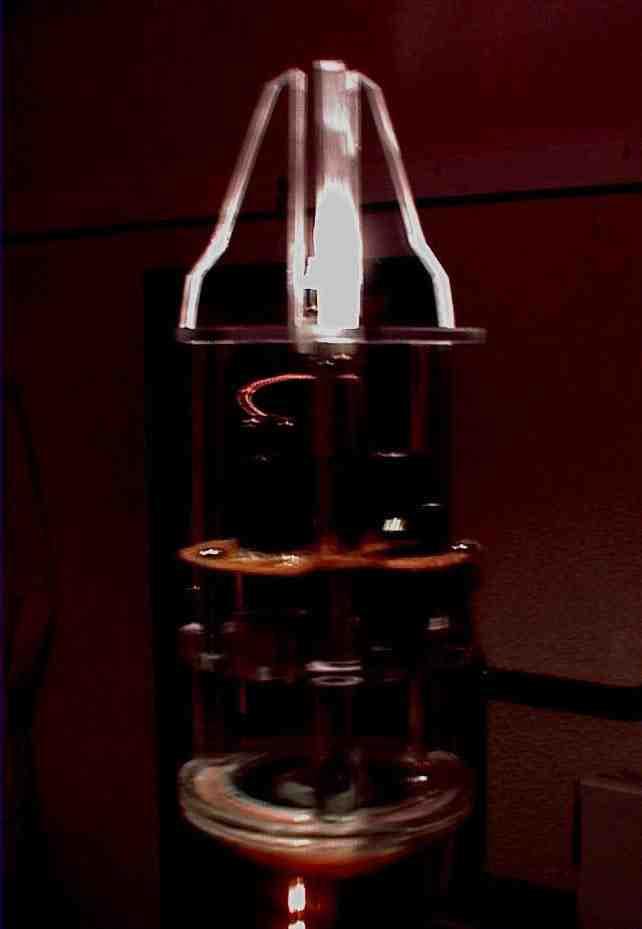
gene1.jpg

gene2.jpg

 ЗАКЛЮЧЕНИЕ

  Явление самоиндукции при ускорении электрического заряда — относительное явление, проявляющееся при относительном ускорении между двумя электрическими зарядами. Когда относительное ускорение существует между одинаковыми видами электрических зарядов, отрицательная энергия может быть запасена в относительном магнитном поле. На этом явлении может быть построена отрицательная катушка индуктивности. Сделать отрицательную катушку индуктивности легко, зарядив внутреннюю часть (подложку) неиндуктивной катушки отрицательно.

Эта информация свободна. Это не может использоваться для патента, торговой марки или никакой собственности вообще. Пожалуйста, распределите без изменения настолько широко насколько возможно.

Оригинал статьи «Отрицательная индуктивность» http://www.geocities.com/nayado/ Сайт FM   http://www.hamen.nm.ru/

Проект происхождение (отрицательная индуктивность)

Эта информация свободна. Это не может использоваться для патента, торговой марки или никакой собственности вообще. Пожалуйста, распространяйте без изменения настолько широко, насколько возможно. Выпущено в марте 1999

Введение

История человечества сделала шаг в сторону непрерывного разрушения. Наука всегда приносит более мощное разрушение. Причина в том, что мир неуклонно развивается в соответствии с физическими законами.

Существующая физика говорит, что разрушение происходит в том же направлении как и поток времени. Чтобы предотвратить разрушение радикально, мы должны найти новый физический поток времени созидания. Другими словами, производить энергию из ничего, как вечный двигатель, описанный в научной фантастике.

Фактически, ничто не может быть произведено из ничего. Термодинамика убедительно доказывает это. Наука говорит, что вечный двигатель не может существовать, это является основой общего представления, есть только положительная энергия.

  Недавно, некоторые физики- теоретики начали рассматривать концепцию мнимого времени и/или отрицательной энергии. Если отрицательная энергия может существовать реально, концепция энергии в физике должна быть изменена и расширена в отрицательной области. И тогда, следует, что вечный двигатель существует. Если вечный двигатель существует, человечество, впервые, может защититься от гибели.

  Таким образом, чтобы заменить разрушение на созидание, прежде всего, должен быть ясен механизм производства отрицательной энергии. Это — цель проекта Происхождения.

 Новая идея, связанная главным образом с электромагнетизмом представлена здесь. Изучая процессы электромагнитных явлений, встречающихся с мнимым временем, дает намек на конкретные шаги по выделению и генерации положительной / отрицательной энергии из ничего.

  Никакой непротиворечивой теории не появится, пока и нет никакого исследования по подтверждению существования вечного двигателя. Понятно что, вечный двигатель до сегодняшнего момента, не существовал.

  Проект Происхождение позволит современности наслаждаться бесконечной энергией и материалами, подойдите к новой эпохе. В этот день, наш старый взгляд на мир рухнет.

Посылая электрический ток в неиндуктивную катушку, находящуюся в отрицательном электрическом поле, можно вызвать явление противоположной самоиндукции. В настоящее время, положительная и отрицательная энергия близка к нулю. Положительная энергия появляется как электроэнергия, и отрицательная энергия появляется как эффект охлаждения и антигравитации.

Поле отрицательной энергии

Свободный электрон это электрон, который оторван от ядра из-за слабой связи с ним. Атом электрически нейтрален, но при потери электрона (отрицательного электрического заряда), атом превращается в положительно заряженный ион.

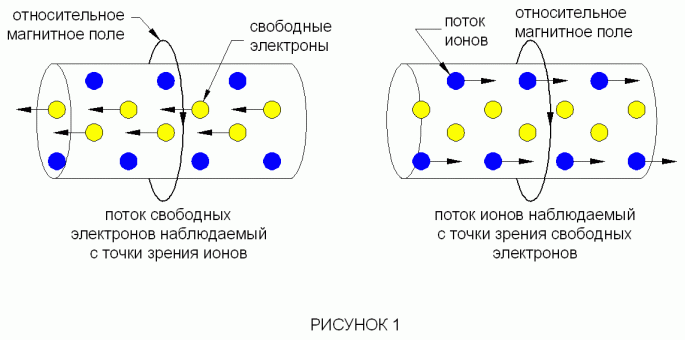
  Ток проводимости это относительный поток из свободных электронов и ионов. Так что электрический ток с точки зрения свободных электронов это поток ионов. Напротив, с точки зрения ионов, ток это — поток свободных электронов. Эти два тока текут в противоположном направлении, но равны и имеют обратную полярность. То есть ток в оба направления равен. Поэтому, магнитное поле, наблюдаемое свободными электронами, равняется тому, что наблюдают ионы.

  Диаг_01.gif

 ДИАГРАММА 1 ток проводимости

Происходит замена тока проводимости, при этом относительная величина потока неизменна, а поток свободных электронов и заменяется потоком ионов. Изменение магнитного поля, вызванного изменением количества потока ионов, наблюдаемых с точки зрения свободных электронов равно изменению магнитного поля, вызванного изменением потока свободных электронов, с точки зрения ионов. Так что индуцированное электрическое поле изменяет магнитное поле, наблюдаемое с точки зрения свободных электронов может наблюдаться в том же самом направлении, как индуцированное электрическое поле изменением магнитного поля, наблюдаемого с точки зрения ионов. Электрические поля, которые имеют то же самое направление, наблюдаемое с каждой точи зрения электронов и ионов, проявляют силы в противоположных направлениях к свободным электронам и ионам, и предотвращают относительное изменение количество потока между свободными электронами и ионами.

  Вышеупомянутое — новая интерпретация, основанная на общем принципе относительности тока проводимости, магнитном поле и наведенном электрическом поле. Из этой интерпретации предполагается следующий основной принцип: созданный электрический / магнитный заряд, если он не связан с другим электрическим / магнитным зарядом, не может электромагнитно существовать и его движение не может быть признано, Мы называем этот фоновым принципом электромагнитного заряда. Поэтому, самоиндукция может рассматриваться, как относительное явление между электрическими зарядами. Наведенное электрическое поле не возникает от отдельно ускоряющегося электрического заряда. Только, когда электрический заряд ускоряется по сравнению с другим зарядом, появляется наведенное электрическое поле. Для сравнения: инерционное гравитационное поле, появляющееся в ускоряющейся массе вызвано другой массой, существующей на заднем (фоновом) плане: Вселенная, которая может рассматриваться как фоновая масса.

  Из фонового принципа электромагнитного заряда следует, что энергия, запасенная в относительном магнитном поле между положительными и отрицательными электрическими зарядами и вызванная их отношением, является эффектом самоиндукции. Когда происходит самоиндукция, созданная работа положительна, при условии, что ток и наведенное электрическое поле находятся в противоположных направлениях. Если они оба находятся в одном направлении, наоборот, работа положительна к току. В первом случае, относительное количество потока между различными видами электрических зарядов увеличилось бы, а во втором — уменьшится. В конце концов, энергия, запасенная в относительном магнитном поле между положительным и отрицательным электрическими зарядами положительна. Нормальный ток проводимости равен этому.

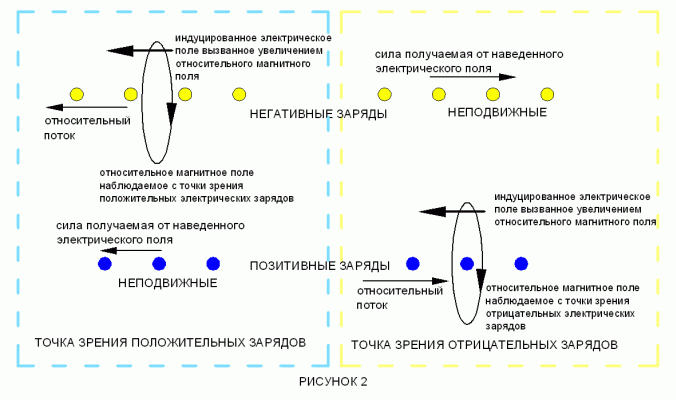
Диаг_02.gif

 ДИАГРАММА 2 явление самоиндукции, появляющееся относительно между положительным зарядом и ускоряющимся отрицательным зарядом.

Это следует от фонового принципа электромагнитного заряда, что энергия, запасенная в относительном магнитном поле между одинаковыми видами электрических зарядов, вызвана явлением их относительной самоиндукции. Когда относительная величина потока между одинаковыми электрическими зарядами изменяется, величина каждого из этих электрических зарядов зависит от наведенного электрического поля, из отношения величин потоков, в направлении в котором происходит ускорение зарядов. Направление, противоположное нормальной самоиндукции, мы называем противоположной самоиндукцией. Когда относительная величина потока между одинаковыми видами электрических зарядов увеличивается, значение работы положительно к относительной величине потока между электрическими зарядами. Напротив, когда она уменьшается, относительная величина потока между электрическими зарядами — значение работы положительно. Энергия, запасенная в относительном магнитном поле между одинаковыми электрическими зарядами отрицательна.

Диаг_03а.gif

ДИАГРАММА 3-a явление противоположной самоиндукции, появляющееся между одинаковыми видами относительно ускоряющихся зарядов

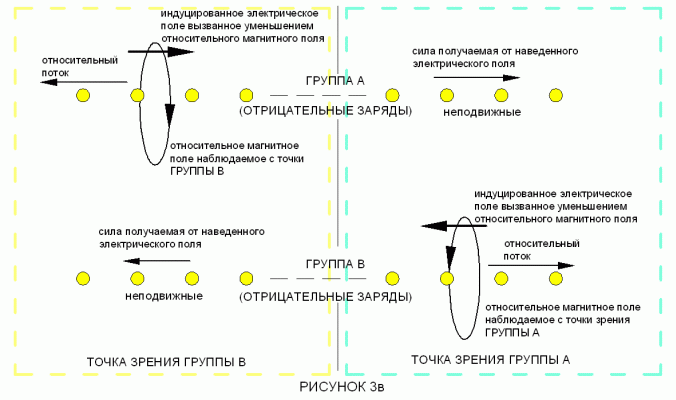
Диаг_03в.gif

 ДИАГРАММА 3-b явление противоположной самоиндукции, появляющееся между одинаковыми видами относительно замедляющихся зарядов

Отрицательная энергия — энергия или вопрос, который следует за мнимым временем.

Из уравнения Дирака, энергия частицы (электрона) может быть положительна или отрицательна.

Отрицательная энергия исключена из физических понятий, поскольку это — не реально. Но верно ли это? Давайте искать условия, с признаками отрицательности среди некоторых популярных уравнений.

Чтобы найти признаки отрицательности, ясно, что время должно быть мнимый числом, а пространство должно быть реальный числом.

Тогда, при условии, что объект принадлежит мнимому времени и реальному пространству, как это проявляется к внешней силе? Судя по уравнению движения, объект будет ускоряться в направлении противоположном к полученной силе. Например, когда предмет притягивается вниз, это ускоряет его вверх.

Между прочим, рассматривая явление противоположной самоиндукции особенно, в условии, когда электрический заряд неподвижной системы наблюдает заряд кинетической системы, ясно, что направление виртуальной силы, которую появившееся наведенное электрическое поле неподвижной системы должно дать этой кинетической системе, обратно направлению силы (направлению ускорения заряда) который получает заряд фактически из кинетической системы .

Катушка индуктивности | Виды катушек, практические опыты

Что такое катушка индуктивности

Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.

Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!

Индуктивность

Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.

Что такое индуктивность?  Если через  провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:

где

В – магнитное поле, Вб

I – сила тока, А

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение

И у нас получится вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с  Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:

С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.

Самоиндукция

Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.

Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:

где

I – сила тока в катушке , А 

U – напряжение в катушке, В 

 R – сопротивление катушки, Ом

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.

И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.

То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть  в разы больше, чем было до размыкания  цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.

Типы катушек индуктивности

Катушки индуктивности делятся в основном на два класса: с магнитным и  немагнитным сердечником. Снизу  на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух – это немагнитный сердечник :-).  Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным  сердечником используется, когда индуктивность не превышает 5 миллигенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.

Дроссели

Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.

Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Опыты с катушкой

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов.  Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

LC-метр  показывает 21 микрогенри.

Ввожу катушку на середину феррита

35 микрогенри. Уже лучше.

Продолжаю вводить катушку на правый край феррита

20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине.  Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности  в переменных катушках индуктивности:

где

1 – это каркас катушки

2 – это витки катушки

3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.

Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки

Индуктивность стала почти 50 микрогенри!

А давайте-ка попробуем расправим витки по всему ферриту

13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.

Убавим витки катушки в два раза. Было 24 витка, стало 12.

Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз.  Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.

Давайте поэкспериментируем с ферритовым кольцом.

Замеряем индуктивность

15 микрогенри

Отдалим витки катушки друг от друга

Замеряем снова

Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка  не играет никакой роли в катушке индуктивности тороидального исполнения.

Мотнем побольше витков. Было 3 витка, стало 9.

Замеряем

Офигеть! Увеличил количество витков  в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.

Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.

Обозначение на схемах

Последовательное и параллельное соединение катушек

При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.

А при параллельном соединении получаем вот так:

При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек.  Это может привести к неправильным показаниям общей индуктивности.

Резюме

Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.

Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:

Беспроводная передача энергии через магнитно-связанные индуктивные катушки / Habr

Введение

Думаю, что многие из читателей видели хотя бы один ролик на популярных видеосервисах, где электричество передается через пустое пространство при помощи индуктивных катушек.

В этой статье мы хотим обратиться к первоосновам процесса беспроводной передачи энергии с помощью магнитного поля. Начав с рассмотрения простейшей индуктивной катушки, и вычисления ее индуктивности, мы постепенно перейдем к теории электрических цепей, в рамках которой, будет показан и обоснован способ передачи максимальной мощности при прочих равных условиях. Итак, начнем.

Магнитное поле одиночного витка с током

Рассмотрим магнитное поле одиночного витка с током. Найдем магнитное поле витка в любой точке пространства. Почему необходимо подобное рассмотрение? Потому что почти во всех книгах, по крайней мере в тех, которые удалось отыскать автору статьи, решение данной задачи ограничивается нахождением лишь одной компоненты магнитного поля и лишь вдоль оси витка — $inline$B_z(z)$inline$, в то время как мы отыщем закон для магнитного поля во всем пространстве.

Иллюстрация к закону Био-Савара-Лапласа

Для нахождения магнитного поля, воспользуемся законом Био-Савара-Лапласа (смотри Википедия — Закон Био-Савара-Лапласа). На рисунке видно, что центр системы координат $inline$O$inline$ совпадает с центром витка. Контур окружности витка обозначен как $inline$C$inline$, а радиус окружности — как $inline$a$inline$.По витку течет ток $inline$I$inline$. $inline$\vec{r}$inline$ — это переменная-радиус-вектор из начала координат в произвольную точку витка. $inline$\vec{r}_0$inline$ — это радиус-вектор в точку наблюдения. Еще нам понадобится полярный угол $inline$\varphi$inline$ — угол между радиус-вектором $inline$\vec{r}$inline$ и осью $inline$OX$inline$. Расстояние от оси витка до точки наблюдения обозначим за $inline$\rho$inline$. И наконец, $inline$\mathrm{d}\vec{r}$inline$ — элементарное приращение радиус-вектора $inline$\vec{r}$inline$.

Согласно закону Био-Савара-Лапласа, элемент контура с током $inline$\mathrm{d}\vec{r}$inline$ создает элементарный вклад в магнитное поле, который дается формулой

$$display$$\mathrm{d}\vec{B}(\vec{r}_0)=\frac{\mu_0 I}{4\pi} \cdot \frac{[\,\mathrm{d}\vec{r} \times (\vec{r}_0-\vec{r})]}{|\vec{r}_0-\vec{r}|^3}$$display$$

Теперь остановимся подробнее на переменных и выражениях, входящих в формулу. С учетом аксиальной симметрии задачи можем записать

$$display$$\vec{r}_0 = (\rho\cos{\varphi}, \rho\sin{\varphi}, z) \overset{\varphi = 0}{\rightarrow} (\rho, 0, z)$$display$$

$$display$$\vec{r} = (a\cos{\varphi}, a\sin{\varphi}, 0)$$display$$

$$display$$\mathrm{d}\vec{r} = (-a\sin{\varphi}, a\cos{\varphi}, 0)\,\mathrm{d}\varphi$$display$$

$$display$$\vec{r}_0-\vec{r} = (\rho -a\cos{\varphi}, -a\sin{\varphi}, z)$$display$$

$$display$$[\mathrm{d}\vec{r} \times (\vec{r}_0-\vec{r})] = \begin{vmatrix} \vec{e}_x& \vec{e}_y& \vec{e}_z\\ -a\sin{\varphi}\,\mathrm{d}\varphi& a\cos{\varphi}\,\mathrm{d}\varphi& 0\\ \rho -a\cos{\varphi}& -a\sin{\varphi}& z \end{vmatrix} = (az\cos{\varphi}, az\sin{\varphi}, a^2 -a\rho\cos{\varphi})\,\mathrm{d}\varphi$$display$$

$$display$$|\vec{r}_0-\vec{r}|^3 = \left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}$$display$$

Для того чтобы найти результирующее магнитное поле, нужно проинтегрировать по всему контуру витка, то есть

$$display$$\vec{B}(\vec{r}_0) = \int_C{\,\mathrm{d}\vec{B}(\vec{r}_0)}$$display$$

После подстановки всех выражений и некоторых тождественных преобразований получаем выражения для аксиальной и радиальной компоненты магнитного поля соответственно

$$display$$B_z(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{\left( a^2 -\rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$

$$display$$B_r(\rho, z) = \frac{\mu_0 I}{4\pi} \int_0^{2\pi}{\frac{a\,z\,\cos{\varphi}\,\mathrm{d}\varphi} {\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}$$display$$

Для нахождения абсолютного значения магнитного поля необходимо просуммировать компоненты по теореме Пифагора $inline$B = \sqrt{B_r^2 + B_z^2}$inline$.

Продемонстрируем полученное решение на примере витка радиуса $inline$a = 0.1$inline$ (м) и $inline$I=1$inline$ (А).

Амплитуда аксиальной компоненты магнитного поля

Амплитуда радиальной компоненты магнитного поля

Абсолютная амплитуда магнитного поля

Заметим, что для витка произвольной формы, на больших расстояниях $inline$z\gg a$inline$, т.е. много больше характерного размера витка, поведение магнитного поля будет стремиться к найденному решению.

Подсказка…

Для подобных вычислений и построения графиков удобно использовать MathCad 15

Катушка индуктивности. Магнитно-связанные катушки

Теперь, когда мы знаем решение для магнитного поля одного витка, можем найти индуктивность катушки, состоящей из $inline$n$inline$ витков. По определению индуктивность — это коэффициент пропорциональности между током в витке и магнитным потоком через площадь сечения витка. Мы пользуемся здесь идеальной моделью катушки, которая безразмерна по направлению своей оси симметрии. Конечно же, на практике такого не бывает. Однако, как приближенные, полученные формулы будут достаточно хороши. Хотя катушки и считаются безразмерными вдоль $inline$OZ$inline$, необходимо задаться ненулевым радиусом сечения провода. Обозначим его $inline$\delta$inline$, и пример равным $inline$\delta=0,1$inline$ (мм). Иначе при интегрировании магнитного потока подынтегральное выражение обратится в бесконечность.

Индуктивно связанные катушки

На рисунке изображены две магнитно связанные катушки. Пусть первая катушка имеет радиус $inline$a_1$inline$ и содержит $inline$n_1$inline$ витков, а вторая — $inline$a_2$inline$ и $inline$n_2$inline$ соответственно. Тогда для нахождения собственных индуктивностей необходимо вычислить магнитный поток каждой катушки через свое собственное сечение.

$$display$$\Phi = \iint_S{\vec{B}\cdot\vec{\,\mathrm{d}S}} = \int_0^{2\pi}{\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi}} = 2\pi\int_0^{a-\delta}{B_z(\rho,z)\rho\,\mathrm{d}\rho}$$display$$

Поскольку в катушке много витков, найдем величину, называемую потокосцепление, дважды умножив на количество витков

$$display$$\Psi = \frac{1}{2}n^2\mu_0 I \int_0^{a-\delta}{\int_0^{2\pi}{\frac{\left( a^2 — \rho a\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a^2 + z^2 -2\rho a\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

По определению, индуктивность это коэффициент пропорциональности $inline$L$inline$ в формуле $inline$\Psi = LI$inline$. Таким образом, получим собственные индуктивности катушек

$$display$$L_1 = \frac{1}{2}n_1^2\mu_0 \int_0^{a_1-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

$$display$$L_2 = \frac{1}{2}n_2^2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_2^2 — \rho a_2\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_2^2 -2\rho a_2\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

Пусть центры катушек разделены расстоянием $inline$d$inline$, лежат на одной оси, и их плоскости витков сориентированы параллельно. Для нахождения взаимной индуктивности, нужно вычислить потокосцепление, образуемое одной катушкой через сечение другой, то есть

$$display$$\Psi_{12} = \frac{1}{2}n_1 n_2\mu_0 I \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + z^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

Тогда взаимная индуктивность катушек дается выражением

$$display$$M_{12} = \frac{1}{2}n_1 n_2\mu_0 \int_0^{a_2-\delta}{\int_0^{2\pi}{\frac{\left( a_1^2 — \rho a_1\cos{\varphi}\right)\,\mathrm{d}\varphi}{\left(\rho^2 + a_1^2 + d^2 -2\rho a_1\cos{\varphi}\right)^{\frac{3}{2}}}}\rho\,\mathrm{d}\rho}$$display$$

Насколько известно автору, такие интегралы можно взять только численно.
Заметим, что как правило $inline$\Psi_{12} = \Psi_{21}$inline$ и $inline$M_{12} = M_{21} = M$inline$. Коэффициентом связи катушек называется величина

$$display$$k = \frac{M}{\sqrt{L_1L_2}}$$display$$

Исследуем зависимость коэффициента связи катушек от расстояния. Для этого рассмотрим две одинаковые катушки с радиусом витков $inline$a_1 = a_2 = 0.1$inline$ (м) и количеством витков $inline$n_1 = n_2 = 100$inline$. При этом собственная индуктивность каждой из катушек составит $inline$L_1 = L_2 = 8.775$inline$ (мГн).

Коэффициент связи катушек от расстояния между ними

График не изменится, если одинаково изменить число витков в обеих катушках, либо одинаково изменить радиус обеих катушек. Коэффициент связи удобно выражать в процентах. Из графика видно, что даже при расстоянии между катушками в 1 (мм) коэффицент связи меньше 100%. Коэффициент падает до 10% на расстоянии порядка 60 (мм), и до 1% на 250 (мм).

Беспроводная передача энергии

Итак, нам известны индуктивности и коэффициент связи. Теперь воспользуемся теорией электрических цепей переменного тока для поиска оптимальных параметров, при которых передаваемая мощность оказалась бы максимальной. Для понимания этого параграфа читатель должен быть знаком с понятием электрического импеданса, а также с законами Кирхгофа и законом Ома. Как известно из теории цепей, две индуктивно-связанные катушки образуют воздушный трансформатор. Для анализа трансформаторов удобна Т-образная схема замещения.

Воздушный трансформатор и его эквивалентная схема

Передающую катушку слева будем условно называть «трасмиттер», а принимающую катушку справа — «ресивер». Между катушками коэффициент связи $inline$k$inline$. На стороне ресивера находится потребитель, представленный нагрузкой $inline$z_L$inline$. Нагрузка в общем случае может быть комплексной. Входное напряжение на стороне трансмиттера $inline$u_1$inline$, а входной ток — $inline$i_1$inline$. Напряжение, передаваемое на ресивер — $inline$u_2$inline$, и передаваемый ток $inline$i_2$inline$. Полный импеданс на стороне трансмиттера обозначим как $inline$z_1$inline$, а полный импеданс на стороне ресивера $inline$z_2$inline$.

Предполагается, что на вход схемы подается синусоидальное напряжение $inline$u_1 = u_{1m}\sin{\omega t}$inline$.

Обозначим $inline$R_{coil\,1}, R_{coil\,2}, L_{coil\,1}, L_{coil\,2}, M$inline$ — сопротивления и индуктивности катушек (две собственные и одна взаимная) соответственно. Тогда, согласно теории трансформатора

$$display$$z_1 = R_{coil\,1} + j\omega (L_{coil\,1} — M)$$display$$

$$display$$z_2 = R_{coil\,2} + j\omega(L_{coil\,2} — M) + R_{load} + j X_{load}$$display$$

С другой стороны, согласно нашим обозначениям

$$display$$z_1 = r_1 + j x_1$$display$$

$$display$$z_2 = r_2 + j x_2$$display$$

где $inline$r_1, r_2$inline$ — полные активные сопротивления на стороне трансмиттера и ресивера соответственно, и $inline$x_1, x_2$inline$ — полные реактивные сопротивления.

Импеданс связи равен $inline$z_3 = j \omega M = j x_3$inline$.

Найдем входной ток цепи

$$display$$i_1 = \frac{u_1}{z_1 + z_2 || z_3}$$display$$

где знак $inline$||$inline$ обозначает параллельное соединение сопротивлений. Тогда напряжение, переданное на ресивер

$$display$$u_2 = u_1 — i_1 z_1 = u_1\left(1 — \frac{z_1}{z_1 + z_2 || z_3}\right)$$display$$

И наведенный ток

$$display$$i_2 = \frac{u_2}{z_2} = \frac{u_1}{z_2}\left(1 — \frac{z_1}{z_1 + z_2 || z_3}\right)$$display$$

Можем найти комплексную мощность, переданную в ресивер

$$display$$s_2 = u_2 i_2^* = p_2 + jq_2$$display$$

Таким образом имеем выражение для комплексной мощности

$$display$$s_2 = |u_1|^2 z_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$

Выражение для активной компоненты мощности

$$display$$p_2 = |u_1|^2 r_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$

Выражение для реактивной компоненты мощности

$$display$$q_2 = |u_1|^2 x_2 \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2$$display$$

В большинстве практических задач требуется передать максимальную активную мощность, поэтому

$$display$$p_2 \rightarrow \mathrm{max} \Rightarrow \left|\frac{z_3}{z_1z_2+z_1z_3+z_2z_3}\right|^2 \rightarrow \mathrm{max}$$display$$

Либо, что то же самое

$$display$$\left|z_1 + z_2 + \frac{z_1z_2}{z_3}\right|^2 \rightarrow \mathrm{min}$$display$$

$$display$$\left|r_1 + jx_1 + r_2 + jx_2 +\frac{(r_1 + jx_1)( r_2 + jx_2)}{jx_3}\right|^2 \rightarrow \mathrm{min}$$display$$

$$display$$\frac{1}{x_3^2}|(r_1x_3 + r_2x_3 + r_1x_2 + r_2x_1) + j(x_1x_3 + x_2x_3 + x_1x_2 — r_1r_2)|^2 \rightarrow \mathrm{min}$$display$$

Для удобства введем функцию

$$display$$f(x_1,x_2) = (r_1x_3 + r_2x_3 + r_1x_2 + r_2x_1) + j(x_1x_3 + x_2x_3 + x_1x_2 — r_1r_2)$$display$$

и исследуем ее на наличие экстремумов

$$display$$|f(x_1,x_2)|^2 \rightarrow \mathrm{min}$$display$$

Откуда получаем систему из двух уравнений

$$display$$\frac{\partial|f|^2}{\partial x_1} = 2\mathbb{Re}(f)r_2 + 2\mathbb{Im}(f)(x_2 + x_3) = 0$$display$$

$$display$$\frac{\partial|f|^2}{\partial x_2} = 2\mathbb{Re}(f)r_1 + 2\mathbb{Im}(f)(x_1 + x_3) = 0$$display$$

Эта система имеет пять решений, два из которых нефизичны, так как приводят к мнимым значениям величин, которым полагается быть действительными. Три других физических решения приведены ниже вместе с соответствующими формулами для мощности
Решение 1

$$display$$x_1 = -x_3,\quad x_2 = -x_3$$display$$

Мощность

$$display$$p_2 = \frac{|u_1|^2\,x_3^2\,r_2}{\left(r_1r_2 + x_3^2\right)^2}, \quad q_2 = -\frac{|u_1|^2\,x_3^3}{\left(r_1r_2 + x_3^2\right)^2}$$display$$

Решение 2 и 3

$$display$$x_1 = \frac{1}{r_2}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}-r_2x_3\right), \quad x_2 = \frac{1}{r_1}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}-r_1x_3\right)$$display$$

$$display$$x_1 = -\frac{1}{r_2}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}+r_2x_3\right), \quad x_2 = -\frac{1}{r_1}\left(\sqrt{r_1r_2\left(x_3^2-r_1r_2\right)}+r_1x_3\right)$$display$$

Мощность для решений 2 и 3

$$display$$p_2 = \frac{|u_1|^2}{4\,r_1}, \quad q_2 = \frac{|u_1|^2\,x_2}{4\,r_1\,r_2}$$display$$

Решение 2 и 3 нужно использовать, когда реактивное сопротивление связи достаточно велико

$$display$$x_3^2 > r_1r_2$$display$$

Когда же это не так, нужно использовать решение 1. Чаще всего в реальных ситуациях $inline$x_3$inline$ окажется мало, поэтому рассмотрим решение 1 несколько подробнее.
Решение 1: $inline$x_1 = -x_3,\quad x_2 = -x_3$inline$. И соответствующая ему активная мощность дается формулой

$$display$$p_2 = \frac{|u_1|^2\,x_3^2\,r_2}{\left(r_1r_2 + x_3^2\right)^2}$$display$$

Из формулы мощности видно, что мощность зависит от реактивного сопротивления связи $inline$x_3 = 2\pi\,f\,k\,\sqrt{L_{coil\,1}L_{coil\,2}}$inline$, а значит и от частоты передачи $inline$f$inline$, и от геометрии взаимного расположения катушек, которая учитывается коэффициентом связи $inline$k$inline$.

Как заметили внимательные читатели, зависимость $inline$p_2(x_3)$inline$ — нелинейная. Функция $inline$p_2(x_3)$inline$ достигает максимума при $inline$x_3 = \sqrt{r_1r_2}$inline$.

Исследование формулы мощности $inline$p_2(x_3)$inline$ на экстремумы

Максимальная активная мощность при $inline$x_3 = \sqrt{r_1r_2}$inline$ равна

$$display$$p_2 = \frac{|u_1|^2}{4\,r_1}$$display$$

Таким образом, вышеозначенная формула представляет абсолютный теоретический предел переданной активной мощности при любых условиях. При этом для реактивной мощности, переданной в ресивер, имеем

$$display$$q_2=\frac{|u_1|^2}{\sqrt{r_1r_2}}$$display$$

Численное моделирование

Продемонстрировать работу всей вышеизложенной теории можно, выполнив симуляцию SPICE модели нашего устройства из двух связанных катушек.

SPICE модель двух индуктивно-связанных катушек

Симуляция выполнена для коэффициента связи $inline$k = 1$inline$%, что соответствует 25 см удаления между катушками. Параметры катушек те же, что и в предыдущем параграфе, принятые для построения графика $inline$k$inline$.

Получается, что реактивные сопротивления каждой из катушек необходимо скомпенсировать конденсаторами $inline$С_1$inline$ и $inline$С_2$inline$. То есть настроить каждый из контуров (передающий и принимающий) в резонанс на заданной частоте. Если предположить, что величина нагрузки действительная, то величины емкостей могут быть найдены из формул

$$display$$C_1 = \frac{1}{\omega^2 L_1}, \quad C_2 = \frac{1}{\omega^2 L_2}$$display$$

Ниже приведены два графика для переданного напряжения и переданной мощности во времени на частоте $inline$f=10$inline$ (кГц).

Переданное напряжение

Переданная мощность

Из рисунков видно, что на расстоянии 25 (см) переданное напряжение оказалось приблизительно в 2.5 меньше входного, а переданная пиковая мощность — приблизительно в 4 раза меньше мощности, потребляемой от входа, что согласуется с полученными формулами.

В заключении опишем, какие меры можно предпринять для увеличения передаваемой мощности:

1. увеличить количество витков в катушках $inline$n_1, n_2$inline$
2. увеличить радиус витков $inline$a_1, a_2$inline$
3. увеличить частоту передачи $inline$f$inline$
4. уменьшить расстояние между катушками $inline$d$inline$
5. ввести магнитный сердечник, принадлежащий обеим катушкам (замкнутый либо открытый)
6. ввести незамкнутый магнитный сердечник, принадлежащий лишь катушке-ресиверу

Пожалуй, написание этой статьи накладывает на автора обязательство изготовить и протестировать такую систему из двух катушек в лабораторных условиях, но это уже совсем другая история. Благодарю за внимание.

Литература

1. Сивухин, Д. В. «Общий курс физики. Т. 3: Электричество и магнетизм.» (1990).
2. Бессонов, Лев Алексеевич. Теоретические основы электротехники. Электромагнитное поле. Общество с ограниченной ответственностью Издательство ЮРАЙТ, 2012.
3. Лаврентьев, М. А., and Б. В. Шабат. «Теория функций комплексной переменной.» (1972).

2. Катушка индуктивности в цепи переменного тока | 3. Реактивное сопр. и импеданс — Индуктивность | Часть2

2. Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.

Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:

 

Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:

 

Простая индуктивная цепь: ток катушки отстает от напряжения на 90^o.

Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:

 

Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90^o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.

 

Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:

 

Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения  и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90^o, бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.

Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.

Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: X_L.

Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:

 

Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:

Частота (Гц)	Реактивное сопротивление (Ом)
60	3.7699
120	7.5398
2500	157.0796

В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360^o. Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360^o. Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.

Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула X_L = 2πfL может быть написана как X_L = ωL.

Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.

При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:

 

 

Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90^o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:

 

 

Ток на катушке индуктивности отстает от напряжения на 90^o.

Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90^o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).

Отрицательная индукция — Большая Энциклопедия Нефти и Газа, статья, страница 1

Отрицательная индукция

Cтраница 1

Отрицательная индукция характеризуется выключением возбуждения другим возбуждением и сопровождающим его активным торможением. Отрицательная индукция проявляется в забывчивости, в непроизвольном переключении внимания.  [1]

Отрицательная индукция характеризуется выключением возбуждения другим возбуждением и сопровождающим его активным торможением.  [2]

Иррадиация и концентрация, положительная и отрицательная индукция процессов обеспечивают взаимосвязь, переход один в другой и непрерывное взаимодействие возбудительных и тормозных процессов. Такое подвижное взаимодействие создает сложный, бесконечно изменяющий свои очертания рисунок ( мозаику) возбуждения и торможения в коре полушарий большого мозга.  [3]

Магнитный насыщающийся элемент, в котором времязадающим параметром является время перемагни-чивания его сердечника от некоторого значения максимальной отрицательной индукции до такой же положительной индукции.  [4]

Улучшение состояния больных и уменьшение силы припадков следует объяснить тем, что необходимый для работы инертный очаг возбуждения по закону отрицательной индукции гасит патологический очаг возбуждения, определяющий возникновение припадка.  [5]

Таким образом, комбинированное управление обеспечивает однозначную управляемость ПМК во всем диапазоне его рабочей характеристики и дает лучшее использование зоны отрицательных индукций сердечника. При этом индукция насыщения может быть повышена до 17 — 18 кгс. Это позволяет более чем в 1 5 раза по сравнению с чисто демпферным управлением снизить габариты дросселей при данной мощности нагрузки и одновременно значительно снизить нагрев силовых транзисторов ( поскольку отсутствует сопротивление смещения), повысив тем самым эксплуатационную надежность схемы.  [7]

Для процесса выработки у человека цепи условных рефлексов из пяти звеньев характерны афферентная генерализация ( максимальное изменение) и торможение второсигнальной си-стем Ъг по принципу одновременной отрицательной индукции. Для формирования системы промежуточного подкрепления ( подцелей) специфична концентрация возбуждения в двигательном анализаторе при одновременной иррадиации возбуждения в области второсигнальной деятельности. Оптимизация пути достижения подкрепления сопровождается дальнейшим прогрессивным укреплением систем временных связей. На первой стадии оптимизации наблюдается элективная иррадиация возбуждения в зрительном и двигательном анализаторах, образование динамического двигательного стереотипа и его последующая автоматизация, сопровождающаяся торможением связей во второй сигнальной системе. На второй стадии оптимизации наблюдается изменение зрительно-двигательного стереотипа ( сокращение звеньев цепи условных рефлексов), растормаживание двигательной активности и иррадиация возбуждения в области второй сигнальной системы.  [8]

Отрицательная индукция характеризуется выключением возбуждения другим возбуждением и сопровождающим его активным торможением. Отрицательная индукция проявляется в забывчивости, в непроизвольном переключении внимания.  [9]

Отрицательная индукция также возникает при чрезмерном увлечении каким-либо предметом изучения, и тогда при работе в другой области мыслительная деятельность затормаживается.  [10]

Однако по мере приближения появления дополнительного сигнала к моменту появления очередного ( следующего) сигнала центрального индикатора время реакции на дополнительный сигнал вновь начинает возрастать. Поэтому вследствие отрицательной индукции возникает торможение тех участков центральной нервной системы, которые включены в функциональную систему реакции на дополнительный сигнал. Это торможение оказывается тем значительнее, чем короче интервал, отделяющий появление дополнительного сигнала от момента, когда должен появиться очередной сигнал центрального индикатора. Вероятно, именно по той причине, что в наших опытах основу реакции на дополнительный и центральный сигнал составляли в какой-то степени самостоятельные функциональные системы, наблюдалось отличие полученных данных от результатов опытов других авторов.  [12]

Таким образом, на основании проведенных серий исследований, можно, очевидно, придти к заключению, что совмещенные действия, связанные, например, с необходимостью одновременного контроля и регулирования ( по показаниям индикаторов) нескольких параметров, осуществляются медленнее и с большим количеством ошибок. Причиной этого является взаимное влияние ( в частности, отрицательная индукция) нервных процессов, протекающих в центральных звеньях функциональных систем, лежащих в основе выполняемых совмещенных реакций. Поэтому в тех случаях, когда сигналы разделяются определенным временным интервалом, создаются более благоприятные условия выполнения реакций. Однако, если одни реакции осуществляются в условиях выработанного двигательного ритмического стереотипа, то реакции на дополнительные сигналы могут тормозиться по мере сближения их ( по времени появления) с моментом предъявления очередного из ритмично следующих сигналов.  [13]

Недавнее событие обычно забывается достаточно быстро, а только что происшедшее или давно свершившееся вспоминается легко. Степень забывания или осознания происшедшего зависит от действия психофизиологического механизма отрицательной индукции, описанное в литературе.  [14]

Таким образом, магнитный элемент через обмотку Wan запоминает полярность импульса, который его перемагничивает до положительной индукции. Сигнал в выходной обмотке & вых, соответствующий 1, появляется при подаче в обмотку считывания сосч импульса тока, создающего отрицательную индукцию — Дв сердечнике.  [15]

Страницы:      1    2

принцип работы, схема, ток и напряжение в нем

В данной статье мы подробно рассмотрим индуктор. Отдельно разберем индуктор на схеме, обратную ЭДС генерируемую индуктором, постоянную времени индуктора, ток и напряжение в индукторе, а так же мощность и энергию в индукторе.

Определение и принцип работы

В наших уроках об электромагнетизме мы увидели, что когда электрический ток протекает через проводник, вокруг проводника возникает магнитный поток. Это создает взаимосвязь между направлением магнитного потока, который циркулирует вокруг проводника, и направлением тока, протекающего через тот же проводник, что приводит к хорошо известной взаимосвязи между током и направлением магнитного потока, называемой «Правило правой руки Флеминга».

Но есть и другое важное свойство, относящееся к намотанной катушке, которая также существует, а именно то, что вторичное напряжение индуцируется в ту же катушку движением магнитного потока, поскольку оно противостоит любым изменениям электрического тока, протекающего по нему.

Типичный индуктор

В своей основной форме Индуктор — это не что иное, как катушка проволоки, намотанная вокруг центрального сердечника. Для большинства катушек ток I, протекающий через катушку, создает магнитный поток NΦ вокруг нее, который пропорционален этому потоку электрического тока.

Индуктор, называемый также дросселем, является еще одним типом пассивного электрического компонента, который является простой катушкой провода предназначенного, чтобы воспользоваться этой взаимосвязью путем индукции магнитного поля, сам по себе, или в активной зоне в результате тока, проходящем через катушки. Это приводит к гораздо более сильному магнитному полю, чем то, которое создавалось бы простой катушкой из проволоки.

Индукторы образованы проволокой, плотно обернутой вокруг сплошного центрального сердечника, который может представлять собой либо прямой цилиндрический стержень, либо непрерывную петлю или кольцо для концентрации их магнитного потока.

Схематическое обозначение индуктора — это катушка с проводом, поэтому катушку с проводом можно также назвать индуктором. Индукторы обычно классифицируются в соответствии с типом внутреннего сердечника, вокруг которого они намотаны, например, полый сердечник, твердый железный сердечник или мягкий ферритовый сердечник, причем различные типы сердечников различаются путем добавления непрерывных или пунктирных параллельных линий рядом с проволочная катушкой, как показано ниже.

Индуктор на схеме

Ток I, который протекает через катушку индуктивности производит магнитный поток, который пропорционален к нему. Но в отличие от конденсатора, который противодействует изменению напряжения на своих пластинах, индуктор противодействует скорости изменения тока, протекающего через него, из-за накопления самоиндуцированной энергии в его магнитном поле.

Другими словами, катушки индуктивности сопротивляются или противостоят изменениям тока, но легко пропустят постоянный ток. Эта способность индуктора противостоять изменениям тока и которая также связывает ток I с его магнитным потоком NΦ как коэффициент пропорциональности, называется индуктивностью, которому присвоен символ L с единицами измерения Генри ( H ).

Поскольку Генри представляет собой относительно большую единицу индуктивности, для младших индукторов Генри используются для обозначения его значения. Например:

Префиксы индуктивности

Префикс	Условное обозначение	мультипликатор	Степень десяти
милли	m	1/1 000	10 -3
микро	μ	1/1000000	10 -6
нано	n	1/1000000000	10 -9

Таким образом, для отображения подразделов Генри мы будем использовать в качестве примера:

• 1mH = 1 милли-Генри   — что равно одной тысячной (1/1000) Генри.
• 100μH = 100 микро-Генри   — что равно одной 100-миллионной ( 1/1 000 000) Генри.

Индукторы или катушки очень распространены в электрических цепях, и существует множество факторов, определяющих индуктивность катушки, таких как форма катушки, число витков изолированного провода, число слоев провода, расстояние между витками, проницаемость материала сердечника, размер или площадь поперечного сечения сердечника и т. д.

Катушка индуктивности имеет площадь поперечного сечения сердечника ( A ) с постоянным числом витков провода на единицу длины ( l ). Таким образом, если катушка N витков связана на величину магнитного потока Φ то катушка имеет потокосцепление NΦ и любой ток I, который протекает через катушку будет производить индуцированный магнитный поток в противоположном направлении по отношению к потоку тока. Затем, согласно закону Фарадея, любое изменение в этой связи магнитного потока производит самоиндуцированное напряжение в одной катушке:

Где:

•    N — число витков
•     А — площадь поперечного сечения в м ²
•    Φ — количество потока в Веберах
•     μ — проницаемость материала сердечника
•     L — длина катушки в метрах
•    di / dt — скорость изменения тока в Амперах в секунду

Изменяющееся во времени магнитное поле индуцирует напряжение, которое пропорционально скорости изменения тока, создающего его, с положительным значением, указывающим на увеличение ЭДС, и отрицательным значением, указывающим на уменьшение ЭДС. Уравнение, связывающее это напряжение, ток и индуктивность с самоиндукцией, может быть найдено путем замены μN ² A / l на L, обозначая постоянную пропорциональности, называемую индуктивностью катушки.

Соотношение между потоком в катушке индуктивности и током, протекающим через катушку индуктивности, имеет вид: NΦ = Li . Поскольку катушка индуктивности состоит из катушки с проводящим проводом, это уменьшает приведенное выше уравнение, чтобы получить самоиндуцированную ЭДС, иногда называемую также обратной ЭДС, индуцированной в катушке.

Обратная ЭДС генерируемая индуктором

Где: 
L — собственная индуктивность, а 
di / dt — скорость изменения тока.

Таким образом, из этого уравнения мы можем сказать, что «самоиндуцированная ЭДС = индуктивность * скорость изменения тока» и цепь с индуктивностью один Генри будет иметь ЭДС 1 вольт, индуцированную в цепи, когда ток, протекающий через цепь, изменяется со скоростью 1 Ампер в секунду.

Катушка индуктивности

Один важный момент, который нужно отметить относительно приведенного выше уравнения. Он только связывает ЭДС, создаваемую через индуктор, с изменениями тока, потому что, если ток индуктора постоянен и не изменяется, например, в постоянном токе, то индуцированное напряжение ЭДС будет равно нулю, поскольку мгновенная скорость изменения тока равна ноль di / dt = 0.

При постоянном токе, протекающем через индуктор и, следовательно, нулевом индуцированном напряжении на нем, индуктор действует как короткое замыкание, равное куску провода, или, по крайней мере, очень низкое значение сопротивления. Другими словами, противодействие протеканию тока, предлагаемого индуктором, очень различно в цепях переменного и постоянного тока.

Постоянная времени индуктора

Теперь мы знаем, что ток не может изменяться мгновенно в индуктивности, потому что для этого ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной di / dt =  ∞ , делая индуцированную ЭДС бесконечной, а бесконечного напряжения не существует. Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.

Рассмотрим схему индуктора выше. Когда переключатель ( S1 ) разомкнут, ток через катушку индуктивности не течет. Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю. Если скорость изменения тока равна нулю, то  в катушке индуктивности нет ЭДС самоиндукции ( V _L= 0 ).

Если мы теперь закроем переключатель (t = 0), ток будет проходить через цепь и медленно подниматься до своего максимального значения со скоростью, определяемой индуктивностью индуктора. Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность по Генри, приводит к тому, что на катушке образуется некоторая самоиндуцированная ЭДС с фиксированным значением, определенная уравнением Фарадея V _L  = Ldi / dt.

Эта самоиндуцированная ЭДС на катушке индуктивности ( V _L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто устойчивое состояние. Ток, который сейчас течет через катушку, определяется только постоянным или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, поскольку скорость изменения тока (di / dt) равна нулю в устойчивом состоянии. Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.

Аналогичным образом, если переключатель ( S1 ) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается удержать ток в своем прежнем значении, индуцируя напряжение в другом направлении. Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.

Ток и напряжение в индукторе

Сколько индуктивного напряжения будет генерироваться индуктором, зависит от скорости изменения тока. В нашем уроке об электромагнитной индукции закон Ленца гласил: «Направление индуцированной ЭДС таково, что оно всегда будет противостоять изменению, которое его вызывает». Другими словами, индуцированная ЭДС всегда будет противопоставлять движение или изменение, которые изначально вызвали индуцированную ЭДС.

Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку, увеличение или уменьшение величины индуцированной ЭДС будет одинаковым.

Мощность в индукторе

Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца. Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС. Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V _L), определяется как:

Мощность в цепи задается как P = V * I, поэтому:

Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.

Энергия в индукторе

Когда мощность поступает в индуктор, энергия накапливается в его магнитном поле. Когда ток, протекающий через индуктор, увеличивается и di / dt становится больше нуля, мгновенная мощность в цепи также должна быть больше нуля, ( P> 0 ), т.е. положительная, что означает, что энергия накапливается в индукторе.

Аналогичным образом, если ток через индуктор уменьшается и di / dt меньше нуля, то мгновенная мощность также должна быть меньше нуля ( P <0 ), т.е. отрицательна, что означает, что индуктор возвращает энергию обратно в цепь. Затем, интегрируя приведенное выше уравнение для мощности, полная магнитная энергия, которая всегда положительна и сохраняется в индуктивности, определяется как:

Где:   
W в джоулях, 
L в Генри и 
I в амперах

Энергия фактически накапливается в магнитном поле, которое окружает индуктор током, текущим через него. В идеальном индукторе, который не имеет сопротивления или емкости, поскольку ток увеличивает энергию, стекающую в индуктор и накапливающуюся там в его магнитном поле без потерь, он не высвобождается до тех пор, пока ток не уменьшится и магнитное поле не разрушится.

Затем в переменном токе, переменного тока индуктор постоянно накапливает и доставляет энергию на каждом цикле. Если ток, протекающий через индуктор, является постоянным, как в цепи постоянного тока, то сохраненная энергия не изменяется, так как P = Li (di / dt) = 0 .

Таким образом, индукторы могут быть определены как пассивные компоненты, так как они могут как накапливать, так и доставлять энергию в цепь, но они не могут генерировать энергию. Идеальный индуктор классифицируется как меньше потерь, что означает, что он может хранить энергию бесконечно, так как энергия не теряется.

Однако, реальные катушки индуктивности всегда будут иметь некоторое сопротивление, связанное с обмотками катушки, и всякий раз, когда ток протекает через энергию сопротивления, теряется в виде тепла по закону Ома ( P = I ²  R ) независимо от того, является ли ток переменным или постоянный.

Тогда основное использование индукторов — это в фильтрационных цепях, резонансных цепях и для ограничения тока. Индуктор может использоваться в цепях для блокировки или изменения переменного тока или диапазона синусоидальных частот, и в этой роли индуктор может использоваться для «настройки» простого радиоприемника или генераторов различных типов. Он также может защитить чувствительное оборудование от разрушительных скачков напряжения и высоких пусковых токов.

В следующем уроке об индукторах мы увидим, что эффективное сопротивление катушки называется индуктивностью, а индуктивность, которая, как мы теперь знаем, является характеристикой электрического проводника, который «противодействует изменению тока», может быть как внутренней, индуцированный, называемый самоиндуктивностью или индуцированный извне, называемый взаимоиндуктивностью.